Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface
Abstract
:1. Introduction
2. Materials and Methods
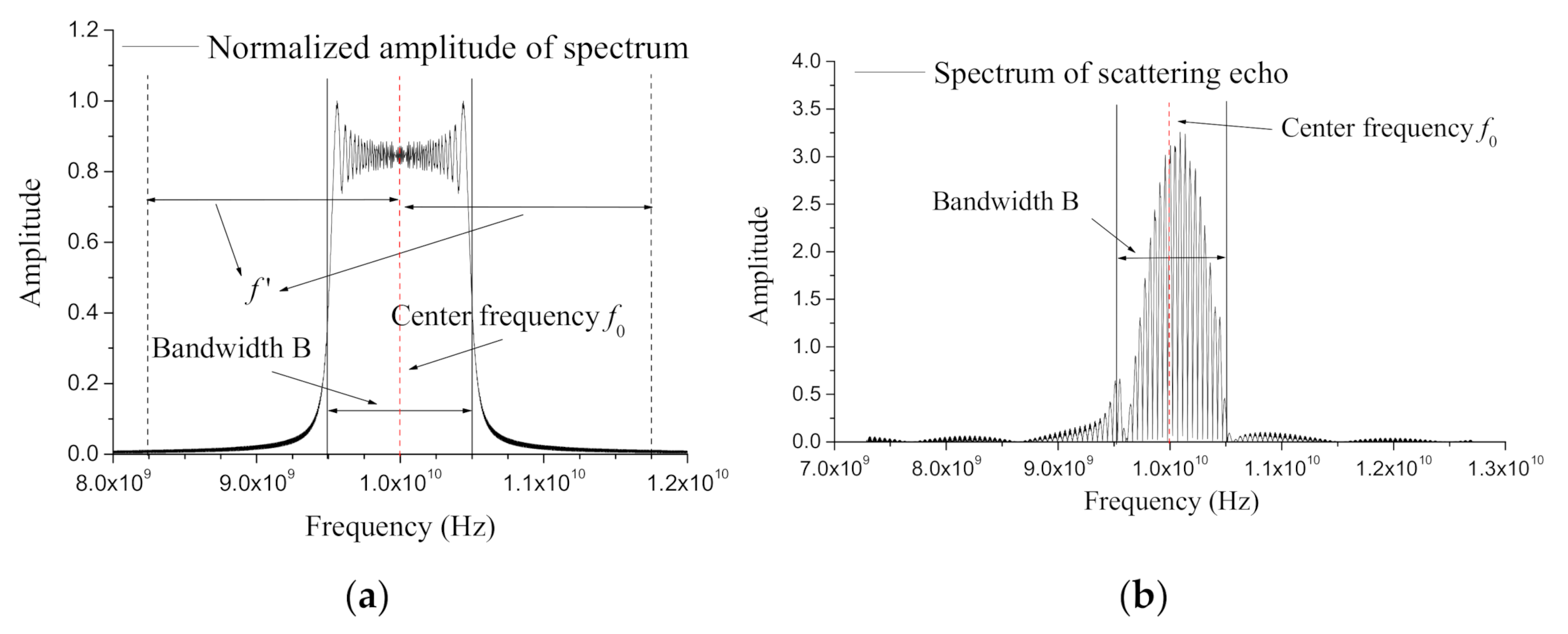
2.1. Scattering Echo Simulation
2.2. Rectangular Wave Beam-Based GO/PO Method
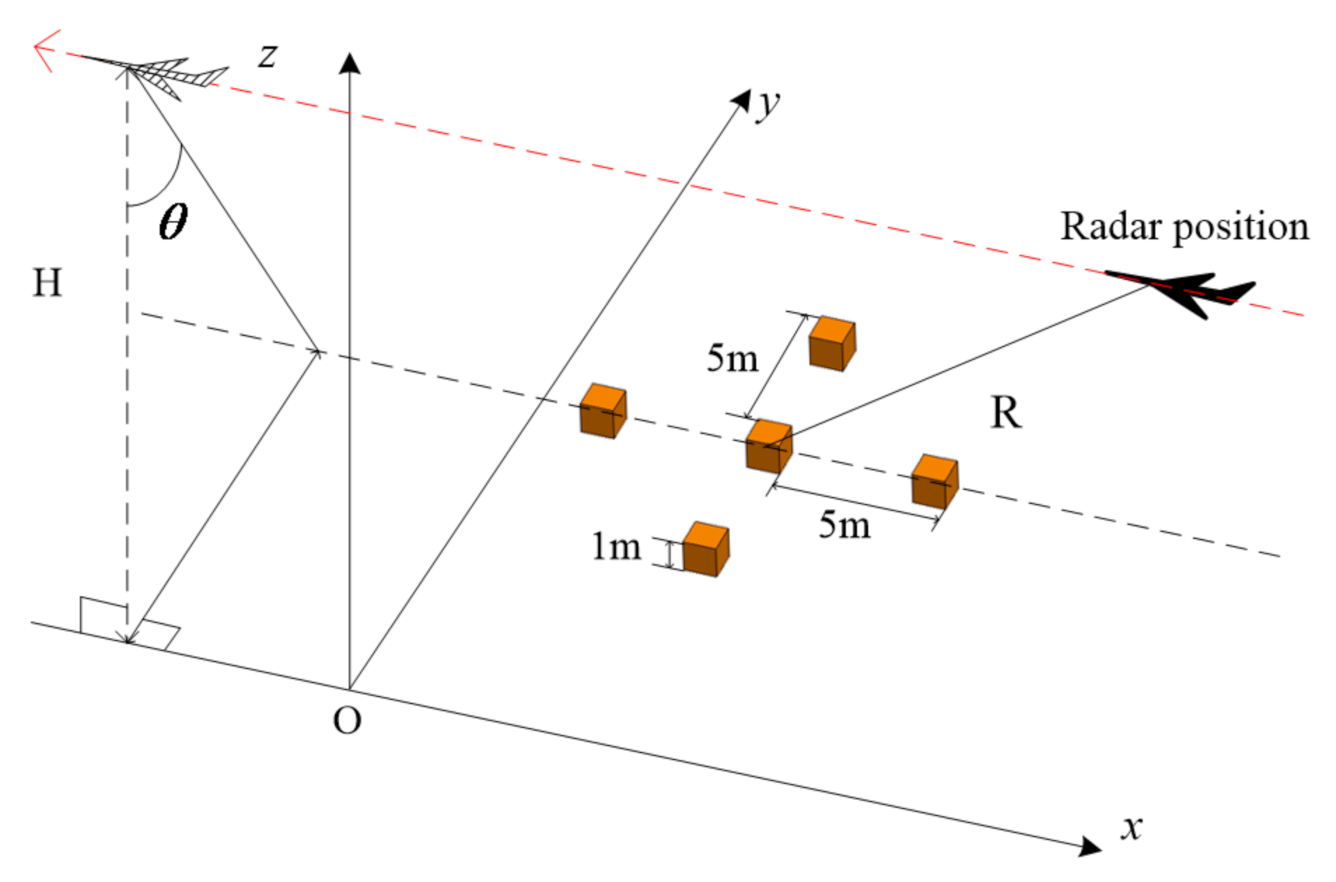
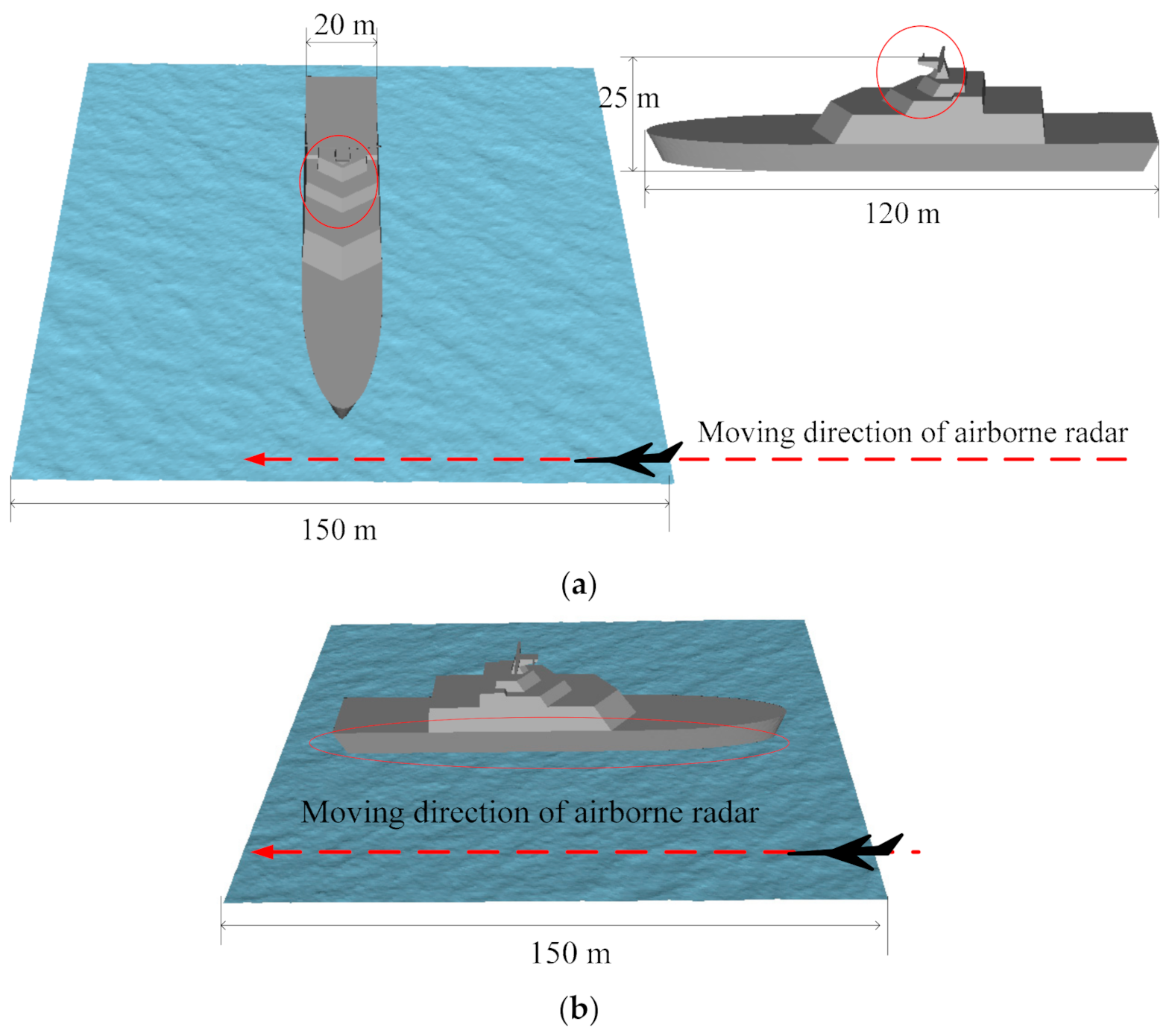
2.3. Scene of Ship and Sea
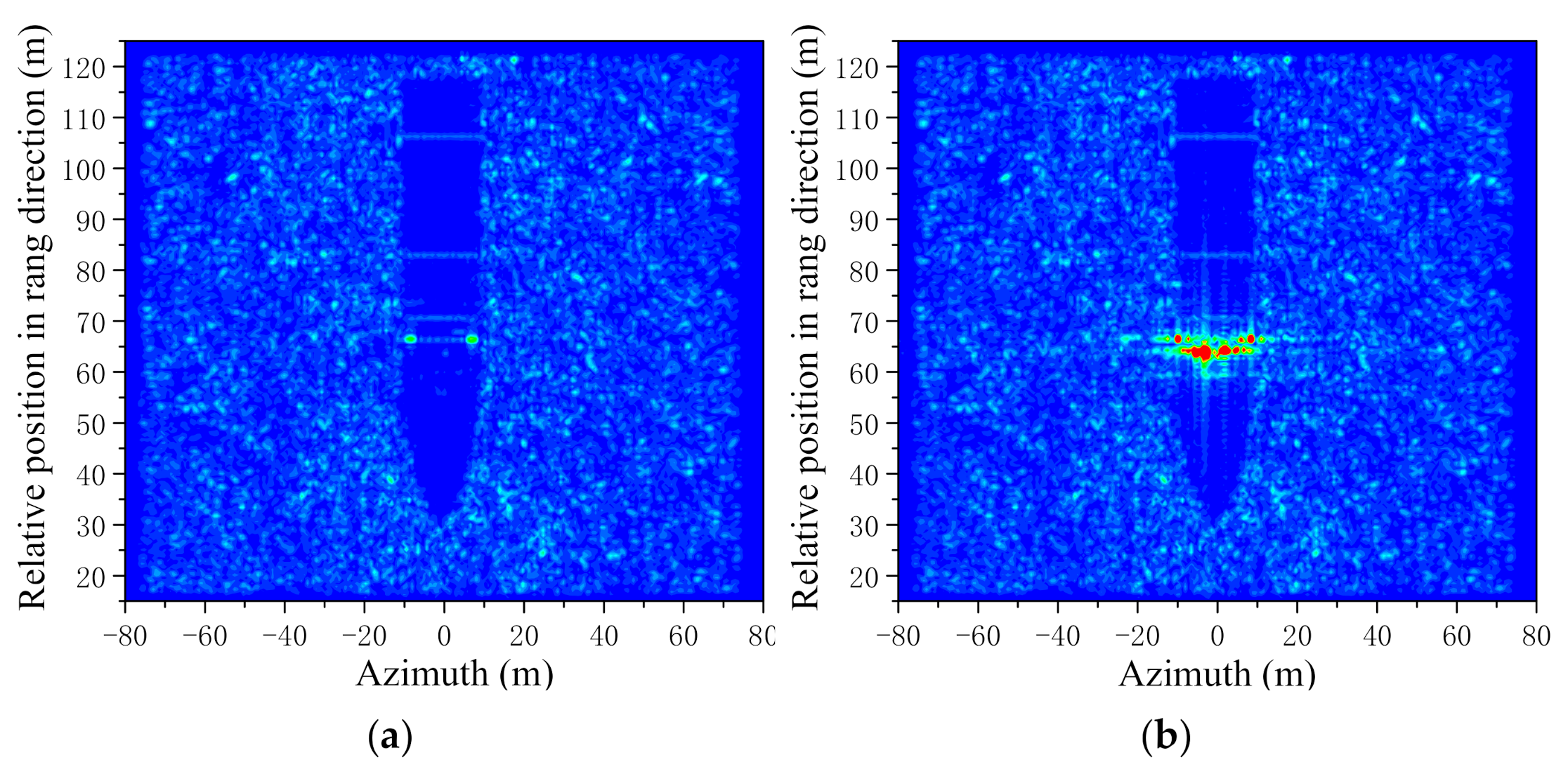
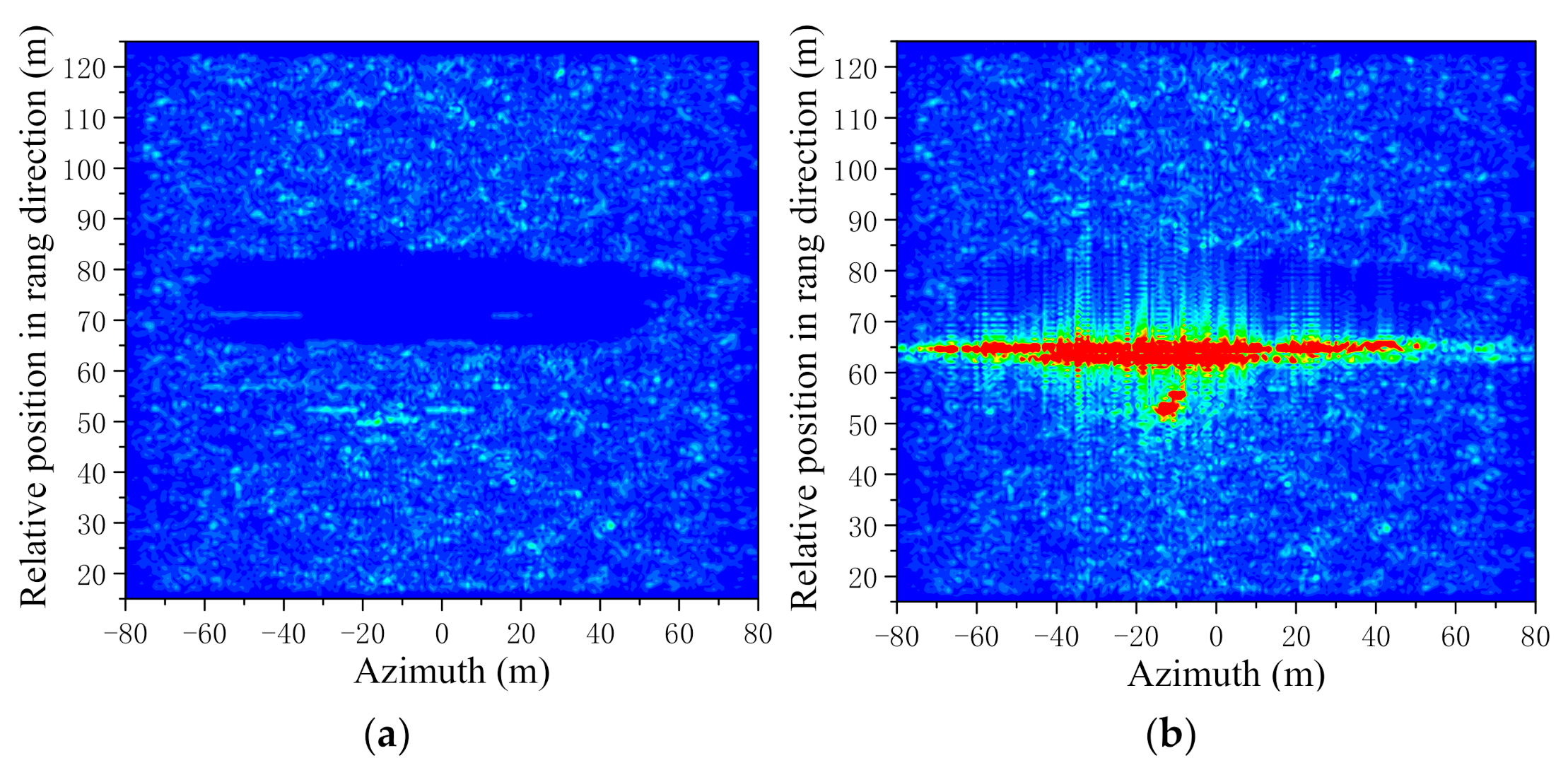
3. Results
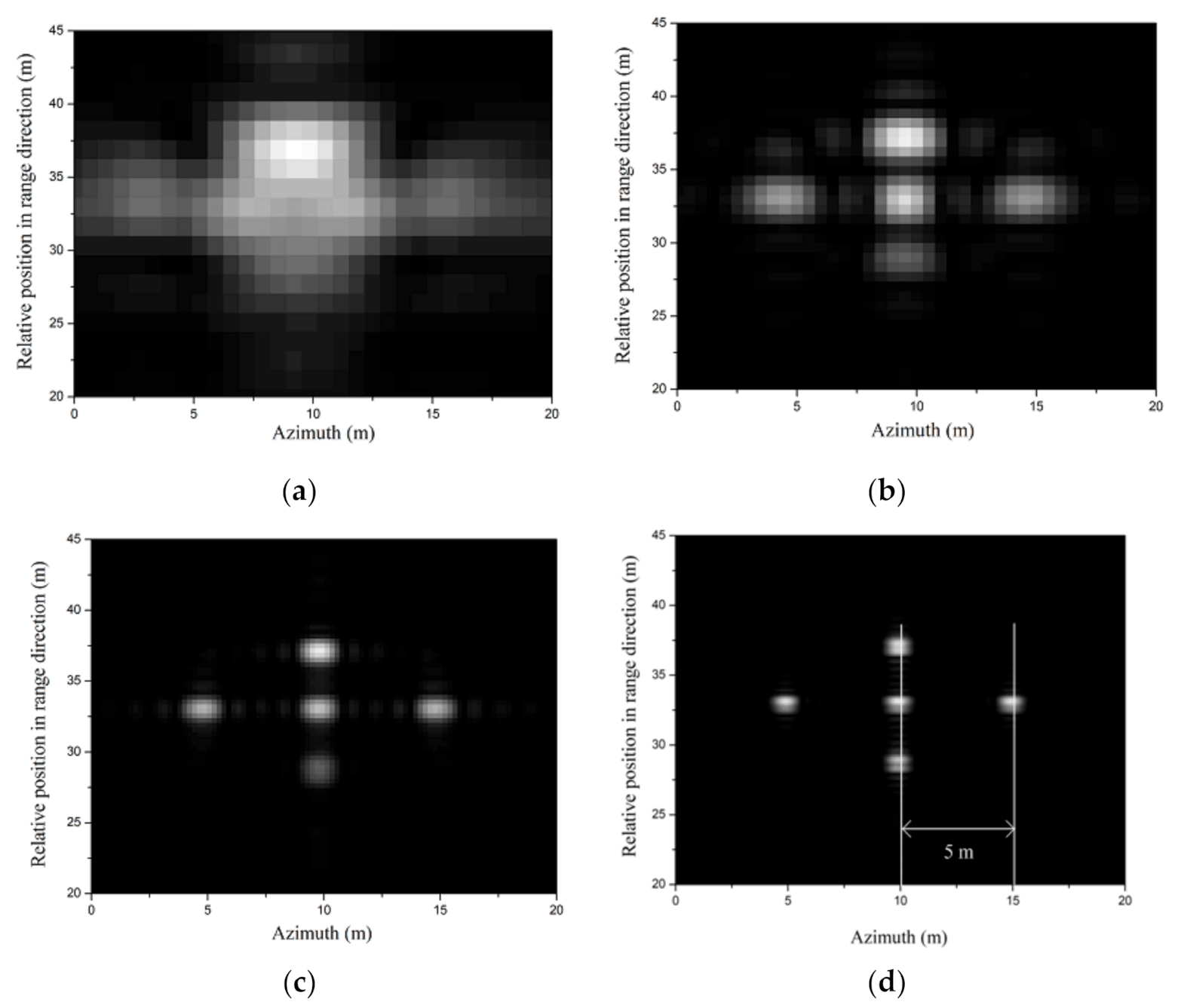
3.1. Results of the SAR Simulation
3.2. Efficiency of the Rectangular Wave Beam-Based GO/PO Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, G.; Kuang, G. Classification on the Monogenic Scale Space: Application to Target Recognition in SAR Image. IEEE Trans. Image Process. 2015, 24, 2527–2539. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Liu, K.; Zou, H.; Zhen, X. Multi-Stream Convolutional Neural Network for SAR Automatic Target Recognition. Remote Sens. 2018, 10, 1473. [Google Scholar] [CrossRef] [Green Version]
- Kajbaf, H.; Case, J.T.; Yang, Z.; Zheng, Y.R. Compressed Sensing for SAR-based Wideband Three-dimensional Microwave Imaging System Using Non-uniform Fast Fourier Transform. IET Radar Sonar Navig. 2013, 7, 658–670. [Google Scholar] [CrossRef]
- Peng, X.; Wang, Y.; Hong, W.; Tan, W.; Wu, Y. Autonomous Navigation Airborne Forward-Looking SAR High Precision Imaging with Combination of Pseudo-Polar Formatting and Overlapped Sub-Aperture Algorithm. Remote Sens. 2013, 5, 6063–6078. [Google Scholar] [CrossRef] [Green Version]
- Gao, G.; Liu, L.; Zhao, L.; Shi, G.; Kuang, G. An adaptive and fast CFAR algorithm based on automatic censoring for target detection in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1685–1697. [Google Scholar] [CrossRef]
- Pourmottaghi, A.; Gazor, S. A CFAR detector in a nonhomogenous Weibull clutter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1747–1758. [Google Scholar] [CrossRef]
- Hou, B.; Chen, X.; Jiao, L. Multilayer CFAR detection of ship targets in very high resolution SAR images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 811–815. [Google Scholar]
- Leng, X.; Ji, K.; Yang, K.; Zou, H.X. A bilateral CFAR algorithm for ship detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1536–1540. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C. Adaptive ship detection in SAR images using variance WIE-based method. Signal, Image Video Process 2016, 10, 1219–1224. [Google Scholar] [CrossRef]
- Wang, X.; Chen, C. Ship Detection for Complex Background SAR Images Based on a Multiscale Variance Weighted Image Entropy Method. IEEE Geosci. Remote Sens. Lett. 2017, 14, 184–187. [Google Scholar] [CrossRef]
- Geng, X.; Shi, L.; Yang, J.; Li, P.; Zhao, L.; Sun, W.; Zhao, J. Ship Detection and Feature Visualization Analysis Based on Lightweight CNN in VH and VV Polarization Images. Remote Sens. 2021, 13, 1184. [Google Scholar] [CrossRef]
- You, J.; Hu, Z.; Peng, C.; Wang, Z. Generation and Annotation of Simulation-Real Ship Images for Convolutional Neural Networks Training and Testing. Appl. Sci. 2021, 11, 5931. [Google Scholar] [CrossRef]
- Zhao, Y.W.; Zhou, P.; Zhang, X.; Zhang, M. Application of improved equivalent edge currents in synthetic aperture radar imaging. J. Syst. Eng. Electron. 2010, 21, 556–571. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, M.; Zhao, Y.W.; Luo, W. An Efficient Slope-deterministic Facet Model for SAR Imagery Simulation of Marine Scene. IEEE Trans. Antennas Propag. 2010, 58, 3751–3756. [Google Scholar] [CrossRef]
- Ghavidel, A.; Camps, A. Time-domain Statistics of the Electromagnetic Bias in GNSS-Reflectometry. Remote Sens. 2013, 7, 11151–11162. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.B.; Lin, H.; Bao, H.J. Kd-tree Based Fast Ray Tracing for RCS Prediction. Prog. Electromagn. Res. 2008, 81, 329–341. [Google Scholar] [CrossRef] [Green Version]
- Rius, J.M.; Ferrando, M.; Jofre, L. GRECO: Graphical Electromagnetic Computing for RCS Prediction in Real Time. IEEE Antennas Propag. Mag. 1993, 35, 7–17. [Google Scholar] [CrossRef] [Green Version]
- Wei, P.B.; Zhang, M.; Niu, W.; Jiang, W.Q. GPU-Based Combination of GO and PO for Electromagnetic Scattering of Satellite. IEEE Trans. Antennas Propag. 2012, 60, 5278–5285. [Google Scholar] [CrossRef]
- Jiang, W.Q.; Zhang, M.; Zhao, Y.; Nie, D.; Jiao, Y.C. Rectangular Wave Beam Based GO/PO Method for RCS Simulation of Complex Target. Prog. Electromagn. Res. M 2017, 53, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.Q.; Zhang, M.; Nie, D.; Jiao, Y.C. Improved GO/PO method and its application to wideband SAR image of conducting objects over rough surface. Waves Random Complex Media 2018, 28, 310–325. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.H.; Cumming, I.G. Processing of Azimuth-Invariant Bistatic SAR Data Using the Range Doppler Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 14–21. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Wang, J.; Liu, Q.H. Frequency-domain backprojection algorithm for synthetic aperture radar imaging. IEEE Geosci. Remote Sens. Lett. 2015, 12, 905–909. [Google Scholar]
- Tong, X.; Bao, M.; Sun, G.; Han, L.; Zhang, Y.; Xing, M. Refocusing of Moving Ships in Squint SAR Images Based on Spectrum Orthogonalization. Remote Sens. 2021, 13, 2807. [Google Scholar] [CrossRef]
- Elfouhaily, T.; Chapron, B.; Katarsos, K. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using the motions of a floating buoy. In Ocean Wave Spectra; Prentice-Hall: Hoboken, NJ, USA, 1963; pp. 111–132. [Google Scholar] [CrossRef]





| Pixel Matrix Size | Time Needed with Proposed Method (s) |
|---|---|
| 128×128 | 16.364 |
| 256 × 256 | 65.224 |
| 512×512 | 260.925 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.-Q.; Wang, L.-Y.; Li, X.-Z.; Liu, G.; Zhang, M. Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface. Remote Sens. 2021, 13, 3186. https://doi.org/10.3390/rs13163186
Jiang W-Q, Wang L-Y, Li X-Z, Liu G, Zhang M. Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface. Remote Sensing. 2021; 13(16):3186. https://doi.org/10.3390/rs13163186
Chicago/Turabian StyleJiang, Wang-Qiang, Liu-Ying Wang, Xin-Zhuo Li, Gu Liu, and Min Zhang. 2021. "Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface" Remote Sensing 13, no. 16: 3186. https://doi.org/10.3390/rs13163186
APA StyleJiang, W.-Q., Wang, L.-Y., Li, X.-Z., Liu, G., & Zhang, M. (2021). Simulation of a Wideband Radar Echo of a Target on a Dynamic Sea Surface. Remote Sensing, 13(16), 3186. https://doi.org/10.3390/rs13163186







