Innovative UAV LiDAR Generated Point-Cloud Processing Algorithm in Python for Unsupervised Detection and Analysis of Agricultural Field-Plots
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Plot Experiment
2.2. UAV LiDAR System and Scanning Parameters
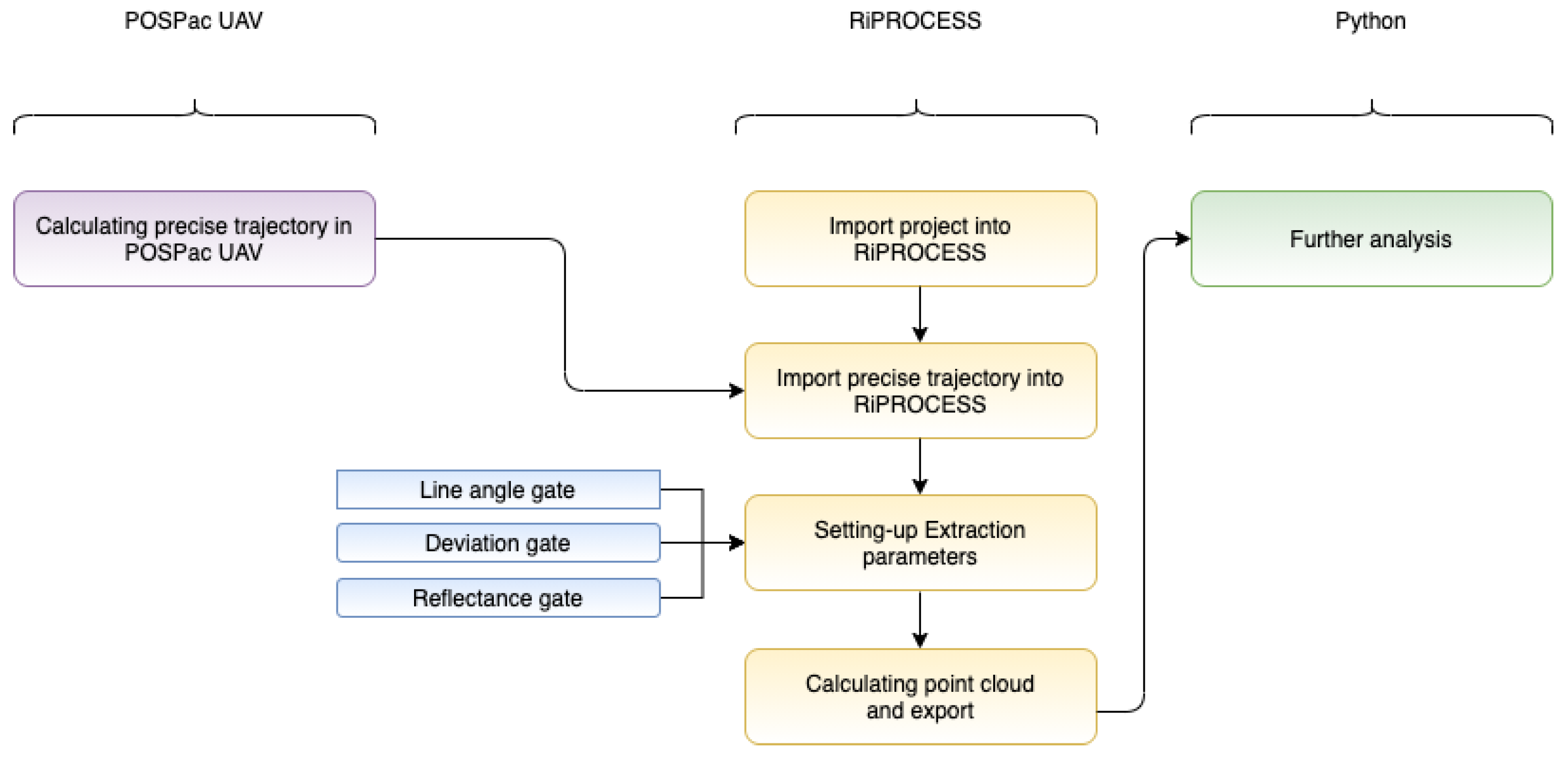
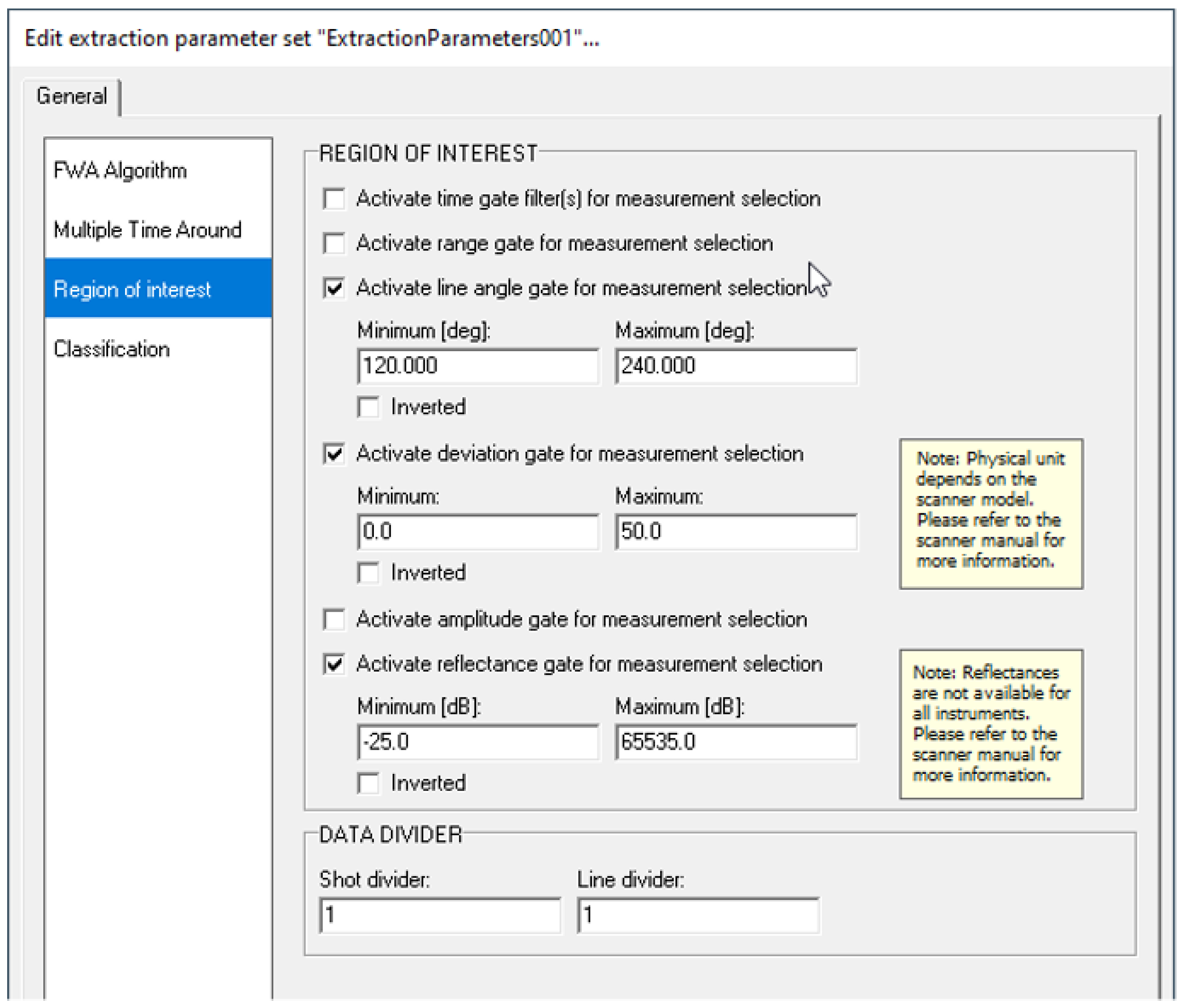
2.3. Pre-Processing of Raw Data
2.4. Pre-Processed Data in Raw Format
3. Results
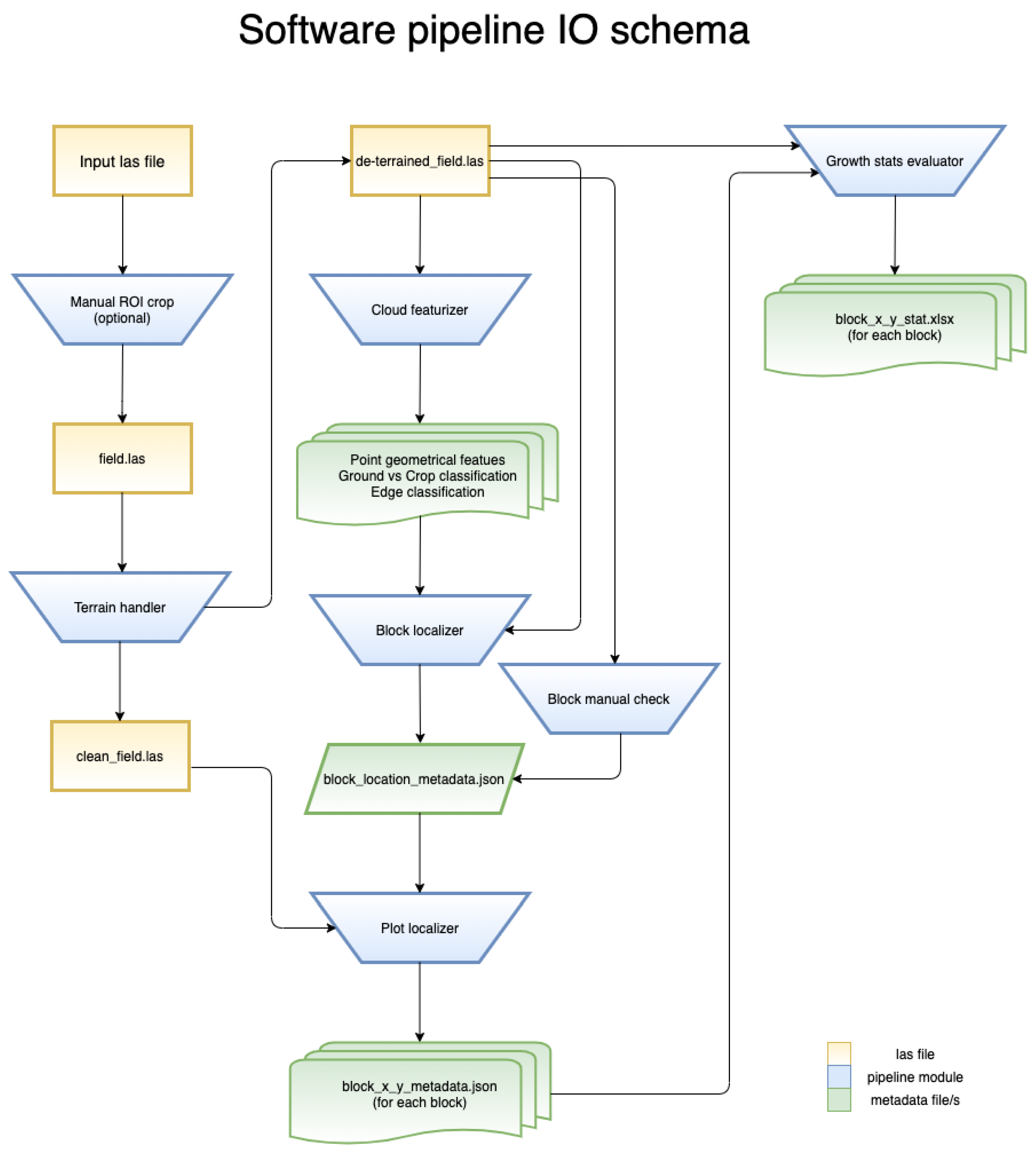
3.1. Point Cloud Processing Algorithm
3.1.1. Manual ROI localization Module (Optional)
- Downsamplimg rate—determines percentage number of downsampled points of raw point cloud which will be visualized.
- Low height quantile—determines percentage amount of points with lowest height value, which are not visualized.
- Up height quantile—determines percentage amount of points with biggest height value, which are not visualized.
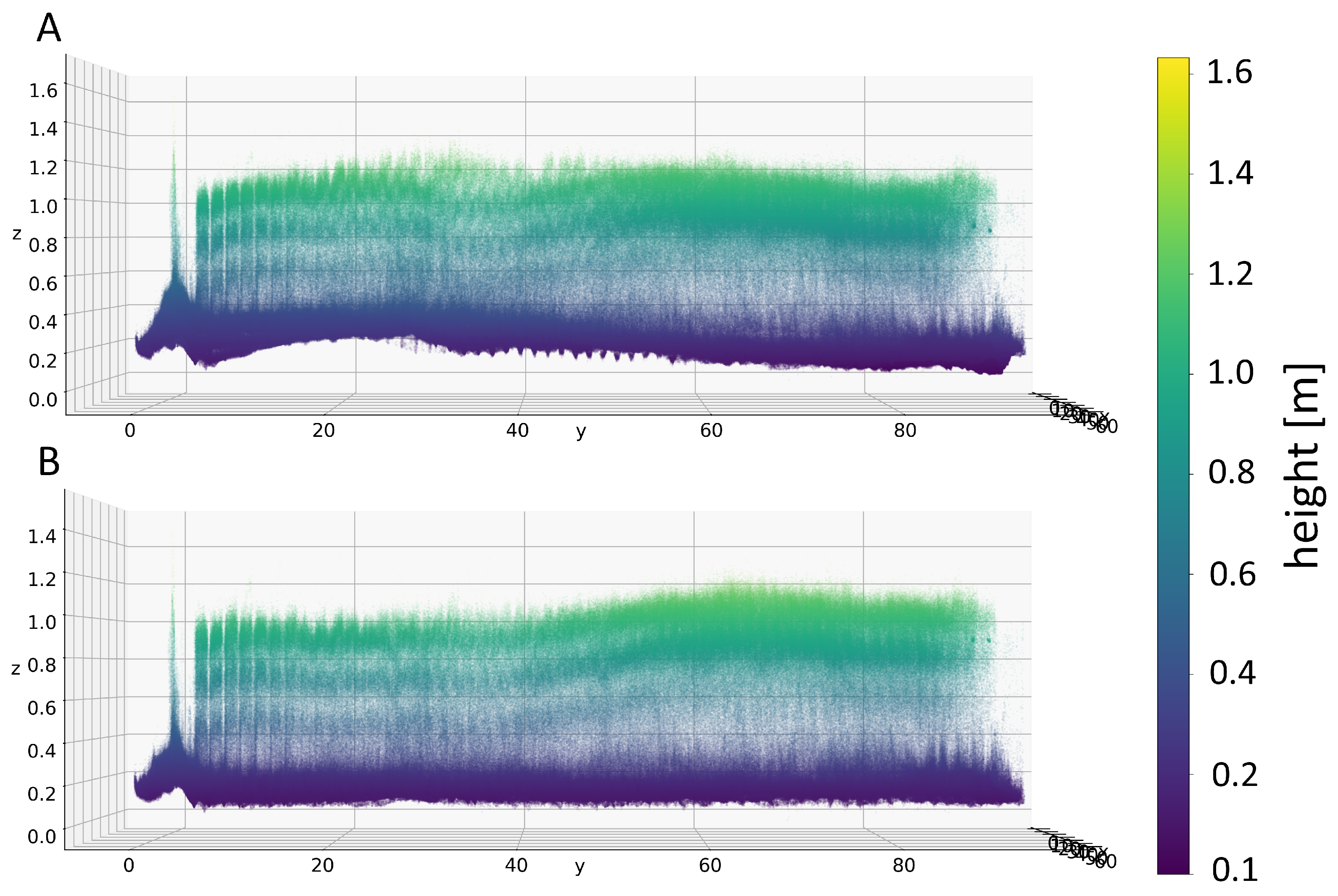
3.1.2. Terrain Adjustment
- Metric determines the metric used in the KDtree algorithm and shape of the local neighborhood. Minkowski metric was used in our analysis.
- Radius defines the size (in meters) of local neighborhood of analyzed point. The radius was used in our analysis.
- Deviance defines how many standard deviations higher than mean distance has to be distance of single point to consider point as outlier. The deviance = 3 was used in our analysis.
- Downsampling rate determines a percentage number of downsampled points which will be processed with module. Since point clouds are huge files in general, to use subset of points can significantly accelerate the computation and decrease processing time.
- Window size defines the size (in meters) of squared sliding window in xy-plane, which used for terrain points selection. The size of 10 was used in our analysis.
- Window stride defines how the sliding window is moved around the ROI area. Sliding windows starts in the origin of coordinate system and is moved in xy-plane with given step (in meters). This step is window stride. The stride 1 was used in our analysis.
- Window quantile defines a percentage of points with lowest value of the z-coordinate in the sliding window, which are selected as the terrain points. In our analysis window quantile was used.
- Metric determines metric used in the KDtree algorithm and shape of the local neighbourhood. Minkowski metric was used in our analysis.
- K defines the certain number of closest terrain points to given grid point.
- Grid resolution defines the number of equidistantly distributed points in x axis range and the same number of equidistantly distributed points in y axis range. In the total gird is formed with (grid resolution) points. The value 100 was used for this parameter in our analysis.
- U degree defines the polynomial order of the spline for first dimension of the parametrical surface space. The value 2 was used in our analysis.
- V degree defines the polynomial order of the spline for second dimension of the parametrical surface space. The value 2 was used in our analysis.
- Delta is used to change the number of evaluated spline points. Increasing the number of points will result in a bigger evaluated points array and decreasing will reduce the size of the array. In our analysis delta parameter was configured as .
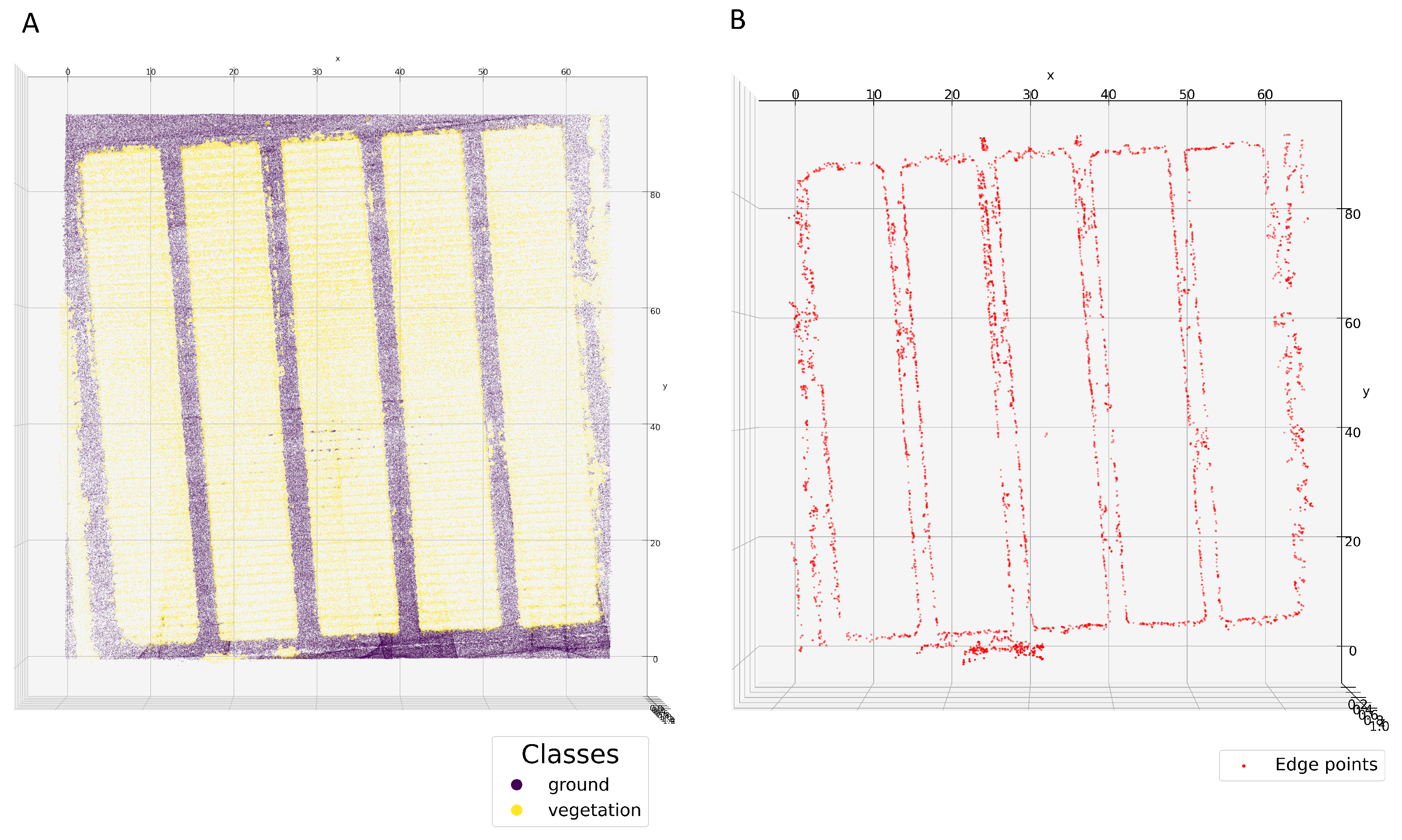
3.1.3. Point Featurization, Classification and Edge Detection
- Downsampling rate determines a percentage number of downsampled points which will be processed with the module. Since point clouds are huge files in general, to use the subset of points can significantly accelerate point cloud featurization and decrease processing time. The value of points was selected for feature evaluation in our analysis.
- Metric determines metric used in the KDtree algorithm and shape of the local neighbourhood. Minkowski metric was used in our analysis.
- K defines the k-nearest neighbours neighbourhood of analyzed point. For the feature evaluation 30 neighbours was used and for the edge detection 50 neighbours.
- Radius defines size (in meters) of the local neighbourhood of analyzed point. The value was used for the feature evaluation.
- Entropy quantile defines a percentage of points with the smallest edge entropy value. These points are considered as the edge points. The value was used in our analysis.
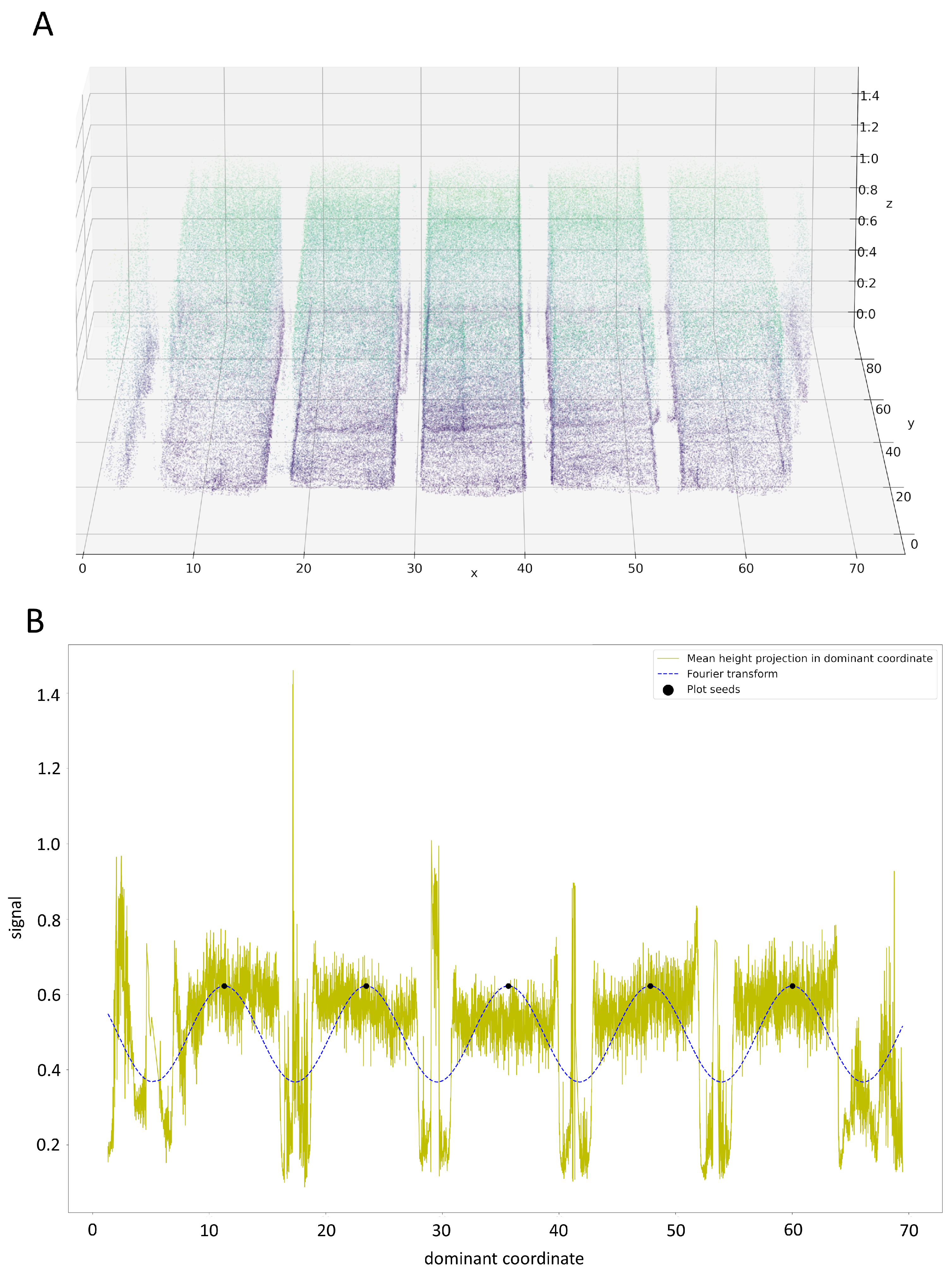
3.1.4. Experimental Block Localization
- Signal span—defines the size of step (in meters) for x and y axis, which is used for the signal computation. A big parameter value is not recommended because it can cause the loss of signal. For the optimal rotation evaluation value was used and for the edge signal evaluation value was used in our analysis.
- w—defines the size (in meters) of analyzed edge point area in x or y coordinate. Value was used in our analysis.
- —defines the smoothing coefficient defining the mutual significancy of cardinality and uniformity for the edge points weight computation.
- Dominant quantile—determines the percentage of reduced edge signal values in the dominant coordinate, which are not considered as the candidates for the experimental block border. In our analysis value was used.
- Not-dominant quantile—determines the percentage of reduced edge signal values in not-dominant coordinate, which are not considered as the candidates for the experimental block border. In our analysis value was used.
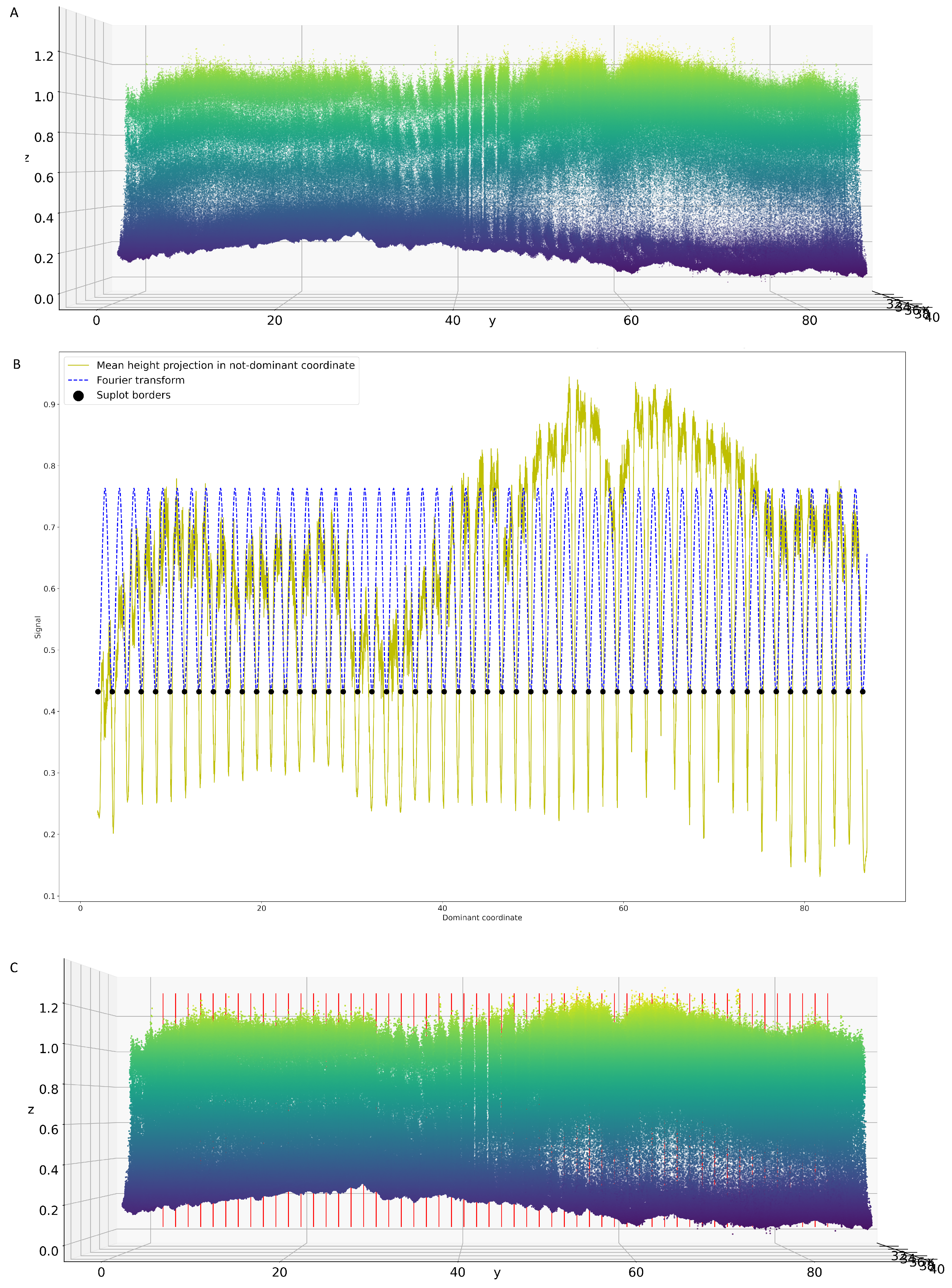
3.1.5. Plots Localization
- Signal span—defines the size of step (in meters) in not-dominant coordinate for the height signal computation. Big parameter value is not recommended, it can cause the loss of signal. Value was used in our analysis.
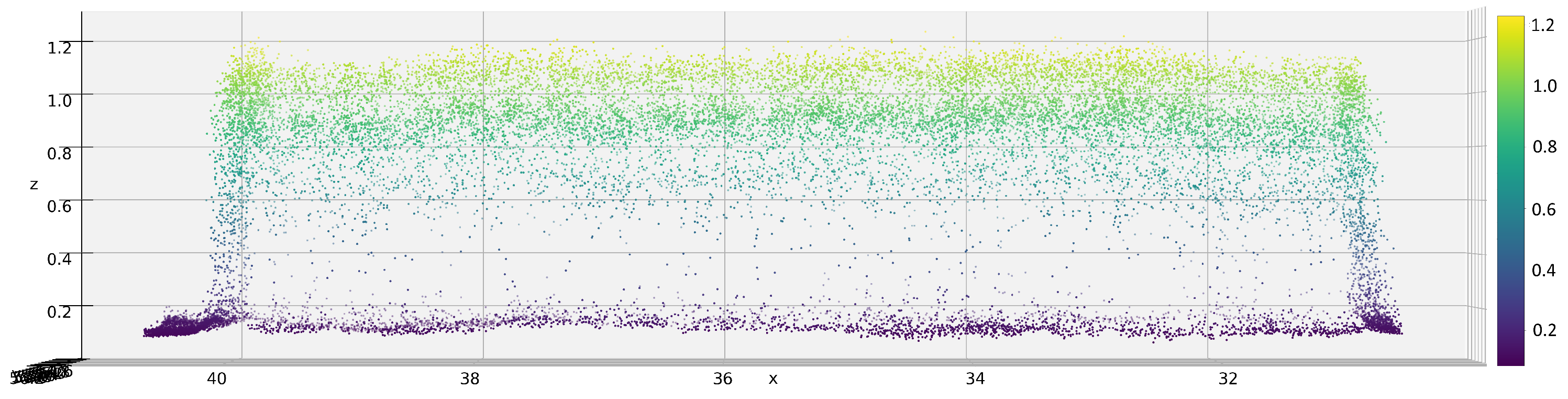
3.1.6. Canopy Characteristic Extraction
- Crop quantile dominant determines a percentage part of the plot area which is removed from plot size in dominant coordinate. It means that half of the crop quantile dominant value is removed from the lower tail and half from the upper tail of the plot dominant coordinate. The reason is to remove noisy borders of plot. Value was used in our analysis.
- Crop quantile not-dominant determines a percentage part of the plot area which is removed from plot size in not-dominant coordinate. It means that half of the crop quantile not-dominant value is removed from the lower tail and half from the upper tail of the plot not-dominant coordinate. The reason is to remove noisy borders of plot. Value was used in our analysis.
- Height quantile filters out from plot point cloud given percentage of points with the lowest value of the z-coordinate. Value was used in our analysis.
- Metric determines metric used in the KDtree algorithm and shape of the local neighbourhood. Minkowski metric was used in our analysis.
- K defines the k-nearest neighbors of cleaned plot points to the given grid point.
- Grid resolution defines the number of equidistantly distributed points in the axis range and the same number of points equidistantly distributed in the axis range. In total gird is formed with the (grid resolution) points. Value of 100 was used for the plot surface fitting with spline.
- U degree defines the polynomial order of spline for first dimension of the surface parametrical. Order 2 was used in our analysis.
- V degree defines the polynomial order of spline for second dimension of the surface parametrical. Order 2 was used in our analysis.
- Delta is used to change the number of evaluated spline points. Increasing the number of points will result in a bigger evaluated points array and while decreasing will reduce the size of the array. In our analysis delta parameter was configured as .
- Block size defines the size (in meters) of the squared and not-overlaping sliding window, which is sliding around the plot area and is used for the volume computation in the small area of sliding window. The principle of plot volume computation is the same as integration. The volume is the sum of volumes calculated in all sliding window areas in the plot area. In our analysis value was used.
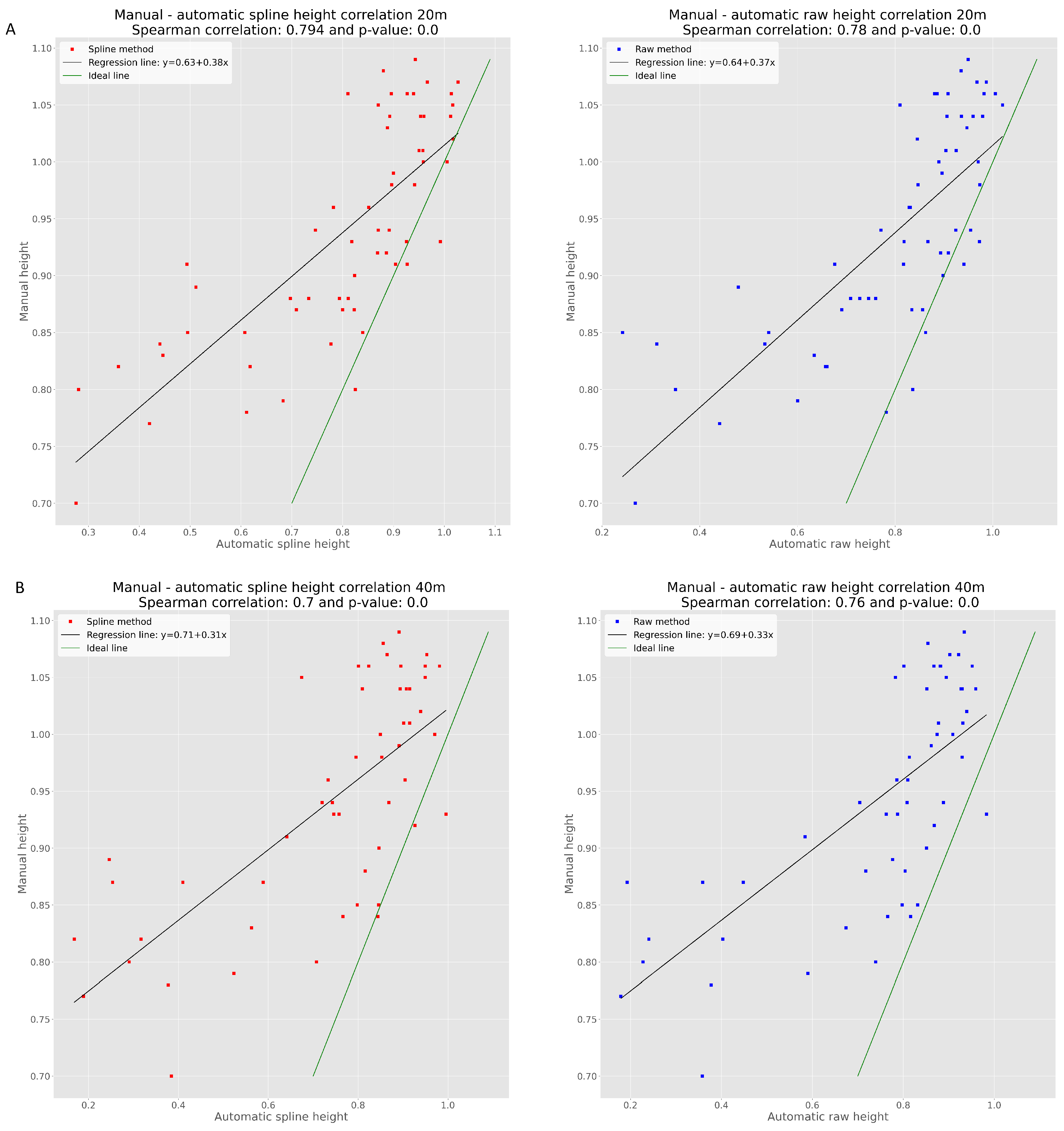
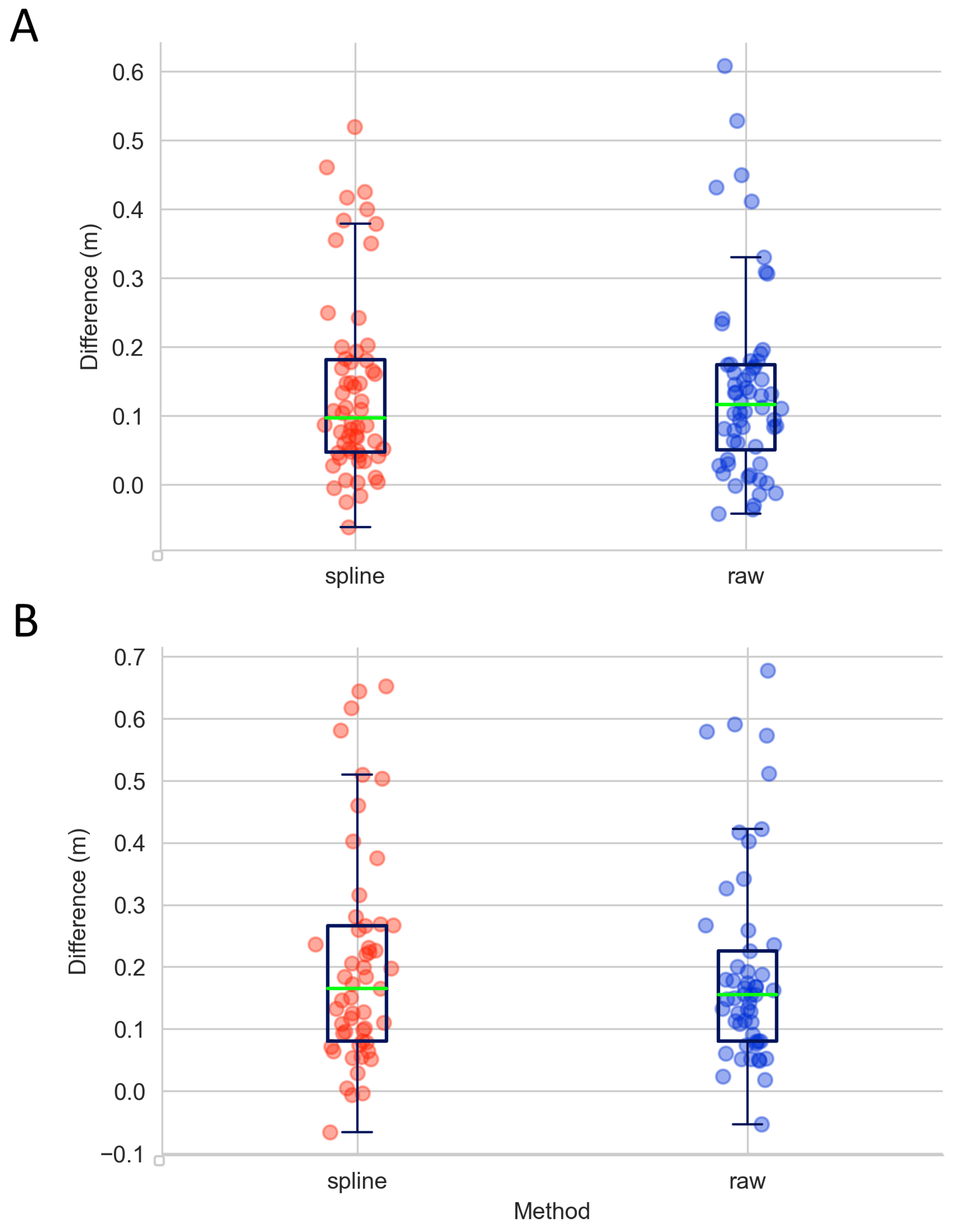
3.2. Validation of Measurements by Manual Measurement of Selected Field-Plots
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, Y. LiDAR: An important tool for next-generation phenotyping technology of high potential for plant phenomics? Comput. Electron. Agric. 2015, 119, 61–73. [Google Scholar] [CrossRef]
- Song, P.; Wang, J.; Guo, X.; Yang, W.; Zhao, C. High-throughput phenotyping: Breaking through the bottleneck in future crop breeding. Crop J. 2021. [Google Scholar] [CrossRef]
- Maesano, M.; Khoury, S.; Nakhle, F.; Firrincieli, A.; Gay, A.; Tauro, F.; Harfouche, A. UAV-based LiDAR for high-throughput determination of plant height and above-ground biomass of the bioenergy grass arundo donax. Remote Sens. 2020, 12, 3464. [Google Scholar] [CrossRef]
- Ten Harkel, J.; Bartholomeus, H.; Kooistra, L. Biomass and crop height estimation of different crops using UAV-based LiDAR. Remote Sens. 2020, 12, 17. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.; Liu, W.; Zhang, Y.; Wang, C.; Xi, X.; Nie, S.; Ma, D.; Lin, Y.; Zhou, G. Maize and soybean heights estimation from unmanned aerial vehicle (UAV) LiDAR data. Comput. Electron. Agric. 2021, 182, 106005. [Google Scholar] [CrossRef]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Hackel, T.; Wegner, J.; Schindler, K. Contour Detection in Unstructured 3D Point Clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ahmed, S.M.; Tan, Y.Z.; Chew, C.M.; Mamun, A.A.; Wong, F.S. Edge and Corner Detection for Unorganized 3D Point Clouds with Application to Robotic. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Applications, 3rd ed.; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Gonzalez, T.; Sahni, S.; Franta, W.R. An Efficient Algorithm for the Kolmogorov-Smirnov and Lilliefors Tests. ACM Trans. Math. Softw. 1977, 3, 60–64. [Google Scholar] [CrossRef]
- Millan, V.E.G.; Rankine, C.; Sanchez-Azofeifa, G.A. Crop loss evaluation using digital surface models from unmanned aerial vehicles data. Remote Sens. 2020, 12, 981. [Google Scholar] [CrossRef] [Green Version]
- Madec, S.; Baret, F.; De Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-throughput phenotyping of plant height: Comparing unmanned aerial vehicles and ground lidar estimates. Front. Plant Sci. 2017, 8, 2002. [Google Scholar] [CrossRef] [PubMed] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polák, M.; Miřijovský, J.; Hernándiz, A.E.; Špíšek, Z.; Koprna, R.; Humplík, J.F. Innovative UAV LiDAR Generated Point-Cloud Processing Algorithm in Python for Unsupervised Detection and Analysis of Agricultural Field-Plots. Remote Sens. 2021, 13, 3169. https://doi.org/10.3390/rs13163169
Polák M, Miřijovský J, Hernándiz AE, Špíšek Z, Koprna R, Humplík JF. Innovative UAV LiDAR Generated Point-Cloud Processing Algorithm in Python for Unsupervised Detection and Analysis of Agricultural Field-Plots. Remote Sensing. 2021; 13(16):3169. https://doi.org/10.3390/rs13163169
Chicago/Turabian StylePolák, Michal, Jakub Miřijovský, Alba E. Hernándiz, Zdeněk Špíšek, Radoslav Koprna, and Jan F. Humplík. 2021. "Innovative UAV LiDAR Generated Point-Cloud Processing Algorithm in Python for Unsupervised Detection and Analysis of Agricultural Field-Plots" Remote Sensing 13, no. 16: 3169. https://doi.org/10.3390/rs13163169
APA StylePolák, M., Miřijovský, J., Hernándiz, A. E., Špíšek, Z., Koprna, R., & Humplík, J. F. (2021). Innovative UAV LiDAR Generated Point-Cloud Processing Algorithm in Python for Unsupervised Detection and Analysis of Agricultural Field-Plots. Remote Sensing, 13(16), 3169. https://doi.org/10.3390/rs13163169




