Critical Points Extraction from Building Façades by Analyzing Gradient Structure Tensor
Abstract
:1. Introduction
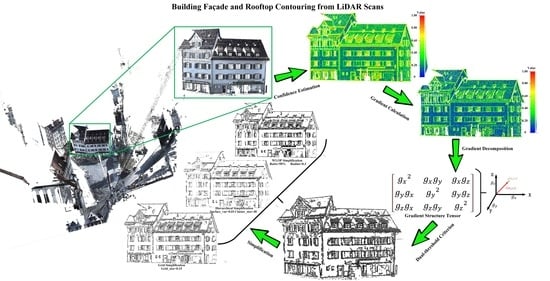
- Building façade contouring framework: We propose a generic framework for building façade contouring from LiDAR and photogrammetric point clouds. The framework consists of five steps including confidence measure estimation, 3D gradient calculation, gradient structure tensor encoding, dual-threshold criterion, and simplification. These steps loosely coupled interact in the pipeline (see Figure 1) to enhance the flexibility of the framework, thereby achieving a tradeoff between geometric accuracy and compact abstraction of building façades.
- Gradient structure tensor encoding: We encode each point’s structure tensor, which describes the gradient variation in the local neighborhood areas. Through analyzing each point’s structure tensor, building point clouds can be roughly labeled into corner points, edge points, boundary points, and constant points (see Section 2.3).
- The solid experiments and effective comparisons: We provide qualitative and quantitative performance evaluations using five datasets, and give two comparisons with the state-of-the-art methods to demonstrate the superiority of the proposed method in terms of topological correctness, geometric accuracy, and compact abstraction.
2. Methodology
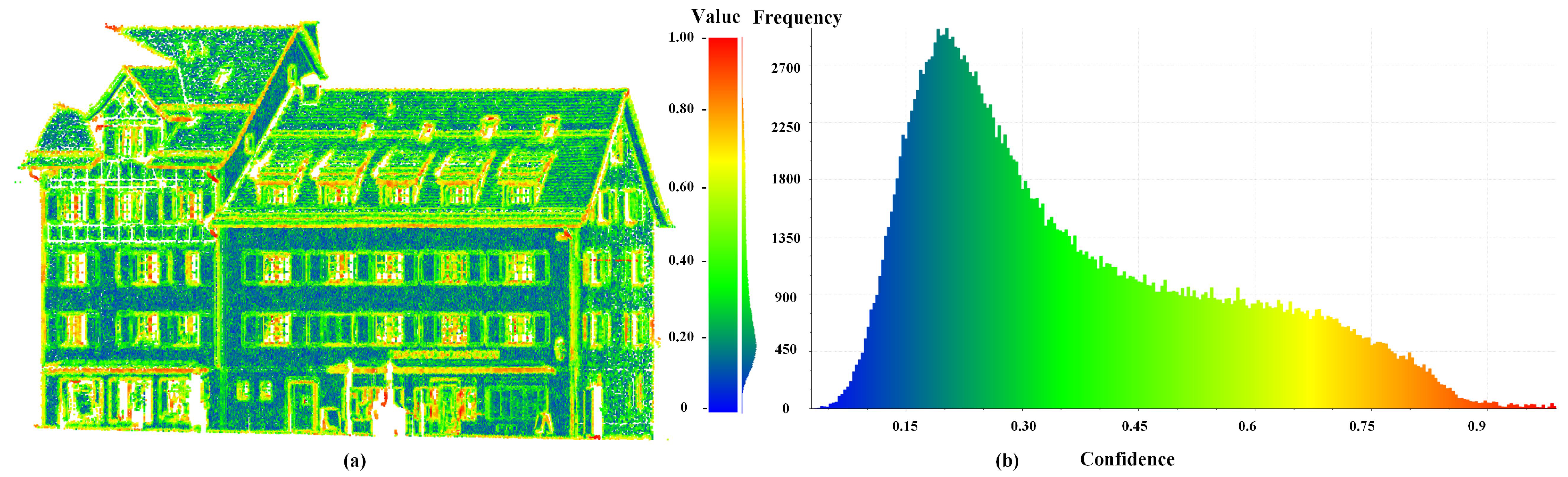
2.1. Confidence Estimation
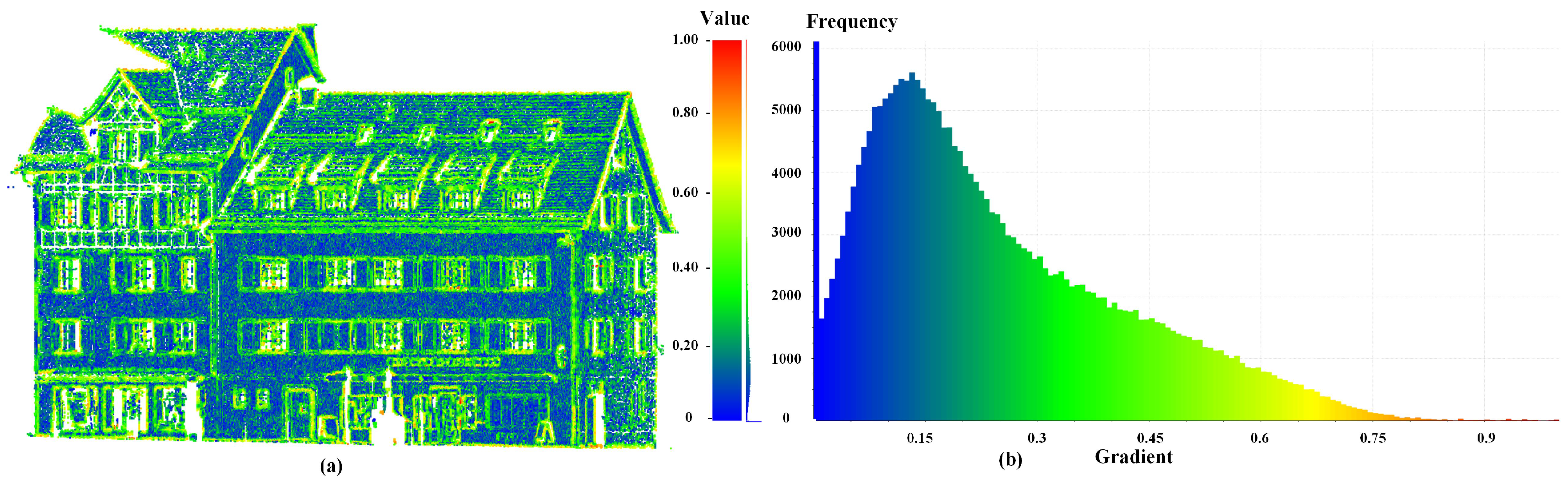
2.2. Gradient Definition in 3D Point Cloud Space
2.3. Gradient Structure Tensor Generation
- Corner points: the current point is most probably at the intersection area of three mutually nonparallel surfaces (façades and rooftop planes). In this case, all three eigenvalues are large.
- Edge points: the current point most likely belongs to the intersection edges generated from façades and/or rooftop planes. In this situation, two eigenvalues are relatively large.
- Boundary points: the current point most probably comes from the outer boundaries or boundaries of inner holes (e.g., window frames) caused by missing data of the façades. In this case, only one large eigenvalue can be observed.
- Constant points: the local neighborhood areas of current point maintain approximately constant gradient values, i.e., arbitrary shifts of 3d voxel windows centered at cause little change value in E (see Equation (4)). All three eigenvalues are small in this case.
2.4. Dual-Threshold Criterion
2.5. Critical Point Refinement through Concept of Simplification
3. Performance Evaluation
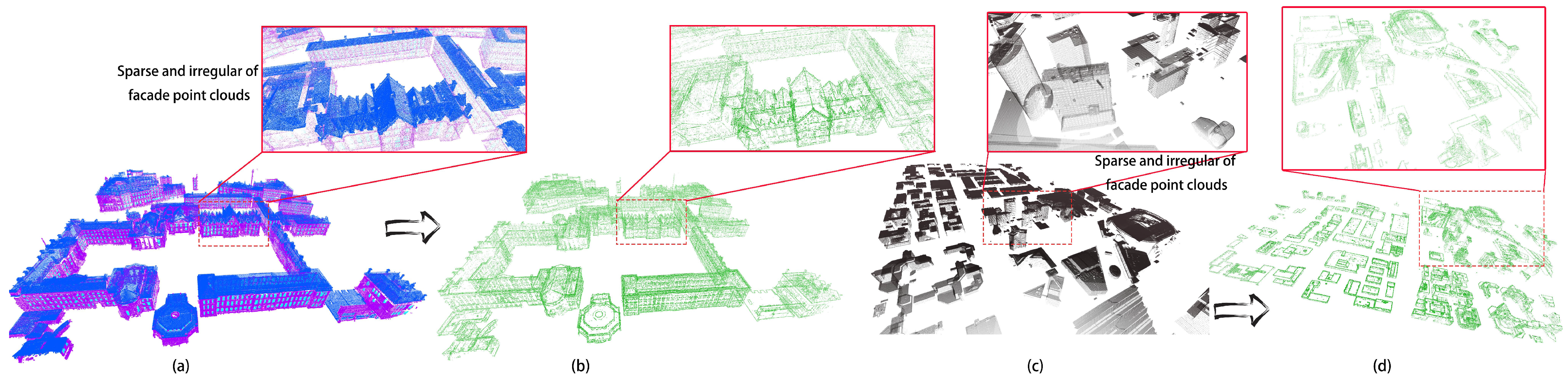
3.1. Dataset Specification
3.2. Parameter Analyzing
3.3. Compactness
3.4. Accuracy
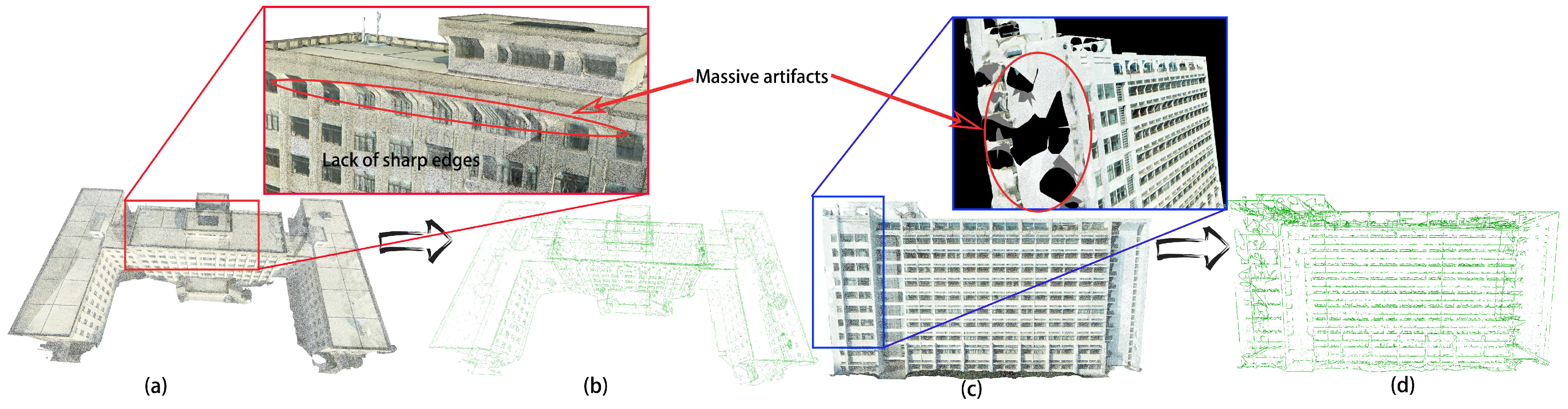
3.5. Comparison
3.6. Robustness
4. Conclusions and Suggestions for Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosenfeld, A.; Thurston, M. Edge and curve detection for visual scene analysis. IEEE Trans. Comput. 1971, 100, 562–569. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, W.; Gu, J. Edge-semantic learning strategy for layout estimation in indoor environment. IEEE Trans. Cybern. 2019, 50, 2730–2739. [Google Scholar] [CrossRef] [Green Version]
- Lepora, N.F.; Church, A.; De Kerckhove, C.; Hadsell, R.; Lloyd, J. From pixels to percepts: Highly robust edge perception and contour following using deep learning and an optical biomimetic tactile sensor. IEEE Robot. Autom. Lett. 2019, 4, 2101–2107. [Google Scholar] [CrossRef] [Green Version]
- Baterina, A.V.; Oppus, C. Image edge detection using ant colony optimization. Wseas Trans. Signal Process. 2010, 6, 58–67. [Google Scholar]
- Sadiq, B.O.; Sani, S.; Garba, S. Edge detection: A collection of pixel based approach for colored images. Int. J. Comput. Appl. 2015, 113, 29–32. [Google Scholar]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Duan, R.l.; Li, Q.x.; Li, Y.h. Summary of image edge detection. Opt. Tech. 2005, 3, 415–419. [Google Scholar]
- Guo, K.Y.; Hoare, E.G.; Jasteh, D.; Sheng, X.Q.; Gashinova, M. Road edge recognition using the stripe Hough transform from millimeter-wave radar images. IEEE Trans. Intell. Transp. Syst. 2014, 16, 825–833. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J.; Chen, D.; Peethambaran, J. Joint clusters and iterative graph cuts for ALS point cloud filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 990–1004. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour detection in unstructured 3d point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1610–1618. [Google Scholar]
- Wang, R.; Peethambaran, J.; Chen, D. LiDAR point clouds to 3-D Urban Models: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Mineo, C.; Pierce, S.G.; Summan, R. Novel algorithms for 3D surface point cloud boundary detection and edge reconstruction. J. Comput. Des. Eng. 2019, 6, 81–91. [Google Scholar] [CrossRef]
- Ahmmed, A.; Paul, M.; Pickering, M. Dynamic point cloud texture video compression using the edge position difference oriented motion model. In Proceedings of the 2021 Data Compression Conference (DCC), Snowbird, UT, USA, 23–26 March 2021; p. 335. [Google Scholar]
- Xia, S.; Chen, D.; Wang, R.; Li, J.; Zhang, X. Geometric primitives in LiDAR point clouds: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 685–707. [Google Scholar] [CrossRef]
- Li, J.; Zhao, P.; Hu, Q.; Ai, M. Robust point cloud registration based on topological graph and Cauchy weighted lq-norm. ISPRS J. Photogramm. Remote Sens. 2020, 160, 244–259. [Google Scholar] [CrossRef]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Guibas, L.J.; Birdal, T. Learning multiview 3D point cloud registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 1759–1769. [Google Scholar]
- Choi, C.; Trevor, A.J.; Christensen, H.I. RGB-D edge detection and edge-based registration. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1568–1575. [Google Scholar]
- Shi, W.; Rajkumar, R. Point-gnn: Graph neural network for 3d object detection in a point cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 1711–1719. [Google Scholar]
- Hu, F.; Yang, D.; Li, Y. Combined edge-and stixel-based object detection in 3D point cloud. Sensors 2019, 19, 4423. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Ferrie, F.P.; Macfarlane, J. A method for detecting windows from mobile LiDAR data. Photogramm. Eng. Remote Sens. 2012, 78, 1129–1140. [Google Scholar] [CrossRef] [Green Version]
- Song, H.; Feng, H.Y. A progressive point cloud simplification algorithm with preserved sharp edge data. Int. J. Adv. Manuf. Technol. 2009, 45, 583–592. [Google Scholar] [CrossRef]
- Li, H.; Zhong, C.; Hu, X.; Xiao, L.; Huang, X. New methodologies for precise building boundary extraction from LiDAR data and high resolution image. Sens. Rev. 2013, 33, 157–165. [Google Scholar] [CrossRef]
- Poullis, C. A framework for automatic modeling from point cloud data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2563–2575. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ewert, D.; Schilberg, D.; Jeschke, S. Edge extraction by merging 3D point cloud and 2D image data. In Proceedings of the 2013 10th International Conference and Expo on Emerging Technologies for a Smarter World (CEWIT), Melville, NY, USA, 21–22 October 2013; pp. 1–6. [Google Scholar]
- Li, Y.; Wu, H.; An, R.; Xu, H.; He, Q.; Xu, J. An improved building boundary extraction algorithm based on fusion of optical imagery and LiDAR data. Optik 2013, 124, 5357–5362. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Zhou, G.; Yan, G. A novel building boundary reconstruction method based on lidar data and images. In International Symposium on Photoelectronic Detection and Imaging 2013: Laser Sensing and Imaging and Applications; SPIE-International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8905, p. 890522. [Google Scholar]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. Remote Sens. 2014, 95, 109–121. [Google Scholar] [CrossRef]
- Demarsin, K.; Vanderstraeten, D.; Volodine, T.; Roose, D. Detection of closed sharp edges in point clouds using normal estimation and graph theory. Comput. Aided Des. 2007, 39, 276–283. [Google Scholar] [CrossRef]
- Borges, P.; Zlot, R.; Bosse, M.; Nuske, S.; Tews, A. Vision-based localization using an edge map extracted from 3D laser range data. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4902–4909. [Google Scholar]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge detection and feature line tracing in 3d-point clouds by analyzing geometric properties of neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Lai, X.; Hou, W. Study on edge detection of LIDAR point cloud. In Proceedings of the 2011 International Conference on Intelligent Computation and Bio-Medical Instrumentation, Wuhan, China, 14–17 December 2011; pp. 71–73. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 679–698. [Google Scholar] [CrossRef]
- Pauly, M.; Mitra, N.J.; Giesen, J.; Gross, M.H.; Guibas, L.J. Example-Based 3d Scan Completion. 2005. Available online: https://infoscience.epfl.ch/record/149337/files/pauly_2005_EBS.pdf (accessed on 6 August 2021).
- Harris, C.G.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September, 1988; pp. 1–6. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.434.4816&rep=rep1&type=pdf (accessed on 6 August 2021).
- Xia, S.; Wang, R. A fast edge extraction method for mobile LiDAR point clouds. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1288–1292. [Google Scholar] [CrossRef]
- Pauly, M.; Gross, M.; Kobbelt, L.P. Efficient simplification of point-sampled surfaces. In Proceedings of the IEEE Visualization, VIS 2002, Boston, MA, USA, 27 October–1 November 2002; pp. 163–170. [Google Scholar]
- Huang, H.; Li, D.; Zhang, H.; Ascher, U.; Cohen-Or, D. Consolidation of unorganized point clouds for surface reconstruction. ACM Trans. Graph. 2009, 28, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Lipman, Y.; Cohen-Or, D.; Levin, D.; Tal-Ezer, H. Parameterization-free projection for geometry reconstruction. ACM Trans. Graph. 2007, 26, 22-es. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Schindler, K.; Pollefeys, M. SEMANTIC3D.NET: A new large-scale point cloud classification benchmark. arXiv 2017, arXiv:1704.03847. [Google Scholar] [CrossRef] [Green Version]
- Du, J.; Chen, D.; Wang, R.; Peethambaran, J.; Mathiopoulos, P.T.; Xie, L.; Yun, T. A novel framework for 2.5-D building contouring from large-scale residential scenes. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4121–4145. [Google Scholar] [CrossRef]
- Zolanvari, S.; Ruano, S.; Rana, A.; Cummins, A.; da Silva, R.E.; Rahbar, M.; Smolic, A. DublinCity: Annotated LiDAR point cloud and its applications. arXiv 2019, arXiv:1909.03613. [Google Scholar]
- Vallet, B.; Brédif, M.; Serna, A.; Marcotegui, B.; Paparoditis, N. TerraMobilita/iQmulus urban point cloud analysis benchmark. Comput. Graph. 2015, 49, 126–133. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2020; pp. 11108–11117. [Google Scholar]







| Modules | Parameters | Recommended Values | Descriptions |
|---|---|---|---|
| Confidence Estimation | r | (, 1.5, 2) | Parameter r defines the neighborhood sphere radius for the calculation of confidence measure. Three scales of the spheres are used to obtain the mean value of each point’s confidence. |
| Gradient Calculation/Structure Tensor Generation/Gaussian Smoothing | N | 40 | It represents how many points are included for calculating gradient and structure tensor of point . |
| Dual-threshold Criterion | [0.6, ] | Gradient threshold. | |
| [5, 30] | Response function threshold. | ||
| Gaussian Smoothing | - | The standard deviation of distance between the current point and its neighbor point set (). | |
| Grid Refinement | 2/3 | It defines the cell size of the 3D grid. The larger cell size is, the less critical points are remained. | |
| Hierarchical Refinement | 0.01 | It controls the local variation of the divided clusters. The values goes from 0 with a coplanar cluster to 1/3 with a fully isotropic cluster. The large it is, the fewer critical points we have. | |
| 30 | It controls the maximum number of the divided clusters.The larger it is, the few critical points we have. | ||
| WLOP Refinement | 50% | It determines the percentage of points to retain. | |
| 0.2 | It controls the degree of regularization. The larger neighbor size is, the more regularized results are obtained. |
| Datasets | Buiding ID | #Building | #Reference | Dual-Threshold | Grid | Hierarchy | WLOP | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | ||||
| TLS | Semantic3D Building 1 | 78,223 | 31,971 | 43.89 | 107.38 | 12.88 | 31.51 | 8.73 | 21.37 | 21.37 | 52.29 |
| Semantic3D Building 2 | 142,346 | 48,949 | 37.90 | 110.21 | 14.16 | 41.17 | 9.00 | 26.18 | 18.67 | 54.31 | |
| Semantic3D Building 3 | 800,048 | 258,267 | 33.00 | 102.22 | 2.12 | 6.54 | 9.43 | 29.21 | 16.50 | 51.11 | |
| Semantic3D Building 4 | 713,975 | 225,596 | 33.84 | 107.09 | 3.99 | 12.63 | 8.02 | 25.39 | 16.89 | 53.44 | |
| Semantic3D Building 5 | 406,525 | 118,602 | 37.95 | 130.09 | 4.33 | 14.83 | 8.50 | 29.13 | 18.91 | 64.83 | |
| Semantic3D Building 6 | 446,521 | 101,665 | 29.65 | 130.24 | 0.98 | 4.32 | 6.75 | 29.65 | 14.83 | 65.11 | |
| Semantic3D Building 7 | 169,399 | 96,377 | 54.43 | 95.67 | 8.25 | 14.50 | 11.53 | 20.27 | 26.99 | 47.43 | |
| Semantic3D Building 8 | 763,570 | 162,936 | 25.03 | 117.31 | 0.92 | 4.31 | 5.42 | 25.40 | 12.51 | 58.63 | |
| ALS | Netherland | 6,047,084 | - | 23.11 | - | 9.08 | - | 1.15 | - | 11.55 | - |
| Dublin | 9,189,507 | - | 14.38 | - | 6.20 | - | 0.72 | - | 7.19 | - | |
| MLS | Paris | 3,738,321 | - | 9.61 | - | 1.23 | - | 1.46 | - | 14.81 | - |
| UAV | Building | 11,192,178 | - | 3.71 | - | 0.49 | - | 0.19 | - | 1.85 | - |
| Building | 6,475,114 | - | 6.45 | - | 0.63 | - | 0.32 | - | 3.22 | - | |
| HLS | Building | 5,118,751 | - | 5.79 | - | 0.56 | - | 0.32 | - | 2.89 | - |
| Building ID | Max (m) | Min (m) | Mean (m) | SD (m) | RMSE (m) | RMSE′ |
|---|---|---|---|---|---|---|
| Semantic3D Building 1 | 2.1129 | 0 | 0.0368 | 0.1819 | 0.1856 | 0.0064 |
| 1.7406 | 0 | 0.0415 | 0.1758 | 0.1807 | 0.0063 | |
| 1.6855 | 0 | 0.0354 | 0.1632 | 0.1670 | 0.0058 | |
| 1.7434 | 0 | 0.0587 | 0.1663 | 0.1764 | 0.0061 | |
| Semantic3D Building 2 | 2.0195 | 0 | 0.0291 | 0.1137 | 0.1174 | 0.0026 |
| 2.0195 | 0 | 0.0372 | 0.1393 | 0.1442 | 0.0031 | |
| 2.0195 | 0 | 0.0271 | 0.1061 | 0.1095 | 0.0024 | |
| 1.9955 | 0 | 0.0538 | 0.1080 | 0.1206 | 0.0026 | |
| Semantic3D Building 3 | 1.9446 | 0 | 0.0052 | 0.0683 | 0.0686 | 0.0017 |
| 1.8483 | 0 | 0.0179 | 0.1010 | 0.1025 | 0.0026 | |
| 1.9141 | 0 | 0.0098 | 0.0707 | 0.0713 | 0.0018 | |
| 1.9094 | 0 | 0.0203 | 0.0684 | 0.0720 | 0.0018 | |
| Semantic3D Building 4 | 3.7826 | 0 | 0.0556 | 0.2779 | 0.2838 | 0.0062 |
| 3.7787 | 0 | 0.0936 | 0.3573 | 0.3693 | 0.0081 | |
| 3.7118 | 0 | 0.0442 | 0.2283 | 0.2325 | 0.0051 | |
| 3.7817 | 0 | 0.0736 | 0.2718 | 0.2816 | 0.0062 | |
| Semantic3D Building 5 | 3.2625 | 0 | 0.0788 | 0.2582 | 0.2703 | 0.0060 |
| 3.2364 | 0 | 0.1477 | 0.3543 | 0.3839 | 0.0085 | |
| 3.2245 | 0 | 0.0769 | 0.2352 | 0.2474 | 0.0055 | |
| 3.2474 | 0 | 0.0931 | 0.2479 | 0.2648 | 0.0059 | |
| Semantic3D Building 6 | 0.7303 | 0 | 0.0568 | 0.1545 | 0.1647 | 0.0087 |
| 0.7226 | 0 | 0.0682 | 0.1525 | 0.1670 | 0.0088 | |
| 0.7230 | 0 | 0.0599 | 0.1526 | 0.1639 | 0.0086 | |
| 0.7175 | 0 | 0.0699 | 0.1497 | 0.1652 | 0.0087 | |
| Semantic3D Building 7 | 1.3306 | 0 | 0.0340 | 0.1069 | 0.1122 | 0.0023 |
| 1.2979 | 0 | 0.0559 | 0.1245 | 0.1365 | 0.0028 | |
| 1.2749 | 0 | 0.0342 | 0.0998 | 0.1055 | 0.0021 | |
| 1.3606 | 0 | 0.0520 | 0.1011 | 0.1137 | 0.0023 | |
| Semantic3D Building 8 | 1.9282 | 0 | 0.0252 | 0.0948 | 0.0982 | 0.0040 |
| 1.8951 | 0 | 0.0433 | 0.1139 | 0.1218 | 0.0050 | |
| 1.9181 | 0 | 0.0279 | 0.0853 | 0.0898 | 0.0037 | |
| 1.8918 | 0 | 0.0381 | 0.0923 | 0.0998 | 0.0041 |
| Dataset | Mean (m) | SD (m) | RMSE (m) | Compactness (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Our Method | Xia’s Method | Our Method | Xia’s Method | Our Method | Xia’s Method | Our Method | Xia’s Method | |
| Semantic3D TLS | 0.0574 | 0.0626 | 0.1507 | 0.1771 | 0.1618 | 0.1889 | 18.33% | 56.09% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Li, J.; Di, S.; Peethambaran, J.; Xiang, G.; Wan, L.; Li, X. Critical Points Extraction from Building Façades by Analyzing Gradient Structure Tensor. Remote Sens. 2021, 13, 3146. https://doi.org/10.3390/rs13163146
Chen D, Li J, Di S, Peethambaran J, Xiang G, Wan L, Li X. Critical Points Extraction from Building Façades by Analyzing Gradient Structure Tensor. Remote Sensing. 2021; 13(16):3146. https://doi.org/10.3390/rs13163146
Chicago/Turabian StyleChen, Dong, Jing Li, Shaoning Di, Jiju Peethambaran, Guiqiu Xiang, Lincheng Wan, and Xianghong Li. 2021. "Critical Points Extraction from Building Façades by Analyzing Gradient Structure Tensor" Remote Sensing 13, no. 16: 3146. https://doi.org/10.3390/rs13163146
APA StyleChen, D., Li, J., Di, S., Peethambaran, J., Xiang, G., Wan, L., & Li, X. (2021). Critical Points Extraction from Building Façades by Analyzing Gradient Structure Tensor. Remote Sensing, 13(16), 3146. https://doi.org/10.3390/rs13163146