Abstract
Two existing double-difference (DD) methods, using either a 3rdSensor or Radiative Transfer Modeling (RTM) as a transfer, are applicable primarily for limited regions and channels, and, thus critical in capturing inter-sensor calibration radiometric bias features. A supplementary method is also desirable for estimating inter-sensor calibration biases at the window and lower sounding channels where the DD methods have non-negligible errors. In this study, using the Suomi National Polar-orbiting Partnership (SNPP) and Joint Polar Satellite System (JPSS)-1 (alias NOAA-20) as an example, we present a new inter-sensor bias statistical method by calculating 32-day averaged differences (32D-AD) of radiometric measurements between the same instrument onboard two satellites. In the new method, a quality control (QC) scheme using one-sigma (for radiance difference), or two-sigma (for radiance) thresholds are established to remove outliers that are significantly affected by diurnal biases within the 32-day temporal coverage. The performance of the method is assessed by applying it to estimate inter-sensor calibration radiometric biases for four instruments onboard SNPP and NOAA-20, i.e., Advanced Technology Microwave Sounder (ATMS), Cross-track Infrared Sounder (CrIS), Nadir Profiler (NP) within the Ozone Mapping and Profiler Suite (OMPS), and Visible Infrared Imaging Radiometer Suite (VIIRS). Our analyses indicate that the globally-averaged inter-sensor differences using the 32D-AD method agree with those using the existing DD methods for available channels, with margins partially due to remaining diurnal errors. In addition, the new method shows its capability in assessing zonal mean features of inter-sensor calibration biases at upper sounding channels. It also detects the solar intrusion anomaly occurring on NOAA-20 OMPS NP at wavelengths below 300 nm over the Northern Hemisphere. Currently, the new method is being operationally adopted to monitor the long-term trends of (globally-averaged) inter-sensor calibration radiometric biases at all channels for the above sensors in the Integrated Calibration/Validation System (ICVS). It is valuable in demonstrating the quality consistencies of the SDR data at the four instruments between SNPP and NOAA-20 in long-term statistics. The methodology is also applicable for other POES cross-sensor calibration bias assessments with minor changes.
1. Introduction
Since its establishment in October 2010 in the NOAA Center for Satellite Applications and Research (STAR), the Integrated Calibration/Validation System (ICVS) has provided both Long-Term Monitoring (LTM) and Near Real-Time (NRT) monitoring on the quality of satellite Raw Data Record (RDR), Temperature Data Record (TDR), and Sensor Data Record (SDR) from more than 30 sensors [1]. These sensors include five instruments onboard the Suomi National Polar-orbiting Partnership (SNPP) and the Joint Polar Satellite System (JPSS)-1, aka NOAA-20, i.e., Cross-track Infrared Sounder (CrIS), Advanced Technology Microwave Sounder (ATMS), Visible Infrared Imaging Radiometer Suite (VIIRS), and Ozone Mapping and Profiler Suite (OMPS) Nadir Mapper (NM) and Nadir Profiler (NP). With same type of sensors flying on multiple satellite platforms, those satellite observations provide an unprecedented opportunity for inter-sensor comparisons and scientific discoveries. It is thus vital to have NRT monitoring of inter-sensor bias distributions for TDR and SDR data among SNPP, NOAA-20, and future JPSS satellites to support various instrument calibration and data validation.
In the past decades, inter-senor radiometric biases among various sensors were intensively studied typically using two double-difference (DD) methods, which are also adopted by ICVS-LTM (hereinafter frequently called ICVS for simplification) for SNPP and NOAA-20 instruments. The first DD method uses the third instrument onboard a different satellite as a transfer (3rdSensor-DD), which is related to Simultaneously Nadir Overpass (SNO) [2,3,4] or Simultaneously Conical Overpass (SCO) analyses [5,6]. The other method uses the Radiative Transfer Model (RTM) as a transfer (RTM-DD) (e.g., [7,8]). These DD methods provide valuable information for cross-sensor calibration biases but are still subject to a few restrictions. The SNO method is applicable over Polar Regions for Low Earth Orbit (LEO)-LEO satellites [2,3,4,5,6], or over low and middle latitude regions for LEO-Geosynchronous Equatorial Orbit (GEO) satellites [9,10]. The assessed channels of this method are limited to common channels between sensors in the SNO method, e.g., only a certain wavelength range of channels overlapped between the CrIS (or VIIRS) and Advanced Baseline Imager (ABI) (see Section 5). In addition, the discrepancies in spatial resolution, central frequency, and polarization can add uncertainties to the SNO analysis and further to the 3rdSensor-DD assessment [7]. The calibration accuracy of the 3rdSensor (transfer sensor) is another potential error source affecting the SNO analysis performance. For the RTM-DD method, on the other hand, the RTM simulation errors at the window and low-sounding channels can be as high as a few Kelvins due to small surface emissivity error (e.g., [11]), which can easily exceed regular inter-sensor calibration radiometric biases. Simulation accuracies at sounding channels are too affected by uncertainties in ingested atmospheric profiles. Besides, simulations under cloudy conditions are still questionable due to a lack of accurate cloud information. Thus, RTM simulation results for inter-sensor comparison are applied primarily to sounding channels under clear skies over open oceans. The abovesaid deficits partially prevent the application of the two DD methods from accurate analysis on regional inter-sensor calibration biases at certain channels. Currently, the NOAA-20 OMPS NP SDR data at wavelengths below 300 nm experience solar intrusions at high latitudes over the Northern Hemisphere where the solar zenith angle (SZA) is greater than 57° [12]. It is challenging if not impossible to use the above DD methods to detect regional features of inter-sensor biases like the OMPS NP data between SNPP and NOAA-20.
Besides the DD methods, the daily global mean method was also used for decades for inter-sensor comparison analysis. This method is useful for inter-sensor comparisons of time-insensitive environment data record (EDR) products such as ocean color products [13]. However, it is not applicable for time-sensitive EDR products such as precipitations due to strong diurnal differences [14]. In comparison with its application to EDR products, this method has more issues in the inter-sensor comparison analysis of radiance in the TDR or SDR data. Previous studies showed an obvious diurnal variation in radiance exists between the same instrument aboard two Polar Operational Environmental Satellites (POES) satellites, whose magnitudes change with atmospheric and/or surface conditions [15,16]. In reality, limited or inconsistent sample sizes of the data over the overlapped regions between two satellite sensors on the same day (see Section 2 below) are usually not sufficient to reduce the diurnal variations within the data (see Section 5 below). The small sample of daily data further prevents the analysis of the zonal mean of the inter-sensor calibration biases. This is especially true for the OMPS NM/NP and VIIRS solar reflective bands because of the large impact induced by SZA discrepancies. While the SZAs are similar for the SNPP and NOAA-20 solar reflective band observations 50 min apart, these two satellites are not observing with the same area on the Earth at the same SZA. For non-overlapped regions, the radiance differences between the two sensors contain larger impacts from diurnal variations due to the discrepancies in atmospheric and/or surface conditions. In addition, for the OMPS NP observations, due to its narrow swath, there are no overlapped areas between SNPP and NOAA-20 observations on the same day. Therefore, the deficiencies in the two existing DD and daily global mean methods call for the development of a supplementary method to estimate the globally-averaged inter-sensor calibration radiometric biases and the regional bias feature with zonally-averaged biases at all channels.
This study develops a new statistical method for inter-sensor calibration radiometric bias assessments by computing 32-day-averaged differences (32D-AD) of Earth-scene radiances within two 16-day global repeating-orbit cycles from the same types of instruments that fly at SNPP and NOAA-20 satellites, respectively [17]. This method is also an extension of the direct (global) mean method from one day to multiple days of data sets (e.g., covering two complete 16-day satellite orbit repeat cycles for the SNPP and JPSS satellites). In contrast to the one-day global mean comparison method, after an orbit repeat cycle, each orbit in the first day typically can cover the entire globe and go back to the starting point of measurement, ensuring fully global coverages by both sensors. Two cycles or 32 days are selected to reduce diurnal differences due to the 50-min orbit differences between SNPP and NOAA-20. This is especially important for inter-sensor calibration radiometric bias estimates at lower sounding and window channels. Moreover, the study addresses the impacts of diurnal variations on 32-day-averaged radiance differences, along with the development of a Quality Control (QC) scheme applicable to ATMS, CrIS, VIIRS, and OMPS NP. Furthermore, the formulae are established upon the QC-passing 32D-AD data sets with and without gridding, respectively. Both globally and zonally averaged inter-sensor radiometric differences for the above instruments are calculated. The formulae are employed to calculate globally-averaged inter-sensor radiometric differences at all channels for the above instruments within the ICVS framework. The OMPS NM will be covered in a separate study. At the overlapped channels, the 32-day globally-averaged biases are compared with those using one or two DD methods for the new method performance validation. In addition, the zonal mean analysis at high upper sounding channels is also conducted. For the OMPS NP, the zonal means are utilized to investigate the impact of solar intrusions on the NOAA-20 NP calibration radiometric biases at channels below 300 nm.
This study is organized as follows. The next section introduces the ICVS-LTM, four instruments onboard SNPP and NOAA-20 platforms, TDR/SDR data, and two DD methods. Section 3 develops the 32D-AD method along with the analysis of diurnal error sources. In Section 4, we develop the procedure to calculate SNPP and NOAA-20 inter-sensor calibration radiometric biases (global average and zonal mean) at each channel using the 32D-AD method. Section 5 describes the application of the method to ATMS, CrIS, VIIRS, and OMPS NP within the ICVS monitoring framework to assess their inter-sensor radiometric biases. The globally-averaged inter-sensor biases from the new method are compared with those using the 3rdSensor-DD and RTM-DD. The chronological length of data sets for inter-sensor biases calculation is discussed. Summary and conclusions are provided in the final section.
2. Descriptions of ICVS-LTM, Instruments, Data, and DD-Methods
2.1. ICVS-LTM
The ICVS-LTM was established to incorporate post-launch onboard and operational monitoring of satellite instrument RDR, TDR, and SDR data, as well as forward calculation of radiance for part of the sensors to meet the challenge of the increasing demand for accurate satellite data quality and inter-sensor data bias assessments in the NRT mode. In practice, the ICVS serves as a web-based dashboard for satellite instrument status and SDR (TDR) data quality. Currently, it monitors more than 30 POES satellite instruments with more than 7000 parameters online. Particularly, it provides monitoring of long-term instrument performance and SDR product quality for ATMS, VIIRS, OMPS NP and NM, and CrIS onboard SNPP and NOAA-20, including trends of inter-satellite calibration radiance biases. As shown in Figure 1, the main functions of ICVS consist of three key components: the Instrument Performance Monitoring System (IPMS), the SDR Quality Assurance System (SQAS), and the ICVS Anomaly Watch Portal (ICVS-AWP). The monitoring detail of each component is referred to (https://www.star.nesdis.noaa.gov/icvs/index.php). The ICVS Severe Weather Event Watch (iSEW) as part of the Satellite Data and Application Demonstration System (DDADS) is referred to [18,19].
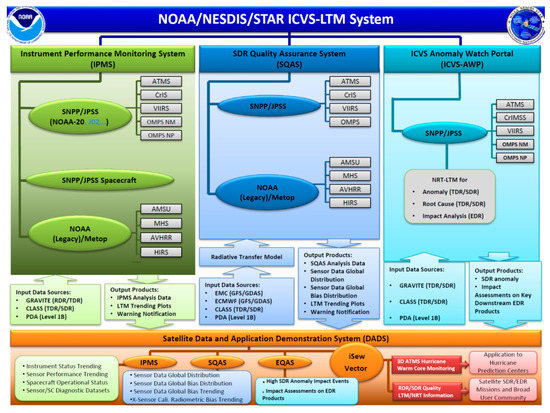
Figure 1.
Diagram of the ICVS-LTM, showing three key components: the Instrument Performance Monitoring System (IPMS), the SDR Quality Assurance System (SQAS), and the ICVS Anomaly Watch Portal (ICVS-AWP) (https://www.star.nesdis.noaa.gov/icvs/index.php, accessed on 5 April 2021), as well as the associated Satellite Data and Application Demonstration System (DADS) which includes the ICVS Severe Weather Event Watch (iSEW).
2.2. Channels Characterizations for Four Instruments
Four instruments aboard SNPP and NOAA-20 are involved in this study, including ATMS, CrIS, OMPS NP, and VIIRS. Detailed descriptions of the instruments can be found in [20,21,22,23]. The following is some brief information on the channel or band wavelength ranges of each instrument. The ATMS is a 22-channel microwave sounder providing both temperature soundings from surface to upper stratosphere and humidity soundings from the surface to upper troposphere. Among the 22 channels, the lowest two channels (23.8 and 31.4 GHz) have a beam width of 5.2°, 13 channels below 60 GHz have a beam width of 2.2°, and the remaining seven channels above 60 GHz have a beam width of 1.1° except for the lowest channel of 88.2 GHz (2.2°) [20]. For each scan cycle, the Earth is viewed at 96 different angles symmetrically around the nadir direction, forming 96 samples of Earth radiometric measurements per scan. The CrIS is a Fourier transform spectrometer, providing sound information of the atmosphere with 2211 spectral channels at full spectral resolution (FSR) mode over three wavelength ranges: short-wave (SW) IR (3.92–4.64 μm), middle-wave (MW) IR (5.71–8.26 μm), and long-wave (LW) infrared (9.14–15.38 μm), with resolution at 0.625 cm−1 for all three bands [21]. Each scan consists of 34 field-of-regards (FORs) with 30 FORs for the Earth scene, while each FOR contains a 3-by-3 field-of-view (FOV) array. For OMPS, one common OMPS sensor on both the SNPP and NOAA-20 is the NP Spectrometer in the spectral range of 250 to 310 nm. It provides ozone profiles in a single ground pixel of 250 × 250 km2 at nadir from SNPP or 25-ground pixels of 50 × 50 km2 at nadir from NOAA-20 [22]. The VIIRS has 22 spectral bands covering the spectrum between 0.412 and 12.01 µm, including 16 moderate-resolution bands (M-bands) with a spatial resolution of 750 m at nadir, 5 imaging resolution bands (I-bands)—375 m at nadir, and one panchromatic DNB with a 750 m spatial resolution [23]. The M-bands include 11 Reflective Solar Bands (RSB) and 5 Thermal Emissive Bands (TEBs), while the I-bands include 3 RSBs and 2 TEBs. The channel or band information of those sensors is listed in Table 1.

Table 1.
Channel or band information of ATMS, CrIS, OMPS NP, and VIIRS [20,21,22,23].
2.3. Data
The data per satellite sensor are typically divided into three levels: Raw Data Records (RDRs or level 0), SDR (or level 1), and EDRs (or level 2). The SDR data associated with calibrated radiance/reflectance/brightness temperatures are used in this study for CrIS, OMPS, and VIIRS. For the ATMS, both TDR and SDR data are generated in the operational data stream. The Advanced Microwave Sounding Unit (AMSU-A) is used as a transfer sensor for the ATMS SNO DD analysis. The operational data stream processing for AMSU-A only produces Temperature Data Records (TDR) associated with antenna temperatures without antenna pattern correction [8,24]. Hence, for the comparison with AMSU-A data, ATMS TDR data are used in the 32D-AD analysis. The SNPP and NOAA-20 SDR data are operationally processed in the NOAA JPSS Interface Data Processing Segment (IDPS) [25]. The TDR data of the AMSU-A onboard European Meteorological Operational satellite programs (Metop) from Metop-A to Metop-C are generated in the NOAA Office of Satellite and Product Operations (OSPO) operational system [26]. All TDR/SDR data are distributed through the Production Distribution and Access (PDA) in near-real-time mode, the Comprehensive Large Array-data Stewardship System (CLASS) and Direct Readout for a board national and international user community.
In this study, the data are analyzed in two ways. For ATMS, CrIS, and VIIRS, which have sufficient orbit coverages, the data are gridded in both latitude and longitude. The gridding here is an average of all original radiance data with the same weighing within the selected spatial resolution of the box (e.g., 1° for ATMS), i.e., a linear process. Since the 32D-AD computation is also a linear process, mathematically, the magnitudes of 32-day data sets in lower resolution are approximately the same as those of 32-day data sets in high (original) resolution. Due to an extremely large volume of data sets covering the globe and 32 days for all channels, the data for ATMS, CrIS, and VIIRS are thus gridded into a 1°, 0.5°, and 0.25° resolution in both the latitude and longitude, respectively, to avoid saving big data sets covering global areas and 32 days for all channels, while the final values of 32D-AD data sets are not significantly affected. The data in ascending or descending nodes are used separately in the 32-AD method unless otherwise given. However, the gridding procedure is not applicable for OMPS NP because it has a very narrow swath coverage of 250 km (see Section 3.1 where the nadir-viewing resolution is 50 × 50 km2 for NOAA-20 and 250 × 250 km2 for SNPP. The original SDR data is thus used in a slightly different computation procedure (see Section 3).
2.4. Two DD Methods
Regarding the 3rdSensor-DD and RTM-DD methods, they have been widely applied to various satellite inter-sensor comparisons (e.g., [3,11,25,26]).
For the 3rdSensor-DD method, the inter-sensor calibration radiometric biases between the SNPP and NOAA-20 instruments are computed using the double-difference via the 3rdSensor as a transfer, based on a series of SNO pairs of measurements, i.e.,
where denote the radiometric measurements in radiance or temperature for per an SNO event. At each SNO, radiometers from both satellites view the same place at the same time at nadir, providing an ideal scenario for the inter-calibration of radiometers aboard the two satellites [2,3]. In (1), and are target sensors for inter-sensor bias computation, while is a bridge (transfer) sensor. In this study, and represent one of the ATMS, CrIS, and VIIRS onboard SNPP and NOAA-20, respectively. For ATMS, is AMSU-A onboard Metop-C; for CrIS and VIIRS, is one of the Advanced Baseline Imager (ABI) onboard the Geostationary satellite (GOES)-16 or GOES-17. The SNO analysis for OMPS NP is still to be conducted in a future study, so it is not included in this study. For convenience, we also use the ABI-DD for the analysis of CrIS and VIIRS, and the AMSU-A-DD for the analysis of ATMS to specify the uniqueness of the bridge sensor.
For the RTM-DD method, its principle is similar to (1) except that an RTM is used as a transfer.
where we use and to signify the radiometric values from either satellite observations or RTM simulations in this method; the subscript ‘’ implies that the simulations for the Earth-scene radiance or antenna temperatures are performed only under clear sky conditions over open oceans. For ATMS, CrIS, and VIIRS, the RTM denotes the Joint Center of Satellite Data Assimilation (JCSDA) Community Radiative Transfer Model (CRTM) [27,28,29]. The analysis data of the European Centre for Medium-Range Weather Forecasts (ECMWF) surface conditions and atmospheric profiles provide inputs to the CRTM. We use the ECMWF analysis data as they are well-validated against numbers of radiosonde measurements, with a bias within one Kelvin at levels from 100 to 1000 hPa [30]. For the OMPS NP, operating at the UV bands, the TomRTM [31] is used to simulate radiance at the NP wavelengths, which was developed initially for observations from the Total Ozone Mapping Spectrometer (TOMS). The ozone atmospheric profiles and surface reflectivity from NASA SNPP Environmental Data Record (EDR) data are acquired from the NASA Science Investigator-led Processing Systems (SIPS) (https://omisips1.omisips.eosdis.nasa.gov/sipslogin.md, accessed on 19 July 2021) are used as inputs to the TomRad for NP SDR data simulations.
3. Development of the 32D-AD Method
Presented as follows, the development of the 32D-AD method includes the rationale of the 32D-AD method, potential error sources due to diurnal variations, and formulas for calculating inter-sensor calibration radiometric biases.
3.1. Principle of 32D-AD Method
Firstly, we introduce the principle of the method using the satellite gridded SDR (TDR) data (hereinafter SDR and TDR are typically omitted). Over a gridded location , there are a series of cross-track Earth-scene radiometric measurements either in radiance or antenna (brightness) temperatures at different scan positions per channel during the 32-day period for an instrument onboard either the SNPP or NOAA-20. and are used to denote the sample sizes of all measurements per channel at by NOAA-20 and SNPP instruments, respectively. The averages of accumulated measurements per location and sensor channel are expressed in the equations:
and
where and denote the averages of 32-day observations at all available scan positions per channel for NOAA-20 and SNPP, respectively; the upper line of the variable is hereinafter used to highlight the average of many measurement data; and The channel index is omitted in the equations throughout this study.
Their difference, is calculated by
where the represents the 32-day-averaged differences (32D-AD) of measurements at all available scan positions per location for the same instrument between the NOAA-20 and SNPP. Explanations of other variables in all the equations in this study are referred to in Table A1 in Appendix A.
For the SNPP and NOAA-20 sensors, if there are no orbit drifts and all measurements are valid, the magnitude of should be the same as that of at all locations for one or more 16-day orbit repeating cycles. In reality, the orbital velocity and satellite altitude can vary slightly with time [32], thus causing certain orbit drift with time. As a consequence, the might not be exactly the same as over each location. Figure 2a,b show the global distributions of the total sample size differences between the SNPP and NOAA-20 CrIS measurements after one day and 32 days, respectively. As expected, the large sample size differences occur on the first day due to the ~50-min passing time gap between SNPP and NOAA-20 (see Figure 2a). Especially, large differences appear over the tropic areas due to discrepancies in the orbit gap locations between two satellites, thus significantly degrade the accuracy of the daily globally-averaged radiance differences due to many inconsistent observations. In addition, there are many data gaps over the polar regions in the one-day gridded data, which are not virtually seen in the map due to the limitation of the used projection. The gaps are caused by the gradually decreased spatial resolution of a given FOV on Earth from low to high latitudes. In contrast, the differences of sample sizes are mostly close to zero after 32-days (two-orbit repeating cycles), although sample size differences can be up to ten or more over the polar regions due to orbit drift of the SNPP and NOAA-20 satellites (see Figure 2b). A similar feature exists in the sample size distribution after one cycle (figure not included). Therefore, the same instrument onboard the SNPP and NOAA-20 platforms can be assumed to have a similar number of observation samples globally after one or more orbit repeating cycles. This essentially mitigates the disadvantage of the one-day global mean where the data from the two sensors have a large discrepancy in coverage over low and middle latitudes.
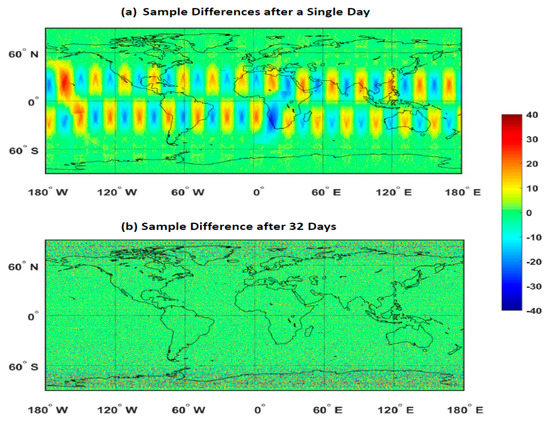
Figure 2.
Global distribution of the differences between (for NOAA-20) and (for SNPP) CrIS measurement sample sizes over each location after one day and 32 days, respectively: (a) One day. (b) 32 days.
Two additional quantities, and are introduced, respectively, to represent the global average and the zonal mean of of the gridded data:
and
The above expressions are given based on the gridded data, which can efficiently produce the global distribution of 32D-AD for two satellite instrument observations. This approach works for sensors such as ATMS, CrIS, and VIIRS that have large swath coverage of satellite observations.
Secondly, for OMPS NPs, instead of the gridding data, the global average and zonal mean are calculated using all available observations without gridding during the 32-day period. This is because some issues potentially exist if the NP SDR data are gridded for inter-sensor comparison. The OMPS NP has a very narrow swath coverage of 250 km, whereas SNPP has a spatial resolution of 250 km and NOAA-20 has a resolution of 50 km. One option is to grid NP SDR data by degrading the NOAA-20 data to match the SNPP FOV as they are present along the orbits for a given day to improve the sorting into latitude boundary boxes. Alternatively, we can grid NP SDR data by upgrading the SNPP data to match the NOAA-20 FOV, where an extra interpolation error could be added. Critically, in either way, the extremely low spatial resolution of data sets can produce uneven sample sizes for accumulated measurements within 32 days between two neighboring grids. Figure 3 displays the global distribution of sample sizes of the 32-day gridded data with a resolution of 3° per channel for NOAA-20 OMPS NP. An obvious stripping pattern is found in the distribution. A similar feature is also found when a higher spatial resolution is used in the grid (figure not included). In addition, the maximum sample size of the 32-day data set per grid is about 10 pixels, thus it hardly removes the impact of the diurnal variations through their average. Consequently, the averaged NP radiance difference per grid can significantly deviate from actual inter-sensor calibration biases due to large diurnal variations. Therefore, the analysis of the NPs in this study focuses on global average and zonal mean differences using 32-day accumulated radiance data for each NP without gridding.
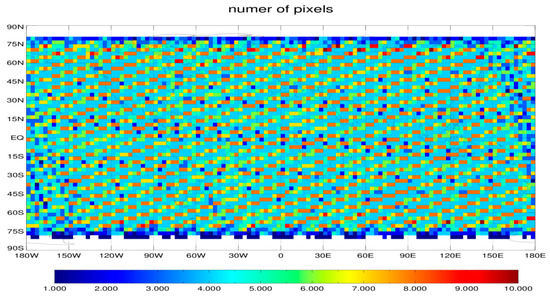
Figure 3.
Global distribution of sample sizes for the 32-day accumulated radiance data per channel for SNPP NP, where the data covers the period from 1 March 2019, to 1 April 2019.
The global mean () and zonal mean ( differences of 32-day non-gridding data between the SNPP and NOAA-20 instrument are computed, respectively, using:
with
Here, represents the global averages of 32-day radiometric observations per satellite sensor, while is the averages of 32-day radiometric observations for a given latitude (range), with . The subscript ‘’ indicates the calculations are applied to the non-gridding data, which is also applicable for the following expressions of zonal mean without gridding.
3.2. Diurnal Error Sources
The 32D-AD method defines three new variables related to the inter-sensor bias assessment for gridded data: and , and two variables for non-gridding data: and . Theoretically, if two satellite instruments measure Earth scenes in the same viewing conditions, they generally characterize the statistical features of global distribution, zonal dependency, and global average for inter-sensor radiometric biases if applicable. However, NOAA-20 passes the same location about 50 min earlier ahead of SNPP, causing certain diurnal variations due to the inconsistency of viewing conditions in measuring the Earth-scene radiance. Thus, it is important to understand the features of diurnal variations in the 32D-AD data sets at various channels. Presented below, we use the grid-based quantities to quantify the impact of the two diurnal error sources.
Figure 4 displays the global distributions of (32-day-averaged brightness temperature differences) at two CrIS channels of 670 and 1450 cm−1, which were calculated using the 32-day data sets at the ascending node covering the period from 27 September to 28 October 2019. The results at 670 cm−1, which is an upper-sounding channel with weak CO2 absorption, have a relatively uniform feature with a mean value close to zero. Certain orbit-pattern features exist especially over low and middle latitudes due to diurnal features, which is confirmed in the simulations in Figure 5a. In contrast, the at 1450 cm−1, which is strongly sensitive to water vapor in the lower troposphere, exhibits a much heterogeneous distribution over tropical- and middle-latitude areas where atmospheric features change rapidly with time. The magnitudes of are up to a couple of Kelvins that are significantly higher than those of SNPP and NOAA-20 CrIS inter-sensor or individual calibration radiometric biases [33,34,35,36]. Those features are primarily caused by diurnal differences between two satellite sensors (see simulations in Figure 5b below). Over other regions including the polar regions, the distribution of 32D-AD values is relatively homogenous with magnitudes close to actual inter-sensor calibration radiometric biases. Similar conclusions are applicable to other sensors.
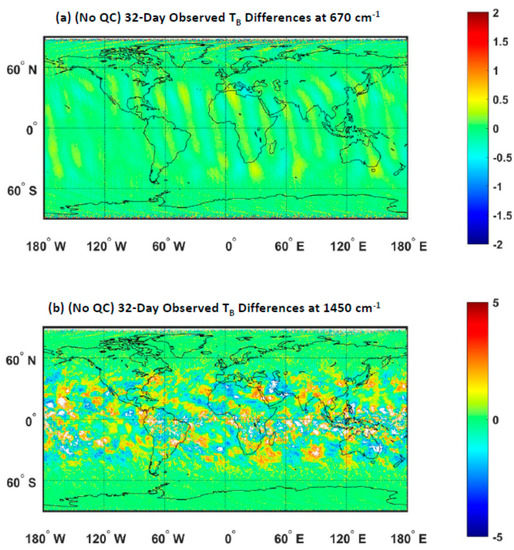
Figure 4.
Global distributions of the 32-day-averaged brightness temperature differences (NOAA-20 CrIS–SNPP CrIS) at two CrIS channels using Equation (5). The data cover the period from 27 September, to 28 October 2019: (a) 670 cm−1. (b) 1450 cm−1.
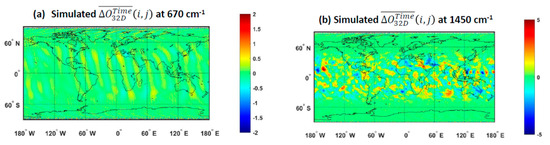
Figure 5.
Global distributions of simulated 32-day-averaged difference) at 670 and 1450 cm−1 corresponding to the orbit time difference of NOAA-20 and SNPP satellites which were calculated using (14) based on 32-day simulations from 27 September to 28 October 2019. (a) 670 cm−1. (b) 1450 cm−1.
According to Figure 4, the 32-day-averaged brightness temperature differences at the two CrIS channels are small and more homogeneous over polar regions than other low latitude regions. The sample sizes of 32D-AD data sets over polar regions for CrIS are smaller than those over other regions. For example, for CrIS SDR data at the 0.5° gridding resolution, the sample sizes of the 32-day data sets per grid over polar regions can be less than 100, but they can be as high as 500 over other regions. Therefore, the uniform feature also addresses that the size/shape change of the sensor footprints over FORs is not a major factor in determining magnitudes of CrIS 32D-AD data when diurnal variations are small. However, as the diurnal variation is strong, an insufficient sample size of data might produce unstable inter-sensor calibration bias estimates. This issue becomes especially critical for the OMPS NPs due to the very small 32-day sample size per grid (mostly below ten) (see Figure 3 below).
To understand the root cause of the above features, the is expressed below according to its contribution components:
i.e.,
where is the measurement difference due to the satellite operational time difference between the two satellites; is the measurement difference due to geographic viewing angle inconsistency for each pair of the measurements.
According to (13), the last two components on the right side of the equation are diurnal error sources for the inter-sensor calibration radiometric bias estimates from .
For it always occurs because of the almost constant satellite operation time difference between SNPP and NOAA-20 for each pair of observations. The magnitudes of this quantity can change with the sensor channel or band since surface or atmospheric properties corresponding to a channel weighting height can change either slowly or rapidly with time. However, it is challenging to quantify the movement or the changing speed from actual satellite observations since various sources of errors mix together with earth-scene radiometric measurements. Here, we conduct a simulation analysis to understand its impact by using CrIS as an example. The for CrIS is estimated using the averaged differences of the CRTM simulated brightness temperatures over 32-day observations at the SNPP and NOAA-20 observation time, i.e.,
where, is the simulated brightness temperature for the lth measurement using the CRTM during the 32-day period at the location ; the superscript and denote the observation time for NOAA-20 and SNPP, respectively; the subscript ‘Point’ is omitted in the variables of The atmospheric and surface data at the local time of NOAA-20 and SNPP observations are interpolated using two ECMWF analysis fields that cover measurement time of SNPP and NOAA-20 satellites.
Figure 5 displays the global distribution of simulated at 650 and 1450 cm−1. Similar patterns are observed between the observed 32D-AD [ and the simulated . The magnitudes of are typically small for sounding channels with weak absorptions, with the magnitudes typically close to zero, which is similar to that in Figure 4a for the observed 32D-AD results. Besides, a similar orbit pattern to Figure 4a occurs over low and middle latitudes, which is caused by diurnal errors due to different inputs of atmospheric and surface parameters corresponding to SNPP and NOAA-20 CrIS measurement time, respectively, in the RTM simulations. At the channel of 1450 cm−1, is highly heterogeneous with a magnitude of up to a few Kelvin over the tropics and the moderate latitude areas. This feature is also similar to the 32D-AD results in Figure 4b, although their magnitudes and coverages are not exactly the same as those in Figure 4b. It is primarily because of the lack of cloudy information in the simulations. In addition, the simulations are not always accurate due to the residual errors in the used atmospheric and surface ancillary data. Therefore, the similar features between Figure 4 and Figure 5 demonstrate that the is a major diurnal error source in .
Compared with the the impact of is typically small for ATMS, CrIS, and VIIRS TEBs because the same type of sensors flying into the two satellites view Earth scenes with the same satellite zenith angle range. An exception occurs for the CrIS, where a small viewing angle difference could exist within 9 FOVs per FOR of measurements between SNPP and NOAA-20. By analyzing the CrIS data sets, it is found that the local zenith angle differences within the 9 FOV pixels between the two CrIS sensors are usually smaller than 0.15°. We use two types of standard profile files to simulate this impact: US76 Standard Atmosphere and Tropical Standard Atmosphere [37]. The local zenith angle differences of 0.15° are assumed for 9 FOV pixels per FOR between SNPP and NOAA-20. According to the RTM simulations, using the US76 Standard Atmosphere, the resultant radiance zonal mean error is on the order of 0.001. A slightly larger impact is observed in the presence of a tropical standard atmosphere, but they are also on the order of 0.003 K for all SW, MW, and LW bands. Thus, the impacts of both and its zonal mean are generally negligible for the above sensors. However, this conclusion is not applicable to VIIRS UV/VIS bands and OMPS channels since the radiances at those channels are very sensitive to SZA [22,23]. Besides, variations of surface properties, aerosols, clouds, and other trace gases can further augment the impact of in the presence of SZA difference.
Therefore, due to combined diurnal variations resulting from both and lower atmospheric and/or surface features can affect largely magnitudes of 32D-AD data sets (i.e., over regions in the presence of rapidly changing atmospheric and surface properties typically at the window and lower sounding channels. Hence, a proper QC scheme mitigating impacts of diurnal errors is critical to the success of the 32D-AD method in deriving inter-sensor calibration radiometric biases from , to be introduced below.
4. Calculation of Inter-Sensor Calibration Radiometric Biases Using the 32D-AD Method
Due to the non-negligible impact of the above-mentioned diurnal variation sources over some regions, a QC scheme is desirable to remove a majority of the outliers that are vitally affected by diurnal errors within the 32D-AD data sets. In this study, the QC scheme consists primarily of one-sigma-rejection criterion for gridding 32D-AD datasets (radiance difference) for ATMS, CrIS, and VIIRS and two-sigma-rejection criterion for non-gridding 32-day data (radiance) sets for OMPS NP. Here, the sigma denotes the standard deviation of 32D-AD data sets for gridded data sets or the standard deviation of 32-day data sets for non-gridded data sets per sensor. The inter-sensor calibration radiometric biases between the same instrument from two different satellites are thus derived from the 32D-AD data sets passing the QC scheme, i.e.,
where and denote the inter-sensor calibration radiometric bias and 32-Day-averaged differences at two ways, with ‘’ or ‘’ defining either global or zonal means of the 32D-AD data sets, i.e., ; the indices of the location and channel are omitted in all variables. The case of ‘’ is only applicable for the part of global distribution particularly at window channels, so it is not generally included in (14). In other words, the computation formulae of globally- or zonally-averaged inter-sensor calibration radiometric biases are the same as these defined in the 32D-AD method in (6)–(9) in Section 3.1, except the data are QC-passing 32D-AD data sets. Figure A1a,b in Appendix B exemplify the diagram of calculating both and using (14) for the gridding SDR data and and for the non-gridding data respectively, after the QC scheme is applied. For ATMS, CrIS and VIIRS, a three-sigma threshold is also applied to original SDR (TDR) data prior to gridding to remove any invalid pixels or pixels with extremely large or small radiance values.
In the QC scheme, the one-sigma threshold is derived based on the statistical analysis of the 32D-AD data sets for each sensor. By using CrIS as an example, the global mean and standard deviation of the 32D-AD data at the channel of 670 cm−1 in Figure 4a are approximately −0.027 and 0.183 K, respectively. The absolute magnitudes of many pixels in the inhomogeneous regions are around 0.4 K with a maximum of 0.8 K, which are much larger than the standard deviation (one-sigma). Similarly, the global mean and standard deviation at the channel of 1450 cm−1 in Figure 4b are about 0.039 K and 1.331 K, correspondingly, while the absolute magnitudes of many pixels in the inhomogeneous regions are in the order of a couple of Kelvins with the maximum of 4.18 K. The absolute magnitudes of those outlier pixels are not just much larger than the standard deviations but also extremely higher than both individual calibration biases and inter-sensor calibration radiometric biases between SNPP and NOAA-20 CrIS [33,34,35,36]. More importantly, the simulation analysis in Figure 5 has confirmed that those extremely large differences are caused by diurnal variations. Hence, using one-sigma to remove the majority of the outliers that are significantly affected by diurnal variations helps improve the data selected to derive the cross-calibration biases. Certainly, the one-sigma QC threshold is a trade-off between reducing diurnal errors and saving sufficient samples containing inter-sensor calibration biases. In fact, we have tested two additional thresholds of two- and three-sigma, which keep the data with larger radiance differences. The resulted global and zonal means are very similar with a negligible difference. This is understandable because most of the 32D-AD data sets distribute within the mean ± one sigma, while the values of the outliers have a relatively random distribution in magnitude and sign thus mostly cancelling in the average.
To demonstrate the performance of the one-sigma QC scheme, Figure 6 shows the global distribution of at 670 cm−1, and 1450 cm−1 using (14). In comparison with Figure 4 where the one-sigma threshold is not applied, many pixels that fail to pass the QC have been removed from the distributions at the two channels. The impact of diurnal variations is noticeably reduced in the global distributions of the 32-day-averaged brightness temperature differences, although the impact of residual diurnal errors still remains in the channel of 1450 cm−1. However, those errors are mostly randomly distributed. Our analysis demonstrates that the impact of those residual diurnal variations can be mostly cancelled through the global average of 32-days of data sets at all channels including lower sounding and window channels (see Section 5 below). For the zonal mean biases, however, the residual impact after the QC is mostly cancelled primarily at upper sounding channels (see Section 5 for more analyses).

Figure 6.
Global distributions of 32-day-averaged brightness temperature differences at 670 and 1450 cm−1 (NOAA-20 CrIS–SNPP CrIS) after the QC is applied, which are the same as Figure 3 except for the QC applied to remove all pixels falling in the QC. (a) 670 cm−1. (b) 1450 cm−1.
To further demonstrate the performance of the one-sigma QC scheme, Figure 7a–d displays the global maps of for ATMS TDR (antenna temperature) data at the channels 1 and 10 before and after the QC scheme is applied. Channel 1 is a window channel that is strongly sensitive to variations of surface and lower atmospheric properties, while channel 10 is an upper temperature sounding channel. As a result, before the QC is applied, the magnitudes of over middle and high latitudes at channel 1 are mostly identical and are close to the observed inter-sensor calibration bias [35,36]. However, variations of surface and lower atmospheric properties appear in the global distribution of at channel 1 over tropical areas resulting in a much higher magnitude than the inter-sensor calibration bias. At channel 10, variations of atmospheric properties are less visible over most of the areas because the variations of upper atmospheric properties are relatively slower and are thus mostly balanced through the 32-day-averaged data at each location. The magnitudes of at channel 10 are mostly close to the observed inter-sensor calibration bias. In contrast with the results without the QC, the global distribution of the QC-passing pixels at the two channels shows a relatively more uniform feature with a magnitude close to the observed inter-sensor calibration bias at corresponding channels for SNPP and NOAA-20 ATMS. It is noticeable that many of the pixels over tropic areas and polar regions at the window and lower sounding channels are removed due to falling in the QC screening, possibly causing unstable assessment of zonal mean biases there due to significantly reduced samples (see Section 5.2 in the following section). Similar performance of the QC scheme with one-sigma rejection is obtained for other channels for ATMS and CrIS and channels for VIIRS (refer to Section 5 for more discussions).
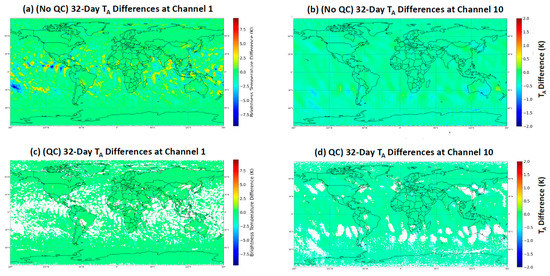
Figure 7.
Global distribution of at channels 1 and 10 for the SNPP and NOAA-20 ATMS TDR (antenna temperature or data with and without the QC scheme applied. The ATMS data are gridded at 1° × 1° resolution covering the period from 1 November 2020, to 2 December 2020. (a) Channel 1 without the QC. (b) Channel 10 without the QC. (c) Channel 1 with the QC. (d) Channel 10 with the QC.
For the OMPS NP, the computations are conducted based on radiance instead of radiance difference, so the threshold of two-sigma is determined based on the statistical features of data sets. Although the distribution of the 32-day datasets slightly deviate from a normal distribution, around 95% of the data can be kept after the two-sigma threshold is applied. Note that the QC with the two-sigma rejection criterion is applied to the individual 16-day accumulated dataset to avoid data over-screening. In this way, the gap of the data loss due to the QC in the first 16-day period can be possibly filled in the second 16-day period. As a result, only a very few percent of pixels are actually removed in the distribution of the 32-day-averaged normalized radiance. The performance of the two-sigma threshold for OMPS NP radiance data will be discussed in the following section.
Next, the above formulae are applied to the SDR (or TDR) data of the four instruments that are monitored by the ICVS to assess the performance of the QC-based 32D-AD formula for calculating inter-sensor calibration radiometric biases.
5. Application to Observations from SNPP and NOAA-20 Instruments within ICVS Framework
The formulae defined in (13) along with (6) to (7) for the gridding data are employed to estimate the globally-averaged inter-sensor calibration radiometric biases for ATMS, CrIS, and VIIRS between SNPP and NOAA-20. The global mean formulae in (14) along with (8) to (9) for the non-gridding datasets are employed to estimate the globally-averaged inter-sensor calibration radiometric biases for OMPS NP between SNPP and NOAA-20. In addition, we will demonstrate the capability of the 32D-AD method in capturing the inter-sensor calibration zonal mean biases at the (upper) sounding channels for ATMS, CrIS, NP, and VIIRS. Particularly, for the NP, the zonal mean feature is used to quantify the impact of solar intrusions on the inter-sensor calibration radiometric biases over the Northern Hemisphere at wavelengths below 300 nm for NOAA-20 NP.
5.1. ATMS
As listed in Table 1, the ATMS sensor consists of 22 channels. Both globally- and zonally-averaged inter-sensor calibration radiometric biases are assessed using the 32D-AD method, as illustrated below.
Firstly, Figure 8 displays the calculated global averages of inter-sensor calibration radiometric biases between SNPP and NOAA-20 ATMS at 22 channels. In the Figure, the 32D-AD calculation is performed by using ATMS data at all satellite view angles ascending and descending, respectively. The inter-sensor calibration biases are within 0.5 K demonstrating that the ATMS TDR data from SNPP and NOAA-20 agree well. The new method also exhibits the stability of 32D-AD computations either using ascending and descending data separately since their magnitudes are approximately identical at 22 channels.

Figure 8.
SNPP and NOAA-20 ATMS inter-sensor calibration radiometric biases at 22 channels using the 32D-AD method, where the data span from 1 November 2020, to 2 December 2020, and 32D-AD datasets are generated in ascending and descending, respectively. The figure also includes the inter-sensor biases at the part of ATMS channels that are calculated using the CRTM-DD and AMSU-A-DD methods. The CRTM-DD represents the double-differences of SNPP and NOAA-20 ATMS Scheme 20. ATMS SDR data via the Metop-C AMSU-A as a transfer. The AMSU-A-DD results are an average of all SNO cases passing the QC with 1 standard deviation between AMSU-A and ATMS from 1 January to 31 December 2020. The CRTM-DD results are an average of the results from 1 to 31 December 2020.
To assess the performance of the 32D-AD results, the results using the AMSU-A-DD and RTM-DD methods are included in Figure 8. Here, the AMSU-A-DD represents the double-differences of SNPP and NOAA-20 ATMS SDR data via the Metop-C AMSU-A as a transfer (see (1)), while the CRTM-DD represents the double-differences of SNPP and NOAA-20 ATMS SDR data via the CRTM as a transfer (see (2)). The AMSU-A-DD results are available in only 15 channels from channel 1 to 16 except for channel 4. In the SNO analysis, a QC threshold is used to discard SNO data that have the deviation from the mean antenna temperature per the selected area (3 pixels × 3 pixels at the center of SNO event) is larger than 3 K [7]. The standard deviation of the AMSU-A-DD datasets per channel is also added to the graph. The CRTM-DD results are an average of the results from 1 December, to 31 December 2020. The calculation details of the CRTM-DD can be found in [38].
Generally, a good agreement is observed among the three methods with some margin. The 32D-AD averages at the 15 AMSU-A-like channels are within the standard deviations of the AMSU-A (SNO)-DD differences, with the best agreements found at the channels from 5 to 13 and channel 15. Small discrepancies among the methods are partially due to uncertainties in each method. For instance, the AMSU-A-DD values at window channels 1, 2, and 15 have a relatively large standard deviation because of the heterogeneous surface/atmospheric conditions within the SNO events for the AMSU-A-DD analysis [7]. This impact of heterogeneous feature still remains even though a separate QC is used in the analysis to discard SNO data that have the deviation from the mean antenna temperature per the selected box is larger than 3 K. In addition, they are affected by the discrepancies in spatial resolution (all channels), polarization (channels 3, 4, and 7), and central frequency (channel 16). In comparison with the averaged CRTM-DD results, a good agreement is also found between the 32D-AD and CRTM-DD methods at the channels from 1–4, 7, 9–15, 17–22, with the absolute difference smaller than 0.1K. The relatively larger discrepancy occurs at channels 5, 6, 8, 9, and 16, with the absolute difference about 0.2 K, and the worst case at channel 16 with a different sign. Channel 16 is a window channel at the center frequency of 88.2 GHz. It is noteworthy that the biases estimated by the AMSU-A-DD and 32D-AD methods are positive and comparable, while the magnitude of the CRTM-DD result is negative. This partially indicates that the CRTM-DD might have a larger uncertainty at this channel. Nonetheless, further analysis is needed in future studies to understand discrepancies among the methods.
Secondly, the zonal means of 32D-AD at the ATMS channels are analyzed to demonstrate the capability of the 32D-AD method in capturing the latitude dependency of inter-sensor biases at upper sounding channels. Figure 9 displays the zonal means of within −80° S to 80° N at 15 channels for the SNPP and NOAA-20 ATMS TDR data in descending node, where the zonal means are computed per 1° and 10° in latitude of running bin separately. The zonal mean per bin of 10° is computed at each running 10° latitude bin, and the number of the latitude in the figure denotes the center of the bin latitudes. This processing is applied to other three sensors in the following analysis. The data above ±80° in latitude are removed due to a relatively lower sample size compared with other latitudes. The window and lower sounding channels from 1 to 4 and 16 to 18 are not included since large diurnal errors still remain with the zonal means. From the zonal means per bin of 1° in latitude in (a), certain fluctuations appear at a few lower sounding channels such as 52.8 GHz, 183.0 ± 1.0 GHz, 183.0 ± 1.8 GHz, and 183.0 ± 3.0 GHz, indicating the impact of residual diurnal errors. To have more statistically robust zonal means, the 10° latitude bin is utilized in (b). Comparing with (a), the SNPP and NOAA-20 ATMS data 32-day difference zonal means per 10° of latitude bin exhibit a relatively more uniform feature in latitude dependence with variation within 0.1 K. Generally, those results demonstrate that the inter-sensor calibration biases for ATMS onboard SNPP and NOAA-20 are less regional or latitude dependent.

Figure 9.
Zonal means of at 15 channels for SNPP and NOAA-20 ATMS TDR data after the QC scheme is applied, where the 15 channels correspond to the channels of 22 ATMS channels by removing 1 to 4 and 16 to 18. In the figure, the data are in the descending node covering the period from 1 November 2020, to 2 December 2020; the zonal bins are calculated per 1° and 10° of running bin, respectively, where the center frequency within the 10° bin is used as the index of latitude per bin. (a) Zonal mean per 1° of latitude bin. (b) Zonal mean per 10° of latitude bin.
5.2. CrIS
The CrIS sensor measures hyper-spectral radiances of 2211 channels in FSR frequencies emitted from the Earth’s surface and its atmosphere, covering three infrared bands from SW, MW, to LW. Similar 32D-AD data analysis is applied to CrIS.
Figure 10 displays the calculated global averages of the inter-sensor calibration radiometric biases at 2211 CrIS channels from 650 to 2545 cm−1. The calculations are given using the CrIS data in ascending (daytime) and descending (nighttime) separately. A good consistency is observed between two data sources, demonstrating that the used QC scheme performs very well. The results also show a very comparable data quality between SNPP and NOAA-20 CrIS SDR since their biases at all channels are smaller than 0.1 K. In addition, the results using the CRTM-DD are also included in the figure. Generally, the magnitudes of the QC-passing 32D-AD results agree with those of the CRTM-DD results with a margin of 0.1 K, with the only exception occurring at the channels near 2385 cm−1. Between the 32D-AD and CRTM-DD results, the mean biases using the CRTM-DD method exhibit a large inter-sensor calibration bias with fluctuations mostly within 0.2 K and the largest error of about 0.9 K around the channel of 2385 cm−1 primarily due to simulation errors. The CRTM simulations are made under clear skies over open oceans, but some uncertainties may still remain in the ECMWF atmospheric and surface analysis data. This is particularly true for the wavenumbers around 2385 cm−1. In addition, some cloud-contaminated data might be mistakenly treated as clear sky pixels, which can result in errors in brightness and temperature simulation. This partially means that the CRTM simulation errors are not entirely cancelled out through the double-difference approach in (2). A similar conclusion is found at other sensors such as ATMS [38], indicating the importance of the CRTM simulation accuracy in the CRTM-DD method.
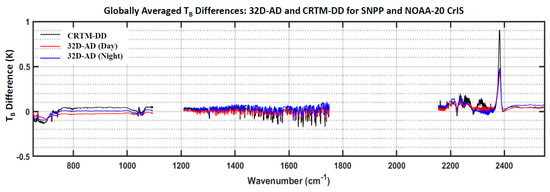
Figure 10.
Comparison of the SNPP and NOAA-20 CrIS inter-sensor calibration radiometric biases at 2211 channels spanning wavenumbers from 650 to 2545 cm−1 using the methods of 32D-AD and RTM-DD, where the data cover the period from 27 September, to 28 October 2019.
The ABI-DD results are further used to validate the SNPP and NOAA-20 CrIS inter-sensor radiometric biases, where the GOES-16 and GOES-17 ABI are used as a transfer, respectively [39]. Figure 11 shows the SNPP and NOAA-20 CrIS inter-sensor calibration radiometric biases at the 9 channels that are overlapped with the ABI broadbands using the two methods, demonstrating a good agreement between the two sensors. Particularly, the ABI-DD and the 32D-AD results agree well with the difference smaller than 0.02 K as the GOES-17 ABI is used as a transfer. Relatively large differences at the ABI channels, from 13 to 14 occur because the SNO cases between CrIS and GOES-16 ABI using the daytime of data occur partially over lands thus experiencing more impact of surface and lower atmospheric inhomogeneities [39].
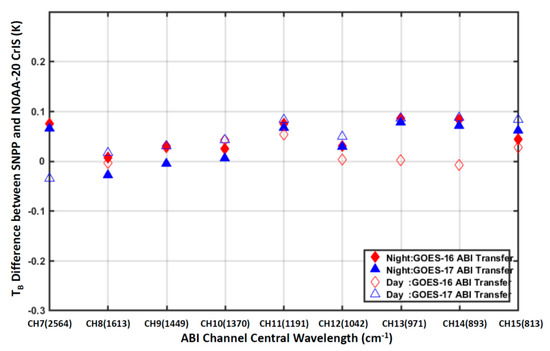
Figure 11.
Comparison of SNPP and NOAA-20 CrIS inter-sensor calibration radiometric biases at 2211 channels spanning wavenumbers from 650 to 2545 cm−1 using the methods of 32D-AD and ABI-DD, where the data cover the period from 27 Scheme 28. October 2019. The results with ‘Night’ and ‘Day’ in the figure correspond to the data in descending and ascending nodes, respectively.
Secondly, the zonal means of the QC-passing 32D-AD data sets from −75° S to 75° N are analyzed to demonstrate the capability of the 32D-AD method in capturing the latitude dependency of inter-sensor biases at upper sounding channels. Most of the channels at wavenumbers from 650 to 720 cm−1 at the LW band, from 1540 to 1700 cm−1 at the MW band, from 2155 to 2375 cm−1 at the SW band, are upper sounding channels. Figure 12 displays the zonal means of from −75° S to 75° N at six upper sounding channels for SNPP and NOAA-20 CrIS using (14-1), where two channels per band are selected and the zonal means are computed per 1° and 10° of bin in latitude, separately. The data beyond the range from −75° S to 75° N are removed in this calculation due to relatively smaller numbers of QC-passing samples, and the center latitude of each 10-degree-bin is used as the index of each bin. Similar to ATMS, the zonal means per 10° latitude bin show a more uniform feature with latitudinal dependence than those using a 1° latitude bin. Variation of up to 0.05 K along with latitude remains in some of the channels due to residual atmospheric variations, but this type of uncertainty is much smaller than those in RTM simulations at the same channel. Those features demonstrate that CrIS data onboard SNPP and NOAA-20 do not exhibit an important regional inter-sensor calibration deviation pattern.
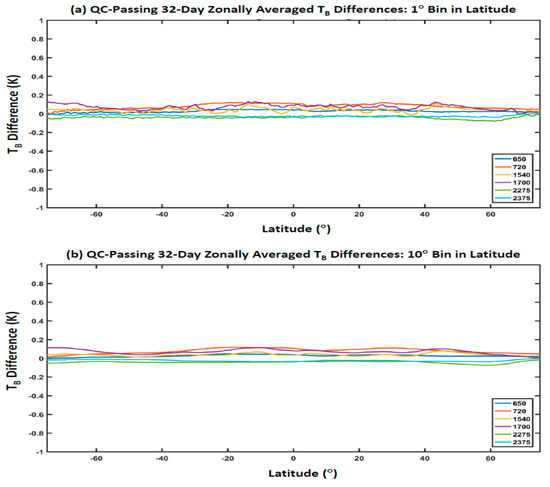
Figure 12.
The zonal mean of from −75° S to 75° N at six upper sounding channels for SNPP and NOAA-20 CrIS, where the data cover the period from 27 September to 28 October 2019, and the selected six channels are 2275 and 2375 cm−1 in the SW band, 1540 and 1700 cm−1 in the MW band, and 650 and 720 cm−1 in the LW band. (a) Zonal mean per bin of 1° latitude. (b) Zonal mean per bin of 10° latitude.
5.3. OMPS NP
To avoid the stripping pattern in the gridded data (see Figure 3), the computation procedure of the 32D-AD global and zonal means for NP (non-gridded data) is different from that for the other sensors (gridded data). As shown in the diagram of Figure A1b in Appendix B, the first step to derive the globally-averaged inter-sensor calibration biases for the data without gridding is to collect all QC-passing radiance data during the 32-day period per channel and sensor. In addition, the QC with the two-sigma rejection criterion is applied to the 16-day accumulated data set to save more QC-passing data. This is because the gap of the 32-day accumulated due to the failure in QC in the first 16-day period can be partially filled in the second 16-day period. As a result, only a very few percent of pixels are actually removed from the 32-day-averaged normalized radiance. Figure 13a,b display the global distributions of the 32-day-averaged normalized radiance (NR) at 297.4 nm for SNPP and NOAA-20 NP, respectively, before the QC was applied. The global distributions of the 32-day-averaged normalized radiance with and without the QC seem very similar for two NPs, so the maps with the QC applied are not shown. The NR distribution for SNPP NP has a very similar feature to that for NOAA-20 NP, demonstrating a good agreement between the two instruments.
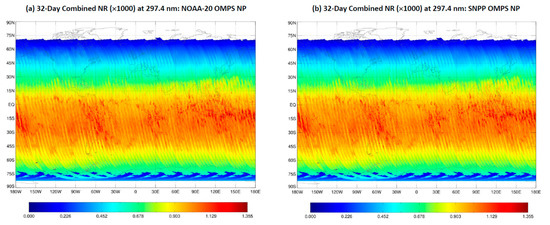
Figure 13.
Global distributions of the 32-day-averaged normalized radiance at 298 nm without QC applied for SNPP and NOAA-20 NP. (a) NOAA-20. (b) SNPP.
After the 32-day observations from each NP instrument are collected, we can compute the global averages of the 32-day observations at all channels and their differences to derive the global averages of inter-sensor calibration radiometric biases. Figure 14a displays the calculated global averages of inter-sensor calibration radiometric biases at wavelengths from 250 to 310 nm. Radiometric biases are expressed by the relative change NOAA-20 NR to SNPP NR (%). The averaged NR differences between NOAA-20 and SNPP NP SDR at wavelengths from 255 to about 296 nm are typically within ±2%, while they are above 2.5% (absolute values) at most channels above 300 nm. The magnitudes of the 32D-AD averages are also well consistent with the double-differences (TomRad-DD) using the TomRad model simulation as a transfer in Figure 14b. Between the two methods, 32D-AD and TomRad-DD, a relatively higher bias (absolute value) occurs in the channels above 300 nm than in other channels. For the 32D-AD method, the feature is partially due to the impact of residual diurnal variations since those channels are lower-sounding channels. For the TomRad-DD method, the simulation accuracy could be degraded if the surface reflectivity is not accurate. The analysis from other sensors also shows that the simulation error is not entirely cancelled in the Rad-DD analysis [38]. Despite the uncertainties in the two methods, our results show that the SNPP and NOAA-20 NP SDR demonstrate a good agreement with margin, because of the high quality of each NP SDR data [26,40,41,42].
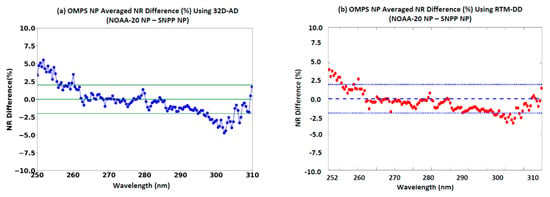
Figure 14.
Comparison of the averaged NP inter-sensor calibration radiometric biases at all NP channels between SNPP and NOAA-20 using the 32D-AD method and TomRad-DD, where the data cover the period from 31 December 2020, to 31 January 2021, over a 32-day period. The dashed lines in the figures represent a ±2% difference. (a) 32D-AD method. (b) TomRad-DD method.
For the zonal means of inter-sensor calibration radiometric biases between two NPs, the 32D-AD zonal mean results above 300 nm are significantly affected by surface variations and lower tropospheric properties (e.g., ozone, aerosols, and clouds). The zonal means of the 32-day observation differences are thus only applied to channels below 300 nm whose weighting heights are in the upper tropospheric or stratosphere [22]. Figure 15a shows the zonal means of the 32D-AD at the following channels using (14–1) to (14-3), 252, 273, 283, 288, 292, 298 nm, which are used in the current NOAA OMPS EDR product retrieval system [42,43]. Due to very limited samples collected during a 32-day period, the zonal mean is computed at each running 10° latitude bin. The magnitudes of the zonally-averaged NR differences (%) over most of the regions are close to those in the global mean of the 32D-AD in Figure 14 for two NPs. However, a large discrepancy between the zonal and global means in the above two figures occurs over the NH middle and high latitude regions. Over NH, it was found that the solar intrusion can cause an anomaly of up to 4% in the NOAA-20 NP radiance at the wavelengths below 300 nm as the solar zenith angles are in the range of 58° to 88° [12]. To confirm this conclusion, (9–2) above is applied to estimate the zonal mean of 32-day-averaged NR for SNPP and NOAA-20 OMPS NPs, respectively. Figure 15b shows the zonal mean of the 32-day accumulated NR datasets at 10 degrees in latitude at the channel of 273 nm for two NPs. Magnitudes of the NOAA-20 NP NRs are generally higher than those of SNPP NR as the latitude is higher than 40 degrees, which explains the anomalous features in the zonal mean in (a). Currently, a solar intrusion correction algorithm was initialized by the NASA OMPS group [12] and is revised to apply to the NOAA OMPS NP SDR operational processing data stream. It is expected that the solar intrusion impact will be removed by re-processing all historical NOAA-20 OMPS SDR data, thus a better agreement between SNPP and NOAA-20 OMPS NR can be seen.
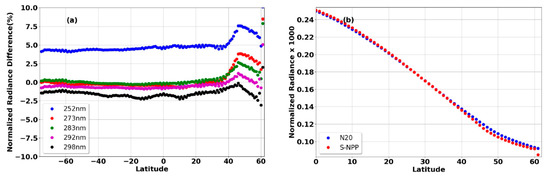
Figure 15.
Zonal means of the 32D-AD for SNPP and NOAA-20 OMPS NP NR data at the channels, 252, 273, 283, 288, 292, 298 nm, which are computed at each 10° latitude running bin. In the calculations, the data beyond the SZA of 75° are removed due to a much smaller sample size. (a) Zonal means of 32D-AD over NH between SNPP and NOAA-20 NPs at the channels, 252, 273, 283, 288, 292, 298 nm. (b) The zonal mean of NP NR at 273 nm over NH for SNPP and NOAA-20 individually.
5.4. VIIRS
For VIIRS, we focused on the 16 M-bands and conducted a similar analysis as for other sensors. In the analysis, the 32D-AD-averaged VIIRS calibration radiometric biases at 16 M-bands are computed using the global average of . For the 11 RSBs from M1 to M11, the reflectance is used, and corresponding inter-sensor bias is introduced using the relative reflectivity difference (%). For the 5 TEBs from M12 to M16, the brightness temperature is used, and corresponding inter-sensor bias is given using the brightness temperature (TB) difference (K). Their globally-averaged inter-sensor calibration biases are plotted in Figure 16a,b, respectively. For comparisons with the ABI-DD and CRTM-DD methods, the ABI-DD results at bands 3, 5, 7, 9-11 are added in Figure 16a and the CRTM-DD result at bands 12 to 16 are in Figure 16b. In addition, for the RSBs, only the daytime data is used, while for the TSBs, the data are analyzed in both daytime and nighttime, separately. The CRTM-DD calculations are made using Equation (2) in Section 2; for the ABI-DD, both GOES-16 and GOES-17 ABIs are used as a transfer for the double-differences of SNPP and NOAA-20 VIIRS by using Equation (1) above.
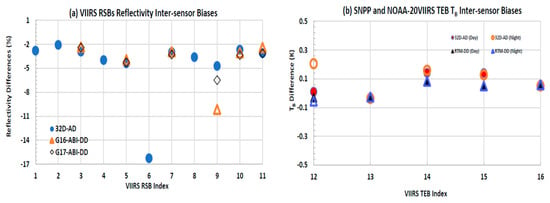
Figure 16.
Comparison of the SNPP and NOAA-20 VIIRS inter-sensor calibration radiometric biases at M-bands using the methods of 32D-AD, ABI-DD, or CRTM-DD. (a) Reflectivity difference (%) at 11 RSB bands using the 32D-AD and ABI-DD for the daytime data. The data for the 32D-AD calculations cover the period from 18 June 2020, to 24 April 2021, and the data for the ABI-DD calculations cover the period from 1 January 2020, to 13 April 2021, to collect sufficient cases. (b) TB differences at 5 TEBs using the 32D-AD and (C)RTM-DD for daytime and nighttime data, separately.
As shown in Figure 16a, confirmed using three different methods, the VIIRS SDR data at all RSBs except for Band 6 (a band with an early saturation issue) shows a very good agreement in quality between SNPP and NOAA-20. The inter-sensor reflectivity differences at the 10 RSBs (band 6 is excluded) are typically within 4%, with the deviation smaller than 0.2% of the reflectance among the three methods. At Band 9, the thin cirrus band, the inter-sensor reflectivity difference is about 4.7% in the 32D-AD method, which is close to 6.4% using the G16-ABI-DD method. In contrast, a bias of 10.1% is found in the G17-ABI-DD. The SNO events between VIIRS and GOES-16 occur mostly over lands, while the SNO events between VIIRS and GOES-17 exist typically over oceans, which is the same as the SNO events between CrIS and GOES-16/17 ABI [39]. Particularly, band 9 is sensitive to heterogeneity with thin cirrus scenes, so the G17-ABI-DD results at this band that are over vigorous thin cirrus regions can be inaccurate over heterogeneous scenes due to limited SNO events. The 32D-AD method shows its advantage over the SNO-DD method due to its large sample size of 32D-AD datasets, where diurnal variations due to scene heterogeneity are significantly decreased. The 32D-AD at the M9 band is more reasonable than the ABI-DD method in estimating the globally-averaged inter-sensor calibration bias. In the RSBs, band 6 is an outlier in the calibration where a large difference of about −16% occurs between two VIIRS sensors. This large discrepancy is related to the saturation rollover issue of this band in the NOAA-20 because the SNPP set of thresholds are used for NOAA-20, while NOAA-20 and SNPP bear RSR differences [44]. For Figure 16b, the brightness temperature differences at the TEBs are within 0.2K. Importantly, for all the TEBs except band 12, the two methods, 32D-AD and CRTM-DD, produce very consistent results, with the deviations smaller than 0.05 K. At band 12, the deviation is about 0.2 K between the 32D-AD and the CRTM-DD for the nighttime data where large CRTM data uncertainty was found. Overall, using the three methods, those results demonstrate that, first, the quality of SNPP and NOAA-20 VIIRS SDR data at 16 M-bands agrees well, which is consistent with the findings in [45,46], and secondly, the 32D-AD method can achieve comparable assessment results as the other two DD methods.
Furthermore, the zonal means of at RSBs are calculated only at bands from 8 to 11 and 5 TEBs because diurnal variations are hardly mitigated from the zonal means at other RSBs. Even for the above VIIRS bands, the zonal mean analysis is also limited to the latitude range below ±65° in latitude because the SZA discrepancy between two VIIRS is larger over high latitudes. Similarly, two sizes of zonal bins are applied to the zonal mean calculation for comparison: one-degree-bin and ten-degree-bin in latitude. The conclusions are similar to those from the other sensors: the ten-degree-bin can produce more uniform features at different latitudes than the one-degree-bin method. This is understandable because the diurnal errors can be better balanced due to larger samples. Even so, some residual diurnal errors remain at the selected bands. For the 4 RSBs, the variation of reflectance bias along with latitude is within 0.001, observing Figure 17a,b, showing a uniform pattern with latitude. However, for the 5 TEBs, which are affected by heterogeneity in atmospheric and/or surface scenes, the variation along with the latitude can exceed 0.1 K. The pattern with the latitude is sometimes opposite in the zonal means between ascending (daytime) and descending (nighttime), observing Figure 17c,d. This instability, which is caused primarily by residual diurnal variations, implies that the current one-sigma-rejection threshold can be further improved over some regions. If the residual diurnal variation in the 32D-AD zonal means can be properly assessed, the inter-sensor biases at the 4 RSBs and 5 TEBs onboard SNPP and NOAA-20 VIIRS would be even less latitude-dependent.
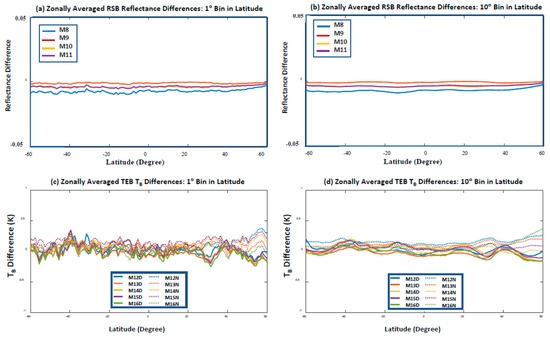
Figure 17.
Zonal means of the 32D-AD at the 4 RSBs from M8 to M11 and 5 TEBs from M12 to M16, which are computed at each 1° latitude bin and the 10° running latitude bin, respectively andthe number on the X-axis is the center of the bin. In (a,b), the data are day time data, while in (c,d), ‘D’ and ‘N’ denote the data during the day time and nighttime respectively. (a) One-degree-bin zonal means for 4 RSBs, (b) ten-degree-bin zonal mean for 4 RSBs, (c) one-degree-bin zonal means for 5 TEBs, and (d) ten-degree-bin zonal mean for 5 TEBs.
5.5. Some Discussions about 32D-AD Method
The above analysis is conducted using two-orbit repeat cycles to ensure a comparable sample size of observations per location and sufficient sample size of datasets for global and zonal means between the same instrument onboard the SNPP and NOAA-20 satellite platforms. This selection is made primarily to ensure the stability of the zonally-averaged inter-sensor calibration radiometric bias assessment although one orbit repeat cycle of data sets should be sufficient for upper sounding channels.
Figure 18a,b display the time series of the globally-averaged brightness temperature differences at 670 and 1450 cm−1 between SNPP and NOAA-20 CrIS, respectively, which are calculated using the datasets from one to 32-days with an one-sigma threshold applied to the datasets per each time period. The calculation procedure for each dataset is the same as that of the 32D-AD except for different time lengths of datasets. According to the results in the figures, the magnitudes of the globally-averaged brightness temperature differences at the two bands fluctuate largely with time when the data set length is less than 10 days. This is understandable since the observations from CrIS in-flying the two satellites are not consistent in observation times and locations over global coverage, thus having significant diurnal differences. This conclusion is applicable to the daily global mean (i.e., one day of the data set) where the diurnal variation actually dominates the globally-averaged brightness temperature differences. This explains why the daily global mean method is usually invalid for inter-sensor radiance comparison. In comparison with the results at 16 days (one orbit repeat cycle), the results at 32 days (two cycles) are very comparable (the differences are smaller than 0.05 K). This implies that an one orbit repeat cycle should be good enough for globally-averaged inter-sensor calibration bias estimates for most of the sensors. A similar conclusion is applied to the other three sensors. Figure 19 shows the time series of the globally-averaged normalized radiance differences at five NP channels between SNPP and NOAA-20. Although the cross-sensor normalized radiance differences are not stable in the first few days, they become typically stable after the first orbit repeating cycle. The magnitudes of the differences at one repeating cycle are also similar to those at two repeating cycles.
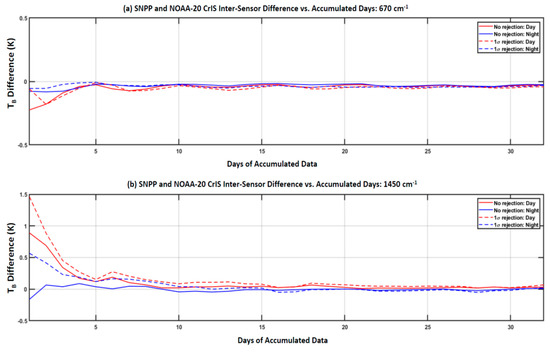
Figure 18.
Time series of the globally-averaged brightness temperature differences at two CrIS channels of 670 and 1450 cm−1 between SNPP and NOAA-20 CrIS, which are calculated using the datasets from one to 32 days with the one-sigma threshold applied to the datasets per each time period. (a) 670 cm−1. (b) 1450 cm−1.

Figure 19.
Time series of the globally-averaged brightness temperature differences at five OMPS NP channels between SNPP and NOAA-20, which are calculated using the datasets from one to 32 days with a two-sigma threshold applied to the data.
The length of one orbit repeat cycle works well for the global mean of cross-sensor calibration bias analysis, but the analysis in the above sub-section has demonstrated that a sufficient sample of data set per bin in latitude is a key for the accuracy of zonally averaged radiance difference between two sensors. Although a QC scheme is utilized to reduce diurnal variations in the analysis, residual diurnal variations still remain in the QC-passing data sets for zonal mean estimates especially at the window and lower sounding channels for ATMS, CrIS, and VIIRS, thus causing unexpected latitude-dependent inter-sensor biases there (see Figure 9, Figure 12 and Figure 17 above). This impact is more critical for OMPS NP at lower-sounding channels (the figure is not shown in this study). In principle, the longer the time series of the datasets, the smaller the diurnal errors. However, the quality of Earth-scene radiance data in either TDR or SDR can slightly change with variational instrument performance with time. For example, instrument Noise Equivalent Differential Temperature (NEDT) and calibration gain are sensitive to time-dependent instrument temperatures, which potentially causes instability of sensor calibration biases [47,48]. The average of a too long time series of datasets might smooth the magnitudes of inter-sensor calibration biases. In addition, timely information of inter-sensor calibration performance is necessary for the analysis related to new POES satellites such as JPSS-2 in early-orbit-verification. Therefore, the trade-off data temporal length is to cover two cycles or 32-days for SNPP and NOAA-20 instruments to have a balance between reducing the impact of diurnal differences and saving basic features of estimates of globally- and zonally-averaged inter-sensor calibration radiometric biases.
In summary, the 32D-AD formulae have been applied to the four instruments to characterize SNPP and NOAA-20 inter-sensor calibration biases at all channels for global means or at most of the sounding channels for zonal means. The globally-averaged inter-sensor biases using the 32D-AD method agree well with those using the 3rdSensor-DD and RTM-DD for the overlapped channels with small margins. Besides, the new method exhibits its advantages over the two existing DD methods in characterizing globally-averaged inter-sensor calibration biases at all channels. It also shows its capability in estimating the zonal mean of inter-sensor calibration biases at upper-sounding channels, which is very helpful to capture regional sensor calibration anomalies. Meanwhile, certain residual diurnal errors still remain in the zonal means over some regions for lower-sounding channels. Thus, improvements in the QC scheme are needed in future studies to further minimize the impact of diurnal variation sources in capturing latitude-dependent inter-sensor calibration radiometric biases.
6. Summary and Conclusions
This study presents a new statistical method based on the 32-day-averaged difference (32D-AD) of radiometric measurements to assess globally- and zonally-averaged inter-sensor calibration radiometric biases between SNPP and NOAA-20 instruments within the ICVS framework. The impact of two types of diurnal errors is also identified in the original 32D-AD datasets. The first type of diurnal error, which occurs for all instruments, is the radiance discrepancy due to the SNPP and NOAA-20 orbit time difference. This impact is usually non-negligible for the window and lower-sounding channels over regions in the presence of rapidly changing atmospheric and surface conditions over time. The second type of diurnal error is the radiance discrepancy primarily due to the SZA difference for solar bands in OMPS and VIIRS. Nonetheless, our analysis reveals that their impacts can be significantly mitigated by using a proper QC threshold scheme that effectively removes the outliers apparently attributable to the diurnal errors. The calculation formulae of the globally- and zonally-averaged inter-sensor calibration biases are thus established using the QC-passing 32D-AD datasets.
Furthermore, within the ICVS framework, the new formulae in the 32D-AD method are applied to four instruments: ATMS, CrIS, OMPS NP, and VIIRS that are flying on the SNPP and NOAA-20 satellites to calculate the globally-averaged inter-sensor calibration radiometric biases at all channels and the zonally-averaged biases typically found at upper sounding channels. Small inter-sensor calibration radiometric biases are observed in the global mean at all channels for those instruments, demonstrating a consistent SDR data quality between SNPP and NOAA-20, consistent with the conclusions from the existing studies [26,35,38,41,46]. For the overlapped channels, the results using the new method typically agree well with those using either the 3rdSensor-DD or RTM-DD methods, with the better agreement with the 3rdSensor-DD method, demonstrating the 32D-AD method performs well for the four instruments. In addition, the 32D-AD method also provides relatively accurate latitude-dependent features of inter-sensor calibration biases at upper sounding channels by calculating the zonal mean of the 32D-AD data. Furthermore, this study assessed the impact of solar intrusion on the NOAA-20 OMPS NP SDR data over the Northern Hemisphere by analyzing the zonal mean feature of 32D-AD between SNPP and NOAA-20 NP SDR data at a few channels below 300 nm. The identified solar intrusions on the NOAA-20 NP radiance are up to 4% depending on the channel and SZA, which is consistent with the findings in [12].
Therefore, the 32D-AD method offers a supplementary approach to the existing DD methods in estimating both globally- and zonally-averaged inter-sensor calibration biases. Currently, the lifetime assessment for the SNPP and NOAA-20 instruments’ global cross-sensor 32-day-averaged differences is monitored within the ICVS framework. The method will also be applied to the inter-sensor calibration radiometric biases associated with the upcoming JPSS-2 satellite. The findings from this study are thus expected to be critically important for the calibration/validation of current and future JPSS TDR/SDR data and the construction of long-term climate data records (CDR) for science exploration. However, it is also worthwhile noting that the zonally-averaged radiance differences using the 32D-AD formulas with the current QC scheme are erroneous over certain regions for the window and lower-sounding channels. Further analysis is needed to improve the QC scheme to make the zonal mean estimation work for all channels, which is important for the latitude dependency analysis of channel calibration performance. In addition, the formulae are established based on SNPP and NOAA-20 instruments, which have 16-day orbit repeating cycles. Some revisions such as the length of days due to dissimilar orbit repeating cycle periods are needed before the formulas in this study are applied to other POES satellite instruments. For example, the length of the orbit repeating cycle varies with the satellite platform, e.g., 29-day for Metop, 11-day for NOAA-18 satellite, etc. The QC scheme should also be updated to reflect the potential impacts of much longer or shorter data lengths. With its potential to be applicable to more sensors by wider user communities, the 32D-AD method, as a complementary method to the existing inter-sensor comparison approaches, can provide valuable and useful information for the inter-sensor calibration radiometric biases assessment.
Author Contributions
Conceptualization, B.Y., M.G., and L.Z.; methodology, B.Y., M.G., X.J., D.L., L.Z., C.P., and Q.L.; software, X.J., D.L., J.H., W.P., N.S., and C.P.; validation, B.Y., X.J., D.L., J.H., W.P., N.S., F.I.-S. and K.Z.; formal analysis, B.Y., X.J., D.L., J.H., and W.P.; investigation, X.J., D.L., J.H., W.P., and C.P.; resources, L.Z.; data curation, X.J., D.L., J.H., W.P., and N.S.; writing—original draft preparation, B.Y.; writing—review and editing, B.Y., J.H., D.L., and N.S.; visualization, B.Y., X.J., D.L., J.H., and W.P.; supervision, B.Y.; project administration, B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research is sponsored by the JPSS funding resource.
Data Availability Statement
All SDR/TDR datasets that support the findings of this study are openly available in NOAA CLASS at https://www.avl.class.noaa.gov/saa/products/catSearch, accessed on 5 April 2021.
Acknowledgments
The authors would like to thank the JPSS Program for supporting the work. The manuscript contents are solely the opinions of the authors and do not constitute a statement of policy, decision, or position on behalf of NOAA or the U. S. Government. We thank Changyong Cao and two anonymous reviewers within the STAR for providing many valuable comments in developing the algorithm; thanks to Kevin Garrett for providing the datasets of the US76 Standard Atmosphere and Tropical Standard Atmosphere profiles and corresponding reference. In addition, we thank Xingpin Liu for useful discussions in the beginning stages of this work. Lastly, the authors thank two anonymous reviewers from the journal review board for providing very valuable comments.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Detailed Descriptions of Variables in the 32D-AD Method

Table A1.
Explanations of major variables used in the 32D-AD method throughout the manuscript. In the table, each variable is defined per channel, but the channel index is omitted; ‘data’ represent either radiance or brightness temperature in SDR data or antenna temperature in TDR data for a given channel and satellite instrument.
Table A1.
Explanations of major variables used in the 32D-AD method throughout the manuscript. In the table, each variable is defined per channel, but the channel index is omitted; ‘data’ represent either radiance or brightness temperature in SDR data or antenna temperature in TDR data for a given channel and satellite instrument.
| 32-day-averaged differences (32D-AD) of gridded data at location for the same type of instruments between NOAA-20 and SNPP, referring to the individual 32D-AD at location | |
| Zonal mean difference of the 32-day gridded data at the ith latitude (range) for the same type of instruments between NOAA-20 and SNPP, referring to the zonal mean of 32D-AD | |
| Same as except for the QC-passing gridded data | |
| Same as except for the data without gridding | |
| Global mean difference of 32-day gridded data for the same type of instruments between NOAA-20 and SNPP, referring to the global mean of 32D-AD | |
| Same as except for the QC-passing gridded data | |
| Same as except for the data without gridding | |
| Same as except for the QC-passing data | |
| Global mean of the 32-day data without gridding per satellite, . | |
| Zonal mean of the 32-day data (no gridding) at a given latitude (range) per satellite | |
| Average of the 32-day gridded data at location per satellite | |
| lth data at the location among the 32-day gridded data per satellite | |
| lth data of accumulated 32-day datasets without gridding per satellite | |
| Sample size of the 32-day data without gridding per satellite | |
| Sample size of the 32-day QC-passing data without gridding per satellite | |
| Sample size of the 32-day data without gridding at the ith latitude (range) per satellite | |
| Same as except for the QC-passing data per satellite | |
| Sample size of the 32-day gridded data at the location by NOAA-20 instrument | |
| Same as except for the QC-passing gridded data per satellite | |
| Same as except for SNPP instrument | |
| and | is determined by the grid resolution of the data in latitude direction, e.g., for 1° × 1° gridded data; is the same as except for QC-passing data |
| and | is determined by the grid resolution of the data in longitude direction, e.g., for 1° × 1° gridded data; and is the same as except for QC-passing data |
Appendix B. 32D-AD Formulae for Estimating Inter-Sensor Calibration Radiometric Biases
Due to the non-negligible impact of the above-mentioned non-sensor error sources over some regions at some channels, a QC scheme is developed to remove the majority of the outliers within the 32D-AD datasets that are vitally affected by non-sensor errors. The inter-sensor calibration radiometric biases between the same instrument from two different satellites are thus derived from the 32D-AD data sets passing the QC scheme, i.e.,
where denotes the inter-sensor calibration radiometric bias at different levels, while the 32D-AD datasets at different levels; ‘’ or ‘’ defining the level of the 32D-AD variables at either the global mean or zonal mean of ; the indices of the location and channel are omitted in all variables. The case of ‘’ is only applicable for the part of global distribution particularly at window channels, so it is not generally included in (Figure A1).
Figure A1a,b exemplify the diagram of calculating both and for gridding SDR data and and for non-gridding data, respectively. The QC scheme is here produced based on the one-sigma-rejection criterion for the radiance difference in the gridding 32D-AD datasets and two-sigma-rejection criterion for the radiance in the non-gridding 32-day datasets, where sigma (σ) denotes the standard deviation of the 32D-AD datasets. The pixels falling in the QC are assumed to be outliers in accumulated 32D-AD or 32-day datasets due to the impact from diurnal error sources.
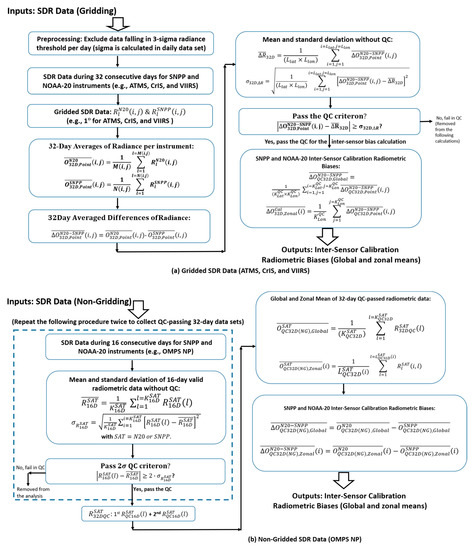
Figure A1.
Diagram of calculating both and for gridding data and and for non-gridding data, respectively. The instruments in (a) include the ATMS, CrIS, and VIIRS, while the instrument in (b) is the OMPS NP in this study. In the diagrams, the sigma () represents the standard deviation for the defined data sets; the subscript ‘ is added to the variables to distinguish from the computations without the QC application; the equations are given in radiance but they are applicable for antenna temperature or brightness temperature. Explanations of other variables are referred to Table A1 in Appendix A. (a) Gridding data. (b) Non-gridding data.
References
- Yan, B.; Sun, N.; Jin, X.; Huang, J.; Liang, D.; Porter, W.; Liang, X.; Kireev, S.; Zhou, L.; Goldberg, M. Exploring New Developments of the STAR Integrated Calibration/Validation System; American Geophysical Union, Fall Meeting: Washington, DC, USA, 2018; Available online: https://ui.adsabs.harvard.edu/abs/2018AGUFM.A23A03B/abstract (accessed on 19 July 2021).
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the intersatellite calibration of radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Cao, C.; Weng, F.; Goldberg, M.; Wu, X.; Xu, H.; Ciren, P. Intersatellite calibration of polar-orbiting radiometers using the SNO/SCO method. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005; p. 4. [Google Scholar] [CrossRef]
- Iacovazzi, R.; Cao, C. Reducing Uncertainties of SNO-Estimated Intersatellite AMSU-A Brightness Temperature Biases for Surface-Sensitive Channels. J. Atmos. Ocean. Technol. 2007, 25, 1048–1054. [Google Scholar] [CrossRef]
- Yan, B.; Weng, F. Intercalibration Between Special Sensor Microwave Imager/Sounder and Special Sensor Microwave Imager. IEEE Trans. Geosci. Remote. Sens. 2008, 46, 984–995. [Google Scholar]
- Yang, S.; Weng, F.; Yan, B.; Sun, N.; Goldberg, M. Special Sensor Microwave Imager (SSM/I) Intersensor Calibration Using a Simultaneous Conical Overpass Technique. J. Appl. Meteor. Climatol. 2011, 50, 77–95. [Google Scholar] [CrossRef]
- Yan, B.; Chen, J. Post-launch Performance Assessment of Metop-C Advanced Microwave Sounding Unit-A (AMSU-A) Instrument Noise and Antenna Temperature Data. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Yan, B.; Chen, J.; Zou, C.-Z.; Ahmad, K.; Qian, H.; Garrett, K.; Zhu, T.; Han, D.; Green, J. Calibration and Validation of Antenna and Brightness Temperatures from Metop-C Advanced Microwave Sounding Unit-A (AMSU-A). Remote Sens. 2020, 12, 2978. [Google Scholar] [CrossRef]
- Uprety, S.; Cao, C.; Shao, X. Geo-Leo intercalibration to evaluate the radiometric performance of NOAA-20 VIIRS and GOES-16 ABI. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 9 September 2019. [Google Scholar] [CrossRef]
- Jin, X.; Yan, B.; Sun, N. Advancing CrIS and ABI Inter-Comparison Applicable for JSTAR Integrated Calibration/Validation System; AGU Fall meeting: Washington, DC, USA, 2019. [Google Scholar]
- Yan, B.; Weng, F. Effects of Microwave Desert Surface Emissivity on AMSU-A Data Assimilation. IEEE Trans. Geosci. Remote. Sens. 2011, 49, 1263–1276. [Google Scholar] [CrossRef]
- Jaross, G.; Huang, L.-K. Update on the NOAA-20 OMPS NP solar intrusion anomaly. In Proceedings of the NASA Ozone Processing Team (OPT) meeting, Greenbelt, MD, USA, 8 August 2020. [Google Scholar]
- Ramachandran, S.; Keegstra, P.; Vogel, R.L.; Soracco, M.; Hughes, K. Ocean color products validation at NOAA CoastWatch. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1182–1185. [Google Scholar] [CrossRef] [Green Version]
- Sungmin, O.; Kirstetter, P.-E. Evaluation of diurnal variation of GPM IMERG derived summer precipitation over the contiguous US using MRMS data. Q. J. R. Meteorol. Soc. 2018, 144, 270–281. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.-Z.; Wang, W. 2009: Diurnal drift correction in the NESDIS/STAR MSU/AMSU atmospheric temperature climate data record. In Proceedings of the SPIE Optical Engineering + Applications, San Diego, CA, USA, 12 August 2009; Volume 7456. [Google Scholar]
- Po-Chedley, S.; Thorsen, T.J.; Fu, Q. Removing Diurnal Cycle Contamination in Satellite-Derived Tropospheric Temperatures: Understanding Tropical Tropospheric Trend Discrepancies. J. Clim. 2015, 28, 2274–2290. [Google Scholar] [CrossRef]
- Yan, B.; Goldberg, M.; Jin, X.; Huang, J.; Sun, N.; Liang, D.; Porter, W.; Zhou, L. SNPP and NOAA-20 Global Inter-Sensor Bias Assessments within ICVS Framework Using 32-Day Averaged Difference Method. In Proceedings of the 2020 IEEE International Geoscience and Remote Sensing Symposium, Virtual Symposium, Waikoloa, HI, USA, 26 September 2020. [Google Scholar]
- Huang, J.; Yan, B.; Sun, N.; Liang, D.; Porter, W.; Liang, X.; Jin, X.; Atkins, T.; Zhou, L.; Goldberg, M. JPSS/STAR ICVS Severe Event Watch System Development and Applications; American Geophysical Union, Fall Meeting: Washington, DC, USA, 2018; Available online: https://ui.adsabs.harvard.edu/abs/2018AGUFMIN33F0898H/abstract (accessed on 21 February 2021).
- Yan, B.; Liang, D.; Porter, W.; Huang, J.; Sun, N.; Zhou, L.; Zhu, T.; Goldberg, M.; Zhang, D.-L.; Liu, Q. Gap filling of advanced technology microwave sounder data as applied to hurricane warm core animations. Earth Space Sci. 2020, 7, e2019EA000961. [Google Scholar] [CrossRef]
- Joint Polar Satellite System (JPSS) Advanced Technology Microwave Sounder (ATMS) SDR Radiometric Calibration Algorithm Theoretical Basic Document (ATBD). 2011. Available online: https://www.star.nesdis.noaa.gov/jpss/documents/ATBD/D0001-M01-S01-001_JPSS_ATBD_ATMS-SDR_A.pdf (accessed on 30 March 2021).
- Rev, C. (Ed.) Joint Polar Satellite System (JPSS) Cross Track Infrared Sounder (CrIS) Sensor Data Records (SDR) Algorithm Theoretical Basis Document (ATBD); Code 474, 474-00032; Goddard Space Flight Center: Greenbelt, Maryland, 2014.
- Joint Polar Satellite System (JPSS) OMPS Nadir Profile Ozone Algorithm Theoretical Basis Document; JPSS Ground Project Code 474-00026; Goddard Space Flight Center: Greenbelt, Maryland, 2014.
- NOAA Technical Report NESDIS 142, Visible Infrared Imaging Radiometer Suite (VIIRS) Sensor Data Record (SDR) User’s Guide, Version 1.3, NOAA National Environmental Satellite, Data, and Information Service, 2017. Available online: https://ncc.nesdis.noaa.gov/documents/documentation/viirs-users-guide-tech-report-142a-v1.3.pdf (accessed on 24 March 2021).
- Yan, B.; Ahmad, K. Derivation and Validation of Sensor Brightness Temperatures for Advanced Microwave Sounding Unit-A Instruments. IEEE Trans. Geosci. Remote. Sens. 2020, 99, 1–11. [Google Scholar] [CrossRef]
- Weng, F.; Zou, X.; Sun, N.; Yang, H.; Tian, M.; Blackwell, W.J.; Wang, X.; Lin, L.; Anderson, K. Calibration of Suomi national polar-orbiting partnership advanced technology microwave sounder. J. Geophys. Res. Atmos. 2013, 118, 11187–11200. [Google Scholar] [CrossRef]
- Yan, B.; Pan, C.; Beck, T.; Xiong, X.; Liang, D.; Chen, J.; Jaross, G.; Flynn, L. NOAA-20 OMPS NP SDR Report for Validated Maturity Review. NOAA JPSS Science Review. 2020. Available online: https://www.star.nesdis.noaa.gov/jpss/documents/AMM/N20/OMPS_NP_SDR_Validated.pdf (accessed on 30 March 2021).
- Han, Y.; van Delst, P.; Liu, Q.; Weng, F.; Yan, B.; Treadon, R.; Derber, J. JCSDA Community Radiative Transfer Model (CRTM)-Version 1. NOAA Tech. Rep. NESDIS 2006, 122, 1–33. [Google Scholar]
- Chen, Y.; Weng, F.; Han, Y.; Liu, Q. Validation of the Community Radiative Transfer Model by using CloudSat data. J. Geophys. Res. Atmos. 2008, 113, D8. [Google Scholar] [CrossRef]
- Ding, S.; Yang, P.; Weng, F.; Liu, Q.; Han, Y.; van Delst, P.; Li, J.; Baum, B. Validation of the community radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1050–1064. [Google Scholar] [CrossRef]
- Carminat, F.; Migliorini1, S.; Ingleby, B.; Bell, W.; Lawrence, H.; Newman, S.; Hocking, J.; Smith, A. Using reference radiosondes to characterize NWP model uncertainty for improved satellite calibration and validation. Atmos. Meas. Tech. 2019, 12, 83–106. [Google Scholar] [CrossRef] [Green Version]
- Eck, F.; Bhartia, P.K.; Kerr, J.B. Satellite estimation of spectral UVB irradiance using TOMS derived total ozone and UV reflectivity. Geophys. Res. Lett. 1995, 22, 611–614. [Google Scholar] [CrossRef]
- Frank, W.; Schabel, M. Effects of orbital decay on satellite-derived lower-tropospheric temperature trends. Nature 1998, 394, 661–664. [Google Scholar]
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 12734–12748. [Google Scholar] [CrossRef]
- Chen, Y.; Han, Y.; Weng, F. Characterization of long-term stability of Suomi NPP Cross-Track Infrared Sounder spectral calibration. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 1147–1159. [Google Scholar] [CrossRef]
- Sanchez, F.; Tobin, D.; Strow, L.; Scott, D.; Mooney, D.; Johnson, D.; Suwinski, L.; Predina, J.; Bolen, D.; Guenther, B.; et al. NOAA-20 CrIS SDR Report for Validated Maturity Review. NOAA JPSS Science Review. 2018. Available online: https://www.star.nesdis.noaa.gov/jpss/documents/AMM/N20/CrIS_SDR_Validated.pdf (accessed on 17 March 2021).
- Sanchez, F.; Strow, L.; Tobin, D.; Scott, D.; Chen, Y.; Tremblay, D.; Knuteson, R.; Johnson, D.; Buttles, C.; Suwinski, L.; et al. SNPP CrIS Instrument: Successfully Restored after Midwave Infrared Band Anomaly, Submitted to the ITGRS. In Proceedings of the 22nd International TOVS Study Conference, Saint-Sauveur, QC, Canada, 31 October–6 November 2019. [Google Scholar]
- McClatchey, R.A.; Fenn, R.W.; Selby, J.E.A.; Volz, F.E.; Garing, J.S. Optical Properties of the Atmosphere; Research Paper 411, AFCRL-72-0497; Defense Technical Information Center: Fort Belvoir, VA, USA, 1972; p. 108.
- Sun, N.; Yan, B.; Liu, Q. Evaluation of Advanced Technology Microwave Sounder (ATMS) Science Data Long-Term Trending through Intersatellite Comparisons. In Proceedings of the 101st AMS Virtual Conference, Online, 10–15 January 2021. [Google Scholar]
- Jin, X.; Yan, B.; Sun, N. Improving SNPP and NOAA-20 CrIS LTM Inter-sensor Radiometric Bias Assessment by Using Interpolating ABI Measurements as Transfer. In Proceedings of the 101st AMS Virtual Conference, Online, 10–15 January 2021. [Google Scholar]
- Pan, C.; Weng, F.; Flynn, L. Spectral performance and calibration of the Suomi NPP OMPS Nadir Profiler sensor. Earth Space Sci. 2017, 4, 737–745. [Google Scholar] [CrossRef]
- Pan., C.; Cao, C.; Flynn, L.; Xiong, X.; Beach, E.; Zhou, L. Performance of OMPS Nadir Profilers’ Sensor Data Records. IEEE Trans. Geosci. Remote. Sens. 2020. [Google Scholar] [CrossRef]
- Flynn, L.; Long, C.; Wu, X.; Evans, R.; Beck, C.T.; Petropavlovskikh, I.; McConville, G.; Yu, W.; Zhang, Z.; Niu, J.; et al. Performance of the Ozone Mapping and Profiler Suite (OMPS) products. J. Geophys. Res. Atmos. 2014, 119, 6181–6195. [Google Scholar] [CrossRef]
- Niu, J.; Flynn, L.E.; Beck, T.; Zhang, Z.; Beach, E. Evaluation and Improvement of the Near-Real-Time Linear Fit SO2; Retrievals from Suomi NPP Ozone Mapping and Profiler Suite. IEEE Trans. Geosci. Remote. Sens. 2021. [Google Scholar] [CrossRef]
- Wang, W.; Cao, C.; Blonski, S.; Gu, Y.; Zhang, B. An Improved Method for VIIRS Radiance Limit Verification and Saturation Rollover Flagging. IEEE Trans. Geosci. Remote. Sens. 2021, in press. [Google Scholar] [CrossRef]
- Cao, C.; Deluccia, F.; Xiong, J.; Weng, F. NPP VIIRS SDR Postlaunch Calibration/Validation. Available online: https://ncc.nesdis.noaa.gov/documents/presentations/ams-viirs-sdr-calval-star-cao-01232012.pdf (accessed on 1 January 2012).
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. Atmos. 2013, 118, 11664–11678. [Google Scholar] [CrossRef]
- Yan, B.; Kireev, S.V. A New Methodology on Noise Equivalent Differential Temperature Calculation for On-Orbit Advanced Microwave Sounding Unit—A Instrument. IEEE Trans. Geosci. Remote. Sens. 2021. [Google Scholar] [CrossRef]
- Yan, B.; Chen, J.; Porter, W.; Kireev, S.; Sun, N.; Zou, C.; Zhou, L. Accurately Quantifying NEDT Performance for In-Orbit AMSU-A and ATMS Instruments by Using a Newly Developed Algorithm. In Proceedings of the 2019 Joint Satellite Conference, Boston, MA, USA, 28 September–4 October 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).