Abstract
Satellite precipitation estimates (SPEs) are promising alternatives to gauge observations for hydrological applications (e.g., streamflow simulation), especially in remote areas with sparse observation networks. However, the existing SPEs products are still biased due to imperfections in retrieval algorithms, data sources and post-processing, which makes the effective use of SPEs a challenge, especially at different spatial and temporal scales. In this study, we used a distributed hydrological model to evaluate the simulated discharge from eight quasi-global SPEs at different spatial scales and explored their potential scale effects of SPEs on a cascade of basins ranging from approximately 100 to 130,000 km2. The results indicate that, regardless of the difference in the accuracy of various SPEs, there is indeed a scale effect in their application in discharge simulation. Specifically, when the catchment area is larger than 20,000 km2, the overall performance of discharge simulation emerges an ascending trend with the increase of catchment area due to the river routing and spatial averaging. Whereas below 20,000 km2, the discharge simulation capability of the SPEs is more randomized and relies heavily on local precipitation accuracy. Our study also highlights the need to evaluate SPEs or other precipitation products (e.g., merge product or reanalysis data) not only at the limited station scale, but also at a finer scale depending on the practical application requirements. Here we have verified that the existing SPEs are scale-dependent in hydrological simulation, and they are not enough to be directly used in very fine scale distributed hydrological simulations (e.g., flash flood). More advanced retrieval algorithms, data sources and bias correction methods are needed to further improve the overall quality of SPEs.
1. Introduction
Precipitation is an important climate variable as well as a major driver of the water cycle [1,2,3]. The traditional method of measuring precipitation is to observe through gauge stations on the ground. However, due to its high cost, the rain gauge network is very sparsely distributed in some regions (e.g., remote areas or high-altitude locations), resulting in its spatial under-representation [4,5]. Radar precipitation is susceptible to many effects (e.g., topography), and usually cannot provide full coverage of precipitation observation [6]. Satellite precipitation estimation is currently the most promising tool, which can provide quasi-global precipitation estimation with high spatial and temporal resolution [7]. Existing state-or-the-art satellite precipitation estimate products (SPEs) include the Precipitation Estimate from Remotely Sensed Information using Artificial Neural Networks (PERSIANN), the Tropical Rainfall Measuring Mission (TRMM), the Global Precipitation Measurement Mission Integrated Multi-satellitE (GPM IMERG) and Global Satellite Mapping of Precipitation (GSMaP) [8,9,10,11,12]. Among them, different satellite estimates incorporate input data from different sensors. For example, the latest PERSIANN Dynamic Infrared-Rain rate model (PDIR), which utilizes climatological data to construct a dynamic cloud-top brightness temperature with the rain rate, contains the spatiotemporal richness and near-instantaneous availability needed for rapid natural hazards response. Other products (e.g., GSMaP) use both IR and passive microwaves (PMW) as input sources and therefore require relatively more processing time. There are also many products (e.g., IMERG Final) that use ground-based observations for bias correction, which are often used for research-level (or climate-scale) studies and are not suitable for real-time monitoring and forecasting. Despite the great development of satellite retrieval algorithms, data sources, post-processing and other technologies, SPEs still suffer biases compared with ground observations [13]. Understanding and quantifying the bias can better serve the updating iteration and application of SPEs [14].
Many studies have been conducted at global or regional scales using various hydrological models for the validation of a wide range of SPEs [15,16,17,18,19,20]. Such studies intuitively enable us to recognize and understand the response of rainfall-runoff processes to input uncertainty and the propagation of input uncertainty in the water cycle [21,22,23,24,25]. For example, Beck et al. [26] selected 9053 small to medium-sized watersheds (catchment area less than 50,000 km2) on a global scale and evaluated 22 global precipitation products, including satellite estimates, reanalysis and merging products, using the HBV hydrological model. Their results showed significant spatial variability in the performance of the different products on a global scale, which emphasizes the importance of assessing and selecting datasets at local scales [26]. Similarly, Mazzoleni et al. [27] selected eight large-sized catchments (Amazon, Brahmaputra, Congo, Danube, Godavari, Mississippi, Rhine and Volga) in different continents around the globe with different catchment areas, climate types and land conditions. Their study also concluded that there is no unique product that outperformed the others in all eight selected basins. In addition, their study proposed an interesting conclusion. That is, the runoff simulation ability of the same product at the outlet of the basin does not indicate its simulation accuracy in internal locations, and they highlighted the importance of using distributed models [27]. The above studies remind us of the importance of pre-evaluation and selection of SPEs for different study areas. More importantly, they demonstrated the existence of scale effects in the application of SPEs. Validating the performance of streamflow simulation only at the basin outlet may not be enough for distributed applications. However, as these studies involve multiple watersheds, they did not discuss this issue in depth.
The scale effect is an important topic and belongs to 1 of the 23 unsolved problems in hydrology [28]. Namely, what are the hydrological laws at the catchment scale and how do they change with scale? In this study, we attempt to answer the question: What is the spatial representation of SPEs as forcing data at the catchment scale? Furthermore, how do they change with scale? In fact, this issue has been discussed in some previous studies. For example, Michaud and Sorooshian [29] designed a couple of experiments with various rain gauge densities to discuss the effect of rainfall-sampling errors on distributed hydrologic simulations. They pointed out that about half of the difference in flood simulations between observation and simulation was due to sampling errors. Mandapaka et al. [30] also took a similar approach to explore the spatial correlation of radar rainfall errors. In addition, they found that the spatial correlation of radar precipitation errors is about 20 km, emphasizing that we need to take care of the differences in runoff simulations due to point-surface rainfall uncertainty. Nijssen and Lettenmaier [31] also used a Monte Carlo and Variable Infiltration Capacity (VIC) model to generate and quantify a large amount of simulated precipitation and their performance. The results showed that when the catchment area is larger than 50,000 km2, the runoff simulation error decreases greatly as the catchment area increases. In another study, the authors indicated that the error was greater for catchments smaller than 400 km2 compared to larger catchments [32]. All the above studies used the Monte Carlo method to generate stochastic rainfall sequences to study the scale effects (or sampling error) of the satellite or radar products used. However, the conclusions they obtained are not entirely consistent due to the small number of relevant cases, so more case studies are needed. Moreover, they did not use real precipitation products or fully reveal the scale effects. As indicated, this still is an unsolved issue [28].
To date, we have a large number of available precipitation products. It is time to revisit the latest precipitation products and their possible scale effects in hydrological application. In this study, we select the Yalong River basin in China as a case. The eight latest quasi-global SPEs are used to drive a distributed hydrological model to validate their applicability and scale effects. This study not only deepens our understanding of satellite precipitation estimates products and their hydrological applications, but also contributes to the study of other rainfall-related topics, such as an estimation of the Areal Reduction Factor (ARF) [33,34] and spatial classification of Rainfall events [35,36,37]. Section 2 introduces the study area, dataset, hydrological model and performance metrics we selected. The main results are described and analyzed in Section 3. Related studies and issues are discussed in Section 4. Section 5 summarizes the conclusions.
2. Materials and Methods
2.1. Study Area
Yalong River is the largest tributary of the Jinsha River in the upper reaches of the Yangtze River of China (Figure 1a). The Yalong River (YLJ) basin is located in the eastern part of the Qinghai-Tibet Plateau and stretches from 96°52′E to 102°48′E longitude and from 26°32′N to 33°58′N latitude. The basin spans 1570 km, with a total area of about 130,000 km2 and significant variation in elevation from north to south (from 7148 m to 115 m). The precipitation in the YLJ basin increases from north to south, with an average annual precipitation of 550 mm in the source area and up to about 1500 mm in the middle and downstream areas (Figure 1d). The runoff distribution is consistent with the precipitation. For better calibration and verification of the hydrological model, we collected flow records from 2006–2015 at four hydrological stations, namely, Tongzilin (TZL), Yajiang (YJ), Daofu (DF) and Ganzi (GZ) (Figure 1b). The average annual discharge at the outlet (TZL) of the basin is about 1860 m3/s. The downstream areas of the YLJ basin are heavily exploited for hydropower production through a complex system of reservoirs (e.g., Pingxiang Hydropower Station and Ertan Hydropower Station). These reservoirs are useful for flood control during the rainy season, guarantee human water use during the dry season and provide abundant power resources through specific scheduling rules.
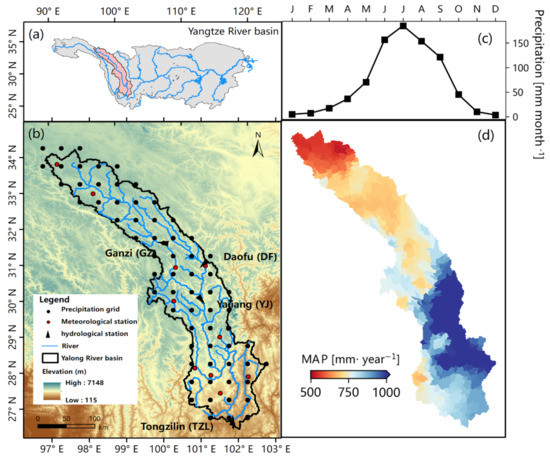
Figure 1.
(a) The location of the Yalong River basin. (b) The terrain and gauge distribution in the Yalong River basin. (c) Basin-averaged precipitation climatology for 2003–2019. (d) Spatial distribution of mean annual precipitation (MAP) for 2003–2019.
2.2. Gauge Precipitation Observations
The China Meteorological Administration (CMA)-observed gridded precipitation (0.5° × 0.5° and daily) was used in this study as a benchmark and reference. This product was developed by interpolating the high-density gauge observations from more than 2400 stations over China [38]. The good quality and spatial representativeness has been confirmed [38] and widely applied in climate change [39], drought monitoring [40,41] and hydrological simulations [42].
2.3. Satellite Precipitation Estimates Products (SPEs)
In this study, eight satellite precipitation estimates products (SPEs) were selected as alternatives to CMA ground observations (Figure 2) and they have also been widely used as alternatives in previous studies. These products differ in algorithms, data sources and bias correction. They can be broadly divided into three categories: (1) Near real-time products with sole IR input (PERSIANN, PERSIANN-CCS and PDIR-Now) and without bias correction, (2) bias-corrected products using rain gauge observations (CMORPH, IMERG Final, GSMaP) and (3) climate data records (PERSIANN-CDR, PERSIANN-CCS-CDR). Detailed information of these products can be found in Table 1 as well as in some earlier studies [9,43].

Figure 2.
The spatial distribution of mean annual precipitation (MAP) (2003–2019) for eight SPEs (a–h) in the YLJ basin.

Table 1.
Satellite precipitation estimates (SPEs) used in this study. GPCP: Global Precipitation Climatology Project dataset; CPC: Climate prediction center dataset; GPCC: Global Precipitation Climatology Centre dataset.
2.3.1. PERSIANN
Precipitation Estimate from Remotely Sensed Information using Artificial Neural Networks (hereafter, PERSIANN) [44] is the first generation of the PERSIANN family of products. PERSIANN uses a modified propagation network and clusters the satellite infrared (IR) imagery into various categories using a self-organizing feature map (SOFM). Meanwhile, the passive microwave (PMW) imagery is used to adapt the parameters of the network.
2.3.2. PCCS
The PERSIANN-Cloud Classification System (hereafter, PCCS) [45] uses a cloud-patch-based algorithm, which extracts features (e.g., cloud coverage) from the satellite images under specified temperature thresholds and classifies them into different categories using SOFM. Then, the relationships between brightness temperature and rainfall rate are fitted to estimate the precipitation using histogram matching and the nonlinear exponential function.
2.3.3. PCDR
The PERSIANN-Climate Data Record (hereafter, PCDR) [46] was intended to develop a long-time historical precipitation record (1983–present). Therefore, it uses more available satellite information from the International Satellite Cloud Climatological Project (ISCCP). Meanwhile, it uses the National Centers for Environmental Prediction (NCEP) Stage IV hourly precipitation data to tune the parameters of the modified PERSIANN model. Finally, the Global Precipitation Climatology Project (GPCP) monthly 2.5 precipitation data are also used to correct the bias of the raw PCDR data.
2.3.4. PCCSCDR
PERSIANN-Cloud Classification System-Climate Data Record (hereafter, PCCSCDR) [47] is a merged product, which concentrates PCCS and PCDR and provides a long-term (1983–present) and high-spatiotemporal-resolution (0.04° × 0.04°, 3 h) precipitation record.
2.3.5. PDIR
PERSIANN-Dynamic Infrared Rain Rate near real-time (PDIR-Now, hereafter, PDIR) [48,49] is the latest generation of the PERSIANN family of products. It incorporates more high-frequency sampled IR imagery and provides near real-time precipitation estimates with a very short time latency (15–60 min). Moreover, the latest PDIR algorithm establishes a dynamic shifting curve between cloud-top brightness temperature and rainfall rate using rainfall climatology to reduce the uncertainties derived from satellite IR images. PIDR dataset is produced at a high spatiotemporal resolution (1 h, 0.04° × 0.04°) with a quasi-global coverage (60°N–60°S).
2.3.6. CMORPH
Bias-corrected Climate Prediction Center Morphing Technique Climate Data Record (BC-CPC-CMORPH V1.0-CDR, hereafter referred to CMORPH) [50] is a reproduced version of CMORPH post-processed with bias correction by incorporating CPC daily gauge analysis over land and the Global Precipitation Climatology Project (GPCP) merged precipitation over the ocean. The original CMORPH technique is a novel method that combines the PMW data from low earth orbiting satellites (LEOS) and IR data from geostationary earth orbiting (GEO) satellites. CMORPH provides high-resolution global satellite precipitation estimates by performing a time-weighted interpolation between the PMW scans. CMORPH are now available at three temporal resolutions (30 min, 1 h and 1 day) and include a quasi-global (60°N–60°S) high-spatial-resolution (0.25° × 0.25°) record from 1998 to present for researchers.
2.3.7. IMERG
The Global Precipitation Measurement Mission Integrated Multi-satellitE (GPM IMERG) [8] provides multi-satellite precipitation estimates retrieved from PMW satellite images. Its main products include the IMERG Early Run (near real-time low-latency), the IMERG Late Run (quasi-Lagrangian time interpolation) and the IMERG Final Run (bias correction). In this study, we selected the IMERG Final Run V6B product (hereafter, IMERG). Its algorithm fully integrates the advantages of morphing technique, PCCS, and Kalman filter. Then, after bias correction by GPCC gauge analysis, research-quality long-term (2000–present) quasi-global (60°N–60°S) high-spatiotemporal-resolution (0.1° × 0.1°, 30 min) precipitation estimates are generated.
2.3.8. GSMaP
Gauge-calibrated Global Satellite Mapping of the Near real-time Precipitation product (GSMaP_Gauge_NRT_v6, hereafter, GSMaP) [11,12] covers quasi-global (60°N–60°S) coverage and provides high-spatiotemporal-resolution (0.1° × 0.1°, 1 h) precipitation estimates. The algorithms of this product are mainly done by the microwave-IR merged algorithm (GSMaP-MVK) and gauge calibration, which makes full use of the multiple-input information, including microwave imager and sounder, GEO IR imager, space-borne precipitation radar, atmospheric condition, sea surface temperature (SST), CPC unified global gauge analysis and topographic data.
2.4. Other Data
Other meteorological forcing data (wind speed, maximum and minimum temperature) were collected from 10 national meteorological stations located in the YLJ basin. For hydrological modeling, the precipitation and temperature data were further interpolated into each sub-basin by using the inverse distance weighting (IDW) method and elevation correction [51]. The wind speed data were also interpolated into each sub-basin using the synergistic mapping (SYMAP) algorithm [52]. Daily (2007–2014) streamflow records for four hydrological stations were collected for model calibration and verification. The 1 km soil types and land use data were clipped from the China soil map-based harmonized world soil database (HWSD) (v1.2) and the Chinese Academy of Sciences Resource and Environmental Science Land use dataset, respectively. The 90 m digital elevation model (DEM) data were downloaded from the National Aeronautics and Space Administration Shuttle Radar Topographic Mission (NASA SRTM).
2.5. Hydrological Model
In this study, we use a distributed hydrological model called the distributed time-variant gain hydrological model (DTVGM) [53,54], which was developed from rainfall-runoff nonlinear theory and can now be fully driven by remote sensing information [55].
First, given a threshold of the sub-basin (100 km2 in this study), we use the drainage network extraction method introduced by Du et al. [56] to spit the whole YLJ basin into 522 sub-basins. The minimum threshold for sub-basin is based on the complexity of hydrological modeling, the running time step, the area of the Yalong River basin, the time scale of the hydrological simulation and the resolution of the forcing data. In each sub-basin (as known as the hydrological response unit, HRU), the runoff is calculated according to the water balance (Equation (1)).
where t is the time step; P is the precipitation (mm); Ep is the potential evapotranspiration (mm); AW represents the soil moisture (mm); WM is the field soil moisture (mm); Subscript u and g represent the upper and lower layers of soil, respectively; Ke, Kr, and Kg are the coefficients of evapotranspiration, interflow runoff and groundwater runoff, respectively; g1 and g2 are factors describing the nonlinear process of runoff; and C is the land cover parameter.
The kinematic wave equation is used for streamflow routing [57,58]. n in the river routing procedure stands for the roughness factor [58]. The degree-day method is used to compute the snowmelt in the upper reaches of the YLJ basin [59].
2.6. Performance Metrics
To evaluate the satellite precipitation estimates products, we selected five metrics as follows: the Pearson Correlation Coefficient (R), the Nash–Sutcliffe efficiency (NSE) [60], the Kling–Gupta efficiency (KGE) [61], the Relative bias (RB) [62] and the Normalized centered root mean square error (NCRMSE) [22]. Among them, R describes the correlation; NSE and KGE are two integrated goodness-of-fit metrics; RB and NCRMSE describe the systematic bias and random bias, respectively. Their equations, intervals and optimal values are summarized in Table 2.

Table 2.
Performance metrics used in this study.
3. Results
We evaluated the performance of each of the eight SPEs at the hydrologic station and sub-basin scales using the calibrated DTVGM hydrologic model from 2001 to 2019. In this paper, we took the discharge simulations driven by the observed precipitation as the reference (or “truth”) and compared the satellite-driven simulations with them. The differences between the satellite-driven and observation-driven simulations were considered as the error of SPEs. We chose the observation-driven simulations instead of the observed discharge at hydrological stations as the reference for the following two considerations: (1) We only used one distributed hydrological model in this study. Although we adequately calibrated the model, there may still be uncertainties in the model structure and model parameters. Using the observation-driven simulations as the reference allowed us to focus on analyzing the uncertainties of different SPEs without considering the influence of the model structure and the model parameter uncertainties. (2) The number of stations with observed discharge is often limited, especially in remote areas. We collected data from four hydrological stations, which was valid for model calibration and verification to some extent but was far from enough for assessing the applicability of SPEs at the sub-basin or grid scale.
3.1. Model Calibration and Verification
In this study, we used CMA precipitation gauge observations to force the DTVGM and four hydrological discharge records to calibrate and verify DTVGM at a daily scale. The discharge simulation was divided into a warm-up period (2006), a calibration period (2007–2010) and a validation period (2011–2014). We manually calibrated the model parameters during the calibration period (2007–2010). The Nash–Sutcliffe efficiency (NSE) and relative bias (RB) were selected as the main objective functions, constraining the NSE > 0.7 and RB between ±10%. Firstly, we adjusted Ke (0 < Ke < 1) to reduce the overall RB of simulation, then tuned Kr (0 < Kr < 1), Kg (0 < Kg < 1), g1 (0 < g1 < 1) and g2 (g2 > 0) to achieve a good enough NSE, and finally fitted the flood peak time by changing different n (0.001 < n < 0.15).
Figure 3 shows the model validation results for the four hydrological stations. Except for the TZL station, all other stations achieved good simulation accuracy (with R > 0.9; NSE and KGE > 0.85; RB < ±10%). In order to ensure the effectiveness of the hydropower plants located in the lower YLJ basin, these reservoirs store more water through regular operations compared to natural conditions. Periodic reservoir operations led to the observation of more undulating hydrologic curves than the smoother hydrologic curves we simulated (Figure 3a). However, we did not consider the effect of downstream, regional, intense reservoir scheduling in this study, which was also not the main objective of our research. Meanwhile, we used the observed precipitation-driven simulated flows as a reference in the following section to ignore the uncertainties in the model structure and model parameters.
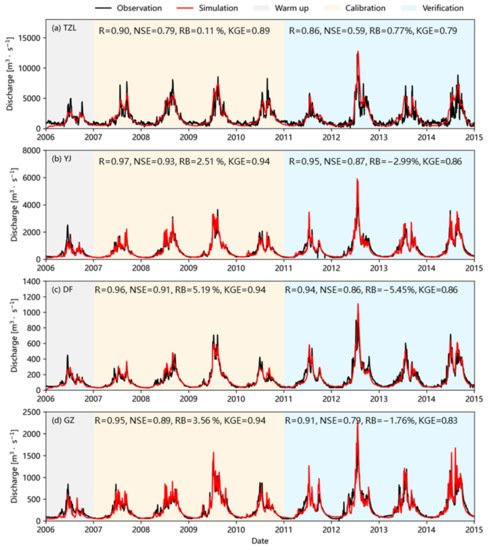
Figure 3.
Model calibration and verification at four hydrological stations. (a) TZL. (b) YJ. (c) DF. (d) GZ. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB).
3.2. Validation of Discharge Simulations at Four Gauged Hydrological Stations and Sub-Basin Scale
By driving the DTVGM model with different SPEs, we obtained corresponding streamflow simulations for four hydrological stations. Figure 4 shows an example of the hydrograph for the TZL station, and those for the other three hydrological stations can be found in the Supplementary Materials (Figures S1–S3). By comparing the streamflow obtained from different datasets, there are quite a lot of mismatches as well as a severe overestimation of flood peaks in PCCS and PERSIANN. The mismatches and overestimation of flood peaks also can be quantified by the low temporal correlation coefficient and high RB values. These two main factors are also responsible for the overall poor performance of PCCS and PERSIANN.

Figure 4.
The model simulation forced by CMA observation and eight different SPEs (a–h) at the TZL station. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE).
Except for PCCS and PERSIANN, the simulations obtained from the other six precipitation products are in high agreement with the reference (CMA). All of them can capture the intra-annual and inter-annual variability well. This is attributed to the fact that they are all bias corrected (except PDIR), whereas the main sources of errors are mainly overestimation and underestimation of flood peaks. For example, PCCSCDR severely overestimates during the high flow period in flood season. PCDR, PDIR and GSMaP also show different degrees of overestimation, while IMERG relatively underestimates the flood peaks. Among the eight products, CMORPH is largely consistent with the reference at the TZL station.
Table 3 summarizes the results for the four hydrological stations, which are distributed at different locations (internal or at the outlet) in the YLJ basin and represent the variation in model performance with the catchment area (Figure 1b). So, these four hydrological stations representing the results of streamflow simulations in four catchments (or sub-basins) from large to small can be used to preliminarily evaluate the performance of different SPEs in different spatial scales and their potential scale effects. To distinguish these products, we divide the results into three columns. The numbers in bold on the left and middle column represent the best values for the near real-time products without bias correction and with bias correction, respectively. Furthermore, the numbers in bold on the right column represent the best values for the climate data records.

Table 3.
Hydrological evaluation of eight SPEs at four hydrological stations of the YLJ basin. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE).
When comparing the accuracy of different products horizontally, the performance ranking of different products is basically the same, despite the differences in the size of the catchment area. For example, in the near real-time family, PDIR expresses the best performance (R, NSE, KGE and RB) for all stations evaluated. Similarly, for the bias-corrected products, IMERG has a better simulation performance than others for three of the stations evaluated (GZ, YJ and DF), except CMORPH outperforms IMERG at the TZL station, with the best values of NSE, KGE, RB and NCRMSE.
As mentioned above, we have drawn some common conclusions about the strengths and weaknesses of the products based on the horizontal comparison of the different products. However, what is more noteworthy is that the performance of these products varies greatly from the stations. For example, although PDIR obtained relatively good results at the TZL station, it performed relatively worse at the YJ, GZ and DF stations, especially the NSE value, which was 0.6 at the TZL station but only 0.32 at the GZ station. Other indicators also showed similar degradation. This phenomenon indicates that the same products may vary greatly when evaluated at different stations, and these stations are outlets of different sub-basins of the whole basin.
Further, by observing the results of these sub-basins with different catchment areas, another interesting conclusion that can be summarized is that this degradation seems to show a regular pattern according to the size of the catchment. For example, the best performance was observed at the TZL station, which has the largest catchment area, while the performance of SPEs deteriorates as the catchment size decreases. However, the generalization of this pattern is hindered by the assessment results at the DF station, which has the smallest catchment area. The performance for different products is better at the DF station than at the GZ station, and even better than at the YJ station.
In general, the comparison of the four hydrological stations allows for a ranking of the products, but this ranking varies somewhat with the stations. The latest generation of the PERSIANN family of products, PDIR, is a very significant improvement over PERSIANN and PCCS, while PCCSCDR, a blended product of PCCS and PCDR, is not a significant improvement. This can be attributed to PCCS, which uses a fixed relationship between the cloud-top brightness temperature and the rain rate, and results in an underestimation in wet regions and an overestimation in dry regions [48,49]. More importantly, the results for the different sites remind us that it is worth noting the spatial characteristics of the model performance more. Does the performance of different SPEs have a scale effect? How does the model performance correlate with the catchment area?
Figure 5 shows the spatial distribution of the five different goodness-of-fit metrics at each sub-basin of the YLJ basin. To better explore the spatial characteristics of the SPEs-driven simulations, we compare and evaluate the performance of each of the eight products at the sub-basin scale. The same color bars are used to describe the relative goodness of the metrics, except for the presence of positive and negative values of the systematic bias (RB), with darker colors representing better results for that indicator. The spatial patterns of the metrics allow us to not only clearly derive the spatial differences between the different SPEs, but also to analyze the differences of each product in different internal locations of the basin. It should be noted that the results for the specific sub-basins are the model performance when the sub-basin is used as an outlet for the catchment.
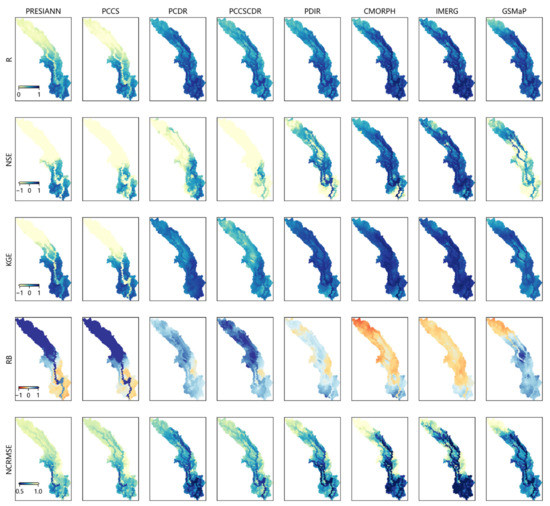
Figure 5.
Spatial distribution of precipitation performance metrics of eight SPEs in YLJ basin. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE).
First, by comparing the different products, we can easily distinguish the advantages and disadvantages of the products, and this is consistent with the results obtained in the previous section at the four hydrological stations. In terms of NSE and KGE, among all products, IMERG and CHORPH belong to the first tier, showing the best performance, while PDIR, GSMaP and PCDR are in the second tier, and their spatial distribution of NSE is relatively poor in the local area of the basin. For example, the NSE of PDIR is even less than 0 near the source part and outlet of the YLJ basin. Further, the same is true for PCDR, with more low values in the middle and upper part of the YLJ basin, while for GSMaP, these cases occur mainly in the middle and lower reaches. PCCSCDR, PCCS and PERSIANN are in the third tier for the YLJ basin, where they express the worst accuracy and temporal correlation. This can be attributed to their severe overestimation in the upper and middle reaches of the YLJ basin (see the spatial distribution of RB in Figure 5), and this overestimation could be dominated by the false alarm precipitation overestimation, and it also leads to the mismatches of flood peaks. Systematic overestimation (or underestimation) of flood peaks also occurs in several other products, such as the overestimation (or underestimation) of PDIR, PCDR and GSMaP (or IMERG and CMORPH). However, these overestimates (or underestimates) did not destroy the temporal correlation.
Then, we focus on the scale effect of discharge simulation. It was not difficult to find that there is a significant spatial variability for the eight SPEs in the internal locations of the whole YLJ basin. Furthermore, the significance of spatial variability varies to a degree with the products. PCCSCDR, PCCS and PERSIANN present the most significant spatial differences, indicating that these datasets are insufficient or even far from adequate for application in the upper areas of the YLJ basin. In contrast, the other products express relatively less spatial variability and perform consistently throughout the whole basin. However, while these products perform poorly in the upstream areas of the catchment, they perform better along with the river network, suggesting that the ability to simulate streamflows driven by SPEs in these regions is very close to that of observation-driven simulations. The common feature of these regions is that they are all near the riverways, with larger catchment areas. This suggests that there is indeed a scale effect in the application of hydrological simulations forcing by SPEs. That is, the error generated in the upstream area of the catchment is attenuated with the streamflow routing. However, for the source part of the catchment, i.e., the sub-basins with smaller flow accumulation area (FAA), there are large differences in model performance. For example, PDIR performs worse at the source and near the outlet of the YLJ basin compared to IMERG, and CMORPH performs worse near the outlet of the basin.
3.3. Spatial Scale Dependence of Simulation Performance
The basic law is that the simulation performance increase with the increase of the catchment area, and there may be a threshold condition triggering the occurrence of this law. To better quantify the relationship between the simulation capacity and the catchment area, as well as to find the threshold condition for the occurrence of the scale effect, we plot the simulation accuracy of all sub-basins and the corresponding flow accumulation area (FAA, or catchment area) of these sub-basins in a two-dimensional coordinate system. Figure 6a–e shows the scores of different metrics as a function of the FAA. Figure 6f shows the distribution of the FAA in different locations of the YLJ basin. Despite the different evaluation metrics used, Figure 6a–e clearly reveals the correlation between the model performance and FAA. It is also worth noting that this relationship does have a threshold, and the threshold is about 20,000 km2, which is determined by all five metrics.
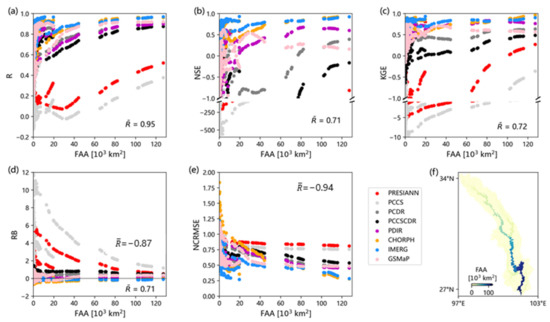
Figure 6.
Hydrological simulation performance metrics (a–e) of eight SPEs as a function of the flow accumulation area (FAA). (f) The distribution of the flow accumulation area (FAA) in the YLJ basin.
When the FAA (or catchment area) is less than 20,000 km2, the model performance behaves more randomly, with different model performances in various locations of the YLJ basin. When the FAA (or catchment area) is larger than 20,000 km2, the model performance increases with the increase of FAA. This reaffirms our hypothesis that the scale effect affects the model performance. For the YLJ basin, 20,000 km2 is a key condition to activate the scale effect.
According to the threshold condition, we further divided the FAA into four intervals (0–20, 20–60, 60–100 and 100–130; ×103 km2) according to their size. The number of sub-basins in the four intervals are 476, 19, 13 and 14, respectively. Meanwhile, we selected the median values of metrics in each interval to represent the average performance of that interval. For better visualization, we use radar plots to depict the capacity of different products. In the radar plot, we uniformly standardize the five metrics to the range of 0 and 1. The method of standardization is shown in Appendix A. In this way, for a specific product, 1 means that the metrics corresponding to that product perform best in the four intervals. Conversely, 0 means that the metrics corresponding to that product performs worst in the four intervals. It is important to note that we have standardized the results between 0 and 1, which can only be applied to compare the relative goodness of products in four intervals. To be able to quantitatively express the model performance of different SPEs and FAA, we summarize the results in Table 4.

Table 4.
The discharge simulation performance (median) of eight products in different catchment area intervals. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE). The values shown in the table are the median of each interval.
Figure 7 shows the relative goodness of the eight products in the four catchment intervals with respect to five metrics. Just as the scale effect obtained in Figure 6, the simulation performance keeps increasing when the catchment area is larger than 20,000 km2. This pattern is expressed in the radar plot as the inclusion relationship of the circles. For example, in Figure 7c, the purple circle encloses the blue circle, while the blue circle encloses the red circle. Likewise, PERSIANN, PCCS, PCCSCDR, and CMORPH show the same patterns. However, PDIR, IMERG and GSMaP show different characteristics. Among them, PDIR and IMERG are mainly the anomalies of the systematic bias (RB). This may be due to the offset effect of positive and negative values in biases. The results may exist in three cases: (1) RB is negative in all upstream areas of the catchment, and its value may increase to a large negative one as it accumulates in the process of streamflow routing; (2) RB is positive in all upstream areas of the catchment, and it will also increase to a large positive one as it accumulates in the process of streamflow routing; (3) there are both positive and negative values in the upstream areas of the catchment, and they may accumulate (or cancel each other out), causing the RB to increase (or decrease). GSMaP does not seem to follow the patterns of the scale effect, which may be due to the relatively good performance in the upstream of the YLJ basin and the poor performance in the downstream regions (Figure 5). Therefore, during the routing process, this routing-induced positive scale effect occurs mainly in the upstream region, which does not further improve the model performance in the downstream region due to the worse performance in these regions. The FFA of the upstream region is roughly between 20,000 and 60,000 km2, corresponding to the results in the radar plot (see Figure 7h). On the other hand, when the catchment area is less than 20,000 km2 (black line in the radar plot), model performance varies in different products, which is highly correlated with the local simulation capacity, without being affected by the river routing. Furthermore, the model performance of the local area may be dominated by the accuracy of precipitation estimates.

Figure 7.
The relative goodness of the eight products (a–h) in the four catchment intervals with respect to five metrics. Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling-Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE). The values shown in the figure are the median of each interval.
3.4. Product Selection Based on Spatial Scale Dependence
In this study, we divided the YLJ basin into 522 sub-basins according to the 100 km2 threshold to expand enough cases for the study of the scale effect. The FAA of different sub-basins ranges from 100 km2 to 130,000 km2. Based on this framework, the simulation capability of different FFA for different SPEs is analyzed. In practical applications, models with different resolutions may be built to achieve the relevant research objectives. For example, flash flood monitoring and early warnings need high-resolution models with as many hydrological response units (HRUs) as possible to capture the local flood characteristics. For water resources planning and reservoir regulation, we only need to obtain the flow conditions at the main stream or outlet of the basin. A coarse-resolution distributed hydrological model, a semi-distributed hydrological model or a lumped model driven by the area mean precipitation can meet the requirements.
Figure 8 shows the relationship between the advantages and disadvantages of different products in different catchment area intervals. Similarly, the five metrics are uniformly standardized to the range of 0–1, where 1 means that the product is the best compared to other products in a certain dimension, and 0 means that the product is the worst compared to other products in that dimension. As shown in the figure, the radar plot can more clearly guide us to identify the strengths and weaknesses of different products. It should be emphasized again that we have scaled down the metrics to between 0 and 1, which can only be applied to compare the relative goodness of different products at the same catchment scale. To quantitatively express the performance of the different products, we summarize the results in the Table 4.
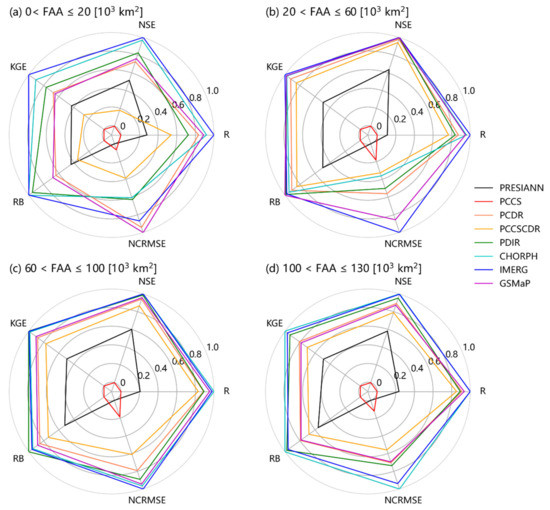
Figure 8.
The relative goodness of different products in different catchment area intervals (a–d). Pearson correlation coefficient (R); Nash–Sutcliffe efficiency (NSE); Kling–Gupta efficiency (KGE); Relative bias (RB); Normalized centered root mean square error (NCRMSE). The values shown in the figure are the median of each interval.
It can be seen from the figure that when the catchment area is less than 20,000 km2, the difference between the eight products is significant, and the best product is IMERG. Meanwhile, IMERG still maintains a high level of simulation performance when the catchment area increases to 100,000 km2. For other products, CMORPH and PDIR have comparable performance and gradually catch up with IMERG in the large catchment. The performance of CMORPH exceeds that of IMERG when the catchment area is larger than 100,000 km2. GSMaP and PCDR are at the same level, followed by PCCSCDR. PERSIANN and PCCS are the worst products for the YLJ basin. Interestingly, for the random error (NCRMSE), although the difference between the eight products is small, the CMORPH and PDIR products perform worse when the catchment area is in the range of 0–100,000 km2, which indicates that the random error of these two products is larger than other products. However, the random error decreases gradually with the increase of the FAA.
4. Discussion
4.1. Comparison with Previous Studies
In this study, we investigate the scale dependence of the accuracy of SPEs-driven streamflow simulations. In the YLJ basin, when the catchment area is larger than 20,000 km2, the simulation accuracy increases with the increase of FFA (or catchment area), which is mainly attributed to the river streamflow routing. It weakens the propagation of errors in upstream areas into downstream areas. On the other hand, when the catchment area is smaller than 20,000 km2, the spatial distribution of simulation accuracy is more stochastic, and its performance is mainly controlled by the local simulation performance. Since we selected only one basin as the case, more evidence is needed to prove whether the results are generalizable. In fact, some previous studies have some degree of similarity with the results we present, or they can be combined with our study to reveal common patterns.
One important law is that when the catchment area is small, the accuracy of flow simulations is dominated by forcing accuracy. A large-scale hydrological simulation experiment confirms this conclusion. Jiang and Bauer-Gottwein [63] selected 300 watersheds with catchment areas smaller than 5000 km2 in mainland China. The authors conclude that these catchments generally follow the rainfall-runoff error propagation and are not influenced by the streamflow routing process. The above studies were conducted in different basins and some other studies were conducted in the same basin with different sub-basins. Terink et al. [64] used the Bootstrap sampling method to set different gauge network densities ranging from 1 to 106 stations in a small watershed in the Netherlands and found that higher densities significantly reduced the uncertainty in runoff simulations and thus increased simulation accuracy. Similarly, the conclusion was confirmed in other studies that the degradation in precipitation resolution introduces errors in the precipitation field and propagates to the runoff simulation [65]. In addition, Cunha et al. [66] selected watersheds (with catchment areas of 20–1600 km2) in central Iowa, showing that the uncertainty in peak flow simulations depends to a large extent on the size of the catchment. Uncertainty decreases with increasing catchment area due to the aggregation effect of the river network, which filters out small-scale uncertainty.
Another issue not covered in this paper but equally important is the temporal scale effect of precipitation, which has been discussed in many previous studies. In these studies, it is also called precipitation time averaging (temporal resolution), or time resampling (sampling error) [29,31,67]. An example is the density scatter plot (see Figure 4 in [64]). In their study, they assessed the quality of IMERG precipitation products at three scales (daily, monthly and annual). The results showed that the quality of precipitation products increased significantly with the increase of time scales. Similar findings can also be found in the assessment of daily and hourly precipitation [68].
However, the high temporal resolution of precipitation is still very important. Li et al. [69] conducted a case study using hourly and daily precipitation to drive SWAT models in a large-scale watershed in eastern China, respectively. The results show that the hourly precipitation-driven runoff simulation is better than the daily simulation because the hourly precipitation is better able to capture the detailed features (e.g., flood peak) of streamflow. Additionally, their results also confirm the existence of a temporal scale effect on the temporal resolution of precipitation. This effect was also confirmed by many other case studies in Tengboche, southern France and America [68,70,71].
In addition, the importance of temporal resolution relative to spatial resolution was emphasized in these studies that included both temporal and spatial resolution discussions. However, this conclusion was limited to smaller study watersheds where precipitation was more uniformly distributed in whole regions [68]. In another study about urban flood simulation, researchers discussed the response of urban hydrological dynamics to the spatial and temporal resolution of precipitation using radar precipitation data and showed that urban flood processes are more sensitive to spatial resolution compared to temporal resolution [72]. Both spatial averaging and temporal averaging result in a flattening of the flood peak simulations [29,67].
In summary, high-precision precipitation estimates with high spatial and temporal resolution are urgently needed, especially for areas with frequent flash floods or urban areas with high-proportioned impervious surfaces. In that case, equally refined high-resolution hydrological models are necessary. The two strategies can work together to improve our understanding and prevention of disasters (e.g., flash floods and urban flooding) [73].
4.2. Statement of Different SPEs in This Study
In this study, we chose eight different remote sensing precipitation products. Our main objective in selecting these products is to increase the diversity of the dataset and thus highlight the generality of the scale effects. Therefore, it is important to state that the generality of the conclusions regarding scale effects is acceptable and this is confirmed by a large number of relevant studies [63,64,65,66,67,68,69,70,71,72]. However, inter-comparisons about product performance are to some extent inappropriate because these data are not used for the same purposes.
PERSIANN, PCCS and PDIR are near real-time products without bias correction and with very short time delay (15 min to 2 days), so they are mainly used for real-time flood or drought monitoring [9,44,45]. PERSIANN and PCCS were among the first generation of global satellite precipitation estimates products, and their algorithm design provided a solid foundation for the advancement of PDIR [48,49]. In addition, they are the foundations of PCDR and PCCSCDR [46,47]. PDIR is a very promising product with a very short delay time (15 to 60 min), relatively high accuracy and the highest spatial resolution (0.04 degree), and it uses the Dynamic Infrared-Rain model, which utilizes climatological data to construct a dynamic cloud-top brightness temperature (Tb)–rain rate relationship to retrieve precipitation. It can be used for a wide range of studies (e.g., atmospheric rivers, flash floods and extreme rainstorms).
CMORPH, IMERG and GSMaP are bias-corrected, near-real-time products. While GSMaP has a relatively short latency (4 h), the other two products have a much longer latency (3 to 4 months). CMORPH (1998 to present) is for the bias-corrected, reprocessed CPC Morphing Technique (CMORPH) high-resolution global satellite precipitation estimates. Bias in raw CMORPH is removed through a comparison against CPC daily gauge analysis over land and adjustment against the Global Precipitation Climatology Project (GPCP) merged analysis of pentad precipitation over ocean [50,74]. IMERG Final provides research-quality, gridded, global, multi-satellite precipitation estimates with quasi-Lagrangian time interpolation, gauge data and climatological adjustment [8]. Its algorithm is intended to intercalibrate, merge and interpolate “all” satellite microwave precipitation estimates, together with microwave-calibrated infrared (IR) satellite estimates, precipitation gauge analyses and potentially other precipitation estimators. The system is run several times for each observation time, first giving a quick estimate (IMERG Early Run) and successively providing better estimates as more data arrive (IMERG Late Run). The final step uses monthly gauge data to create research-level products (IMERG Final Run). So for IMERG Final, incorporating data from multiple sources and being fully bias corrected makes it the best performer in this study. These three datasets achieved very good accuracy with bias correction. This also confirms the importance of bias correction.
PCDR and PCCSCDR are climate-scale data records (CDR). PCDR and PCCSCDR are consistent from 1983 to present at a high resolution. The consistency in them is from the consistent global IR and GPCP datasets utilized in creating these datasets. These datasets are unique and useful for climate studies (i.e., historical trend analysis or climate change). Although PCCSCDR did not exceed the accuracy of PCDR in this study (YLJ basin), PCCSCDR has a higher spatial resolution (0.04 degree) compared to PCDR. It may exceed PCDR in other regions and can be used for some local studies [47].
In addition, the results of this study can only illustrate the basic performance of these data in the Yalong River basin. In other regions, the data may behave differently. Therefore, end-users should select products in a targeted manner according to the specific usage.
5. Conclusions
In this study, we evaluated eight satellite precipitation estimate products in a set of nested watersheds in the YLJ basin in China. The selected eight satellite products include Remotely Sensed Information using Artificial Neural Networks (PERSIANN), the PERSIANN-Cloud Classification System (PCCS), the PERSIANN-Climate Data Record (PCDR), the PERSIANN-Cloud Classification System-Climate Data Record (PCCSCDR), PERSIANN-Dynamic Infrared Rain Rate near real-time (PDIR), the Bias-corrected Climate Prediction Center Morphing technique Climate Data Record (CMORPH), the Global Precipitation Measurement Mission Integrated Multi-satellitE Final Run V6B (IMERG) and Gauge-calibrated Global Satellite Mapping of Near Real-time Precipitation product version 6 (GSMaP). The SPEs-driven simulated flow processes were evaluated for 522 catchments and four hydrological stations based on simulations driven by gauge observations, respectively. The 522 selected catchments range in size from 100 km2 to 130,000 km2. The results of this study indicate that the quality of satellite-driven runoff simulations is characterized regionally at different spatial scales. Despite the different satellite precipitation estimates products, they tend to have poorer model performance upstream of the catchment and better performance downstream of the catchment (areas close to the river network). In addition, the scale effects contribute to these regional characteristics of simulation performance. Due to regional averaging and river routing, the “parent” basins are better simulated than the “son” basins, but this law is triggered under a threshold value (20,000 km2 in this study).
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13163061/s1, Figure S1: Model simulation forced by CMA observation and eight different SPEs (a–h) at YJ station, Figure S2: Model simulation forced by CMA observation and eight different SPEs (a–h) at DF station, Figure S3: Model simulation forced by CMA observation and eight different SPEs (a–h) at GZ station.
Author Contributions
Conceptualization, Y.Z., A.Y., P.N., B.A., S.S. and K.H.; methodology, Y.Z. and A.Y.; software, Y.Z. and A.Y.; validation, Y.Z.; data curation, Y.Z., A.Y., P.N. and B.A.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z., A.Y., P.N., B.A., S.S. and K.H.; visualization, Y.Z.; supervision, A.Y. and S.S.; project administration, A.Y. and S.S.; funding acquisition, A.Y. and S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of China (No. 2018YFE0196000), U.S. Department of Energy (DOE Prime Award DE-IA0000018), the National Natural Science Foundation of China (No. 51879009), the Second Tibetan Plateau Scientific Expedition and Research Program (No. 2019QZKK0405), and the China Scholarship Council (CSC grant No. 202106040071).
Data Availability Statement
The PERSIANN family of products can be freely download from the CHRS Data Portal (http://chrsdata.eng.uci.edu/; accessed on 21 December 2020); the GSMaP dataset is publicly available (at https://sharaku.eorc.jaxa.jp/GSMaP/index.htm; accessed on 21 December 2020); IMERG dataset is publicly available (at https://gpm.nasa.gov/data/directory; accessed on 21 December 2020); the CMORPH dataset is publicly available (at https://www.ncdc.noaa.gov/cdr/atmospheric/precipitation-cmorph; accessed on 21 December 2020). The CMA precipitation dataset and meteorological forcing data can be obtained from the China Meteorological Administration (http://data.cma.cn/en; accessed on 21 December 2020). The soil types are publicly available from the China soil map based harmonized world soil database (HWSD) (v1.2) at (http://www.fao.org/soils-portal/soil-survey/soil-maps-and-databases/harmonized-world-soil-database-v12/en/; accessed on 21 December 2020); The land use data are free available from the Chinese National Tibetan Plateau Third Pole Environment Data Center at (http://data.tpdc.ac.cn/en/data/a75843b4-6591-4a69-a5e4-6f94099ddc2d/; accessed on 21 December 2020) provided by the Chinese Academy of Sciences Resource and Environmental Science Data Center. The DEM data were download from the National Aeronautics and Space Administration Shuttle Radar Topographic Mission at (https://www2.jpl.nasa.gov/srtm/; accessed on 21 December 2020).
Acknowledgments
We thank the editors and reviewers for their constructive comments and suggestions, which greatly improved the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Standardization Scaling in the Radar Plot
For R, NSE and KGE, the scaling (0–1) was transformed by:
For NCRMSE, the scaling (0–1) was transformed by:
For RB, the scaling (0–1) was transformed by:
where and are scaled and original values of metrics, respectively; is the absolute value of .
References
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef] [Green Version]
- Feng, X.; Wang, Z.; Wu, X.; Yin, J.; Qian, S.; Zhan, J. Changes in Extreme Precipitation across 30 Global River Basins. Water 2020, 12, 1527. [Google Scholar] [CrossRef]
- Schreiner McGraw, A.P.; Ajami, H. Impact of Uncertainty in Precipitation Forcing Data Sets on the Hydrologic Budget of an Integrated Hydrologic Model in Mountainous Terrain. Water Resour. Res. 2020, 56, e2020WR027639. [Google Scholar] [CrossRef]
- Tang, G.; Behrangi, A.; Long, D.; Li, C.; Hong, Y. Accounting for spatiotemporal errors of gauges: A critical step to evaluate gridded precipitation products. J. Hydrol. 2018, 559, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Xiong, A. Validation and comparison of a new gauge-based precipitation analysis over mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Li, C.; Tang, G.; Hong, Y. Cross-evaluation of ground-based, multi-satellite and reanalysis precipitation products: Applicability of the Triple Collocation method across Mainland China. J. Hydrol. 2018, 562, 71–83. [Google Scholar] [CrossRef]
- Foufoula-Georgiou, E.; Guilloteau, C.; Nguyen, P.; Aghakouchak, A.; Hsu, K.; Busalacchi, A.; Turk, F.J.; Peters-Lidard, C.; Oki, T.; Duan, Q.; et al. Advancing Precipitation Estimation, Prediction, and Impact Studies. Bull. Am. Meteorol. Soc. 2020, 101, E1584–E1592. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 1 Day 0.1-Degree × 0.1-Degree V06; Savtchenko, A., Greenbelt, M.D., Eds.; Goddard Earth Sciences Data and Information Services Center (GES DISC): Washington, DC, USA, 2019. Available online: https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGDF_06/summary (accessed on 21 December 2020). [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef] [Green Version]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizume, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K. Global precipitation map using satellite-borne microwave radiometers by the GSMaP project: Production and validation. IEEE Trans. Geosci. Remote 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Aonashi, K.; Awaka, J.; Hirose, M.; Kozu, T.; Kubota, T.; Liu, G.; Shige, S.; Kida, S.; Seto, S.; Takahashi, N. GSMaP passive microwave precipitation retrieval algorithm: Algorithm description and validation. J. Meteor. Soc. Jpn. 2009, 87, 119–136. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114, D24101. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Yong, B.; Shen, Y.; Liu, J.; Hong, Y.; Zhang, J. Comparison analysis of six purely satellite-derived global precipitation estimates. J. Hydrol. 2020, 581, 124376. [Google Scholar] [CrossRef]
- Su, J.; Lü, H.; Zhu, Y.; Wang, X.; Wei, G. Component Analysis of Errors in Four GPM-Based Precipitation Estimations over Mainland China. Remote Sens. 2018, 10, 1420. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Wang, Y.; Chen, L.; Wang, Z.; Zhu, H.; Li, B. Inter-Comparison and Evaluation of Remote Sensing Precipitation Products over China from 2005 to 2013. Remote Sens. 2018, 10, 168. [Google Scholar] [CrossRef] [Green Version]
- Gebregiorgis, A.S.; Kirstetter, P.E.; Hong, Y.E.; Gourley, J.J.; Huffman, G.J.; Petersen, W.A.; Xue, X.; Schwaller, M.R. To What Extent is the Day 1 GPM IMERG Satellite Precipitation Estimate Improved as Compared to TRMM TMPA-RT? J. Geophys. Res. Atmos. 2018, 123, 1694–1707. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef] [Green Version]
- Nwachukwu, P.N.; Satge, F.; Yacoubi, S.E.; Pinel, S.; Bonnet, M. From TRMM to GPM: How Reliable Are Satellite-Based Precipitation Data across Nigeria? Remote Sens. 2020, 12, 3964. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Li, L.; Wang, J.; Qi, W.; Xu, C.; Kim, J. Evaluation of Multi-Satellite Precipitation Datasets and Their Error Propagation in Hydrological Modeling in a Monsoon-Prone Region. Remote Sens. 2020, 12, 3550. [Google Scholar] [CrossRef]
- Ehsan Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N.; Polcher, J.; Albergel, C.; Dutra, E.; Fink, G.; Martínez-de La Torre, A.; Munier, S. Assessment of precipitation error propagation in multi-model global water resource reanalysis. Hydrol. Earth Syst. Sci. 2019, 23, 1973–1994. [Google Scholar] [CrossRef] [Green Version]
- Falck, A.S.; Maggioni, V.; Tomasella, J.; Vila, D.A.; Diniz, F.L.R. Propagation of satellite precipitation uncertainties through a distributed hydrologic model: A case study in the Tocantins–Araguaia basin in Brazil. J. Hydrol. 2015, 527, 943–957. [Google Scholar] [CrossRef]
- Zhu, D.; Peng, D.Z.; Cluckie, I.D. Statistical analysis of error propagation from radar rainfall to hydrological models. Hydrol. Earth Syst. Sci. 2013, 17, 1445–1453. [Google Scholar] [CrossRef] [Green Version]
- Pan, M.; Li, H.; Wood, E. Assessing the skill of satellite-based precipitation estimates in hydrologic applications. Water Resour. Res. 2010, 46, W09535. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef] [Green Version]
- Mazzoleni, M.; Brandimarte, L.; Amaranto, A. Evaluating precipitation datasets for large-scale distributed hydrological modelling. J. Hydrol. 2019, 578, 124076. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G.; Bierkens, M.F.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.; Sivapalan, M. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Michaud, J.D.; Sorooshian, S. Effect of rainfall-sampling errors on simulations of desert flash floods. Water Resour. Res. 1994, 30, 2765–2775. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Krajewski, W.F.; Ciach, G.J.; Villarini, G.; Smith, J.A. Estimation of radar-rainfall error spatial correlation. Adv. Water Resour. 2009, 32, 1020–1030. [Google Scholar] [CrossRef]
- Nijssen, B.; Lettenmaier, D. Effect of precipitation sampling error on simulated hydrological fluxes and states: Anticipating the Global Precipitation Measurement satellites. J. Geophys. Res. Atmos. 2004, 109, D02103. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Hossain, F.; Gebremichael, M.; Borga, M. Understanding the Scale Relationships of Uncertainty Propagation of Satellite Rainfall through a Distributed Hydrologic Model. J. Hydrometeorol. 2010, 11, 520–532. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Critical examination of area reduction factors. J. Hydrol. Eng. 2014, 19, 769–776. [Google Scholar] [CrossRef]
- Biondi, D.; Greco, A.; De Luca, D.L. Fixed-area vs storm-centered areal reduction factors: A Mediterranean case study. J. Hydrol. 2021, 595, 125654. [Google Scholar] [CrossRef]
- Greco, A.; De Luca, D.L.; Avolio, E. Heavy Precipitation Systems in Calabria Region (Southern Italy): High-Resolution Ob-served Rainfall and Large-Scale Atmospheric Pattern Analysis. Water 2020, 12, 1468. [Google Scholar] [CrossRef]
- Houze, R.A., Jr. Structures of atmospheric precipitation systems—A global survey. Radio Sci. 1981, 16, 671–689. [Google Scholar] [CrossRef]
- Willems, P. A spatial rainfall generator for small spatial scales. J. Hydrol. 2001, 252, 126–144. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, J.; Xu, Y. Establishment and assessment of the grid precipitation datasets in China for recent 50 years. J. Meteor. Sci. 2014, 34, 414–420. (In Chinese) [Google Scholar]
- Qu, S.; Wang, L.; Lin, A.; Zhu, H.; Yuan, M. What drives the vegetation restoration in Yangtze River basin, China: Climate change or anthropogenic factors? Ecol. Indic. 2018, 90, 438–450. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Chen, S.; Ndayisaba, F. Evaluation of PERSIANN-CDR for Meteorological Drought Monitoring over China. Remote Sens. 2016, 8, 379. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.; Zhong, R.; Wang, Z.; Wu, X.; Chen, X.; Wang, P.; Lian, Y. Monitoring hydrological drought using long-term satellite-based precipitation data. Sci. Total Environ. 2019, 649, 1198–1208. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.; Yang, H.; Sweetapple, C. An ensemble-based dynamic Bayesian averaging approach for discharge simulations using multiple global precipitation products and hydrological models. J. Hydrol. 2018, 558, 405–420. [Google Scholar] [CrossRef]
- Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS Data Portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef] [Green Version]
- Hsu, K.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteor. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteor. 2004, 43, 1834–1852. [Google Scholar] [CrossRef] [Green Version]
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavy precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Ombadi, M.; Gorooh, V.A.; Shearer, E.J.; Sadeghi, M.; Sorooshian, S.; Hsu, K.; Bolvin, D.; Ralph, M.F. PERSIANN Dynamic Infrared–Rain Rate (PDIR-Now): A Near real-Time, Quasi-Global Satellite Precipitation Dataset. J. Hydrometeorol. 2020, 21, 2893–2906. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Shearer, E.J.; Ombadi, M.; Gorooh, V.A.; Hsu, K.; Sorooshian, S.; Logan, W.S.; Ralph, M. PERSIANN Dynamic Infrared–Rain Rate Model (PDIR) for High-Resolution, Real-Time Satellite Precipitation Estimation. Bull. Am. Meteorol. Soc. 2020, 101, E286–E302. [Google Scholar] [CrossRef]
- Xie, P.P.; Joyce, R.; Wu, S.R.; Yoo, S.-H.; Yarosh, Y.; Sun, F.Y.; Lin, R. NOAA CDR Program (2019): NOAA Climate Data Record (CDR) of CPC Morphing Technique (CMORPH) High Resolution Global Precipitation Estimates, Version 1; NOAA National Centers for Environmental Information: College Park, MD, USA, 2019. Available online: https://www.ncei.noaa.gov/access/metadata/landing-page/bin/iso?id=gov.noaa.ncdc:C00948 (accessed on 22 December 2020). [CrossRef]
- Xu, C.; Wang, J.; Li, Q. A new method for temperature spatial interpolation based on sparse historical stations. J. Clim. 2018, 31, 1757–1770. [Google Scholar] [CrossRef]
- Shepard, D.S. Computer Mapping: The SYMAP Interpolation Algorithm; Springer: Berlin/Heidelberg, Germany, 1984; pp. 133–145. [Google Scholar]
- Xia, J. Identification of a constrained nonlinear hydrological system described by Volterra Functional Series. Water Resour. Res. 1991, 27, 2415–2420. [Google Scholar] [CrossRef]
- Xia, J.; Wang, G.; Tan, G.; Ye, A.; Huang, G.H. Development of distributed time-variant gain model for nonlinear hydrological systems. Sci. China Ser. D Earth Sci. 2005, 48, 713–723. [Google Scholar] [CrossRef]
- Ye, A.; Duan, Q.; Zheng, H.; Li, L.; Wang, C. A Distributed Time-Variant Gain Hydrological Model Based on Remote Sensing. J. Resour. Ecol. 2010, 3, 222–230. [Google Scholar] [CrossRef]
- Du, C.; Ye, A.; Gan, Y.; You, J.; Duan, Q.; Ma, F.; Hou, J. Drainage network extraction from a high-resolution DEM using parallel programming in the NET Framework. J. Hydrol. 2017, 555, 506–517. [Google Scholar] [CrossRef]
- Ye, A.; Duan, Q.; Zhan, C.; Liu, Z.; Mao, Y. Improving kinematic wave routing scheme in Community Land Model. Hydrol Res. 2013, 44, 886–903. [Google Scholar] [CrossRef] [Green Version]
- Ye, A.; Zhou, Z.; You, J.; Ma, F.; Duan, Q. Dynamic Manning’s roughness coefficients for hydrological modelling in basins. Hydrol Res. 2018, 49, 1379–1395. [Google Scholar] [CrossRef]
- Bormann, K.J.; Evans, J.P.; McCabe, M.F. Constraining snowmelt in a temperature-index model using simulated snow densities. J. Hydrol. 2014, 517, 652–667. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Camici, S.; Massari, C.; Ciabatta, L.; Marchesini, I.; and Brocca, L. Which rainfall score is more informative about the per-formance in river discharge simulation? A comprehensive assessment on 1318 basins over Europe. Hydrol. Earth Syst. Sci. 2020, 24, 4869–4885. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Terink, W.; Leijnse, H.; van den Eertwegh, G.; Uijlenhoet, R. Spatial resolutions in areal rainfall estimation and their impact on hydrological simulations of a lowland catchment. J. Hydrol. 2018, 563, 319–335. [Google Scholar] [CrossRef]
- Vergara, H.; Hong, Y.; Gourley, J.J.; Anagnostou, E.N.; Maggioni, V.; Stampoulis, D.; Kirstetter, P. Effects of Resolution of Satellite-Based Rainfall Estimates on Hydrologic Modeling Skill at Different Scales. J. Hydrometeorol. 2014, 15, 593–613. [Google Scholar] [CrossRef] [Green Version]
- Cunha, L.K.; Mandapaka, P.V.; Krajewski, W.F.; Mantilla, R.; Bradley, A.A. Impact of radar-rainfall error structure on estimated flood magnitude across scales: An investigation based on a parsimonious distributed hydrological model. Water Resour. Res. 2012, 48, W10515. [Google Scholar] [CrossRef]
- Sampson, A.A.; Wright, D.B.; Stewart, R.D.; LoBue, A. The Role of Rainfall Temporal and Spatial Averaging in Seasonal Simulations of the Terrestrial Water Balance. Hydrol. Process. 2020, 34, 2531–2542. [Google Scholar] [CrossRef]
- Huang, Y.; Bárdossy, A.; Zhang, K. Sensitivity of hydrological models to temporal and spatial resolutions of rainfall data. Hydrol. Earth Syst. Sci. 2019, 23, 2647–2663. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Huang, S.; He, R.; Wang, G.; Tan, M.L.; Yang, X.; Zheng, Z. Impact of temporal rainfall resolution on daily streamflow simulations in a large-sized river basin. Hydrol. Sci. J. 2020, 65, 2630–2645. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef] [Green Version]
- Demaria, E.M.; Nijssen, B.; Valdés, J.B.; Rodriguez, D.A.; Su, F. Satellite precipitation in southeastern South America: How do sampling errors impact high flow simulations? Int. J. River Basin Manag. 2014, 12, 1–13. [Google Scholar] [CrossRef]
- Bruni, G.; Reinoso, R.; van de Giesen, N.C.; Clemens, F.H.L.R.; Ten Veldhuis, J.A.E. On the sensitivity of urban hydrodynamic modelling to rainfall spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2015, 19, 691–709. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.; Wang, H.; Jia, P.; Tang, G.; Wang, D.; Ma, Z.; Yan, H. Application of the GPM-IMERG Products in Flash Flood Warning: A Case Study in Yunnan, China. Remote Sens. 2020, 12, 1954. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).