Study of the Spatiotemporal Characteristics of the Equatorial Ionization Anomaly Using Shipborne Multi-GNSS Data: A Case Analysis (120–150°E, Western Pacific Ocean, 2014–2015)
Abstract
:1. Introduction
2. Data and Processing Methods
2.1. Kinematic GNSS Data Acquisition
2.2. Ionosphere TEC Derived from Dual-Frequency GNSS Observations
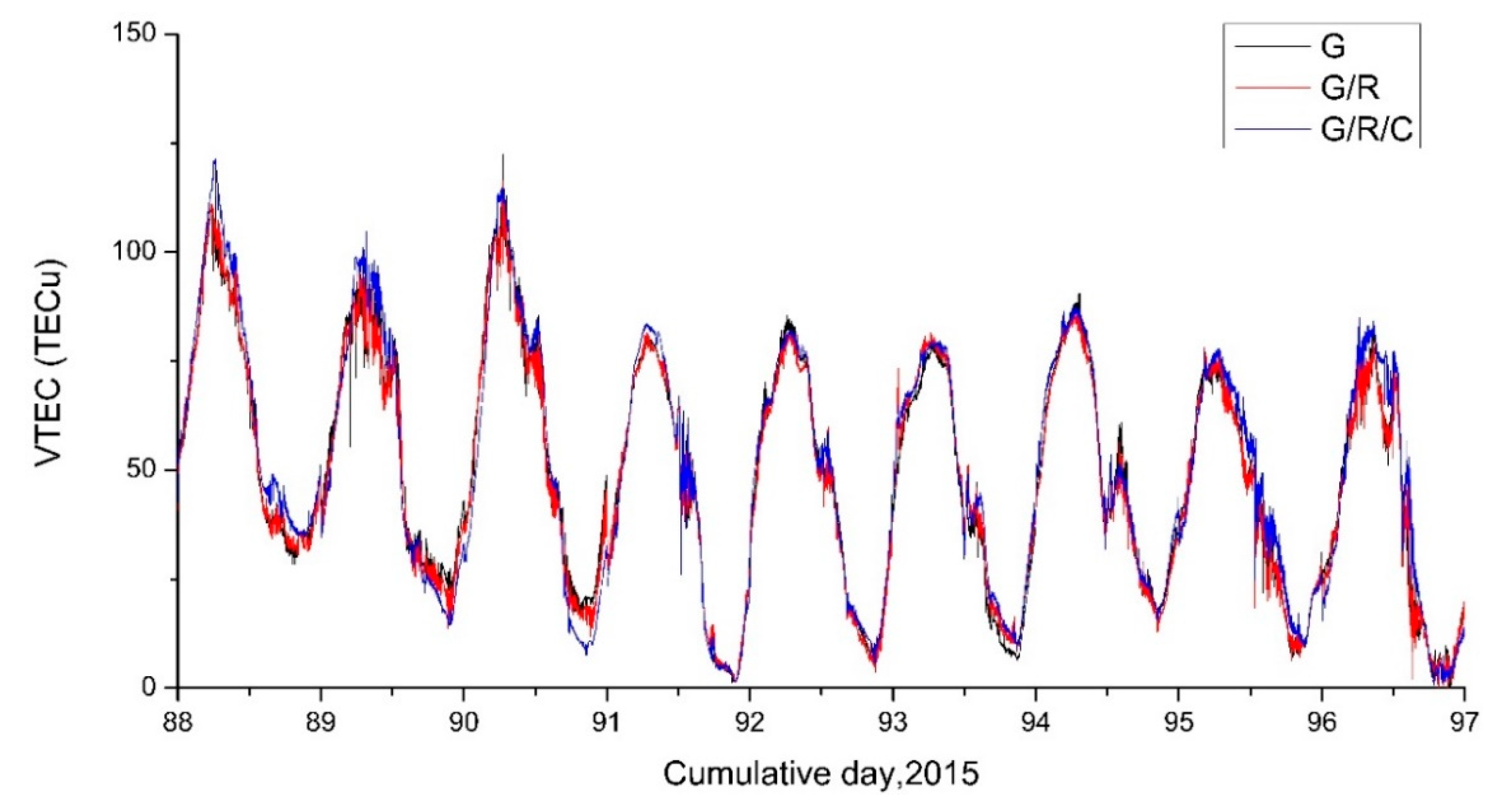
2.3. Comparison of Different Satellite System Combinations
3. Results and Analysis
3.1. Comparison of Different Satellite System Combinations
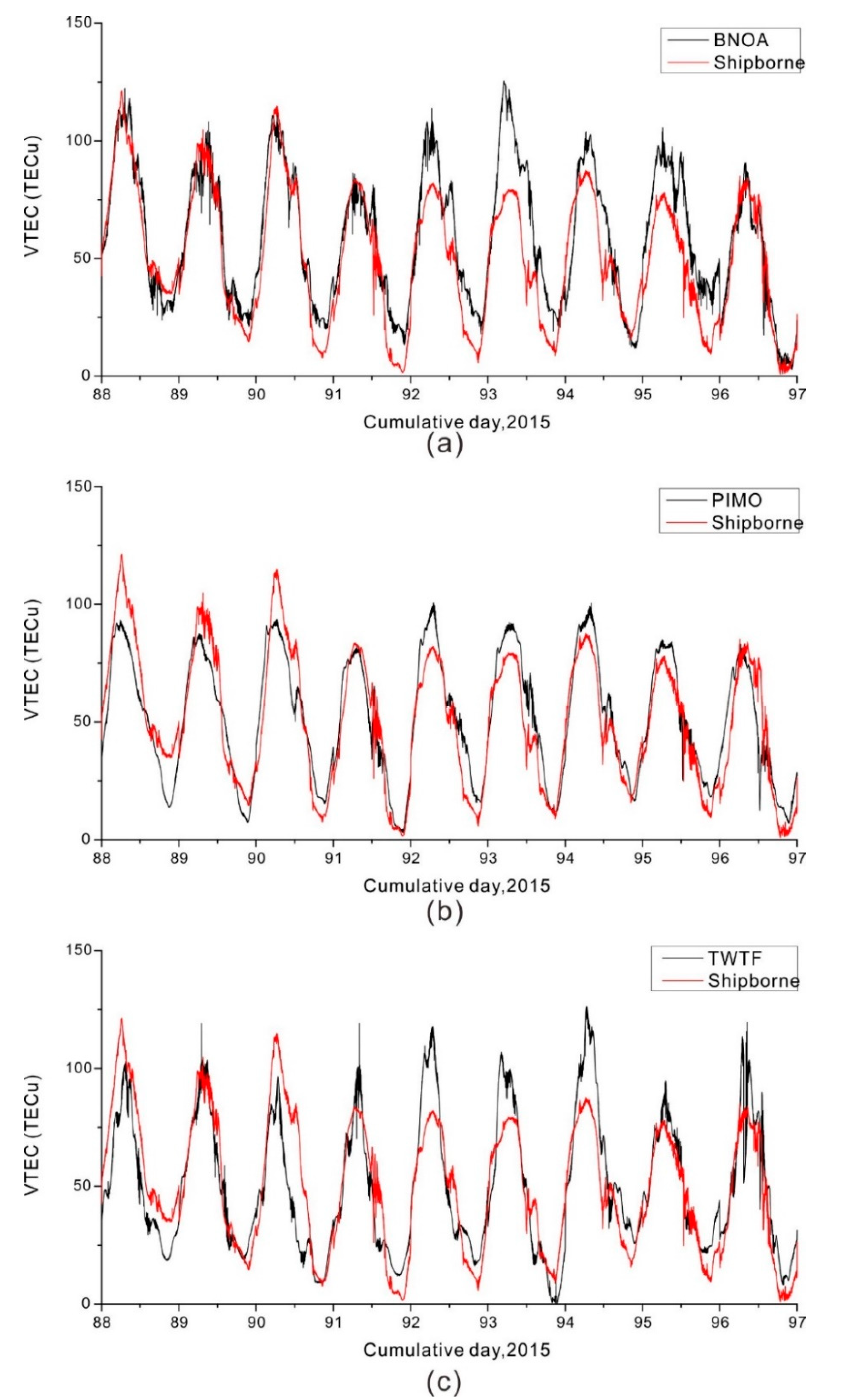
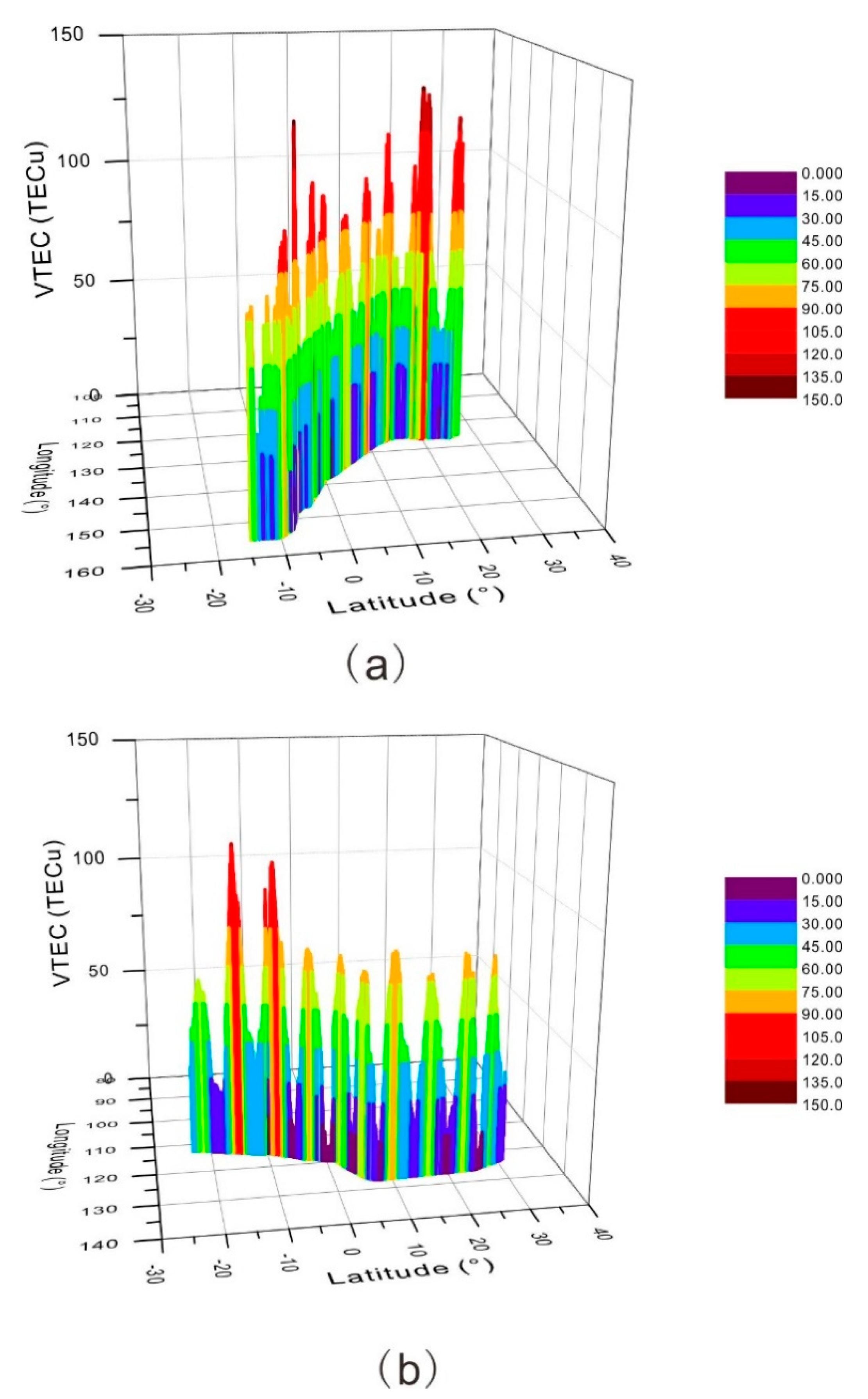
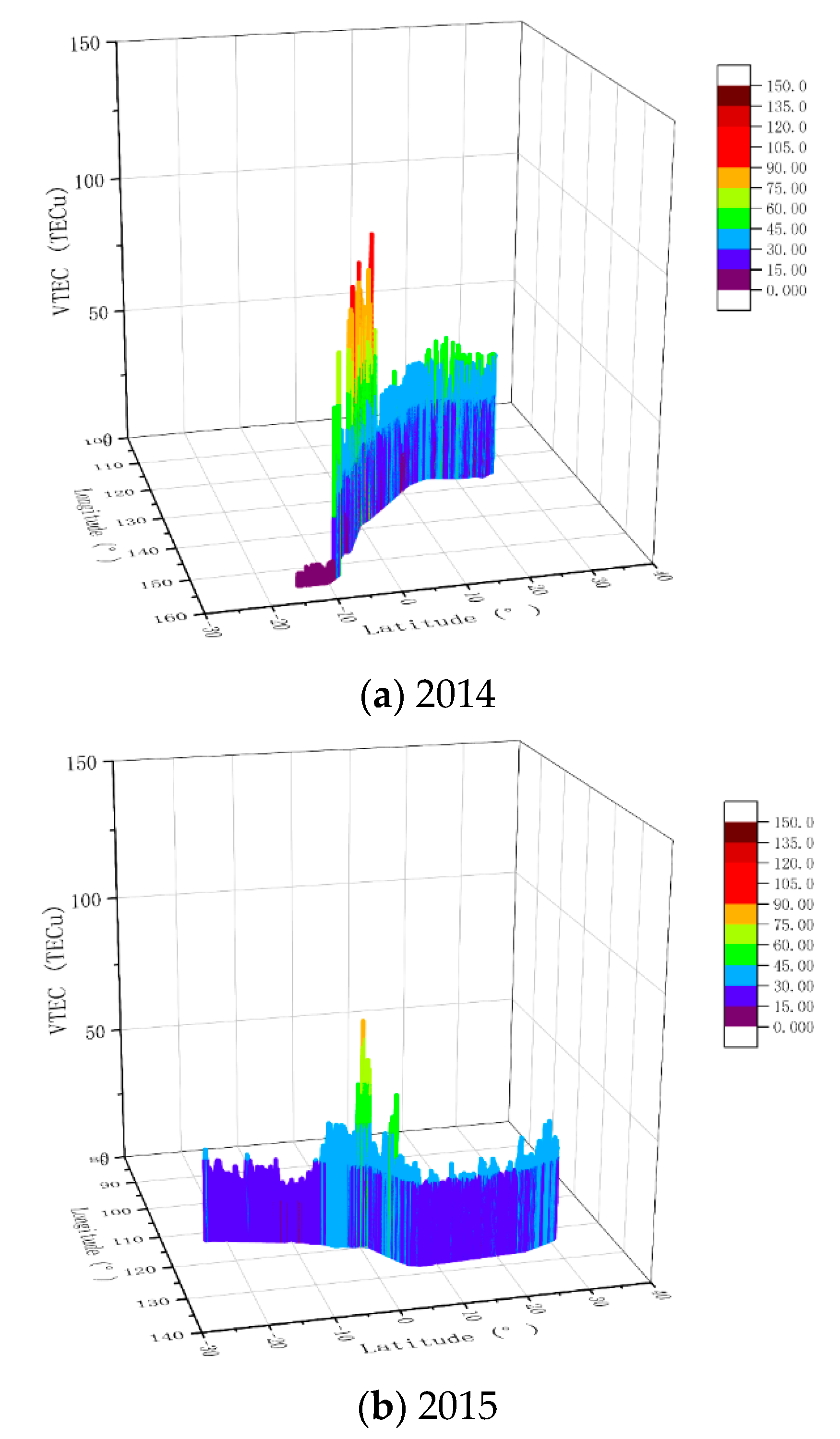
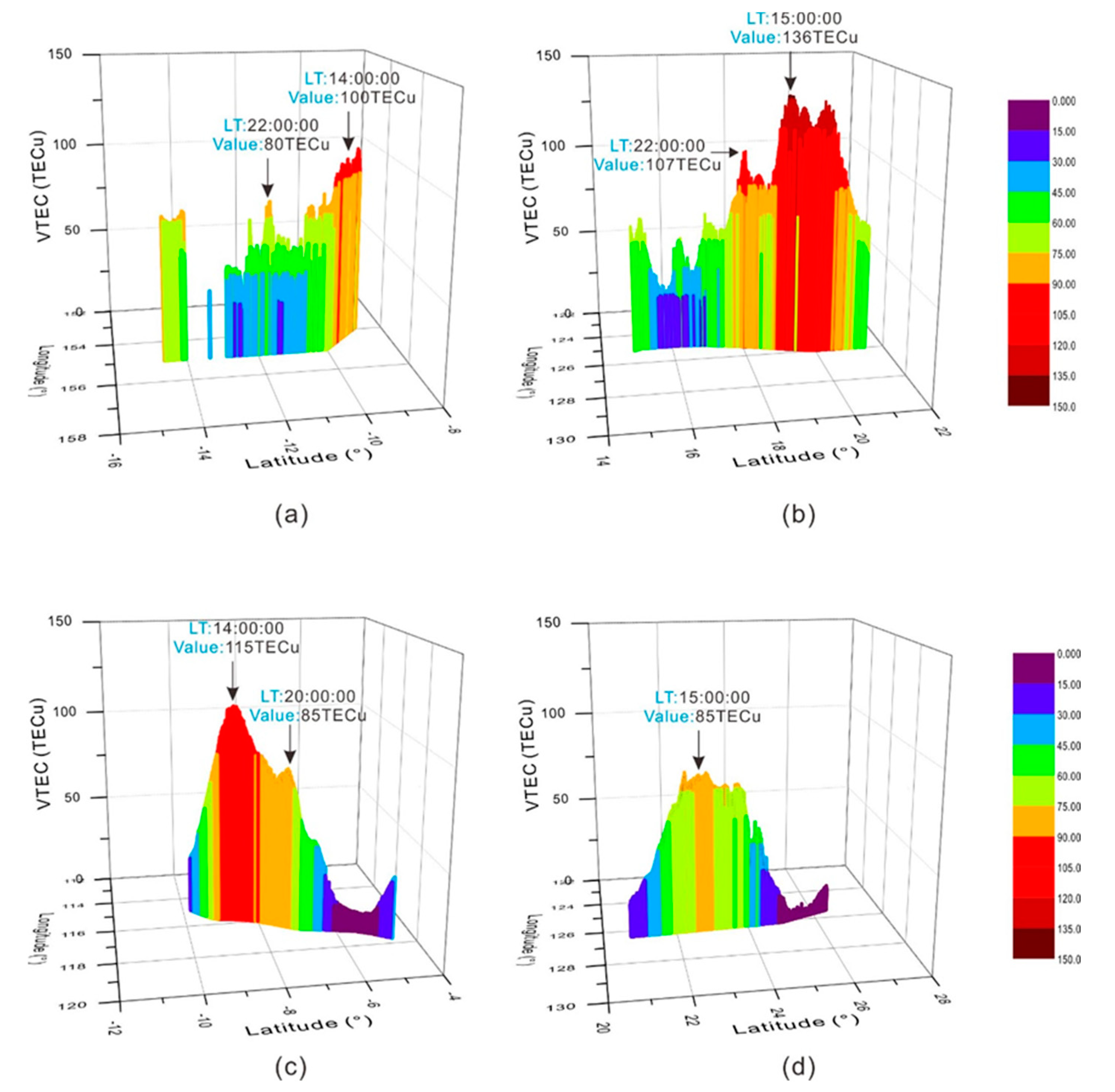
3.2. Analysis of Spatiotemporal Characteristics of Kinematic Ionospheric TEC
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Appleton, E.V. Two Anomalies in the Ionosphere. Nat. Cell Biol. 1946, 157, 691. [Google Scholar] [CrossRef]
- Croom, S.; Robbins, A.; Thomas, J.O. Two Anomalies in the Behaviour of the F2 Layer of the Ionosphere. Nat. Cell Biol. 1959, 184, 2003–2004. [Google Scholar] [CrossRef]
- Hanson, W.B.; Moffett, R.J. lonization transport effects in the equatorialFregion. J. Geophys. Res. Space Phys. 1966, 71, 5559–5572. [Google Scholar] [CrossRef]
- Gadsden, M. An Introduction to the Ionosphere and Magnetosphere. Phys. Bull. 1973, 24, 448. [Google Scholar] [CrossRef]
- Martyn, D.F. Theory of height and ionization density changes at the maximum of a Chapman-like region, taking account of ion production, decay, diffusion and tidal drift. In Proceedings of the Physics of the Ionosphere, Cavendish Laboratory, Cambridge, UK, September 1954; The Physical Society: London, UK, 1955; p. 254. [Google Scholar]
- Sethia, G.; Chandra, H.; Rastogi, R.G. Equatorial electrojet control on the low latitude ionospheric total electron content. Proc. Indian Acad. Sci. Sect. A 1979, 88, 87–91. [Google Scholar]
- Townsend, R.E.; Cannata, R.W.; Prochaska, R.D.; Rattray, G.E.; Holbrook, J.C. Source Book of the Solar-Geophysical Environment. Air Force Glob. Weather. Cent. Offutt Afb Ne 1982. [Google Scholar]
- Richmond, A.D. Modeling the ionosphere wind dynamo: A review. Pure Appl. Geophys. 1989, 131, 413–435. [Google Scholar] [CrossRef]
- Balan, N.; Bailey, G.J.; Abdu, M.A.; Oyama, K.I.; Richards, P.G.; MacDougall, J.; Batista, I.S. Equatorial plasma fountain and its effects over three locations: Evidence for an additional layer, the F3 layer. J. Geophys. Res. Space Phys. 1997, 102, 2047–2056. [Google Scholar] [CrossRef]
- Venkatesh, K.; Fagundes, P.R.; Prasad, D.S.V.V.D.; Denardini, C.M.; De Abreu, A.J.; De Jesus, R.; Gende, M. Day-to-day variability of equatorial electrojet and its role on the day-to-day characteristics of the equatorial ionization anomaly over the Indian and Brazilian sectors. J. Geophys. Res. Space Phys. 2015, 120, 9117–9131. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Patel, K.; Singh, A.K. TEC variation over an equatorial and anomaly crest region in India during 2012 and 2013. GPS Solut. 2015, 20, 617–626. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Yuan, Y.; Ou, J. Auto-covariance estimation of variable samples (ACEVS) and its application for monitoring random ionospheric disturbances using GPS. J. Geod. 2001, 75, 438–447. [Google Scholar] [CrossRef]
- Prieto-Cerdeira, R.; Orús-Pérez, R.; Breeuwer, E.; Lucas-Rodriguez, R.; Falcone, M. Performance of the Galileo single-frequency ionospheric correction during in-orbit validation. GPS World 2014, 25, 53–58. [Google Scholar]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Wang, W.-M.; Wang, B.; Yang, S.-G. Analysis and prediction of ionospheric total electron content of the Equatorial Ionization Anomaly around 120°E longitude. Chin. J. Geophys. 2012, 7, 2185–2192. [Google Scholar]
- Kumar, S.; Priyadarshi, S.; Krishna, S.G.; Singh, A.K. GPS-TEC variations during low solar activity period (2007–2009) at Indian low latitude stations. Astrophys. Space Sci. 2012, 339, 165–178. [Google Scholar] [CrossRef]
- Ouattara, F.; Gnabahou, D.A.; Mazaudier, C.A. Seasonal, Diurnal, and Solar-Cycle Variations of Electron Density at Two West Africa Equatorial Ionization Anomaly Stations. Int. J. Geophys. 2012, 2012, 1–9. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Z.; Shi, S.; Zhang, B.B. Using IGS to analyze the variation of anomaly equatorial ionization. Sci. Surv. Mapp. 2016, 41, 44–47. [Google Scholar]
- Romero-Hernandez, E.; Denardini, C.M.; Takahashi, H.; Gonzalez-Esparza, J.A.; Nogueira, P.A.B.; De Padua, M.B.; Lotte, R.G.; Negreti, P.D.S.; Jonah, O.F.; Resende, L.C.A.; et al. Daytime ionospheric TEC weather study over Latin America. J. Geophys. Res. Space Phys. 2018, 123, 10345–10357. [Google Scholar] [CrossRef]
- Ram, S.T.; Su, S.-Y.; Liu, C.H. FORMOSAT-3/COSMIC observations of seasonal and longitudinal variations of equatorial ionization anomaly and its interhemispheric asymmetry during the solar minimum period. J. Geophys. Res. Space Phys. 2009, 114, 06311. [Google Scholar] [CrossRef]
- Huang, L.; Huang, J.; Wang, J.; Jiang, Y.; Deng, B.; Zhao, K.; Lin, G. Analysis of the north–south asymmetry of the equatorial ionization anomaly around 110°E longitude. J. Atmos. Sol. Terr. Phys. 2013, 102, 354–361. [Google Scholar] [CrossRef]
- Walker, G.O.; Ma, J.H.K.; Golton, E. The equatorial ionospheric anomaly in electron content from solar minimum to solar maximum for South East Asia. Ann. Geophys. 1994, 12, 195–209. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H.; Wan, W.; Zhang, H. Equatorial ionization anomaly in the low-latitude topside ionosphere: Local time evolution and longitudinal difference. J. Geophys. Res. Space Phys. 2016, 121, 7166–7182. [Google Scholar] [CrossRef]
- Lin, C.H.; Hsiao, C.C.; Liu, J.Y.; Liu, C.H. Longitudinal structure of the equatorial ionosphere: Time evolution of the four-peaked EIA structure. J. Geophys. Res. Space Phys. 2007, 112, 12305. [Google Scholar] [CrossRef]
- Huang, H.; Lu, X.; Liu, L.; Wang, W.; Li, Q. Transition of Interhemispheric Asymmetry of Equatorial Ionization Anomaly During Solstices. J. Geophys. Res. Space Phys. 2018, 123, 10283–10300. [Google Scholar] [CrossRef]
- Chou, M.Y.; Lin, C.C.H.; Tsai, H.F.; Lin, C.Y. Ionospheric electron density inversion for Global Navigation Satellite Systems radio occultation using aided Abel inversions. J. Geophys. Res. Space Phys. 2017, 122, 1386–1399. [Google Scholar] [CrossRef]
- Feng, J.; Han, B.; Zhao, Z.; Wang, Z. A New Global Total Electron Content Empirical Model. Remote Sens. 2019, 11, 706. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.Y.; Lin, C.C.H.; Liu, T.J.Y.; Rajesh, P.K.; Chou, M.Y. Simulation and Validation of FORMOSAT-7/COSMIC-2 Space Weather Products: Global Iono-spheric Specification Electron Density Structure and Aided Abel Electron Density Profile. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019; Volume 2019, p. SA13B-3249. [Google Scholar]
- Yunbin, Y.; Xingliang, H.; Jikun, O. Models and methods for precise determination of Ionospheric delay using GPS. Prog. Nat. Sci. 2007, 17, 187–196. [Google Scholar] [CrossRef]
- Wang, C.; Shi, C.; Fan, L.; Zhang, H. Improved Modeling of Global Ionospheric Total Electron Content Using Prior Information. Remote Sens. 2018, 10, 63. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Ou, J. A generalized trigonometric series function model for determining ionospheric delay. Prog. Nat. Sci. 2004, 14, 1010–1014. [Google Scholar] [CrossRef]
- Yuan, Y. Study on the New Methods of Correcting Ionospheric Delay and Ionospheric Model Using GPS Data. J. Grad. Sch. Chin. Acad. Sci. 2002, 19, 209–214. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Wang, D.; Wang, J.; Wu, Z.; Gao, J.; Zhang, T.; Yang, C.; Qin, X.; Chen, X. Study of the Spatiotemporal Characteristics of the Equatorial Ionization Anomaly Using Shipborne Multi-GNSS Data: A Case Analysis (120–150°E, Western Pacific Ocean, 2014–2015). Remote Sens. 2021, 13, 3051. https://doi.org/10.3390/rs13153051
Luo X, Wang D, Wang J, Wu Z, Gao J, Zhang T, Yang C, Qin X, Chen X. Study of the Spatiotemporal Characteristics of the Equatorial Ionization Anomaly Using Shipborne Multi-GNSS Data: A Case Analysis (120–150°E, Western Pacific Ocean, 2014–2015). Remote Sensing. 2021; 13(15):3051. https://doi.org/10.3390/rs13153051
Chicago/Turabian StyleLuo, Xiaowen, Di Wang, Jinling Wang, Ziyin Wu, Jinyao Gao, Tao Zhang, Chunguo Yang, Xiaoming Qin, and Xiaolun Chen. 2021. "Study of the Spatiotemporal Characteristics of the Equatorial Ionization Anomaly Using Shipborne Multi-GNSS Data: A Case Analysis (120–150°E, Western Pacific Ocean, 2014–2015)" Remote Sensing 13, no. 15: 3051. https://doi.org/10.3390/rs13153051
APA StyleLuo, X., Wang, D., Wang, J., Wu, Z., Gao, J., Zhang, T., Yang, C., Qin, X., & Chen, X. (2021). Study of the Spatiotemporal Characteristics of the Equatorial Ionization Anomaly Using Shipborne Multi-GNSS Data: A Case Analysis (120–150°E, Western Pacific Ocean, 2014–2015). Remote Sensing, 13(15), 3051. https://doi.org/10.3390/rs13153051





