1. Introduction
The rapid increase in population and economic development across East Asia has led to high atmospheric sulfur dioxide (SO
2) concentrations in the region, although the trend has been decreasing in recent years [
1,
2,
3,
4,
5,
6]. Most of the SO
2 in the atmosphere is emitted from anthropogenic sources such as fossil fuel combustion, although some is also emitted from natural sources such as volcanoes [
7,
8,
9]. These SO
2 emissions can, either directly or indirectly, adversely affect human health and the environment [
9]. The significant effects of atmospheric SO
2 on human health include cardiopulmonary disease, pulmonary edema, eye irritation, asthma attacks, and an increase in mortality rate [
10,
11,
12]. Examples of adverse environmental effects include acid deposition [
13,
14,
15,
16,
17], photochemical smog [
18,
19,
20], and heavy haze [
21,
22,
23,
24,
25]. Chemical reactions transform SO
2 into sulfate and sulfuric acid [
26]. SO
2 and various sulfuric aerosols are also known to affect radiative forcing by acting as cloud condensation nuclei and scattering solar radiation, thereby having a cooling effect on the atmosphere [
27,
28,
29,
30]. SO
2 has a lifetime of 1 to 2 days and can be transported over long distances from hotspots or its source areas to downwind locations [
31,
32]. The transported SO
2 may affect the chemical composition of the atmosphere in the receptor area as a result of enhanced SO
2 loading and sulfuric aerosols. To establish an effective SO
2 reduction strategy in a receptor area, it is necessary to quantify the impact of the long-range transport of SO
2 (LRT-SO
2) amounts in the receptor area.
Satellite observations provide regional and global coverage over short time intervals of one to several days, and recent studies [
33,
34,
35] have investigated emission trends and LRT-SO
2 using such data. One such study [
35] of LRT-SO
2 was conducted using data obtained from the Ozone Monitoring Instrument (OMI), which is a UV–Vis hyperspectral sensor onboard the low Earth orbit Aura satellite. Other studies [
36,
37,
38,
39] have focused on the detection of LRT-SO
2 emitted from volcanic eruptions. The LRT-SO
2 emitted from the Asian continent has been observed using OMI [
33,
34]. Lee et al. [
40] used data from the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography (SCIAMACHY) to detect LRT-SO
2 from Asia to the Korean Peninsula and validated this approach through a comparison with Multi-Axis Differential Optical Absorption Spectroscopy (MAX-DOAS) data and in situ measurements. Donkelaar et al. [
41] estimated the LRT-SO
2 contribution from East Asia and North America using data from Chemical Transport Models (CTMs) and from aircraft and satellites, i.e., MODIS and the Multi-angle Imaging SpectroRadiometer (MISR). Li et al. [
33] reported LRT-SO
2 from northern China based on OMI data and HTSPLIT backward trajectory calculation. In addition, Hsu et al. [
34] reported LRT-SO
2 from China and the Pacific Ocean, mainly using OMI data, and utilized the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) data for aerosol layer information, which is used to estimate the SO
2 plume layer height. Another study [
35] also reported an episode of high SO
2 concentrations over northern India as a result of LRT-SO
2 from Africa using OMI and HYSPLIT backward trajectory analysis data, and utilized the CALIPSO data to retrieve the vertical distribution of aerosol layers.
All of these studies [
33,
34,
35,
40,
41] reported LRT-SO
2 detection in various regions, and some of them [
33,
34] reported satellite-based LRT-SO
2 observation. Other studies [
35,
40,
41] have investigated the effect of LRT-SO
2 on local air quality. For better understanding the contribution of LRT-SO
2 to changes in SO
2 amounts in receptor regions, it is important to quantify the flow rate of LRT-SO
2, which is calculated from the amount of SO
2 transferred from source areas to receptor areas.
Park et al. [
42] calculated, for the first time, the flow rates of SO
2 transported from Asia to the Korean Peninsula, Japan, and the northwest Pacific Ocean using their own LRT-SO
2 flow rate calculation method based on OMI SO
2 vertical column density (VCD) data [
43,
44], HYSPLIT simulations [
45], and planetary boundary layer (PBL) height information [
46]. Park et al. [
42] used daily OMI SO
2 data so that the LRT-SO
2 flow rate at a receptor area could be obtained with a daily temporal and spatial resolution. If SO
2 VCD data can be obtained at a higher temporal resolution than daily ones, a better understanding of the continuous movement of the SO
2 plume and its flow into receptor areas can be developed. The geostationary environment monitoring spectrometer (GEMS), launched in February 2020, was developed to monitor diurnal variations in air pollutants caused by time-dependent emissions, photochemistry, and meteorological variability [
47]. GEMS is the first hyperspectral UV–Vis sensor onboard a geostationary Earth orbit satellite, and it is capable of providing hourly SO
2 VCD information all over Asia, from India to Japan in a west-to-east direction, and from Indonesia to northern China in a south-to-north direction. We used an LRT-SO
2 flow rate calculation algorithm that had been introduced in a previous study [
42]. In the present study, the LRT-SO
2 flow rate calculation algorithm used hourly SO
2 VCDs as input data for hourly calculation of SO
2 flow rate. However, it is important to understand the uncertainties associated with these SO
2 flow rate estimates.
The aim of this study is to quantify the contribution of the GEMS SO
2 slant column density (SCD) retrieval errors and wind data uncertainties to the errors associated with estimates of LRT-SO
2 flow rate. We used the LRT-SO
2 flow rate algorithm [
42] to calculate the LRT-SO
2 flow rates for both anthropogenic and volcanic SO
2 emissions based on the synthetic GEMS radiances over the Korean Peninsula. The GEMS synthetic radiances were generated using a Radiative Transfer Model (RTM) based on the linearized pseudo-spherical scalar and vector discrete ordinate radiative transfer (VLIDORT v2.6 [
48]) code, with inputs of trace gases and aerosol data from the GEOS-Chem simulation [
49].
Section 2 describes how we calculated the contributions from errors associated with the GEMS SO
2 SCDs and wind data to the errors in the LRT-SO
2 flow rate estimates.
Section 2 also provides detailed descriptions of the GEOS-Chem input data and the conditions used for the simulations and those of VLIDORT.
Section 3 shows the effects of the GEMS SO
2 SCD retrieval errors and wind data uncertainties on the LRT-SO
2 flow rate errors over the Korean Peninsula, as calculated for several anthropogenic and volcanic SO
2 transport events.
2. Data and Methods
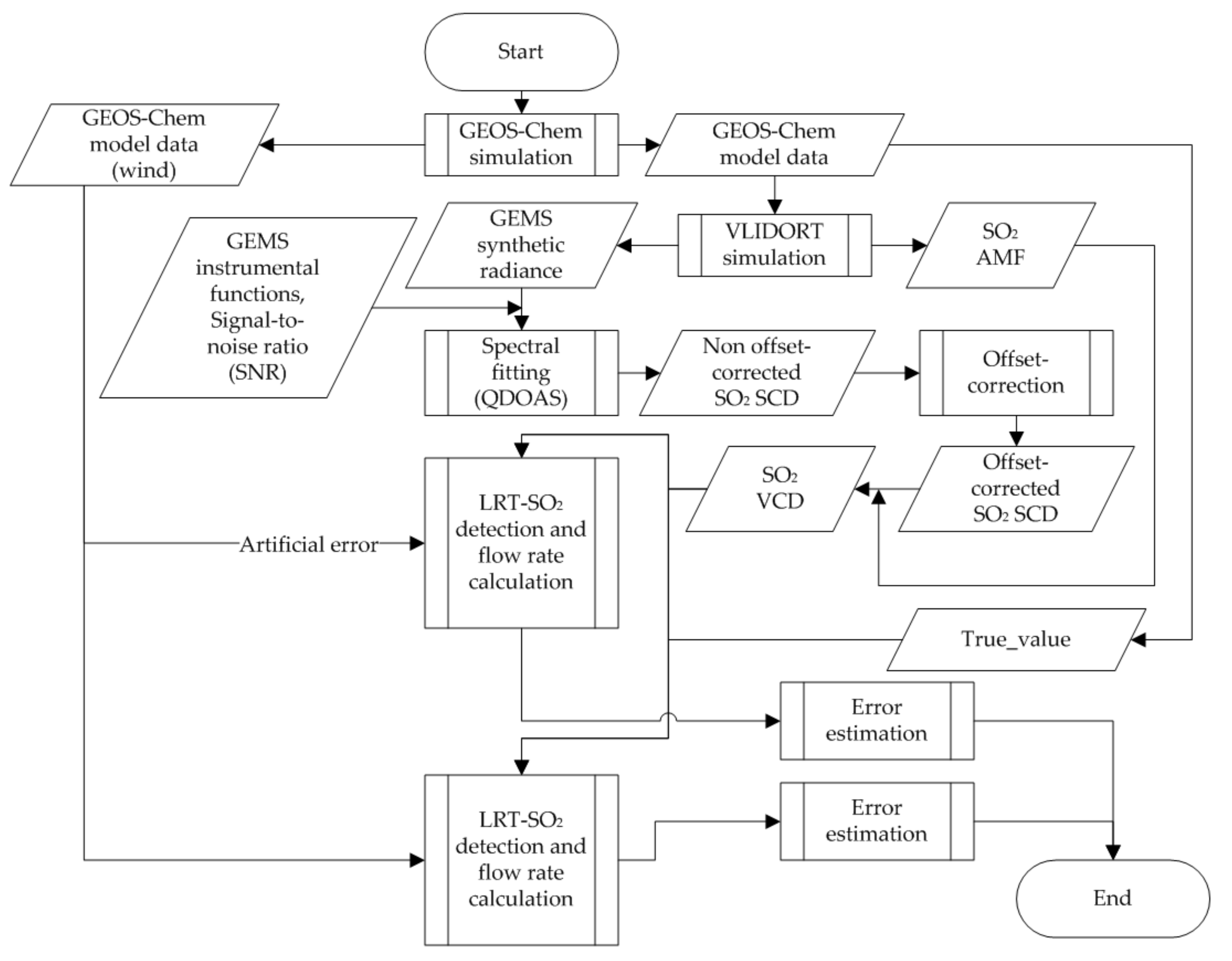
Figure 1 shows each step of the present study. We generated the GEMS synthetic radiances using the RTM (VLIDORT v2.6 [
48]) and GEOS-Chem model [
49] data. The SO
2 air mass factor (AMF) was also calculated with the RTM simulation. The SO
2 SCD retrieved from these GEMS synthetic radiances and the calculated (modeled) SO
2 AMF were used to retrieve the SO
2 VCDs. Thus, we focus on the SO
2 SCD retrieval error in this present study. AMF is another source of uncertainty in SO
2 VCD retrieval using the DOAS method [
50]. The effect of AMF uncertainty was not accounted for in this study but will be considered in a separate study. To estimate the effect of GEMS SO
2 AMF uncertainties on the calculation of LRT-SO
2 flow rate, we first need to quantify the uncertainty of GEMS SO
2 AMF. To quantify the uncertainty of GEMS SO
2 AMF, the uncertainties and errors in the input data (most of which are GEMS L2 products), such as aerosol optical properties, aerosol layer height, cloud fraction, cloud pressure, surface reflectance, ozone column, and SO
2 vertical profile, which are used to calculate the GEMS SO
2 AMF, should be estimated. However, uncertainties and errors of the input data, most of which are GEMS L2 products, have not been evaluated. Therefore, the effect of GEMS SO
2 AMF uncertainty on the calculation of LRT-SO
2 flow rate can be investigated in a separate study once the uncertainties and errors of GEMS L2 products, which are used to calculate GEMS SO
2 AMF are quantified. That is, we considered that the SO
2 SCD relative error was equal to the SO
2 VCD relative error. We calculated the SO
2 VCD error from the difference between the retrieved and true SO
2 VCDs. The GEMS synthetic radiances were convoluted with GEMS instrumental functions [
47,
51]. The SO
2 SCDs were retrieved from these GEMS synthetic radiances. Thus, differences between true SO
2 SCDs and retrieved SO
2 SCDs can occur owing to the effects of GEMS instrumental functions and noise, and SCD error caused by the performance of SO
2 retrieval. The details of the SO
2 SCD retrieval method are described in
Section 2.4. Here, the true SO
2 SCD and AMF were calculated directly from the RTM simulation. Having retrieved the SO
2 VCDs from the synthetic radiances and quantified the error, we used the SO
2 VCDs to detect the LRT-SO
2 event and to calculate the flow rate of the SO
2. Finally, the uncertainty associated with the LRT-SO
2 flow rate was estimated based on the validation datasets using the GEOS-Chem data. The method used to calculate the uncertainty of the LRT-SO
2 flow rate is described in
Section 2.4.
2.1. GEOS-Chem
We used a 3-D global CTM GEOS-Chem [
49] (
www.geos-chem.org, accessed on 3 August 2021) to provide hourly trace gases (SO
2, HCHO, NO
2, and O
3) and aerosol concentrations to RTM simulations for generating the GEMS synthetic radiances. The GEOS-Chem output was also used in the validation of flow rate calculation as the true value. GEOS-Chem version 12.3.0 driven by the Goddard Earth Observation System-Forward Processing (GEOS-FP) assimilated meteorological fields at 0.25° × 0.3125° horizontal resolution and 47 vertical layers (from surface to ~0.01 hPa) were used. Nested simulations over a custom defined domain (110°E–140°E, 20°N–50°N) were conducted using boundary conditions from a GEOS-Chem global simulation at 2° × 2.5° resolution. For anthropogenic emissions inventory, we used version KORUSv2 [
52] developed by Konkuk University to support the Korea–United States Air Quality (KORUS-AQ) campaign [
53]. For other settings, including natural emissions and model chemistry, we refer the reader to Lee et al. [
54].
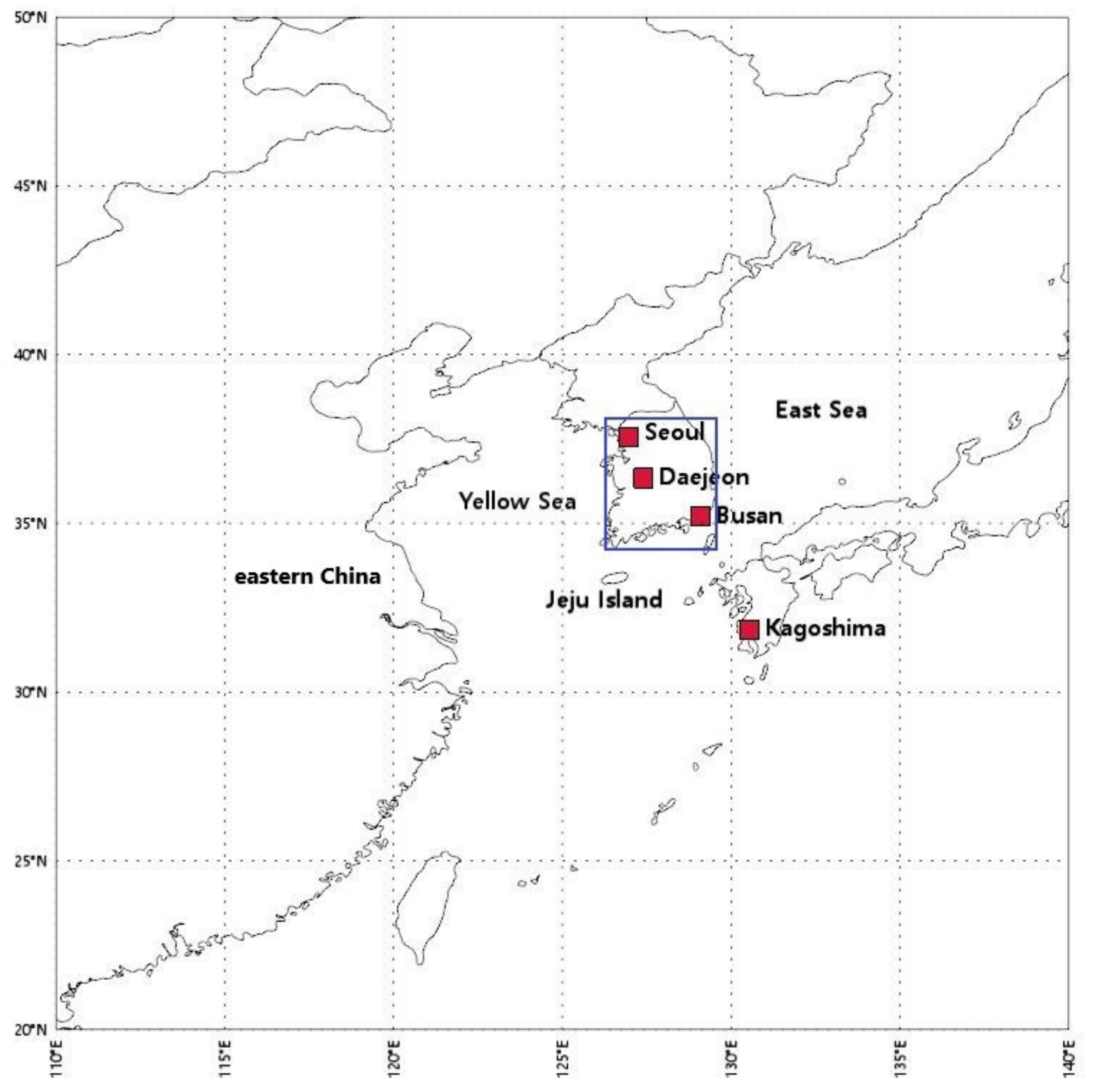
To calculate the true LRT-SO
2 flow rate, we performed the GEOS-Chem simulation twice: with and without anthropogenic and natural emissions over the blue rectangle in
Figure 2. This blue rectangle defines the receptor area where the LRT-SO
2 flow rate was estimated. The output from the simulation with full emissions was used as input to calculate the flow rate of SO
2. The output from the simulation without emissions over the blue rectangle was used to calculate the true LRT-SO
2 flow rate. We then estimated the errors associated with the calculated SO
2 flow rate. We quantified the SO
2 flow rate errors via a comparison between the true LRT-SO
2 flow rate and the calculated LRT-SO
2 flow rate.
2.2. OMI Level 2 SO2
We used the OMI Level 2 (L2) SO
2 data from the domain area shown in
Figure 2 to define the SO
2 column contributed by regional emissions (i.e., the background SO
2 amount). The OMI sensor is onboard the Earth Observing System (EOS)/Aura satellite, which was launched on 15 July 2004 and flies in a sun-synchronous polar orbit with an equator-crossing time of around 13:45 local time (LT) in the ascending node at an altitude of 705 km altitude [
43]. We used the OMI L2 SO
2 column data, which were produced from an updated algorithm in 2015. These OMI data are archived at NASA’s Goddard Earth Sciences Data and Information Services Center (GES DISC). They consist of daily global L2 gridded (L2G) SO
2 data from the OMI, having a spectral resolution of 0.45 nm in the UV band and a spatial resolution of 13 × 24 km (along track × cross track) at nadir [
43].
2.3. HYSPLIT Backward Trajectory Model
We defined an LRT-SO
2 event at a receptor pixel when the contribution of LRT-SO
2 from the source areas was considered to have changed the atmospheric SO
2 level in the receptor pixel. We used the HYSPLIT backward trajectory model (version 4.9), developed by the National Oceanic and Atmospheric Administration, Air Resources Laboratory (NOAA/ARL) [
45], to identify the travel route of the air mass. We used the National Centers for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) reanalysis meteorological data for the HYSPLIT backward trajectory simulation. Air mass backward trajectories from each receptor site were calculated every 0.1 km above ground level (agl) for each event. Stohl [
55] reported that HYSPLIT simulated trajectory endpoints have uncertainties of ~20% of the travel distance. However, another study [
56] reported that these uncertainties could exceed 20% in the first few time steps. Given a short average transport time of 2 days in the present study, we set the random errors of wind data to range from −15% to +15% for estimating the effect of wind data uncertainty on LRT-SO
2 flow rate calculation.
2.4. Method
To quantify the uncertainties associated with the retrieval of the SO
2 flow rate, the SO
2 VCD was retrieved from the generated synthetic radiance by entering simple, known SO
2 in the CTM, and the flow rate was then calculated using the retrieved SO
2 VCD and known wind information.
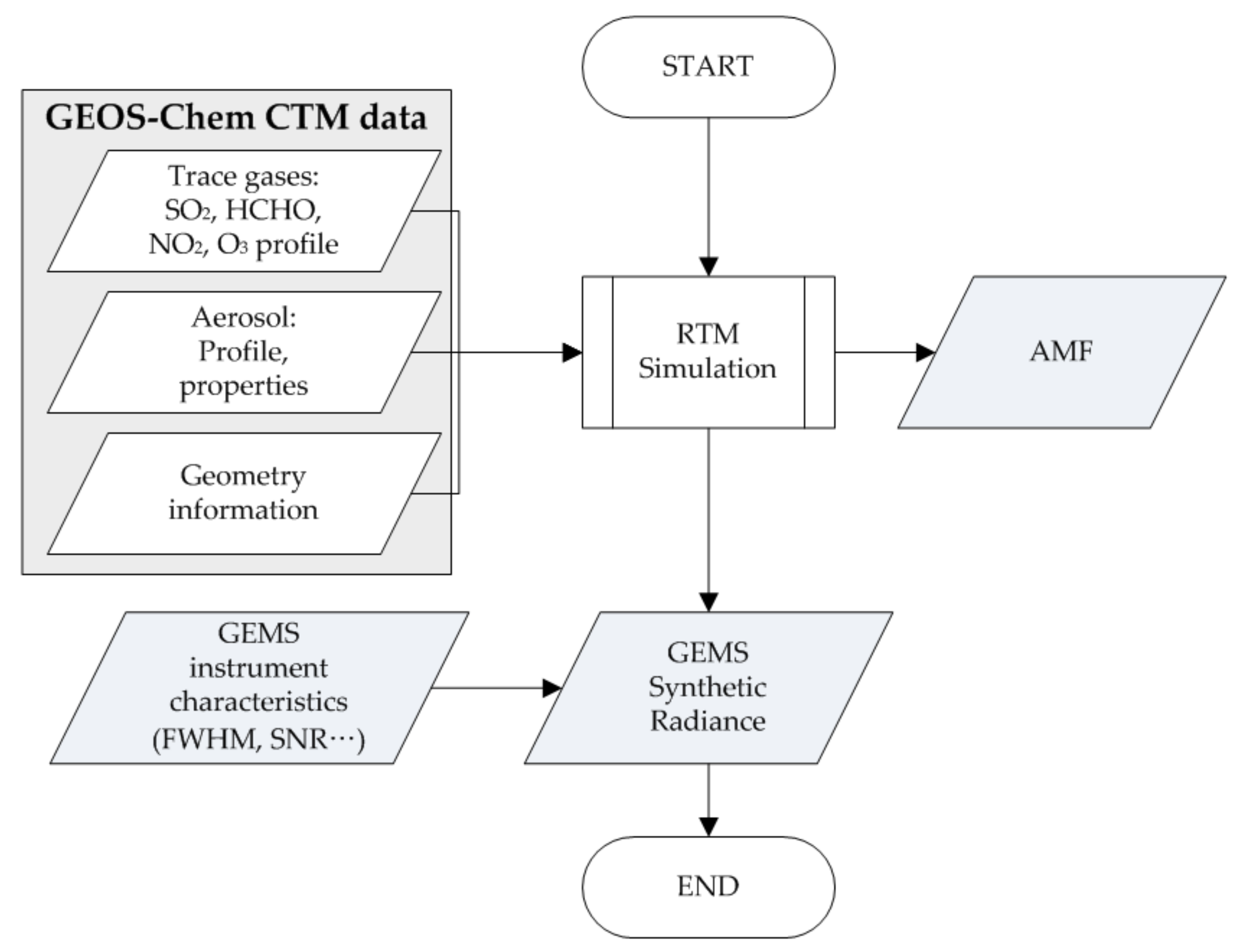
Figure 3 shows a flowchart of synthetic radiance generation using RTM (VLIDORT, v2.6) with inputs from the GEOS-Chem model, which was simulated with full emissions (see
Section 2.1). The vertical profiles of trace gases, aerosol, pressure, and temperature data were obtained from GEOS-Chem. We also used the aerosol properties (aerosol peak height, single-scattering albedo, and aerosol type) and geometry information obtained from the GEOS-Chem. In the present study, we carried out instrument modeling according to the Observing System Simulation Experiment (OSSE) [
50,
51,
57,
58]. First, synthetic radiances were generated using VLIDORT from 310 to 326 nm with a 0.2 nm sampling resolution. Second, the generated synthetic radiances were convoluted with GEMS instrumental functions. Noise was added to the convoluted synthetic radiances to satisfy a signal-to-noise ratio (SNR) of 1440 according to Equation (1). The operational GEMS SO
2 retrieval algorithm present its product over either 2 × 2 or 4 × 4 pixels. However, an SNR of 1440 (4 × 4 pixels) was used in this present study because the GEOS-Chem model [
49], which assimilated meteorological fields at 0.25° × 0.3125° (the spatial resolution of the assimilated field is approximately the same as 4 × 4 GEMS pixels) was used for the calculation of SO
2 flow rate. In this study, noise was added using the following equation [
51,
57,
58]:
where
and
are the ith SNR and radiance at wavelength
, respectively;
is the average value of all synthetic radiances from 310 to 326 nm; and
is its corresponding SNR.
We adopted the GEMS SO
2 operational algorithm to retrieve SO
2 SCDs in this present study because this study aimed to determine whether it is possible to calculate the SO
2 flow rate over the GEMS measurement domain using the GEMS SO
2 products. The GEMS SO
2 operational algorithm [
47,
59], which requires SO
2 retrieval over a whole GEMS measurement domain within 30 min, is a combined algorithm of Principal Component Analysis (PCA) [
44] and multi-window DOAS [
60]. Currently, PCA is the operational SO
2 retrieval algorithm in the OMI and the Ozone Mapping and Profiler Suite (OMPS) [
61]. Multi-window DOAS was used as the operational SO
2 retrieval algorithm in TROPOMI [
60]. However, PCA cannot be used for GEMS synthetic radiances in the present study because PCs, which are extracted from synthetic radiances, tend to be influenced by the SO
2 absorption effect. Once PCs influenced by the SO
2 absorption effect are used to retrieve SO
2 SCDs, the SO
2 SCDs cannot be retrieved from the synthetic radiances using the SO
2 contaminated PCs and SO
2 absorption cross-section. Therefore, in the present study, we used the multi-window DOAS method, which is used partly as the GEMS SO
2 operational algorithm, to quantify SO
2 SCD retrieval error.
We used SO
2 VCDs retrieved from the synthetic radiances to determine the pixels affected by LRT-SO
2 and to calculate the LRT-SO
2 flow rate.
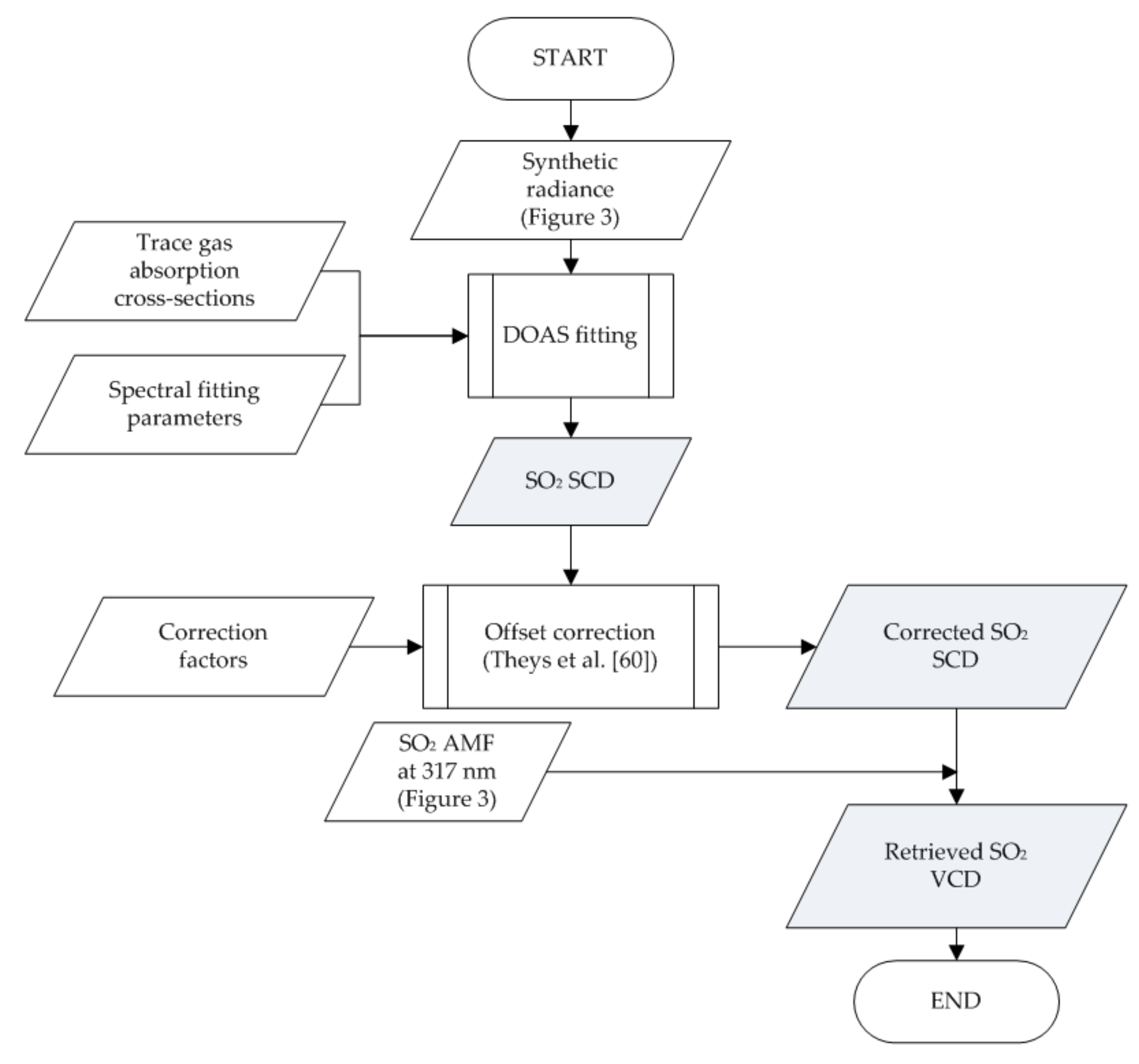
Figure 4 summarizes the SO
2 VCD retrieval from the synthetic radiances. In general, we used the DOAS technique [
62] to retrieve the SO
2 SCD, which is the total amount of SO
2 integrated over the light path length, which is affected by absorption and scattering in the atmosphere and reflected by the surface between the sun and a satellite sensor. The optical density fitting was carried out over the wavelength range (310–326 nm) using the QDOAS software [
63]. This spectral interval, which includes a strong SO
2 absorption band that peaks between about 310 and 313 nm, was found to have the smallest spectral fitting residual (optical density of residual = 0.021). We used the SO
2 and O
3 cross-sections to retrieve the SO
2 SCD. In addition, we used the same cross sections to generate the synthetic radiance as were used to retrieve the SO
2 SCD. The SO
2 absorption cross-section is from Vandaele et al. [
64]. The O
3 (223 K and 293 K) absorption cross-sections are from Bogumil et al. [
65]. We used a fifth-order polynomial to account for Rayleigh and Mie scattering. All absorption cross-sections were convolved using the GEMS slit function. The SO
2 and O
3 spectra were I
o-corrected using the QDOAS software.
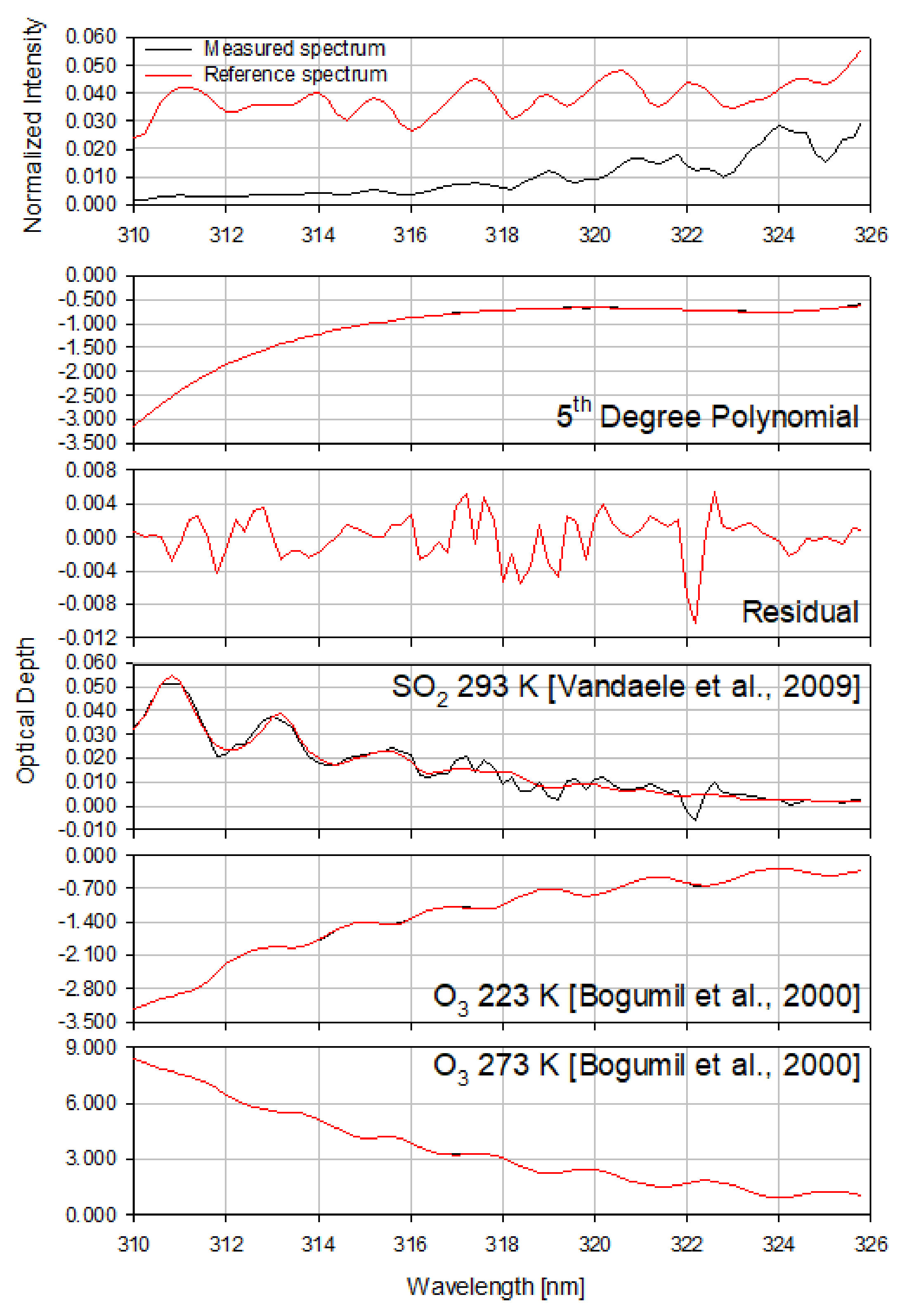
Figure 5 shows an example of DOAS spectral fitting for SO
2 SCD retrieval in the Kagoshima volcanic area, Japan at 06:00 (UTC) 09 April 2016.
The retrieved SO
2 SCDs were offset-corrected [
60].
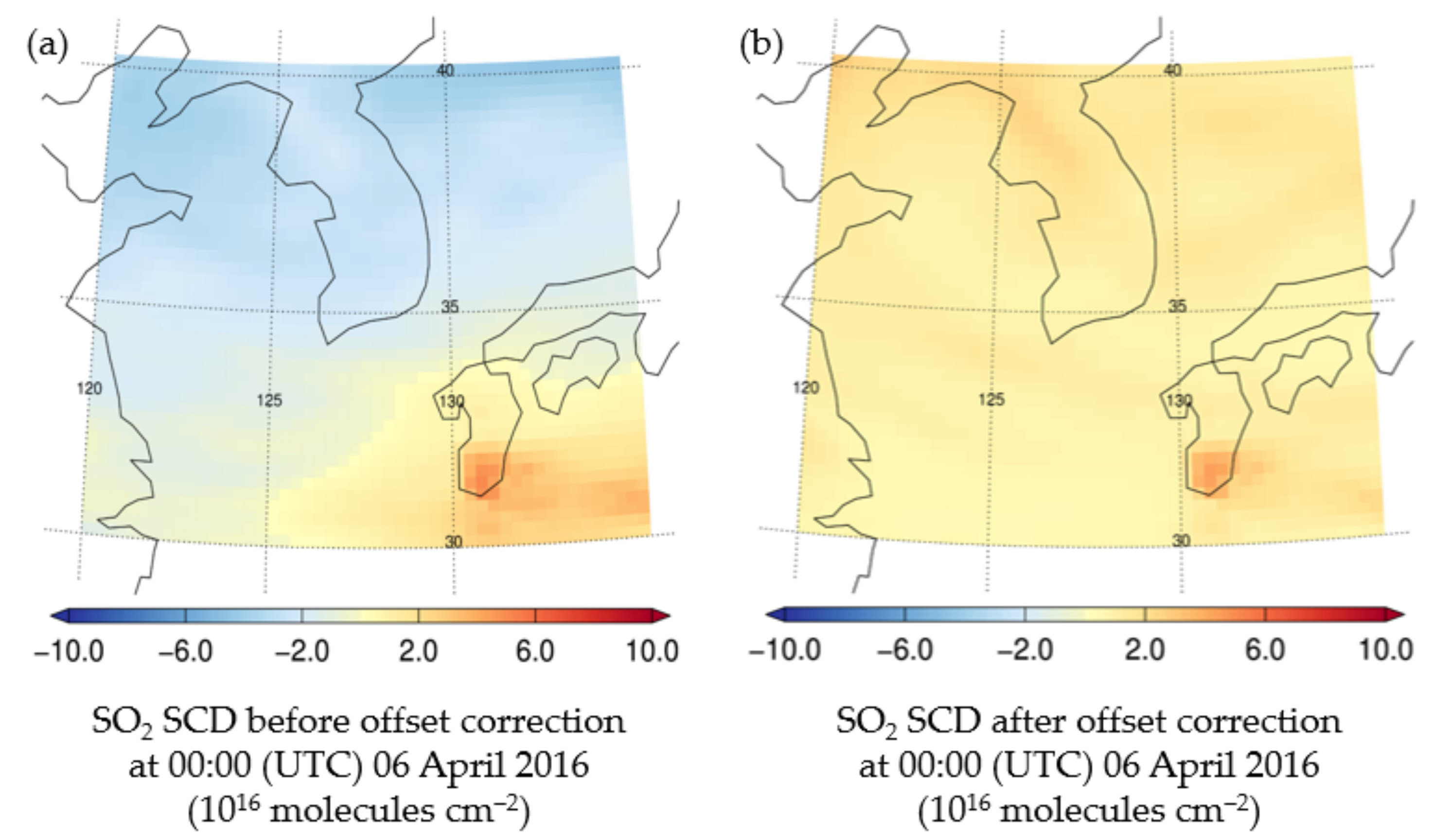
Figure 6 shows examples of the SO
2 SCD distributions at 00:00 (UTC) 06 April 2016 over the receptor area.
Figure 6a,b shows the SO
2 SCDs before and after the offset correction, respectively. The biases shown in Figure 10 can be attributed to the ozone effect, which is a well-known, common problem with most algorithms that retrieve SO
2 SCDs from UV sensors onboard satellites [
57]. As shown in
Figure 6, the SO
2 SCD before ozone correction (the so-called “offset correction”) is much smaller than the SO
2 SCD after offset correction. Therefore, the SO
2 SCDs contained a negative bias owing to this ozone effect. The negative biases of the SO
2 SCDs due to the ozone effect can be partly reduced after the offset correction. Thus, the negative biases presented in Figure 10 are part of the SO
2 SCD retrieval error due to the ozone effect. However, the magnitude of these biases can vary depending on the SO
2 retrieval algorithm used.
The AMF was calculated using the VLIDORT RTM, and the same inputs were used to simulate the synthetic radiances. The AMFs were used to convert the offset-corrected SO
2 SCDs into SO
2 VCDs (AMF = SCD/VCD). The AMF was calculated at 317 nm, which is the center of the fitting window. The error of the retrieved SO
2 VCD also contained an uncertainty, as a 2% difference was calculated between SO
2 AMF at 317 and 318 nm. Differences between true SO
2 VCDs and retrieved SO
2 VCDs can be attributed mainly to the SO
2 SCD retrieval error and partly to the uncertainty of AMF caused by the GEMS SO
2 AMF calculated at a center wavelength. The scattering weight,
, and the shape factor,
(z
), in each layer can be expresses as the AMF, as follows [
66]:
where
is the geometric AMF. A detailed description of VLIDORT and the AMF calculations can be found in Spurr and Christi [
48].
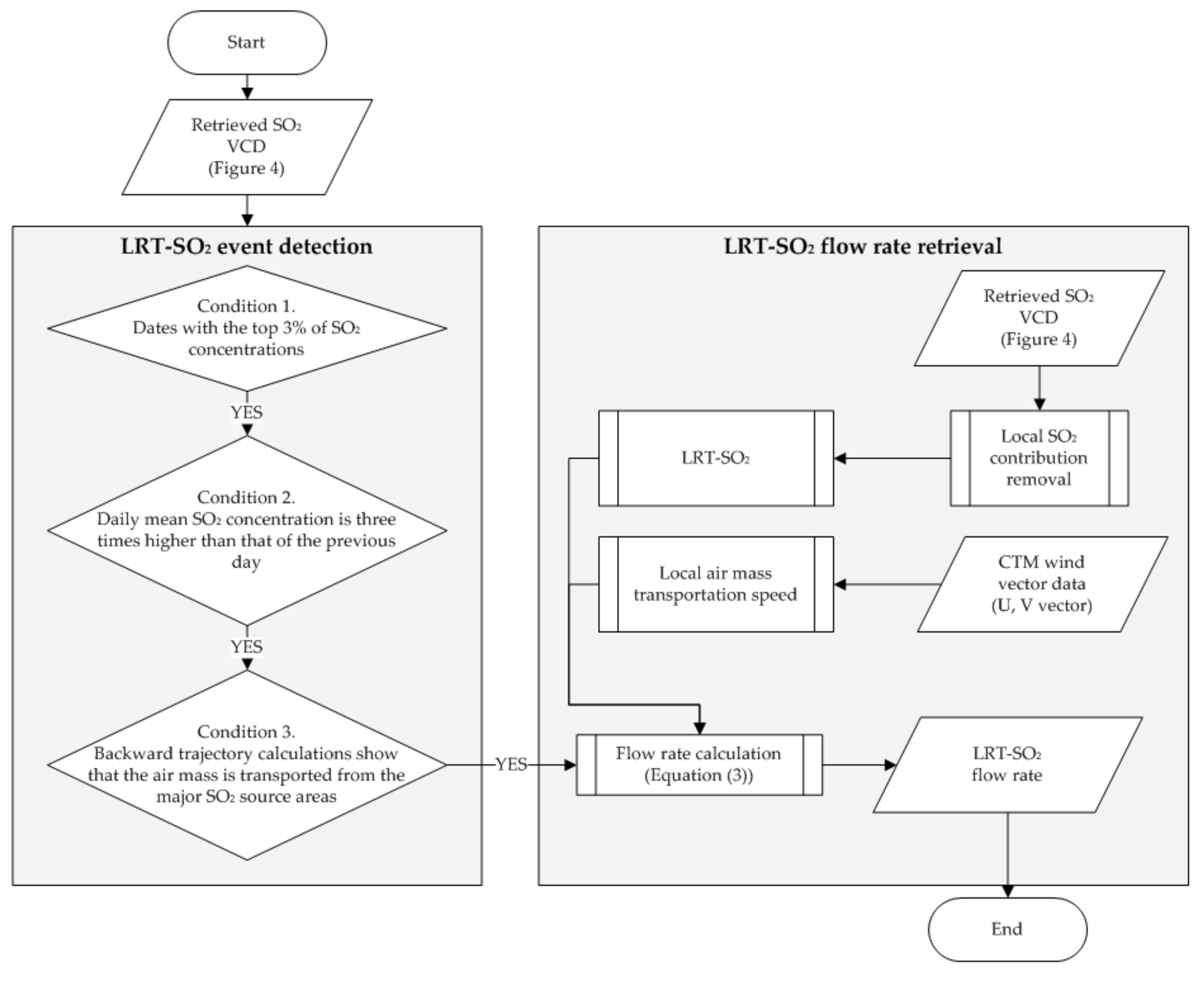
Figure 7 shows the methods used to determine the LRT-SO
2 events and to calculate the SO
2 flow rate. First, we categorized the LRT-SO
2 events as periods when SO
2 levels in a pixel were increased by LRT-SO
2 from continental Asia or volcanic areas. Three conditions (left grey rectangle in
Figure 7) were used to categorize the pixel with the LRT-SO
2 event. A detailed description of these conditions can be found in Park et al. [
42]. For this study, we used the SO
2 column densities obtained from the CTM simulation for condition 1, whereas surface SO
2 concentrations from in situ measurements were used by Park et al. [
42]. Second, we calculated the flow rate of the LRT-SO
2 over the pixel with the LRT-SO
2 event, as shown in
Figure 7 (grey rectangle on the right-hand side).
The LRT-SO
2 flow rate was calculated using Equation (3), where
and
denote the LRT-SO
2 column and the average transportation speed of the air mass, respectively. To calculate the LRT-SO
2 column amount (
), the contribution from local SO
2 emissions needs to be quantitatively estimated. A previous study used in situ ground measurements to quantify SO
2 from local contributions [
42] because continuously monitored SO
2 data are useful in quantifying the locally contributed SO
2. However, in the present study, we used the SO
2 VCD obtained from the OMI L2 SO
2 data to quantify SO
2 amount from local sources as in situ ground measurement data are not available for all pixels where the LRT-SO
2 flow rate needs to be calculated. The local SO
2 VCD was calculated by averaging the OMI SO
2 column data that were available for the 15 days before and after each event date, excluding the data measured on the event date. We excluded the data measured on the event date because it is possible that calculated local SO
2 VCD is overestimated owing to the LRT-SO
2 on the event date. We calculated LRT-SO
2 column based on Equation (4) as follows:
where
is the LRT-SO
2 column (i.e., the SO
2 column at each synthetic radiance pixel due to LRT-SO
2), and SO
2VCD and SO
2VCD
local represent the SO
2 VCD measured for each pixel and SO
2 VCD from local contributions, respectively. The mean value of
(1.3 × 10
16 molecules cm
−2) was much larger than 2.5 × 10
15 molecules cm
−2, which is the sum of the mean SO
2VCD
local and the standard deviation of SO
2VCD
local (4.0 × 10
14 molecules cm
−2). This present study used Equation (4) to estimate LRT-SO
2, as suggested by a previous study [
42]. However, Equation (4) may underestimate the LRT-SO
2 column when LRT-SO
2 is affected by the local SO
2 column and may overestimate the LRT-SO
2 column when the local SO
2 column is underestimated compared with a real local SO
2 column.
We also calculated the local air mass transportation speed (
) by averaging the local transportation speeds of the air masses. Air mass transportation speeds were calculated from the U and V vectors used for the GEOS-Chem simulation. We calculated the air mass transport speed for cases of volcanic and anthropogenic emission. We calculated the air mass transport speed for volcanic emission case using the U and V vectors of the air masses that originated from surface to ~0.01 hPa. On the other hand, we calculated the air mass transport speed using the U and V vectors of the air masses that originated within the PBL in the source area and were transported to the receptor area because the anthropogenic SO
2 is assumed to be located mostly within the PBL in the source areas [
67,
68]. We used the PBL data that were simulated by GEOS-Chem. We also used the OMI L2 SO
2 data to define the SO
2 source areas. The areas with high SO
2 emissions reported in previous studies [
1,
69,
70] and the areas with a high SO
2 column in the OMI L2 SO
2 data were coincident, and these areas were defined as the source areas. A more detailed description of this procedure can be found in Park et al. [
42].
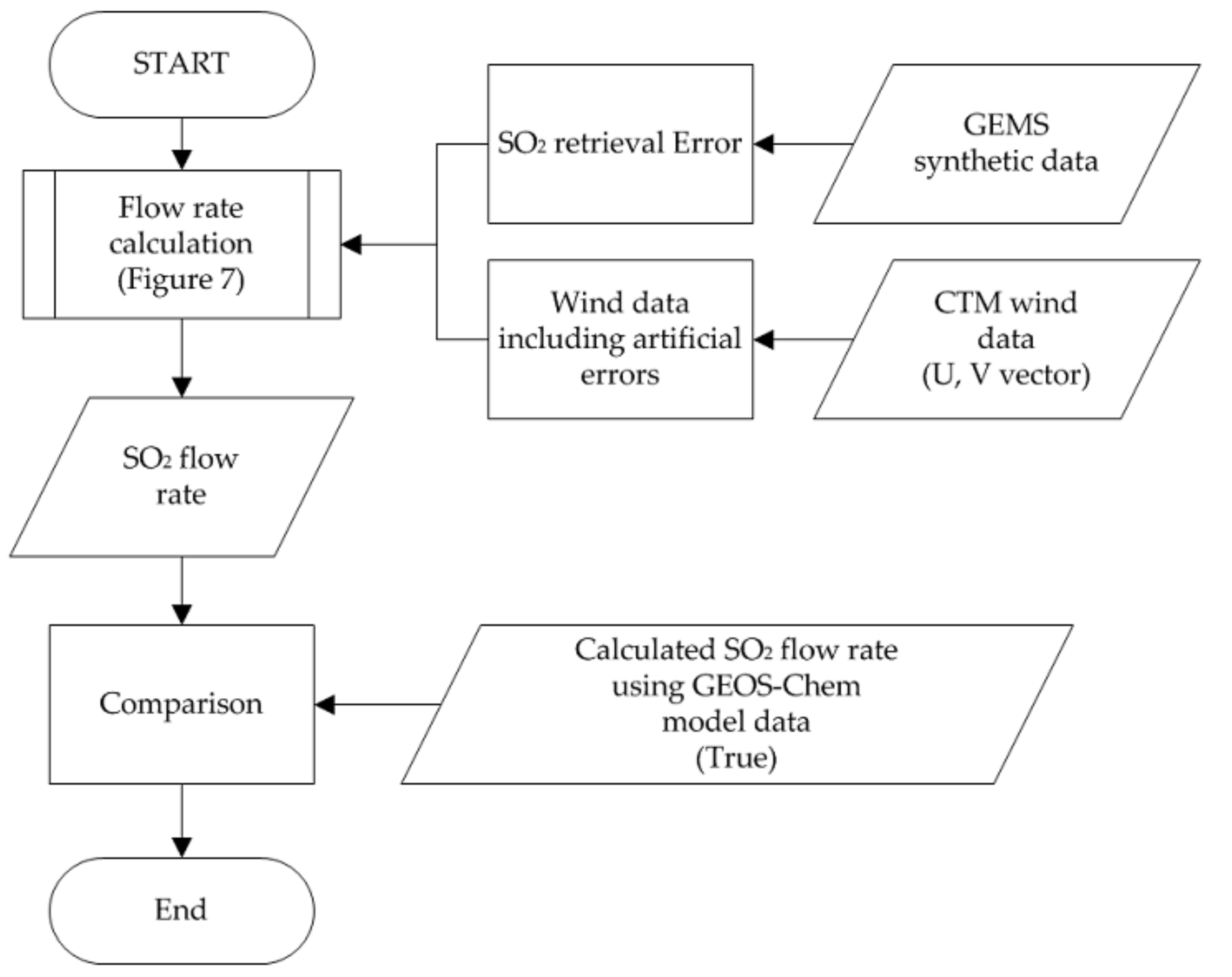
We investigated the uncertainties in the LRT-SO
2 flow rate under the SNR of 1440 condition and for various wind data with random errors ranging from −15% to +15% (
Figure 8). The absolute percentage difference (APD) between the LRT-SO
2 flow rate and the true LRT-SO
2 flow rate was calculated as follows:
where the true flow rate of SO
2 is calculated as the LRT flow rate of SO
2 based on GEOS-Chem SO
2 profile data. In addition, the retrieved flow rate of SO
2 is calculated as the LRT flow rate of SO
2 based on SO
2 VCDs, which are retrieved as shown in
Figure 4.
3. Results
Table 1 lists the LRT-SO
2 events and the event dates determined using the three conditions shown in
Figure 7. All events in
Table 1 represent high-SO
2 events when LRT-SO
2 reaches the Korean Peninsula or the sea around the Korean Peninsula (e.g., the Yellow Sea, East Sea, or South Sea). In addition, all events in
Table 1 were affected by either a combination of anthropogenic emissions and volcanic eruptions, or just volcanic SO
2 emissions. Mount Shindake, which is located in Japan (Kagoshima), erupted on 29 May 2015 and has continued to erupt since then. Events 1, 5, and 6 were additionally affected by anthropogenic sources because SO
2 emitted from the Asian continent was transported to the Korean Peninsula by the trade winds.
Once the GEMS synthetic radiances were produced for the event dates in
Table 1 (
Figure 3), the SO
2 VCDs were retrieved from these radiances according to the DOAS technique described in
Figure 4. Then, the LRT-SO
2 flow rate over the Korean Peninsula was calculated based on the algorithms (shown in
Figure 7) with the inputs of the retrieved SO
2 VCDs and wind data that were used to run GEOS-Chem.
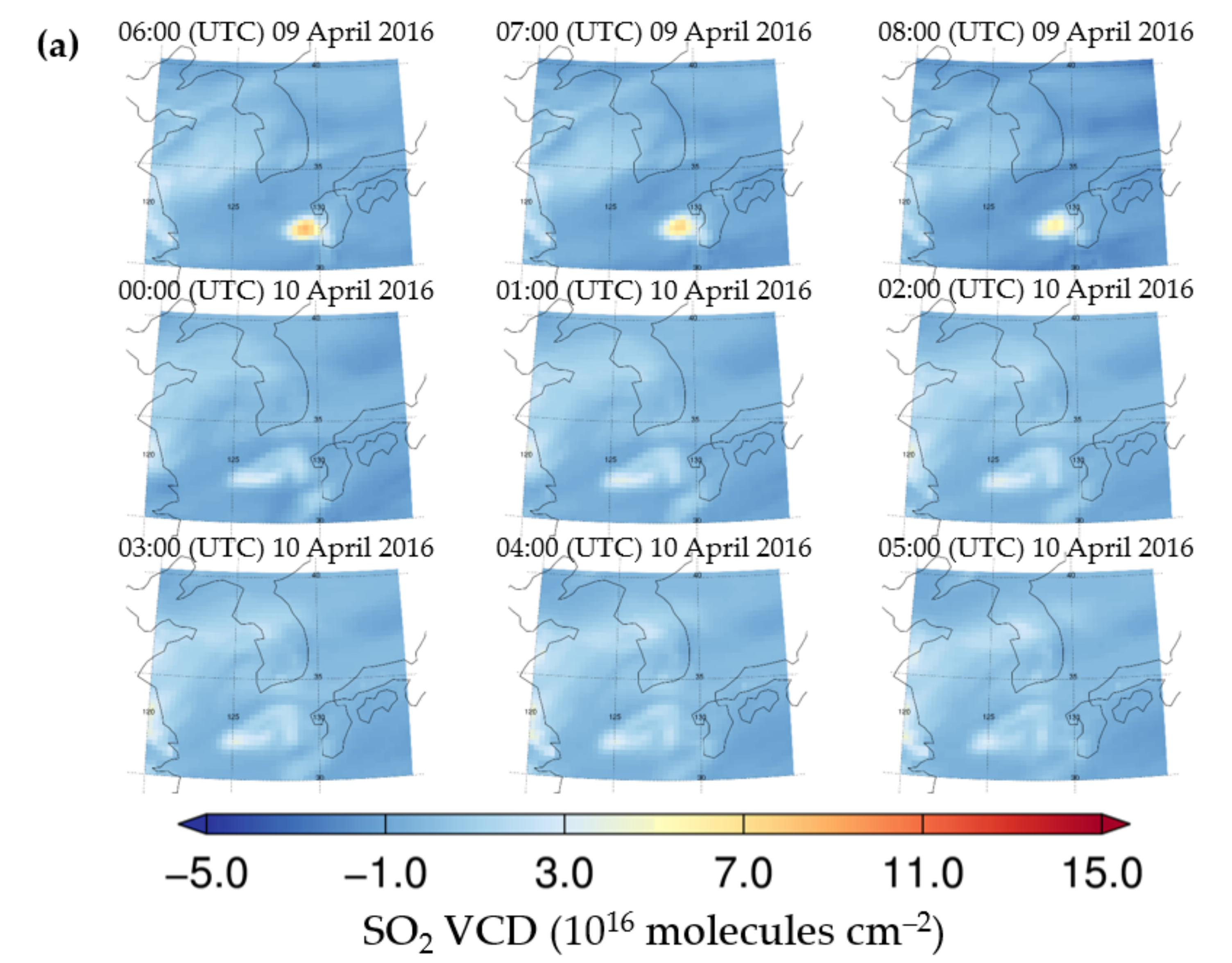
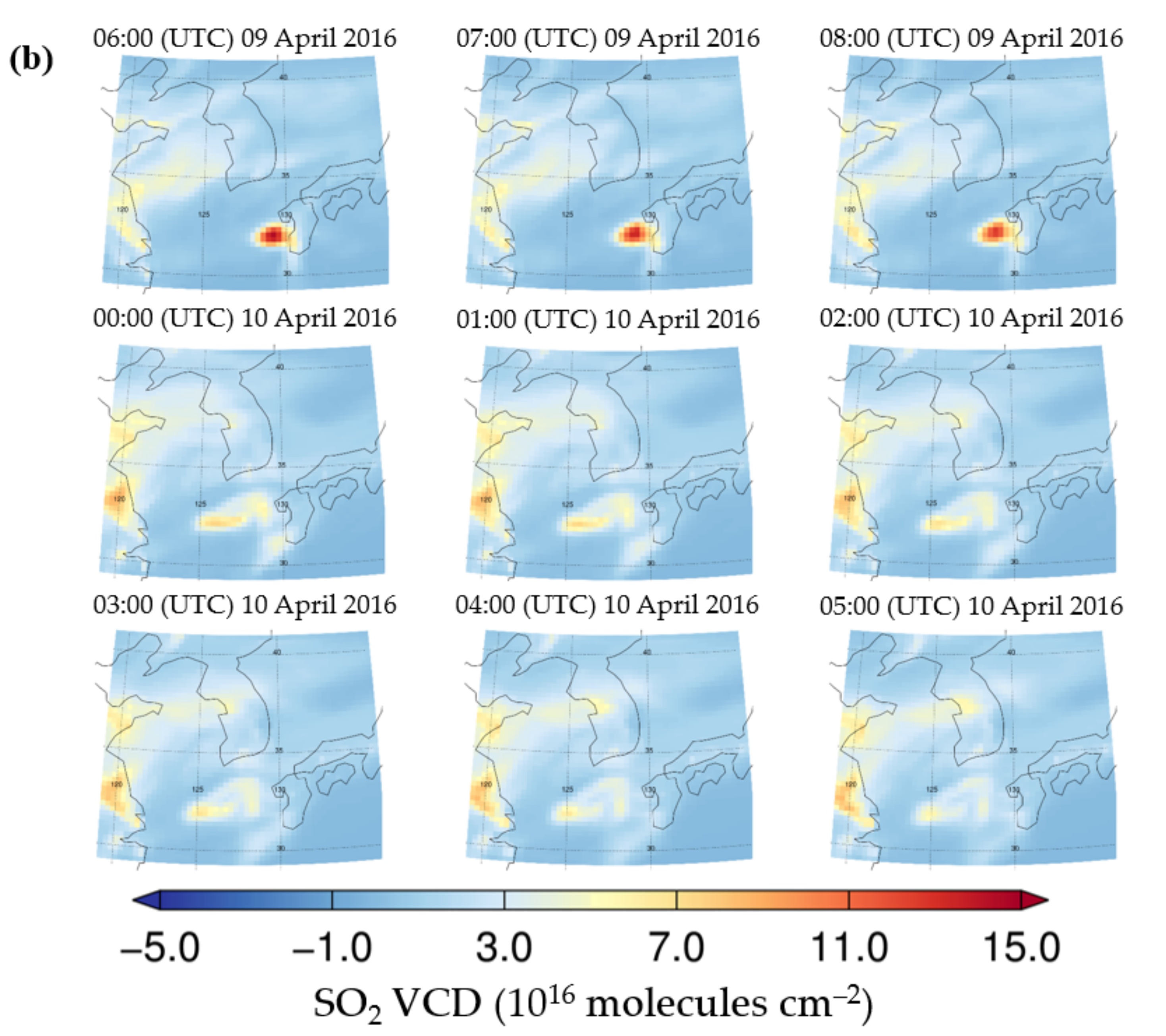
Figure 9a shows the SO
2 VCD retrieved from the GEMS synthetic radiance (SO
2 VCD
Retrieved) on 09–10 April 2016, and
Figure 9b shows the SO
2 VCD simulated from the GEOS-Chem (SO
2 VCD
True) on the same date.
Figure 9 shows examples of SO
2 VCD
Retrieved and SO
2 VCD
True for event 1 in
Table 1.
Figure 9 shows high SO
2 VCDs over eastern China and Kagoshima in Japan.
Figure 9 shows how the volcanic SO
2 plume from Kagoshima was transported to the southern part of the Korean Peninsula. The maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True values over the southern part of the Korean Peninsula were 0.2 (0.2) and 1.2 (1.1) × 10
16 molecules cm
−2, respectively, before the volcanic SO
2 plume arrived. However, the maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True values over the southern part of the Korean Peninsula were 6.2 (4.1) and 14.1 (11.4) × 10
16 molecules cm
−2, respectively, after the arrival of the volcanic SO
2 plume. In addition, LRT-SO
2 from Asia to the Korean Peninsula was well-detected. In terms of anthropogenic SO
2 effects, the maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True over the Korean Peninsula (near Seoul) were 0.2 (0.1) and 2.4 (2.1) × 10
16 molecules cm
−2, respectively, before the anthropogenic SO
2 plume was transported from eastern China. However, the maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True for Seoul were 2.1 (1.9) and 5.3 (4.6) × 10
16 molecules cm
−2, respectively, when the anthropogenic SO
2 plume arrived from eastern China.
Figure 10 shows the SO
2 VCD
Retrieved and SO
2 VCD
True from event 3 in
Table 1. High-SO
2 VCDs occurred over eastern China and Kagoshima in Japan, and a volcanic SO
2 plume from Kagoshima was transported across several cities in Korea (Busan, Daejeon, and Seoul). Before the volcanic SO
2 plume reached these cities, the maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True levels were −0.2 (−0.6) and 0.4 (0.1) × 10
16 molecules cm
−2 over Busan, −0.4 (−0.5) and 1.1 (0.6) × 10
16 molecules cm
−2 in Daejeon, and −0.7 (−0.9) and 2.1 (1.3) × 10
16 molecules cm
−2 in Seoul. The maximum (average) SO
2 VCD
Retrieved and SO
2 VCD
True values were 3.2 (2.7) and 6.5 (5.9) × 10
16 molecules cm
−2 over Busan, 4.1 (3.8) and 6.8 (6.1) × 10
16 molecules cm
−2 over Daejeon, and 2.8 (2.5) and 3.9 (3.4) × 10
16 molecules cm
−2 over Seoul after the volcanic SO
2 plume reached them.
The spatial distribution of SO
2 VCD
Retrieved agrees well with that of the true SO
2 VCDs in
Figure 9 and
Figure 10. However, the value of SO
2 VCD
Retrieved tends to underestimate SO
2 VCD
True. It should be remembered that the SO
2 VCD error represents the SO
2 SCD retrieval error in this study. The SO
2 SCD retrieval error is the difference between the true and retrieved SO
2 SCD values (see
Section 2 for a more detailed explanation). To investigate the uncertainty of the flow rate of LRT-SO
2, which is calculated using SO
2 VCD
Retrieved, the accuracy of the SO
2 VCD
Retrieved obtained in this study needs to be quantified. To understand the accuracy of SO
2 VCD
Retrieved, we compared the true SO
2 VCD values with those retrieved for all events in
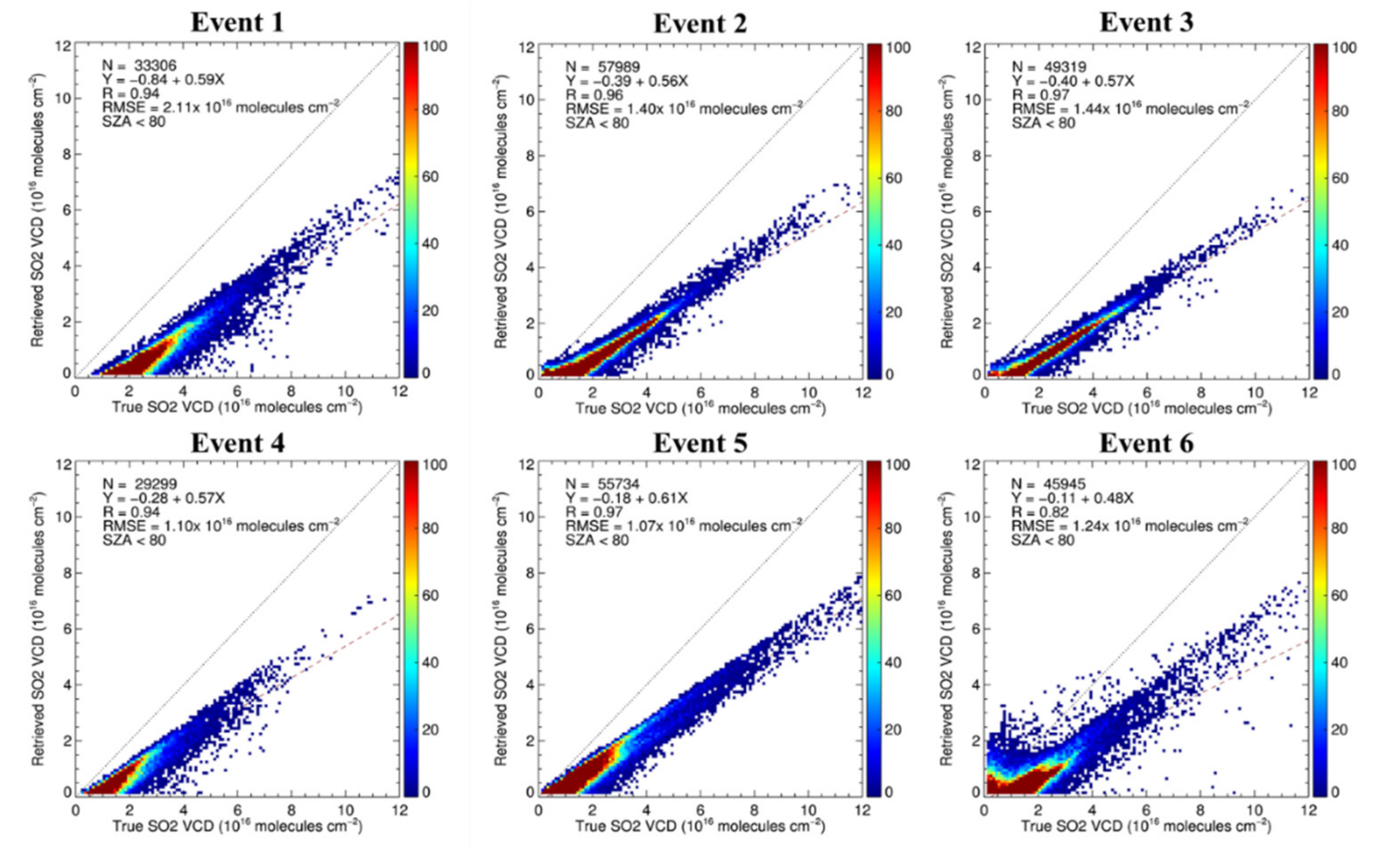
Figure 11. For the comparisons, we selected pixels with (1) a range of VCDs from 5.0 × 10
14 to 1.2 × 10
17 molecules cm
−2, (2) a DOAS fitting residual <
0.001, (3) an SCD error < 20%, and (4) a solar zenith angle < 70°. The scatter plots (
Figure 11) show the correlation between the retrieved SO
2 VCD
Retrieved and SO
2 VCD
True. On all of these plots, the dashed red line and dotted black line represent the regression line and 1:1 line, respectively. The colors and color bar in
Figure 11 indicate the data number for the values.
Table 2 lists the correlation coefficient (R), slope, intercept, and root mean square error (RMSE) between true SO
2 VCDs and those retrieved for each event.
Figure 11 and
Table 2 show the correlation between the SO
2 VCD
Retrieved and SO
2 VCD
True. The correlation coefficient (R) varies from 0.82 to 0.97, and the slope varies from 0.48 to 0.61. The RMSE values range from 1.10 to 2.11 × 10
16 molecules cm
−2, which equates to a retrieval uncertainty of about 40% to 80% of the retrieved SO
2 column densities. In particular, for event 6, the correlation coefficient and slope show poor agreement between the SO
2 VCD
Retrieved and SO
2 VCD
True, which is associated with the low magnitude of SO
2 VCD in comparison with those for other events. The average SO
2 VCD
True values range from 2.1 to 3.2 × 10
16 molecules cm
−2 for events 1 through 5, but the value is 1.8 × 10
16 molecules cm
−2 for event 6, which implies that lower SO
2 VCD
True values lead to an increase in the percentage uncertainty associated with the retrieved SO
2 VCD.
Once SO
2 VCDs were obtained from the GEMS synthetic radiances and their error was calculated (
Figure 11 and
Table 2), the SO
2 VCDs were used to detect the LRT-SO
2 events and to calculate the flow rate of the SO
2.
Figure 12 shows the detection of the LRT-SO
2 plume for the period 09–10 April 2016. The red shading represents the pixels that were affected by LRT-SO
2 according to the method described in
Figure 7, and the blue shading indicates those not affected by LRT-SO
2. The three conditions outlined in
Figure 7 were applied to determine the pixels affected by LRT-SO
2 for event 1 (9–10 April 2016) using the retrieved SO
2 VCDs. The red pixels show northward movement of the SO
2 plume that originated from the Kagoshima volcanic area in Japan. The LRT-SO
2 was found over Kagoshima at 00:00 (UTC) on 9 April 2016 and near Jeju Island at 03:00 (UTC) on 10 April 2016. In addition to the volcanic SO
2 transport during event 1, SO
2 transport from eastern China was also found over the Yellow Ocean between 01:00 and 06:00 (UTC) on 9 April 2016 and over the middle of the Korean Peninsula between 02:00 and 06:00 (UTC) on 10 April 2016, as shown in
Figure 12.
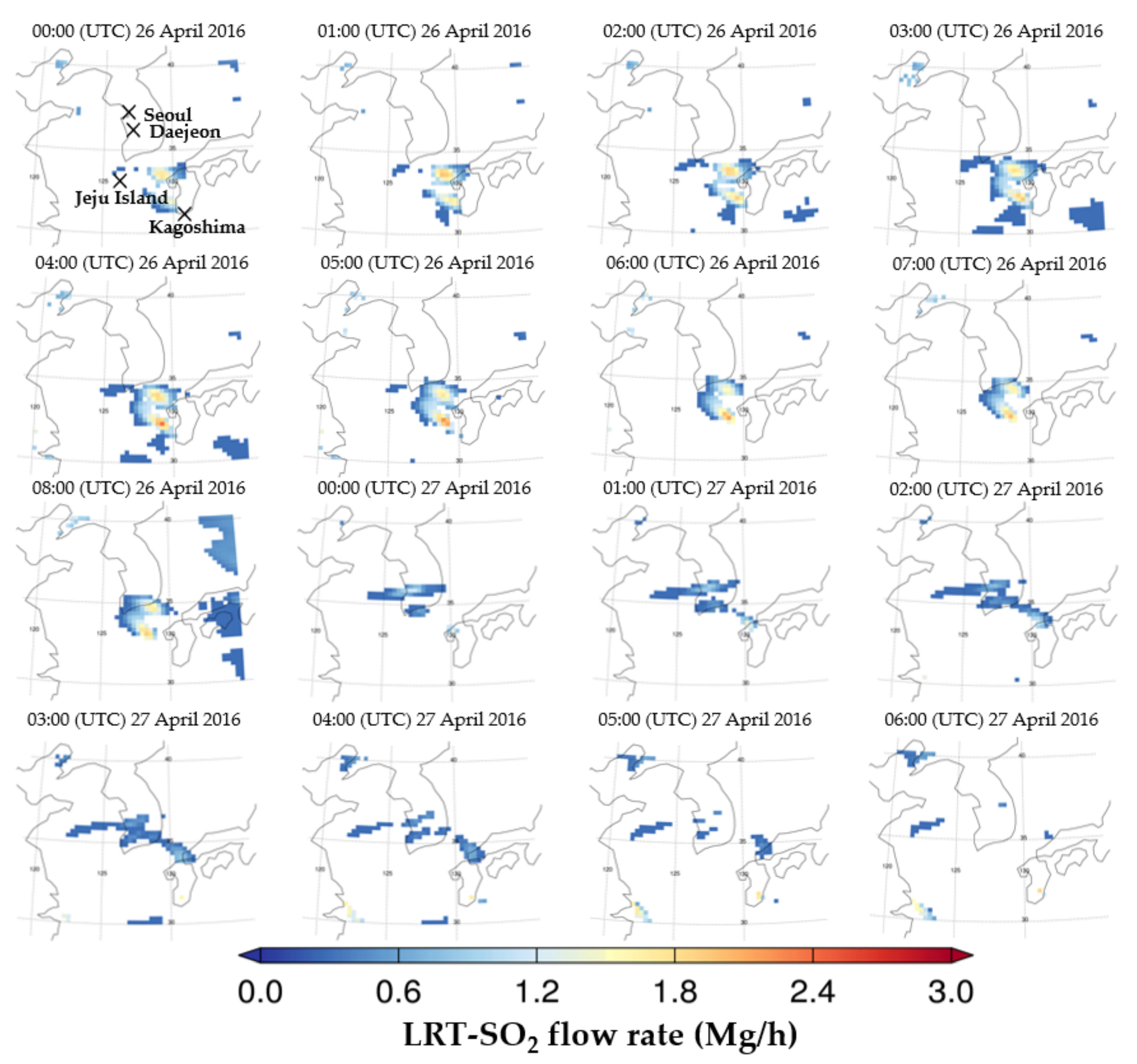
Figure 13 shows the pixels affected by LRT-SO
2 throughout event 3. The pixels affected by transported volcanic SO
2 were also determined by the method described in
Figure 7. Volcanic SO
2 plumes emitted from Kagoshima reached the southern part of the Korean Peninsula at 05:00 (UTC) on 26 April 2016. Volcanic SO
2 plumes were present over the Korean Peninsula from 05:00 (UTC) on 26 April 2016 to 04:00 (UTC) on 27 April 2016. The volcanic SO
2 VCD
Retrieved value was 7.2 × 10
16 molecules cm
−2 over Kagoshima (the volcanic SO
2 source area) at 05:00 (UTC) on 26 April 2016 when the plume began to affect the Korean Peninsula. The volcanic SO
2 VCD
Retrieved was 5.3 × 10
16 molecules cm
−2 over Daejeon at 04:00 (UTC) on 27 April 2016.
The LRT-SO
2 flow rates were calculated using Equation (3) and the method described in
Figure 7.
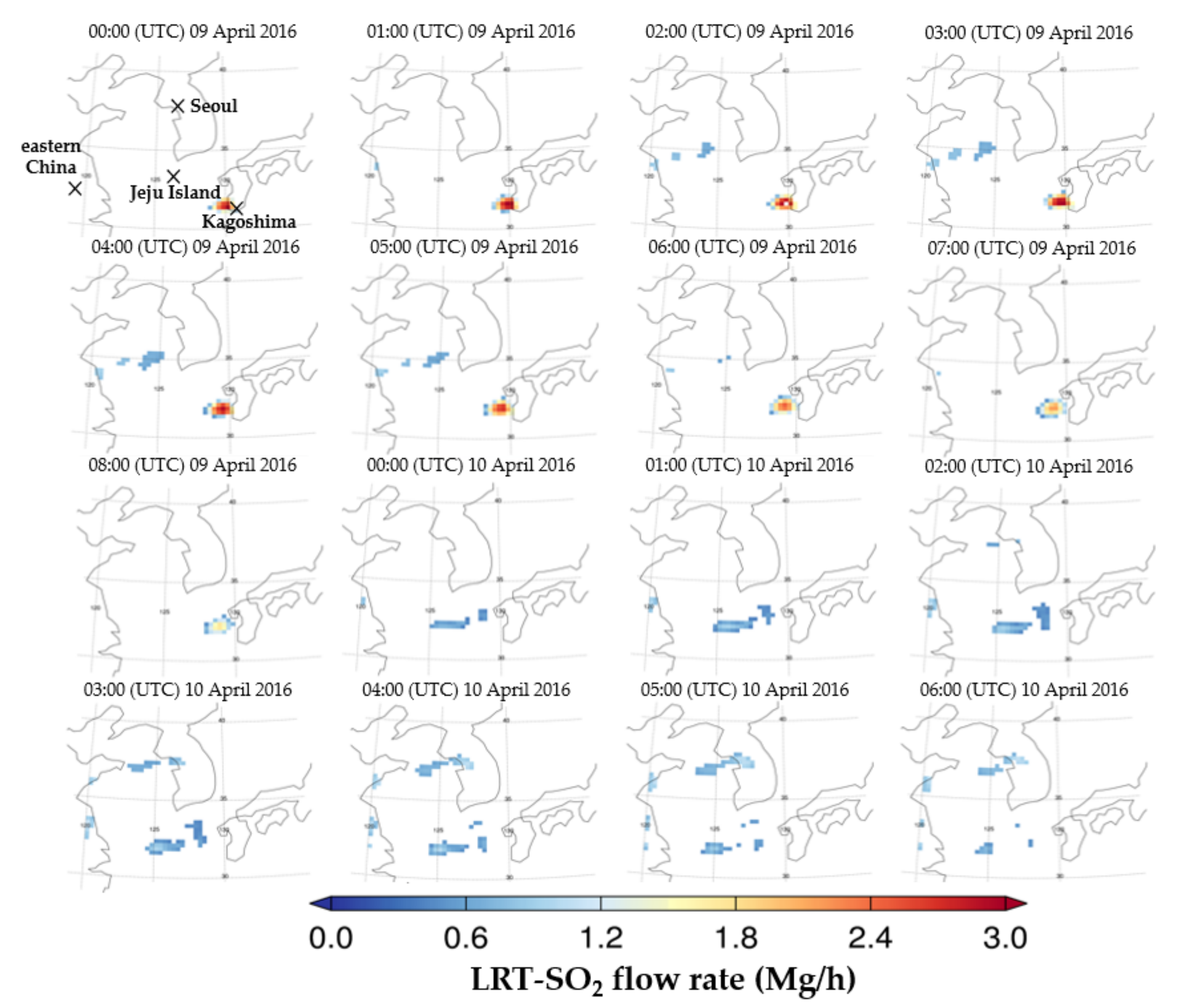
Figure 14 shows the SO
2 flow rates calculated for the pixels that were determined to be affected by LRT-SO
2 during event 1 (
Figure 12). As shown in
Figure 12 and
Figure 14, the transported SO
2 plumes were well-captured and observed to move from the Kagoshima volcanic area in Japan to the South Ocean of the Korean Peninsula and from industrial areas of eastern China to west of the Korean Peninsula. In the case of the LRT-SO
2 from the Kagoshima volcanic area, the average, maximum, and minimum values of the SO
2 flow rate over the southern part of the Korean Peninsula (near Jeju Island) were calculated to be 1.4, 2.1, and 1.1 Mg/h, respectively. For the SO
2 transported from industrial areas of eastern China, the corresponding values over the Yellow Sea were 0.32, 0.51, and 0.38 Mg/h, respectively. To evaluate the accuracy of these calculated SO
2 flow rates, we compared our SO
2 flow rate estimates with the true SO
2 flow rates. The true SO
2 flow rate was calculated using the method described in
Section 2 and
Figure 7. For the volcanic SO
2 plume, the average of the calculated SO
2 flow rate (true flow rate) over the southern Korean Peninsula (near Jeju Island) was 1.1 (2.3) Mg/h whereas it was 0.8 (1.8) Mg/h over the Yellow Ocean for the anthropogenic SO
2 plume from eastern China. The difference between the average calculated SO
2 flow rates and the true rates was 3.1 and 1.2 Mg/h for the volcanic and anthropogenic SO
2 plumes, respectively.
Figure 15 shows the SO
2 flow rates calculated for the pixels that were determined to be affected by the LRT-SO
2 during event 3 (
Figure 13). We found a general decrease in LRT-SO
2 flow rates with distance from the volcanic SO
2 source region. The calculated LRT-SO
2 flow rates (true flow rate) for pixels defined as being affected by long-range transportation was 2.3 (3.7) Mg/h over the Kagoshima region (03:00 (UTC) 26 April 2016), 1.1 (2.8) Mg/h over Jeju (07:00 (UTC) 26 April 2016), and 0.8 (2.1) Mg/h over Daejeon (01:00 (UTC) 27 April 2016). In the case of Daejeon, SO
2 VCD
Retrieved increased from 0.3 × 10
16 molecules cm
−2 on 26 April 2016 (01:00 UTC), which was before the SO
2 LRT event, to 2.1 × 10
16 molecules cm
−2 on 27 April 2016 (01:00 UTC), when the Kagoshima volcanic SO
2 had just arrived.
The maximum, minimum, and average LRT-SO2 flow rates during event 3 were 1.89, 0.13, and 0.94 Mg/h, respectively, whereas those for the true SO2 flow rates were 4.43, 0.14, and 0.96 Mg/h, respectively. The differences between the two sets of values were caused mostly by the SO2 SCD retrieval error associated with the DOAS spectral fitting method. However, uncertainties in the SO2 flow rate calculation are also created by uncertainties in the wind data, SO2 AMF, and SO2 SCD. The uncertainties in the SO2 flow rate calculations were evaluated by accounting for uncertainties in the wind data and SO2 SCD and are discussed in the next section.
Error Estimation
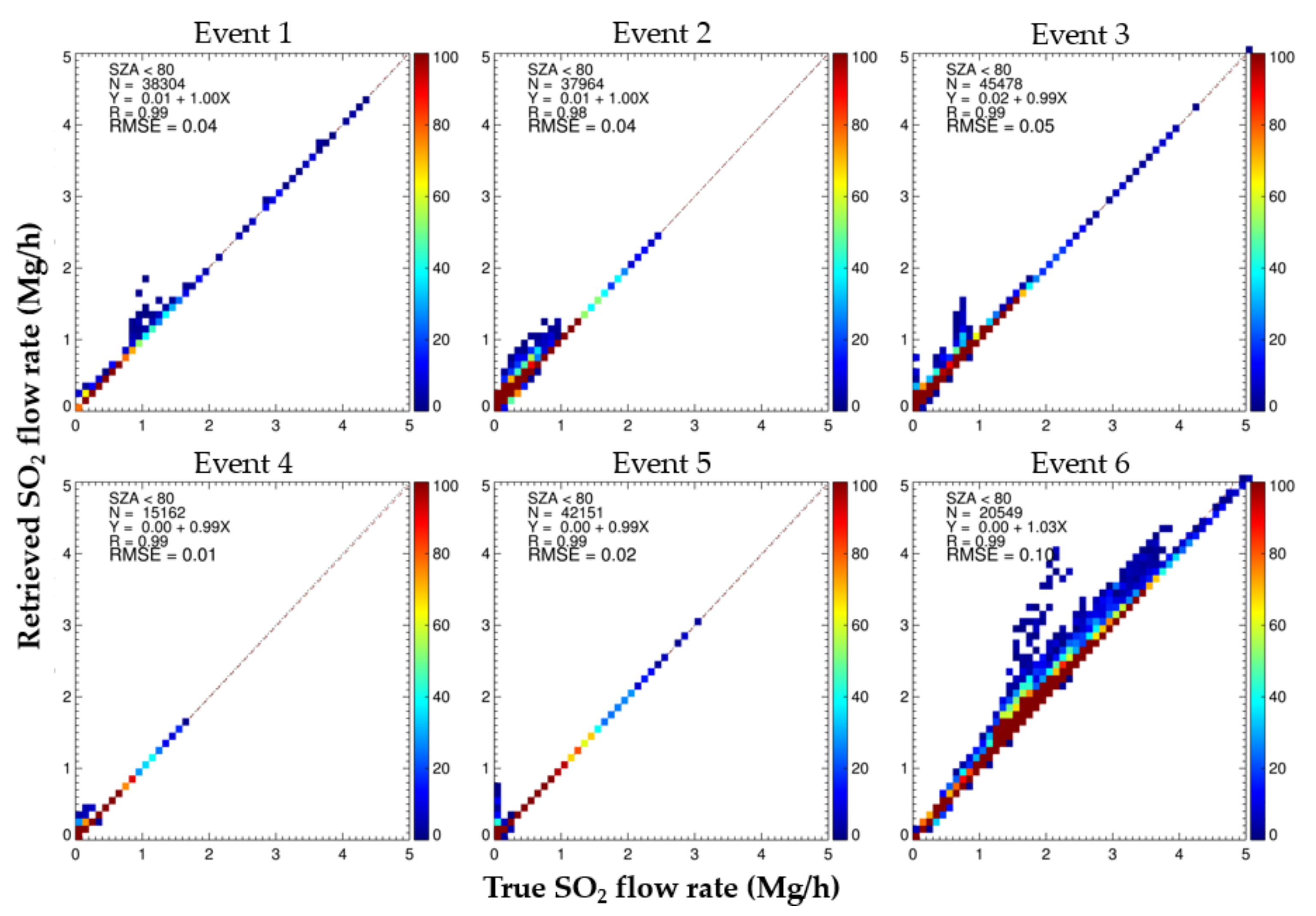
We compared our calculated SO
2 flow rates with those of the true ones to estimate the magnitude of the errors associated with the calculated values. The true SO
2 flow rates were calculated using the method shown in
Figure 8, with inputs of true wind data and true SO
2 column density. The true SO
2 column densities do not contain a retrieval error or the contribution of the SO
2 emissions from the receptor areas because they were simulated using the GEOS-Chem SO
2 column with the SO
2 emission off in the receptor region on the Korean Peninsula. We evaluated the accuracy of the LRT-SO
2 flow rates calculated under the conditions of the true SO
2 VCDs and wind data. The correlation coefficient, slope, and intercept between the calculated flow rates and the true values ranged from 0.98 to 0.99, from 0.99 to 1.03, and from 0.00 to 0.02 Mg/h, respectively (
Figure 16). The SO
2 emissions from the Korean Peninsula contributed 0.01–0.10 Mg/h of the RMSE in the SO
2 flow rate calculation (
Table 3). For all events except event 2, we obtained a difference of less than 8% between the true SO
2 flow rate and those calculated under the conditions of no errors in the SO
2 retrieval and wind data. These small differences can be attributed to uncertainties in the SO
2 flow rate calculation method, such as uncertainty in the local SO
2 column removal (
Figure 7 and Equation (4)).
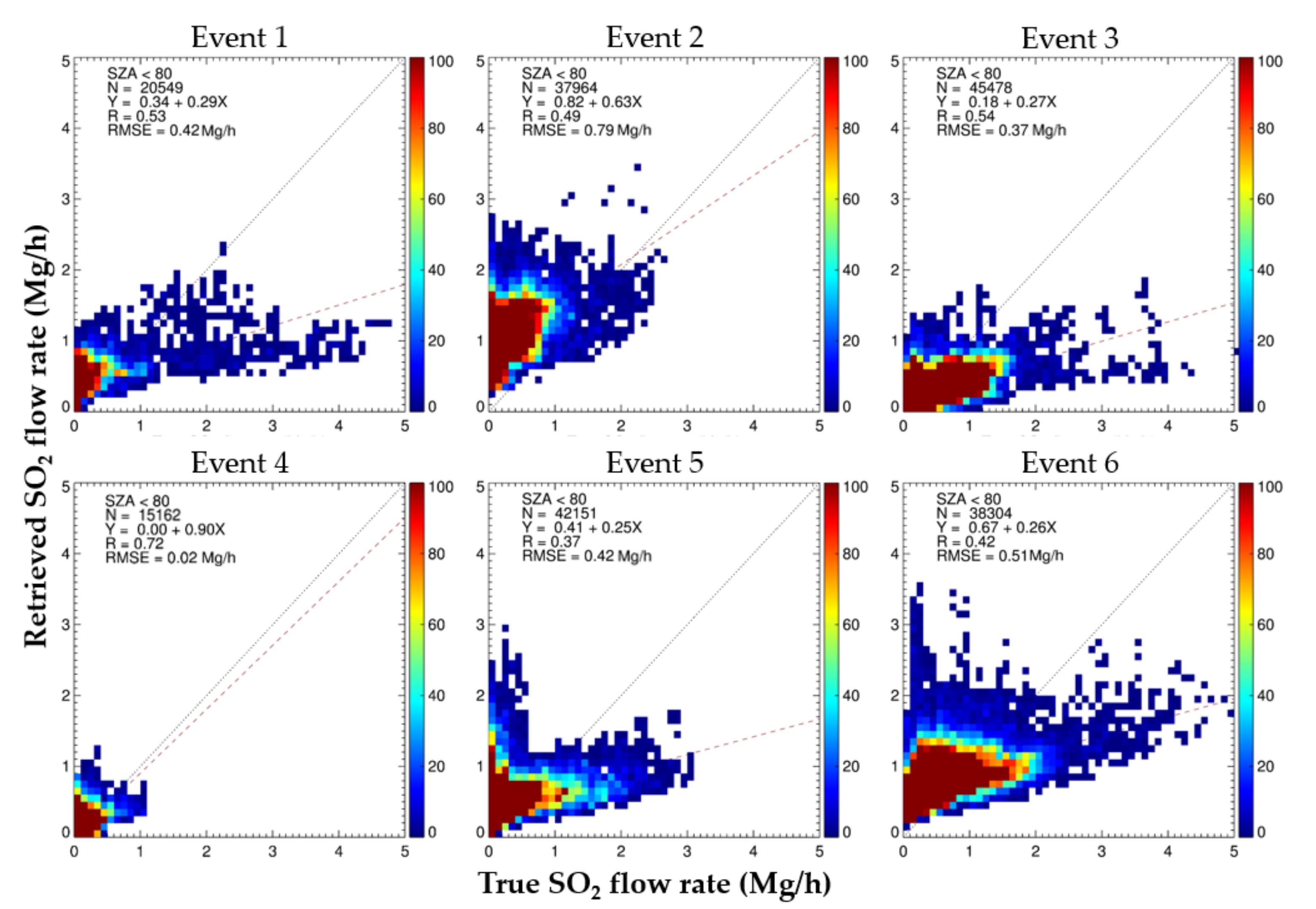
We investigated the uncertainties in LRT-SO
2 flow rate retrieval associated with both the GEMS SO
2 L2 data and the wind data. The calculated SO
2 flow rates in
Figure 17 were obtained using the true wind data, which were used as the inputs for the GEOS-Chem simulation, as well as the SO
2 column densities retrieved from the GEMS synthetic radiances, and these account for the SNR of 1440 for the SO
2 spectral fitting wavelength range. The SO
2 flow rates were calculated for a solar zenith angle of less than 70°. The calculated SO
2 flow rates in
Figure 17 contain GEMS retrieval errors only.
Figure 17 shows the correlation between the true SO
2 flow rates and those calculated under the conditions of the GEMS SO
2 retrieval error but with no errors in wind data for all events in
Table 1. The slope and intercept between the true and calculated SO
2 flow rates range from 0.23 to 0.63 and from 0.09 to 0.82 Mg/h, respectively. As shown in
Figure 17, the RMSE for all events ranges from 0.14 to 0.79 Mg/h and the minimum and maximum R values are 0.37 and 0.72, respectively. These statistics of the SO
2 flow rate calculation are mostly due to errors in the SO
2 SCD retrieval from GEMS.
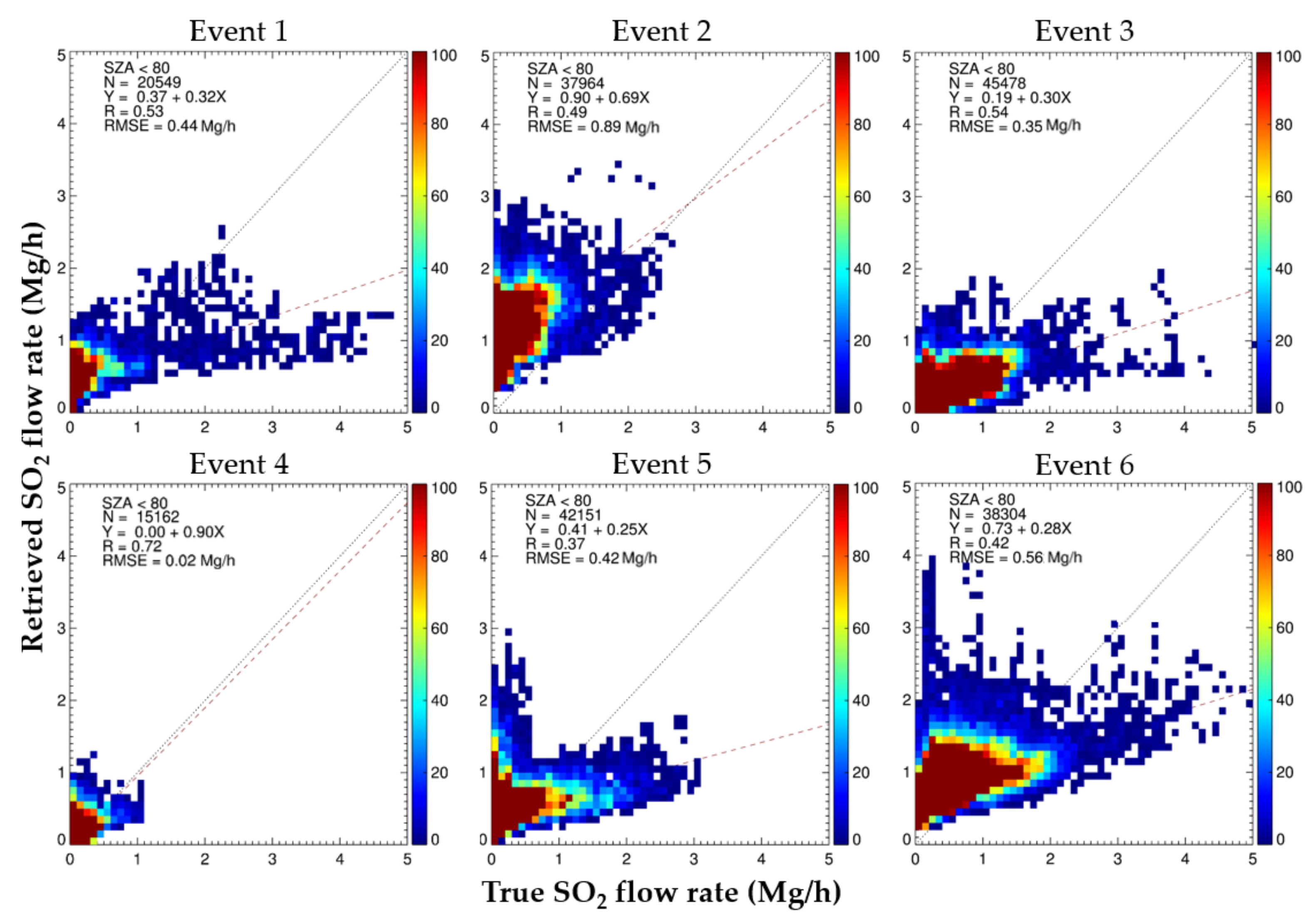
Figure 18 shows the correlation between the true SO
2 flow rates and those calculated in the presence of uncertainties in both wind data and SO
2 VCD retrievals for all events in
Table 1. To evaluate the effects of wind data uncertainty in addition to that associated with the SO
2 VCD retrievals from the GEMS synthetic radiances, we calculated the SO
2 flow rates using the wind data used in the GEOS-Chem simulations but with random errors added that ranged from −15% to 15%, following Stohl [
55]. When the uncertainties in both the SO
2 VCD retrieval and wind data were present, the errors in the SO
2 flow rates were much larger than those generated from only the SO
2 VCD retrieval error. The average true SO
2 flow rates (standard deviation) and those calculated in the presence of both the SO
2 VCD retrieval error and wind data uncertainty were 1.17 (
0.44) and 1.04 (
0.70) Mg/h, respectively. As shown in
Figure 18, the RMSE for all events ranges from 0.02 to 0.79 Mg/h. The minimum and maximum R values between the true SO
2 flow rates and those calculated were 0.37 and 0.72, respectively.
Table 4 lists the R values, slope, intercept, and RMSE between the true LRT-SO
2 flow rate and calculated LRT-SO
2 flow rates in the presence of the GEMS SO
2 retrieval error and no uncertainty in wind data, whereas
Table 5 shows the values in the presence of both the GEMS SO
2 retrieval error and uncertainty in the wind data. The R values in
Figure 17 are similar to those in
Figure 18. The correlation coefficients between the true and calculated SO
2 flow rates range from 0.37 to 0.72 in
Figure 17 and from 0.37 to 0.72 in
Figure 18. The differences in the slope, intercept, and RMSE values shown in
Table 4 and
Table 5 range from 0.0% to 11.1%, from 0.0% to 9.7%, and from 5.4% to 12.6%, respectively. In particular, when comparing
Table 4 and
Table 5, there is a large difference in the SO
2 flow rate calculation errors of event 2. The large SO
2 flow rate error for event 2 in
Table 5 is due to the uncertainty (
15%) of the calculated transport speed. When LRT-SO
2 flow rate was calculated in the condition of an SNR of 1440 without wind data uncertainties, the RMSE and standard deviation ranged from 0.02 to 0.79 Mg h
−1 and ±0.13 to ±0.95 Mg h
−1, respectively, as shown in
Figure 17 and
Table 4. However, the LRT-SO
2 flow rate was calculated in the presence of both an SNR of 1440 and wind data uncertainties, with RMSE and standard deviation ranging from 0.02 to 0.89 Mg h
−1 and from ±0.15 to ±1.55 Mg h
−1, respectively, as shown in
Figure 18 and
Table 5. RMSE and standard deviation tended to slightly increase in the presence of an SNR of 1440 and wind data uncertainties compared with those in the presence of only an SNR of 1440. In this study, errors related to AMF were not accounted for in the GEMS SO
2 retrieval error. According to a previous study [
50], the SO
2 AMF errors caused by uncertainties in aerosol properties and surface reflectance were calculated as being between 46% and 173.4%. We calculated the SO
2 flow rate error based on the SNR of 1440. However, spatial pixel-binning is required to enhance the SNR and to reduce the GEMS SO
2 retrieval error and the SO
2 flow rate calculation error.
4. Discussion
SO
2 is one of the less-reactive atmospheric gas species compared with other reactive trace gases, such as NO
x, OH, O
3, and HCHO, and it can last in the atmosphere for several days [
31,
32]. Thus, SO
2 is transported on the regional and global scales. Several studies [
33,
34,
35] investigated LRT-SO
2. Hsu et al. [
34] reported that the SO
2 plume emitted from anthropogenic sources in eastern China is transported to eastern Pacific Ocean. Li et al. [
33] also showed that the SO
2 plume emitted from China is transported to northwestern Pacific Ocean. Both Li et al. [
33] and Hsu et al. [
34] used OMI SO
2 data to observe LRT-SO
2.
The transport of SO
2 emission from Dalaffilla volcano has also been well-detected and reported in a previous study [
35] using the OMI SO
2 data. These studies used the satellite SO
2 data only for the detection of SO
2 plume transport. Park et al. [
42] proposed a method to estimate LRT-SO
2 values using the daily OMI SO
2 column, in situ data, and the HYSPLIT model. This previous study contributed to flow rate estimates and the assessment of their uncertainties from source areas over northeast Asia and the northwestern Pacific at several receptor locations. Subsequently, the GEMS instrument was launched in February 2020, and it is now theoretically possible to estimate the hourly SO
2 flow rate. However, it is important to understand the effects of GEMS SO
2 SCD retrieval errors on these LRT-SO
2 flow rate estimates. In particular, UV hyperspectral sensors, including GEMS, are known to have poor sensitivity to surface SO
2 levels because of the strong interference by ozone absorption and the SNR over the spectral fitting window for surface SO
2 retrieval. In this study, we attempted to estimate the LRT-SO
2 flow rate based on the synthetic GEMS radiances for several anthropogenic and volcanic SO
2 events over the Korean Peninsula and surrounding areas. Errors in the LRT-SO
2 flow rate estimates were quantified and related to errors in the GEMS SO
2 SCD retrieval and wind data uncertainty for those events. Although uncertainties associated with the AMF calculations were not accounted for in this study, our simulations showed that the accuracy of the LRT-SO
2 flow rate estimates depends primarily on the GEMS SO
2 SCD retrieval errors, which are partly associated with the SNR of 1440 over the 310–326 nm band. The RMSE and standard deviation between the true LRT-SO
2 flow rate and calculated LRT-SO
2 flow rates are found to be increased slightly due to the wind data uncertainty. Thus, a larger SO
2 SCD retrieval error leads to a larger uncertainty in the LRT-SO
2 flow rate estimates. In the present study, the multi-window DOAS algorithm [
59,
60], which is used partly as the GEMS SO
2 operational algorithm [
59], was used to quantify the SO
2 SCD retrieval error. However, there are still chances to reduce the SO
2 SCD retrieval error using other SO
2 retrieval algorithms although the GEMS operational algorithm requires fast retrieval within 30 min. Spatial pixel-binning can increase the GEMS radiance SNR, although it decreases the spatial resolution. An increased SNR can reduce the SO
2 SCD retrieval error, which eventually leads to an increase in SO
2 flow rate estimates.
5. Conclusions
We calculated LRT-SO2 flow rates using hourly synthetic GEMS measurements over Northeast Asia. We retrieved the SO2 VCD from the GEMS synthetic radiances using the multi-window DOAS algorithm. The SO2 VCDs retrieved and the true SO2 VCDs show ranges from −1.1 to 6.2 and from 0.4 to 14.1 × 1016 molecules cm−2. In addition, the mean values of the SO2 VCDs retrieved and the true SO2 VCDs were calculated as 1.7 and 3.1 × 1016 molecules cm−2, respectively. The retrieved SO2 VCDs were compared with the true SO2 VCDs calculated from the SO2 vertical profile used as the input data of the GEOS-Chem simulation. This comparison showed a high correlation coefficient (from 0.82 to 0.97).
The LRT-SO2 flow rates were calculated for three synthetic anthropogenic and three volcanic SO2 transport events. We investigated the effects of the GEMS SO2 retrieval error and meteorological data uncertainties on the LRT-SO2 flow rate calculation error. When there is only the GEMS SO2 retrieval error, which did not include the SO2 AMF error in this study, the R value, intercept, slope, and RMSE between the calculated and true SO2 flow rates ranged from 0.37 to 0.72, from 0.23 to 0.90 Mg/h, from 0.00 to 0.82, and from 0.02 to 0.79 Mg/h, respectively. In the presence of both the GEMS SO2 VCD retrieval error and wind data uncertainty, the corresponding values ranged from 0.37 to 0.72, from 0.25 to 0.90 Mg/h, from 0.00 to 0.90, and from 0.02 to 0.89 Mg/h, respectively.
When only an SNR of 1440 was accounted in LRT-SO2 flow rate calculation, the RMSE and standard deviation were calculated ranges from 0.02 to 0.79 Mg/h and from 0.13 to 0.95 Mg/h, respectively. However, when both an SNR of 1440 and wind data uncertainties were accounted for in the LRT-SO2 flow rate calculation, RMSE and standard deviation were calculated, ranging from 0.02 to 0.89 Mg/h and from 0.15 to 1.55 Mg/h, respectively.
In addition to the effects of SO2 SCD error and wind data uncertainty, the effect of AMF uncertainty on the SO2 flow rate estimates needs to be calculated. The SO2 AMF errors caused by uncertainties in aerosol properties and surface reflectance were calculated to be between 46% and 173.4%. Future studies should consider the effect of the temporal and spatial pixel-binning level on the GEMS SO2 retrieval error as well as on the SO2 flow rate calculation errors.