Measurement of the Sea Surface Height with Airborne GNSS Reflectometry and Delay Bias Calibration
Abstract
:1. Introduction
2. Altimetry of Reflected GNSS Signals
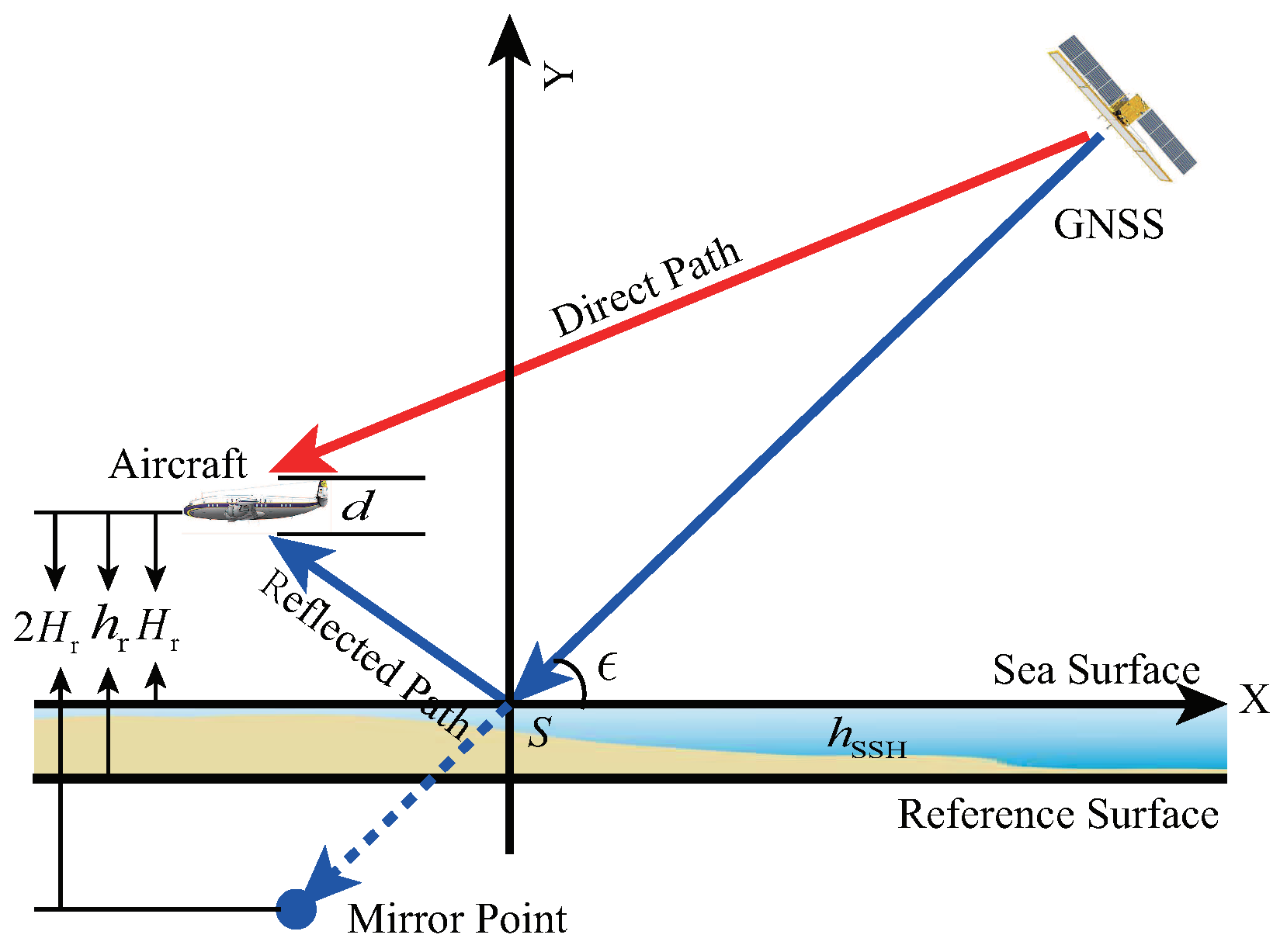
2.1. Geometry Model
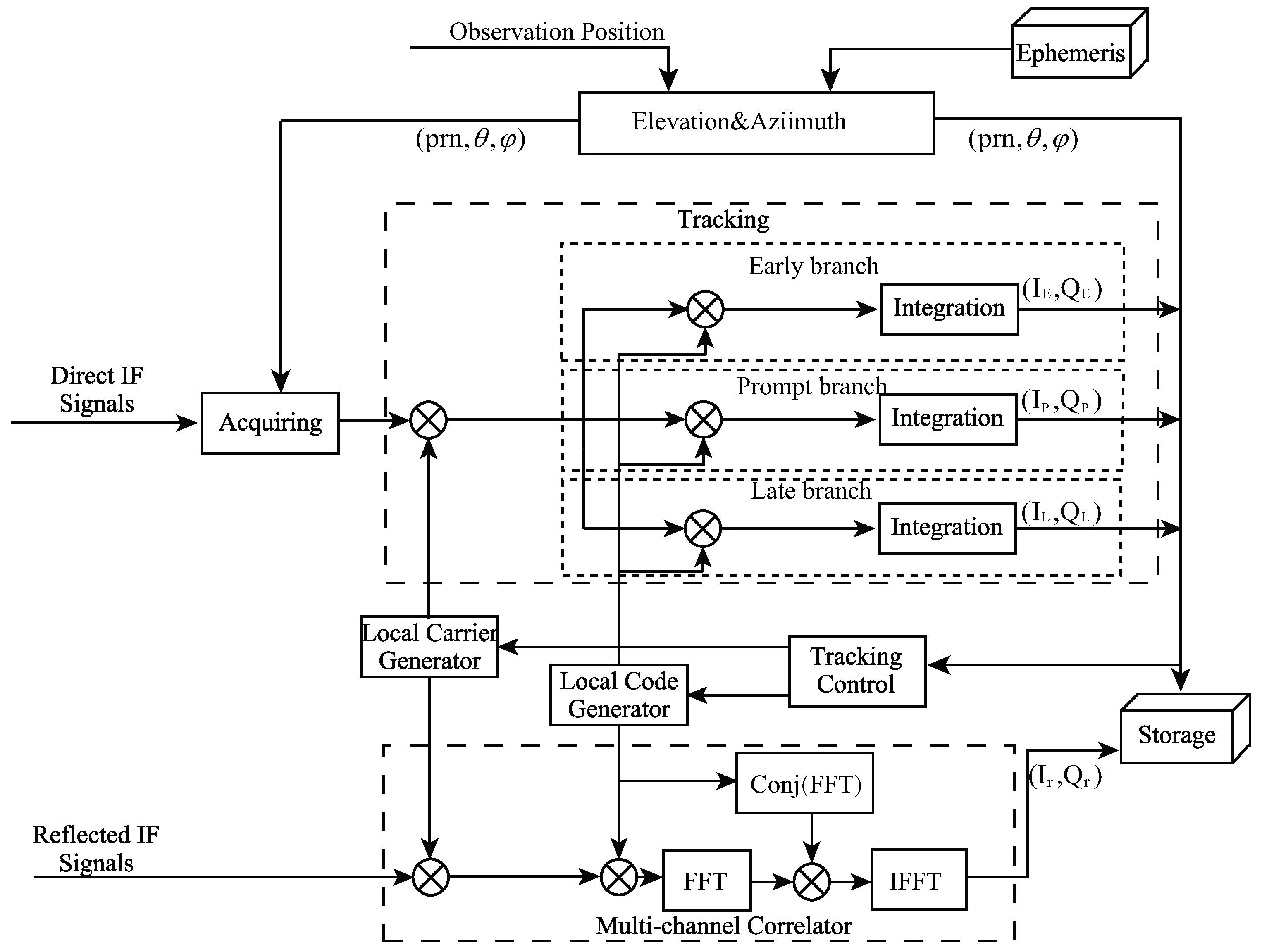
2.2. Delay Estimation
3. Specular Delay Bias
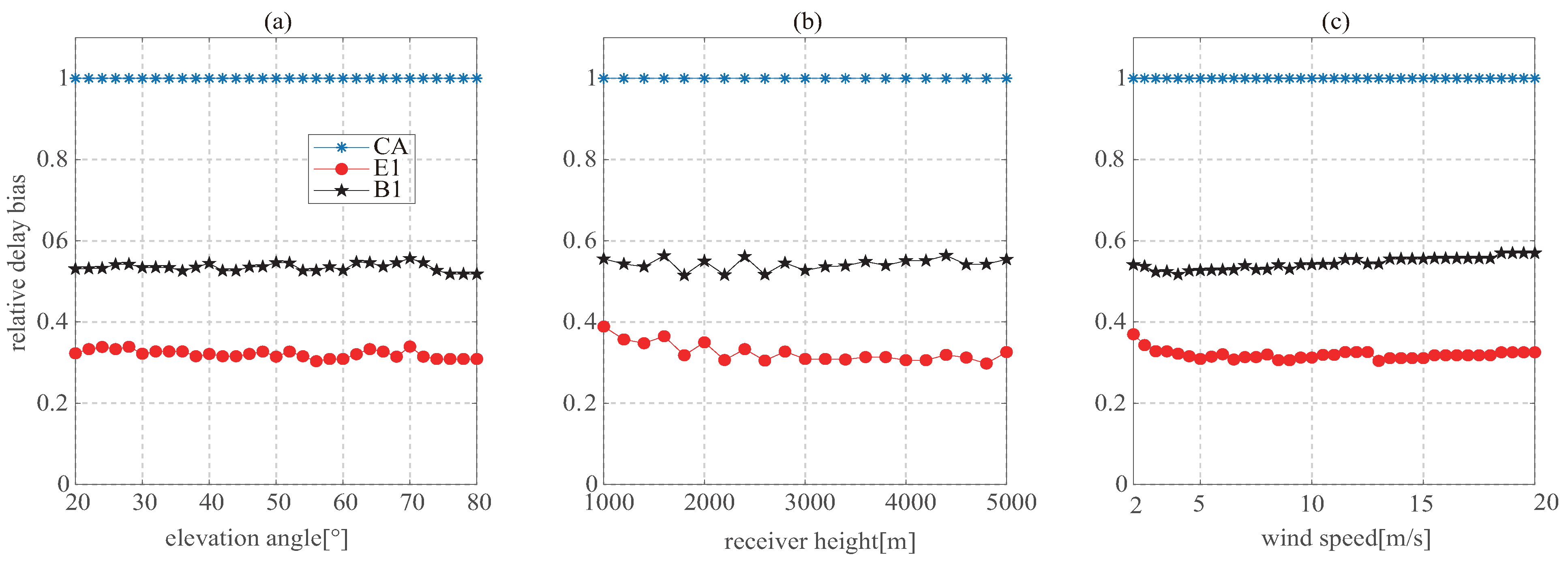
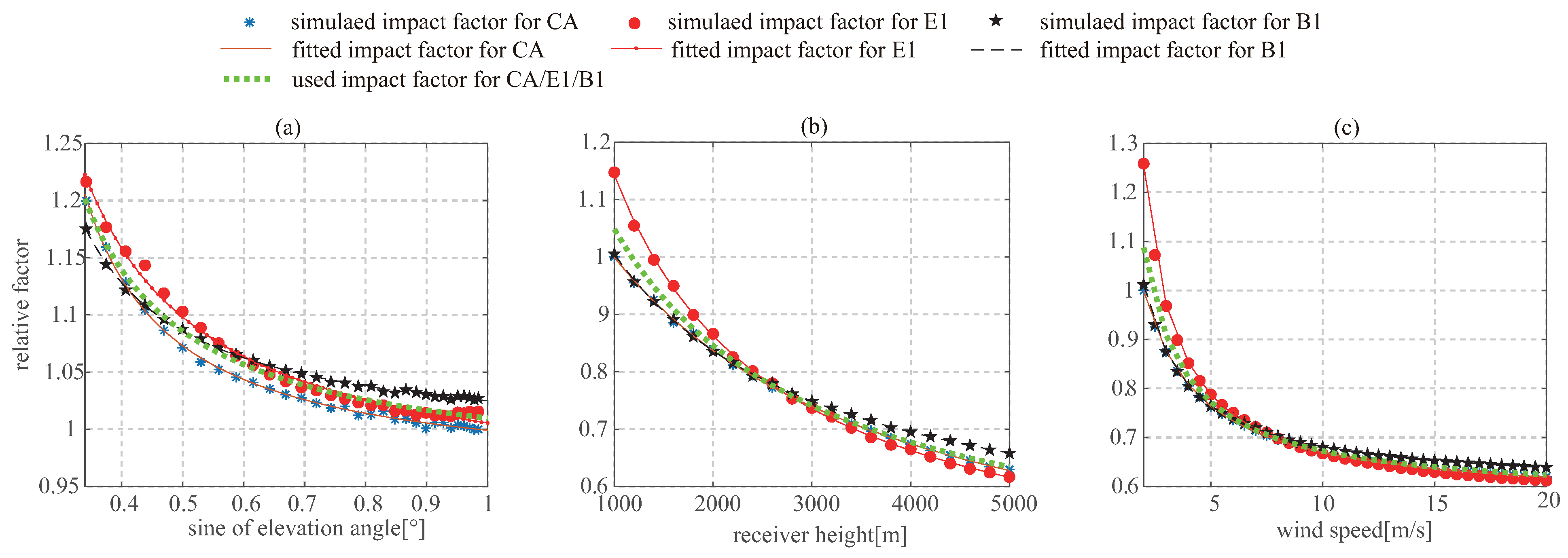
3.1. Elevation Angle
3.2. Height
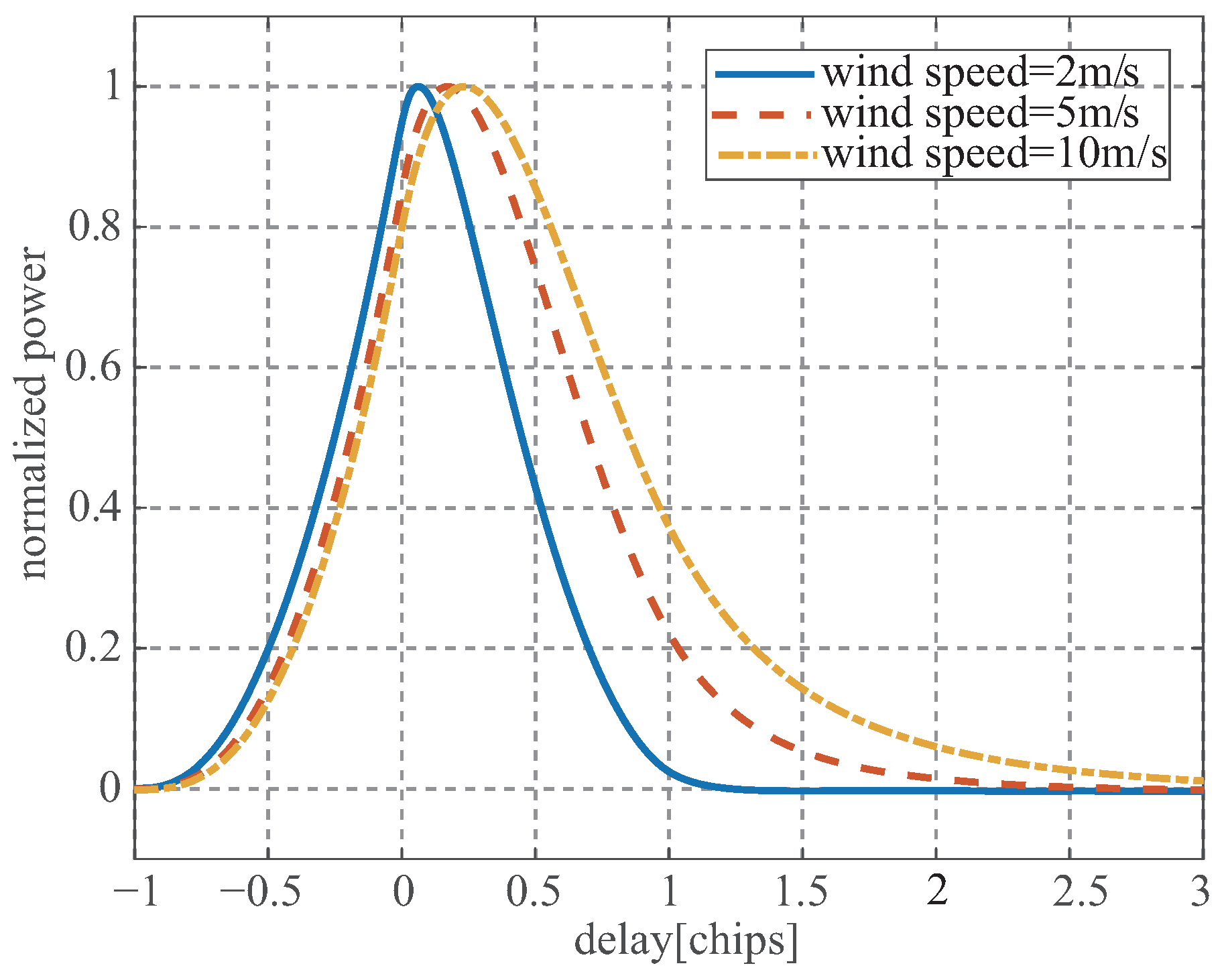
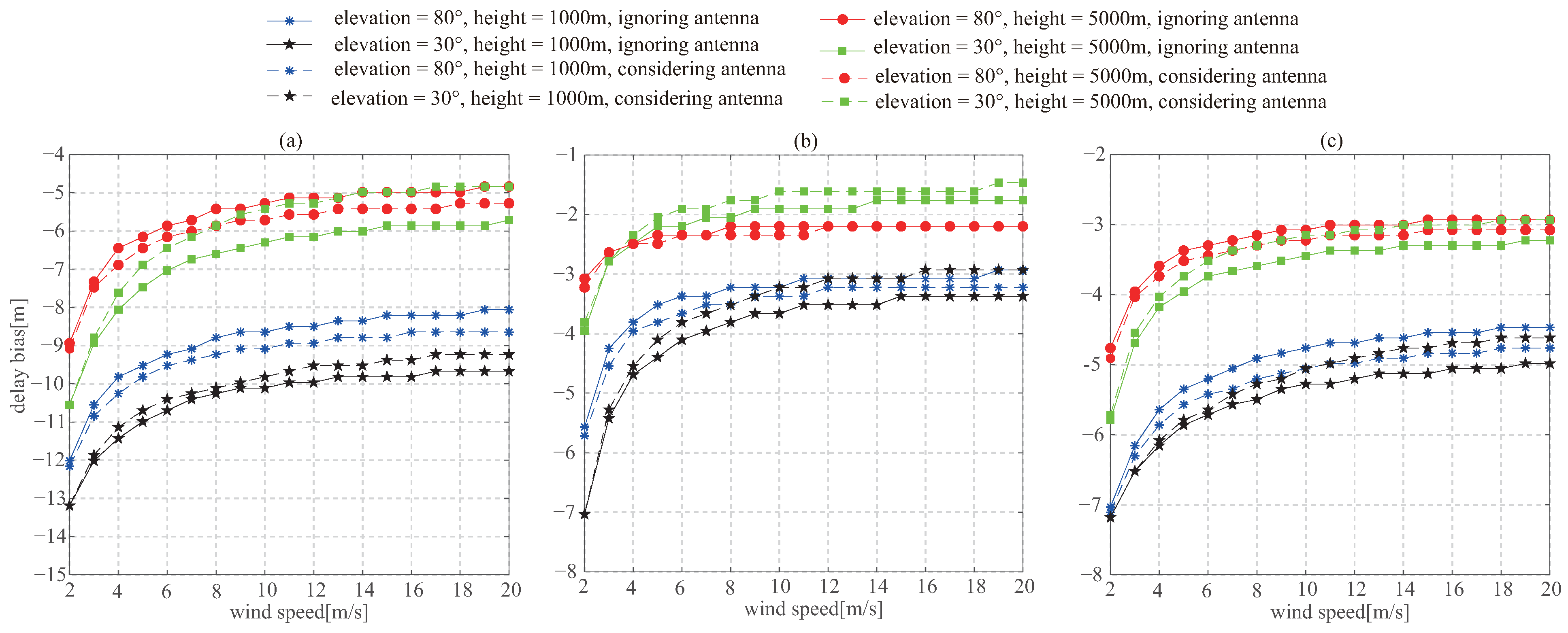
3.3. Wind Speed
3.4. Pseudorandom Noise Code
3.5. LHCP Antenna
4. Calibration of the Specular Delay Bias
4.1. Analytical Model
- a group of elevation angles, receiver heights, and wind speeds are randomly generated and recorded as , respectively, where ;
- the elevation angle, receiver height, and wind speed in the above group are replaced with the given references to produce the other three groups, recorded as , and , respectively;
- the above four groups of parameters are used as the input to simulate the delay waveforms of GPS CA, Galileo E1b, and BeiDou B1I through Equation (6);
- the delay bias is estimated and recorded as , , and for GPS CA; , , and for Galileo E1b; and , , and for BeiDou B1I;
- , and are computed for GPS CA, Galileo E1b, and BeiDou B1I as
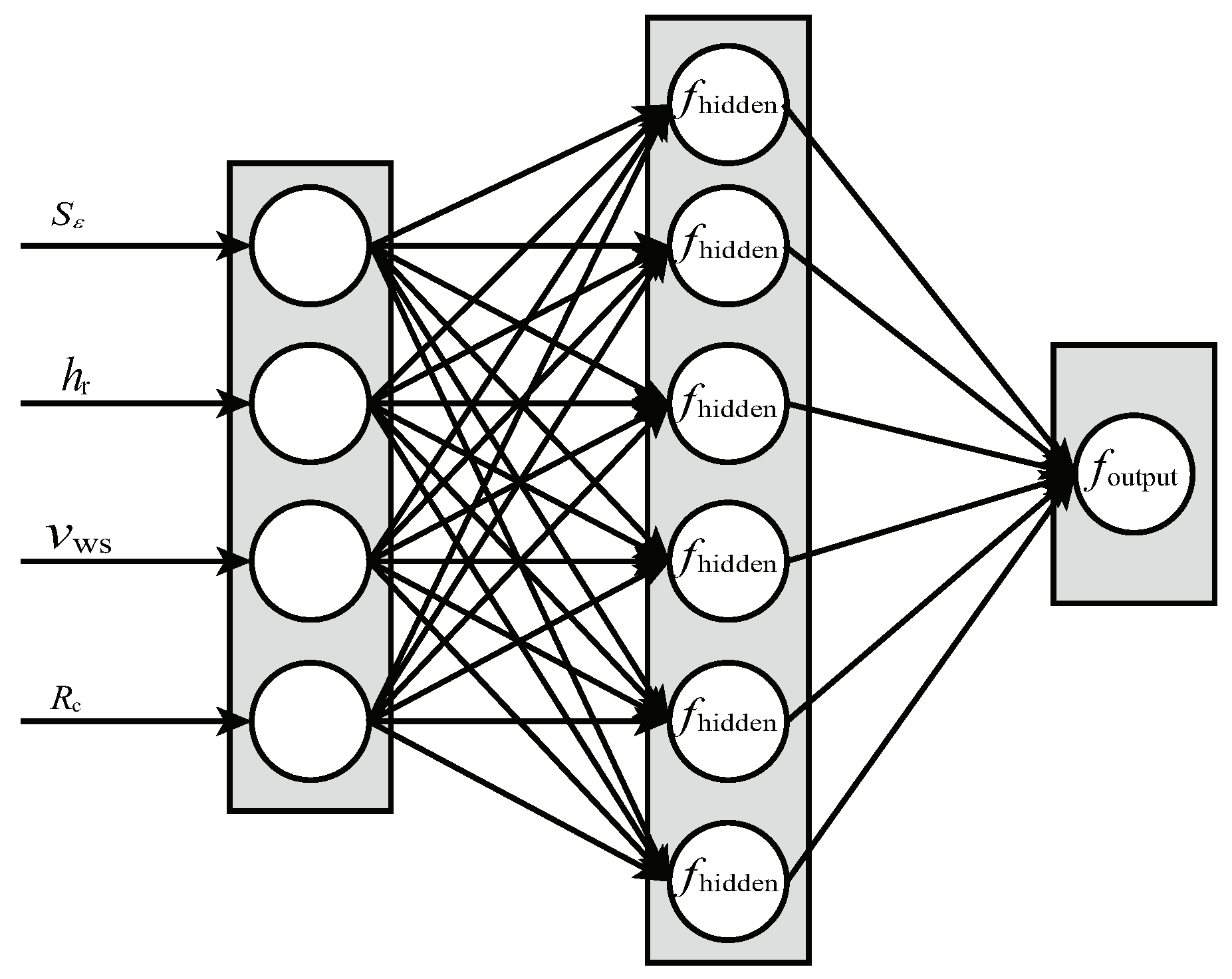
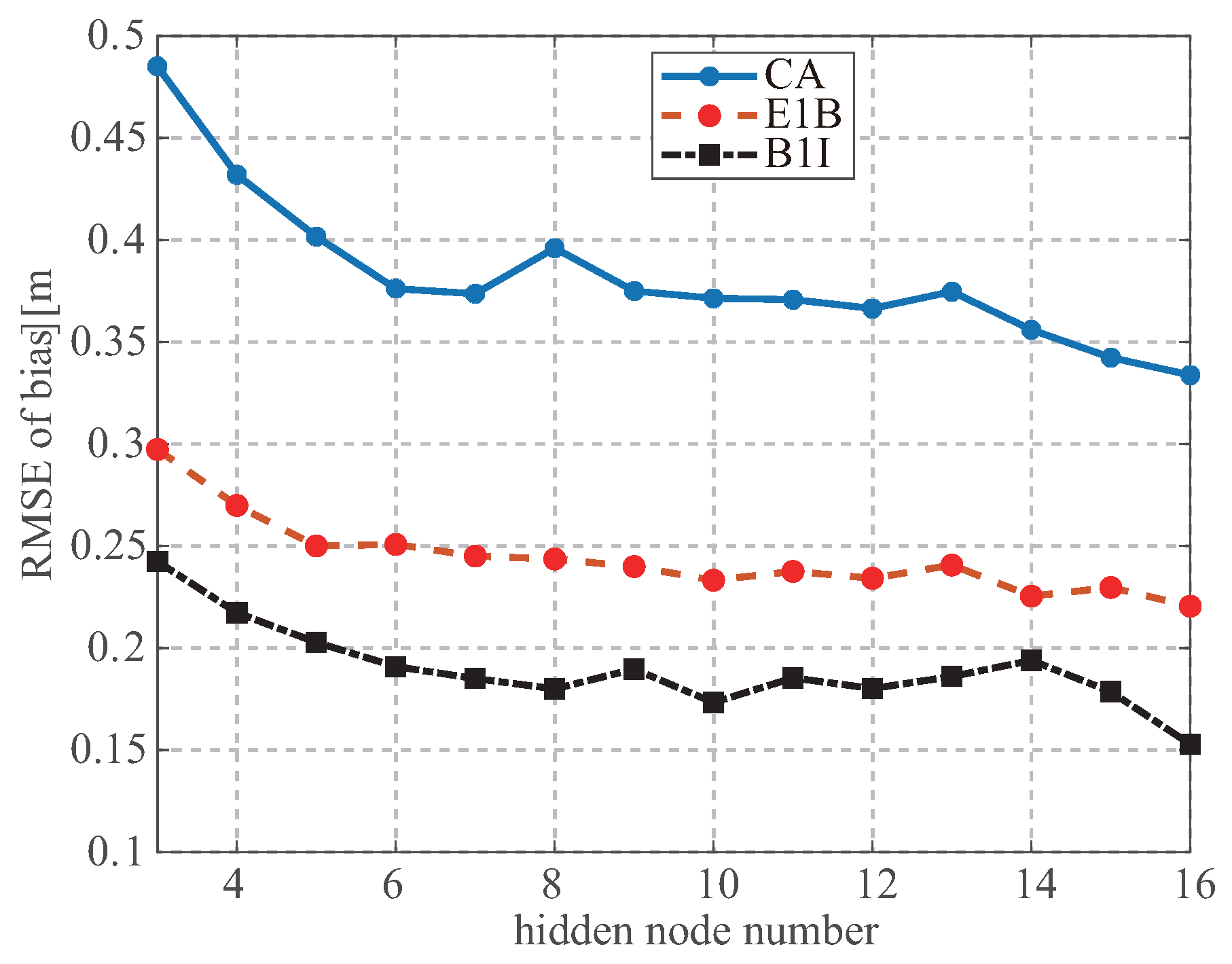
4.2. Neural Network
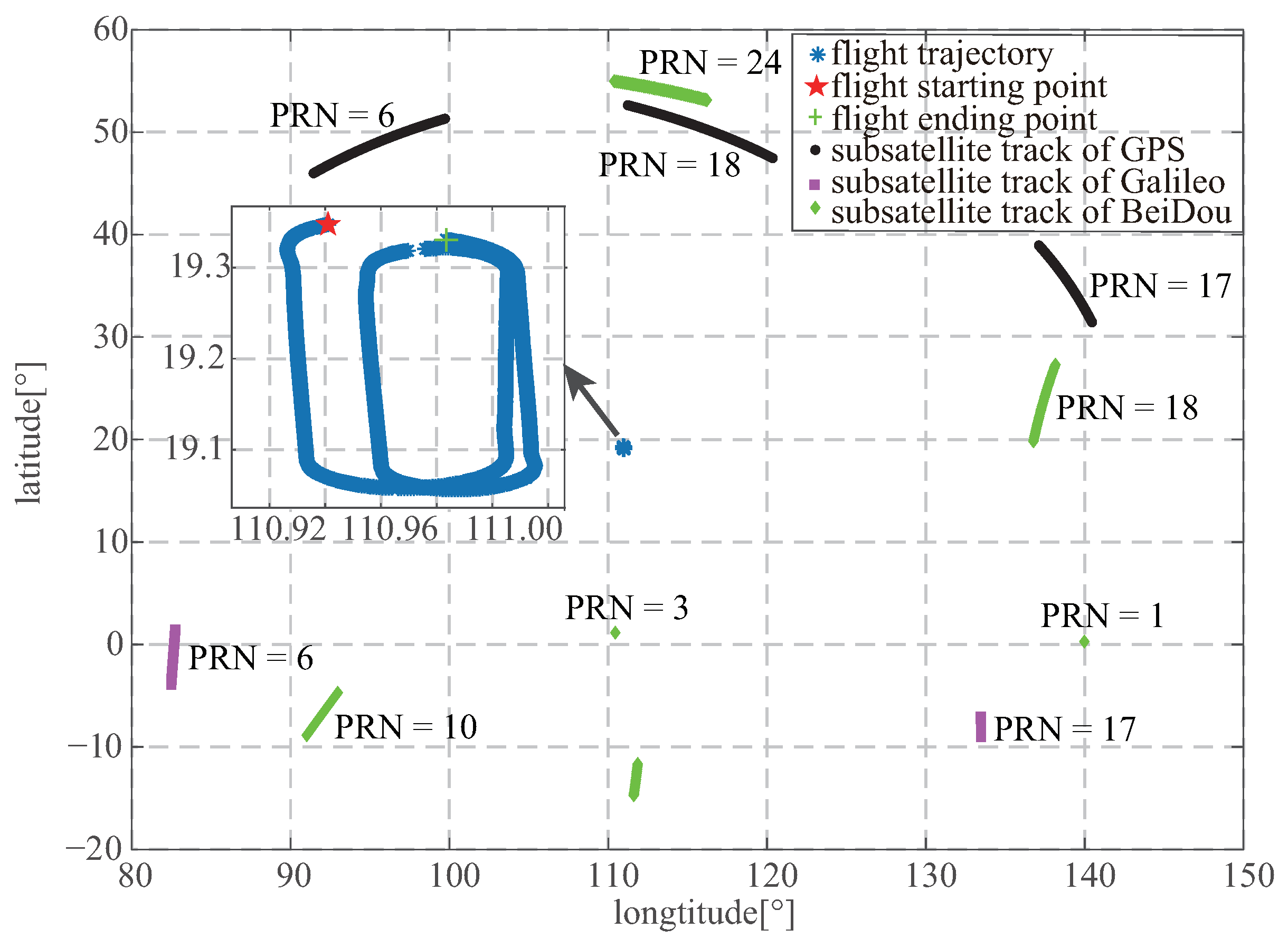
4.3. Multisatellite Observation
- The elevation angles of the chosen satellites should be as different as possible;
- The frequency spectra of the delay waveform should be as different as possible.
5. Validation
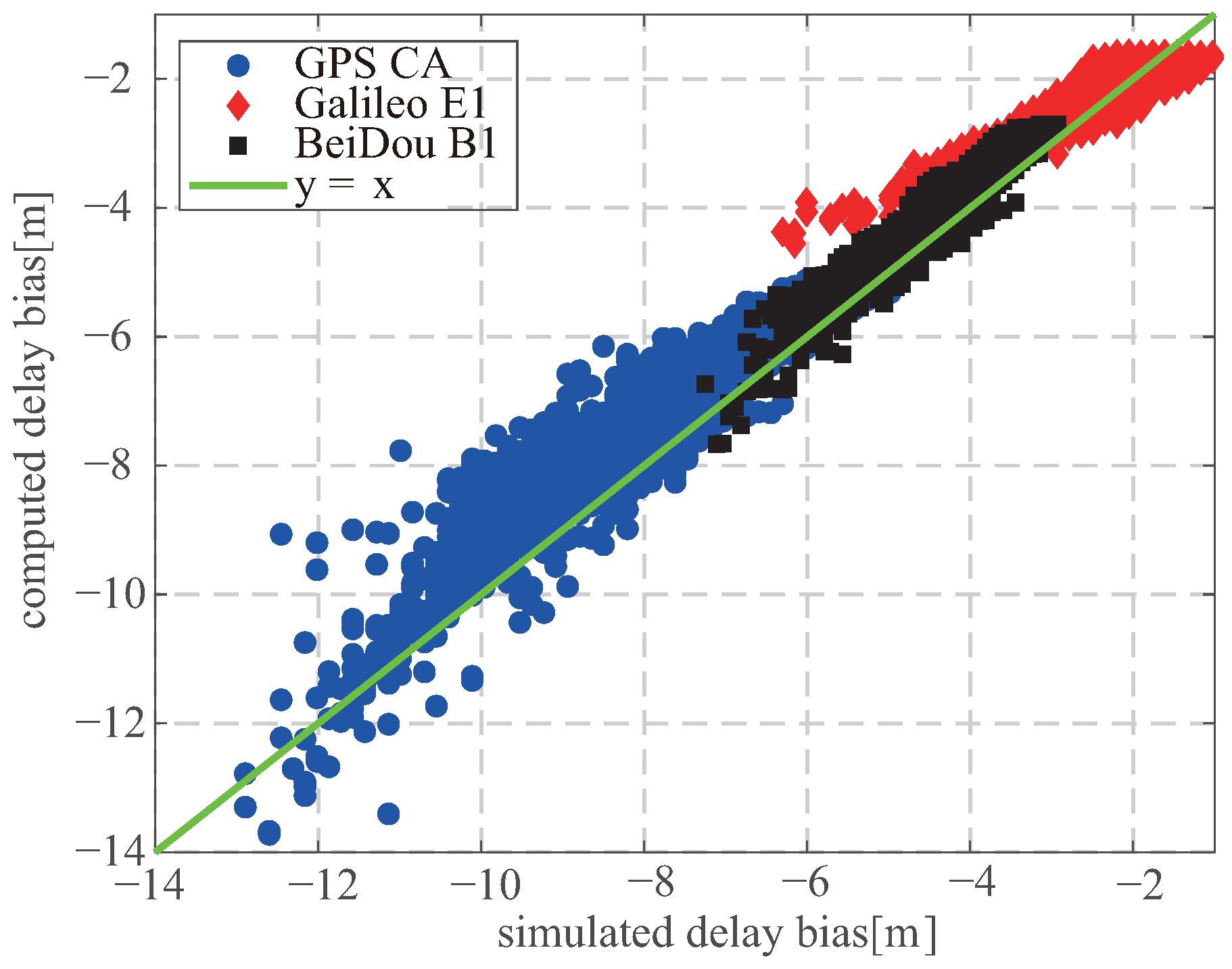
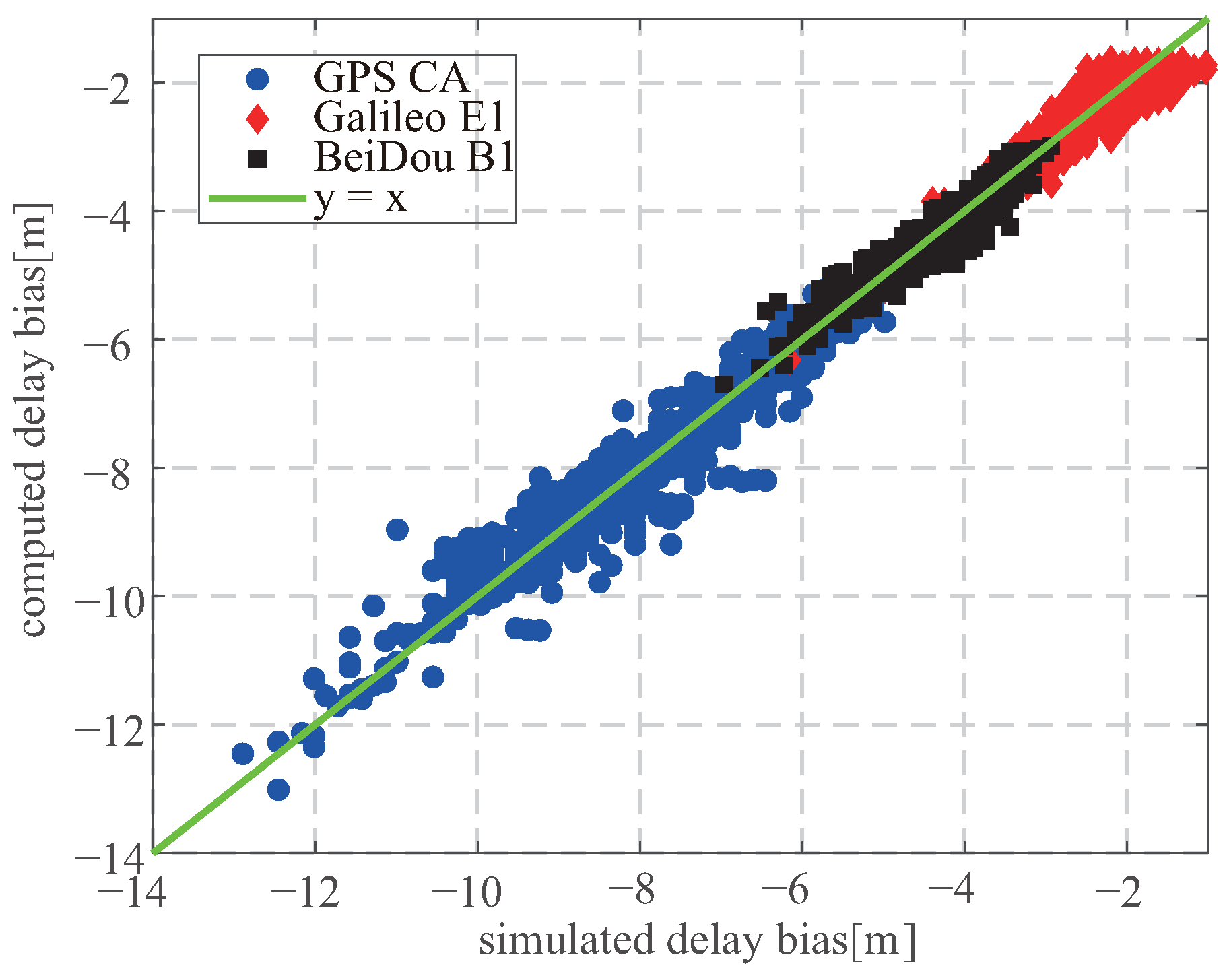
5.1. Simulation
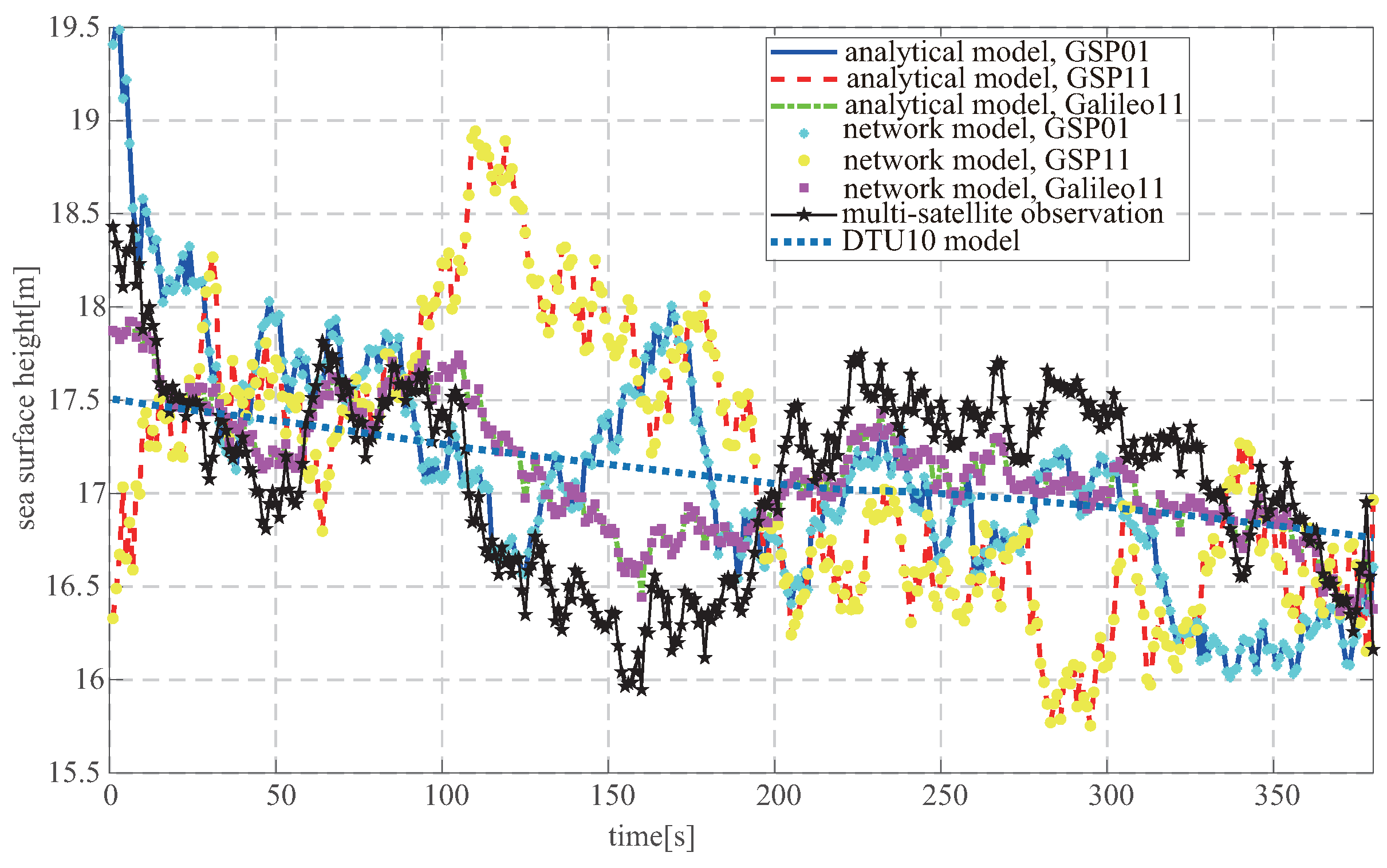
5.2. Experiment
- The receiver position and elevation angle of the GNSS satellite are computed from the direct signal and IGS ephemeris;
- The peak of the derivative waveform is retracked to estimate the delay from the incoherently averaged waveforms;
- and are calibrated to obtain ;
- Equation (3) is used to compute the receiver height referring to the sea surface;
- The sea surface height is retrieved using Equation (4), and a moving average is obtained for the retrieved heights;
- A comparison is made with the DTU10 data to obtain the bias and RMSE of the retrieved sea surface height.
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. Eur. Space Agency 1993, 17, 331–355. [Google Scholar]
- Yu, K.; Rizos, C.; Dempster, A. Sea surface altimetry based on airborne GNSS signal measurements. In Proceedings of the International Society for Photogrammetry, and Remote Sensing (ISPRS) Congress, Melbourne, Australia, 5 August–1 September 2012; pp. 347–352. [Google Scholar]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-Reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Zuffada, C.; Lowe, S.T.; Lee, T.; Zlotnicki, V. Analysis of GNSS-R Altimetry for Mapping Ocean Mesoscale Sea Surface Heights Using High-Resolution Model Simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4631–4642. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Wind speed retrieval algorithm for the cyclone global navigation satellite system (CYGNSS) mission. IEEE Trans. Geosci. Remote Sens. 2016, 54, 441–4432. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosello, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophis. Res. Lett. 2015, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.; Portabella, M.; Foti, G.; Stoffelen, A.; Gommenginger, C.; He, Y. Toward the Generation of a Wind Geophysical Model Function for Spaceborne GNSS-R. IEEE Trans. Geosci. Remote Sens. 2019, 57, 655–666. [Google Scholar] [CrossRef]
- Alonso-Arroyo, A.; Zavorotny, V.U.; Camps, A. Sea ice detection using, U.K. TDS-1 GNSS-R data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4989–5001. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Cardellach, E.; Fabra, F.; Rius, A.; Rib, S.; Martn-Neira, M. First spaceborne phase altimetry over sea ice using TechDemoSat-1 GNSS-R signals. Geophys. Res. Lett. 2017, 44, 8369–8376. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Rizos, C.; Qiao, L. Single-pass sub-meter spacebased GNSS-R ice altimetry: Results from TDS-1. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 3782–3788. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Nasters, D. Utilizing calibrated GPS reflected signals to estimate soil reflectivity and dielectric constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-Llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2015, 20, 525–537. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Cardellach, E.; Xie, F. GNSS Remote Sensing: Theory, Methods and Applications; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New ocean winds satellite mission to probe hurricanes and tropical convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar]
- Jing, C.; Niu, X.; Duan, C.; Lu, F.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Rius, A.; Martn-Neira, M.; Fabra, F.; Nogus-Correig, O.; Rib, S.; Kainulainen, J.; Camps, A.; DAddio, S. Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Rius, A.; Nogués-Correig, O.; Ribó, S.; Cardellach, E.; Oliveras, S.; Valencia, E.; Park, H.; Tarongí, J.M.; Camps, A.; van der Marel, H.; et al. Altimetry with GNSS-R interferometry: First proof of concept experiment. GPS Solut. 2012, 16, 231–241. [Google Scholar] [CrossRef]
- Onrubia, R.; Pascual, D.; Park, H. Satellite Cross-Talk Impact Analysis in Airborne Interferometric Global Navigation Satellite System-Reflectometry with the Microwave Interferometric Reflectometer. Remote Sens. 2019, 11, 1120. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Lofgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Qian, X.; Wu, X. Sea level change from BeiDou Navigation Satellite System-Reflectometry (BDS-R): First results and evaluation. Glob. Planetray Chang. 2011, 149, 20–25. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Williams, S.D. A 10-year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry With GNSS Reflected Signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 102–112. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Lake level and surface topography measured with spaceborne GNSS-Reflectometry from CYGNSS mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13332–13341. [Google Scholar] [CrossRef]
- Rius, A.; Cardellach, E.; Martin-Neira, M. Altimetric Analysis of the Sea-Surface GPS-Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]
- Mashburn, J.; Axelrad, J.; Lowe, S.T.; Larson, K.M. An Assessment of the Precision and Accuracy of Altimetry Retrievals for a Monterey Bay GNSS-R Experiment. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 4660–4668. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Rib, S.; Rius, A. Assessment of Spaceborne GNSS-R Ocean Altimetry Performance Using CYGNSS Mission Raw Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Rib, S.; Martin-Neira, M. Revisiting the GNSS-R Waveform Statistics and Its Impact on Altimetric Retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2854–2871. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2002, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Martin-Neira, M.; D’Addio, S.; Buck, C.; Floury, N.; Prieto-Cerdeira, R. The PARIS Ocean Altimeter In-Orbit Demonstrator. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2209–2237. [Google Scholar] [CrossRef]
- Rib, S.; Arco, J.C.; Oliveras, S.; Cardellach, E.; Rius, A.; Buck, C. Experimental results of an X-band PARIS receiver using digital satellite TV opportunity signals scattered on the sea surface. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5704–5711. [Google Scholar] [CrossRef]
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Hajj, G.A.; Zuffada, C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal. Radio Sci. 2003, 17, 1089. [Google Scholar] [CrossRef]
- Balakhder, A.M.; Al-Khaldi, M.M.; Johnson, J.T. On the Coherency of Ocean and Land Surface Specular Scattering for GNSS-R and Signals of Opportunity Systems. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10426–10436. [Google Scholar] [CrossRef]
- Trees, H.L.V. Detection, Estimation and Modulation Theory. Part III: Radar-Sonar Signal Processing and Gaussian Signals in Noise; Wiley: New York, NY, USA, 1971; pp. 294–302. [Google Scholar]
- Chen, K.S.; Tzeng, Y.C.; Chen, P.C. Retrieval of ocean winds from satellite scatterometer by a neural network. IEEE Trans. Geosci. Remote Sens. 2002, 37, 247–256. [Google Scholar] [CrossRef]
- Attali, J.G.; Gilles, P. Approximations of Functions by a Multilayer Perceptron: A New Approach. Neural Netw. 1997, 10, 1069–1081. [Google Scholar] [CrossRef]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.U.; Katzberg, S.J. Wind speed measurement using forward scattered GPS signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef] [Green Version]
- Shash, R.; Garrison, J.L.; Grant, M.S. Demonstration of bistatic radar for ocean remote sensing using communication satellite signals. IEEE Geophys. Res. Lett. 2012, 9, 619–623. [Google Scholar]
- Gleason, S.T. Remote Sensing of Ocean, Ice and Land Surfaces Using Bistatically Scattered GNSS Signals from Low Earth Orbit. Ph.D. Thesis, University of Surrey, Surrey, UK, 2006. [Google Scholar]
- Mannikus, R.; Soomere, T.; Vika, M. Variation in the mean, seasonal and extreme water level on the Latvian coast, the eastern Baltic sea, during 1961–2018. Estuar. Costal Shelf Sci. 2020, 245, 106827. [Google Scholar] [CrossRef]
- Andersen, O.B. The DTU10 gravity field and mean sea surface. In Proceedings of the Second International Symposium of the Gravity Field of the Earth (IGFS2), Fairbanks, AK, USA, 20–22 September 2010. [Google Scholar]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006; pp. 153–240. [Google Scholar]
- Pascual, D.; Camps, A.; Martin, F.; Park, H.; Arroyo, A.A.; Onrubia, R. Precision bounds in GNSS-R ocean altimetry. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1416–1423. [Google Scholar] [CrossRef]
- Li, W.; D’Addio, S.; Martin-Neria, M. Partial Interferometric Processing of Relfetced GNSS Signals for Ocean Altimetry. IEEE Geophys. Res. Lett. 2014, 11, 1509–1513. [Google Scholar]
- Lowe, S.T.; Meehan, T.; Young, L. Direct Signal Enhanced Semicodeless Processing of GNSS Surface-Reflected Signals. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1469–1472. [Google Scholar] [CrossRef]
- Ho, S.C.; Shah, R.; Garrison, J.L.; Mohammed, P.N.; Schoenwald, A.; Pannu, R.; Piepmeier, J.R. Wideband Ocean Altimetry Using Ku-Band and K-Band Satellite Signals of Opportunity: Proof of Concept. IEEE Geophys. Res. Lett. 2019, 16, 1012–1016. [Google Scholar] [CrossRef]



| elevation angle | 0.96 | −0.11 | −0.16 |
| receiver height | 0.41 | 1810.95 | 1123.74 |
| wind speed | 0.58 | 0.88 | −0.13 |
| Purelin [m] | Tanh [m] | Sigmoid [m] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CA | E1b | B1I | CA | E1b | B1I | CA | E1b | B1I | |
| purelin | 0.83 | 0.49 | 0.40 | 0.68 | 0.50 | 0.34 | 1.03 | 0.56 | 0.37 |
| tanh | 0.38 | 0.26 | 0.16 | 0.44 | 0.27 | 0.23 | 1.23 | 0.25 | 0.21 |
| sigmoid | 0.43 | 0.25 | 0.24 | 0.41 | 0.24 | 0.21 | 1.22 | 0.23 | 0.19 |
| Simulation Parameter | Unit | Value |
|---|---|---|
| flight height | m | 3500 |
| receiver bandwidth | MHz | 10 |
| temperature | C | 25 |
| down-looking antenna beam width | 30 | |
| sea surface height | m | 0.16 |
| wind speed | m/s | 3.83∼4.15 |
| incoherent number | - | 1000 |
| GNSS | - | GPS/Galileo/BeiDou |
| Method | GPS 18 [m] | Galileo 06 [m] | BeiDou 10 [m] |
|---|---|---|---|
| Uncalibrated | −5.41 | −1.68 | −2.77 |
| Analytical model | −0.51 | −0.03 | −0.25 |
| Network model | −0.02 | 0.18 | 0.05 |
| Multisatellite observation | 0.16 | ||
| Method | GPS 18 [m] | Galileo 06 [m] | BeiDou 10 [m] |
|---|---|---|---|
| Uncalibrated | 0.49 | 0.42 | 0.22 |
| Analytical model | 0.47 | 0.42 | 0.22 |
| Network model | 0.47 | 0.42 | 0.22 |
| Multisatellite observation | 0.56 | ||
| PRN | 07 | 17 | 18 |
|---|---|---|---|
| Elevation angle | ∼50.04 | ∼ | ∼ |
| Method | GPS 01 [m] | GPS 11 [m] | Galileo 11 [m] |
|---|---|---|---|
| Uncalibrated | 4.57 | 4.20 | 1.65 |
| Analytical model | 0.80 | −0.27 | 0.25 |
| Network model | −0.48 | −0.94 | 0.02 |
| Multisatellite observation | 0.46 | ||
| Method | GPS 01 [m] | GPS 11 [m] | Galileo 11 [m] |
|---|---|---|---|
| Uncalibrated | 0.48 | 0.63 | 0.23 |
| Analytical model | 0.48 | 0.65 | 0.23 |
| Network model | 0.48 | 0.64 | 0.23 |
| Multisatellite observation | 0.49 | ||
| Satellite 1 | Satellites | Bias [m] | RMSE [m] | |
|---|---|---|---|---|
| GPS 01 | GPS 11 | 18.53 | 6.63 | 4.86 |
| GPS 01 | Galileo 11 | 1.05 | 0.43 | −0.08 |
| GPS 11 | Galileo 11 | 0.86 | 0.48 | 0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Yang, D.; Zhang, G.; Xing, J.; Zhang, B.; Yang, L. Measurement of the Sea Surface Height with Airborne GNSS Reflectometry and Delay Bias Calibration. Remote Sens. 2021, 13, 3014. https://doi.org/10.3390/rs13153014
Wang F, Yang D, Zhang G, Xing J, Zhang B, Yang L. Measurement of the Sea Surface Height with Airborne GNSS Reflectometry and Delay Bias Calibration. Remote Sensing. 2021; 13(15):3014. https://doi.org/10.3390/rs13153014
Chicago/Turabian StyleWang, Feng, Dongkai Yang, Guodong Zhang, Jin Xing, Bo Zhang, and Lei Yang. 2021. "Measurement of the Sea Surface Height with Airborne GNSS Reflectometry and Delay Bias Calibration" Remote Sensing 13, no. 15: 3014. https://doi.org/10.3390/rs13153014
APA StyleWang, F., Yang, D., Zhang, G., Xing, J., Zhang, B., & Yang, L. (2021). Measurement of the Sea Surface Height with Airborne GNSS Reflectometry and Delay Bias Calibration. Remote Sensing, 13(15), 3014. https://doi.org/10.3390/rs13153014






