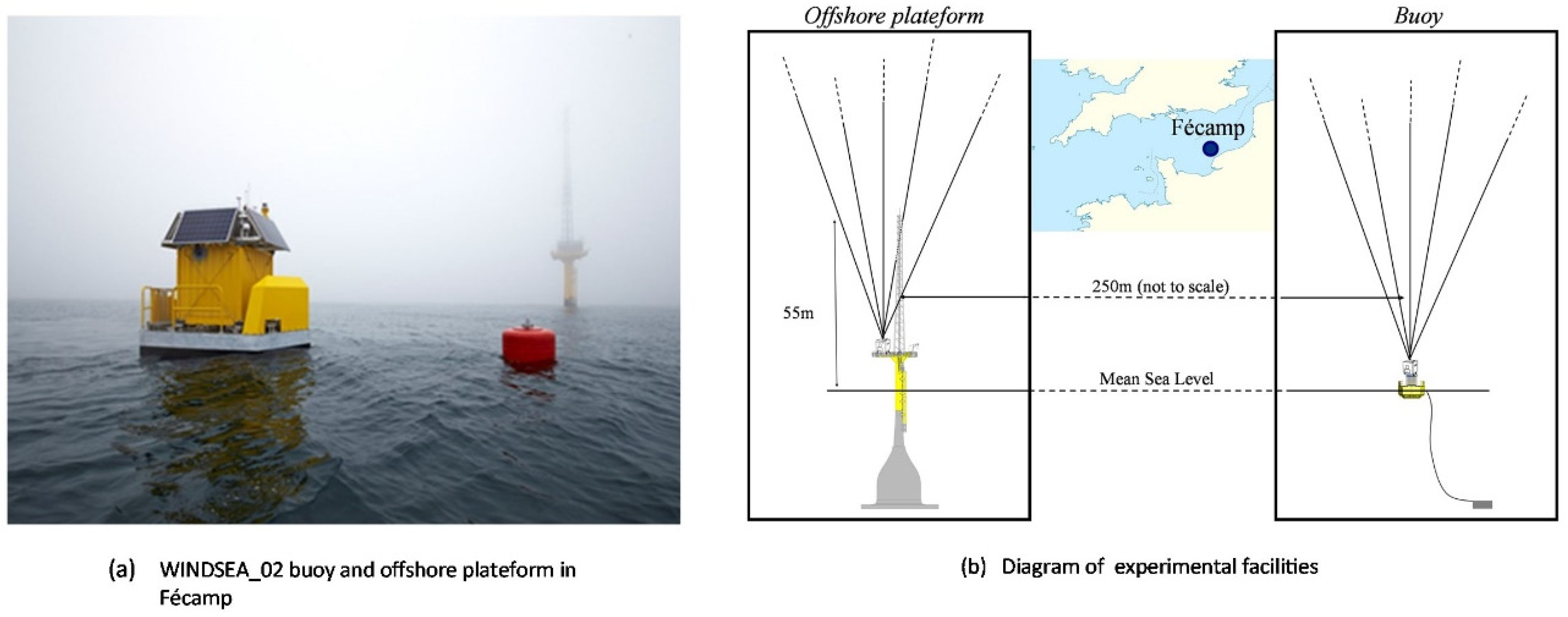
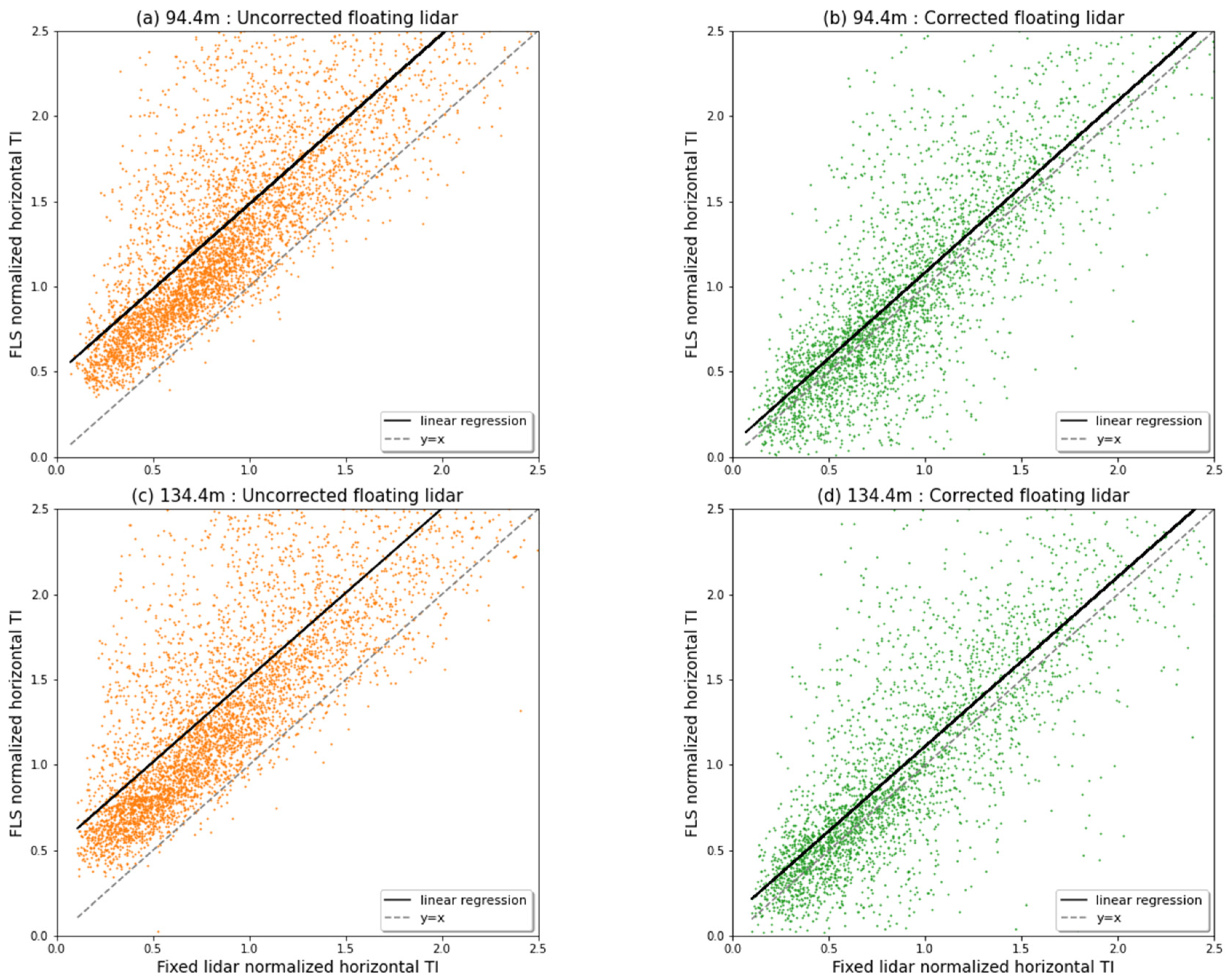
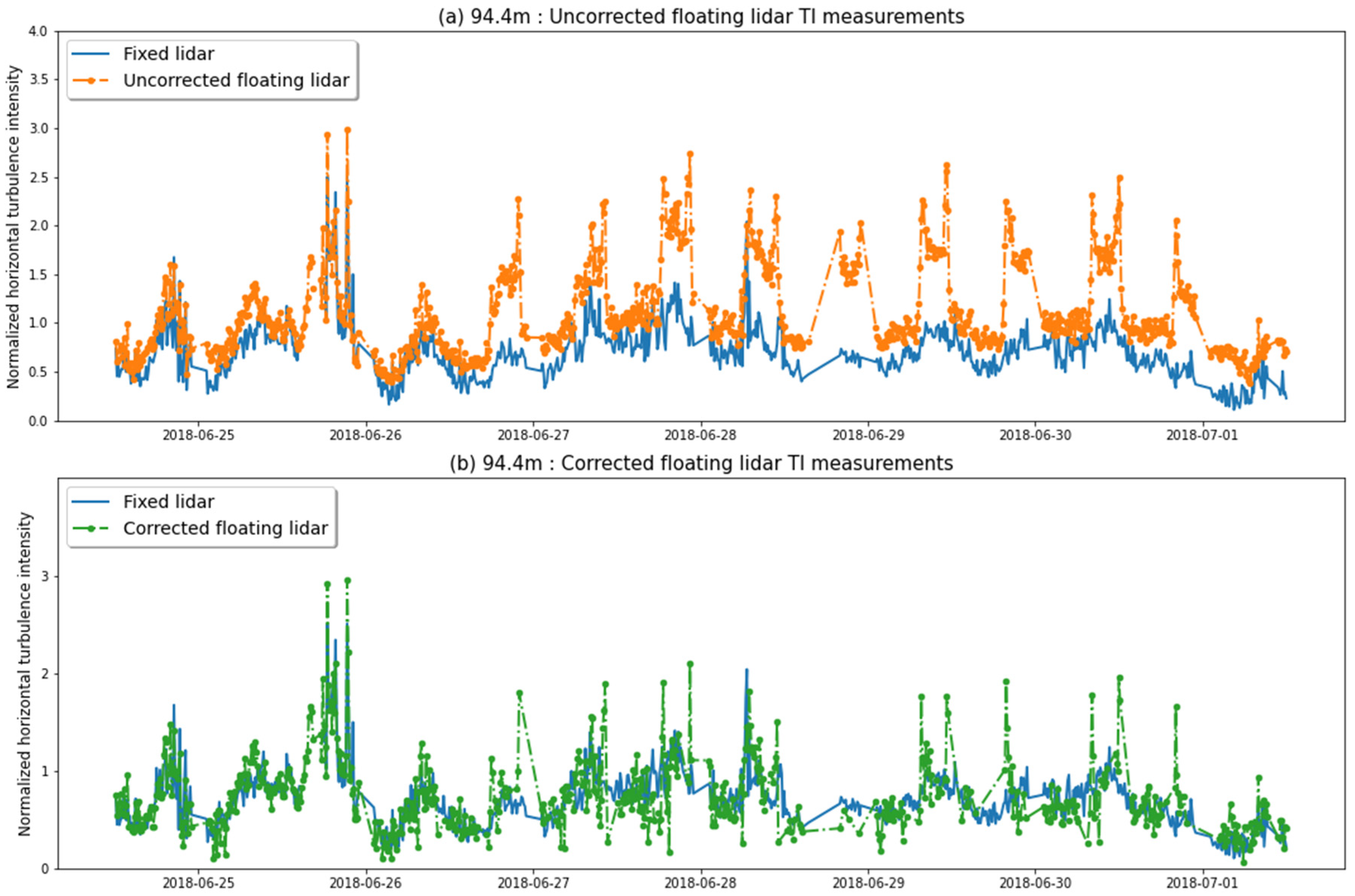
The buoy motion influences the wind LIDAR velocity measurement in several ways. We separate three distinct effects; the effect of motion on the cone geometry and on the perceived relative velocity; the effect of subsampling due to the temporal averaging of several pulses in the same beam direction, and; the interaction effect between the different beam measurements.
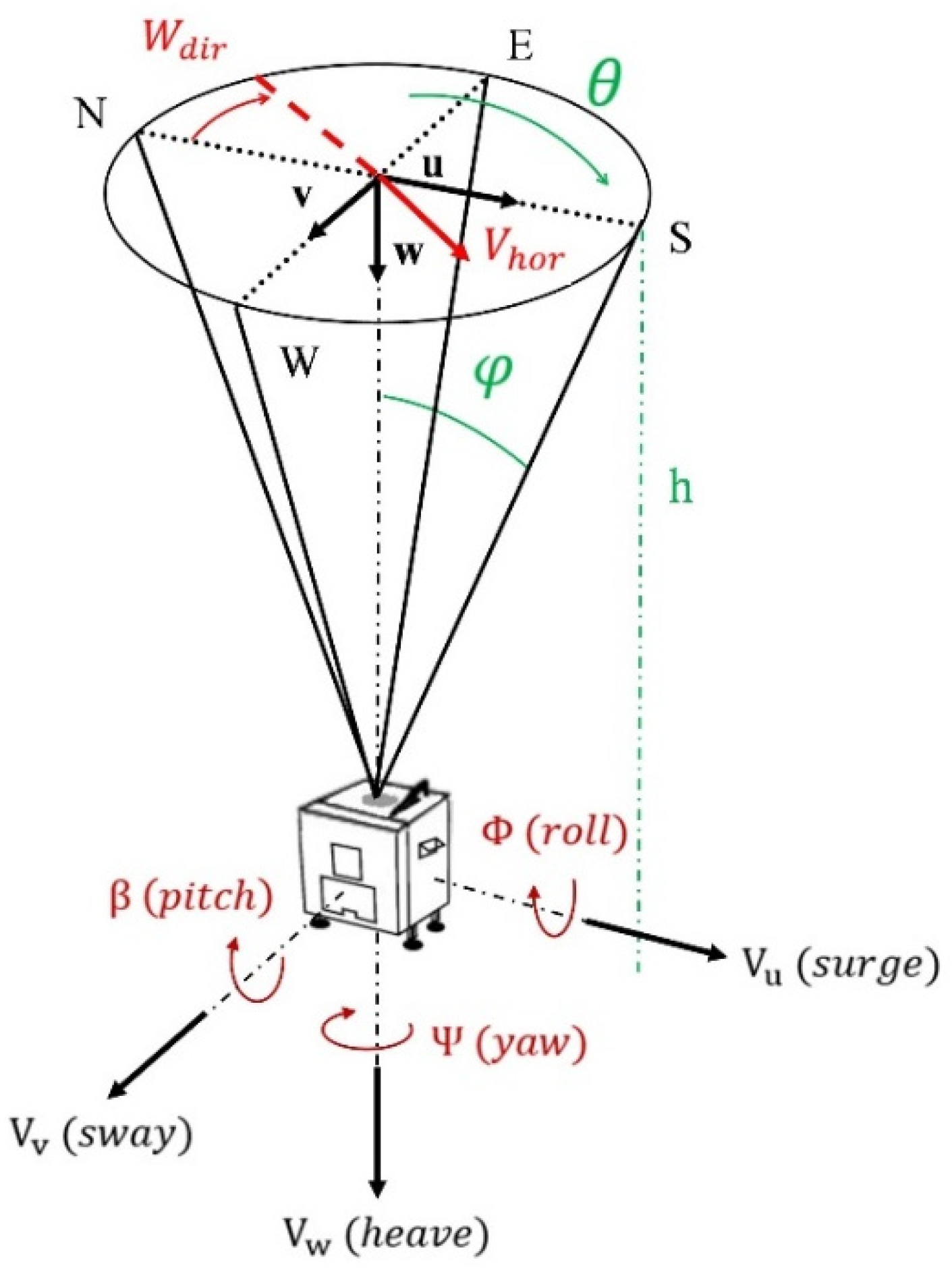
In order to understand the influence of the various degrees of freedom of motion on the LIDAR measurement, we consider the case of a purely horizontal non-turbulent wind (
). As the directions of the WindCube v2
® measurement beams are symmetrical in the horizontal plane, roll and pitch have a similar effect on the beams having the same relative position to their rotation axis. Therefore, for the sake of simplicity, we combine these two motions and decompose the rotational motions into two effects: Tilt and yaw. The motions are represented by zero-centred sinusoids, defined by an amplitude
and period
, of the form:
For a gradual understanding, we first study the reaction of a single LIDAR beam measurement to a period of tilt and yaw. In a second step, we study the effect of the temporality of the measurements, including the effect of subsampling and the effect of interaction between the different beam directions. Based on the study of the order of magnitude of the IMU measurements, we consider the amplitudes: , ) and m/s.
4.2.2. Tilt Motion
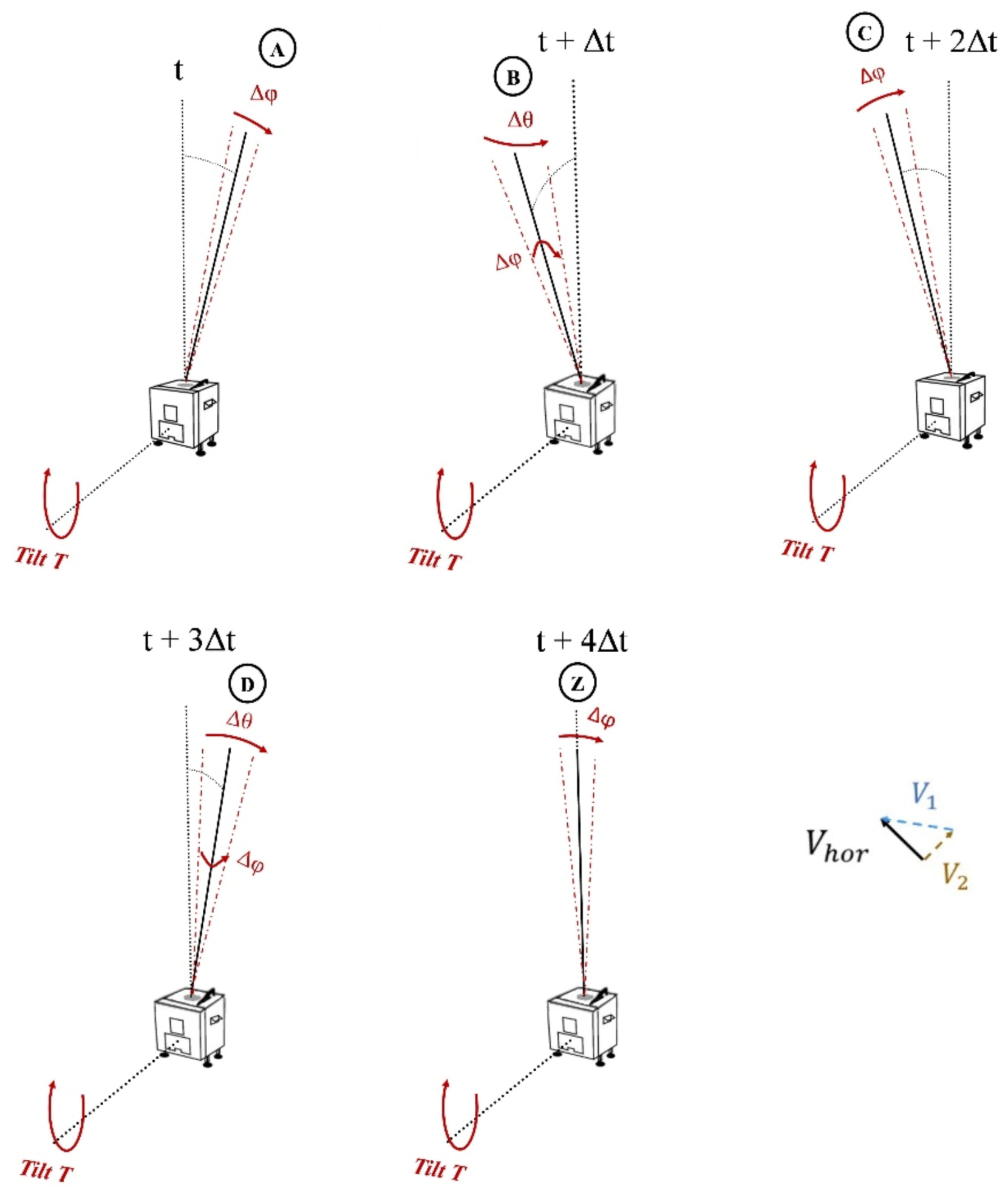
In this section, care has been taken to make all the results independent of the nature of the tilt (pitch or roll), so the directions of the rays are defined by A, B, C, D and Z for zenith. The effect of tilt on the angles
and
of the beams in the different directions of the WindCube v2
® is studied in
Figure 4. The horizontal velocity is decomposed into two components:
component in the A–C beams plane and the
component in the B–D beams plane.
For beams A and C, the tilt only affects the angle . And for beams B and D, the tilt modifies and . The effect on the measurements is a composition of two angular effects. In the Z case, the ray is at the zenith and the tilt has an effect only on φ. As the horizontal velocity measurement is only affected by the measurements of the beams A, B, C and D, we do not study here in detail the zenith beam.
We first focus on the rays in the normal plane to the tilt axis (beams A–C). In this plane, only the angle
is affected by the rotational movement, it evolves in a linear way with the tilt:
. Therefore, only the
component of the incident horizontal wind affects the radial wind speed measurement. We present here the effect of motion on the measurement of beam A. The radial wind speed is calculated according to the Equation (6):
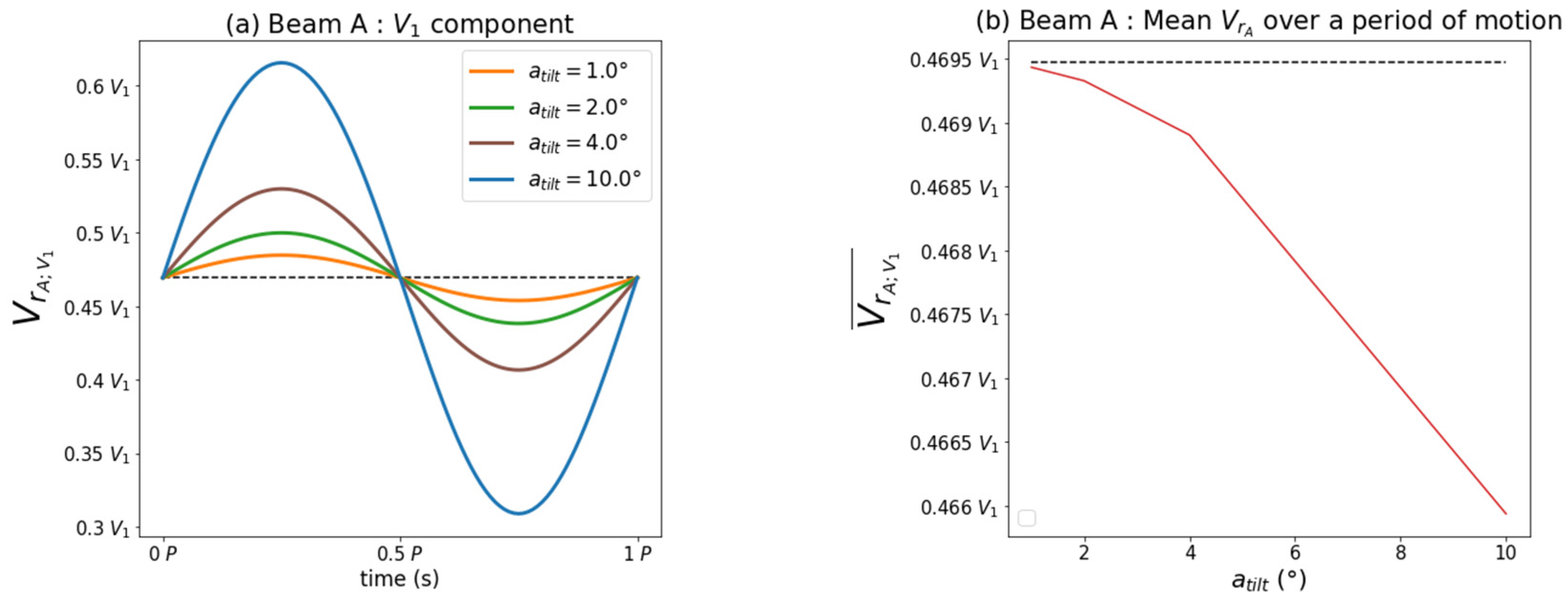
The tilt of the LIDAR has the effect of increasing or decreasing the value of
which directly affects the value of the measured readial velocity (
Figure 5a). The larger the value of
, the more aligned the beam is with the horizontal velocity and the greater the radial wind speed measurement. In
Figure 5b, it is observed that this effect is not uniformly distributed around the value
. The properties of the sine function around the angle
bring more influence to the decrease of the angle than to its increase. Thus, the average measurement of the beam A is affected by the tilting motion. For an entire period of tilt of amplitude
, the average measurement of the beam is decreased by less than 1%.
We note that the same tilting movement has an opposite effect on the radial wind speed measured by beam C. Thus, if the measurements were carried out simultaneously at both directions A and C, the tilting movement would have very little influence on the measurement of the velocity component by the WindCube v2®. However, in a real case, the measurements are not simultaneous and this effect has a strong influence on the LIDAR measurement.
Now, we focus on the beams in the plane parallel to the tilt axis (beams B-D). In this plane, the motion simultaneously affects the angles
and
of the beams. Here, we present the effect of the tilt on the radial wind speed measurement from beam B.
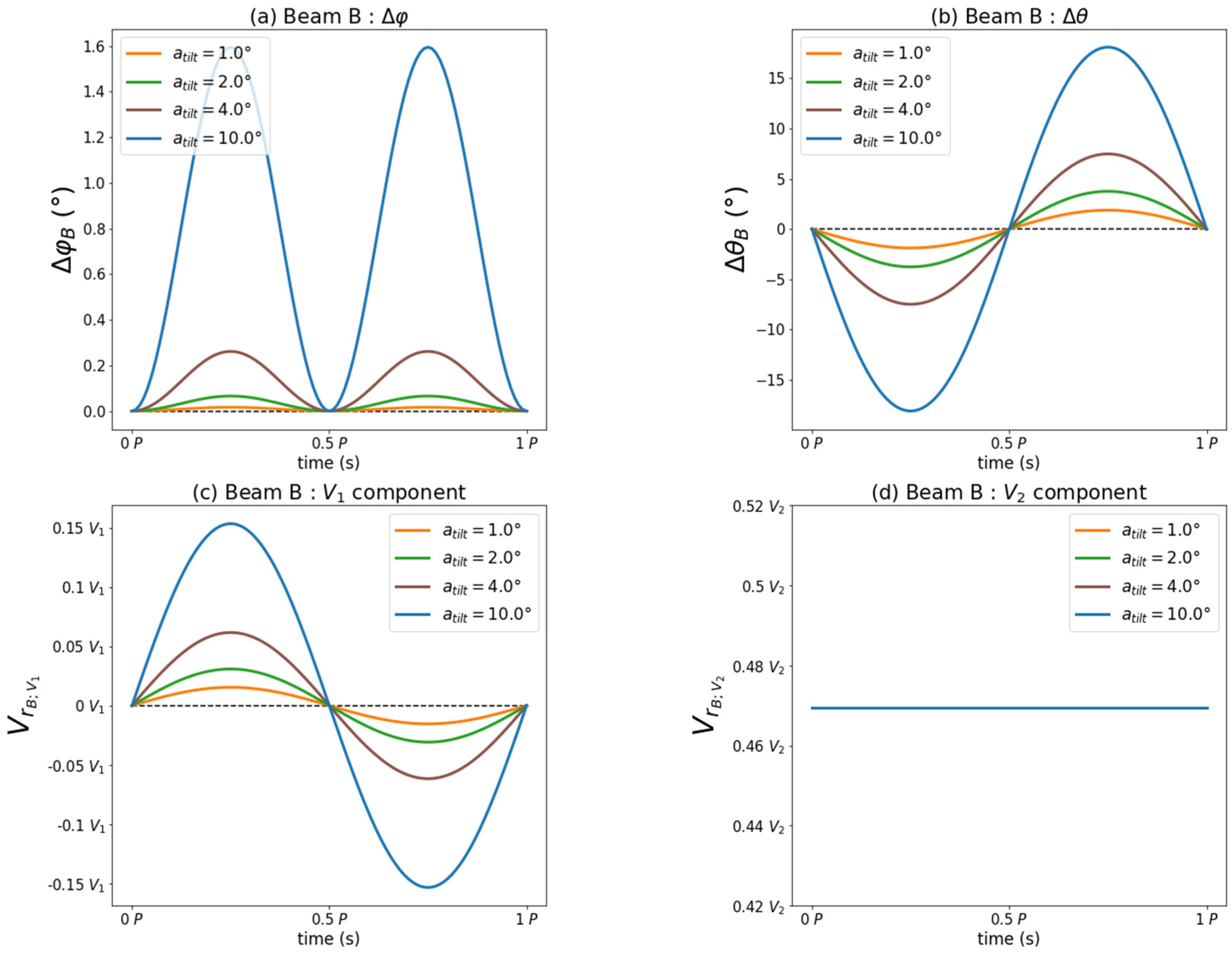
Figure 6a,b show the influence of a period of sinusoidal motion on the variation of angles
and
of beam B:
and
. The variation is defined as the difference of the angle subjected to the motion with respect to its original position. The angle
evolves counterclockwise for a positive inclination. While the angle
is accentuated whatever the sign of the tilt
. Since the angles
and
are modified by the tilt, the measurements of the radius B are impacted by both wind components
and
:
The measurement of the
component of the radial wind speed is impacted by the tilt motion (
Figure 6c). Since beam B is originally perpendicular to the wind component
, it is not supposed to measure it. However, the tilt modifies
and the measurement of beam B is impacted by the
component. The measurement of the
component is not affected by the tilt movement (
Figure 6d). The effects induced by the simultaneous changes in the angles
and
compensate each other to remove this error.
We note that the same tilting movement has an equivalent effect on the radial wind speed measurement of beam D. If the measurements were made simultaneously at both directions B and D, the effects of the tilting movements on the two opposite beams would be additive.
We can now determine the dominant effect induced by tilting on the horizontal wind measurement. For a tilt along a given axis, only the component of the incident wind, perpendicular to the axis of rotation, has an influence on the measurement of the four non-vertical rays. We consider here the case of a whole period of sinusoidal motion of amplitude and we evaluate the order of magnitude of the influence of this motion on the measurement of the different rays. While the average measurement is barely affected by the tilting motion, a large amount of variability is introduced into the time series of the measurement. The effects on the rays parallel (beams B–D) and perpendicular (beams A–C) to the axis of rotation introduce an equivalent standard deviation on the radial wind speed measurement, of the order of . However, the influence on the horizontal velocity variation is not equivalent. In order to estimate this influence, let us assume an incident wind following the component () and a variation introduced by a tilt on the measurement of the wind component in the plane of each pair of rays. Considering , using a Reynolds decomposition and the Equation (2), we compare:
The effect of a variation of
in the measurement of the component measured by A-C rays:
The effect of a variation of
in the measurement of the component measured by B-D rays:
There is an order of magnitude of discrepancy between the two estimates: . In the case of an isolated tilt , the most influential effect on the horizontal wind measurement is the variation of the angle on the beams perpendicular to the rotation axis (beams A–C).
4.2.3. Yaw Movement
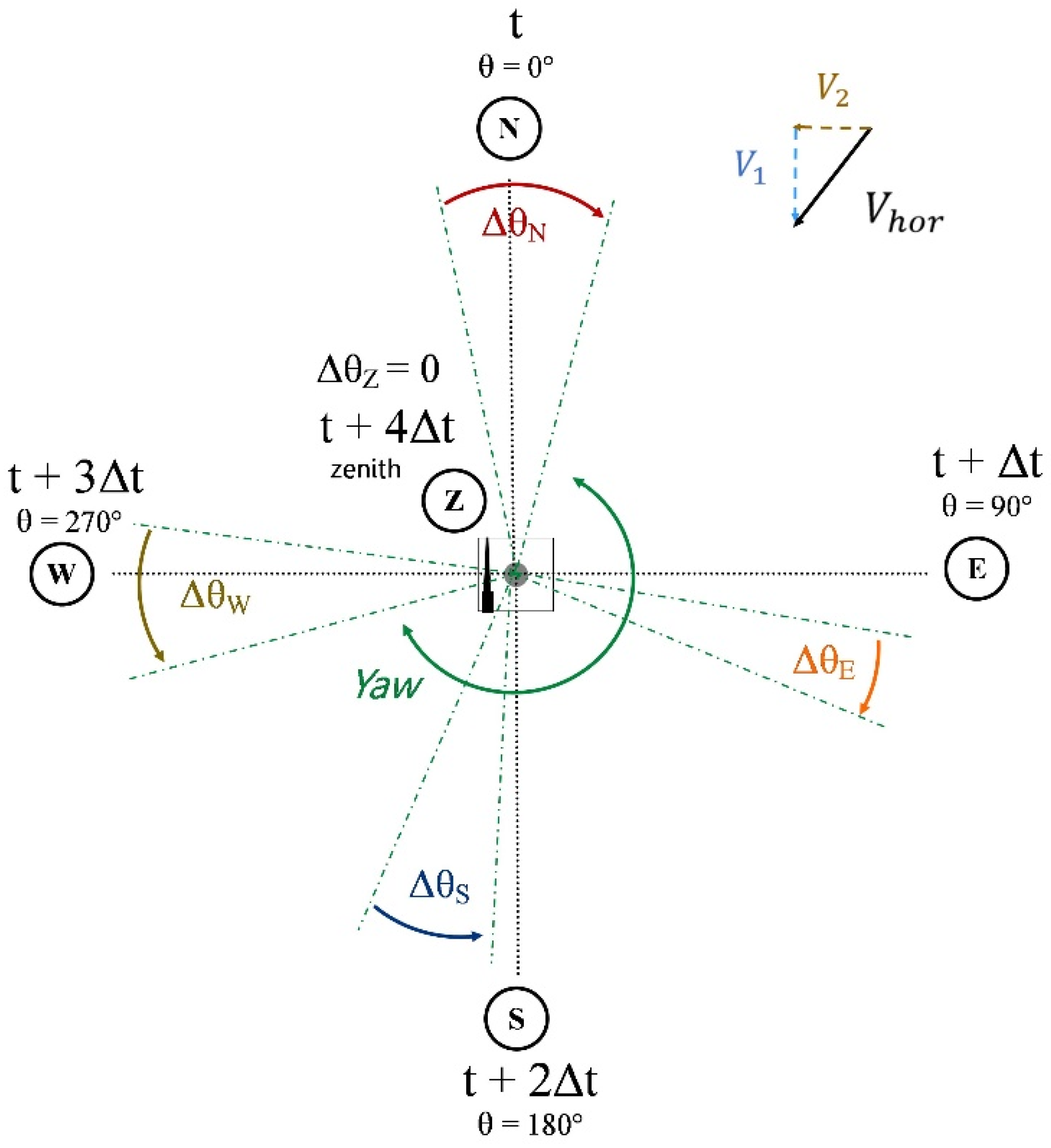
As yaw only has one degree of freedom, we relate to the rays here by their more common label:
. The effect of yaw
on the angle
of the different WindCube rays v2 is studied in
Figure 7. The horizontal velocity is decomposed into two components: the
component in the N-S beams plane and the
component in the E-W beams plane.
and
correspond to the
and
axes in the WindCube v2
® reference frame (
Figure 1).
For the four non-vertical beams, yaw is in the same plane as the angle , so it is linearly affected by the rotation: . For the beam at the zenith, an isolated yaw motion has no effect on its geometry. However, it is important to bear in mind that yaw will affect the vertical measurement in the case of a tilted LIDAR.
As the angles
of the non-vertical rays are modified by yaw, the measurements of the four rays are impacted by the two wind components
and
. Here we present the effect of motion on the measurement of the N beam:
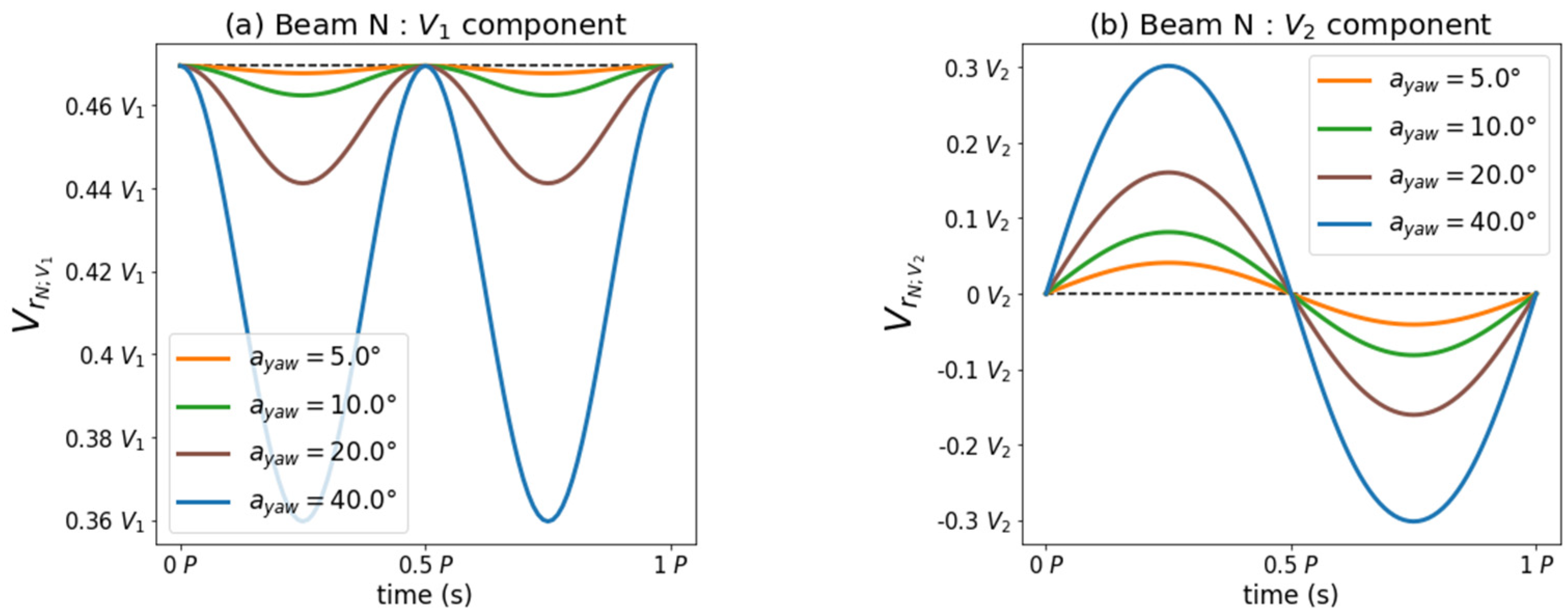
The ray N is originally aligned with the
component of the incident wind (
Figure 7). Thus, the radial wind speed measurement
is decreased by the LIDAR motion regardless of the yaw direction (
Figure 8a). The
component depends on the direction of rotation because it depends on the orientation of the beam with respect to the
component of the incident wind (
Figure 8b).
We note that, in the hypothetical case of a simultaneous measurement of all the rays, the effect of the yaw on the horizontal speeds measured by the four non-vertical rays would be cancelled and only the direction of the wind measured would be modified. However, in the real case, the influence of the yaw depends on the movement-measurement temporality and yaw motion affects the LIDAR’s horizontal speed measurements.
4.2.4. Effect of Motion Subsampling for an Isolated Beam
Now, we take into account the timing of the alternative measurements of the rays. We recall here that the approximate
LOS measurement times of the five rays are defined by:
. The measurement of a given beam occurs approximately every 4.2 s and for a duration of about 0.8 to 1 s. During a
LOS measurement time, the six degrees of freedom of motion of the buoy shift. The radial wind speed measurement is an average of a large number of measurements subjected to different movements. In addition to this phenomenon, a motion subsampling effect is induced by the incremental evolution of the beam direction, which returns to its original position every 4.2 s. These phenomena apply to rotational (roll, pitch, yaw) and translational (surge, sway, heave) motions and can strongly influence the radial wind speed measurement of one line-of-sight. In order to observe the influence of subsampling on the measured radial wind speed, we consider the ray A described in
Section 4.2.2, aligned to the component
, subjected to a tilting motion
of amplitude
.
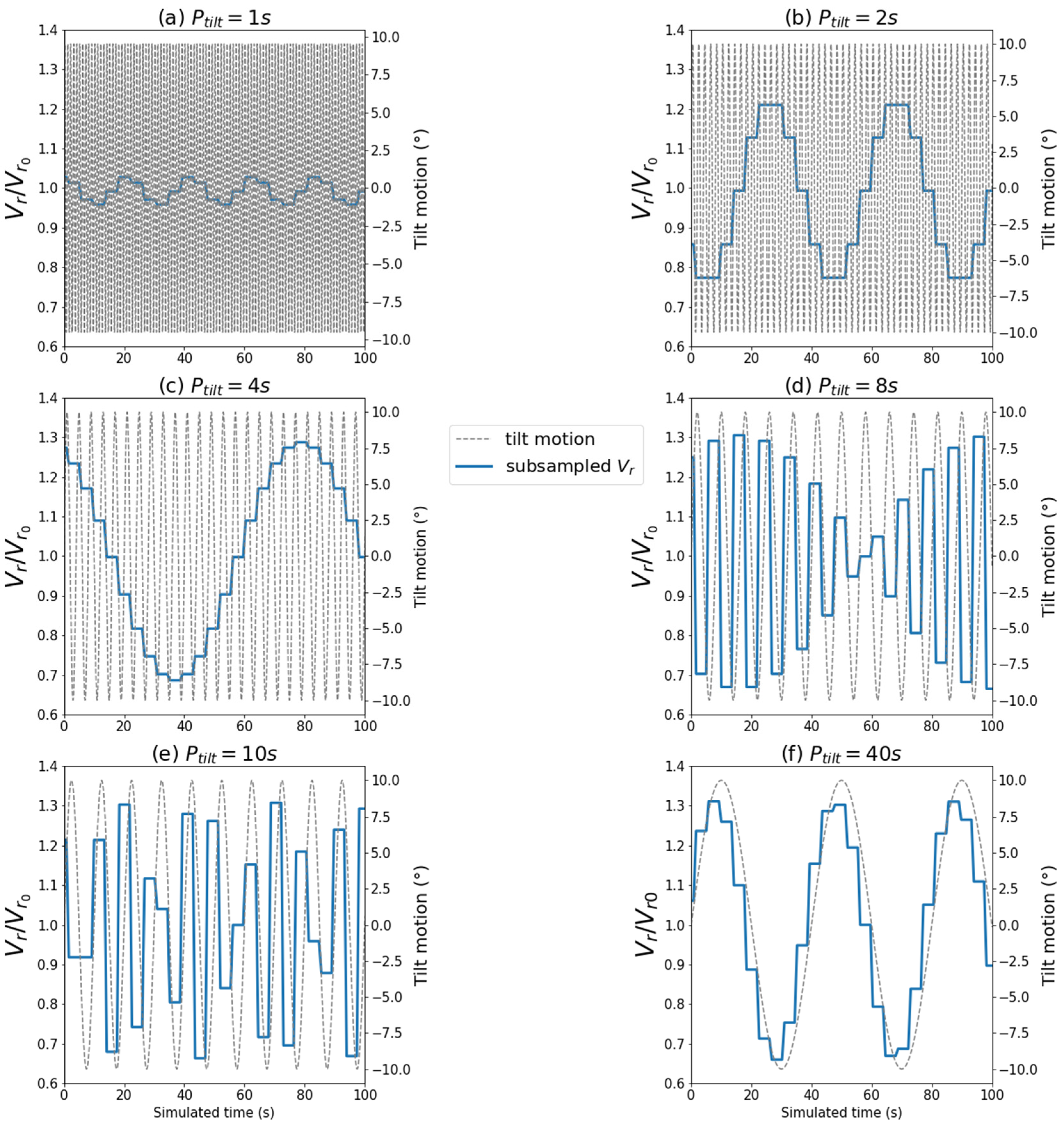
Figure 9 shows an example of subsampling and averaging on the radial wind speed measurement. The radial wind speed is calculated with Equation (24) and is normalized by the value measured in the motionless case
.
For motion periods , we see that the period of the measured radial wind speed signal is larger than the period of the tilt motion. The radial wind speed is affected by a subsample of the motion. For motion periods , harmonics due to the subsampling phenomenon are introduced but the period of the motion is respected by the radial wind speed measurements. These harmonics affect the standard deviation of the measurement and may also change the mean value of the measurement. For the period , the period of the motion is sufficiently greater than the period of one rotation of the LIDAR beam for the two signals to follow the same evolution.
4.2.5. Influence of a 10-min Sinusoidal Motion on the Measurement of the Entire LIDAR
The floating LIDAR measurement of a component of the horizontal wind is calculated from the radial speed measurements of two opposite rays. Thus, the horizontal speed is calculated from the measurement of the four non-vertical rays. As the radial velocities are measured alternately, they do not experience the same motion. At the scale of a 10-min measurement, each ray experiences a different subsampling of the LIDAR motion. In this section, we consider sinusoidal tilt, yaw and heave motions. The heave was chosen to represent the effect of translational velocity as it is the component with the greatest impact on the horizontal velocity measurement [
16]. As in the WindCube v2
® operation, we compute the lidar measurement statistics from the recorded data from each
LOS measurement. We normalize the velocities and standard deviations evaluated throughout this section by the incident horizontal wind speed
. All the simulations in this section are carried out under similar wind conditions (
).
Figure 10 and
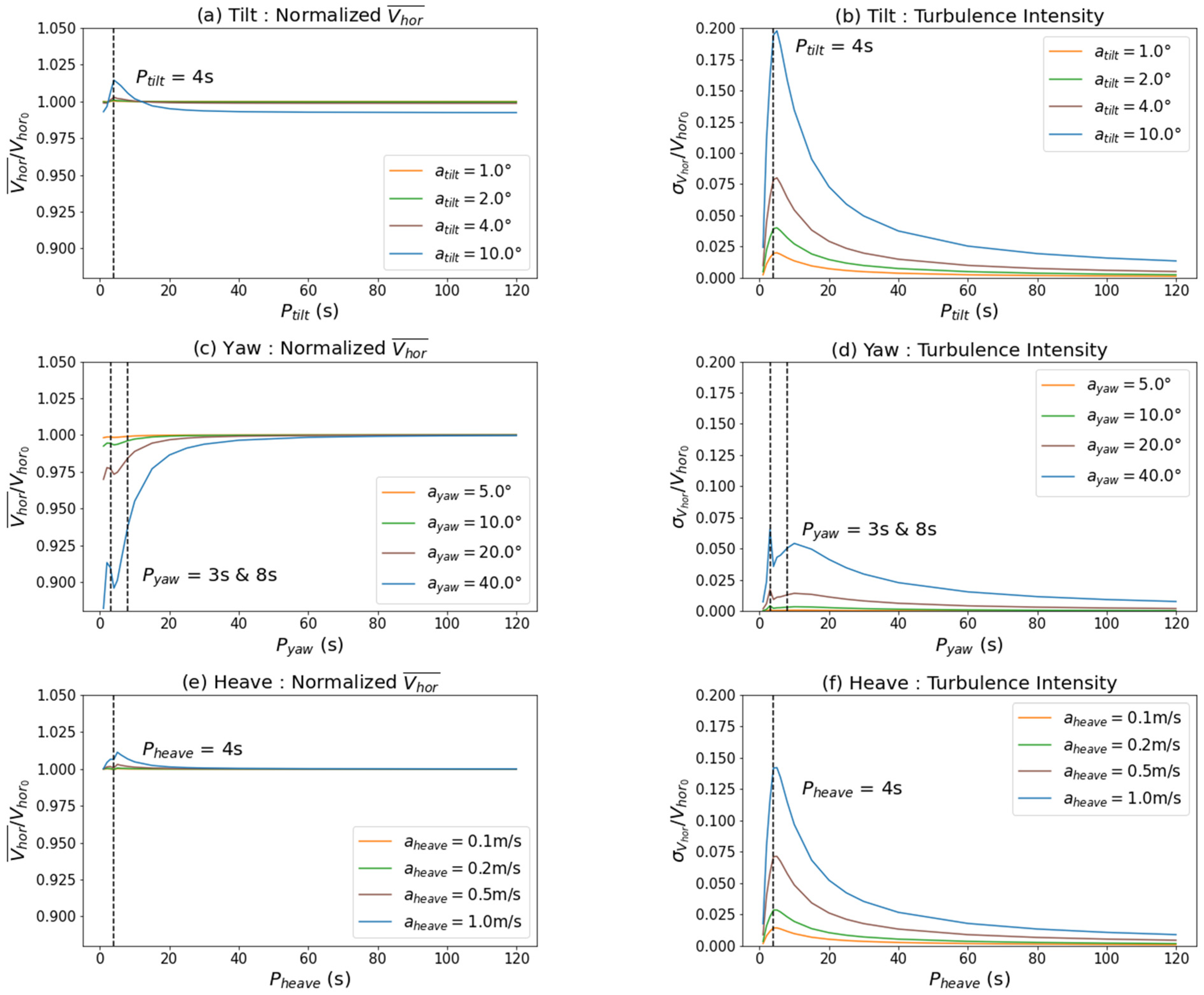
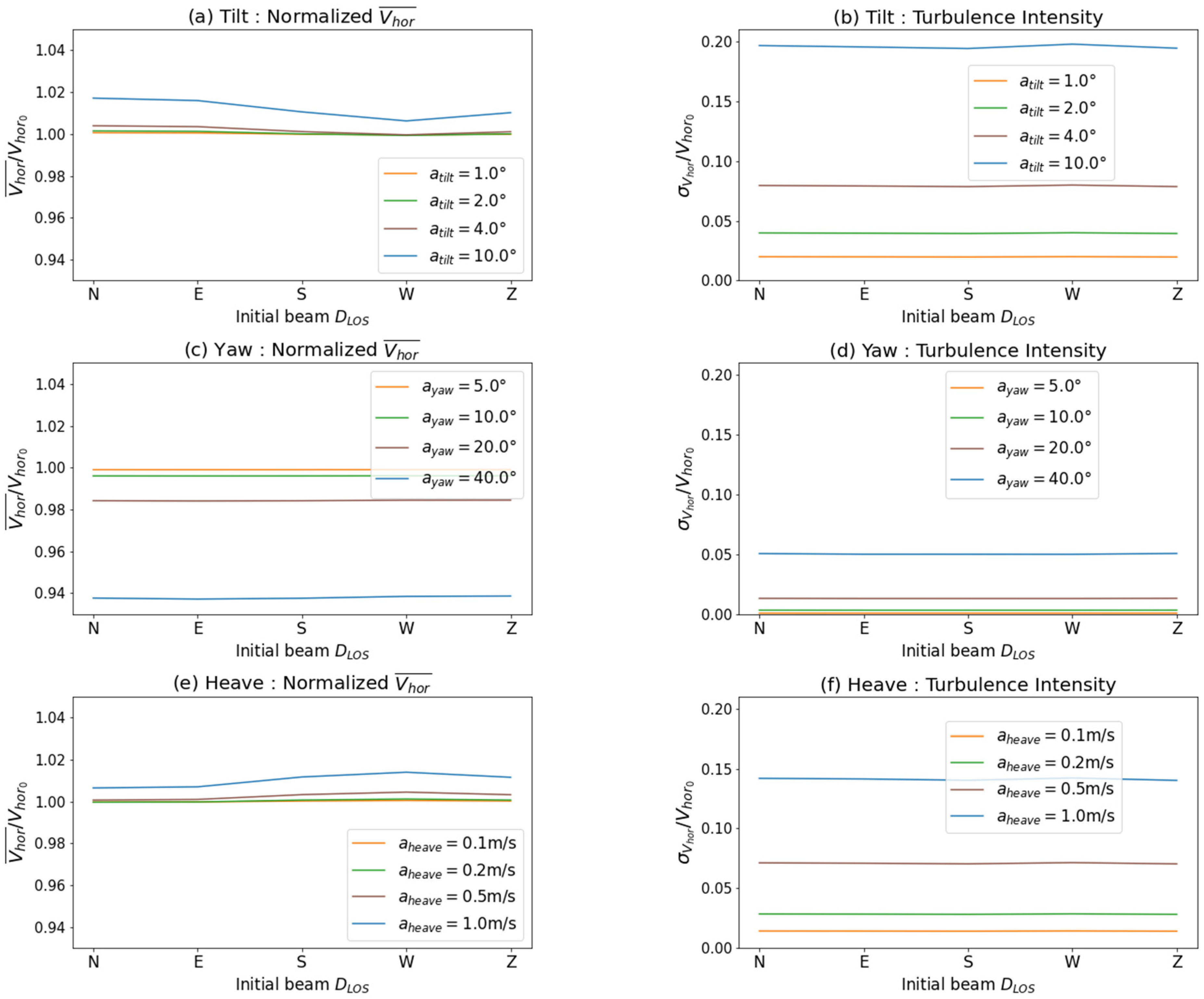
Figure 11 show the influence of the period of the sinusoidal motion, and the direction of the initial beam in the model, respectively. The mean horizontal velocities and standard deviations are compared. Since the incident horizontal velocity is turbulence-free, the calculated standard deviation is entirely induced by the motion. The effect of the initial direction of the laser beam is evaluated at the period having the greatest impact on the LIDAR measurement, called resonance period. We discuss all the figures according to the type of motion: tilt, yaw and heave. Finally, we study the dominant effects on the LIDAR error as a function of sea conditions.
We start with the tilt motion, it is applied in the axis perpendicular to the incident wind direction (i.e., roll for
). The average horizontal velocity measurement (
Figure 10a) evaluated by the model is either smaller or greater than the incident horizontal wind speed
as a function of the tilt period. The error induced by an extreme motion (
) is up to 1 to 2% at the resonance period
, the initial direction of the measurement beam in the model strongly influences the magnitude of this error (
Figure 11a).
The standard deviation of the horizontal velocity (
Figure 11b) fluctuates with the period and amplitude of the motion, reaching its maximum value at the resonance period
. The order of magnitude of the TI induced by an extreme motion is 0.2 at the resonance period. The standard deviation of the horizontal velocity is only slightly influenced by the initial direction of the beam (
Figure 11b).
Now, we study the effect of yaw motion. It has a similar influence on all the 4 non-vertical beams. However, the difference in the timing of evaluations introduces a compositional effect between the subsampling encountered by each ray. The average horizontal velocity measurement evaluated by the model (
Figure 10c) is always lower than the horizontal incident wind speed
. The underestimation for a yaw at resonance periods (
= 3 s & 8 s) and amplitude
= 40° is of the order of 10%.
The standard deviation of the horizontal velocity (
Figure 10d) varies with the period and amplitude of the sinusoidal motion, its maximum value being encountered at the resonance period
= 3 s. The order of magnitude of the motion-induced TI for a tilt amplitude
= 40° is about 0.05 at the resonance periods.
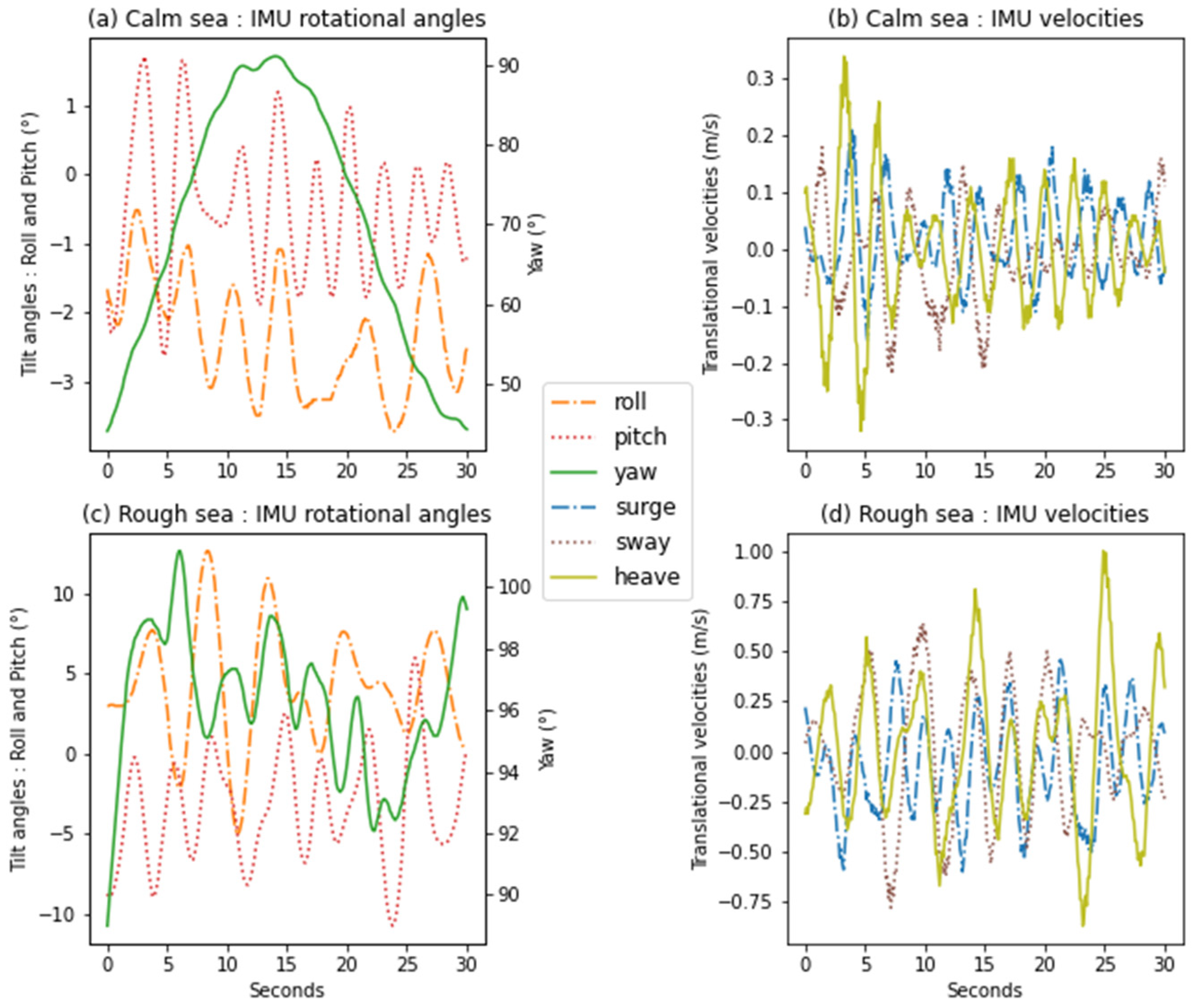
The initial direction of the beam in the model has little influence on the horizontal velocity measurement of the floating LIDAR in the case of yaw motion (
Figure 11c,d). And we specify that the case studied here of a yaw of high amplitude evolving at high frequency was not encountered in our experimental study (
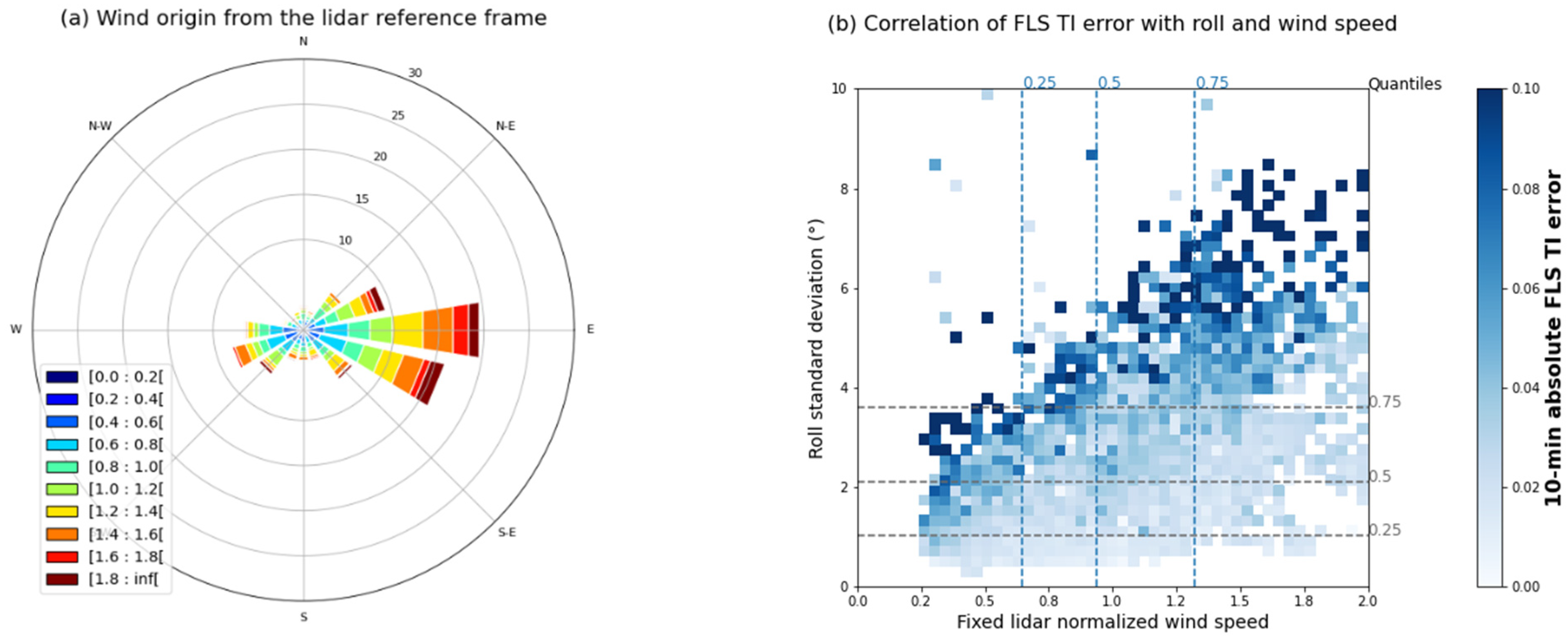
Section 4.1). The measured yaw from the WINDSEA_02 buoy shows a high amplitude/low frequency in calm sea conditions and a low amplitude/high frequency in rough sea conditions.
Now, we focus of the effect of heave. The translational movements of the buoy appear as an added component to the velocity vector measured by the LIDAR. The difference in the temporality of the evaluations introduces a compositional effect between the subsamples encountered by the rays. The average horizontal velocity measurement (
Figure 10e) evaluated by the model is always higher than the horizontal incident wind speed
. The overestimation for a heave at resonance period (
= 4 s) and amplitude
= 1 m/s is of the order of 1%, the initial direction of the ray strongly influences the magnitude of this error (
Figure 11e).
The standard deviation of the horizontal velocity (
Figure 10f) varies with the period and amplitude of the sinusoidal motion, the maximum value is encountered at the resonance period. The order of magnitude of the motion-induced TI for a tilt amplitude
= 1 m/s is 0.15 at the resonance period. The initial direction of the beam has little effect on the standard deviation of the horizontal velocity estimated by the model (
Figure 11f).
Now, we want to assess the motions with the greatest impact on the LIDAR measurement in different sea conditions. The horizontal wind speed measured by a LIDAR subjected to a tilt, yaw or heave motion depends on the period of the motion. Resonance periods are observed for each of these phenomena. Each of the observed resonance period are close to the time required for the LIDAR to perform a
LOS measurement for each of its beams (~4 s). The initial direction of the measuring beam also has an influence on the average value of the horizontal velocity for tilt and heave. In the context of our turbulence intensity measurement correction method presented in
Section 3.1, we note that the default choice of the first measuring ray influences the value of
. The standard deviation of the horizontal velocity is only slightly influenced by the initial direction of the ray. However, this quantity is by definition linked to the average horizontal velocity.
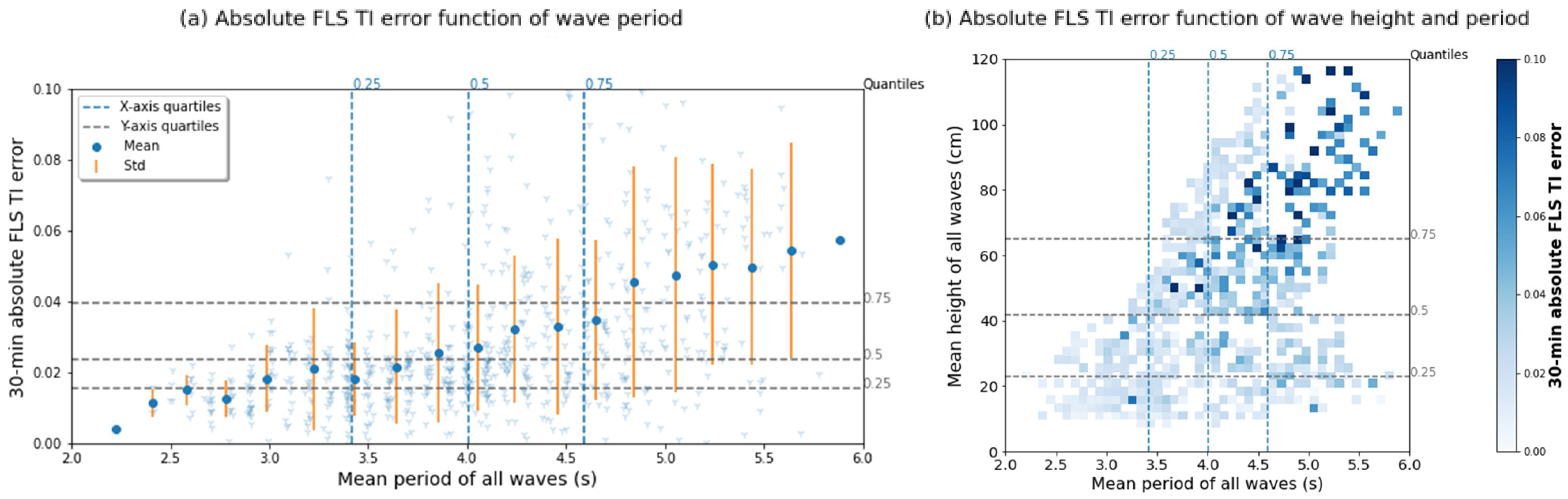
We shall study the order of magnitude of the motion-induced bias on the LIDAR measurement as a function of the sea conditions presented in
Section 4.1. We note that the turbulence intensity value presented here corresponds to the motion-induced TI evaluated in a turbulence-free atmosphere, it should not be added to the atmospheric turbulence as a bias, the relationship is quadratic (Equation (9)).
In calm sea conditions, the three motions lead to motion-induced TI of the same order of magnitude (0.01 to 0.04) and the horizontal speed is mainly impacted by the yaw (relative underestimation of about 1%). The initial direction of the beam has little influence on the average horizontal wind value.
In rough sea conditions, yaw has very little influence on the horizontal wind measurement. The tilt and heave motions cause a huge motion-induced TI of the same order of magnitude (0.1 to 0.2). As a comparison, atmospheric turbulence intensities exceeding 0.1 are very rare in an open sea area [
23,
24]. The mean horizontal velocity is also impacted by tilt and heave motions with a relative overestimation of the order of 1 to 2%, corroborating the order of magnitude of error reported by Gottschall et al. [
15].