Measurement of Solar Absolute Brightness Temperature Using a Ground-Based Multichannel Microwave Radiometer
Abstract
1. Introduction
2. Materials and Methods
2.1. Principle of the Solar TB Measurement Using a GMR
2.2. Atmospheric Mean Radiating Temperature
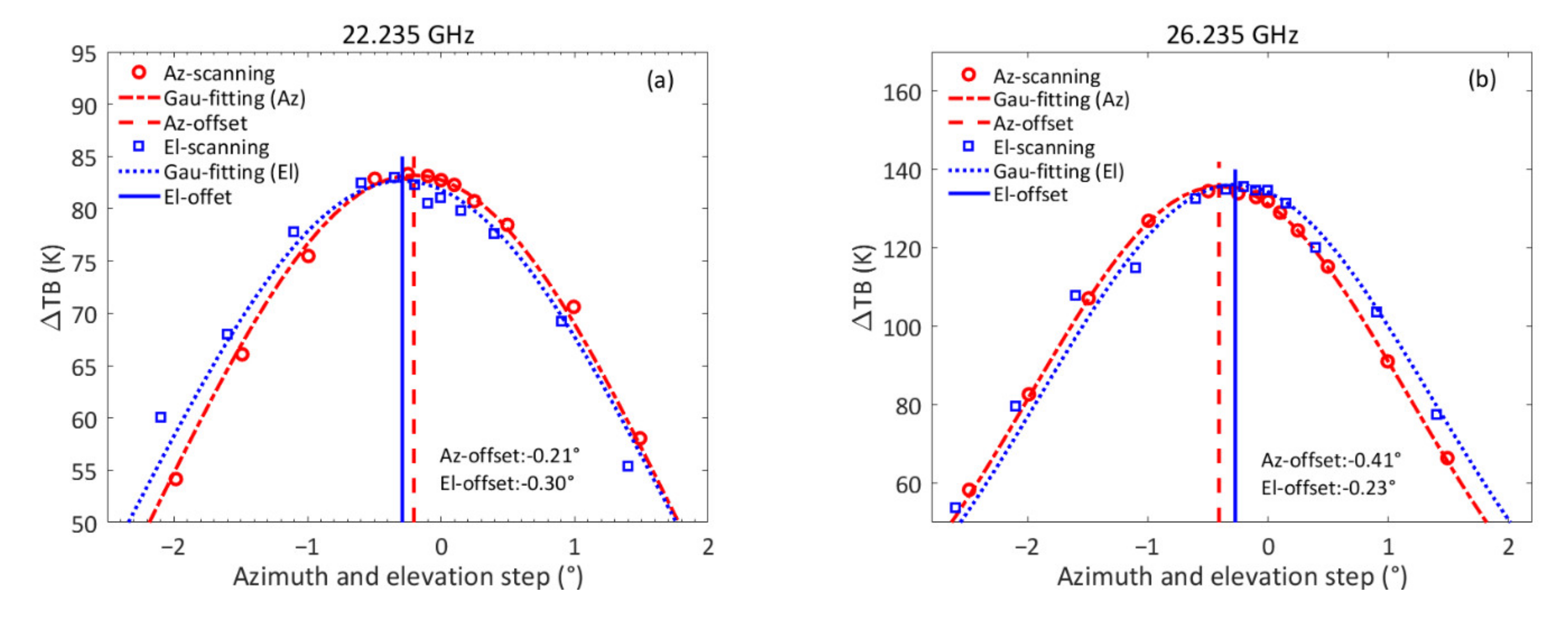
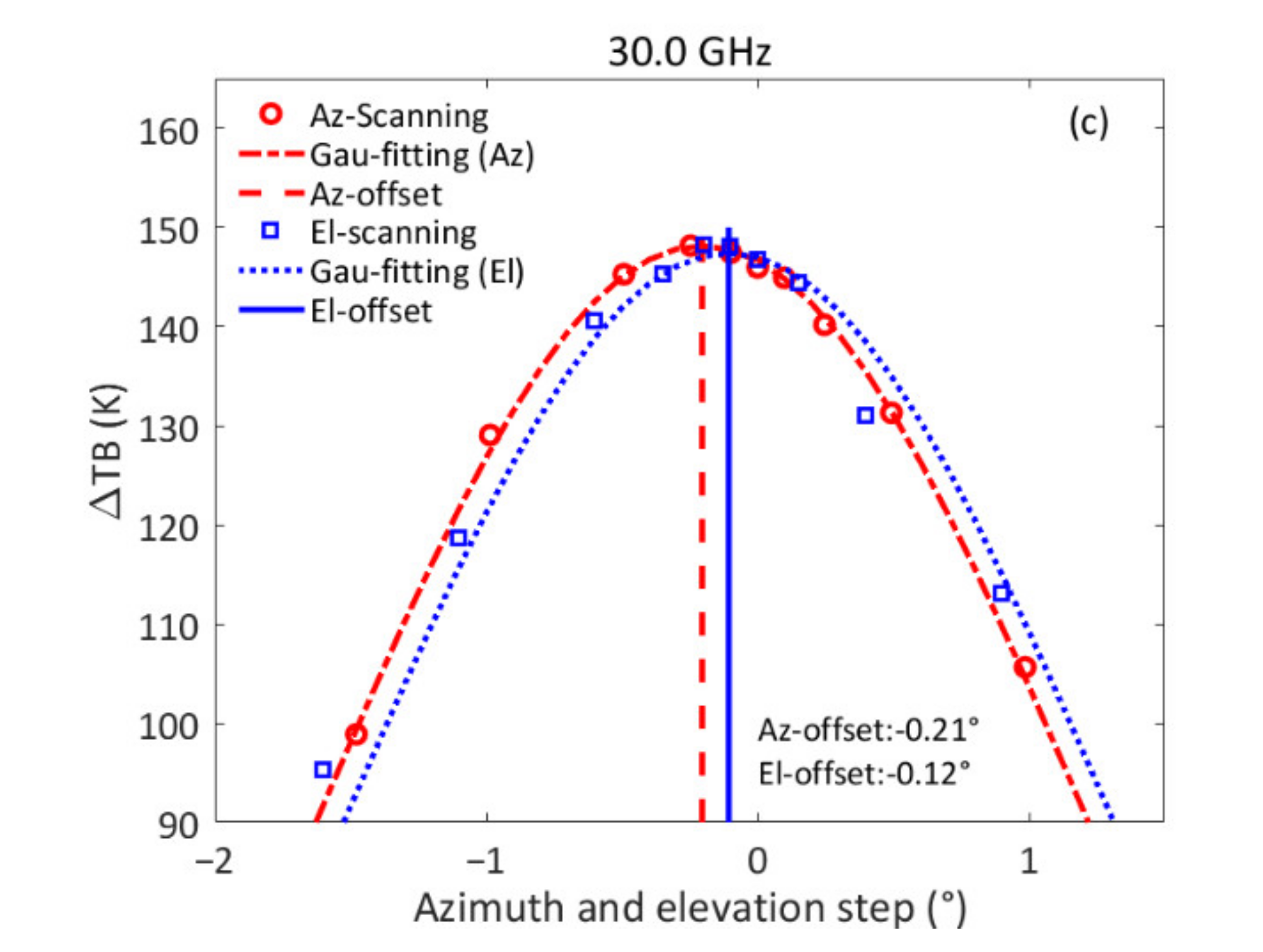
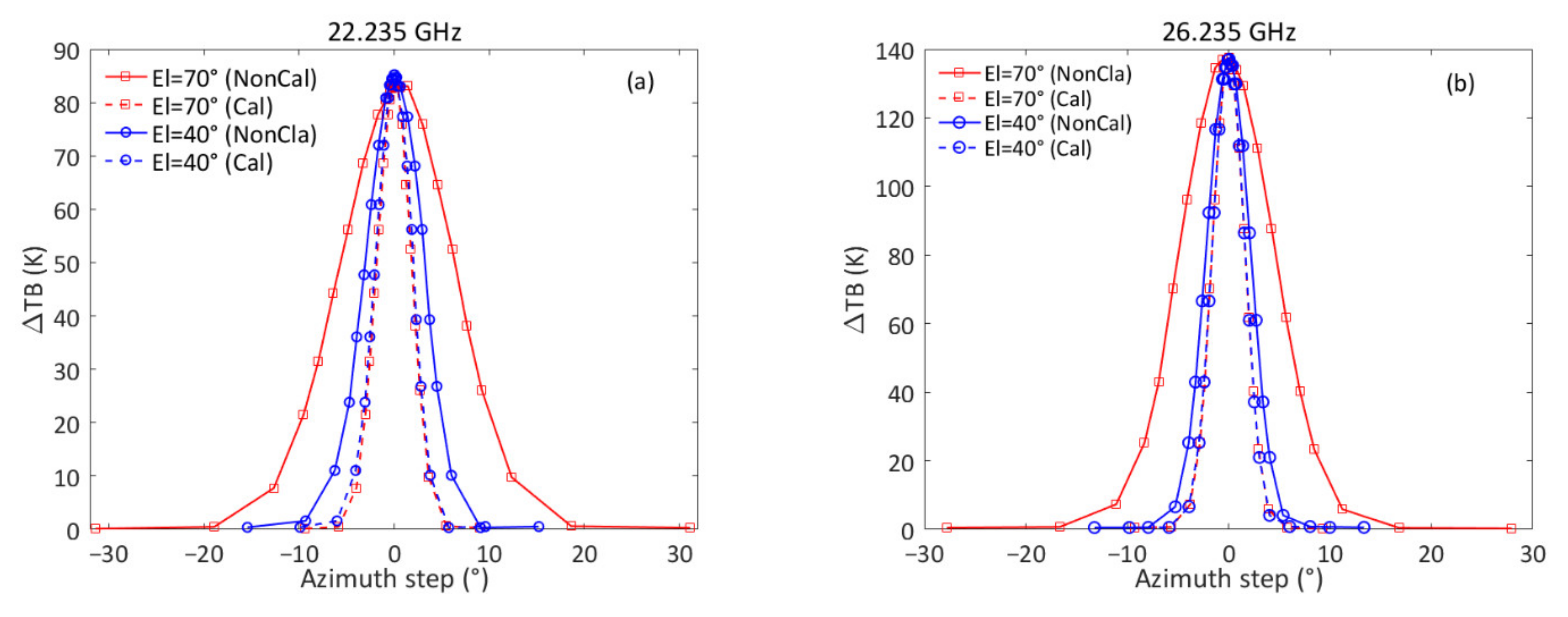
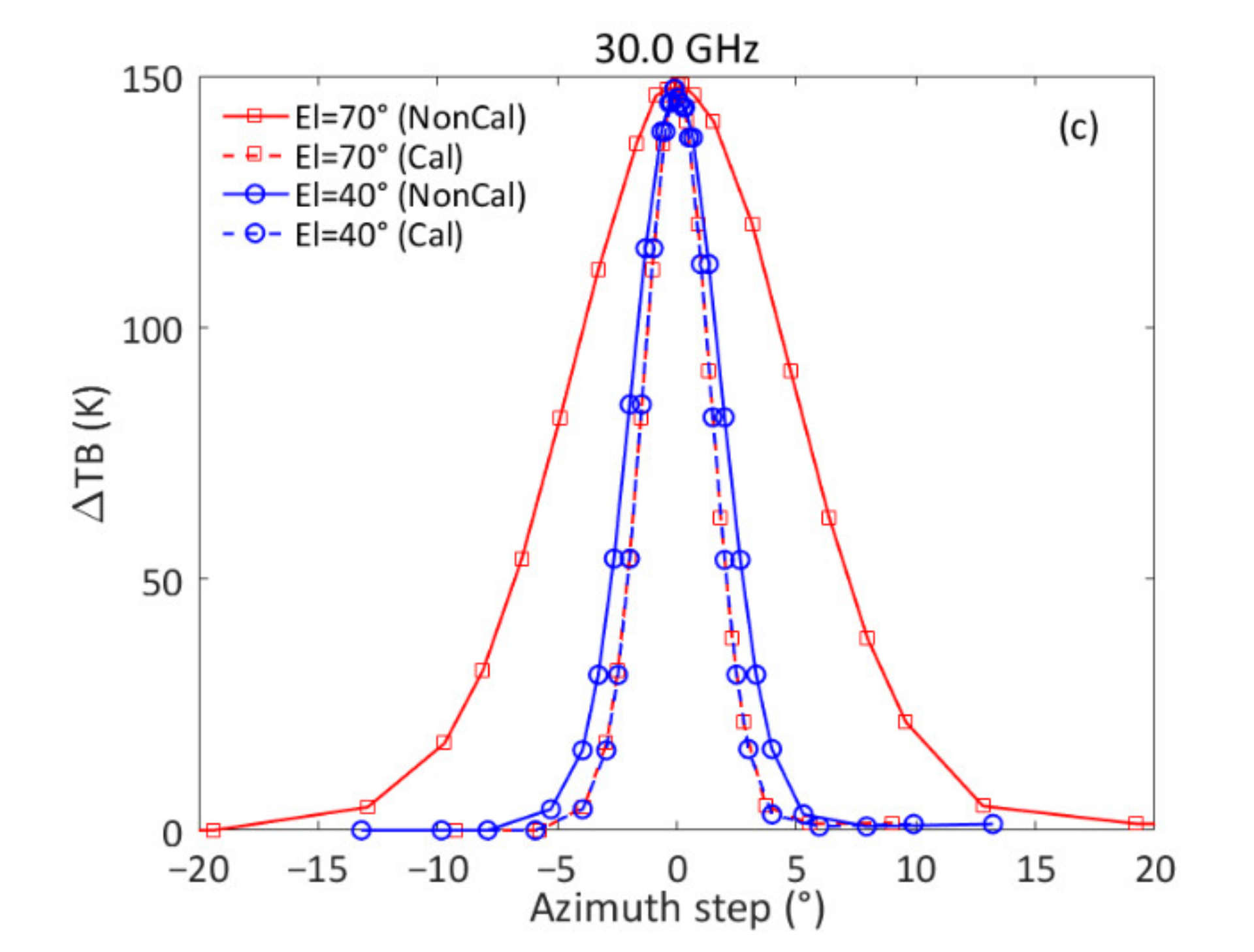
2.3. Measurement of the Antenna Pattern
2.4. Calibration of the Earth-Sun Distance
2.5. Data and Instrument for Observations
3. Results
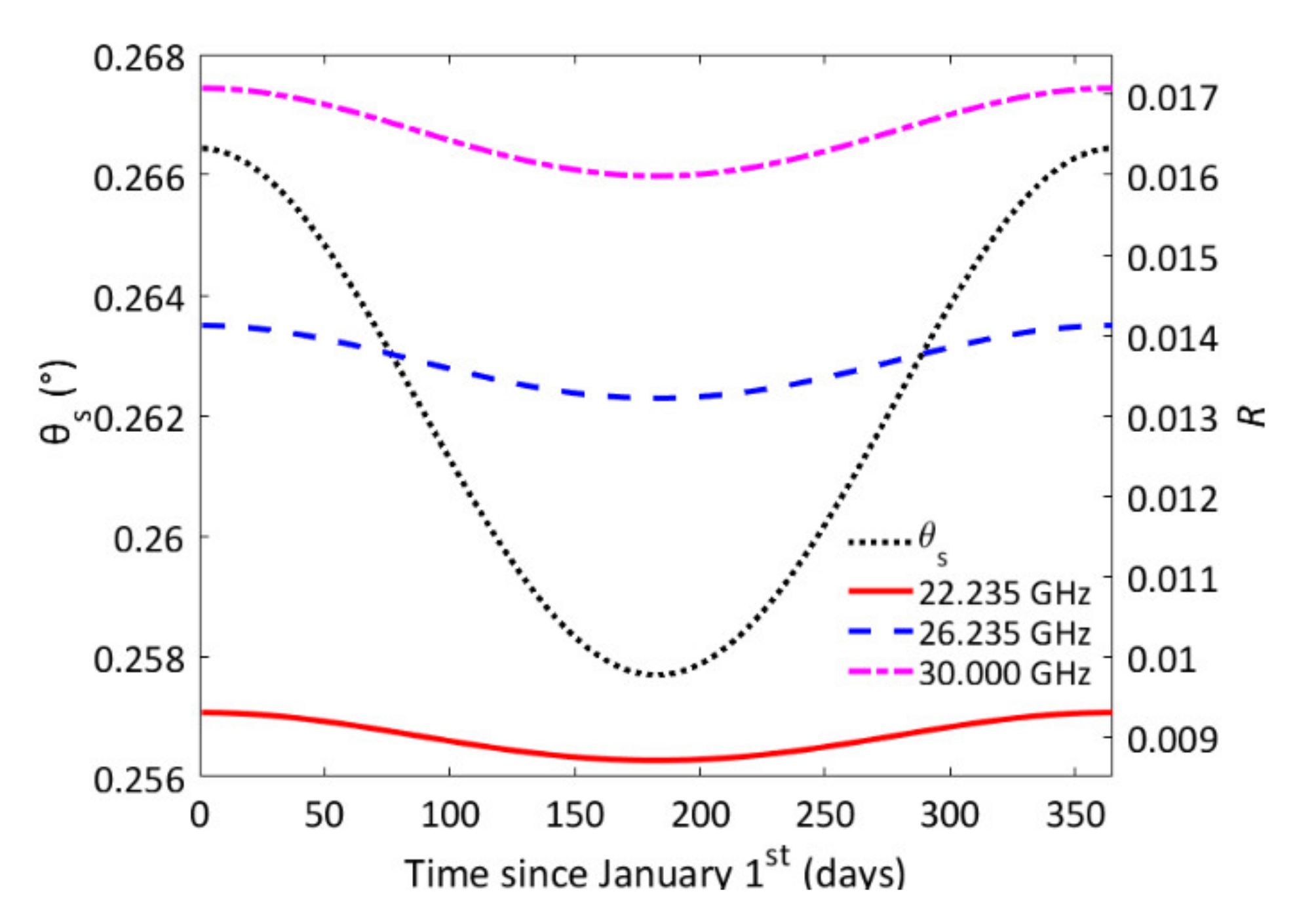
3.1. Mean Radiative Temperature
3.2. Observation of the Solar TB Increment
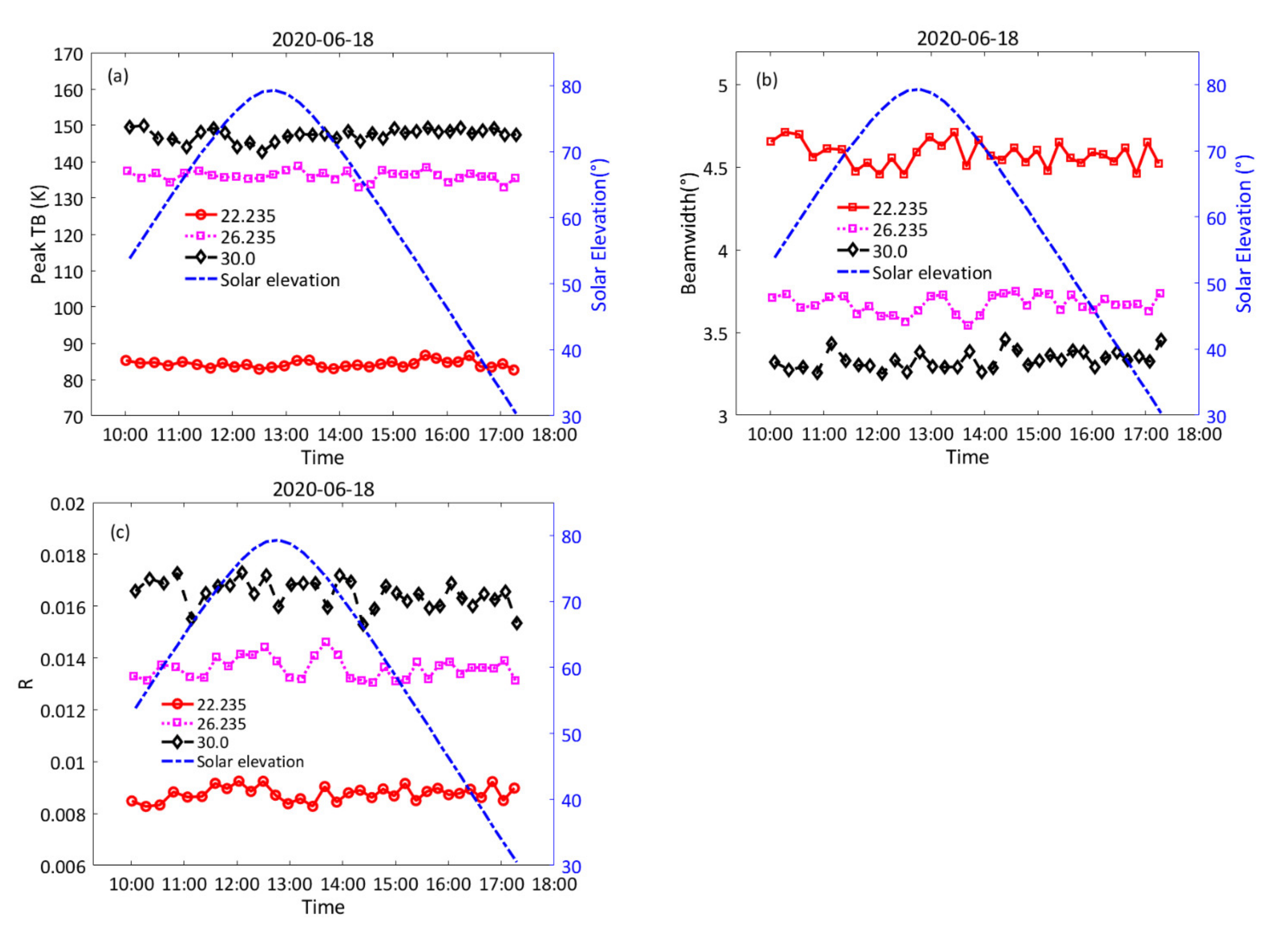
3.3. Measurement of the Antenna Pattern
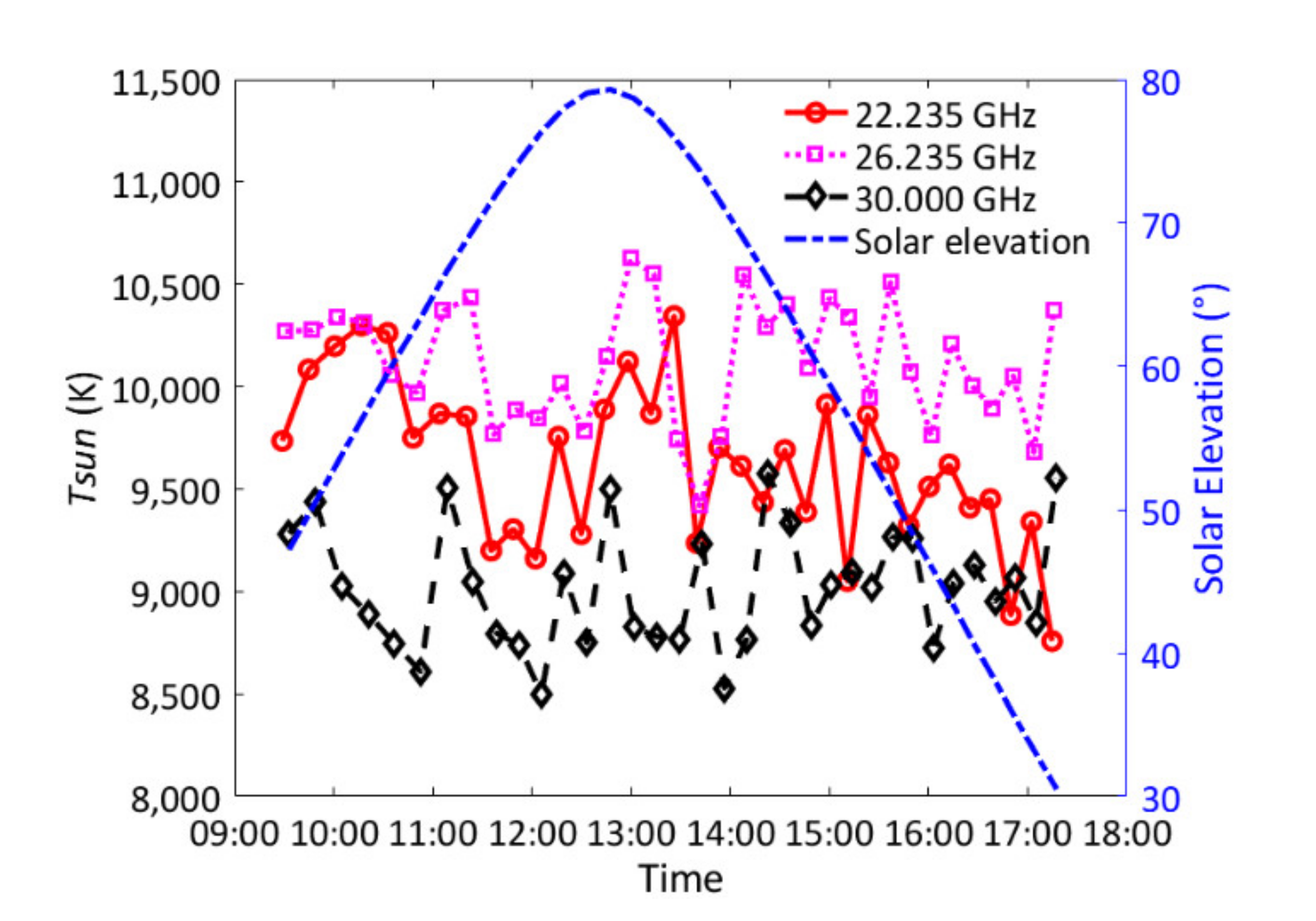
3.4. TB of the Sun
4. Discussion
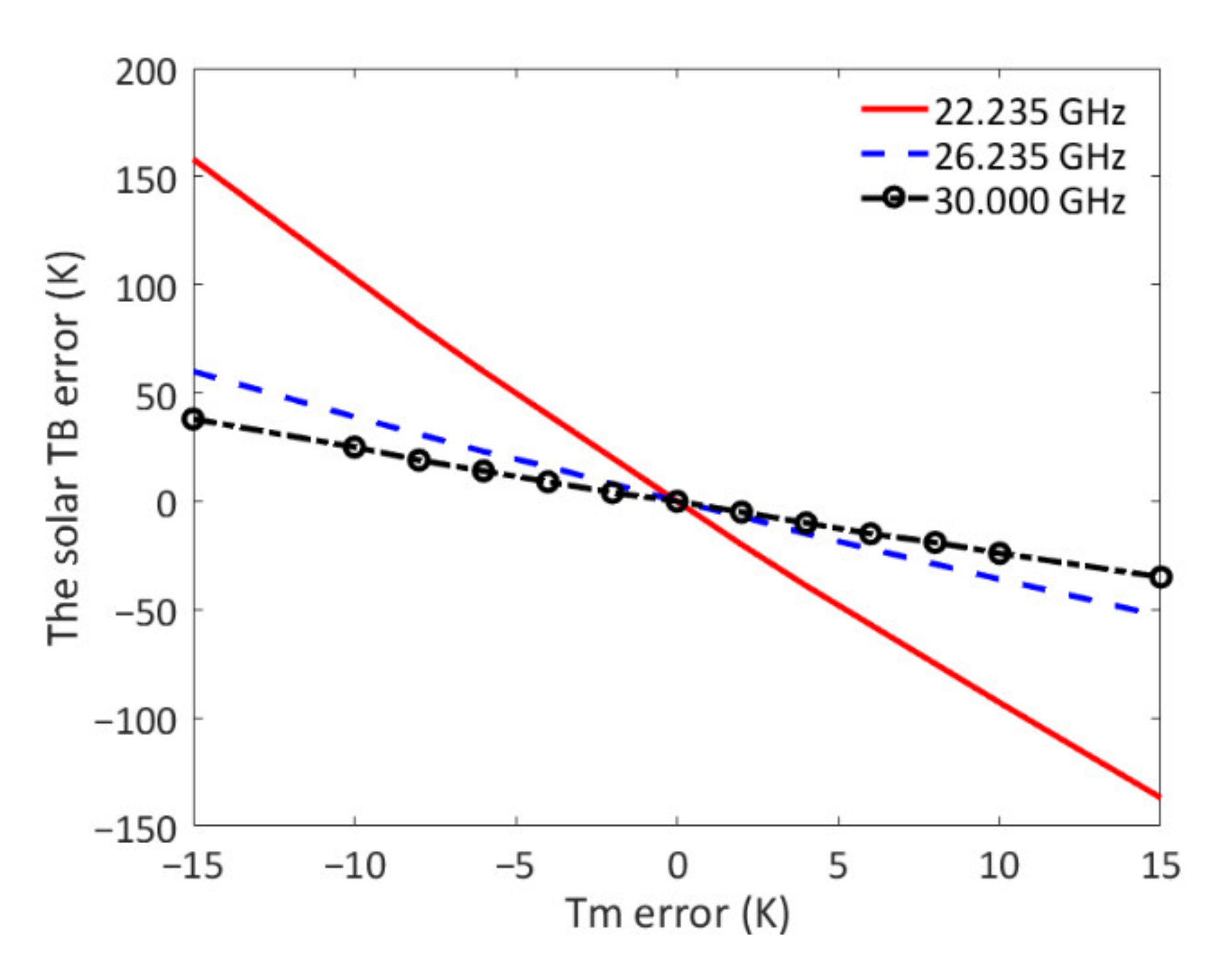
4.1. Effect of the Mean Radiative Temperature
4.2. Effect of the Earth-Sun Distance
4.3. Effect of the Antenna Alignment
4.4. Calibration of the Angle Distortion in the Azimuth
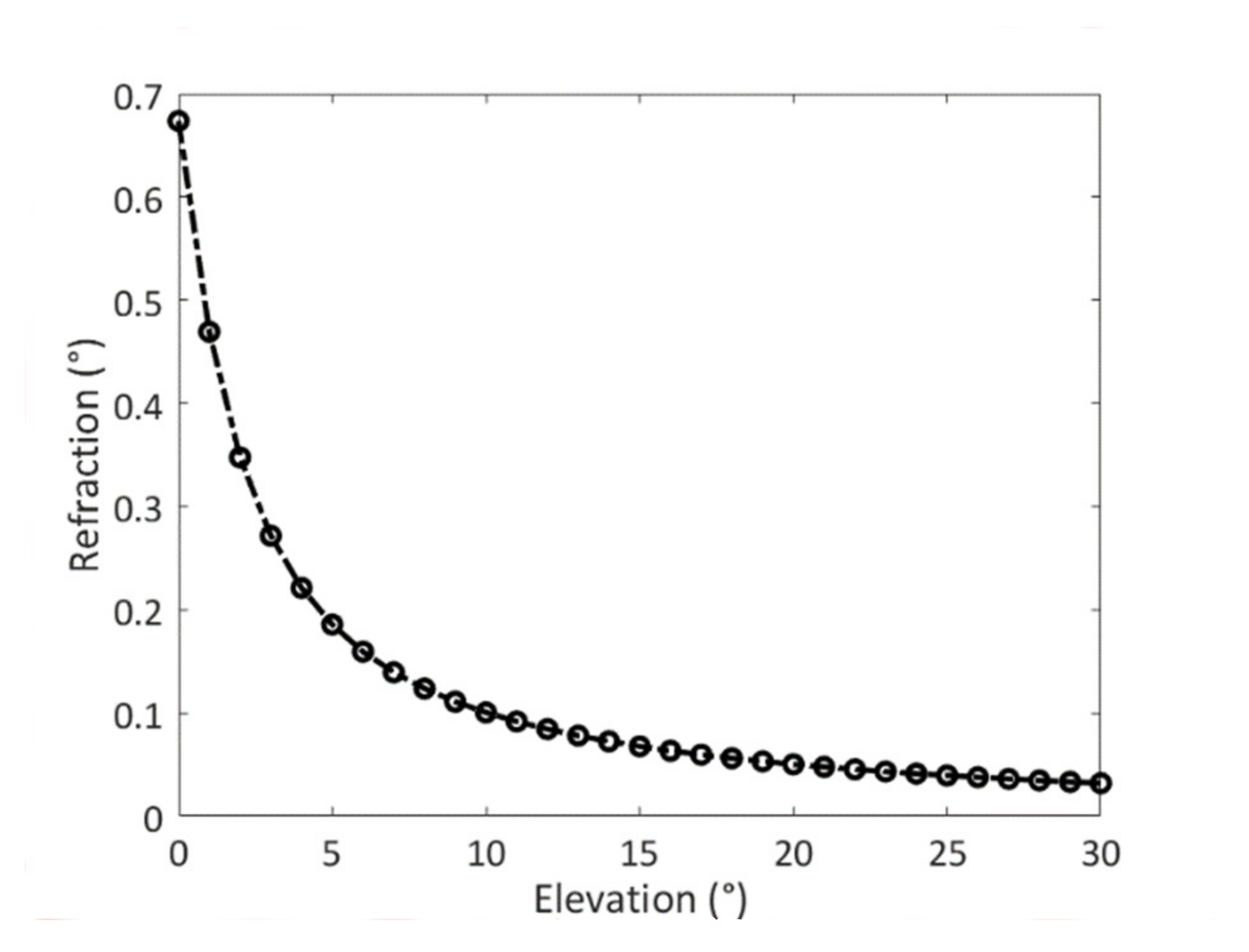
4.5. Atmospheric Refraction and the Non-Stratified Atmospheric Condition
4.6. Long-Term Observation
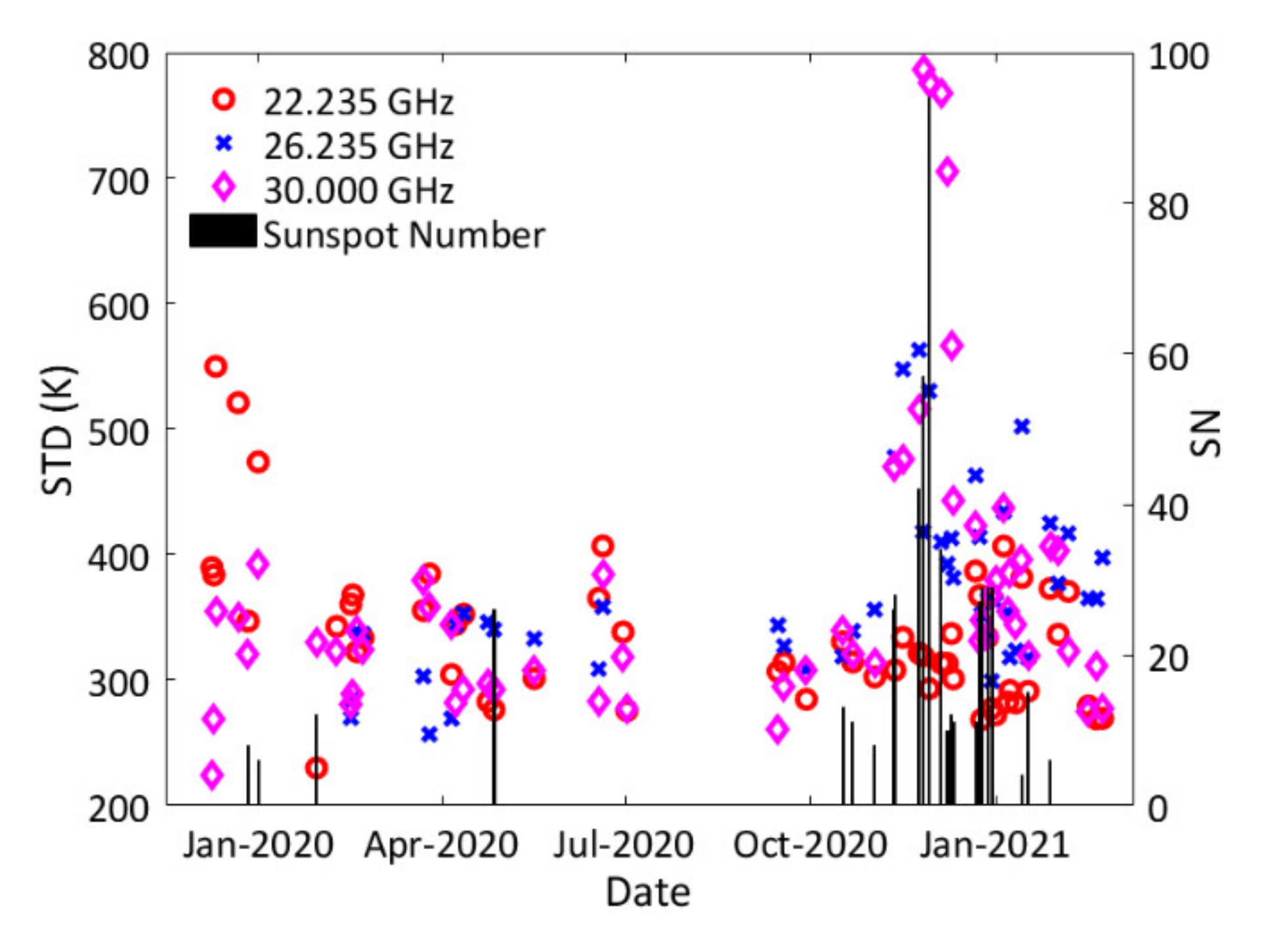
4.7. Effect of the Solar Activity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mattioli, V.; Milani, L.; Magde, K.M.; Brost, G.A.; Marzano, F.S. Retrieval of Sun Brightness Temperature and Precipitating Cloud Extinction Using Ground-Based Sun-Tracking Microwave Radiometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 10, 3134–3147. [Google Scholar] [CrossRef]
- Ulich, B.L. Absolute brightness temperature measurements at 2.1-mm wavelength. Icarus 1974, 21, 254–261. [Google Scholar] [CrossRef]
- Gabella, M.; Huuskonen, A.; Sartori, M.; Holleman, I.; Boscacci, M.; Germann, U. Evaluating the Solar Slowly Varying Component at C-Band Using Dual- and Single-Polarization Weather Radars in Europe. Adv. Meteorol. 2017, 2017, 4971765. [Google Scholar] [CrossRef]
- Iwai, K.; Shimojo, M.; Asayama, S.; Minamidani, T.; White, S.; Bastian, T.; Saito, M. The Brightness Temperature of the Quiet Solar Chromosphere at 2.6 mm. Sol. Phys. 2017, 292, 22. [Google Scholar] [CrossRef]
- Ulich, B.; Haast, R. Absolute calibration of millimeter-wavelength spectral line. Astrophys. J. Suppl. Ser. 1976, 30, 247–258. [Google Scholar] [CrossRef]
- Ulich, B.; Davis, J.; Rhodes, P.; Hollis, J. Absolute brightness temperature measurements at 3.5-mm wavelength. IEEE Trans. Antennas Propag. 1980, 28, 367–377. [Google Scholar] [CrossRef]
- Kosugi, T.; Ishiguro, M.; Shibasaki, K. Polar-cap and coronal-hole-associated brightenings of the sun at millimeter wavelengths. Publ. Astron. Soc. Jpn. 1986, 38, 1–11. [Google Scholar]
- White, S.M.; Loukitcheva, M.; Solanki, S.K. High-resolution millimeter-interferometer observations of the solar chromosphere. Astron. Astrophys. 2006, 456, 697–711. [Google Scholar] [CrossRef]
- Ahn, M.-H.; Won, H.Y.; Han, D.; Kim, Y.-H.; Ha, J.-C. Characterization of downwelling radiance measured from a ground-based microwave radiometer using numerical weather prediction model data. Atmos. Meas. Tech. 2016, 9, 281–293. [Google Scholar] [CrossRef]
- Bianco, L.; Friedrich, K.; Wilczak, J.M.; Hazen, D.; Wolfe, D.; Delgado, R.; Oncley, S.P.; Lundquist, J.K. Assessing the accuracy of microwave radiometers and radio acoustic sounding systems for wind energy applications. Atmos. Meas. Tech. 2017, 10, 1707–1721. [Google Scholar] [CrossRef]
- Cadeddu, M.P.; Liljegren, J.C.; Turner, D.D. The atmospheric radiation measurement (ARM) program network of microwave radiometers: Instrumentation, data, and retrievals. Atmos. Meas. Tech. 2013, 6, 2359–2372. [Google Scholar] [CrossRef]
- Xu, G.; Xi, B.; Zhang, W.; Cui, C.; Dong, X.; Liu, Y.; Yan, G. Comparison of atmospheric profiles between microwave radiometer retrievals and radiosonde soundings. J. Geophys. Res. Atmos. 2015, 120, 10313–10323. [Google Scholar] [CrossRef]
- Yang, J.; Min, Q. Retrieval of atmospheric profiles in the New York State Mesonet using one-dimensional variational algorithm. J. Geophys. Res. Atmos. 2018, 123, 7563–7575. [Google Scholar] [CrossRef]
- Cimini, D.; Rosenkranz, P.W.; Tretyakov, M.Y.; Koshelev, M.; Romano, F. Uncertainty of atmospheric microwave absorption model: Impact on ground-based radiometer simulations and retrievals. Atmos. Chem. Phys. Discuss. 2018, 18, 15231–15259. [Google Scholar] [CrossRef]
- Caumont, O.; Cimini, D.; Löhnert, U.; Alados-Arboledas, L.; Bleisch, R.; Buffa, F.; Ferrario, M.E.; Haefele, A.; Huet, T.; Madonna, F.; et al. Assimilation of humidity and temperature observations retrieved from ground-based microwave radiometers into a convective-scale NWP model. Q. J. R. Meteorol. Soc. 2016, 142, 2692–2704. [Google Scholar] [CrossRef]
- Che, Y.; Ma, S.; Xing, F.; Li, S.; Dai, Y. An improvement of the retrieval of temperature and relative humidity profiles from a combination of active and passive remote sensing. Meteorol. Atmos. Phys. 2018, 131, 681–695. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Hu, F.; Cao, X.; Chu, Y. Remote sensing of lightning by a ground-based microwave radiometer. Atmos. Res. 2014, 150, 143–150. [Google Scholar] [CrossRef]
- Jiang, S.; Pan, Y.; Lei, L.; Ma, L.; Li, Q.; Wang, Z. Remote sensing of the lightning heating effect duration with ground-based microwave radiometer. Atmos. Res. 2018, 205, 26–32. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, Z.; Lei, L.; Pan, Y.; Lyu, W.; Zhang, Y. Preliminary study on the relationship between the brightness temperature pulses observed with a ground-based microwave radiometer and the lightning current integral values. Atmos. Res. 2020, 245, 105072. [Google Scholar] [CrossRef]
- Marzano, F.S.; Mattioli, V.; Milani, L.; Magde, K.M.; Brost, G.A. Sun-Tracking Microwave Radiometry: All-Weather Estimation of Atmospheric Path Attenuation at Ka-, V-, and W-Band. IEEE Trans. Antennas Propag. 2016, 64, 4815–4827. [Google Scholar] [CrossRef]
- Lei, L.; Wang, Z.; Qin, J.; Zhu, L.; Chen, R.; Lu, J.; Ma, Y. Feasibility for Operationally Monitoring Ground-Based Multichannel Microwave Radiometer by Using Solar Observations. Atmosphere 2021, 12, 447. [Google Scholar] [CrossRef]
- D’Orazio, A.; de Sario, M.; Gramegna, T.; Petruzzelli, V.; Prudenzano, F. Optimisation of tipping curve calibration of microwave radiometer. Electron. Lett. 2003, 39, 905. [Google Scholar] [CrossRef]
- Han, Y.; Westwater, E. Analysis and improvement of tipping calibration for ground-based microwave radiometers. IEEE Trans. Geosci. Remote. Sens. 2000, 38, 1260–1276. [Google Scholar] [CrossRef]
- Zhang, M.; Gong, W.; Ma, Y.; Wang, L.; Chen, Z. Transmission and division of total optical depth method: A universal calibration method for Sun photometric measurements. Geophys. Res. Lett. 2016, 43, 2974–2980. [Google Scholar] [CrossRef]
- Schneebeli, M.; Mätzler, C. A calibration scheme for microwave radiometers using tipping curves and Kalman filtering. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4201–4209. [Google Scholar] [CrossRef]
- Coates, R. Measurements of Solar Radiation and Atmospheric Attenuation at 4.3-Millimeters Wavelength. Proc. IRE 1958, 46, 122–126. [Google Scholar] [CrossRef]
- Ulich, B. A radiometric antenna gain calibration method. IEEE Trans. Antennas Propag. 1977, 25, 218–223. [Google Scholar] [CrossRef]
- Holleman, I.; Huuskonen, A.; Kurri, M.; Beekhuis, H. Operational Monitoring of Weather Radar Receiving Chain Using the Sun. J. Atmos. Ocean. Technol. 2010, 27, 159–166. [Google Scholar] [CrossRef]
- Altube, P.; Bech, J.; Argemí, O.; Rigo, T.; Pineda, N. Intercomparison and Potential Synergies of Three Methods for Weather Radar Antenna Pointing Assessment. J. Atmos. Ocean. Technol. 2016, 33, 331–343. [Google Scholar] [CrossRef]
- Reimann, J.; Hagen, M. Antenna Pattern Measurements of Weather Radars Using the Sun and a Point Source. J. Atmos. Ocean. Technol. 2016, 33, 891–898. [Google Scholar] [CrossRef]
- Tapping, K.F. The 10.7cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Lahaye, T. Measuring the eccentricity of the Earth’s orbit with a nail and a piece of plywood. Eur. J. Phys. 2012, 33, 1167–1178. [Google Scholar] [CrossRef][Green Version]
- Yu, F.J. Calculating the eccentricity of the Earth’s orbit by approximate orbital equation. Coll. Phys. 2017, 36, 23–24. (In Chinese) [Google Scholar]
- Renju, R.; Raju, C.S.; Mathew, N.; Antony, T.; Moorthy, K.K. Microwave radiometer observations of interannual water vapor variability and vertical structure over a tropical station. J. Geophys. Res. Atmos. 2015, 120, 4585–4599. [Google Scholar] [CrossRef]
- Qi, X.; Wang, J.; Zhao, L.; Ji, J. Antenna beam angle calibration method via solar electromagnetic radiation scan. J. Eng. 2019, 2019, 7890–7893. [Google Scholar] [CrossRef]
- Huuskonen, A.; Holleman, I. Determining Weather Radar Antenna Pointing Using Signals Detected from the Sun at Low Antenna Elevations. J. Atmos. Ocean. Technol. 2007, 24, 476–483. [Google Scholar] [CrossRef]
- Darlington, T.; Kitchen, M.; Sugier, J.; de Rohan-Truba, J. Automated real-time monitoring of radar sensitivity and antenna pointing accuracy. In Proceedings of the 31st Conference on Radar Meteorology, Seattle, WA, USA, 6–12 August 2003; pp. 538–541. [Google Scholar]
- Gabella, M.; Leuenberger, A. Dual-Polarization Observations of Slowly Varying Solar Emissions from a Mobile X-Band Radar. Sensors 2017, 17, 1185. [Google Scholar] [CrossRef] [PubMed]
- Shimabukuro, F.I.; Stacey, J.M. Brightness temperature of the quiet Sun at centimeter and millimeter wavelengths. Astrophys. J. 1968, 152, 777–782. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, S.; Zhang, Z.; Xu, J. Analysis of Sunspot Time Series (1749–2014) by Means of 0–1 Test for Chaos Detection. In Proceedings of the 2015 11th International Conference on Computational Intelligence and Security (CIS), Shenzhen, China, 19–20 December 2015; pp. 215–218. [Google Scholar] [CrossRef]
- Covington, A.E. Micro-Wave Solar Noise Observations During the Partial Eclipse of November 23, 1946. Nature 1947, 159, 405–406. [Google Scholar] [CrossRef]
- Kaufmann, P.; Scalise, E.; Dos Santos, P.M.; Schaal, R.E.; Fortunato, R.A.A. Microwave observations of the 4 January, 1973 solar eclipse. Sol. Phys. 1973, 33, 69–73. [Google Scholar] [CrossRef]
- Chatterjee, T.N.; Datta, S.K.; Datta, A.K.; Chatterjee, S.; Tarafdar, G.; Bera, J.; Rahman, M.; Bera, R.; Mitra, A.; Karmakar, P.K.; et al. Observation of microwave radio Sun during total solar eclipse on October 24, 1995 by Eastern Centre for Research in Astrophysics (ECRA). Indian J. Phys. Sect. B 1996, 70, 169–173. [Google Scholar]
- Sawant, H.S.; Srivastava, N.; Trigoso, H.E.; Sobral, J.H.A.; Fernandes, F.C.R.; Cecatto, J.R.; Subramanian, K.R. Radio Observation of Total Solar Eclipse of November 3, 1994 at Chapecoó (BRZIL). Adv. Space Res. 1997, 20, 2359–2363. [Google Scholar] [CrossRef]

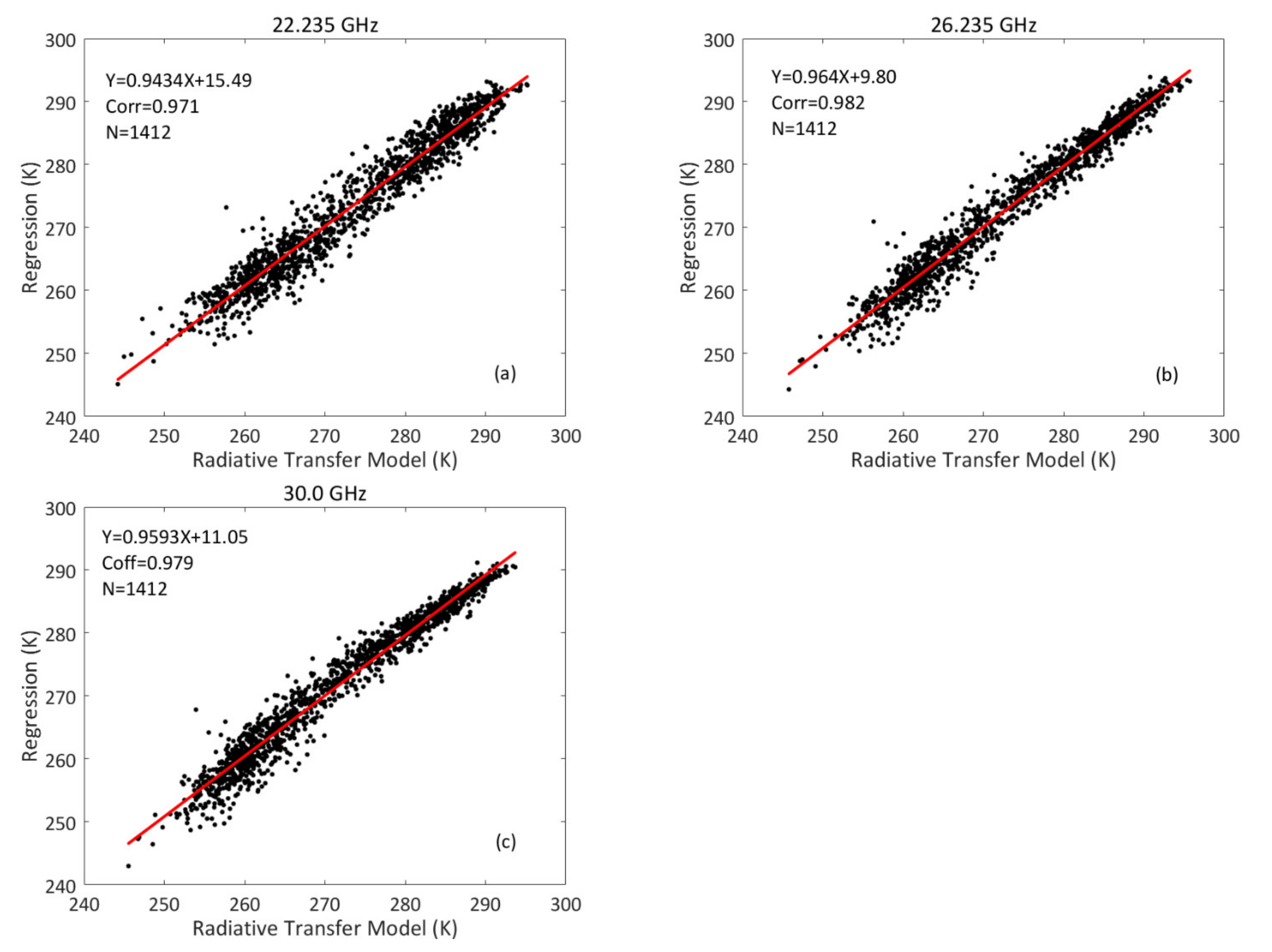
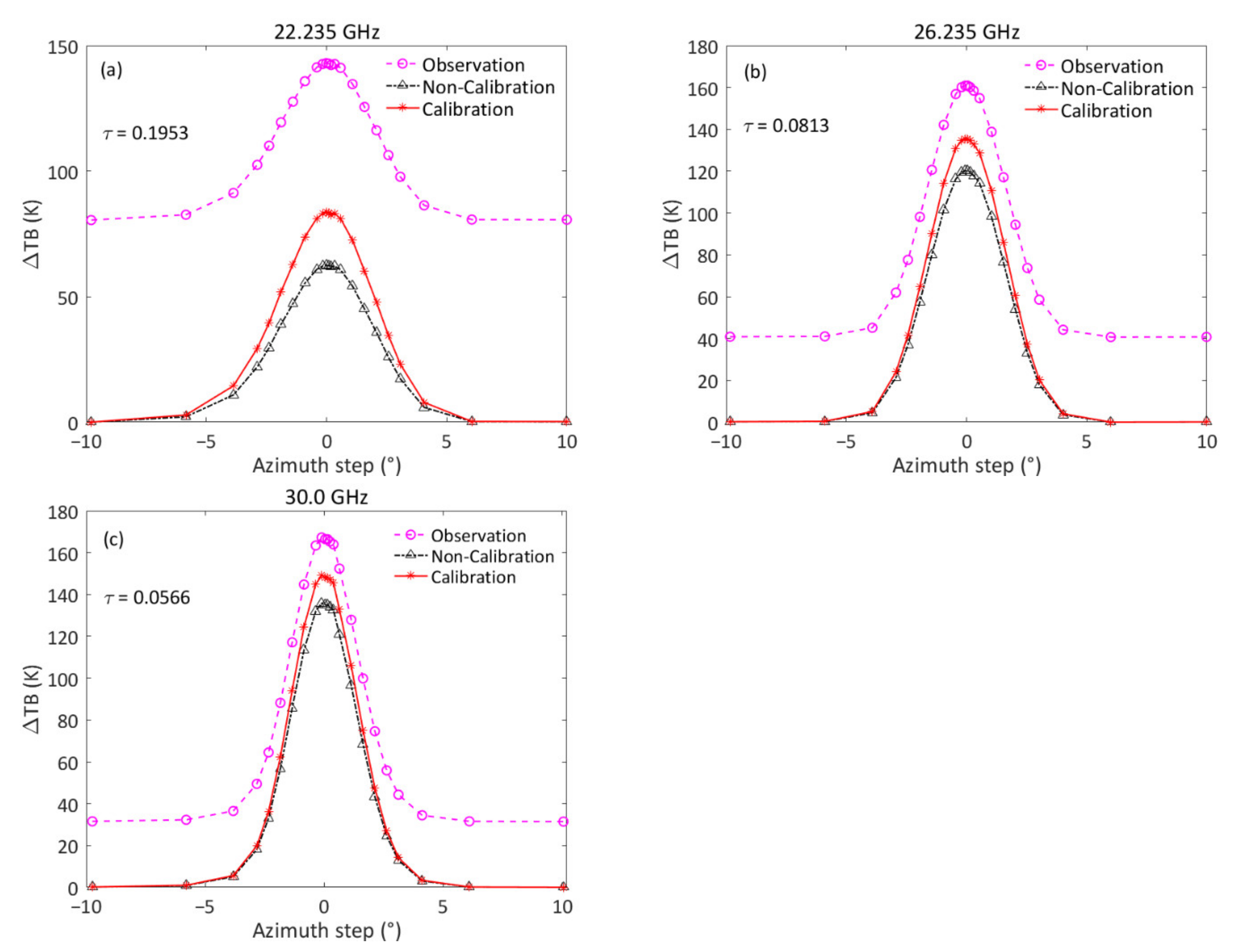

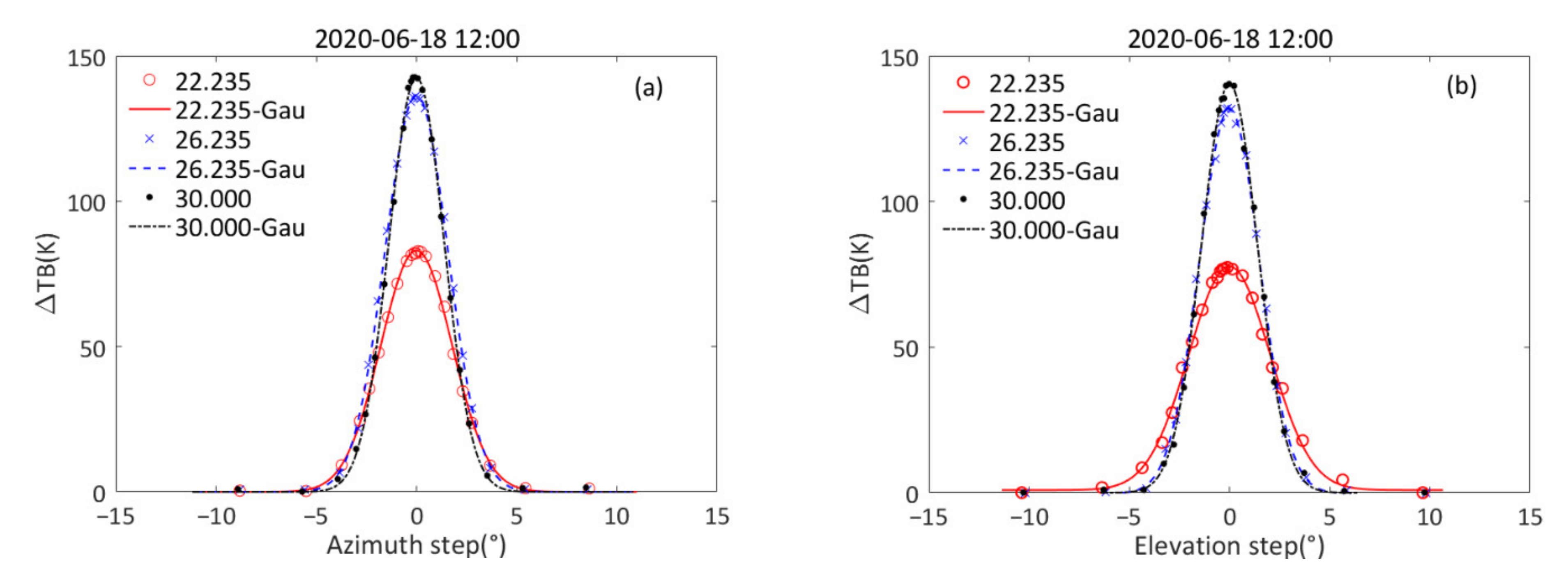
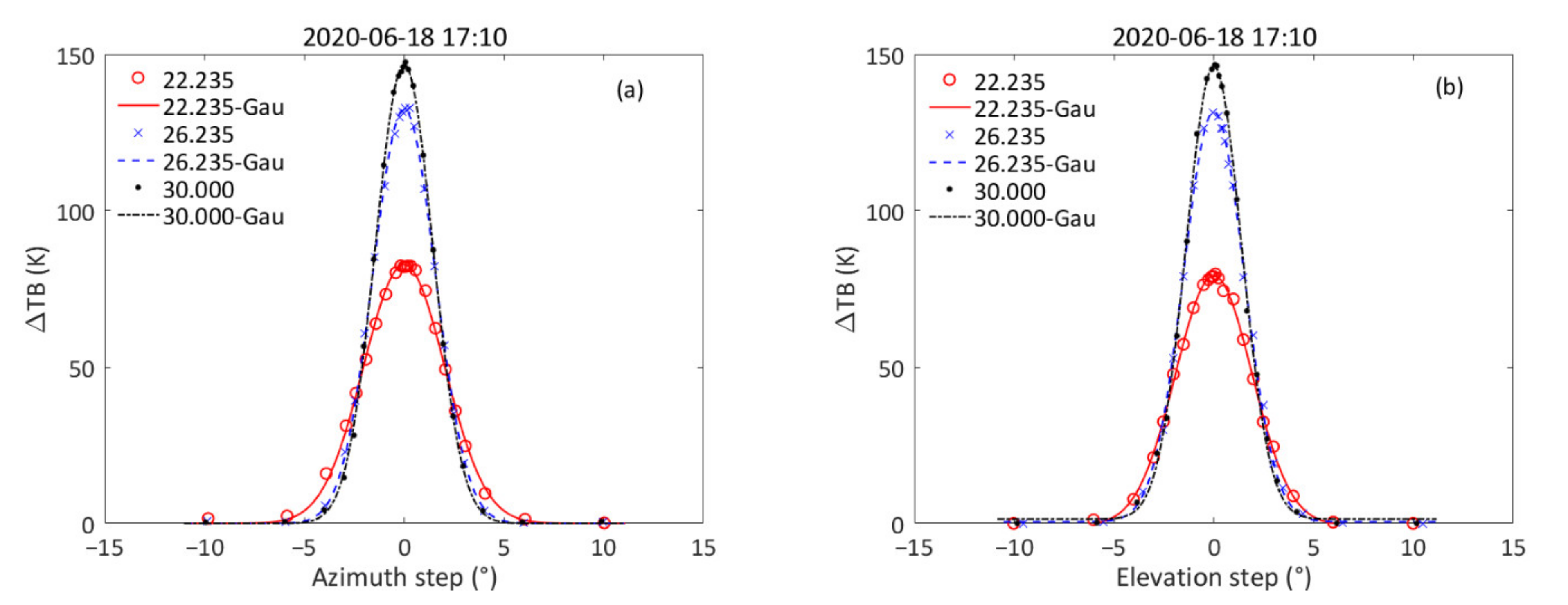



| Frequency (GHz) | a0 | a1 | a2 | a3 | BIAS (K) | RMS (K) |
|---|---|---|---|---|---|---|
| 22.235 | 184.9 | 0.797 | 0.187 | −0.1547 | 2.09 | 2.65 |
| 26.235 | 132.5 | 0.862 | 0.200 | −0.1208 | 1.66 | 2.17 |
| 30.000 | 108.7 | 0.855 | 0.204 | −0.0968 | 1.75 | 2.26 |
| Frequency (GHz) | Peak TB (K) | Beamwidth (°) | R | |||
|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | |
| 22.235 | 84.3 | 0.99 | 4.58 | 0.10 | 0.0087 | 0.00027 |
| 26.235 | 136.5 | 1.25 | 3.68 | 0.08 | 0.0135 | 0.00037 |
| 30.000 | 147.6 | 1.54 | 3.34 | 0.08 | 0.0164 | 0.00052 |
| Frequency (GHz) | Tsun (K) | |
|---|---|---|
| Mean | STD | |
| 22.235 | 9622.8 | 396.9 |
| 26.235 | 10,119.3 | 296.9 |
| 30.000 | 9015.4 | 294.4 |
| Frequency (GHz) | Beamwidth (°) | R | Tsun (K) | |||
|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | |
| 22.235 | 4.59 | 0.06 | 0.0092 | 0.0002 | 9950 | 334 |
| 26.235 | 3.72 | 0.10 | 0.0140 | 0.0004 | 10,351 | 370 |
| 30.000 | 3.38 | 0.05 | 0.0168 | 0.0005 | 9217 | 375 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, L.; Wang, Z.; Ma, Y.; Zhu, L.; Qin, J.; Chen, R.; Lu, J. Measurement of Solar Absolute Brightness Temperature Using a Ground-Based Multichannel Microwave Radiometer. Remote Sens. 2021, 13, 2968. https://doi.org/10.3390/rs13152968
Lei L, Wang Z, Ma Y, Zhu L, Qin J, Chen R, Lu J. Measurement of Solar Absolute Brightness Temperature Using a Ground-Based Multichannel Microwave Radiometer. Remote Sensing. 2021; 13(15):2968. https://doi.org/10.3390/rs13152968
Chicago/Turabian StyleLei, Lianfa, Zhenhui Wang, Yingying Ma, Lei Zhu, Jiang Qin, Rui Chen, and Jianping Lu. 2021. "Measurement of Solar Absolute Brightness Temperature Using a Ground-Based Multichannel Microwave Radiometer" Remote Sensing 13, no. 15: 2968. https://doi.org/10.3390/rs13152968
APA StyleLei, L., Wang, Z., Ma, Y., Zhu, L., Qin, J., Chen, R., & Lu, J. (2021). Measurement of Solar Absolute Brightness Temperature Using a Ground-Based Multichannel Microwave Radiometer. Remote Sensing, 13(15), 2968. https://doi.org/10.3390/rs13152968







