Effect Analysis of the Digital Spectrometer FFT Algorithm on THz Atmospheric Limb Sounder (TALIS) System Sensitivity
Abstract
1. Introduction
2. Materials and Methods
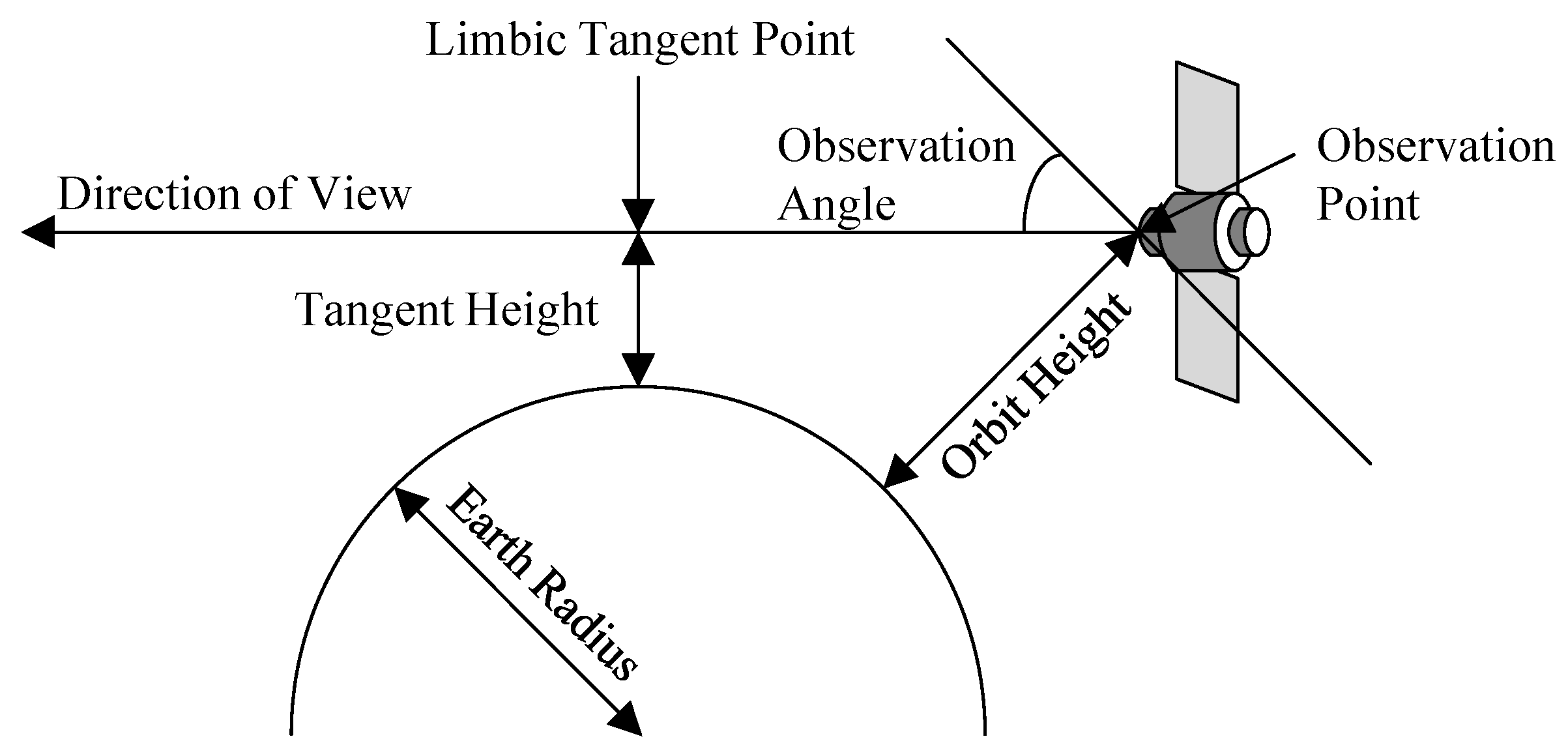
2.1. TALIS Overview
2.2. Digital Spectrometer Parameter Selection
2.2.1. Bandwidth and the Number of Channels
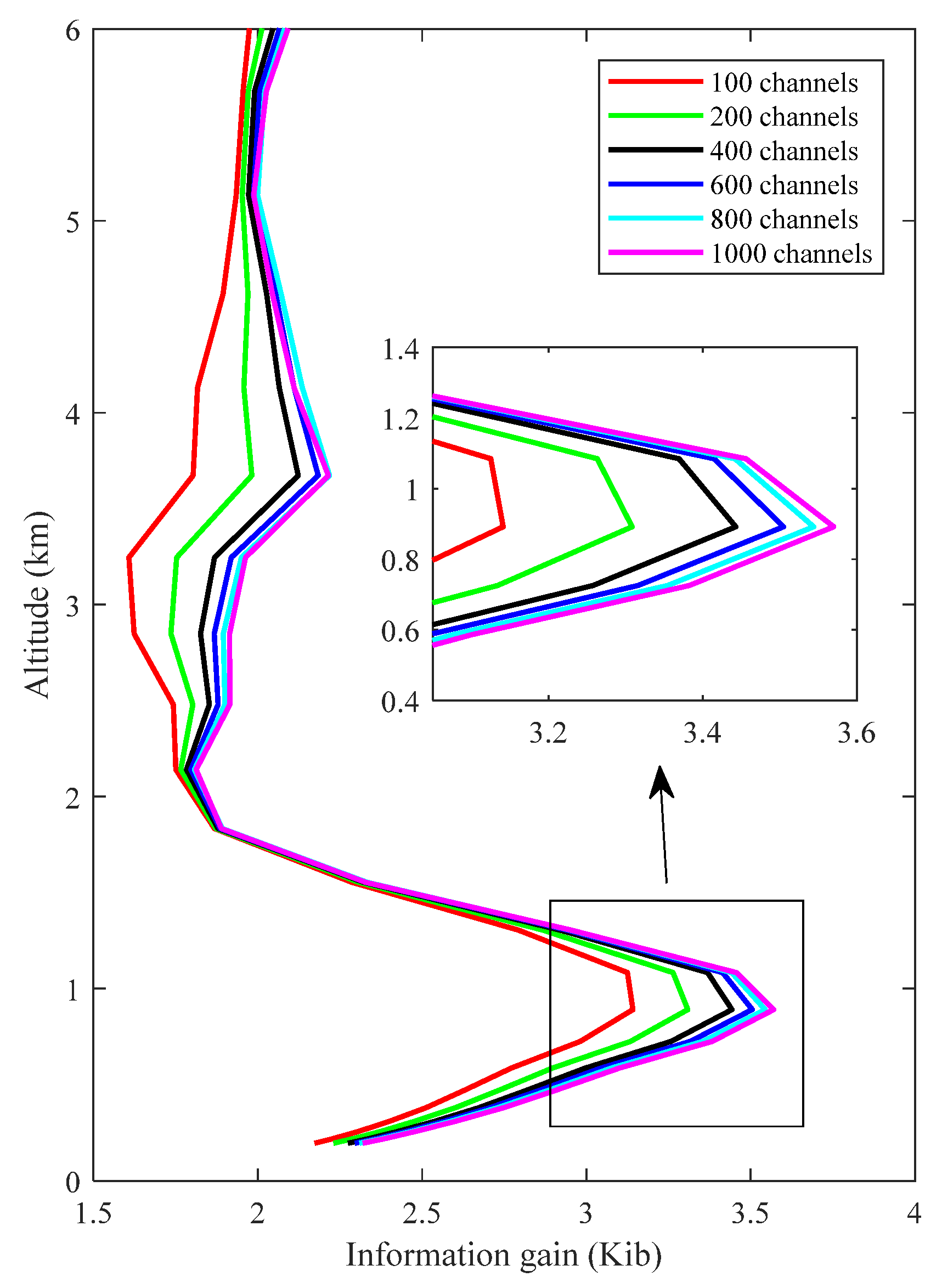
2.2.2. Parameter Analysis
3. Results
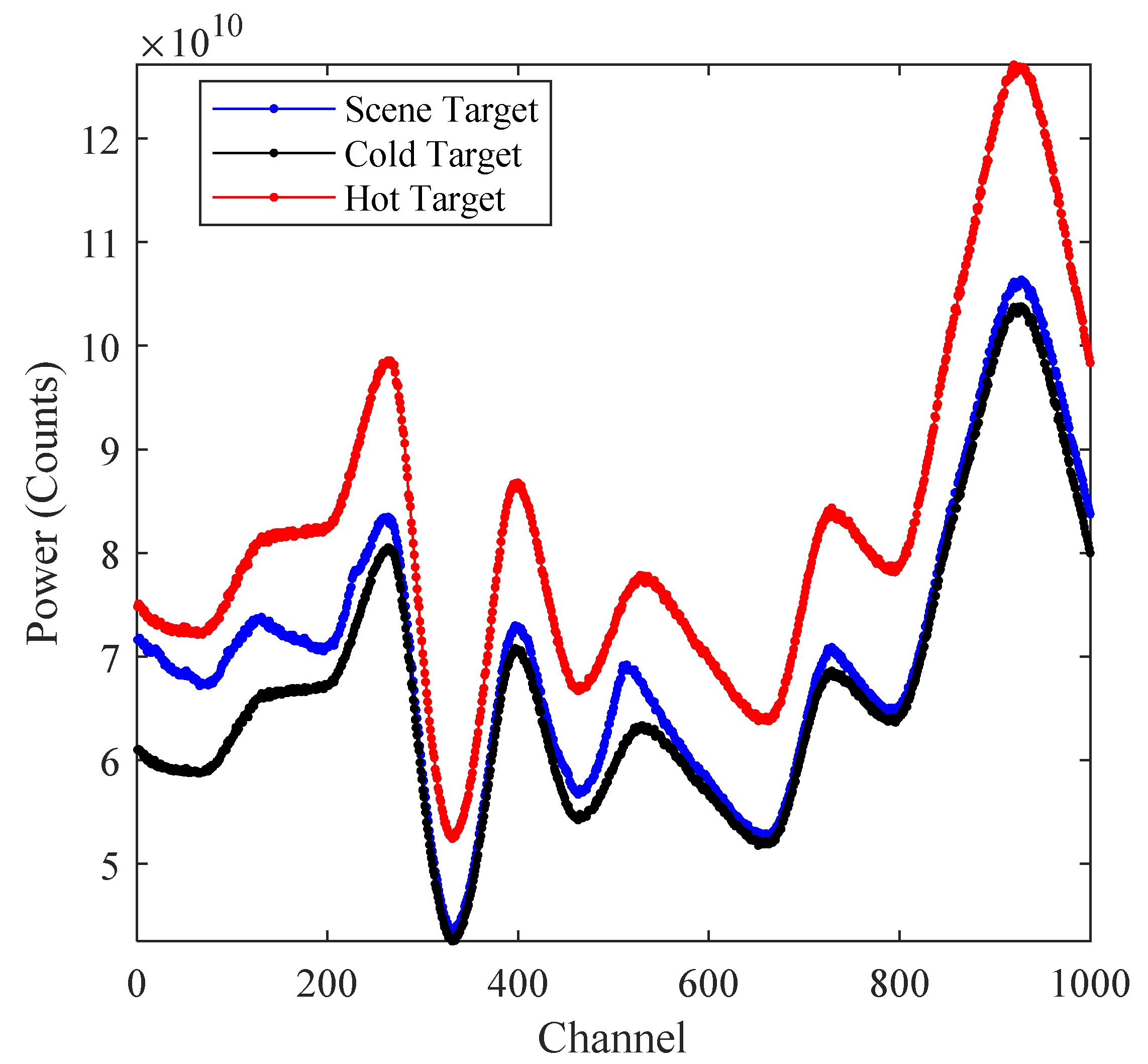
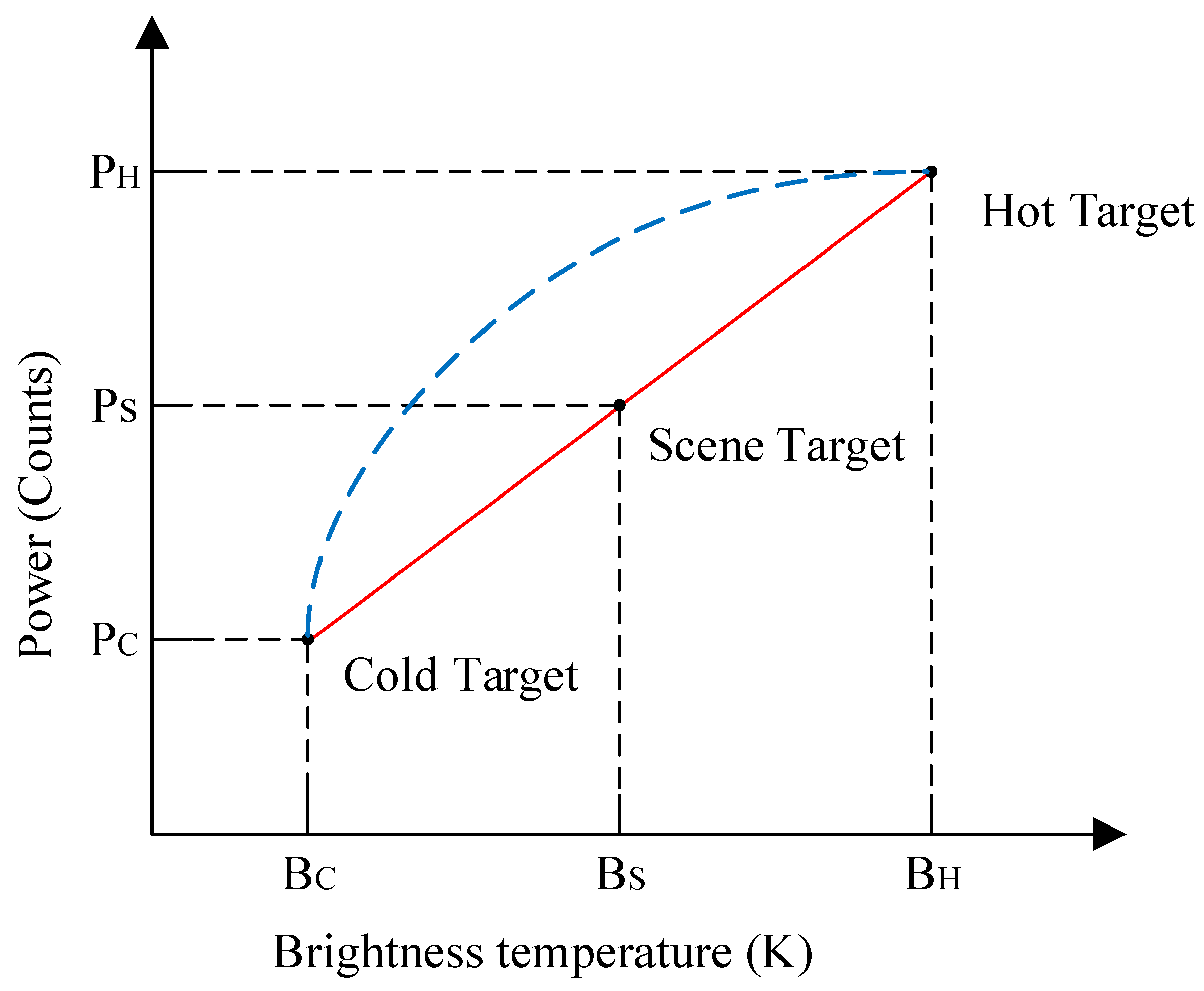
3.1. Effect of the Digital Spectrometer FFT Algorithm
3.2. Simulation Process
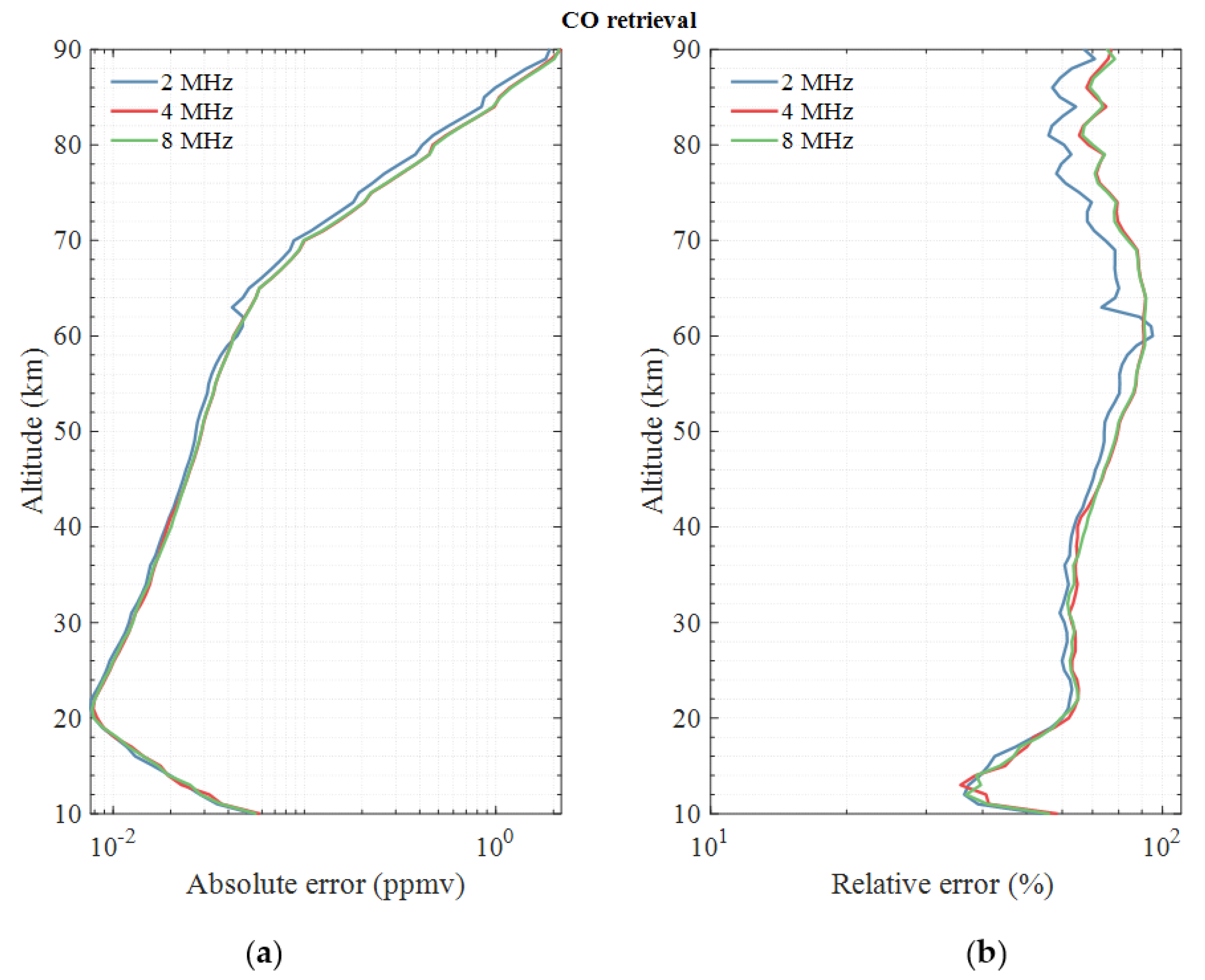
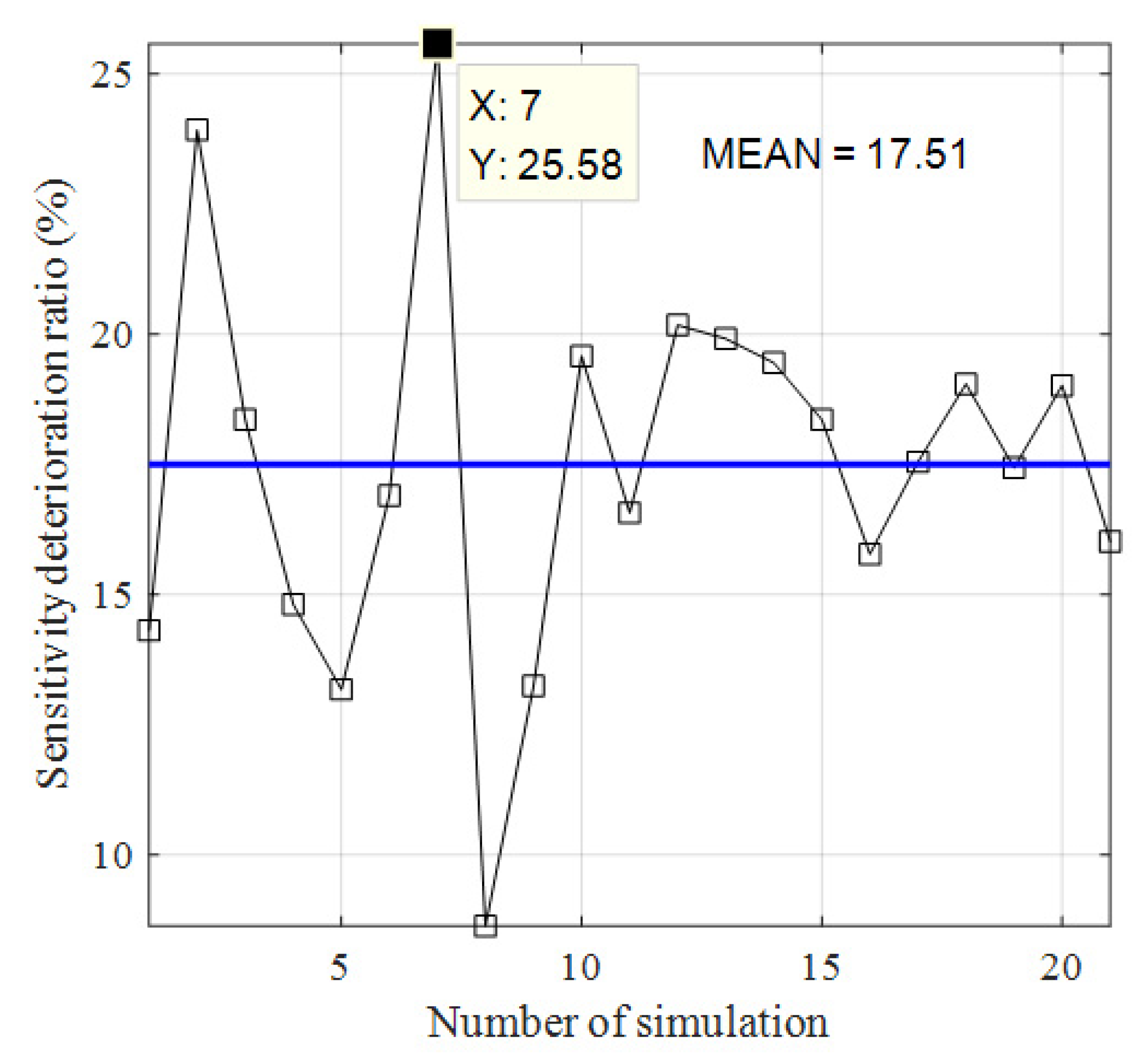
3.3. Sensitivity Analysis
- Full-band auto-correlation (abbreviated as F-AC) method: After the quantization process of the TALIS system simulation model, the value in each channel is subtracted from the mean value and then squared to obtain the sub-band auto-correlation result of the channel for each packet of data. Then the results of all the sub-band channels are summed to the full band to obtain the value of this packet.
- Full-band FFT (abbreviated as F-FFT) method: After the quantization process of the TALIS system simulation model, the FFT algorithm is performed for the results of all channels to obtain the amplitude spectrum, after which the amplitude spectrum is squared to obtain the results of the PSD for each packet of data. The results of PSD for all sub-band channels are summed to the full band to obtain the value of this packet.
- Sub-band ideal (abbreviated as S-Ideal) method: According to Equation (2), the ideal sub-band sensitivity and ideal full-band sensitivity should be related by times, under the condition of constant system noise temperature, integration time, spectral resolution, and so on, where C denotes the number of channels, so the ideal sub-band sensitivity can be obtained based on the ideal full-band sensitivity.
- Sub-band FFT (abbreviated as S-FFT) method, which includes two calculation ways, the sub-band FFT calculated value (abbreviated as S-FFT-C) method and the sub-band FFT real value (abbreviated as S-FFT-R) method.
- S-FFT-C method: After the quantization process of the TALIS system simulation model, FFT algorithm is performed for the results of all channels to obtain the amplitude spectrum, after which the amplitude spectrum is squared to obtain the results of the PSD for each packet of data. Unlike the F-FFT method, the calculation of sub-band sensitivity no longer involves the accumulation of power values of all channels within each packet of data but instead directly corresponds to the accumulation of each packet of data for each channel.
- S-FFT-R method: The previous process is the same as S-FFT-C, and the cumulative value corresponding to each packet of data for each channel is obtained. After that, the cumulative value of each sub-band channel needs to be summed again to the full-band value. The cumulative value of each sub-band channel is divided by this full-band value and multiplied by the final value of the F-AC method obtained in method (1).
4. Discussion
- (1)
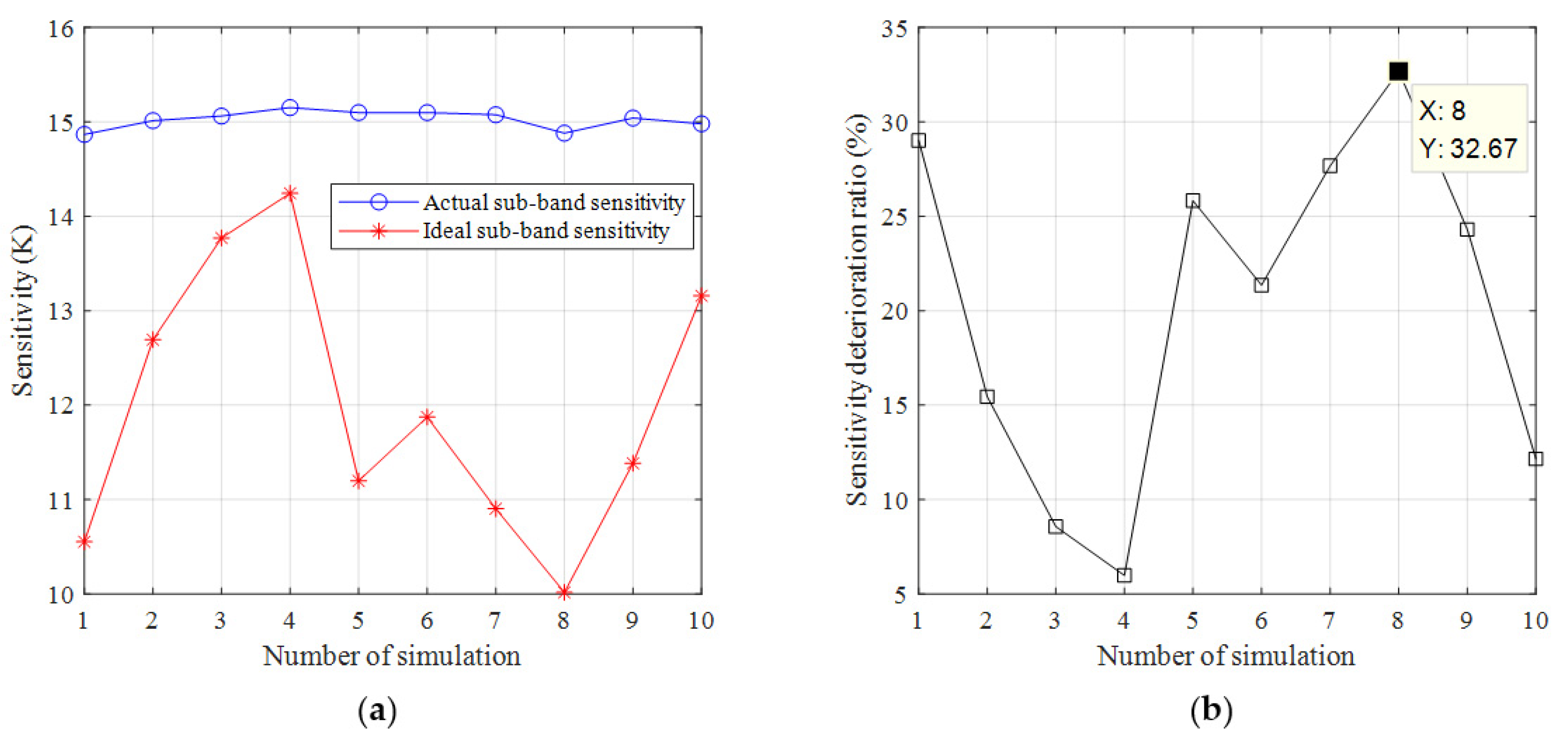
- For different integration time, we chose 0.5–80 ms and the intermediate 1 ms, 5 ms, 10 ms, 20 ms, and 50 ms as the simulation conditions, limited by the computer memory. The spectral resolution of 2 MHz and the quantization bits of 8-bit were kept constant at the same time. The simulation results are shown in Table 5 and Figure 12.
- (2)
- For different spectral resolutions, we chose 0.25–16 MHz and the intermediate 0.5 MHz, 1 MHz, 2 MHz, 4 MHz, and 8 MHz as the simulation conditions. The corresponding numbers of channels were set to 8000, 4000, 2000, 1000, 500, 250, and 125. The integration time of 5 ms and the quantization bits of 8-bit were kept constant at the same time. The simulation results are shown in Table 6 and Figure 13.
- (3)
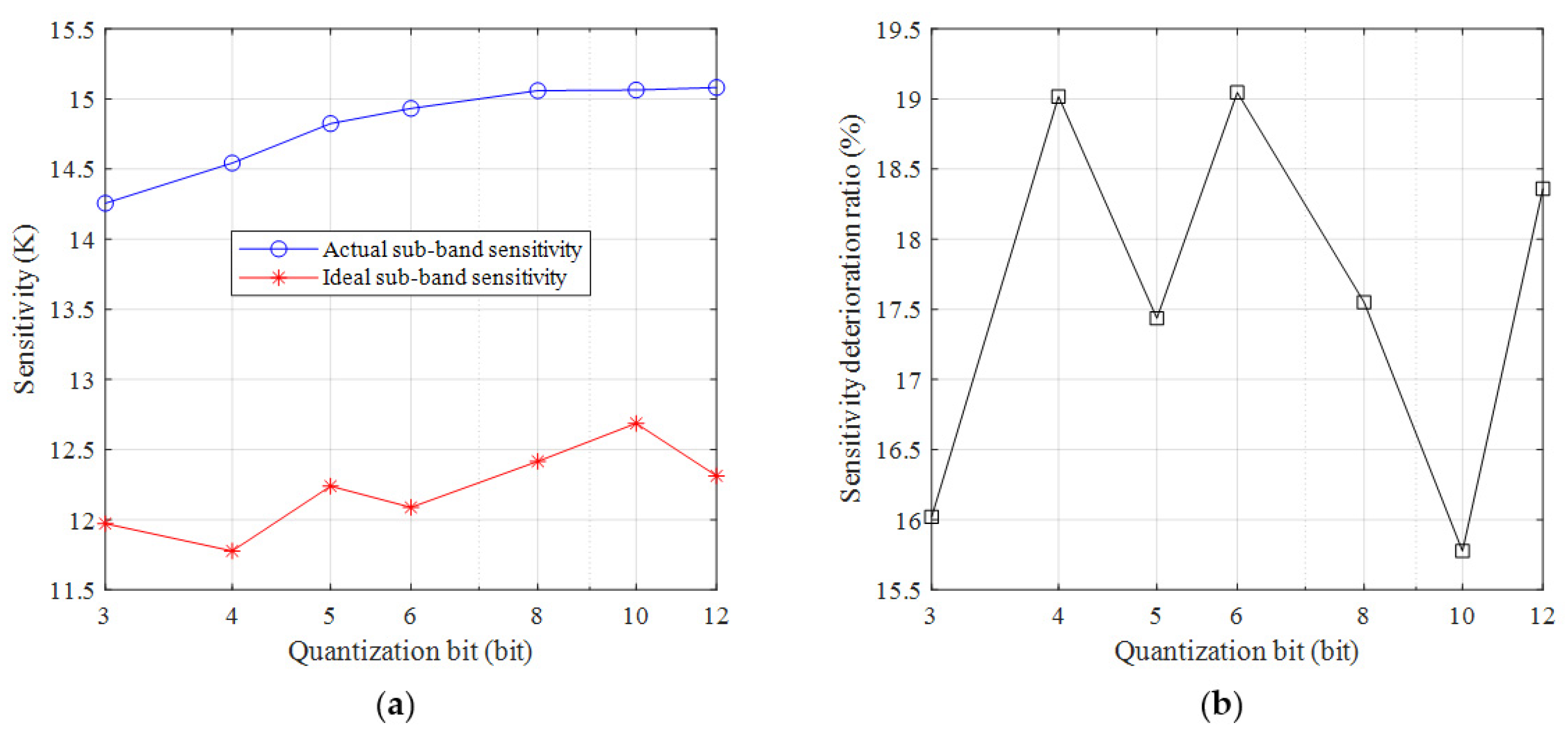
- For different quantization bits, we chose 12-bit to 3-bit and the intermediate 10-bit, 8-bit, 6-bit, 5-bit, and 4-bit as the simulation conditions. The integration time of 5 ms and the spectral resolution of 2 MHz were kept constant at the same time. The simulation results are shown in Table 7 and Figure 14.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.M.; Zhang, S.W. Scheme design of the K band spectrum analysis microwave radiometer. J. Terahertz Sci. Electron. Inf. Technol. 2013, 11, 747–752. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Li, J. Development of Microwave Limb Sounder. Adv. Mater. Microw. Opt. 2012, 500, 204–211. [Google Scholar] [CrossRef]
- Wu, D.L.; Read, W.G.; Shippony, Z.; Leblanc, T.; Duck, T.J.; Ortland, D.A.; Sica, R.J.; Argall, P.S.; Oberheide, J.; Hauchecorne, A.; et al. Mesospheric temperature from UARS MLS: Retrieval and validation. J. Atmos. Sol. Terr. Phys. 2003, 65, 245–267. [Google Scholar] [CrossRef]
- Waters, J.W.; Read, W.G.; Froidevaux, L.; Jarnot, R.F.; Cofield, R.E.; Flower, D.A.; Lau, G.K.K.; Pickett, H.M.; Santee, M.L.; Wu, D.L.; et al. The UARS and EOS microwave limb sounder (MLS) experiments. J. Atmos. Sci. 1999, 56, 194–218. [Google Scholar] [CrossRef]
- Barath, F.T.; Chavez, M.C.; Cofield, R.E.; Flower, D.A.; Frerking, M.A.; Gram, M.B.; Harris, W.M.; Holden, J.R.; Jarnot, R.F.; Kloezeman, W.G.; et al. The Upper-Atmosphere Research Satellite Microwave Limb Sounder Instrument. J. Geophys. Res. Atmos. 1993, 98, 751–762. [Google Scholar] [CrossRef]
- Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jimenez, C.; Megie, G.; et al. An overview of the Odin atmospheric mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
- Frisk, U.; Hagström, M.; Ala-Laurinaho, J.; Andersson, S.; Berges, J.-C.; Chabaud, J.-P.; Dahlgren, M.; Emrich, A.; Florén, H.-G.; Florin, G.; et al. The Odin satellite-I. Radiometer design and test. Astron. Astrophys. 2003, 402, L27–L34. [Google Scholar] [CrossRef]
- Olberg, M.; Frisk, U.; Lecacheux, A.; Olofsson, A.O.H.; Baron, P.; Bergman, P.; Florin, G.; Hjalmarson, A.; Larsson, B.; Murtagh, D.; et al. The Odin satellite-II. Radiometer data processing and calibration. Astron. Astrophys. 2003, 402, L35–L38. [Google Scholar] [CrossRef]
- Pickett, H.M. Microwave Limb Sounder THz module on Aura. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1122–1130. [Google Scholar] [CrossRef]
- Jarnot, R.F.; Perun, V.S.; Schwartz, M.J. Radiometric and spectral performance and calibration of the GHz bands of EOS MLS. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1131–1143. [Google Scholar] [CrossRef]
- Waters, J.W.; Froidevaux, L.; Harwood, R.S.; Jarnot, R.F.; Pickett, H.M.; Read, W.G.; Siegel, P.H.; Cofield, R.E.; Filipiak, M.J.; Flower, D.A.; et al. The Earth Observing System Microwave Limb Sounder (EOS MLS) on the Aura satellite. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1075–1092. [Google Scholar] [CrossRef]
- Ochiai, S.; Kikuchi, K.-i.; Nishibori, T.; Manabe, T. Gain Nonlinearity Calibration of Submillimeter Radiometer for JEM/SMILES. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 962–969. [Google Scholar] [CrossRef]
- Kikuchi, K.; Nishibori, T.; Ochiai, S.; Ozeki, H.; Irimajiri, Y.; Kasai, Y.; Koike, M.; Manabe, T.; Mizukoshi, K.; Murayama, Y.; et al. Overview and early results of the Superconducting Submillimeter-Wave Limb-Emission Sounder (SMILES). J. Geophys. Res. Atmos. 2010, 115, D23306. [Google Scholar] [CrossRef]
- Imai, K.; Manago, N.; Mitsuda, C.; Naito, Y.; Nishimoto, E.; Sakazaki, T.; Fujiwara, M.; Froidevaux, L.; von Clarmann, T.; Stiller, G.P.; et al. Validation of ozone data from the Superconducting Submillimeter-Wave Limb-Emission Sounder (SMILES). J. Geophys. Res. Atmos. 2013, 118, 5750–5769. [Google Scholar] [CrossRef]
- Villanueva, G.; Hartogh, P. The High Resolution Chirp Transform Spectrometer for the Sofia-Great Instrument. Exp. Astron. 2006, 18, 77–91. [Google Scholar] [CrossRef]
- Pointon, L. The Jodrell Bank 1024-channel digital autocorrelation spectrometer. J. Phys. E Sci. Instrum. 1977, 10, 833–837. [Google Scholar] [CrossRef]
- Muller, S.C.; Murk, A.; Monstein, C.; Kampfer, N. Intercomparison of Digital Fast Fourier Transform and Acoustooptical Spectrometers for Microwave Radiometry of the Atmosphere. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2233–2239. [Google Scholar] [CrossRef]
- Zeng, C.; Han, Y.; Liu, B.; Sun, P.; Li, X.; Chen, P. Optical design of a high-resolution spectrometer with a wide field of view. Opt. Lasers Eng. 2021, 140. [Google Scholar] [CrossRef]
- De Miguel-Hernandez, J.; Hoyland, R.J.; Gomez Renasco, M.F.; Rubino-Martin, J.A.; Viera-Curbelo, T.A. A High-Sensitivity Fourier Transform Spectrometer for Cosmic Microwave Background Observations. IEEE Trans. Instrum. Meas. 2020, 69, 4516–4523. [Google Scholar] [CrossRef]
- Wang, W.Y.; Wang, Z.Z.; Duan, Y.Q. Preliminary Evaluation of the Error Budgets in the TALIS Measurements and Their Impact on the Retrievals. Remote Sens. 2020, 12, 468. [Google Scholar] [CrossRef]
- Benz, A.O.; Grigis, P.C.; Hungerbuhler, V.; Meyer, H.; Monstein, C.; Stuber, B.; Zardet, D. A broadband FFT spectrometer for radio and millimeter astronomy. Astron. Astrophys. 2005, 442, 767–773. [Google Scholar] [CrossRef][Green Version]
- Stanko, S.; Klein, B.; Kerp, J. A field programmable gate array spectrometer for radio astronomy. Astron. Astrophys. 2005, 436, 391–395. [Google Scholar] [CrossRef]
- Iwai, K.; Kubo, Y.; Ishibashi, H.; Naoi, T.; Harada, K.; Ema, K.; Hayashi, Y.; Chikahiro, Y. OCTAD-S: Digital fast Fourier transform spectrometers by FPGA. Earth Planets Space 2017, 69, 95. [Google Scholar] [CrossRef]
- Emrich, A.; Andersson, S. Autocorrelation spectrometers for space borne (sub)millimetre spectroscopy. In Proceedings of the Submillimetre Far-infrared Space Instrumentation, Noordwijk, The Netherlands, 24–26 September 1996; pp. 257–260. [Google Scholar]
- Klein, B.; Philipp, S.D.; Krämer, I.; Kasemann, C.; Güsten, R.; Menten, K.M. The APEX digital fast Fourier transform spectrometer. Astron. Astrophys. 2006, 454, L29–L32. [Google Scholar] [CrossRef]
- Jiang, H.M.; Liu, H.; Guzzino, K.; Kubo, D.; Li, C.T.; Chang, R.; Chen, M.T. A 5 Giga Samples Per Second 8-Bit Analog to Digital Printed Circuit Board for Radio Astronomy. Publ. Astron. Soc. Pac. 2014, 126, 761–768. [Google Scholar] [CrossRef]
- Ebenezer, E.; Ramesh, R.; Subramanian, K.R.; SundaraRajan, M.S.; Sastry, C.V. A new digital spectrograph for observations of radio burst emission from the Sun. Astrophys 2001, 367, 1112–1116. [Google Scholar] [CrossRef]
- Duan, Y.; Wang, Z.; Xiao, Y.; Wang, W. Simulating Radiometric Resolution of Microwave Humidity and Temperature Sounder Onboard the FY-3D Satellite. IEEE Trans. Instrum. Meas. 2020, 69, 6582–6594. [Google Scholar] [CrossRef]
- Tian, M.; Zou, X.L.; Weng, F.Z. Use of Allan Deviation for Characterizing Satellite Microwave Sounder Noise Equivalent Differential Temperature (NEDT). IEEE Geosci. Remote Sens. Lett. 2015, 12, 2477–2480. [Google Scholar] [CrossRef]
- Klein, B.; Hochgurtel, S.; Kramer, I.; Bell, A.; Meyer, K.; Gusten, R. High-resolution wide-band fast Fourier transform spectrometers. Astron. Astrophys. 2012, 542, 1075. [Google Scholar] [CrossRef]
- Hagen, J.; Luder, A.; Murk, A.; Kampfer, N. Frequency-Agile FFT Spectrometer for Microwave Remote Sensing Applications. Atmosphere 2020, 11, 490. [Google Scholar] [CrossRef]
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the Atmospheric Radiative Transfer Simulator–version 2.2, the planetary toolbox edition. Geosci. Model Dev. 2018, 11, 1537–1556. [Google Scholar] [CrossRef]
- Wang, W.Y.; Wang, Z.Z.; Duan, Y.Q. Performance evaluation of THz Atmospheric Limb Sounder (TALIS) of China. Atmos. Meas. Tech. 2020, 13, 13–38. [Google Scholar] [CrossRef]
- Jordanov, V.T.; Knoll, G.F. Digital Synthesis of Pulse Shapes in Real-Time for High-Resolution Radiation Spectroscopy. Nucl. Instrum. Methods A 1994, 345, 337–345. [Google Scholar] [CrossRef]
- Shiunn-Jang, C.; Kuo-Jiann, C. An enhanced Fourier transform spectrometer with a search algorithm. IEEE Trans. Instrum. Meas. 1996, 45, 127–135. [Google Scholar] [CrossRef]
- Li, J.; Lu, D.-F.; Qi, Z.-M. A Modified Equation for the Spectral Resolution of Fourier Transform Spectrometers. J. Lightwave Technol. 2015, 33, 19–24. [Google Scholar] [CrossRef]
- Wang, W.Y. Simulation Study on Application for THz Atmospheric Limb Sounder. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar]
- Soref, R.A.; De Leonardis, F.; Passaro, V.M.N.; Fainman, Y. On-Chip Digital Fourier-Transform Spectrometer Using a Thermo-Optical Michelson Grating Interferometer. J. Lightwave Technol. 2018, 36, 5160–5167. [Google Scholar] [CrossRef]
- Duan, Y.; Wang, Z.; Xu, H.; Wang, W. Simulation of the Spectrum Response for the THz Atmosphere Limb Sounder (TALIS). Sensors 2020, 20, 498. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Yu, C.Y.; Kubo, D.; Chen, M.T.; Guzzino, K. A Low-cost 4 Bit, 10 Giga-samples-per-second Analog-to-digital Converter Printed Circuit Board Assembly for FPGA-based Backends. Publ. Astron. Soc. Pac. 2016, 128, 115002. [Google Scholar] [CrossRef]
- Yiu, P.; Iturbe, X.; Keymeulen, D.; Berisford, D.; Hand, K.; Carlson, R.; Wadsworth, W.; Dybwad, J.P.; Levy, R. Adaptive Controller for a Fourier Transform Spectrometer with Space Applications. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Teng, H.F.; Zhang, U.H.; Chiueh, T.H.; Wong, S.K.; Li, H.H.; Chen, Y.L. Ultrawideband 1-b Digital Spectrometer. IEEE Trans. Instrum. Meas. 2015, 64, 299–307. [Google Scholar] [CrossRef]






| Spectrometer Type | Limitation |
|---|---|
| FBS | Poor channel consistency and frequency crosstalk |
| DACS | Consumes large amounts of digital resources |
| AOS | Large size, complex structure, not easy to integrate |
| CTS | Narrow bandwidth |
| AACS | Low system stability and few channels |
| Payload | Spectrometer Type | Maximum Bandwidth | Spectral Resolution |
|---|---|---|---|
| UARS-MLS | FBS | 510 MHz | 2–128 MHz |
| Odin-SMR | DACS, AOS | 1.2 GHz | 0.15–1 MHz |
| EOS-MLS | FBS, DACS | 1.3 GHz | 0.1–500 MHz |
| JEM/SMILES | AOS | 1.3 GHz | 1.4 MHz |
| TALIS | FFTS | 2 GHz | 2.3 MHz |
| Radiometer (GHz) | System Noise Temperature (K) | Spectral Band (GHz) |
|---|---|---|
| 118 | 1000 | S1: 115.35–117.35, 117.75–119.75 |
| 190 | 1000 | S2: 175.50–177.50, 202.70–204.70 |
| S3: 178.90–180.90, 199.30–201.30 | ||
| S4: 183.00–185.00, 195.20–197.20 | ||
| 240 | 1000 | S5: 229.66–231.66, 247.66–249.66 |
| S6: 232.16–234.16, 245.16–247.16 | ||
| S7: 234.66–236.66, 242.66–244.66 | ||
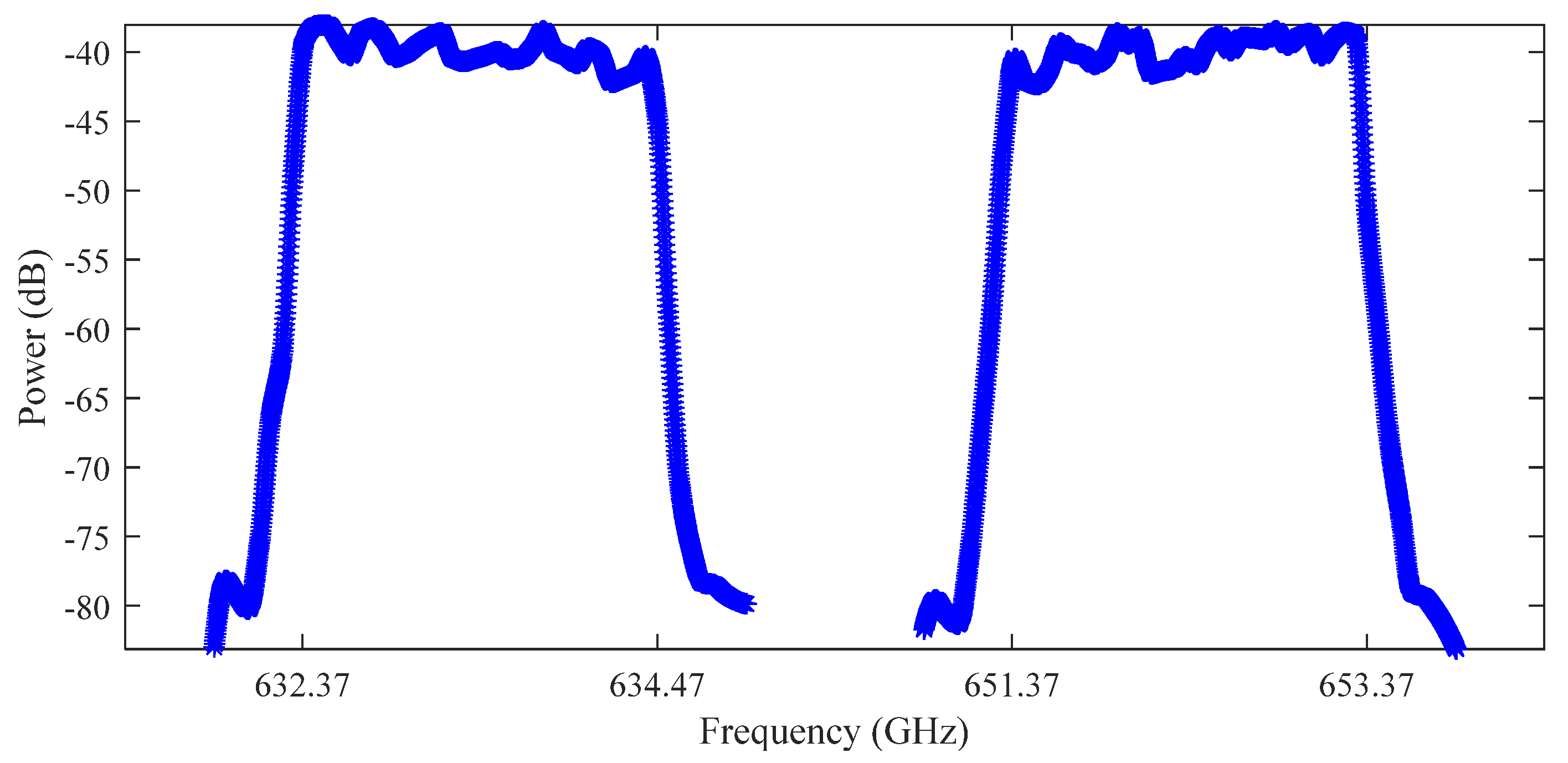
| 640 | 2300 | S8: 624.47–626.47, 659.27–661.27 |
| S9: 627.37–629.37, 656.37–658.37 | ||
| S10: 632.37–634.37, 651.37–653.37 | ||
| S11: 634.87–636.87, 648.87–650.87 |
| Number of Simulation | F-AC Method (K) | F-FFT Method (K) | S-Ideal Method (K) | S-FFT Method | |
|---|---|---|---|---|---|
| S-FFT-C Method (K) | S-FFT-R Method (K) | ||||
| 1 | 0.33 | 0.34 | 10.55 | 14.87 | 14.87 |
| 2 | 0.40 | 0.40 | 12.69 | 15.01 | 15.01 |
| 3 | 0.44 | 0.43 | 13.77 | 15.06 | 15.06 |
| 4 | 0.45 | 0.45 | 14.24 | 15.15 | 15.15 |
| 5 | 0.36 | 0.35 | 11.20 | 15.10 | 15.10 |
| 6 | 0.38 | 0.38 | 11.87 | 15.10 | 15.10 |
| 7 | 0.34 | 0.34 | 10.90 | 15.07 | 15.07 |
| 8 | 0.32 | 0.31 | 10.02 | 14.88 | 14.88 |
| 9 | 0.36 | 0.36 | 11.39 | 15.04 | 15.04 |
| 10 | 0.42 | 0.41 | 13.16 | 14.98 | 14.98 |
| Average | 0.38 | 0.38 | 11.98 | 15.03 | 15.03 |
| Sensitivity Method | Sensitivity Type | Sensitivity under Different Integration Time (K) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.5 ms | 1 ms | 5 ms | 10 ms | 20 ms | 50 ms | 80 ms | ||
| F-AC-AVR | Ideal full-band | 1.29 | 0.81 | 0.39 | 0.29 | 0.21 | 0.12 | 0.09 |
| F-FFT-AVR | Actual full-band | 1.29 | 0.81 | 0.39 | 0.29 | 0.21 | 0.12 | 0.09 |
| S-Ideal-AVR | Ideal sub-band | 40.75 | 25.59 | 12.24 | 9.06 | 6.53 | 3.95 | 2.79 |
| S-FFT-C-AVR S-FFT-R-AVR | Actual sub-band | 47.56 | 33.64 | 14.99 | 10.64 | 7.52 | 4.75 | 3.75 |
| 47.56 | 33.64 | 14.99 | 10.64 | 7.52 | 4.75 | 3.75 | ||
| Sensitivity Method | Sensitivity Type | Sensitivity under Different Spectral Resolutions (K) | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.25 MHz | 0.5 MHz | 1 MHz | 2 MHz | 4 MHz | 8 MHz | 16 MHz | ||
| F-AC-AVR | Ideal full-band | 0.16 | 0.21 | 0.28 | 0.41 | 0.56 | 0.78 | 1.12 |
| F-FFT-AVR | Actual full-band | 0.16 | 0.21 | 0.28 | 0.41 | 0.55 | 0.78 | 1.12 |
| S-Ideal-AVR | Ideal sub-band | 14.15 | 13.46 | 12.49 | 12.97 | 12.45 | 12.39 | 12.57 |
| S-FFT-C-AVR S-FFT-R-AVR | Actual sub-band | 15.49 | 15.52 | 15.53 | 15.55 | 15.60 | 15.47 | 15.60 |
| 15.49 | 15.52 | 15.53 | 15.55 | 15.60 | 15.47 | 15.60 | ||
| Sensitivity Method | Sensitivity Type | Sensitivity under Different Quantization Bits (K) | ||||||
|---|---|---|---|---|---|---|---|---|
| 3-bit | 4-bit | 5-bit | 6-bit | 8-bit | 10-bit | 12-bit | ||
| F-AC-AVR | Ideal full-band | 0.38 | 0.37 | 0.39 | 0.38 | 0.39 | 0.40 | 0.39 |
| F-FFT-AVR | Actual full-band | 0.38 | 0.37 | 0.39 | 0.38 | 0.39 | 0.40 | 0.39 |
| S-Ideal-AVR | Ideal sub-band | 11.97 | 11.78 | 12.24 | 12.09 | 12.42 | 12.69 | 12.31 |
| S-FFT-C-AVR S-FFT-R-AVR | Actual sub-band | 14.26 | 14.54 | 14.82 | 14.93 | 15.06 | 15.06 | 15.08 |
| 14.26 | 14.54 | 14.82 | 14.93 | 15.06 | 15.06 | 15.08 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Lu, H.; Wang, Z.; He, W.; Wang, W. Effect Analysis of the Digital Spectrometer FFT Algorithm on THz Atmospheric Limb Sounder (TALIS) System Sensitivity. Remote Sens. 2021, 13, 2921. https://doi.org/10.3390/rs13152921
Xu H, Lu H, Wang Z, He W, Wang W. Effect Analysis of the Digital Spectrometer FFT Algorithm on THz Atmospheric Limb Sounder (TALIS) System Sensitivity. Remote Sensing. 2021; 13(15):2921. https://doi.org/10.3390/rs13152921
Chicago/Turabian StyleXu, Haowen, Hao Lu, Zhenzhan Wang, Wenming He, and Wenyu Wang. 2021. "Effect Analysis of the Digital Spectrometer FFT Algorithm on THz Atmospheric Limb Sounder (TALIS) System Sensitivity" Remote Sensing 13, no. 15: 2921. https://doi.org/10.3390/rs13152921
APA StyleXu, H., Lu, H., Wang, Z., He, W., & Wang, W. (2021). Effect Analysis of the Digital Spectrometer FFT Algorithm on THz Atmospheric Limb Sounder (TALIS) System Sensitivity. Remote Sensing, 13(15), 2921. https://doi.org/10.3390/rs13152921






