Application of SAR Data for Tropical Cyclone Intensity Parameters Retrieval and Symmetric Wind Field Model Development
Abstract
1. Introduction
2. Data
2.1. Sentinel-1 EW Mode Data
2.2. SFMR Wind Speed Measurements
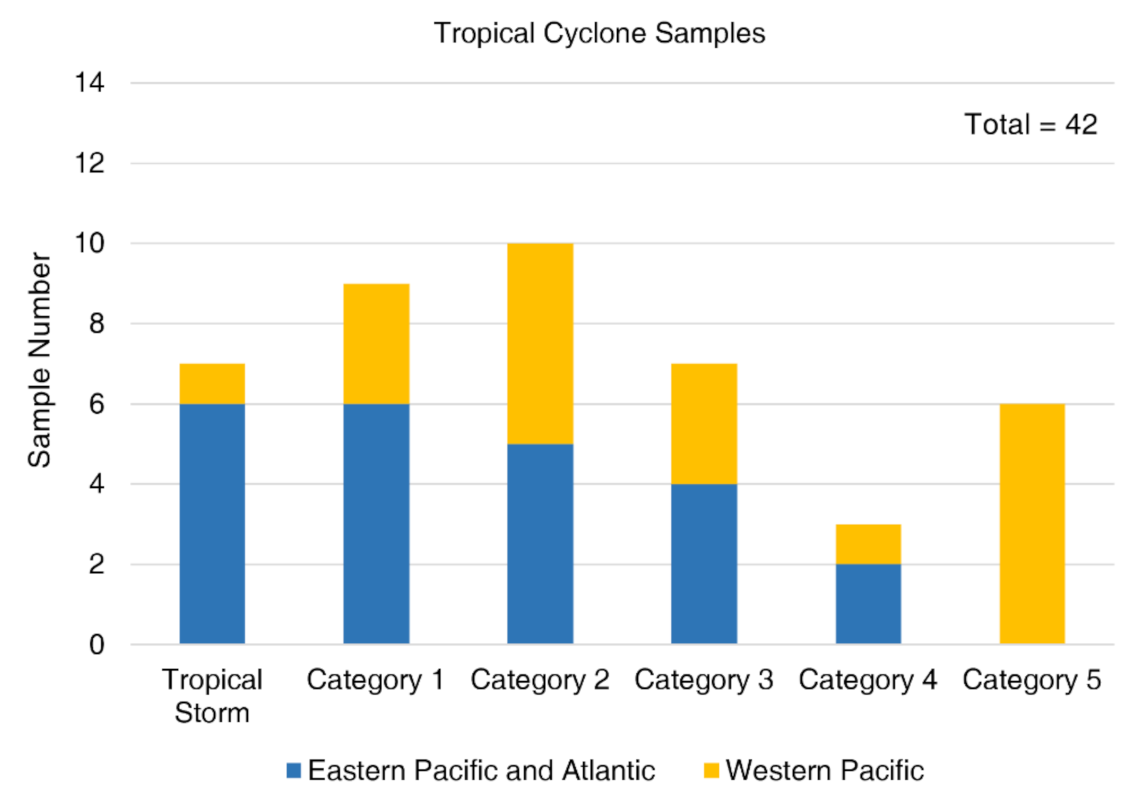
2.3. TC Best-Track Data
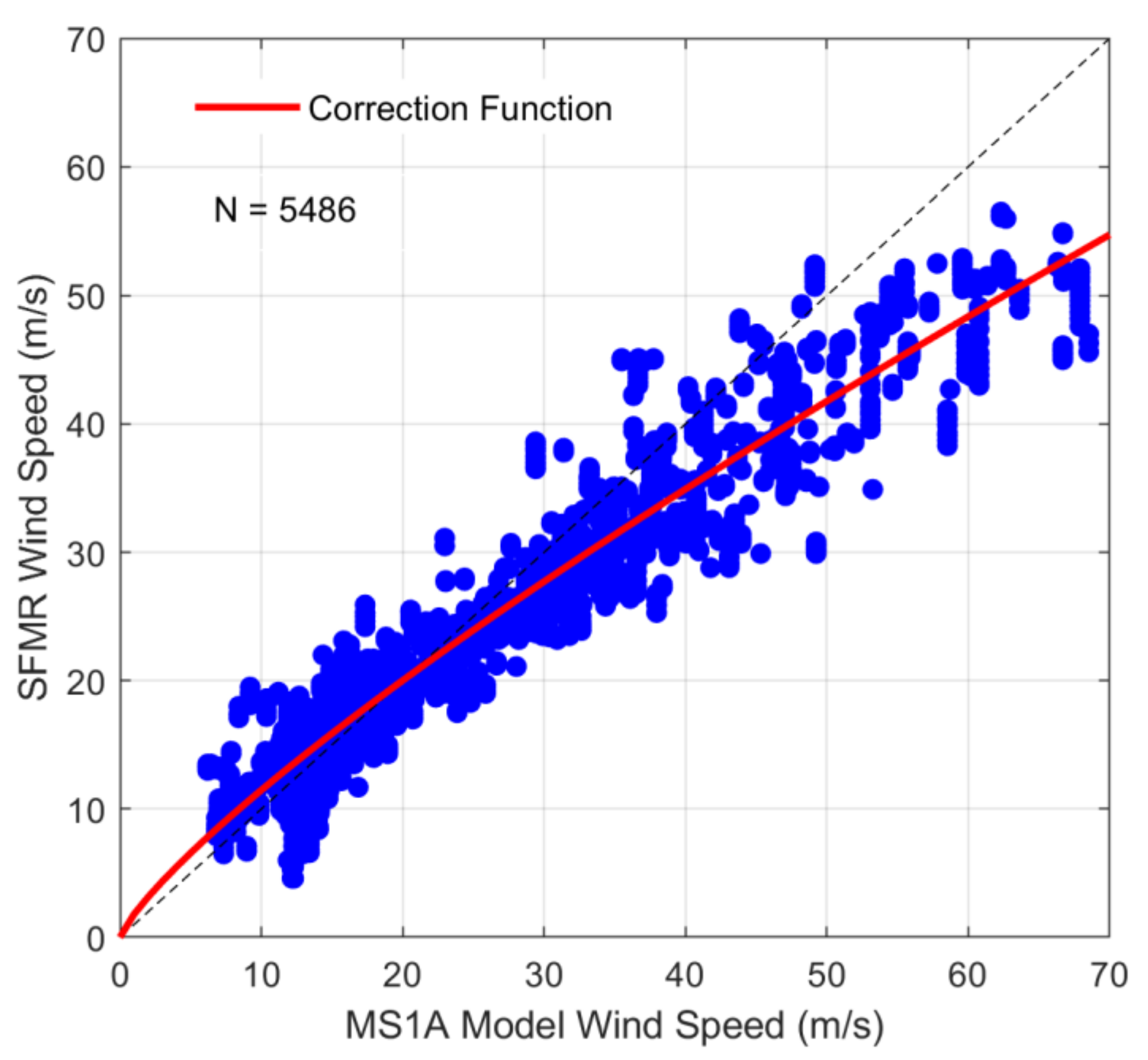
3. MS1A Modification
4. TC Intensity Parameters Retrieval
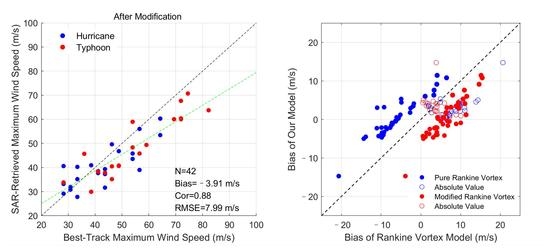
4.1. Surface Maximum Wind Speed
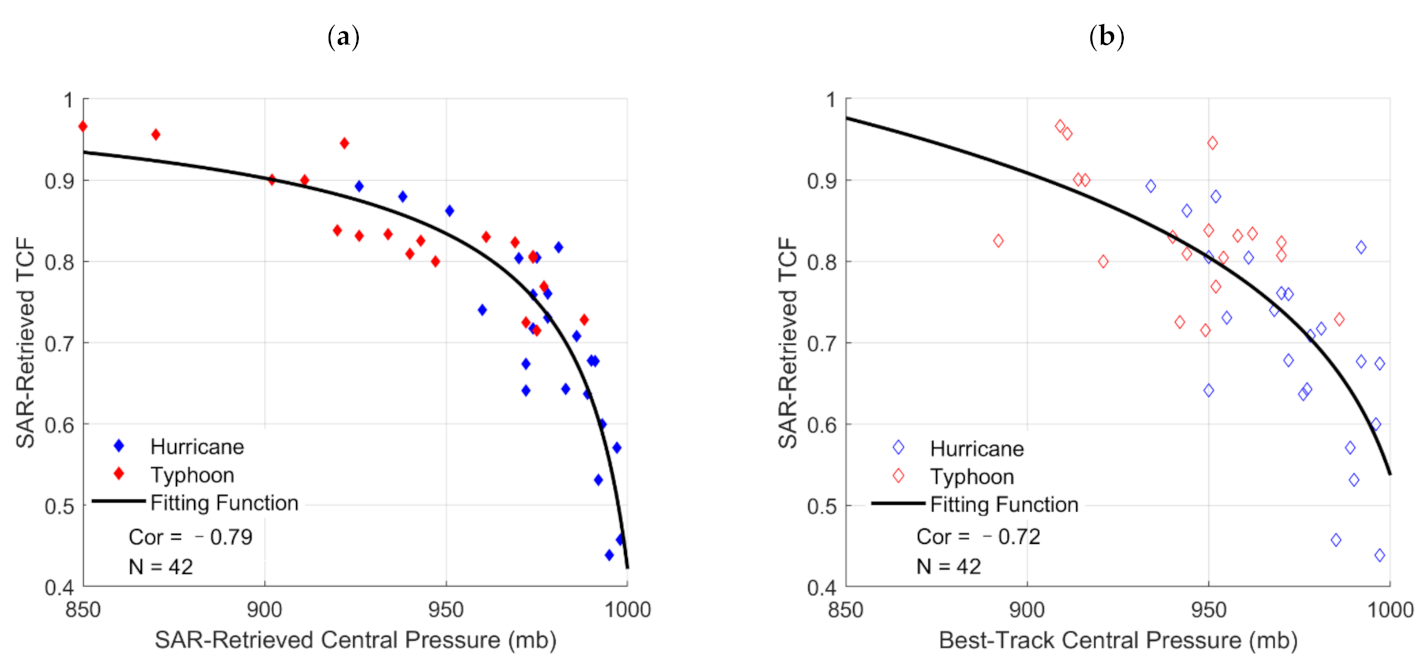
4.2. Tropical Cyclone Fullness
4.3. Central Surface Pressure
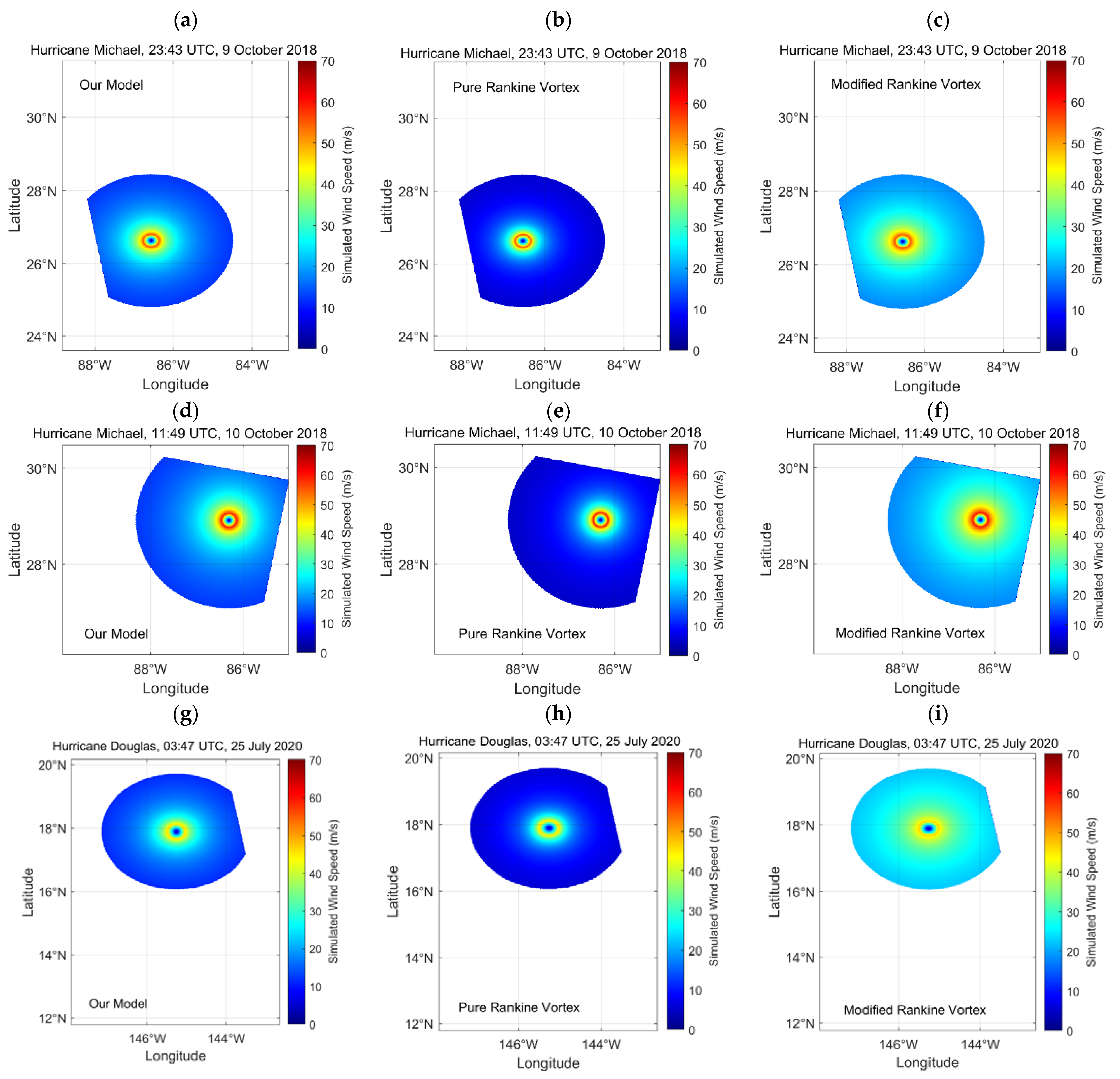
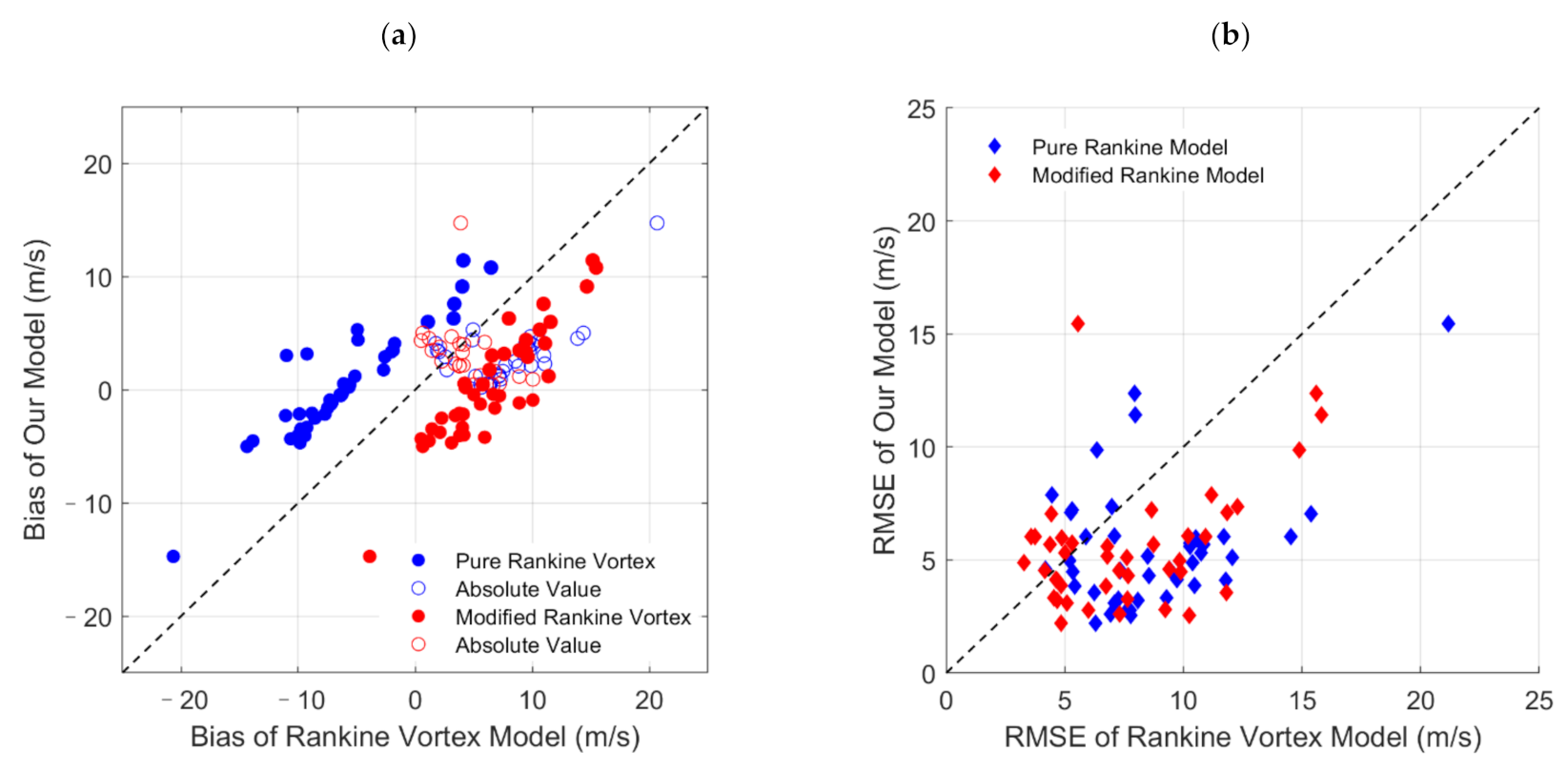
5. Wind Field Model Development
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Typhoon | |||
|---|---|---|---|
| Name | Area | SAR Instrument | Acquisition Time (UTC) |
| Megi | Western Pacific | Sentinel-1A | 20160926 09:34 |
| Jongdari | Western Pacific | Sentinel-1B | 20180725 20:46 |
| Sentinel-1A | 20180726 20:37 | ||
| Sentinel-1B | 20180727 08:22 | ||
| Shanshan | Western Pacific | Sentinel-1A | 20180808 08:23 |
| Soulik | Western Pacific | Sentinel-1B | 20180818 08:38 |
| 20180818 20:45 | |||
| Jebi | Western Pacific | Sentinel-1B | 20180829 07:55 |
| Sentinel-1A | 20180831 20:39 | ||
| Mangkhut | Western Pacific | Sentinel-1B | 20180911 20:47 |
| Sentinel-1A | 20180914 09:50 | ||
| Trami | Western Pacific | Sentinel-1A | 20180925 21:20 |
| 20180928 09:35 | |||
| Kon-Rey | Western Pacific | Sentinel-1A | 20181002 21:11 |
| Yutu | Western Pacific | Sentinel-1A | 20181025 20:31 |
| Hagibis | Western Pacific | Sentinel-1A | 20191008 20:30 |
| Halong | Western Pacific | Sentinel-1A | 20191105 19:57 |
| Sentinel-1B | 20191106 19:49 | ||
| Sentinel-1A | 20191107 19:39 | ||
| Hurricane | |||
|---|---|---|---|
| Name | Area | SAR Instrument | Acquisition Time (UTC) |
| Lester | East Pacific | Sentinel-1A | 20160826 13:39 |
| 20160830 14:45 | |||
| 20160831 03:15 | |||
| Gaston | Atlantic | Sentinel-1A | 20160826 21:16 |
| 20160827 09:21 | |||
| 20160829 21:41 | |||
| 20160830 09:45 | |||
| 20160901 20:29 | |||
| Hermine | Atlantic | Sentinel-1A | 20160904 22:32 |
| Karl | Atlantic | Sentinel-1A | 20160923 22:22 |
| Miriam | East Pacific | Sentinel-1A | 20180831 03:32 |
| Florence | Atlantic | Sentinel-1A | 20180904 08:34 |
| 20180908 09:39 | |||
| Helene | Atlantic | Sentinel-1B | 20180912 08:18 |
| Sergio | East Pacific | Sentinel-1A | 20181006 14:06 |
| 20181007 02:34 | |||
| 20181009 14:29 | |||
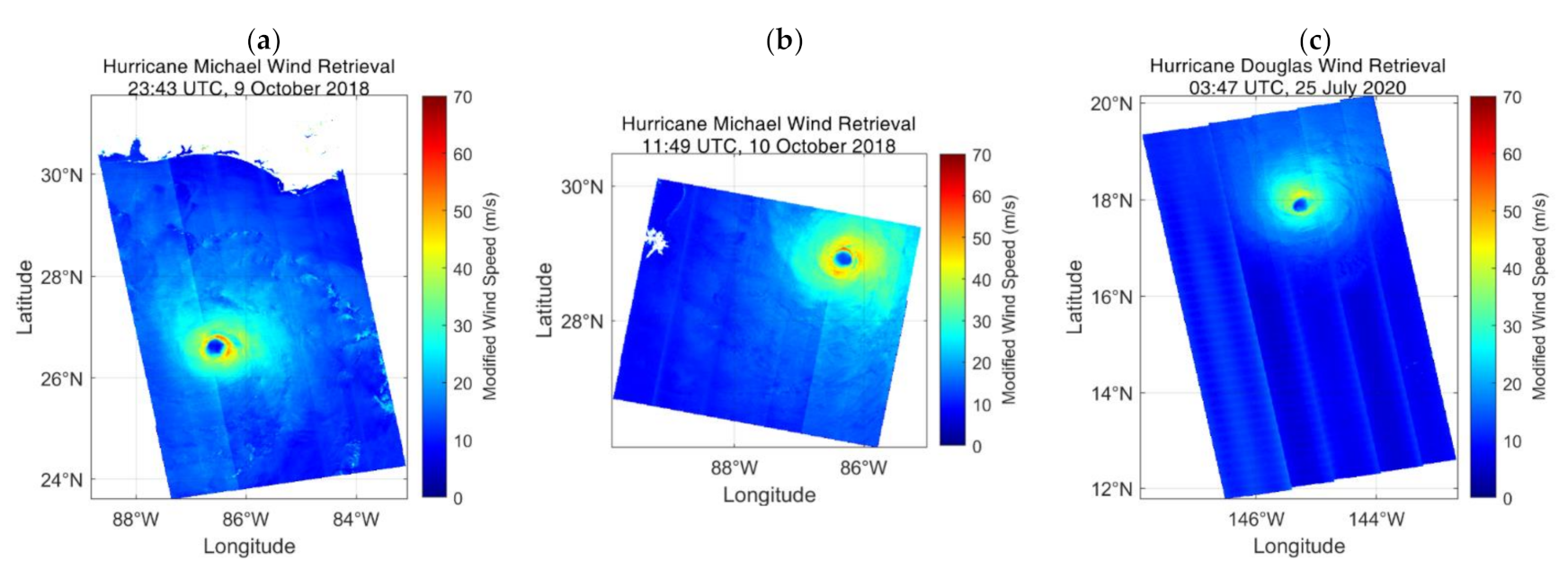
| Michael | Atlantic | Sentinel-1A | 20181009 23:43 |
| 20181010 11:49 | |||
| Leslie | Atlantic | Sentinel-1A | 20181013 07:15 |
| Juliette | East Pacific | Sentinel-1A | 20190904 13:39 |
| Douglas | East Pacific | Sentinel-1A | 20200725 03:47 |
| Teddy | Atlantic | Sentinel-1A | 20200922 10:16 |
References
- Katsaros, K.B.; Vachon, P.W.; Liu, W.T.; Black, P.G. Microwave Remote Sensing of Tropical Cyclones from Space. J. Oceanogr. 2002, 58, 137–151. [Google Scholar] [CrossRef]
- Kossin, J.P. Hurricane Wind–Pressure Relationship and Eyewall Replacement Cycles. Weather Forecast. 2015, 30, 177–181. [Google Scholar] [CrossRef]
- Guo, X.; Tan, Z.-M. Tropical cyclone fullness: A new concept for interpreting storm intensity. Geophys. Res. Lett. 2017, 44, 4324–4331. [Google Scholar] [CrossRef]
- Simpson, R.H.; Saffir, H. The hurricane disaster-potential scale. Weatherwise 1974, 27, 186. [Google Scholar]
- Knaff, J.A.; Zehr, R.M. Reexamination of Tropical Cyclone Wind–Pressure Relationships. Weather Forecast. 2006, 22, 71–88. [Google Scholar] [CrossRef]
- Xie, L.; Bao, S.; Pietrafesa, L.J.; Foley, K.; Fuentes, M. A Real-Time Hurricane Surface Wind Forecasting Model: Formulation and Verification. Mon. Weather Rev. 2006, 134, 1355–1370. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Holland, G.J.; Belanger, J.I.; Fritz, A. A Revised Model for Radial Profiles of Hurricane Winds. Mon. Weather Rev. 2010, 138, 4393–4401. [Google Scholar] [CrossRef]
- Merrill, R.T. A Comparison of Large and Small Tropical Cyclones. Mon. Weather Rev. 1984, 112, 1408–1418. [Google Scholar] [CrossRef]
- Hill, K.A.; Lackmann, G.M. Influence of Environmental Humidity on Tropical Cyclone Size. Mon. Weather Rev. 2009, 137, 3294–3315. [Google Scholar] [CrossRef]
- Chan, K.T.F.; Chan, J.C.L. Size and Strength of Tropical Cyclones as Inferred from QuikSCAT Data. Mon. Weather Rev. 2012, 140, 811–824. [Google Scholar] [CrossRef]
- Yu, P.; Johannessen, J.A.; Yan, X.-H.; Geng, X.; Zhong, X.; Zhu, L. A Study of the Intensity of Tropical Cyclone Idai Using Dual-Polarization Sentinel-1 Data. Remote Sens. 2019, 11, 2837. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Yang, X.; Pichel, W.G.; DeMaria, M.; Long, D.; Li, Z. Tropical Cyclone Morphology from Spaceborne Synthetic Aperture Radar. Bull. Am. Meteorol. Soc. 2013, 94, 215–230. [Google Scholar] [CrossRef]
- Klotz, B.W.; Jiang, H. Global composites of surface wind speeds in tropical cyclones based on a 12 year scatterometer database. Geophys. Res. Lett. 2016, 43, 480–488. [Google Scholar] [CrossRef]
- Shao, W.; Yuan, X.; Sheng, Y.; Sun, J.; Zhou, W.; Zhang, Q. Development of Wind Speed Retrieval from Cross-Polarization Chinese Gaofen-3 Synthetic Aperture Radar in Typhoons. Sensors 2018, 18, 412. [Google Scholar] [CrossRef]
- Horstmann, J.; Falchetti, S.; Wackerman, C.; Maresca, S.; Caruso, M.J.; Graber, H.C. Tropical Cyclone Winds Retrieved From C-Band Cross-Polarized Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2887–2898. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, C.; Sun, J.; Xie, L. Tropical Cyclone Wind Speed Retrieval from Dual-Polarization Sentinel-1 EW Mode Products. J. Atmos. Ocean. Technol. 2020, 37, 1713–1724. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Hwang, P.; Zhang, B.; Yang, X. Bridging the gap between cyclone wind and wave by C -band SAR measurements. J. Geophys. Res. Oceans 2017, 122, 6714–6724. [Google Scholar] [CrossRef]
- Hwang, P.A.; Zhang, B.; Perrie, W. Depolarized radar return for breaking wave measurement and hurricane wind retrieval. Geophys. Res. Lett. 2010, 37, 70–75. [Google Scholar] [CrossRef]
- Phillips, O.M. Radar Returns from the Sea Surface—Bragg Scattering and Breaking Waves. J. Phys. Oceanogr. 1988, 18, 1065–1074. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-Polarized Synthetic Aperture Radar: A New Potential Measurement Technique for Hurricanes. Bull. Am. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef]
- Zhang, G.; Perrie, W.; Zhang, B.; Yang, J.; He, Y. Monitoring of tropical cyclone structures in ten years of RADARSAT-2 SAR images. Remote Sens. Environ. 2020, 236, 111449. [Google Scholar] [CrossRef]
- Gao, Y.; Guan, C.; Sun, J.; Xie, L. A Wind Speed Retrieval Model for Sentinel-1A EW Mode Cross-Polarization Images. Remote Sens. 2019, 11, 153. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A Hurricane Wind Speed Retrieval Model for C-Band RADARSAT-2 Cross-Polarization ScanSAR Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Hwang, P.A.; Stoffelen, A.; van Zadelhoff, G.-J.; Perrie, W.; Zhang, B.; Li, H.; Shen, H. Cross-polarization geophysical model function for C-band radar backscattering from the ocean surface and wind speed retrieval. J. Geophys. Res. Oceans 2015, 120, 893–909. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined Co- and Cross-Polarized SAR Measurements Under Extreme Wind Conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F.J. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteorol. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
- Combot, C.; Mouche, A.; Knaff, J.; Zhao, Y.; Zhao, Y.; Vinour, L.; Quilfen, Y.; Chapron, B. Extensive High-Resolution Synthetic Aperture Radar (SAR) Data Analysis of Tropical Cyclones: Comparisons with SFMR Flights and Best Track. Mon. Weather Rev. 2020, 148, 4545–4563. [Google Scholar] [CrossRef]
- Uhlhorn, E.W.; Black, P.G.; Franklin, J.L.; Goodberlet, M.; Carswell, J.; Goldstein, A.S. Hurricane Surface Wind Measurements from an Operational Stepped Frequency Microwave Radiometer. Mon. Weather Rev. 2007, 135, 3070–3085. [Google Scholar] [CrossRef]
- Klotz, B.W.; Uhlhorn, E.W. Improved Stepped Frequency Microwave Radiometer Tropical Cyclone Surface Winds in Heavy Precipitation. J. Atmos. Ocean. Technol. 2014, 31, 2392–2408. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, J.; Zhang, J.; Guan, C. Extreme Wind Speeds Retrieval Using Sentinel-1 IW Mode SAR Data. Remote Sens. 2021, 13, 1867. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Knaff, J.; Zhao, Y.; Zhang, B.; Combot, C. Copolarized and Cross-Polarized SAR Measurements for High-Resolution Description of Major Hurricane Wind Structures: Application to Irma Category 5 Hurricane. J. Geophys. Res. Oceans 2019, 124, 3905–3922. [Google Scholar] [CrossRef]
- Alpers, W.; Zhang, B.; Mouche, A.; Zeng, K.; Chan, P.W. Rain footprints on C-band synthetic aperture radar images of the ocean—Revisited. Remote Sens. Environ. 2016, 187, 169–185. [Google Scholar] [CrossRef]
- Katsaros, K.; Vachon, P.W.; Black, P.; Dodge, P.; Uhlhorn, E. Wind Fields from SAR: Could They Improve Our Understanding of Storm Dynamics? Johns Hopkins APL Tech. Dig. 2000, 21, 86–93. [Google Scholar] [CrossRef][Green Version]
- Reppucci, A.; Lehner, S.; Schulz-Stellenfleth, J.; Brusch, S. Tropical Cyclone Intensity Estimated From Wide-Swath SAR Images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1639–1649. [Google Scholar] [CrossRef]
- Xu, F.; Li, X.; Wang, P.; Yang, J.; Pichel, W.G.; Jin, Y.-Q. A Backscattering Model of Rainfall Over Rough Sea Surface for Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3042–3054. [Google Scholar] [CrossRef]
- Velden, C.; Harper, B.; Wells, F.; Beven, J.L.; Zehr, R.; Olander, T.; Mayfield, M.; Guard, C.; Lander, M.; Edson, R.; et al. Supplement To: The Dvorak Tropical Cyclone Intensity Estimation Technique: A Satellite-Based Method that Has Endured for over 30 Years. Bull. Am. Meteorol. Soc. 2006, 87, S6–S9. [Google Scholar] [CrossRef]
- Rappaport, E.N.; Jiing, J.-G.; Landsea, C.W.; Murillo, S.T.; Franklin, J.L. The Joint Hurricane Test Bed: Its First Decade of Tropical Cyclone Research-To-Operations Activities Reviewed. Bull. Am. Meteorol. Soc. 2012, 93, 371–380. [Google Scholar] [CrossRef]
- Carrasco, C.A.; Landsea, C.W.; Lin, Y.-L. The Influence of Tropical Cyclone Size on Its Intensification. Weather Forecast. 2014, 29, 582–590. [Google Scholar] [CrossRef]
- Leroux, M.-D.; Meister, J.; Mekies, D.; Dorla, A.-L.; Caroff, P. A Climatology of Southwest Indian Ocean Tropical Systems: Their Number, Tracks, Impacts, Sizes, Empirical Maximum Potential Intensity, and Intensity Changes. J. Appl. Meteorol. Clim. 2018, 57, 1021–1041. [Google Scholar] [CrossRef]
- Knaff, J.A.; Sampson, C.R.; DeMaria, M.; Marchok, T.P.; Gross, J.M.; McAdie, C.J. Statistical Tropical Cyclone Wind Radii Prediction Using Climatology and Persistence. Weather Forecast. 2005, 22, 781–791. [Google Scholar] [CrossRef]
- Rappin, E.D.; Nolan, D.S.; Majumdar, S.J. A Highly Configurable Vortex Initialization Method for Tropical Cyclones. Mon. Weather Rev. 2013, 141, 3556–3575. [Google Scholar] [CrossRef]
- Mallen, K.J.; Montgomery, M.T.; Wang, B. Reexamining the Near-Core Radial Structure of the Tropical Cyclone Primary Circulation: Implications for Vortex Resiliency. J. Atmos. Sci. 2005, 62, 408–425. [Google Scholar] [CrossRef]
- Sapp, J.W.; Alsweiss, S.O.; Jelenak, Z.; Chang, P.S.; Carswell, J. Stepped Frequency Microwave Radiometer Wind-Speed Retrieval Improvements. Remote Sens. 2019, 11, 214. [Google Scholar] [CrossRef]

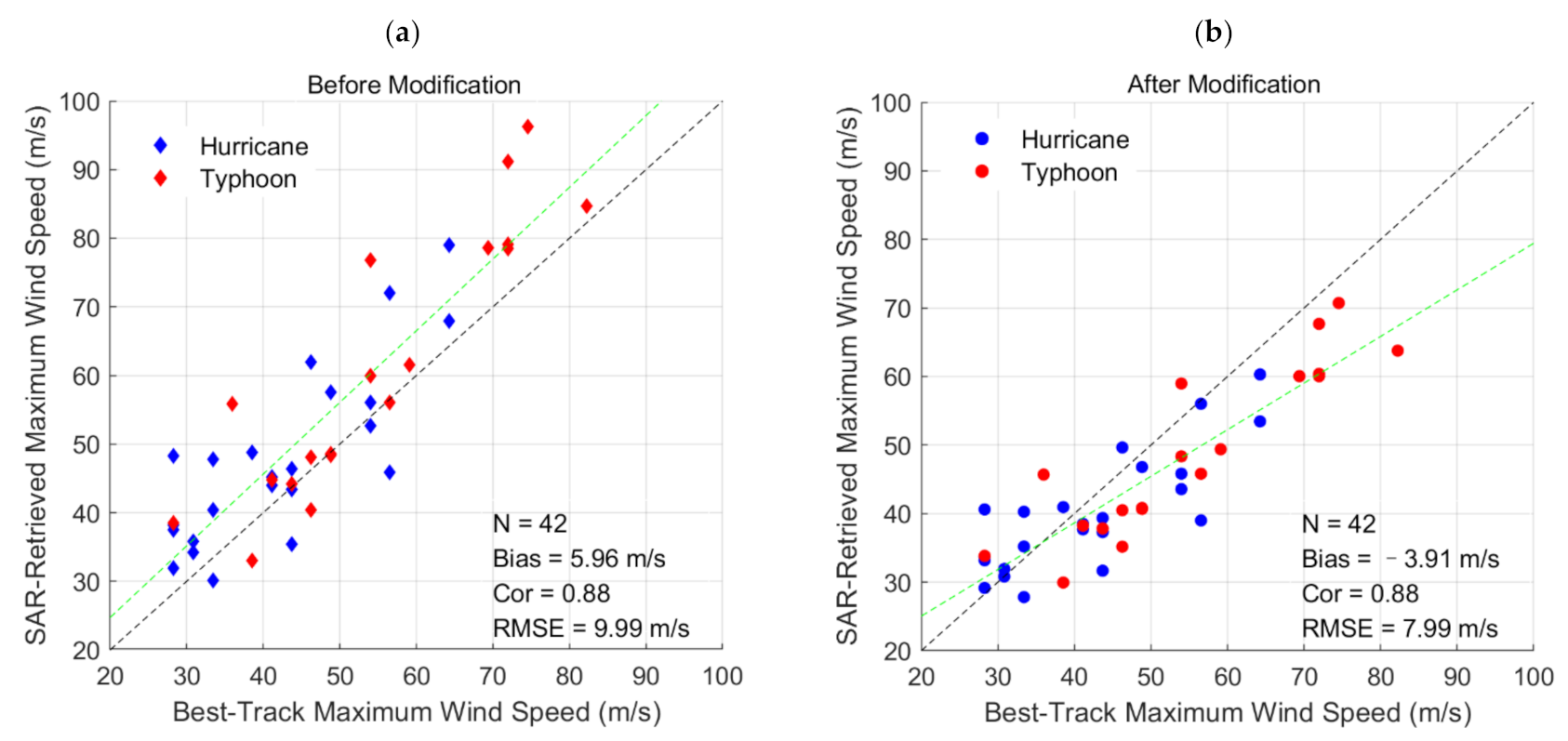
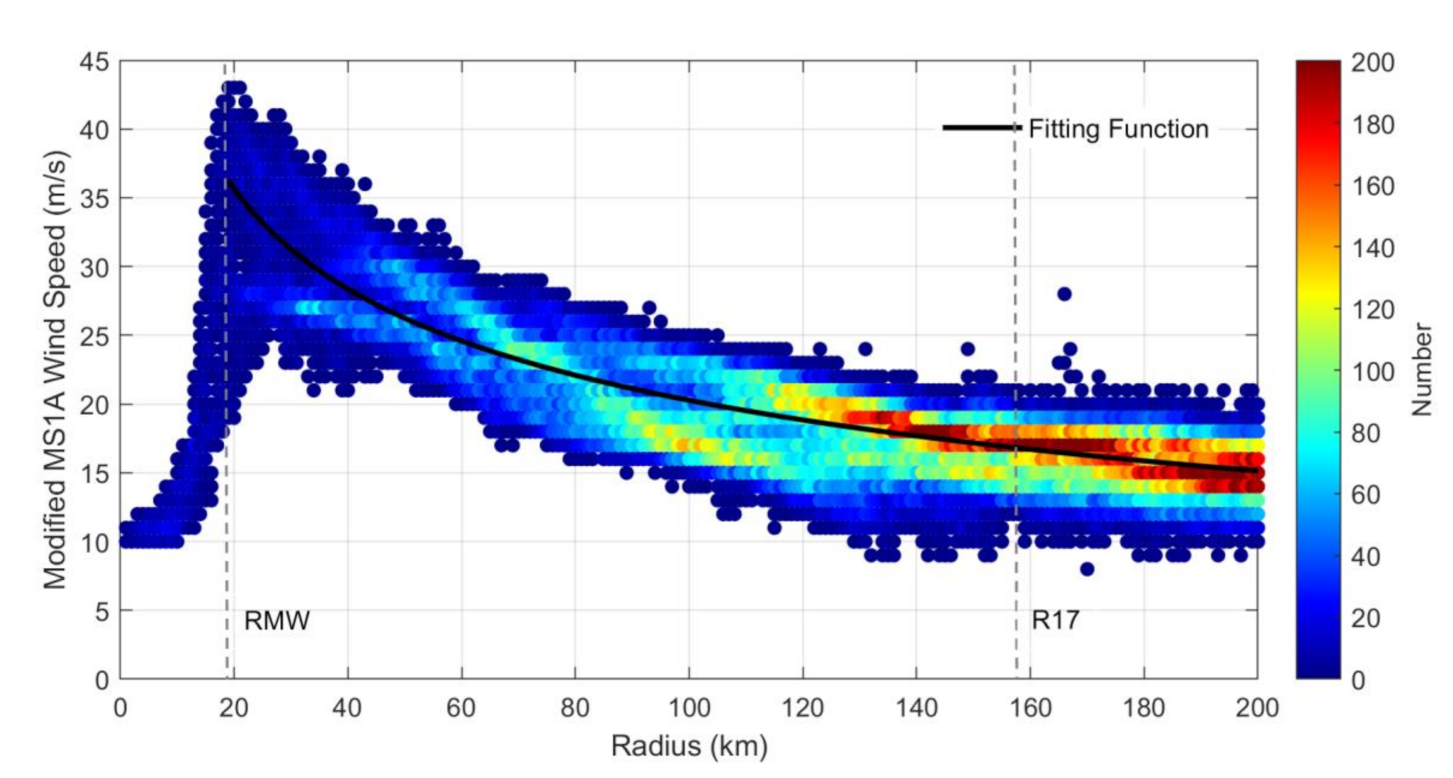
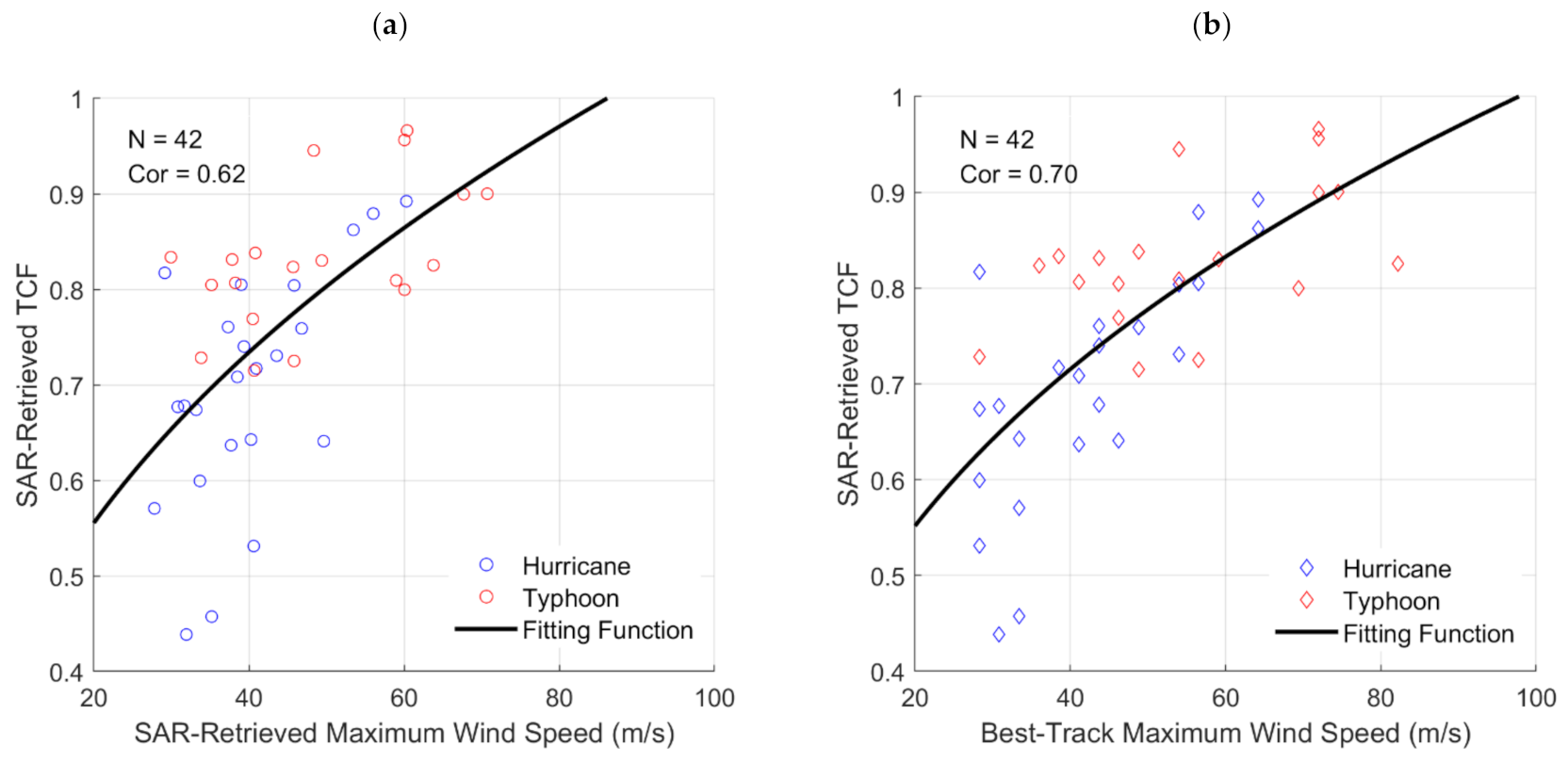
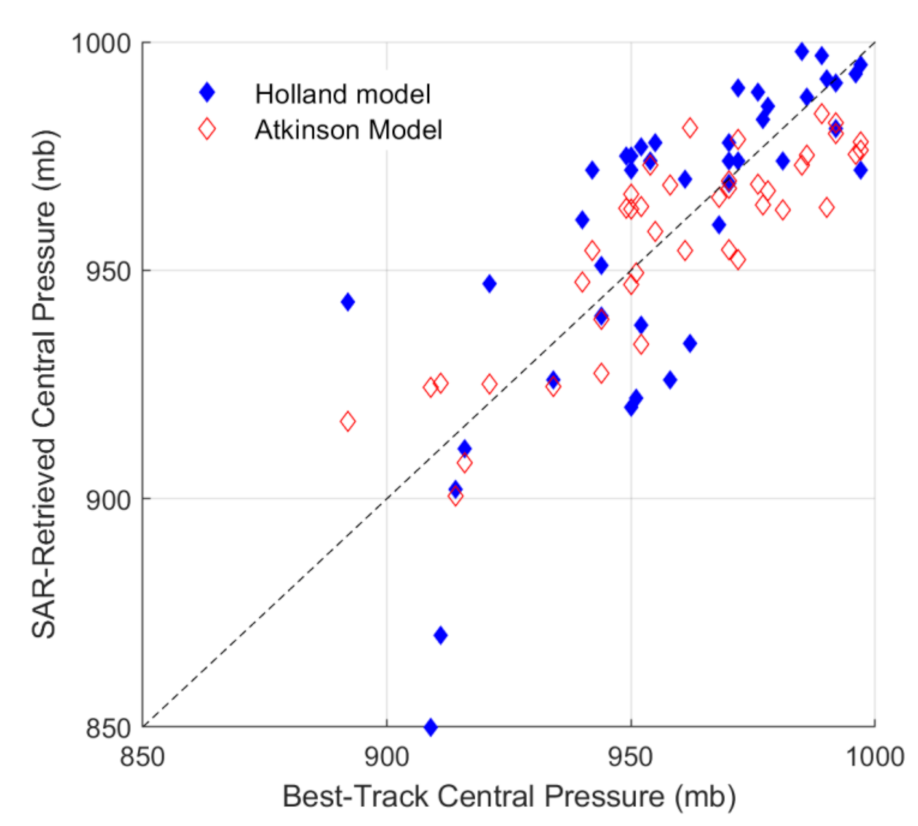

| TC Name | Area | Category | SAR Instrument | Acquisition Time (UTC) | Wind Reference | Collocations |
|---|---|---|---|---|---|---|
| Michael | Atlantic | 3 | Sentinel-1A | 20181009 23:43 | AFRC 1 SFMR NOAA SFMR | 2789 |
| Atlantic | 4 | Sentinel-1A | 20181010 11:49 | AFRC SFMR NOAA SFMR | 2588 | |
| Douglas | East Pacific | 2 | Sentinel-1A | 20200725 03:47 | AFRC SFMR | 109 |
| Wind Range (m/s) | Collocation Number | Averaged Bias (m/s) | Cor | RMSE (m/s) |
|---|---|---|---|---|
| 0–20 | 2702 | −0.51 | 0.69 | 2.51 |
| 20–40 | 2332 | 2.88 | 0.88 | 5.35 |
| >40 | 452 | 6.00 | 0.59 | 9.02 |
| All Data | 5486 | 1.46 | 0.96 | 4.68 |
| Model | Bias (mb) | Cor | RMSE (mb) |
|---|---|---|---|
| Holland Model | 1.17 | 0.77 | 21.29 |
| Atkinson Model | −2.64 | 0.86 | 13.54 |
| Model | Averaged Bias (m/s) | Averaged Absolute Bias (m/s) | Averaged RMSE (m/s) |
|---|---|---|---|
| Our Model | 0.27 | 3.78 | 5.52 |
| Pure Rankine Vortex Model | −6.25 | 7.31 | 8.72 |
| Modified Rankine Vortex Model | 6.47 | 6.65 | 7.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Zhang, J.; Sun, J.; Guan, C. Application of SAR Data for Tropical Cyclone Intensity Parameters Retrieval and Symmetric Wind Field Model Development. Remote Sens. 2021, 13, 2902. https://doi.org/10.3390/rs13152902
Gao Y, Zhang J, Sun J, Guan C. Application of SAR Data for Tropical Cyclone Intensity Parameters Retrieval and Symmetric Wind Field Model Development. Remote Sensing. 2021; 13(15):2902. https://doi.org/10.3390/rs13152902
Chicago/Turabian StyleGao, Yuan, Jie Zhang, Jian Sun, and Changlong Guan. 2021. "Application of SAR Data for Tropical Cyclone Intensity Parameters Retrieval and Symmetric Wind Field Model Development" Remote Sensing 13, no. 15: 2902. https://doi.org/10.3390/rs13152902
APA StyleGao, Y., Zhang, J., Sun, J., & Guan, C. (2021). Application of SAR Data for Tropical Cyclone Intensity Parameters Retrieval and Symmetric Wind Field Model Development. Remote Sensing, 13(15), 2902. https://doi.org/10.3390/rs13152902