Improving CyGNSS-Based Land Remote Sensing: Track-Wise Data Calibration Schemes
Abstract
:1. Introduction
2. Datasets
2.1. CyGNSS Data
2.2. SMAP SM Product
3. Method and Model
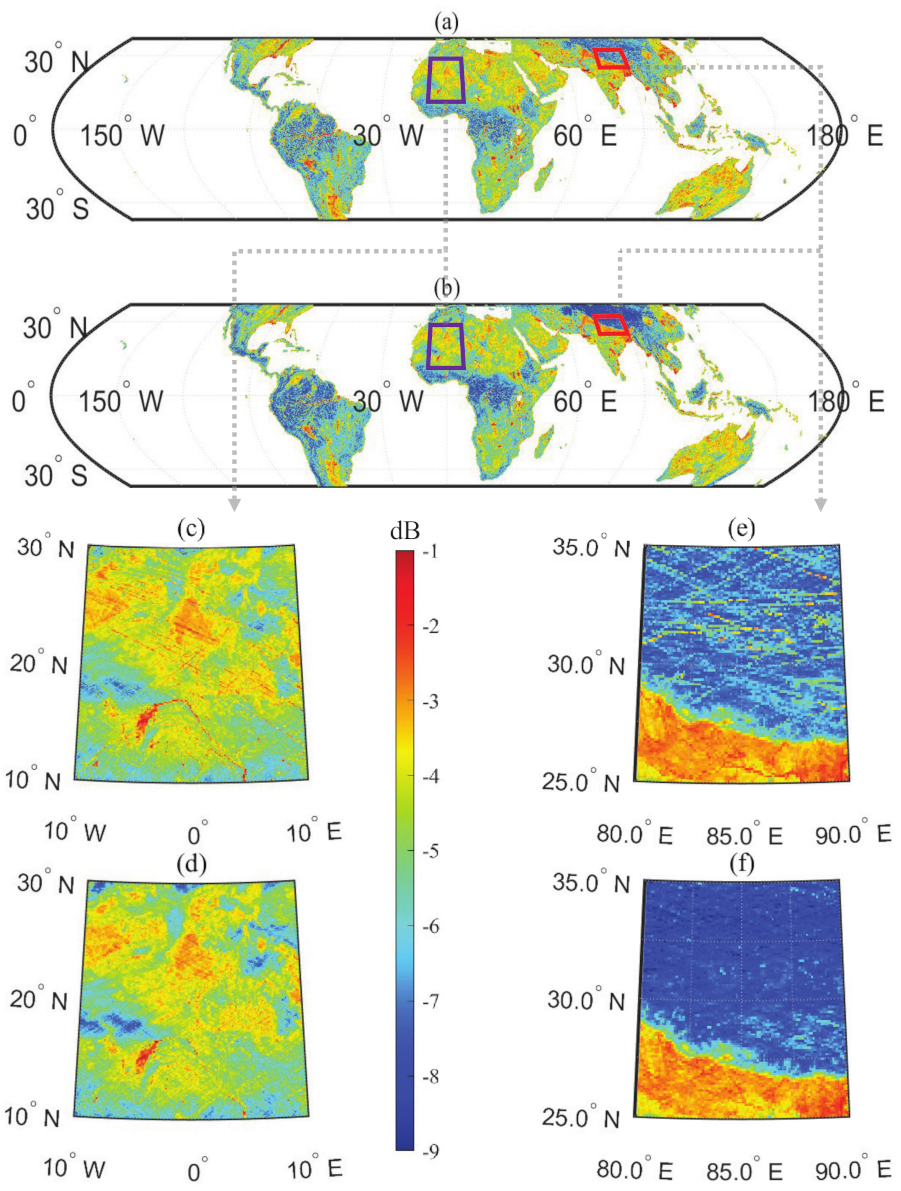
3.1. Derivation of CyGNSS
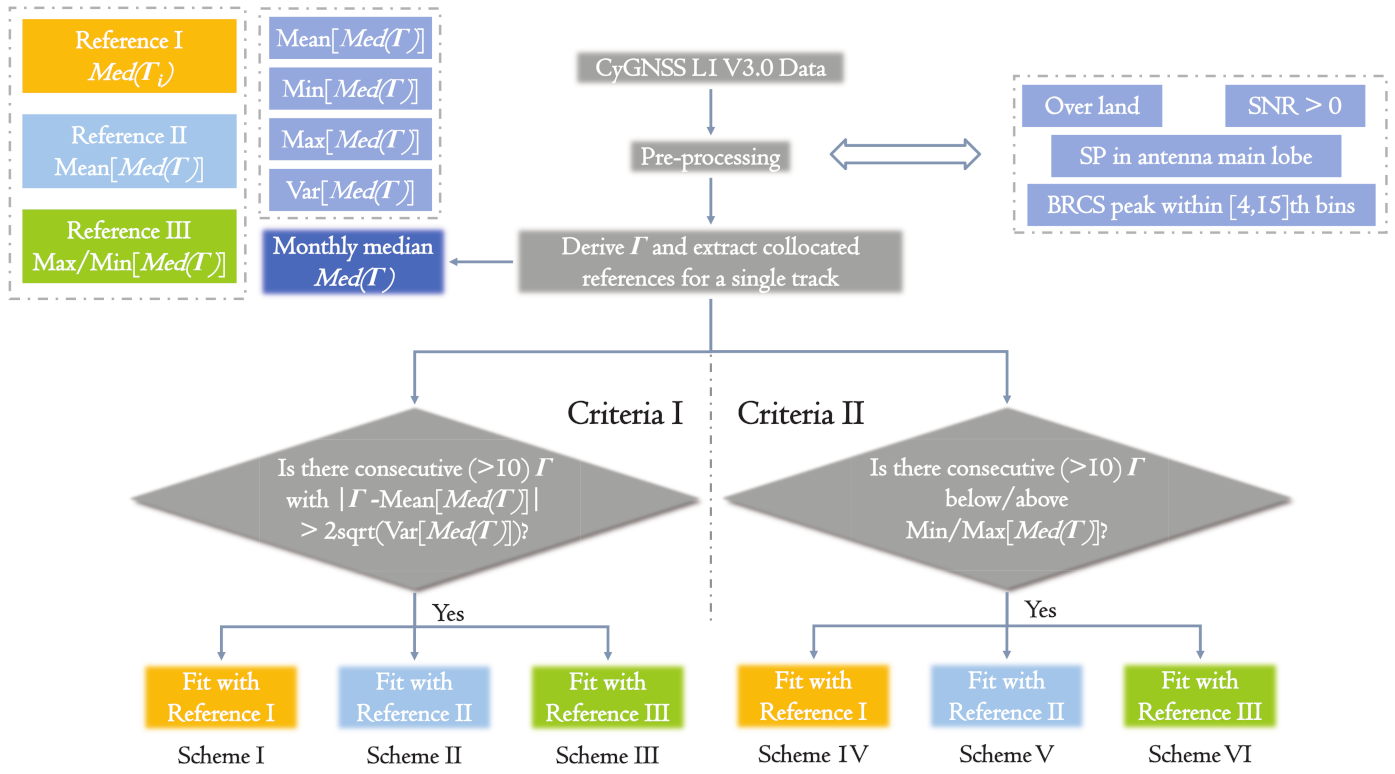
3.2. Track-Wise Calibration Schemes
3.3. SM Retrieval Model
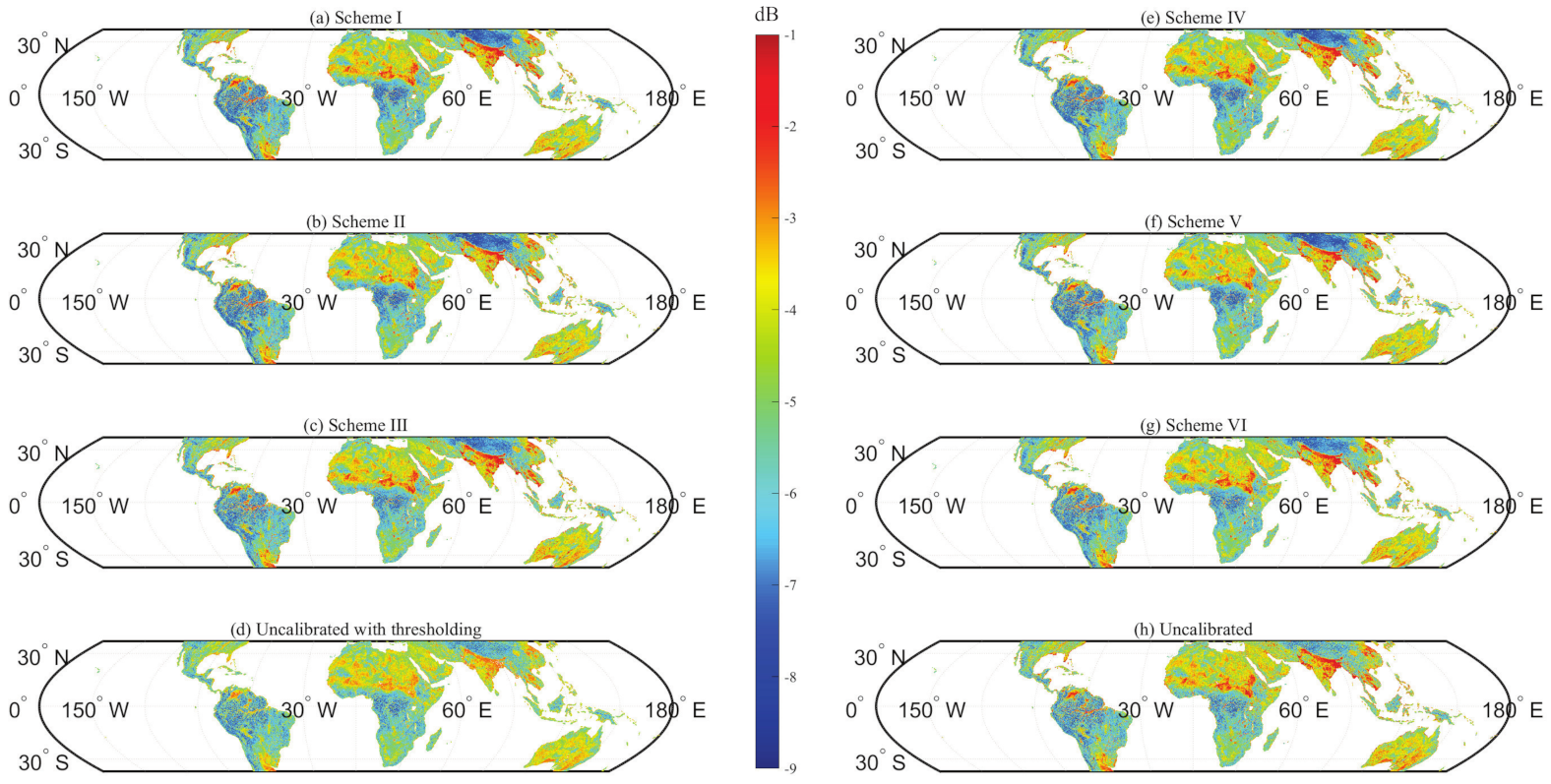
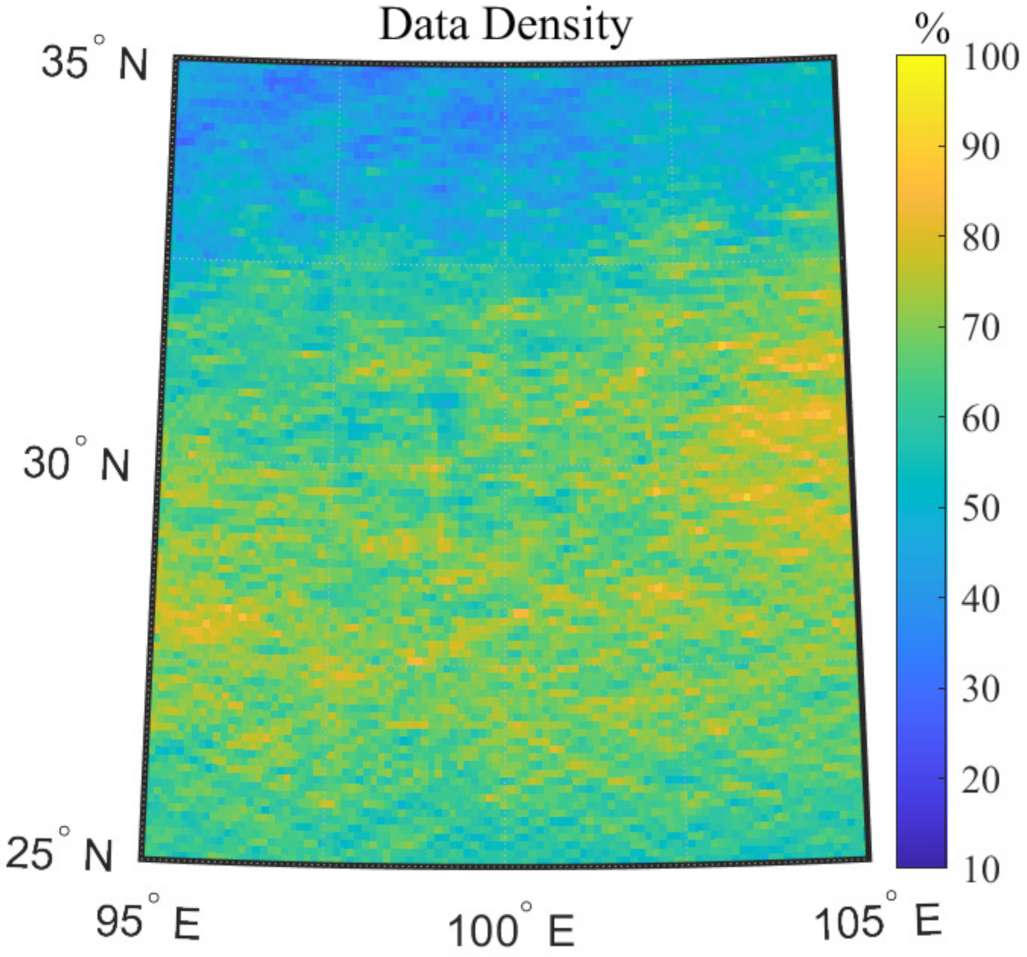
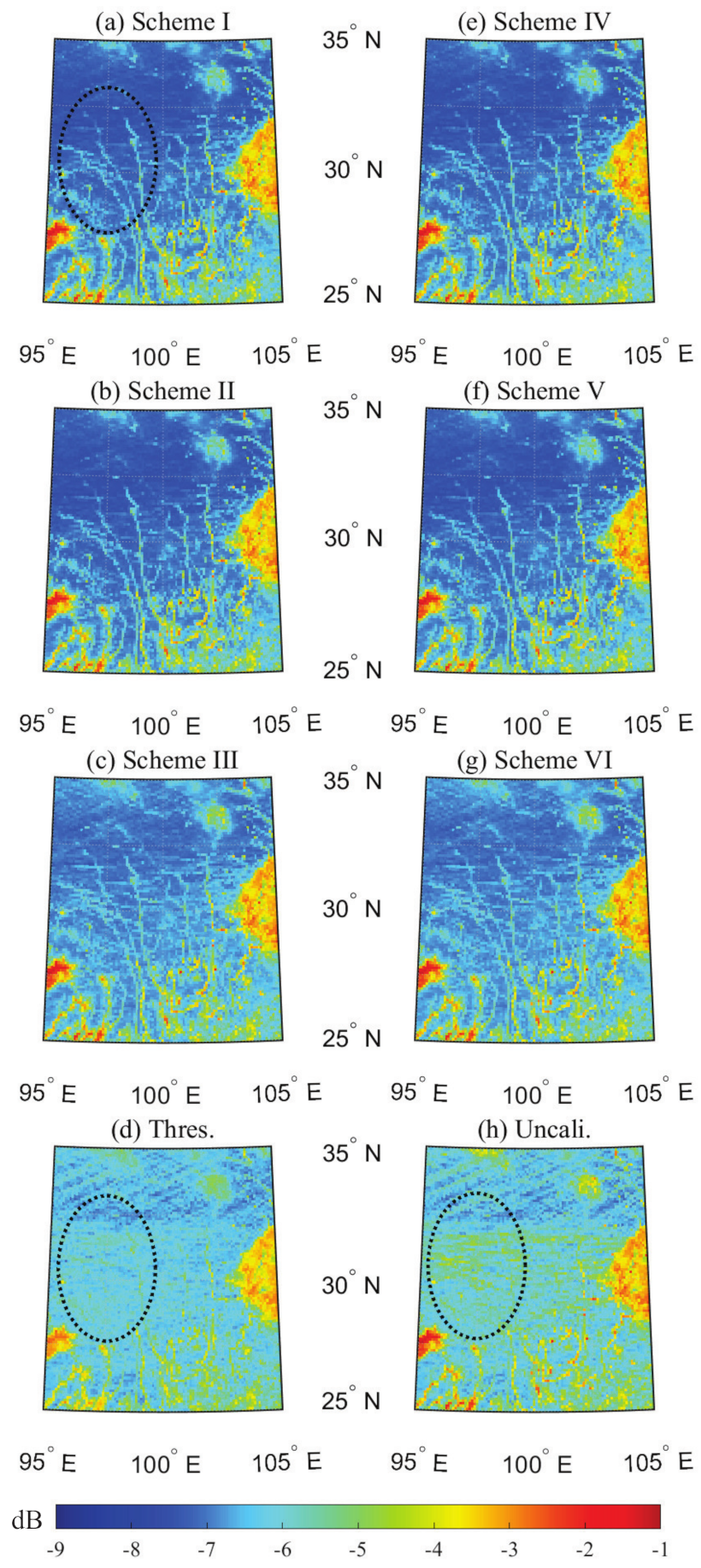
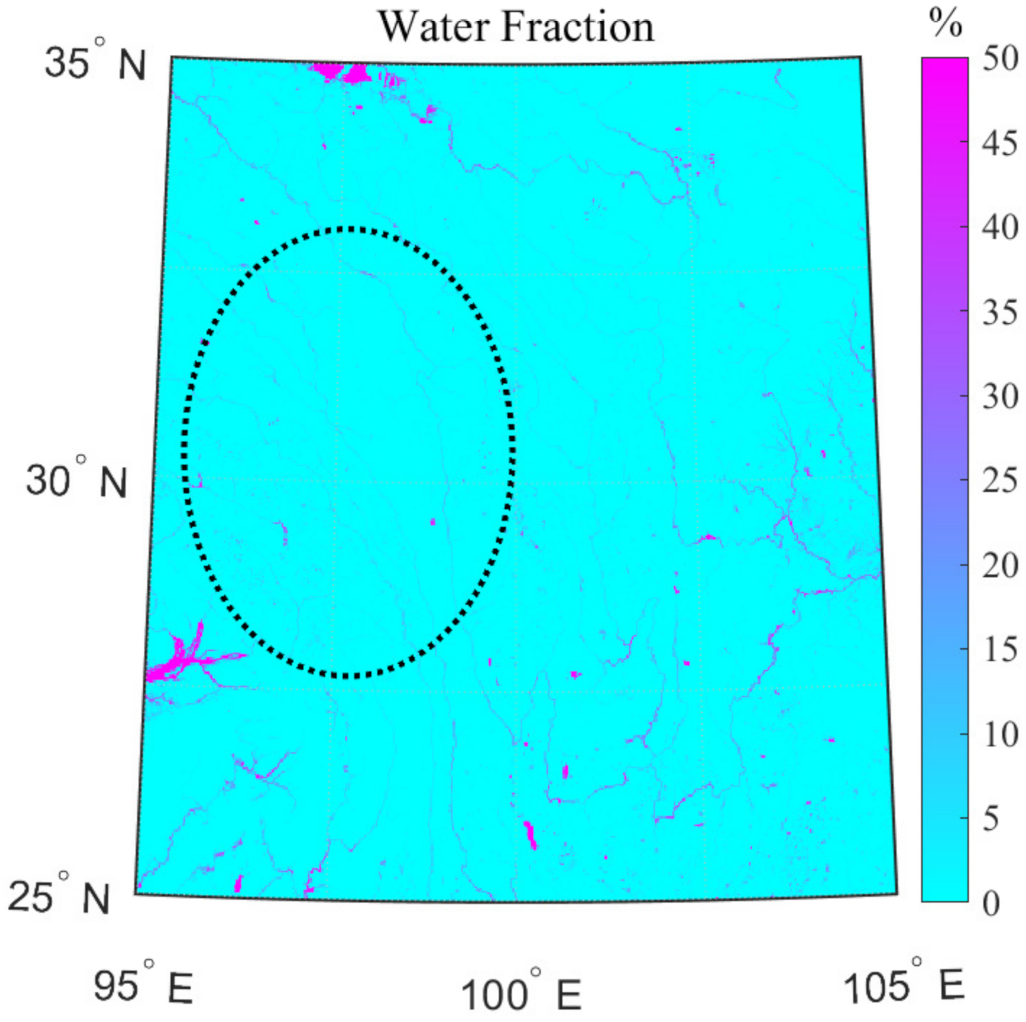
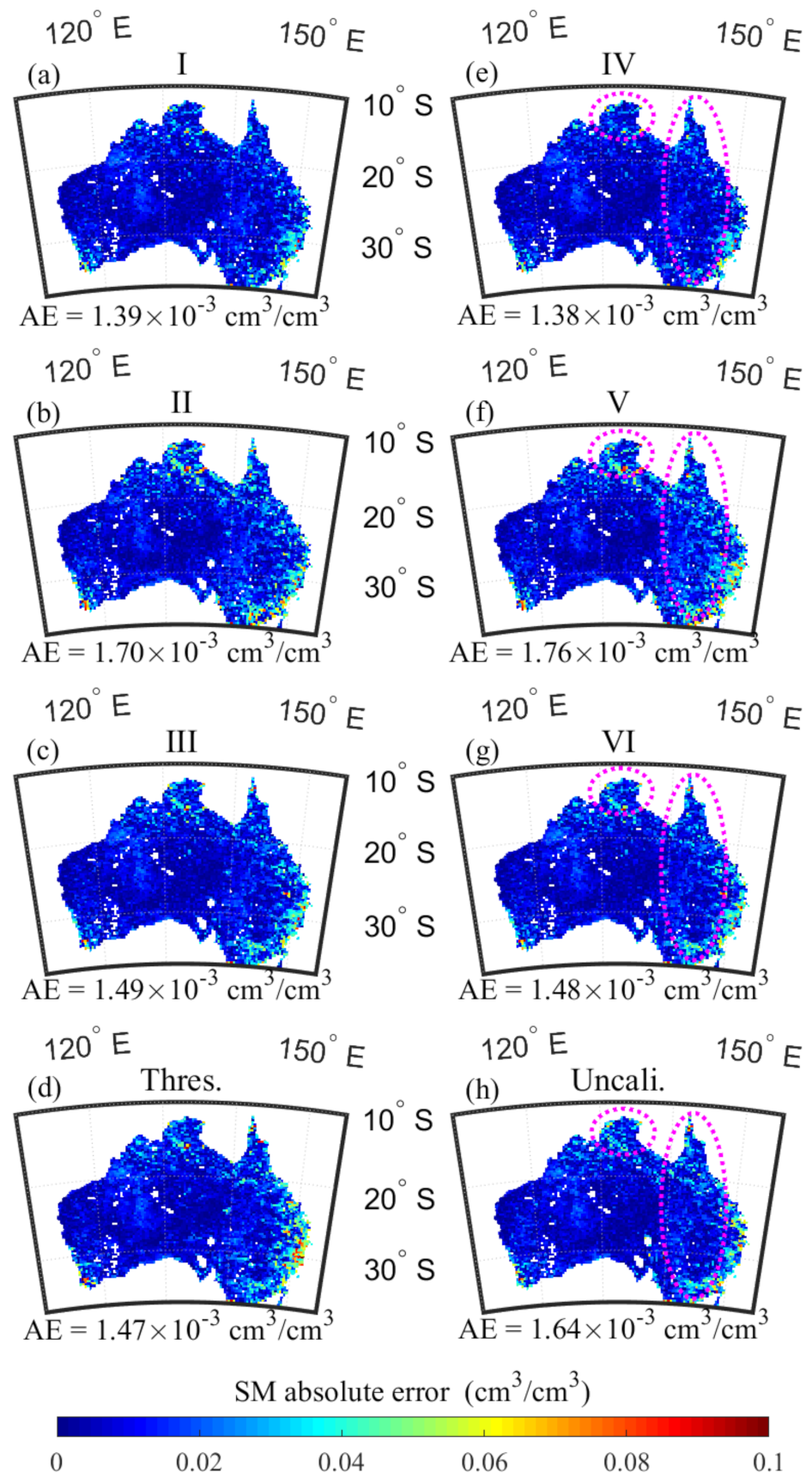
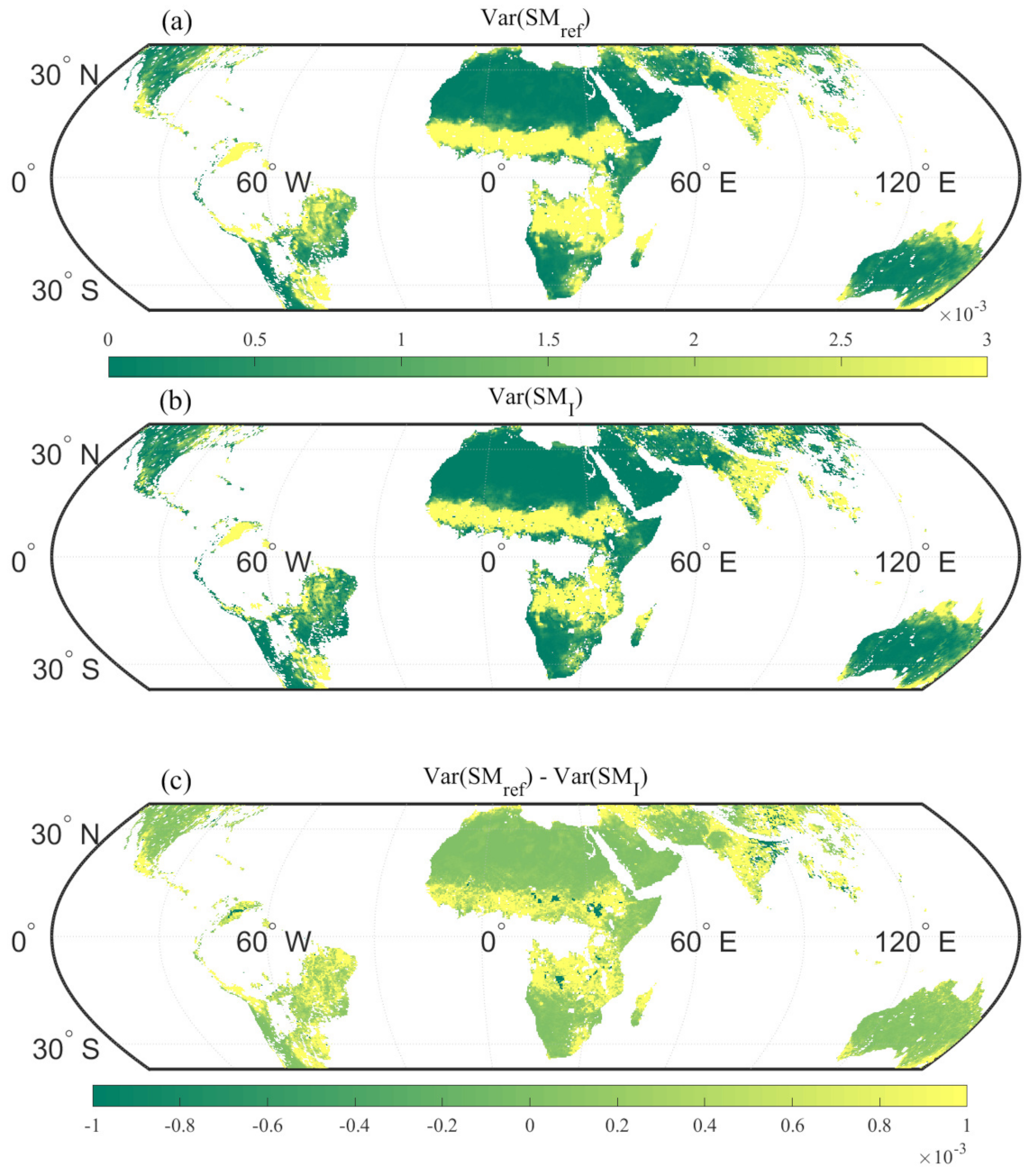
4. Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CyGNSS | Cyclone Global Navigation Satellite System |
| EIRP | Effective Instantaneous Radiative Power |
| GNSS | Global Navigation Satellite System |
| GNSS-R | Global Navigation Satellite System-Reflectometry |
| SM | Soil Moisture |
| BRCS | Bistatic Radar Cross Section |
| GPS | Global Positioning System |
| SP | Specular Point |
| NBRCS | Normalized Bistatic Radar Cross Section |
| LES | Leading-Edge Slope |
| SNR | Signal-to-Noise Ratio |
| SMAP | Soil Moisture Active Passive |
| EASE-Grid | Equal-Area Scalable Eartd Grid |
| PRN | Pseudo-Random Number |
| PSNR | Peak Signal-to-Noise Ratio |
| RMSE | Root Mean Square Error |
| AE | Absolute Errors |
References
- Jin, S.; Komjathy, A. GNSS reflectometry and remote sensing: New objectives and results. Adv. Space Res. 2010, 46, 111–117. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Roselló, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.P.; Ruf, C.S.; Jales, P.; Gommenginger, C. Spaceborne GNSS-R minimum variance wind speed estimator. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6829–6843. [Google Scholar] [CrossRef]
- Liu, Y.; Collett, I.; Morton, Y.J. Application of neural network to GNSS-R wind speed retrieval. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9756–9766. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Foti, G. Quantification of the relationship between sea surface roughness and the size of the glistening zone for GNSS-R. IEEE Geosci. Remote Sens. Lett. 2018, 15, 237–241. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martin-Neira, M.; Fabra, F.; Nogues-Correig, O.; Ribo, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the precision of interferometric GNSS-R ocean altimetry using airborne experimental data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Li, W.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Assessment of spaceborne GNSS-R ocean altimetry performance using CYGNSS mission raw data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 238–250. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea Ice Remote Sensing Using GNSS-R: A Review. Remote Sens. 2019, 11, 2565. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Alvarez, N.; Holt, B.; Jaruwatanadilok, S.; Podest, E.; Cavanaugh, K.C. An Arctic sea ice multi-step classification based on GNSS-R data from the TDS-1 mission. Remote Sens. Environ. 2019, 230, 111202. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Sea ice thickness measurement using spaceborne GNSS-R: First results with TechDemoSat-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 577–587. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W. Tsunami Detection and Parameter Estimation From GNSS-R Delay-Doppler Map. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4650–4659. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Podest, E.; Jensen, K.; McDonald, K.C. Classifying inundation in a tropical wetlands complex with GNSS-R. Remote Sens. 2019, 11, 1053. [Google Scholar] [CrossRef] [Green Version]
- Gerlein-Safdi, C.; Ruf, C.S. A CYGNSS-based algorithm for the detection of inland waterbodies. Geophys. Res. Lett. 2019, 46, 12065–12072. [Google Scholar] [CrossRef]
- Ghasemigoudarzi, P.; Huang, W.; De Silva, O.; Yan, Q.; Power, D. A machine learning method for inland water detection using CYGNSS data. IEEE Geosci. Remote Sens. Lett. 2021, in press. [Google Scholar] [CrossRef]
- Ghasemigoudarzi, P.; Huang, W.; De Silva, O.; Yan, Q.; Power, D.T. Flash flood detection from CYGNSS data using the RUSBoost algorithm. IEEE Access 2020, 8, 171864–171881. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil moisture sensing using spaceborne GNSS reflections: Comparison of CYGNSS reflectivity to SMAP soil moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High spatio-temporal resolution CYGNSS soil moisture estimates using artificial neural networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.; Jin, S.; Chen, H.; Yan, Q.; Savi, P.; Jin, Y.; Yuan, Y. Temporal-spatial soil moisture estimation from CYGNSS using machine learning regression with a pre-classification approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4879–4893. [Google Scholar] [CrossRef]
- Yan, Q.; Gong, S.; Jin, S.; Huang, W.; Zhang, C. Near real-time soil moisture in China retrieved from CyGNSS reflectivity. IEEE Geosci. Remote Sens. Lett. 2021, in press. [Google Scholar] [CrossRef]
- Gleason, S.; O’Brien, A.; Russel, A.; Al-Khaldi, M.M.; Johnson, J.T. Geolocation, calibration and surface resolution of CYGNSS GNSS-R land observations. Remote Sens. 2020, 12, 1317. [Google Scholar] [CrossRef] [Green Version]
- Dong, Z.; Jin, S. Evaluation of the land GNSS-Reflected DDM coherence on soil moisture estimation from CYGNSS data. Remote Sens. 2021, 13, 570. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-series retrieval of soil moisture using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Wang, T.; Ruf, C.S.; Gleason, S.; O’Brien, A.J.; McKague, D.S.; Block, B.P.; Russel, A. Dynamic calibration of GPS effective isotropic radiated power for GNSS-Reflectometry earth remote sensing. IEEE Trans. Geosci. Remote Sens. 2021, 1–12. [Google Scholar] [CrossRef]
- Said, F.; Jelenak, Z.; Park, J.; Soisuvarn, S.; Chang, P.S. A ‘track-wise’ wind retrieval algorithm for the CYGNSS mission. In Proceedings of the IGARSS 2019–2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8711–8714. [Google Scholar] [CrossRef]
- Ruf, C.; Twigg, D. Level 1 and 2 Trackwise Corrected Climate Data Record Algorithm Theoretical Basis Document. 2020. Available online: https://clasp-research.engin.umich.edu/missions/cygnss/reference/148-0389 (accessed on 20 May 2021).
- Cardellach, E.; Nan, Y.; Li, W.; Padullés, R.; Ribó, S.; Rius, A. Variational retrievals of high winds using uncalibrated cygnss observables. Remote Sens. 2020, 12, 3930. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111947. [Google Scholar] [CrossRef]
- Chew, C.; Small, E. Description of the UCAR/CU soil moisture product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
- O’Neill, P.; Chan, S.; Njoku, E.; Jackson, T. Smap l3 Radiometer Global Daily 36 km Ease-Grid Soil Moisture, Version 7; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2016. [Google Scholar]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]

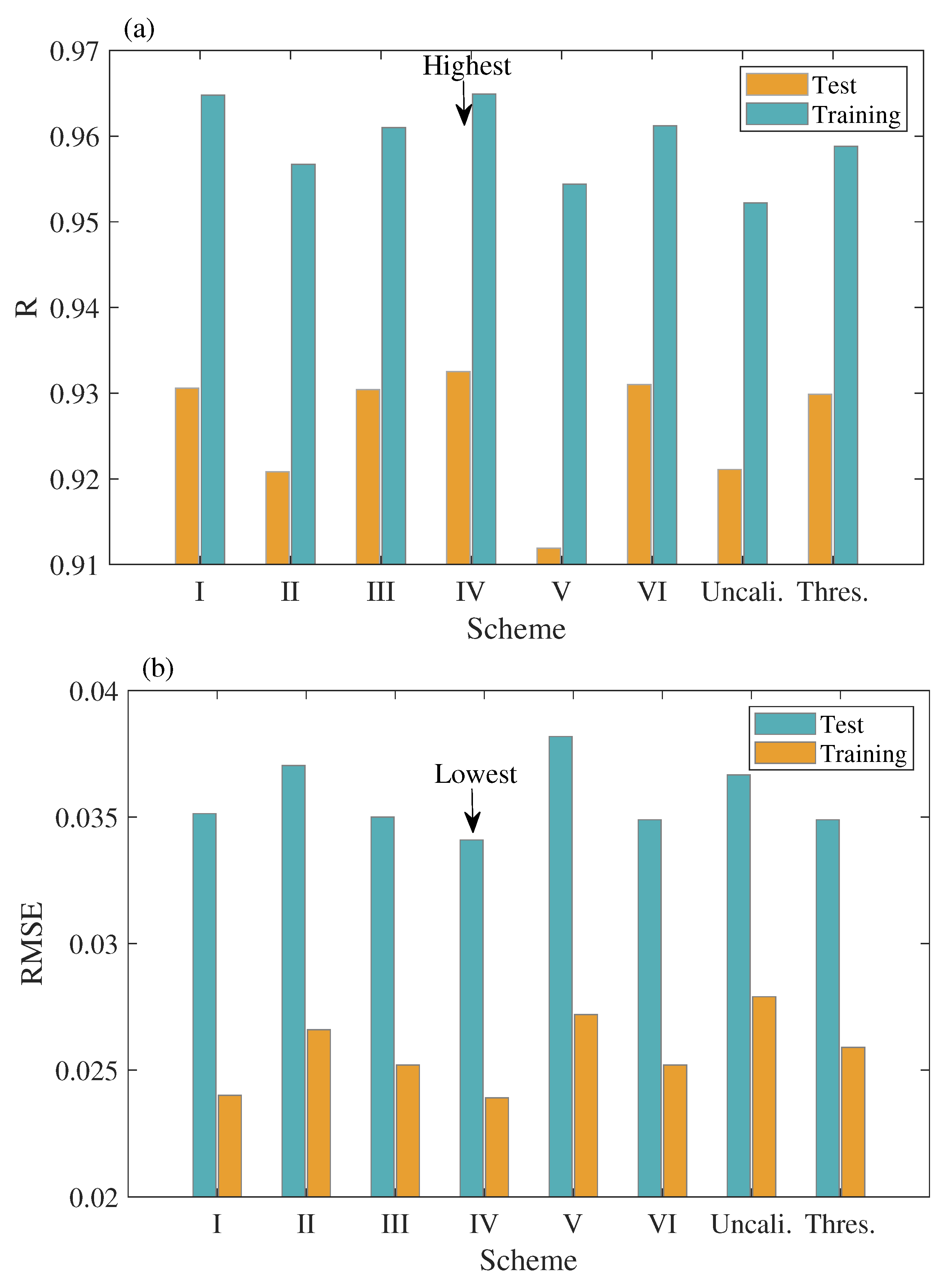
| Scheme | I | II | III | IV | V | VI | Uncali. | Thres. | |
|---|---|---|---|---|---|---|---|---|---|
| Year | |||||||||
| 2021 | 27.18 | 27.10 | 26.04 | 26.89 | 26.61 | 26.03 | 23.50 | 25.43 | |
| 2020 | 26.92 | 26.80 | 25.88 | 26.87 | 26.58 | 25.88 | 23.51 | 25.24 | |
| 2019 | 27.32 | 27.22 | 26.39 | 26.61 | 25.96 | 26.41 | 24.13 | 25.68 | |
| 2018 | 27.77 | 27.75 | 27.13 | 26.77 | 26.25 | 27.12 | 25.35 | 26.41 | |
| I | II | III | IV | V | VI | Uncali. | Thres. | |
|---|---|---|---|---|---|---|---|---|
| Training | 15.52 | 17.31 | 16.27 | 15.46 | 17.75 | 16.25 | 17.96 | 16.74 |
| Test | 22.11 | 23.32 | 22.15 | 21.69 | 23.48 | 22.12 | 23.15 | 22.34 |
| Overall | 19.71 | 21.13 | 20.01 | 19.42 | 21.39 | 19.99 | 21.26 | 20.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Hu, T.; Jin, S.; Huang, W.; Jia, Y.; Chen, T.; Wang, J. Improving CyGNSS-Based Land Remote Sensing: Track-Wise Data Calibration Schemes. Remote Sens. 2021, 13, 2844. https://doi.org/10.3390/rs13142844
Yan Q, Hu T, Jin S, Huang W, Jia Y, Chen T, Wang J. Improving CyGNSS-Based Land Remote Sensing: Track-Wise Data Calibration Schemes. Remote Sensing. 2021; 13(14):2844. https://doi.org/10.3390/rs13142844
Chicago/Turabian StyleYan, Qingyun, Ting Hu, Shuanggen Jin, Weimin Huang, Yan Jia, Tiexi Chen, and Jian Wang. 2021. "Improving CyGNSS-Based Land Remote Sensing: Track-Wise Data Calibration Schemes" Remote Sensing 13, no. 14: 2844. https://doi.org/10.3390/rs13142844
APA StyleYan, Q., Hu, T., Jin, S., Huang, W., Jia, Y., Chen, T., & Wang, J. (2021). Improving CyGNSS-Based Land Remote Sensing: Track-Wise Data Calibration Schemes. Remote Sensing, 13(14), 2844. https://doi.org/10.3390/rs13142844











