An Adaptive Piecewise Harmonic Analysis Method for Reconstructing Multi-Year Sea Surface Chlorophyll-A Time Series
Abstract
:1. Introduction
2. Materials and Methods
2.1. Conventional HANTS Algorithm
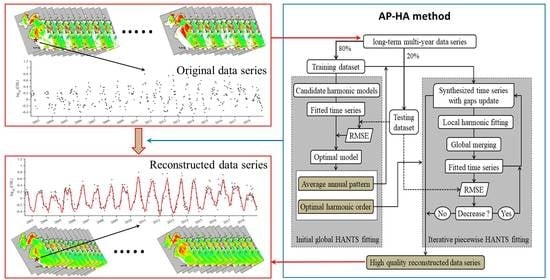
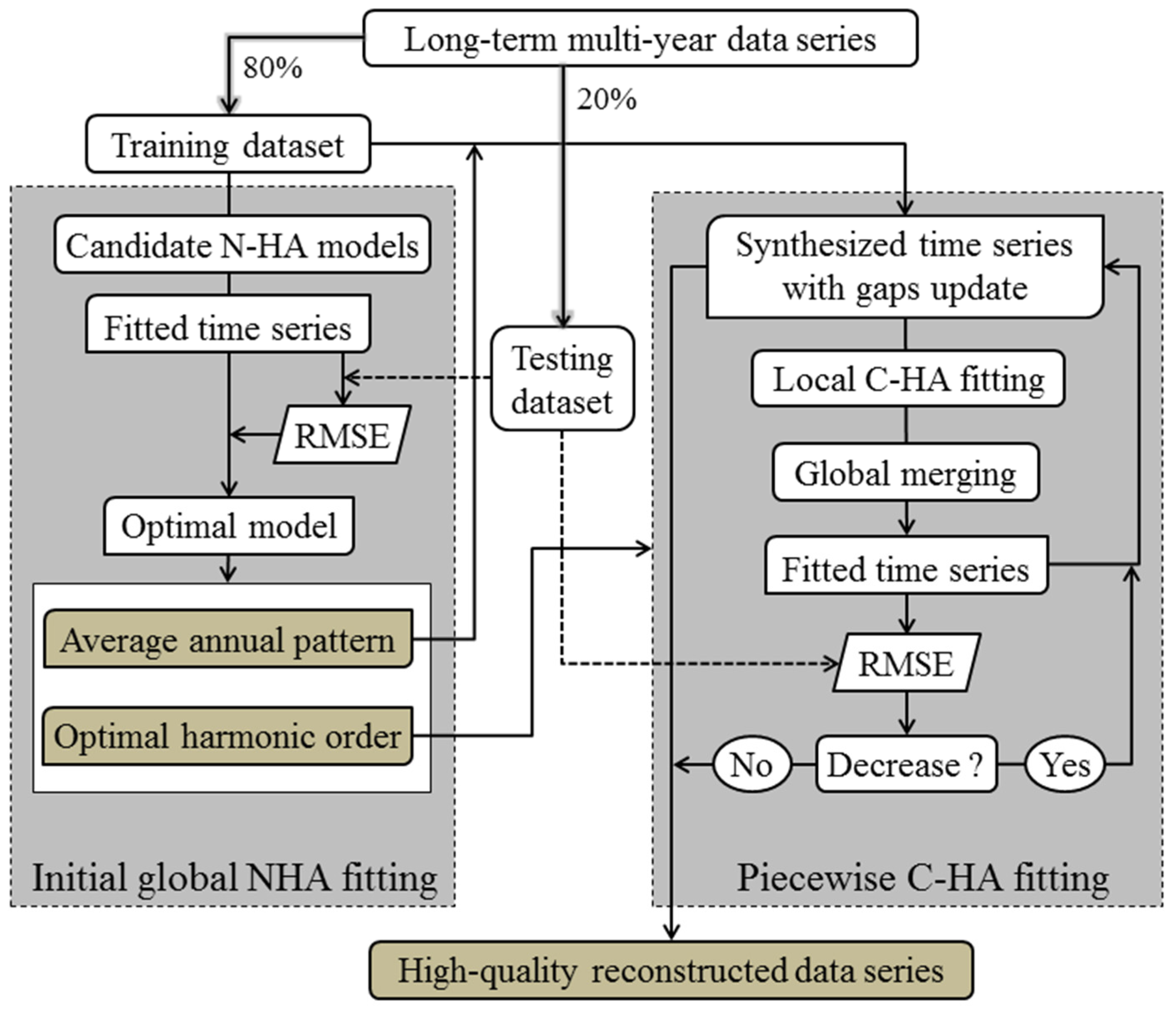
2.2. Algorithm of Adaptive Piecewise HANTS (AP-HA) Method
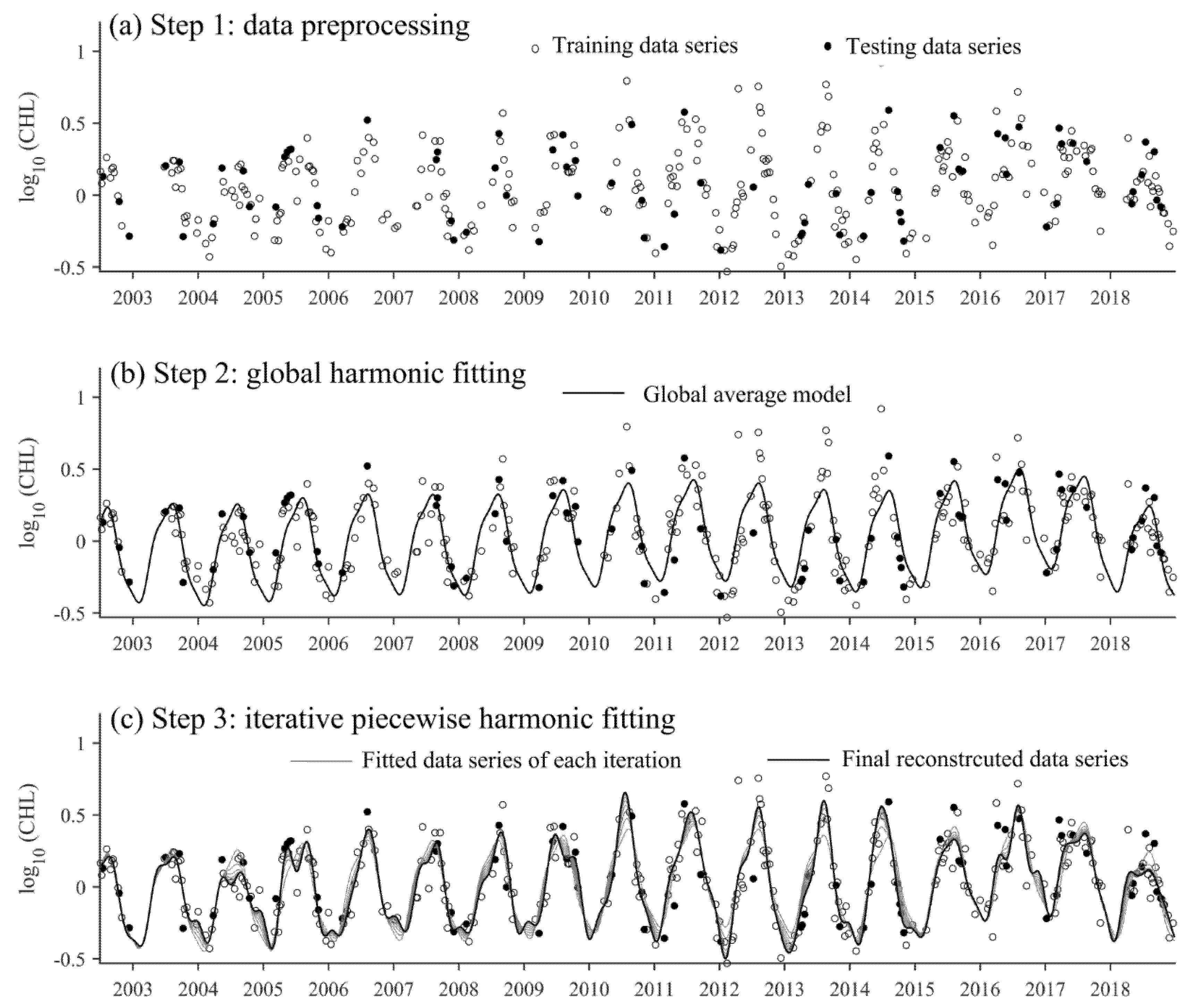
2.2.1. Step 1: Preprocessing of the Original Data Series
2.2.2. Step 2: Initial Global HANTS Fitting
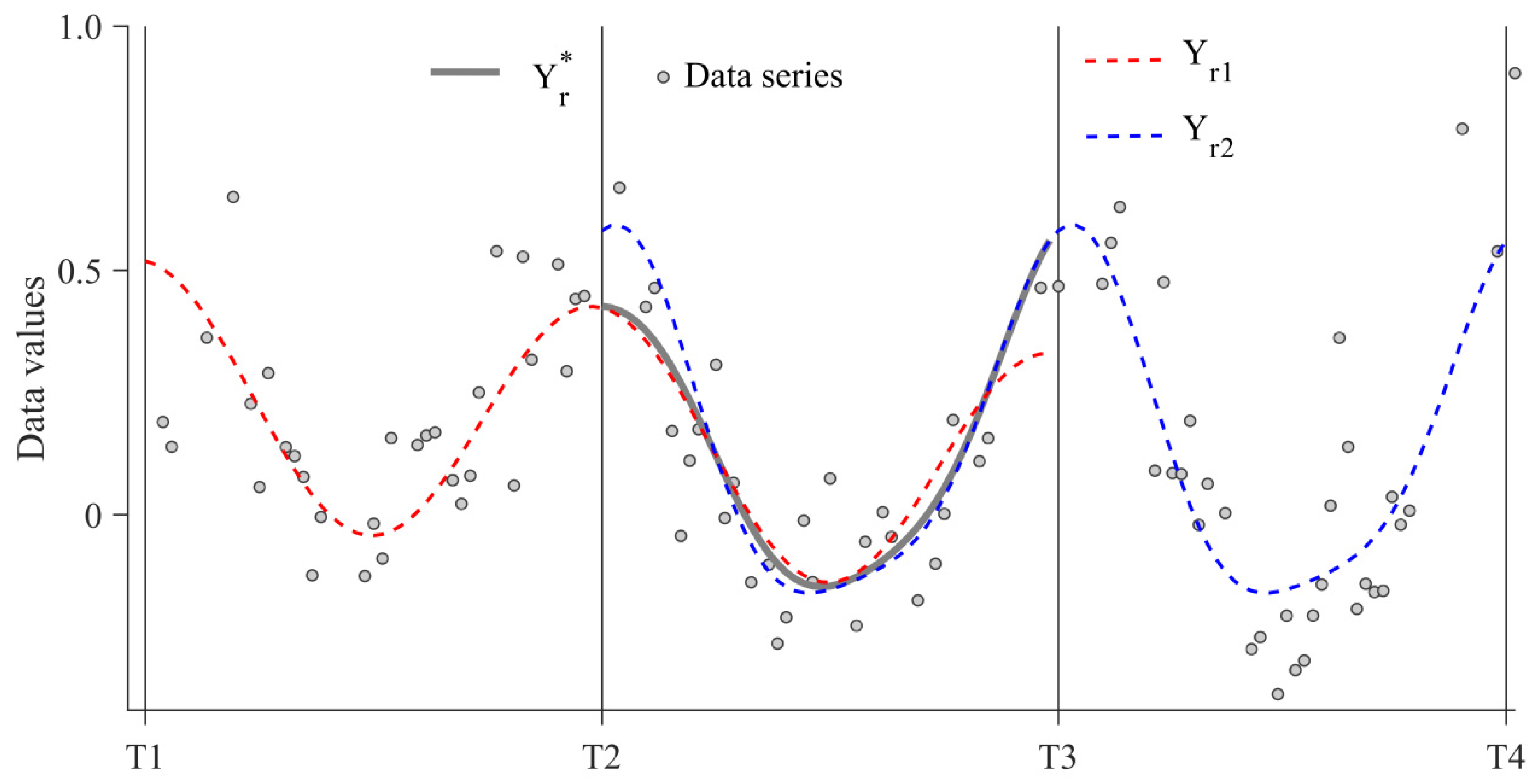
2.2.3. Step 3: Iterative Piecewise HANTS Fitting
2.3. Evaluation Strategy
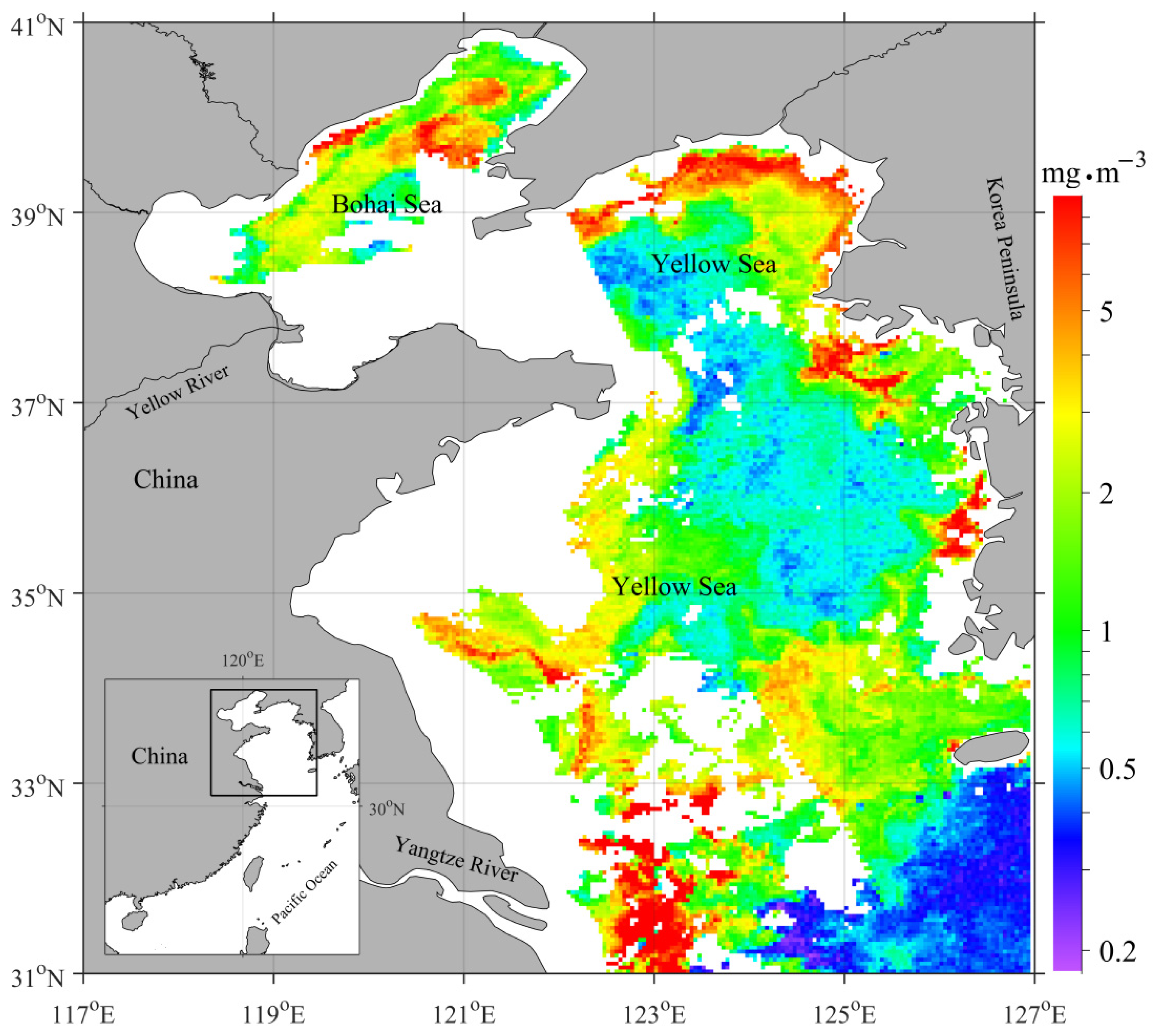
2.4. Sea Surface Chlorophyll-a Dataset
3. Results
3.1. Illustrating the AP-HA Implementation on a Profile
3.2. Overall Quantitative Evaluation
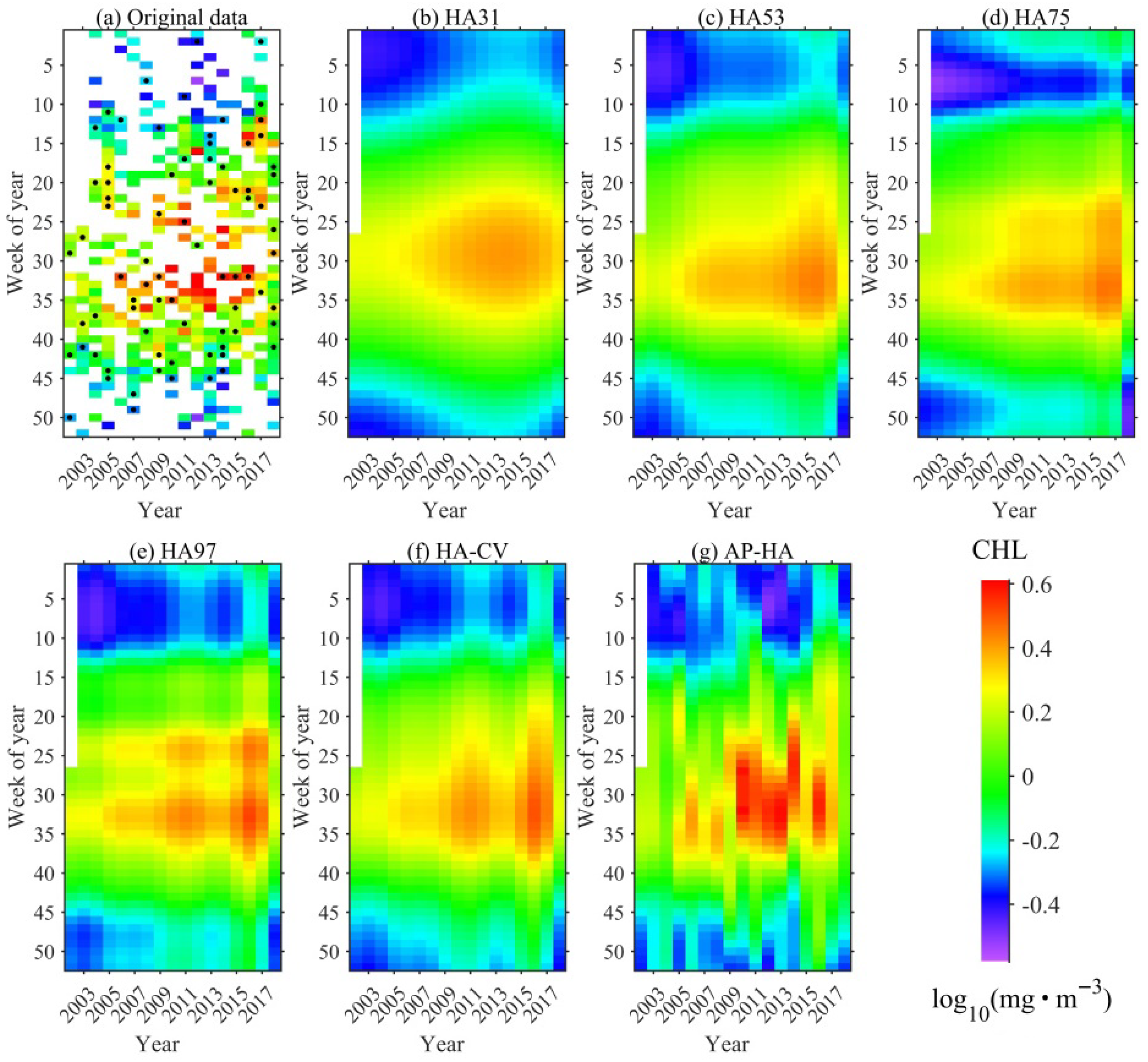
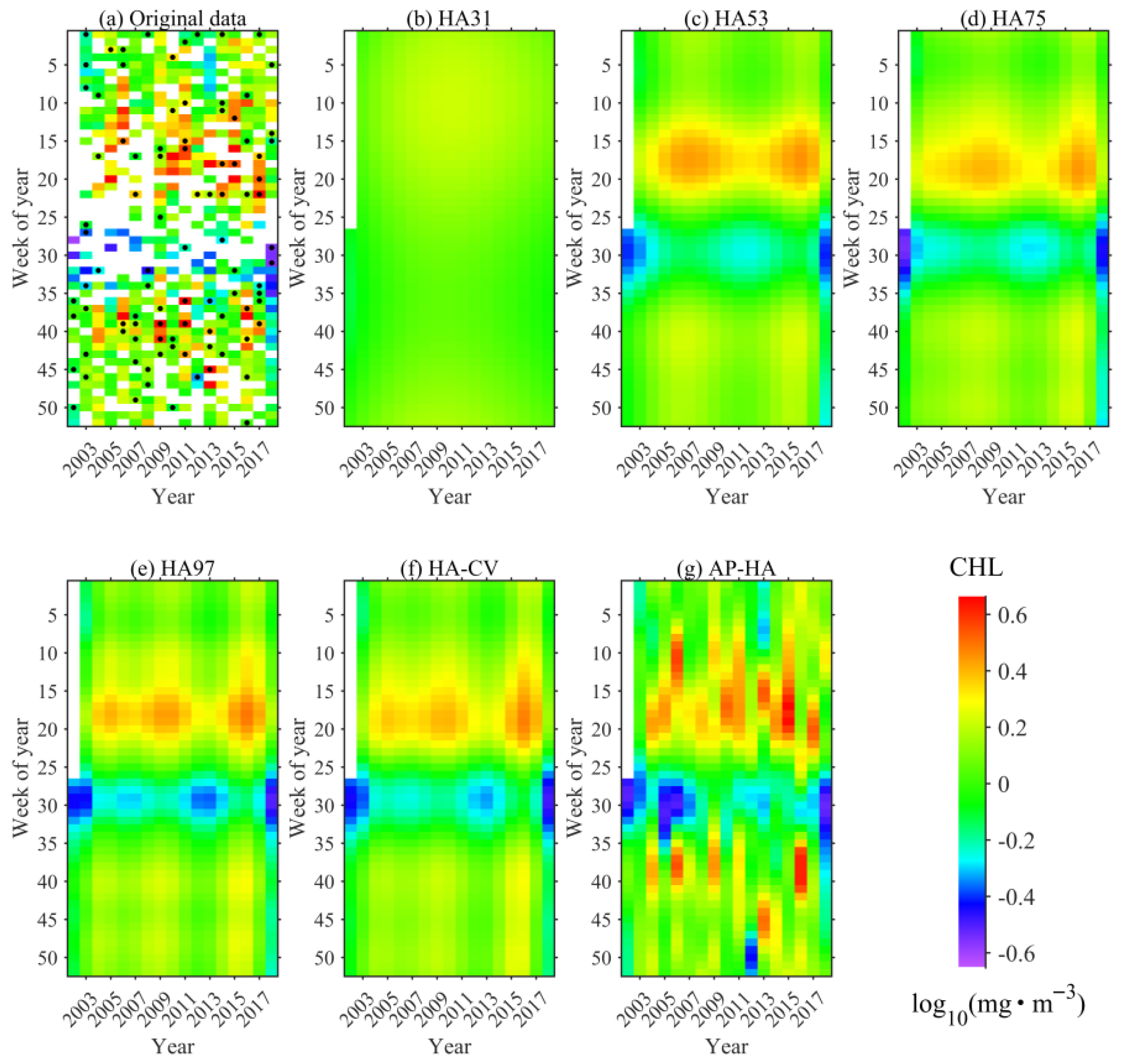
3.3. Visual Inspection of Typical Data Series
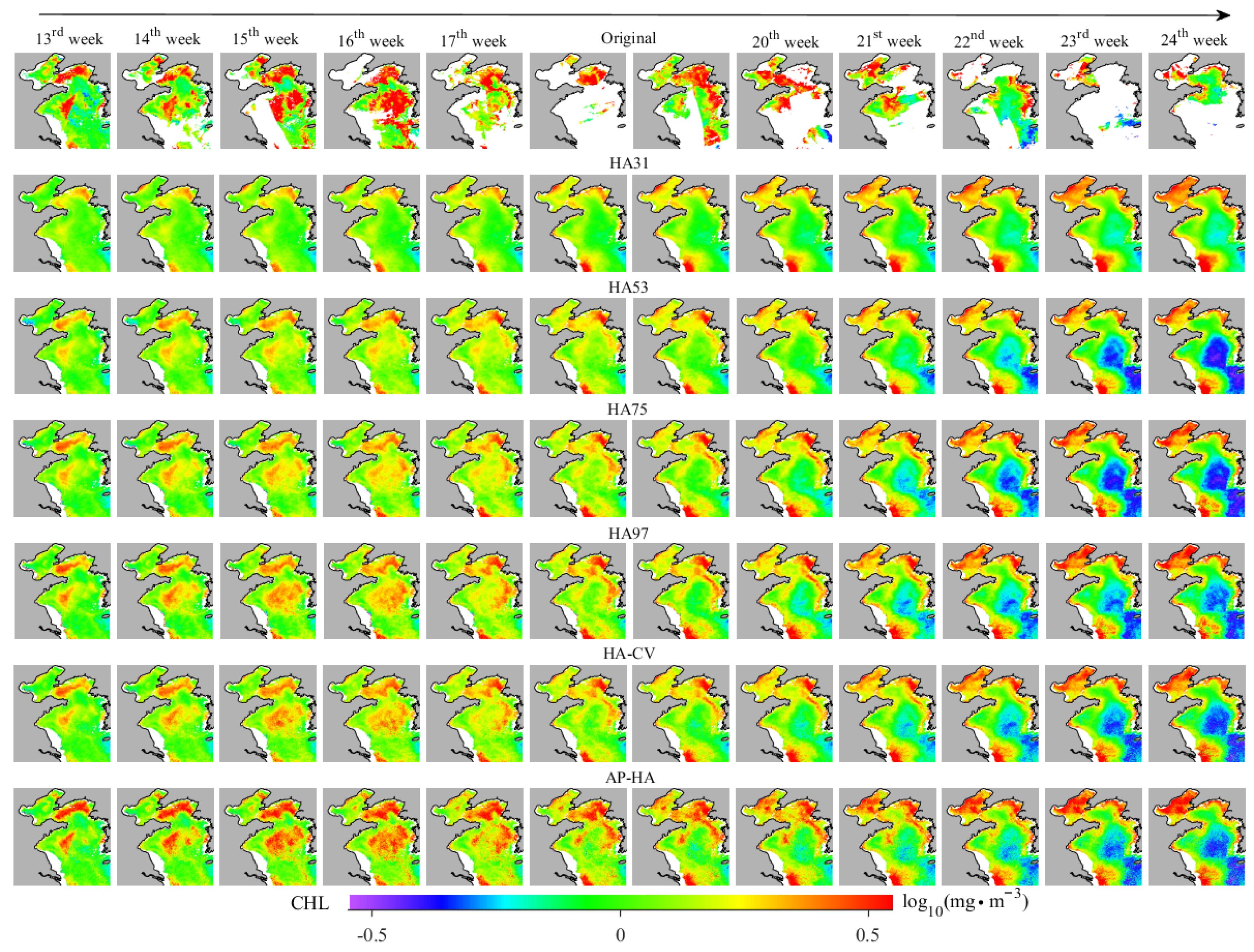
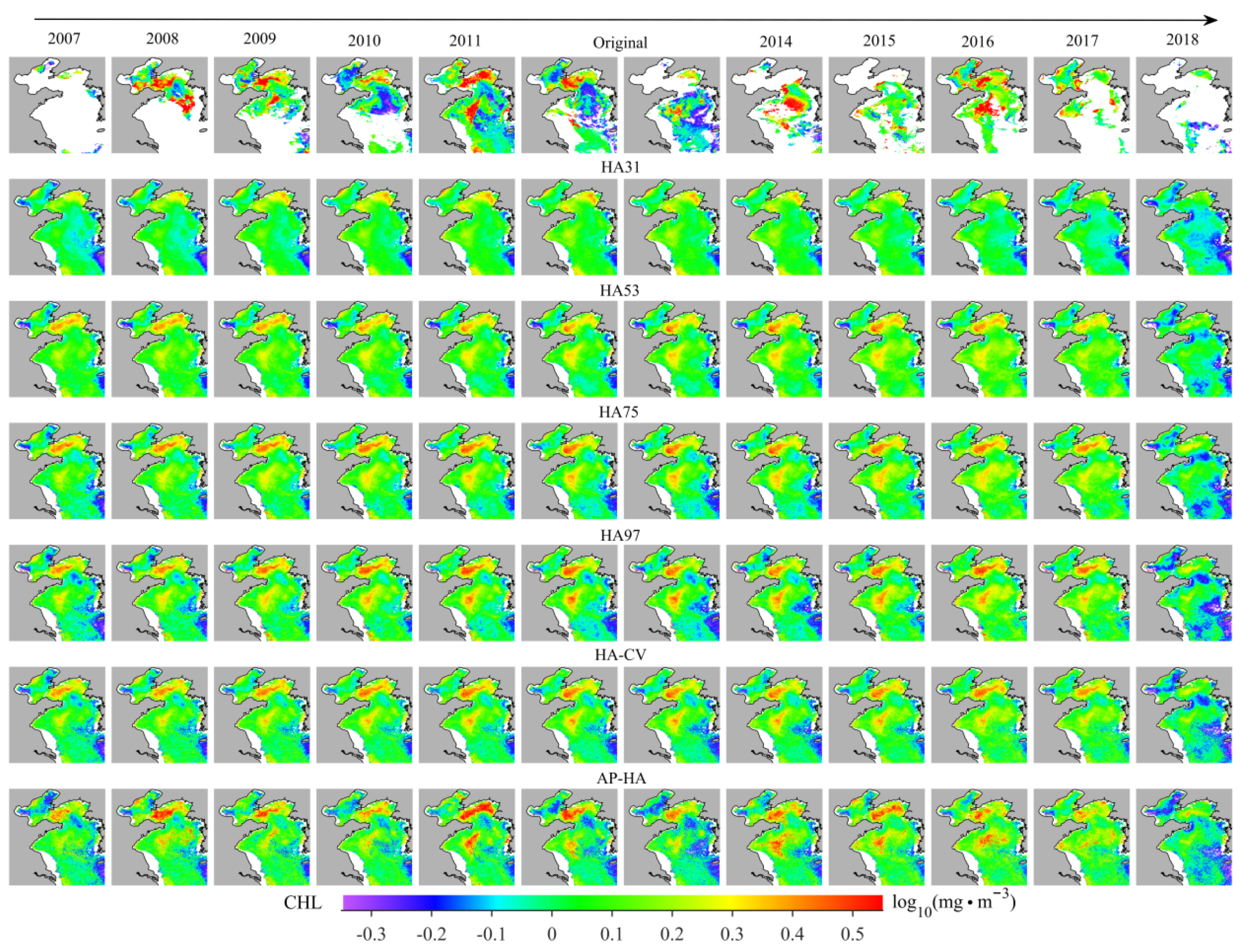
3.4. Results of Reconstructed CHL Images
4. Discussion
4.1. Improvements in AP-HA Method
4.2. Limitations and Perspective
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Piao, S.L.; Fang, J.Y.; Zhou, L.M.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Glob. Chang. Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Gregg, W.W.; Conkright, M.E. Decadal changes in global ocean chlorophyll. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef] [Green Version]
- Gregg, W.W.; Woodward, R.H. Improvements in coverage frequency of ocean color: Combining data from SeaWiFS and MODIS. Trans. Geosci. Remote Sens. 1998, 36, 1350–1353. [Google Scholar] [CrossRef]
- Pottier, C.; Garcon, V.; Larnicol, G.; Sudre, J.; Schaeffer, P.; Le Traon, P.Y. Merging SeaWiFS and MODIS/Aqua ocean color data in North and Equatorial Atlantic using weighted averaging and objective analysis. Trans. Geosci. Remote Sens. 2006, 44, 3436–3451. [Google Scholar] [CrossRef] [Green Version]
- Bai, K.; Chang, N.-B.; Chen, C.-F. Spectral information adaptation and synthesis scheme for merging cross-mission ocean color reflectance observations from MODIS and VIIRS. Trans. Geosci. Remote Sens. 2016, 54, 311–329. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Barale, V.; Jaquet, J.-M.; Ndiaye, M. Algal blooming patterns and anomalies in the Mediterranean Sea as derived from the SeaWiFS data set (1998–2003). Remote Sens. Environ. 2008, 112, 3300–3313. [Google Scholar] [CrossRef]
- Chen, S.; Hu, C. Estimating sea surface salinity in the northern Gulf of Mexico from satellite ocean color measurements. Remote Sens. Environ. 2017, 201, 115–132. [Google Scholar] [CrossRef]
- Demarcq, H.; Reygondeau, G.; Alvain, S.; Vantrepotte, V. Monitoring marine phytoplankton seasonality from space. Remote Sens. Environ. 2012, 117, 211–222. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Gao, Z.Q.; Liu, D.Y. Multivariate DINEOF reconstruction for creating long-term cloud-free chlorophyll-a data records from SeaWiFS and MODIS: A case study in Bohai and Yellow Seas, China. J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1383–1395. [Google Scholar] [CrossRef]
- Liu, X.M.; Wang, M.H. Gap filling of missing data for VIIRS global ocean color products using the DINEOF method. Trans. Geosci. Remote Sens. 2018, 56, 4464–4476. [Google Scholar] [CrossRef]
- Pukhtyar, L.D.; Stanichny, S.V.; Timchenko, I.E. Optimal interpolation of the data of remote sensing of the sea surface. Phys. Oceanogr. 2009, 19, 225–239. [Google Scholar] [CrossRef]
- Cole, H.; Henson, S.; Martin, A.; Yool, A. Mind the gap: The impact of missing data on the calculation of phytoplankton phenology metrics. J. Geophys. Res. Ocean. 2012, 117, C08030. [Google Scholar] [CrossRef]
- Racault, M.-F.; Sathyendranath, S.; Platt, T. Impact of missing data on the estimation of ecological indicators from satellite ocean-colour time-series. Remote Sens. Environ. 2014, 152, 15–28. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, A.S.; Visser, A.W.; MacKenzie, B.R.; Payne, M.R. Accuracy and precision in the calculation of phenology metrics. J. Geophys. Res. Ocean. 2014, 119, 8438–8453. [Google Scholar] [CrossRef]
- Jönsson, P.; Cai, Z.; Melaas, E.; Friedl, M.A.; Eklundh, L. A method for robust estimation of vegetation seasonality from Landsat and Sentinel-2 time series data. Remote Sens. 2018, 10, 635. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Wardlow, B.D.; Xiang, D.; Hu, S.; Li, D. A review of vegetation phenological metrics extraction using time-series, multispectral satellite data. Remote Sens. Environ. 2020, 237, 111511. [Google Scholar] [CrossRef]
- Wasmund, N.; Nausch, G.; Gerth, M.; Busch, S.; Burmeister, C.; Hansen, R.; Sadkowiak, B. Extension of the growing season of phytoplankton in the western Baltic Sea in response to climate change. Mar. Ecol. Prog. Ser. 2019, 622, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Roy, D.P. Spatially and temporally complete Landsat reflectance time series modelling: The fill-and-fit approach. Remote Sens. Environ. 2020, 241, 111718. [Google Scholar] [CrossRef]
- Hermance, J.F.; Jacob, R.W.; Bradley, B.A.; Mustard, J.F. Extracting phenological signals from multiyear AVHRR NDVI time series: Framework for applying high-order annual splines with roughness damping. Trans. Geosci. Remote Sens. 2007, 45, 3264–3276. [Google Scholar] [CrossRef]
- Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky-Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Atzberger, C.; Eilers, P.H.C. A time series for monitoring vegetation activity and phenology at 10-daily time steps covering large parts of South America. Int. J. Digit. Earth 2011, 4, 365–386. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Harmonic analysis of time-series AVHRR NDVI data. Photogramm. Eng. Remote Sens. 2001, 67, 461–470. [Google Scholar]
- Atkinson, P.M.; Jeganathan, C.; Dash, J.; Atzberger, C. Inter-comparison of four models for smoothing satellite sensor time-series data to estimate vegetation phenology. Remote Sens. Environ. 2012, 123, 400–417. [Google Scholar] [CrossRef]
- Cai, Z.Z.; Jonsson, P.; Jin, H.X.; Eklundh, L. Performance of smoothing methods for reconstructing NDVI time-series and estimating vegetation phenology from MODIS data. Remote Sens. 2017, 9, 1271. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.G.; Shang, R.; Liu, Y.; Lu, X.L. Global evaluation of gap-filling approaches for seasonal NDVI with considering vegetation growth trajectory, protection of key point, noise resistance and curve stability. Remote Sens. Environ. 2017, 189, 164–179. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Hermance, J.F. Stabilizing high-order, non-classical harmonic analysis of NDVI data for average annual models by damping model roughness. Int. J. Remote Sens. 2007, 28, 2801–2819. [Google Scholar] [CrossRef]
- Padhee, S.K.; Dutta, S. Spatio-Temporal reconstruction of MODIS NDVI by regional land surface phenology and harmonic analysis of time-series. GISci. Remote Sens. 2019, 56, 1261–1288. [Google Scholar] [CrossRef]
- Huan, Y.; Sun, D.; Wang, S.; Zhang, H.; Qiu, Z.; Bilal, M.; He, Y. Remote sensing estimation of phytoplankton absorption associated with size classes in coastal waters. Ecol. Indic. 2021, 121, 107198. [Google Scholar] [CrossRef]
- Moore, T.S.; Brown, C.W. Incorporating environmental data in abundance-based algorithms for deriving phytoplankton size classes in the Atlantic Ocean. Remote Sens. Environ. 2020, 240, 111689. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, D.Y.; Tang, D.L. Application of a generalized additive model (GAM) for estimating chlorophyll-a concentration from MODIS data in the Bohai and Yellow Seas, China. Int. J. Remote Sens. 2017, 38, 639–661. [Google Scholar] [CrossRef]
- Vargas, M.; Brown, C.W.; Sapiano, M.R.P. Phenology of marine phytoplankton from satellite ocean color measurements. Geophys. Res. Lett. 2009, 36, L01608. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Q.; Gao, Z.Q. Contrasting chlorophyll-a seasonal patterns between nearshore and offshore waters in the Bohai and Yellow Seas, China: A new analysis using improved satellite data. Cont. Shelf Res. 2020, 203. [Google Scholar] [CrossRef]
- Campbell, J.W. The lognormal distribution as a model for bio-optical variability in the sea. J. Geophys. Res. 1995, 100, 13237–13254. [Google Scholar] [CrossRef]
- Bradley, B.A.; Jacob, R.W.; Hermance, J.F.; Mustard, J.F. A curve fitting procedure to derive inter-annual phenologies from time series of noisy satellite NDVI data. Remote Sens. Environ. 2007, 106, 137–145. [Google Scholar] [CrossRef]
- Yang, Y.; Luo, J.; Huang, Q.; Wu, W.; Sun, Y. Weighted double-logistic function fitting method for reconstructing the high-quality sentinel-2 NDVI time series data set. Remote Sens. 2019, 11, 2342. [Google Scholar] [CrossRef] [Green Version]
| Dataset | HA31 | HA53 | HA75 | HA97 | HA-CV | AP-HA |
|---|---|---|---|---|---|---|
| Training | 0.224 | 0.198 | 0.192 | 0.188 | 0.195 | 0.155 |
| Testing | 0.229 | 0.207 | 0.281 | 0.303 | 0.197 | 0.188 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Gao, Z.; Ning, J. An Adaptive Piecewise Harmonic Analysis Method for Reconstructing Multi-Year Sea Surface Chlorophyll-A Time Series. Remote Sens. 2021, 13, 2727. https://doi.org/10.3390/rs13142727
Wang Y, Gao Z, Ning J. An Adaptive Piecewise Harmonic Analysis Method for Reconstructing Multi-Year Sea Surface Chlorophyll-A Time Series. Remote Sensing. 2021; 13(14):2727. https://doi.org/10.3390/rs13142727
Chicago/Turabian StyleWang, Yueqi, Zhiqiang Gao, and Jicai Ning. 2021. "An Adaptive Piecewise Harmonic Analysis Method for Reconstructing Multi-Year Sea Surface Chlorophyll-A Time Series" Remote Sensing 13, no. 14: 2727. https://doi.org/10.3390/rs13142727
APA StyleWang, Y., Gao, Z., & Ning, J. (2021). An Adaptive Piecewise Harmonic Analysis Method for Reconstructing Multi-Year Sea Surface Chlorophyll-A Time Series. Remote Sensing, 13(14), 2727. https://doi.org/10.3390/rs13142727