Abstract
In potato (Solanum tuberosum) production, the number of tubers harvested and their sizes are related to the plant population. Field maps of the spatial variation in plant density can therefore provide a decision support tool for spatially variable harvest timing to optimize tuber sizes by allowing densely populated management zones more tuber-bulking time. Computer vision has been proposed to enumerate plant numbers using images from unmanned aerial vehicles (UAV) but inaccurate predictions in images of merged canopies remains a challenge. Some research has been done on individual potato plant bounding box prediction but there is currently no information on the spatial structure of plant density that these models may reveal and its relationship with potato yield quality attributes. In this study, the Faster Region-based Convolutional Neural Network (FRCNN) framework was used to produce a plant detection model and estimate plant densities across a UAV orthomosaic. Using aerial images of 2 mm ground sampling distance (GSD) collected from potatoes at 40 days after planting, the FRCNN model was trained to an average precision (aP) of 0.78 on unseen testing data. The model was then used to generate predictions on quadrants imposed on orthorectified rasters captured at 14 and 18 days after emergence. After spatially interpolating the plant densities, the resultant surfaces were highly correlated to manually-determined plant density (R2 = 0.80). Further correlations were observed with tuber number (r = 0.54 at Butter Hill; r = 0.53 at Horse Foxhole), marketable tuber weight per plant (r = −0.57 at Buttery Hill; r = −0.56 at Horse Foxhole) and the normalized difference vegetation index (r = 0.61). These results show that accurate two-dimensional maps of plant density can be constructed from UAV imagery with high correlation to important yield components, despite the loss of accuracy of FRCNN models in partially merged canopies.
1. Introduction
Potato (Solanum tuberosum) plant density is a basic measurement of plant population whose spatial variation has been linked to significant variations in yield and tuber size distribution [1,2,3,4]. Increasing plant spacing significantly reduces the plant population and subsequently decreases yield [5]. Potatoes are known to form multiple main stems per planted tuber and the stems are considered to be the ideal unit of plant population due to previous studies that have linked stem density to tuber number at harvest [1]. However, potatoes are also known to form multiple secondary stems originating below the ground, which makes it difficult to determine an accurate stem number from above the ground without digging up the plant [1]. Currently, the opportunity to accurately assess stem population is taken during yield sampling, when plants are uprooted for the purpose of estimating tuber numbers. Stem number assessments at this stage are used to parameterize yield prediction models. For early-season assessments and calculations of plant population, the practical approach for estimating plant population involves the use of the weight of the tubers planted per unit area as a standard seed rate that directly relates to plant density rather than stem density [1]. This enables farmers to determine the effective plant density in the field in order to evaluate the efficiency of planting operations, seed germination rates, and to accordingly adjust yield expectations. Plant density also affects the number of tubers produced by a plant and their size distribution [1]. This means accurate prediction of spatial variation in plant density can enable the adoption of spatially variable management to optimized tuber size distribution at harvest. Currently, farmers predominantly evaluate plant density using visual counts of emerged plants from a sample of locations during the establishment phase of crop development [6]. The reliability of this method ultimately depends on the sample size used to make the assessment and the assumption that the sample is representative of the actual spatial variation in the field. Apart from the inherent irreproducibility of sampling-based designs, the sample sizes needed to reliably meet these assumptions in large fields makes this method impractical. Reliable, efficient, and reproducible methods of plant density determination are therefore an important need in precision agriculture.
A potential solution for estimation of potato plant density is by remotely sensing potato plants, leveraging on the advances in computer vision and aerial image photogrammetry. Unmanned aerial vehicles (UAV) fitted with imaging sensors provide a platform for remote sensing of canopy development with the potential to determine the variation in plant density for precision agriculture applications. A common application of remote sensing in agriculture has been the generation of spatial variation maps using vegetation indices derived from multispectral camera data. These maps have been extensively used to infer spatial variation in vegetation health, utilizing the known spectral responses of vegetation to plant health and molecular constitution [7]. Classification algorithms applied at spatio-temporal scales are useful for the evaluation of fractional vegetation cover characteristics [8]. Fractional vegetation cover of land surfaces has been measured temporally and used as a proxy for crop growth rate [8], providing the potential to simulate crop growth characteristic curves that are required in time-step yield forecasting crop models. Therefore, remote sensing of plant canopy development, using sensors mounted on UAVs, irrigation equipment and tractors provides the potential to operationalize crop modelling at an unprecedented spatial scale, as well as deliver the data needed for high throughput assessment of plant establishment in precision agriculture, quick evaluation of viability of populations in breeding lines and other applications. Apart from pixel-level image analysis applications, there is considerable interest in leveraging advances in artificial intelligence technologies in remote sensing for non-destructive and non-invasive evaluation of properties of interest within crop canopies such as plant heights with light detection and ranging, instances of diseases or pests and stem population counts [9,10].
Several computer vision algorithms have been proposed for determining plant counts from aerial images of different crops using traditional image analysis and machine learning approaches. The most prevalent approach involves feature extraction using traditional image analysis followed by any machine learning regression approach for predicting numerical image class labels from extracted features. Several variations of this two-step approach have been used to produce plant-counting models in wheat [11], rapeseed [12], potatoes [13], and other crops. In weed-free fields, images of emerged plants before canopy consolidation consist mostly of green pixels of the objects of interest against a background dominated by soil [14]. This dichotomy is utilized in the feature extraction step to classify and consolidate connected foreground pixels as objects of interest using reflectance values of the pixels. Colour indices are often used to generate two-dimensional greyscale images from truecolor (RGB) or multispectral images. Once the colour indices are applied, the generation of a binary mask representing the dichotomy between the foreground and background often involves the selection of a threshold that is either learned from the image using the Otsu algorithm [13] or subjectively selected [6]. The binary masks are used to generate the feature sets for machine learning like the number of blobs, and their total pixel area. While these approaches return satisfactory binary masks in some situations, subjective selection of a threshold is clearly not expected to be robust in all environments. The most common algorithm-based approach for automatic threshold selection to overcome the subjective threshold selection problem is the Otsu algorithm, which unfortunately becomes sub-optimal when vegetation indices produce multi-modal frequency histograms [15]. The reliability of the subsequent feature extraction and regression or classification modelling is therefore contingent upon further data-cleaning methods deployed to clean the binary mask, which reduced the reproducibility of downstream models.
Traditional image analysis, fused with machine learning was used by [13] to predict plant numbers in potatoes, with accurate predictions in well separated plants but mixed results in instances containing overlapped plants. Following up on this work, [14] trained a deep learning-based Mask R-CNN model, predicting potato and lettuce instances using bounding boxes and sizing the extent of each instance with a mask. This overcame the need for manual feature extraction and demonstrated the efficacy of the deep learning approach. A framework based on a fully convolutional neural network to count potato plants in merged canopies was also developed by [16]. However, both the Mask R-CNN [14] and the two-step computer vision [13] approaches suffer from a loss of accuracy in distinguishing overlapping plants. Homogeneity in potato plants, and the difficulty of separating individual plant units in merged canopies during data annotation makes it difficult to train models that can accurately distinguish individual plants after potato canopy consolidation. A potential solution to this problem would be to conduct imaging before canopy consolidation. However, potato emergence rates vary spatially with soil temperature, disease incidence, and treatments that alter apical-dominance at the seed-lot level [6]. Additionally, calcium deficiency at the terminal bud can induce the loss of apical dominance, which necessitates branching and determines the number of sprouts per tuber, causing a spatial variation in canopy growth rates across the field [17]. Variations in planting depth also cause variations in the number of days to emergence, with deeper planted tubers taking up to a week longer to emerge than shallower planted tubers within a field [18]. These factors make it necessary to delay image acquisition, so as to minimize the chance of underestimating emergence.
Accurate mapping of centroids of plants in merged canopy was reported by [16] using a custom CentroidNet architecture supported by a fully convolutional network learning the centroid origin of leaves in overlapping potato canopies. The premise of this method is that potato leaves grow outwardly from the location of the planted tuber, and the model can therefore detect the location of a plant by learning the vectors pointing to the centroid of a plant object. In merged canopies, this assumption may be violated by the fact that potato leaves grow outward from their subtending stem and each stem eventually grows independently from its mother tuber [1]. Therefore, overestimation can be expected in multi-stem plants using the CentroidNet. Indeed, [16] report observing false positives due to oddly shaped plants, which may be primary or secondary stems. Evidence suggests that accurate potato plant counting remains an object detection problem that is best modelled from UAV data before canopy overlap when individual plants are discernible to data annotators. The practical need for plant counting algorithms to farmers is the generation of a plant density map across the field from the detected objects, making this primarily an object detection problem, and the accurate pixel-wise segmentation problem is secondary. Faster R-CNN (FRCNN), the detection framework under the Mask R-CNN framework therefore provides an adequate and simplified training protocol. Training FRCNN models also requires less hyperparameter tuning requirements than MASK-RCNN [14].
The ultimate goal of plant counting algorithms is to replace the need for manual estimations of plant density across a field, which is done by interpolation of manually collected count data. The accurate production of 2D density maps that represent the spatial variation in plant density is therefore more pertinent than fine-grain plant-by-plant accuracy because the economic and practical feasibility of site-specific management is contingent upon the establishment of a practically manageable range of spatial autocorrelation [19]. Management decisions on variables that respond to plant density (e.g., yield) are also likely to only be economically interesting if the plant density exhibits relatively long-range spatial autocorrelation. Large differences in the range of autocorrelation in potato yields from 12 m to 425 m have been reported [19]. In commercial production, farmers aim to produce uniform plant density across the field and any variation is likely to come from factors such as a systematic fault in the planting operation, low viability of a batch of seed, or soil-borne factors that affect seed germination [5]. Such systematic sources of variation are likely to exhibit spatial autocorrelation relative to the size of the field. Therefore, plant density maps need to capture this spatial structure rather than merely capturing local variation. This provides a geostatistical solution to the problem of plant-density determination using computer vision and deep learning algorithms in fields with slightly merged canopies. In a large orthomosaic of UAV imagery, plant detection can be conducted on a sliding window as suggested by [14] then a filtering step can be added post-detection, discarding all images containing overlapped plants. This would create a sparse matrix of detections across the field from which geostatistical interpolation can be used to generate a continuous representative 2D density map. The 2D density map can then be related to variation in yield parameters or used to test the utility of other sources of variation like satellite-derived early-season NDVI. With the main potato-related papers in this field focused solely on detection [13,14,16], this approach has not been reported in literature.
In this paper, we demonstrate plant counting in potatoes as a detection problem solvable by a FRCNN model without the need for instance segmentation. For the first time, we produce geostatistically interpolated 2D plant density plots, compare them to satellite-derived early-season NDVI density plots and evaluate the relationships between the density plots and potato yield attributes.
2. Materials and Methods
2.1. Data Capture and Modelling
The study site for model development was a commercially planted potato crop (cv Amora) planted at Harper Adams University, Shropshire, United Kingdom (Table 1). The field was planted on 27 March 2019 at a targeted 25 cm between planting stations. First emergence was observed on 18 April 2019, after which a 10-day interval was allowed before imaging, allowing the emergence of a sufficient number of plants for annotating a training dataset. Consequently, aerial images were captured on 28 April 2019 at 30 m altitude using a Mavic Air UAV hosting a 2.54 cm CMOS sensor producing 12 MP images with an 88° field of view (FOV).

Table 1.
Summary of the locations, varieties, and crop stage of the images used in the study.
To prevent data leakage, the initial image acquisition was restricted to a designated sub-section of the field for training the model, while the remaining portion of the field was used for validating the model. Thirty images were randomly selected from the collected image set and divided into 338 × 304 pixel sub-images, creating 1000 images for annotation. With a ground sampling distance of 2 mm per pixel, the images contained enough perceptual detail to manually produce bounding boxes for plant objects and the earliness of the image acquisition made it possible to delineate overlapping plant clusters and place an independent bounding box for each distinct plant. The 1000 images contained instances of blur and distortion, which were artefacts of the image acquisition process. These were prevalent at areas of change in direction during the drone flight. It was therefore necessary to identify and remove these images because they were difficult to annotate reliably during the generation of training and testing data for the deep learning algorithms. Additionally, headlands with no vegetation were also captured by the UAV. The headlands contained no vegetation and were therefore not considered useful for the training process. Collectively, it was decided that all images with distorted pixels or with headlands containing no potatoes would be excluded from the training dataset. Accordingly, a visual inspection of the 1000 training images was conducted, resulting in the exclusion of 172 images due to the exclusion criteria. The resulting 828 images were partitioned into a training set of 580 and a testing set of 248 images. The images were then manually annotated using Matlab’s [20] Image Labeller application. All generated bounding boxes were stored as labels to create a training dataset for transfer learning with a CNN.
The flow chart of the training pipeline is as illustrated in Figure 1. Transfer learning was conducted using FRCNN with a VGG-16 network backbone, pre-trained on the ImageNet dataset [21]. The VGG-16, developed at the University of Oxford by the Visual Geometry Group (from which the name VGG-16 is derived) is a convolutional neural network architecture that was used in the winning entry of the ImageNet Large Scale Visual Recognition Challenge of 2014. It has since been used to solve many computer vision problems even after the evolution of deeper architectures like the residual networks. In its unmodified form, the VGG-16 is principally used to solve computer vision problems based on 3-channel (mostly RGB) images because it takes input of 224 × 224 RGB images through a sequence of convolutional layers with minimal 3 × 3 filters, a fixed 1-pixel stride and max-pooling with a stride of 2 [22]. Three fully connected layers follow the convolutional layers, with the final fully connected layer containing a number of channels equal to the number of training classes (in this case 2, representing the potato plants and background) and followed by a soft-max layer. The FRCNN framework utilizes the VGG-16 final convolutional feature map to train a region proposal network (RPN) and spatially locate the objects within the convolutional feature map. To create a potato plant detector, the final convolutional feature map of VGG-16 was used to train a RPN, and the last max-pooling layer was replaced by an ROI (region of interest) max-pooling layer as proposed by [23] followed by FRCNN’s classification and regression layers. The training was conducted on an Nvidia GeForce GTX 1070 GPU with CUDA version 10.1.243 and 8 GB Video RAM. The training was run for 100 epochs which completed in 6 h. The hyperparameters used included a learning rate of 0.0001 and a mini-batch size of 4. Stochastic gradient descent was used to optimize loss with a momentum of 0.95. To minimize gradient explosion, extreme gradient values were clipped to ensure that the L2-norm equalled the threshold of 1.
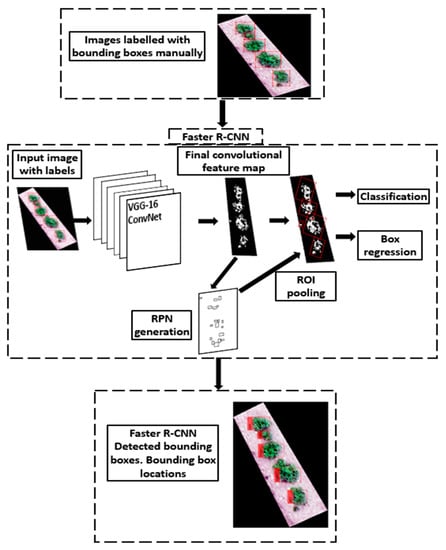
Figure 1.
Faster-RCNN-based transfer learning process for producing a potato plant detection model.
2.2. Model Testing
FRCNN model performance was evaluated as follows. Firstly, model performance diagnostics on unseen data were conducted using the test dataset. Accordingly, the bounding boxes of the FRCNN detections were compared with the manual annotations made on the test images. The intersection over union (IoU) of all bounding boxes with ground truth data were computed then all predicted bounding boxes with more than 0.5 IoU were classified as true positives (TP) while those with less than 0.5 were classified as false positives (FP). The TP and FP instances were computed for each image and the precision of the detection was evaluated as follows:
At the standard IoU threshold of 0.5, a high rate of FP was expected, resulting from random bias in the ground truth bounding boxes, as opposed to the refined bounding boxes generated by the FRCNN model. A high FP rate was expected to penalize recall and F1-scores; therefore, the precision metric was used. From an end-product standpoint, it was considered more important to accurately detect the presence of a plant while its accurate sizing is not as important, prompting the choice of precision over recall. The aP of the model was computed averaging across all bounding boxes in all the test dataset images.
The model was also evaluated for the accurate generation of an observed plant count at 30 different sites across the Horse Foxhole Farm collected 14 days after emergence. Accordingly, an aerial imagery survey covering the entire field was conducted on 2nd May 2019 at 30 m altitude using a DJI Phantom 4 pro UAV with a global positioning device for geo-referencing images. The UAV was equipped with a Hasselblad L1D-20c aerial camera with a 2.54 cm CMOS sensor producing 20 MP still images with a 70° field of view (FOV). The UAV and image acquisition interval ensured an 80% overlap in adjacent images at a ground sampling distance of 8 mm. A second field named Buttery Hill (Table 1) was also evaluated using the model. Images at Buttery Hill were acquired using the DJI phantom 4 at an increased altitude of 80 m with a ground sampling distance of 22 mm per pixel on 1 May 2020, 43 days after planting and 18 days after emergence. At each of the two fields, a single geo-referenced raster for the entire field was produced by stitching all the images together with structure-from-motion techniques using Pix4D [24]. In brief, Pix4D deploys feature matching algorithms to detect similar features in overlapping images from the UAV, then uses the geolocation and height of each image to triangulate the geolocation and height of the matched features across images. This enables the creation of a point cloud from which an orthophotograph of the entire field is generated.
The flow chart of the process to generate of 2D density plots from the UAV orthomosaics was as illustrated in Figure 2. To predict a plant density map at the two fields, a grid of 1 m2 sized quadrant was imposed on the orthorectified raster of each field in order to run the FRCNN model. Truncated quadrants of less than 1 m2 were inevitably created at the edges of each field. These quadrants were also included in the analysis. After running the FRCNN model, it was necessary to determine the presence of merged plants which could not be reliably counted. To do this, each image with all the detected bounding boxes overlaid was converted to a binary mask. All pixels located within the perimeter of a bounding box were converted of ones and all other pixels were converted to zeros. This generated a binary mask of all the bounding boxes. The length of the major axis of each bounding box was then calculated and converted to centimetres using the ground sampling distance of the image, in order to size the length of the plant object. All the image processing was conducted using the image processing toolbox of MATLAB [20].
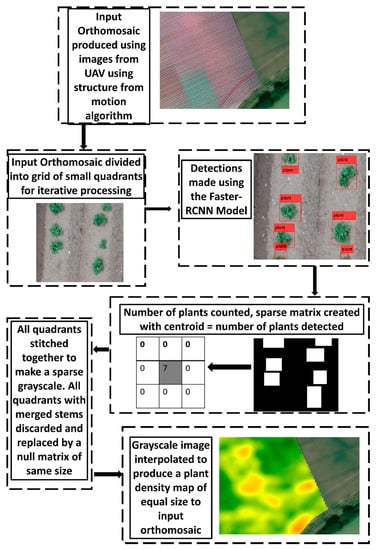
Figure 2.
Flow chart for the production of a plant density plot from a transfer-learning model.
A cursory assessment of the average size of a non-overlapped plant was conducted on the images and twenty-five centimetres was chosen as a threshold to represent the length of the major axis (diagonal) of a bounding box at which it would be considered to represent a merged group of plants. All quadrants where a merged plant was discovered were removed from the analysis and the quadrant was replaced by an equally-sized null matrix. This was done in order to facilitate the use of only valid individual plant detections in the geostatistical interpolation of the plant densities across the entire field. Replacement of all quadrants containing merged plants with a null matrix meant missing data were declared at the spatial location of the quadrant, removing a potentially spurious data point during geostatistical interpolation. For all valid detections, a null matrix equal to the size of the quadrant was also produced then the centroid pixel of the matrix was assigned a value equal to the number of plants that was detected in the quadrant by the FRCNN model. For the quadrant, this created a sparse matrix with only the centroid pixel containing a non-zero value. The series of sparse and null matrices were then stitched together, positioned at the original locations of the quadrants from which they were derived, effectively re-constituting a greyscale image of the same dimensions as the original orthorectified raster. The greyscale image was saved as a Tagged Image File Format (TIFF) file and associated with the “world file” of the original geo-referenced raster. This processing created a georeferenced greyscale image predominated by zeros, with a series of non-zero pixels representing estimated plant densities from the FRCNN model at the non-zero pixel locations. The raster was then vectorised into spatial sampling points in arcGIS [25] and all null-valued points were discarded, leaving a point sampling dataset of estimated plant densities across the field. The points dataset was then interpolated across the entire field to produce a continuous 2-D plant density plot of the field using a Gaussian variogram in ArcGIS [25].
At Horse Foxhole, atmospherically corrected (Level—2A) Sentinel-2 satellite imagery was acquired from the Copernicus Open Access Hub on 12 May 2019. The date was chosen due to the absence of clouds in the satellite imagery after manual inspection. Additionally, this was the date on which the first discernible green vegetation spanning all of Horse Foxhole was visible in the satellite images. Manual inspection was also conducted to ensure that there was spectral mixing with soil features in the images, indicating the lack of canopy closure. The satellite imagery of 10 m spatial resolution was clipped to the field boundaries of Horse Foxhole then processed in ArcGIS to calculate the NDVI of Horse Foxhole. The pixel values of the NDVI at 10 m spatial resolution were extracted then an interpolated surface of the whole field at 1 m spatial resolution was created by kriging with a Gaussian variogram model. Similarly, a manual inspection was conducted on the Sentinel-2 satellite imagery at Buttery Hill for cloud-free images. However, no further analysis of satellite imagery was conducted at Buttery Hill because all available cloud-free images met the exclusion criteria of having either bare soil (before emergence) or merged canopies without visual spectral mixing between vegetation and soil.
In both fields, 30 sampling sites were randomly selected, and plant densities determined at each point using a 1 m row of plants. At harvest, the potato yield components were determined including marketable yield per square metre, average tuber weight, number of total and marketable tubers (per plant and square metre), and number of stems per square metre. The utility of plant density predictions from the interpolated surfaces of the FRCNN model and the NDVI in inferring the yield components was evaluated using the Pearson’s product moment correlation (PPMC). The accuracy of the interpolated FRCNN surfaces in predicting the actual plant densities were evaluated using the root mean squared error (RMSE).
3. Results
Using the test dataset of 248 images from Horse Foxhole, the FRCNN model achieved an aP score of 0.78. Figure 3 shows the actual vs. predicted number of plant objects in the test dataset drawn from the same pool as the training data. Overall, the model predicted the actual number of plants in an image to within 2 stems error as illustrated in Figure 3 (RMSE = 1.59). The model had a nRMSE of 0.19 and R2 of 0.80, though the scatter plot revealed relatively larger variation between observations and model predictions at higher plant densities, elucidating the decrease in model accuracy in closely spaced and potentially merged plants. Manual assessments showed that the model under-predicted the ground-truth bounding boxes in images with merged plants.
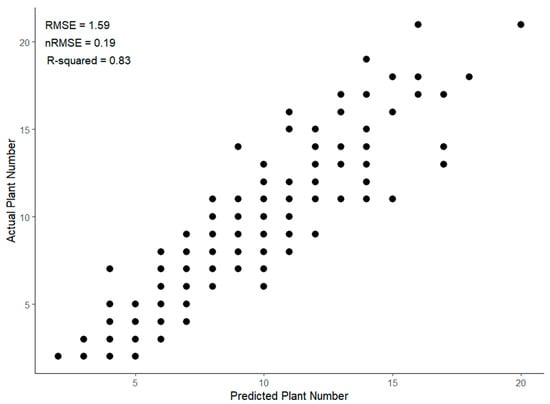
Figure 3.
Actual vs. predicted potato plant numbers in a test dataset of potato plants using predictions from a Faster-RCNN transfer learning model.
Some images contained potato plants that were emerging from the ground but had not formed enough above-ground foliage to be confidently annotated. The model learned and labelled these as potato plants, leading to over-prediction in a small number of instances. An illustration of this is in Figure 4 where the model predicted one more plant than the originally annotated ground truth on account of a single planting station that had delayed emergence and was not annotated in the ground truth but predicted by the model. In practical terms, the model predictions were closer to the actual plant density than the ground truth labels in this instance. Due to the clear linear relationship between the predicted and actual plant counts, reliable plant density maps of the whole field could be constructed from the model and compared to observed densities.

Figure 4.
Visualisation of the bounding-box predictions from a Faster-RCNN transfer-learning model (red colour) against manually labelled bounding boxes (yellow colour) at Horse Foxhole Field (image width = 1.5 m).
The plant density map of Horse Foxhole (Figure 5) revealed considerable systematic spatial variation in the plant stand, showing higher plant densities in the edges of the field compared to the middle. This was determined to result from an inconsistent seed metering mechanism during planting at the edges, resulting in very high plant densities. This was rectified when the middle section of the field was planted, culminating in the observed differences. The variation in predicted plant density coincided with the variation observed in NDVI (Figure 6), showing that early-season NDVI sensed by the sentinel-2 is partially influenced by the plant density on the ground. NDVI was not measured at Buttery Hill due to the lack of cloud-free images before significant canopy consolidation in the Sentinel-2 repository, therefore the NDVI map and plant density map are not shown.
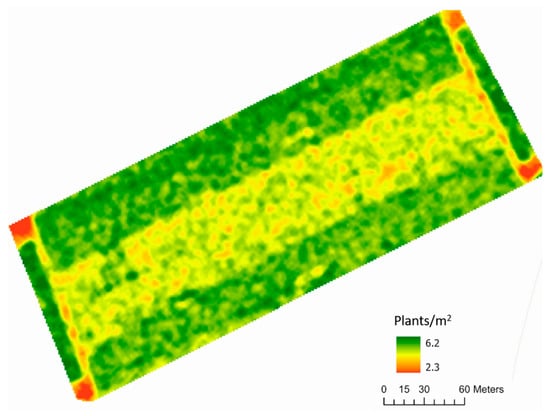
Figure 5.
An interpolated predicted plant density plot of Horse Foxhole field, predicted using the Faster-RCNN transfer learning model.
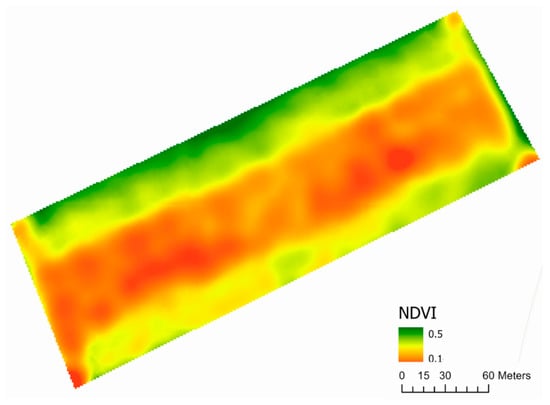
Figure 6.
An interpolated plot of early-season NDVI in the Horse Foxhole field constructed from a Sentinel-2 (10 m spatial resolution) satellite image.
Comparison of the actual plant populations at Horse Foxhole and Buttery Hill against the predictions from the FRCNN model (Figure 7) by RMSE showed that the model performed comparably with the test dataset.
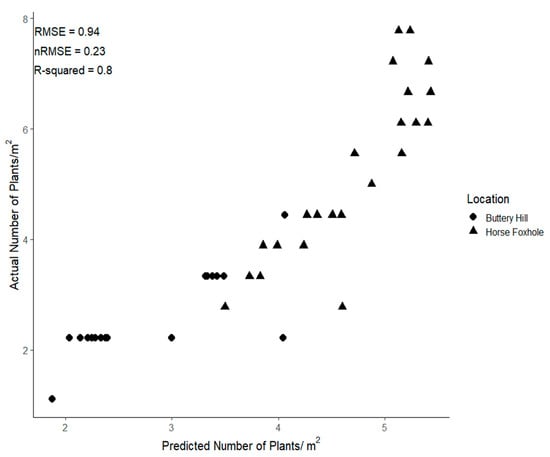
Figure 7.
Actual plant density at Buttery Hill and Horse Foxhole vs. predicted densities from the Faster-RCNN transfer learning model.
An RMSE of ~1 plant, and nRMSE of 0.24 were observed, showing good accuracy at low plant densities but largely under-predicted at the high plant densities at Horse Foxhole. Overall, there was less variation in planting density at Buttery Hill compared to Horse Foxhole where high actual plant densities of up to eight plants per square metre were observed, corresponding to approximately 12 cm spacing between plants. There was a large degree of overlap between plants at these plant densities, causing the model to miss some detections and subsequently return lower plant densities than expected. However, the model still highly captured the variation in plant densities (R2 = 0.80) and therefore the density map produced was a reflectance of observed variation.
Table 2 shows the mean and standard deviation of the potato yield components at Horse Foxhole and Buttery Hill. Overall, inconsistent plant spacing at Horse Foxhole had a large effect on the plant population density, with an average five plants being planted per square metre while Buttery Hill had three plants per square metre. There was also larger variation at Horse Foxhole with a standard deviation of two plants (STD = 1.58) compared to Buttery Hill (STD = 0.77). Buttery Hill produced more tubers per plant than Horse Foxhole, but the mean tuber weight was smaller (74 g and 103 g, respectively). Correlation analysis showed a highly significant correlation between the FRCNN plant density predictions and the actual plant densities as shown in Table 3. At both sites, there was a correlation of exactly 0.87 between predicted and measured plant density. Furthermore, there was a strong correlation (r = 0.61) between plant density predicted by the FRCNN model and the NDVI derived from the Sentinel-2 satellite, quantitatively buttressing the visual similarity between the FRCNN plant density map (Figure 5) and the NDVI map (Figure 6). The FRCNN-predicted plant density, actual plant density and NDVI all showed a similar pattern in their correlation coefficients with potato yield components. Increasing plant density was associated with decreasing tuber number per plant (r = −0.61 at Buttery Hill and r = −0.78 at Horse Foxhole). Similarly, a negative significant correlation was observed between NDVI and the number of tubers per plant at Horse Foxhole.

Table 2.
Summary statistics of the plant density and Potato yield components at Buttery Hill and Horse Foxhole fields.

Table 3.
Correlation coefficients showing the relationship between actual plant density, potato yield components and plant density predicted from the Faster-RCNN transfer learning model at Buttery Hill and Horse Foxhole fields.
The weight of tubers per plant was also negatively associated with plant density at both sites and a similar negative relationship was observed with NDVI at Horse Foxhole. Despite the significant relationships between plant population and the weight per plant, no strong correlation with yield per square metre was observed at both sites. Similarly, no correlation between marketable yield and NDVI was observed at Horse Foxhole. The negative correlation between predicted plant density and tuber weight per plant at Horse Foxhole (r = −0.82, p < 0.001) coincided with a positive correlation between predicted plant density and total tuber number (r = 0.41, p = 0.01). However, while the tuber number per unit area was positively related to the predicted plant density (r = 0.41 at Horse Foxhole and r = 0.54 at Buttery Hill), the overall yield per unit area was not significantly different. As observed in Table 3, high PPN at Horse Foxhole were negatively correlated with tuber weight (r = −0.62). The tuber weight per square metre at Buttery Hill was only weakly correlated to predicted and actual plant density although the tuber weight per plant was negatively correlated (r = −0.57) and the total tuber number was positively correlated (r = 0.54).
4. Discussion
The predictive precision obtained by our FRCNN model (0.78) is much higher than previously reported 0.41 mean average precision by [14], who used a Mask-RCNN architecture on overlapped plants. Though utilizing Mask-RCNN offers the prospective advantage of filtering individual plant masks from overlapping potato plants over ordinary FRCNN, [14] concede that accurate annotation of individual plants from canopy images of overlapped plants is difficult for domain experts and subsequently the trained models struggle to make accurate detections. Additionally, Mask-RCNN’s detection framework is based on FRCNN, however, [14] conducted their study using images taken later than four weeks after emergence, while our image acquisition was restricted to fewer than three weeks after emergence. Therefore, large improvements in precision observed in this study are partially due to less overlapping plants in the images, on account of earlier image acquisition. While [16] report accurate mapping of individual plant centroids in merged canopies, they did not report the average precision of their models. However, the inherent assumptions of the CentroidNet model in relation to potato plants reveal an underlying limitation that at least needs to be acknowledged; the radial expansion of a cluster of potato leaves from a centroid location is only likely to be valid in non-overlapping single-stem plants. Each planted potato tuber produces multiple competing stems that eventually function as independent plants, complicating the unit of plant density [1]. The direction of vectors learned from canopy leaf images are therefore expected to point towards the centroid of individual stems and not the overall plant object. Similarly, it is not practical for data annotation to be conducted in potatoes after a large degree of canopy consolidation because of the difficulty in assigning perceived individual main stems and leaves to individual plant units accurately. [14] also acknowledge this limitation in their data annotation and [13] acknowledge it as a source of error in their random-forest-based classification of potato plant numbers in an image from extracted plant object features. Because of these limitations, it can be considered impractical to conduct plant detection on images containing overlapped plants. While earlier image acquisition can solve the limitations, asynchrony in potato emergence days makes it difficult to determine an optimum day for obtaining a representative plant population. Beyond the scope of this study, striking a balance between premature and late imaging provides one potential solution to these challenges, which can be studied for each variety by evaluating model accuracy as a function of the number of days after planting. However, this would entail variety-specific recommendations for imaging time, which also need further calibration against factors that affect emergence rate like planting depth and average soil temperature. In this study, a geostatistical approach was chosen to create a sparse matrix of accurate plant density predictions at locations where no overlapping plants were observed.
In the two-stage (FRCNN detection then geostatistical interpolation) approach used in this study, we demonstrate that an accurate 2D surface of the variation in plant population density can be created from partially merged canopies, by conducting detections on non-overlapping plants and interpolating across the whole surface. Except for soil temperature and disease incidence, the factors that have been reported to contribute to asynchrony in potato emergence like variety, seed-tuber physiological age and apical-dominance-altering seed treatments vary at the seed-lot level [6]. It is therefore reasonable to assume that spatial variation in plant emergence early in the season is attributable to systematic inefficiencies in planting operations. With an nRMSE of 0.19 for the determination of actual plant numbers per image as well as a high R2 value (0.83), the current FRCNN model exhibits the robustness required to produce reliable field maps of spatial variation in plant density to inform precision agriculture decisions. Comparably, the image-analysis-based algorithm by [13] reported a high R2 value of 0.96. However, as noted by both [13] and [14], the algorithm is heavily dependent on the accurate production of a noise-free binary mask based on the Excess Green vegetation index, which is not always guaranteed and cannot distinguish between weeds and potato plants. The current FRCNN model therefore provides a robust modelling pipeline free of the complexity of generating potato image masks from vegetation indices deployed in the Mask-RCNN and random-forest-based image analysis algorithm.
The high correlation between satellite-imagery-derived NDVI and the FRCNN model results we report represents novel evidence of a link between early-season NDVI and potato plant density. Before canopy consolidation, NDVI is influenced by soil brightness in coarse-resolution imagery, which is normally corrected using the soil-adjusted vegetation index [26] when evaluating vegetation health. In the present study, non-adjusted NDVI was used with the premise that the level of interference from soil is dependent on the number of plants in the pixel. The high correlation value (r = 0.61) between the FRCNN modelled plant densities and the NDVI values substantiates this premise. A limitation to the use of satellite data for this purpose is the uncertain availability of cloud-free images after emergence before canopy consolidation (highlighted in this study by the lack of available cloud-free images within this window at Buttery Hill). Nevertheless, early-season NDVI can be calculated from UAVs hosting red and NIR sensors, down-sampled to reproduce the spectral mixing observed in satellite imagery.
Our findings agree with [3] that there is a significant negative effect of plant density on the number of tubers per plant. Additionally, [3] found a negative correlation between tuber size (measured as average tuber fresh weight in g) and plant density, in line with our results. In controlled-treatment studies, the effects of plant density on yield are largely inevitable due to large fixed differences in plant density between treatments that are not typically observed in commercial production field. Previous studies [2,3,4,5] report significant positive association between plant density and yield, in line with our observations at Buttery Hill. However, the relationship was not observed at Horse Foxhole, with yield more related to stem number than plant number. Literature [27] also points to a more significant relationship between yield and stem number than yield and plant number, with the latter explaining a negligible portion of the variation (R2 = 0.06).
Ultimately, the association between plant density and yield appears to be tenuous. While our findings suggest that areas of high plant density within a field produced more tubers per unit area, the number of marketable tubers at harvest was smaller. Assuming exponential growth in dry matter production over time [28,29], marketable tuber numbers can potentially be increased by delaying harvest timing in high density areas to allow for more tuber bulking. A utility of our main findings is that plant density maps produced from UAVs can be used as a basis for management and harvest decisions, such as variable in-season nitrogen management to delay senescence for tuber bulking purposes and subsequently incorporate variable vine desiccation and harvest timing.
5. Conclusions
This study demonstrated the feasibility of FRCNN-based models in the prediction of potato plant population and the subsequent production of representative 2D-density maps which can inform decisions on precision agriculture. This study leveraged prior information on the loss of accuracy of computer vision-based potato plant detection models once significant canopy consolidation is observed. The study integrated geostatistics to filter high quality model detections in non-overlapped field sections and interpolate 2D surfaces that provide useful insight beyond localized plant detection. Asynchrony in potato emergence means the trade-off between early and late image acquisition will always need to be balanced in order to make plant population assessments at the right time. Nevertheless, the goal of using UAVs in plant population modelling is mainly the accurate estimation of variation at the field-relevant spatial scale rather than per-plant pin-point accuracy. Therefore, the filtering and subsequent interpolation of reliable non-merged FRCNN predictions provides a work-around to the problems of overlapping plants. This study also demonstrated that plant density maps produced from the integration of deep learning with geostatistical analysis are consistent with early-season satellite-imagery-derived NDVI scores. For the first time, this finding shows the validity of using satellite data to estimate plant population at emergence stage in potatoes. In this case, this finding also shows that UAVs can be used to provide a high throughput method of calibrating or verifying functions produced from multispectral analysis of satellite data. Plant counting algorithms for potatoes have captured the interest of several computer vision and deep learning researchers, and therefore improvements in the CNN architecture and object detection frameworks can be reasonably expected, especially in the direction on the CentroidNet architecture. However, it was shown that a simple framework like FRCNN are adequate for predicting plant population and the resultant predictions were shown to correlate with yield components, therefore showing that useful models can be obtained without the ever-increasing complexities of modelling the “perfect” plant detector with novel convolutional neural network architecture.
Author Contributions
Conceptualization, J.K.M.; methodology, J.K.M., J.M.M., E.W.H.; validation, J.K.M., E.W.H.; investigation, J.M.M., J.K.M.; resources, J.M.M.; data curation, J.K.M.; writing—original draft preparation, J.K.M.; writing—review and editing, J.K.M., J.M.M., E.W.H., R.G.; visualization, J.K.M.; supervision, J.M.M., E.W.H.; project administration, J.M.M.; funding acquisition, J.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Agriculture and Horticulture Development Board, Stoneleigh Park, Kenilworth, Warwickshire, CV8 2TL, United Kingdom Project Number 11140054.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to Intellectual Property Regulations.
Acknowledgments
Acknowledgement to the Crops and Environment Research Centre of Harper Adams University (TF10 8NB, Edgmond, Shropshire, United Kingdom) for providing the experimental sites for this study and the National Centre for Precision Farming at Harper Adams University for the operation of UAVs during image acquisition.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, E.J.; Wurr, D.C.E. Plant density. In Potato Crop; Springer: Dordrecht, The Netherlands, 1992; pp. 292–333. [Google Scholar] [CrossRef]
- Arsenault, W.J.; LeBlanc, D.A.; Tai, G.C.C.; Boswall, P. Effects of nitrogen application and seedpiece spacing on yield and tuber size distribution in eight potato cultivars. Am. J. Potato Res. 2001. [Google Scholar] [CrossRef]
- Knowles, N.R.; Knowles, L.O. Manipulating stem number, tuber set, and yield relationships for northern- and southern-grown potato seed lots. Crop Sci. 2006. [Google Scholar] [CrossRef]
- Love, S.L.; Thompson-Johns, A. Seed piece spacing influences yield, tuber size distribution, stem and tuber density, and net returns of three processing potato cultivars. HortScience 1999. [Google Scholar] [CrossRef] [Green Version]
- Bohl, W.H.; Stark, J.C.; McIntosh, C.S. Potato Seed Piece Size, Spacing, and Seeding Rate Effects on Yield, Quality and Economic Return. Am. J. Potato Res. 2011, 88, 470–478. [Google Scholar] [CrossRef]
- Sankaran, S.; Quirós, J.J.; Knowles, N.R.; Knowles, L.O. High-Resolution Aerial Imaging Based Estimation of Crop Emergence in Potatoes. Am. J. Potato Res. 2017, 94, 658–663. [Google Scholar] [CrossRef]
- Gates, D.M.; Keegan, H.J.; Schleter, J.C.; Weidner, V.R. Spectral Properties of Plants. Appl. Opt. 1965. [Google Scholar] [CrossRef]
- dos Santos, L.M.; de Souza Barbosa, B.D.; Diotto, A.V.; Andrade, M.T.; Conti, L.; Rossi, G. Determining the Leaf Area Index and Percentage of Area Covered by Coffee Crops Using UAV RGB Images. IEEE J. Sel. Top Appl. Earth Obs. Remote Sens. 2020, 13, 6401–6409. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Song, S.; Xu, K.; Hu, T.; Yang, Q.; Wu, F.; Xu, G.; Ma, Q.; Guan, H.; et al. Non-destructive estimation of field maize biomass using terrestrial lidar: An evaluation from plot level to individual leaf level. Plant Methods 2020, 16, 69. [Google Scholar] [CrossRef]
- Franceschini, M.H.D.; Bartholomeus, H.; van Apeldoorn, D.F.; Suomalainen, J.; Kooistra, L. Feasibility of Unmanned Aerial Vehicle Optical Imagery for Early Detection and Severity Assessment of Late Blight in Potato. Remote Sens. 2019, 11, 224. [Google Scholar] [CrossRef] [Green Version]
- Fernandez-Gallego, J.A.; Lootens, P.; Borra-Serrano, I.; Derycke, V.; Haesaert, G.; Roldán-Ruiz, I.; Araus, J.L.; Kefauver, S.C. Automatic wheat ear counting using machine learning based on RGB UAV imagery. Plant J. 2020, 103, 1603–1613. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, J.; Yang, C.; Zhou, G.; Ding, Y.; Shi, Y.; Zhang, D.; Xie, J.; Liao, Q. Rapeseed Seedling Stand Counting and Seeding Performance Evaluation at Two Early Growth Stages Based on Unmanned Aerial Vehicle Imagery. Front. Plant Sci. 2018, 9, 1362. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Han, J.; Zhang, L.; Bian, C.; Jin, L.; Liu, J. The estimation of crop emergence in potatoes by UAV RGB imagery. Plant Methods 2019, 15, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Machefer, M.; Lemarchand, F.; Bonnefond, V.; Hitchins, A.; Sidiropoulos, P. Mask R-CNN Refitting Strategy for Plant Counting and Sizing in UAV Imagery. Remote Sens. 2020, 12, 3015. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Long, J.; Chen, H. An Improved Median-based Otsu Image Thresholding Algorithm. AASRI Procedia 2012, 3, 468–473. [Google Scholar] [CrossRef]
- Dijkstra, K.; van de Loosdrecht, J.; Schomaker, L.R.B.; Wiering, M.A. CentroidNet: A Deep Neural Network for Joint Object Localization and Counting. In Machine Learning and Knowledge Discovery in Databases; ECML PKDD 2018. Lecture Notes in Computer Science; Brefeld, U., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Jefferies, R.A.; Lawson, H.M. A key for the stages of development of potato (Solatium tuberosum). Ann. Appl. Biol. 1991, 119, 387–399. [Google Scholar] [CrossRef]
- Bohl, W.H.; Love, S.L. Effect of planting depth and hilling practices on total, U.S. No. 1, and field greening tuber yields. Am. J. Potato Res. 2005, 82, 441–450. [Google Scholar] [CrossRef]
- Taylor, J.A.; Chen, H.; Smallwood, M.; Marshall, B. Investigations into the opportunity for spatial management of the quality and quantity of production in UK potato systems. Field Crop Res. 2018. [Google Scholar] [CrossRef] [Green Version]
- MATLAB. version 9.8.0 (R2020a); The MathWorks Inc.: Natick, MA, USA, 2020; Available online: https://www.mathworks.com/products/get-matlab.html (accessed on 11 September 2020).
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Li, F.-F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015—Conference Track Proceedings, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Pix4dmapper Pro. Available online: https://pix4d.com/product/pix4dmapper/ (accessed on 13 July 2020).
- ESRI. ArcGIS Pro (Version 2.5.2); Environmental Systems Research Institute: West Redlands, CA, USA, 2020; Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview (accessed on 22 September 2020).
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Bussan, A.J.; Mitchell, P.D.; Copas, M.E.; Drilias, M.J. Evaluation of the effect of density on potato yield and tuber size distribution. Crop Sci. 2007. [Google Scholar] [CrossRef]
- Goudriaan, J.; Monteith, J.L. A Mathematical Function for Crop Growth Based on Light Interception and Leaf Area Expansion. Ann. Bot. 1990, 66, 695–701. [Google Scholar] [CrossRef] [Green Version]
- Haverkort, A.J.; MacKerron, D.K.L. (Eds.) Potato Ecology and Modelling of Crops under Conditions Limiting Growth; Springer: Dordrecht, The Netherlands, 1995; Volume 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).