Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission †
Abstract
1. Introduction
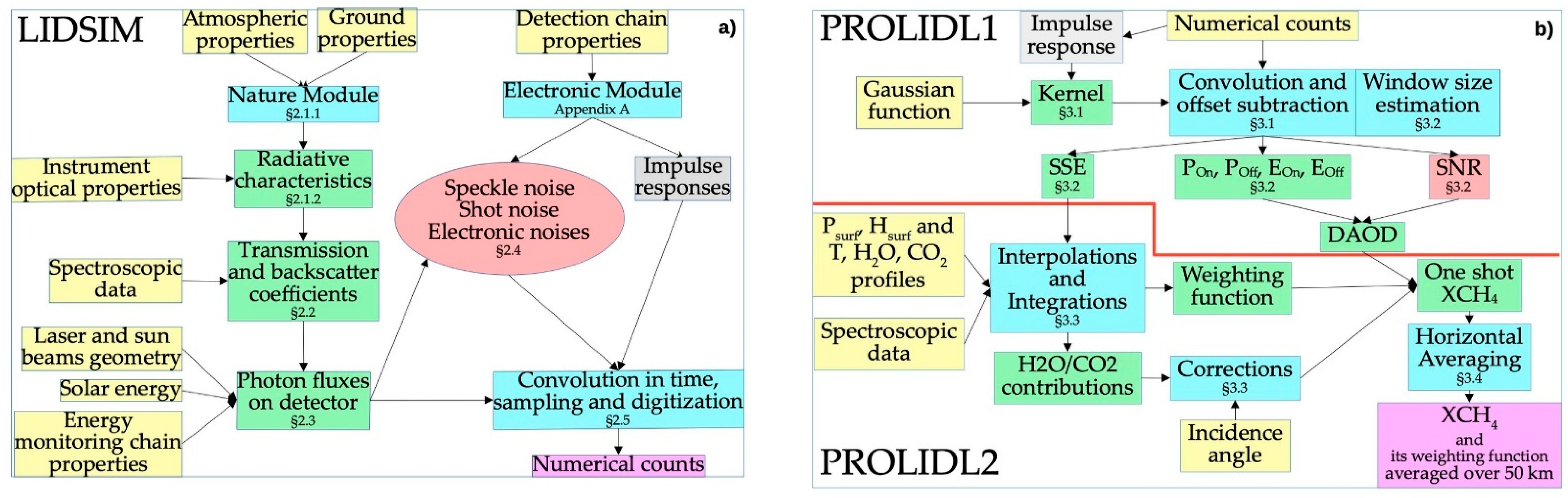
2. LIDSIM: Simulating Lidar Signal
2.1. Ground and Atmosphere Description
2.1.1. Physical and Chemical Properties
2.1.2. Radiative Properties
2.2. From Radiative Properties to Transmission and Backscatter Coefficients
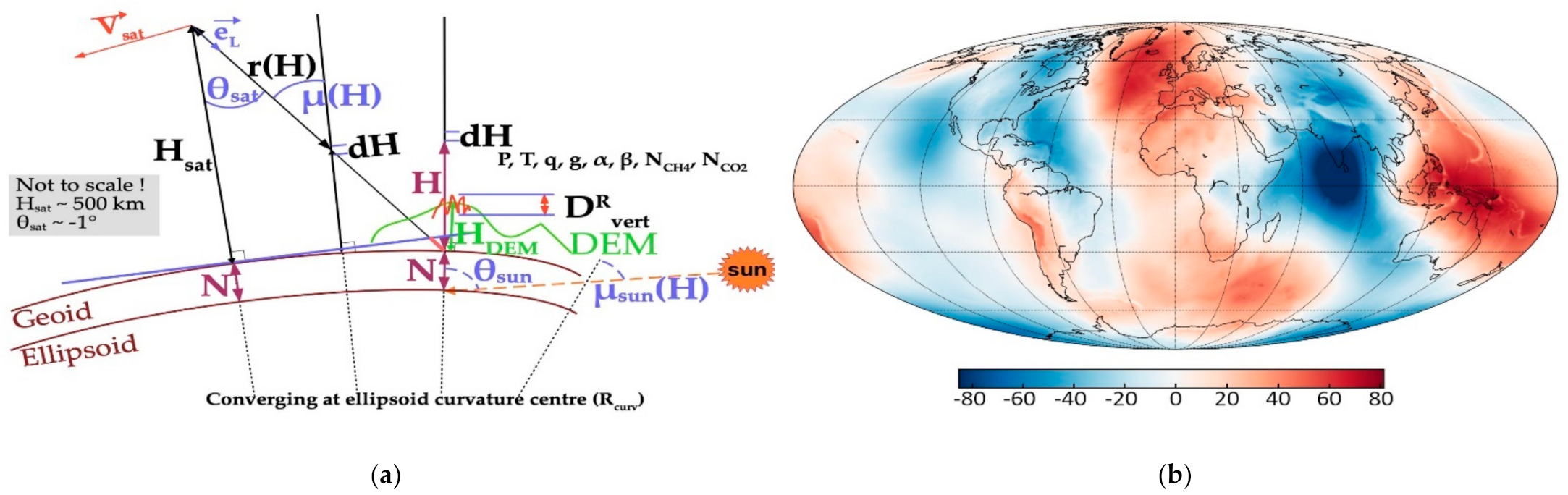
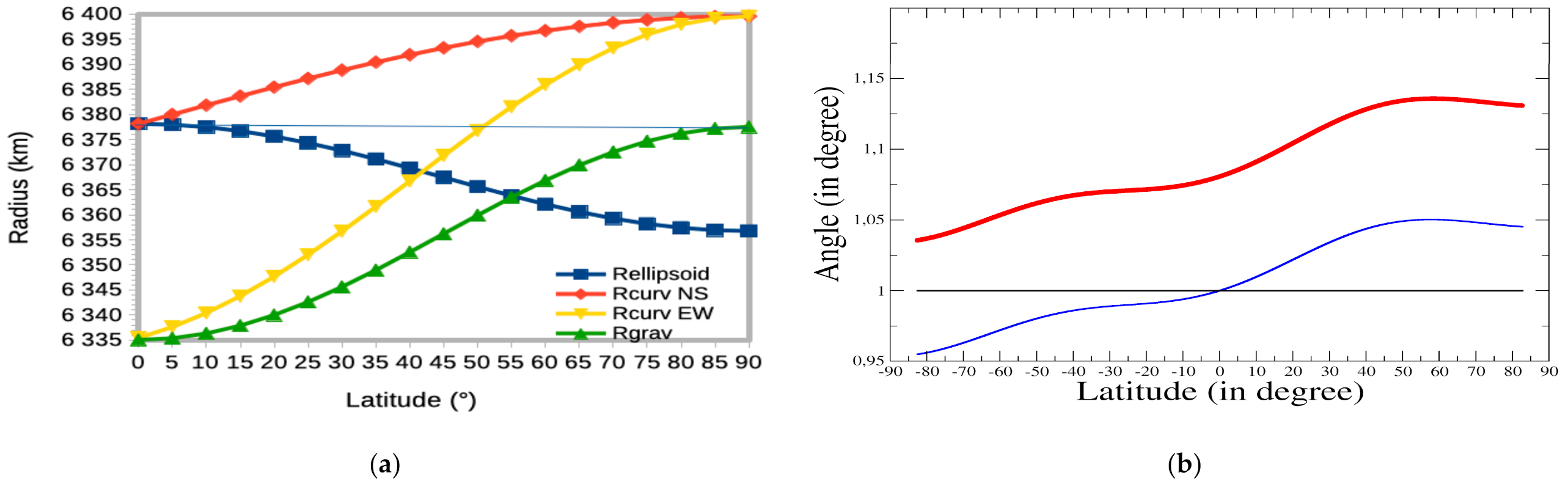
2.2.1. Observation Geometry and Vertical Coordinates
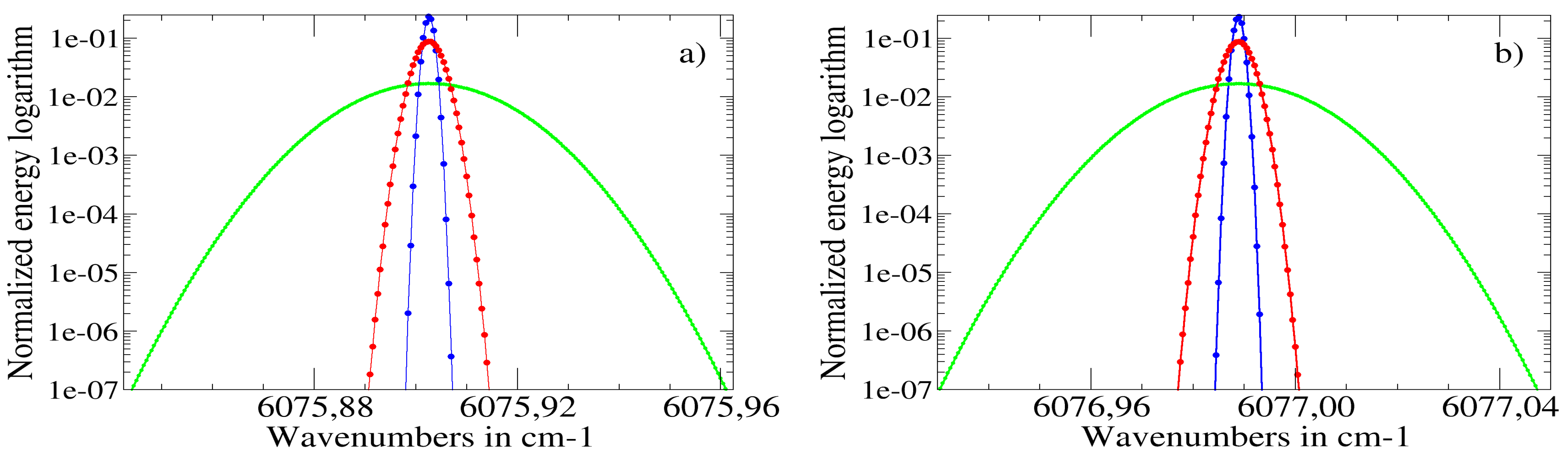
2.2.2. Spectral Distribution of the Lidar Emission and Doppler Effects
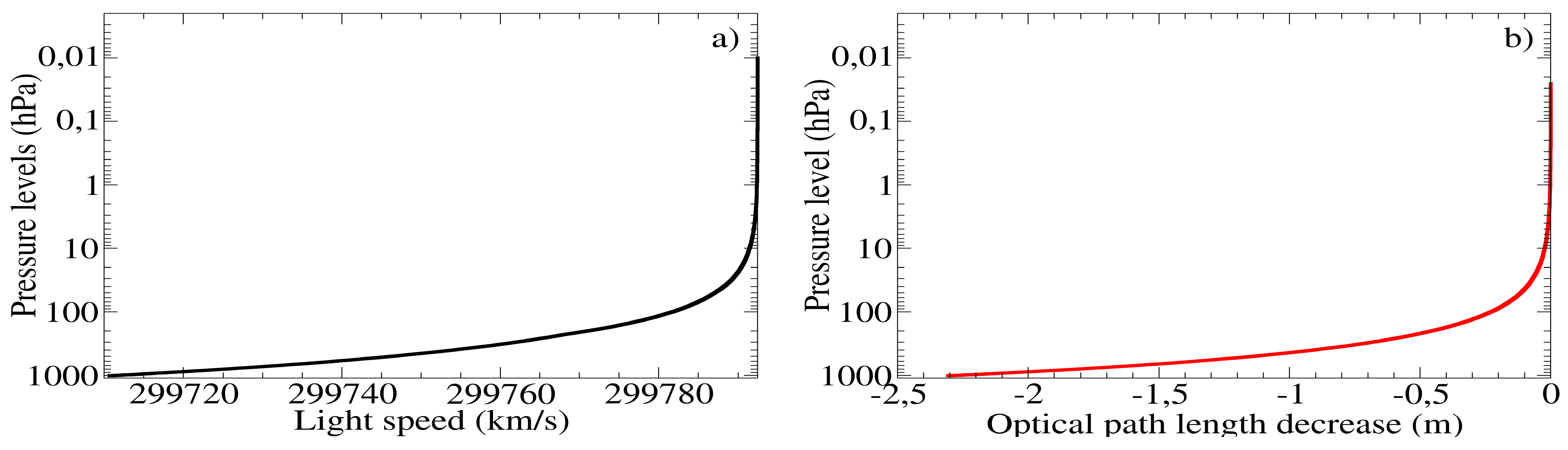
2.2.3. Vertical Distribution of Transmission and Backscatter Coefficients
2.3. Radiative Fluxes on the Detector
2.3.1. From Emitted Lidar Pulses to Backscattered Fluxes on the Detector
2.3.2. Solar Flux
2.3.3. Energy Monitoring Fluxes
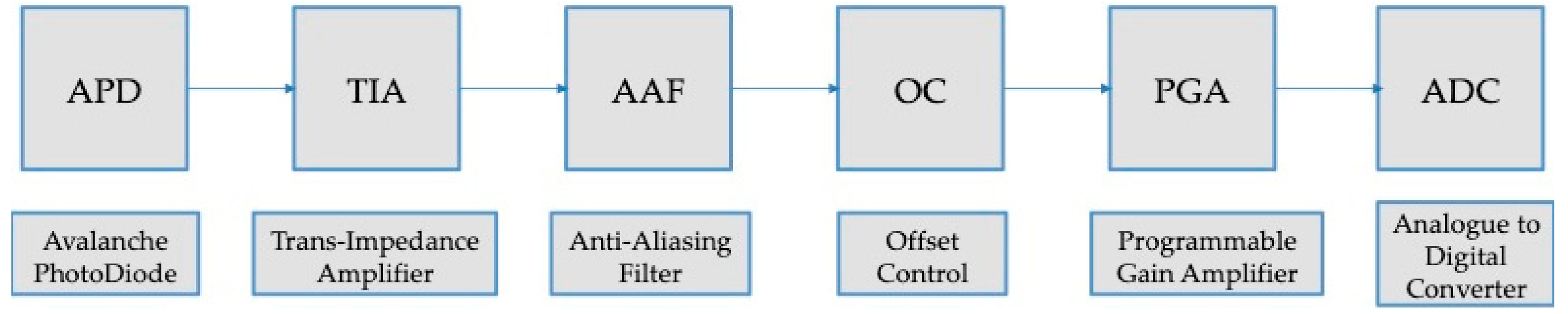
2.4. Electronic Chain and Noises
2.4.1. Speckle Effects
2.4.2. Shot Noise
2.4.3. Photoelectric Effect and Avalanche Process in the APD
2.4.4. Electronics Noises
2.5. From Radiative Fluxes to Digitised Signal
3. PROLID: Processing Lidar Data
3.1. Preliminary Treatments
3.2. Estimations
3.2.1. Elevation of the Scattering Target
3.2.2. Energy Peaks and Their Variability
3.2.3. DAOD along the Optical Path
3.3. XCH4 Retrieval
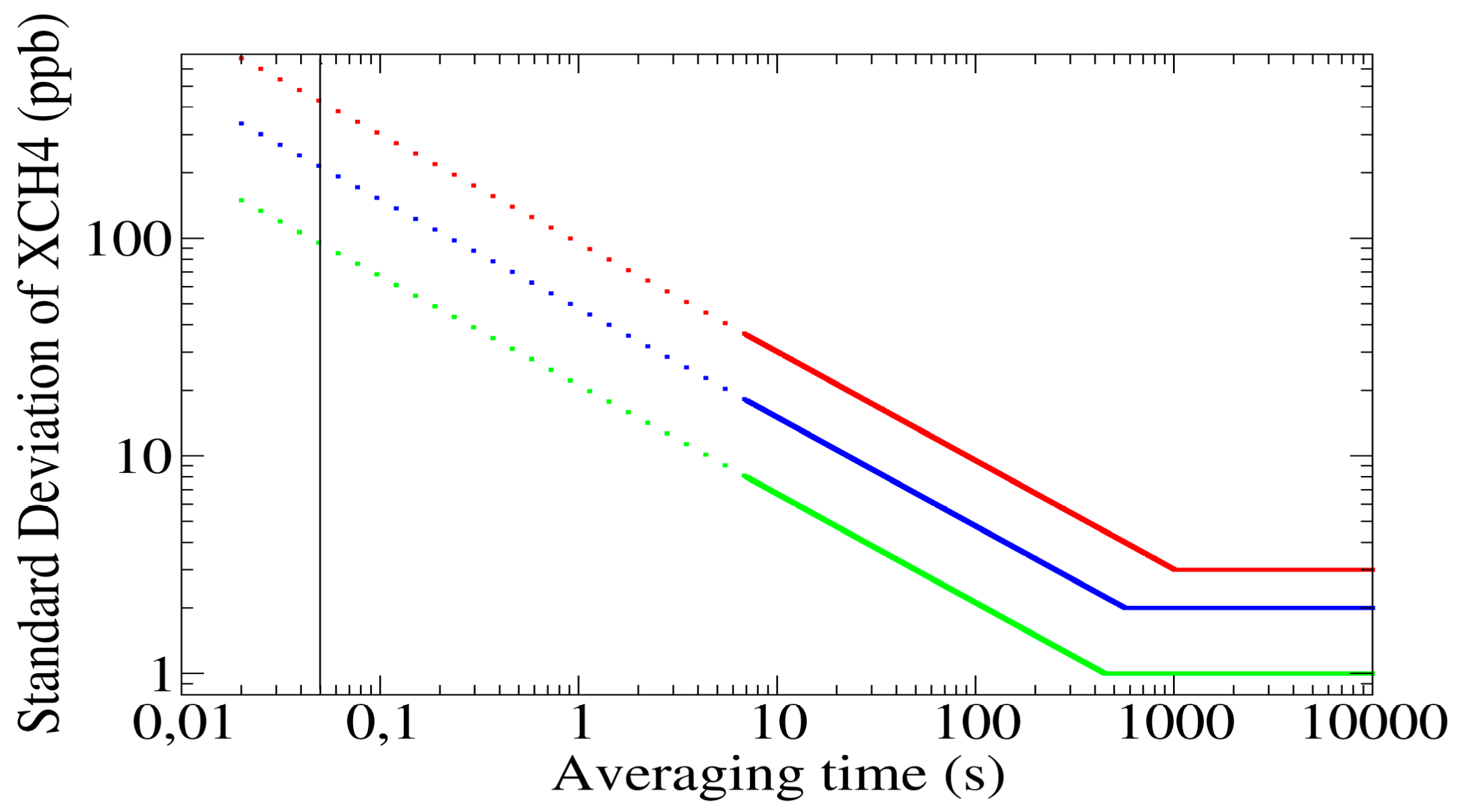
3.4. Averaging
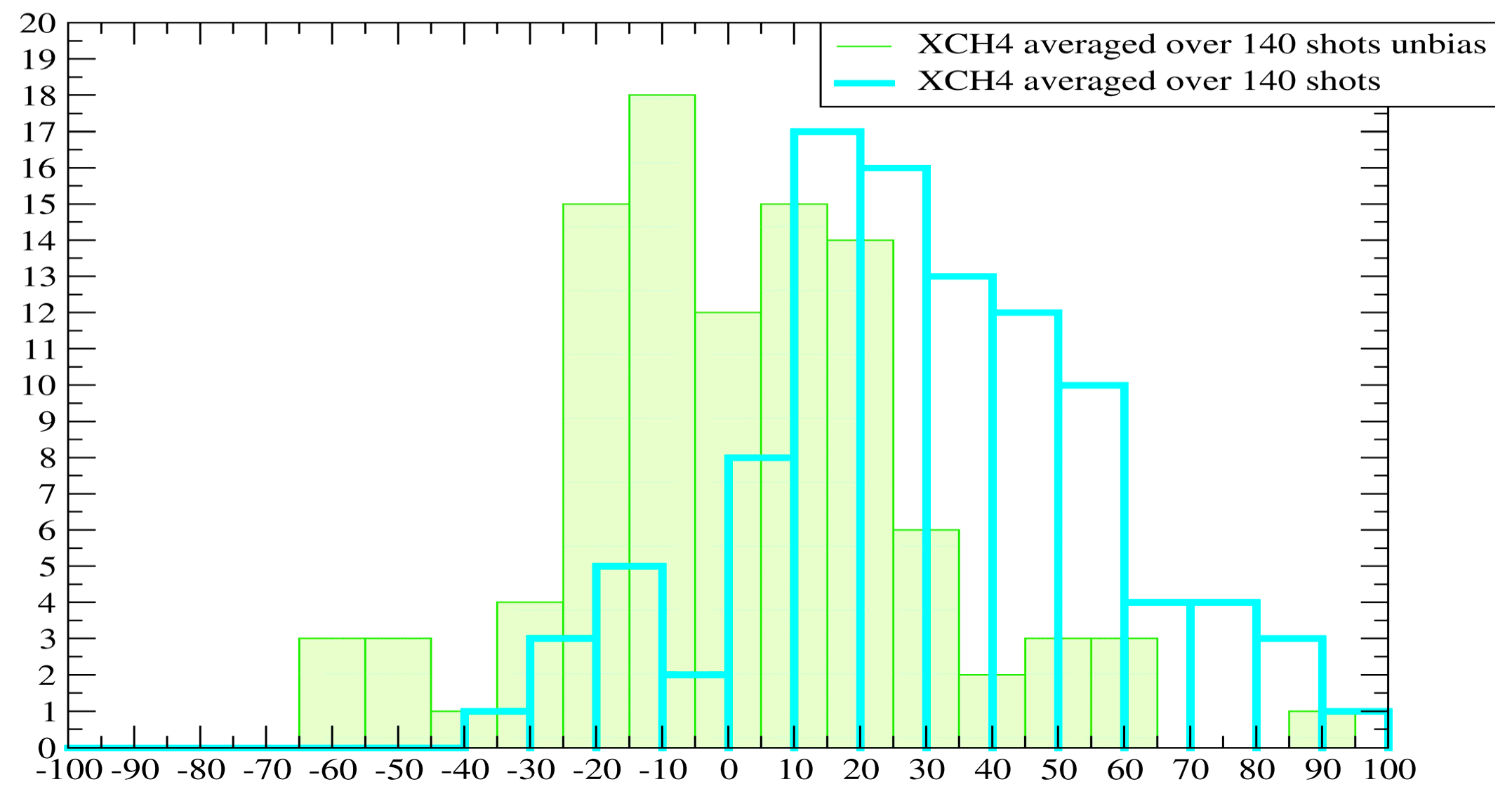
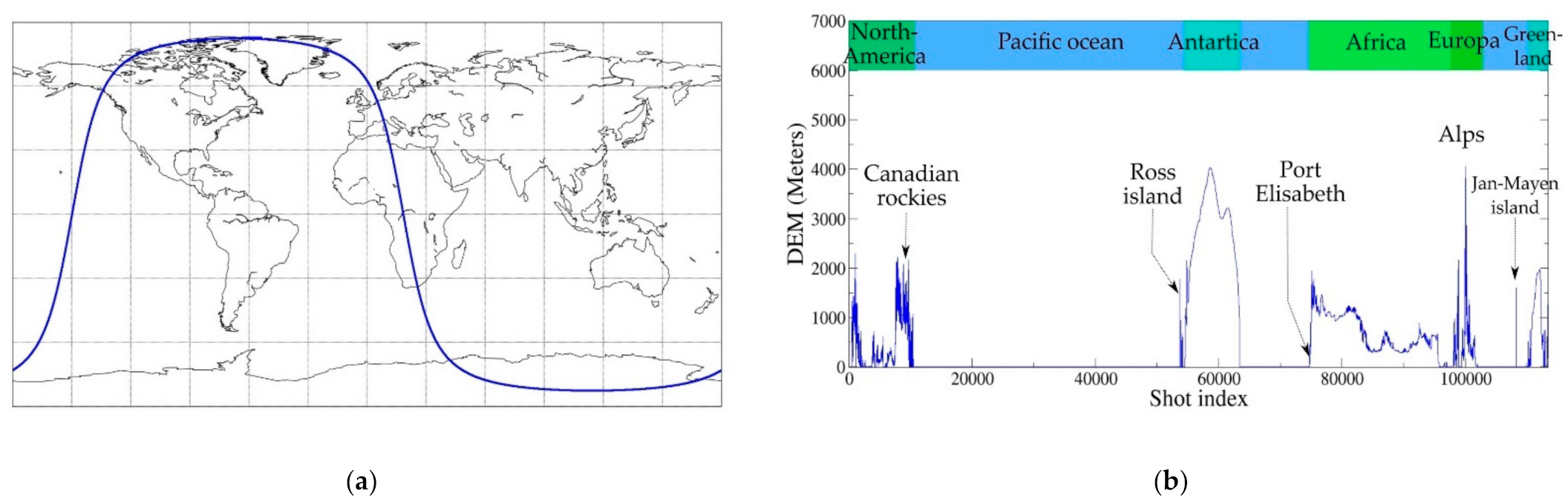
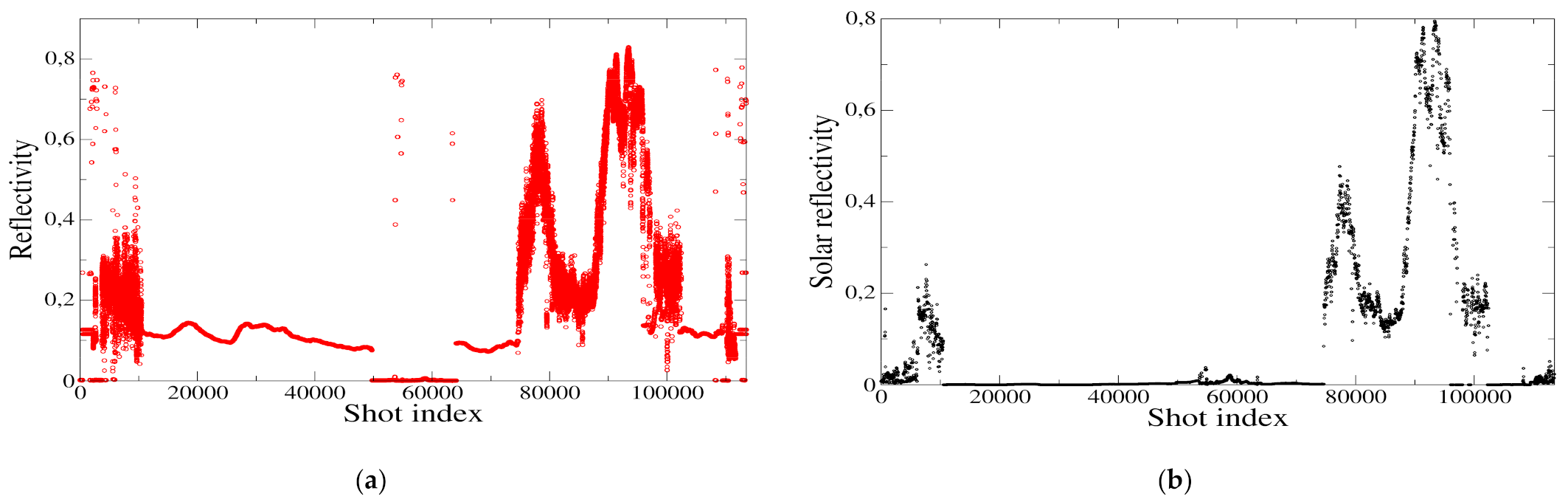
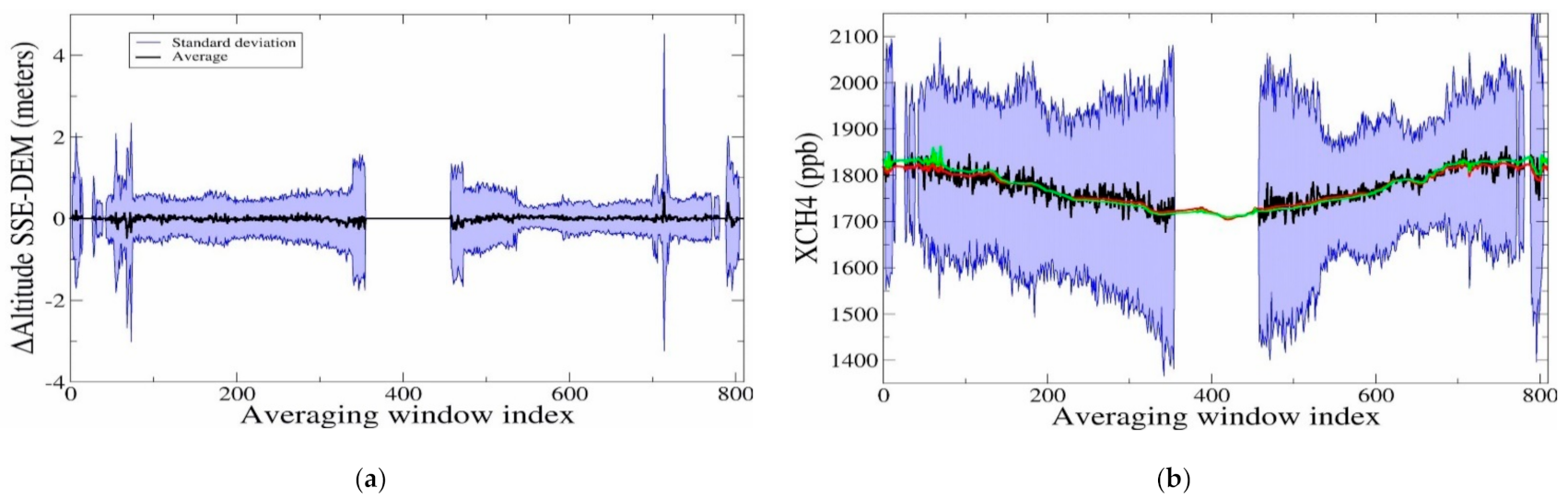
4. Results and Discussion
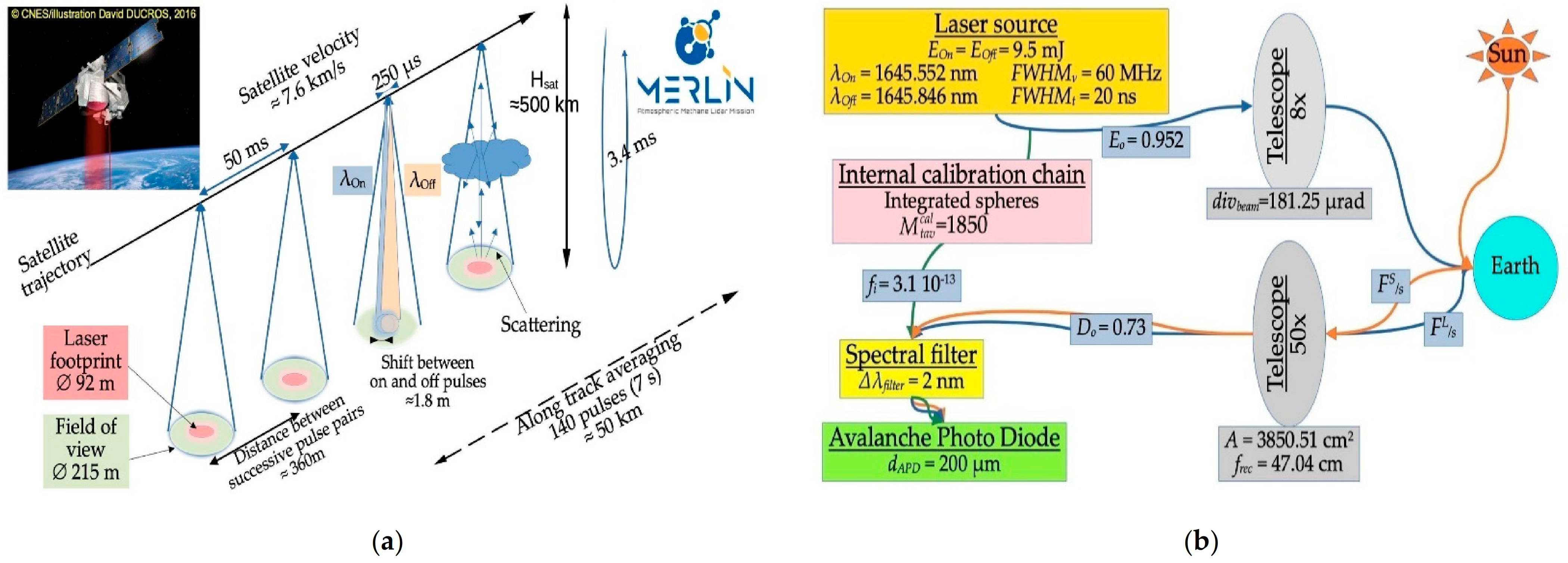
4.1. Order of Magnitude of Some Characteristic Values
4.2. Signal Validation
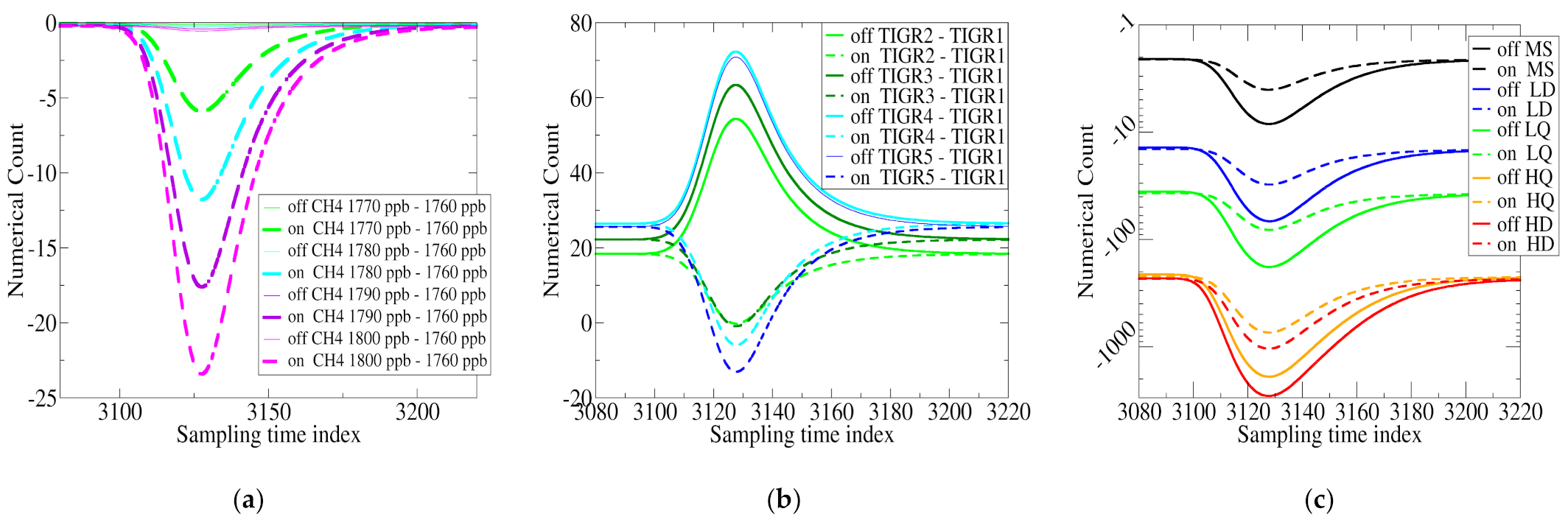
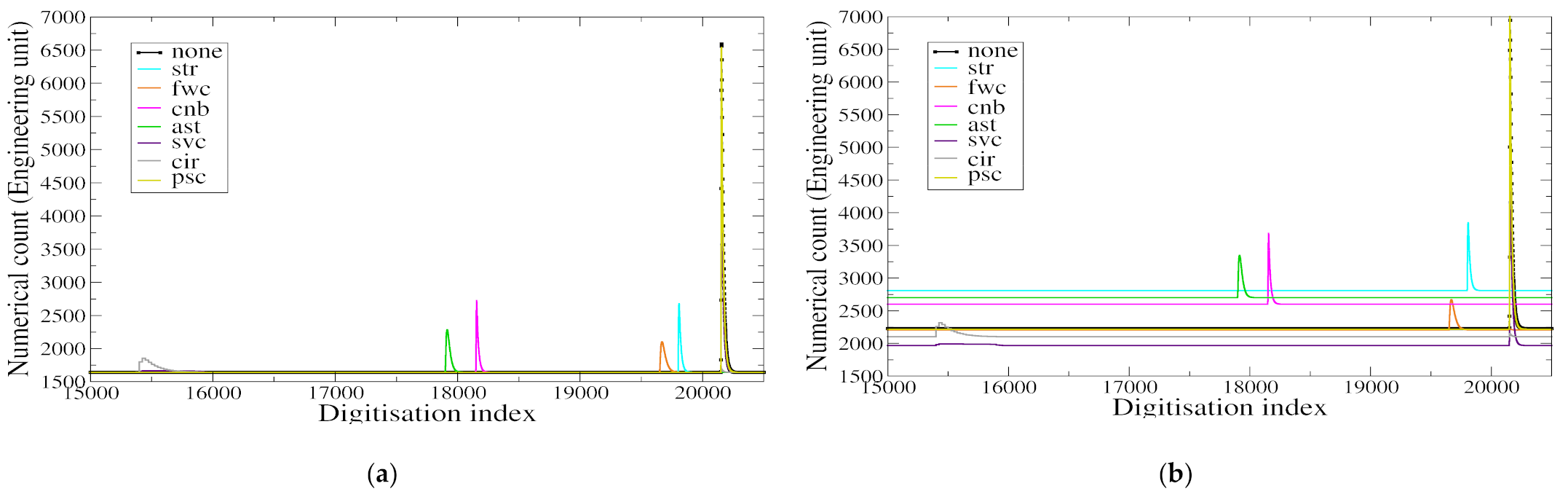
4.3. Noise Impact
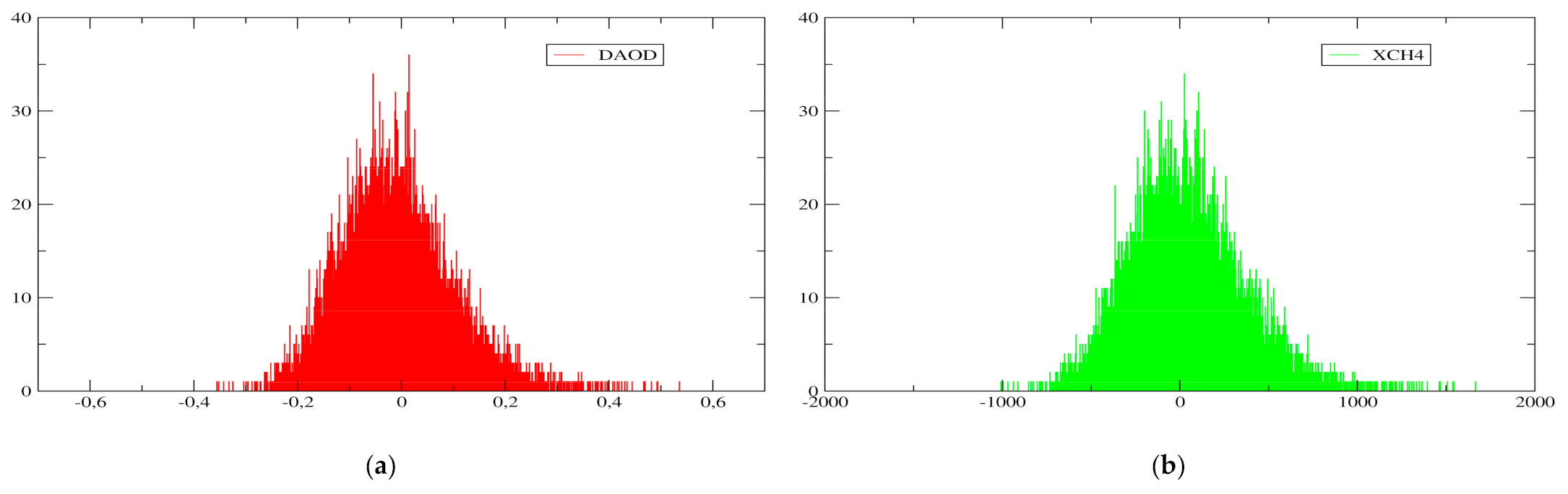
4.4. Full Orbit Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
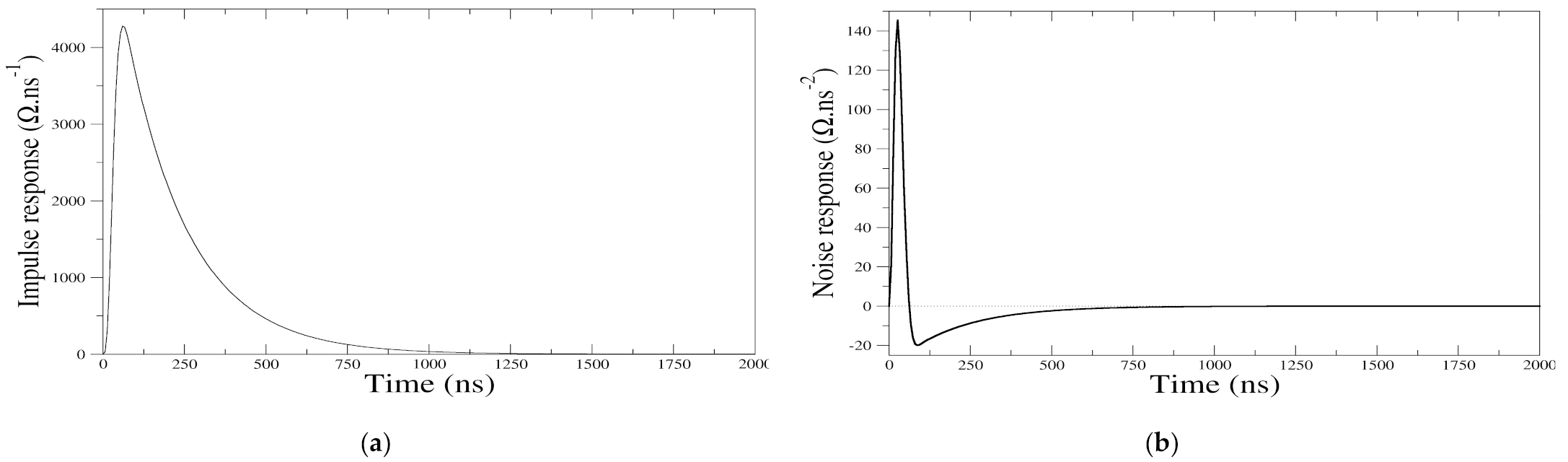
Appendix A. Impulse Response Functions

Appendix B. Interpolation Procedure for Resampling a Data Set While Maintaining the Total Number of Photons
References
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.B.; Bovensmann, H.; Burrows, J.P.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef]
- Bousquet, P.; Pierangelo, C.; Bacour, C.; Marshall, J.; Peylin, P.; Ayar, P.V.; Ehret, G.; Bréon, F.M.; Chevallier, F.; Crevoisier, C.; et al. Error Budget of the MEthane Remote LIdar missioN and Its Impact on the Uncertainties of the Global Methane Budget. JGR Atmos. 2018, 123, 766–785. [Google Scholar] [CrossRef]
- Crevoisier, C.; Clerbaux, C.; Guidard, V.; Phulpin, T.; Armante, R.; Barret, B.; Camy-Peyret, C.; Chaboureau, J.P.; Coheur, P.F.; Crpeau, L.; et al. Towards IASI-new generation (IASI-NG): Impact of improved spectral resolution and radiometric noise on the retrieval of thermodynamic, chemistry and climate variables. Atmos. Meas. Tech. 2014, 7, 4367–4385. [Google Scholar] [CrossRef]
- Irizar, J.; Melf, M.; Bartsch, P.; Koehler, J.; Weiss, S.; Greinacher, R.; Erdmann, M.; Kirschner, V.; Perez Albinana, A.; Martin, D. Sentinel-5/UVNS. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 12 July 2019; Volume 11180, p. 1118004. [Google Scholar] [CrossRef]
- Cressot, C.; Chevallier, F.; Bousquet, P.; Crevoisier, C.; Dlugokencky, E.J.; Fortems-Cheiney, A.; Frankenberg, C.; Parker, R.; Pison, I.; Scheepmaker, R.A.; et al. On the consistency between global and regional methane emissions inferred from SCIAMACHY, TANSO-FTS, IASI and surface measurements. Atmos. Chem. Phys. 2014, 14, 577–592. [Google Scholar] [CrossRef]
- GAW Report n°213. In Proceedings of the 17th WMO/IAEA Meeting on Carbon Dioxide, Other Greenhouse Gases and Related Tracers Measurement Techniques (GGMT-2013), Beijing, China, 10–13 June 2013; World Meteorological Organization: Geneva, Switzerland, 2014.
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption Lidar: A sensitivity analysis. Appl. Phys. B Lasers Opt. 2008, 90, 593–608. [Google Scholar] [CrossRef]
- Frankenberg, C.; Aben, I.; Bergamaschi, P.; Dlugokencky, E.J.; Van Hees, R.; Houweling, S.; Van der Meer, P.; Snel, R.; Tol, P. Global column-averaged methane mixing ratios from 2003 to 2009 as derived from SCHIAMACHY:Trends and variability. J. Geophys. Res. Atmos. 2011, 116, D04302. [Google Scholar] [CrossRef]
- Butz, A.; Guerlet, S.; Hasekamp, O.; Schepers, D.; Galli, A.; Aben, I.; Frankenberg, C.; Hartmann, J.M.; Tran, H.; Kuze, A.; et al. Toward accurate CO2 and CH4 observations from GOSAT. Geophys. Res. Lett. 2011, 38, L14812. [Google Scholar] [CrossRef]
- Morino, I.; Uchino, O.; Inoue, M.; Yoshida, Y.; Yokota, T.; Wennberg, P.O.; Toon, G.C.; Wunch, D.; Roehl, C.M.; Notholt, J.; et al. Preliminary validation of column-averaged volume mixing ratios of carbon dioxide and methane retrieved from GOSATshort-wavelength infrared spectra. Atmos. Meas. Tech. 2011, 4, 1061–1076. [Google Scholar] [CrossRef]
- Crevoisier, C.; Nobileau, D.; Fiore, A.M.; Armante, R.; Chedin, A.; Scott, N.A. Tropospheric methane in the tropics—First year from IASI hyperspectral infrared observations. Atmos. Chem. Phys. 2009, 9, 6337–6350. [Google Scholar] [CrossRef]
- Hu, H.; Landgraf, J.; Detmers, R.; Borsdorff, T.; Aan de Brugh, J.; Aben, I.; Butz, A.; Hasekamp, O. Toward Global Mapping of Methane with TROPOMI: First Results and Intersatellite Comparison to GOSAT. Geophys. Res. Lett. 2018, 45, 3682–3689. [Google Scholar] [CrossRef]
- Glumb, R.; Davis, G.; Lietzke, C. The TANSO-FTS-2 instrument for the GOSAT-2 greenhouse gas monitoring mission. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 6 November 2014; pp. 1238–1240. [Google Scholar] [CrossRef]
- Kiemle, C.; Quatrevalet, M.; Ehret, G.; Amediek, A.; Fix, A.; Wirth, M. Sensitivity studies for a space-based methane lidar mission. Atmos. Meas. Tech. 2011, 4, 2195–2211. [Google Scholar] [CrossRef]
- Nikolov, S.; Wührer, C.; Kühl, C.; Bode, M.; Hupfer, W.; Lucarelli, S. MERLIN: Design of an IPDA LIDAR instrument. CEAS Space J. 2019, 11, 437–457. [Google Scholar] [CrossRef]
- Amediek, A.; Fix, A.; Wirth, M.; Ehret, G. Development of an OPO system at 1.57 μm for integrated path DIAL measurement of atmospheric carbon dioxide. Appl. Phys. 2008, 92, 295. [Google Scholar] [CrossRef]
- Tellier, Y.; Pierangelo, C.; Wirth, M.; Gibert, F.; Marnas, F. Averaging bias correction for the future space-borne methane IPDA lidar mission MERLIN. Atmos. Meas. Tech. 2018, 11, 5865–5884. [Google Scholar] [CrossRef]
- Fix, A.; Quatrevalet, M.; Amediek, A.; Wirth, M. Energy calibration of integrated path differential absorption lidars. Appl. Opt. 2018, 57, 7501–7514. [Google Scholar] [CrossRef]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Büdenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. CHARM-F a new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef] [PubMed]
- Wirth, M. MERLIN ATBD: Algorithm Theoretical Basis Document Part 1/Top Level Algorithms for Primary L1/2 Products: MLN-PLDP-ATBD-90001-PI, Version 1, Revision 2; CNES: Toulouse, France, 2018.
- Newell, D.; Tiesinga, E. The International System of Units (SI), 2019 Edition, Special Publication (NIST SP), National Institute of Standards and Technology, Gaithersburg, MD, USA. Available online: https://doi.org/10.6028/NIST.SP.330-2019 (accessed on 1 July 2021).
- Haynes, W.M. (Ed.) Handbook of Chemistry and Physics, 97th ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 2643. ISBN 978-1498754293. [Google Scholar]
- COESA (Committee on Extension to the Standard Atmosphere). U.S. Standard Atmosphere, 1976; U.S. Government Printing Office: Washington, DC, USA, 1976. Available online: https://www.ngdc.noaa.gov/stp/space-weather/online-publications/miscellaneous/us-standard-atmosphere-1976/us-standard-atmosphere_st76-1562_noaa.pdf (accessed on 1 July 2021).
- Chevallier, F.; Chédin, A.; Chéruy, F.; Morcrette, J.-J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation. Q. J. R. Meteorol. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- Reference Model of the Atmosphere. Internal Report, ESA, EOP-PI/2006-12-19 Issue 02. 2006. Available online: https://earth.esa.int/eogateway/documents/20142/37627/Aeolus-L1B-Algorithm-ATBD.pdf (accessed on 1 July 2021).
- Capderou, M. Handbook of Satellite Orbits; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Morcrette, J.J.; Boucher, O.; Jones, L.; Salmond, D.; Bechtold, P.; Beljaars, A.; Benedetti, A.; Bonet, A.; Kaiser, J.W.; Razinger, M.; et al. Aerosol analysis and forecast in the ECMWF Integrated Forecast System. Part I: Forward modelling. J. Geophys. Res. 2009, 114, D06206. [Google Scholar] [CrossRef]
- Benedetti, A.; Morcrette, J.J.; Boucher, O.; Dethof, A.; Engelen, R.J.; Fisher, M.; Flentje, H.; Huneeus, N.; Jones, L.; Kaiser, W.; et al. Aerosol analysis and forecast in the ECMWF Integrated Forecast System. Part II: Data assimilation. J. Geophys. Res. 2009, 114, D13205. [Google Scholar] [CrossRef]
- Agusti-Panareda, A.; Diamantakis, M.; Bayona, V.; Klappenbach, F.; Butz, A. Improving the inter-hemispheric gradient of total column atmospheric CO2 and CH4 in simulations with the ECMWF semi-Lagrangian atmospheric global model. Geosci. Model Dev. 2017, 10, 1–18. [Google Scholar] [CrossRef]
- Robinson, N.; Regetz, J.; Guralnick, R.P. EarthEnv-DEM90: A nearly-global, void-free, multi-scale smoothed, 90m digital elevation model from fused ASTER and SRTM data. ISPRS J. Photogramm. Remote Sens. 2014, 87, 57–67. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); US Department of the Interior; US Geological Survey Open File Report, 2011. Available online: http://pubs.usgs.gov/of/2011/1073/pdf/of2011-1073.pdf (accessed on 1 July 2021).
- Jacquinet-Husson, N.; Armante, R.; Scott, N.A.; Chedin, A.; Crépeau, L.; Boutammine, C.; Bouhdaoui, A.; Crevoisier, C.; Capelle, V.; Boonne, C.; et al. The 2015 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 2016, 327, 31–72. [Google Scholar] [CrossRef]
- Delahaye, T.; Maxwell, S.E.; Reed, Z.D.; Lin, H.; Hodges, J.T.; Sung, K.; Devi, V.; Warneke, T.; Tran, H. Precise methane absorption measurements in the 1.64 μm spectral region for the MERLIN mission. JGR Atmos. 2016, 121, 7360–7370. [Google Scholar] [CrossRef]
- Delahaye, T.; Ghysels, M.; Hodges, J.T.; Sung, K.; Armante, R.; Tran, H. Measurement and modeling of air-broadened methane absorption in the MERLIN spectral region at low temperatures. JGR Atmos. 2019, 124, 3556–3564. [Google Scholar] [CrossRef]
- Vasilchenko, S.; Tran, H.; Mondelain, D.; Kassi, S.; Campargue, A. Accurate absorption spectroscopy of water vapour near 1.64 µm in support of the MEthane Remote LIdar missioN (MERLIN). J. Quant. Spectrosc. Radiat. Transf. 2019, 235, 332–342. [Google Scholar] [CrossRef]
- Scott, N.A.; Chédin, A. A fast line-by-line method for atmospheric absorption computations: The Automatized Atmospheric Absorption Atlas. J. Appl. Meteor. 1981, 20, 802–812. [Google Scholar] [CrossRef]
- Chéruy, F.; Scott, N.A.; Armante, R.; Tournier, B.; Chedin, A. Contribution to the development of radiative transfer models for high spectral resolution observations in the infrared. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 597–611. [Google Scholar] [CrossRef]
- Ngo, N.H.; Lisak, D.; Tran, H.; Hartmann, J.-M. An isolated line-shape model to go beyond the Voigt profile in spectroscopic databases and radiative transfer codes. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 89–100. [Google Scholar] [CrossRef]
- Vaughan, J.M.; Brown, D.W.; Nash, C.; Alejandro, S.B.; Koenig, G.G. Atlantic atmospheric aerosol studies: 2. Compendium of airborne backscatter measurements at 10.6μm. JGR Atmos. 1995, 100, 1043–1065. [Google Scholar] [CrossRef]
- Meador, W.E.; Weaver, W.R. Two-stream approximations to radiative transfer in planetary atmospheres: A unified description of existing methods and a new improvement. J. Atmos. Sci. 1980, 37, 630–643. [Google Scholar] [CrossRef]
- Peng, Y.; Lohmann, U.; Leaitch, R.; Banic, C.; Couture, M. The cloud albedo-cloud droplet effective radius relationship for clean and polluted clouds from RACE and FIRE.ACE. JGR Atmos. 2002, 107, AAC 1-1–AAC 1-6. [Google Scholar] [CrossRef]
- Vermote, E.F.; Roger, J.C.; Ray, J.P. MODIS Surface Reflectance User’s Guide (Collection 6, Version 1.4). May 2015. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD09_UserGuide_v1.4.pdf (accessed on 1 July 2021).
- Bréon, F.-M.; Maignan, F.; Leroy, M.; Grant, I. Analysis of hopt spot directional signatures measured from space. JGR Atmos. 2002, 107, AAC 1-1–AAC 1-15. [Google Scholar] [CrossRef]
- Maignan, F.; Bréon, F.-M.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the hot spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar] [CrossRef]
- Noveltis Consortium. A Surface Reflectance DAtabase for ESA’s Earth Observation Missions (ADAM) Technical Note 4 for ESA Study Contract Nr C4000102979, NOV-3895-NT-12121. 2013. Available online: https://nebula.esa.int/sites/default/files/neb_study/1089/C4000102979ExS.pdf (accessed on 1 July 2021).
- Imagery, National and Agency, Mapping Department of Defense. World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems. (TR8350.2); National Imagery and Mapping Agency: St. Louis, MO, USA, 2000.
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–162. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef]
- Ciddor, P.E. Refractive index of air: New equations for the visible and near infrared. Appl. Optics. 1996, 35, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Mahnke, P.; Klingenberg, H.H.; Fix, A.; Wirth, M. Dependency of injection seeding and spectral purity of a single resonant KTP optical parametric oscillator on the phase matching condition. Appl. Phys. 2007, 89, 1–7. [Google Scholar] [CrossRef][Green Version]
- Toon, G.C. Solar Line List for GGG2014, TCCON Data Archive; The Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014. [CrossRef]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Cassé, V.; Gibert, F.; Edouart, D.; Chomette, O.; Crevoisier, C. Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar. Atmosphere 2019, 10, 540. [Google Scholar] [CrossRef]
- Ohtsubo, J.; Asakura, T. Velocity measurement of a diffuse object by using time-varying speckles. Opt. Quant. Electron. 1976, 8, 523–529. [Google Scholar] [CrossRef]
- Liu, Z.; Hunt, W.; Vaughan, M.; Hostetler, C.; McGill, M.; Powell, K.; Winker, D.; Hu, Y. Estimating random errors due to shot noise in backscatter lidar observations. Appl. Opt. 2006, 45, 4437–4447. [Google Scholar] [CrossRef] [PubMed]
- Mandel, L. Fluctuations of Photon Beams: The Distribution of the Photo-Electrons. Proc. Phys. Soc. 1959, 74, 233–243. [Google Scholar] [CrossRef]
- Teich, M.C.; Saleh, B.E.A. Effects of random deletion and additive noise on bunched and antibunched photon-counting statistics. Opt. Lett. 1982, 7, 365–367. [Google Scholar] [CrossRef]
- Mc Intyre, R.J. Distribution of gains in uniformly multiplying avalanche photodiodes: Theory. IEEE Trans. Electron Devices 1972, 19, 703–713. [Google Scholar] [CrossRef]
- Burgess, R.E. Homophase and heterophase fluctuations in semiconducting crystals. Discuss. Faraday Soc. 1959, 28, 151–158. [Google Scholar] [CrossRef]
- Van Vliet, K.M.; Rucker, L.M. Noise associated with reduction, multiplication and branching processes. Phys. Stat. Mech. Appl. 1979, 95, 117–140. [Google Scholar] [CrossRef]
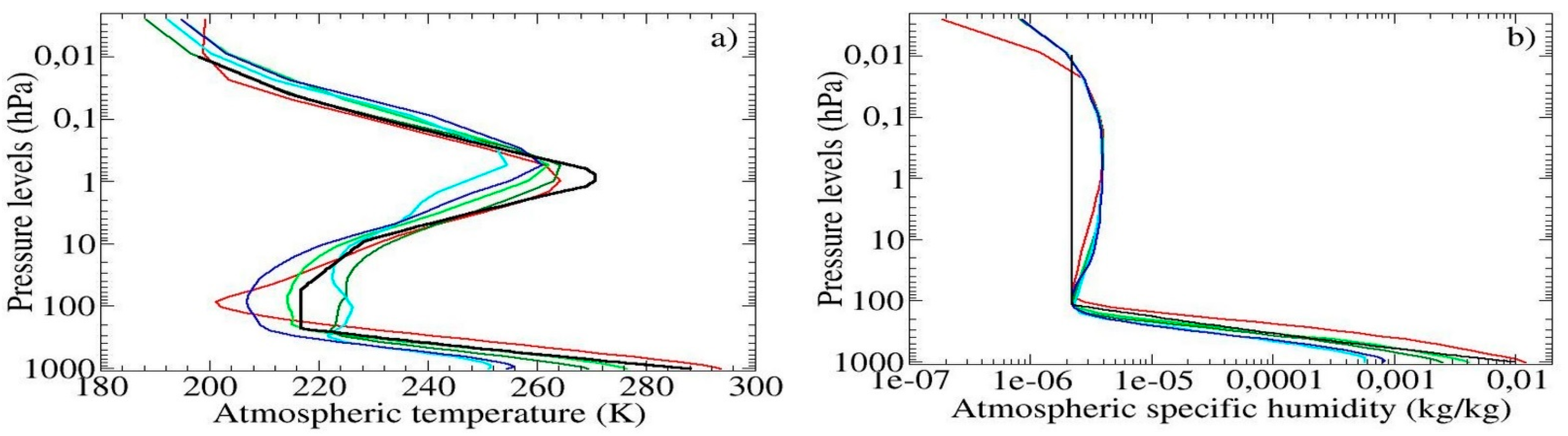
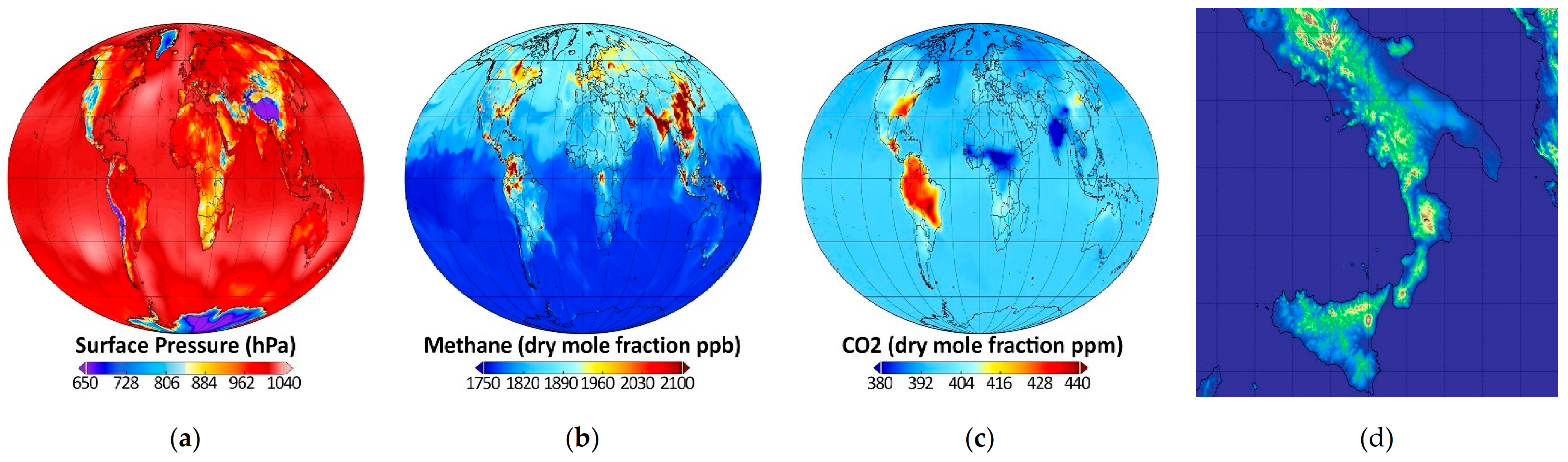

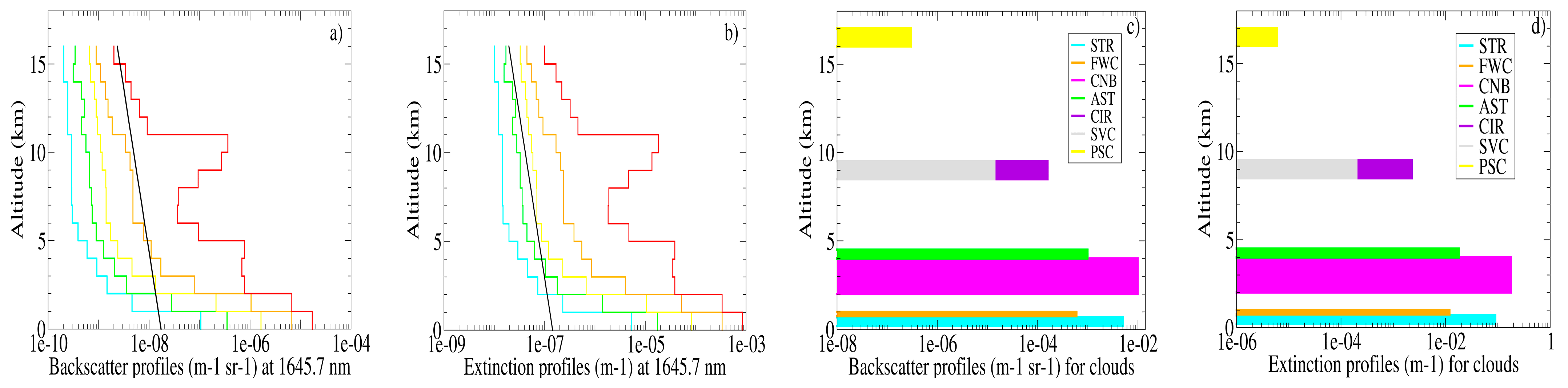
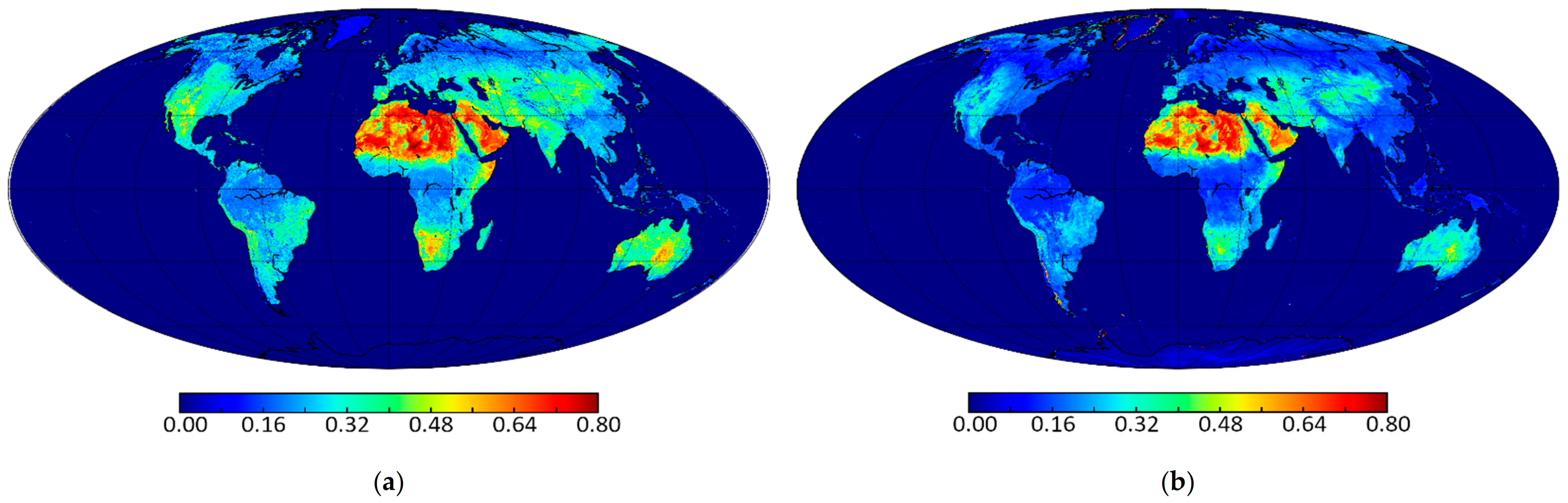





| Instrument | Satellite | Agency | Launch Date | References |
|---|---|---|---|---|
| SCIAMACHY A | ENVISAT E | ESA I | 2002 (end of the mission in 2012) | [8] |
| TANSO-FTS B | GOSAT F | JAXA J | 2009 | [9,10] |
| IASI C | MetOp G satellite series | EUMETSAT K | 2006, 2012 and 2018 | [11] |
| TROPOMI D | Sentinel-5P H | ESA I | 2017 | [12] |
| TANSO-FTS-2 B | GOSAT-2 F | JAXA J-NIES L-MOE M | 2018 | [13] |
| Target | Breakthrough | Threshold | |
|---|---|---|---|
| XCH4 Random Error | 8 ppb | 18 ppb | 36 ppb |
| XCH4 Systematic Error | 1 ppb | 2 ppb | 3 ppb |
| Horizontal resolution | 50 km | ||
| P | Sc | Tc | A/Sc | T/Tc | Mtav | |
|---|---|---|---|---|---|---|
| Laser flux | 1 | = 105 mm2 | ∞ | 3667 | 0 | 3668 |
| Solar flux | 0 | = 19 mm2 | = 4.52 × 10−3 ns | 20266 | 2950 | ∞ |
| η | F | K | |||||
|---|---|---|---|---|---|---|---|
| 0.715 | 7.18 | 2882 | 1850 | 998,798 Ω | 1638.4 or 13.5 mV | 383.5 or 3.16 mV | 9.98 × 10−7 |
| Ref = 0.1 | Ref = 0.01 | |
|---|---|---|
| Ncal | 18 786 photons | id |
| NOff | 8 539 photons | 865 photons |
| NOn | 2 608 photons | 268 photons |
| Nsun(70°) | 56.41 photons or 4.85 mV ± 1.73 mV | 5.641 photons or 0.485 mV ± 0.55 mV |
| Nsun(80°) | 27.21 photons or 2.34 mV ± 1.20 mV | 2.721 photons or 0.234 mV ± 0.38 mV |
| Nnoise | 187.30 ph + 0.91 ph or ± 3.16 mV ± 0.22 mV | id |
| SNRcal | 29.5 without sun 29.1 with the sun at 70° | id |
| SNROff | 20.4 without sun 19.5 with the sun at 70° | 2.75 without sun smaller but nearly the same with the sun at 70° |
| SNROn | 7.8 without sun 7.4 with the sun at 70° | 0.86 without sun smaller but nearly the same with the sun at 70° |
| SSE (in m) | XCH4 (in ppb) | |||||
|---|---|---|---|---|---|---|
| Experiment | Per Shot | Per Cell | Per Shot | Per Cell | ||
| without Noise | with Noise | with Noise | without Noise | with Noise | with Noise | |
| Number of points | 113,400 | 96,385 (85%) | 669 (83%) | 113,400 | 96,239 (85%) | 669 (83%) |
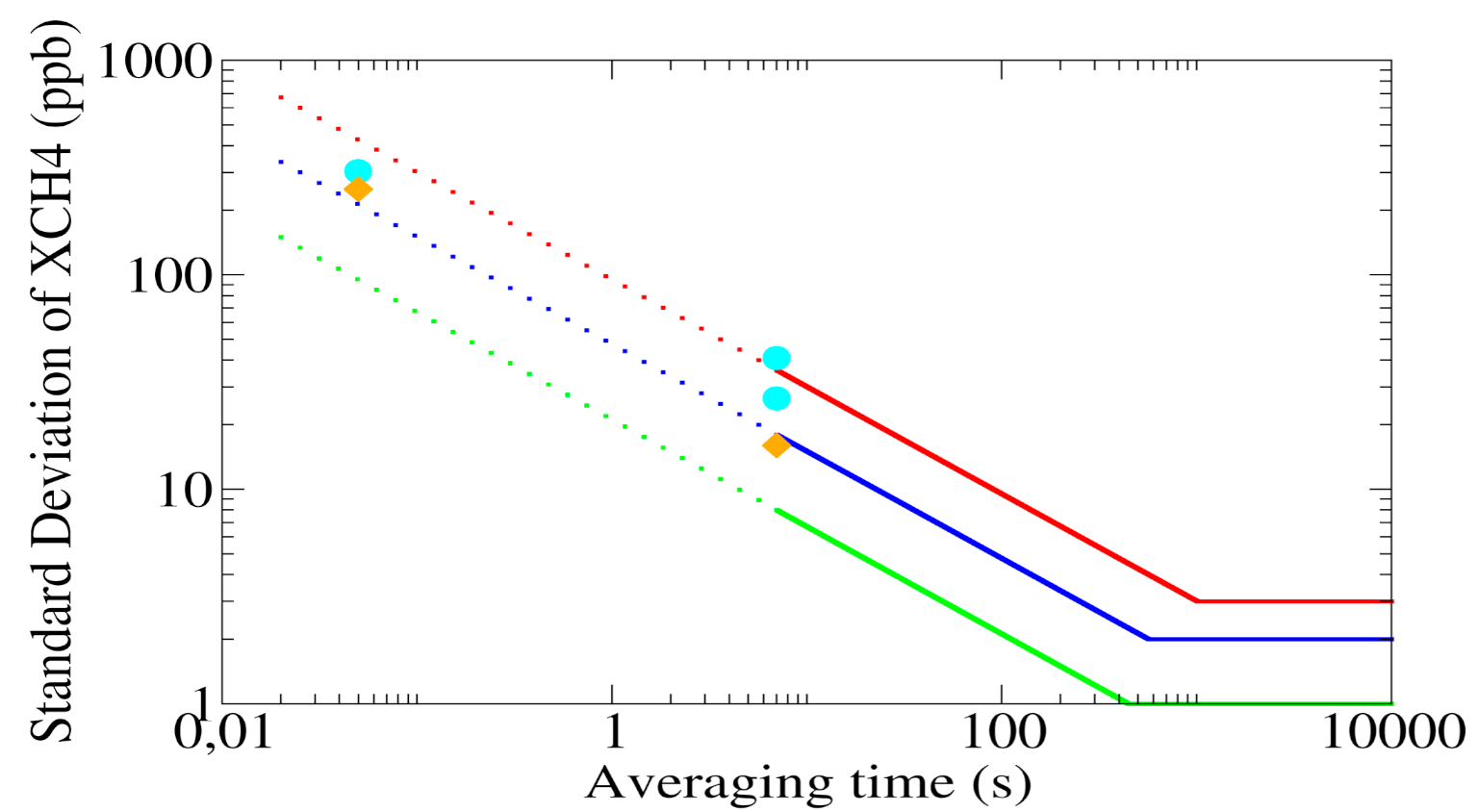
| Bias | 0.02 | 0. | 0. | 0.07 | 11.3 | 1.2 |
| Standard deviation | 0.03 | 1.7 | 0.1 | 0.10 | 250.3 | 16.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassé, V.; Armante, R.; Bousquet, P.; Chomette, O.; Crevoisier, C.; Delahaye, T.; Edouart, D.; Gibert, F.; Millet, B.; Nahan, F.; et al. Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission. Remote Sens. 2021, 13, 2679. https://doi.org/10.3390/rs13142679
Cassé V, Armante R, Bousquet P, Chomette O, Crevoisier C, Delahaye T, Edouart D, Gibert F, Millet B, Nahan F, et al. Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission. Remote Sensing. 2021; 13(14):2679. https://doi.org/10.3390/rs13142679
Chicago/Turabian StyleCassé, Vincent, Raymond Armante, Philippe Bousquet, Olivier Chomette, Cyril Crevoisier, Thibault Delahaye, Dimitri Edouart, Fabien Gibert, Bruno Millet, Frédéric Nahan, and et al. 2021. "Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission" Remote Sensing 13, no. 14: 2679. https://doi.org/10.3390/rs13142679
APA StyleCassé, V., Armante, R., Bousquet, P., Chomette, O., Crevoisier, C., Delahaye, T., Edouart, D., Gibert, F., Millet, B., Nahan, F., & Pierangelo, C. (2021). Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission. Remote Sensing, 13(14), 2679. https://doi.org/10.3390/rs13142679






