A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products
Abstract
:1. Introduction
2. Experiment Description and Data Retrieval
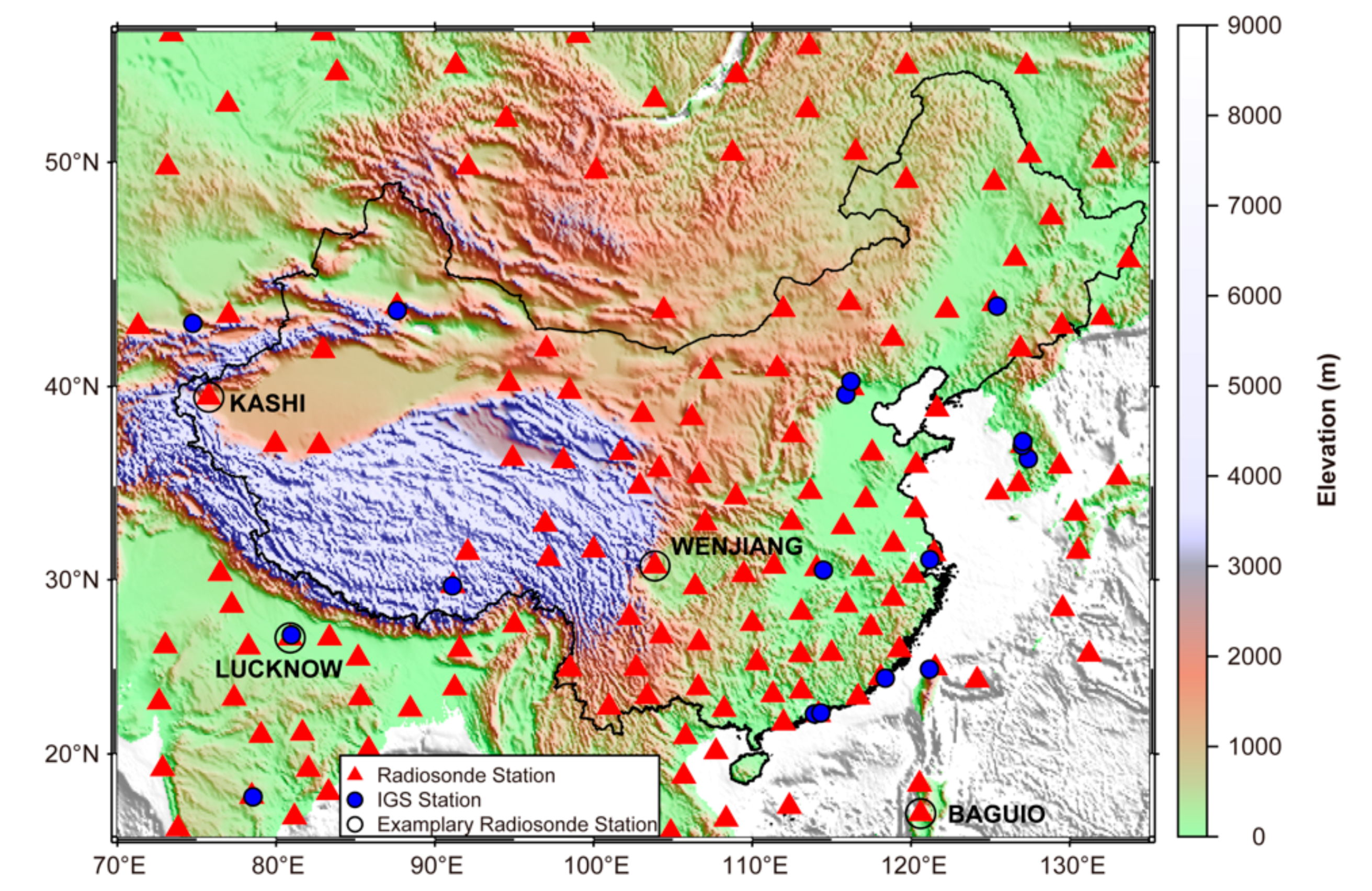
2.1. Data Description
2.2. Retrieval of ZHD, ZWD, and Tm Using GRAPES_MESO and Radiosonde Data
2.3. Interpolating GRAPES Products to Any Location
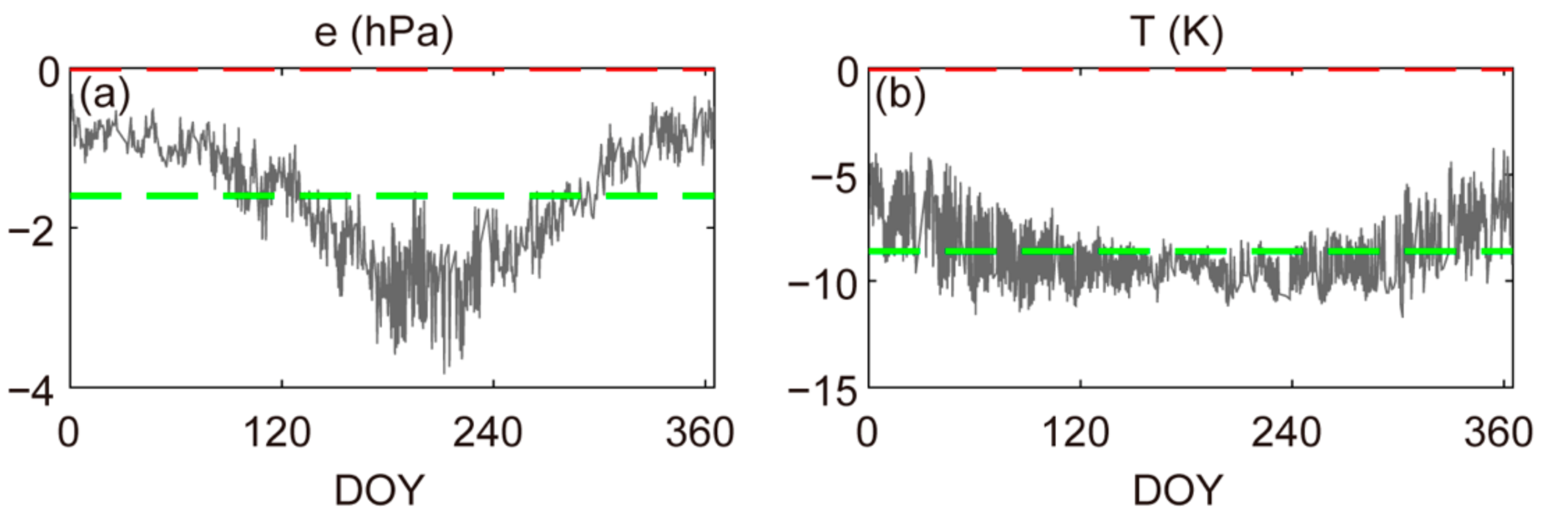
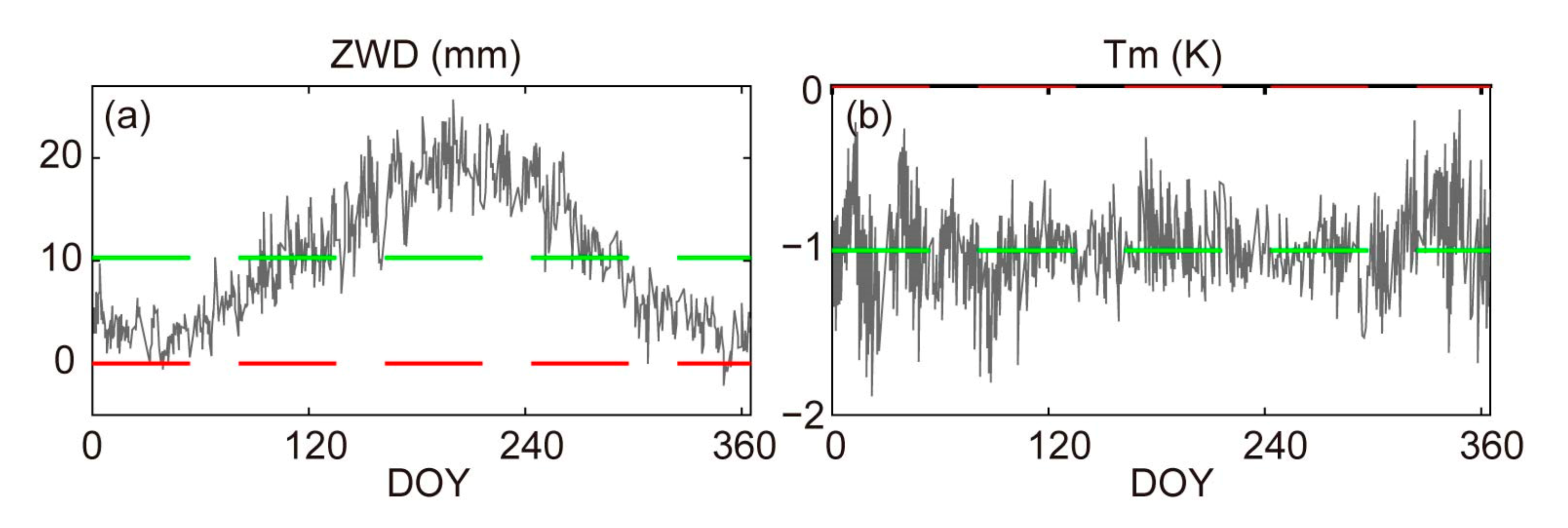
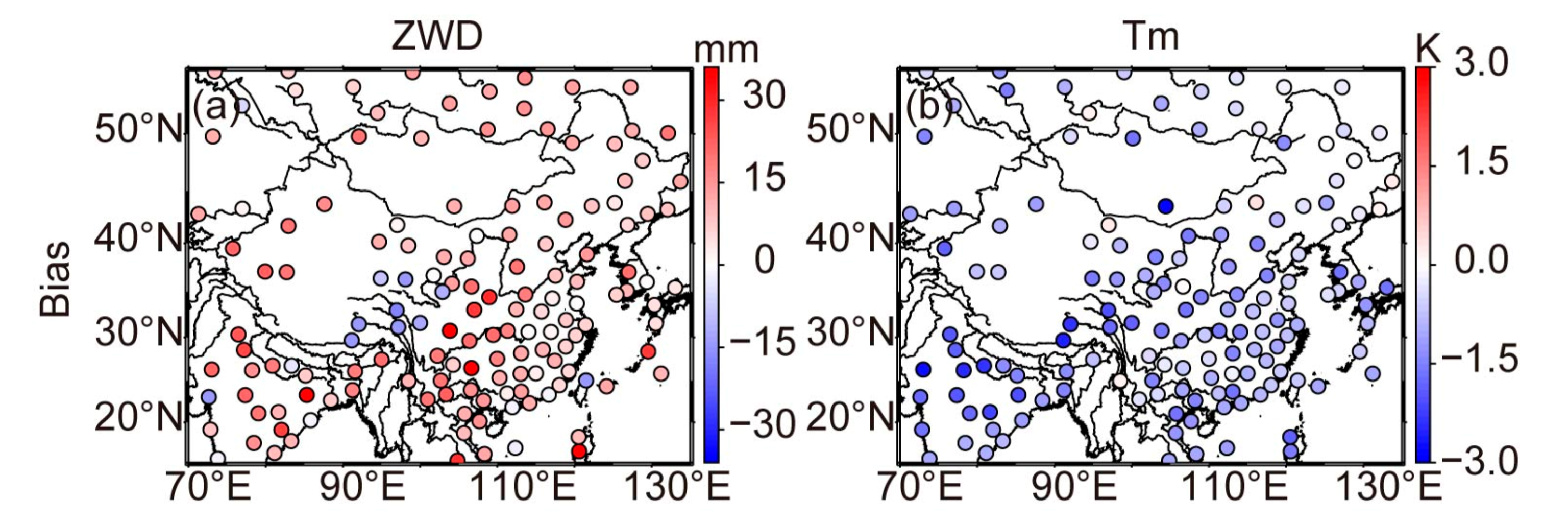
3. Biases in ZWD and Tm
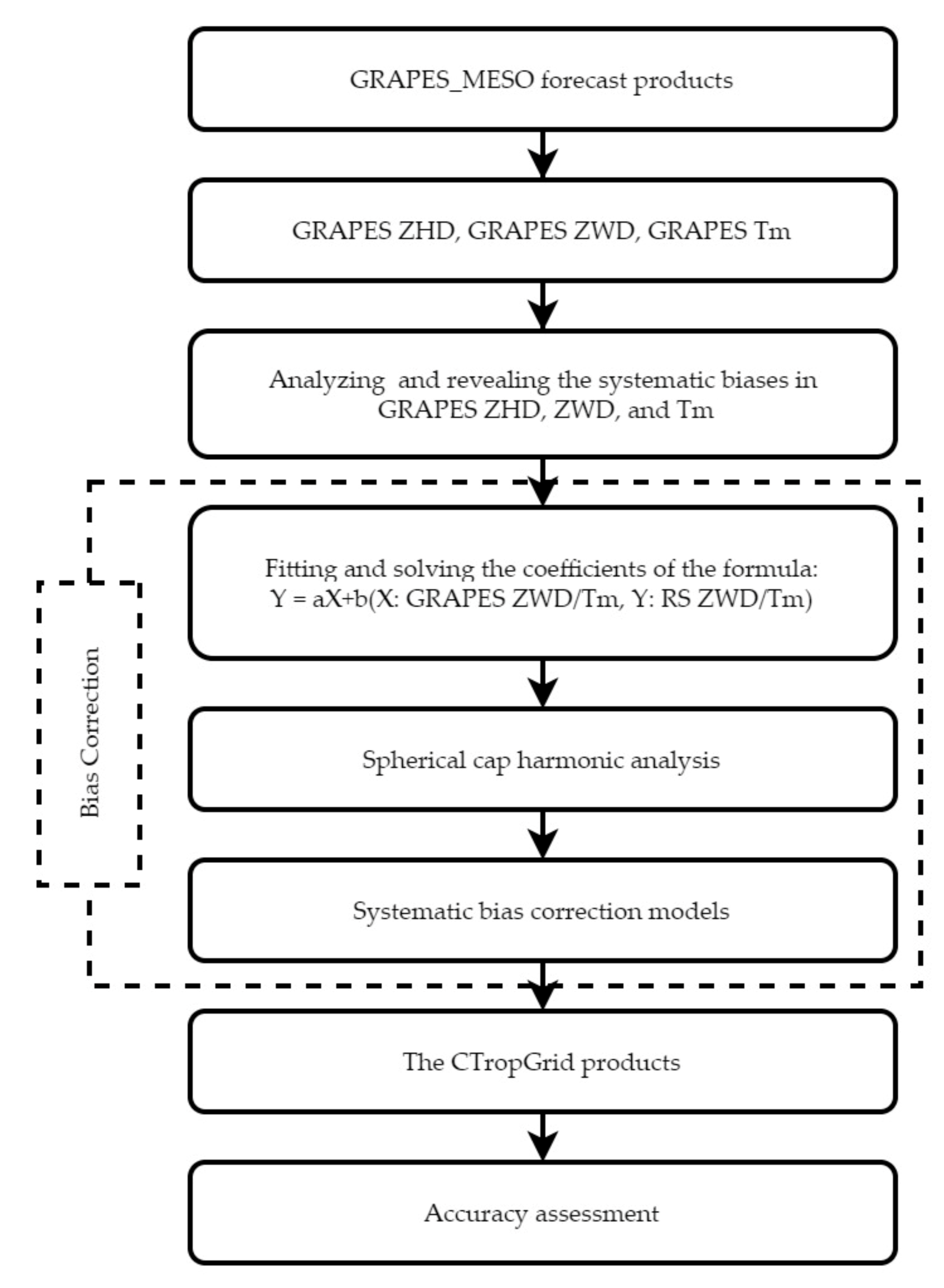
4. Bias Correction
4.1. Correcting Systematic Biases between GRAPES-Based and Radiosonde-Based ZWD(Tm)
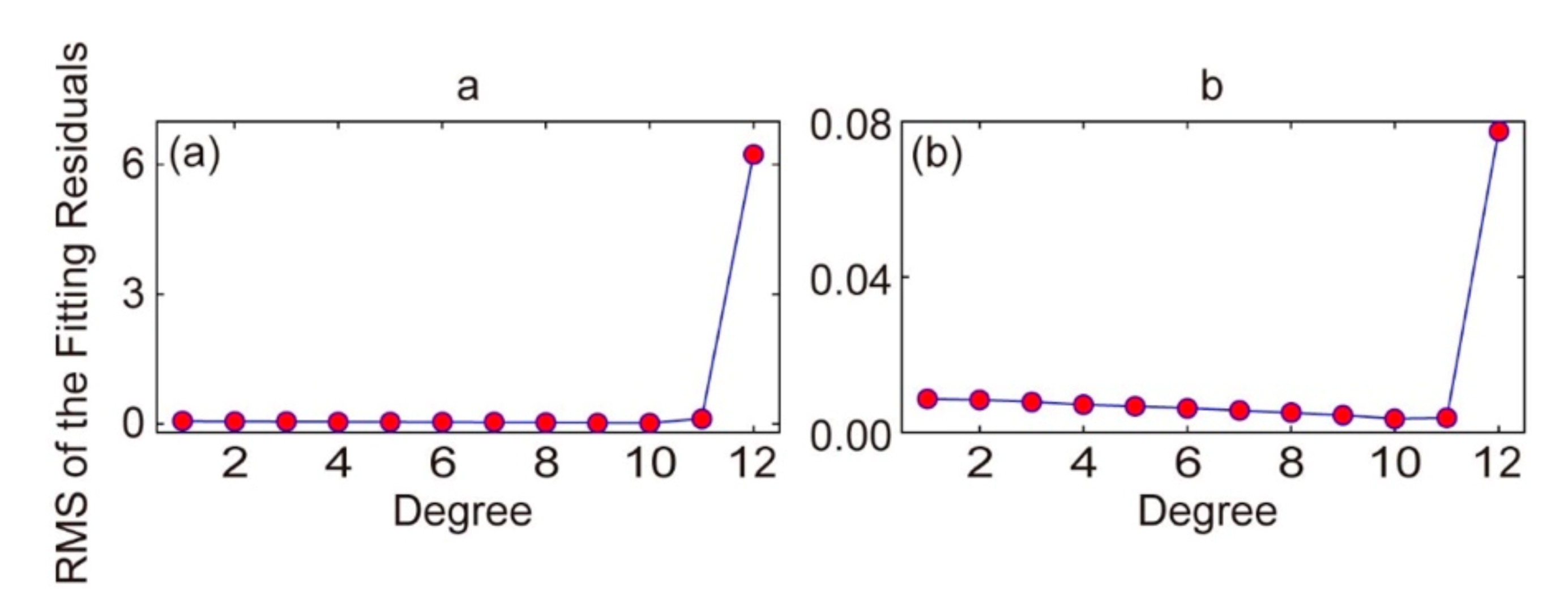
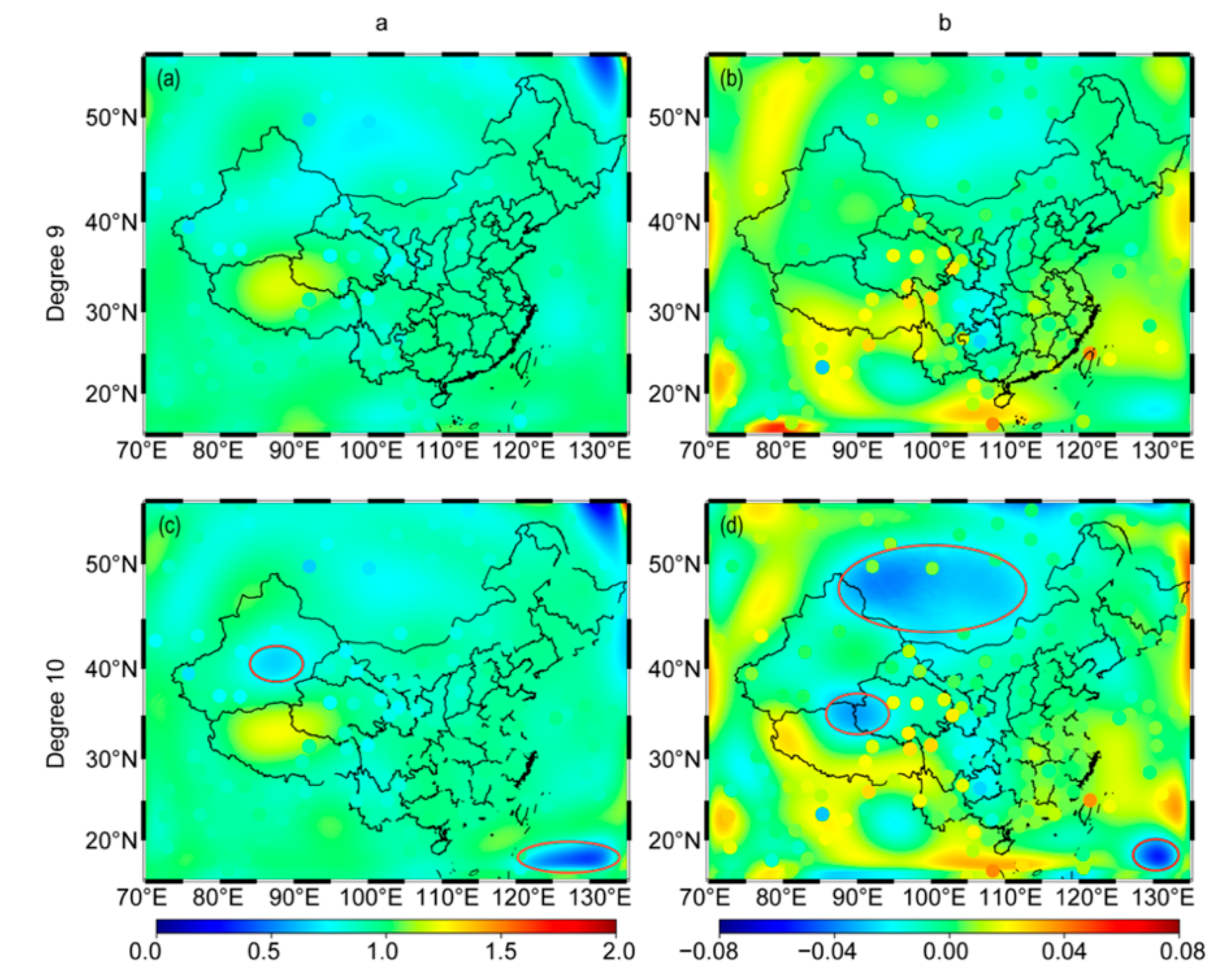
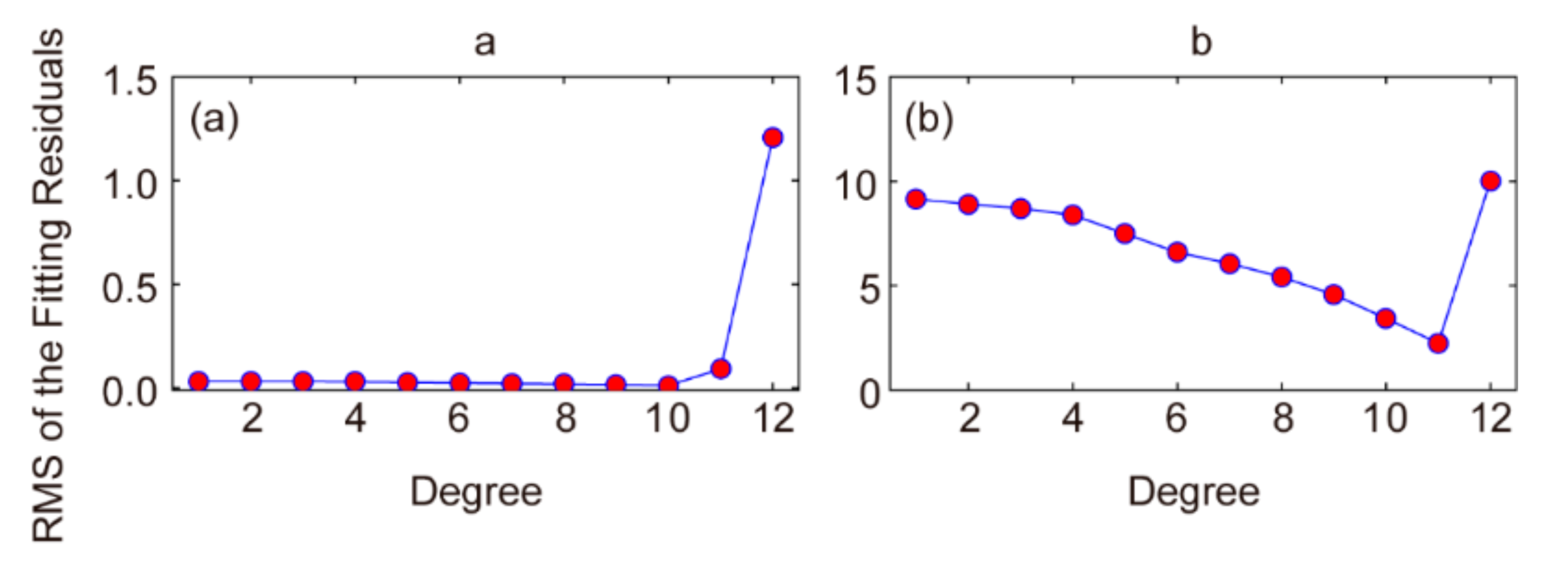
4.2. Interpolating and Using a Spherical Cap Harmonic (SCH) Model
5. Results
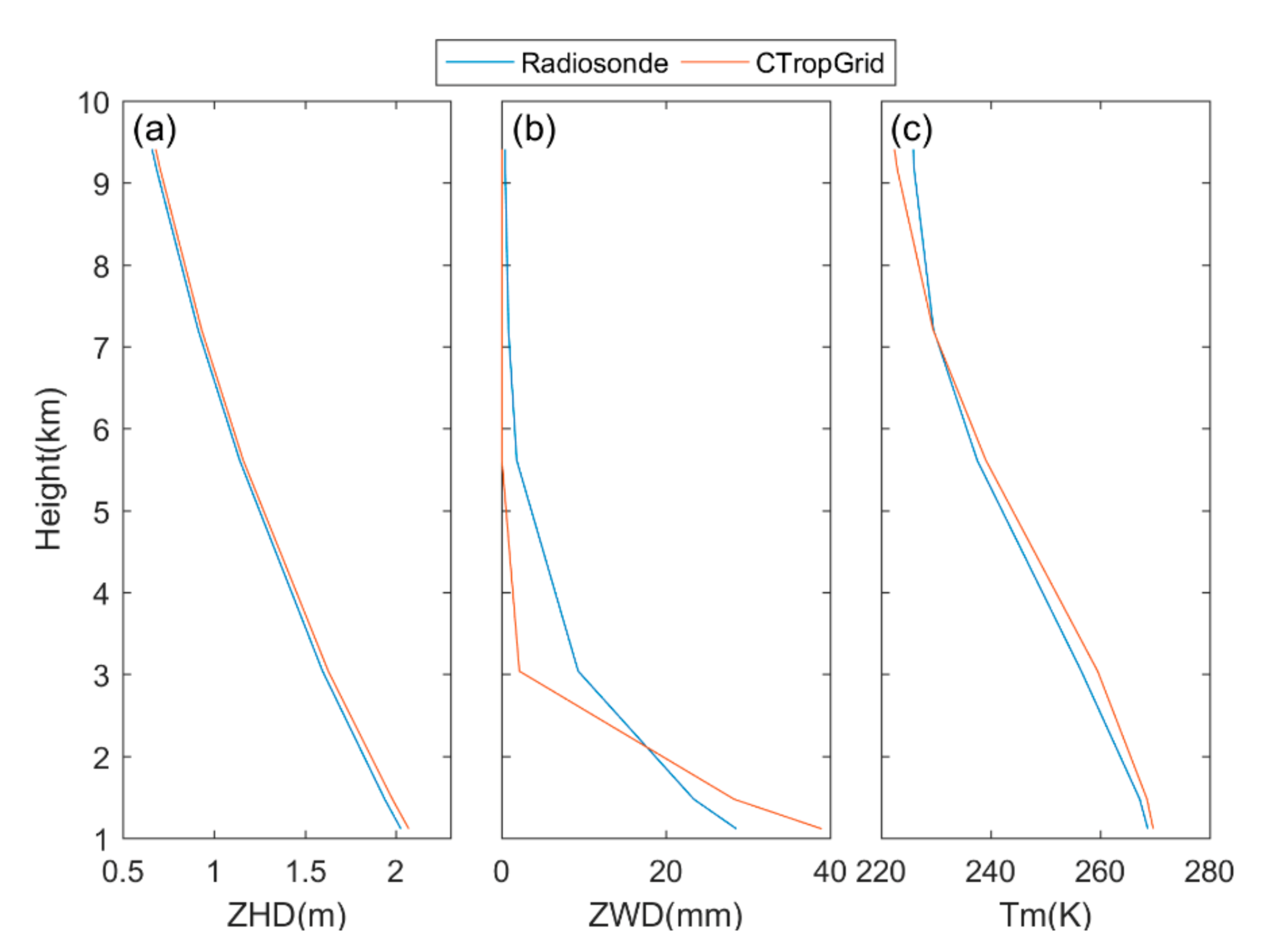
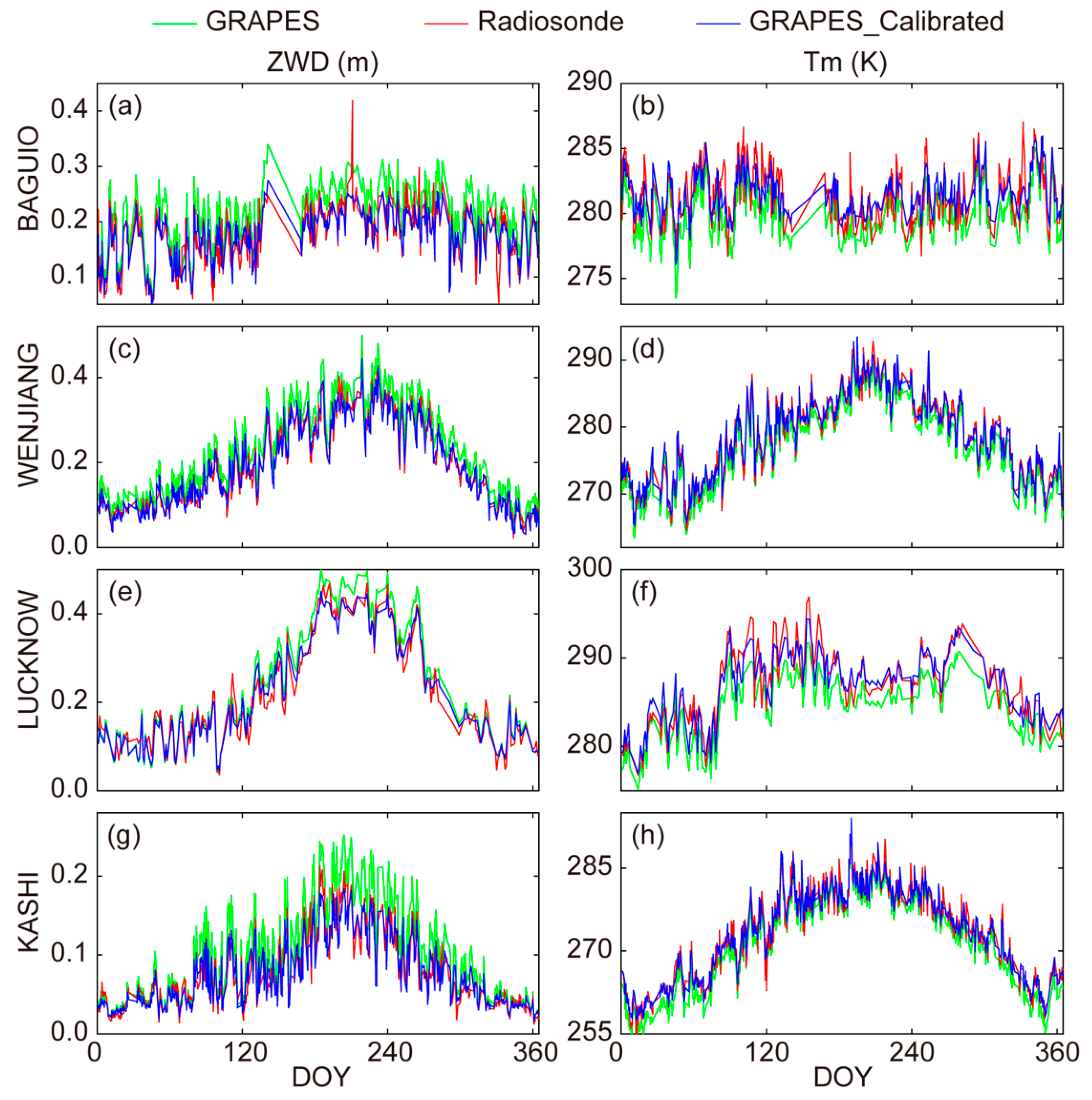
5.1. Validation with Radiosonde Data
5.1.1. Overall Performance
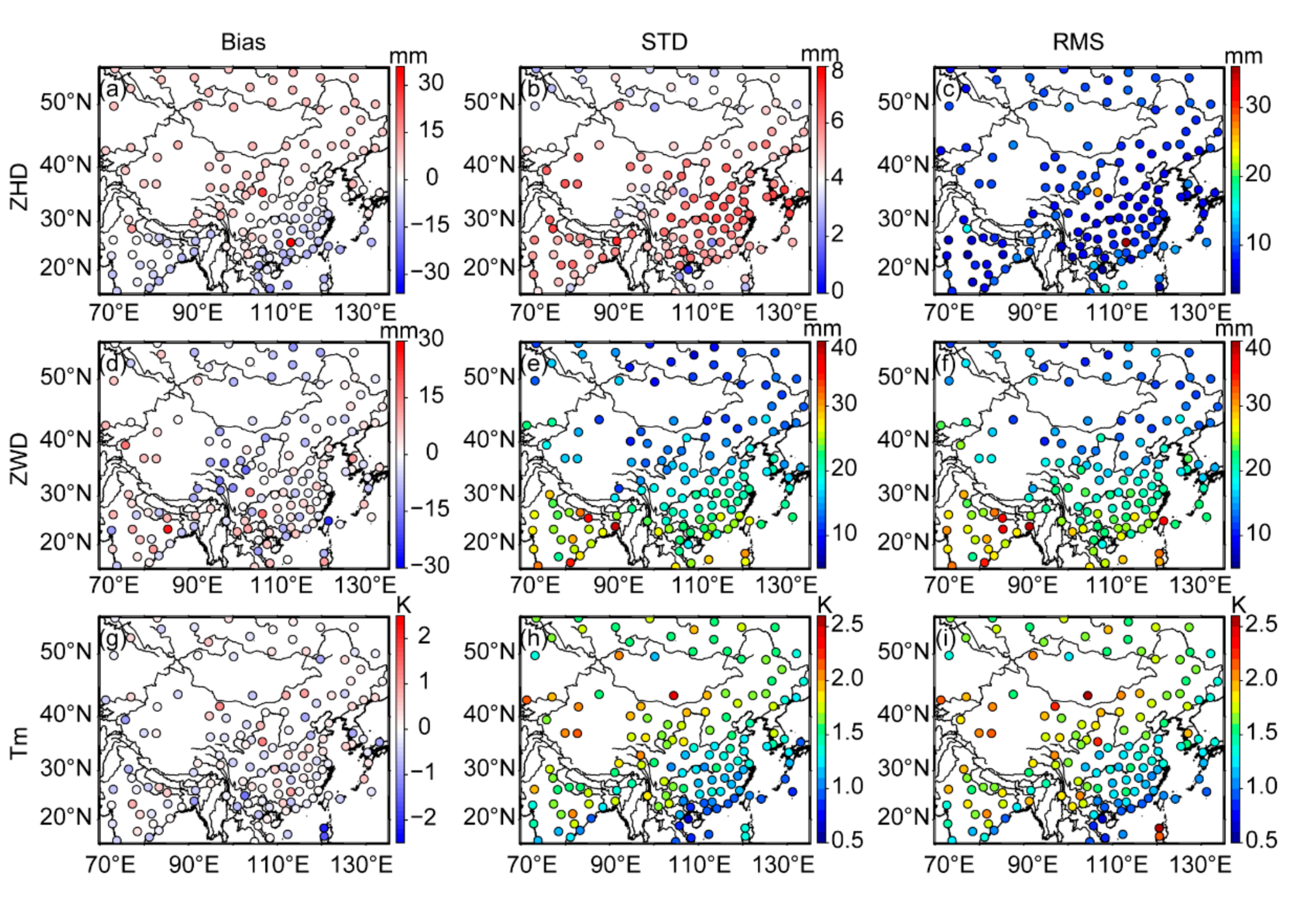
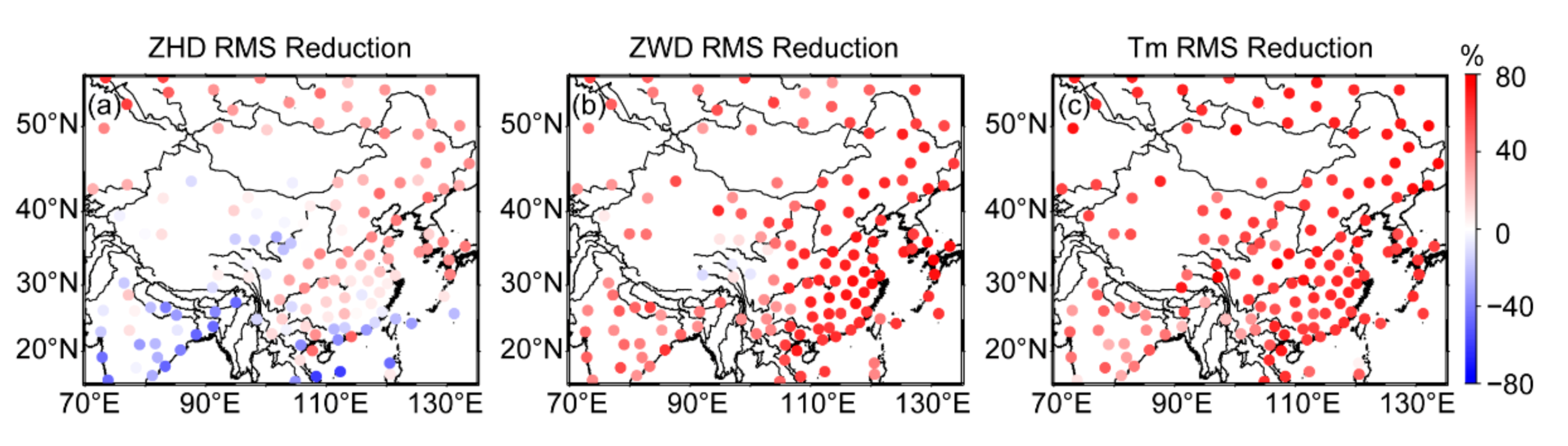
5.1.2. Spatial Variations of Accuracy
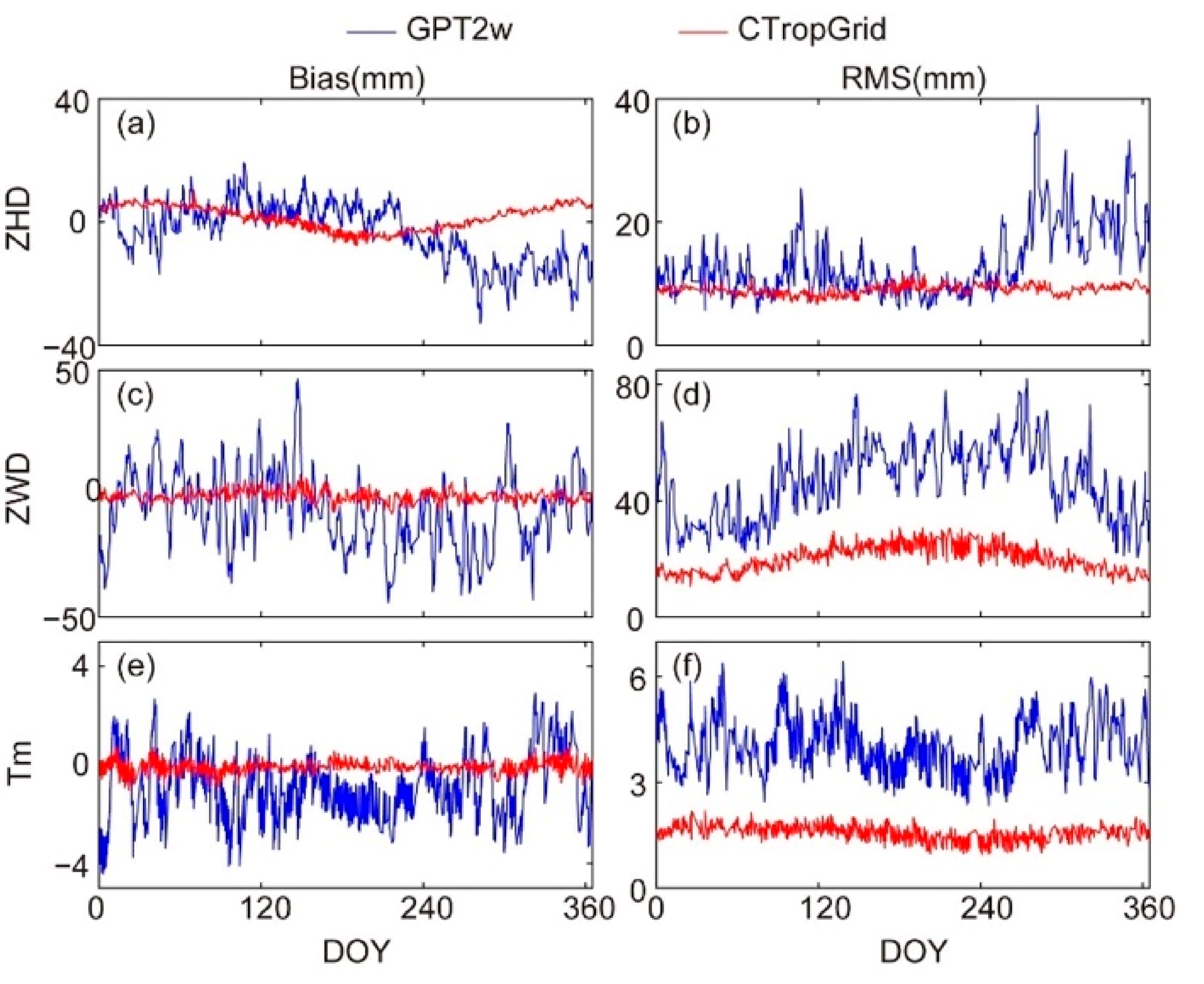
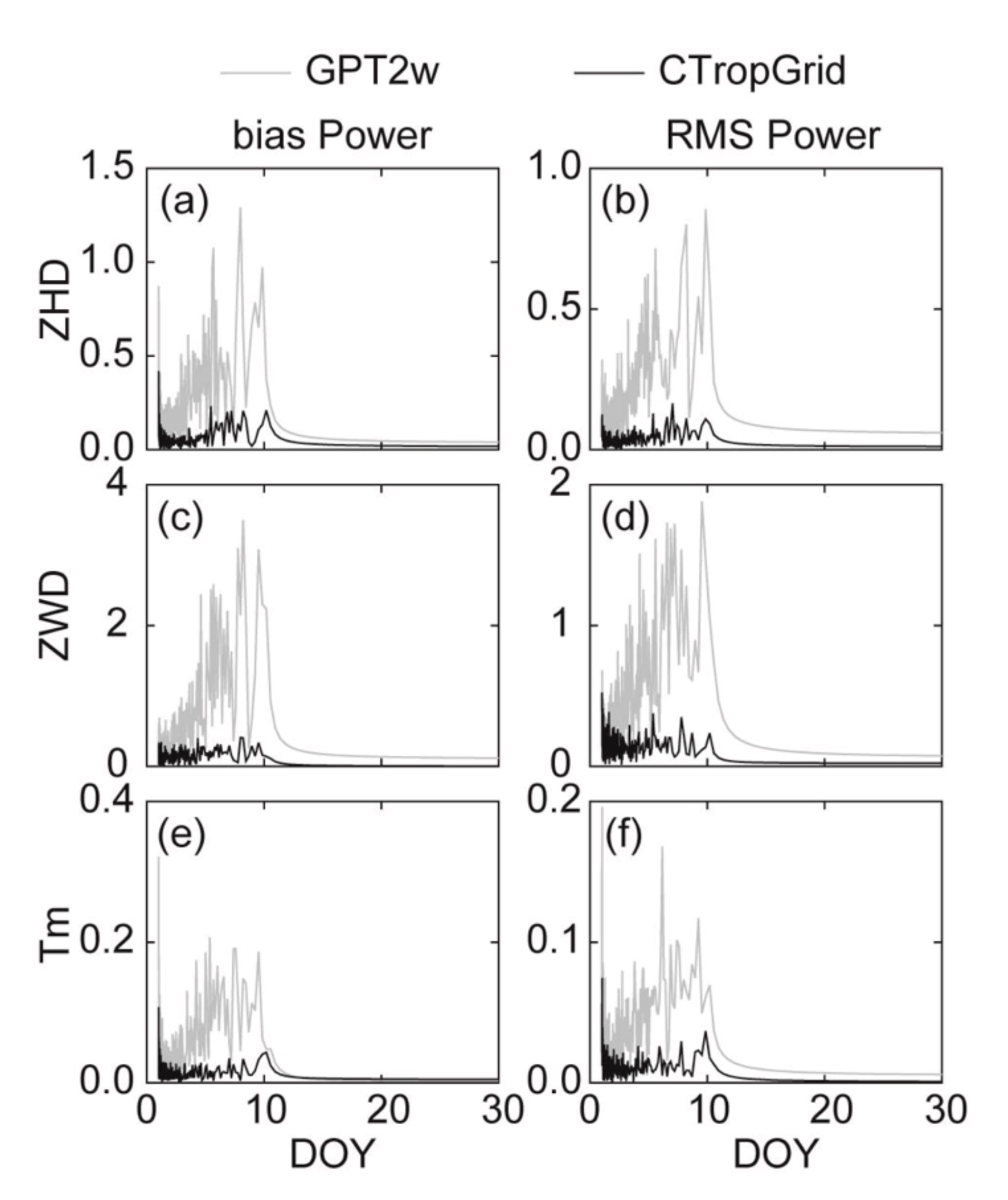
5.1.3. Temporal Variations of Accuracy
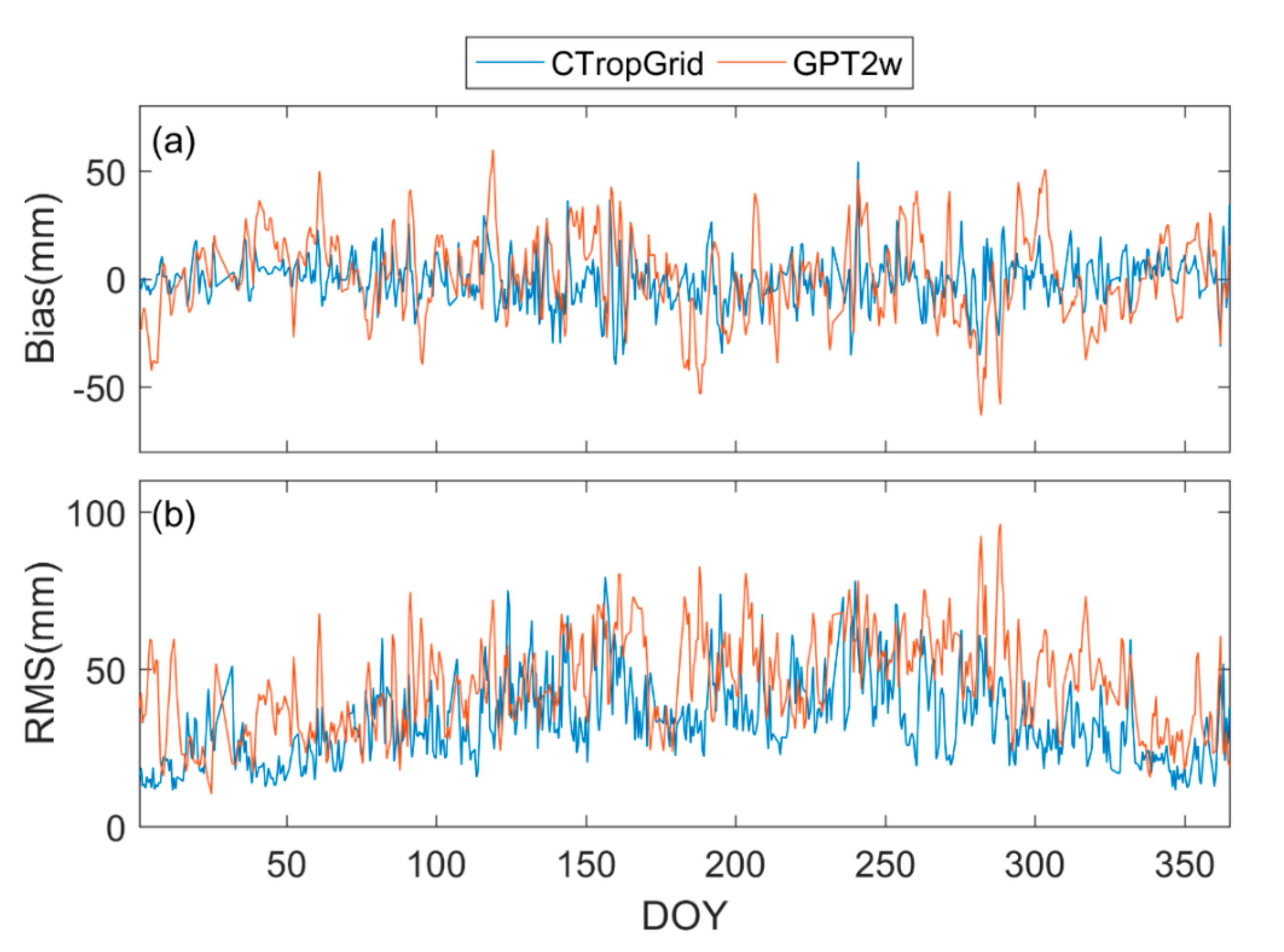
5.2. Validate the CTropGrid Products with IGS ZTD
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Chen, Q.; Song, S.; Heise, S.; Liou, Y.-A.; Zhu, W.; Zhao, J. Assessment of ZTD derived from ECMWF/NCEP data with GPS ZTD over China. GPS Solut. 2011, 15, 415–425. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.-U.; Cho, J.-H.; Park, P.-H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. 2007, 112, D09110. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Ou, J.; Chai, Y.; Li, Z.; Liou, Y.-A.; Wang, N. New versions of the BDS/GNSS zenith tropospheric delay model IGGtrop. J. Geod. 2014, 89, 73–80. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a priori zenith hydrostatic delay errors on GPS estimates of station heights and zenith total delays. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.M.; Zhang, K.F.; Wu, S.Q.; Fan, S.J.; Cheng, Y.Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Chen, P.; Ma, Y.; Liu, H.; Zheng, N. A New Global Tropospheric Delay Model Considering the Spatiotemporal Variation Characteristics of ZTD with Altitude Coefficient. Earth Space Sci. 2020, 7, e2019EA000888. [Google Scholar] [CrossRef]
- Li, S.; Xu, T.; Jiang, N.; Yang, H.; Wang, S.; Zhang, Z. Regional Zenith Tropospheric Delay Modeling Based on Least Squares Support Vector Machine Using GNSS and ERA5 Data. Remote Sens. 2021, 13, 1004. [Google Scholar] [CrossRef]
- Saastamoinen, J.H. Atmospheric Correction for the Troposphere and the Stratosphere in Radio Ranging Satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Hopfield, H.S. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Bohm, J.; Moller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Lagler, K.; Schindelegger, M.; Bohm, J.; Krasna, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2017, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Boehm, J.; Kouba, J.; Schuh, H. Forecast Vienna Mapping Functions 1 for real-time analysis of space geodetic observations. J. Geod. 2008, 83, 397–401. [Google Scholar] [CrossRef]
- Krueger, E.; Schüler, T.; Arbesser-Rastburg, B. The standard tropospheric correction model for the European satellite navigation system Galileo. In Proceedings of the XXVIIIth general assembly of International Union of Radio Science (URSI), New Delhi, India, 23–29 October 2005. [Google Scholar]
- Schuler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS tropospheric correction model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhang, B.; Yao, Y.; Liu, L.; Sun, Z.; Yan, X. A Refined Regional Model for Estimating Pressure, Temperature, and Water Vapor Pressure for Geodetic Applications in China. Remote Sens. 2020, 12, 1713. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Ou, J.; He, Y. IGGtrop_SH and IGGtrop_rH: Two Improved Empirical Tropospheric Delay Models Based on Vertical Reduction Functions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5276–5288. [Google Scholar] [CrossRef]
- Yao, Y.; Hu, Y.; Yu, C.; Zhang, B.; Guo, J. An improved global zenith tropospheric delay model GZTD2 considering diurnal variations. Nonlinear Process. Geophys. 2016, 23, 127–136. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; He, C.; Zhang, B.; Xu, C. A new global zenith tropospheric delay model GZTD. Chin. J. Geophys. 2013, 56, 2218–2227. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. An ERA5-Based Model for Estimating Tropospheric Delay and Weighted Mean Temperature Over China With Improved Spatiotemporal Resolutions. Earth Space Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Sun, J.L.; Wu, Z.L.; Yin, Z.D.; Ma, B. A simplified GNSS tropospheric delay model based on the nonlinear hypothesis. GPS Solut. 2017, 21, 1735–1745. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Zhang, B.; Ou, J. A grid-based tropospheric product for China using a GNSS network. J. Geod. 2017, 92, 765–777. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. A Comprehensive Evaluation and Analysis of the Performance of Multiple Tropospheric Models in China Region. IEEE Trans. Geosci. Remote Sens. 2016, 54, 663–678. [Google Scholar] [CrossRef]
- Yao, Y.B.; Zhu, S.; Yue, S.Q. A globally applicable, season-specific model for estimating the weighted mean temperature of the atmosphere. J. Geod. 2012, 86, 1125–1135. [Google Scholar] [CrossRef]
- Yao, Y.B.; Zhang, B.; Yue, S.Q.; Xu, C.Q.; Peng, W.F. Global empirical model for mapping zenith wet delays onto precipitable water. J. Geod. 2013, 87, 439–448. [Google Scholar] [CrossRef]
- Yao, Y.B.; Xu, C.Q.; Zhang, B.; Cao, N. GTm-III: A new global empirical model for mapping zenith wet delays onto precipitable water vapour. Geophys. J. Int. 2014, 197, 202–212. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Jiang, W.; Liu, L.; Chen, H.; Ye, S. A new global grid model for the determination of atmospheric weighted mean temperature in GPS precipitable water vapor. J. Geod. 2019, 93, 159–176. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Ou, J.; Li, Y.; Zhang, B. GPS PPP-derived precipitable water vapor retrieval based on Tm/Ps from multiple sources of meteorological data sets in China. J. Geophys. Res. Atmos. 2017, 122, 4165–4183. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Chen, H.; Jiang, W. An improved atmospheric weighted mean temperature model and its impact on GNSS precipitable water vapor estimates for China. GPS Solut. 2019, 23, 1–16. [Google Scholar] [CrossRef]
- Emardson, T.R.; Derks, H.J.P. On the relation between the wet delay and the integrated precipitable water vapour in the European atmosphere. Meteorol. Appl. 2000, 7, 61–68. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Meng, X.; Shi, J.; Zhang, D.; Zhao, Y. An improved weighted mean temperature (Tm) model based on GPT2w with Tm lapse rate. GPS Solut. 2020, 24, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Ding, M. A second generation of the neural network model for predicting weighted mean temperature. GPS Solut. 2020, 24, 1–6. [Google Scholar] [CrossRef]
- Hadas, T.; Teferle, F.N.; Kazmierski, K.; Hordyniec, P.; Bosy, J. Optimum stochastic modeling for GNSS tropospheric delay estimation in real-time. GPS Solut. 2016, 21, 1069–1081. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Holden, L.; Kealy, A.; Choy, S.; Hordyniec, P. Assessment of forecast Vienna Mapping Function 1 for real-time tropospheric delay modeling in GNSS. J. Geod. 2019, 93, 1501–1514. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Li, Z.; Heinkelmann, R.; Nilsson, T.; Dick, G.; Ge, M.; Schuh, H. GNSS tropospheric gradients with high temporal resolution and their effect on precise positioning. J. Geophys. Res. Atmos. 2016, 121, 912–930. [Google Scholar] [CrossRef] [Green Version]
- Wang, L. Assimilation of soil moisture and temperature in the GRAPES_Meso model using an ensemble Kalman filter. Meteorol. Appl. 2019, 26, 483–489. [Google Scholar] [CrossRef] [Green Version]
- Hagemann, S.; Bengtsson, L.; Gendt, G. On the determination of atmospheric water vapor from GPS measurements. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Rüeger, J. Refractive index formulae for radio waves, JS28 integration of techniques and corrections to achieve accurate engineering. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002. [Google Scholar]
- Hu, Y.; Yao, Y. A new method for vertical stratification of zenith tropospheric delay. Adv. Space Res. 2019, 63, 2857–2866. [Google Scholar] [CrossRef]
- Yao, Y.; Sun, Z.; Xu, C.; Xu, X. Global Weighted Mean Temperature Model Considering Nonlinear Vertical Reduction. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 106–111. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, X. An Improved Rainfall Forecasting Model Based on GNSS Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4891–4900. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Liu, J.; Shi, C.; Huang, J.; Zheng, G.; Zhang, R.; Haase, J.S.; Lou, Y. The Use of Ground-Based GPS Precipitable Water Measurements over China to Assess Radiosonde and ERA-Interim Moisture Trends and Errors from 1999 to 2015. J. Clim. 2017, 30, 7643–7667. [Google Scholar] [CrossRef]
- Twisk, J.W. Applied Longitudinal Data Analysis for Epidemiology: A Practical Guide; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Yao, Y.; Xu, X.; Xu, C.; Peng, W.; Wan, Y. GGOS tropospheric delay forecast product performance evaluation and its application in real-time PPP. J. Atmos. Sol. Terr. Phys. 2018, 175, 1–17. [Google Scholar] [CrossRef]
- Boneau, C.A. The effects of violations of assumptions underlying the t test. Psychol. Bull. 1960, 57, 49–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thébault, E.; Mandea, M.; Schott, J.J. Modeling the lithospheric magnetic field over France by means of revised spherical cap harmonic analysis (R-SCHA). J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Haines, G.V.; Torta, J.M. Determination of equivalent current sources from spherical cap harmonic models of geomagnetic feld variations. Geophys. J. Int. 1994, 118, 499–514. [Google Scholar] [CrossRef] [Green Version]
- Desantis, A. Translated Origin Spherical Cap Harmonic-Analysis. Geophys. J. Int. 1991, 106, 253–263. [Google Scholar] [CrossRef] [Green Version]
- De Santis, A.; Torta, J.M. Spherical cap harmonic analysis: A comment on its proper use for local gravity feld representation. J. Geod. 1997, 71, 526–532. [Google Scholar] [CrossRef]
- Li, J.; Chao, D.; Ning, J. Spherical cap harmonic expansion for local gravity feld representation. Manuscr. Geod. 1995, 20, 265. [Google Scholar]
- Liu, J.B.; Chen, R.Z.; Wang, Z.M.; Zhang, H.P. Spherical cap harmonic model for mapping and predicting regional TEC. GPS Solut. 2011, 15, 109–119. [Google Scholar] [CrossRef]
- De Franceschi, G.; Desantis, A.; Pau, S. Ionospheric Mapping by Regional Spherical Harmonic-Analysis—New Developments. Adv. Space Res. 1994, 14, 61–64. [Google Scholar] [CrossRef]
- Hwang, C.; Chen, S.-K. Fully normalized spherical cap harmonics: Application to the analysis of sea-level data from TOPEX/POSEIDON and ERS-1. Geophys. J. Int. 1997, 129, 450–460. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Yao, Y.; Xin, L.; Xu, X. Precipitable water vapor fusion: An approach based on spherical cap harmonic analysis and Helmert variance component estimation. J. Geod. 2019, 93, 2605–2620. [Google Scholar] [CrossRef]
- Hackman, C.; Byram, S.M. IGS troposphere working group 2013. IGS Cent. Bur. 2012, 183. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
| Method | ZHD (mm) | ZWD (mm) | Tm (K) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | STD | RMS | Bias | STD | RMS | Bias | STD | RMS | |
| CTropGrid | 1.5 | 5.2 | 8.9 | −0.7 | 19.0 | 20.2 | −0.1 | 1.5 | 1.5 |
| [−15.8, 35.8] | [0.7, 7.3] | [3.0, 35.9] | [−24.1, 26.2] | [7.9, 38.3] | [10.2, 38.7] | [−2.2, 1.3] | [0.7, 2.5] | [0.7, 2.6] | |
| GPT2w | 0.6 | 9.3 | 10.1 | −7.0 | 43.8 | 45.5 | −0.7 | 3.5 | 3.8 |
| [−4.0, 45.4] | [4.0, 21.0] | [4.4, 45.8] | [−61.8, 20.5] | [13.8, 78.1] | [13.8, 79.0] | [−7.1, 3.8] | [1.4, 5.7] | [1.4, 7.7] | |
| Model | Bias (mm) | STD (mm) | RMS (mm) |
|---|---|---|---|
| GPT2w | 1.0 [−13.9, 21.8] | 45.2 [17.5, 67.0] | 46.3 [20.9, 67.2] |
| CTropGrid | −0.7 [−16.8, 23.6] | 34.1 [22.7, 49.6] | 35.8 [24.7, 49.8] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.; Zhang, B.; Li, J.; Yao, Y.; Liu, L.; Ran, Q.; Xiong, Z. A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products. Remote Sens. 2021, 13, 2644. https://doi.org/10.3390/rs13132644
Cao L, Zhang B, Li J, Yao Y, Liu L, Ran Q, Xiong Z. A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products. Remote Sensing. 2021; 13(13):2644. https://doi.org/10.3390/rs13132644
Chicago/Turabian StyleCao, Liying, Bao Zhang, Junyu Li, Yibin Yao, Lilong Liu, Qishun Ran, and Zhaohui Xiong. 2021. "A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products" Remote Sensing 13, no. 13: 2644. https://doi.org/10.3390/rs13132644
APA StyleCao, L., Zhang, B., Li, J., Yao, Y., Liu, L., Ran, Q., & Xiong, Z. (2021). A Regional Model for Predicting Tropospheric Delay and Weighted Mean Temperature in China Based on GRAPES_MESO Forecasting Products. Remote Sensing, 13(13), 2644. https://doi.org/10.3390/rs13132644







