Collision Avoidance on Unmanned Aerial Vehicles Using Neural Network Pipelines and Flow Clustering Techniques

Abstract

Unmanned Autonomous Vehicles (UAV), while not a recent invention, have recently acquired a prominent position in many industries, and they are increasingly used not only by avid customers, but also in high-demand technical use-cases, and will have a significant societal effect in the coming years. However, the use of UAVs is fraught with significant safety threats, such as collisions with dynamic obstacles (other UAVs, birds, or randomly thrown objects). This research focuses on a safety problem that is often overlooked due to a lack of technology and solutions to address it: collisions with non-stationary objects. A novel approach is described that employs deep learning techniques to solve the computationally intensive problem of real-time collision avoidance with dynamic objects using off-the-shelf commercial vision sensors. The suggested approach’s viability was corroborated by multiple experiments, firstly in simulation, and afterward in a concrete real-world case, that consists of dodging a thrown ball. A novel video dataset was created and made available for this purpose, and transfer learning was also tested, with positive results.

1. Introduction

UAVs evolved from an emerging innovation, to a common technology in the consumer and commercial sectors of the economy [1,2,3]. This paper addresses a safety key issue that, most of the time, is discarded by UAV manufacturers, but that is critical for a massive deploy in urban environments, to allow UAVs to achieve the same levels of autonomy as cars [4], which is the collision avoidance with highly dynamic objects. The proposed solution works in the symbiosis with standard autonomous fly and avoid architecture [5]. This level of safety and reliability must be maintained regardless of operating conditions or the occurrence of unanticipated events. Due to carelessness, and disregard for these type of events, multiple disasters have happen in the past [6,7,8,9,10,11,12], which will increase considerably with the expected exponential increase in the number of UAVs deployed.

This sudden progress of UAVs and, more importantly, their commercial application in an ever-larger spectrum of scenarios increases the need for safer and more reliable algorithms [13,14,15,16]. The UAVs are a forefront of upheaval developments of sensing technologies (e.g., thermal, multispectral, and hyperspectral) in multiple areas that may change parts of society by creating new solutions and applications [17,18,19,20,21,22].

The increased safety in the UAV operation offered by the proposed solution allows new and interesting usage scenarios, such as urban event filming. A novel Collision Avoidance algorithm is proposed, which utilizes a Neural Network Pipeline (NNP) that consists of a Convolutional Neural Network (CNN) to extract features from video frames, a Recursive Neural Network (RNN) that takes advantage of the video temporal characteristics, and feeds a Feed-forward Neural Network (FNN) that is capable of estimating if there is an incoming collision. In parallel, an algorithm based on optical flow and flow agglomeration uses the latest two frames to calculate the closer object trajectory. The output of this algorithm is only taken into consideration whenever the NNP detects an incoming collision. Having the closest object trajectory, it is trivial to calculate a reactive escape trajectory.

To prevent a collision with a dynamic obstacle (such as an animal) or an incoming object (such as a thrown ball), a UAV needs to detect them as fast as possible and execute a safe maneuver to avoid them. The higher the relative speed between the UAV and the object, the more critical the role of perception latency becomes [23,24,25].

Researchers elaborated Collision-Avoidance Vector Field (CAVF) in the presence of static and moving obstacles [26] but did not tackle the problems of estimating the objects speed in real scenarios, where the sensors generate not so accurate data, and the objects are not well defined. Some solutions using deep reinforced learning are starting to appear in literature [27,28,29], which explore Neural Networks for autonomous navigation, but still only show a low Technology Readiness Level (TRL) and are not yet ready for industrial applications.

Compared to collision avoidance algorithms for static objects, the avoidance of dynamic objects have not yet been that much explored, since the task is much harder [5,30]. There are some works, such as the one from Poiesi and Cavallaro where multiple image processing algorithms that estimate the time of collision of incoming objects [31] are explored. The detection is accurate, but the algorithm takes more than 10 s to process each frame, making the solution not applicable in real time scenarios with state-of-the-art hardware. In addition, Faland et al. [32] delved into the event cameras to generate a computing efficient sensing pipeline, that was capable of avoiding a ball thrown towards a quad-copter at speeds up to 9 m/s similar to the work done in Reference [24]. To have a comparable test-bed, this use-case was considered for testing our algorithm, requiring the creation of a novel dataset with over 600 videos of different individuals throwing balls at a UAV.

The contributions of this article are then threefold:

• the development of an efficient and simple but robust software architecture for reacting and avoiding collisions with static or dynamic obstacles that are not known beforehand;
• proposal of a dataset of different individuals throwing balls at a UAV;
• and collision Avoidance Algorithm that uses an NNP for predicting collisions, and an Object Trajectory Estimation (OTE) algorithm using Optical Flow.

The rest of this paper is structured in the following sections: Section 2 presents the proposed solutions, being fully explained to facilitate replicability. Initially, a high level overview of the Framework for Collision avoidance for autonomous UAVs is provided in Section 2.1, and the main novelties of this architecture is the collision module, which is detailed, respectively, in Section 2.2, divided in the NNP and the Flows processing. Section 3 describes the experimental testing of the solution, followed by Section 4 that analyzes the data collected, which validates our approach and implementation. The paper presents its main conclusions and possible future research work in Section 5.

2. Materials and Methods

To tackle the collision avoidance task in UAVs, the architecture in Figure 1 is proposed. Initially, a generic view of all the modules and technologies is provided. Afterward, a detailed explanation is provided for the avoidance of incoming objects.

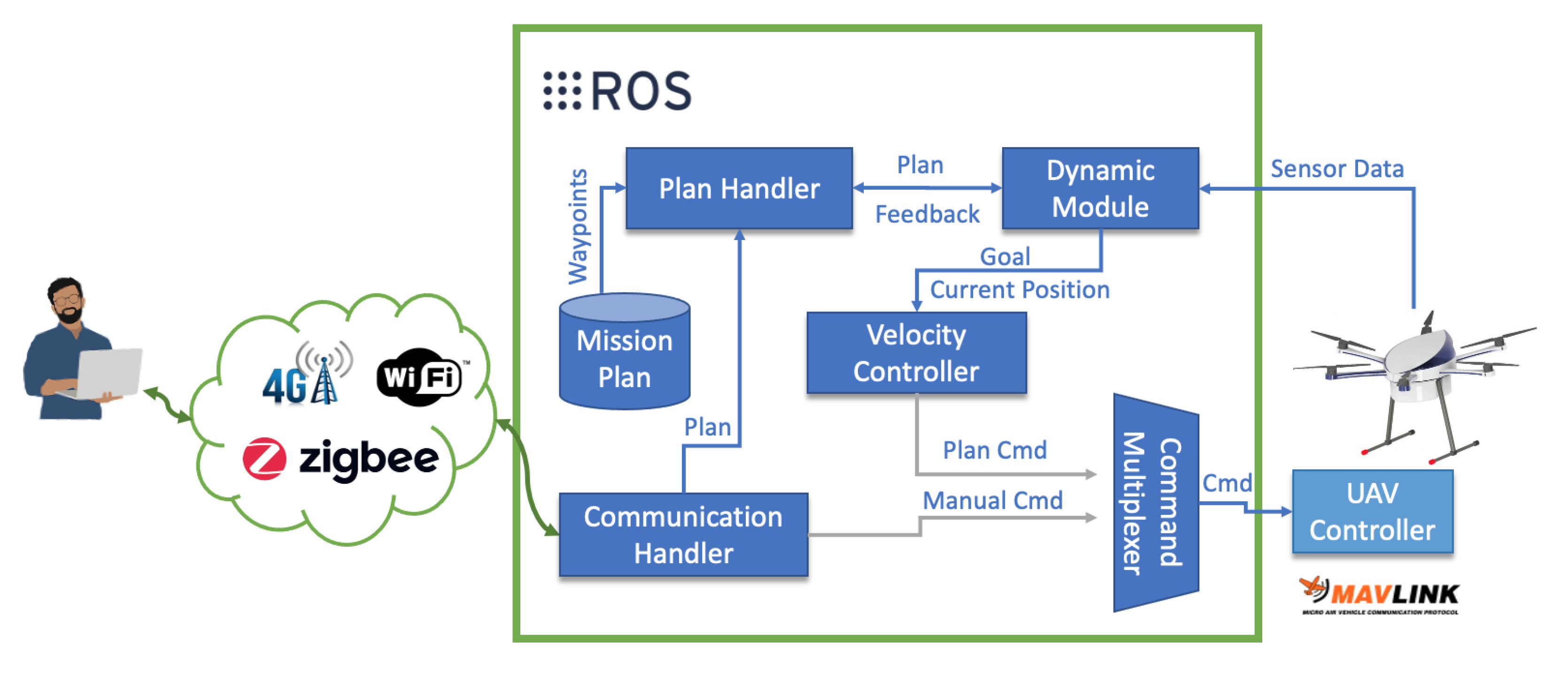
2.1. Collision Avoidance Framework for Autonomous Uavs

The communication between blocks is executed throughout ROS topics and services using the publisher/subscriber paradigm [33,34]. The cloud between the user and the UAV can be performed through the Wi-Fi, Zigbee and/or 4G protocols. In this way, the user is able to remotely communicate with/control the UAV, regardless of the distance. An architecture of the main modules is depicted in Figure 1.

The proposed architecture can be divided into five main blocks:

• Communication Handler: The Communication Handler block is responsible for maintaining interoperability between the user and the UAV. It is also responsible for triggering the pre-saved UAV mission through an activation topic.
• Plan Handler: This block is responsible for sending each waypoint of the complete mission to the Positioning Module block through a custom service in order to increase the security of communication and the entire system pipeline [35]. In this custom service, the Positioning block asks the Plan Handler block for the next point of the mission to be reached. In turn, the Plan Handler block returns the next point, where they contain the local coordinates of the intended destination.
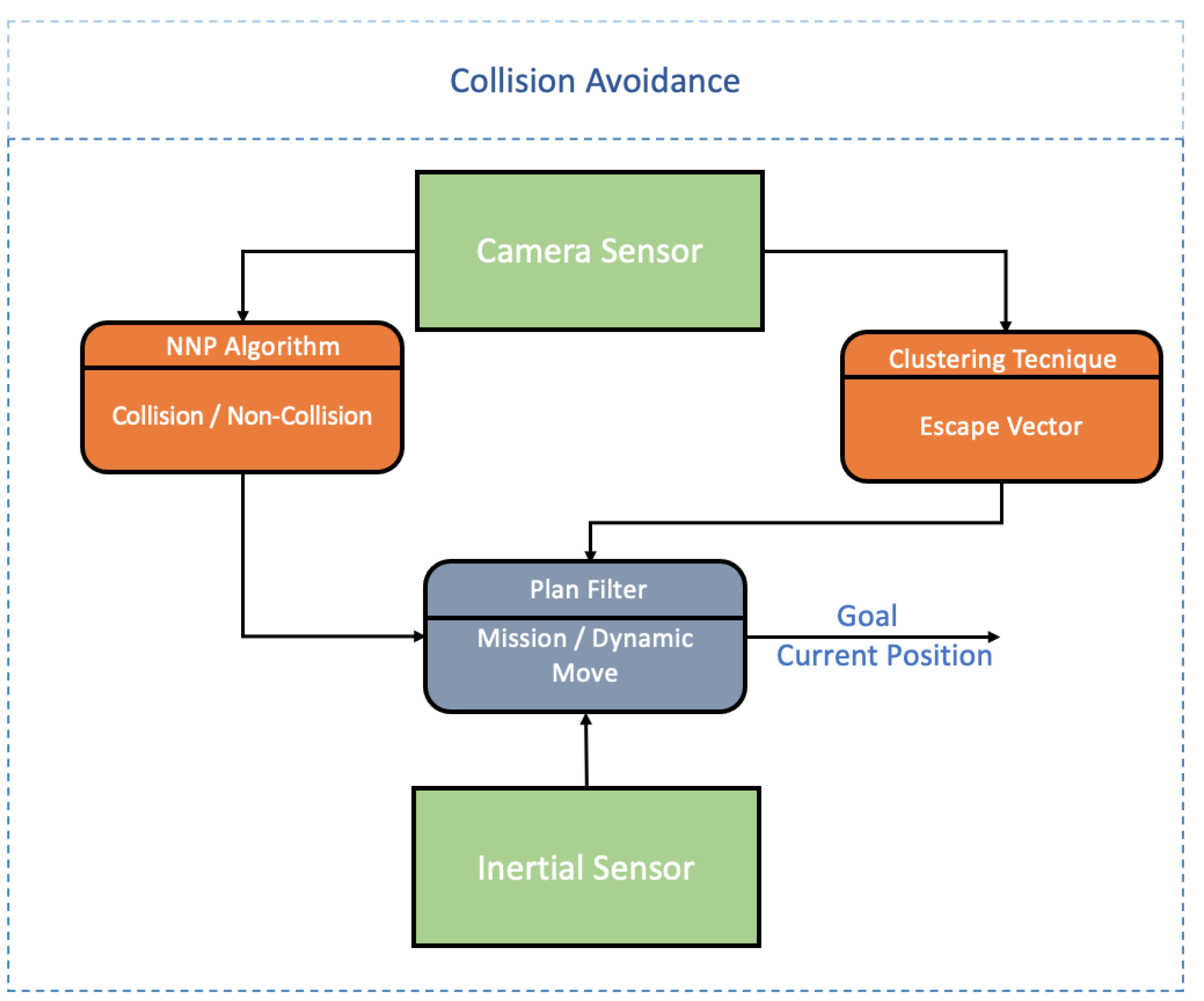
• Dynamic Module: This module computes possible dynamic object collisions. Through the camera, the inertial sensors, and the algorithm proposed in Section 2.2, it is possible to detect and avoid dynamic objects. Figure 2 presents the connections required for this module works.
  It is possible to observe in Figure 2 that there are 2 distinct processes: NNP for the static and dynamic obstacles prediction and detection; Clustering technique for grouping different objects in the same image and its, respectively, 2D movement direction to know the UAV escape trajectory.
  Through the inertial sensor, it is possible to know the UAV position and how to avoid when the obstacle avoidance algorithm is activated. In case the algorithm is not activated, the pre-defined mission by the user is carried out, through the Plan Handler module. The UAV position and the desired destination are then sent to the Velocity Controller block that navigates the UAV to the desired destination.
• Velocity Controller: The Velocity Controller block calculates the velocity required to reach the desired destination (with the mavros package [36]) using the inputs from the Positioning Module block and the Dynamic Module. This controller extends a proportional–integral–derivative (PID) controllers, where the variables change depending on the type of UAV, and the UAV’s velocity calculation on the three axes were based on Reference [37], where:

  $$e{P}^{\left(t\right)}=g{P}^{\left(t\right)}-c{P}^{\left(t\right)},$$

  (1)

  and

  $$e{D}^{\left(t\right)}=\left|\right|\left(e{P}^{\left(t\right)}\right)\left|\right|,$$

  (2)

  where $e{P}^{\left(t\right)}$ represents the error position, $g{P}^{\left(t\right)}$ the goal position, $c{P}^{\left(t\right)}$ the current position at time instant t, and $e{D}^{\left(t\right)}$ is the distance error position $e{P}^{\left(t\right)}$.
  With Equations (1) and (2), it is possible to normalize the error, as shown in Equation (3).

  $$e{N}^{\left(t\right)}=\frac{e{P}^{\left(t\right)}}{e{D}^{\left(t\right)}},$$

  (3)

  where $e{N}^{\left(t\right)}$ is the error normalized.
  If the distance is lower than a certain threshold, $\tau$ (in this work, the threshold value value is set to $\tau =4$ m), Equation (4) is activated.

  $$v{P}^{\left(t\right)}=e{P}^{\left(t\right)}·{\left(\frac{e{D}^{\left(t\right)}}{\tau }\right)}^{SF},$$

  (4)

  where $v{P}^{\left(t\right)}$ is the velocity vector, and $SF$ is the Smooth Factor (the $SF$ was set to 2 [37]).
  If the distance is higher than 4 m (threshold), Equation (5) is then used.

  $$v{P}^{\left(t\right)}=e{N}^{\left(t\right)}·PMV.$$

  (5)
  In Equation (5), $PMV$ is the Param Max Velocity and is equal to 2.
  In this way, it is allowed to dynamically vary the UAV speed depending on the UAV distance in relation to the desired destination without any sudden changes regarding the UAV’s acceleration;
• Command Multiplexer: The Command Multiplexer (CM) block subscribes to a list of topics, which are publishing commands and multiplexes them according to a priority criteria. The input with the highest priority controls the UAV by mavros package [36] with the mavlink protocol [38], becoming the active controller.

2.2. The Proposed Collision Avoidance Algorithm

To detect and avoid a possible collision with moving objects, a combination of two novel algorithms is proposed, that should be executed in parallel threads to boost performance. The first uses a NNP that predicts if there is an incoming collision. The second analyzes the pixel flows and applies clustering techniques estimate the image objects motion, allowing the calculation of the dynamic object trajectory. Only when NNP detects a collision are the results of the objects flow considered. A pseudo-code example is shown in Algorithm 1.

Whenever a possible collision is detected, the algorithm can use the latest available escape trajectory to dodge the incoming object. If the processing time of the NNP is greater than 1/fps, an additional thread must be added, which keeps reading the frames in parallel and updating the frame buffer that is used by the NNP. This thread makes sure that both the NNP and the OTE are using the latest frames, with no lost frames, or variable sequencing.

Algorithm 1: Proposed Algorithm for collision avoidance with moving objects.

# message publisher

reactiveCmdPub = ros.Publisher ()

# last known escape vector

escapeVector = {x: 0.0 , y: 0.0 , z: 0.0}

# OAF algorithm will constantly update the escapeVector var

opticalFlowThread = threading.Thread (target = OAF)

# Callback for Hybrid Collision Avoidance function

# it should be called whenever a new frame is obtained

def hca(videoFrame):

# Use the DCA algorithm to detect collisions

if(dcaProcessFrame (videoFrame)):

reactiveCmdPub.pub (escapeVector)

Section 2.2.1 will describe the NNP model that was developed in this article, and Section 2.2.2 will address the algorithm developed in order to agglomerate different incoming objects detected in a given image.

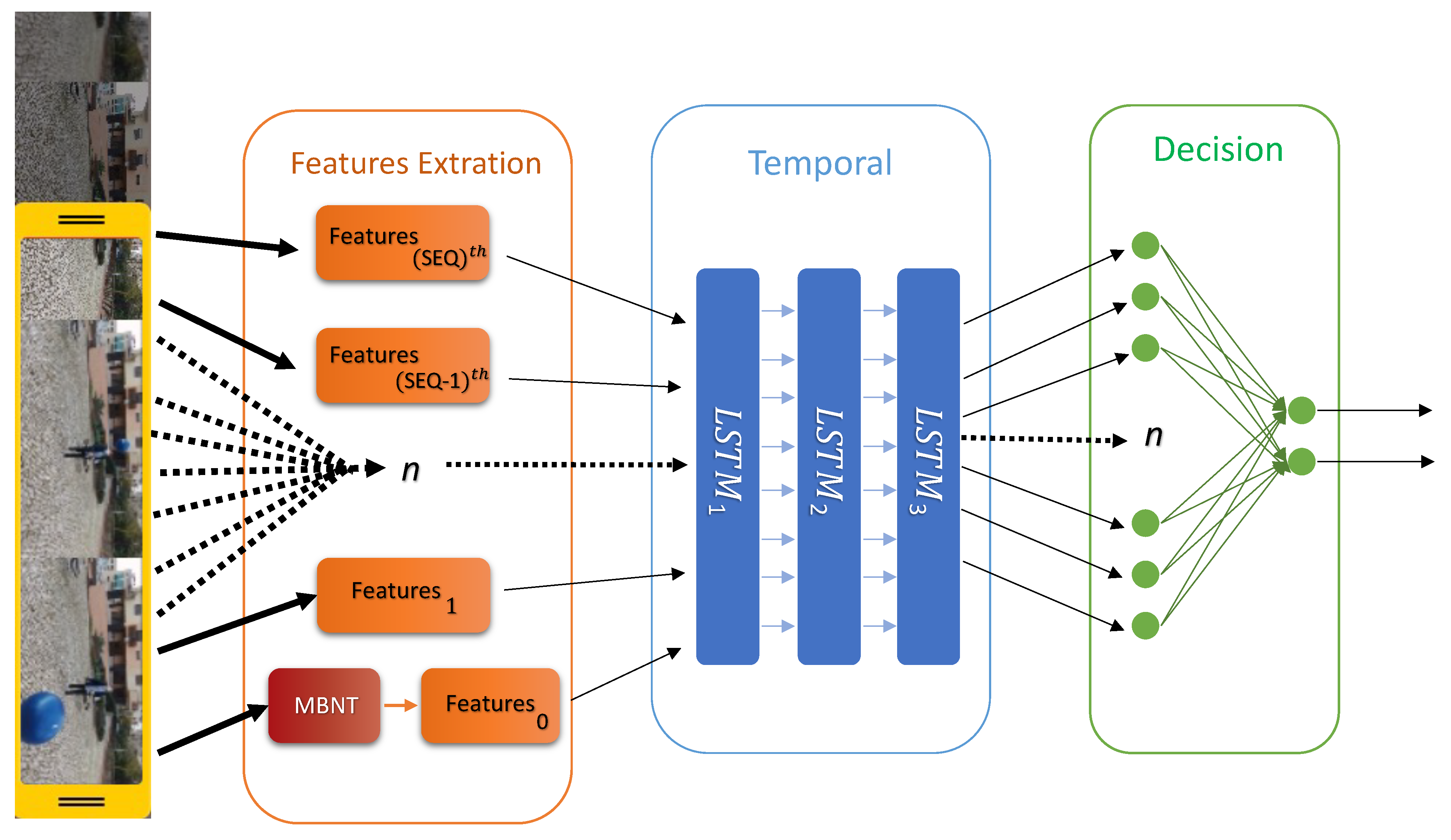
2.2.1. Neural Network Pipeline

A UAV must detect and perform a safe maneuver to avoid a collision with a incoming obstacle (such as an animal) or an incoming target (such as a tossed ball). Researchers [23,24,25] have defined perception latency as the time used to perceive the environment and process the captured data to generate control commands. This is a key metric when designing collision avoidance algorithms. The higher the relative speed between the UAV and object, the more critical the role of perception latency becomes.

This article proposes an innovative approach that makes use of a NNP. The task was divided into three sections to make it easier to solve. The first block is called Feature Extraction (FE), and it uses a CNN to generate feature vectors for video frames. The second block uses RNNs and the input of several $SEQ$ feature vectors to manage the video temporal information (stream). Finally, the third block receives the outcome of the previous RNN and employs a FNN to generate a decision. Figure 3 depicts the proposed architecture. These blocks will be discussed in more detail in the following subsections. Implementations, visualization functions, and additional details are available at https://github.com/dario-pedro/uav-collision-avoidance/tree/master/train-models (accessed on 20 May 2021).

Feature Extraction

The process of FE can be summarized in processing each frame with a CNN, which produces a vector, that can be interpreted as the frame key features that will ultimately be used by the NNP to detect a collision. Due to performance reasons, a MobileNetV2 (MNV2) [39] was selected. This CNN’s model is built on an inverted residual configuration, under which the standard residual block’s input and output are thin bottleneck layers, in contrast to residual models that use extended representations in the input and lightweight depth-wise convolutions to process features in the middle expansion layer [39]. This allows it to achieve the best trade-off between accuracy and computation for a low-power processor as the one present in UAVs [39,40,41]. For the input, it requires a $224\times 224\times 3$ matrix, and, after processing, it generates a $7\times 7\times 1280$ output matrix, which is converted into a 1280 vector by applying a 2D Global Average Pooling [42].

Temporal Correlation and Decision

A RNN is used to achieve the temporal association of the function data derived from each frame. A 3-depth blocks Long Short Term Memory (LSTM) [43] architecture is proposed in this article, which receives a series $\phi$ of 25 input vectors, representing approximately 1 s of video at a frame rate of 25 (the average video framerate of the selected dataset, the ColANet). The first layer contains eight LSTMs, while the second and third layers each contain two LSTMs. Dropout and batch normalization are applied after the first three layers. Furthermore, the final RNN layer is linked to a Feed-forward Neural Network with four neurons, which is then linked to two output neurons.

In a real-world use-case, the architecture is implemented using a sliding window technique, with the function queue still including the last 25 feature vectors and being fed into the RNN. When a new video frame becomes available, the FE processes it and adds the new feature vector to the features queue by moving the previous values. Furthermore, the resulting decision of the last frame is the consequence of the RNN and FNN for a group of 25 function vector arrays. Algorithm 2 describes the steps required to process a new video frame, assuming that all neural networks have already been loaded.

Algorithm 2: Neural Network Pipeline—processing the latest video frame.

SEQ_LEN = 25

features_queue = deque (maxlen=SEQ_LEN) # Double-ended queue

def dcaProcessFrame(videoFrame):

# Resize image to cnn input size

img = video_frame.resize (224,224,3)

# ML libs predict functions outputs arrays

cnn_pred = cnn_model.predict(img) [0]

# Shift add the image features to the features queue

features_queue.append cnn_pred)

# Check if enough images have been seen

if(len(features_queue) >= SEQ_LEN):

rnn_pred = rnn_model.predict(features_queue)[0]

return decision_model.predict(rnn_pred)[0] # return result

else:

return 0 # return no collision

Comparing solutions, such as conv3d [44], which apply convolutions to a 3D space, the processing is streamlined and, therefore, highly optimized. Just the last frame has to be interpreted by the CNN and the output features inserted into a queue that is forwarded to the RNN. Following that, the RNN and FNN are executed, which will provide a prediction.

2.2.2. Object Trajectory Estimation

The NNP presented is capable of detecting collisions or estimating escape trajectories. But, for practical scenarios, some federal organizations fear deploying algorithms that are only based on Neural Network (NN) architectures because they lack a results explanation [45]. Furthermore, if the task of the AI algorithm is simplified to the collision prediction, it increases its performance. For this reason, an Object Motion Estimator (OME) that utilizes Optical Flow (OF), and that can run on a parallel thread, was developed.

The OF is defined as the change of light in the image, e.g., the retina or the camera sensor, associated with the motion of the scene relative to the eyeball or the camera. In a bio-inspired sense, shifts in the light captured by the retina result in a movement perception of the objects projected onto the retina. In the technical context of computer vision, a set of video frames contain the movement of the observer and the environment combined.

NVIDIA Turing GPUs include dedicated hardware for OF computing. This dedicated hardware uses sophisticated algorithms to generate highly accurate flow vectors that are robust for frame-to-frame variations in intensity and track true object motion. Computation is significantly faster than other methods with comparable accuracy. The NVIDIA library for the pyramidal version of Lucas-Kanade method, which computes the optical flow vectors for a sparse feature set, was used to estimate the objects movement. The result of this algorithm on two frames at $t-1$ and t is illustrated at Figure 4. In Figure 4c, it is possible to observe the magnitude and direction of the flows matrix, each represented by a red arrow.

Calculating the OF of an image generates a matrix of flows that can be used to estimate the objects flow. Nevertheless, some flows are outliers and others are tracks of the object and parts of the background that were covered and became unveiled. In literature, there are multiple algorithms capable of clustering data. Nevertheless, none of them are tailored for the concrete case of low-processing, highly variable, objects flows. For this reason, a novel algorithm that filters and agglomerates flows in groups, outputting an aggregated flow result, with the goal of obtaining the closest object true flow is proposed. This algorithm is entitled Optical Flow Clustering. The most known clustering techniques were also implemented in order to benchmark the proposed algorithm.

To facilitate the comparison between metrics and results, the algorithms were divided by: the feature vectors representation and normalization of the flow data; appropriate distance measures and data reduction; and data clustering techniques.

Flow Vectors

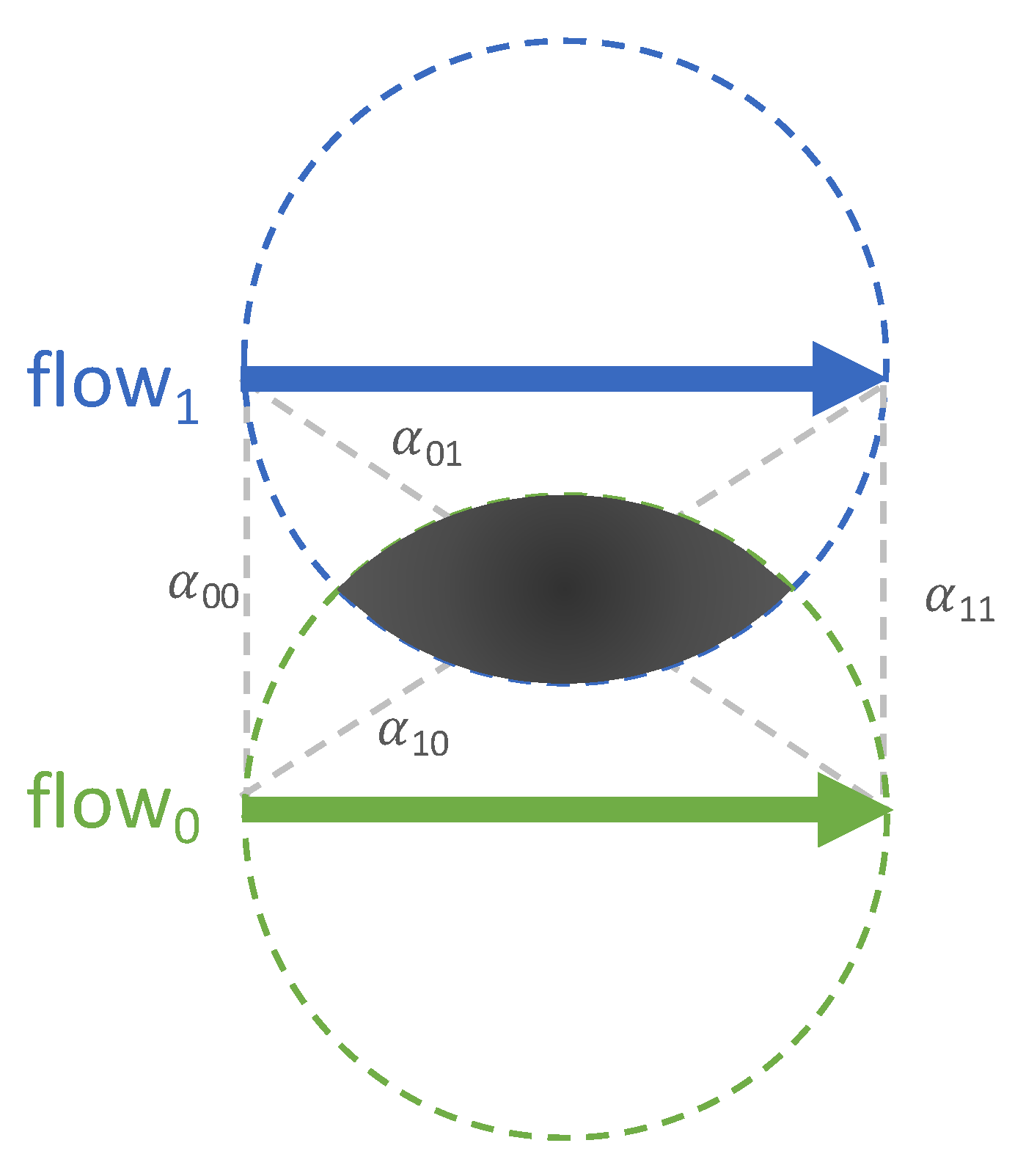
To obtain the feature space $\chi$, a four-dimensional vector space with N feature vectors $f={\left(\begin{array}{cccc}x& y& u& v\end{array}\right)}^T$ is considered, where $p={\left(\begin{array}{cc}x& y\end{array}\right)}^T$ are image pixel location coordinates, and $\psi ={\left(\begin{array}{cc}u& v\end{array}\right)}^T$ are velocity vectors.

The $\Re \left(v\right)$ is the magnitude of a vector, and $\Theta \left(v\right)=\angle (v_i,v_j)$ is the angle between any two vectors $v_i$ and $v_j$, with $1\le i,j<N$. The N function vectors are drawn at random from dense optical flow fields obtained for the measurement duration using a real-time variational method recently published [46]. Flow vectors with the smallest magnitude are discarded (by default 10%). Random sampling is used for statistical purposes, so clustering can be processed in miliseconds. We omit time details from the function vectors since the examined video sequences are comparatively small. By subtracting the average and dividing by the standard deviation, we normalize the image position coordinates x and y, as well as the velocity components u and v.

Flow Distances and Dimension Reduction

Three distance measures are defined: $D(i,j):=D(f_i,f_j)$ between any two feature vectors, with $1\le i,j<N$ :

• Euclidian: $D_E(i,j)=\sqrt{{\sum }_K^k{\left(k_i-k_j\right)}^2}$;
• Manhattan: $D_{Mt}(i,j)={\sum }_K^k\left|k_i-k_j\right|$; and
• Mahanalobis: $D_{Mh}(i,j)={\sum }_K^k{\left(k_i-k_j\right)}^{{\Sigma }^{-1}}{\left(k_i-k_j\right)}^T$, where $\Sigma$ is the covariance matrix between the components of the feature vectors.

Dimension reduction assists in data compression and reduces computation time. It also aids in the removal of some unnecessary functions. Furthermore, it reduces the time needed for clustering computation. For this reason, some dimension reduction techniques were also integrated:

• Isomap [47] is a low-dimensional embedding approach that is commonly used to compute a quasi-isometric, low-dimensional embedding of a series of high-dimensional data points. Centered on a rough approximation of each data point’s neighbors on the manifold, the algorithm provides a straightforward procedure for estimating the intrinsic geometry of a data manifold. Isomap is highly efficient and can be applied to a wide variety of data sources and dimensionalities.
• Multidimensional Scaling (MDS) [48,49,50] is a technique for displaying the degree of resemblance between particular cases in a dataset. MDS is a method for converting the information about the pairwise ’distances’ among a collection of vectors into a structure of points mapped into an abstract Cartesian space.
• T-distributed Stochastic Neighbor Embedding (t-SNE) [51,52] is a mathematical method for visualizing high-dimensional data by assigning a position to each datapoint on a two or three-dimensional map. Its foundation is Stochastic Neighbor Embedding. It is a nonlinear dimensionality reduction technique that is well-suited for embedding high-dimensional data for visualization in a two- or three-dimensional low-dimensional space. It models each high-dimensional object by a two- or three-dimensional point in such a way that identical objects are modeled by neighboring points and dissimilar objects are modeled by distant points with a high probability.

Flow Clustering

In order to generate the region of interested of the incoming object, the following clustering methods have been implemented:

• Kmeans [53] is a vector quantization clustering technique that attempts to divide n observations into c clusters, with each observation belonging to the cluster with the closest mean (cluster centers or cluster centroid), which serves as the cluster’s prototype. As a consequence, the data space is partitioned into Voronoi cells [54].
• Agglomerative Ward (AW) [55] is a Agglomerative Clustering technique that recursively merges the pair of clusters that minimally increase the wards distance criterion. Ward suggested a general agglomerative hierarchical clustering procedure in which the optimal value of an objective function is used to pick the pair of clusters to merge at each node.
• Agglomerative Average (AA) [56] is a clustering technique that recursively merges pairs of clusters, ordered by by the minimum average distance criterion, which is the average of the distances between each observation.

In addition to the state-of-the-art clustering techniques, a novel algorithm, entitled Optical Flow Clustering was developed, which is finely tailored for the collision detection. To process the OFC, initially it is necessary to calculate the image normalization factor (Equation (6)), $\varrho$:

$$\varrho =W^2+H^2,$$

(6)

where W is the image width, and H the image height. Then, the OF matrix is obtained, by computing the flow between $fram{e}_{t-1}$ and $fram{e}_t$. The resulting flows need to be filtered to reduce noise and ensure that only meaningful flows are considered for agglomeration. The value should be normalized by $\varrho$ to compare to the flow threshold, ${\varphi }_T$. A standard value for ${\varphi }_T$ is 1%, varying mostly with the camera stabilization (which induces noise). This filtering can be obtain by Equation (7).

$$\sqrt{\frac{x_w^2+y_h^2}{\varrho }}\ge {\varphi }_T.$$

(7)

The next step is an iterative procedure. It starts by considering two flows $f_0$ and $f_1$, from which the current position $P_{r0}=(x_0,y_0)$ and $P_{r1}=(x_1,y_1)$ is obtained, along with the flow ending position $(x_{0d},y_{0d})$ and $(x_{1d},y_{1d})$, which is $(x_n+f_{nx},y_n+f_{ny})$. An example of these flows and positions is illustrated in Figure 5.

Using these positions, it is possible to calculate the $\alpha$ distances:

$$\left[\begin{array}{cc}{\alpha }_{00}& {\alpha }_{01}\\ {\alpha }_{10}& {\alpha }_{11}\end{array}\right]=\left[\begin{array}{cc}\sqrt{\frac{{(y_0-y_1)}^2+{(x_0-x_1)}^2}{\varrho }}& \sqrt{\frac{{(y_0-y_{1d})}^2+{(x_0-x_{1d})}^2}{\varrho }}\\ \sqrt{\frac{{(y_{0d}-y_1)}^2+{(x_{0d}-x_1)}^2}{\varrho }}& \sqrt{\frac{{(y_{0d}-y_{1d})}^2+{(x_{0d}-x_{1d})}^2}{\varrho }}\end{array}\right].$$

(8)

The $\alpha$ distances presented in Equation (8) are used to verify if two flows can be merged, by comparing their values with ${\alpha }_{threshold}$. If the calculated value is below the ${\alpha }_{threshold}$, it is a valid flow to be merged. Whenever the values of the flows increase greatly and share the same direction, all the $\alpha$ distances might be larger then the ${\alpha }_{threshold}$, but still represent a flow from the same object. For this reason, it is important to calculate the distance of the centers of both flows $D_c$ and the radius of the enclosing circumferences $R_{fn}$ (Equations (9) and (10)):

$$D_c=\sqrt{\frac{{\left(\left|y_0-y_{0d}\right|-\left|y_1-y_{1d}\right|\right)}^2+{\left(\left|x_0-x_{0d}\right|-\left|x_1-x_{1d}\right|\right)}^2}{2}},$$

(9)

and

$$\left\{\begin{array}{c}{R}_{f0}=\sqrt{\frac{{(y_0-y_{0d})}^2+{(x_0-x_{0d})}^2}{2}}\\ R_{f1}=\sqrt{\frac{{(y_1-y_{1d})}^2+{(x_1-x_{1d})}^2}{2}}\end{array}.\right.$$

(10)

Figure 6 represents the intersection of the enclosing circumferences, which can be verified by the condition $R_{f0}>D_c+R_{f1}or{R}_{f1}>D_c+R_{f0}$.

Whenever the $\alpha$ distance or the intersection of the enclosing circumferences is verified, calculate $\left\{y_{min},x_{min};y_{max},x_{max}\right\}$ of the considered positions and merge Flows $f_0$ and $f_1$. The merge can be obtained by Equations (11) and (12):

$$P_{r0}(x,y)=\frac{P_{r0}·{\nu }_{f0}+P_{r1}·{\nu }_{f1}}{{\nu }_{f0}+{\nu }_{f1}},$$

(11)

$$F_{r0}(x,y)={\P }_{r1}-{\P }_{r0}.$$

(12)

Then, the $f_1$ is removed from the flow list. For a given region group, this processed is iterated considering the next $P_{r1}$ the left value of the list. When no flows can be agglomerated, that flow is stored and the next two flows are considered. This process is executed through the entire list of flows, and only stops whenever no flows are merged in a full search. The final result are regions containing the group of flows, and the cumulative flow values at the center of the regions. Figure 7 represents the result of the OFC on the flows processed and previously represented in Figure 4.

The output of the OFC are regions, that can be considered as moving objects. The incoming colliding object is considered to be region with the bigger area (supposedly closer to the camera). For example, on Figure 8, the hand of the person throwing the ball towards the UAV has produced a region with flows, which is smaller than the flow produced by the ball, and that needs to be discarded. By the incoming colliding object flow is possible to calculate an escape trajectory v, which is the perpendicular vector $v^{\perp }$, giving preference to rising solutions. Note that a perpendicular 2D vector $v^{\perp }$ always has two solutions, (${90}^{\circ }$ and $-{90}^{\circ }$). For a UAV, it is usually safer to go up; therefore, dodging objects by rising the UAV is considered safer). The OFC algorithm is depicted in pseudo-code in Algorithm 3.

Algorithm 3: Optical Flow Clustering algorithm.

# threshold to filter the flows

flowThreshold = 1

# N value for normalize the flows with image width and image height

N = math.sqrt(pow(w,2) + pow(h,2))

# threshold to filter the alpha distances

distanceThreshold = 15

# Callback for Hybrid Collision Avoidance function

# it should be called whenever a new frame is obtained

def OAF(frame1,frame2):

# obtain the optical flow from the 2 frames

flows = cv2.cuda_OpticalFlow.calc(frame1,frame2)

# filter meaningful flows

flows = filterFlows(flows,flowThreshold)

aggregating = True # control variable

regions = [] # object regions

while aggregating: # stop when there is no flows to merge

aggregating = False

for i in len(flows)-1:

for j in len(flows)-1:

if (i != j): # do not compare with self

# calculate the flows

alphas = calculateAlphas (flows[i],flows[j])

# radius and centers

rac = calculateRaC (flows[i],flows[j])

if (validAggregate(alphas,rac,distanceThreshold)):

# force a full scan

aggregating = True

# merge flows into flow [j]

mergeFlows (flows[j],flows[i])

if flows[j] not in regions:

# new region found - append it

regions.append (flows[j])

del flows[i] # remove the merged flow

break # go back to the first for cycle

3. Results

This section validates the performance of the proposed algorithm through numerical results and is organized in three parts. The first one presents the training results of the NNP, the second showcases the real environment results to assess the performance of the proposed algorithm from both accuracy and operational time point of views. The third part will compare the obtained results with the SoA methods.

3.1. NNP Training and Results

To train the proposed NNP, the creation of a new dataset focused on the selected testing scenario, the avoidance of a thrown ball, was required. The techniques proposed in ColANet [57] were used as guidelines, and the new dataset was made available at https://ballnet.qa.pdmfc.com/ (accessed on 20 May 2021). This dataset has 600 videos, which represent a total of 20,000 images. Frameworks for machine learning Tensorflow and Keras were used to aid in the creation and training of the models of the NNP [58].

At first, the MNV2 model was created in Tensorflow using the transfer learning method [59]. The weights were pre-trained with the ImageNet dataset, which contains 1.4 million images and 1000 categories of web images [60]. ImageNet is a fairly diverse dataset, containing categories, such as plane and eagle; however, this information facilitates the FE processes and transfers the general world perception.

First, the MNV2 layer used for FE is determined. The final classification layer (on top, like most models, which go from bottom to top) is useless. Typically, it is a standard practice to use the final layer before the last flattening layer. This layer is referred to as the ’bottleneck layer’. As compared to the final/top layer, bottleneck features maintain a lot of generality. This can be accomplished by loading a network without the classification layers at the end, which is suitable for FE.

Secondly, all layers are frozen before compiling the model, avoiding weights from changing during training. Then, a classification block is applied, which consists of a global average pooling 2D layer to convert the features to a single 1280-element vector per image and a dense layer to convert these features to a single prediction per image. Since this prediction would be viewed as a raw prediction value, no activation mechanism is needed. Positive numbers indicate a collision, while negative numbers indicate no collision.

Using a binary cross-entropy loss and an Adam optimizer [61] with a $1\times {10}^{-4}$ learning rate and a $1\times {10}^{-6}$ decay rate, the final classification layer was trained to have some knowledge of the objective target. The logistic regression loss can be represented as Equation (13) for the classification problem under consideration.

$$J\left(\mathbf{w}\right)=-\frac{1}{N}\sum _{i=1}^N\left[y_{i}log\left({\widehat{y}}_i\right)+(1-y_i)log(1-{\widehat{y}}_i)\right],$$

(13)

where w denotes the model parameters (weights), N denotes the number of images, $y_i$ denotes the target label, and ${\widehat{y}}_i$ denotes the projected label. Equation (14) gives the accuracy metric:

$$\mathtt{accuracy}(y,\widehat{y})=\frac{1}{N}\sum _{i=0}^{N}1({\widehat{y}}_i=y_i).$$

(14)

The training results of the added classifier are seen in Figure 9 for the first 20 epochs (before fine-tuning). Using only single frame knowledge, the model predicted collisions with 54.4% accuracy at the end of the 20 epochs (validation accuracy). Following that, a refined version of the MNV2 base model was trained. To do this, all layers were unfrozen. It is vital to emphasize that the first step is needed, since, if a randomly initialized classifier is applied on top of a pre-trained model, and all layers are jointly trained, the magnitude of the gradient updates will be too high (due to the classifier’s random weights) and the pre-trained model will forget what it has learned (the transferred knowledge). The fine-tuned FE’s training results are the last 20 epochs of Figure 9 and obtained a final validation precision of 66.8%. The disparity between training and validation began to increase on the final epochs, indicating the beginning of over-fitting, and no further epochs were trained as a result.

The MNV2 network has been fine-tuned to produce a model that is highly oriented to the collision classification challenge. On the one hand, this is positive because it helps the CNN to emphasize certain features, but, on the other hand, it is negative because it does not generalize well (potentially contributing to overfitting data) and gives more weight to features present in the dataset. As a result, the RNN and FNN blocks’ training will be achieved in just two iterations. The first iteration employs the MNV2 with ImageNet pre-trained weights. The second iteration employs the MNV2 with ImageNet pre-trained weights that have been fine-tuned in the novel dataset.

Initially, the RNN+FNN blocks are trained using CNN resulting data that has not been fine-tuned with dataset data. Some restrictions must be applied to the data in order to ready it for the second block:

• The input data must be a SEQ-length sequence. In this article, a value of 25 was used, but any value between 20 and 50 produced comparable results.
• The sequences produced must only contain frames from a single video. Working with video data on GPUs is not an easy process, and creating video sequences adds another layer of complexity. The model perceives the dataset as a continuous stream of data, and this constraint must be applied to prevent the model from learning jumps between videos (false knowledge).
• The goal for the whole series is the last frame target label.

The Adam optimizer [61] was used, with a learning rate of $1\times {10}^{-4}$ and a decay rate of $1\times {10}^{-6}$. Figure 10 shows the training results of the RNN with the FNN classification layer with moved FE weights and fine-tuned FE.

3.2. Real Environment

The avoidance of a thrown ball was tested to validate the algorithm in a similar use-case to previous research works [32]. A Parrot Bebop 2 was connected to a Legion with a 2060 GPU, running the proposed framework.

At first, the trained NNP weights were used, but the results were worse then expected. After some troubleshooting, the authors realized that by using the recorded videos, a constant framerate of approximately 29 fps was obtained. However, when working with the livestreaming video from the UAV, a framerate high variance was experienced, oscillating between 5 to 30 fps. On top of that, the compression algorithm used by the Parrot Bebop in livestream mode also reduces the video quality, creation yet another major difference against the trained NNP. The transmission delay is also an issue, and, for simplification, it will be left out of this paper.

To solve this issue, a set of image augmentation techniques were applied to the dataset. It consisted in randomly exposing the model to videos at variable framerate (by dropping frames), compressed frames (constant within the video, variable per epoch), and applied the most traditional augmentations, such as rotation, translation, and zoom (yet again, constant per video). After training and deploying this new model, a normal behavior was obtained. The NNP result is far from perfect, but this is due to the fact that the score is measured at the frame level. On the testing results, the NNP often detects a collision a few frames before or after the ideal moment annotated on the dataset, lowering the score. This is not critical, as long as the detection is obtained at a moment previously enough for the dodge routine.

Some of the latest UAVs in market (e.g., Skydio 2, HEIFU [62,63]) already have Nvidia Single Board Computer (SBC)s, being capable of running such algorithms directly on the aircraft, therefore being capable of running the proposed architecture directly on the UAV. The NNP and OME were integrated in a Jetson Nano (SBC) used by HEIFU), which managed to run the entire algorithm pipeline in an average of 0.18 s, demonstrating that it is a viable option for SoA UAVs.

In order to study the proposed OME algorithm, 8 frames from 8 different videos (total of 64 frames) were selected. Figure 11 illustrates these frames, which were manually annotated with a red mask on the ball, allowing the creation of ground truth mask by the filtering by color. The NNP were correctly outputing collision for all the selected frames; therefore, it is possible to evaluate the performance of the OME algorithm (the most critical part of the dodging trajectory estimation). The results of the overall approach are further analyzed on the next subsection.

4. Discussion

The NNP appers to be a vilable solution for the detection of incoming objects.

Table 1. Collision avoidance trained models’ results comparison.

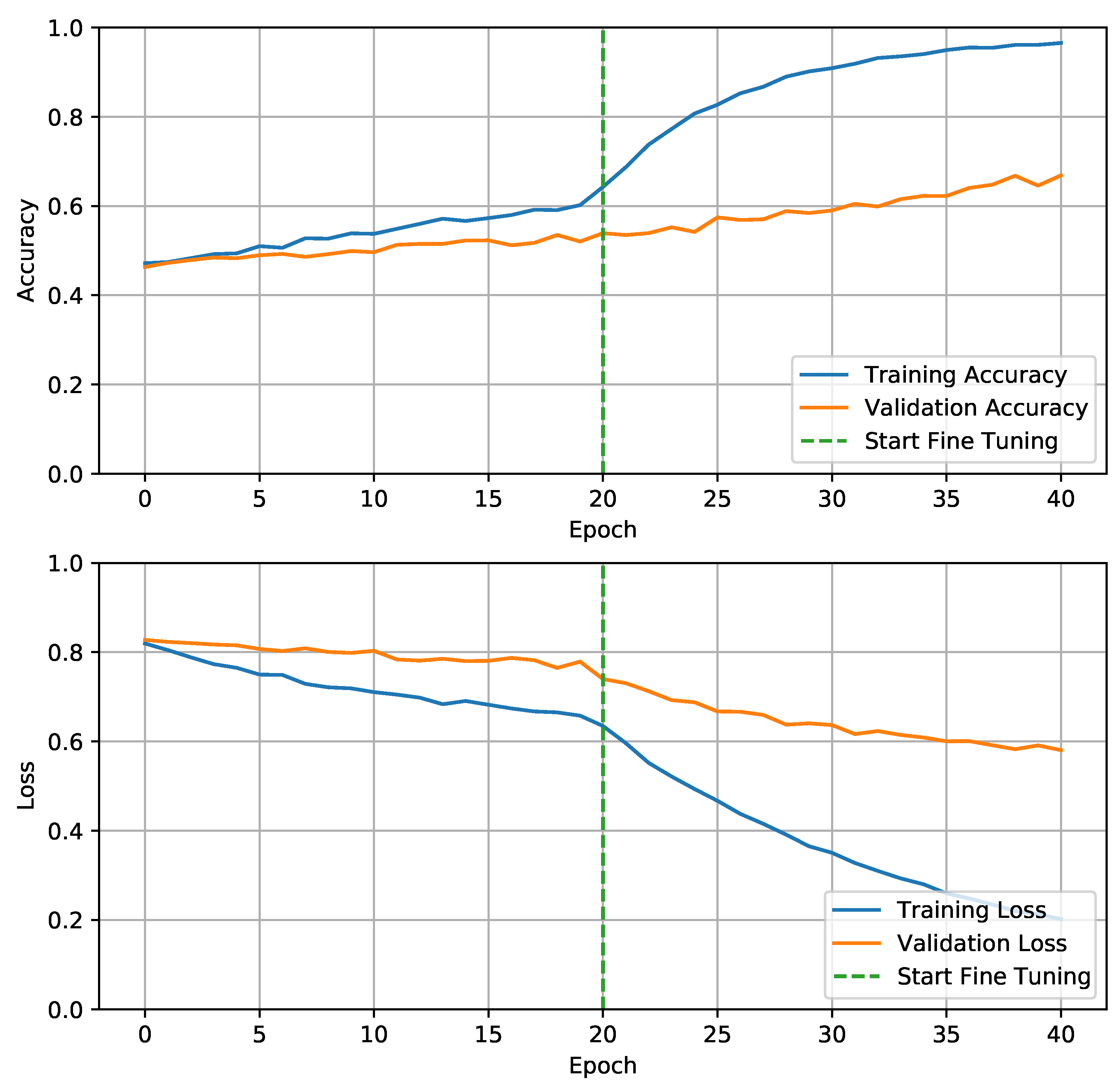
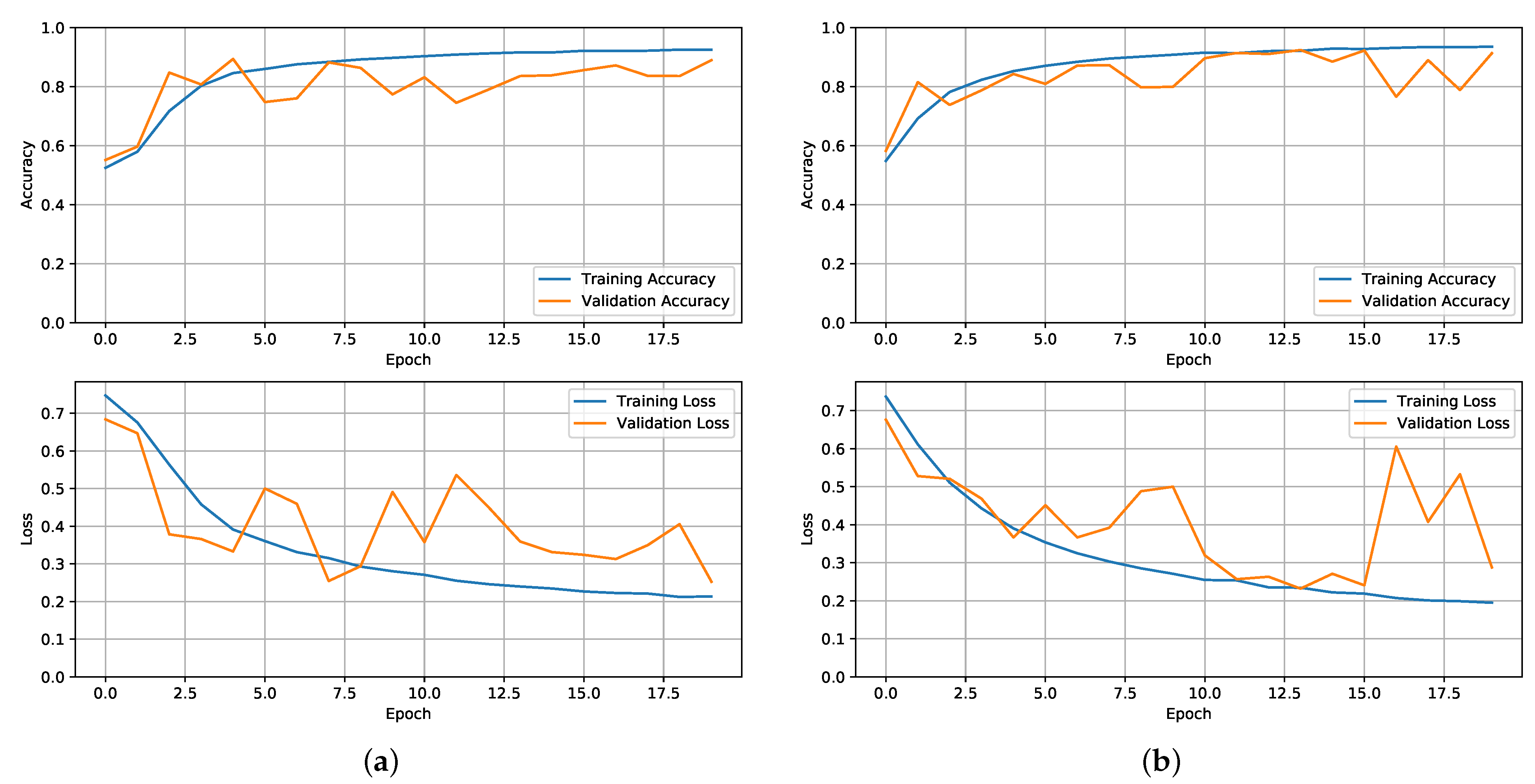
Metrics	${\mathbf{FE}}_1$ MNV2	Fine-Tuned MNV2	NNP w/ MNV2	NNP w/ Fine-Tuned MNV2
Training Accuracy	64.6%	97.4%	92.6%	93.4%
Validation Accuracy	54.4%	66.8%	89.4%	91.4%

summarizes the outcomes of the proposed models pipelines. It is possible to infer that it is a viable solution for the detection of incoming collisions, but more research, datasets, and testing are needed. On unseen data, the trained MNV2 achieved an accuracy of 66.8%, while the complete NNP using temporal features from an untrained MNV2 achieved an accuracy of over 89%. This confirms the theory that temporal information is important in the collision detection problem (or possibly in any video-related classification problem).

Fine-tuning the MNV2 improved the results of the NNP, but it is a slight trade-off between generalization and dataset performance. The presented dataset is relatively small and narrow, with a limited range of environments and variability. Because of the model’s proclivity to overfit, this makes preparation more difficult. The models can be further generalize and show better results as the amount of available UAVs datasets grows.

Futhermore, the OME is capable of calculating escape trajectories for the closest detected object. For each frame illustrated in Figure 11, the previous frame and the current frame were fed into the OME algorithm, that outputted a region for the incoming object. Using this output and the ground truth mask $GT$, it is possible to calculate the True Positive (TP) and False Positive (FP) (normalized by the object size $\sum G{T}_f$). For a given frame f and a different OME algorithm i, where & is the bitwise AND between matrix, it can calculated by Equation (15):

$$\left\{\begin{array}{c}T{P}_{fi}=\frac{G{T}_f\&OM{E}_{fi}}{\sum G{T}_f}\\ F{P}_{fi}=\frac{\overline{G{T}_f}\&OM{E}_{fi}}{\sum G{T}_f}\end{array}.\right.$$

(15)

In Figure 12, it is possible to observe the TP for each frame that is under analyses. The top-5 performing algorithms were picked for a better visualization. The OFC and the Agglomerative algorithms without dimension reduction were the ones that achieved the higher results. Moreover, on Figure 13 is depicted the processing time in ms of the algorithms per frame. The application of dimension reduction does not reduce processing time, according to this Figure 13. This is most likely due to the low complexity of the applied clustering algorithms. The OFC appears as a trade-off between accuracy and processing time.

Just analyzing the TP might be misleading because an algorithm might be detecting bigger regions, which always encapsulate the incoming object and, therefore, outperform other algorithms. On the other hand, when analyzing the FP, some algorithms detect a bigger area around the object, which intuitively is justified by the movement of the object which generate a flow vector between the previous and the current frame. This algorithm should not penalize the algorithm because, ultimately, it is estimating the incoming object correctly. For this reason, a new metric entitled $FPPerformance$ is introduced. The $FPPerformance$ takes into consideration the impact of the error in the decision. For this, after computing the $\overline{G{T}_f}\&OM{E}_{fi}$, for each point of the resulting mask, it has calculated the distance to the nearest point on the object. This new matrix of distances is named as $FD$. Afterwards, the $F{P}_{Performance}$ can be calculated by:

$$F{P}_{Performance}=\frac{\sum F{D}_{fi}}{\sum G{T}_f\&OM{E}_{fi}}.$$

(16)

Using Equation (16), it is possible to plot the results in Figure 14, which illustrate the FP Performance on the multiple frames. The OFC generate very few points outside the region of the incoming object; therefore, it is always below 0.15 FP Performance, which is a desirable threshold. Values above this threshold might lead to agglomeration of other objects and, therefore, a miss perception of another direction, which could lead to a wrong escape trajectory.

All the results have been summarized in

Table 2. Results comparison of the OME algorithm in the selected and annotated 64 frames.

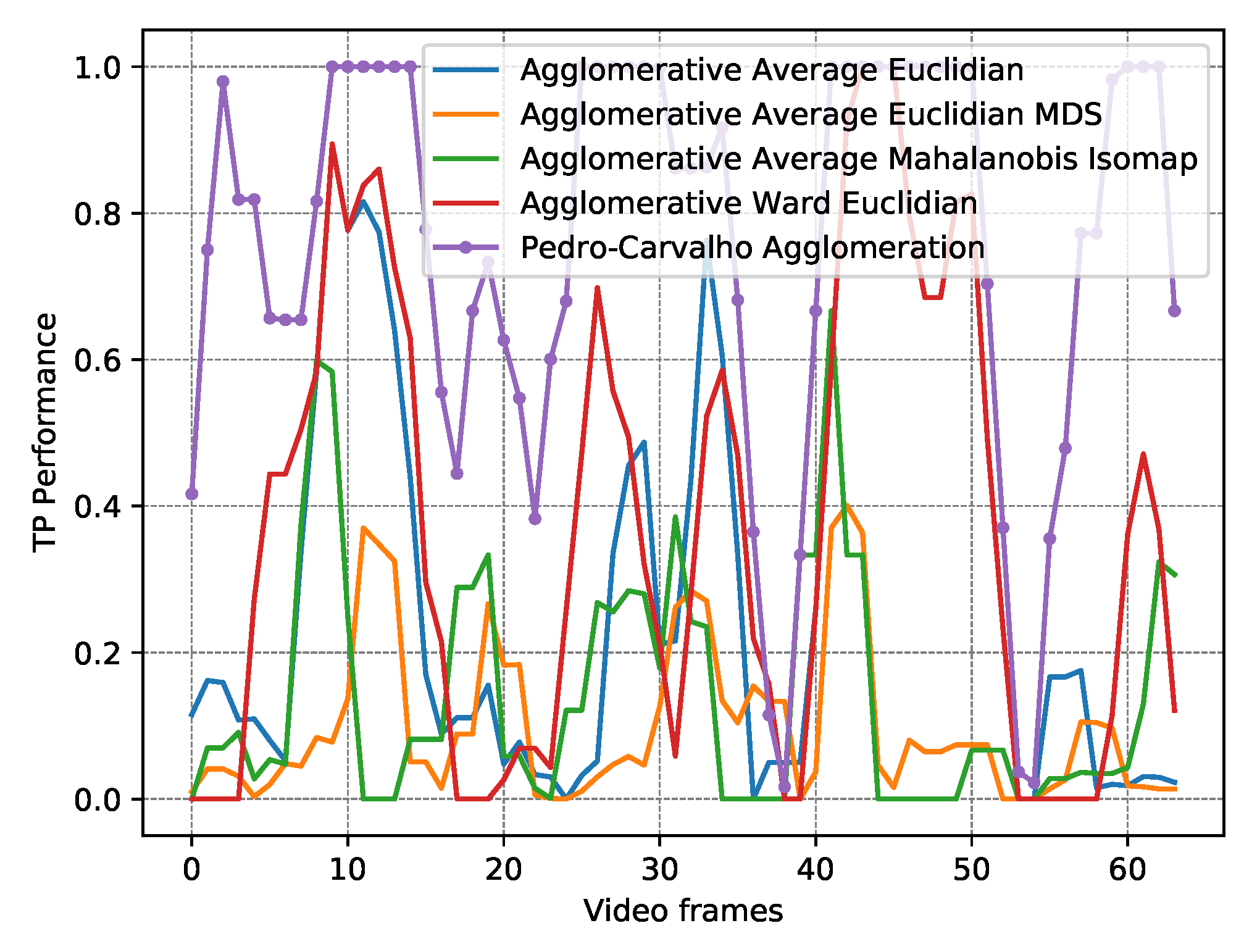
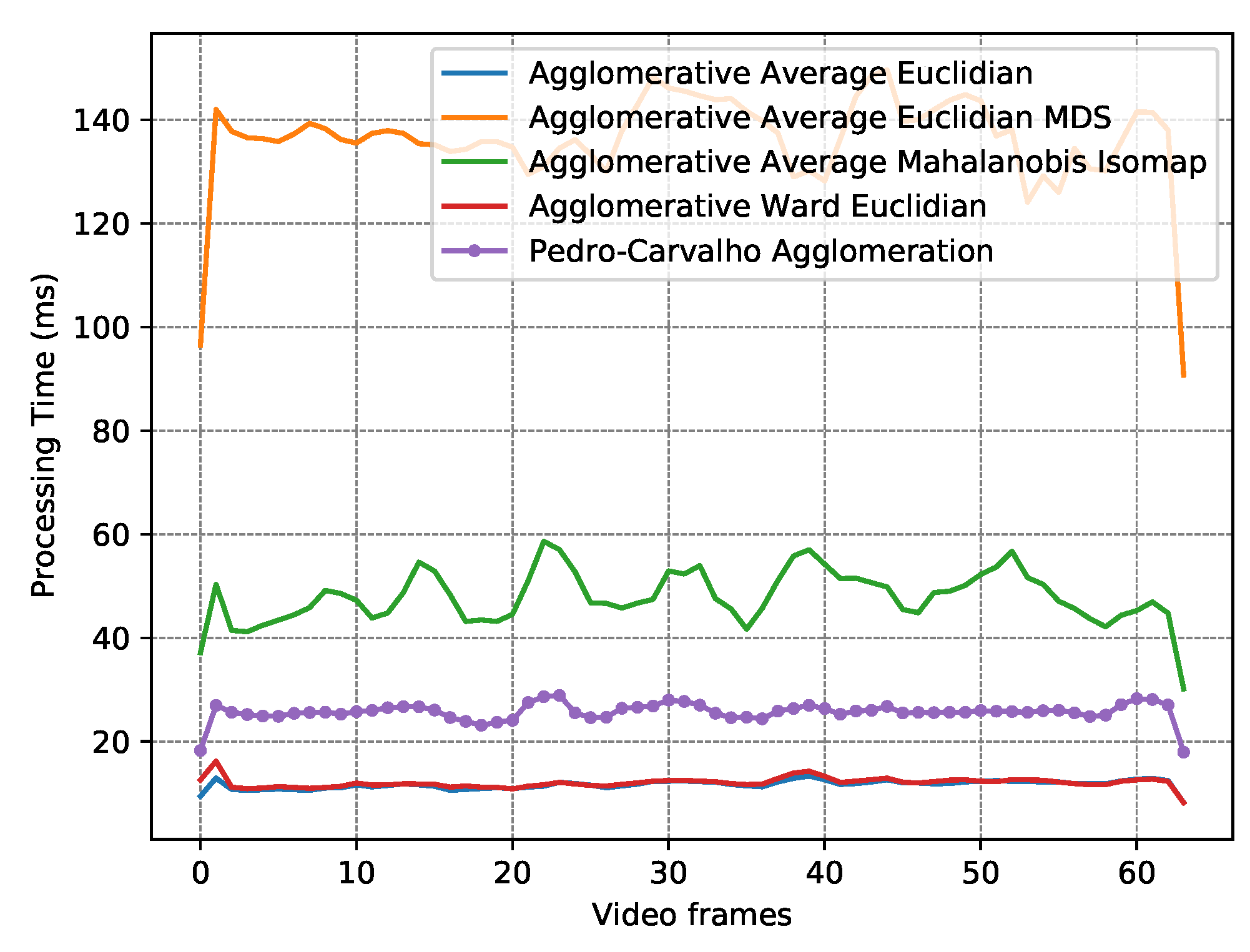
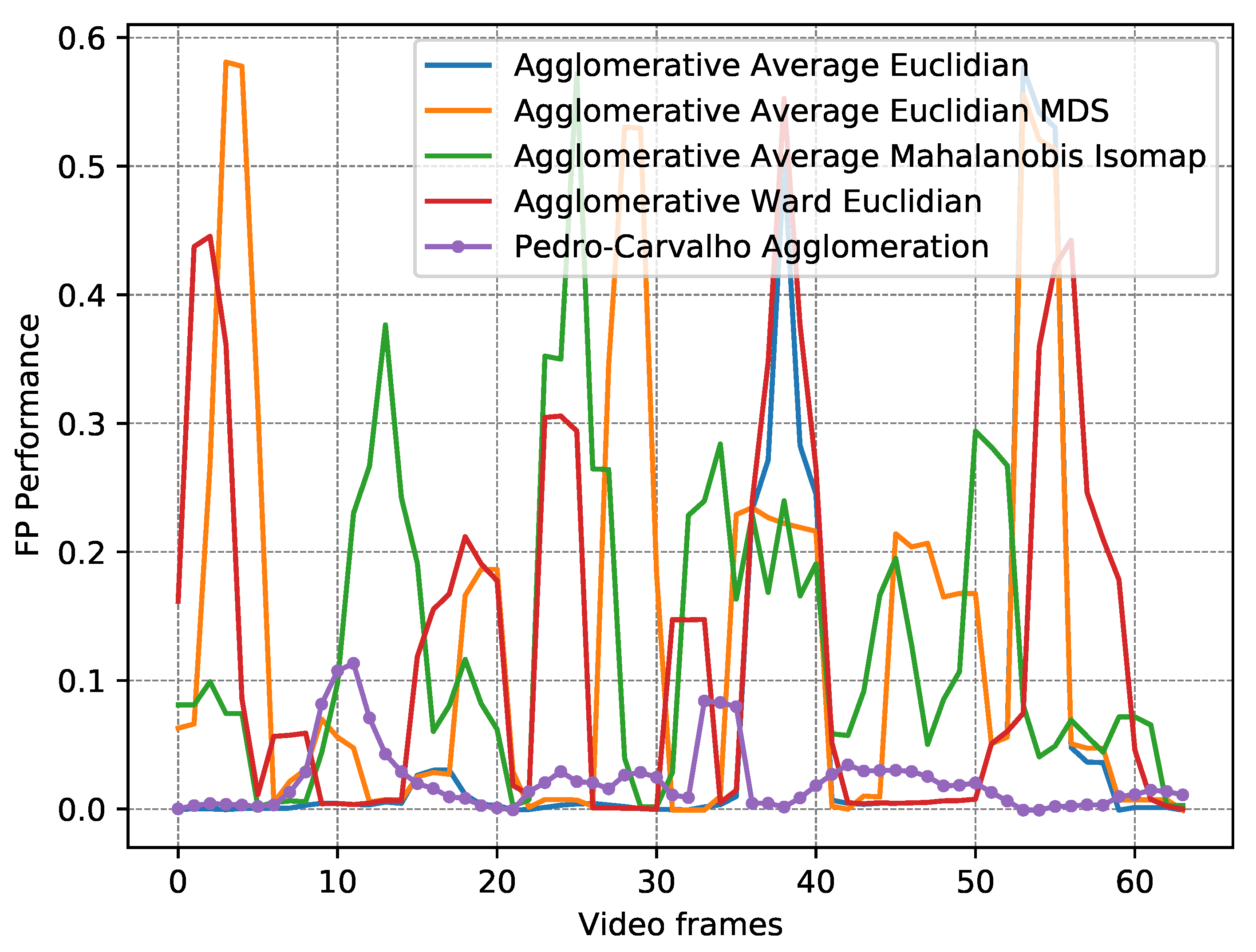
Algorithm	Distance Metric	Dimension Reduction	Mean TP	Mean FP	RMSE	FP Perf. (Min / Mean / Max)	Mean Time (ms)
OFC Agg.	- -	- -	0.76	3.40	0.50	0.00/0.02/0.06	25.99
AA [56]	Euclidian	- -	0.33	0.96	0.43	0.00/0.06/0.22	11.84
AA [56]	Manhattan	- -	0.33	0.96	0.43	0.00/0.06/0.22	8.69
AA [56]	Mahalanobis	- -	0.33	1.29	0.46	0.00/0.10/0.37	33.67
AW [55]	Euclidian	- -	0.37	1.82	0.47	0.00/0.13/0.27	12.23
AW [55]	Manhattan	- -	0.37	1.82	0.47	0.00/0.13/0.27	9.11
AA [56]	Mahalanobis	Isomap [47]	0.14	2.03	0.41	0.05/0.13/0.24	48.51
AA [56]	Euclidian	MDS [48]	0.10	1.43	0.37	0.02/0.14/0.28	137.63
AA [56]	Manhattan	MDS [48]	0.13	1.36	0.39	0.01/0.14/0.37	138.84
Kmeans [53]	Manhattan	- -	0.43	2.43	0.48	0.01/0.15/0.35	25.01
AA [56]	Euclidian	Isomap [47]	0.09	2.18	0.48	0.06/0.16/0.24	26.11
AA [56]	Manhattan	Isomap [47]	0.09	2.18	0.48	0.06/0.16/0.24	21.95
Kmeans [53]	Euclidian	- -	0.41	2.58	0.48	0.01/0.16/0.45	29.10
AA [56]	Mahalanobis	MDS [48]	0.13	1.81	0.39	0.02/0.17/0.48	159.93
AW [55]	Mahalanobis	- -	0.33	2.49	0.46	0.00/0.18/0.48	34.07
Kmeans [53]	Mahalanobis	- -	0.38	3.08	0.47	0.01/0.19/0.50	49.76
Kmeans [53]	Mahalanobis	Isomap [47]	0.18	4.67	0.44	0.07/0.23/0.41	64.07
AW [55]	Mahalanobis	Isomap [47]	0.18	3.91	0.46	0.07/0.24/0.40	48.91
AA [56]	Mahalanobis	t-SNE [51]	0.16	2.92	0.42	0.06/0.24/0.37	1057.79
AW [55]	Mahalanobis	t-SNE [51]	0.17	3.15	0.43	0.06/0.25/0.39	1058.15
Kmeans [53]	Mahalanobis	t-SNE [51]	0.19	3.51	0.43	0.06/0.26/0.36	1075.77
AA [56]	Euclidian	t-SNE [51]	0.13	2.97	0.45	0.12/0.29/0.43	1017.39
AA [56]	Manhattan	t-SNE [51]	0.13	2.97	0.45	0.12/0.29/0.43	1039.02
Kmeans [53]	Euclidian	Isomap [47]	0.10	4.37	0.49	0.07/0.29/0.44	41.11
Kmeans [53]	Euclidian	t-SNE [51]	0.13	3.43	0.45	0.10/0.30/0.47	1034.63
Kmeans [53]	Manhattan	Isomap [47]	0.08	4.70	0.47	0.07/0.31/0.49	36.56
Kmeans [53]	Manhattan	t-SNE [51]	0.13	3.43	0.46	0.10/0.31/0.47	1056.44
AW [55]	Euclidian	t-SNE [51]	0.11	3.31	0.47	0.09/0.32/0.50	1017.83
AW [55]	Manhattan	t-SNE [51]	0.11	3.31	0.47	0.09/0.32/0.50	1039.30
AW [55]	Euclidian	Isomap [47]	0.11	4.97	0.49	0.08/0.33/0.52	26.52
AW [55]	Manhattan	Isomap [47]	0.11	4.97	0.49	0.08/0.33/0.52	22.40
AW [55]	Manhattan	MDS [48]	0.06	4.15	0.44	0.20/0.42/0.63	139.31
AW [55]	Euclidian	MDS [48]	0.07	4.77	0.45	0.21/0.45/0.90	138.09
AW [55]	Mahalanobis	MDS [48]	0.08	4.92	0.50	0.17/0.52/0.99	160.31
Kmeans [53]	Manhattan	MDS [48]	0.03	6.08	0.42	0.36/0.54/0.78	158.46
Kmeans [53]	Mahalanobis	MDS [48]	0.04	5.84	0.44	0.24/0.54/0.82	179.07
Kmeans [53]	Euclidian	MDS [48]	0.03	6.33	0.42	0.30/0.58/1.00	158.76

, which is ordered by decreasing mean FP performance. The TP, FP, and the processing time are presented as the mean of all frames. Furthermore, the Root Mean Square Error (RMSE), and the min/max FP performance results are also presented. It’s possible to conclude that for the object trajectory estimation the proposed solution is capable to solve the problem with approximately $2\%$ error. When the algorithm is running live, with continuous frames being fed to the algorithm, the error should statistically decrease because it was measured per frame [64,65]. Further studies are required to analyze the performance impact with the speed variability of the incoming object, the speed variability of the observer, especially angular movements that might induce false trajectories [66]. In addition, environments with multiple moving objects require some attention, as might be the case in most crowded cities.

5. Conclusions and Future Work

In this work, a safer architecture for UAVs’ navigation was presented. This architecture features a block that is responsible for the collision avoidance with dynamic objects (such as a thrown ball). This block uses a NNP composed of a CNN for feature extraction, a RNN for temporal analyses, and a FNN for outputting the detection. Whenever this NNP outputs an incoming collision, an escape vector is calculated by a OME algorithm running in parallel. The OME uses the optical flow between the previous and the current frame, and a clustering algorithm to estimate the trajectory of the incomming object. A novel OF clustering algorithm for this use-case was introduced, which was named OFC, that outperform the state-of-art techniques.

To train the NNP a new dataset with 600 videos, with subjects throwing balls at a UAV was created. The videos were annotated and convert into 37,655 images. The NNP demonstrated an on-time detection, which allows the UAV to estimate a trajectory and to dodged the incoming ball. Both the results on the NNP and the OME demonstrated promising results, achieving $9\%$ error on frame collision detection (multiple consecutive frames drop this percentage) by the NNP, and approximately $2\%$ error on the trajectory estimation by the OME. The tackled use case is just an introduction to the capabilities of the proposed technique, as it only a scenario that consisted of a thrown ball, and presented a dataset for that purpose. The NNP knowledge can also be transferred to other scenarios with the enlargement of the dataset, and this solution only requires a simple monocular camera, which can be found in most commercial UAVs. The benefits of using these cameras are their small size, less weight, lower power consumption, flexibility, and mounting simplicity. On the other hand, they are highly dependent on weather conditions, might lack image clarity depending on the background color contrast. Regarding the proposed algorithms, the drawbacks identified are the processing requirements of the NNP, which are still not available in most of the out-of-shelf UAVs, and on the professional categories, it is still a significant amount of computational processing and power consumption. In addition, the OME might be accurate in processing the object trajectory, but any minor error can compromise the dodging maneuver. Finally, fast reactions might be dangerous if flying in cluttered environments, or if the UAV has considerable dimensions.

Compared with the current state-of-art, the proposed approach can be applied to standard UAVs using regular video sensors. Even though, in this paper, only the collision of an incoming thrown ball was explored, the authors believe that the algorithm can be easily adapted to multiple use-cases (with static or dynamic obstacles) by increasing the dataset scenarios. The solutions in the literature are in comparison harder to apply or unable of handling fast-moving objects.

This work will be continued with further updates on the modules presented in this article. The list below summarizes some of the key innovative ideas that will drive the future work:

• NNP improvement to estimate an escape vector, as postulated in the ColANet dataset;
• Optical Flow with depth estimation (using an depth camera), allowing the estimation of the distance to the object, therefore adjusting the escape speed, and facilitating the selection of the nearest object.
• CUDA implementation of the OFC algorithm to speed up computation time.
• Live tests on HEIFU hexacopters with the algorithms taking advantage of the on board GPU.