Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data
Abstract
:1. Introduction
2. Methodology
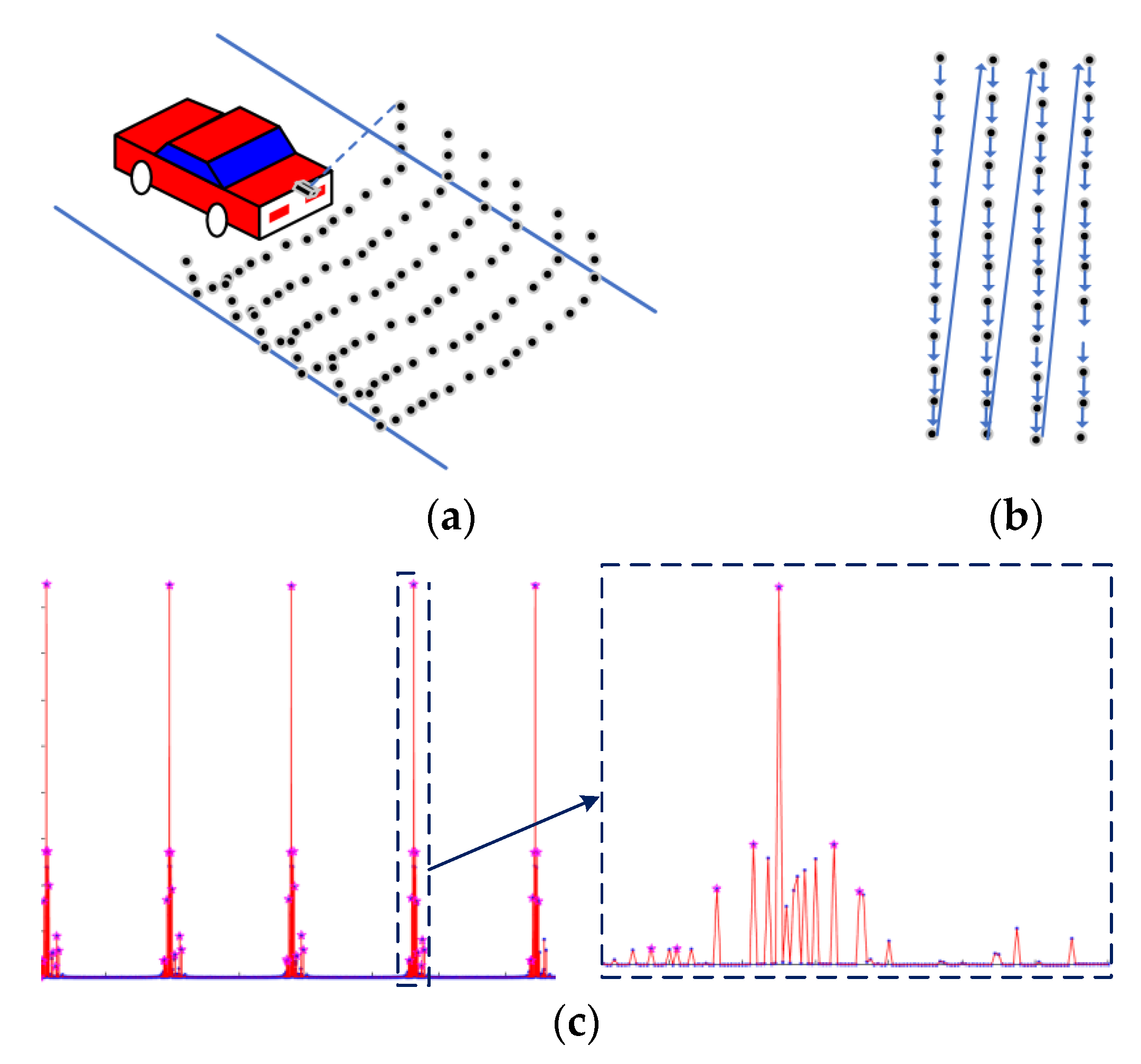
2.1. Pavement Extraction
2.2. Road Marking Extraction
2.2.1. Rasterization of Pavement Point Clouds
2.2.2. Adaptive Threshold Segmentation
2.2.3. Euclidean Clustering of Road Marking Point Clouds
- (1)
- Starting from any point in point set , add to the point set .
- (2)
- Add the points in the range of centered on into point set , as shown in Figure 7a.
- (3)
- Repeat step (2) with each newly added point in point set as the center, until no new points are added to point set , as shown in Figure 7b,c.
- (4)
- Start a new clustering by repeating steps (1)–(3) from the remaining points in P until all points are handled, as shown in Figure 7d.
2.3. Road Markings Vectorization
- Determination of the growth point. Suppose the total number of road marking clusters is n. Starting from the arbitrary cluster cluster_i(i∈[1,n]). If the distance between the MBR center of cluster_j(j∈[1,n], j≠i) and the MBR center of cluster_i is less than r (r = 20 m), cluster_j will be put into set clusterSet_r, as shown in Figure 8.
- Determination of the direction of growth. The direction of growth is determined by the direction of the vehicle trajectory, as shown in Figure 9.
- Firstly, calculate the coordinate azimuth between the MBR center of cluster_i and the MBR center of the clusters concluded in the set clusterSet_r. Secondly, calculate the difference (see Figure 9) between the azimuth and the azimuth of cluster_i. The clusters that satisfy Equation (22) will be put into set clusterSet_A. The parameter in this paper is set as 5°.Thirdly, calculate the difference (see Figure 9) between the azimuth of the cluster_j and the azimuth of the growth direction. The clusters that satisfy Equation (23) will be put into set clusterSet_A’. The parameter A in this paper is set as 5°.
- Calculate the similarity between cluster_i and the cluster concluded in the set clusterSet_A’ according to Equation (21). The clusters that satisfy Equation (24) are named as clusterSet_Si. The parameter Si in this paper is set as 0.58.
- If the set clusterSet_Si does not exist, the line segment growth will be over. Set the cluster_i to be any unconnected cluster and start a new line segment growth. Repeat steps until all of the road marking clusters are connected.
- In set clusterSet_Si, find out the cluster nearest to cluster_i, and mark it as cluster_j. cluster_j is the next cluster to be connected.
- Update the growth point to the MBR center of cluster_j and repeat the above steps until all of the clusters have been processed.



3. Experimental Data and Scheme
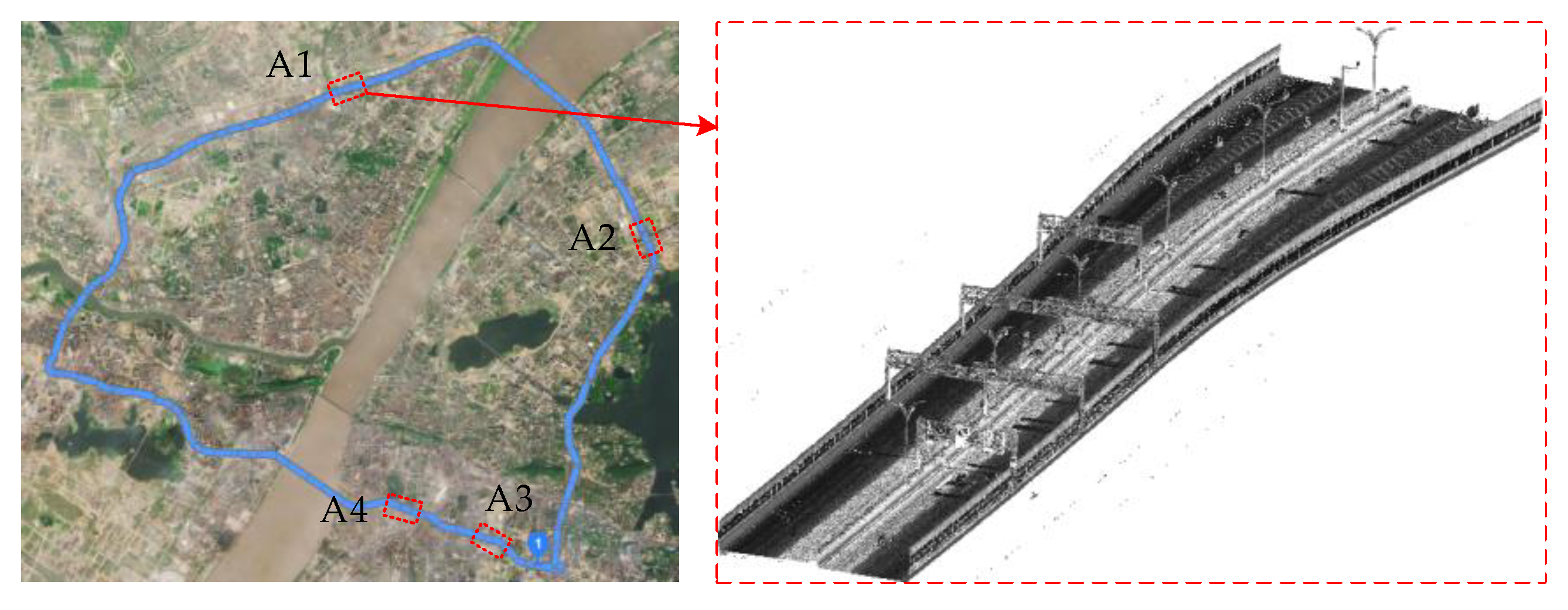
3.1. Experimental Data
3.2. Experimental Scheme
4. Experimental Results
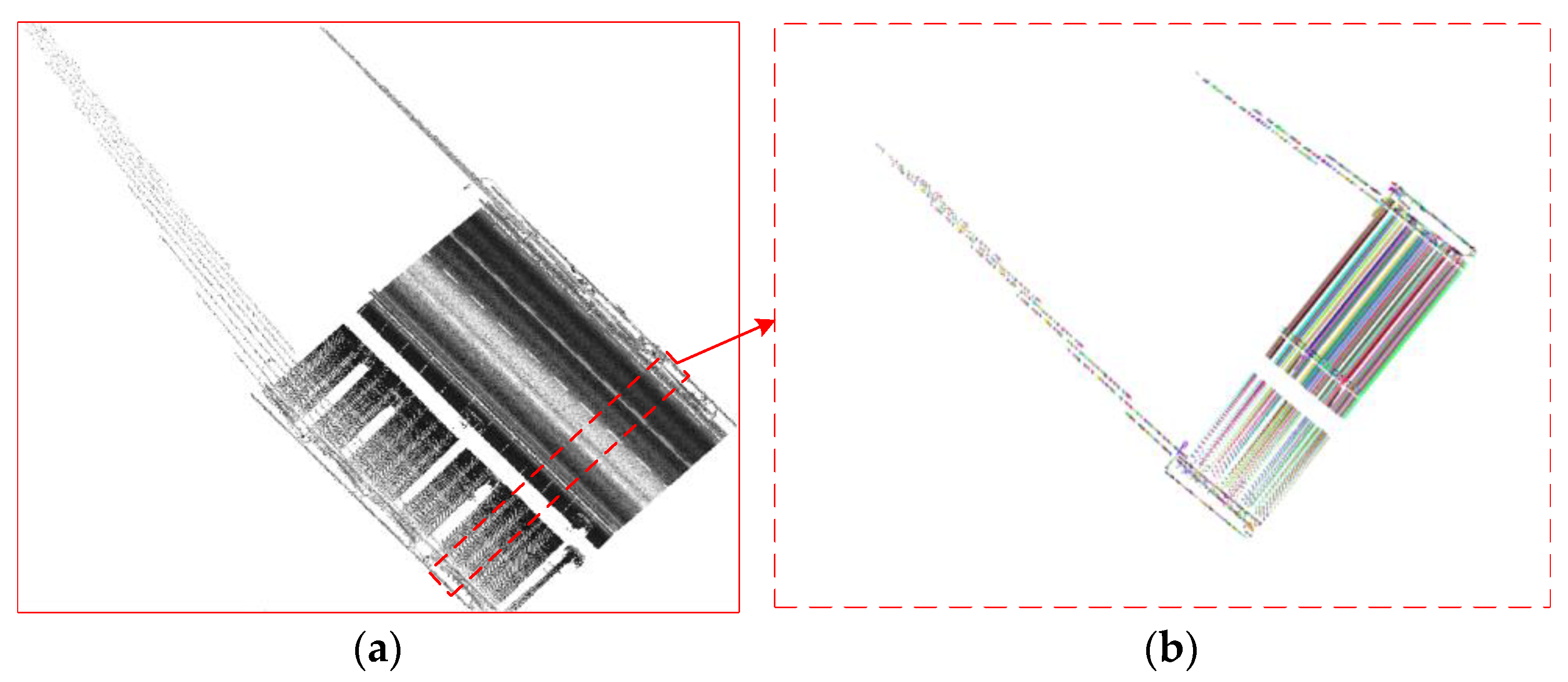
4.1. Pavement Extraction
4.2. Rasterization of Pavement Point Clouds
4.3. Binarization of Pavement Image
4.4. Euclidean Clustering
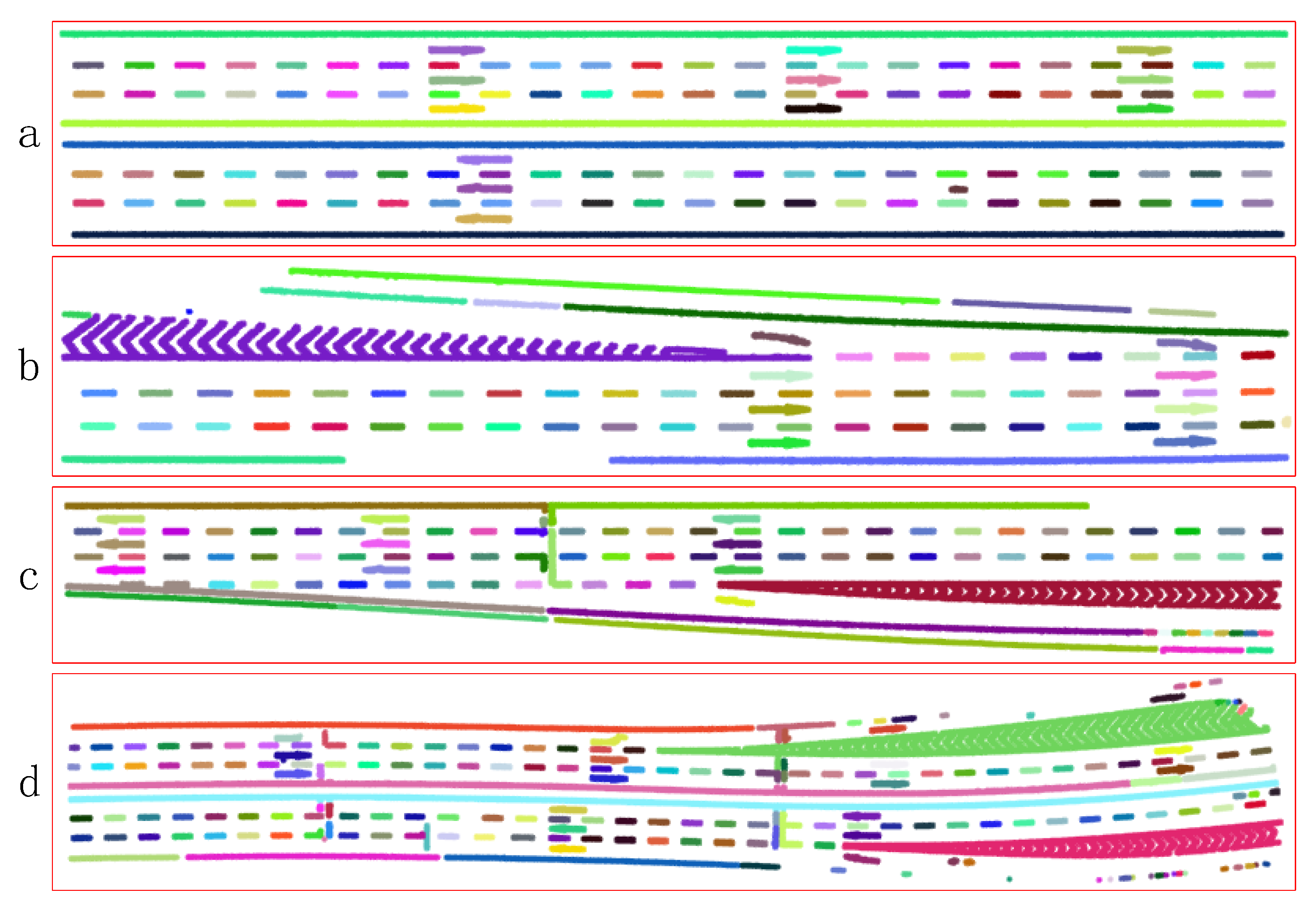
4.5. Recognition of Road Markings
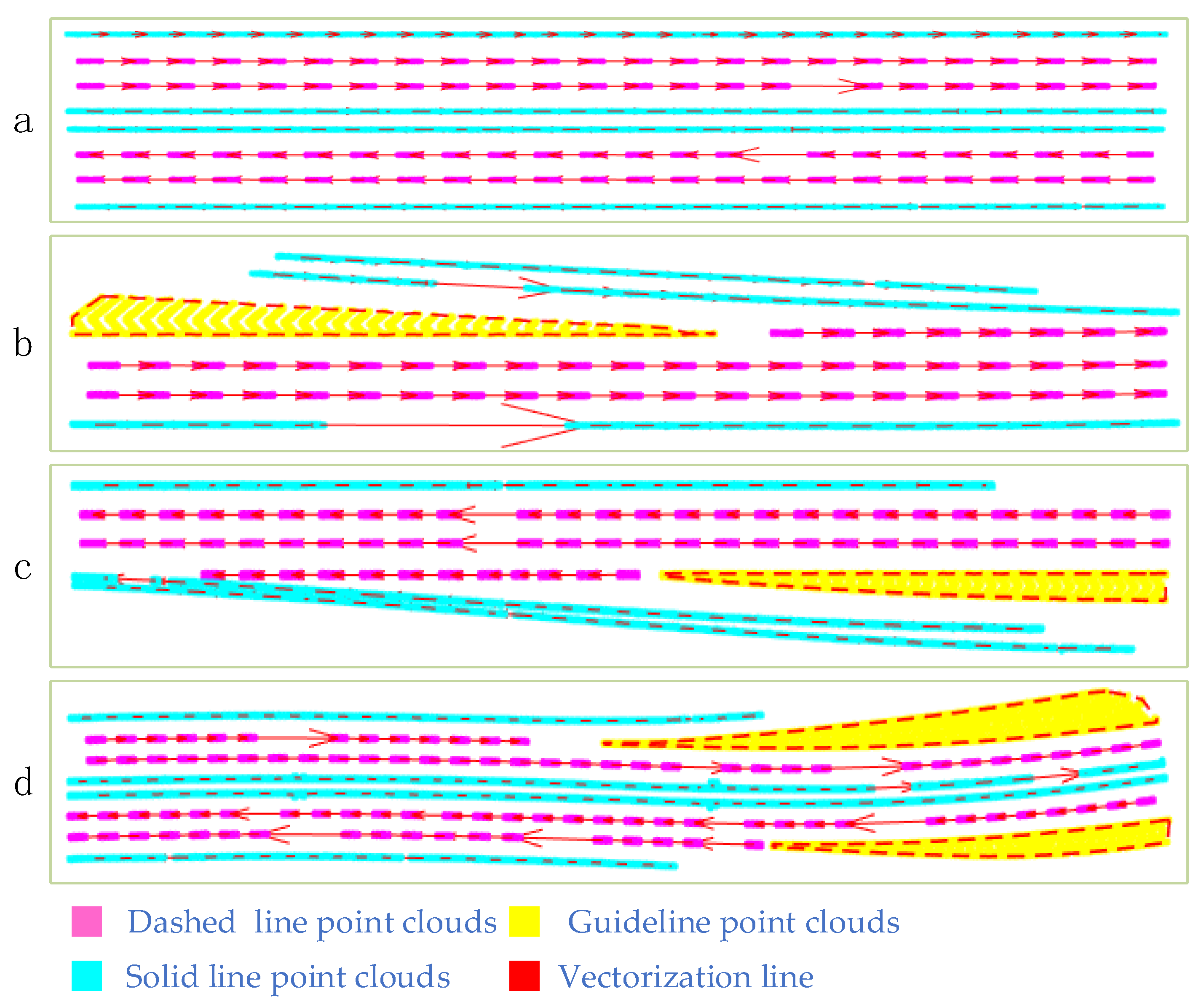
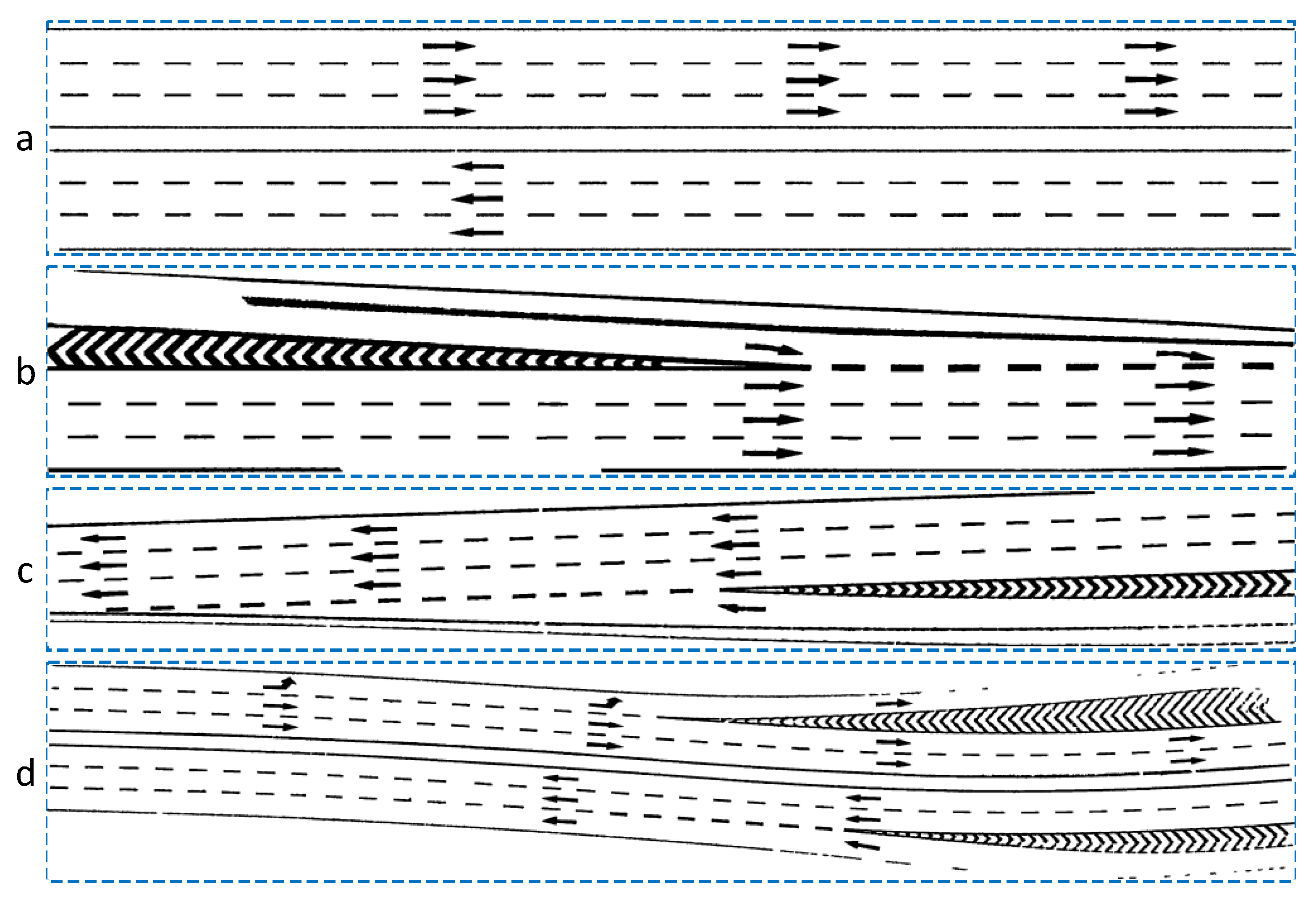
4.6. Vectorization of Road Markings
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, Y.; Patel, A.; Wen, C.; Bullock, D.; Habib, A. Intensity Thresholding and Deep Learning Based Lane Marking Extraction and Lane Width Estimation from Mobile Light Detection and Ranging (LiDAR) Point Clouds. Remote Sens. 2020, 12, 1379. [Google Scholar] [CrossRef]
- Li, Z.; Cai, Z.; Xie, J.; Ren, X. Road markings extraction based on threshold segmentation. In Proceedings of the IEEE 2012 9th International Conference on Fuzzy System and Knowledge Discovery (FSKD)—Chongqing, Sichuan, Chian, 29–31 May 2012; pp. 1924–1928. [Google Scholar]
- Chen, T.; Chen, Z.; Shi, Q.; Huang, X. Road marking detection and classification using machine learning algorithms. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 617–621. [Google Scholar]
- Rebut, J.; Bensrhair, A.; Toulminet, G. Image segmentation and pattern recognition for road marking analysis. In Proceedings of the 2004 IEEE International Symposium on Industrial Electronics, Ajaccio, France, 4–7 May 2004; Volume 1, pp. 727–732. [Google Scholar]
- Jung, S.; Youn, J.; Sull, S. Efficient lane detection based on spatiotemporal images. IEEE Trans. Intell. Transp. Syst. 2015, 17, 289–295. [Google Scholar] [CrossRef]
- Hernández, D.C.; Seo, D.; Jo, K.-H. Robust lane marking detection based on multi-feature fusion. In Proceedings of the 2016 9th International Conference on Human System Interactions (HSI), Portsmouth, UK, 6–8 July 2016; pp. 423–428. [Google Scholar]
- Azimi, S.M.; Fischer, P.; Körner, M.; Reinartz, P. Aerial LaneNet: Lane-marking semantic segmentation in aerial imagery using wavelet-enhanced cost-sensitive symmetric fully convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2018, 57, 2920–2938. [Google Scholar] [CrossRef] [Green Version]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan line based road marking extraction from mobile LiDAR point clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Li, J.; Yu, Y.; Ji, Z.; Wang, C. Using mobile LiDAR data for rapidly updating road markings. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2457–2466. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Jia, F.; Cheng, W. Learning hierarchical features for automated extraction of road markings from 3-D mobile LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 709–726. [Google Scholar] [CrossRef]
- Wang, H.; Luo, H.; Wen, C.; Cheng, J.; Li, P. Road Boundaries Detection Based on Local Normal Saliency from Mobile Laser Scanning Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2085–2089. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Wang, C.; Chapman, M.; Yang, B. Using mobile laser scanning data for automated extraction of road markings. ISPRS J. Photogramm. Remote Sens. 2014, 87, 93–107. [Google Scholar] [CrossRef]
- Yang, B.; Fang, L.; Li, Q.; Li, J. Automated extraction of road markings from mobile LiDAR point clouds. Photogramm. Eng. Remote Sens. 2012, 78, 331–338. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Li, J.; Yu, Y.; Junior, J.M.; Gonçalves, W.N.; Chapman, M.A. Capsule-based networks for road marking extraction and classification from mobile LiDAR point clouds. IEEE Trans. Intell. Transp. Syst. 2021, 22, 1981–1995. [Google Scholar] [CrossRef]
- Wellner, P.D. Adaptive Thresholding for the DigitalDesk. Xerox 1993. [Google Scholar]
- Bradley, D.; Roth, G. Adaptive thresholding using the integral image. J. Graph. Tools 2007, 12, 13–21. [Google Scholar] [CrossRef]
- Yao, J.; Cao, X.; Zhao, Q.; Meng, D.; Xu, Z. Robust subspace clustering via penalized mixture of Gaussians. Neurocomputing 2018, 278, 4–11. [Google Scholar] [CrossRef]
- Yao, L.; Chen, Q.; Qin, C.; Wu, H.; Zhang, S. Automatic Extraction of Road Markings from Mobile Laser-Point Cloud Using Intensity Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3, 2113–2119. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.; Yi, L.; Su, H.; Guibas, L. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. PointCNN—Convolution On X-Transformed Points. Adv. Neural Inf. Process. Syst. 2018, 31, 828–838. [Google Scholar]
- Thomas, H.; Qi, C.; Deschaud, J.; Marcotegui, B.; Goulette, F.; Guibas, L. KPConv-Flexible and Deformable Convolution for Point Clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6410–6419. [Google Scholar]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Zhang, H.; Wang, C.; Li, J. Extraction and Classification of Road Markings Using Mobile Laser Scanning Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1182–1196. [Google Scholar] [CrossRef]










| Parameter Type | Value |
|---|---|
| Scanner model | RIEGL VUX-1 |
| Scanning mode | Single line cross section scanning |
| Vehicle speed | 35~40 km/h |
| Scanning frequency | 200 hz |
| Scanning speed | 500,000 points/s |
| Vertical field of view | 330° |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 5 m | 25° | ||
| 7 m | 0.05 m | ||
| 650 | 350 | ||
| 0.08 m |
| Category | Total | TP | FN | FP | Precision | Recall | F-Score |
|---|---|---|---|---|---|---|---|
| Broken line | 325 | 310 | 16 | 3 | 0.95 | 0.99 | 0.97 |
| Guideline | 4 | 4 | 0 | 4 | 1.00 | 0.5 | 0.66 |
| Straight arrow | 38 | 37 | 1 | 13 | 0.97 | 0.74 | 0.84 |
| Left turn arrow | 1 | 0 | 1 | 0 | 0 | - | - |
| Right turn arrow | 3 | 3 | 0 | 0 | 1 | 1 | 1 |
| Test Data | Completeness | Correctness | F-Score | |
|---|---|---|---|---|
| a | (7, 1.28) | 0.94 | 0.73 | 0.83 |
| b | (14, 1.38) | 0.86 | 0.79 | 0.82 |
| c | (13, 1.43) | 0.82 | 0.83 | 0.83 |
| d | (13, 1.36) | 0.90 | 0.78 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, L.; Qin, C.; Chen, Q.; Wu, H. Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data. Remote Sens. 2021, 13, 2612. https://doi.org/10.3390/rs13132612
Yao L, Qin C, Chen Q, Wu H. Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data. Remote Sensing. 2021; 13(13):2612. https://doi.org/10.3390/rs13132612
Chicago/Turabian StyleYao, Lianbi, Changcai Qin, Qichao Chen, and Hangbin Wu. 2021. "Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data" Remote Sensing 13, no. 13: 2612. https://doi.org/10.3390/rs13132612
APA StyleYao, L., Qin, C., Chen, Q., & Wu, H. (2021). Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data. Remote Sensing, 13(13), 2612. https://doi.org/10.3390/rs13132612







