Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices
Abstract
:1. Introduction
2. Background
2.1. CNN and RS Classification
2.2. Traditional Remote Sensing Accuracy Assessment Standards and Best Practices
2.3. RS DL Accuracy Assessment Background
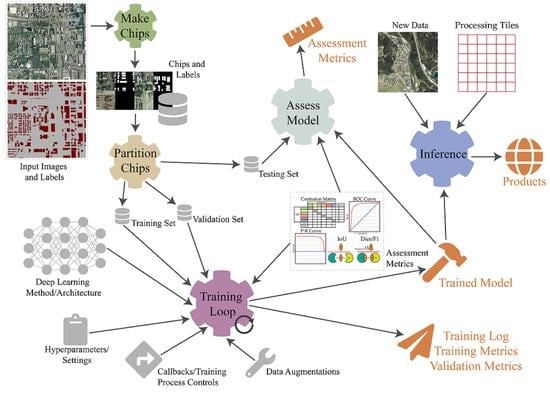
3. Recommendations and Best Practices for RS DL Accuracy Assessment
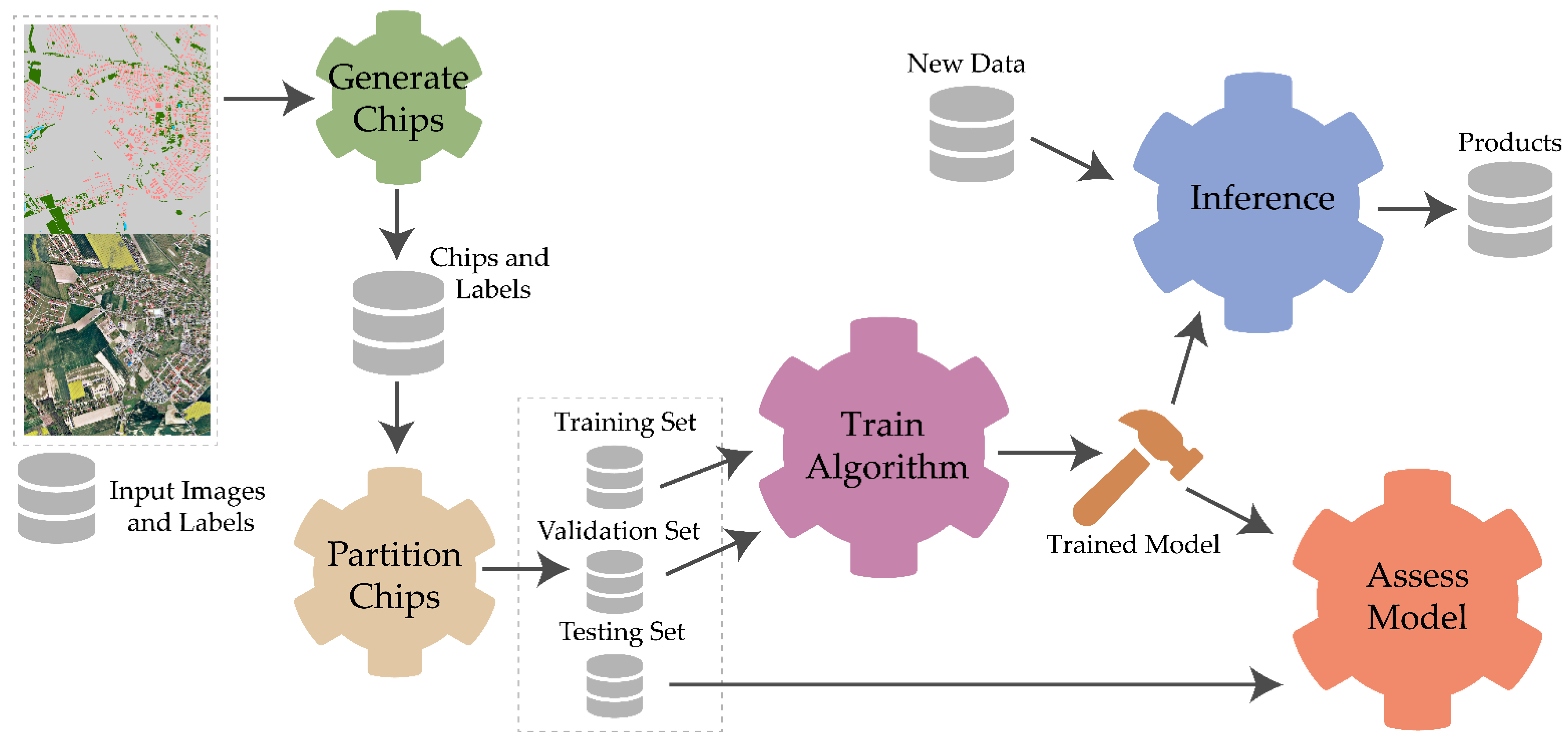
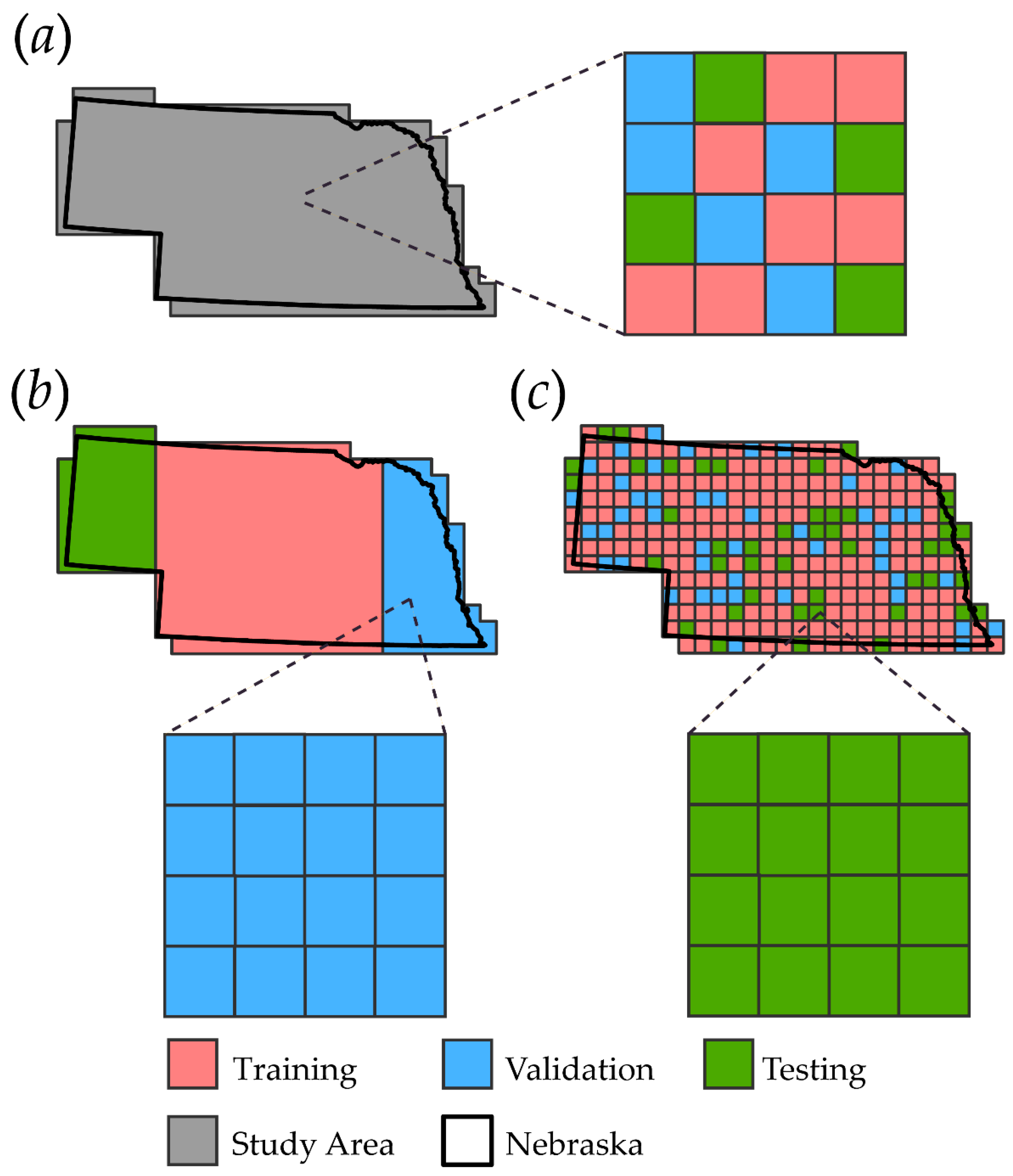
3.1. Training, Validation, and Testing Partitions
3.2. Assessing Model Generalization
3.3. Assessment Metrics
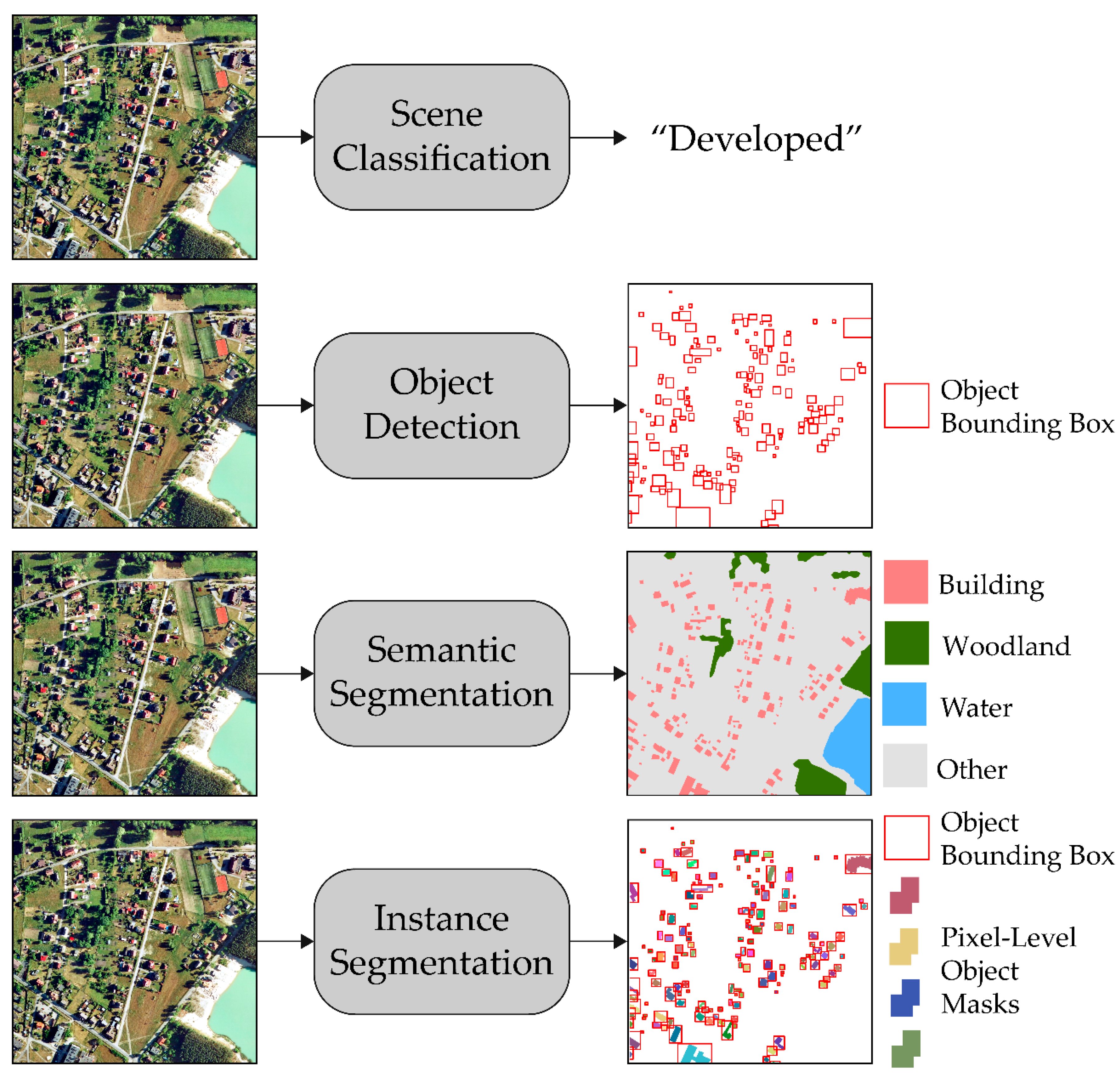
3.3.1. Scene Classification
3.3.2. Semantic Segmentation
3.3.3. Object Detection and Instance Segmentation
3.4. Creating Benchmark Datasets
- The methods used for generating training, validation, and testing partitions should be documented.
- Tables and/or code should be provided to replicate the defined data partitions. Alternatively, the data partitions can be separated into different folders.
- Class codes and descriptions should be defined.
- The testing dataset should approximate the relative proportions of classes or features on the landscape in order to support the generation of population-level metrics. Sampling should either be comprehensive (i.e., wall-to-wall) or probabilistic.
- If the dataset is meant to support the assessment of model generalization to new data and/or geographic extents, the recommended validation configuration should be documented.
- The accuracy of the reference data should be assessed and reported.
- Example code should be provided as a benchmark.
- Any complexities or limitations of the dataset should be defined.
3.5. Reporting Standards
- The number of training, validation, and testing chips should be reported, along with the chip size, classes and associated numeric codes, class definitions, and means of partitioning the samples (i.e., simple random, geographically stratified, tessellation stratified random, etc.). The relative proportions of each mapped category or abundance of features of interest on the actual landscape should be described.
- If a subset of image chips from the entire dataset and/or mapped extent is used, the method for this subsampling should be described.
- If the validation/testing sample unit was not the image chip (i.e., pixels, pixel blocks, or areal units), the unit should be stated and explained. If a minimum mapping unit (MMU) is used, this should be stated and the rationale for its use documented.
- Providing code and data on a public access site is particularly helpful. If doing so, this should include code or a description that allows the data partitions used in the original study to be replicated. For example, providing code that will replicate the partitions when executed, and/or specifying random seeds could be used to enhance replicability.
- The supporting documentation or code should allow the generation of a confusion matrix and associated derived metrics that are estimates of the population characteristics. If the testing sample does not directly provide an estimate of the population properties, methods for estimating the population confusion matrix from the sample confusion matrix should be provided.
- Any thresholds used to generate metrics should be reported (e.g., IoU thresholds or probability thresholds to generate binary metrics).
- For object detection and/or instance segmentation, it should be stated whether bounding boxes and/or pixel-level masks were used to perform the assessment, and whether assessment relied on feature counts or areas.
- If model generalization is assessed, the form of generalization should be defined along with the sampling methods, geographic extents, and/or new datasets used.
- Any limitations of the input data should be described.
4. Outstanding Issues and Challenges
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maxwell, A.; Warner, T.; Guillén, L. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 1: Literature Review. Remote Sens. 2021, 13, 2450. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Stehman, S.V.; Foody, G.M. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ. 2019, 231, 111199. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Hoeser, T.; Bachofer, F.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review—Part II: Applications. Remote Sens. 2020, 12, 3053. [Google Scholar] [CrossRef]
- Hoeser, T.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review-Part I: Evolution and Recent Trends. Remote Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. DeepSat: A Learning Framework for Satellite Imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, New York, NY, USA, 3 November 2015; pp. 1–10. [Google Scholar]
- Ren, Z.; Sudderth, E.B. Three-Dimensional Object Detection and Layout Prediction Using Clouds of Oriented Gradients. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1525–1533. [Google Scholar]
- Wei, X.; Fu, K.; Gao, X.; Yan, M.; Sun, X.; Chen, K.; Sun, H. Semantic pixel labelling in remote sensing images using a deep convolutional encoder-decoder model. Remote Sens. Lett. 2017, 9, 199–208. [Google Scholar] [CrossRef]
- Dai, J.; He, K.; Sun, J. Instance-Aware Semantic Segmentation via Multi-task Network Cascades. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3150–3158. [Google Scholar]
- Li, Y.; Qi, H.; Dai, J.; Ji, X.; Wei, Y. Fully Convolutional Instance-Aware Semantic Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Venice, Italy, 22–29 October 2017; pp. 4438–4446. [Google Scholar]
- Boguszewski, A.; Batorski, D.; Ziemba-Jankowska, N.; Zambrzycka, A.; Dziedzic, T. LandCover. ai: Dataset for Automatic Mapping of Buildings, Woodlands and Water from Aerial Imagery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the Transactions on Petri Nets and Other Models of Concurrency XV, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [Green Version]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Handa, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Robust Semantic Pixel-Wise Labelling. arXiv 2015, arXiv:1505.07293. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Zhou, Z.; Siddiquee, M.R.; Tajbakhsh, N.; Liang, J. UNet++: Redesigning Skip Connections to Exploit Multiscale Features in Image Segmentation. IEEE Trans. Med. Imaging 2020, 39, 1856–1867. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Granada, Spain, 20 September 2018; pp. 3–11. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–16 October 2018. [Google Scholar]
- Pinheiro, P.O.; Collobert, R.; Dollar, P. Learning to Segment Object Candidates. arXiv 2015, arXiv:1506.06204. [Google Scholar]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Matterport/Mask_RCNN; Matterport, Inc.: Sunnyvale, CA, USA, 2021.
- Cheng, T.; Wang, X.; Huang, L.; Liu, W. Boundary-Preserving Mask R-CNN. In Transactions on Petri Nets and Other Models of Concurrency XV; Maciej, K., Kordon, F., Lucia, P., Eds.; Springer: Heidelberg, Germany, 2020; pp. 660–676. [Google Scholar]
- Foody, G. Thematic Map Comparison. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Foody, G.M. Harshness in image classification accuracy assessment. Int. J. Remote Sens. 2008, 29, 3137–3158. [Google Scholar] [CrossRef] [Green Version]
- Stehman, S.V. Thematic map accuracy assessment from the perspective of finite population sampling. Int. J. Remote Sens. 1995, 16, 589–593. [Google Scholar] [CrossRef]
- Stehman, S. Statistical Rigor and Practical Utility in Thematic Map Accuracy Assessment. Photogramm. Eng. Remote Sens. 2001, 67, 727–734. [Google Scholar]
- Stehman, S.V. Comparison of Systematic and Random Sampling for Estimating the Accuracy of Maps Generated from Remotely Sensed Data. PE & RS-Photogramm. Eng. Remote Sens. 1992, 58, 1343–1350. [Google Scholar]
- Stehman, S.V.; Foody, G.M. Others Accuracy assessment. In The SAGE Handbook of Remote Sensing; Sage: London, UK, 2009; pp. 297–309. [Google Scholar]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Stehman, S.V. Basic probability sampling designs for thematic map accuracy assessment. Int. J. Remote Sens. 1999, 20, 2423–2441. [Google Scholar] [CrossRef]
- Stehman, S.V. Practical Implications of Design-Based Sampling Inference for Thematic Map Accuracy Assessment. Remote Sens. Environ. 2000, 72, 35–45. [Google Scholar] [CrossRef]
- Stehman, S.V. A Critical Evaluation of the Normalized Error Matrix in Map Accuracy Assessment. Photogramm. Eng. Remote Sens. 2004, 70, 743–751. [Google Scholar] [CrossRef]
- Stehman, S.V. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens. 2009, 30, 5243–5272. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area and map accuracy for stratified random sampling when the strata are different from the map classes. Int. J. Remote Sens. 2014, 35, 4923–4939. [Google Scholar] [CrossRef]
- Stehman, S.V.; Czaplewski, R.L. Design and Analysis for Thematic Map Accuracy Assessment: Fundamental Principles. Remote Sens. Environ. 1998, 64, 331–344. [Google Scholar] [CrossRef]
- Stehman, S.V.; Wickham, J.D. Pixels, blocks of pixels, and polygons: Choosing a spatial unit for thematic accuracy assessment. Remote Sens. Environ. 2011, 115, 3044–3055. [Google Scholar] [CrossRef]
- Congalton, R. Accuracy Assessment of Remotely Sensed Data: Future Needs and Directions. In Proceedings of the Pecora, Singapore, 31 August–2 September 1994; ASPRS: Bethesda, MD, USA, 1994; Volume 12, pp. 383–388. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Congalton, R.G.; Oderwald, R.G.; Mead, R.A. Assessing Landsat Classification Accuracy Using Discrete Multivariate Analysis Statistical Techniques. Photogramm. Eng. Remote Sens. 1983, 49, 1671–1678. [Google Scholar]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- Stehman, S.V. Impact of sample size allocation when using stratified random sampling to estimate accuracy and area of land-cover change. Remote Sens. Lett. 2012, 3, 111–120. [Google Scholar] [CrossRef]
- Clinton, N.; Holt, A.; Scarborough, J.; Yan, L.; Gong, P. Accuracy Assessment Measures for Object-based Image Segmentation Goodness. Photogramm. Eng. Remote Sens. 2010, 76, 289–299. [Google Scholar] [CrossRef]
- Kucharczyk, M.; Hay, G.; Ghaffarian, S.; Hugenholtz, C. Geographic Object-Based Image Analysis: A Primer and Future Directions. Remote Sens. 2020, 12, 2012. [Google Scholar] [CrossRef]
- Lizarazo, I. Accuracy assessment of object-based image classification: Another STEP. Int. J. Remote Sens. 2014, 35, 6135–6156. [Google Scholar] [CrossRef]
- Radoux, J.; Bogaert, P.; Fasbender, D.; Defourny, P. Thematic accuracy assessment of geographic object-based image classification. Int. J. Geogr. Inf. Sci. 2011, 25, 895–911. [Google Scholar] [CrossRef]
- Radoux, J.; Bogaert, P. Good Practices for Object-Based Accuracy Assessment. Remote Sens. 2017, 9, 646. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A. Thematic Classification Accuracy Assessment with Inherently Uncertain Boundaries: An Argument for Center-Weighted Accuracy Assessment Metrics. Remote Sens. 2020, 12, 1905. [Google Scholar] [CrossRef]
- Li, W.; Wang, Z.; Wang, Y.; Wu, J.; Wang, J.; Jia, Y.; Gui, G. Classification of High-Spatial-Resolution Remote Sensing Scenes Method Using Transfer Learning and Deep Convolutional Neural Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1986–1995. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Foody, G.M. Explaining the unsuitability of the kappa coefficient in the assessment and comparison of the accuracy of thematic maps obtained by image classification. Remote Sens. Environ. 2020, 239, 111630. [Google Scholar] [CrossRef]
- Howard, J.; Gugger, S. Deep Learning for Coders with Fastai and PyTorch; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Subramanian, V. Deep Learning with PyTorch: A Practical Approach to Building Neural Network Models Using PyTorch; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Howard, J.; Gugger, S. Fastai: A Layered API for Deep Learning. Information 2020, 11, 108. [Google Scholar] [CrossRef] [Green Version]
- Graf, L.; Bach, H.; Tiede, D. Semantic Segmentation of Sentinel-2 Imagery for Mapping Irrigation Center Pivots. Remote Sens. 2020, 12, 3937. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Singh, A.; Kalke, H.; Loewen, M.; Ray, N. River Ice Segmentation with Deep Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7570–7579. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Jorgenson, M.T.; Kent, K. Transferability of the Deep Learning Mask R-CNN Model for Automated Mapping of Ice-Wedge Polygons in High-Resolution Satellite and UAV Images. Remote Sens. 2020, 12, 1085. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Bester, M.S.; Guillen, L.A.; Ramezan, C.A.; Carpinello, D.J.; Fan, Y.; Hartley, F.M.; Maynard, S.M.; Pyron, J.L. Semantic Segmentation Deep Learning for Extracting Surface Mine Extents from Historic Topographic Maps. Remote Sens. 2020, 12, 4145. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Pourmohammadi, P.; Poyner, J.D. Mapping the Topographic Features of Mining-Related Valley Fills Using Mask R-CNN Deep Learning and Digital Elevation Data. Remote Sens. 2020, 12, 547. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Witharana, C.; Liljedahl, A.K.; Kanevskiy, M. Deep Convolutional Neural Networks for Automated Characterization of Arctic Ice-Wedge Polygons in Very High Spatial Resolution Aerial Imagery. Remote Sens. 2018, 10, 1487. [Google Scholar] [CrossRef] [Green Version]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Can semantic labeling methods generalize to any city? the inria aerial image labeling benchmark. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3226–3229. [Google Scholar]
- Robinson, C.; Hou, L.; Malkin, K.; Soobitsky, R.; Czawlytko, J.; Dilkina, B.; Jojic, N. Large Scale High-Resolution Land Cover Mapping with Multi-Resolution Data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12726–12735. [Google Scholar]
- Qi, K.; Yang, C.; Hu, C.; Guan, Q.; Tian, W.; Shen, S.; Peng, F. Polycentric Circle Pooling in Deep Convolutional Networks for High-Resolution Remote Sensing Image Recognition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 632–641. [Google Scholar] [CrossRef]
- Land Cover Data Project 2013/2014. Available online: https://www.chesapeakeconservancy.org/conservation-innovation-center/high-resolution-data/land-cover-data-project/ (accessed on 29 April 2021).
- Prakash, N.; Manconi, A.; Loew, S. Mapping Landslides on EO Data: Performance of Deep Learning Models vs. Traditional Machine Learning Models. Remote Sens. 2020, 12, 346. [Google Scholar] [CrossRef] [Green Version]
- Ii, D.J.G.; Haupt, S.E.; Nychka, D.W.; Thompson, G. Interpretable Deep Learning for Spatial Analysis of Severe Hailstorms. Mon. Weather Rev. 2019, 147, 2827–2845. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Real, R. AUC: A misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [Green Version]
- Pham, M.-T.; Courtrai, L.; Friguet, C.; Lefèvre, S.; Baussard, A. YOLO-Fine: One-Stage Detector of Small Objects under Various Backgrounds in Remote Sensing Images. Remote Sens. 2020, 12, 2501. [Google Scholar] [CrossRef]
- Chen, J.; Wan, L.; Zhu, J.; Xu, G.; Deng, M. Multi-Scale Spatial and Channel-wise Attention for Improving Object Detection in Remote Sensing Imagery. IEEE Geosci. Remote Sens. Lett. 2020, 17, 681–685. [Google Scholar] [CrossRef]
- Oh, S.; Chang, A.; Ashapure, A.; Jung, J.; Dube, N.; Maeda, M.; Gonzalez, D.; Landivar, J. Plant Counting of Cotton from UAS Imagery Using Deep Learning-Based Object Detection Framework. Remote Sens. 2020, 12, 2981. [Google Scholar] [CrossRef]
- Henderson, P.; Ferrari, V. End-to-End Training of Object Class Detectors for Mean Average Precision. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016; pp. 198–213. [Google Scholar]
- Zheng, Z.; Zhong, Y.; Ma, A.; Han, X.; Zhao, J.; Liu, Y.; Zhang, L. HyNet: Hyper-scale object detection network framework for multiple spatial resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2020, 166, 1–14. [Google Scholar] [CrossRef]
- COCO-Common Objects in Context. Available online: https://cocodataset.org/#detection-eval (accessed on 3 April 2021).
- Wu, T.; Hu, Y.; Peng, L.; Chen, R. Improved Anchor-Free Instance Segmentation for Building Extraction from High-Resolution Remote Sensing Images. Remote Sens. 2020, 12, 2910. [Google Scholar] [CrossRef]
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.-S. Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Koutsoukas, A.; Monaghan, K.J.; Li, X.; Huan, J. Deep-learning: Investigating deep neural networks hyper-parameters and comparison of performance to shallow methods for modeling bioactivity data. J. Cheminform. 2017, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Musgrave, K.; Belongie, S.; Lim, S.-N. A Metric Learning Reality Check. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Sejnowski, T.J. The unreasonable effectiveness of deep learning in artificial intelligence. Proc. Natl. Acad. Sci. USA 2020, 117, 30033–30038. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Warner, T. Kernel-Based Texture in Remote Sensing Image Classification. Geogr. Compass 2011, 5, 781–798. [Google Scholar] [CrossRef]
- Kim, M.; Madden, M.; Warner, T.A. Forest Type Mapping using Object-specific Texture Measures from Multispectral Ikonos Imagery. Photogramm. Eng. Remote Sens. 2009, 75, 819–829. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Warner, T.A.; Madden, M.; Atkinson, D.S. Multi-scale GEOBIA with very high spatial resolution digital aerial imagery: Scale, texture and image objects. Int. J. Remote Sens. 2011, 32, 2825–2850. [Google Scholar] [CrossRef]
- Fern, C.; Warner, T.A. Scale and Texture in Digital Image Classification. Photogramm. Eng. Remote Sens. 2002, 68, 51–63. [Google Scholar]
- Foody, G.M. Sample size determination for image classification accuracy assessment and comparison. Int. J. Remote Sens. 2009, 30, 5273–5291. [Google Scholar] [CrossRef]
- Cortes, C.; Mohri, M. Confidence Intervals for the Area Under the ROC Curve. Adv. Neural Inf. Process. Syst. 2005, 17, 305–312. [Google Scholar]
- Demler, O.V.; Pencina, M.J. Misuse of DeLong test to compare AUCs for nested models. Stat. Med. 2012, 31, 2577–2587. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, A.E.; Warner, T.A. Is high spatial resolution DEM data necessary for mapping palustrine wetlands? Int. J. Remote Sens. 2018, 40, 118–137. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P. Predicting Palustrine Wetland Probability Using Random Forest Machine Learning and Digital Elevation Data-Derived Terrain Variables. Photogramm. Eng. Remote Sens. 2016, 82, 437–447. [Google Scholar] [CrossRef]
- Wright, C.; Gallant, A. Improved wetland remote sensing in Yellowstone National Park using classification trees to combine TM imagery and ancillary environmental data. Remote Sens. Environ. 2007, 107, 582–605. [Google Scholar] [CrossRef]
- Fuller, R.; Groom, G.; Jones, A. The Land-Cover Map of Great Britain: An Automated Classification of Landsat Thematic Mapper Data. Photogramm. Eng. Remote Sens. 1994, 60, 553–562. [Google Scholar]
- Foody, G. Approaches for the production and evaluation of fuzzy land cover classifications from remotely-sensed data. Int. J. Remote Sens. 1996, 17, 1317–1340. [Google Scholar] [CrossRef]
- Foody, G.M. Local characterization of thematic classification accuracy through spatially constrained confusion matrices. Int. J. Remote Sens. 2005, 26, 1217–1228. [Google Scholar] [CrossRef]
- Berberoglu, S.; Lloyd, C.; Atkinson, P.; Curran, P. The integration of spectral and textural information using neural networks for land cover mapping in the Mediterranean. Comput. Geosci. 2000, 26, 385–396. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Olmo, M.C.; Abarca-Hernandez, F.; Atkinson, P.; Jeganathan, C. Random Forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Rivas, M. Evaluation of different machine learning methods for land cover mapping of a Mediterranean area using multi-seasonal Landsat images and Digital Terrain Models. Int. J. Digit. Earth 2014, 7, 492–509. [Google Scholar] [CrossRef]
- Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
- Stow, D.A.; Hope, A.; McGuire, D.; Verbyla, D.; Gamon, J.; Huemmrich, F.; Houston, S.; Racine, C.; Sturm, M.; Tape, K.; et al. Remote sensing of vegetation and land-cover change in Arctic Tundra Ecosystems. Remote Sens. Environ. 2004, 89, 281–308. [Google Scholar] [CrossRef] [Green Version]
- Rees, W.; Williams, M.; Vitebsky, P. Mapping land cover change in a reindeer herding area of the Russian Arctic using Landsat TM and ETM+ imagery and indigenous knowledge. Remote Sens. Environ. 2003, 85, 441–452. [Google Scholar] [CrossRef]
- Bartsch, A.; Höfler, A.; Kroisleitner, C.; Trofaier, A.M. Land Cover Mapping in Northern High Latitude Permafrost Regions with Satellite Data: Achievements and Remaining Challenges. Remote Sens. 2016, 8, 979. [Google Scholar] [CrossRef] [Green Version]
- Cingolani, A.M.; Renison, D.; Zak, M.R.; Cabido, M.R. Mapping Vegetation in a Heterogeneous Mountain Rangeland Using Landsat Data: An Alternative Method to Define and Classify Land-Cover Units. Remote Sens. Environ. 2004, 92, 84–97. [Google Scholar] [CrossRef]
- Rigge, M.; Homer, C.; Shi, H.; Wylie, B. Departures of Rangeland Fractional Component Cover and Land Cover from Landsat-Based Ecological Potential in Wyoming, USA. Rangel. Ecol. Manag. 2020, 73, 856–870. [Google Scholar] [CrossRef]
- Herold, M.; Scepan, J.; Clarke, K. The Use of Remote Sensing and Landscape Metrics to Describe Structures and Changes in Urban Land Uses. Environ. Plan. A Econ. Space 2002, 34, 1443–1458. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Wang, Y.; Li, J.; Chang, X.; Cao, Y.; Xie, J.; Gong, J. High-resolution urban land-cover mapping and landscape analysis of the 42 major cities in China using ZY-3 satellite images. Sci. Bull. 2020, 65, 1039–1048. [Google Scholar] [CrossRef]
- Dennis, M.; Barlow, D.; Cavan, G.; Cook, P.A.; Gilchrist, A.; Handley, J.; James, P.; Thompson, J.; Tzoulas, K.; Wheater, C.P.; et al. Mapping Urban Green Infrastructure: A Novel Landscape-Based Approach to Incorporating Land Use and Land Cover in the Mapping of Human-Dominated Systems. Land 2018, 7, 17. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Shao, G. Object-Based Land-Cover Mapping with High Resolution Aerial Photography at a County Scale in Midwestern USA. Remote Sens. 2014, 6, 11372–11390. [Google Scholar] [CrossRef] [Green Version]
- Witharana, C.; Bhuiyan, A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Daanen, R.; Griffin, C.G.; Kent, K.; Jones, M.K.W. Understanding the synergies of deep learning and data fusion of multispectral and panchromatic high resolution commercial satellite imagery for automated ice-wedge polygon detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
- Mou, L.; Hua, Y.; Zhu, X.X. Relation Matters: Relational Context-Aware Fully Convolutional Network for Semantic Segmentation of High-Resolution Aerial Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7557–7569. [Google Scholar] [CrossRef]
- Luo, S.; Li, H.; Shen, H. Deeply supervised convolutional neural network for shadow detection based on a novel aerial shadow imagery dataset. ISPRS J. Photogramm. Remote Sens. 2020, 167, 443–457. [Google Scholar] [CrossRef]
| Group | Examples | Reference |
|---|---|---|
| Scene Classification | AlexNet ResNet Xception | [15] [16] [17] |
| Object Detection | Single Shot Detector (SSD) Yolo v3 Faster R-CNN | [18] [19] [20] |
| Semantic Segmentation | SegNet UNet UNet++ DeepLab DeepLabv3+ | [21,22] [23] [24,25] [26] [27] |
| Instance Segmentation | DeepMask Mask R-CNN Boundary Preserving Mask R-CNN | [28] [29,30] [31] |
| Reference Data | |||
|---|---|---|---|
| Positive | Negative | ||
| Classification Result | Positive | TP | FP |
| Negative | FN | TN | |
| Metric | Equation | Relation to Traditional RS Measures |
|---|---|---|
| Overall Accuracy (OA) | Overall Accuracy | |
| Recall | PA for positives | |
| Precision | UA for positives | |
| Specificity | PA for negatives | |
| Negative Predictive Value (NPV) | UA for negatives |
| Reference | Row Total | Precision (UA) | F1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Barren | Building | Grassland | Road | Tree | Water | |||||
| Classification | Barren | 0.2248 | 0.0000 | 0.0006 | 0.0000 | 0.0000 | 0.0000 | 0.2253 | 0.9974 | 0.9943 |
| Building | 0.0000 | 0.0454 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0455 | 0.9989 | 0.9946 | |
| Grassland | 0.0020 | 0.0000 | 0.1548 | 0.0000 | 0.0002 | 0.0000 | 0.1570 | 0.9861 | 0.9909 | |
| Road | 0.0000 | 0.0004 | 0.0000 | 0.0255 | 0.0000 | 0.0000 | 0.0260 | 0.9819 | 0.9899 | |
| Tree | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.1749 | 0.0000 | 0.1750 | 0.9996 | 0.9993 | |
| Water | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.3712 | 0.3712 | 1.0000 | 1.0000 | |
| Column Total | 0.2268 | 0.0459 | 0.1555 | 0.0256 | 0.1751 | 0.3712 | ||||
| Recall (PA) | 0.9912 | 0.9903 | 0.9957 | 0.9981 | 0.9989 | 1.0000 | ||||
| Reference | Row Total | Precision (UA) | F1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Barren | Building | Grassland | Road | Tree | Water | |||||
| Classification | Barren | 0.9912 | 0.0000 | 0.0037 | 0.0000 | 0.0000 | 0.0000 | 0.9949 | 0.9962 | 0.9937 |
| Building | 0.0000 | 0.9903 | 0.0000 | 0.0019 | 0.0000 | 0.0000 | 0.9922 | 0.9981 | 0.9942 | |
| Grassland | 0.0088 | 0.0000 | 0.9957 | 0.0000 | 0.0011 | 0.0000 | 1.0056 | 0.9902 | 0.9929 | |
| Road | 0.0000 | 0.0097 | 0.0002 | 0.9981 | 0.0000 | 0.0000 | 1.0079 | 0.9902 | 0.9941 | |
| Tree | 0.0000 | 0.0000 | 0.0004 | 0.0000 | 0.9989 | 0.0000 | 0.9993 | 0.9996 | 0.9993 | |
| Water | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Column Total | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | ||||
| Recall (PA) | 0.9912 | 0.9903 | 0.9957 | 0.9981 | 0.9989 | 1.0000 | ||||
| Reference | Row Total | Precision (UA) | F1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Barren | Building | Grassland | Road | Tree | Water | |||||
| Classification | Barren | 0.0033 | 0.0000 | 0.0010 | 0.0000 | 0.0000 | 0.0000 | 0.0043 | 0.7647 | 0.8633 |
| Building | 0.0000 | 0.0277 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0277 | 0.9989 | 0.9946 | |
| Grassland | 0.0000 | 0.0000 | 0.2715 | 0.0000 | 0.0007 | 0.0000 | 0.2721 | 0.9975 | 0.9966 | |
| Road | 0.0000 | 0.0003 | 0.0000 | 0.0157 | 0.0000 | 0.0000 | 0.0160 | 0.9803 | 0.9891 | |
| Tree | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.6199 | 0.0000 | 0.6200 | 0.9998 | 0.9994 | |
| Water | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0598 | 0.0598 | 1.0000 | 1.0000 | |
| Column Total | 0.0033 | 0.0280 | 0.2726 | 0.0157 | 0.6206 | 0.0598 | ||||
| Recall (PA) | 0.9912 | 0.9903 | 0.9957 | 0.9981 | 0.9989 | 1.0000 | ||||
| Reference | Row Total | Precision (UA) | F1 Score | |||||
|---|---|---|---|---|---|---|---|---|
| Buildings | Woodlands | Water | Other | |||||
| Classification | Buildings | 0.007 | 0.000 | 0.000 | 0.003 | 0.009 | 0.827 | 0.716 |
| Woodlands | 0.000 | 0.325 | 0.000 | 0.019 | 0.344 | 0.931 | 0.937 | |
| Water | 0.000 | 0.001 | 0.053 | 0.004 | 0.058 | 0.961 | 0.938 | |
| Other | 0.001 | 0.023 | 0.002 | 0.562 | 0.588 | 0.956 | 0.955 | |
| Column Total | 0.008 | 0.349 | 0.056 | 0.588 | ||||
| Recall (PA) | 0.705 | 0.944 | 0.916 | 0.955 | ||||
| Class | Sample Size (No. Pixels) |
|---|---|
| Buildings | 246,966 |
| Woodlands | 9,035,022 |
| Water | 1,531,777 |
| Other | 15,433,404 |
| Geographic Region | Precision | Recall | Specificity | NPV | F1 Score | OA |
|---|---|---|---|---|---|---|
| 1 | 0.914 | 0.938 | 0.999 | 0.993 | 0.919 | 0.999 |
| 2 | 0.883 | 0.915 | 0.999 | 0.999 | 0.896 | 0.998 |
| 3 | 0.905 | 0.811 | 0.998 | 0.993 | 0.837 | 0.992 |
| 4 | 0.910 | 0.683 | 0.998 | 9.983 | 0.761 | 0.983 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maxwell, A.E.; Warner, T.A.; Guillén, L.A. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices. Remote Sens. 2021, 13, 2591. https://doi.org/10.3390/rs13132591
Maxwell AE, Warner TA, Guillén LA. Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices. Remote Sensing. 2021; 13(13):2591. https://doi.org/10.3390/rs13132591
Chicago/Turabian StyleMaxwell, Aaron E., Timothy A. Warner, and Luis Andrés Guillén. 2021. "Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices" Remote Sensing 13, no. 13: 2591. https://doi.org/10.3390/rs13132591
APA StyleMaxwell, A. E., Warner, T. A., & Guillén, L. A. (2021). Accuracy Assessment in Convolutional Neural Network-Based Deep Learning Remote Sensing Studies—Part 2: Recommendations and Best Practices. Remote Sensing, 13(13), 2591. https://doi.org/10.3390/rs13132591