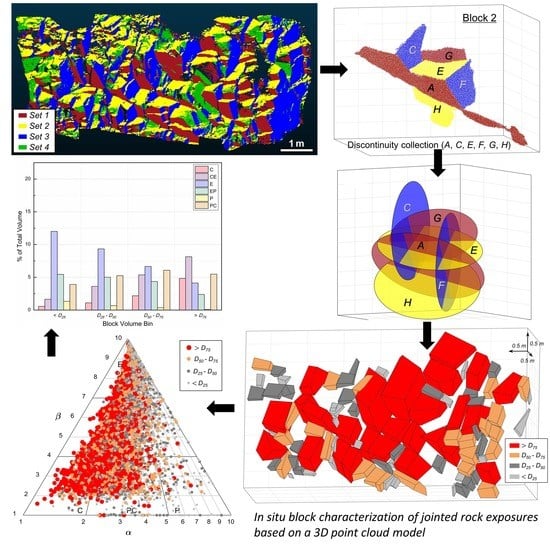
In-Situ Block Characterization of Jointed Rock Exposures Based on a 3D Point Cloud Model
Abstract
:1. Introduction
2. Study Sites
2.1. Site 1: A Road Cut Slope in Catalonia, Spain
2.2. Site 2: Yinshan Open-pit Copper Mine in Dexing, China
2.3. A Synthetic Test Model: The Dataset of Cardboard Boxes
3. Methodology
3.1. Treatment of Data Source
3.2. Identification of Discontinuities from PCM
3.3. PCM-DDN: Global Searching of Block Candidates
3.4. PCM-DDN: Polyhedral Modeling
3.5. PCM-DDN: Block Characterization
3.6. PCM-SDS: Deriving Fundamental Discontinuity Parameters
3.7. PCM-SDS: 3D Stochastic DFN Simulation
3.8. PCM-SDS: Block Extraction and Characterization
4. Results
4.1. Results of the Synthetic Box Model
4.2. Comparison of the Results of Site 1 Using Two Procedures
5. Discussion
5.1. Practical Application of the Proposed Method
- (1)
- (2)
- Blasting design, e.g., explosive consumption and fragmentation energy optimization for mining or tunneling [73]. Taking a quarry project as an example, the IBSD curve and the block shape distribution are important for blasting design and quarry yield prediction. The blasting can be considered as a transformation from IBSD to fragmented size distribution (or blasted block size distribution, BBSD) and the main framework of the energy-block- transition (E-B-T) model can be established [74] (Figure 15c).
- (3)
- (4)
- Stability evaluation and support design of slopes or excavations in jointed rock masses [8].
- (5)
5.1.1. Practical Applicability of PCM-DDN
5.1.2. Practical Applicability of PCM-SDS
5.2. Comparison with an Representative Analytical Approach
5.2.1. The Persistence Factor Estimation
5.2.2. Comparison with Calculation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Priest, S.D. Discontinuity Analysis for Rock Engineering; Chapman & Hall: London, UK, 1993; pp. 219–254. [Google Scholar]
- Kalenchuk, K.S.; Diederichs, M.S.; McKinnon, S. Characterizing block geometry in jointed rockmasses. Int. J. Rock Mech. Min. Sci. 2006, 43, 1212–1225. [Google Scholar] [CrossRef]
- Palmstrom, A. Measurements of and correlations between block size and rock quality designation (RQD). Tunn. Undergr. Sp. Technol. 2005, 20, 362–377. [Google Scholar] [CrossRef]
- Goodman, R.E. Introduction to Rock Mechanics; Wiley: New York, NY, USA, 1989; Volume 2, pp. 221–388. [Google Scholar]
- Buyer, A.; Aichinger, S.; Schubert, W. Applying photogrammetry and semi-automated joint mapping for rock mass characterization. Eng. Geol. 2020, 264, 105332. [Google Scholar] [CrossRef]
- Morelli, G.L. Empirical Assessment of the Mean Block Volume of Rock Masses Intersected by Four Joint Sets. Rock Mech. Rock Eng. 2016, 49, 1759–1771. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J. Comparing rockfall scar volumes and kinematically detachable rock masses. Eng. Geol. 2017, 219, 64–73. [Google Scholar] [CrossRef]
- Dong, X.; Xu, Q.; Huang, R.; Liu, Q.; Kieffer, D.S. Reconstruction of Surficial Rock Blocks by Means of Rock Structure Modelling of 3D TLS Point Clouds: The 2013 Long-Chang Rockfall. Rock Mech. Rock Eng. 2020, 53, 671–689. [Google Scholar] [CrossRef] [Green Version]
- Goodman, R.; Shi, G. Block Theory and its Application to Rock Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Sturzenegger, M.; Stead, D.; Elmo, D. Terrestrial remote sensing-based estimation of mean trace length, trace intensity and block size/shape. Eng. Geol. 2011, 119, 96–111. [Google Scholar] [CrossRef]
- Fekete, S.; Diederichs, M. Integration of three-dimensional laser scanning with discontinuum modelling for stability analysis of tunnels in blocky rockmasses. Int. J. Rock Mech. Min. Sci. 2013, 57, 11–23. [Google Scholar] [CrossRef]
- Yao, W.; Mostafa, S.; Yang, Z. Assessment of block size distribution in fractured rock mass and its influence on rock mass mechanical behavior. AIP Adv. 2020, 10, 35124. [Google Scholar] [CrossRef] [Green Version]
- ISRM International society for rock mechanics commission on standardization of laboratory and field tests: Suggested methods for the quantitative description of discontinuities in rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [CrossRef]
- Kim, B.H.; Cai, M.; Kaiser, P.K.; Yang, H.S. Estimation of Block Sizes for Rock Masses with Non-persistent Joints. Rock Mech. Rock Eng. 2006, 40, 169. [Google Scholar] [CrossRef]
- Hoek, E.; Carter, T.G.; Diederichs, M.S. Quantification of the Geological Strength Index Chart. In Proceedings of the 47th US Rock Mechanics /Geomechanics Symposium, San Francisco, CA, USA, 23–26 June 2013. [Google Scholar]
- Chen, N.; Kemeny, J.; Jiang, Q.; Pan, Z. Automatic extraction of blocks from 3D point clouds of fractured rock. Comput. Geosci. 2017, 109, 149–161. [Google Scholar] [CrossRef]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Hardy, A.J.; Ryan, T.M.; Kemeny, J.M. Block size distribution of in situ rock masses using digital image processing of drill core. Int. J. Rock Mech. Min. Sci. 1997, 34, 303–307. [Google Scholar] [CrossRef]
- Lu, P.; Latham, J.-P. Developments in the Assessment of In-situ Block Size Distributions of Rock Masses. Rock Mech. Rock Eng. 1999, 32, 29–49. [Google Scholar] [CrossRef]
- Latham, J.-P.; Van Meulen, J.; Dupray, S. Prediction of in-situ block size distributions with reference to armourstone for breakwaters. Eng. Geol. 2006, 86, 18–36. [Google Scholar] [CrossRef]
- Deere, D.U. Technical description of rock cores for engineering purpose. Felsmech. Ing. 1963, 1, 16–22. [Google Scholar]
- Palmstrom, A. The volumetric joint count―a useful and simple measure of the degree of rock mass jointing. In Proceedings of the 4th International Congress IAEG, New Delhi, India, 10–15 December1982; pp. 221–228. [Google Scholar]
- Palmstrom, A. Characterization of jointing density and the quality of rock masses (in Norwegian). Intern. Rep. Norw. AB Berdal 1974, 26, 3. [Google Scholar]
- Palmström, A.; Singh, R. The deformation modulus of rock masses—Comparisons between in situ tests and indirect estimates. Tunn. Undergr. Sp. Technol. 2001, 16, 115–131. [Google Scholar] [CrossRef]
- Şen, Z.; Eissa, E.A. Rock quality charts for log-normally distributed block sizes. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 1–12. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Uno, H.; Tasaka, Y.; Minami, M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2004, 41, 3–19. [Google Scholar] [CrossRef]
- Elmouttie, M.K.; Poropat, G. V A Method to Estimate In Situ Block Size Distribution. Rock Mech. Rock Eng. 2012, 45, 401–407. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J. Evaluation of Maximum Rockfall Dimensions Based on Probabilistic Assessment of the Penetration of the Sliding Planes into the Slope. Rock Mech. Rock Eng. 2020. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Latham, J.-P.; Poole, A.B. Predictions of block size distribution for quarrying. Q. J. Eng. Geol. Hydrogeol. 1991, 24, 91–99. [Google Scholar] [CrossRef]
- Saroglou, H.; Marinos, V.; Marinos, P.; Tsiambaos, G. Rockfall hazard and risk assessment: An example from a high promontory at the historical site of Monemvasia, Greece. Nat. Hazards Earth Syst. Sci. 2012, 12, 1823–1836. [Google Scholar] [CrossRef] [Green Version]
- Jern, M. Determination of the In situ Block Size Distribution in Fractured Rock, an Approach for Comparing In-situ Rock with Rock Sieve Analysis. Rock Mech. Rock Eng. 2004, 37, 391–401. [Google Scholar] [CrossRef]
- Stavropoulou, M. Discontinuity frequency and block volume distribution in rock masses. Int. J. Rock Mech. Min. Sci. 2014, 65, 62–74. [Google Scholar] [CrossRef]
- Stavropoulou, M.; Xiroudakis, G. Fracture Frequency and Block Volume Distribution in Rock Masses. Rock Mech. Rock Eng. 2020, 53, 4673–4689. [Google Scholar] [CrossRef]
- Riquelme, A.J.; Abellán, A.; Tomás, R.; Jaboyedoff, M. A new approach for semi-automatic rock mass joints recognition from 3D point clouds. Comput. Geosci. 2014, 68, 38–52. [Google Scholar] [CrossRef] [Green Version]
- Ferrero, A.; Migliazza, M.; Umili, G. Rock mass characterization by means of advanced survey methods. Rock Eng. Rock Mech. Struct. Rock Masses 2014, 17–27. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Couture, R.; Locat, P. Structural analysis of Turtle Mountain (Alberta) using digital elevation model: Toward a progressive failure. Geomorphology 2009. [Google Scholar] [CrossRef]
- Salvini, R.; Mastrorocco, G.; Esposito, G.; Di Bartolo, S.; Coggan, J.; Vanneschi, C. Use of a remotely piloted aircraft system for hazard assessment in a rocky mining area (Lucca, Italy). Nat. Hazards Earth Syst. Sci. 2018, 18, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial laser scanning of rock slope instabilities. Earth Surf. Process. Landforms 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Abellán, A.; Vilaplana, J.M.; Martínez, J. Application of a long-range Terrestrial Laser Scanner to a detailed rockfall study at Vall de Núria (Eastern Pyrenees, Spain). Eng. Geol. 2006, 88, 136–148. [Google Scholar] [CrossRef]
- Vanhaekendover, H.; Lindenbergh, R.; Ngan-Tillard, D.; Slob, S.; Wezenberg, U. Deterministic in-situ block size estimation using 3D terrestrial laser data. In Proceedings of the ISRM Regional Symposium-EUROCK, Vigo, Spain, 27–29 May 2014. [Google Scholar]
- Mavrouli, O.; Corominas, J.; Jaboyedoff, M. Size Distribution for Potentially Unstable Rock Masses and In Situ Rock Blocks Using LIDAR-Generated Digital Elevation Models. Rock Mech. Rock Eng. 2015, 48, 1589–1604. [Google Scholar] [CrossRef] [Green Version]
- Battulwar, R.; Zare-Naghadehi, M.; Emami, E.; Sattarvand, J. A state-of-the-art review of automated extraction of rock mass discontinuity characteristics using three-dimensional surface models. J. Rock Mech. Geotech. Eng. 2021. [Google Scholar] [CrossRef]
- Slob, S. Automated Rock Mass Characterisation Using 3-D Terrestrial Laser Scanning. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherland, 2010. [Google Scholar]
- Wu, F.; Wu, J.; Bao, H.; Li, B.; Shan, Z.; Kong, D. Advances in statistical mechanics of rock masses and its engineering applications. J. Rock Mech. Geotech. Eng. 2021, 13, 22–45. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- Giordan, D.; Adams, M.S.; Aicardi, I.; Alicandro, M.; Allasia, P.; Baldo, M.; De Berardinis, P.; Dominici, D.; Godone, D.; Hobbs, P. The use of unmanned aerial vehicles (UAVs) for engineering geology applications. Bull. Eng. Geol. Environ. 2020, 79, 3437–3481. [Google Scholar] [CrossRef] [Green Version]
- Kong, D.; Saroglou, C.; Wu, F.; Sha, P.; Li, B. Development and application of UAV-SfM photogrammetry for quantitative characterization of rock mass discontinuities. Int. J. Rock Mech. Min. Sci. 2021, 141, 104729. [Google Scholar] [CrossRef]
- Gigli, G.; Casagli, N. Semi-automatic extraction of rock mass structural data from high resolution LIDAR point clouds. Int. J. Rock Mech. Min. Sci. 2011, 48, 187–198. [Google Scholar] [CrossRef]
- Vöge, M.; Lato, M.J.; Diederichs, M.S. Automated rockmass discontinuity mapping from 3-dimensional surface data. Eng. Geol. 2013, 164, 155–162. [Google Scholar] [CrossRef]
- Lato, M.; Diederichs, M.S.; Hutchinson, D.J.; Harrap, R. Optimization of LiDAR scanning and processing for automated structural evaluation of discontinuities in rockmasses. Int. J. Rock Mech. Min. Sci. 2009, 46, 194–199. [Google Scholar] [CrossRef]
- Kong, D.; Wu, F.; Saroglou, C. Automatic identification and characterization of discontinuities in rock masses from 3D point clouds. Eng. Geol. 2020. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Zhu, H. A new method for automated discontinuity trace mapping on rock mass 3D surface model. Comput. Geosci. 2016, 89, 118–131. [Google Scholar] [CrossRef]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. Nesti-net: Normal estimation for unstructured 3d point clouds using convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3DmFV: Three-Dimensional Point Cloud Classification in Real-Time Using Convolutional Neural Networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Liu, Q.; Kaufmann, V. Integrated Assessment of Cliff Rockfall Hazards by Means of Rock Structure Modelling Applied to TLS data: New Developments. In Proceedings of the ISRM Regional Symposium—EUROCK, Salzburg, Austria, 7–10 October 2015. [Google Scholar]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: New York, NY, USA, 1981; ISBN 147570450X. [Google Scholar]
- Hammah, R.E.; Curran, J.H. On distance measures for the fuzzy K-means algorithm for joint data. Rock Mech. Rock Eng. 1999, 32, 1–27. [Google Scholar] [CrossRef]
- Schubert, E.; Sander, J.; Ester, M.; Kriegel, H.P.; Xu, X. DBSCAN revisited, revisited: Why and how you should (still) use DBSCAN. ACM Trans. Database Syst. 2017, 42, 1–21. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Zhu, Y.; Ting, K.M.; Carman, M.J. Density-ratio based clustering for discovering clusters with varying densities. Pattern Recognit. 2016, 60, 983–997. [Google Scholar] [CrossRef]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial LiDAR point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2014. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Gottsbacher, L.K.J. Calculation of the Young’s Modulus for Rock Masses with 3DEC and Comparing It with Empirical Methods. Master’s Thesis, Graz University of Technology, Graz, Austria, 2017. [Google Scholar]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Umili, G.; Bonetto, S.M.R.; Mosca, P.; Vagnon, F.; Ferrero, A.M. In Situ Block Size Distribution Aimed at the Choice of the Design Block for Rockfall Barriers Design: A Case Study along Gardesana Road. Geosciences 2020, 10, 223. [Google Scholar] [CrossRef]
- Golder Associates. FracMan Software. Available online: https://www.golder.com/fracman/ (accessed on 28 June 2021).
- Itasca Consulting Group Inc. 3DEC Software. Available online: https://www.itascacg.com/software/3dec (accessed on 28 June 2021).
- Rasmussen, L.L. UnBlocksgen: A Python library for 3D rock mass generation and analysis. SoftwareX 2020, 12, 100577. [Google Scholar] [CrossRef]
- Kim, B.-H.; Peterson, R.L.; Katsaga, T.; Pierce, M.E. Estimation of rock block size distribution for determination of Geological Strength Index (GSI) using discrete fracture networks (DFNs). Min. Technol. 2015, 124, 203–211. [Google Scholar] [CrossRef]
- Kluckner, A.; Söllner, P.; Schubert, W.; Pötsch, M. Estimation of the in situ Block Size in Jointed Rock Masses using Three-Dimensional Block Simulations and Discontinuity Measurements. In Proceedings of the 13th ISRM International Congress of Rock Mechanics, Montreal, Canada, 10–13 May 2015. [Google Scholar]
- Macciotta, R.; Gräpel, C.; Skirrow, R. Fragmented rockfall volume distribution from photogrammetry-based structural mapping and discrete fracture networks. Appl. Sci. 2020, 10, 6977. [Google Scholar] [CrossRef]
- Yarahmadi, R.; Bagherpour, R.; Taherian, S.-G.; Sousa, L.M.O. Discontinuity modelling and rock block geometry identification to optimize production in dimension stone quarries. Eng. Geol. 2018, 232, 22–33. [Google Scholar] [CrossRef]
- Latham, J.-P.; Lu, P. Development of an assessment system for the blastability of rock masses. Int. J. Rock Mech. Min. Sci. 1999, 36, 41–55. [Google Scholar] [CrossRef]
- Salmi, E.F.; Sellers, E.J. A review of the methods to incorporate the geological and geotechnical characteristics of rock masses in blastability assessments for selective blast design. Eng. Geol. 2021, 281, 105970. [Google Scholar] [CrossRef]
- Palmstrøm, A. Characterizing rock masses by the RMi for use in practical rock engineering: Part 1: The development of the Rock Mass index (RMi). Tunn. Undergr. Sp. Technol. 1996, 11, 175–188. [Google Scholar] [CrossRef]
- Rives, T.; Razack, M.; Petit, J.-P.; Rawnsley, K.D. Joint spacing: Analogue and numerical simulations. J. Struct. Geol. 1992, 14, 925–937. [Google Scholar] [CrossRef]
- Laughton, C.; Nelson, P.P. The Development of Rock Mass Parameters For Use In the Prediction of Tunnel Boring Machine Performance. In Proceedings of the ISRM International Symposium—EUROCK 96, Turin, Italy, 2–5 September 1996. [Google Scholar]
- Ruiz-Carulla, R.; Corominas, J.; Mavrouli, O. A fractal fragmentation model for rockfalls. Landslides 2017, 14, 875–889. [Google Scholar] [CrossRef]
- Ruiz-Carulla, R.; Corominas, J. Analysis of Rockfalls by Means of a Fractal Fragmentation Model. Rock Mech. Rock Eng. 2020, 53, 1433–1455. [Google Scholar] [CrossRef]
- Einstein, H.H.; Veneziano, D.; Baecher, G.B.; O’Reilly, K.J. The effect of discontinuity persistence on rock slope stability. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 227–236. [Google Scholar] [CrossRef]
- Elmo, D.; Donati, D.; Stead, D. Challenges in the characterisation of intact rock bridges in rock slopes. Eng. Geol. 2018, 245, 81–96. [Google Scholar] [CrossRef]


















| Set | Orientation (°) | Trace Length (m) | Normal Set Spacing (m) | ||||
|---|---|---|---|---|---|---|---|
| Fisher Distribution | Log Normal Distribution | Log Normal Distribution | |||||
| Dip Dir | Dip | Mean | Standard Deviation | Mean | Standard Deviation | ||
| Set 1 | 127 | 56 | 15.17 | 0.27 | 0.135 | 0.34 | 0.016 |
| Set 2 | 291 | 45 | 35.09 | 0.55 | 0.304 | 0.15 | 0.067 |
| Set 3 | 227 | 83 | 34.89 | 0.45 | 0.386 | 0.25 | 0.061 |
| Set 4 | 279 | 81 | 37.96 | 0.44 | 0.107 | 0.18 | 0.119 |
| Block ID | Manually Measured Size (m3) | Extracted Size (m3) | Percent Deviation |
|---|---|---|---|
| 1 | 0.2160 | 0.2111 | 2.27% |
| 2 | 0.4320 | 0.4307 | 0.30% |
| 3 | 0.0689 | 0.0701 | 1.74% |
| 4 | 0.3645 | 0.3780 | 3.70% |
| 5 | 0.0506 | 0.0531 | 4.94% |
| 6 | 0.0540 | 0.0561 | 3.89% |
| 7 | 0.0630 | 0.0642 | 1.90% |
| 8 | 0.0180 | 0.0187 | 3.89% |
| 9 | 0.0270 | 0.0284 | 5.19% |
| Method | Block Size (m3) | Block Orientation (Dip Dir/Dip, °) | |||
|---|---|---|---|---|---|
| D25 | D50 | D75 | Mean | ||
| PCM-DDN | 0.005 | 0.014 | 0.038 | 0.041 | 115/26 |
| PCM-SDS: Model ID 75 | 0.006 | 0.035 | 0.120 | 0.101 | 124/17 |
| PCM-SDS: All models 1 | M: 0.005 | M: 0.027 | M: 0.092 | M: 0.084 | -- |
| SD: 0.003 | SD: 0.014 | SD: 0.044 | SD: 0.060 | ||
| Set | Orientation (°) | Trace Length (m) | Normal Set Spacing (m) | Persistence Factor | ||||
|---|---|---|---|---|---|---|---|---|
| Fisher Distribution | Log Normal Distribution | Log Normal Distribution | -- | |||||
| Dip Dir | Dip | Mean | Standard Deviation | Mean | Standard Deviation | Value Range | ||
| Set 1 | 305 | 81 | 93.76 | 1.14 | 0.601 | 0.25 | 0.069 | 85–100% |
| Set 2 | 6 | 76 | 99.60 | 1.52 | 0.862 | 0.61 | 0.240 | 85–100% |
| Set 3 | 108 | 42 | 273.68 | 1.52 | 1.183 | 0.745 | 0.387 | 90–100% |
| Method | Block Size (m3) | Block Orientation (Dip dir/Dip, °) | |||
|---|---|---|---|---|---|
| D25 | D50 | D75 | Mean | ||
| PCM-SDS: Model ID 61 | 0.009 | 0.053 | 0.212 | 0.192 | 306/33 |
| PCM-SDS: All models 1 | M: 0.008 | M: 0.051 | M: 0.196 | M: 0.179 | -- |
| SD: 0.004 | SD: 0.025 | SD: 0.092 | SD: 0.079 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, D.; Wu, F.; Saroglou, C.; Sha, P.; Li, B. In-Situ Block Characterization of Jointed Rock Exposures Based on a 3D Point Cloud Model. Remote Sens. 2021, 13, 2540. https://doi.org/10.3390/rs13132540
Kong D, Wu F, Saroglou C, Sha P, Li B. In-Situ Block Characterization of Jointed Rock Exposures Based on a 3D Point Cloud Model. Remote Sensing. 2021; 13(13):2540. https://doi.org/10.3390/rs13132540
Chicago/Turabian StyleKong, Deheng, Faquan Wu, Charalampos Saroglou, Peng Sha, and Bo Li. 2021. "In-Situ Block Characterization of Jointed Rock Exposures Based on a 3D Point Cloud Model" Remote Sensing 13, no. 13: 2540. https://doi.org/10.3390/rs13132540
APA StyleKong, D., Wu, F., Saroglou, C., Sha, P., & Li, B. (2021). In-Situ Block Characterization of Jointed Rock Exposures Based on a 3D Point Cloud Model. Remote Sensing, 13(13), 2540. https://doi.org/10.3390/rs13132540