Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska
Abstract
:1. Introduction
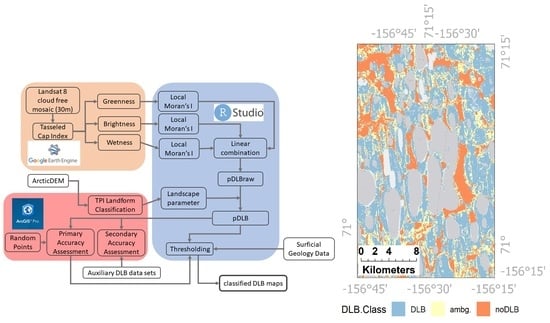
2. Materials and Methods
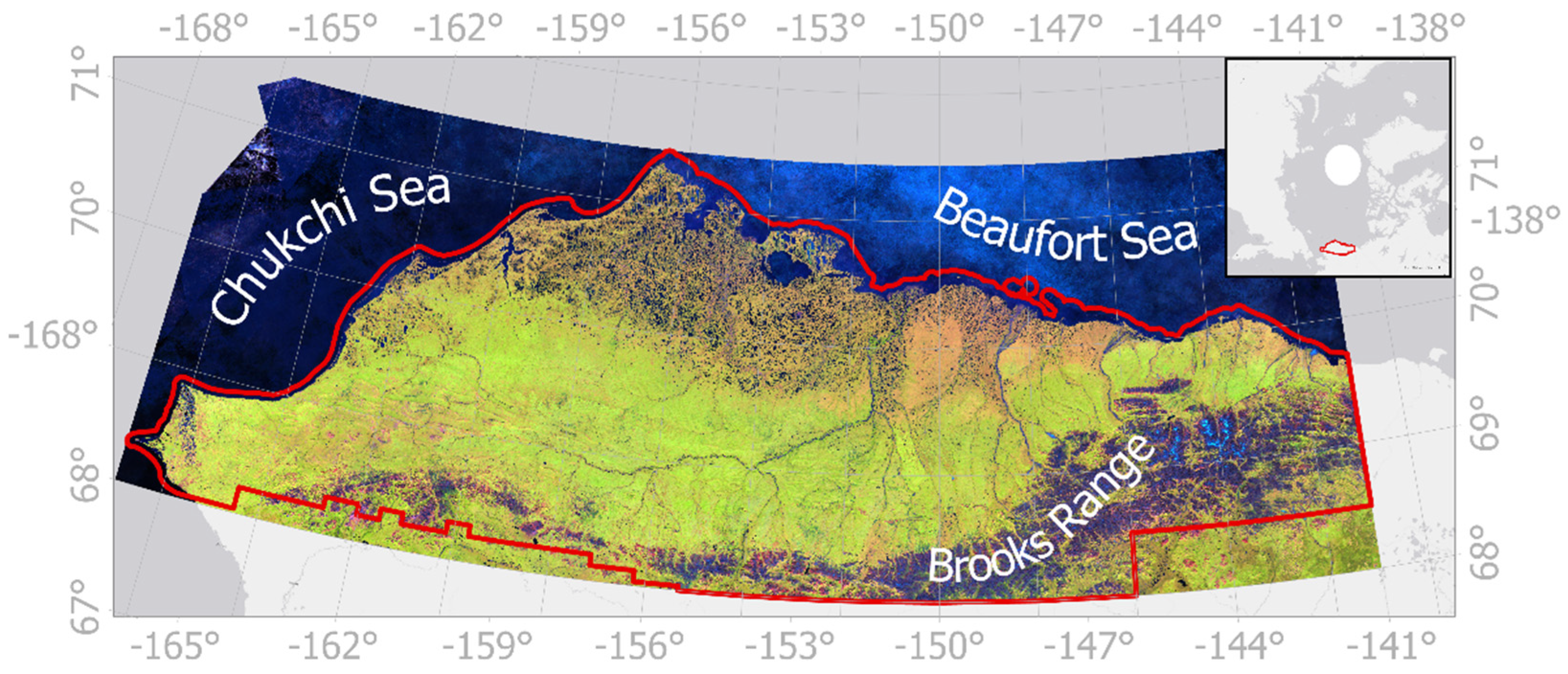
2.1. Study Area
2.2. Data Selection and Pre-Processing
2.2.1. Landsat-8 Mosaic

2.2.2. Landform Classification
2.2.3. Ancillary Geospatial Datasets
2.3. Local Moran’s I Statistic
2.4. Remote Sensing-Based Statistical Classification Approach
2.5. Accuracy Assessment and Calibration
2.6. Quantifying Area of Lakes and Drained Lake Basins
2.7. Classifying Drained Lake Basins
3. Results
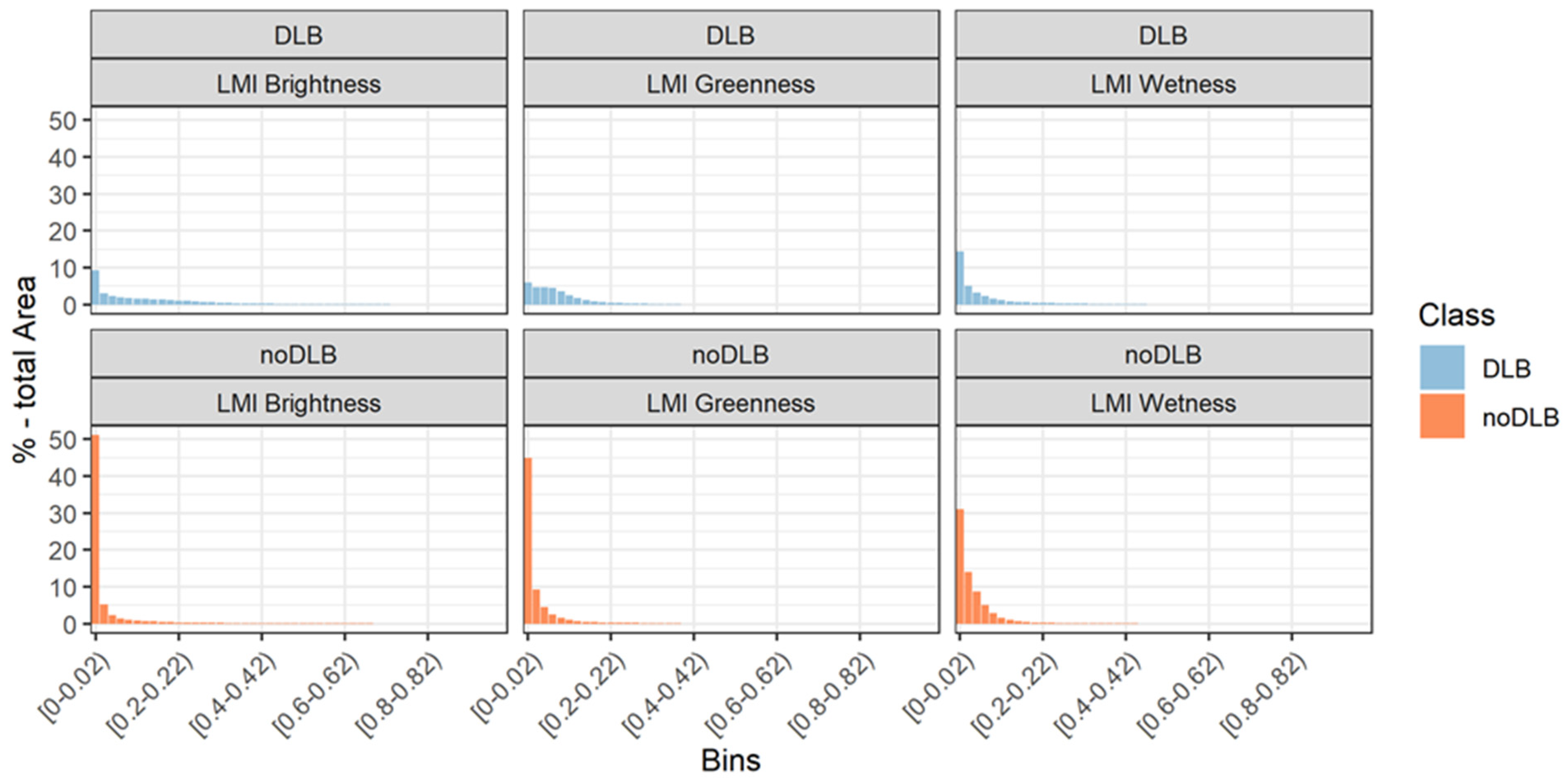
3.1. Local Moran’s I Statistic Based on Tasseled Cap Transformation
3.2. Defining Drained Lake Basins
3.3. Accuracy Assessment
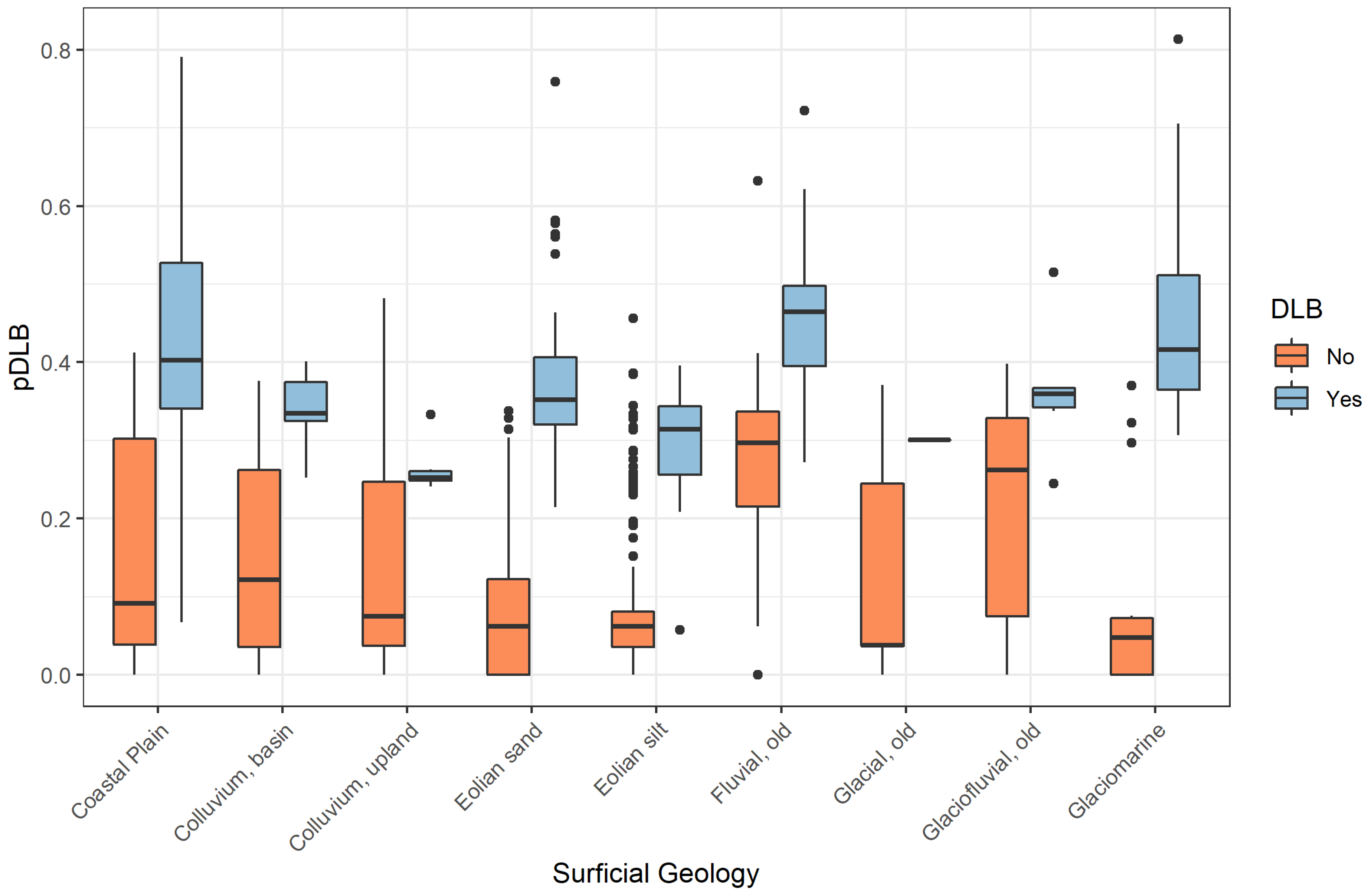
3.4. Areas of Lakes and DLBs for Regions with Different Surficial Geology
4. Discussion
4.1. DLB Data Product
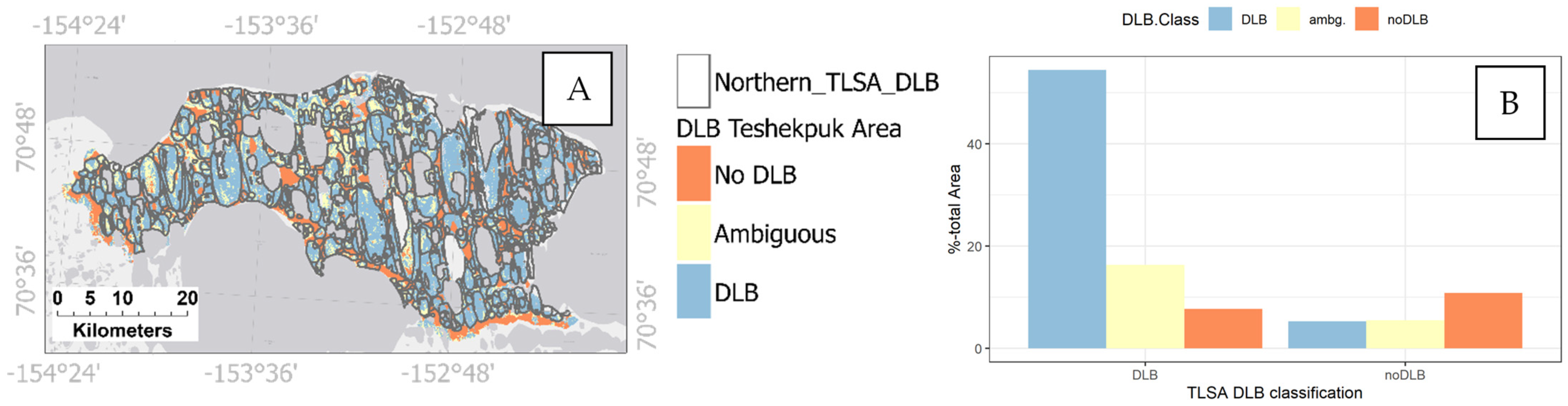
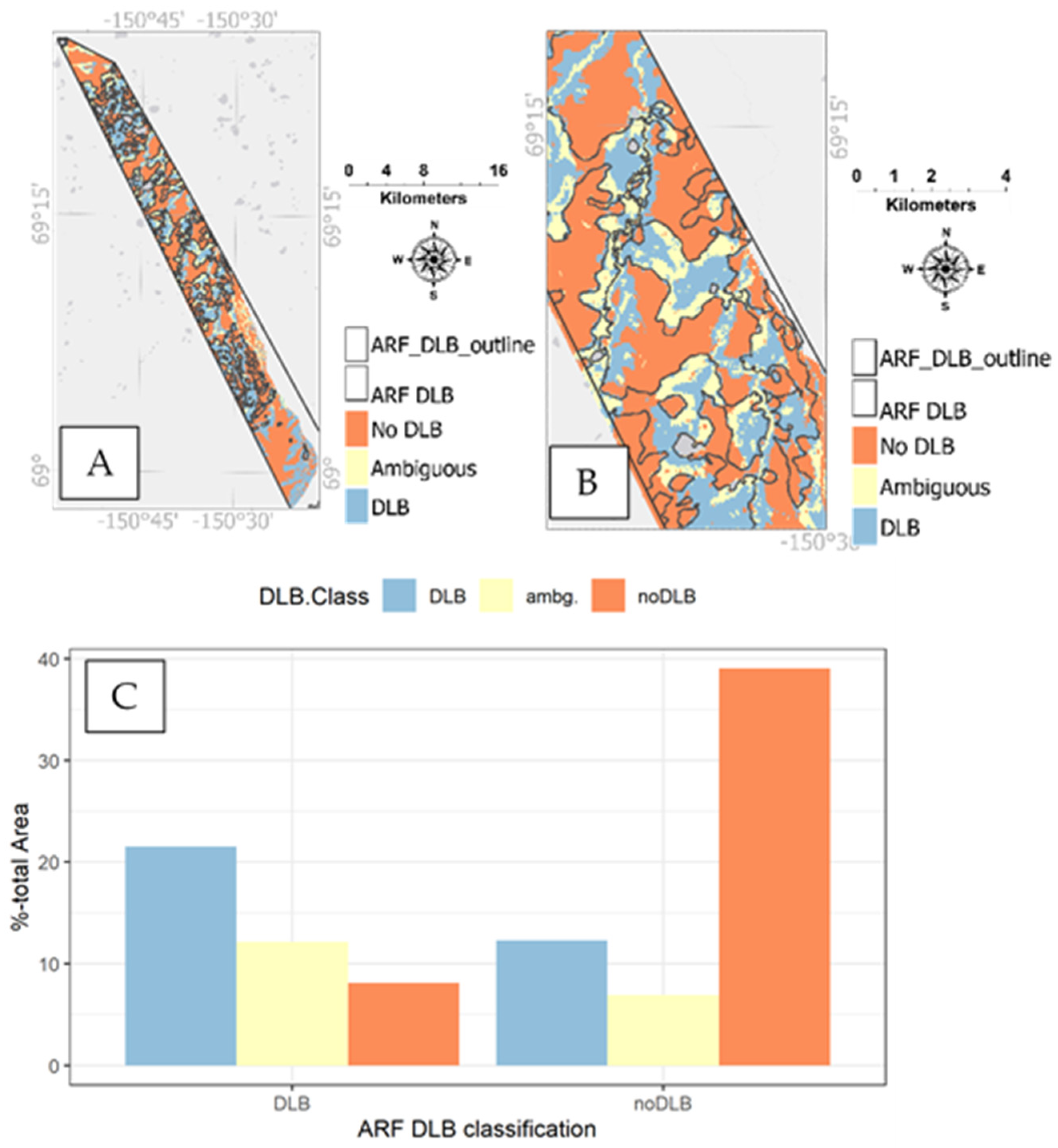
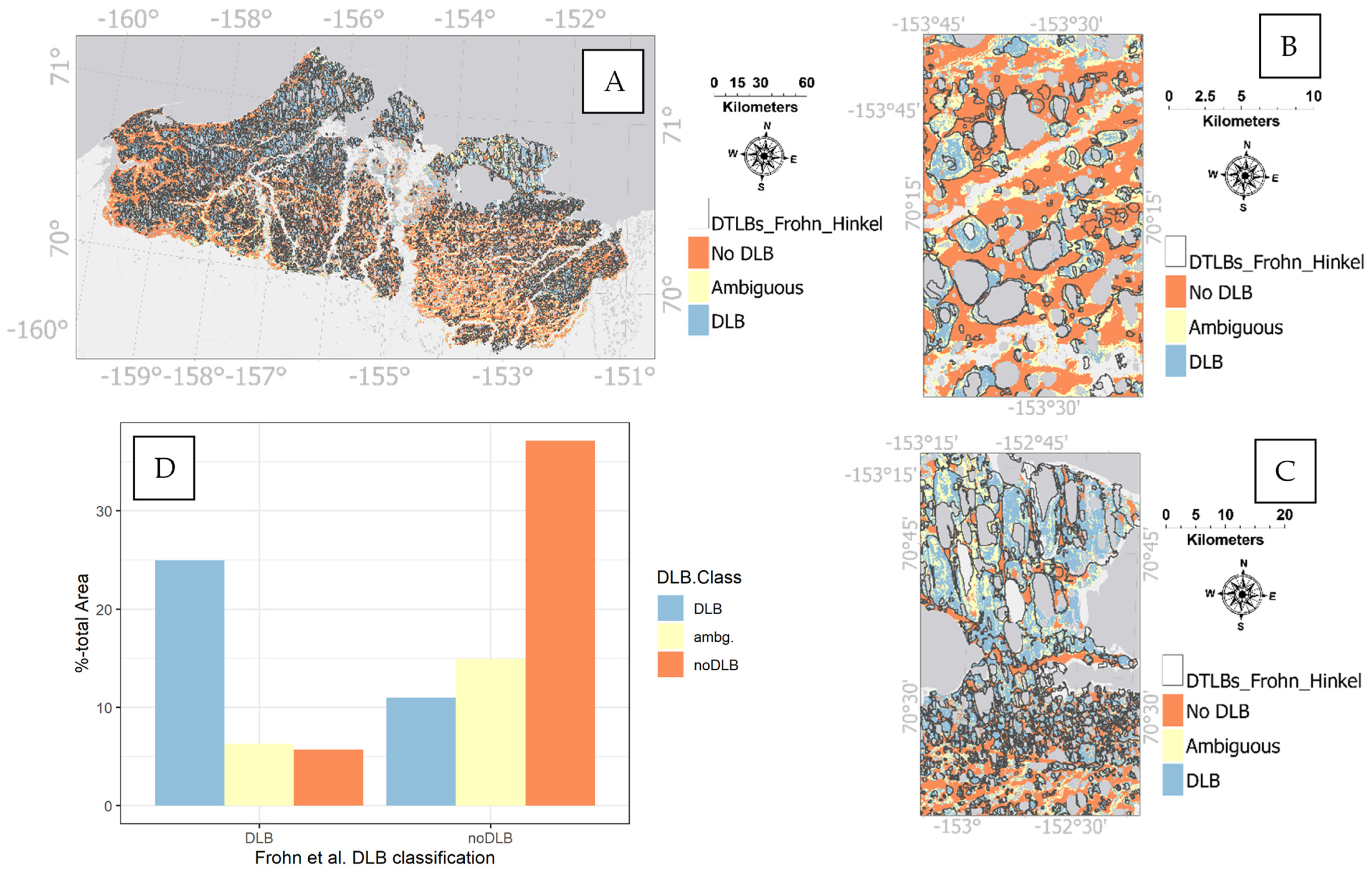
4.2. Comparison of DLB Classification with Previously Published Datasets
4.3. Lakes and Drained Lake Basins on the North Slope of Alaska
4.4. Potential Applications and Upscaling of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lara, M.J.; Nitze, I.; Grosse, G.; Martin, P.; McGuire, A.D. Reduced Arctic Tundra Productivity Linked with Landform and Climate Change Interactions. Sci. Rep. 2018, 8, 2345. [Google Scholar] [CrossRef] [PubMed]
- Lantz, T.C. Vegetation Succession and Environmental Conditions Following Catastrophic Lake Drainage in Old Crow Flats, Yukon. Arctic 2017, 70, 177–189. [Google Scholar] [CrossRef]
- Hashemi, J.; Zona, D.; Arndt, K.A.; Kalhori, A.; Oechel, W.C. Seasonality Buffers Carbon Budget Variability across Heterogeneous Landscapes in Alaskan Arctic Tundra. Environ. Res. Lett. 2021, 16, 35008. [Google Scholar] [CrossRef]
- Arp, C.D.; Jones, B.M.; Hinkel, K.M.; Kane, D.L.; Whitman, M.S.; Kemnitz, R. Recurring Outburst Floods from Drained Lakes: An Emerging Arctic Hazard. Front. Ecol. Environ. 2020, 18, 384–390. [Google Scholar] [CrossRef]
- Grosse, G.; Jones, B.M.; Arp, C.D. Thermokarst lakes, drainage, and drained basins. In Treatise on Geomorphology; Shroder, J.F., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 8, pp. 325–353. [Google Scholar]
- Frohn, R.C.; Hinkel, K.M.; Eisner, W.R. Satellite Remote Sensing Classification of Thaw Lakes and Drained Thaw Lake Basins on the North Slope of Alaska. Remote Sens. Environ. 2005, 97, 116–126. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Frohn, R.C.; Nelson, F.E.; Eisner, W.R.; Beck, R.A. Morphometric and Spatial Analysis of Thaw Lakes and Drained Thaw Lake Basins in the Western Arctic Coastal Plain, Alaska. Permafr. Periglac. Process. 2005, 16, 327–341. [Google Scholar] [CrossRef]
- Jorgenson, M.T.; Shur, Y. Evolution of Lakes and Basins in Northern Alaska and Discussion of the Thaw Lake Cycle. J. Geophys. Res. Earth Surf. 2007, 112, F02S17. [Google Scholar] [CrossRef]
- Kanevskiy, M.; Shur, Y.; Jorgenson, M.T.; Ping, C.L.; Michaelson, G.J.; Fortier, D.; Stephani, E.; Dillon, M.; Tumskoy, V. Ground Ice in the Upper Permafrost of the Beaufort Sea Coast of Alaska. Cold Reg. Sci. Technol. 2013, 85, 56–70. [Google Scholar] [CrossRef]
- Jones, M.C.; Grosse, G.; Jones, B.M.; Walter Anthony, K. Peat Accumulation in Drained Thermokarst Lake Basins in Continuous, Ice-Rich Permafrost, Northern Seward Peninsula, Alaska. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef]
- Jones, B.M.; Arp, C.D. Observing a Catastrophic Thermokarst Lake Drainage in Northern Alaska. Permafr. Periglac. Process. 2015, 26, 119–128. [Google Scholar] [CrossRef]
- Farquharson, L.M.; Mann, D.H.; Grosse, G.; Jones, B.M.; Romanovsky, V.E. Spatial Distribution of Thermokarst Terrain in Arctic Alaska. Geomorphology 2016, 273, 116–133. [Google Scholar] [CrossRef] [Green Version]
- Veremeeva, A.; Nitze, I.; Günther, F.; Grosse, G.; Rivkina, E. Geomorphological and Climatic Drivers of Thermokarst Lake Area Increase Trend (1999–2018) in the Kolyma Lowland Yedoma Region, North-eastern Siberia. Remote Sens. 2021, 13, 178. [Google Scholar] [CrossRef]
- Hughes-Allen, L.; Bouchard, F.; Laurion, I.; Séjourné, A.; Marlin, C.; Hatté, C.; Costard, F.; Fedorov, A.; Desyatkin, A. Seasonal Patterns in Greenhouse Gas Emissions from Thermokarst Lakes in Central Yakutia (Eastern Siberia). Limnol. Oceanogr. 2021, 66, S98–S116. [Google Scholar] [CrossRef]
- Serikova, S.; Pokrovsky, O.S.; Laudon, H.; Krickov, I.V.; Lim, A.G.; Manasypov, R.M.; Karlsson, J. High Carbon Emissions from Thermokarst Lakes of Western Siberia. Nat. Commun. 2019, 10, 1552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morgenstern, A.; Grosse, G.; Günther, F.; Fedorova, I.; Schirrmeister, L. Spatial Analyses of Thermokarst Lakes and Basins in Yedoma Landscapes of the Lena Delta. Cryosphere 2011, 5, 849–867. [Google Scholar] [CrossRef] [Green Version]
- Sibley, P.K.; White, D.M.; Cott, P.A.; Lilly, M.R. Introduction to Water Use from Arctic Lakes: Identification, Impacts, and Decision Support. J. Am. Water Resour. Assoc. 2008, 44, 273–275. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.M.; Arp, C.D.; Hinkel, K.M.; Beck, R.A.; Schmutz, J.A.; Winston, B. Arctic Lake Physical Processes and Regimes with Implications for Winter Water Availability and Management in the National Petroleum Reserve Alaska. Environ. Manag. 2009, 43, 1071–1084. [Google Scholar] [CrossRef]
- Alessa, L.; Kliskey, A.; Lammers, R.; Arp, C.; White, D.; Hinzman, L.; Busey, R. The Arctic Water Resource Vulnerability Index: An Integrated Assessment Tool for Community Resilience and Vulnerability with Respect to Freshwater. Environ. Manag. 2008, 42, 523–541. [Google Scholar] [CrossRef] [PubMed]
- Derksen, D.V.; Eldridge, W.D.; Weller, M.W. Habitat Ecology of Pacific Black Brant and Other Geese Moulting near Teshekpuk Lake, Alaska. Wildfowl 1982, 33, 39–57. [Google Scholar]
- Arp, C.D.; Jones, B.M.; Schmutz, J.A.; Urban, F.E.; Jorgenson, M.T. Two Mechanisms of Aquatic and Terrestrial Habitat Change along an Alaskan Arctic Coastline. Polar Biol. 2010, 33, 1629–1640. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.M.; Grosse, G.; Arp, C.D.; Jones, M.C.; Walter Anthony, K.M.; Romanovsky, V.E. Modern Thermokarst Lake Dynamics in the Continuous Permafrost Zone, Northern Seward Peninsula, Alaska. J. Geophys. Res. Biogeosci. 2011, 116, G00M03. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Jones, B.M.; Eisner, W.R.; Cuomo, C.J.; Beck, R.A.; Frohn, R. Methods to Assess Natural and Anthropogenic Thaw Lake Drainage on the Western Arctic Coastal Plain of Northern Alaska. J. Geophys. Res. Earth Surf. 2007, 112, F02S16. [Google Scholar] [CrossRef] [Green Version]
- Marsh, P.; Russell, M.; Pohl, S.; Haywood, H.; Onclin, C. Changes in Thaw Lake Drainage in the Western Canadian Arctic from 1950 to 2000; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2009; Volume 23, pp. 145–158. [Google Scholar]
- Jones, B.M.; Arp, C.D.; Grosse, G.; Nitze, I.; Lara, M.J.; Whitman, M.S.; Farquharson, L.M.; Kanevskiy, M.; Parsekian, A.D.; Breen, A.L.; et al. Identifying Historical and Future Potential Lake Drainage Events on the Western Arctic Coastal Plain of Alaska. Permafr. Periglac. Process. 2020, 31, 110–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nitze, I.; Grosse, G.; Jones, B.M.; Romanovsky, V.E.; Boike, J. Remote Sensing Quantifies Widespread Abundance of Permafrost Region Disturbances across the Arctic and Subarctic. Nat. Commun. 2018, 9, 5423. [Google Scholar] [CrossRef] [PubMed]
- Nitze, I.; Cooley, S.W.; Duguay, C.R.; Jones, B.M.; Grosse, G. The Catastrophic Thermokarst Lake Drainage Events of 2018 in Northwestern Alaska: Fast-Forward into the Future. Cryosphere 2020, 14, 4279–4297. [Google Scholar] [CrossRef]
- Van Der Kolk, H.J.; Heijmans, M.M.P.D.; Van Huissteden, J.; Pullens, J.W.M.; Berendse, F. Potential Arctic Tundra Vegetation Shifts in Response to Changing Temperature, Precipitation and Permafrost Thaw. Biogeosciences 2016, 13, 6229–6245. [Google Scholar] [CrossRef] [Green Version]
- Sellmann, P.V.; Brown, J.; Lewellen, R.I.; McKim, H.; Merry, C. The Classification and Geomorphic Implications of Thaw Lakes on the Arctic Coastal Plain, Alaska; US Department of Defense, Department of the Army, Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, Germany; New Hampshire, NE, USA, 1975; Volume 344. [Google Scholar]
- Wang, J.; Sheng, Y.; Hinkel, K.M.; Lyons, E.A. Drained Thaw Lake Basin Recovery on the Western Arctic Coastal Plain of Alaska Using High-Resolution Digital Elevation Models and Remote Sensing Imagery. Remote Sens. Environ. 2012, 119, 325–336. [Google Scholar] [CrossRef]
- Labrecque, S.; Lacelle, D.; Duguay, C.R.; Lauriol, B.; Hawkings, J. Contemporary (1951–2001) Evolution of Lakes in the Old Crow Basin, Northern Yukon, Canada: Remote Sensing, Numerical Modeling, and Stable Isotope Analysis. Arctic 2009, 62, 225–238. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Lu, P.; Li, Z. Semi-Automated Detection of Thaw Lakes in Permafrost Areas in Qinghai-Tibet Plateau from Sentinel-2 Images Using Markov Random Field. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium; Institute of Electrical and Electronics Engineers (IEEE), Yokohama, Japan, 28 July–2 August 2019; pp. 4036–4039. [Google Scholar]
- Simpson, C.E.; Arp, C.D.; Sheng, Y.; Carroll, M.L.; Jones, B.M.; Smith, L.C. Landsat-Derived Bathymetry of Lakes on the Arctic Coastal Plain of Northern Alaska. Earth Syst. Sci. Data 2021, 13, 1135–1150. [Google Scholar] [CrossRef]
- Bartsch, A.; Pointner, G.; Leibman, M.O.; Dvornikov, Y.A.; Khomutov, A.; Trofaier, A.M. Circumpolar Mapping of Ground-Fast Lake Ice. Front. Earth Sci. 2017, 5, 12. [Google Scholar] [CrossRef] [Green Version]
- Al-Roubaiey, A.; Sheltami, T.; Mahmoud, A.; Shakshuki, E.; Mouftah, H. AACK: Adaptive Acknowledgment Intrusion Detection for MANET with Node Detection Enhancement. In Proceedings of the 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, Australia, 20–23 April 2010; Volume 17, pp. 634–640. [Google Scholar] [CrossRef]
- Surdu, C.M.; Duguay, C.R.; Pour, H.K.; Brown, L.C. Ice Freeze-up and Break-up Detection of Shallow Lakes in Northern Alaska with Spaceborne SAR. Remote Sens. 2015, 7, 6133–6159. [Google Scholar] [CrossRef] [Green Version]
- Engram, M.; Anthony, K.W.; Meyer, F.J.; Grosse, G. Synthetic Aperture Radar (SAR) Backscatter Response from Methane Ebullition Bubbles Trapped by Thermokarst Lake Ice. Can. J. Remote Sens. 2013, 38, 667–682. [Google Scholar] [CrossRef]
- Zhang, S.; Pavelsky, T.M. Remote Sensing of Lake Ice Phenology across a Range of Lakes Sizes, ME, USA. Remote Sens. 2019, 11, 1718. [Google Scholar] [CrossRef] [Green Version]
- Engram, M.; Arp, C.D.; Jones, B.M.; Ajadi, O.A.; Meyer, F.J. Analyzing Floating and Bedfast Lake Ice Regimes across Arctic Alaska Using 25 years of Space-Borne SAR Imagery. Remote Sens. Environ. 2018, 209, 660–676. [Google Scholar] [CrossRef]
- Pointner, G.; Bartsch, A.; Dvornikov, Y.; Kouraev, A. Mapping Potential Signs of Gas Emissions in Ice of Lake Neyto, Yamal, Russia Using Synthetic Aperture Radar and Multispectral Remote Sensing Data. Cryosphere 2021, 15, 1907–1929. [Google Scholar] [CrossRef]
- Nitze, I.; Grosse, G.; Jones, B.M.; Arp, C.D.; Ulrich, M.; Fedorov, A.; Veremeeva, A. Landsat-Based Trend Analysis of Lake Dynamics across Northern Permafrost Regions. Remote Sens. 2017, 9, 640. [Google Scholar] [CrossRef] [Green Version]
- Hinkel, K.M.; Eisner, W.R.; Bockheim, J.G.; Nelson, F.E.; Peterson, K.M.; Dai, X. Spatial Extent, Age, and Carbon Stocks in Drained Thaw Lake Basins on the Barrow Peninsula, Alaska. Arctic Antarct. Alp. Res. 2003, 35, 291–300. [Google Scholar] [CrossRef] [Green Version]
- Regmi, P.; Grosse, G.; Jones, M.C.; Jones, B.M.; Anthony, K.W. Characterizing Post-Drainage Succession in Thermokarst Lake Basins on the Seward Peninsula, Alaska with TerraSAR-X Backscatter and Landsat-Based NDVI Data. Remote Sens. 2012, 4, 3741–3765. [Google Scholar] [CrossRef] [Green Version]
- Marcus, M.G.; Wahrhaftig, C. Physiographic Divisions of Alaska. Geogr. Rev. 1967, 57, 581. [Google Scholar] [CrossRef]
- Osterkamp, T.E.; Payne, M.W. Estimates of Permafrost Thickness from Well Logs in Northern Alaska. Cold Reg. Sci. Technol. 1981, 5, 13–27. [Google Scholar] [CrossRef]
- Van Everdingen, R.O.; Terminology Working Group. Multi-Language Glossary of Permafrost and Related Ground-Ice Terms in Chinese, English, French, German, Icelandic, Italian, Norwegian, Polish, Romanian, Russian, Spanish, and Swedish; International Permafrost Association: Calgary, Alberta, 1998. [Google Scholar]
- Hinkel, K.M.; Nelson, F.E. Spatial and Temporal Patterns of Active Layer Thickness at Circumpolar Active Layer Monitoring (CALM) Sites in Northern Alaska, 1995–2000. J. Geophys. Res. Atmos. 2003, 108, 8168. [Google Scholar] [CrossRef]
- Walker, D.A.; Jia, G.J.; Epstein, H.E.; Raynolds, M.K.; Chapin, I.S.; Copass, C.; Hinzman, L.D.; Knudson, J.A.; Maier, H.A.; Michaelson, G.J.; et al. Vegetation-Soil-Thaw-Depth Relationships along a Low-Arctic Bioclimate Gradient, Alaska: Synthesis of Information from the ATLAS Studies. Permafr. Periglac. Process. 2003, 14, 103–123. [Google Scholar] [CrossRef]
- Walker, D.A.; Reynolds, M.K.; Daniëls, F.J.A.; Einarsson, E.; Elvebakk, A.; Gould, W.A.; Katenin, A.E.; Kholod, S.S.; Markon, C.J.; Melnikov, E.S.; et al. The Circumpolar Arctic Vegetation Map. J. Veg. Sci. 2005, 16, 267–282. [Google Scholar] [CrossRef]
- Walker, D.A.; Kuss, P.; Epstein, H.E.; Kade, A.N.; Vonlanthen, C.M.; Raynolds, M.K.; Daniëls, F.J.A. Vegetation of Zonal Patterned-Ground Ecosystems along the North America Arctic Bioclimate Gradient. Appl. Veg. Sci. 2011, 14, 440–463. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Li, H.; Wan, W.; Fang, Y.; Zhu, S.; Chen, X.; Liu, B.; Hong, Y. A Google Earth Engine-Enabled Software for Efficiently Generating High-Quality User-Ready Landsat Mosaic Images. Environ. Model. Softw. 2019, 112, 16–22. [Google Scholar] [CrossRef]
- Johansen, K.; Phinn, S.; Taylor, M. Mapping Woody Vegetation Clearing in Queensland, Australia from Landsat Imagery Using the Google Earth Engine. Remote Sens. Appl. Soc. Environ. 2015, 1, 36–49. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, X.; Yao, J.; Zhang, X.; Zhang, H. Mapping the Annual Dynamics of Cultivated Land in Typical Area of the Middle-Lower Yangtze Plain Using Long Time-Series of Landsat Images Based on Google Earth Engine. Int. J. Remote Sens. 2020, 41, 1625–1644. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, Y.; Ling, F.; Wang, Q.; Li, W.; Li, X. Water Bodies’ Mapping from Sentinel-2 Imagery with Modified Normalized Difference Water Index at 10-m Spatial Resolution Produced by Sharpening the Swir Band. Remote Sens. 2016, 8, 354. [Google Scholar] [CrossRef] [Green Version]
- Jorgenson, M.T.; Kanevskiy, M.; Shur, Y.; Grunblatt, J.; Ping, C.-L.; Michaelson, G. Permafrost Database Development, Characterization, and Mapping for Northern Alaska; Item Type Technical Report Permafrost Database Development, Characterization, and Mapping for Northern Alaska Final Report Prepared for U.S. Fish and Wildlife Service; Arctic LandscapeConservation Cooperative: Anchorage, AK, USA, 2014. [Google Scholar]
- Raynolds, M.K.; Walker, D.A. Increased Wetness Confounds Landsat-Derived NDVI Trends in the Central Alaska North Slope Region, 1985–2011. Environ. Res. Lett. 2016, 11, 085004. [Google Scholar] [CrossRef] [Green Version]
- Fraser, R.; Olthof, I.; Carrière, M.; Deschamps, A.; Pouliot, D. A Method for Trend-Based Change Analysis in Arctic Tundra Using the 25-Year Landsat Archive. Polar Rec. 2012, 48, 83–93. [Google Scholar] [CrossRef]
- Brooker, A.; Fraser, R.H.; Olthof, I.; Kokelj, S.V.; Lacelle, D. Mapping the Activity and Evolution of Retrogressive Thaw Slumps by Tasselled Cap Trend Analysis of a Landsat Satellite Image Stack. Permafr. Periglac. Process. 2014, 25, 243–256. [Google Scholar] [CrossRef]
- Olthof, I.; Fraser, R.H. Detecting Landscape Changes in High Latitude Environments Using Landsat Trend Analysis: 2. Classification. Remote Sens. 2014, 6, 11558–11578. [Google Scholar] [CrossRef] [Green Version]
- Nitze, I.; Grosse, G. Detection of Landscape Dynamics in the Arctic Lena Delta with Temporally Dense Landsat Time-Series Stacks. Remote Sens. Environ. 2016, 181, 27–41. [Google Scholar] [CrossRef]
- Baig, M.H.A.; Zhang, L.; Shuai, T.; Tong, Q. Derivation of a Tasselled Cap Transformation Based on Landsat 8 At-Satellite Reflectance. Remote Sens. Lett. 2014, 5, 423–431. [Google Scholar] [CrossRef]
- Porter, C.; Morin, P.; Howat, I.; Noh, M.-J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. ArcticDEM, V3; Harvard Dataverse: Cambridge, MA, USA, 2018. [Google Scholar] [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA Spatial Modeling of Plant Species Distribution. Plant Ecol. 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Weiss, A.D. Topographic Position and Landforms Analysis. In Proceedings of the 2001 ESRI User Conference, San Diego, CA, USA, 9–13 July 2001; Volume 200. [Google Scholar]
- Wilson, J.P. Digital Terrain Analysis [EReserve]; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Jenness Enterprises. Topographic Position Index (Tpi_jen.Avx) Extension for ArcView 3.x, v. 1.3a. Jenness Enterprises. 2006. Available online: www.Jennessent.Com/Arcview/Tpi.Htm (accessed on 25 June 2021).
- Liu, M.; Hu, Y.; Chang, Y.; He, X.; Zhang, W. Land Use and Land Cover Change Analysis and Prediction in the Upper Reaches of the Minjiang River, China. Environ. Manag. 2009, 43, 899–907. [Google Scholar] [CrossRef] [PubMed]
- Tagil, S.; Jenness, J. GIS-Based Automated Landform Classification and Topographic, Landcover and Geologic Attributes of Landforms around the Yazoren Polje, Turkey. J. Appl. Sci. 2008, 8, 910–921. [Google Scholar] [CrossRef] [Green Version]
- Illés, G.; Kovács, G.; Heil, B. Comparing and Evaluating Digital Soil Mapping Methods in a Hungarian Forest Reserve. Can. J. Soil Sci. 2011, 91, 615–626. [Google Scholar] [CrossRef]
- Liu, H.; Bu, R.; Liu, J.; Leng, W.; Hu, Y.; Yang, L.; Liu, H. Predicting the Wetland Distributions under Climate Warming in the Great Xing’an Mountains, Northeastern China. Ecol. Res. 2011, 26, 605–613. [Google Scholar] [CrossRef]
- Jones, B.M.; Grosse, G.; Arp, C.D.; Miller, E.; Liu, L.; Hayes, D.J.; Larsen, C.F. Recent Arctic Tundra Fire Initiates Widespread Thermokarst Development. Sci. Rep. 2015, 5, 15865. [Google Scholar] [CrossRef] [Green Version]
- Jones, B.; Kolden, C.; Jandt, R.; Abatzoglou, J.; Urban, F.; Arp, C. Fire Behavior, Weather, and Burn Severity of the 2007 Anaktuvuk River Tundra Fire, North Slope, Alaska. Arctic Antarct. Alp. Res. 2009, 41, 309–316. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Hijmans, R.J.; van Etten, J.; Sumner, M.; Cheng, J.; Baston, D.; Bevan, A.; Bivand, R.; Busetto, L.; Canty, M.; Fasoli, B.; et al. Raster: Geographic Data Analysis and Modeling; Version 3.4-13; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Ohmann, J.L.; Gregory, M.J.; Roberts, H.M.; Cohen, W.B.; Kennedy, R.E.; Yang, Z. Mapping change of older forest with nearest-neighbor imputation and Landsat time-series. For. Ecol. Manag. 2012, 272, 13–25. [Google Scholar] [CrossRef]
- Smith, B.; McDermid, G.J. Examination of fire-related succession within the dry mixed-grass subregion of Alberta with the use of MODIS and Landsat. Rangel. Ecol. Manag. 2014, 67, 307–317. [Google Scholar] [CrossRef]
- Adams, B.; Iverson, L.; Matthews, S.; Peters, M.; Prasad, A.; Hix, D. Mapping forest composition with Landsat time series: An evaluation of seasonal composites and harmonic regression. Remote Sens. 2020, 12, 610. [Google Scholar] [CrossRef] [Green Version]
- Lara, M.J.; Chipman, M.L. Periglacial Lake Origin Influences the Likelihood of Lake Drainage in Northern Alaska. Remote Sens. 2021, 13, 852. [Google Scholar] [CrossRef]
- Muster, S.; Roth, K.; Langer, M.; Lange, S.; Cresto Aleina, F.; Bartsch, A.; Morgenstern, A.; Grosse, G.; Jones, B.; Sannel, A.B.K.; et al. PeRL: A Circum-Arctic Permafrost Region Pond and Lake Database. Earth Syst. Sci. Data 2017, 9, 317–348. [Google Scholar] [CrossRef] [Green Version]
- Anthony, K.M.W.; Zimov, S.A.; Grosse, G.; Jones, M.C.; Anthony, P.M.; Iii, F.S.C.; Finlay, J.C.; Mack, M.C.; Davydov, S.; Frenzel, P.; et al. A Shift of Thermokarst Lakes from Carbon Sources to Sinks during the Holocene Epoch. Nature 2014, 511, 452–456. [Google Scholar] [CrossRef]
- Turetsky, M.R.; Abbott, B.; Jones, M.C.; Walter Anthony, K.M.; Olefeldt, D.; Schuur, E.A.G.; Grosse, G.; Kuhry, P.; Hugelius, G.; Koven, C.; et al. Carbon Release through Abrupt Permafrost Thaw. Nat. Geosci. 2020, 13, 138–143. [Google Scholar] [CrossRef]
- Olefeldt, D.; Goswami, S.; Grosse, G.; Hayes, D.; Hugelius, G.; Kuhry, P.; Mcguire, A.D.; Romanovsky, V.E.; Sannel, A.B.K.; Schuur, E.A.G.; et al. Circumpolar Distribution and Carbon Storage of Thermokarst Landscapes. Nat. Commun. 2016, 7, 13043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Strauss, J.; Schirrmeister, L.; Grosse, G.; Fortier, D.; Hugelius, G.; Knoblauch, C.; Romanovsky, V.; Schädel, C.; von Deimling, T.S.; Schuur, E.A.; et al. Deep Yedoma Permafrost: A Synthesis of Depositional Characteristics and Carbon Vulnerability. Earth Sci. Rev. 2017, 172, 75–86. [Google Scholar] [CrossRef] [Green Version]
- Brosius, L.S.; Walter Anthony, K.M.; Treat, C.; Lenz, J.; Jones, M.; Bret-Harte, M.S.; Grosse, G. Spatiotemporal Patterns of Northern Lake Formation since the Last Glacial Maximum. Quat. Sci. Rev. 2021, 253, 106773. [Google Scholar] [CrossRef]
- Treat, C.C.; Jones, M.C.; Brosius, L.S.; Grosse, G.; Anthony, K.W.; Frolking, S. The Role of Wetland Successional Processes in Methane Emissions from High-Latitude Wetlands during the Holocene. Quat. Sci. Rev. 2021, 257, 106864. [Google Scholar] [CrossRef]
- Bergstedt, H.; Jones, B.; Hinkel, K.; Farquharson, L.; Gaglioti, B. Drained Lake Basin classification based on Landsat-8imagery, North Slope, Alaska 2014–2019. Arctic Data Center 2021. [Google Scholar] [CrossRef]
- Bergstedt, H.; Jones, B.M.; Arp, C. Drained Lake basins on the younger outer coastal plain north of Teshekpuk Lake, North Slope, Alaska, 2010–2014. Arctic Data Center 2021. [Google Scholar] [CrossRef]
- Bergstedt, H.; Jones, B.; Grosse, G.; Arp, C.; Miller, E.; Liu, L.; Hayes, D.; Larsen, C. Drained Lake basins in the area of the 2007 Anaktuvuk River Tundra Fire, North Slope, Alaska. Arctic Data Center 2021. [Google Scholar] [CrossRef]




| Landsat-8 TCT | Blue Band 2 | Green Band 3 | Red 4 Band 4 | NIR Band 5 | SWIR1 Band 6 | SWIR2 Band 7 |
|---|---|---|---|---|---|---|
| Brightness | 0.3029 | 0.2786 | 0.4733 | 0.5599 | 0.5080 | 0.1872 |
| Greenness | −0.2941 | −0.2430 | −0.5424 | 0.7276 | 0.0713 | −0.1608 |
| Wetness | 0.1511 | 0.1973 | 0.3283 | 0.3407 | −0.7117 | −0.4599 |
| TCT4 | −0.8239 | 0.0849 | 0.4396 | −0.0580 | 0.2013 | −0.2773 |
| TCT5 | −0.3294 | 0.0557 | 0.1056 | 0.1855 | −0.4349 | 0.8085 |
| TCT6 | 0.1079 | −0.9023 | 0.4119 | 0.0575 | −0.0259 | 0.0252 |
| Landforms | DLB Area Classified as Landform in % | Non-DLB Area Classified as Landform in % | Area % of Landform Classified as DLB | LP |
|---|---|---|---|---|
| Streams | 10.5 | 13.7 | 22.9 | 0.7 |
| Mid-slope drainages, shallow valleys | 2.8 | 2.1 | 34.1 | 0.5 |
| Upland drainages, head waters | 0.3 | 0.6 | 16.3 | 0.4 |
| U-shaped valleys | 16.1 | 14.1 | 30.6 | 1 |
| Plains | 61.6 | 33.7 | 41.5 | 1 |
| Open slopes | 5.9 | 0.05 | 16.1 | 0.8 |
| Upland plains | 0.01 | 2.35 | 16.3 | 0.2 |
| Local ridges, mid-slope ridges, small hills, mountain tops, high ridges | 2.5 | 20.8 | 15.1 | 0 |
| LMI TCT | Greenness | Brightness | Wetness |
|---|---|---|---|
| DLB Mean | 0.08 | 0.12 | 0.06 |
| Non-DLB Mean | 0.03 | 0.03 | 0.03 |
| p-Value | <0.001 | <0.001 | <0.001 |
| t-value | 1591.3 | 1475.1 | 553.7 |
| DF | 845,5903 | 756,8750 | 777,3206 |
| Coefficient Version | Coeff. B | Coeff. G | Coeff. W | pDLBraw Mean within DLB | pDLBraw Mean outside DLB | p-Value | t-Value | DF |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 1 | 0.49 | 0.17 | <0.001 | −15.157 | 298 |
| 2 | 1 | −1 | −1 | 0.53 | 0.23 | <0.001 | −9.3428 | 276.67 |
| 3 | −1 | −1 | 1 | 0.36 | 0.18 | <0.001 | −8.5516 | 296.02 |
| 4 | −1 | 1 | −1 | 0.45 | 0.16 | <0.001 | −14.553 | 292.37 |
| 5 | 1 | 1 | −2 | 0.41 | 0.1 | <0.001 | −16.834 | 253.5 |
| 6 | 2 | 2 | −1 | 0.42 | 0.08 | <0.001 | −20.691 | 205.84 |
| 7 | 1 | 2 | −1 | 0.44 | 0.1 | <0.001 | −21.497 | 246.61 |
| Surficial Geology | Lake Area [km2] | DLB Area [km2] | Area Ratio DLB/Lakes | Ranges of DLB Area | Massive Ground Ice Content | pDLB Thresholds |
|---|---|---|---|---|---|---|
| Glaciomarine | 1415.40 | 1049.53 | 0.74 | 1049.53–1389.45 | 10–30% | 0.23 |
| Glaciofluvial, old | 23.94 | 12.13 | 0.5 | 12.13–59.35 | 5–30% | 0.31 |
| Glacial, young | 36.17 | - | - | - | 10–80% | - |
| Glacial, old | 31.70 | 0.07 | 0.002 | 0.07–0.28 | 10–80% | 0.17 |
| Fluvial, old | 1579.88 | 504.14 | 0.32 | 504.14–1069.58 | 5–30% | 0.39 |
| Eolian silt | 502.78 | 35.49 | 0.07 | 35.49–12,438.35 | 30–70% | 0.18 |
| Eolian sand | 4098.44 | 2082.32 | 0.51 | 2082.32–5410.78 | 5–10% | 0.21 |
| Colluvium upland | 45.51 | 1.02 | 0.02 | 1.02–11,177.98 | 5–10% | 0.16 |
| Colluvium basin | 13.36 | 272.66 | 20.4 | 272.66–306.83 | 10–30% | 0.28 |
| Coastal plain | 4725.8 | 5599.32 | 1.18 | 5599.32–12,162.36 | 10–30% | 0.25 |
| Reference Datasets | DLB Classification | ||
|---|---|---|---|
| DLB | Ambiguous | Non-DLB | |
| DLB | 64.46% | 31% | 4.54% |
| Non-DLB | 4.6% | 12.2% | 83.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergstedt, H.; Jones, B.M.; Hinkel, K.; Farquharson, L.; Gaglioti, B.V.; Parsekian, A.D.; Kanevskiy, M.; Ohara, N.; Breen, A.L.; Rangel, R.C.; et al. Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska. Remote Sens. 2021, 13, 2539. https://doi.org/10.3390/rs13132539
Bergstedt H, Jones BM, Hinkel K, Farquharson L, Gaglioti BV, Parsekian AD, Kanevskiy M, Ohara N, Breen AL, Rangel RC, et al. Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska. Remote Sensing. 2021; 13(13):2539. https://doi.org/10.3390/rs13132539
Chicago/Turabian StyleBergstedt, Helena, Benjamin M. Jones, Kenneth Hinkel, Louise Farquharson, Benjamin V. Gaglioti, Andrew D. Parsekian, Mikhail Kanevskiy, Noriaki Ohara, Amy L. Breen, Rodrigo C. Rangel, and et al. 2021. "Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska" Remote Sensing 13, no. 13: 2539. https://doi.org/10.3390/rs13132539
APA StyleBergstedt, H., Jones, B. M., Hinkel, K., Farquharson, L., Gaglioti, B. V., Parsekian, A. D., Kanevskiy, M., Ohara, N., Breen, A. L., Rangel, R. C., Grosse, G., & Nitze, I. (2021). Remote Sensing-Based Statistical Approach for Defining Drained Lake Basins in a Continuous Permafrost Region, North Slope of Alaska. Remote Sensing, 13(13), 2539. https://doi.org/10.3390/rs13132539