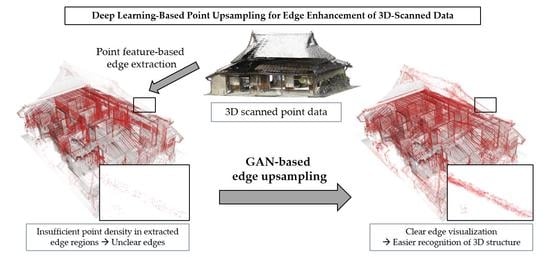
Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization
Abstract
:1. Introduction
2. Eigenvalue-Based 3D Feature Values
3. Methods for Transparent Visualization and Edge Highlighting
3.1. Stochastic Point-Based Rendering (SPBR)
3.2. Opacity-Based Edge Highlighting
3.3. Resampling for Controlling Point Density
4. Proposed Method for Edge-Highlighting Visualization
4.1. Steps of the Proposed Method
- Random downsampling of the 3D-edge regions: Execute downsampling for points in the 3D-edge regions. We randomly eliminate points with such that the resultant point distribution obeys the selected opacity function (type (a), (b), or (c)). Points with are eliminated;
- Deep learning-based upsampling of the 3D-edge regions: Execute the deep learning-based upsampling for the points obtained in STEP 1;
- Point integration and visualization: Merge the original 3D-scanned points, which include points of the non-edge regions, with the upsampled edge points obtained in STEP 2. Then, stochastic point-based rendering is applied to the integrated point dataset. In this step, we obtain a transparent image of the target 3D-scanned point cloud data with clear edge highlighting.
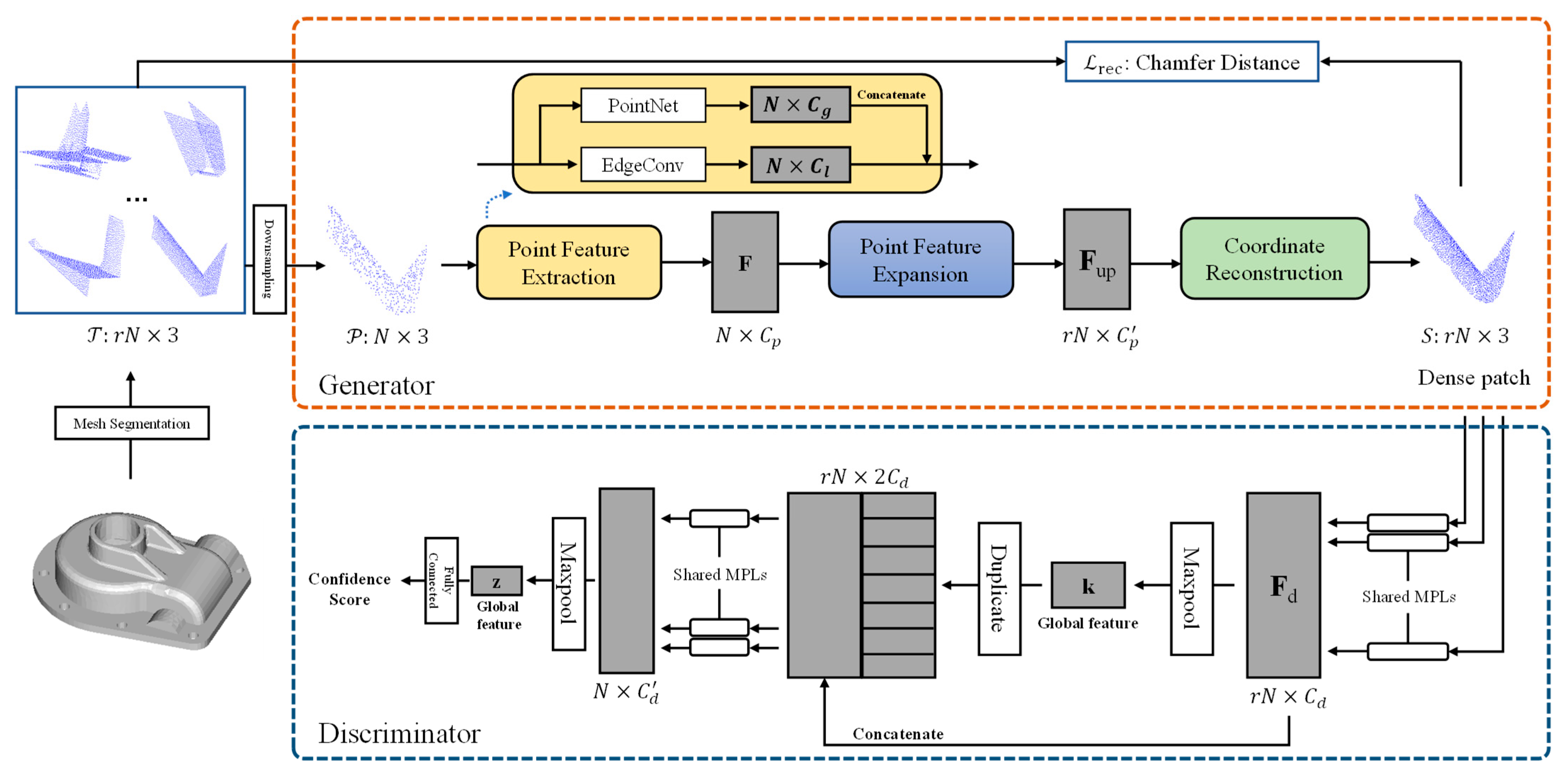
4.2. Proposed Upsampling Network
4.2.1. Overview
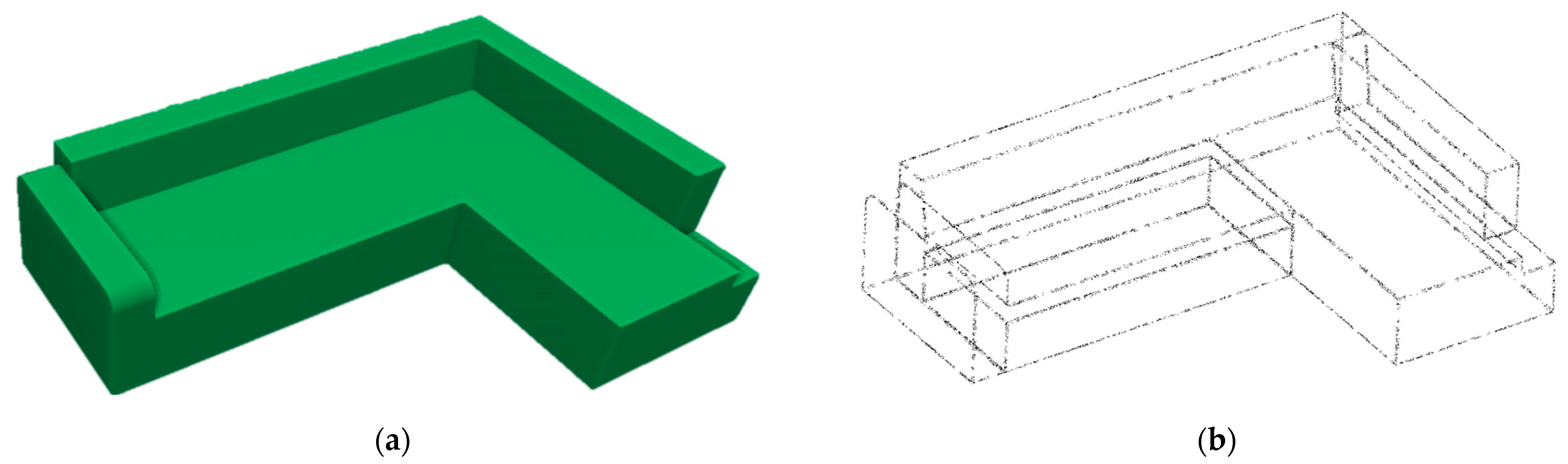
4.2.2. Preparing the Training Data and Ground Truth
4.2.3. Generator
4.2.4. Discriminator
4.2.5. Loss Function
5. Upsampling and Visualization Results and Evaluation of the Proposed Method
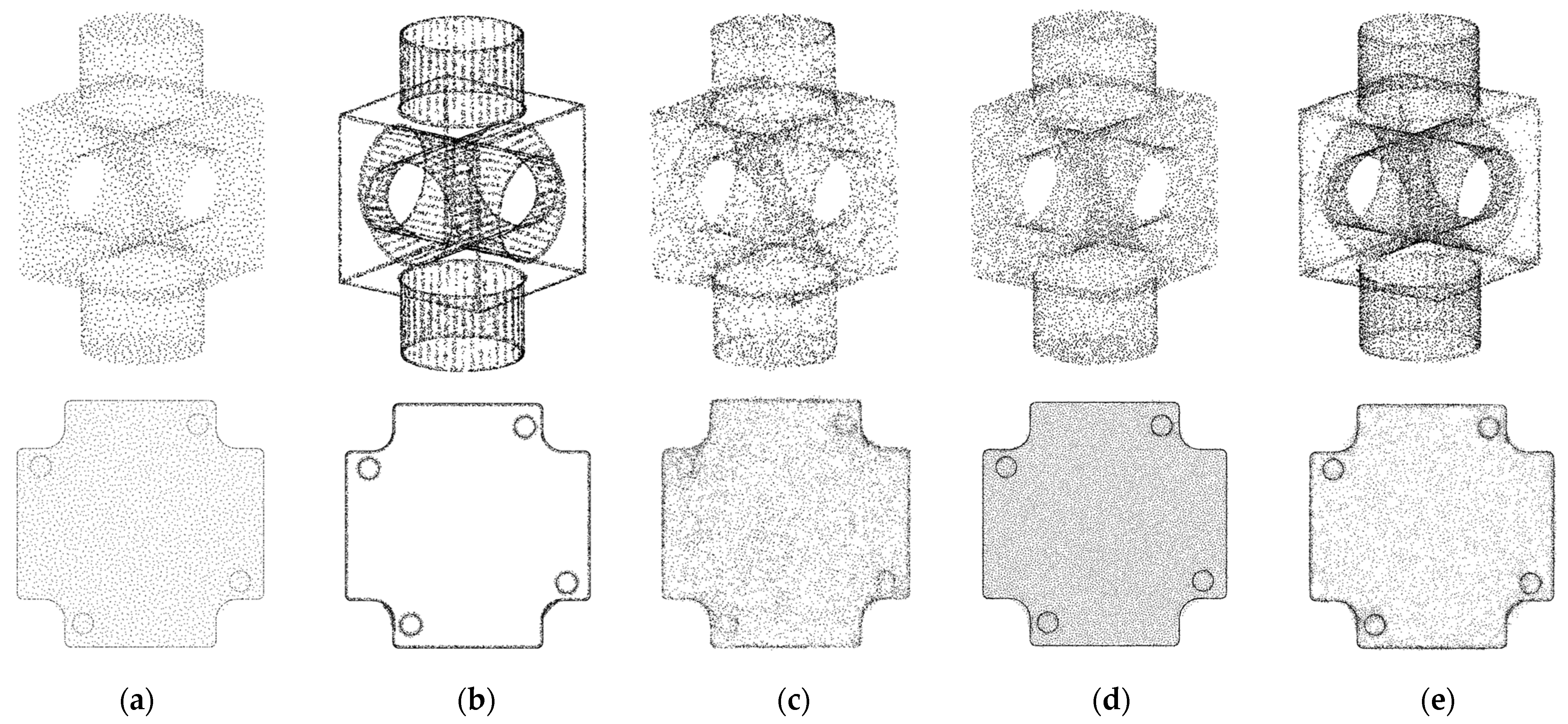
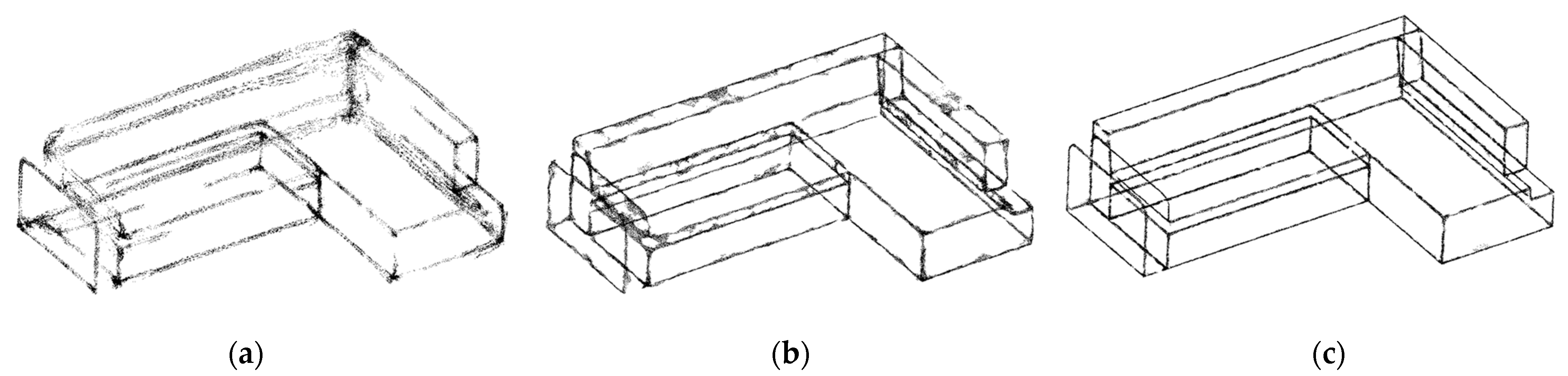
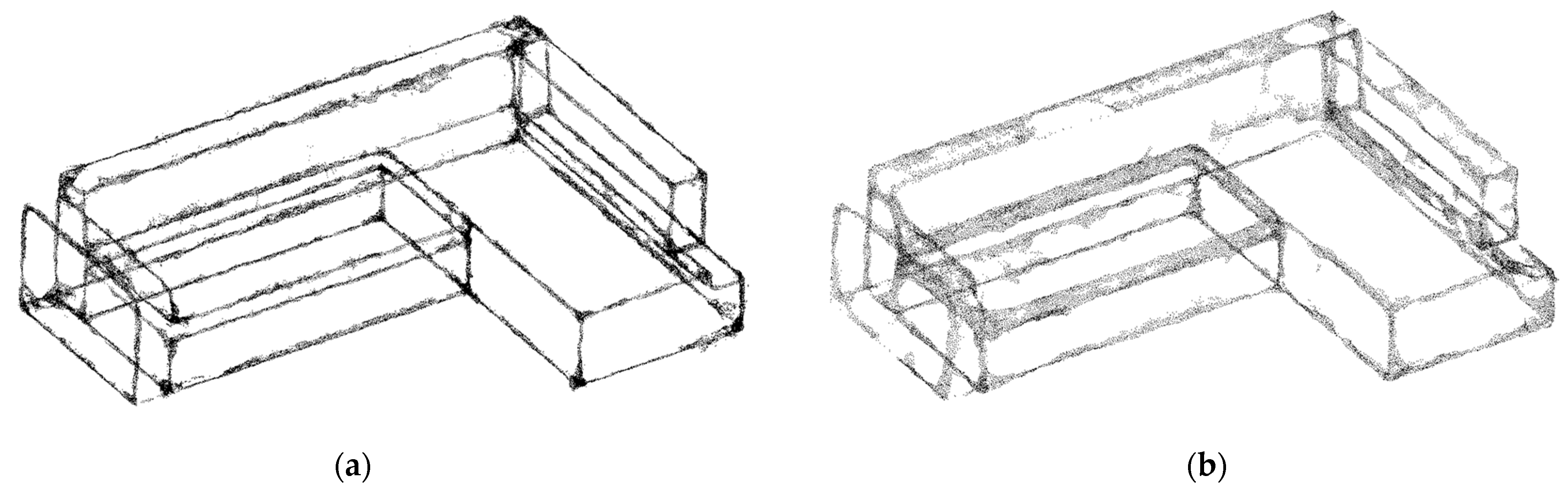
5.1. Verifying the Robustness of Upsampling Networks on Simulated Edges
5.2. Datasets and Implementation Details
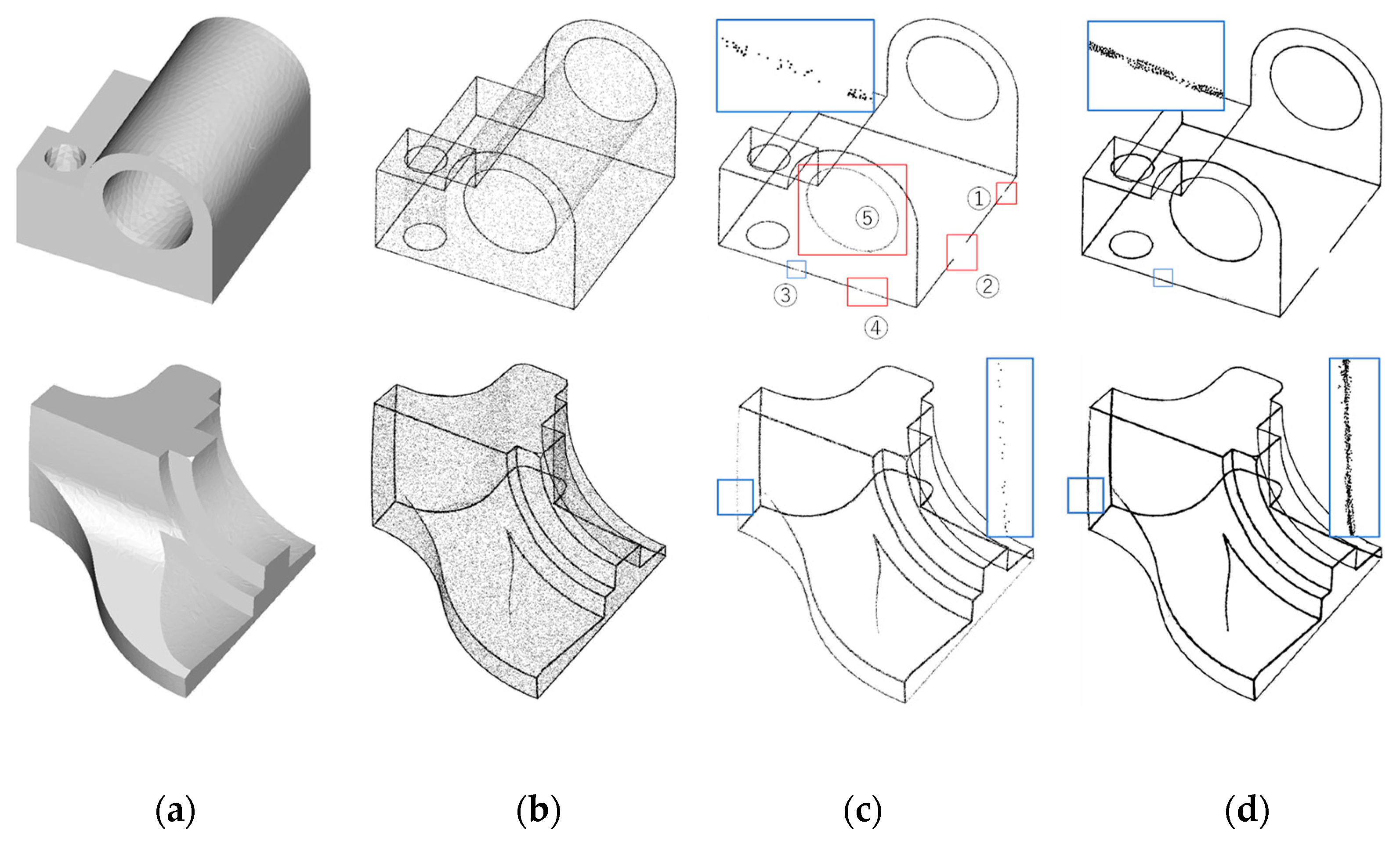
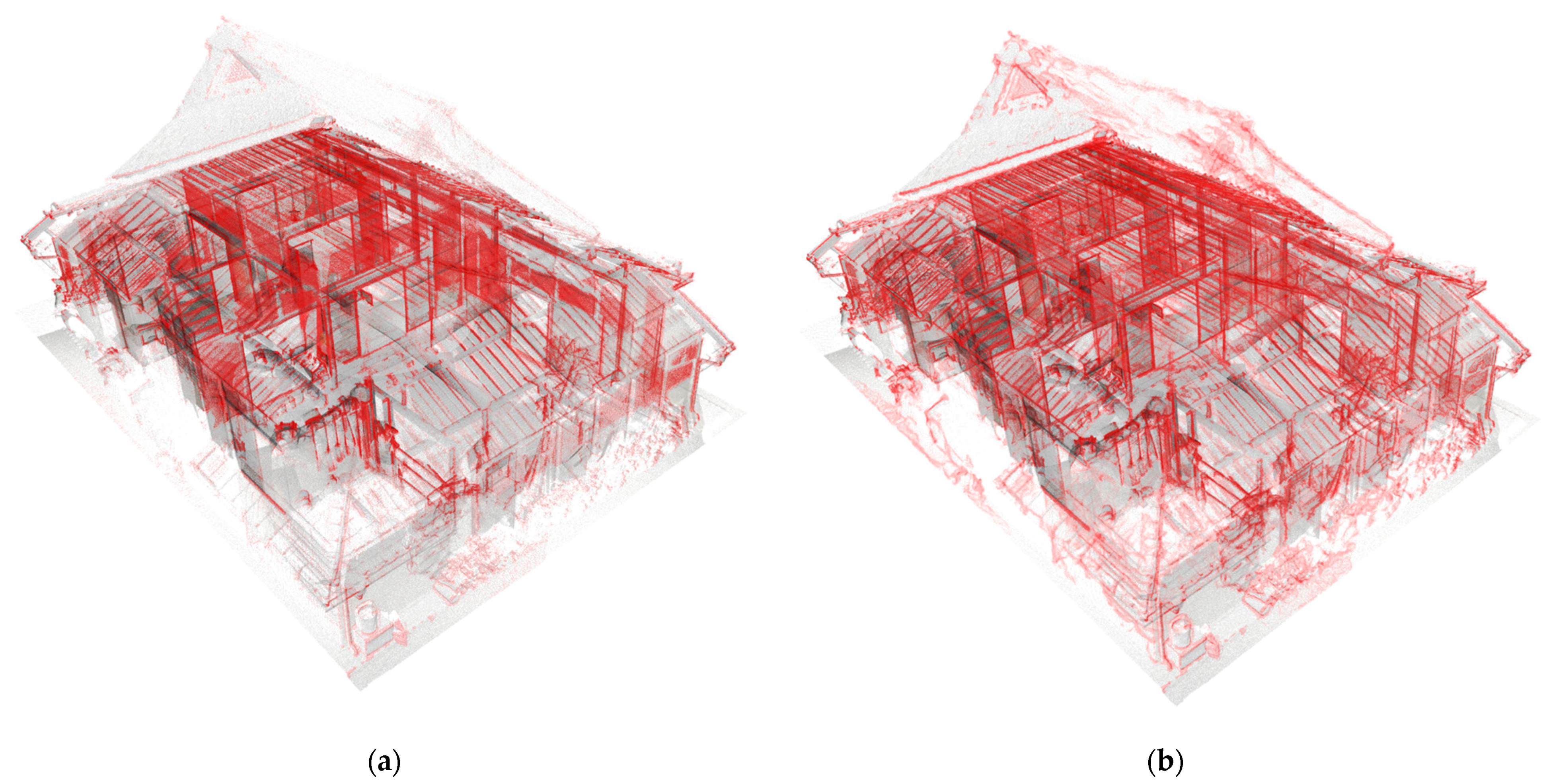
5.3. Application to Real 3D-Scanned Data
5.3.1. Results of Upsampling and Visualization for 3D-Edge Regions
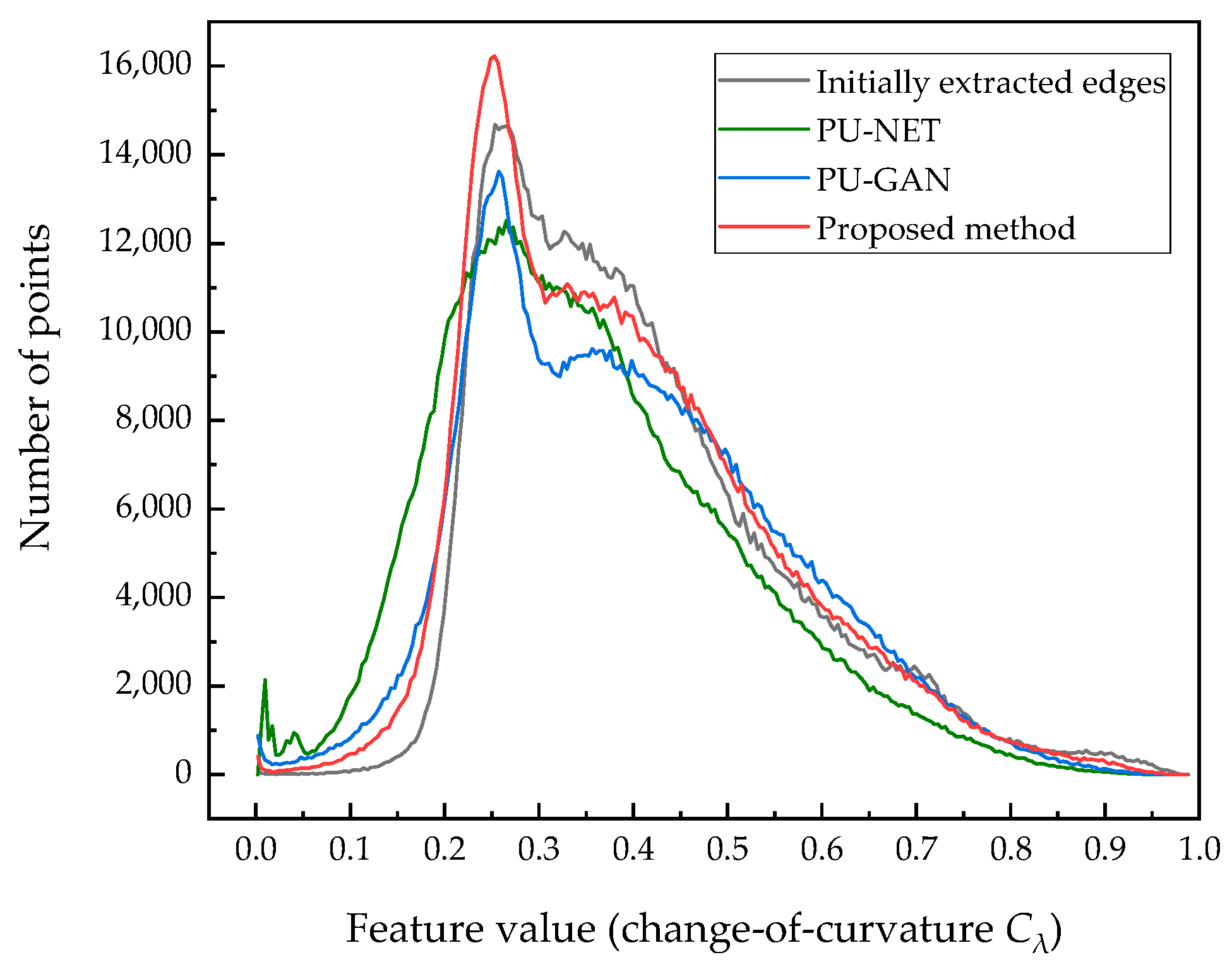
5.3.2. Comparison with Existing Upsampling Networks
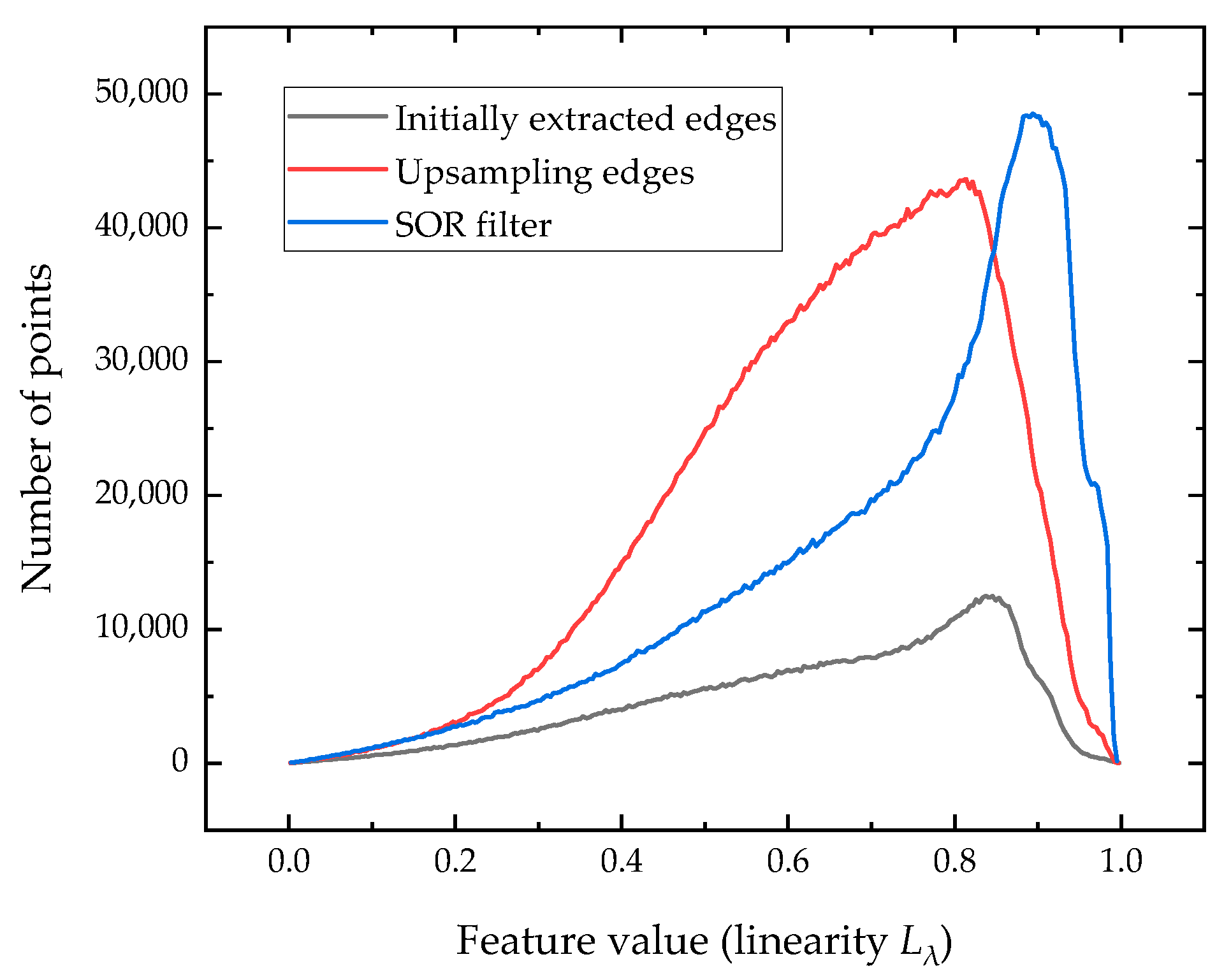
5.4. Use of Statistical Outlier Removal (SOR) Filter for Noisy Data
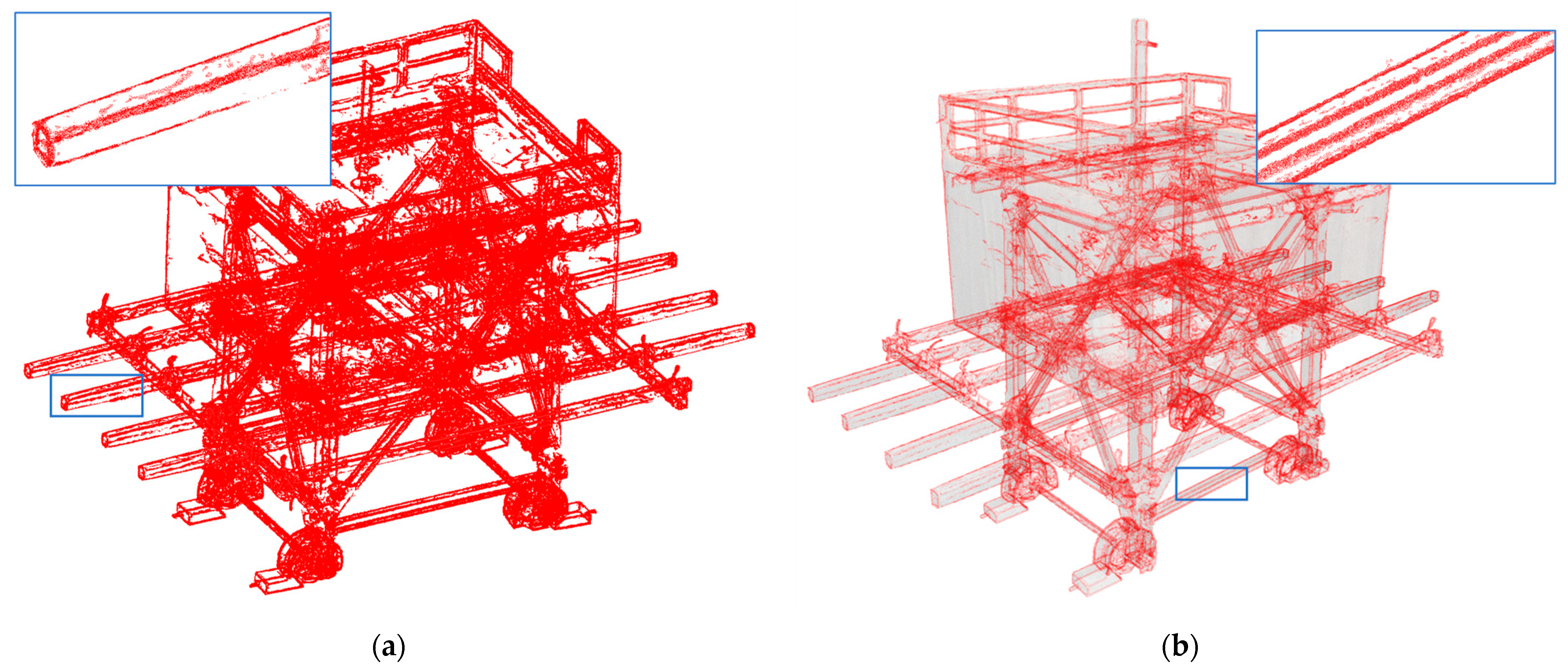
5.5. Visibility Improvement of Soft Edges Using Our Upsampling Network
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanaka, S.; Hasegawa, K.; Okamoto, N.; Umegaki, R.; Wang, S.; Uemura, M.; Okamoto, A.; Koyamada, K. See-Through Imaging of Laser-Scanned 3D Cultural Heritage Objects Based on Stochastic Rendering of Large-Scale Point Clouds. In Proceedings of the ISPRS Annals of Photogrammetry, Remote Sensing & Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; Volume III-3. [Google Scholar]
- Kawakami, K.; Hasegawa, K.; Li, L.; Nagata, H.; Adachi, M.; Yamaguchi, H.; Thufail, F.I.; Riyanto, S.; Tanaka, S.; Brahmantara. Opacity-based edge highlighting for transparent visualization of 3D scanned point clouds. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, 5, 373–380. [Google Scholar] [CrossRef]
- Tanaka, S.; Hasegawa, K.; Shimokubo, Y.; Kaneko, T.; Kawamura, T.; Nakata, S.; Ojima, S.; Sakamoto, N.; Tanaka, H.T.; Koyamada, K. Particle-Based Transparent Rendering of Implicit Surfaces and its Application to Fused Visualization. In Proceedings of the Eurographics Conference on Visualization (EuroVis), Vienna, Austria, 5–8 June 2012. [Google Scholar]
- Uchida, T.; Hasegawa, K.; Li, L.; Adachi, M.; Yamaguchi, H.; Thufail, F.I.; Riyanto, S.; Okamoto, A.; Tanaka, S. Noise-robust transparent visualization of large-scale point clouds acquired by laser scanning. ISPRS J. Photogramm. Remote. Sens. 2020, 161, 124–134. [Google Scholar] [CrossRef]
- Alexa, M.; Behr, J.; Cohen-Or, D.; Fleishman, S.; Levin, D.; Silva, C. Computing and rendering point set surfaces. IEEE Trans. Vis. Comput. Graph. 2003, 9, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Lipman, Y.; Cohen-Or, D.; Levin, D.; Tal-Ezer, H. Parameterization-free projection for geometry reconstruction. ACM Trans. Graph. 2007, 26, 22. [Google Scholar] [CrossRef]
- Huang, H.; Li, D.; Zhang, H.; Ascher, U.; Cohen-Or, D. Consolidation of unorganized point clouds for surface reconstruction. ACM Trans. Graph. 2009, 28, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Tuzel, O. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4490–4499. [Google Scholar]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection From Point Cloud. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 770–779. [Google Scholar]
- Huang, Z.; Yu, Y.; Xu, J.; Ni, F.; Le, X. PF-Net: Point Fractal Network for 3D Point Cloud Completion. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2020; pp. 7659–7667. [Google Scholar]
- Wen, X.; Li, T.; Han, Z.; Liu, Y.-S. Point Cloud Completion by Skip-Attention Network With Hierarchical Folding. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2020; pp. 1936–1945. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 652–660. [Google Scholar]
- Zhang, Y.; Rabbat, M. A Graph-CNN for 3D Point Cloud Classification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 6279–6283. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-Shape Convolutional Neural Network for Point Cloud Analysis. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 8887–8896. [Google Scholar]
- Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 4558–4567. [Google Scholar]
- Wang, W.; Yu, R.; Huang, Q.; Neumann, U. SGPN: Similarity Group Proposal Network for 3D Point Cloud Instance Segmentation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA; pp. 2569–2578. [Google Scholar]
- Yu, L.; Li, X.; Fu, C.-W.; Cohen-Or, D.; Heng, P.A. PU-Net: Point Cloud Upsampling Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 2790–2799. [Google Scholar]
- Yifan, W.; Wu, S.; Huang, H.; Cohen-Or, D.; Sorkine-Hornung, O. Patch-based Progressive 3D Point Set Upsampling. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 5958–5967. [Google Scholar]
- Li, R.; Li, X.; Fu, C.-W.; Cohen-Or, D.; Heng, P.-A. PU-GAN: A Point Cloud Upsampling Adversarial Network. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2019; pp. 7203–7212. [Google Scholar]
- Chang, A.X.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012 2015. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3D ShapeNets: A deep representation for volumetric shapes. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2015; pp. 1912–1920. [Google Scholar]
- West, K.F.; Webb, B.N.; Lersch, J.R.; Pothier, S.; Triscari, J.M.; Iverson, A.E. Context-Driven Automated Target Detection in 3D Data. In Proceedings of the Automatic Target Recognition XIV, Orlando, FL, USA, 21 September 2004. [Google Scholar]
- Rusu, R.B. Semantic 3D Object Maps for Everyday Manipulation in Human Living Environments. KI Künstliche Intell. 2010, 24, 345–348. [Google Scholar] [CrossRef] [Green Version]
- Weinmann, M.; Jutzi, B.; Mallet, C. Semantic 3D scene interpretation: A framework combining optimal neighborhood size selection with relevant features. ISPRS Ann. Photogramm. Remote. Sens. Spat. Inf. Sci. 2014, II-3, 181–188. [Google Scholar] [CrossRef] [Green Version]
- Jutzi, B.; Gross, H. Nearest neighbour classification on laser point clouds to gain object structures from buildings. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 4–7. [Google Scholar]
- Corsini, M.; Cignoni, P.; Scopigno, R. Efficient and Flexible Sampling with Blue Noise Properties of Triangular Meshes. IEEE Trans. Vis. Comput. Graph. 2012, 18, 914–924. [Google Scholar] [CrossRef] [Green Version]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Comput. Vis. Pattern Recognit. 2017, arXiv:1706.02413 2017. [Google Scholar]
- Yu, L.; Li, X.; Fu, C.-W.; Cohen-Or, D.; Heng, P.A. EC-Net: An Edge-Aware Point Set Consolidation Network. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2018; pp. 398–414. [Google Scholar]
- Chen, N.; Liu, L.; Cui, Z.; Chen, R.; Ceylan, D.; Tu, C.; Wang, W. Unsupervised Learning of Intrinsic Structural Representation Points. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2020; pp. 9118–9127. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Achlioptas, P.; Diamanti, O.; Mitliagkas, I.; Guibas, L. Learning Representations and Generative Models for 3d Point Clouds. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 40–49. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2018; pp. 206–215. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. Pcn: Point Completion Network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 2463–2471. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Paul Smolley, S. Least Squares Generative Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 2794–2802. [Google Scholar]
- Visionair. Available online: http://www.infra-visionair.eu (accessed on 21 March 2021).
- Kingma, D.P.; Ba, J. Adam: A method for Stochastic Optimization. In Proceedings of the International Conference Learn Represent (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- Berger, M.; Levine, J.A.; Nonato, L.G.; Taubin, G.; Silva, C.T. A benchmark for surface reconstruction. ACM Trans. Graph. 2013, 32, 1–17. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef] [Green Version]
- ShapeNetCore. Available online: https://shapenet.org (accessed on 4 June 2021).
- Rusu, R.B.; Cousins, S. 3d is Here: Point Cloud Library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Li, W.; Shigeta, K.; Hasegawa, K.; Li, L.; Yano, K.; Adachi, M.; Tanaka, S. Transparent Collision Visualization of Point Clouds Acquired by Laser Scanning. ISPRS Int. J. Geo-Inf. 2019, 8, 425. [Google Scholar] [CrossRef] [Green Version]





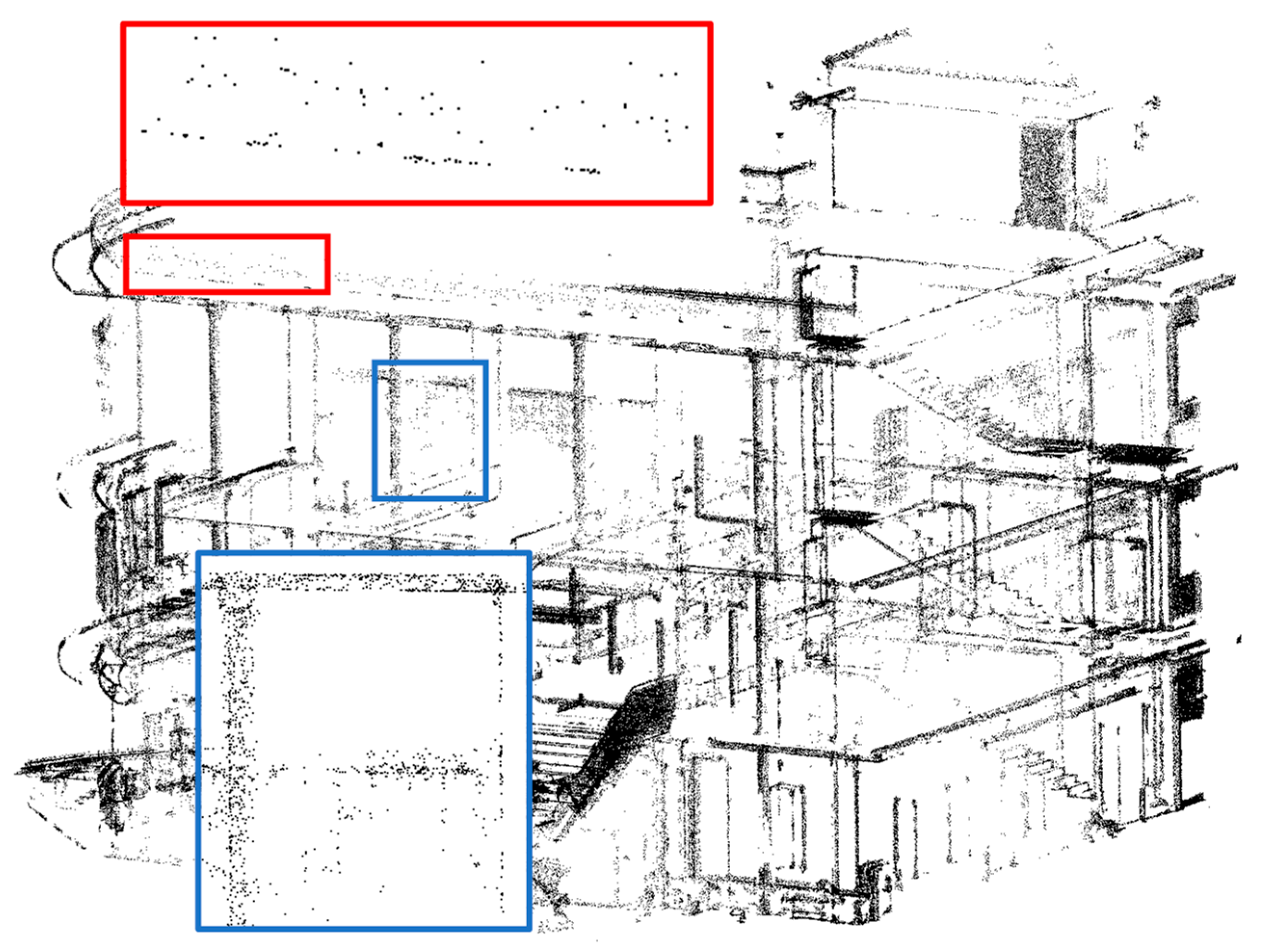
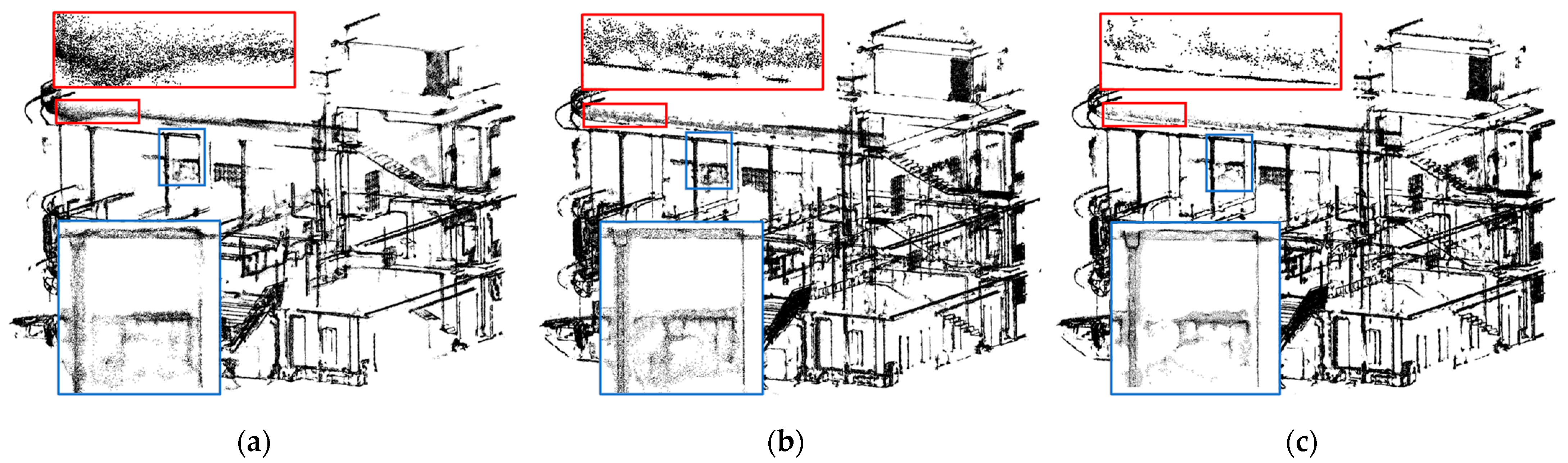

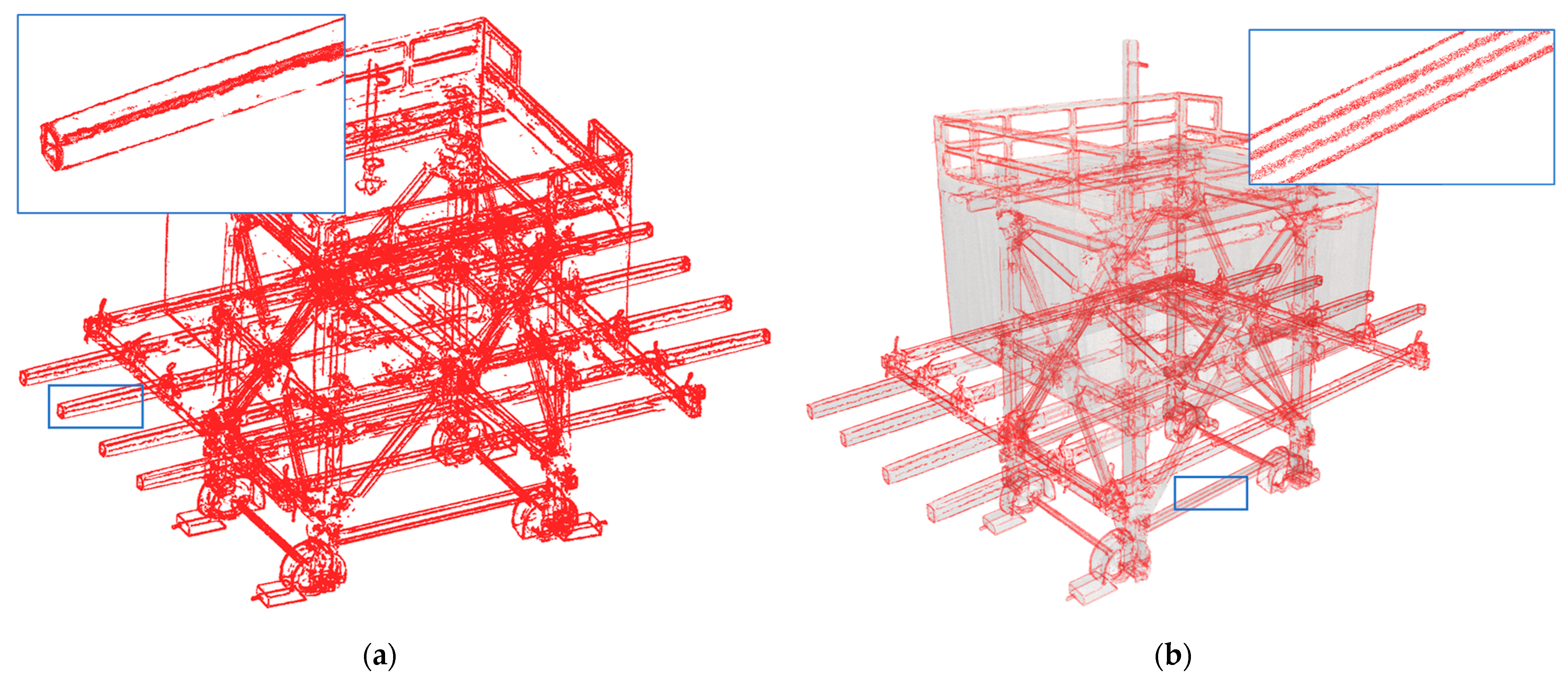


| Objects | Scale [m] | Data | Number of Points | |
|---|---|---|---|---|
| Joint | Original point cloud | 50,000 | 1.55 | |
| Extracted edges | 2283 | 1.41 | ||
| Modified edges | 1072 | 1.19 | ||
| Upsampling result | 4290 | 2.99 | ||
| Fandisk | Original point cloud | 50,000 | 2.05 | |
| Extracted edges | 2518 | 1.95 | ||
| Modified edges | 1441 | 1.62 | ||
| Upsampling result | 5764 | 2.69 |
| Objects | Methods | Hausdorff Distance | ||
|---|---|---|---|---|
| Block | PU-NET | 65.26% | 3.19 | 0.31 |
| PU-GAN | 58.53% | 3.42 | 0.32 | |
| Proposed method | 82.37% | 1.63 | 0.29 | |
| Cover rear | PU-NET | 62.62% | 1.51 | 0.72 |
| PU-GAN | 53.77% | 1.71 | 0.72 | |
| Proposed method | 79.83% | 1.15 | 0.67 |
| Data | Scale [m] | Number of Points | |
|---|---|---|---|
| Original point cloud | 24,074,424 | 8.46 | |
| Initially extracted edges | 3,821,874 | 3.33 | |
| Upsampling edges | 15,287,496 | 6.34 |
| Data | Scale [m] | Number of Points | |
|---|---|---|---|
| Original point cloud | 5,234,550 | 5.21 | |
| Initially extracted edges | 1,211,452 | 4.38 | |
| Upsampling edges | 4,845,808 | 4.84 |
| Hausdorff Distance | |||
|---|---|---|---|
| PU-NET | 75.00% | 4.42 | 0.89 |
| PU-GAN | 84.02% | 3.53 | 1.44 |
| Proposed method | 92.71% | 2.65 | 0.64 |
| Number of Edge Points | |||
|---|---|---|---|
| Initially extracted edges | 1,200,278 | 95.32% | 0.64 |
| Upsampling edges | 4,801,112 | 95.67% | 0.66 |
| SOR filter | 3,661,036 | 97.17% | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Hasegawa, K.; Li, L.; Tsukamoto, A.; Tanaka, S. Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization. Remote Sens. 2021, 13, 2526. https://doi.org/10.3390/rs13132526
Li W, Hasegawa K, Li L, Tsukamoto A, Tanaka S. Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization. Remote Sensing. 2021; 13(13):2526. https://doi.org/10.3390/rs13132526
Chicago/Turabian StyleLi, Weite, Kyoko Hasegawa, Liang Li, Akihiro Tsukamoto, and Satoshi Tanaka. 2021. "Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization" Remote Sensing 13, no. 13: 2526. https://doi.org/10.3390/rs13132526
APA StyleLi, W., Hasegawa, K., Li, L., Tsukamoto, A., & Tanaka, S. (2021). Deep Learning-Based Point Upsampling for Edge Enhancement of 3D-Scanned Data and Its Application to Transparent Visualization. Remote Sensing, 13(13), 2526. https://doi.org/10.3390/rs13132526