1. Introduction
With the development of remote sensing technology, hyperspectral images (HSIs) have been of wide concern and gradually applied in many fields [
1,
2]. In the field of HSIs, as a fundamental task, HSI classification is a task of assigning category labels to each pixel in the HSI and has attracted more and more attention.
An HSI usually contains hundreds of spectral bands, so it has abundant spectral information in addition to the usual spatial information of the image. In the early stages of HSI classification, there were many works based on spectral or spatial characteristics [
3]. Support vector machines (SVMs) were used to address the problem by using spectral information [
4]. In the past ten years, many works were based on spectral–spatial feature learning for HSI classification [
5,
6]. The performance of sparse representation was improved by using the spatial neighborhood information of samples [
7]. In [
8], principal component analysis (PCA) was used for unsupervised extraction of spectral features and data dimensionality reduction, and edge-preserving features were obtained by edge-preserving filtering, and the resulting features were classified by an SVM classifier. A hierarchical subspace and ensemble learning algorithm was proposed to solve the problem of hyperspectral image classification, in which spectral–spatial features were also applied [
9]. Although most of these methods based on spectral–spatial features have achieved better results than those based on spectral information alone, they usually rely on hand-crafted or shallow-based descriptors. Therefore, the robustness and classification accuracy of these traditional methods still need to be improved.
In recent years, deep learning has been widely adopted in HSI classification because of its advantage of automatically learning discrimination features from raw data [
10]. Autoencoders (AEs) were applied to extract the deep features of the image in an unsupervised manner [
11,
12]. In [
13], the spectral information of each pixel was regarded as a sequence, and sequence features were extracted by recurrent neural networks (RNNs) for HSI classification. In [
14], AE and RNN were combined to construct a new network for HSI classification.
Convolutional neural networks (CNNs) have been widely used in the field of HSI classification because of the advantages of spatial extraction and weight sharing mechanisms [
15,
16]. In [
17], 1D CNNs were employed to extract the spectral features for HSI classification. The spectral images in HSIs were treated as the channels of conventional images, and then 2D CNNs were designed to extract the spatial features for HSI classification [
18]. A 3D CNN that combined spectral and spatial information was used for HSI classification [
19]. A spectral–spatial residual network (SSRN) adopted a 3D CNN and residual connections to improve the classification accuracy [
20]. Batch normalization (BN) was used to regularize the training process in SSRN, making the training processing of the deep learning model more efficient. A 3D CNN has advantages over a 1D CNN and a 2D CNN in simultaneously extracting spectral and spatial features, while it requires more computation. To reduce the computational burden of 3D CNNs, 3D and 2D CNNs were mixed in a hybrid network (HybridSN) for HSI classification [
21]. Overall, deep spectral–spatial feature learning has become a new trend in the classification of HSIs. Among these deep learning methods, it is difficult to achieve satisfactory results with the existing unsupervised network methods. Although these deep learning methods trained in a supervised manner can obtain encouraging results, they usually require sufficient labelled samples for training. However, obtaining labelled samples of hyperspectral images often consumes a lot of human and material resources. Therefore, training a deep learning model for hyperspectral image classification with limited samples is still a challenge.
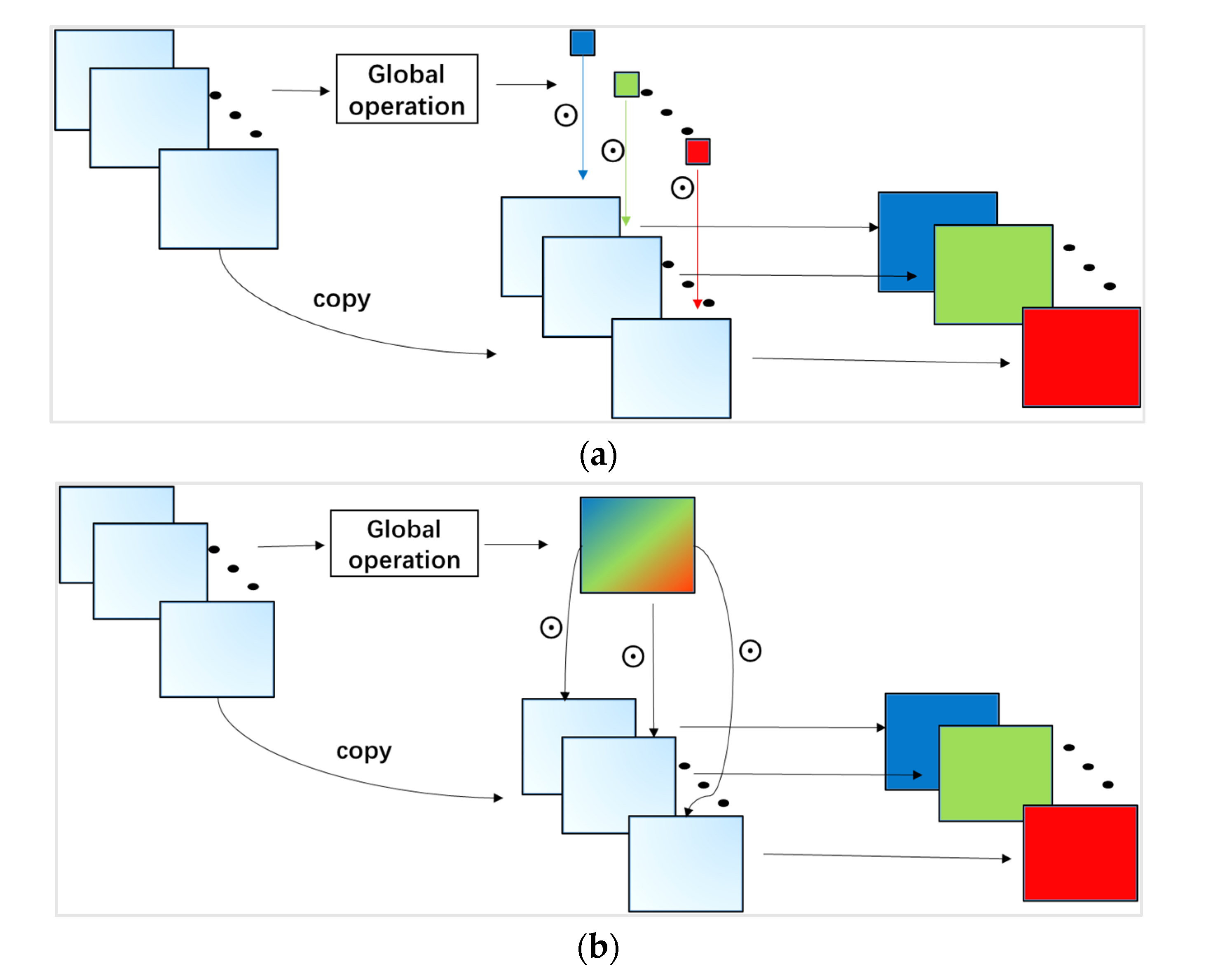
Recently, some deep learning methods have introduced the attention mechanism to alleviate these problems in HSI classification [
22,
23]. The attention mechanism is inspired by the human visual mechanism [
24,
25]. When people observe a scene, they always pay more attention to the area of interest to obtain more meaningful information. In [
26], the global pooling operations in the spectral dimension and spatial dimension were used to assign the attention to the interesting features. In [
27], the spatial correlation and spectral band correlation were used to compute the attention weights of feature learning. In [
28], a cascaded dual-scale crossover network (CDSCN) was proposed for HSI classification, which can obtain the parts of interest in the images through the multiplication of dual branch features. These methods use different ways to obtain attention features, thereby improving the classification performance. In addition to these attention methods, there may be other ways to extract attention features.
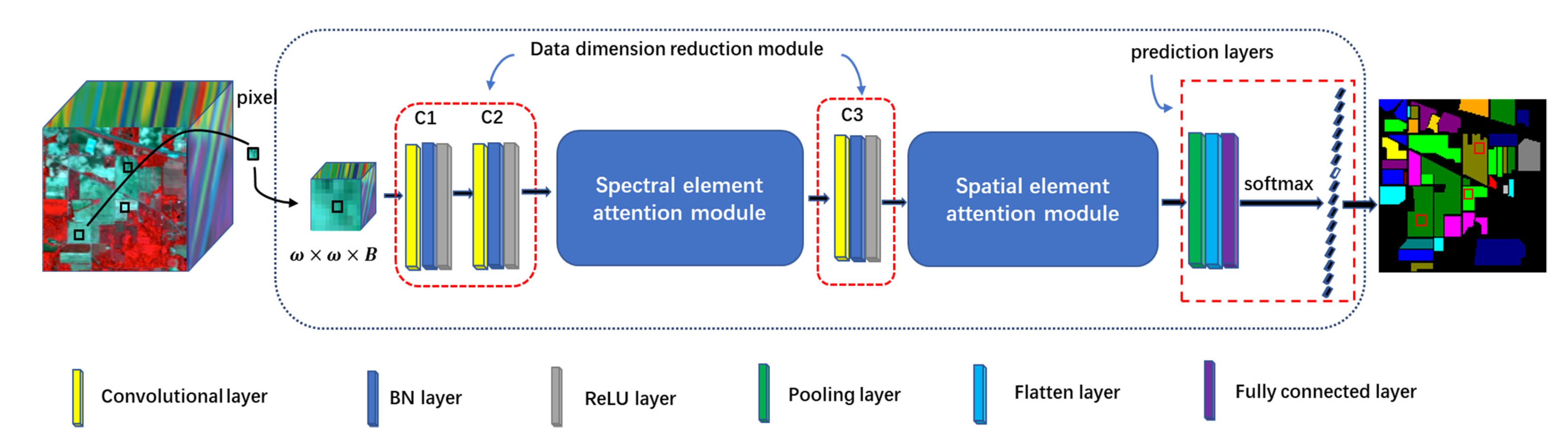
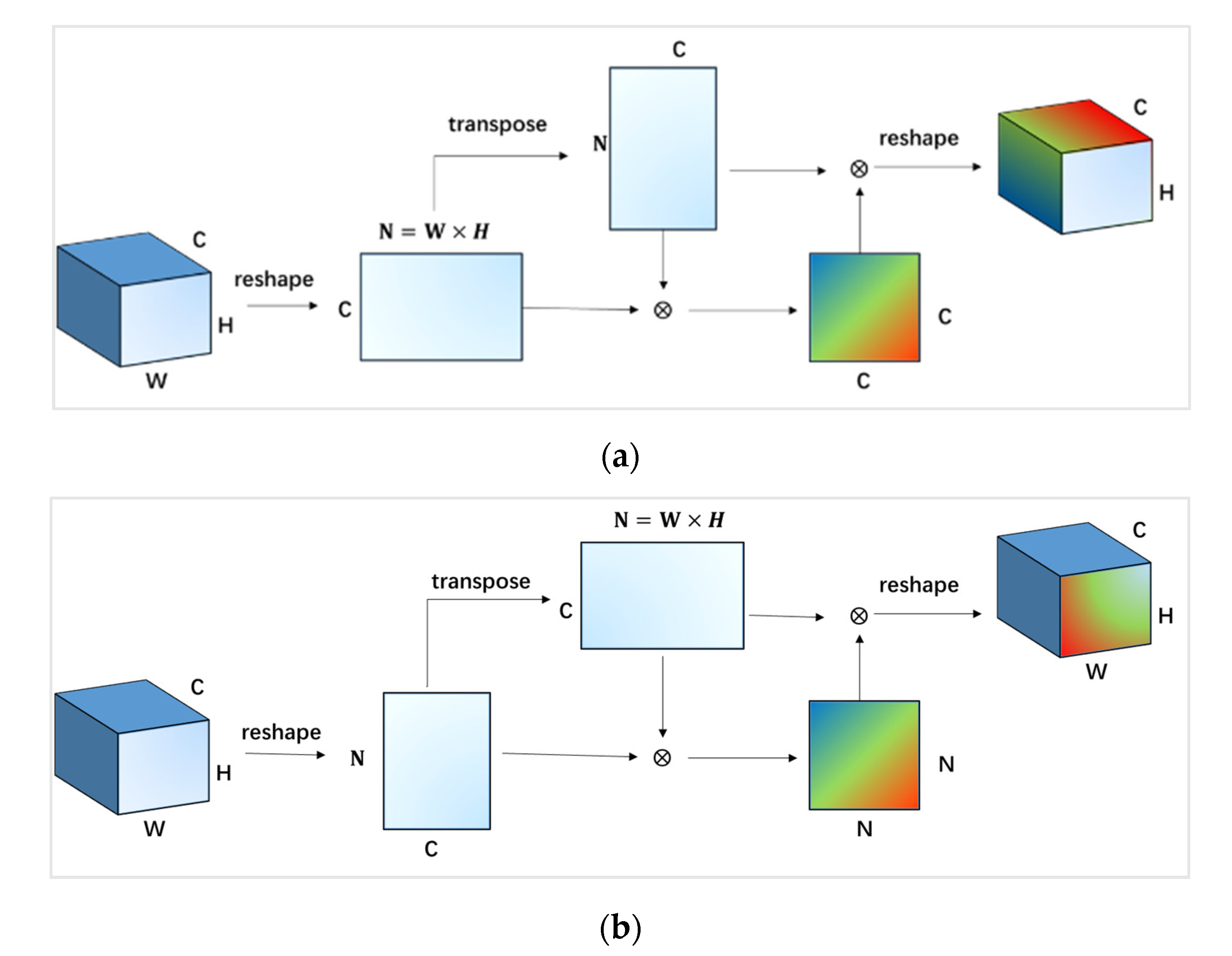
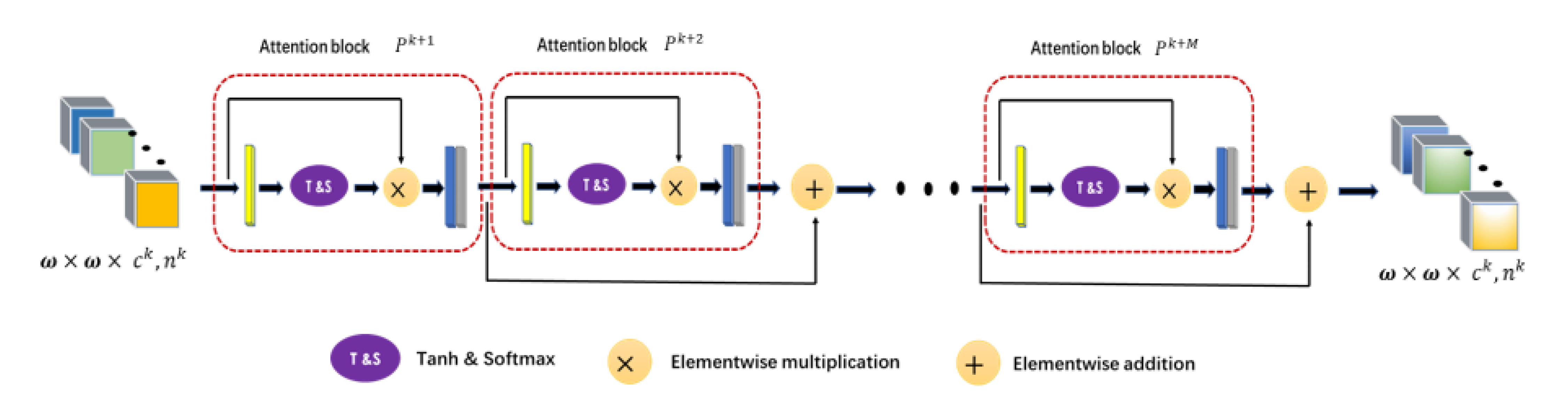
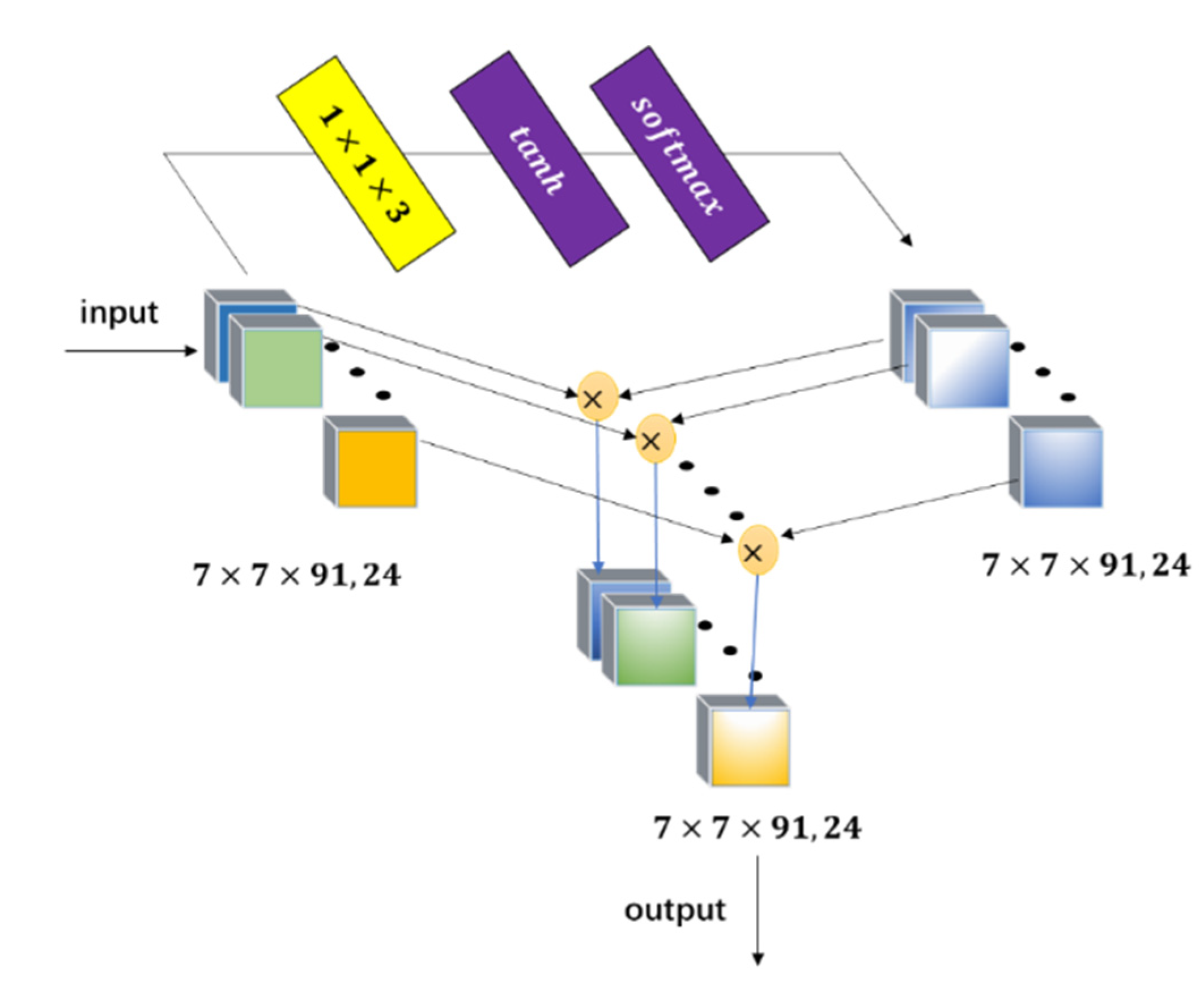
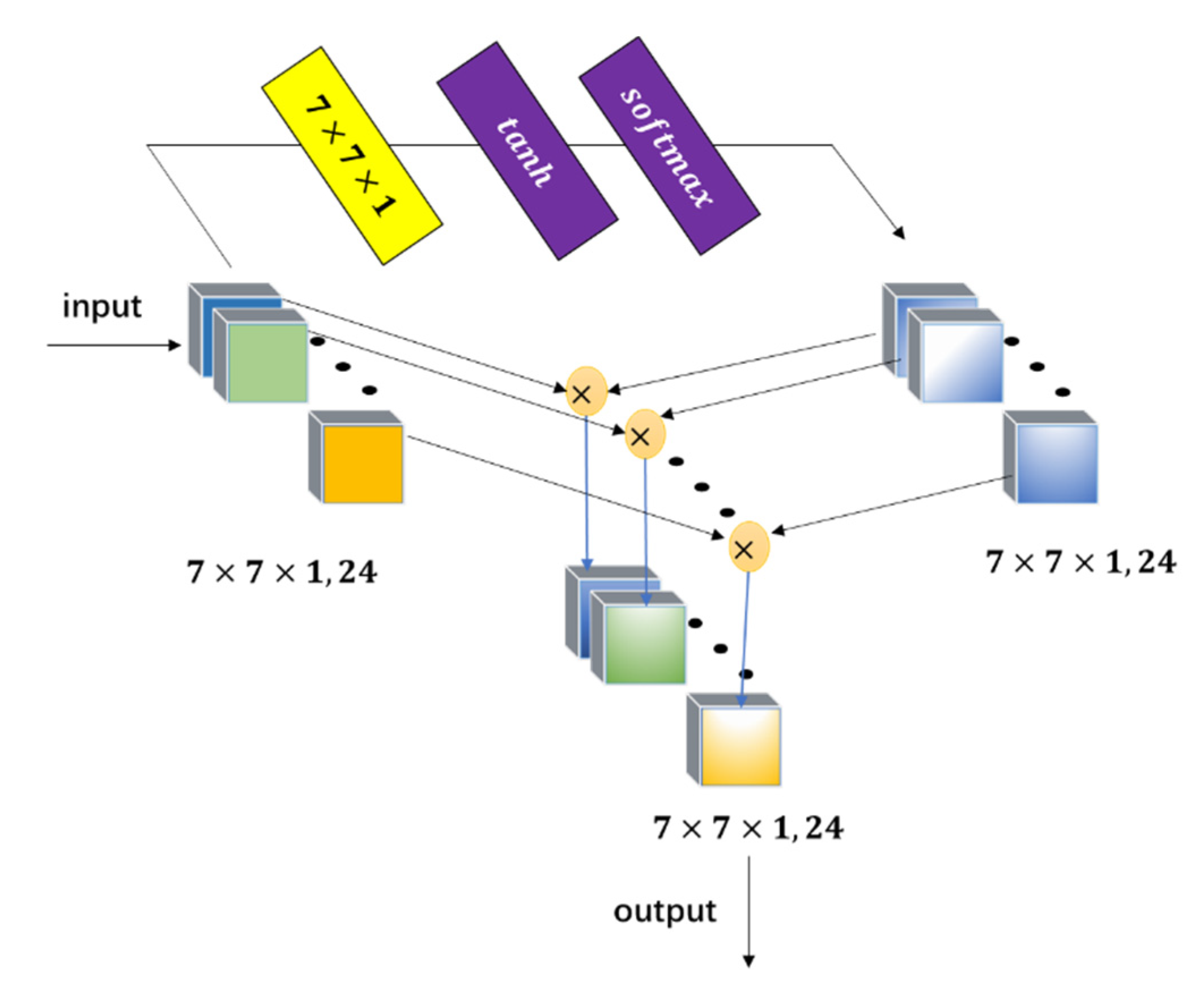
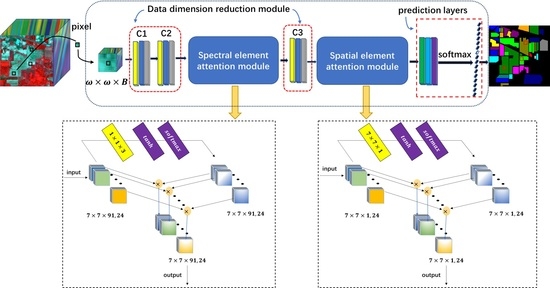
In this paper, a 3D cascaded spectral–spatial element attention network (3D-CSSEAN) is proposed for HSI classification. In 3D-CSSEAN, an element attention mechanism is used to extract spectral and spatial attention features, as shown in
Figure 1. This method is different from the attention method mentioned above. It uses several activation functions to assign weights to all elements in the 3D feature tensor and obtains attention features through elementwise multiplication. The overall framework of 3D-CSSEAN is shown in
Figure 2. It first uses convolution operations for data dimensionality reduction and shallow feature extraction. Then two attention modules are used to extract attention features. The following pooling operation is used to reduce the dimensionality of features. Finally, a fully connected layer and softmax activation layer are used to generate classification results. The main contributions of this work can be summarized in the following three aspects.
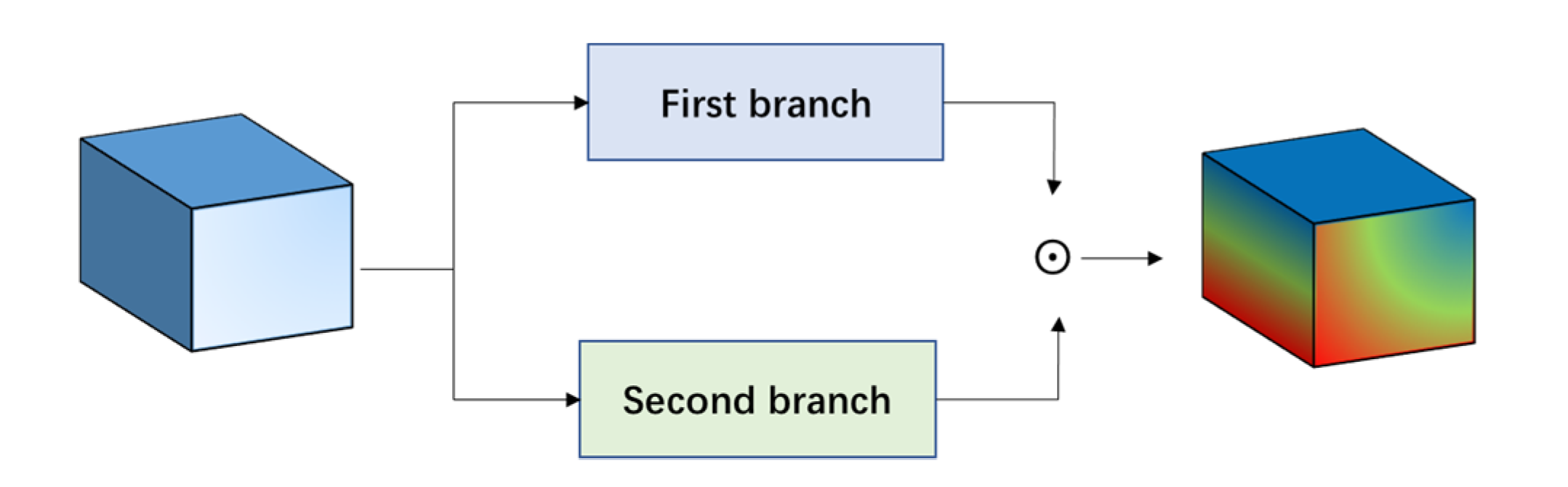
First, a cascade element attention network is proposed to extract meaningful features, which can give different weight responses to each element in the 3D data. Two element attention modules are employed to enhance the important spectral features and strengthen the interesting spatial features, respectively.
Second, the proposed element attention modules are implemented through several simple activation operations and elementwise multiplication operations. Therefore, the implementation of the attention module does not add too many parameters, which makes the network model suitable for small sample learning.
Third, the proposed attention modules can be easily plug and play, and can be achievable based on a single branch, so it is more time-efficient.
The rest of this paper is organized as follows: In
Section 2, the existing attention methods for HSI classification are discussed. The proposed 3D-CSSEAN model is described in detail in
Section 3. Experimental results and analysis are presented in
Section 4. In
Section 5, the influence of attention block numbers and different training sample numbers on the model are discussed. Finally, conclusions are summarized in
Section 6.
4. Experimental Results
4.1. Experimental Setup
This section evaluates the performance of our method on three public hyperspectral image data sets. The Indian Pines data set includes 16 vegetation classes and has 224 bands from 400 to 2500 nm. After removing water absorption bands, it had 145 × 145 pixels with 200 bands. The Kennedy Space Center data set includes 13 classes and has 224 bands from 400 to 2500 nm. After removing water absorption bands, it had 512 × 453 pixels with 176 bands. The Salinas Scene data set includes 16 classes and has 224 bands from 360 to 2500 nm. After removing water absorption bands, it had 512 × 217 pixels with 204 bands.
In the Indian Pines data set, the labeled samples were unbalanced. In the Kennedy Space Center data set, the number of labeled samples was small. Compared with the Indian Pines and Kennedy Space Center, the labeled samples in the Salinas Scene data set were larger and more balanced. Therefore, these three data sets represented three different situations. The performance of the proposed method was verified in three different cases, which could better demonstrate the generalization ability of the method. For the Indian Pines and Kennedy Space Center data sets, about 5%, 5%, and 90% of the labeled samples were randomly select as training, validation, and testing data sets, respectively. For the Salinas Scene data set, due to the large number of overall labeled samples, a smaller training ratio was set. The ratio was about 1%:1%:98% for the Salinas Scene data set. Moreover, all three data sets were normalized to a Gaussian distribution with zero mean and unit variance. The overall accuracy (OA%), average accuracy (AA%), and Kappa coefficient () were used to evaluate the classification performance of the proposed methods. The higher these index values, the better the classification performance of the method. Each method was randomly run ten times, and the mean and standard deviation of the classification index were reported. All the experiments were implemented with a GTX 2080Ti GPU, 16 GB of RAM, Python 3.6, TensorFlow 1.10, and the Keras 2.1.0 framework.
To express more clearly,
Table 1 shows the shape of input data and output data and the specific parameters of the convolutional operation in the 3D-CSSEAN for the Indian Pines data set. The settings of Kennedy Space Center and Salinas Scene data sets are same as Indian Pines except for the band number of the input data.
and
in
Table 1 indicate the convolution operation in the spectral element attention module and spatial element attention module, respectively. For each convolutional layer,
were set to be 24 for each convolutional layer, and experiments show that the change of
in a small range had little impact on the result.
4.2. Comparison and Analysis of Experimental Results
To evaluate the superiority and effectiveness of the proposed 3D-CSSEAN model, some machine learning and deep learning classification methods were compared with it. These methods included a traditional machine learning method SVM, state-of-the-art 3D deep learning models such as SSRN [
20] and HybridSN [
21], and the latest attention networks, such as CDSCN [
28] and MAFN [
32]. SVM was implemented by scikit-learn tools of the machine learning. The Radial Basis Function (RBF) was selected as the kernel function on the three data sets. The grid search method was used to determine the best values of parameters
and
. Other comparison methods were implemented through code published in their papers [
20,
21,
28,
32]. For fairness of comparison, the input image patch size was set to
for all methods except HybridSN, where
was the band number of the HSI. For HybridSN, in order to make the network work without changing the network structure, the input image patch size was set to
, which was the closest parameter setting. For SVM and HybridSN, the number of PCA principal components was set to 30, which is the same as in the literature on HybridSN [
21].
Classification results of the different methods on testing data of the three data set are reported in
Table 2,
Table 3 and
Table 4. As shown, 3D-CSSEAN achieved the best results on most indicators compared with the other methods. In our cases, the classification performances of all deep learning methods were better than those of SVM, which indicates that these deep learning models are generally superior to the traditional machine learning method in HSI classification. On the Indian Pines data set, the 3D-CSSEAN, MAFN, and CDSCN achieved better results than other methods. These results show that in the case of imbalanced categories, these attention models pay more attention to meaningful features, so they achieved better results. Compared with the two other attention methods, the 3D-CSSEAN increased the score at least 0.89%, 1.52%, and 1.01% in the OA, AA, and Kappa, respectively. Moreover, the AA of the 3D-CSSEAN was 0.89% higher than the best result of the other compared methods. These results indicate that the proposed method has good stability and robustness under the condition of unbalanced samples.
On the Kennedy Space Center data set, the 3D-CSSEAN, SSRN, CDSCN, and MAFN achieved at least 22% improvement compared to HybridSN and SVM. The reasons for this may be that HybridSN and SVM use PCA for dimension reduction, while the 3D-CSSEAN, SSRN, CDSCN, and MAFN are end-to-end network structures. The data dimension reduction module in the end-to-end is implemented in a supervised way, so the effect is better than the unsupervised way of PCA. Compared with SSRN and CDSCN, the 3D-CSSEAN achieved 2% and 1.75% improvement on OA, respectively. As for the latest MAFN, the 3D-CSSEAN also achieved comparable results. MAFN was slightly better than the 3D-CSSEAN on AA. The possible reason is that the spatial distribution of some categories in the Kennedy Space Center data set was relatively scattered. MAFN uses the correlation-based attention method to extract spatial features. Correlation-based methods may better capture the connections between scattered samples of these categories, so as to obtain more ideal results. The increase in accuracy of these categories can improve AA. On the Salinas Scene data set, all methods achieved higher than the 94% overall accuracy, while the 3D-CSSEAN was 0.42, 0.47, and 0.55 higher than the best result of the other methods on OA, Kappa, and AA, respectively.
In general, the three attention methods, CDSCN, MAFN and 3D-CSSEAN, achieved good results, indicating that the attention features extracted by them are beneficial to classification. These results indicated that the proposed element attention method can also effectively improve the classification performance. According to the results of the three data sets, the 3D-CSSEAN has good generalization ability on different data sets.
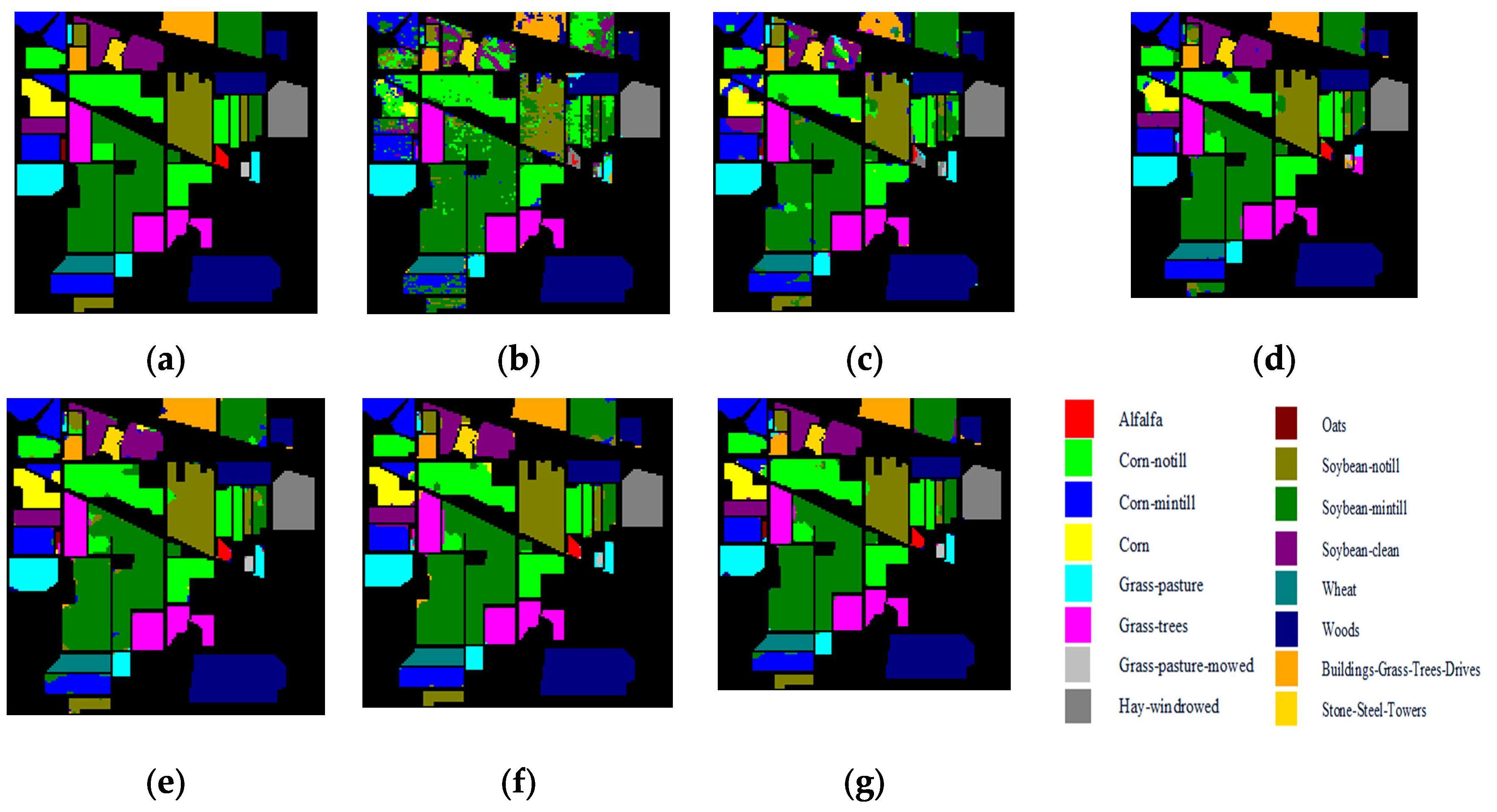
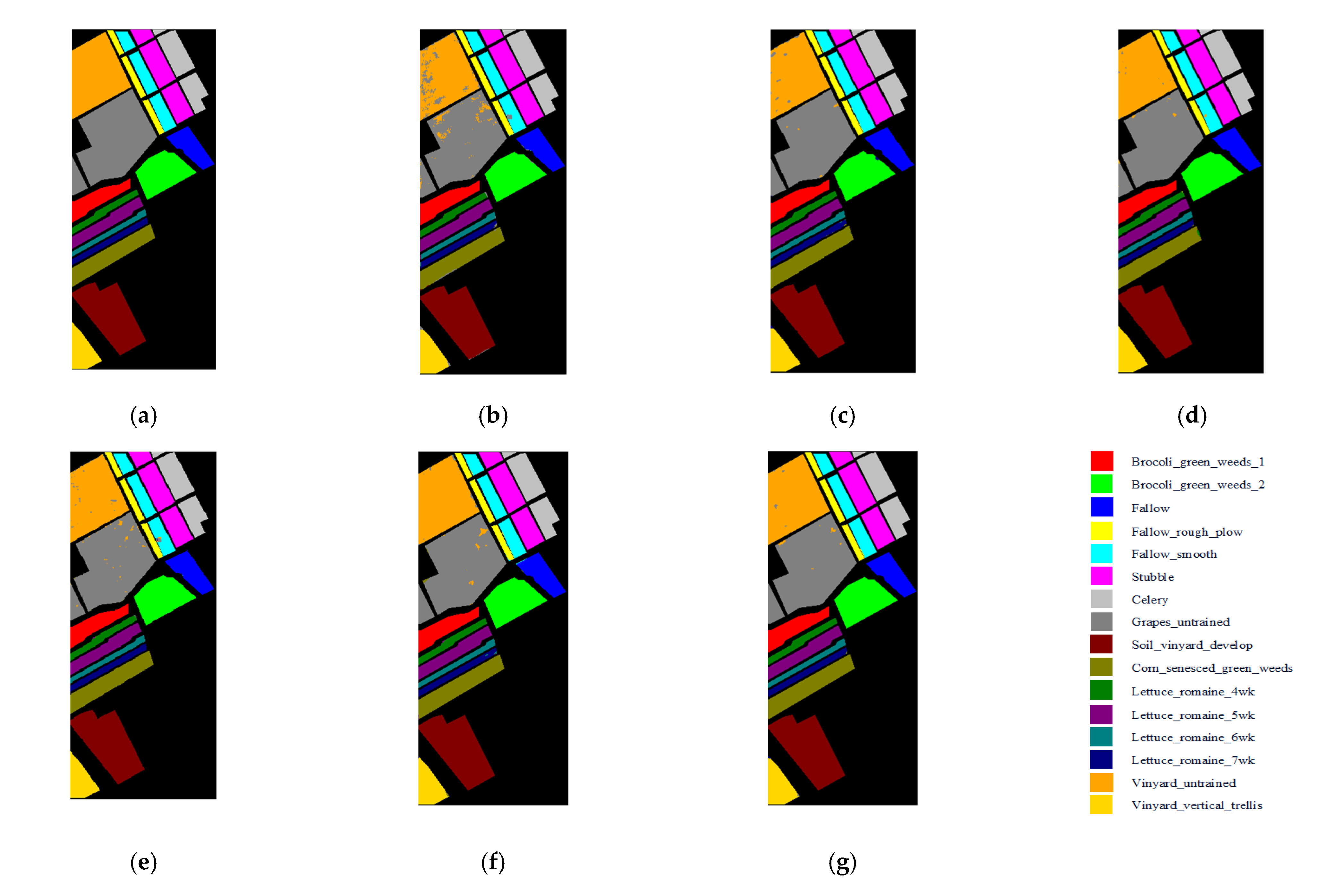
The classification maps of the five methods and the corresponding ground truth maps of the three data sets are shown in
Figure 12,
Figure 13 and
Figure 14. It can be clearly seen from these results that the higher the classification accuracy, the better the continuity of the classification map. For the Indian Pines data set, there were obvious noise and discontinuous regions, as shown in
Figure 12b, while the classification effect of the 3D-CSSEAN was relatively good. As shown in
Figure 13, although there are very few labeled samples in the Kennedy Space Center data set, the 3D-CSSEAN still achieved good results. On the contrary, many obvious misclassified pixels can be seen in
Figure 13b,c. All methods achieved over 94% overall accuracy on Salinas Scene data sets; however, there were still significant differences, which can be observed in
Figure 14. It can be seen from
Figure 14g that the 3D-CSSEAN still performed well at the edge of the category and the easily confused area.
Training and testing times provide a direct measure of the computational efficiency of HSI classification methods. In
Table 5, the training time and the test time on the test data of different methods are shown. As presented in
Table 5, because their inputs were the data under dimension reduction through PCA, the training time of SVM and HybridSN was significantly lower than that of other methods. Additionally, the time efficiency of the 3D-CSSEAN was higher than that of SSRN, CDSCN, and MAFN. As for MAFN, this may be because it uses a mixture of global operation-based and correlation-based methods to extract attention features, so it is relatively time-consuming. In particular, the training and testing time of the 3D-CSSEAN was about half that of the CDSCN method. The possible reason for this is that CDSCN adopts the dual branches mode, while the 3D-CSSEAN adopts the single branch mode, and thus it can save about half of the running time.
4.3. Ablation Studies
Three ablation experiments were conducted to analyze the contribution of different attention modules to HSI classification. The results are shown in
Table 6. NONE means the 3D-CSSEAN without spectral and spatial attention module. SPE-EAN indicates the 3D-CSSEAN only with the spectral attention module, and SPA-EAN indicates the 3D-CSSEAN only with the spatial attention module. The experimental results showed that any kind of attention module is helpful for classification. The role of the spatial attention module is more obvious than that of the spectral attention module. In terms of OA indicators, SPA-EAN increased 1.25%, 0.87%, and 1.06% more than SPE-EAN on Indian Pines, Kennedy Space Center, and Salinas Scene data sets, respectively. These results suggest that the spatial element attention module is more conducive to acquiring discriminative features for classification. The OA obtained by the 3D-CSSEAN had obvious improvement compared with the module without spectral–spatial attention. The OA of the 3D-CSSEAN was 3.17%, 3.66%, and 1.99% higher than without attention modules on Indian Pines, Kennedy Space Center, and Salinas Scene data sets, respectively. It can be seen from the results of ablation experiments that the proposed cascaded spectral–spatial element attention module can obtain more meaningful spectral and spatial features, thereby improving the final classification results.
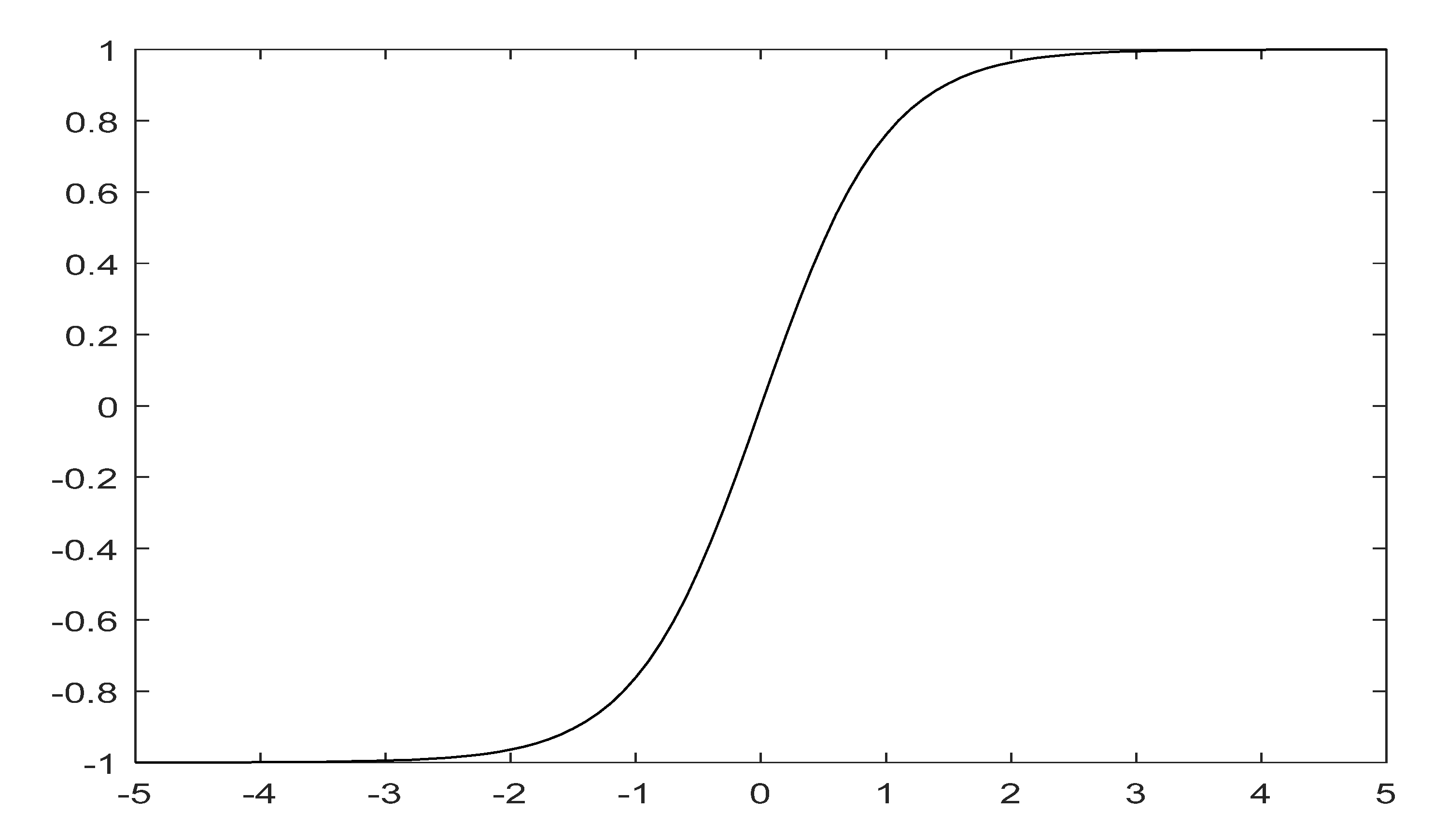
To verify the contribution of
activation function to the classification task, a series of experiments was conducted on the three data sets. Experiment results are shown in
Table 7. As can be seen from
Table 7, AA, Kappa, and OA were all improved on the three data sets by using the
function. Compared with the model without
, the OA score’s enhancements obtained by the 3D-CSSEAN with
were 0.56% (Indian Pines), 0.49% (Kennedy Space Center), and 0.12% (Salinas Scene). The AA score’s increases were 0.49% (Indian Pines), 0.82% (Kennedy Space Center), and 0.04% (Salinas Scene). The Kappa coefficient’s improvements were 0.64% (Indian Pines), 0.55% (Kennedy Space Center), and 0.14% (Salinas Scene). These results indicate that the
function is beneficial to enhance the separability of features and improve the classification performance. In addition, the standard deviation of all the results also decreased through using the
function. This also shows that the stability of the model is improved by using the
function.
5. Discussion
5.1. Influence of the Attention Block Number
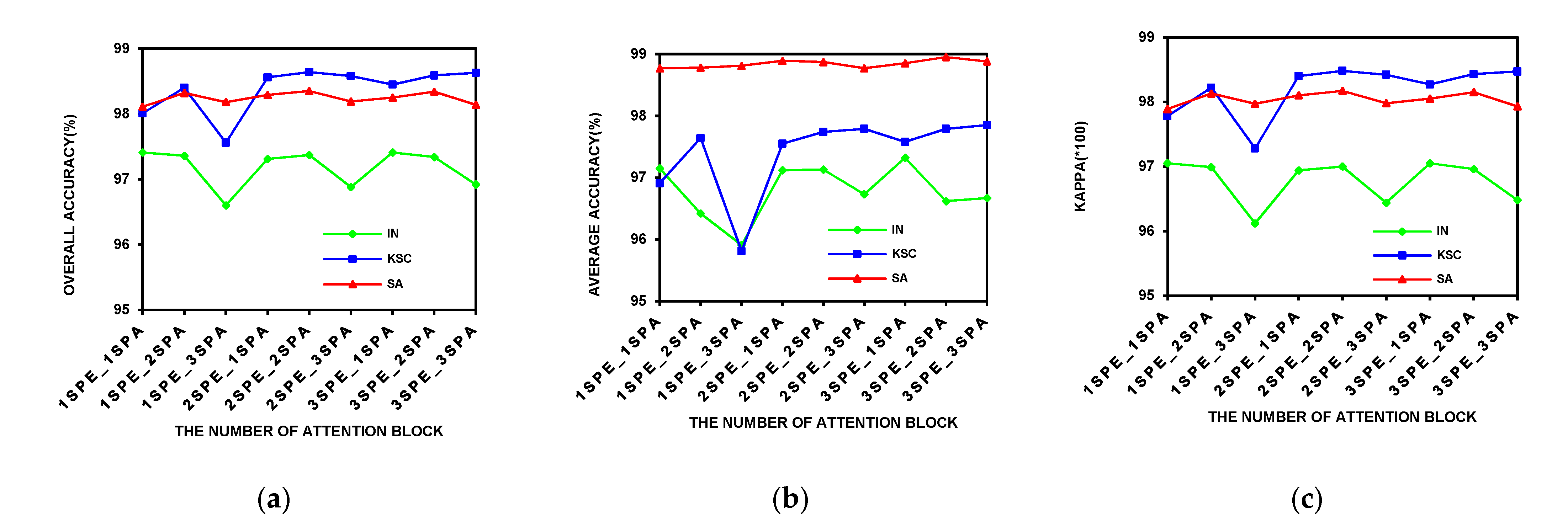
On three public data sets, the influence of the attention block number on the classification performance was analyzed. The experimental results are shown in
Figure 15. In the figure,
of the horizontal axis represents
attention blocks in the spectral element attention module and
attention blocks in the spatial element attention module.
Figure 15a–c, respectively, show the influence of the attention block number on overall accuracy, average accuracy, and Kappa coefficient. As can be seen from the figure, on the Salinas Scene data set, the number of attention blocks had little effect on the results. Particularly, the model with
achieved good performance of OA at over 98%, indicating that the network structure with only one spectral element attention block cascading to one spatial element attention block extracted enough features for the improvement of the classification performance.
On the Indian Pines and Kennedy Space Center data sets, when the number of the spectral attention block was 1, three indicators all fluctuated greatly with the increase of spatial attention modules. In the case of , all the indicators were significantly reduced. This result shows that when the spectral features are not sufficiently extracted, blindly adding spatial depth features will not bring good results. When the spectral feature block was greater than 2, the indicators on the Kennedy Space Center data set tended to be stable, and at the same time, the fluctuation range on the Indian Pines data set was also narrowing.
When the number of spectral attention modules was 2, and the number of spatial attention modules was from 1 to 2, both OA and Kappa increased slightly on the three data sets. In the case of , the best OA was achieved on Kennedy Space Center and Salinas Scene data sets. As for the Indian Pines data set, when the number of attention module increased, the improvement in classification performance was limited. Furthermore, as the number of attention block increased, the time efficiency was bound to decrease. Overall, the network with could achieve the best or very close to the best on three indicators. In addition, it had good performance on the three data sets, indicating that its generalization performance was better. Based on the above analysis, the network structure of our final model is .
5.2. Influence of Different Training Sample Numbers
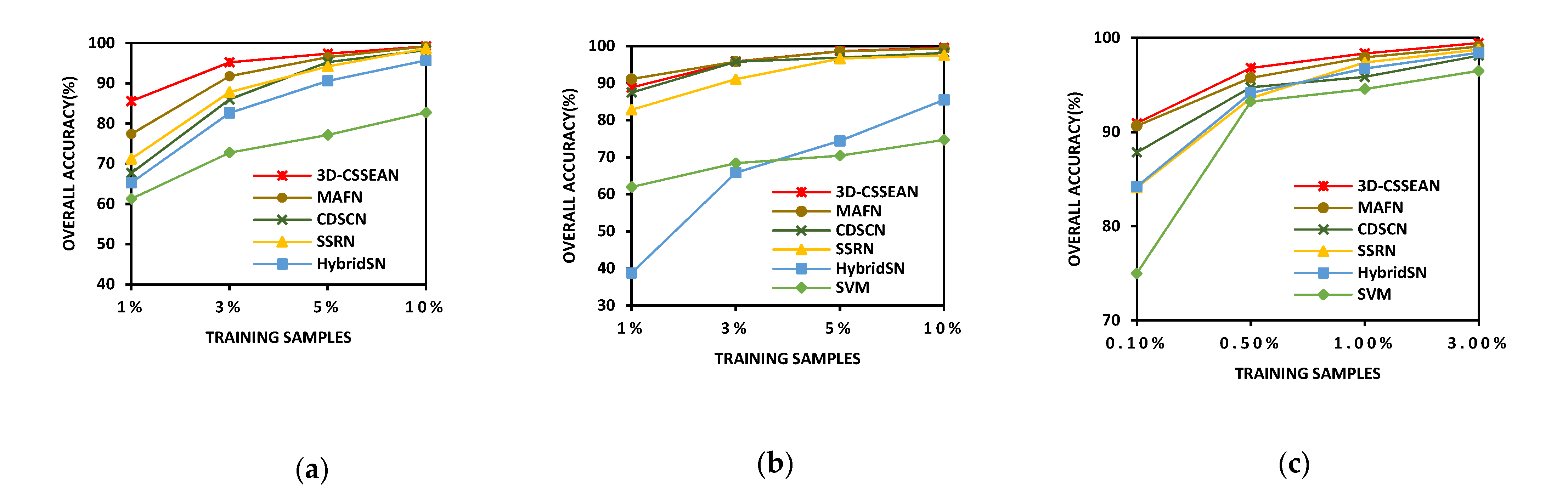
To evaluate the performance of the proposed 3D-CSSEAN, in this paper, under different numbers of training samples, four groups of labeled samples with different percentages were randomly selected as training samples for experiments. Specifically, 1%, 3%, 5%, and 10% of each category were randomly selected from the labeled samples as training samples on the Indian Pines data set and Kennedy Space Center data set, and 0.1%, 0.5%, 1%, and 3% of each category were randomly selected from the labeled samples as training samples on the Salinas Scene data set. The experiment results are shown in
Figure 16.
On the Indian Pines data set, the advantages were more obvious when 1% and 3% of the labeled samples were used for training. Meaningful features extracted by the 3D-CSSEAN were more conducive to improving the classification performance in the case of small samples. Moreover, there was a significant decrease in the OA of CDSCN when only 3% of the labeled samples were used for training, indicating that CDSCN is prone to overfitting small training data. However, the 3D-CSSEAN did not increase many training parameters in the implementation of the attention module, and thus this problem can be avoided to some extent. On the Kennedy Space Center data set, the three different attention models, the 3D-CSSEAN, MAFN, and CDSCN, achieved better results than other methods, especially at 1% and 3%. These results indicate that these three attention features are beneficial for classification on the Kennedy Space Center data set. On the Salinas Scene data set, all methods achieved relatively close results, but the results of the 3D-CSSEAN were always the highest. In most cases, all methods could achieve good results, but in 0.10% of cases, the 3D-CSSEAN and MAFN had more obvious advantages.
In general, on Indian Pines and Salinas Scene data sets, the 3D-CSSEAN consistently outperformed the other approaches on all the training samples. As for the Kennedy Space Center data set, the results of the 3D-CSSEAN and MAFN were very close, and these results were better than those from the other comparison methods. Through these experimental investigations, it can be concluded that the 3D-CSSEAN has better classification performance and robustness in different training sample sets, and especially in the case of small samples, this advantage is more obvious. In addition, the MAFN method based on multiple attention combinations also demonstrated its competitiveness, especially on the Kennedy Space Center data set, where the spatial distribution of categories was relatively scattered. This shows that the combination of multiple attention methods is a promising research direction. In the future, perhaps the combination of the proposed element attention method and other attention methods will also produce more competitive results.
6. Conclusions
In this paper, a 3D cascaded spectral–spatial element attention network (3D-CSSEAN) is proposed to extract the meaningful features for hyperspectral image classification. The spectral element attention module and the spatial element attention module can make the network focus on primary spectral features and meaningful spatial features. Two element attention modules were implemented through several simple activation functions and elementwise multiplication. Therefore, the proposed model not only can obtain features that facilitate classification, but also has high computational efficiency. Since the implementation of the attention module does not add too many training parameters, it also makes the network structure suitable for small sample learning.
To evaluate the effectiveness of the method, extensive experiments were implemented on three public data sets: Indian Pines, Kennedy Space Center and Salinas Scene. Compared with the machine learning method, the popular deep learning methods and the attention methods, the proposed method obtained better classification performance. In cases with small samples, the advantages of the proposed method are more obvious. These results verify that the attention features obtained by the 3D-CSSEAN are beneficial for classification, and the 3D-CSSEAN is suitable for small sample learning. To evaluate the effectiveness of attention modules, several ablation experiments were conducted. From the results of the ablation experiments, both the spectral element attention module and the spatial element attention module have improved classification performance.
Extensive experiments showed that in the case of limited training samples, how to extract more meaningful features for classification is a direction worth exploring. In addition, the fusion of multiple attention features may be a kind of potential method, but how to ensure time efficiency may be a direction to be studied in the future.