Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm
Abstract
1. Introduction
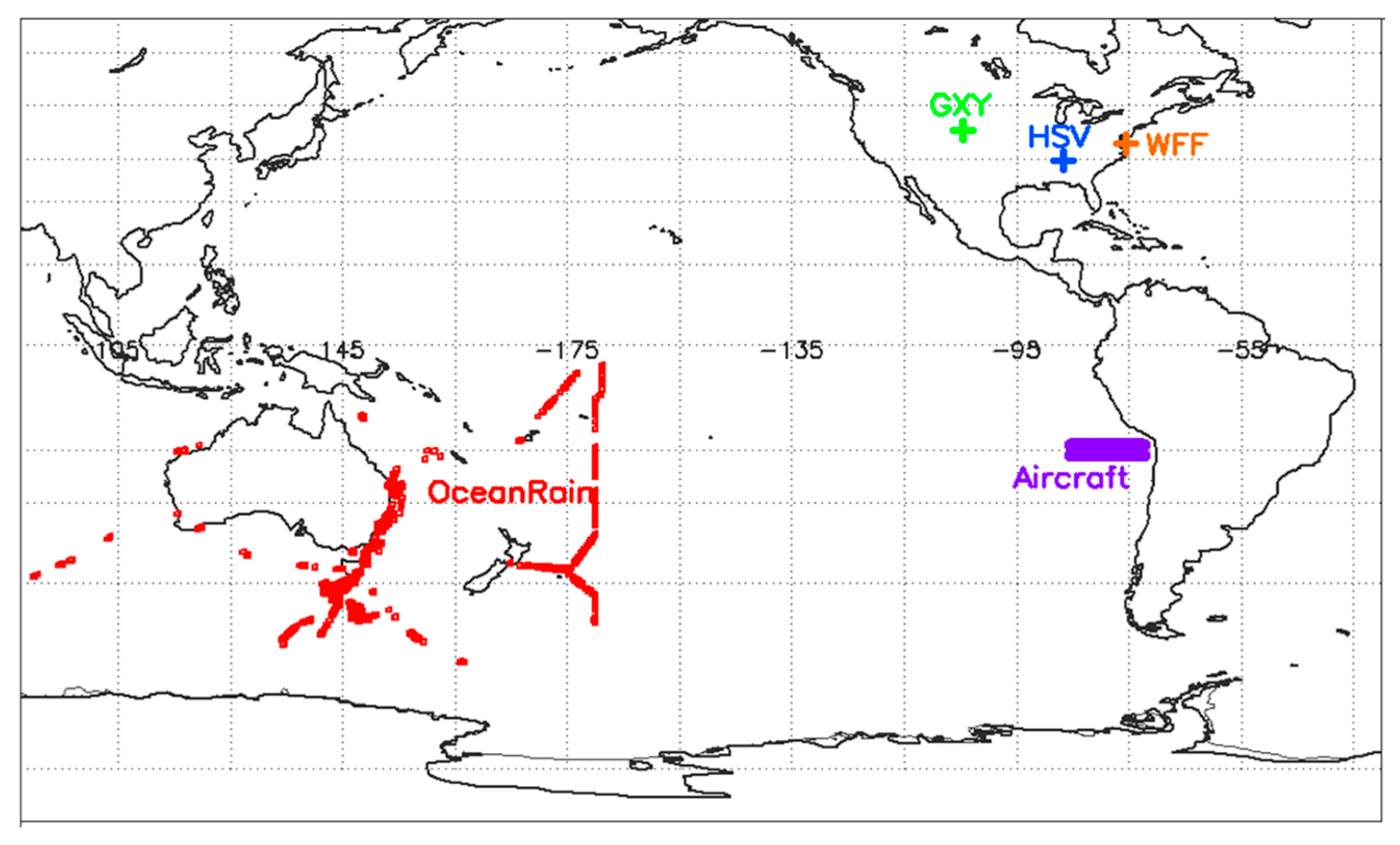
2. Instrumentation and Data Collection
- (a)
- Measured DSDs from semi-arid Greeley (GXY), Colorado, USA, and sub-tropical Huntsville (HSV), Alabama, USA, are collated together to form about 2928 3-min averaged DSDs. At each site the 2DVD and MPS instruments were placed inside a 2/3-scaled DFIR (Double Fence Intercomparison Reference windshield [30]). An identical instrument suite was recently installed at the Wallops Precipitation Research Facility (henceforth WFF), to represent a mid-latitude coastal location. Since all three sites had identical instruments, the comparison between them would not have the uncertainty and other complications of using different sensors. The data quality procedures typically follow Schoenhuber et al. [7,8], with some caveats noted by [31].
- (b)
- The NCAR C-130 was operated off the coast of Chile [32] equipped with a ‘fast’ 1-s 2D-C probe in stratocumulus drizzle (warm rain). The total number of 1-s DSDs was 4142, all quality controlled (J. Jensen, NCAR, personal communication).
- (c)
- (d)
- Simulations of gamma DSDs with uncorrelated NW, Dm, and shape parameter (μ).
- (e)
- The outer rain bands of: (a) Category-1 Hurricane Dorian, described by Thurai et al. [34] and modeled using a cloud particle model by Bringi et al. [35], which traversed the WFF disdrometer network site for ≈8 h; (b) tropical storm Irma (<14 h) near the Huntsville site; (c) tropical depression Nate, which was very shallow at times with negligible echo above the melting layer and ‘pure’ warm rain at times (overall <16 h) near Huntsville. Figure 1 shows the locations marked as WFF and HSV. The outer rainbands were typically stratiform in nature and occurred in the down shear left quadrant. The reason for including these DSDs is because the dynamics are known to be very different from the stratiform rain produced by mesoscale convective complexes.
3. Data Analysis
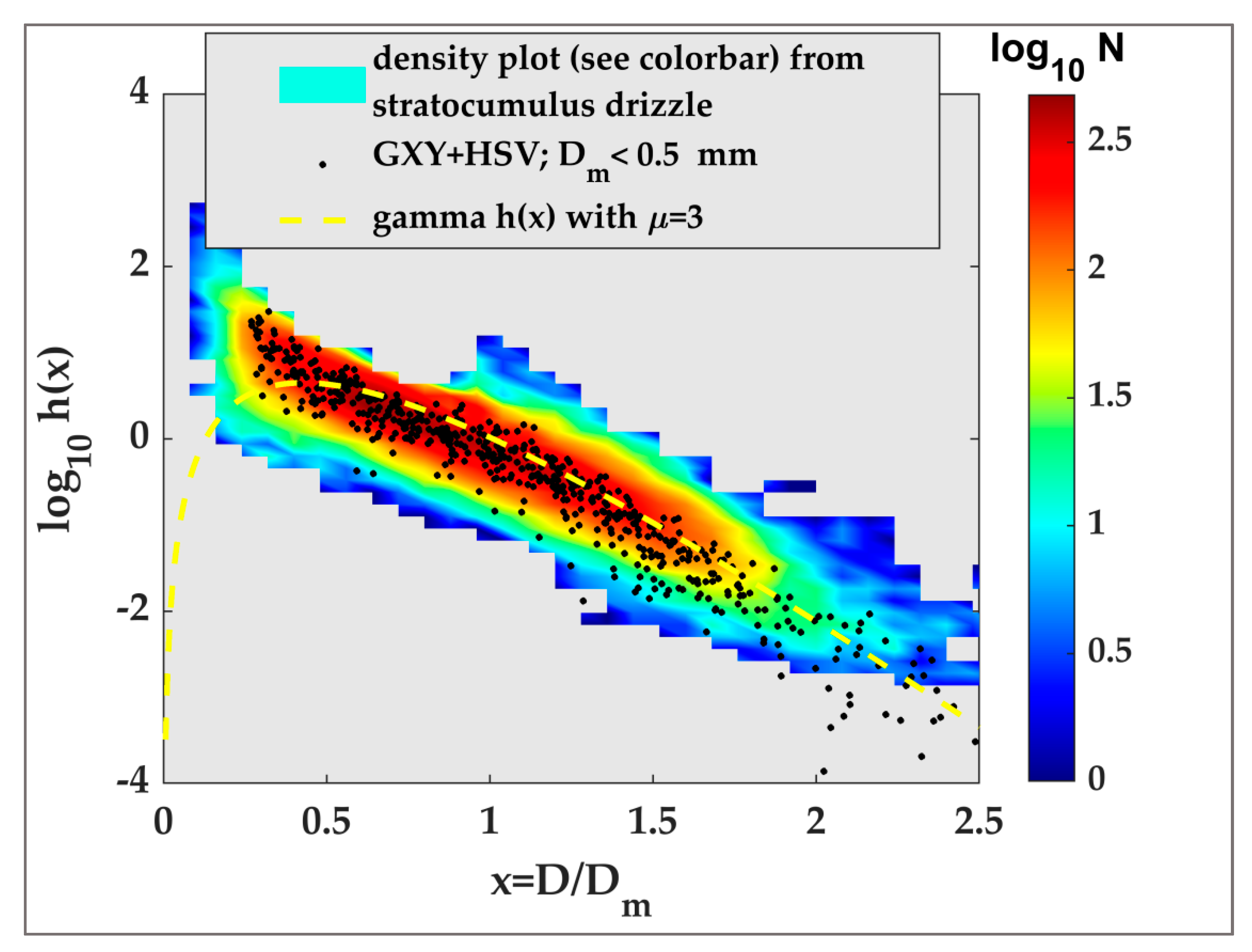
3.1. The ‘Intrinsic’ DSD Shape: Marine Stratocumulus Drizzle versus Semi-Arid and Sub-Tropical Regimes
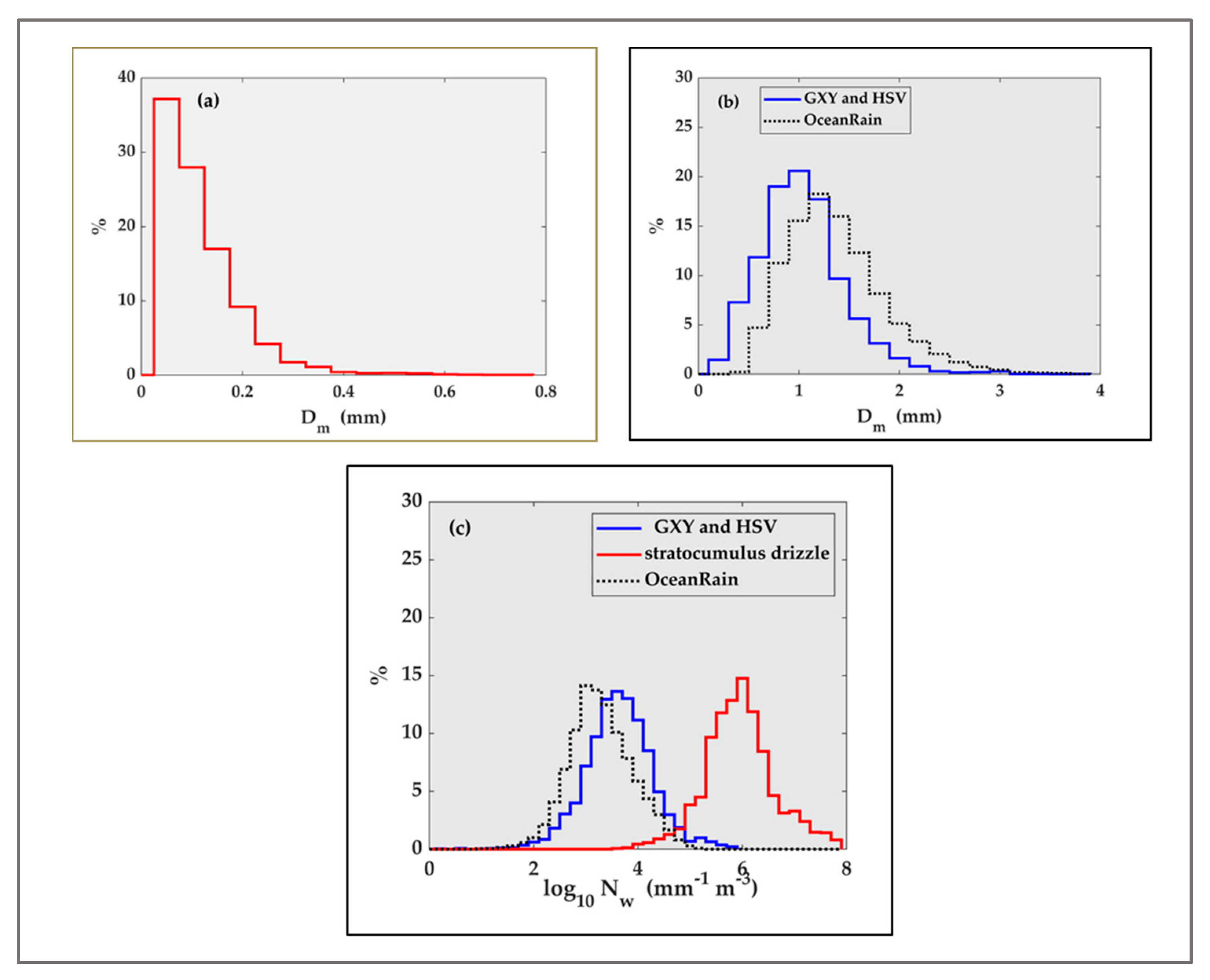
3.2. Histograms of DSD Parameters
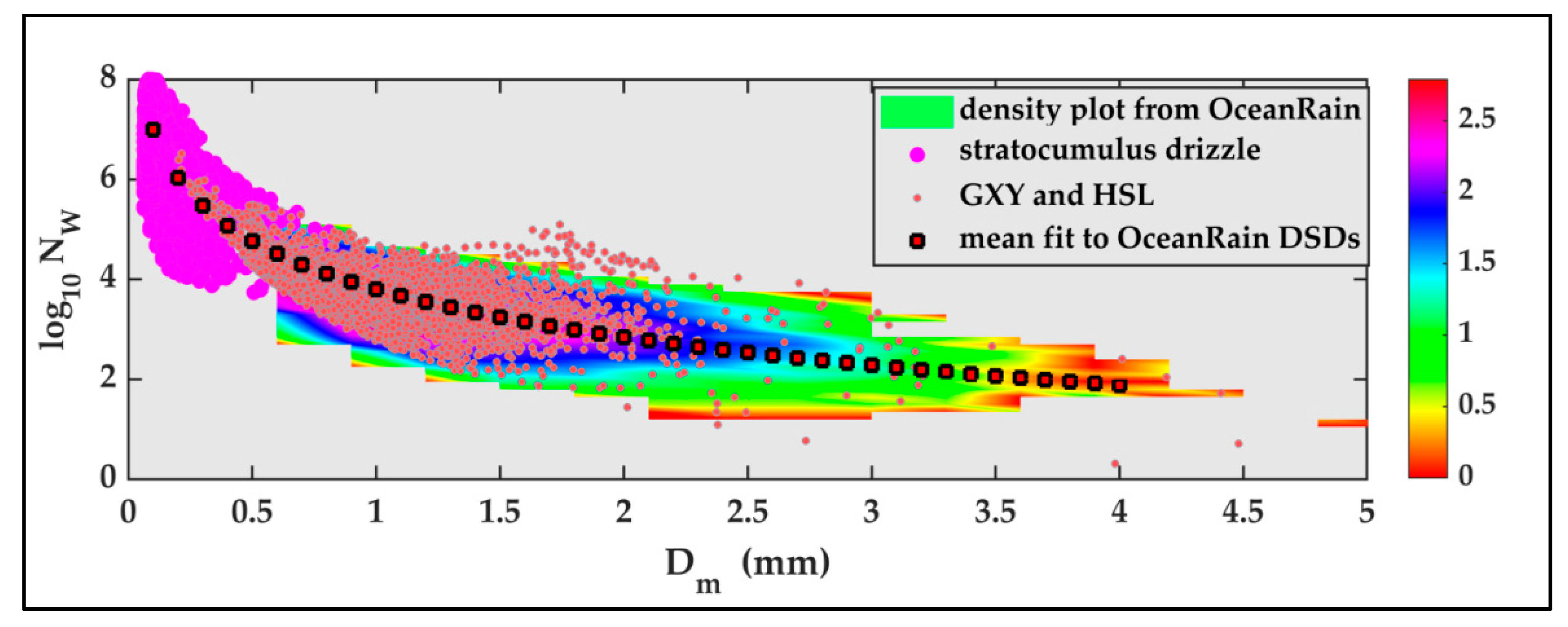
3.3. NW versus Dm
- (a)
- From the high resolution (25 microns) ‘fast’ 2D cloud probe aircraft DSD data, we found that the drizzle Dm is generally <0.5 mm with NW spanning at least two orders of magnitude for any given Dm;
- (b)
- The NW–Dm points from GXY-HSV appear to smoothly merge with the drizzle data for Dm < 0.35 mm;
- (c)
- The mean power law fit from [22], from their OceanRain DSDs, shown as ‘squares’, is an excellent fit through the entire size range covered by all datasets (with the exception of drizzle; see Appendix A), despite the large variability of NW for any given Dm. This is a major finding of this paper.
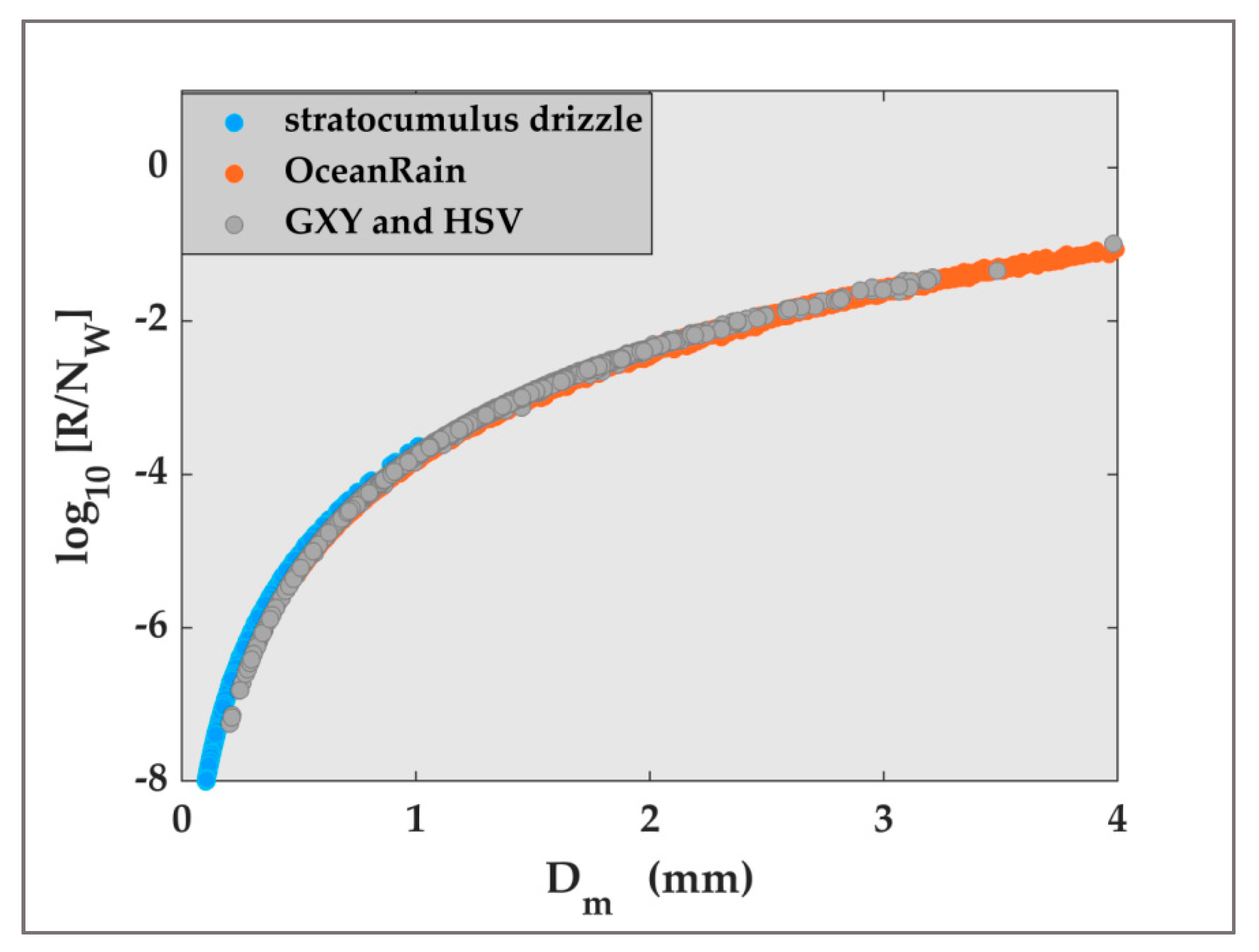
3.4. The Relationship between Rain Rate and DSD Gamma Parameters
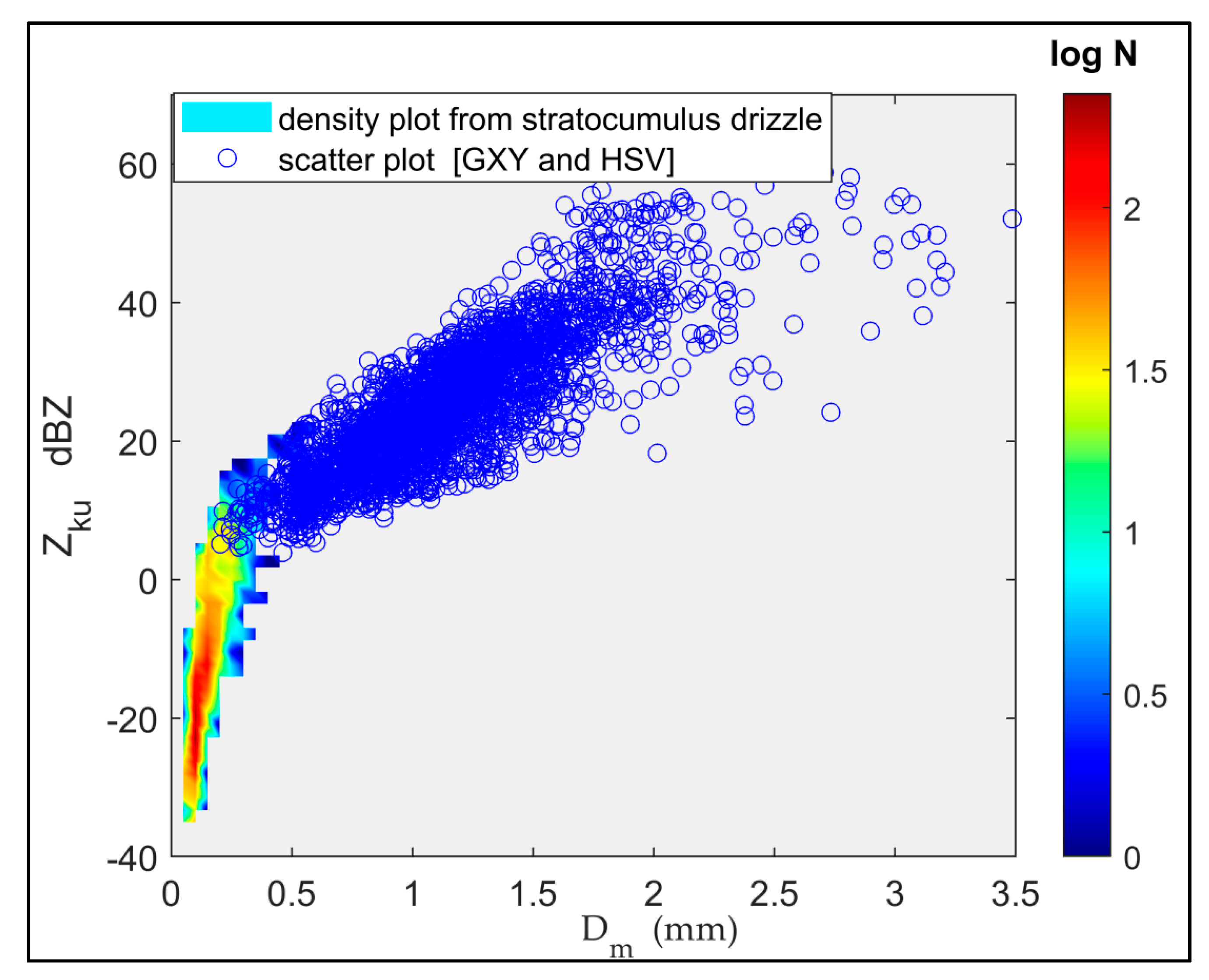
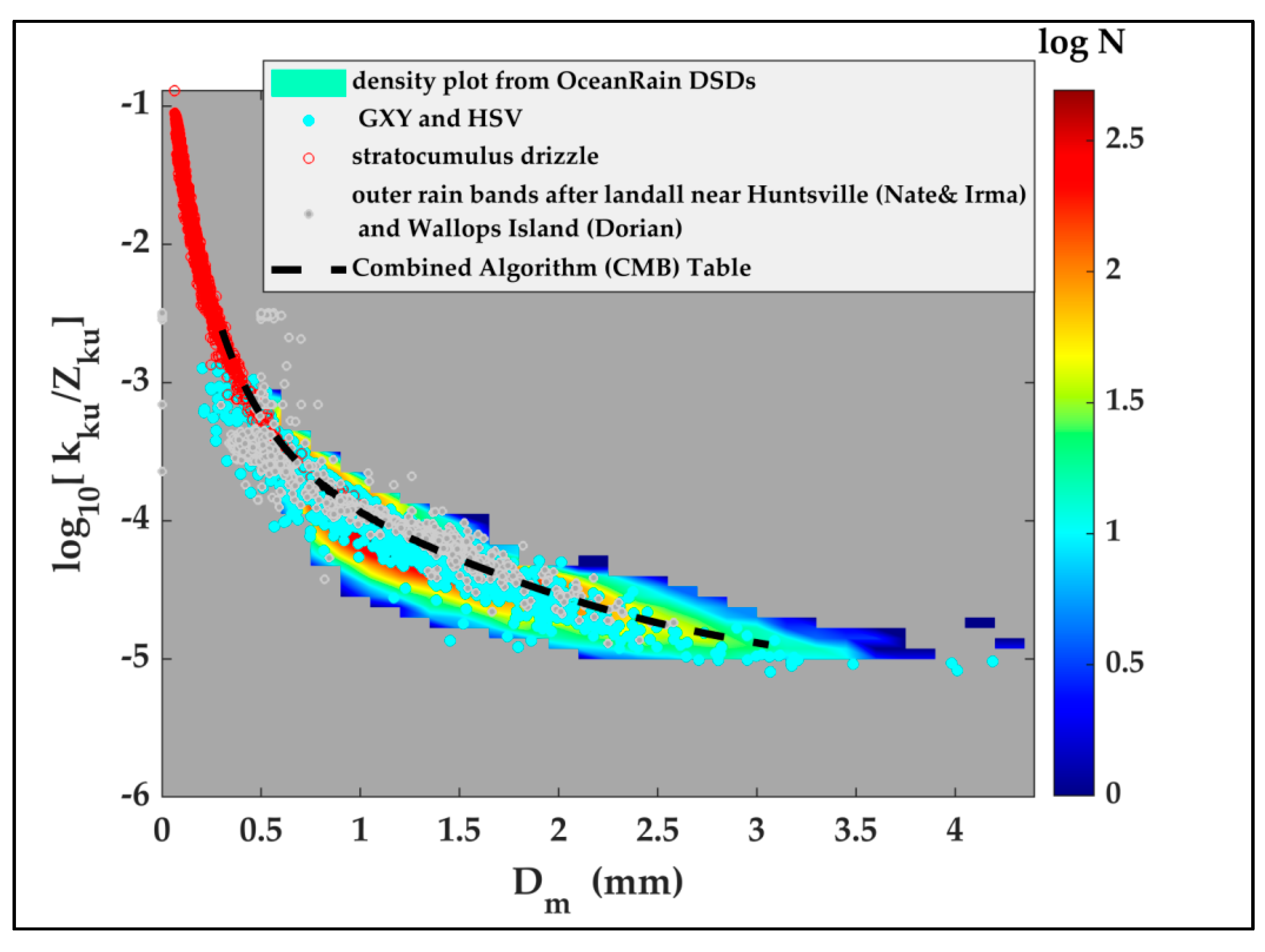
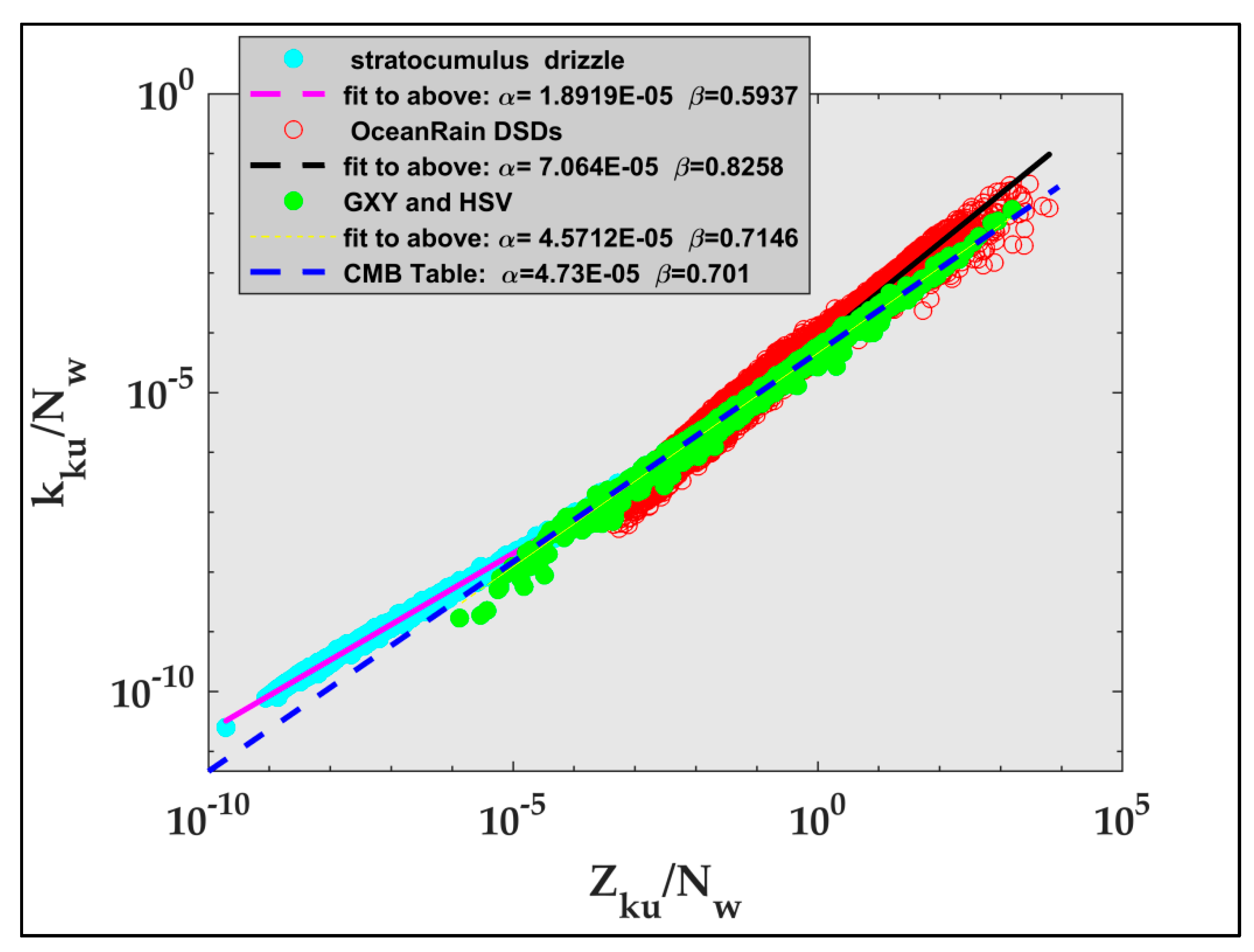
3.5. The Relation between Normalized Radar Quantities and Dm
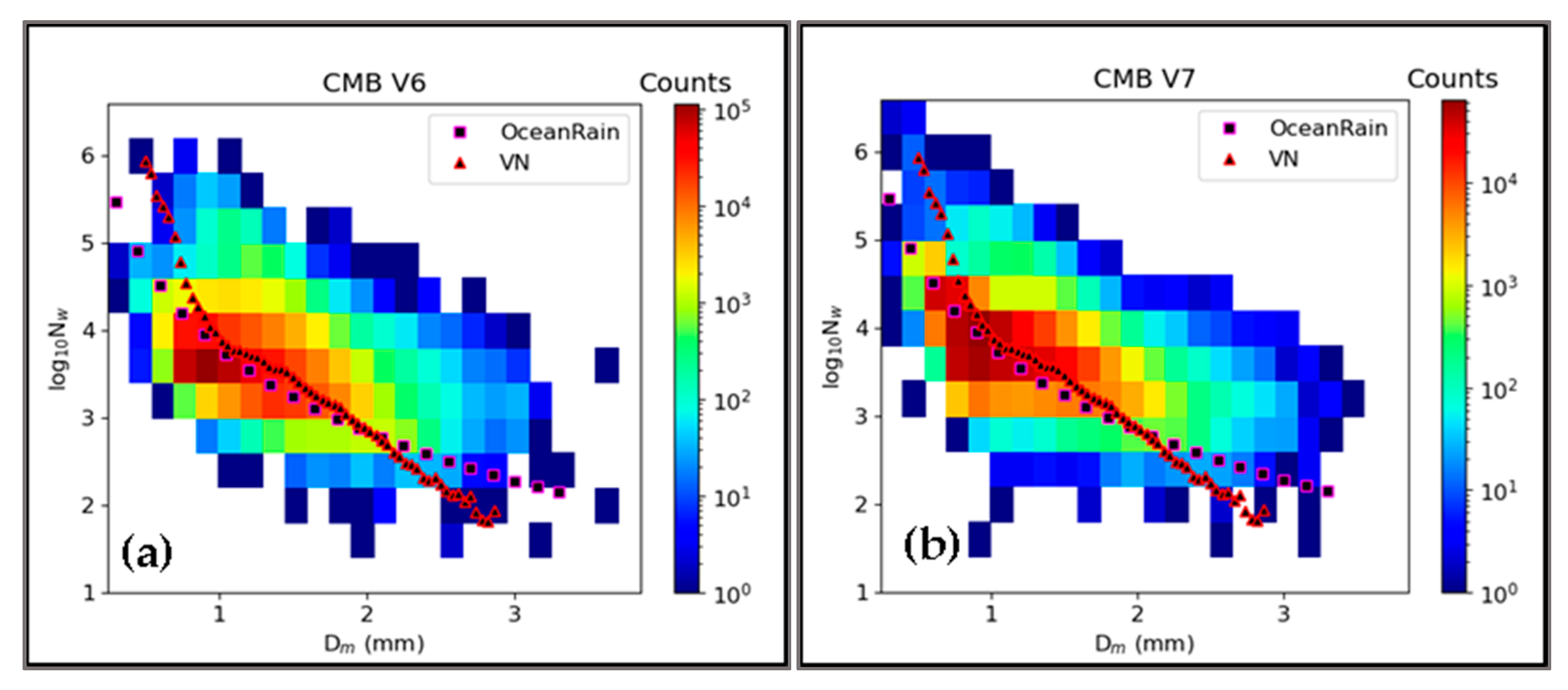
4. Application to the CMB Algorithm
5. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. NW versus Dm Fitted Curve

| Fitted Parameters | Fitted Values for GXY-HSV Dataset | Fitted Values for OceanRain Dataset |
|---|---|---|
| p0 | 8.3 | 11.8 |
| p1 | −0.06 | 0.07 |
| p2 | 0.446 | 0.342 |
| p3 | 0.194 | −0.007 |
References
- Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The concept of “normalized”distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
- Bringi, V.N.; Huang, G.; Chandrasekar, V.; Gorgucci, E. A methodology for estimating the parameters of a gamma raindrop size distribution model from polarimetric radar data: Application to a squall-line event from the TRMM/Brazil campaign. J. Atmos. Ocean. Technol. 2002, 19, 633–645. [Google Scholar] [CrossRef]
- Lee, G.; Zawadzki, I.; Szyrmer, W.; Sempere-Torres, D.; Uijlenhoet, R. A general approach to double-moment normalization of drop size distributions. J. Appl. Meteorol. 2004, 43, 264–281. [Google Scholar] [CrossRef]
- Morrison, H.; Kumjian, M.R.; Martinkus, C.P.; Prat, O.P.; Van Lier-Walqui, M. A general N-moment normalization method for deriving raindrop size distribution scaling relationships. J. Appl. Meteorol. Climatol. 2019, 58, 247–267. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Baumgardner, D.; Kok, G.; Dawson, W.; O’Connor, D.; Newton, R. A new ground-based precipitation spectrometer: The Meteorological Particle Sensor (MPS). In Proceedings of the 11th Conference on Cloud Physics, Ogden, UT, USA, 2–3 June 2002. Paper 8.6. [Google Scholar]
- Schoenhuber, M.; Lammer, G.; Randeu, W.L. One decade of imaging precipitation measurement by 2D-video-distrometer. Adv. Geosci. 2007, 10, 85–90. [Google Scholar] [CrossRef]
- Schönhuber, M.; Lammer, G.; Randeu, W.L. The 2D-Video-Distrometer. In Precipitation: Advances in Measurement, Estimation and Prediction; Michaelides, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–31. ISBN 978-3-540-77654-3. [Google Scholar]
- Thurai, M.; Bringi, V.N. Application of the generalized gamma model to represent the full rain drop size distribution spectra. J. Appl. Meteorol. Climatol. 2018, 57, 1197–1210. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.; Gatlin, P.N.; Petersen, W.A.; Wingo, M.T. Measurements and modeling of the full rain drop size distribution. Atmosphere 2019, 10, 39. [Google Scholar] [CrossRef]
- Williams, C.R.; Kruger, A.; Gage, K.S.; Tokay, A.; Cifelli, R.; Krajewski, W.F.; Kummerow, C. Comparison of simultaneous rain drop size distributions estimated from two surface disdromters and a UHF profiler. Geophys. Res. Lett. 2000, 27, 1763–1766. [Google Scholar] [CrossRef]
- Kozu, T.; Iguchi, T.; Shimomai, T.; Kashiwagi, N. Raindrop size distribution modeling from a statistical rain parameter relation and its application to the TRMM precipitation radar rain retrieval algorithm. J. Appl. Meteorol. Climatol. 2009, 48, 716–724. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
- Petersen, W.A.; Kirstetter, P.E.; Wang, J.; Wolff, D.B.; Tokay, A. The GPM Ground Validation Program. In Satellite Precipitation Measurement; Springer: Cham, Germany, 2020; pp. 471–502. [Google Scholar]
- Grecu, M.; Olson, W.S.; Munchak, S.J.; Ringerud, S.; Liao, L.; Haddad, Z.; Kelley, B.L.; McLaughlin, S.F. The GPM Combined Algorithm. J. Atmos. Ocean. Technol. 2016, 33, 2225–2245. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). In Algorithm Theoretical Basis Document (ATBD); 2019; Version 6; p. 39. Available online: https://gpm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V06.pdf (accessed on 19 June 2021).
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The Global Precipitation Measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef] [PubMed]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Hitschfeld, W.; Bordan, J. Errors inherent in the radar measurement of rainfall at attenuating wavelengths. J. Meteorol. 1954, 11, 58–67. [Google Scholar] [CrossRef]
- Bringi, V.N.; Tolstoy, L.; Thurai, M.; Petersen, W.A. Estimation of spatial correlation of rain drop size distribution parameters and rain rate using NASA’s S-band polarimetric radar and 2D-video disdrometer network: Two case studies from MC3E. J. Hydrometeor. 2015, 16, 1207–1221. [Google Scholar] [CrossRef]
- Viltard, N.; Kummerow, C.; Olson, W.S.; Hong, Y. Combined use of the radar and radiometer of TRMM to estimate the influence of drop size distribution on rain retrievals. J. Appl. Meteorol. 2000, 39, 2103–2114. [Google Scholar] [CrossRef]
- Protat, A.; Klepp, C.; Louf, V.; Petersen, W.A.; Alexander, S.P. The latitudinal variability of oceanic rainfall properties and its implication for satellite retrievals: 1. Drop size distribution properties. J. Geophys. Res. Atmos. 2019, 124, 13291–13311. [Google Scholar] [CrossRef]
- Protat, A.; Klepp, C.; Louf, V.; Petersen, W.A.; Alexander, S.P.; Barros, A.; Leinonen, J.; Mace, G.G. The latitudinal variability of oceanic rainfall properties and its implication for satellite retrievals: 2. The relationships between radar observables and drop size distribution parameters. J. Geophys. Res. Atmos. 2019, 124, 13312–13324. [Google Scholar] [CrossRef]
- Duncan, D.I.; Eriksson, P.; Pfreundschuh, S.; Klepp, C.; Jones, D.C. On the distinctiveness of observed oceanic raindrop distributions. Atmos. Chem. Phys. 2019, 19, 6969–6984. [Google Scholar]
- Olson, W.S.; Masunaga, H.; GPM Combined Radar-Radiometer Algorithm Team. GPM Combined Radar-Radiometer Precipitation Algorithm Theoretical Basis Document (Version 4); NASA: Washington, DC, USA, 2019.
- Gatlin, P.N.; Petersen, W.A.; Pippitt, J.L.; Berendes, T.A.; Wolff, D.B.; Tokay, A. The GPM validation network and evaluation of satellite-based retrievals of the rain drop size distribution. Atmosphere 2020, 11, 1010. [Google Scholar] [CrossRef]
- Chase, R.J.; Nesbitt, S.W.; McFarquhar, G.M. Evaluation of the Microphysical Assumptions within GPM-DPR Using ground-based observations of rain and snow. Atmosphere 2020, 11, 619. [Google Scholar] [CrossRef]
- Tokay, A.; D’Adderio, L.P.; Wolff, D.B.; Petersen, W.A. Development and evaluation of the raindrop size distribution parameters for the NASA global precipitation measurement mission ground validation program. J. Atmos. Ocean. Technol. 2020, 37, 115–128. [Google Scholar] [CrossRef]
- Liao, L.; Meneghini, R.; Iguchi, T.; Tokay, A. Characteristics of DSD bulk parameters: Implication for radar rain retrieval. Atmosphere 2020, 11, 670. [Google Scholar] [CrossRef]
- Rasmussen, R.; Baker, B.; Kochendorfer, J.; Meyers, T.; Landolt, S.; Fischer, A.P.; Black, J.; Thériault, J.M.; Kucera, P.; Gochis, D.; et al. How well are we measuring snow: The NOAA/FAA/NCAR winter precipitation test bed. Bull. Am. Meteorol. Soc. 2012, 93, 811–829. [Google Scholar] [CrossRef]
- Larsen, M.; Schönhuber, M. Identification and characterization of an anomaly in 2-dimensional video disdrometer data. Atmosphere 2018, 9, 315. [Google Scholar] [CrossRef]
- Wood, R.; Mechoso, C.R.; Bretherton, C.S.; Weller, R.A.; Huebert, B.; Straneo, F.; Albrecht, B.A.; Coe, H.; Allen, G.; Vaughan, G.; et al. The VAMOS Ocean-cloud-atmosphere-land study regional experiment (VOCALS-REx): Goals, platforms, and field operations. Atmos. Chem. Phys. 2011, 11, 627–654. [Google Scholar] [CrossRef]
- Klepp, C.; Michel, S.; Protat, A.; Burdanowitz, J.; Albern, N.; Kähnert, M.; Dahl, A.; Louf, V.; Bakan, S.; Buehler, S.A. OceanRAIN, a new in-situ shipboard global ocean surface-reference dataset of all water cycle components. Sci. Data 2018, 5, 180122. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; Wolff, D.B.; Marks, D.A.; Pabla, C.S. Drop size distribution measurements in outer rainbands of hurricane dorian at the NASA wallops precipitation-research facility. Atmosphere 2020, 11, 578. [Google Scholar] [CrossRef]
- Bringi, V.; Seifert, A.; Wu, W.; Thurai, M.; Huang, G.-J.; Siewert, C. Hurricane dorian outer rain band observations and 1D particle model simulations: A case study. Atmosphere 2020, 11, 879. [Google Scholar] [CrossRef]
- Abel, S.J.; Boutle, I.A. An improved representation of the rain size spectra for single-moment microphysics schemes. Quart. J. R. Meteorol. Soc. 2012, 138, 2151–2162. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path- and area-integrated rainfall measurement by microwave attenuation in the 1–3 cm band. J. Appl. Meteorol. Climatol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Barber, P.; Yeh, C. Scattering of electromagnetic waves by arbitrarily shaped dielectric bodies. Appl. Opt. 1975, 14, 2864–2872. [Google Scholar] [CrossRef]
- Iguchi, T.; Kozu, T.; Meneghini, R.; Awaka, J.; Okamoto, K. Rain-profiling algorithm for the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2038–2052. [Google Scholar] [CrossRef]
- Schwaller, M.R.; Morris, K.R. A ground validation network for the global precipitation measurement mission. J. Atmos. Ocean. Technol. 2011, 28, 301–319. [Google Scholar] [CrossRef]
- Meneghini, R.; Kozu, T.; Kumagai, H.; Boncyk, W.C. A study of rain estimation methods from space using dual-wavelength radar measurements at near-nadir incidence over ocean. J. Atmos. Ocean. Technol. 1992, 9, 364–382. [Google Scholar] [CrossRef]
- Haddad, Z.S.; Meagher, J.P.; Durden, S.L.; Smith, E.A.; Im, E. Drop size ambiguities in the retrieval of precipitation profiles from dual-frequency radar measurements. J. Atmos. Sci. 2006, 63, 204–217. [Google Scholar] [CrossRef][Green Version]
- Meneghini, R.; Iguchi, T.; Kozu, T.; Liao, L.; Okamoto, K.; Jones, J.A.; Kwiatkowski, J. Use of the surface reference technique for path attenuation estimates from the TRMM precipitation radar. J. Appl. Meteorol. 2000, 39, 2053–2070. [Google Scholar] [CrossRef]
- Ferreira, F.; Amayenc, P.; Oury, S.; Testud, J. Study and tests of improved rain estimates from the TRMM precipitation radar. J. Appl. Meteorol. 2001, 40, 1878–1899. [Google Scholar] [CrossRef]
- Grecu, M.; Anagnostou, E.N. Use of passive microwave observations in a radar rainfall-profiling algorithm. J. Appl. Meteorol. 2002, 41, 702–715. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.; Wolff, D.; Marks, D.; Pabla, C. Testing the drop-size distribution-based separation of stratiform and convective rain using radar and disdrometer data from a mid-latitude coastal region. Atmosphere 2021, 12, 392. [Google Scholar] [CrossRef]




| Dataset | Instruments | Number of DSDs | Location |
|---|---|---|---|
| Ground-based (green, blue, and orange ‘+’ marks in Figure 1) |
| A total of 2928 3-min ‘complete’ DSDs | Three fixed locations
|
| C-130 penetrations in stratocumulus drizzle off the coast of Chile (purple area in Figure 1) | ‘fast’ 2D-cloud probe (25 micron resolution) | 1-s data: 4412 DSDs | 1.4 km altitude, off the coast of Chile in stratocumulus drizzle. |
| Open ocean (shown as red squares in Figure 1) | ODM 470 optical disdrometer | 1-min DSDs: 14,213 | Ocean regions surrounding Australia plus south-west Pacific. |
| Outer rain bands * (blue and orange ‘+’ marks in Figure 1) |
| A total of 1403 3-min ‘complete’ DSDs | Two fixed locations
|
| DSD Source | Figure 10: R = α NW(1-β) Zkuβ | Figure 11: R = α NW(1-β) Zkaβ | ||
|---|---|---|---|---|
| Stratocumulus drizzle | α = 0.0015 | β = 0.6423 | α = 0.0014 | β = 0.6412 |
| OceanRain | α = 0.0012 | β = 0.633 | α = 0.0017 | β = 0.7339 |
| GXY-HSV | α = 0.0015 | β = 0.664 | α = 0.0018 | β = 0.7336 |
| CMB Table | α = 0.00143 | β = 0.666 | α =0.00219 | β = 0.727 |
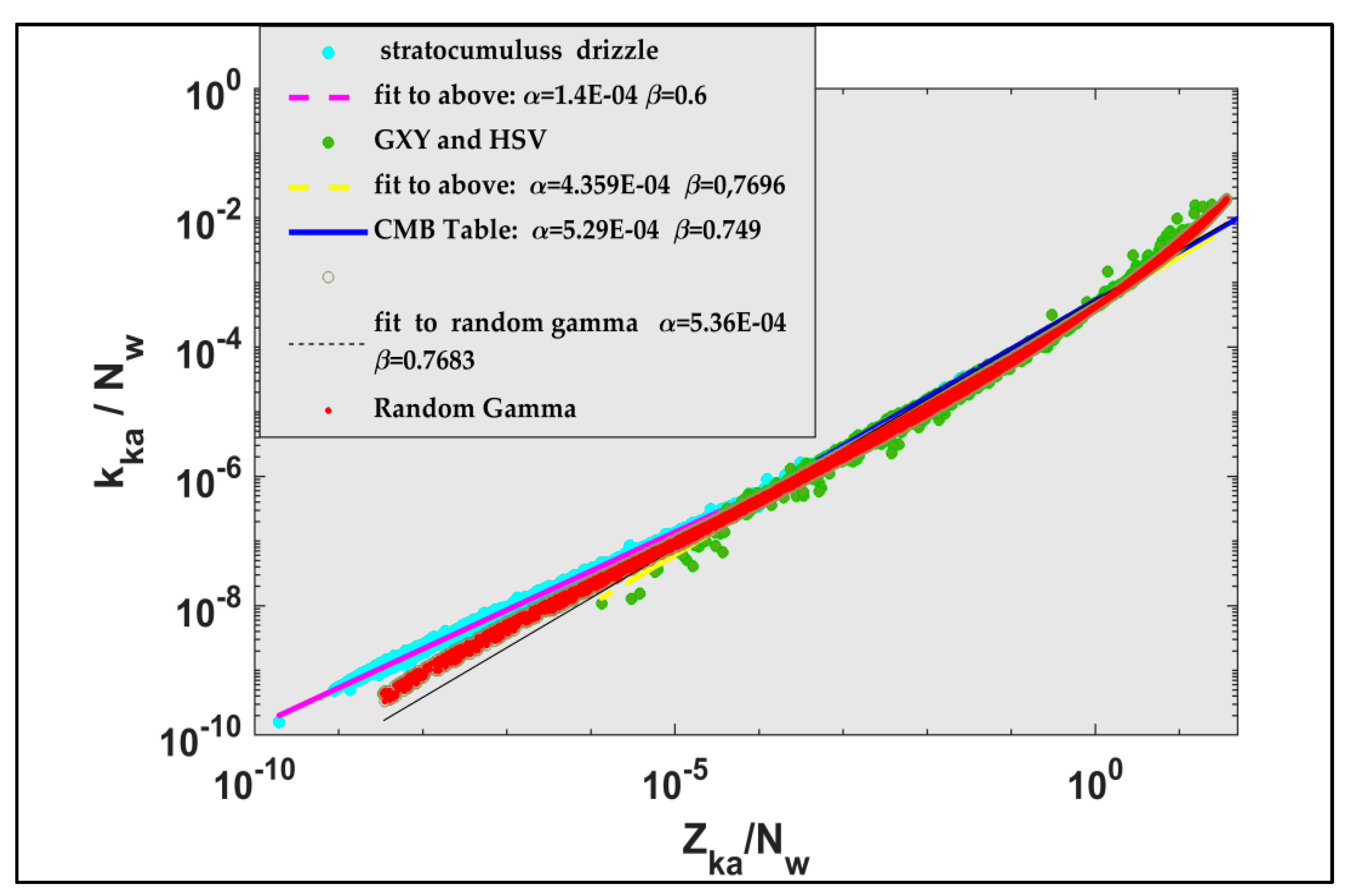
| DSD Source | Figure 12: kKu = α NW(1-β) ZKuβ | Figure 13: kKa = α NW(1-β) ZKaβ | ||
|---|---|---|---|---|
| Stratocumulus drizzle | α = 1.89 × 10−5 | β = 0.5937 | α = 1.4 × 10−4 | β = 0.6 |
| OceanRain | α = 7.064 × 10−5 | β = 0.8258 | α = 7.0 × 10−4 | β = 0.715 |
| GXY-HSV | α = 4.57 × 10−5 | β = 0.7146 | α = 4.36 × 10−4 | β = 0.769 |
| CMB Table | α = 4.73 × 10−5 | β = 0.701 | α =5.29 × 10−4 | β = 0.749 |
| Random Gamma | α = 4.55 × 10−5 | β = 0.721 | α =5.36 × 10−4 | β = 0.768 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bringi, V.; Grecu, M.; Protat, A.; Thurai, M.; Klepp, C. Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm. Remote Sens. 2021, 13, 2412. https://doi.org/10.3390/rs13122412
Bringi V, Grecu M, Protat A, Thurai M, Klepp C. Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm. Remote Sensing. 2021; 13(12):2412. https://doi.org/10.3390/rs13122412
Chicago/Turabian StyleBringi, Viswanathan, Mircea Grecu, Alain Protat, Merhala Thurai, and Christian Klepp. 2021. "Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm" Remote Sensing 13, no. 12: 2412. https://doi.org/10.3390/rs13122412
APA StyleBringi, V., Grecu, M., Protat, A., Thurai, M., & Klepp, C. (2021). Measurements of Rainfall Rate, Drop Size Distribution, and Variability at Middle and Higher Latitudes: Application to the Combined DPR-GMI Algorithm. Remote Sensing, 13(12), 2412. https://doi.org/10.3390/rs13122412








