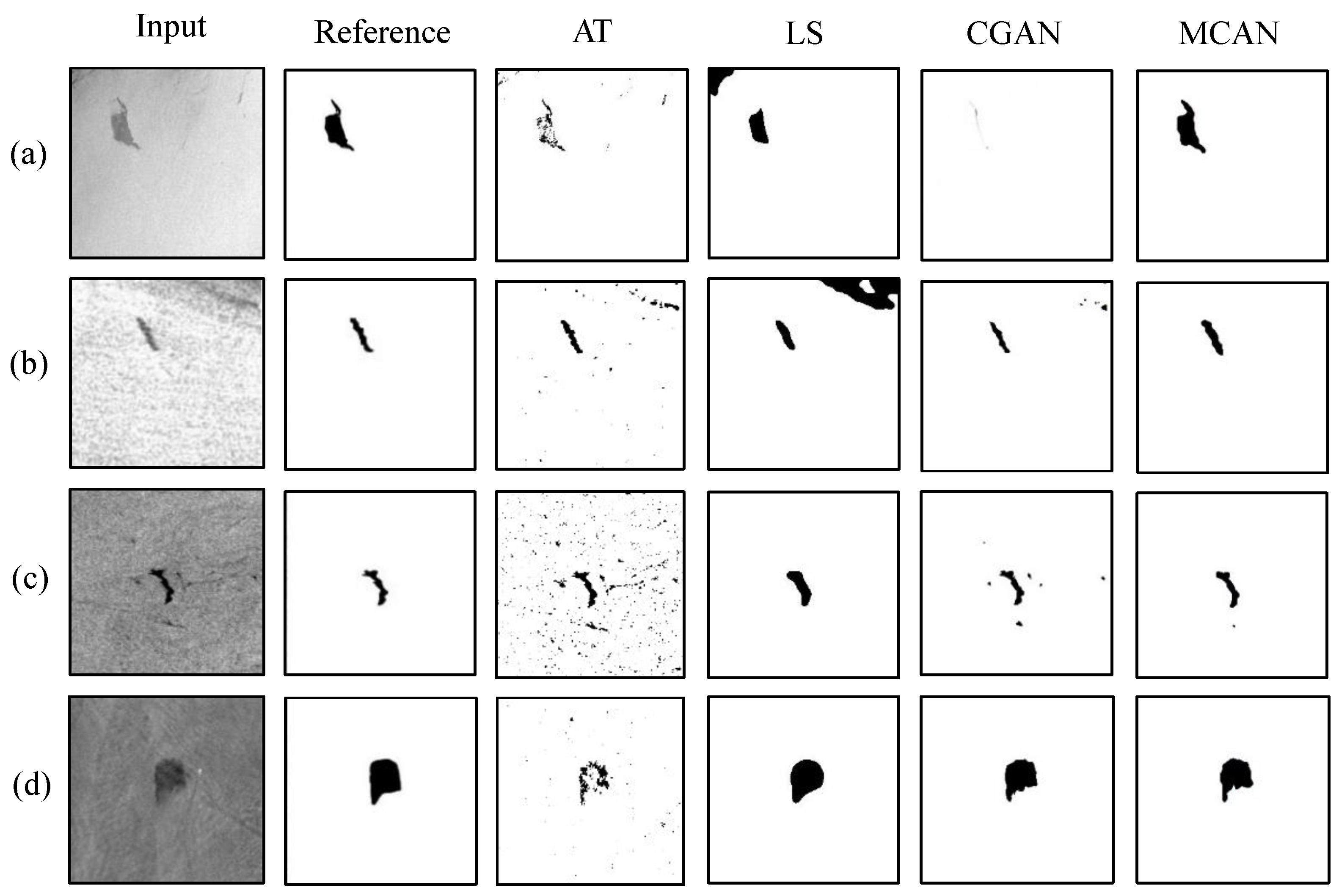
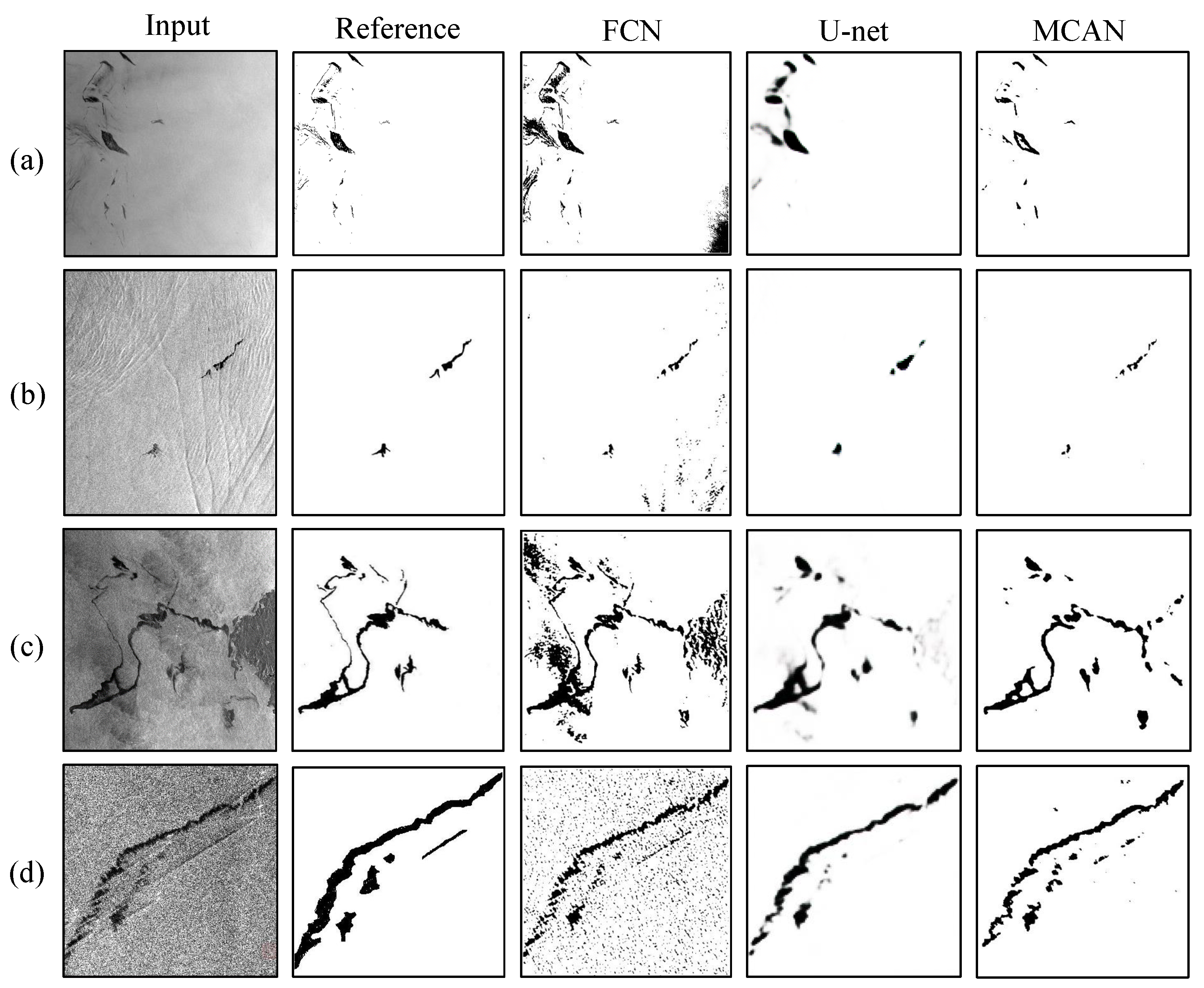
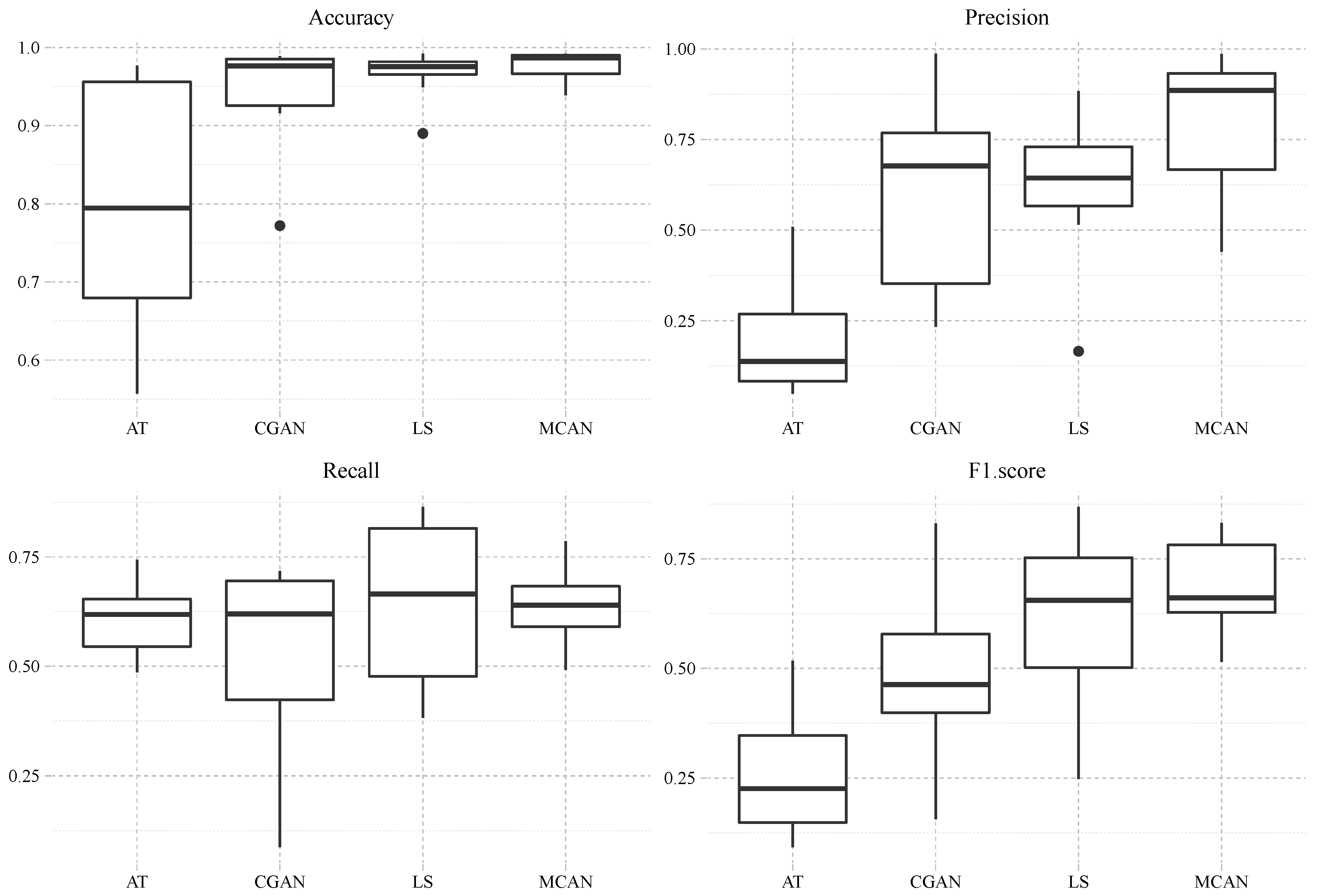
1. Introduction
Frequent oil spill accidents have caused great harm to marine life and national economies in recent years. Accurately detecting oil spills in remote sensing images plays an important role in environmental protection and emergency responses for marine accidents. Among the many monitoring methods that use remote sensing, synthetic aperture radar (SAR) is an essential tool for observing oil spills with its broad view and all-time and all-weather data acquisition [
1,
2,
3]. Oil spill detection based on SAR images is an indispensable research topic in the field of ocean remote sensing [
4,
5,
6,
7].
The principle of oil spill detection lies in the differential display between oil and water in oil spill observation images [
8,
9]. As oil spills can weaken the Bragg scattering and result in dark regions in the observation images, numerous researchers are dedicated to analyzing the physical characteristics of oil spills. In particular, the polarimetric characteristics have been effectively used to enhance the comprehensive observation effect [
10,
11]. Moreover, other kinds of techniques for oil spill detection based on semplice image processing have mainly drawn support from energy minimization [
12], which is the optimization objective of energy functions.
Mdakane and Kleynhans [
5] achieved efficient oil spill detection with an automatic segmentation framework that combines automated threshold-based and region-based algorithms. Ren et al. [
13] took the shapes of elongated oil spills and their details into consideration with a dual-smoothing framework that operates at both the label and pixel levels. Ren et al. [
14] proposed a solution to the problem of manual labeling with one-dot fuzzy initialization. Chen et al. [
15] exploited a segmentation method with multipliers of alternating directions to handle blurry SAR images. Energy-minimization-based segmentation is not too computationally expensive, but relies heavily on the initialization information; such information is usually scarce, as it is provided by manually segmented images.
Machine-learning-based oil spill detection models have been investigated extensively in recent years, as they have been proven to have the ability to intelligently extract the internal information of SAR images. Inchoate detection models tend to find oil spills in three steps [
16,
17,
18,
19,
20,
21]: dark-spot detection, feature extraction, and dark-spot classification. An early machine-learning-based model used adaptive thresholding for dark-spot detection and extracted four features in order to conduct the subsequent dark-spot classification [
4]. Brekke and Solberg [
22] developed an improved two-step classification procedure for oil spill detection in SAR images, consisting of a regularized statistical classifier and an automatic confidence estimation of the detected slicks. Singha et al. [
23] employed two different artificial neural networks (ANNs) in sequence; the first ANN outputs candidate pixels belonging to oil spills, and the corresponding feature parameters drive the second ANN to classify objects into oil spills or lookalikes. Xu et al. [
24] made a comparative study of classification techniques by analyzing classifiers, including support vector machines, artificial neural networks, tree-based ensemble classifiers (bagging, bundling, and boosting), generalized additive models, and penalized linear discriminant analysis. Taravat et al. [
25] proposed an automated dark-spot detection approach combining the Weibull multiplicative model and pulse-coupled neural network techniques; the proposal differentiates between dark spots and background.
Machine-learning-based methods use step-by-step operations and can seldom be implemented as end-to-end detection pipelines. Such stepwise schemes rely on complex procedures and do not guarantee efficient oil spill detection.
Recently, deep learning has been investigated for target recognition [
2,
26] and oil spill detection [
27,
28,
29]. Gallego et al. [
30] used a deep residual encoder–decoder network for oil spill detection in one step. The encoder receives the input image and creates a latent representation, and the decoder takes this intermediate representation and outputs the oil spill detection results. Nieto-Hidalgo et al. [
31] proposed a two-stage convolutional neural network to detect oil spills from side-looking airborne radar images. The first network performs a coarse detection, and the second one provides a precise pixel classification. Shaban et al. [
32] used a two-stage deep learning framework that considers the unbalanced nature of datasets for oil spill identification. The first network classifies oil spill image patches via a 23-layer convolutional neural network, and the second network performs semantic segmentation using a five-stage U-Net. Li et al. [
33] discussed two automatic detection models that combine a fully convolutional network (FCN) [
34] with Resnet [
35] and Googlenet [
36] for oil spill images, with no restrictions on the size of the input. These methods achieve effective detection in an end-to-end fashion, and they tend to outperform ordinary machine-learning-based methods.
Other approaches for the same purpose employ adversarial training mechanisms, including generative adversarial networks (GANs) [
37,
38,
39,
40,
41] and conditional adversarial networks (CANs) [
42,
43]. CANs are capable of learning the transformation of observation images into detection maps in accordance with the users’ expectations. Yu et al. [
44] used a detection model with adversarial f-divergence learning for automatic oil spill identification. The network utilized in adversarial f-divergence learning is a typical CAN. CAN-based oil spill detection methods are reliable and achieve good accuracy.
The intelligent detection methods described above are driven by a training process. Most machine-learning-based oil spill detection methods depend on large amounts of training data to guarantee accurate detection results. Significant amounts of oil spill observation data are challenging to obtain, and training an oil spill detection model with small amounts of data remains a challenge in the literature. To eliminate the dependence on vast observation data of oil spills, we developed a multiscale conditional adversarial network (MCAN) to achieve such a goal with small amounts of training data.
MCAN consists of a series of adversarial networks at multiple scales. Both images of observed oil spills and detection maps are used in coarse-to-fine representations at multiple scales. Each adversarial network of the MCAN at each scale is composed of a generator and a discriminator. The generator captures the observed image’s characteristics and produces an oil spill detection map as authentically as possible. The discriminator distinguishes the generated detection map from the reference data. The output of each generator is used as the input of the following finer-scale generator and the current-scale discriminator. The training procedure of each scale is conducted independently in an adversarial fashion.
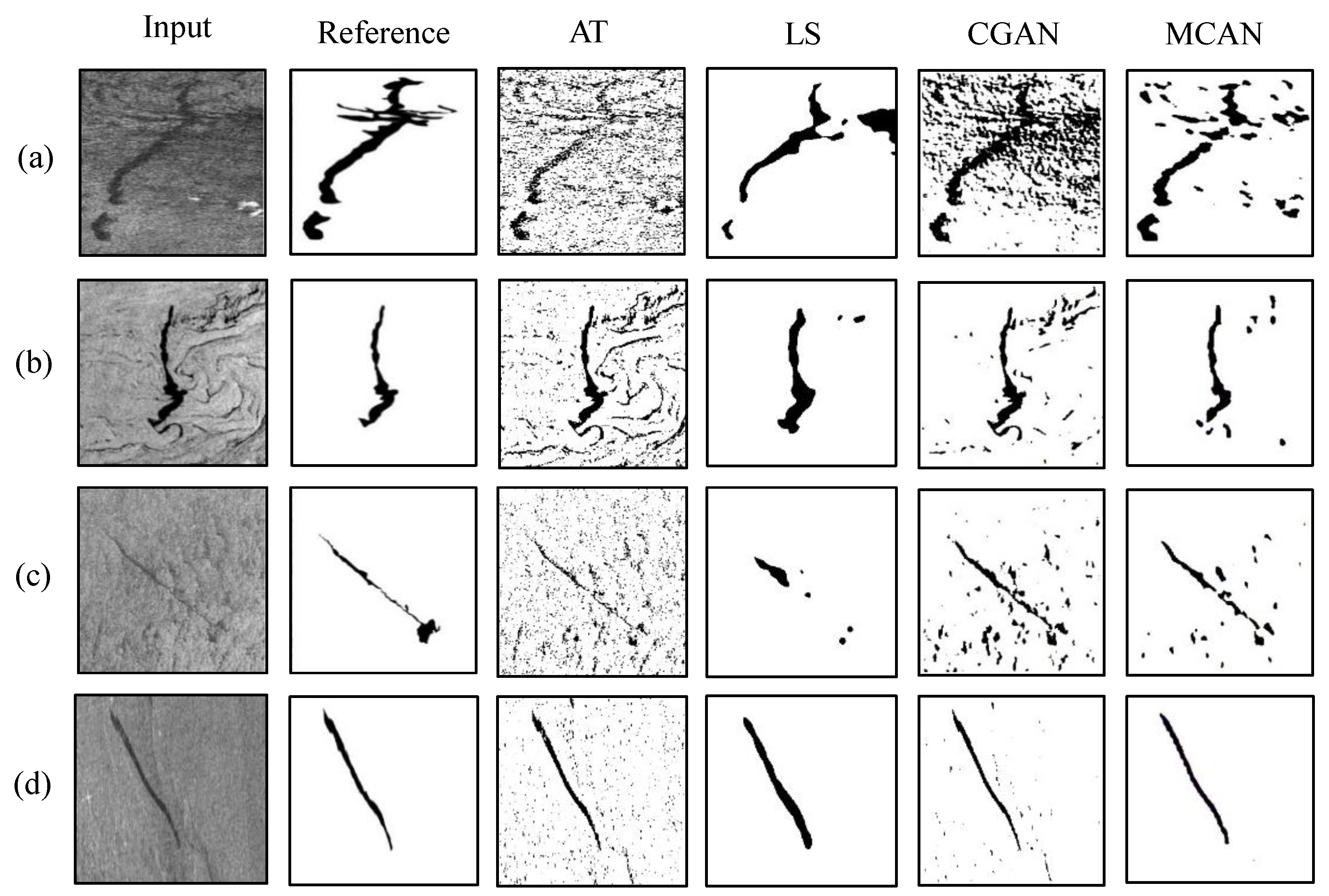
The three features (i.e., (i) multiscale processing, (ii) coarse-to-fine data flow in a cascade, and (iii) independent adversarial training) enable MCAN to comprehensively capture data characteristics, and they empower it with the capability of learning with small amounts of data. The experimental results validate that MCAN produces accurate detection maps for sophisticated oil spill regions based on only four training data samples. The detection performance of MCAN outperforms those of other methods.
The main contributions of this article are summarized as follows.
We propose a novel oil spill detection method based on MCAN, which employs a lightweight network for each generator and discriminator.
We implement adversarial training independently at each scale and achieve a coarse-to-fine data flow of oil spill features in a cascade.
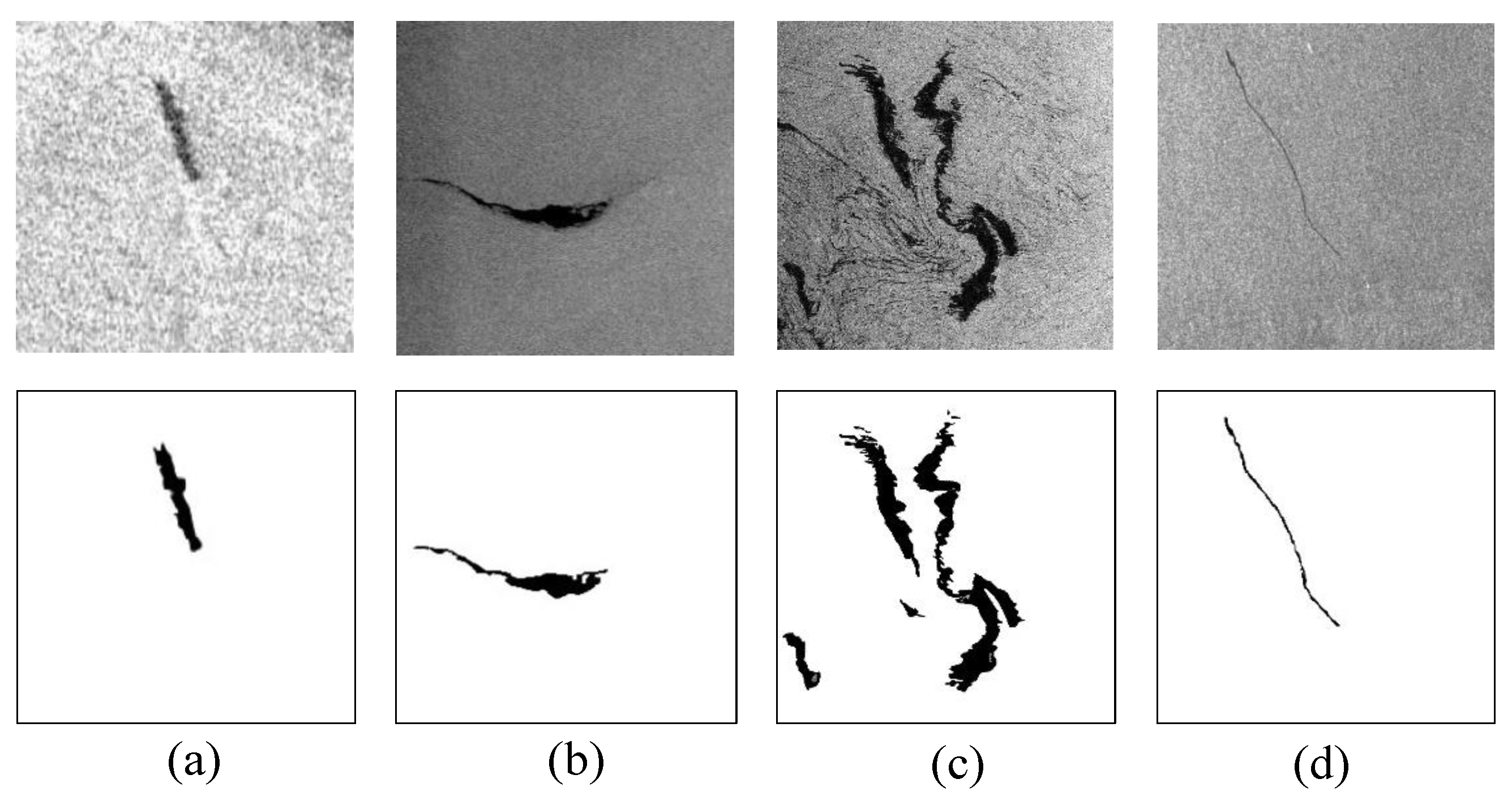
We elaborately set small training data with different characteristics to conduct an experimental evaluation.
The rest of this article is structured as follows.
Section 2 describes our MCAN framework and presents the training procedure.
Section 3 provides the experimental settings and evaluations.
Section 4 discusses the experimental results. Finally,
Section 5 presents conclusions about the proposed method and its performance.
2. Materials and Methods
Adversarial learning with one generator and one discriminator is widely used in the task of semantic segmentation. The generator is trained by a loss function that is automatically learned from the discriminator. The discriminator learns the distribution between the real and generated maps, allowing for flexible losses and alleviating the need for manual tuning.
Oil spill detection with small-data training is a promising and practically significant learning method. It requires a well-designed network and, in the case under study, an efficient training mode in order to learn an effective oil spill detection model. Adversarial learning is adequate for small-data training. This section describes how to detect oil spills via a multiscale conditional adversarial network (MCAN) trained with few samples.
2.1. The MCAN Architecture
We denote an oil spill observation image as , the reference data of the oil spill region as , and the corresponding oil spill detection map produced by the MCAN as . Both and are binary images in which 0 represents the oil spill and 1 represents the ocean surface. We establish multiscale representations for , , and , starting from the 0-th scale.
The representations and at the n-th scale are obtained by downsampling (by averaging values) the 0-th-scale data by a factor , where r is usually set to 2. We denote by the n-th generator network, which produces . The size of is of that of , and is considered as the n-th-scale representation for . Representations across scales from the N-th scale to the 0-th scale form the coarse-to-fine multiscale representation set that is used in the MCAN oil spill detection.
We propose a multiscale conditional adversarial network consisting of a series of generators and discriminators at multiple scales. The generator and the discriminator process representations at the n-th scale.
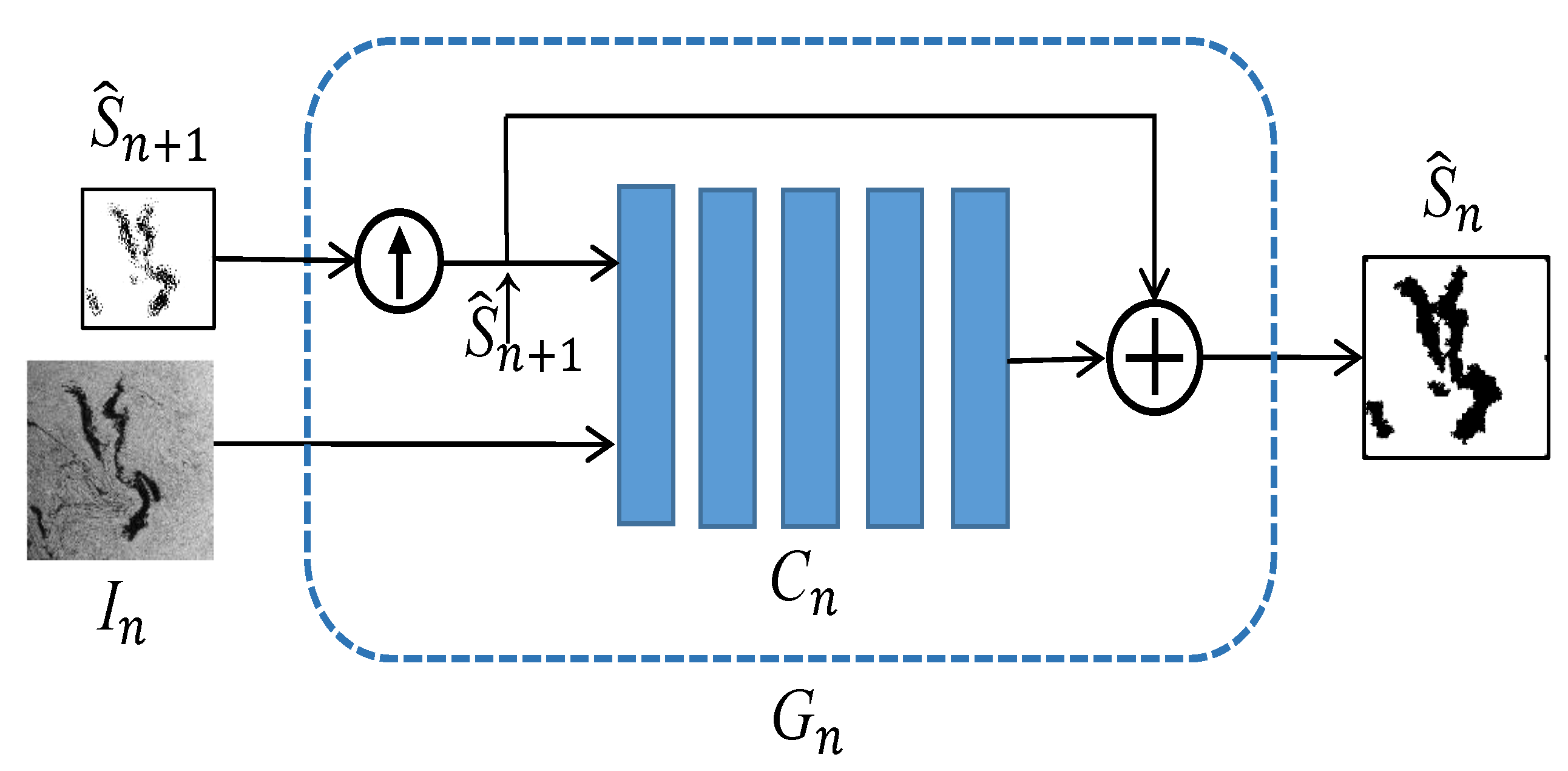
Figure 1 illustrates the architecture of MCAN. The oil spill observation image
and the oil spill detection map
are the input and output of the overall MCAN framework, respectively. The generator
takes both the oil spill observation image
at the
n-th scale and the generated oil spill detection map
at the
-th scale as input and produces the generated oil spill detection map
as the output. The discriminator
takes
or
as input, and it separately outputs the corresponding discriminant scores.
aims to distinguish between the reference oil spill detection map
and the generated oil spill detection map
.
Figure 2 shows the architecture of the generator
at the
n-th scale. The inputs of
are the observation image
and the detection map
from the
-th scale. By upsampling
by a factor
r, we obtain
with the same size of
. The convolutional network
processes the pair
with five convolutional blocks. Each block consists of three layers, including a convolutional layer, a batch normalization (BN) layer, and a LeakyReLU (or Tanh) layer. The sum of the convolutional network’s output and
forms the output of
, i.e., an oil spill detection map
at the
n-th scale. The operation within
is:
The sum is a typical residual learning scheme that enhances the representational power of the convolutional network. At the n-th scale, the generator aims to produce the oil spill detection map as authentically as possible.
At the coarsest scale, the generator
only takes the oil spill observation image
as input and outputs its oil spill detection map
, which is represented as follows:
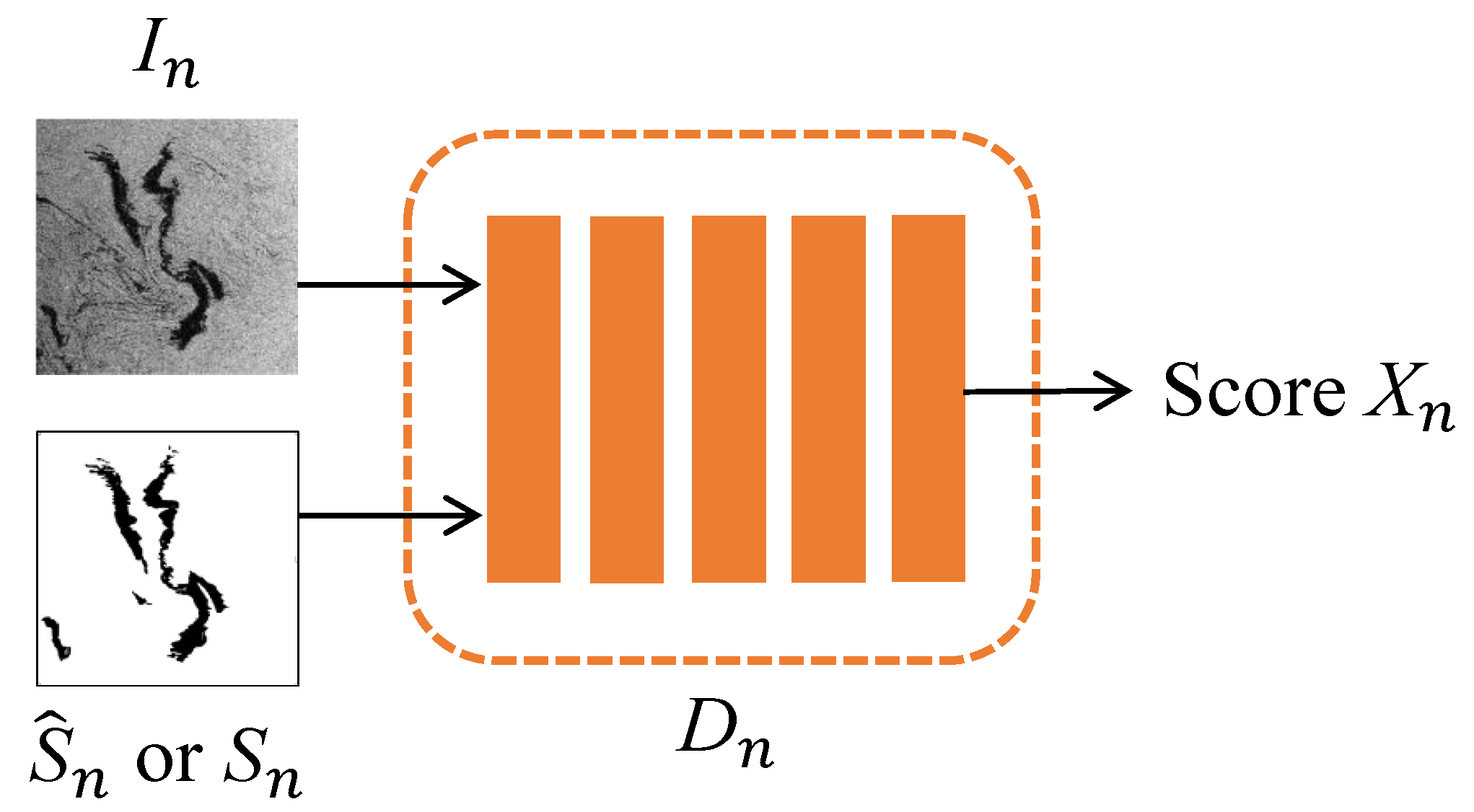
Figure 3 shows the architecture of the discriminator
at the
n-th scale. The network used in
has five convolutional blocks. Each of the first four blocks has a convolutional layer, a batch normalization (BN) layer, and a LeakyReLU layer. The fifth one only has a convolutional layer.
The input of
is either
or
. The output of
is a discriminant score
that reflects the confidence on the detection map:
where
is the average of the feature map
that is output from
’s final convolutional layer. Each element of
corresponds to a patch of the input image. The last output of
integrates all of the elements of
and aims to classify if each patch in the input image is real or generated.
penalizes the generated pair
and favors the actual pair
. At the
n-th scale, the discriminator
tries to distinguish the generated
from the reference data
.
2.2. Training MCAN
The training of MCAN is conducted hierarchically from the
N-th scale to the 0-th scale. At each scale, the training is performed independently in the same manner using a Wasserstein GAN–gradient penalty (WGAN-GP) loss [
39] for stable training. Once the training at the
-th scale has concluded, the generated detection map
is used for the training at the
n-th scale.
The training loss for the generator
is:
where
is a balance parameter. The term
is the adversarial loss that encourages
to generate a detection map
that is as close as possible to the reference data
. The term
is the
norm loss. It penalizes the per-pixel distance between the reference data
and the generated
. Minimizing (
4) trains
to generate detection maps as authentically as possible, and finally, they successfully fool the discriminator.
The training loss for the discriminator
is given as:
where
is a balance parameter, and
denotes a random variable that samples uniformly between
and
. The term
represents the adversarial loss that strengthens the discrimination power of
; it makes
try its best to classify
as false and
as true. The term
is the gradient penalty loss. It results in stable gradients that neither vanish nor explode [
39]. Minimizing (
5) trains
to distinguish the generated detection map from the reference data.
The training procedure of the proposed MCAN is described in Algorithm 1. The input consists of original SAR images and their corresponding reference data of oil spill detection results. The output is the trained parameter set of MCAN. For example, consider the training sample
and its reference data
. If MCAN is set to have three scales,
and
are downsampled to obtain
and
. The training procedure is conducted from generator
and discriminator
. Firstly, the output of
is computed by
. Secondly,
takes
and
separately as input. The parameters of
are updated by Equation (
5), and the parameters of
are updated according to Equation (
4). Thirdly,
and
are concatenated as the input of
to obtain the output
.
and
are updated as Equation (
5) and Equation (
4), respectively. Finally,
and
are concatenated as the input of
to obtain the output
.
and
are updated by Equations (
5) and (
4), respectively. At this point, the two images
and
go through one training iteration to update the parameters of MCAN. The next training sample pair will follow the same procedure as that for
and
.
| Algorithm 1 Training Procedure of the Proposed MCAN Oil Spill Detection Method. |
|
|
for all training epochs do for all scales do Input a downsampled sample and from the -th scale Compute train : Compute as Equation ( 5) and update the parameters of train : Compute as Equation ( 4) and update the parameters of end for end for
|
2.3. Rationale
The capability of MCAN of learning with small data is threefold.
Firstly, the multiscale strategy comprehensively captures the characteristics of oil spills. The multiscale representations characterize oil spills from the coarsest representation at the N-th scale, which reflects the global layouts, to the finest representation at the 0-th scale, which has rich local details. It comprehensively depicts oil spills from both the global and local perspectives and exhibits a representational diversity with few samples.
Secondly, the multiscale learning strategy intrinsically takes advantage of the multiscale representational diversity of the small oil spill data to hierarchically train multiple generators and discriminators. The cascaded coarse-to-fine data flow enhances the model’s representational power due to the benefit of the processing scheme, in which the output of each generator is used as the input of the following finer-scale generator.
Thirdly, data diversity is further increased via the adversarial training in a multiscale manner, where the data generated at one scale are used in training at the subsequent finer scale.
Therefore, MCAN comprehensively mines the characteristics of oil spills on a small-data basis, providing an effective oil spill detection strategy in a situation of limited observations.