Abstract
Satellite imagery has been used to monitor and assess Harmful Algal Blooms (HABs), specifically, cyanobacterial blooms in Lake Erie (the USA and Canada) for over twelve years. In recent years, imagery has been applied to the other Great Lakes as well as other U.S. lakes. The key algorithm used in this monitoring system is the cyanobacterial index (CI), a measure of the chlorophyll found in cyanobacterial blooms. The CI is a “spectral shape” (or curvature) algorithm, which is a form of the second derivative around the 681 nm (MERIS/OLCI) or 678 nm (MODIS) band, which is robust and implicitly includes an atmospheric correction, allowing reliable use for many more scenes than analytical algorithms. Monitoring of cyanobacterial blooms with the CI began with the European Space Agency’s (ESA) Medium Resolution Imaging Spectrometer (MERIS) sensor (2002–2012). With the loss of data from MERIS in the spring of 2012, the monitoring system shifted to using NASA’s Moderate Resolution Imaging Spectroradiometer (MODIS). MODIS has bands that allow computation of a CI product, which was intercalibrated with MERIS at the time to establish a conversion of MODIS CI to MERIS CI. In 2016, ESA launched the Ocean and Land Color Imager (OLCI), the replacement for MERIS, on the Sentinel-3 spacecraft. MODIS can serve two purposes. It can provide a critical data set for the blooms of 2012–2015, and it offers a bridge from MERIS to OLCI. We propose a basin-wide integrated technique for intercalibrating the CI algorithm from MODIS to both MERIS and OLCI. This method allowed us to intercalibrate OLCI CI to MERIS CI, which would then allow the production of a 20-year and ongoing record of cyanobacterial bloom activity. This approach also allows updates as sensor calibrations change or new sensors are launched, and it could be readily applied to spectral shape algorithms.
Keywords:
intercalibration; MERIS; OLCI; MODIS; cyanobacteria; remote sensing; great lakes; Harmful Algal Blooms (HABs) 1. Introduction
Blooms of cyanobacteria are generally considered a harbinger for anthropogenic eutrophication [1]. Potentially massive blooms can have long durations and detrimental environmental and human health impacts [2]. Cyanobacterial blooms are often toxic and can contribute to hypoxia when the blooms senesce and increase the biological oxygen demand. These blooms have a particular affinity for warm stratified water, and as such, blooms of cyanobacteria may become more prevalent in the context of a warming climate [3]. Cyanobacteria can produce various toxins (such as microcystins, anatoxins, and saxitoxin) that pose a health risk and cause mortalities in domestic and wild animal populations [4]. Additionally, several species have compounds such as geosmin that can cause taste and odor issues in drinking water. As a result of these detrimental influences, cyanobacterial blooms are classified as Harmful Algal Blooms (HAB) and should be monitored to reduce potential deleterious impacts.
Perhaps the most effective monitoring, detection, and assessment tool for describing cyanobacterial bloom dynamics is synoptic remote sensing [5,6]. In order to detect any significant increase in cyanobacterial bloom concentration and frequency, there must be an effective and robust algorithm to estimate the extent and severity of these blooms. After an effective algorithm is determined, there needs to be a way to merge the detection technique across different sensors as new ones are deployed and older ones cease operations. These satellite intercalibrations work under the basic premise that two instruments should make identical observations over the same place and time with consistent spatial and spectral responses and identical view angles [7]. Obviously, this is impossible in a real-world situation. However, it is possible to compensate for any error effect by applying a correction if biases are small and the relationship between the two remotely sensed parameters is linear. Many intercalibration studies have been conducted using consistent, bright targets as the intermediary. For example, Yu et al. [8] use the Sonoran Desert, a consistently bright target that is visible to both the GOES-East and GOES-West satellites, to perform an intercalibration between the two satellites based on getting the same reflectance from each sensor. Bouvet et al. [9] describe an important new calibration network (The Radiometric Calibration Network; RadCalNet) that can be used for vicarious calibration based on a set of reference sites of relatively stable surface reflectance in different parts of the world. This network is an important advancement in calibration for land targets. The aquatic environment is far too dynamic for a similar correction technique (and also, the MODIS ocean color bands saturate over bright land targets). A more typical approach for aquatic applications is a point-by-point or pixel-to-pixel matchup [10,11]. The pixel-to-pixel matchup has some caveats. Spatial heterogeneity in water bodies can be substantial and subject to change. Instrument characteristics (ground field-of-view, sensor response functions and others) can all introduce mismatches between sensors even when viewing the same point on the water. The result is noise and biases in the resulting comparison. Here, we propose a technique using pixel integration across the cyanobacterial blooms detected within a basin as a means of reducing analytical error. We compare this technique with the more traditional pixel-to-pixel intercalibration analysis.
1.1. CI Algorithm Usage
Since 2009, the National Oceanic and Atmospheric Administration (NOAA) has released short-term (<1 week) forecasts of cyanobacterial blooms in the western basin of Lake Erie [12]. The primary product used is a satellite proxy for cyanobacterial biomass called the cyanobacterial index (CI). The CI has been used extensively in various freshwater systems throughout the United States [13,14,15,16]. While the algorithm was initially developed by Wynne et al. [17,18] for the MERIS sensor on-board the Envisat spacecraft, it has since been successfully applied to MODIS [10,11]. This was necessary as the Envisat spacecraft ceased operation in April 2012. In early 2016, ESA launched the follow-on mission to MERIS, the Ocean and Land Color Imager (OLCI) on the Sentinel 3A spacecraft that is now operated by the European Organization for the Exploration of Meteorological Satellites (EUMETSAT). A second OLCI sensor was launched on the Sentinel 3B satellite in 2018 (Figure 1). The MODIS sensor is deployed on two spacecraft: Terra (launched December 1999) and Aqua (launched May 2002). Both MODIS sensors are well past their designed mission life and could become inoperable at any time. The OLCI and MERIS sensors are less noisy and have a higher spatial resolution (for MERIS, high-resolution images were only available when specifically recorded or captured by direct broadcast [16]) and would generally be preferred to MODIS for monitoring cyanobacterial blooms [19]. As a result, it is advantageous to develop a way to calibrate the CI algorithm among the three sensors to create a seamless time-series blending the MODIS, MERIS, and OLCI sensors. Having a method for comparing the CI values between sensors is imperative as it could help direct monitoring of cyanobacterial blooms over decadal timescales and address the efficacy of management decisions designed to decrease the detrimental impacts of cyanobacterial blooms. Furthermore, having a technique to compare algorithms across remotely sensed platforms satisfactorily could be beneficial to intercalibrating other biogeophysical algorithms between sensors. Having interoperability between sensors allows for increased observational frequency, as well as an increase in spatial coverage. This will assist in overcoming data gaps due to clouds, orbital patterns, or sunglint.

Figure 1.
The time period when each sensor was actively collecting data. An arrow indicates that the sensor was still collecting data at the time of this writing.
The process described here has three steps: first, to intercalibrate the CI product between MERIS and MODIS; second, to intercalibrate MODIS-to-OLCI CI; third, to use MODIS as a bridge to establish a relationship between OLCI-to-MERIS CI (Figure 1).
1.2. Characteristics of the MODIS, OLCI, and MERIS Sensors
The characteristics of the three sensors that are relevant to this study are described in Table 1. The OLCI, MERIS, and MODIS Terra sensors all have overpass times of approximately 10:30 a.m. local time. The MODIS Aqua sensor has an overflight time in the afternoon, approximately 3 h later. This time lag is sufficiently long to allow bloom locations to shift, introducing a significant bias when scenes from this sensor are compared to comparable ones collected during the earlier OLCI and MERIS overpasses. To ensure the greatest similarity in data collection in space and time [7], only the MODIS Terra data will be used in this study for intercalibrating the different satellite sensors. Consequently, any reference to the MODIS sensor onboard the Terra satellite will be referred hereafter as MODIST. The few references the MODIS instrument on the Aqua satellite will be denoted as MODIS-Aqua.

Table 1.
The sensor spectral and spatial resolution of the bands used in this study. The center wavelength is the input used in Equations (1) and (2).
MODIST has an exact orbital repeat time of 16 days on a 705 km high orbit in descending node. The MERIS sensor has a repeat time of 35 days, which allows global coverage in ~3 days at an orbit height of 800 km. The OLCI sensor has a repeat time of 27 days at an orbital height of 815 km. OLCI has a spatial resolution of 300 m, as did MERIS when data was collected in the Full Resolution (FR) mode. FR collection was not routine over the USA and Canada until 2008 when the Canadian Center for Remote Sensing began acquiring direct broadcast data. The MERIS data set was routinely resampled onboard to a 1200-m spatial resolution in the Reduced Resolution (RR) mode. The RR data was more reliably archived and will be used here, as the FR data was not reliably archived over much of North America. While the algorithm has been applied successfully to all three sensors (OLCI, MODIS, and MERIS) in a variety of water bodies, the validation of the algorithm is not the focus of this manuscript. For more detailed results of the algorithmic performance with these sensors, the reader is directed to Wynne et al. [19] for a detailed look into MODIS, Wynne et al. [18] for validation of MERIS, and Mishra et al. [16] for application to OLCI.
1.3. Study Area
The Laurentian Great Lakes lie between the border of Canada and the United States and feature three catchments that are routinely affected by cyanobacterial blooms: western Lake Erie, Saginaw Bay, and Green Bay [20] (Figure 2). These are large water bodies that have been routinely experienced cyanobacterial blooms over the last 20 years and will be the regions of interest for this study. These lakes are used by millions of people to supply drinking water, and cyanobacterial blooms can be detrimental to human health. For example, in 2014, the metropolitan area of Toledo, OH (USA), issued a “Do Not Drink” order on its municipal water supply due to contamination from the biotoxin, microcystin, caused by cyanobacterial blooms [21]. Green Bay and Lake Erie are separated by over 500 km and do not necessarily appear in the same swath on MERIS (1150 km) or OLCI (1270 km). The CI algorithm has been routinely run on all three basins to monitor and detect cyanobacterial blooms [22]. Western Lake Erie has the largest blooms of the three catchments, and these blooms exhibit a large degree of interannual variability in size and severity (interannual variability is >20 fold) [19]. Saginaw Bay has intermediate-sized blooms with a small degree of interannual variability [19]. Green Bay exhibits the smallest blooms of the three basins, with a high degree of interannual variability in its cyanobacterial biomass [20]. These three regions will be used to make the three CI intercalibration factors (MERIS-to-MODIST, MODIST-to-OLCI, and MERIS-to-OLCI). Using three distinct basins in three different lakes (Figure 2) will yield a more robust dataset as opposed to using only one single basin. All three basins are shallow, relatively warm, eutrophic environments that have the preponderance of their nutrients delivered by a single river. The Fox River supplies 60% of nutrients into Green Bay [23], the Saginaw River supplies approximately 90% of the nutrients into Saginaw Bay [24], and the Maumee River, along with the smaller Cuyahoga and Sandusky Rivers, supplies approximately half of the nutrients into western Lake Erie [25] (Figure 2).
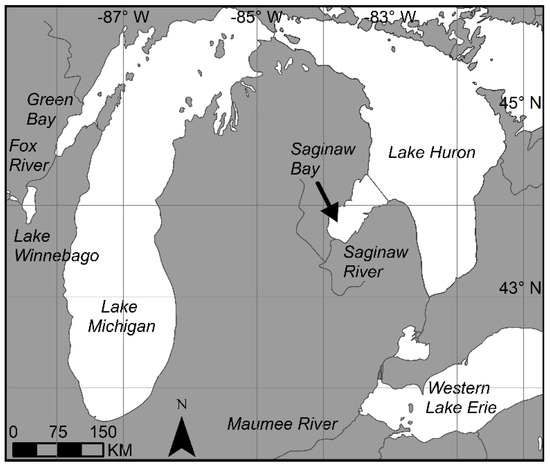
Figure 2.
The locations of the places of interest described in the text.
2. Methods
2.1. Algorithm
The cyanobacteria index (CI) is the algorithm that will be evaluated here. It has been used for over a decade to monitor for cyanobacteria in freshwater bodies. The CI algorithm [17,18] is defined as:
where SS is the spectral shape around the band (about 680 nm) that corresponds to the strong chlorophyll-a absorption peak (Table 1). The SS takes the form of a second derivative and is sometimes called a baseline algorithm:
where ρ is the dimensionless Rayleigh-corrected surface reflectance determined from the instrument-observed top-of-atmosphere radiance by only removing Rayleigh radiances and molecular absorption transmission loss, both corrected for elevation. See Table 1 for band information for each of the sensors such as ρ, and CI is dimensionless.
MERIS-reduced resolution L1B, OLCI-reduced resolution L1B, and Terra L0 imagery were downloaded and processed with NOAA’s Satellite Automated Processing System (SAPS), with methods presented in Wynne et al. [26]. SAPS used the NASA l2gen “rho_s” option to generate the Rayleigh-corrected reflectance, ρ, used in Equation (2). These were mapped, using nearest neighbor, to the same Albers Equal Area protection with a pixel size of 1100 m [26] (Table 1). The results allow consistent comparison of the three sensors.
2.2. Image processing
2.2.1. How Image Pairs Were Selected
For calibration, high-quality image pairs with well-defined cyanobacterial blooms are needed to avoid any artifacts or biases resulting from noise such as sunglint, thin clouds, haze, etc. Image pairs were selected using a sequence of steps. Dates with same-day pairs during blooms were identified. The cyanobacterial bloom season in the Laurentian Great Lakes lasts from 1 June to 31 October and is generally highest in July–October [27]. All images shown here were chosen from the July–October time period from 2002 through 2011 for the MERIS–MODIST matchups and from 2016 to 2019 for the OLCI–MODIST matchups. If one of the images was substantially off-nadir or experienced adjacency effects [28,29], the image pair was rejected. Each image pair was also rejected if the wind speed during acquisition time from either sensor exceeded 8 m s−1 to avoid perceived changes in surface cyanobacterial biomass due to vertical mixing [18]. The remaining image pairs were screened by visually inspecting the RGB true color composites (which are all processed with the same enhancement). Evidence of extensive clouds, cloud shadows, or sun glint in the bloom area in either image led to a rejection of that image pair. Each image pair used for the MODIST-to-MERIS intercalibration is listed in Supplementary Table S1 (n = 42), and each image pair used for the MODIST-to-OLCI intercalibration is listed in Supplementary Table S2 (n = 19). Example image pairs that were rejected based on a visual inspection are described in Supplementary Table S3.
The time differences of the final image pairs were considered acceptable. The largest time difference in the overflight times between the two different spacecraft was 78 min (Figure 3). The average time difference between MERIS and MODIST’s data acquisition was 26 min, with MODIST having an earlier overpass 19 times and MERIS having an earlier overpass 23 times. The OLCI and MODIST image pairs were similar with an average time difference between image acquisition of 25 min, with MODIST having an earlier overpass 8 times and OLCI having an earlier overpass 11 times.
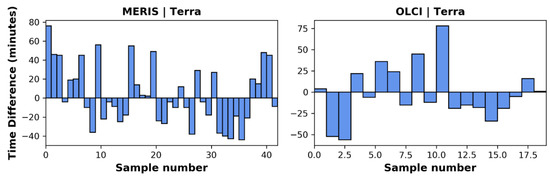
Figure 3.
The left panel shows the time difference in over pass between MERIS and Terra (MERIS–Terra) image pairs used in the analysis here. The right panel shows the time difference in overpass times between OLCI and Terra (OLCI–Terra) image pairs used.
2.2.2. Image Quality Assurance
Radiance signal from the adjacent area surrounding a pixel (the object pixel) can propagate into the sensor field-of-view due to subsequent scattering and cause perturbations in the spectral signature at the pixel in question. This process is usually termed as adjacency effect [29]. In open ocean waters, the adjacency effect may not be an issue due to the spatial homogeneity. However, in coastal waters, it can affect the radiometric quality of the image data. In this study, adjacency issues affecting pixel quality were dealt with as follows. Initially, a 3 × 3 pixel neighborhood surrounding each pixel in the image was identified. Next, if at least one invalid pixel was identified within the 3 × 3 pixel neighborhood as being invalid due to clouds, sun glint, adjacency to land, etc., that pixel was flagged as unusable. When any two images were subsequently being compared as part of the satellite sensor intercalibration analysis, only the pixel pairs that did not suffer for adjacency effects were used. This assured only the highest quality data set was used in the subsequent analyses.
2.3. Pixel to Pixel Technique
The most common technique used for satellite intercalibration is the pixel-to-pixel technique. In this method, the value of corresponding pixels in regions of interest from paired images collected by two different sensors are extracted. In this study, CI values from paired pixels were extracted from the images (MODIST/MERIS or MODIST/OCLI), and least-squares regression analyses were performed. The regression line was forced through the origin, and if this was not so, the low values on the low end might become less than the slope intercept, rendering them meaningless. The intercalibration correction factor (assuming that the relationship of the data pairs passes through the origin) was the slope of the best fit linear regression line of the CI values for each sensor pair. This allowed determining intercalibration factors, which allowed the CI values between sensors to be interconverted [10,11,30]. Henceforth, this approach will be referred to as the pixel technique.
2.4. Integrated Pixel Technique
An alternative to cross-validating satellite imagery on a pixel-to-pixel basis is instead to compare the integrated pixel values across the same regions from paired MERIS, OLCI, or MODIST images. This approach involves first identifying within paired satellite images all pairs of pixels that both have a positive CI value and have no image quality issues in either image (Section 2.2.2). These pixels were then summed to produce an aggregate, or integrated, CI value for each image. This is not an averaging but, instead, a sum of all of the CI positive values from each image. These pairs of summed CI values were then used as the basis for least-square regression analyses to determine the CI relationships between the MODIST, MERIS, and OLCI sensors. As a result, each image pair produces a single pair of values, unlike the pixel technique, which may produce many pairs of values for each pair of images. Henceforth, this approach will be referred to as the integrated technique. As in the pixel technique, the regression line was forced through the origin, and if this was not so, the low values on the low end might become less than the slope intercept, rendering them meaningless.
The integrated technique has a major advantage over the pixel technique. It inherently reduces one key source of error, the mismatch from the spatiotemporal change in bloom distribution between the two sensor overpass times. Cyanobacterial blooms often are patchy with considerable spatial heterogeneity. The dynamic nature of the coastal environment can cause significant changes between overpasses due to shifts in these patches. These changes can cause mismatches in pixel-to-pixel inter-comparisons. However, an integrated technique would be expected to reduce the error from the spatiotemporal variability of the bloom by aggregating across the patchiness in the CI field.
2.5. Model Evaluation
Leave-one-out cross-validation, often used in data-scarce scenarios, is an n-fold cross-validation approach where n is the total number of samples in the dataset. In each fold, the process leaves one sample out for model validation and uses the remaining samples for model calibration, making it similar to a jack-knife estimation [31]. Thus, in each iteration, the model is calibrated with (n−1) data points and validated on the left-out single data point, allowing a validation for each data point. Similar to that idea, here, we followed the leave-one-lake-out validation approach for cross-validation. Least-square regression models for sensor intercalibration were adjusted, using data from two study regions (e.g., Western Lake Erie and Saginaw Bay) and validated using the third region (e.g., Green Bay) as an independent dataset, giving a “leave-one-lake-out” approach. The model (M) was then applied to the appropriate sensor (typically MODIST) for the third lake, and the MERIS or OLCI values for that lake were used as the observed (O) reference data. Thus, the models were calibrated three times, using data from pairs of lakes in combination, as well as validated three times. This “leave-one-lake-out” approach demonstrated the robustness of the regression coefficients or correction factors with a geographically independent data set. Additionally, instead of a single slope, this validation approach provided an uncertainty range around the mean slopes.
The arithmetic mean of the regression coefficients from the three sets of calibration coefficients relating the MERIS-to-MODIST CI and OLCI-to-MODIST CI were finally used to convert OLCI CI observations to MERIS CI-equivalent observations, thereby connecting the MERIS and OLCI time-series. Calibrating for combinations of each of the three regions separately allows an assessment of calibration consistency and validation with the third region.
Error Metrics
We used bias and Mean Absolute Error (MAE) as error metrics [32] for evaluating the calibrations. Bias quantifies the systematic error or the difference between the modeled value (M) (in this case, the MERIS/OLCI CI modeled from MODIST CI) and the observed or reference value (O) (actual MERIS/OLCI CI). As the analysis used log-transformed data, the mean multiplicative bias was determined:
where M is the modeled CI; O is the observed; n is the sample size (number of pixels for the pixel technique or number of image pairs for the integrated image technique). The closer the multiplicative bias is to a value of 1, the less bias the comparisons have and the better the model accuracy. For example, a bias of 1.2 indicates a model that overestimates by about 20%, and a mean bias of 0.8 indicates a model that underestimates by about 20% (there is not an exact match between multiplicative error and percentage error [32].
The MAE captures the error magnitude, highlighting the absolute error between the observed and modeled quantities. The MAE is defined as:
Equation (4) uses the same variables as Equation (3). The MAE in Equation (4) is multiplicative also. An MAE value of 1.2 indicates that the error is about 1.2× the observed value. Multiplicative error metrics are most appropriate for distributions that have errors that are proportional to magnitude.
3. Results
3.1. MERIS-to-MODIST Comparison
3.1.1. Pixel Technique MERIS and MODIST
The pixel-to-pixel matchups for all MERIS-MODIST CI pairs in Supplementary Table S1 produced a slope of 2.76 with an R2 of 0.82 (Figure 4 (left)). The residuals (or difference between pairs) in Figure 4 (right) suggests a skewed error distribution, with a high density of pixels below the zero residual line. The correction factor using the pixel technique to convert from MODIST to MERIS is
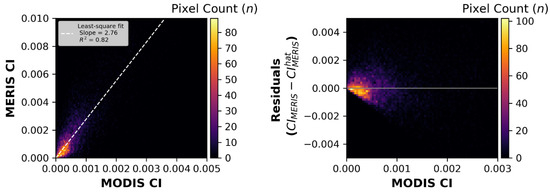
Figure 4.
The left panel shows the calibration based on the pixel-by-pixel matchups between the MODIS Terra and MERIS sensors. The right panel shows the residual errors around the calibration shown on the left. Note the negative bias.
The value of 2.76 (vs. unity) is expected, as the CI algorithm uses different wavelengths for the λ3 term in Equation (2): 748 nm band for MODIST vs. 709 nm band for both MERIS and OLCI. Because water absorbs about 3-fold more at 748 nm than 709 nm, the ρ (water reflectance) at 709 nm will be about 3× that for ρ at 748 nm, resulting in a similarly higher value for the MERIS CI compared to that for MODIST. The error metrics are presented in Table 2.

Table 2.
Metrics described in Section 2.5 between the MERIS–MODIST intercalibration for the pixel technique and integrated technique described in Section 2.3 and Section 2.4, respectively.
3.1.2. Integrated Technique MERIS and MODIST
The integrated technique uses the same 42 image pairs from Section 3.1.1 (see Supplementary Table S2). The intercalibration correlation between the two returned a slope of 2.92 (compared to 2.76 for the pixel technique) and an R2 of 0.97 (Figure 5). Therefore, the correction factor to convert from MODIST to MERIS using the integrated technique is:
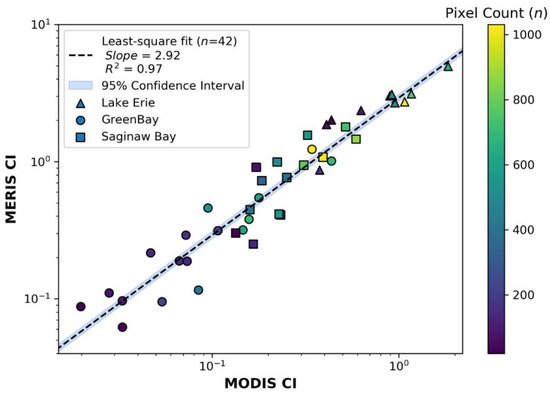
Figure 5.
The matchups between the MODIS TERRA and MERIS sensors using the integrated technique detailed in Section 2.4. The images used to generate these plots are seen in Supplementary Table S1. The symbol shapes represent the three different basins used with triangles from western Lake Erie, circles from Green Bay, and squares from Saginaw Bay.
As noted before, the value of 2.92 is consistent with the difference in the λ3 term, with error metrics in Table 2. Both the integrated technique and the pixel technique had a negligible mean bias (1.009 and 1.003, respectively). However, the pixel technique had a much larger error, with an MAE 44% greater than the integrated technique. The technique also generated a slightly smaller slope (5.5%) than the integrated technique (2.76 vs. 2.92). The integrated technique also showed a uniform distribution of values close to the regression line, indicating linearity and consistency across the range. The difference between the two techniques lies primarily in the challenge of using the pixel technique to successfully match the pixels because discrepancies caused by any bloom movement or differences in ground field-of-view between sensors can manifest as errors due to local biases. Supplementary Table S3 shows examples of image pairs that were not selected as they were deemed flawed, along with the rationale for rejection.
3.1.3. MERIS and MODIST Statistics on Intercalibration
The calibration approach using “leave-one-lake-out” gave quite similar results between regions (Table 3, Figure 6A–C). Figure 6D–F shows the observed MERIS CI to modeled MERIS CI (using MODIST CI) relationships for each of the three regions. All regions behave similarly, with Green Bay having a slightly higher bias relative to western Lake Erie and Saginaw Bay and western Lake Erie has the lowest MAE of the three regions. In the case of this intercalibration, the validation data was outside the calibration range; however, the intercalibration still performed sufficiently, showing linearity and consistency in slope. This consistency indicated extrapolation outside the calibration range is valid.

Table 3.
Least-square fit parameters from MERIS–MODIST intercalibration using different combinations of the regions as seen in Figure 6A–C. WLE, SB, and GB, respectively, represent Western Lake Erie, Green Bay, and Saginaw Bay. Percentages in the slopes indicate the difference of that pair from a calibration based on all regions.

Figure 6.
Various calibration fit parameters. Panel (A) shows the fit between MODIS and MERIS using image pairs from western Lake Erie and Saginaw Bay. Panel (B) shows the fit between MODIS TERRA and MERIS using image pairs from western Lake Erie and Green Bay. Panel (C) shows the fit between MODIS TERRA and MERIS using image pairs from Green Bay and Saginaw Bay. Panel (D) shows the observed MERIS CI to predicted MERIS CI from Green Bay. Panel (E) shows the observed MERIS CI to predicted MERIS CI from Saginaw Bay. Panel (F) shows the observed MERIS CI to predicted MERIS CI from western Lake Erie.
3.2. OLCI-to-MODIST Comparison
3.2.1. Pixel Technique OLCI to MODIST
The pixel-to-pixel intercalibration between OLCI and MODIST image pairs (Supplemental Table S2) produced a slope of 2.75 and an R2 of 0.86 (Figure 7). As was the case in the MERIS-to-MODIST analysis, the residuals show a skewed error distribution, with a high density of pixels in the mid-range (0.00–0.001), showing a negative bias. The relationship to go from MODIST to OLCI using the pixel technique is seen in Equation (7).
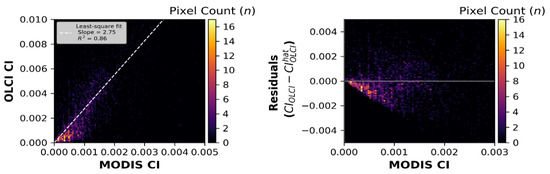
Figure 7.
The left panel shows calibration based on the pixel-by-pixel matchups between the MODIS. Terra and OLCI sensors. (The images used to generate these plots are seen in Supplementary Table S2). The right panel shows the residual errors around the calibration shown in the left panel.
Unlike the MERIS–MODIST intercalibration, where both techniques showed negligible bias, the integrated technique for OLCI to MODIST led to a significantly smaller bias (down ~24% to 0.94). Likewise, the MAE showed ~29% less error using the integrated technique relative to the pixel technique.
3.2.2. Integrated Technique OLCI to MODIST
The intercalibration using the integrated technique (Figure 8) uses the same image pairs as the pixel technique (Supplemental Table S2). The R2 increases from 0.86 to 0.98 relative to the pixel technique, and the slope decreases slightly from 2.75 to 2.71. The equation to go from MODIST to OLCI using the integrated technique is shown in Equation (8).

Figure 8.
The matchups between the MODIS TERRA and OLCI sensors using the integrated technique detailed in Section 2.4. The images used to generate these plots are seen in Supplementary Table S2. The symbol shapes represent the three different basins used with triangles from western Lake Erie, circles from Green Bay, and squares from Saginaw Bay.
No residual bias around the regression line is evident, unlike for the pixel-to-pixel intercalibration. Most values fall close to the regression line, and those at the lower end are equally distributed above and below the line, with two points well above (points 15 and 11) and three below (points 8, 17, and 12) (Figure 8; Supplementary Tables S1 and S2).
While both the pixel technique and the integrated technique produced equivalent slopes for OLCI (2.75 vs 2.71, respectively) (Table 4), the subsequent error metrics (bias and MAE) were much different. For OLCI, the integrated technique had a slight negative bias (0.94), while the pixel technique had a strong negative bias (0.77). This differs from the MODIST–MERIS, where both techniques had a negligible bias. The pixel technique also had a much larger error (1.76) than the integrated technique (1.25), just as was seen with MERIS. In this case, the pixel technique produced substantially large errors that may lead to lower confidence in the resulting calibration.

Table 4.
Metrics described in Section 2.5 between the OLCI–MODIST intercalibration for the pixel technique and integrated technique described in Section 2.3 and Section 2.4, respectively.
3.2.3. MERIS and MODIST Statistics on Intercalibration
Figure 9A–C shows the calibration fit parameters for the OLCI–MODIST intercalibration for each combination of the three regions, with results summarized in Table 5. Figure 9D–F shows the observed OLCI to modeled OLCI (using MODIST) relationships for each of the three regions. There is more discrepancy within the regions using the OLCI to MODIST intercalibration among the three geographical regions than there was between the MERIS–MODIST intercalibration. Likewise, there was much more variability geographically in the MAE, with western Lake Erie and Saginaw Bay having quite similar values (>1% change) but with Green Bay having a much lower error with MAE some 12% lower.
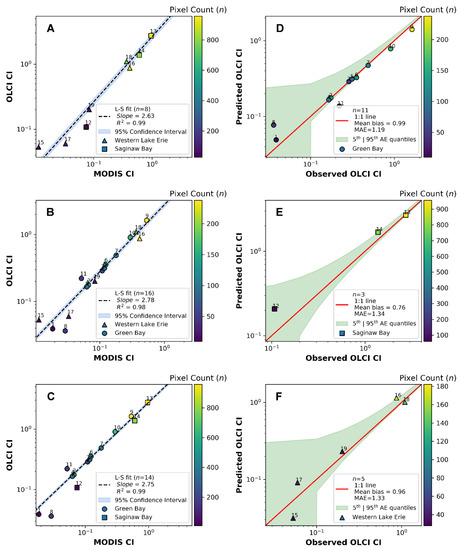
Figure 9.
Various calibration fit parameters. Panel (A) shows the fit between MODIS TERRA and OLCI using image pairs from western Lake Erie and Saginaw Bay. Panel (B) shows the fit between MODIS and OLCI using image pairs from western Lake Erie and Green Bay. Panel (C) shows the fit between MODIS and OLCI using image pairs from Green Bay and Saginaw Bay. Panel (D) shows the observed OLCI CI to predicted OLCI CI from Green Bay. Panel (E) shows the observed OLCI CI to predicted OLCI CI from Saginaw Bay. Panel (F) shows the observed OLCI CI to predicted OLCI CI from western Lake Erie.

Table 5.
Least-square fit parameters from the OLCI–MODIST CI intercalibration as seen in Figure 9A–C based on the integrated technique. Percentages in the slopes indicate the difference of that pair from a calibration based on all regions.
3.3. MERIS–OLCI Intercalibration
The final intercalibration coefficients estimated from the leave-one-lake-out approach and based on the integrated technique are summarized in Table 6. These coefficients are the slopes of the regression lines between all three sensors for all three regions. To compare OLCI to MERIS, the relationships between MODIST and MERIS/OLCI were used as an intermediary using the cross-regional averages (Table 6). Using the calibration coefficients from Table 6 yields the following set of equations (Equations (9) and (10) represent the updated Equations (6) and (8), respectively, after replacing the slopes with the cross-regional average slopes.):

Table 6.
Final intercalibration coefficients between sensors and regions.
Currently, the MERIS calibration is more stable than the OLCI calibration, likely because there has been sufficient time to properly calibrate the sensor, therefore converting OLCI to MERIS is the more appropriate choice as compared to converting MERIS to OLCI. Substituting the CIMODIST with the CIOLCI from Equation (11) into Equation (9) yields:
Solving Equation (12) will yield the final relationship between the CIMERIS and the CIOLCI expressed as:
4. Discussion
The need to merge cyanobacterial index (CI) data from multiple sensors for environmental analyses will become increasingly common [33]. This will be necessary to determine the efficacy of management strategies to control cyanobacterial bloom intensity, such as nutrient reductions on decadal time scales. If agricultural best management practices are amended, the need to synoptically differentiate any impacts through the changing of these practices must be taken into account [34]. The timing, severity, location, and size of cyanobacterial blooms can be used to test the efficacy of these changes. Further, if there are differences in the physical manifestation of the bloom (i.e., timing, severity, location, and size), this could be a harbinger for an ecological shift within a given ecosystem. This study examined both the traditional pixel-to-pixel technique and a new image-to-image integrated technique for intercalibrating the CI algorithm from the MODIST, MERIS, and OLCI sensors. Being able to reliably compare the CI values between sensors will allow the production of a >20 year CI time-series in numerous geographically dispersed water bodies. These time-series will prove useful in retrospectively evaluating previous management decisions and in documenting temporal changes in cyanobacterial bloom intensity.
In this study, the image-to-image integrated technique exhibited much lower error and reduced bias than the pixel-to-pixel technique. The residual CI distributions produced by the pixel technique showed skewed bias in the residuals (Figure 4B and Figure 7B), which did not occur with the integrated technique (Figure 5 and Figure 8). Additionally, as the MODIST CI increased, the more negative the MERIS or OLCI residuals became when using the pixel technique (Figure 4B and Figure 7B). The integrated technique did not exhibit such biases over the entire range of CI values, with the higher values converging on the 1:1 line (Figure 5 and Figure 8). Pixel-to-pixel comparisons would be expected to have this problem because any shifts in the distribution of the variable being measured between overflight times or alignment issues can introduce noise confounding intercalibration (Figure 4B and Figure 7B for the pixel technique; 5 and 8 for the pixel technique for integrated technique). The integrated technique, in contrast, provides a more robust analysis option for evaluating the influence of individual image pairs on the calibration (e.g., Figure 6A–C and Figure 9A–C). In a pixel-to-pixel technique, the statistical influence of the pixels from individual scenes cannot be readily evaluated and would require more complex analysis. Any skewing of pixels from CI image pairs at the low or high end (those pairs with maximum statistical leverage) would bias the results of the comparison. Skewing could occur with even a one or two-pixel offset in the actual (or apparent) location of an intense bloom between two images. This problem is mostly removed by the integration technique, as the offset pixels are contained within the integrated region of the bloom.
The calibration coefficient between the MODIST and MERIS for the pixel and integrated techniques differed by 5% (Table 4), while the coefficient between the pixel and integrated technique for the MODIST–OLCI matchup differed by 1%. However, as noted above, the pixel technique for MODIST to OLCI had a severe bias, which can lead to questions on the accuracy of the calibration. The integrated technique did not have this problem. OLCI appeared to miss the lowest CI values (Figure 7) that MODIST and MERIS detect. MERIS has had much more time for calibration, and it is now at the fourth reprocessing. As the OLCI calibration is developed and improves, it is likely to see shifts in the calibration, potentially reducing the difference. Most calibration is conducted on a band-by-band basis. Subtle inter-band differences within the uncertainties of the band calibration can affect a shape algorithm such as the CI [35]. A spectral shape method can detect these residual differences, providing a means of improving the inter-band calibration [35]. The integrated technique can provide a more reliable method for intercalibrating other biophysical variables across sensors as well. A similar approach has been used to calibrate MODIS [36,37]. Specifically, data sets were integrated over space and time to compare satellites for such issues as trends and calibrating for cross-scan polarization.
We carried out sensitivity analysis using bootstrap simulation to find out how stable the slope parameters were with respect to the effect from the points of leverage or influence. We repeated the simulation for 1000 runs for MERIS–MODIS analysis. OLCI–MODIS sensitivity analysis was repeated 171 times based on the number of unique permutations possible with a sample size of 17. At every step of the iteration, 39 out of 42 of the MERIS–MODIS samples and 17 out of 19 samples were randomly selected without replacement. By doing so, 5% and 10% of MERIS–MODIS and OLCI–MODIS pairs were left out to evaluate their influence on the regression slope. The median slope from the sensitivity analysis was identical to the reported slopes in Figure 5 and Figure 7 (Table 7). The variability of the MERIS–OLCI slope is expected to be within 2.87–2.99, which is −1.7% and +2.4% of the median value of 2.92. Similarly, the OLCI–MODIS slope is likely to be within 2.61–2.81 (−3.7% or +3.5% around the median of 2.71). While more samples may lead to more robust statistics, special attention was given to image quality, and only the very best image pairs were selected for analysis.

Table 7.
Descriptive statistics of regression slopes from the bootstrap simulation.
This study shows the CI intercalibration is consistent between the three basins in the Laurentian Great Lakes and that the integration technique is robust. The intercalibration coefficients presented here were consistent with no outliers compared to those derived with the pixel-to-pixel technique used in Wynne et al. [10]. We should note that the CI algorithm does not require an atmospheric correction [26]. It was based on the Maximum Chlorophyll Index (MCI) presented by Gower et al. [38], who used top-of-atmosphere reflectance. The calibration coefficient between MODIS and MERIS derived here was much higher than in Wynne et al. [10], primarily due to an issue with the measurement units. The original MERIS reflectance data sets were expressed as L2 files from the original ESA processing as having units of per steradian (sr−1) (although presented as dimensionless). This translates as having the initial L2 products being off by a factor of π sr. By multiplying the 1.33 correction factor derived by Wynne et al. [10] by π, the new factor becomes 4.17, which is considerably closer to the correction factor of 2.94 derived here. The remaining ~30 % difference (between 4.17 and 2.94) could be explained by several reasons. ESA has recalibrated and reprocessed the MERIS data several times since the analysis of Wynne [10]. This study also used rigorous quality assurance for both the image pairs selected and the pixels used for analysis. Further, Wynne et al. [10] used only MODIS Aqua imagery, which is collected about 3 h later than MERIS and OLCI. By employing MODIS Terra imagery in this study, which has comparable overpass times to MERIS and OLCI, it was possible to reduce any impacts of wind events or biomass changes in surface waters unaccounted for in the original calibration study. This, in turn, reduced misfit, thereby improving the calibrations.
While this study focuses on intercalibrating the CI algorithm among three large satellite missions in the Great Lakes, the techniques presented here could be adapted to other areas and sensors. The integrated technique could be applied to any remotely sensed image products from any number of sensors and algorithms. The integrated technique is not designed to better approximate an in situ measurement but instead to determine how well an algorithm from one sensor approximates the same algorithm on a different sensor. As a result, the integrated technique could also be applied to small satellites, such as CubeSats, which generally have poor absolute radiometric calibration, but show linearity. Two excellent review articles highlight water quality parameters that could be tested using the integrated technique for sensor intercalibration [39,40].
5. Conclusions
Using an integrated technique for intercalibration provides better metrics and more consistent results for calibrating an algorithm between the sensors than the pixel technique. The more typical pixel-to-pixel technique did produce equivalent calibration coefficients (slopes) for MODIST to OLCI but with greater uncertainty. The comparison of three separate lakes separated by up to 500 km showed a robust and consistent result. This integrated technique allows us to calibrate across the three sensors, MERIS, OLCI, MODIST, and by inference, also MODIS-Aqua (as NASA calibrates Terra to Aqua). The results further allow us to adjust OLCI data sets to match MERIS. For the calibration identified here, OLCI underestimates the CI relative to MERIS by 6% (Equation (13)). The results of this study allow the development of a consistent time-series across MERIS, MODIS, and OLCI for the CI product. The calibration should work in other lakes which are large enough for detection by these sensors. The correction can be updated using the same scenes with changes in calibration. The results will help in the analysis of time-series and in the comparison of MERIS and OLCI for climate changes in cyanobacterial blooms. The integrated technique can be applied to other algorithms and sensors to allow continuity in longer-term datasets.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13122305/s1, Table S1: MODIST-MERIS image pairs used for intercalibration, Table S2: MODIST–OLCI image pairs used for intercalibration, Table S3: shows an explanation of why image pairs were accepted or rejected from inclusion in Table 2.
Author Contributions
Conceptualization, T.T.W., S.M. and R.P.S.; methodology, T.T.W., S.M., A.M. and R.P.S.; validation, T.T.W., S.M., A.M. and R.P.S.; formal analysis, T.T.W., S.M., A.M. and R.P.S.; investigation, T.T.W., S.M., A.M. and R.P.S.; writing—original draft preparation, T.T.W., S.M., R.W.L. and R.P.S.; writing—review and editing, T.T.W., S.M., A.M., R.W.L. and R.P.S.; visualization, T.T.W., S.M., A.M., R.W.L. and R.P.S.; supervision, T.T.W., S.M., A.M. and R.P.S.; project administration, T.T.W. and R.P.S.; funding acquisition, R.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded through the Great Lakes Restoration Initiative.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is available on request. The scientific results and conclusions, as well as any views or opinions expressed herein, are those of the author(s) and do not necessarily reflect the official policy or position of the NOAA or Department of Commerce.
Acknowledgments
The authors would like to acknowledge Bryan Eder’s assistance with the creation of the map in Figure 2. The authors would like to thank Richard Johansen and Molly Reif for insightful comments that strengthened this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Boesch, D. Barriers and Bridges in Abating Coastal Eutrophication. Front. Mar. Sci. 2019, 6, 123. [Google Scholar] [CrossRef]
- Michalak, A.M.; Anderson, E.J.; Beletsky, D.; Boland, S.; Bosch, N.S.; Bridgeman, T.B.; Chaffin, J.D.; Cho, K.; Confesor, R.; Daloglu, I.; et al. Record-setting algal bloom in Lake Erie caused by agricultural meteorological trends consistent with expected future conditions. Proc. Natl. Acad. Sci. USA 2012, 110, 6448–6452. [Google Scholar] [CrossRef] [PubMed]
- Paerl, H.W.; Huisman, J. Blooms like it hot. Science 2008, 320, 57–58. [Google Scholar] [CrossRef] [PubMed]
- Chorus, I.; Bartram, J. Toxic Cyanobacteria in Water: A Guide to Their Public Health Consequences, Monitoring and Management; World Health Organization: London, UK, 1999. [Google Scholar]
- Kutser, T.; Metsamaa, L.; Strömbeck, N.; Vahtmäe, E. Monitoring cyanobacterial blooms by satellite remote sensing. Estuar. Coast. Shelf Sci. 2006, 67, 303–312. [Google Scholar] [CrossRef]
- Kutser, T. Passive optical remote sensing of cyanobacteria and other intense phytoplankton blooms in coastal and inland waters. Int. J. Remote Sens. 2009, 30, 4401–4425. [Google Scholar] [CrossRef]
- Chander, G.; Hewison, T.; Fox, N.; Wu, X.; Xiong, X.; Blackwell, W.J. Overview of Intercalibration of Satellite Instruments. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1056–1080. [Google Scholar] [CrossRef]
- Yu, F.; Wu, X.; Grotenhuis, M.; Qian, H. Intercalibration of GOES Imager visible channels over the Sonoran Desert. J. Geophys. Res. Atmos. 2014, 119, 8639–8658. [Google Scholar] [CrossRef]
- Bouvet, M.; Thome, K.; Berthelot, B.; Bialek, A.; Czapla-Myers, J.; Fox, N.P.; Goryl, P.; Henry, P.; Ma, L.; Marcq, S.; et al. RadCalNet: A Radiometric Calibration Network for Earth Observing Imagers Operating in the Visible to Shortwave Infrared Spectral Range. Remote Sens. 2019, 11, 2401. [Google Scholar] [CrossRef]
- Wynne, T.; Stumpf, R.; Briggs, T. Comparing MODIS and MERIS spectral shapes for cyanobacterial bloom detection. Int. J. Remote Sens. 2013, 34, 6668–6678. [Google Scholar] [CrossRef]
- Moradi, M. Comparison of the efficacy of MODIS and MERIS data for detecting cyanobacterial blooms in the southern Caspian Sea. Mar. Pollut. Bull. 2014, 87, 311–322. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Fahnenstiel, G.L.; Dyble, J.; Schwab, D.J.; Joshi, S.J. Evolution of a cyanobacterial bloom forecast system in western Lake Erie: Development and initial evaluation. J. Great Lakes Res. 2013, 39, 90–99. [Google Scholar] [CrossRef]
- Lunetta, R.S.; Schaeffer, B.A.; Stumpf, R.P.; Keith, D.L.; Jacobs, S.A.; Murphy, M.S. Evaluation of cyanobacteria cell count de-tection derived from MERIS imagery across the eastern USA. Remote Sens. Environ. 2015, 157, 24–34. [Google Scholar] [CrossRef]
- Schaeffer, B.; Loftin, K.; Stumpf, R.; Werdell, P. Agencies Collaborate, Develop a Cyanobacteria Assessment Network. EOS 2015, 96. [Google Scholar] [CrossRef]
- Clark, J.M.; Schaeffer, B.A.; Darling, J.A.; Urquhart, E.A.; Johnson, J.M.; Ignatius, A.R.; Myer, M.H.; Loftin, K.A.; Werdell, J.P.; Stumpf, R.P. Satellite monitoring of cyanobacterial harmful algal bloom frequency in recreational waters and drinking water sources. Ecol. Indic. 2017, 80, 84–95. [Google Scholar] [CrossRef]
- Mishra, S.; Stumpf, R.P.; Schaeffer, B.A.; Werdell, P.J.; Loftin, K.A.; Meredith, A. Measurement of Cyanobacterial Bloom Magnitude using Satellite Remote Sensing. Sci. Rep. 2019, 9, 18310. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Warner, R.A.; Tester, P.A.; Dyble, J.; Fahnenstiel, G.L. Relating spectral shape to cyanobacterial blooms in the Laurentian Great Lakes. Int. J. Remote Sens. 2008, 29, 3665–3672. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Tomlinson, M.C.; Dyble, J. Characterizing a cyanobacterial bloom in western Lake Erie using satellite imagery and metrological data. Limnol. Oceanogr. 2010, 55, 2025–2036. [Google Scholar] [CrossRef]
- Wynne, T.T.; Stumpf, R.P.; Litaker, R.W.; Hood, R.R. Cyanobacterial bloom phenology in Saginaw Bay from MODIS and a comparative look with western Lake Erie. Harmful Algae 2021, 103, 101999. [Google Scholar] [CrossRef]
- Sayers, M.; Fahnenstiel, G.L.; Shuchman, R.A.; Whitley, M. Cyanobacterial blooms in three eutrophic basins of the Great Lakes: A comparative analysis using remote sensing. Int. J. Remote Sens. 2016, 37, 4147–4148. [Google Scholar] [CrossRef]
- Steffen, M.M.; Davis, T.W.; McKay, R.M.; Bullerjahn, G.S.; Krausfeldt, L.E.; Stough, J.M.A.; Neitzey, M.L.; Gilbert, N.E.; Boyer, G.L.; Johengen, T.H.; et al. Ecophysiological examination of the Lake Erie Mi-crocystis bloom in 2014: Linkages between biology and the water supply shutdown of Toledo, Ohio. Environ. Sci. Technol. 2017, 51, 6745–6755. [Google Scholar] [CrossRef] [PubMed]
- NOAA. Harmful Algal Bloom Monitoring System. 2021. Available online: https://coastalscience.noaa.gov/research/stressor-impacts-mitigation/hab-monitoring-system/ (accessed on 11 January 2021).
- Dolan, D.M.; Chapra, S.C. Great Lakes total phosphorus revisited: 1. Loading analysis and update (1994–2008). J. Great Lakes Res. 2012, 38, 730–740. [Google Scholar] [CrossRef]
- Bierman, V.J.; Dolan, D.M.; Kasprzyk, R.; Clark, J.L. Retrospective analysis of the response of Saginaw Bay, Lake Huron, to reductions in phosphorus loadings. Environ. Sci. Technol. 1984, 18, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Baker, D.B.; Confesor, R.; Ewing, D.E.; Johnson, L.T.; Kramer, J.W.; Merryfield, B.J. Phosphorus loading to Lake Erie from the Maumee, Sandusky and Cuyahoga rivers: The importance of bioavailability. J. Great Lakes Res. 2014, 40, 502–517. [Google Scholar] [CrossRef]
- Wynne, T.T.; Meredith, A.; Stumpf, R.P.; Briggs, T.O.; Litaker, R.W. Harmful Algal Bloom Forecasting Branch Ocean Color Satellite Imagery Processing Guidelines; NOAA Technical Memorandum NOS NCCOS 252; NOAA: Silver Spring, MD, USA, 2018; 48p. [Google Scholar]
- Wynne, T.T.; Stumpf, R.P. Spatial and Temporal Patterns in the Seasonal Distribution of Toxic Cyanobacteria in Western Lake Erie from 2002–2014. Toxins 2015, 7, 1649–1663. [Google Scholar] [CrossRef]
- Matthews, M.; Odermatt, D. Improved algorithm for routine monitoring of cyanobacteria and eutrophication in inland and near-coastal waters. Remote Sens. Environ. 2015, 156, 374–382. [Google Scholar] [CrossRef]
- Otterman, J.; Fraser, R.S. Adjacency effects on imaging by surface reflection and atmospheric scattering: Cross radiance to zenith. Appl. Opt. 1979, 18, 2852–2860. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, D.; Xu, H.; Wu, C. Intercalibration between DMSP/OLS and VIIRS night-time light images to evaluate city light dynamics of Syria’s major human settlement during Syrian Civil War. Int. J. Remote Sens. 2017, 38, 5934–5951. [Google Scholar] [CrossRef]
- Webb, G.I.; Sammut, C.; Perlich, C.; Horváth, T.; Wrobel, S.; Korb, K.B.; Noble, W.S.; Leslie, C.; Lagoudakis, M.G.; Quadrianto, N.; et al. Leave-One-Out Cross-Validation. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2011; pp. 600–601. [Google Scholar] [CrossRef]
- Seegers, B.N.; Stumpf, R.P.; Schaeffer, B.A.; Loftin, K.A.; Werdell, P.J. Performance metrics for the assessment of satellite data products: An ocean color case study. Opt. Express 2018, 26, 7404–7422. [Google Scholar] [CrossRef]
- Poom-Medina, J.L.; Jimenez-Escalona, J.C.; Villa-Martinez, H.A. Comparison of two data sets from two different satellite sensors at @490 nm in the same space-temporal window over the Gulf of California area. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI, Strasbourg, France, 9–12 September 2019; International Society for Optics and Photonics: Bellingham, WA, USA, 2019; Volume 11149, p. 1114910. [Google Scholar] [CrossRef]
- Zhang, W.; Wilson, R.S.; Burnett, E.; Irwin, E.G.; Martin, J.F. What motivates farmers to apply phosphorus at the “right” time? Survey evidence from the Western Basin of Lake Erie. J. Great Lakes Res. 2016, 42, 1343–1356. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Werdell, J.P. Adjustment of ocean color sensor calibration through multi-band statistics. Opt. Express 2010, 18, 401–412. [Google Scholar] [CrossRef]
- Kwiatkowska, E.J.; Franz, B.A.; Meister, G.; McClain, C.R.; Xiong, X. Cross calibration of ocean-color bands from moderate resolution imaging spectroradiometer on Terra platform. Appl. Opt. 2008, 47, 6796–6810. [Google Scholar] [CrossRef]
- Meister, G.; Franz, B.A.; Kwiatkowska, E.J.; McClain, C.R. Corrections to the Calibration of MODIS Aqua Ocean Color Bands Derived From SeaWiFS Data. IEEE Trans. Geosci. Remote. Sens. 2011, 50, 310–319. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Goncalves, P. Global monitoring of plankton blooms using MERIS MCI. Int. J. Remote Sens. 2008, 29, 6209–6216. [Google Scholar] [CrossRef]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [PubMed]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel spectra-derived features for empirical retrieval of water quality parameters: Demonstrations for OLI, MSI, and OLCI sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).