An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring
Abstract
1. Introduction
2. Materials and Methods
2.1. The Characteristics and Extraction of a Multipath
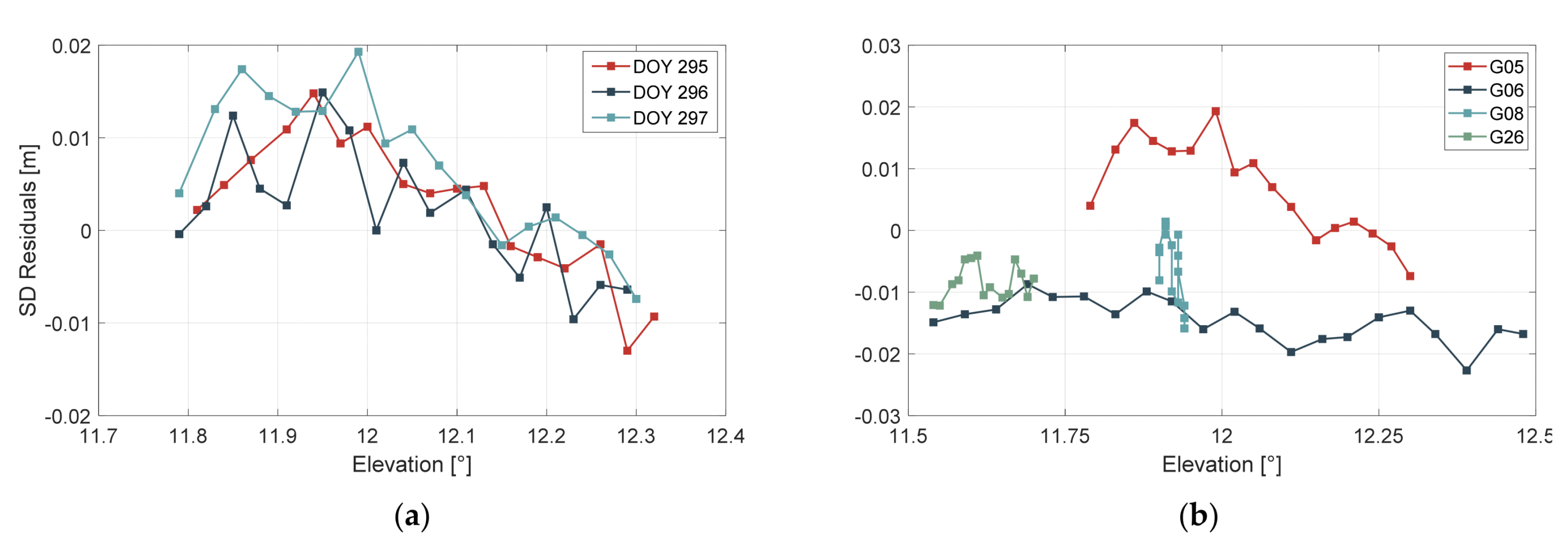
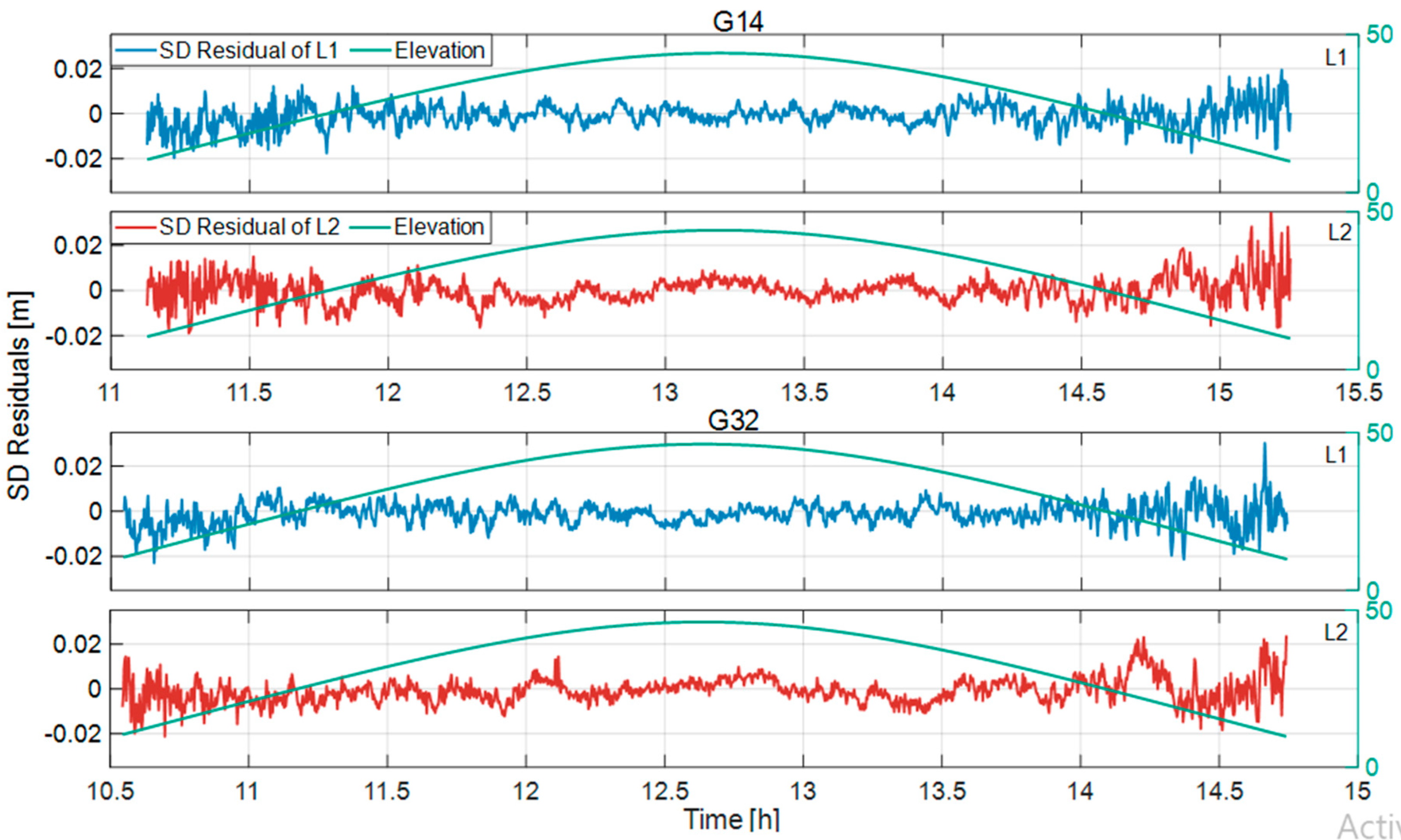
2.1.1. The Characteristics of a Multipath
2.1.2. The Extraction of SD Residuals Based on the SD Model
2.2. The Improved MHM Algorithm (MHM_V)
2.2.1. The Introduction of VMD
| Algorithm 1: VMD algorithm used to decompose the SD residual time series |
| 1: Initialize , where n is the iteration number. |
| 2: repeat the entire cycle, . |
| 3: For do |
| 4: Update for all , using Equation (6); |
| 5: Update , using Equation (8); |
| 6: end for |
| 7: Do dual ascent for all , using Equation (7); |
| 8: until Iterative constraints satisfied: |
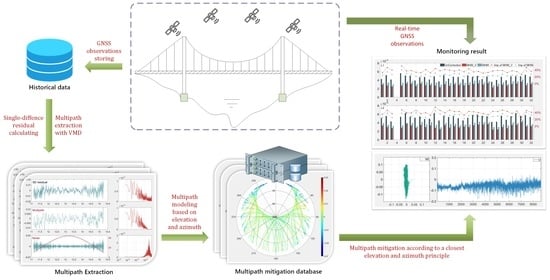
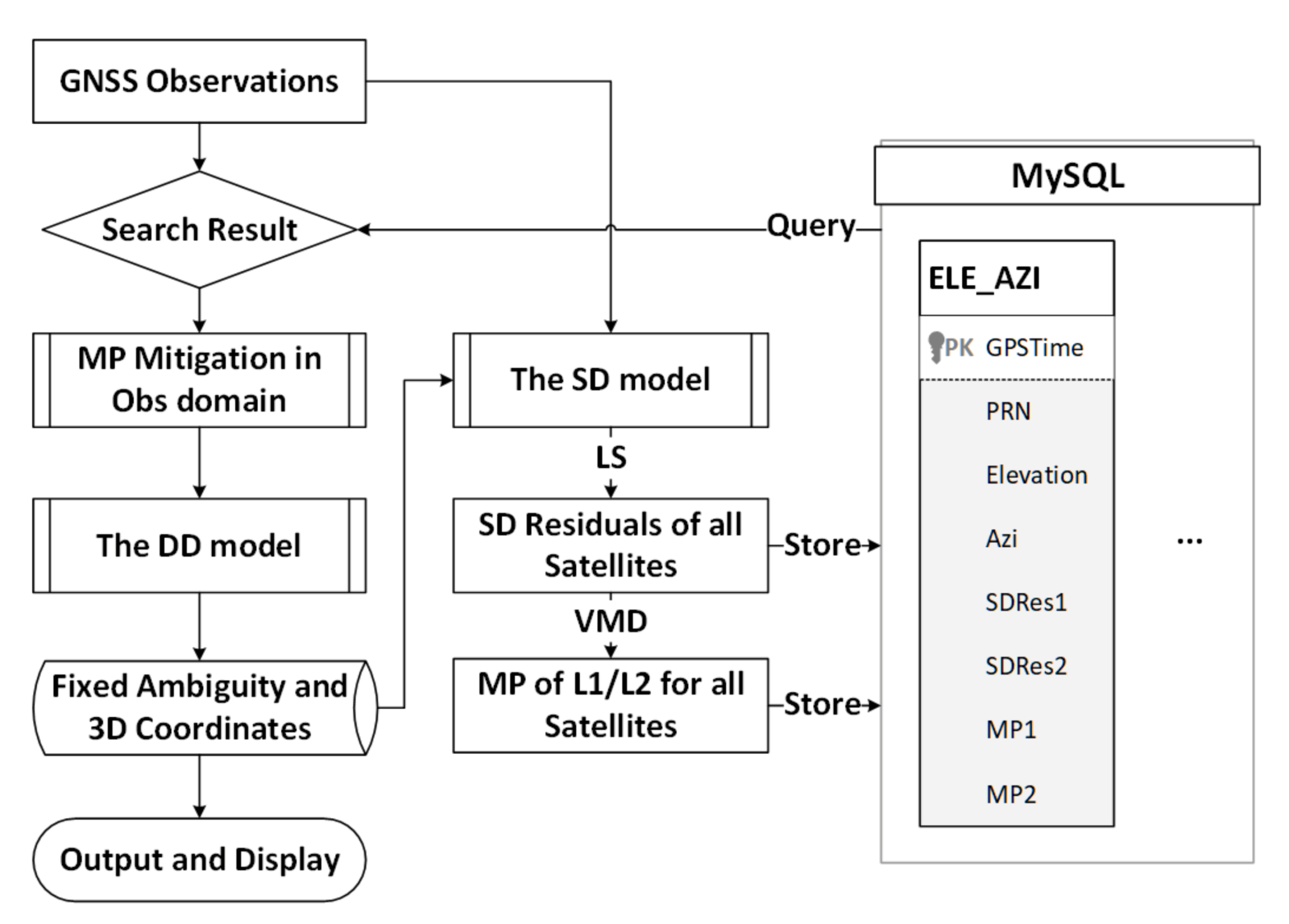
2.2.2. The Algorithm Flow of MHM_V
- The dynamic model is used to calculate the current daily observation data, and the integer solution of ambiguity and three-dimensional coordinates are obtained based on the double-difference model.
- The integer ambiguity and three-dimensional coordinates in step 1 are substituted into the single-difference model, and the single-difference residuals of all satellites are obtained.
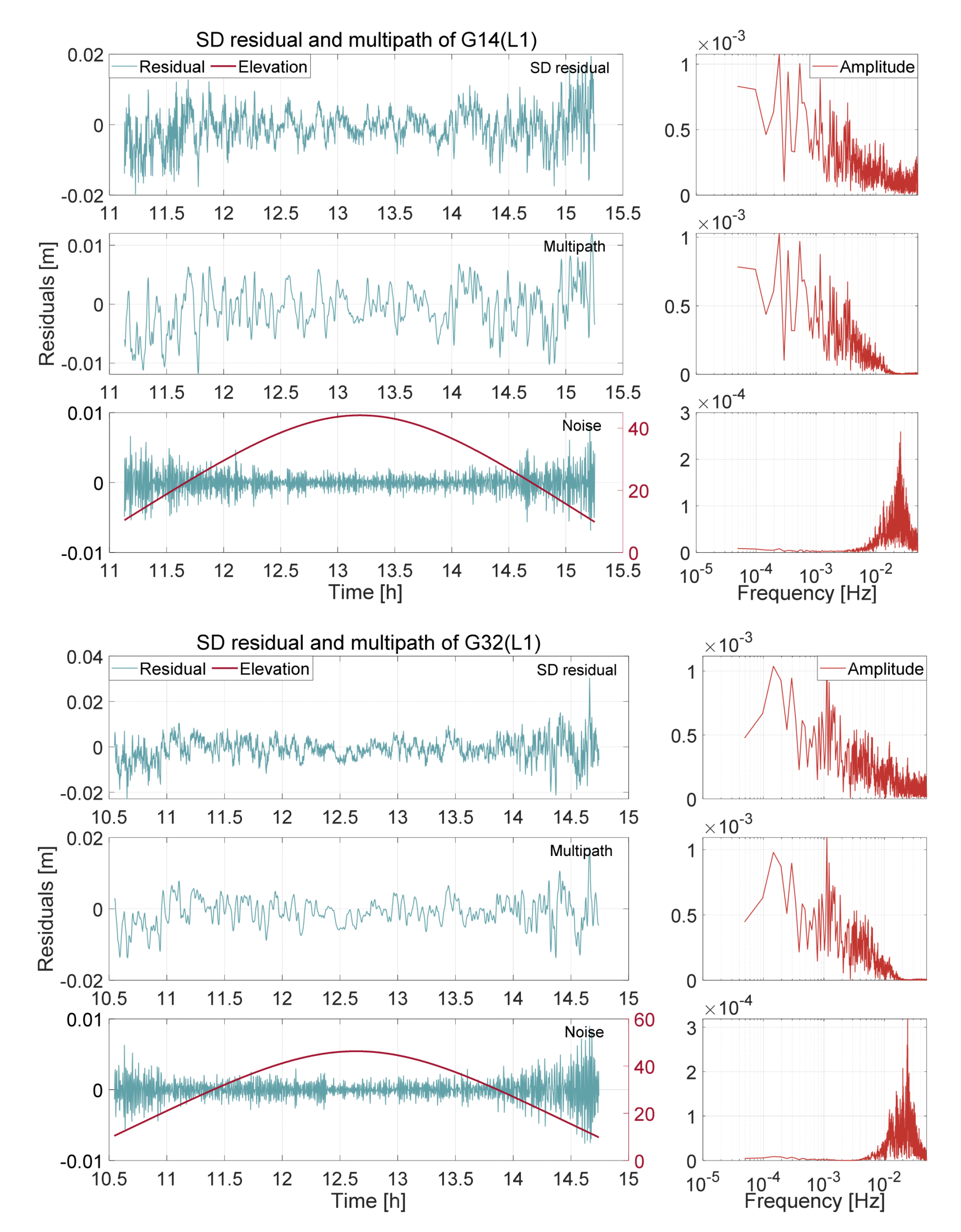
- The multipath is extracted from the SD residual by the VMD algorithm, and the multipath mitigation model is established and stored in the database.
- In the case that the multipath mitigation model has been established, using the principle of the nearest elevation and azimuth, the multipath correction value is searched from the database, corrected to the double difference observation, and then steps 1–3 are repeated.
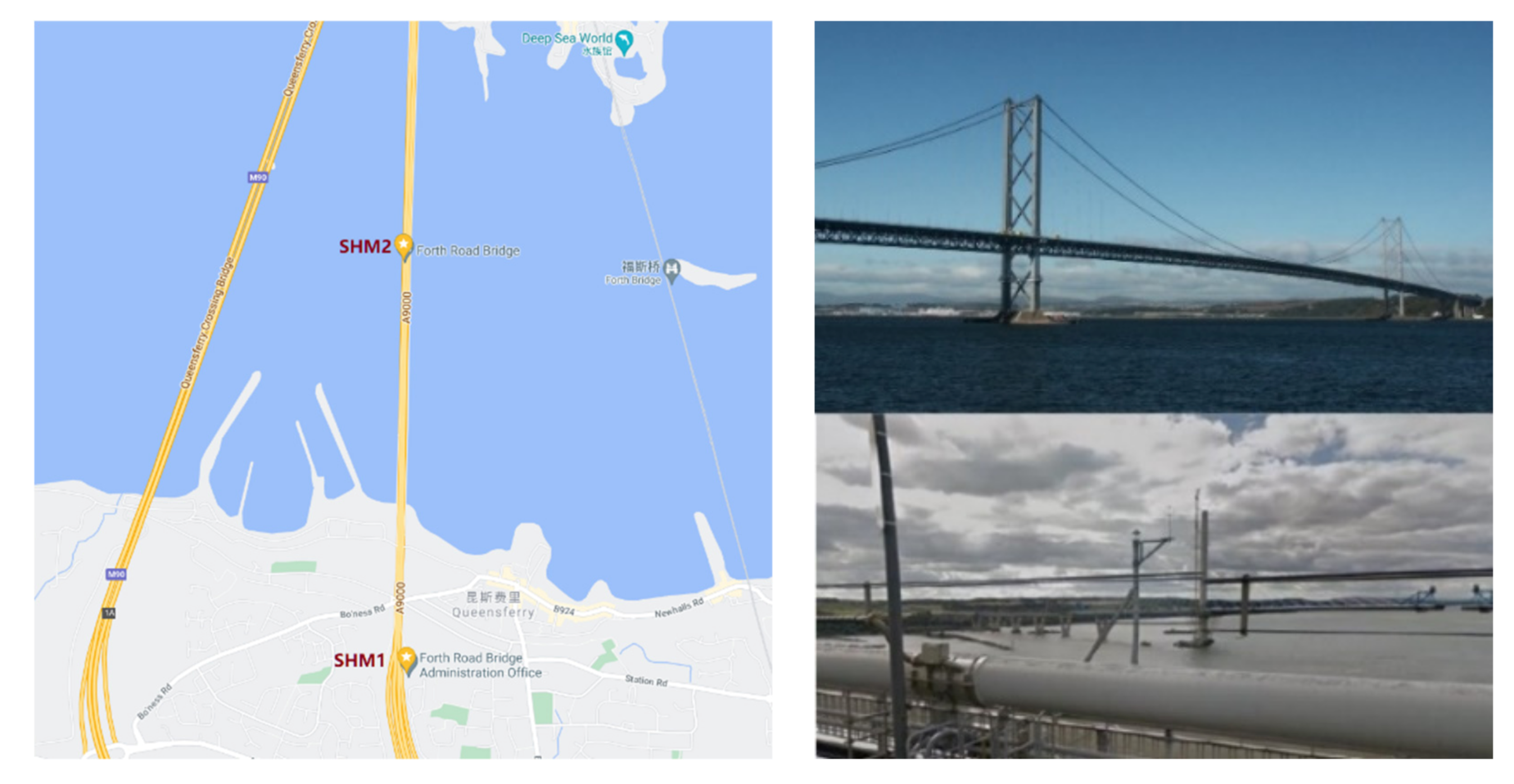
3. Results
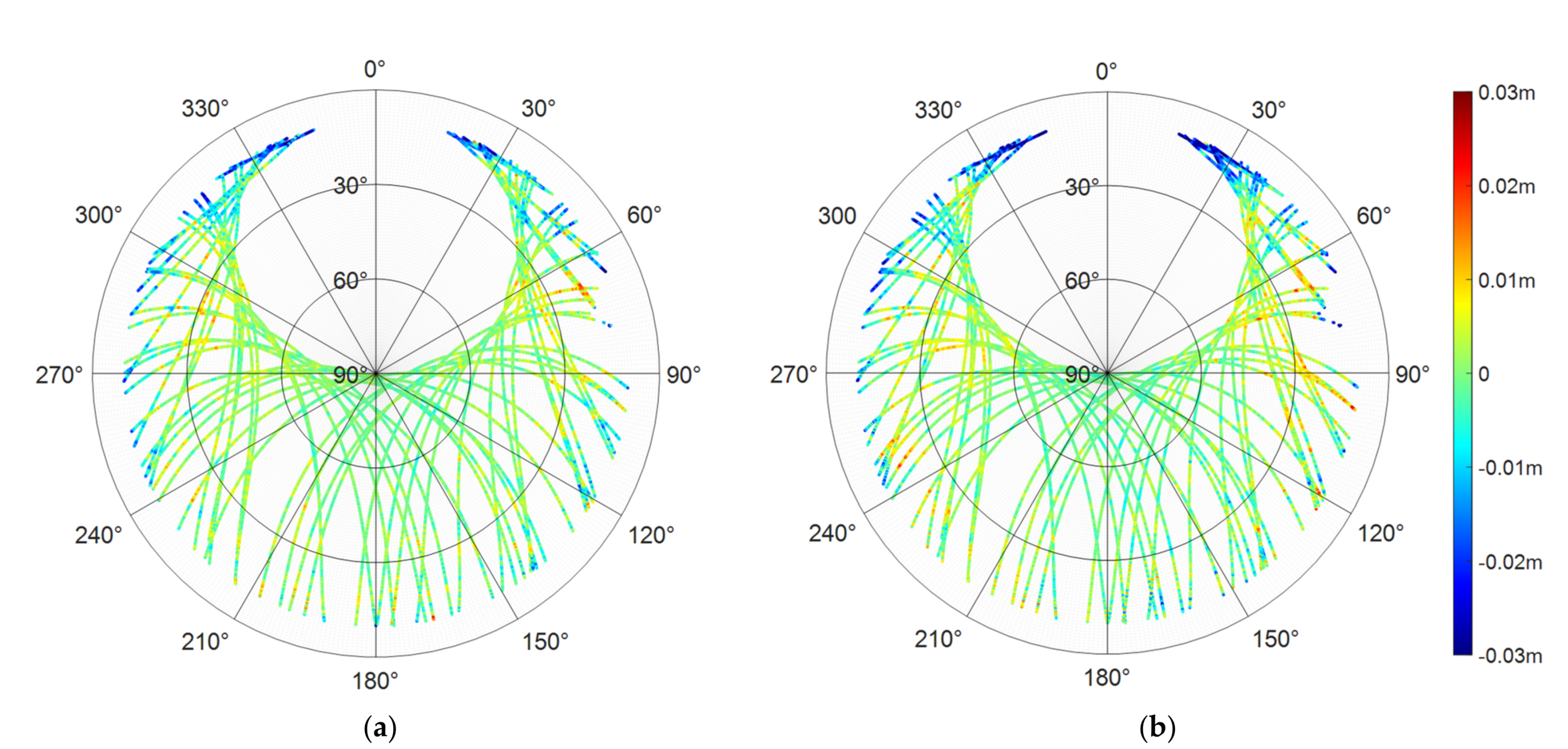
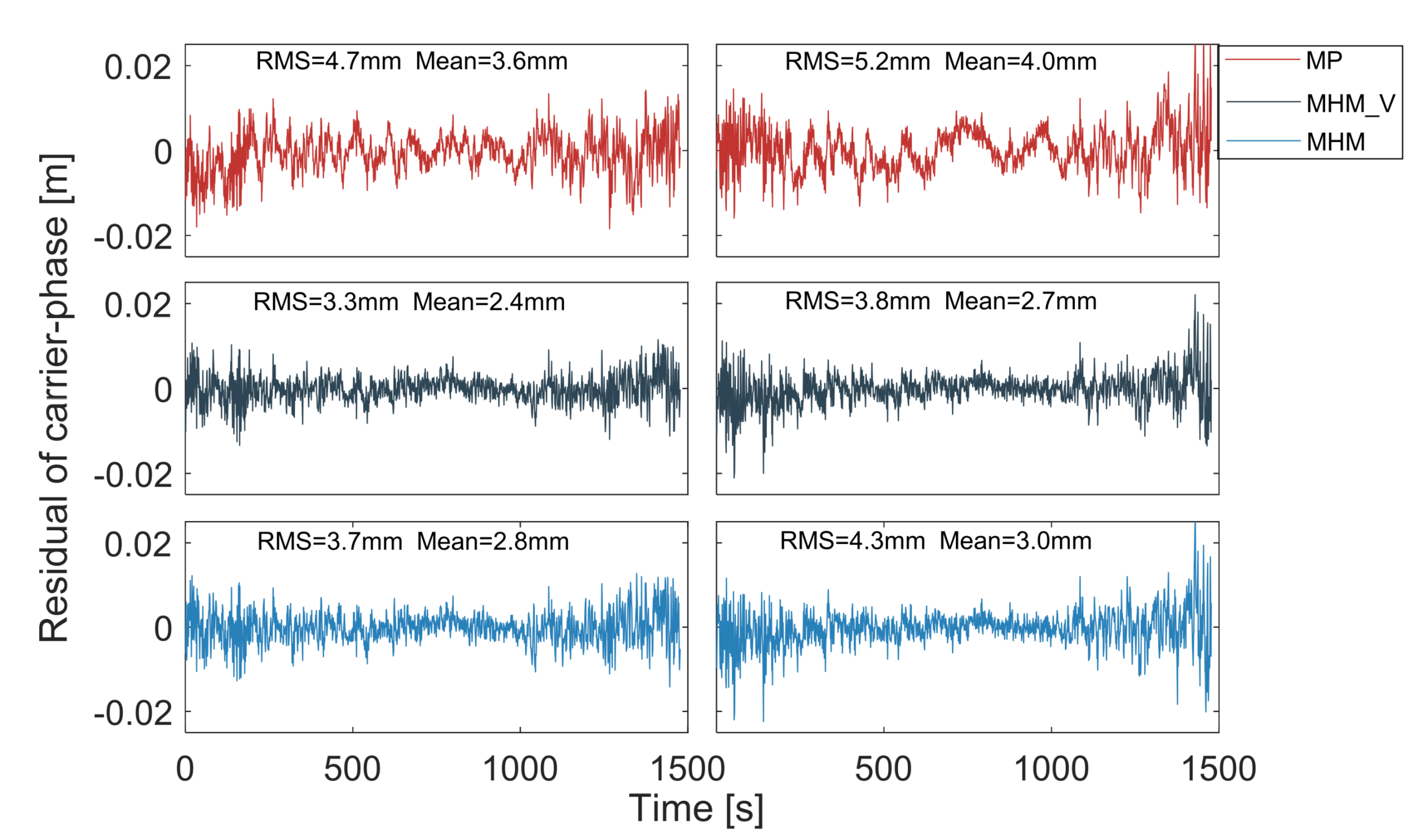
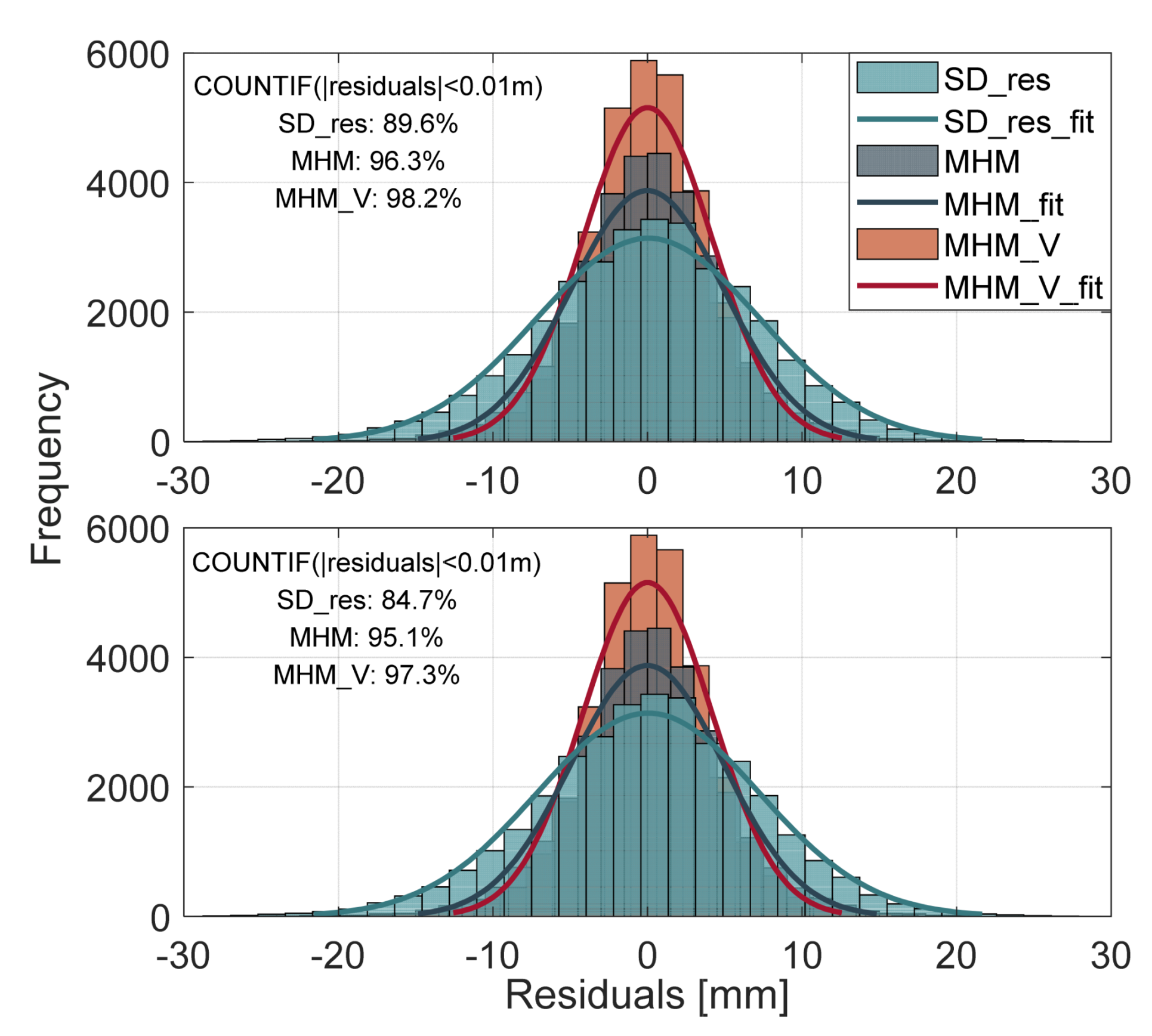
3.1. Multipath Extraction
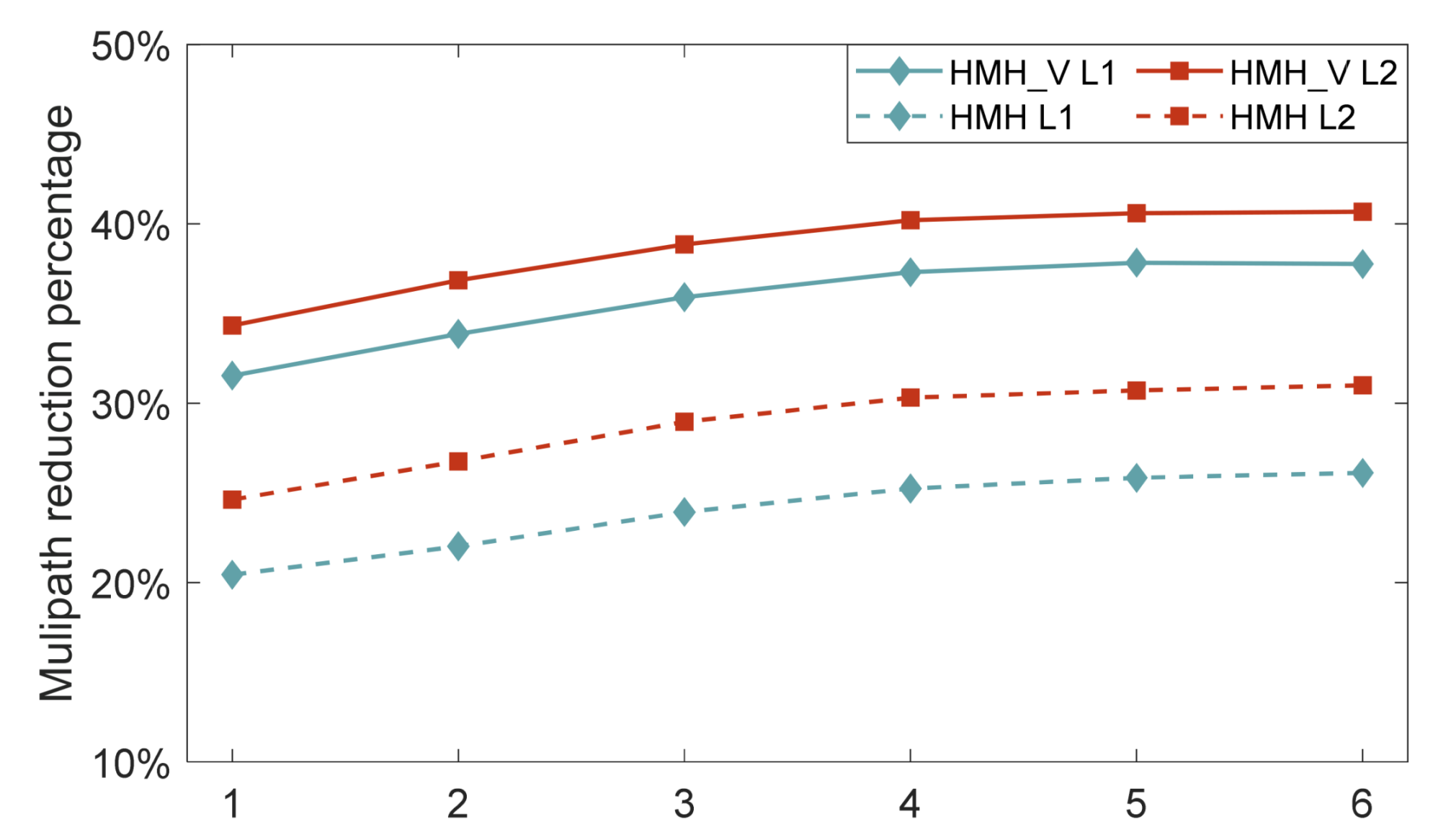
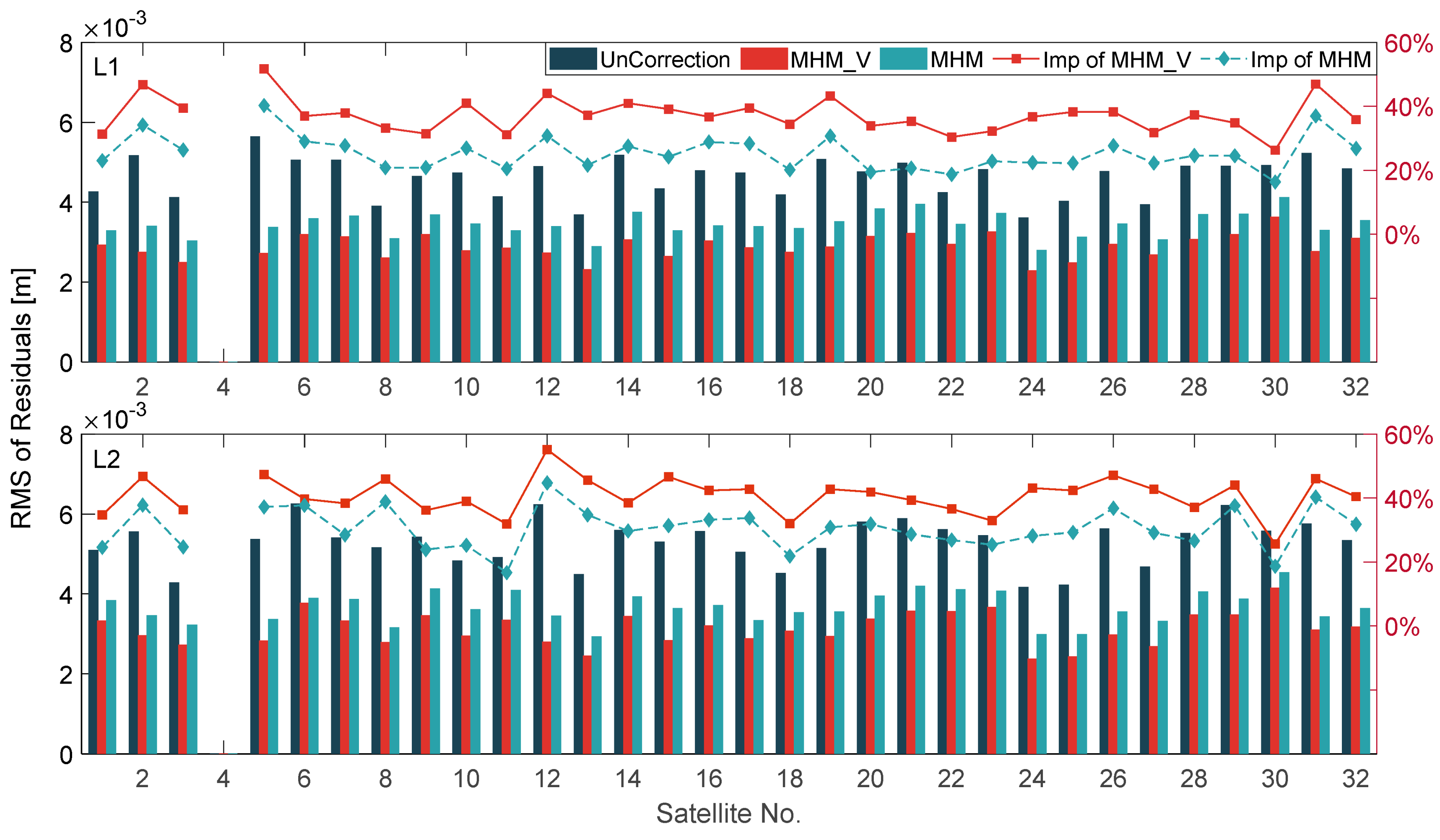
3.2. Analysis of Ambiguity Resolution Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, G. GPS Theory, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2003; pp. 122–132. [Google Scholar]
- Braasch, M.S. Multipath effects. Parkinson 1996, 11, 505–514. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lau, L.; Mok, E. Improvement of GPS Relative Positioning Accuracy by Using SNR. J. Surv. Eng. 1999, 125, 185–202. [Google Scholar] [CrossRef]
- Bilich, A.; Larson, K.M. Mapping the GPS multipath environment using the signal-to-noise ratio (SNR). Radio Sci. 2007, 42, 1–16. [Google Scholar] [CrossRef]
- Rost, C.; Wanninger, L. Carrier phase multipath mitigation based on GNSS signal quality measurements. J. Appl. Geodesy 2009, 3, 81–87. [Google Scholar] [CrossRef]
- Satirapod, C.; Rizos, C. Multipath mitigation by wavelet analysis for GPS basestation applications. Surv. Rev. 2005, 38, 2–10. [Google Scholar] [CrossRef]
- Bernelli-Zazzera, F.; Campana, R.; Gottifredi, F.; Marradi, L. GPS Attitude Determination by Kalman Filtering: Simulation of Multipath Rejection; AAS 98-199: Breckenridge, CO, USA, 1998. [Google Scholar]
- Zhong, P.; Ding, X.; Zheng, D. Study of GPS multipath effects with method of CVVF. Acta Geod. Cartogr. Sin. 2005, 34, 161–167. [Google Scholar]
- Zheng, D.; Zhong, P.; Ding, X.; Chen, W. Filtering GPS time-series using a Vondrak filter and cross-validation. J. Geod. 2005, 79, 363–369. [Google Scholar] [CrossRef]
- Genrich, J.F.; Bock, Y. Rapid resolution of crustal motion at short ranges with the global positioning system. J. Geophys. Res. Space Phys. 1992, 97, 3261–3269. [Google Scholar] [CrossRef]
- Agnew, D.C.; Larson, K.M. Finding the repeat times of the GPS constellation. GPS Solut. 2006, 11, 71–76. [Google Scholar] [CrossRef]
- Atkins, C.; Ziebart, M. Effectiveness of observation-domain sidereal filtering for GPS precise point positioning. GPS Solut. 2015, 20, 111–122. [Google Scholar] [CrossRef]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified sidereal filtering: Implications for high-rate GPS positioning. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath efect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Ragheb, A.E.; Clarke, P.; Edwards, S.J. GPS sidereal filtering: Coordinate- and carrier-phase-level strategies. J. Geod. 2007, 81, 325–335. [Google Scholar] [CrossRef]
- Cohen, C.; Parkinson, B. Mitigating multipath error in GPS-based attitude determination. In Proceedings of the Advances in the Astronautical Sciences, AAS Guidance and Control Conference, San Diego, CA, USA, 4–8 February 1991; pp. 74–78. [Google Scholar]
- Wübbena, G.; Schmitz, M.; Matzke, N. On GNSS in situ-station calibration of near feld multipath. In Proceedings of the International Symposium on GNSS Space Based and Ground Based Augmentation Systems and Applications, Brussels, Belgium, 11–14 November 2010. [Google Scholar]
- Lidberg, M.; Eksröm, C.; Johansson, J.M. Site-Dependent Efects in High-Accuracy Applications of GNSS; EUREF Publication No. 17, Band 42; Mitteilungen des Bundesamtes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2009; pp. 132–138. [Google Scholar]
- Bender, M.; Dick, G.; Wickert, J.; Schmidt, T.; Song, S.; Gendt, G.; Ge, M.; Rothacher, M. Validation of GPS slant delays using water vapour radiometers and weather models. Meteorol. Z. 2008, 17, 807–812. [Google Scholar] [CrossRef]
- Moore, M.; Watson, C.; King, M.; McClusky, S.; Tregoning, P. Empirical modelling of site-specific errors in continuous GPS data. J. Geod. 2014, 88, 887–900. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Luo, X.; Knöpfler, A.; Mayer, M. Generating statistically robust multipath stacking maps using congruent cells. GPS Solut. 2014, 19, 83–92. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, P.; Li, X.; Ge, M.; Guo, F.; Sang, J.; Schuh, H. Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning. J. Geod. 2019, 93, 2037–2051. [Google Scholar] [CrossRef]
- Chang, G.; Chen, C.; Yang, Y.; Xu, T. Tikhonov Regularization Based Modeling and Sidereal Filtering Mitigation of GNSS Multipath Errors. Remote. Sens. 2018, 10, 1801. [Google Scholar] [CrossRef]
- Wang, D.; Meng, X.; Gao, C.; Pan, S.; Chen, Q. Multipath extraction and mitigation for bridge deformation monitoring using a single-difference model. Adv. Space Res. 2017, 60, 2882–2895. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling. J. Geod. 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Qin, H.; Xue, X.; Yang, Q. GNSS multipath estimation and mitigation based on particle filter. IET Radar Sonar Navig. 2019, 13, 1588–1596. [Google Scholar] [CrossRef]
- Jia, Q.; Wu, R.; Wang, W.; Lu, D.; Wang, L.; Li, J. Multipath interference mitigation in GNSS via WRELAX. GPS Solut. 2016, 21, 487–498. [Google Scholar] [CrossRef]
- Su, M.; Zheng, J.; Yang, Y.; Wu, Q. A new multipath mitigation method based on adaptive thresholding wavelet denoising and double reference shift strategy. GPS Solut. 2018, 22, 40. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Baykut, S.; Akgül, T.; Ergintav, S. EMD-based analysis and denoising of GPS data. In Proceedings of the 2009 IEEE 17th Signal Processing and Communications Applications Conference, Antalya, Turkey, 9–11 April 2009; pp. 644–647. [Google Scholar]
- Dodson, A.H.; Meng, X.; Roberts, G.W. Adaptive method for multipath mitigation and its application for structural deflection monitoring. In Proceedings of the Int Symp Kinemat Syst Geod, Geomat Navig (KIS 2001), Banff, AB, Canada, 5–8 June 2001; pp. 101–110. [Google Scholar]
- Yan, F.L. Gps/pseudolites technology based on emd-wavelet in the complex field conditions of mine. Procedia Earth Planet. Sci. 2009, 1, 1293–1300. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Jegadeeshwaran, R.; Sugumaran, V. Vibration based fault diagnosis of a hydraulic brake system using variational mode decomposition (vmd). Sdhm Struct. Durab. Health Monit. 2014, 10, 81–97. [Google Scholar]
- An, X.; Yang, J. Denoising of hydropower unit vibration signal based on variational mode decomposition and approximate entropy. Trans. Inst. Meas. Control. 2016, 38, 282–292. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Sivavaraprasad, G.; Padmaja, R.S.; Ratnam, D.V. Mitigation of Ionospheric Scintillation Effects on GNSS Signals Using Variational Mode Decomposition. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 389–393. [Google Scholar] [CrossRef]
- Zhang, R.; Gao, C.; Pan, S.; Shang, R. Fusion of GNSS and Speedometer Based on VMD and Its Application in Bridge Deformation Monitoring. Sensors 2020, 20, 694. [Google Scholar] [CrossRef] [PubMed]
- Georgiadou, Y.; Kleusberg, A. On carrier signal multipath efects in relative GPS positioning. Manuscr Geod. 1988, 13, 172–179. [Google Scholar]
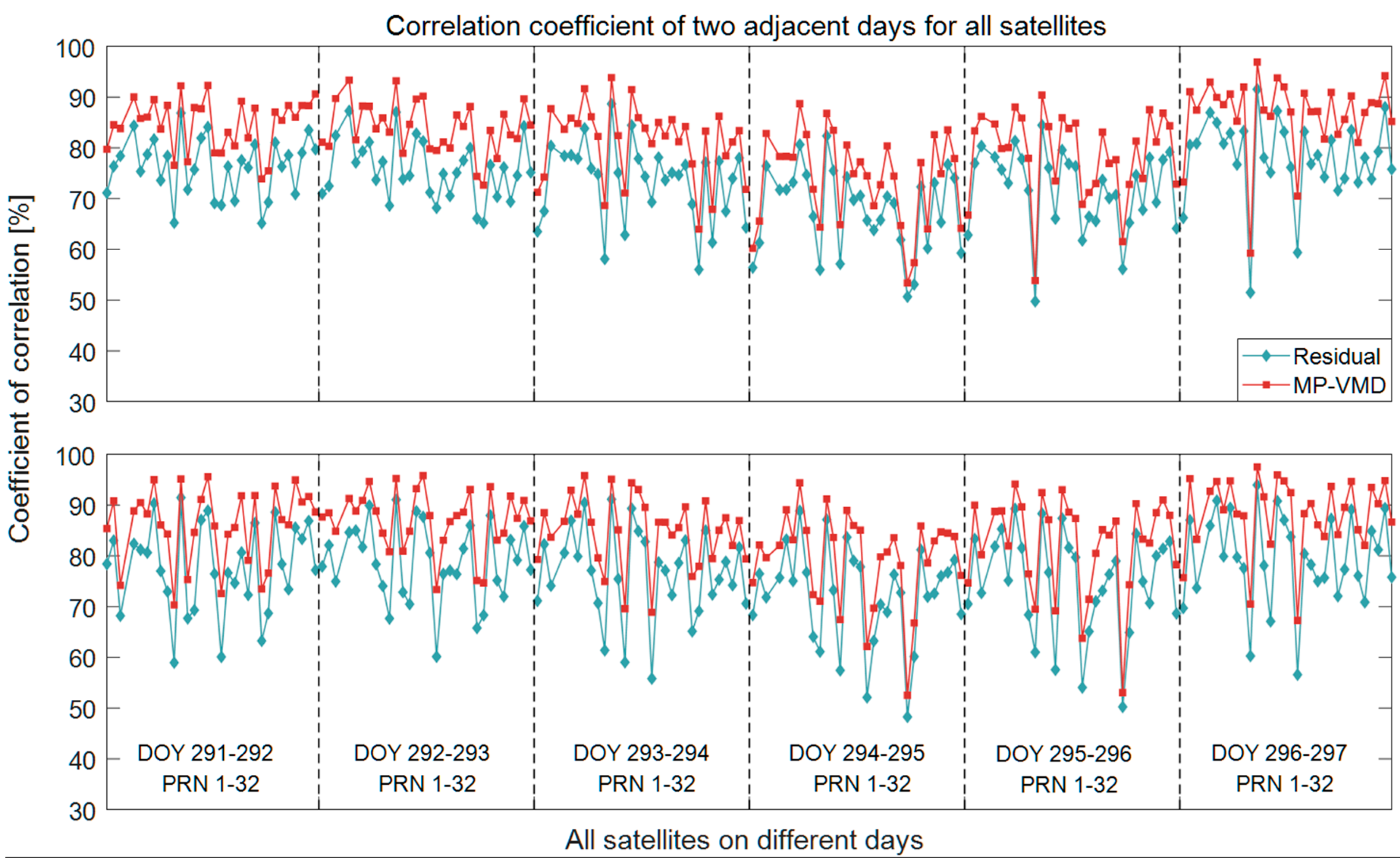
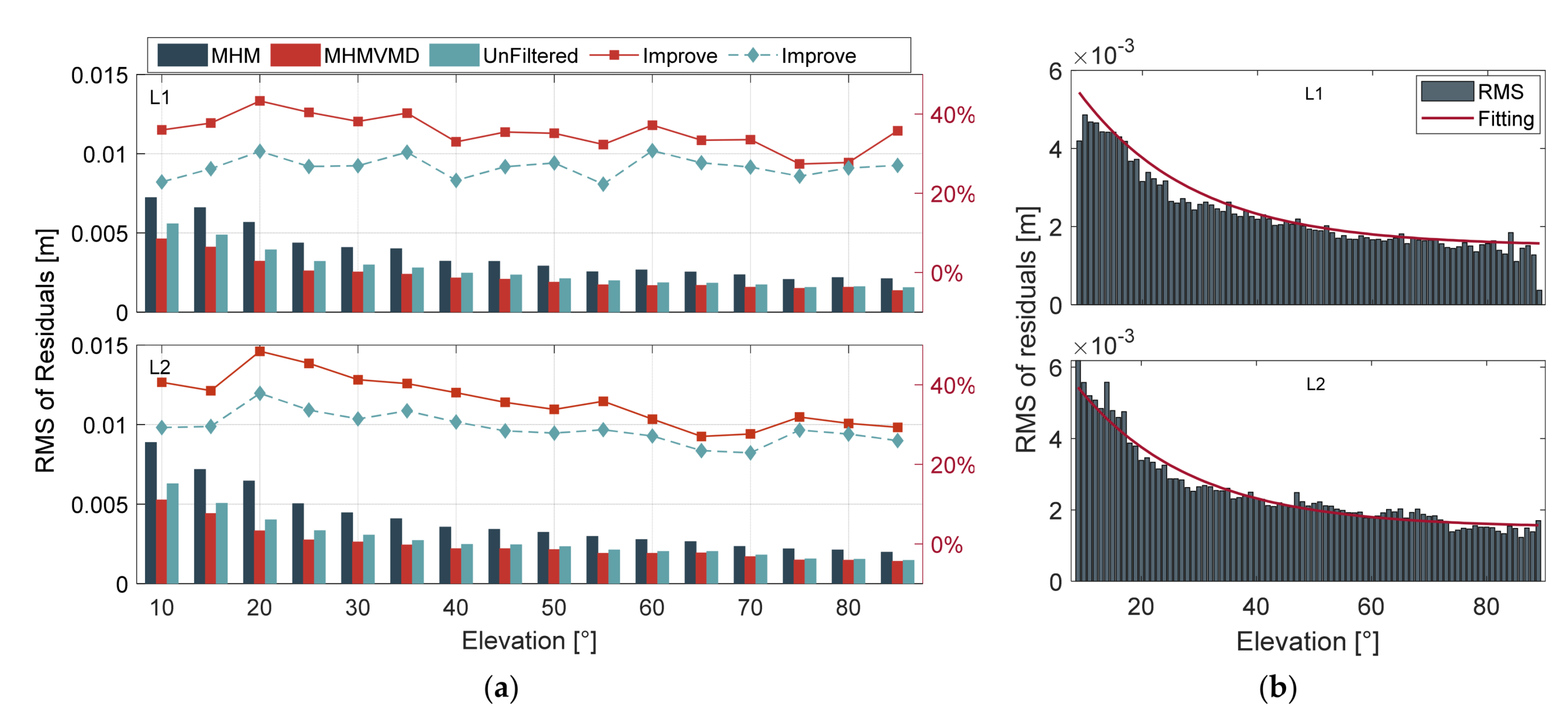
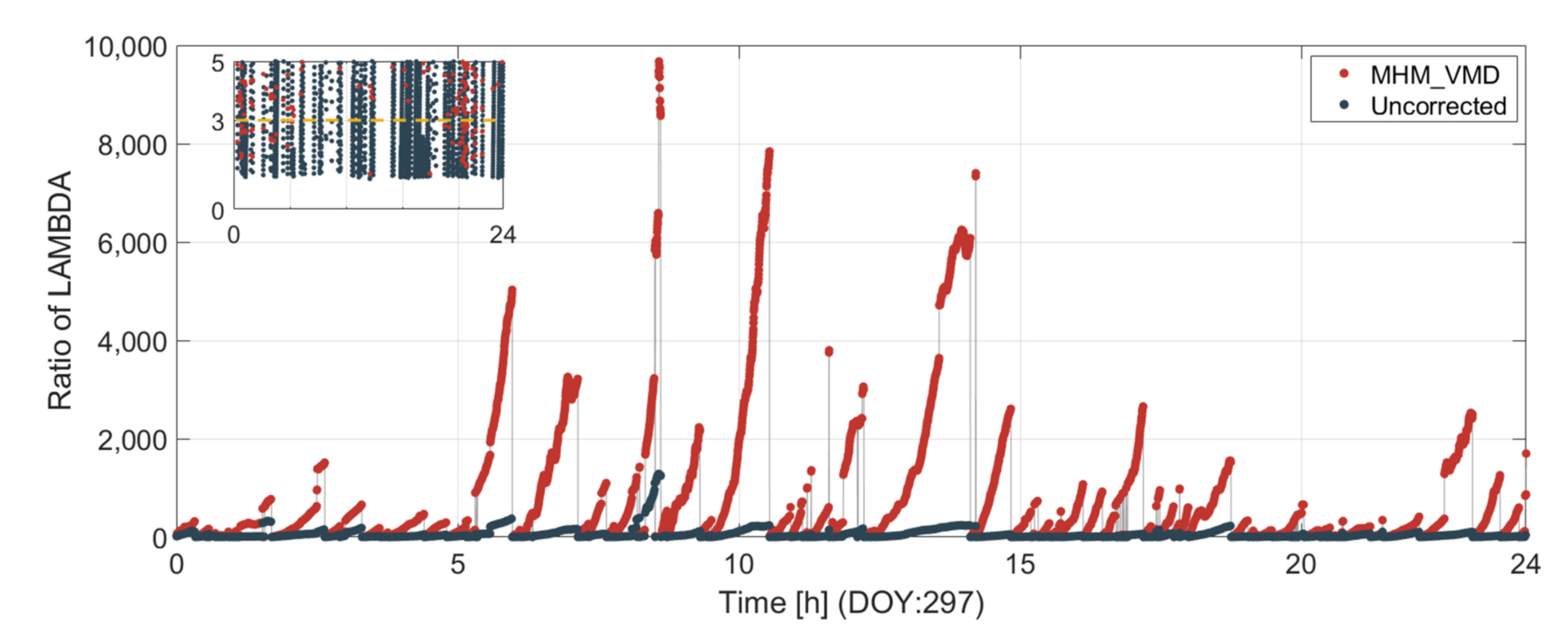
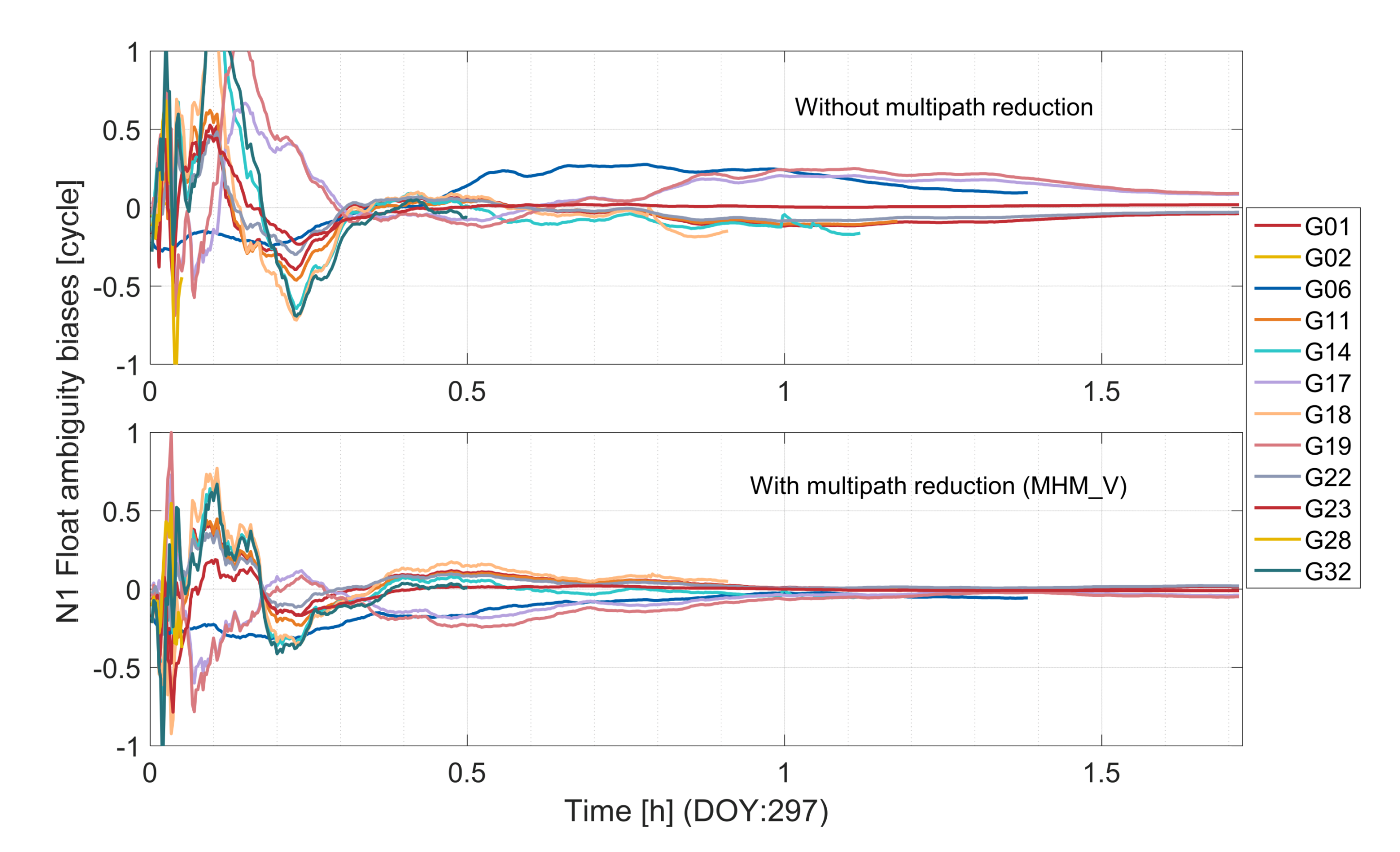
| DOY | L1 | L2 | ||||
|---|---|---|---|---|---|---|
| SD_res | MP_VMD | Promotion Ratio | SD_res | MP_VMD | Promotion Ratio | |
| 291–292 | 0.763 | 0.843 | 11.2% | 0.778 | 0.861 | 10.8% |
| 292–293 | 0.757 | 0.840 | 11.1% | 0.787 | 0.871 | 10.6% |
| 293–294 | 0.734 | 0.812 | 10.7% | 0.766 | 0.848 | 10.7% |
| 294–295 | 0.677 | 0.738 | 9.0% | 0.722 | 0.796 | 10.2% |
| 295–296 | 0.719 | 0.788 | 9.7% | 0.748 | 0.824 | 10.2% |
| 296–297 | 0.780 | 0.866 | 11.1% | 0.795 | 0.883 | 11.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Gao, C.; Zhao, Q.; Peng, Z.; Shang, R. An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring. Remote Sens. 2021, 13, 2259. https://doi.org/10.3390/rs13122259
Zhang R, Gao C, Zhao Q, Peng Z, Shang R. An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring. Remote Sensing. 2021; 13(12):2259. https://doi.org/10.3390/rs13122259
Chicago/Turabian StyleZhang, Ruicheng, Chengfa Gao, Qing Zhao, Zihan Peng, and Rui Shang. 2021. "An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring" Remote Sensing 13, no. 12: 2259. https://doi.org/10.3390/rs13122259
APA StyleZhang, R., Gao, C., Zhao, Q., Peng, Z., & Shang, R. (2021). An Improved Multipath Mitigation Method and Its Application in Real-Time Bridge Deformation Monitoring. Remote Sensing, 13(12), 2259. https://doi.org/10.3390/rs13122259