Abstract
The neutral atmospheric delay is one of the major error sources in Space Geodesy techniques such as Global Navigation Satellite Systems (GNSS), and its modeling for high accuracy applications can be challenging. Improving the modeling of the atmospheric delays (hydrostatic and non-hydrostatic) also leads to a more accurate and precise precipitable water vapor estimation (PWV), mostly in real-time applications, where models play an important role, since numerical weather prediction models cannot be used for real-time processing or forecasting. This study developed an improved version of the Hourly Global Pressure and Temperature (HGPT) model, the HGPT2. It is based on 20 years of ERA5 reanalysis data at full spatial (0.25° × 0.25°) and temporal resolution (1-h). Apart from surface air temperature, surface pressure, zenith hydrostatic delay, and weighted mean temperature, the updated model also provides information regarding the relative humidity, zenith non-hydrostatic delay, and precipitable water vapor. The HGPT2 is based on the time-segmentation concept and uses the annual, semi-annual, and quarterly periodicities to calculate the relative humidity anywhere on the Earth’s surface. Data from 282 moisture sensors located close to GNSS stations during 1 year (2020) were used to assess the model coefficients. The HGPT2 meteorological parameters were used to process 35 GNSS sites belonging to the International GNSS Service (IGS) using the GAMIT/GLOBK software package. Results show a decreased root-mean-square error (RMSE) and bias values relative to the most used zenith delay models, with a significant impact on the height component. The HGPT2 was developed to be applied in the most diverse areas that can significantly benefit from an ERA5 full-resolution model.
1. Introduction
The neutral atmosphere is a refractive medium, which affects the propagation of an electromagnetic signal. The refractive index in this medium is slightly greater than unity, causing the speed of the signal to be lower than it would be in a vacuum and an increase in the signal travel time between the satellite and the sensors located on the Earth’s surface [1]. Refraction also bends the signal path, further increasing the travel time. A consequence of these effects is expanding the equivalent path length, generally seen as a propagation delay and known as tropospheric delay [2,3,4,5]. This delay varies between 2.3 to 2.6 m at sea level and can be divided into two components, the hydrostatic delay, that depends on the dry gas mixture present in the atmosphere, and the non-hydrostatic delay, also referred to as wet delay, which depends on the water vapor distribution [6]. The hydrostatic component varies mainly with the atmospheric pressure, and therefore it fluctuates relatively slowly. This component can be calculated using a surface pressure with high accuracy, with the Hopfield model [7] or the Saastamoinen model [8]. The wet delay part is relatively small, varying between 0 and 0.5 m, but very challenging to predict due to water vapor dynamics in the troposphere [9]. It can be calculated using temperature and water vapor pressure profiles, made available only by radiosondes or numerical weather prediction (NWP) models. The wet component can be estimated from surface meteorological measurements in the absence of vertical profiles but with less accuracy [10]. This component is one of the major error sources remaining in Space Geodesy.
Since radiosonde vertical profiles are sparse in space and time and observations of surface meteorological parameters near GNSS stations are not frequent, solutions based on data from climatological data or NWP models emerge to provide estimates of these parameters for any point on Earth. Regional models have been developed over the past two decades (e.g., [11,12,13,14,15,16]), but in this study we refer only to models of global application. The University of New Brunswick developed a series of models (UNB series) based on the U.S. standard atmosphere [17], which was adopted in Wide Area Augmentation Systems (WAAS). The TropGrid2 model [18], an upgraded version of the TropGrid model [19], is based on 9 years of atmospheric data provided by the National Oceanic and Atmospheric Administration (NOAA) with a horizontal resolution of 1° × 1°. This model considers the annual and diurnal variations but neglects the semi-annual variation. The Improved Tropospheric Grid (ITG) model [20] is based on atmospheric data with 2.5° × 2.5° horizontal resolution, interpolated from the ERA-Interim dataset [20]. This model uses the annual, semi-annual, and diurnal variations to provide the temperature, pressure, weighted mean temperature, zenith wet delay, and temperature lapse rate. With the implementation of the European Galileo navigation system, the European Space Agency (ESA) developed a new model [21] based on ERA-15 reanalysis data with a 1.5° × 1.5° global grid [22]. This model is characterized by different periodicities depending on the atmospheric parameter to be estimated. However, ECMWF strongly recommends that the ERA-Interim or ERA5 products be used rather than the ERA-15 [23,24]. The improved tropospheric grid (ITG) [20] model is based on 10 years of a 2.5° × 2.5° global grid of ERA-Interim data and considers the annual, semi-annual, and diurnal variations to provide the temperature, pressure, weighted mean temperature, zenith wet delay, and temperature lapse rate. More recently, a series of models, designated as Global Pressure and Temperature (GPT), became widely used. These models are derived from the reanalysis of NWP products provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). The GPT model [25] is based on spherical harmonics up to degree and order nine to obtain means and annual amplitudes of temperature and pressure used as input for a periodic function, providing pressure and temperature values for a specific location and time [25]. Three more versions of this model were developed: GPT2 [26], GPT2w [27], and GPT3 [28]. The GPT2 model is based on 10 years of a 5° × 5° grid resolution of monthly means estimated from the ERA-Interim reanalysis data. It includes two new parameters, the temperature lapse rate and the water vapor pressure, and a semi-annual amplitude to represent each parameter, but the diurnal variation is ignored. In an improved version of GPT2, the GPT2w, the amplitudes for the annual and semi-annual variation can be interpolated from a 5° × 5° or 1° × 1° grid resolution, and two new output parameters were included, the weighted mean temperature and the water vapor decrease factor. The last GPT version, GPT3, reveals some improvements over its predecessor. The amplitude values can also be interpolated from two different resolution grids, and two new output parameters were added, the hydrostatic north-east gradients and wet north-east gradients. Details about these models can be seen in [25,26,27,28]. The last version of the GPT series is considered the most accurate tropospheric model and the most used in the main GNSS processing packages, e.g., GAMIT/GLOBK or Bernese. However, for all these models, the best horizontal resolution is 1° × 1°, and the highest temporal resolution is 6 hours. At these resolutions, the temperature, the pressure, and mainly the water vapor can change significantly, depending on many factors, such as a complex terrain, atmospheric coastal interactions, or regional vulnerability to extreme atmospheric events. The HGPT model [29] provides surface pressure, surface air temperature, zenith hydrostatic delay, and weighted mean temperature values for any location and was developed to overcome these limitations. It is based on the time-segmentation concept and uses 20 years of ERA5 reanalysis [30] data provided by ECMWF at full spatial (0.25° × 0.25°) and temporal (1-h) resolution to estimate the annual, semi-annual, and quarterly periodicities for each hour. The weighted mean temperature is estimated from the surface temperature using a linear regression, where the linear coefficients are determined using a 20-year time series of monthly ERA5 data. The amplitudes and initial phase variations are estimated as a periodic function that includes a linear trend to account for the global climate change scenario; see [29] for details.
In this study, we present an improved version of the HGPT [29], named HGPT2. The HGPT2 follows the same concept of time segmentation and uses three periodicities, the annual, semi-annual, and quarterly, to obtain estimates of relative humidity. The periodicities coefficients are based on a Fourier analysis using 20 years of ERA5 dew point temperature data. The model provides the zenith non-hydrostatic delay (commonly referred to as zenith wet delay), calculated using the Saastamoinen wet formulation [8,10], and the precipitable water vapor (PWV) [31]. The zenith total delay can be obtained by adding the zenith hydrostatic and wet delays, as well the water vapor pressure, and the saturated water vapor pressure can be quickly calculated from the temperature and relative humidity, e.g., using the Wexler equations. The model function coefficients are bilinearly interpolated in space using an efficient subroutine developed in Fortran, Matlab, and Python, available at https://github.com/pjmateus/hgpt_model (accessed on 29 January 2020), along with the coefficient files in binary format. These subroutines can be easily modified to obtain the delay between the receivers and the satellites (slant path delays). Three statistical metrics: (i) the root-mean-square error (RMSE), (ii) the bias, and (iii) the Pearson correlation coefficient were used to characterize the HGPT2 model’s accuracy in space and time. We downloaded from the Scripps Orbit and Permanent Array Center (SOPAC) and the University NAVSTAR Consortium (UNAVCO) servers a database of meteorological observations (RINEX met-files), globally distributed, to assess the HGPT2-derived relative humidity. Additionally, we evaluated the performance of the GPT series versus HGPT2 regarding the estimation of relative humidity. As proof of concept, we processed 38 GNSS sites belonging to the International GNSS Service (IGS) using the GAMIT/GLOBK packages with and without the HGPT2 solutions (surface temperature, pressure, and relative humidity). The most significant impact was seen in the height component, with a considerable decrease of the solution biases.
The HGPT2 is the first global model that makes use of the ERA5 full horizontal and temporal resolution. The ERA5 model has several significant innovative features compared to discontinued reanalysis models (ERA-15, ERA-40, or the ERA-Interim). The major improvements are attributed to an increased horizontal grid spacing (of several tens of kilometers to about 30 km), an increase of the number of vertical levels (from about 60 to 137), and an increase of the temporal resolution (from 6 to 1 hour), which allows for a better temporal representation of the water vapor dynamics. Other factors are the new 4D-Var data assimilation system, based on Cycle 41r2 of the Integrated Forecasting System (IFS), which was operational at ECMWF in 2016 [32], and the number of observations that are assimilated per day (from 0.75 million per day in 1979 to about 24 million per day in 2020). ERA5 benefits from a decade of developments in model physics, numeric, and data assimilation, boosting a more realistic representation of convective systems, gravity waves, tropical cyclones, and other meso- to synoptic-scale atmospheric structures [30,33,34].
The structure of this paper is as follows: in Section 2 the current model formulation and computation of the grid coefficients are introduced; in Section 3 the results are presented and discussed; Section 4 describes the assessment materials and methods; and, finally, in Section 5 we draw some conclusions.
2. Model Formulation
The main differences between HGPT2 and HGPT are (1) the estimation of relative humidity (RH), based on 20 years of ERA5 reanalysis data at full spatial (0.25° × 0.25°) and temporal (1-h) resolutions; (2) the computation of the zenith non-hydrostatic delay (or zenith wet delay (ZWD)); and (3) the computation of the precipitable water vapor (PWV) using the ZWD and the weighted mean temperature () calculated by the previous version. Both versions of the model maintain the same inputs, five parameters (date, , , , h_type), where the date can be in modified Julian date (MJD) of Gregorian date format, is the longitude, is the latitude, is the altitude, and h_type identifies the type of altitude, ellipsoidal or orthometric.
2.1. ERA5 Relative Humidity
The relative humidity (RH) parameter is not available from the ERA5 single-level dataset, but only from the pressure levels dataset that required vertical interpolation to the surface level. To avoid interpolation, we use 20 years of dew point temperature () simulations available in the single-level dataset at 2 meters from the surface. The ERA5 model grid has 721 grid points in latitude and 1440 grid points in longitude (a total of 1,038,240 grid points). A time series with 175,320 simulations was obtained for each grid point (between January 1, 1999, 00:00 UTC, and December 31, 2018, 23:00 UTC), totalizing about 3.64 × 109 simulations for the entire grid. We used the Wexler formulation to calculate the saturated water vapor pressure () and the water vapor pressure (). The Wexler formulations are based on more recent experimental data than most used formulations due to their numerical simplicity and have gained considerable international acceptance. The Wexler equation to compute the saturation vapor pressure over water is given by [35]:
where is the saturation vapor pressure over water in the pure phase, in Pascal, is the temperature, in Kelvin, and the coefficients are
- g0 = −2.8365744 × 103
- g1 = −6.028076559 × 103
- g2 = 1.954263612 × 101
- g3 = −2.737830188 × 10−2
- g4 = 1.6261698 × 10−5
- g5 = 7.0229056 × 10−10
- g6 = −1.8680009 × 10−13
- g7 = 2.7150305
The Wexler equation to compute the saturation vapor pressure over ice is given by [36]:
where the coefficients are
- k0 = −5.8666426 × 103
- k1 = 2.232870244 × 101
- k2 = 1.39387003 × 10−2
- k3 = −3.4262402 × 10−5
- k4 = 2.7040955 × 10−8
- k5 = 6.7063522 × 10−1
In the presence of other gases, the ideal saturation vapor pressures given in Equations (1) and (2) differ from the effective saturation vapor pressure. We can relate the effective saturation vapor pressure to the ideal by
where is the effective saturation vapor pressure, is the ideal saturation vapor pressure (as given in Equations (1) and (2)), and is the enhancement factor, which varies with ideal the saturated water vapor (), pressure (), and temperature () conditions, given by [37]:
and
where is the natural exponential function, and and have the same units. The and coefficients for water are
- A0 = −1.6302041 × 10−1
- A1 = 1.8071570 × 10−3
- A2 = −6.7703064 × 10−6
- B3 = 8.5813609 × 10−9
- B0 = −5.9890467 × 101
- B1 = 3.4378043 × 10−1
- B2 = −7.7326396 × 10−4
- B3 = 6.3405286 × 10−7
The and coefficients for ice are
- A0 = −6.0190570 × 10−2
- A1 = 7.3984060 × 10−4
- A2 = −3.0897838 × 10−6
- A3 = 4.3669918 × 10−9
- B0 = −9.4868712 × 101
- B1 = 7.2392075 × 10−1
- B2 = −2.1963437 × 10−3
- B3 = 2.4668279 × 10−6
Coefficients for specific temperature ranges can be consulted in [37]. The , , , and coefficients presented here agree with the International Temperature Scale of 1990 (ITS-90). Minor differences between these coefficients and Wexler’s original coefficients can be found, since the originals comply with the ITS-68 (for details, see [37]). The effective water vapor pressure () was obtained by exchanging by in Equations (2) and (3). The relative humidity is calculated (in percentage) using Equation (6):
2.2. HGPT2 Relative Humidity
The HGPT2 model follows the time-segmentation concept, which is focused on a set of hourly coefficients to determine the relative humidity at anytime and anywhere on Earth. The mean value and three periodic functions were considered to account for the annual, semi-annual, and quarterly periodicities, as given by Equation (7):
where , and are the mean, annual, semi-annual, and quarterly amplitudes, respectively; is the modified Julian date (MJD) and is the MJD for the first observation (); is the hour (UTC); , and are the annual, semi-annual, and quarterly initial phases, respectively. Firstly, the relative humidity time series with 1-h resolution obtained using Equation (6) is divided into 24 times series, one for each hour of the day (00 h to 23 h). This task is performed for each pixel, resulting in 24,917,760 time series to evaluate. Secondly, a Fast Fourier Transform (FFT) analysis as a function of the location and time is performed on each time series. The amplitude and phase values for each hour corresponding to the annual, semi-annual, and quarterly signals are extracted and saved to a binary file. To save time and improve computational efficiency, only the grid for a requested hour is loaded at every run of the HGPT2 subroutine.
2.3. HGPT2 Zenith Wet Delay
To obtain the zenith wet delay (ZWD) we apply the Saastamoinen wet model [8,10], given by
where is the surface air temperature (K), is the surface water vapor pressure (hPa), and ZWD is the zenith wet delay (m). Equation (8) is a simplified model designed using Essen and Froome’s refractivity constants [38] and for mid-latitudes and average conditions [10]. It is possible to improve the model accuracy by estimating new constants that better represent local conditions; see Mendes (1999) [39] for details. Since the HGPT already determined the zenith hydrostatic delay (ZHD), the ZTD is easily calculated by ZTD = ZHD + ZWD.
2.4. HGPT2 Precipitable Water Vapor
The precipitable water vapor (PWV) is the height of the condensed water vapor contained in a vertical column of a unit cross-sectional area extending between the Earth’s surface and the upper edge of the troposphere, commonly expressed in millimeter units. The PWV quantity is often preferable to the ZWD in the meteorology community, since it is easily related to the amount of water potentially available in the atmosphere for precipitation. The PWV can be estimated using the ZWD and the atmosphere mean temperature () [31] as
where is the liquid water density, is the specific gas constant for water vapor [40], are refractivity constants (as given by the best average solution proposed by Rüeger [41], i.e., , , ), and , with being the ratio of the molar masses of water vapor () and dry air (). is defined as the inverse of the water vapor column-weighted inverse temperature and can be calculated along a vertical profile [31], defined as
where is the thickness of the ith layer atmosphere, is the number of atmospheric layers, and are the water vapor pressure and temperature of the ith layer atmosphere, respectively. The right part of Equation (9) is called the dimensionless constant of proportionality, normally represented by () [31]. To obtain using Equation (10), it is necessary to know and along vertical profiles, which are only measured by radiosondes or simulated by NWMs. On the other hand, shows a high correlation with the surface air temperature () and can be estimated from it using a linear function, , where and are the linear regression coefficients estimated from ERA5 data during one year to account for the seasonality and geographic variability intrinsic to . The novelty in the HGPT2 model is Equation (9), since the linear regression coefficients ( and ) are estimated in the previous version. See details in [29].
2.5. HGPT2 Height-Dependent Values Correction
In the HGPT2 model, all the estimated values are referred to the ERA5 surface elevation grid, whose vertical datum is based on the WGS84 Earth gravitational model (EGM 96) geoid [33]. To adjust the estimated values altitudes to orthometric altitudes, we apply the equations presented by Xu [6] (page 56). The only difference is that instead of using a constant temperature lapse rate value (6.5 °C km−1), we introduced the lapse rate latitudinal variation, given by [42]:
where is the temperature lapse rate, and is the latitude. In the specific case of GNSS data processing, we must consider that the GNSS station heights are referenced to the WGS84 ellipsoid. A transformation from ellipsoidal heights to the mean sea level system is also necessary and achieved by subtracting the geoid height (undulation) to the ellipsoidal height [29]. All these adjustments are implemented in HGPT2.
3. Results and Discussion
This section presents and discusses the spatial distribution of each relative humidity coefficient estimated using the methodology described previously. Figure 1 shows the mean value () and the three mean amplitudes (, and ) in Equation (7), for each pixel (full ERA5 spatial resolution) and considering 20 years of reanalysis data (between 1 January 1999, 00:00 UTC, and 31 December 2018, 23:00 UTC). Figure 1a shows the mean RH (global) spatial distribution, revealing smaller values over the tropical, subtropical, and temperate deserts (dry deserts zones) and mountain systems such as the Himalayas, Andes, and the Rocky Mountains. The higher values are concentrated over the tropical rainforest zones and over the ocean, with the diurnal cycle showing a weak variability. Variations in the daily cycle of up to 60% arise in the African and Australian continents and, although with less variation, in India and Mexico (not shown). Figure 1b shows the mean annual amplitude, with variations up to 38% in the African Sahel and over the tropical moist forests (south of Africa). The semi-annual amplitude shows variations up to 18%, mainly over India and east of the African continent, and the quarterly amplitude contributes with a variation up to 8%, primarily over the east of the African continent, in tropical shrubland zones (Figure 1c,d). The annual amplitude displays variations in the diurnal cycle up to 28% over Europe, west America, Canada, and the central part of Asia. The semi-annual amplitude reaches 14%, mainly in the center of the African continent, and about 10% to the south of the Amazon basin, south of the Asian continent, and northwest of Canada. The quarterly amplitude displays a maximum cycle variation of 6% east of the African continent and about 3% northwest of the Asian continent (not shown).
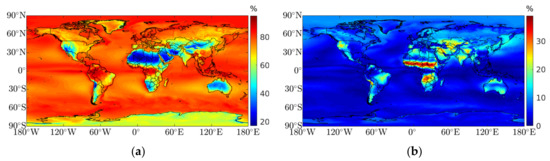
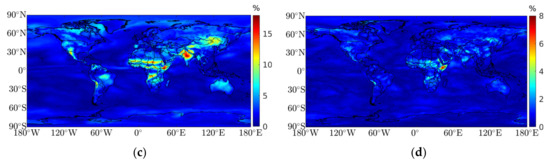
Figure 1.
Global distribution of mean coefficients for relative humidity: (a) mean values (%); (b) mean annual amplitude contribution (%); (c) mean semi-annual contribution (%); and (d) mean quarterly contribution (%).
Usually, other models adopted 5° × 5°, 2.5° × 2.5°, or 1° × 1° horizontal grid resolutions to estimate the model coefficients. However, even when considering the highest resolution grid, the water vapor present in a cell can have significant variations. In order to investigate the extent of this variation, the standard deviation for the mean value () and each periodicity ( and ) were calculated for each window of 4 × 4 grid points (about 12,544 km2), which was approximately the 1° × 1° horizontal grid. Figure 2 shows the average of the standard deviation calculated for each amplitude. For the mean value, variations up to 28% can be found at the Andes and the west coast of the African continent, and about 20% on the west coast of the United States and Australian coasts, among other places, but with a greater incidence on the land-sea boundaries where complex atmospheric interactions occur (Figure 2a). The annual, semi-annual, and quarterly amplitudes display almost the same spatial pattern (Figure 2b–d). Although the semi-annual and quarterly amplitudes show higher variability in regions far from the coast, all three amplitudes show a higher variability incidence in the south of the Asian continent, mainly between the Himalayas and the north of the Taklamakan Desert, the African continent, and the west coast of the United States (Figure 2b–d). Combining all amplitudes, we found variations up to 48% in cells of 1° × 1° horizontal resolution, which are not considered by the other models in the literature, that can have a significant impact on the ZTD and ZWD estimation. Such variations justify the use of a full ERA5 spatial resolution for applications that require the highest precision in estimating relative humidity.
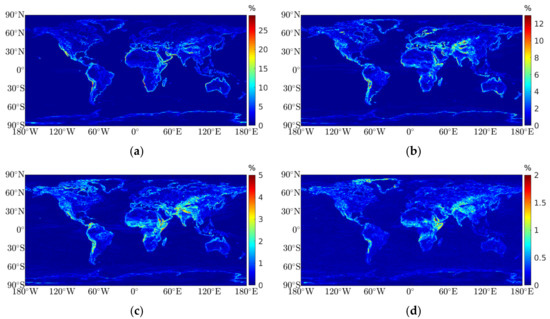
Figure 2.
Maximum spatial variability for each relative humidity periodicity, calculated using a window of 4 × 4 grid points, approximately a 1° × 1° horizontal grid: (a) mean values (%); (b) annual amplitude (%); (c) semi-annual amplitude (%); (d) quarterly amplitude (%).
Similarly to what was done in a previous study [13], we chose the same two points, with very distinct climatological and topographical characteristics—the Sahara desert (λ = 0°, ϕ = 25° N) and the Amazon Rainforest (λ = 65° W, ϕ = 0°)—to apply Equation (7) for a one-year time-span (2020) against ERA5 simulations. Figure 3 shows a good agreement between both models, demonstrating that the time-segmentation model is able to tackle the high variability of the water vapor content in the atmosphere and to reproduce the relative humidity diurnal cycle with accuracy.
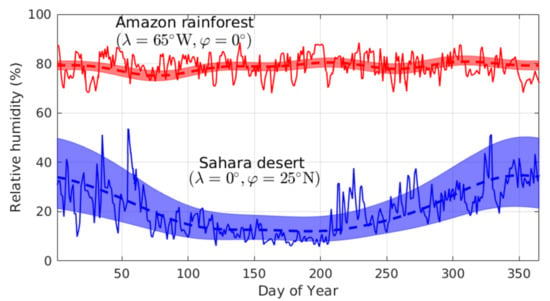
Figure 3.
Relative humidity at two distinct locations with different climatological and topographical characteristics. In blue: over the Sahara Desert (λ = 0°, ϕ = 25°N), and in red: over the Amazon Rainforest (λ = 65°W, ϕ = 0°) during 1 year (2020). The bluish shaded area represents the diurnal cycle, obtained using Equation (7). The dashed line represents the model daily mean, and the continuous line represents the daily mean of ERA5 simulations.
The HGPT2 uses the Saastamoinen wet model (Equation (8)) to obtain the ZWD, and the ZTD is the sum of the two components, the ZWD and the ZHD (calculated using the Saastamoinen hydrostatic model [8]). Figure 4a,b shows an example of the ZTD and ZWD calculated for 1 August 2020, 12:00 UTC. As expected, the ZTD decreases with altitude (lower surface pressure), showing smaller values in mountain regions and higher values at sea level, namely along the equatorial region, due to the presence of high levels of water vapor (Figure 4a). Figure 4b also reflects that ZWD tends to decrease as the latitude increases, since the ZWD depends significantly on the temperature and water vapor pressure. The ZWD quantity can be easily converted to PWV using a constant of proportionality () and interpreted as the height (length units) of an equivalent column of liquid water that would result if the water vapor were condensed (Figure 4c). The atmospheric water vapor has an active role in dynamic processes that shape the atmosphere’s global circulation, and its simulation is challenging due to its high variability in time and space. In the HGPT2, the PWV is calculated based on Equation (9), that uses meteorological surface variables, estimated from different periodicities, to obtain the ZWD and .
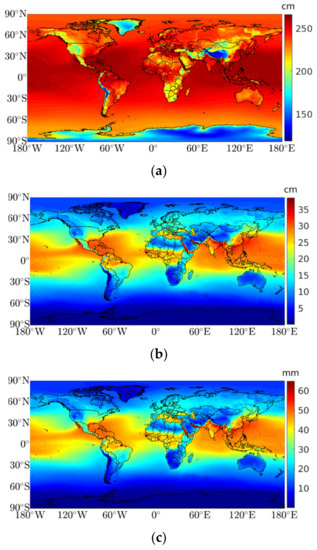
Figure 4.
Example of ZTD, ZWD, and PWV maps calculated on August 1, 2020, 12:00 UTC: (a) ZTD obtained from the sum of the two components (ZHD and ZWD), in cm; (b) ZWD obtained using the Saastamoinen wet model (see Equation (8)), in cm; and (c) PWV calculated using the ZWD and a constant of proportionality ( second term of Equation (9)), in mm.
4. Accuracy Assessment
In this section, we compare the HGPT2-derived relative humidity and precipitable water vapor against ERA5-derived relative humidity during 1 year (hourly data). The ERA5 dew point temperature, surface temperature, and pressure were used to obtain the partial surface pressure () and saturated partial pressure () through the Wexler equations (see Section 2.1). Finally, the RH is calculated using Equation (6). We used the RMSE, bias and Pearson spatial correlation coefficient to characterize the HGPT2 model’s accuracy in space and time. The RMSE indicates how close the estimated values are to the observed values and has the same units as the estimated (and observed) values, given by [43]:
where and are the observations and the corresponding model values, respectively, and is the number of observations. The bias reflects the difference between the estimated expected value and the true value at the same units as estimated (and true) values, given by
Concerning the Pearson correlation coefficient (), it is a dimensionless measure of the linear correlation between two sets of data, and given by
where and represent the covariance and variance, respectively. Figure 5 shows the mean relative humidity RMSE, bias, and Pearson correlation coefficient (). Lower RMSE values can be found on polar and tropic zones, with higher values in the temperate zones (well-defined wet and dry seasons), mostly inland. The mean global RMSE is 7.17%, inland 8.2%, and over oceans 6.5% (Figure 5a). Figure 5b shows the mean bias, where positive values indicate an overestimation of the HGPT2, notorious in the central zone of the United States and over Iraq and Syria. The negative values indicate an underestimation, with greater incidence in Mainland Australia and South Africa. The mean global bias is 0.9%, overland 0.8%, and over oceans 0.9%. The correlation is strong inland, with a mean value of 0.6 (which increases to 0.8, if we exclude Antarctica), and less strong over oceans, with a mean value of 0.4.
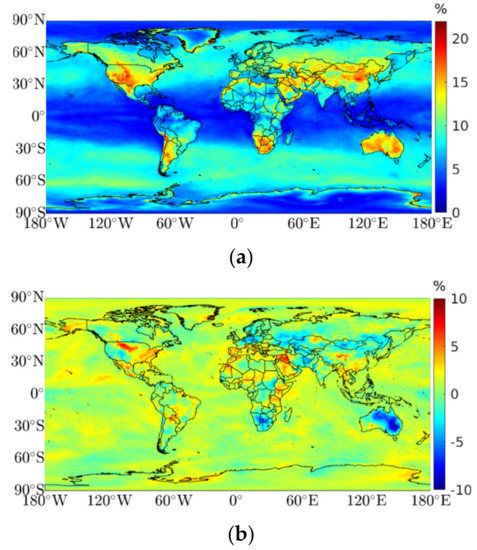
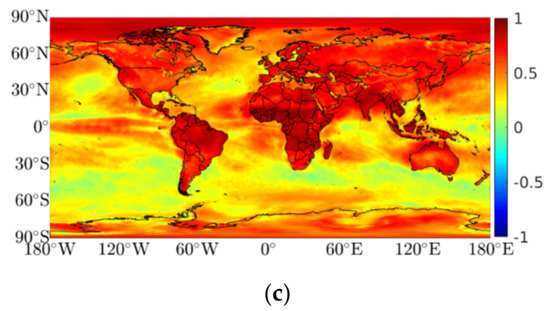
Figure 5.
Comparison of 1 year (2020) of ERA5 RH (modeled from surface dew point temperature, pressure, and temperature) with HGPT2 RH; (a) mean RMSE values (in %); (b) mean bias values, positive (negative) values indicate an overestimation (underestimation) of the HGPT2 model (in %); and (c) mean Pearson correlation coefficient values.
PWV maps were calculated every hour during 1 year (2020) and compared with the maps calculated by ECMWF using the simulations of the ERA5 model. Figure 6a–c displays the mean RMSE, bias, and Pearson correlation coefficient. The mean global RMSE is 5.0 mm, inland 3.5 mm, and over oceans 5.7 mm. The highest RMSE can be seen over the Red Sea, Arabian Sea, and north of Bengal Bay. The smallest values are found at the poles, where the amount of water vapor is almost non-existent (Figure 6a). The mean bias values show a similar behavior, with a mean bias near zero at the poles and higher values at the tropics and temperate zones, with a global mean bias of –0.2 mm (0.8 mm inland and –0.8 mm over the oceans)—see Figure 6b. The correlation is strong inland, with a mean value of 0.74. Areas without correlation can be seen throughout the tropics, the west coast of the United States, and the Arabian Peninsula. The global mean value is 0.7, and over the oceans 0.6. We also calculated the PWV monthly means between January 2016 and December 2020 and compared with the MODIS/Terra level-3 atmospheric precipitable water product with 1° × 1° spatial resolution. The MODIS/Terra (Moderate-Resolution Imaging Spectroradiometer) PWV estimates are based on a near-infrared algorithm that uses only daytime measurements with a solar zenith angle less than 72 degrees; details about the algorithm can be seen in [44]. Figure 6d shows the 5-year mean RMSE, very similar to the map displayed in Figure 6a. However, it reveals a mean global RMSE of 3.7 mm (less 1.3 mm), inland 2.9 mm (less 0.6 mm), and over oceans 4.3 mm (less 1.4 mm). The mean bias and mean Pearson correlation coefficient values are also very similar to Figure 6b,c (not shown).
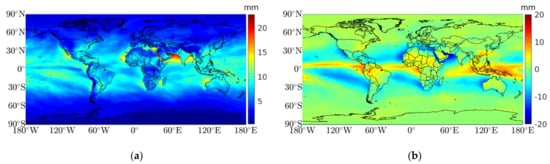
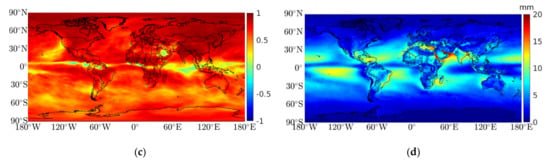
Figure 6.
Comparison of 1 year (2020) of ERA5 PWV (calculated by ECMWF) with HGPT2 PWV; (a) mean RMSE values (in mm); (b) mean bias values, positive (negative) values indicate an overestimation (underestimation) of the HGPT2 model (in mm); (c) mean Pearson correlation coefficient values; and (d) mean RMSE values obtained by comparing 5 years of MODIS monthly data and HGPT2 estimates.
The Scripps Orbit and Permanent Array Center (SOPAC) and the University NAVSTAR Consortium (UNAVCO) provide a database of meteorological observations, recorded near-surface and close to GNSS receivers at several permanent sites scattered worldwide, in RINEX format (here designated as met-files). They include the observation time (GNSS time), relative humidity, temperature, and pressure (the type of observations is dependent on the type of the meteorological sensors)—generally recorded at intervals of a few minutes. However, some sites have small sporadic data gaps, ranging from a few minutes to a few days. For this study, we used met-files with observations for the full year of 2020. A total of about 300 GNSS sites with met-files were available, but we have only considered 282 sites, as relative humidity data was missing for some sites. The in situ RH observations and the RH output from HGPT2 were evaluated based on the RMSE of the differences, the bias, and the correlation coefficient. To understand if the RH provided by the proposed model has advantages over the most used models, we made the same analysis with the Global Pressure and Temperature 2 wet (GPT2w) [27] and with the Global Pressure and Temperature 3 [28]. Both models are developed at the Technical University of Vienna and are based on 10 years of data derived from the ERA-Interim model (available by ECMWF and precedent to the ERA5 model). The GPT3 is the latest version of the GPT (Global Pressure and Temperature) series model and has some improvements over the GPT2w version. The model coefficients are available in two different resolutions, 5° × 5° and 1° × 1°. The code and grid files can be downloaded at https://vmf.geo.tuwien.ac.at/index.html (accessed on 29 January 2020). The output of the GPT2w and the GPT3 model is the water vapor pressure (), and the RH can be determined in two steps: (1) applying the Wexler’s formulation (Equations (1)–(3)) to calculate the saturated water vapor pressure () using the output surface pressure and temperature; and (2) applying Equation (6) to calculate the RH. The statistical results of the mean RMSE, bias, and correlation coefficient (ρ) are shown in Table 1. From the analysis of this table, we can conclude that the differences for the statistic parameters concerning GPT2w and GPT3 are relatively small, with a slight advantage of GPT3, with the best grid resolution. When comparing HGPT2 and GPT3, the mean RMSE decreased 3.4%, an improvement of 17.6%, the mean bias value decreased 0.3%, an improvement of 15%, and the mean correlation value increased from 0.3 to 0.6, an expected result, since neither the GPT2w nor the GPT3 have variation in the daytime cycle—unlike HGPT2, which is based on the concept of time segmentation.

Table 1.
Mean RMSE, bias, and correlation coefficient (ρ) for GPT2w, GPT3 (two grid resolution), and HGPT2, calculated using 282 met-files with RH observations for 1 year (2020), hourly data.
A more effective validation was done by processing a set of 38 stations belonging to the IGS network using the GAMIT/GLOBK package [4]. Figure 7 shows the distribution of the 38 GNSS stations chosen for this analysis. We selected data from 70 days that were divided into two periods to account for the seasonal variations. The first period was from 1 January to 8 February (winter in the northern hemisphere), and the second period from 1 July to 31 July (winter in the southern hemisphere). The first run was done with the default values, i.e., GPT3, atmospheric values estimated every 2 h, and the Global Mapping Function (GMF)—see Table 2.
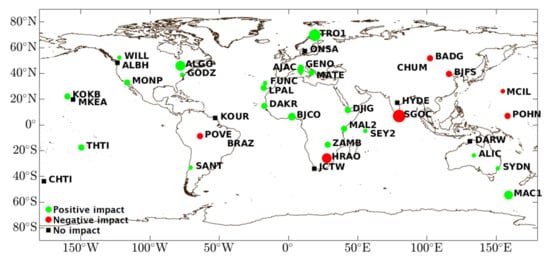
Figure 7.
Weight-root-mean-square (WRMS) variation between the two runs (with and without HGPT2) for the station height. Green circles show stations with a positive impact, red circles stations with a negative impact, and black squares stations with no impact. The circle size indicates the magnitude of the impact: negative for values from −0.8 to −0.1 mm, and positive values from 0.1 to 0.7 mm.

Table 2.
Processing main parameters in the GAMIT/GLOBK software. The main difference is the source of the meteorological observation. The first run uses the default options; in the second run, the surface pressure, temperature, and relative humidity at each GNSS station location is provided by the HGPT2 model through met-files. Each run has data from the 70 days selected. The bold option indicates the differences between runs.
The GPT3 model, as implemented in GAMIT/GLOBK, reads from an external table the zenith hydrostatic delay (ZHD), temperature, water vapor pressure, lapse rate, and dry and wet mapping functions. The relative humidity is then calculated using the input water vapor pressure and temperature through Magnus Teten’s formulation [48]. In the second run, the surface pressure, temperature, and relative humidity are read by GAMIT/GLOBK from met-files, and the hydrostatic delay is computed using the input values given by the Saastamoinen model. For each DOY and GNSS station, one met-file was created with hourly resolution (a total of 2475 met-files, which corresponds to 176,400 observations) using the outputs of the HGPT2 model. We combined both solutions (two-time slots) in a unique solution and used the weight-root-mean-square (WRMS) [49] (p. 16.551, Equation (3)) error to determine the degree of improvement in the repeatability of the position components, namely in the vertical component, by the inclusion of the meteorological daily cycle variability. Significant biases occur in the station height, while biases on horizontal (N and E) directions are minimal, so its analysis will be ignored in this study. Comparing the WRMS between both runs, an improvement was found in 22 stations (59%) and a worsening in seven (18%); no differences were found for the remaining nine stations (23%). The WRMS varied from –0.8 mm (a worsening) to 0.7 mm (an improvement) between the two runs. Figure 7 shows each station’s results; the green circles show stations with a positive impact, the red circles stations with a negative impact, and the black squares stations with no impact. The circle size indicates the magnitude of the impact. Two stations, SGOC and HRAO, show the worst comparative solution, with –0.8 and –0.6 mm, respectively. The behavior of these two sites is not clear, and therefore a more detailed analysis is needed. The remaining five stations (BADG, BJFS, MCIL, POHN, and POVE) show small values, between –0.1 and –0.2 mm. Overall, the HGPT2 model improved the quality of the repeatability in 59% of all sites.
5. Conclusions
In this study, an improvement of the ERA5-based hourly global pressure and temperature (HGPT) is presented, named HGPT2. This model follows the same concept that its predecessor, time segmentation, to obtain estimates of relative humidity anywhere on the Earth’s surface. It uses 20 years of ECMWF ERA5 reanalysis data at full spatial (0.25° × 0.25°) and temporal (1-h) resolution to obtain the mean and three periodicities for each hour (annual, semi-annual, and quarterly). The HGPT2 adds three new outputs, the relative humidity (RH), the zenith wet delay (ZWD), and the precipitable water vapor (PWV). The water vapor pressure and saturated water vapor pressure are easily calculated from temperature and relative humidity (e.g., applying the Wexler’s formulation).
The most used zenith delay models (e.g., GPT series) interpolate their coefficients from a 5° × 5° or 1° × 1° horizontal grid resolution. We found mean relative humidity variations up to 48% in cells of 1° × 1° not considered by these models. The spatial and temporal resolution of ERA5 will significantly improve the relative humidity estimations, not only at seacoasts, where there are land-sea-atmosphere complex interactions, but also in inland areas, enhancing hydrological modeling. We compared the relative humidity from HGPT2, GPT2w (5° and 1° grid resolution), and GPT3 (5° and 1° grid resolution) with in situ observations recorded in 282 met-files (1-year interval) and made available at the SOPAC and UNAVCO FTP sites. Our results indicate an improvement of 18% (in RMSE) and 15% (in bias) and a considerable increase in the mean correlation value, from 0.27 to 0.61. The HGPT2-derived PWV values were compared with ERA5 and MODIS/Terra PWV products (monthly resolution). The mean global RMSE was 5.0 mm and 3.7 mm, respectively. We used the GAMIT/GLOBK package to process 38 GNSS stations belonging to the IGS network in two steps—the first with the default setup, and the second using the HGPT2 output. The results for the height component indicate an improvement in 22 stations (59%) and a worsening in seven (18%), while nine (23%) show no differences.
Author Contributions
Conceptualization, P.M. and V.B.M.; methodology, P.M. and V.B.M.; software, P.M.; validation, P.M. and V.B.M.; formal analysis, P.M. and V.B.M.; investigation, P.M.; resources, P.M.; data curation, P.M.; writing—original draft preparation, P.M.; writing—review and editing, V.B.M. and S.M.P.; visualization, S.M.P.; supervision, V.B.M.; project administration, P.M.; funding acquisition, P.M. and V.B.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FCT-Instituto Dom Luiz under Project UIDB/50019/2020- IDL.
Data Availability Statement
Met-files available by the Scripps Orbit and Permanent Array Center (SOPAC) can be found at http://garner.ucsd.edu/pub/met/ (accessed on 29 January 2020) (requires authentication) and by the University NAVSTAR Consortium (UNAVCO) at ftp://data-out.unavco.org/pub/rinex/met/ (accessed on 29 January 2020). ERA5 hourly data on single levels from 1979 to the present can be found at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 29 January 2020) (includes PWV fields and dew point temperature). MODIS/Terra data are available at https://ladsweb.modaps.eosdis.nasa.gov/archive/allData/61/ (accessed on 29 January 2020). Subroutines developed in Fortran, Matlab, and Python are available at https://github.com/pjmateus/hgpt_model (accessed on 29 January 2020), along with the coefficient files in binary format.
Acknowledgments
We are grateful to the European Centre for Medium-Range Weather Forecasts (ECMWF) for making the hourly climate simulations (ERA5) available and free through the Climate Data Store; to the Scripps Orbit and Permanent Array Center (SOPAC) and the University NAVSTAR Consortium (UNAVCO), which make free and available surface observations; and to the Department of Earth, Atmospheric and Planetary Sciences, MIT, for making the GAMIT/GLOBK software free and available and for the support given. Thank you also for the GPT series provided by Global Geodetic Observing System (GGOS), which is available at https://vmf.geo.tuwien.ac.at/ (accessed on 29 January 2020).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS-Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and more. Choice Rev. Online 2008, 45. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. 1992, 97. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; Floyd, M.A.; McClusky, S.C. GAMIT Reference Manual Reference Manual GPS Analysis at MIT. 2018. Available online: http://geoweb.mit.edu/gg/GAMIT_Ref.pdf (accessed on 1 March 2020).
- Tralli, D.M.; Lichten, S.M. Stochastic estimation of tropospheric path delays in global positioning system geodetic measurements. Bull. Géod. 1990, 64, 127–159. [Google Scholar] [CrossRef]
- Xu, G. GPS: Theory, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 9783540727149. [Google Scholar]
- Hopfield, H.S. Two-Quartic Tropospheric Refractivity Profile for Correcting Satellite Data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géod. 1972, 46, 279–298. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric water vapor, convection, and climate. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction—Part II. Refraction corrections in satellite geodesy. Bull. Géod. 1973, 47, 13–34. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Zhang, C.; Li, Y.; Li, J. A regional zenith tropospheric delay (Ztd) model based on gpt3 and ann. Remote Sens. 2021, 13, 838. [Google Scholar] [CrossRef]
- Yang, L.; Gao, J.; Zhu, D.; Zheng, N.; Li, Z. Improved zenith tropospheric delay modeling using the piecewise model of atmospheric refractivity. Remote Sens. 2020, 12, 876. [Google Scholar] [CrossRef]
- Long, F.; Hu, W.; Dong, Y.; Wang, J. Neural network-based models for estimating weighted mean temperature in china and adjacent areas. Atmosphere 2021, 12, 169. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Q.; Verhagen, S.; Psychas, D.; Dun, H. Kriging interpolation in modelling tropospheric wet delay. Atmosphere 2020, 11, 1125. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Yao, Y. An ERA5-Based Model for Estimating Tropospheric Delay and Weighted Mean Temperature Over China With Improved Spatiotemporal Resolutions. Earth Sp. Sci. 2019, 6, 1926–1941. [Google Scholar] [CrossRef]
- Li, J.; Zhang, B.; Yao, Y.; Liu, L.; Sun, Z.; Yan, X. A refined regional model for estimating pressure, temperature, and water vapor pressure for geodetic applications in China. Remote Sens. 2020, 12, 1713. [Google Scholar] [CrossRef]
- Leandro, R.F.; Langley, R.B.; Santos, M.C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques. GPS Solut. 2008, 12, 65–70. [Google Scholar] [CrossRef]
- Schüler, T. The TropGrid2 standard tropospheric correction model. GPS Solut. 2014, 18, 123–131. [Google Scholar] [CrossRef]
- Krueger, E.; Schueler, T.; Hein, G.; Martellucci, A.; Blarzino, G. Galileo tropospheric correction approaches developed within GSTB-V1. In Proceedings of the GNSS 2004—European Navigation Conference, Rotterdam, The Netherlands, 16–19 May 2004. [Google Scholar]
- Yao, Y.; Xu, C.; Shi, J.; Cao, N.; Zhang, B.; Yang, J. ITG: A New Global GNSS Tropospheric Correction Model. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef]
- Martellucci, A.; Cerdeira, A.R.P. Review of tropospheric, ionospheric and multipath data and models for global navigation satellite systems. In Proceedings of the European Conference on Antennas and Propagation, EuCAP 2009, Berlin, Germany, 23–27 March 2009; pp. 3697–3702. [Google Scholar]
- Gibson, J.K.; Kållberg, P.; Uppala, S.; Hernandez, A.; Nomura, A.; Serrano, E. ECMWF Re-Analysis Project Report Series 1. 1999. Available online: https://www.ecmwf.int/sites/default/files/elibrary/1997/9584-era-description.pdf (accessed on 1 March 2020).
- Trenberth, K.E.; Stepaniak, D.P.; Hurrell, J.W.; Fiorino, M. Quality of reanalyses in the tropics. J. Clim. 2001, 14, 1499–1510. [Google Scholar] [CrossRef]
- Shea, D. National Center for Atmospheric Research Staff NCAR Climate Data Guide 2016. Available online: https://climatedataguide.ucar.edu/climate-data/era-15 (accessed on 1 March 2020).
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined discrete and empirical troposphere mapping functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Mateus, P.; Catalão, J.; Mendes, V.B.; Nico, G. An ERA5-Based Hourly Global Pressure and Temperature (HGPT) Model. Remote Sens. 2020, 12, 1098. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Bevis, M. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP|ECMWF. 2018. Available online: https://www.ecmwf.int/node/18765 (accessed on 29 January 2020).
- Copernicus Climate Change Service (C3S) ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 29 January 2020).
- Hoffmann, L.; Günther, G.; Li, D.; Stein, O.; Wu, X.; Griessbach, S.; Heng, Y.; Konopka, P.; Müller, R.; Vogel, B.; et al. From ERA-Interim to ERA5: The considerable impact of ECMWF’s next-generation reanalysis on Lagrangian transport simulations. Atmos. Chem. Phys 2019, 19, 3097–3124. [Google Scholar] [CrossRef]
- Wexler, A. Vapor pressure formulation for water in range 0 to 100 Degrees C. A revision. J. Res. Natl. Bur. Stand. 1976, 80A, 775–785. [Google Scholar] [CrossRef]
- Wexler, A. Vapor Pressure Formulation for Ice. J. Res. Natl. Bur. Stand. 1977, 81A, 5–20. [Google Scholar] [CrossRef]
- Hardy, B. ITS-90 Formulations for Water Vapor Pressure, Frostpoint Temperature, Dewpoint Temperature, and Enhancement Factors in range −100 to +100 C. In Proceedings of the Third International Symposium on Humidity and Moisture, Teddington, UK, 6–8 April 1998; pp. 1–8. [Google Scholar]
- Essen, L.; Froome, K.D. Dielectric constant and refractive index of air and its principal constituents at 24,000 Mc./s. Nature 1951, 167, 512–513. [Google Scholar] [CrossRef]
- Mendes, V.B. Modeling the Neutral-Atmospheric Propagation Delay in Radiometric Space Techniques; University of New Brunswick: Fredericton, NB, Canada, 1999; p. 353. [Google Scholar]
- Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA Recommended Values of the Fundamental Physical Constants: 2010. J. Phys. Chem. Ref. Data 2012, 41, 043109. [Google Scholar] [CrossRef]
- Rüeger, J.M.; Jean Rüeger, A.M. Refractive Index Formulae for Radio Waves. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002; pp. 19–26. [Google Scholar]
- Neumann, J. Latitudinal variation of tropospheric temperature lapse rate. Arch. Meteorol. Geophys. Bioklimatol. Ser. A 1955, 8, 351–353. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 100, ISBN 978-0-12-385022-5. [Google Scholar]
- Hubanks, P.; Platnick, S.; King, M.; Ridgway, B. Monthly Mean Liquid Water Cloud Optical Thickness from Aqua/MODIS for MODIS Atmosphere L3 Gridded Product Algorithm Theoretical Basis Document (ATBD) & Users Guide. 2006. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod30.pdf (accessed on 29 January 2020).
- Tregoning, P.; van Dam, T. Atmospheric pressure loading corrections applied to GPS data at the observation level. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Murray, F.W. On the Computation of Saturation Vapor Pressure. J. Appl. Meteorol. 1967, 6, 203–204. [Google Scholar] [CrossRef]
- Larson, K.M.; Agnew, D.C. Application of the Global Positioning System to Crustal Deformation Measurement: 1. Precision and Accuracy. J. Geophys. Res. 1991, 96, 16547–16565. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).