Detection of Upper and Lower Planetary-Boundary Layer Curves and Estimation of Their Heights from Ceilometer Observations under All-Weather Conditions: Case of Athens, Greece
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Data Pre-Processing
2.3. Methodology
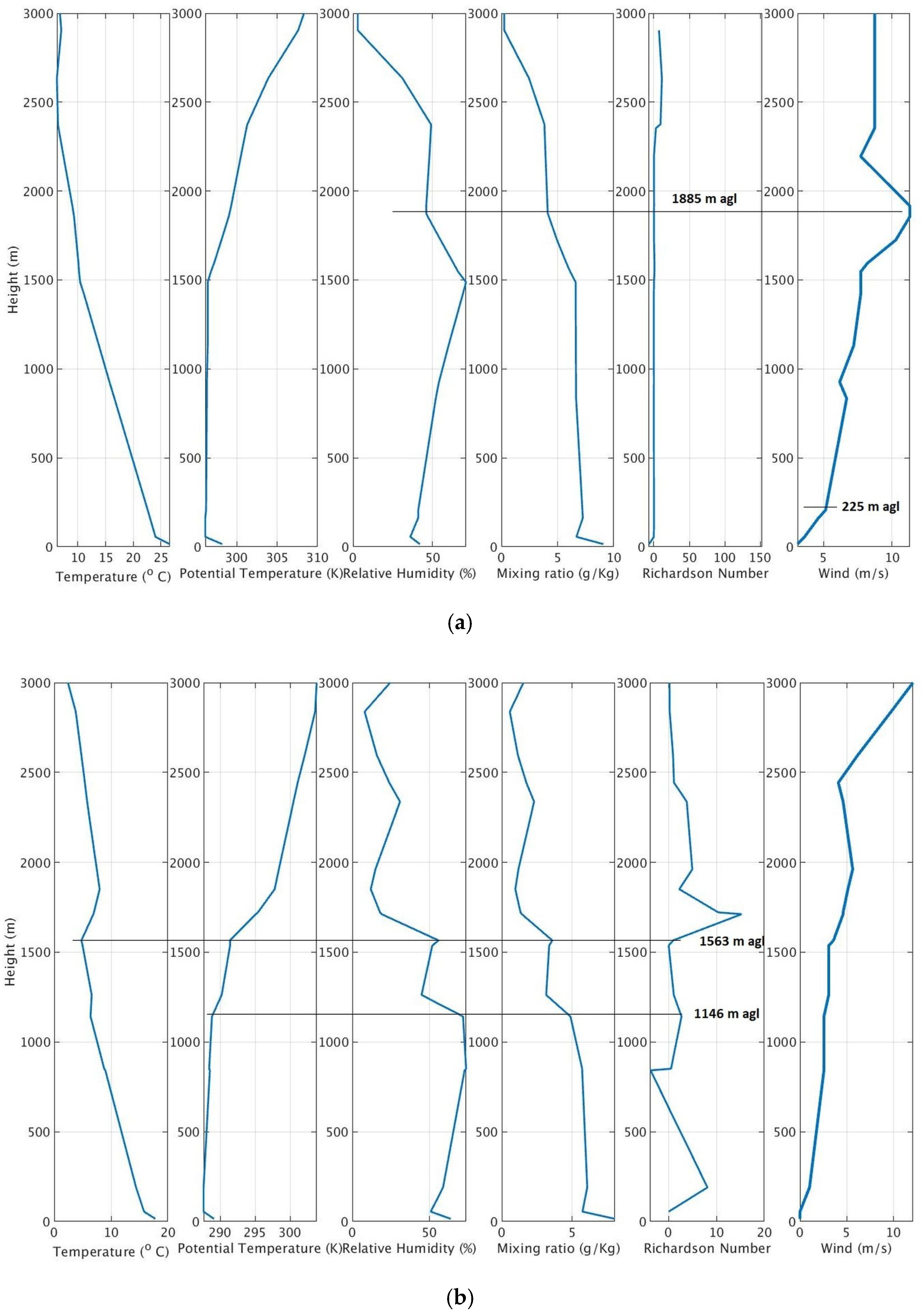
2.3.1. Retrieval of the MLH from Radiosonde Soundings
2.3.2. Methods for Retrieving MLH from Ceilometers
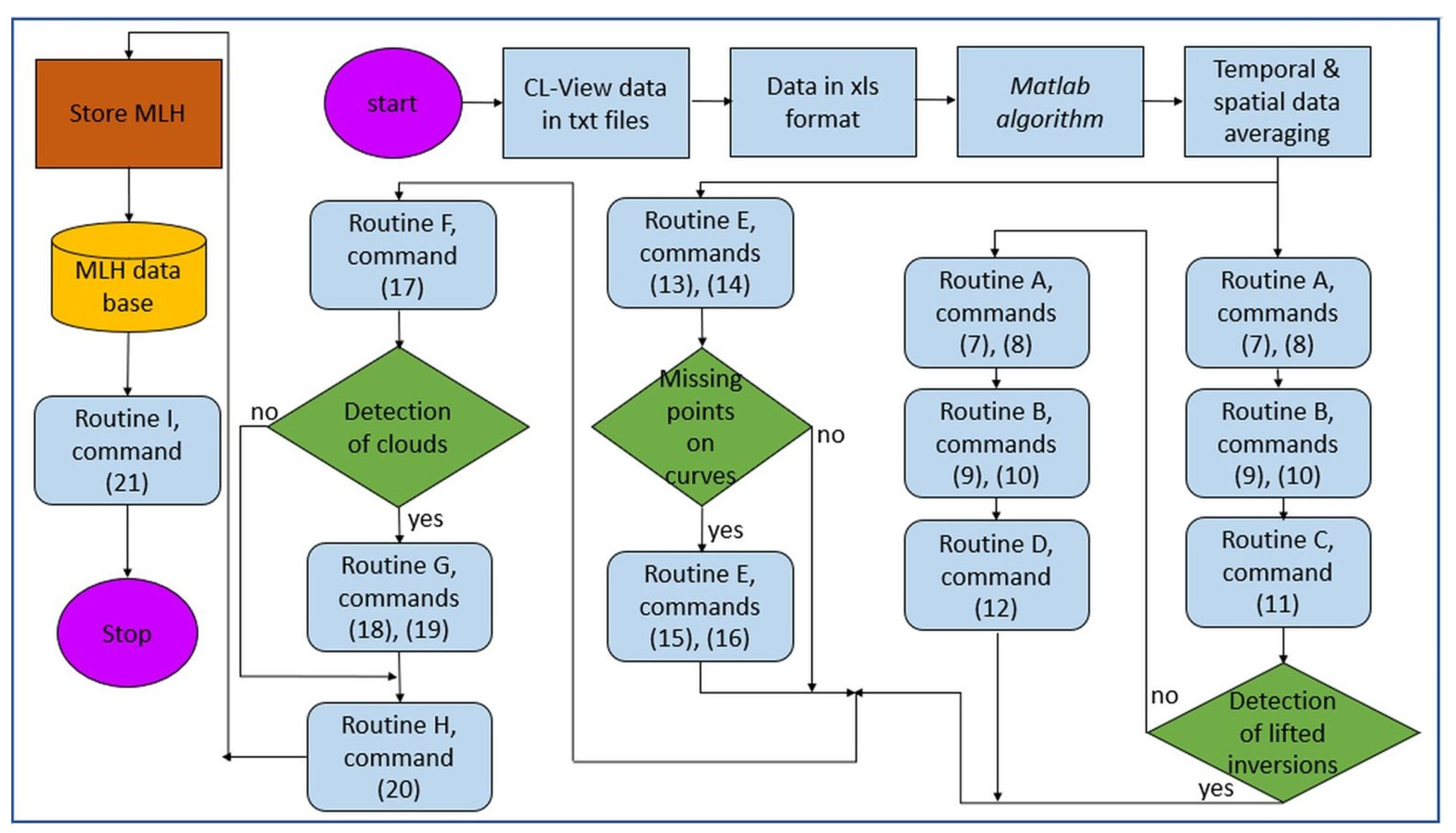
2.3.3. New Algorithm for Retrieving the MLH from Ceilometers
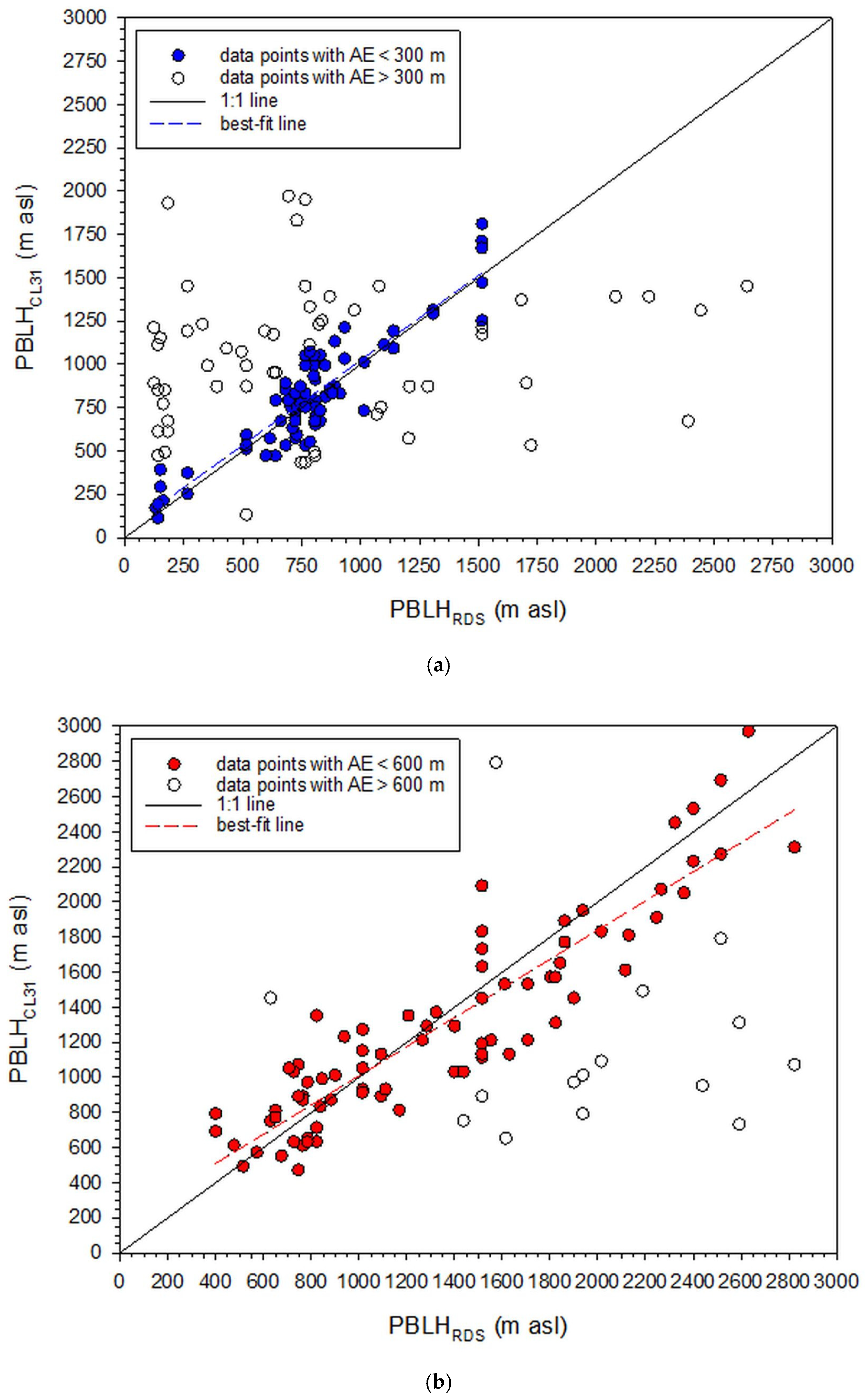
2.4. Evaluation of the Algorithm
2.5. Statistics of the Algorithm-Derived PBL Height
3. Results
3.1. Month-Hour PBL Diagrams
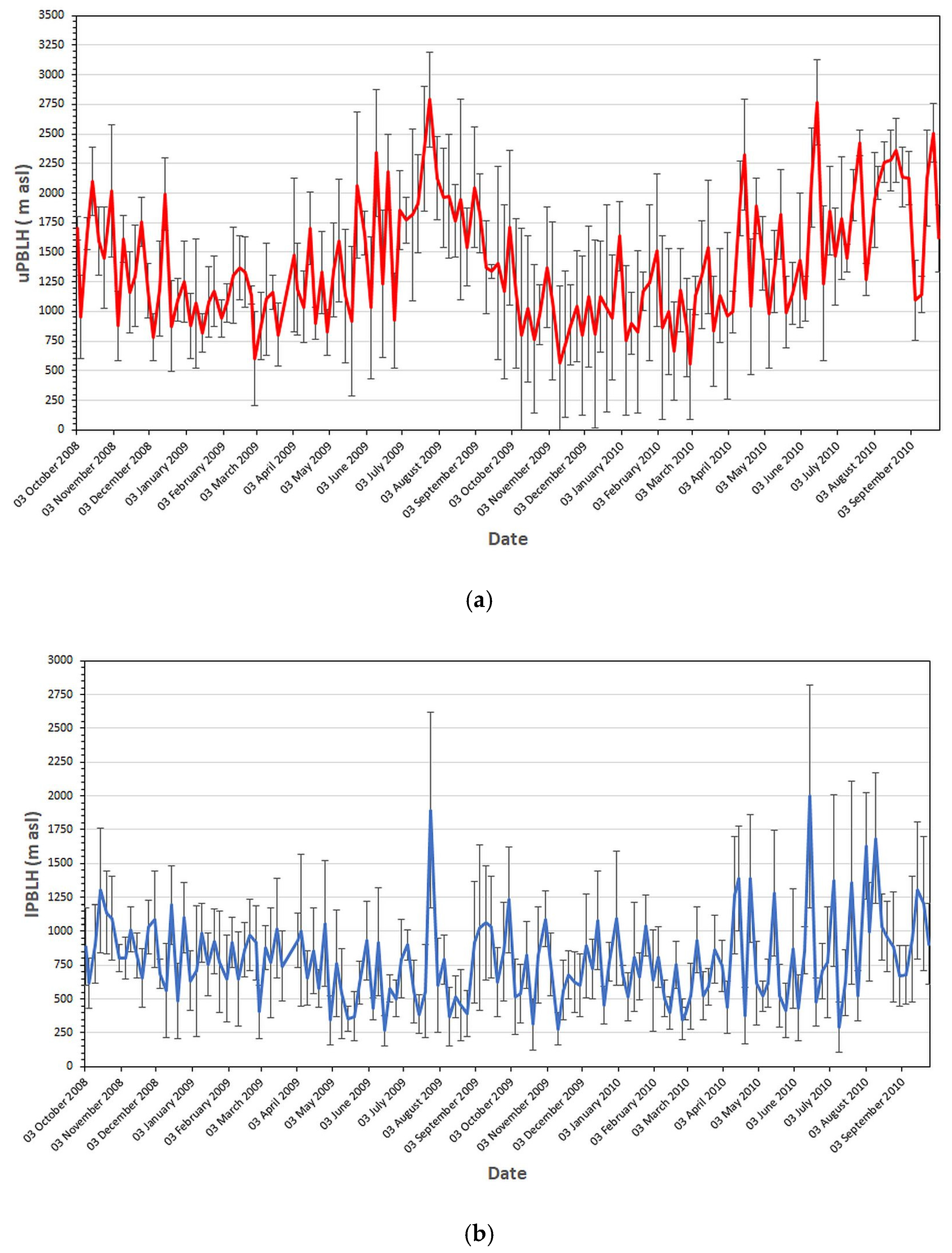
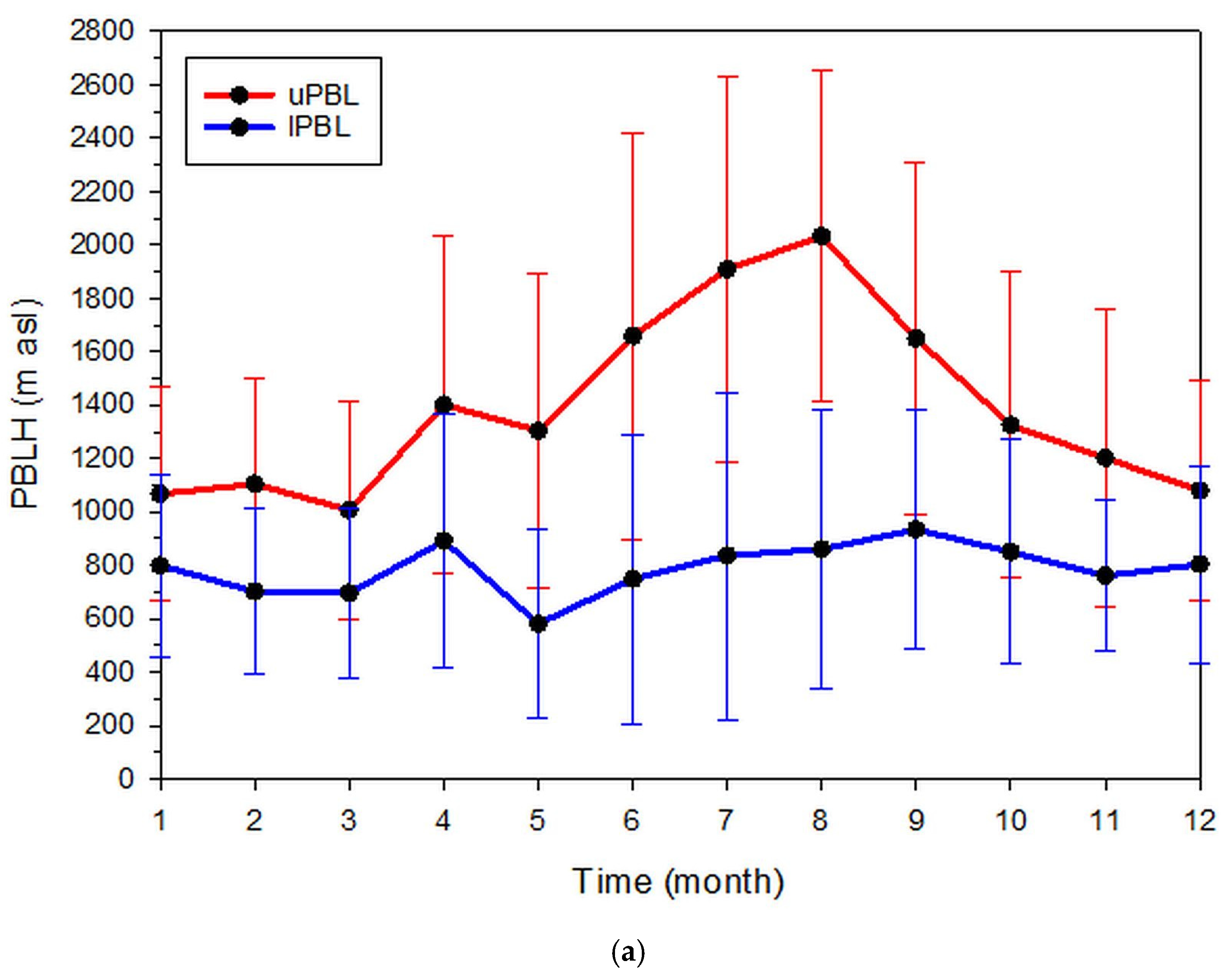
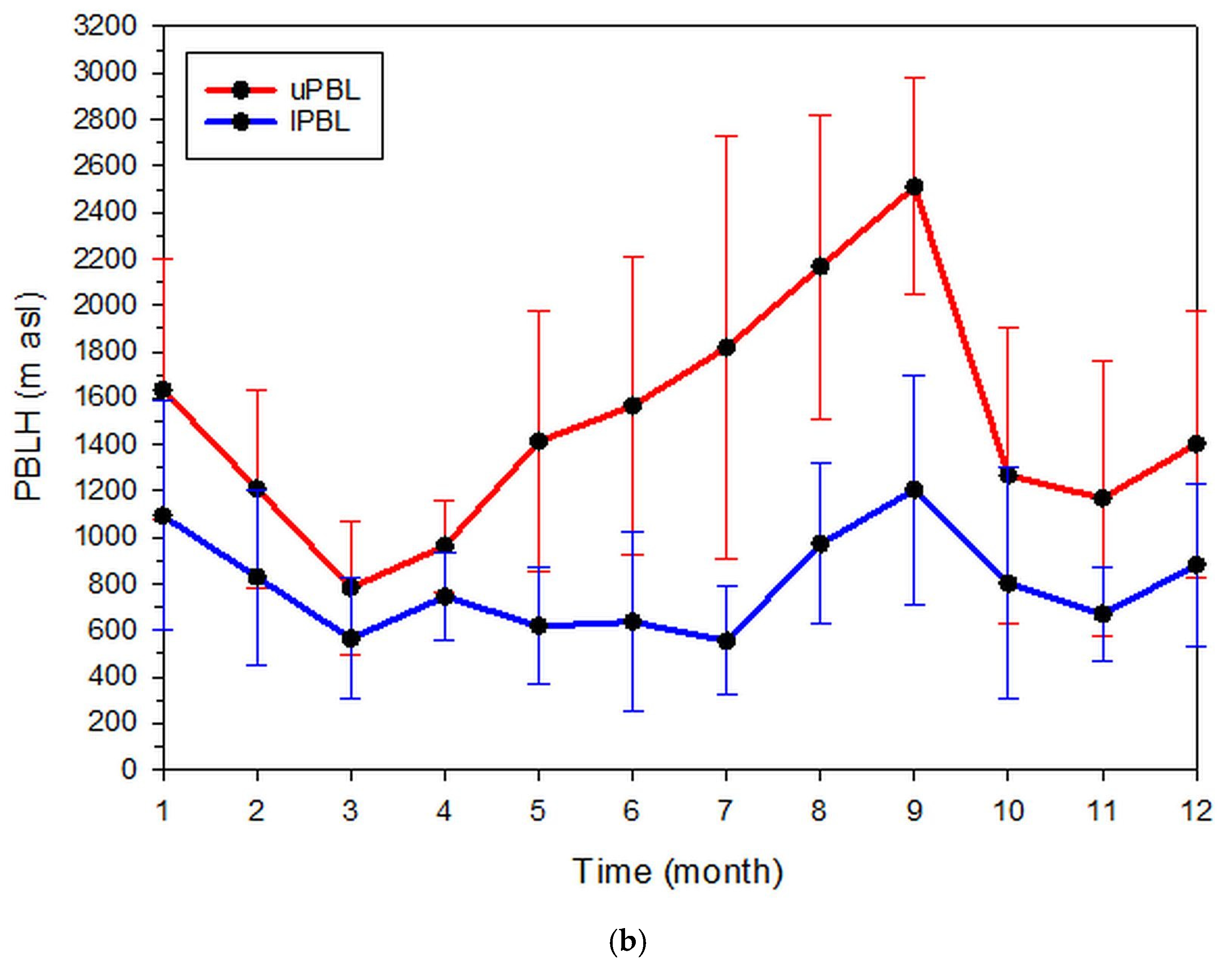
3.2. Inter-Annual PBL-Height Variation
3.3. Intra-Annual PBL-Height Variation
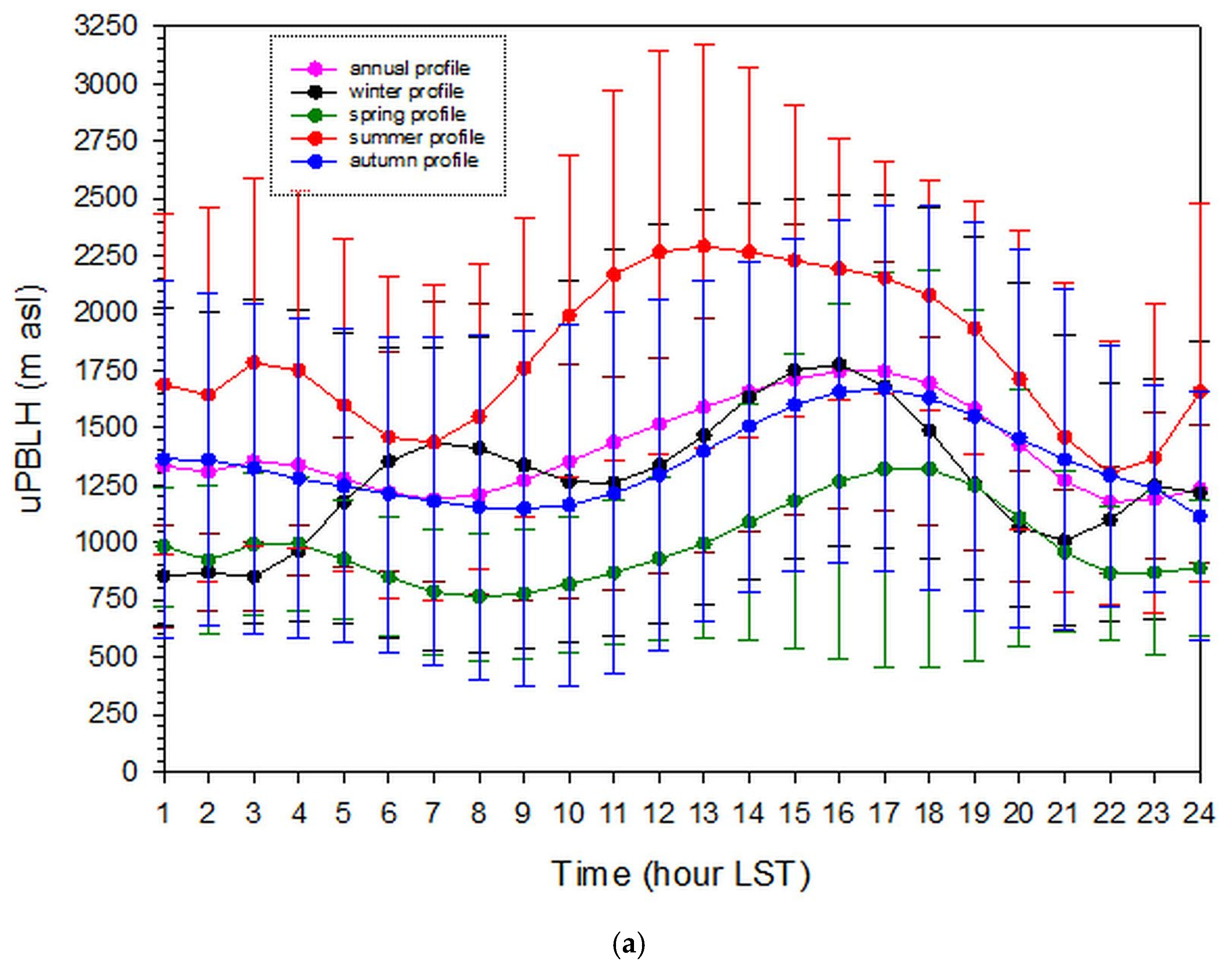
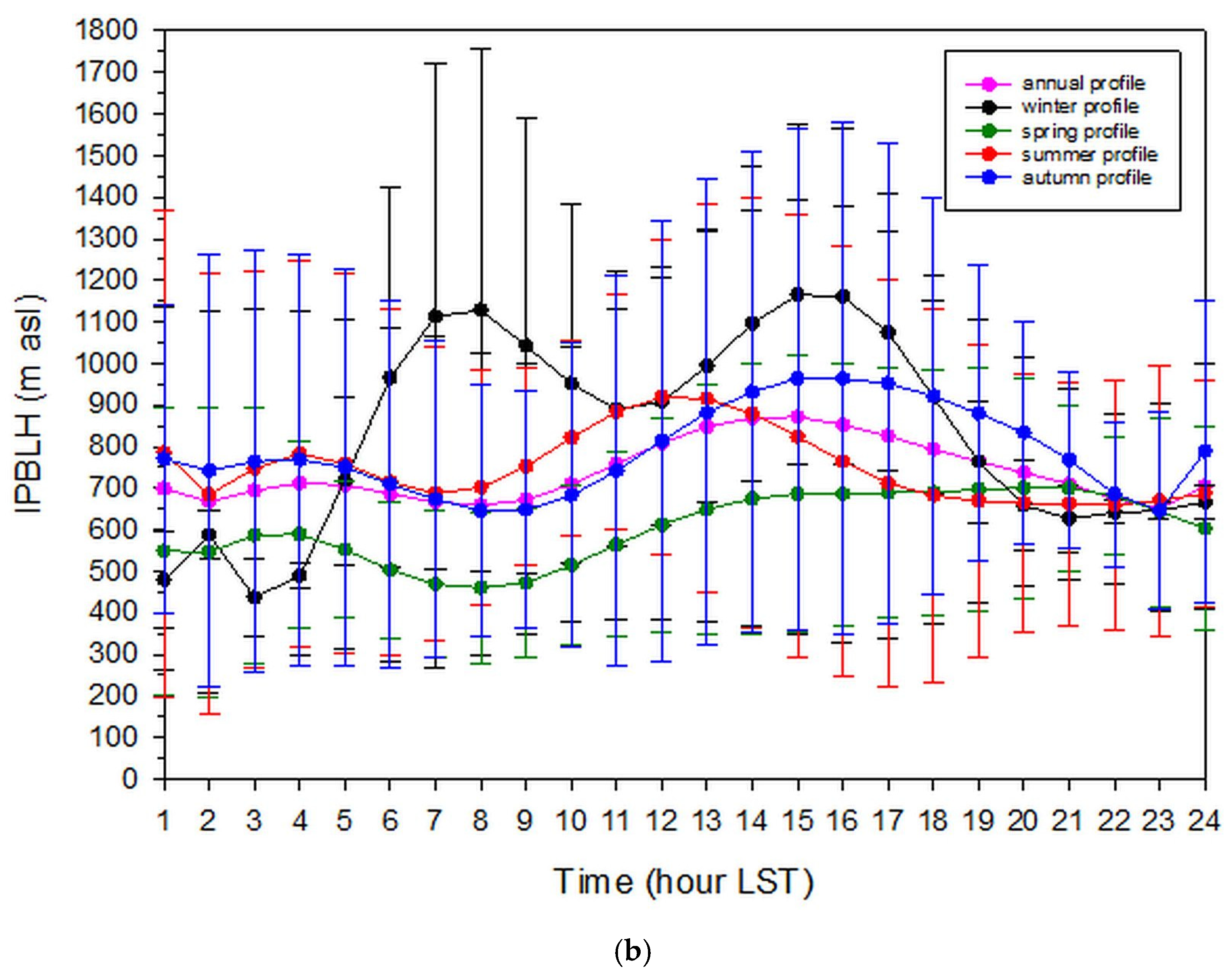
3.4. Seasonal PBL-Height Variation
3.5. Intra-Daily PBL-Height Variation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and inter-comparison of operational methods for the determination of the Mixing Height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Compton, J.C.; Delgado, R.; Berkoff, T.A.; Hoff, R.M. Determination of Planetary Boundary layer height on short spatial and temporal scales: A demonstration of the covariance wavelet transforms in ground-based wind profiler and lidar measurements. J. Atmos. Ocea. Tech. 2013, 30, 1566–1575. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. 2010, 115, D16113. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kim, J.; Cho, C.-H. An automated monitoring of atmospheric mixing height from routine radiosonde profiles over S. Korea using a web-based data transfer method. Environ. Monit. Assess. 2014, 186, 3253–3263. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, K.C. Estimation of atmospheric mixing layer height from radiosonde data. Atmos. Meas. Tech. 2014, 7, 1701–1709. [Google Scholar] [CrossRef]
- Ferrero, L.; Riccio, A.; Perrone, M.G.; Sangiori, G.; Ferrini, B.S.; Bolzacchini, E. Mixing height determination by tethered balloon-based particle soundings and modeling simulations. Atmos. Res. 2011, 102, 145–156. [Google Scholar] [CrossRef]
- Dai, C.; Wang, Q.; Kalogiros, J.A.; Lenschow, D.H.; Gao, Z.; Zhou, M. Determining Boundary-Layer Height from aircraft measurements. Bound. Layer Meteorol. 2014, 152, 277–302. [Google Scholar] [CrossRef]
- Eremsaa, N.; Karppinen, A.; Joffre, S.M.; Räsänen, J.; Talvitie, H. Mixing layer height determination by ceilometer. Atmos. Chem. Phys. 2006, 6, 1485–1493. [Google Scholar] [CrossRef]
- Feng, X.; Wu, B.; Yan, N. A method for deriving the Boundary Layer Mixing height from MODIS atmospheric profile data. Atmosphere 2015, 6, 1346–1361. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, S.; Wang, L.; Gao, Z.; Zhang, Y.; Zou, H.; Miao, S.; Li, Y.; Huang, M.; Yim, S.H.L.; et al. Diurnal evolution of the wintertime Boundary Layer in urban Beijing, China: Insights from doppler lidar and a 325-m meteorological tower. Remote Sens. 2020, 12, 3935. [Google Scholar] [CrossRef]
- Wang, D.; Stachlewska, I.S.; Song, X.; Heese, B.; Nemuc, A. Variability of the Boundary Layer over an urban continental site based on 10 years of active remote sensing observations in Warsaw. Remote Sens. 2020, 12, 340. [Google Scholar] [CrossRef]
- De Bruine, M.; Apituley, A.; Donovan, D.P.; Klein Baltink, H.; Haij, M.J.D. Pathfinder: Applying graph theory to consistent tracking of daytime mixed layer height with backscatter lidar. Atmos. Meas. Tech. 2017, 10, 1893–1909. [Google Scholar] [CrossRef]
- Liu, B.; Guo, J.; Gong, W.; Shi, Y.; Jin, S. Boundary Layer Height as estimated from radar wind profilers in four cities in China: Relative contributions from aerosols and surface features. Remote Sens. 2020, 12, 1657. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Mixing height determination for dispersion modeling. Report of Working Group 2. In Harmonization in the Preprocessing of Meteorological Data for Atmospheric Dispersion Models; Office for Official Publications of the European Communities: Luxembourg, 1998. [Google Scholar]
- Emeis, S.; Jahn, C.; Münkel, C.; Münsterer, C.; Schäfer, K. Multiple atmospheric layering and mixing-layer height in the Inn valley observed by remote sensing. Meteorol. Zeit. 2007, 16, 415–424. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary-Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Piringer, M.; Joffre, S.; Baklanov, A.; Christen, A.; Doserti, M.; De Ridder, K.; Emeis, S.; Mestayer, P.; Tombrou, M.; Middleton, D.; et al. The surface energy budget and the mixing height in urban areas–activities and recommendations of COST-Action 715. Bound. Layer Meteorol. 2007, 124, 3–24. [Google Scholar] [CrossRef]
- Tsaknakis, G.; Papayannis, A.; Kokkalis, P.; Amiridis, V.; Kambezidis, H.D.; Mamouri, R.E.; Georgoussis, G.; Avdikos, G. Inter-comparison of lidar and ceilometer retrievals for aerosol and planetary boundary layer profiling over Athens, Greece. Atmos. Meas. Tech. 2011, 4, 1261–1273. [Google Scholar] [CrossRef]
- Knippertz, P.; Stuut, J.-B.W. Mineral Dust: A Key Player in the Earth System; Springer: Cham, The Netherlands, 2014. [Google Scholar]
- Mielonen, T.; Aaltonen, V.; Lihavainen, H.; Hyvärinen, A.P.; Arola, A.; Komppula, M.; Kivi, R. Biomass-burning aerosols observed in northern Finland during the 2010 wildfires in Russia. Atmosphere 2013, 4, 17–34. [Google Scholar] [CrossRef]
- Wiegner, M.; Gasteiger, J.; Groß, S.; Schnell, F.; Freudenthaler, V.; Forkel, R. Characterization of the Eyjafjallajökull ash-plume: Potential of lidar remote sensing. Phys. Chem. Earth 2012, 45, 79–86. [Google Scholar] [CrossRef]
- Nemuc, A.; Stachlewska, I.S.; Vasilescu, J.; Górska, A.; Nicolae, D.; Talianu, C. Optical properties of long-range transported volcanic ash over Romania and Poland during Eyjafjallajökull eruption in 2010. Acta Geophys. 2014, 62, 350–366. [Google Scholar] [CrossRef]
- Martucci, G.; Milroy, C.; O’Dowd, C.D. Detection of cloud-base height using Jenoptik CHM15K and Vaisala CL-31 ceilometers. J. Atmos. Ocean. Technol. 2010, 27, 305–318. [Google Scholar] [CrossRef]
- Vaisala CL31 Ceilometer. Available online: https://www.vaisala.com/en/products/instruments-sensors-and-other-measurement-devices/weather-stations-and-sensors/cl31 (accessed on 21 May 2021).
- Wiegner, M.; Gasteiger, J. Correction to water vapor absorption for aerosol remote sensing with ceilometers. Atmos. Meas. Tech. 2015, 8, 3971–3984. [Google Scholar] [CrossRef]
- Münkel, C.; Eresmaa, N.; Räsänen, J.; Karpinen, A. Retrieval of mixing height and dust concentration with lidar ceilometer. Bound. Layer Meteorol. 2007, 124, 117–128. [Google Scholar] [CrossRef]
- Danchovski, V. Summertime urban Mixing Layer Height over Sofia, Bulgaria. Atmosphere 2019, 10, 36. [Google Scholar] [CrossRef]
- Hirsikko, A.; O’Connor, E.J.; Komppula, M.; Korhonen, K.; Pfüller, A.; Giannakaki, E.; Wood, C.R.; Bauer-Pfundstein, M.; Poikonen, A.; Karppinen, T.; et al. Observing wind, aerosol particles, cloud and precipitation: Finland’s new ground-based remote-sensing network. Atmos. Meas. Tech. 2014, 7, 1351–1375. [Google Scholar] [CrossRef]
- E-PROFILE (EUMETNET Profiling Programme). Available online: https://e-profile.eu/#/cm_profile (accessed on 21 May 2021).
- EUMETNET (European Meteorological Services Network). Available online: https://www.eumetnet.eu (accessed on 21 May 2021).
- Haman, C.L.; Lefer, B.; Morris, G.A. Seasonal variability in the diurnal evolution of the Boundary Layer in a near-coastal urban environment. J. Atmos. Ocean. Technol. 2012, 29, 697–710. [Google Scholar] [CrossRef]
- Stachlewska, I.S.; Piądłowski, M.; Migacz, S.; Szkop, A.; Zielińska, A.; Swaczyna, P.L. Ceiloemeter observations of the boundary layer over Warsaw, Poland. Acta Geophys. 2012, 60, 1386–1412. [Google Scholar] [CrossRef]
- Mues, A.; Rupakheti, M.; Münkel, C.; Lauer, A.; Bozem, H.; Hoor, P.; Butler, T.; Lawrence, M.G. Investigation of the mixing layer height derived from ceilometer measurements in the Kathmandu Valley and implications for local air quality. Atmos. Chem. Phys. 2017, 17, 8157–8176. [Google Scholar] [CrossRef]
- COST Action 1303 (TOPROF). Towards Operational Ground-Based Profiling with Ceilometers, Doppler Lidars and Microwave Radiometers for Improving Weather Forecasts. Available online: https://www.cost.eu/actions/ES1303/#tabs|Name:overview (accessed on 21 May 2021).
- Uzan, L.; Egert, S.; Alpert, P. Ceilometer evaluation of the eastern Mediterranean summer BLH–first study at two Israeli sites. Atmos. Meas. Tech. 2016, 9, 4387–4398. [Google Scholar] [CrossRef]
- Kokkalis, P.; Alexiou, D.; Papayannis, A.; Rocadenbosch, F.; Soupiona, O.; Raptis, P.I.; Mylonaki, M.; Tzanis, C.G.; Christodoulakis, J. Application and testing of the Extended-Kalman-Filtering Technique for determining the Planetary Boundary-Layer height over Athens, Greece. Bound. Layer Meteorol. 2020, 176, 125–147. [Google Scholar] [CrossRef]
- Emeis, S.; Münkel, C.; Vogt, S.; Müller, W.J.; Schäfer, K. Atmospheric boundary-layer structure from simultaneous SODAR, RASS, and ceilometer measurements. Atmos. Environ. 2004, 38, 273–286. [Google Scholar] [CrossRef]
- De Haij, M.J.; Wauben, W.M.F.; Baltink, H.K.; Apituley, A. Determination of the mixing layer height by a ceilometer. In S03-P01, Proceedings of the 8th International Symposium on Tropospheric Profiling, Delft, The Netherlands, 19–23 October, 2009; Apituley, A., Russchenberg, H.W.J., Monna, W.A.A., Eds.; KNMI: Delft, The Netherlands, 2009; pp. 1–4. [Google Scholar]
- Emeis, S.; Schäfer, K.; Münkel, C. Long-term observations of the urban mixing-layer height with ceilometers. Ser. Earth Environ. Sci. 2008, 1, 012027. [Google Scholar] [CrossRef]
- Lotteraner, C.; Piringer, M. Mixing-layer height time series from operational ceilometer aerosol-layer heights. Bound. Layer Meteorol. 2016, 161, 265–287. [Google Scholar] [CrossRef]
- Cho, C.; Kim, S.W.; Rupakheti, M.; Park, J.-S.; Panday, A.; Yoon, S.C.; Kim, J.-H.; Kim, H.; Jeon, H.; Sung, M.; et al. Wintertime aerosol optical and radiative properties in the Kathmandu Valley during the SusKat-ABC field campaign. Atmos. Chem. Phys. 2017, 17, 12617–12632. [Google Scholar] [CrossRef]
- Di Giuseppe, F.; Riccio, A.; Caporaso, L.; Bonafé, G.; Gobbi, G.P.; Angelini, F. Automatic detection of atmospheric boundary layer height using ceilometer backscatter data assisted by a boundary layer model. Q. J. R. Meteorol. Soc. 2012, 138, 649–663. [Google Scholar] [CrossRef]
- Salmond, J.A.; McKendry, I.G. A review of turbulence in the very stable nocturnal boundary layer and its implication for air quality. Prog. Phys. Geogr. 2005, 29, 171–188. [Google Scholar] [CrossRef]
- Mahrt, L. Nocturnal boundary-layer regimes. Bound. Layer Meteorol. 1998, 88, 255–278. [Google Scholar] [CrossRef]
- Melas, D.; Kambezidis, H.D. The depth of the Internal Boundary Layer over an urban area under sea-breeze conditions. Bound. Layer Meteorol. 1992, 61, 247–264. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Peppes, A.A.; Melas, D. An environmental experiment over Athens urban area under sea-breeze conditions. Atmos. Res. 1995, 36, 139–156. [Google Scholar] [CrossRef]
- Levitin, J.; Kambezidis, H.D. Numerical modelling of the Thermal Internal Boundary Layer evolution using Athens field experimental data. Bound. Layer Meteorol. 1997, 84, 207–217. [Google Scholar] [CrossRef]
- Savijärvi, H.; Niemelä, S.; Tisler, P. Coastal winds and low-level jets: Simulations for sea gulfs. Q. J. R. Meteorol. Soc. 2005, 131, 625–637. [Google Scholar] [CrossRef]
- Münkel, C.; Räsänen, J. Enhanced single lens lidar ceilometer for mixing height and dust concentration retrieval. In Proceedings of the 14th International Conference on Knowledge Technologies and Data-Driven Business, Graz, Austria, 14–17 September 2005. [Google Scholar]
- Münkel, C. Boundary layer and air quality monitoring with a commercial lidar ceilometer. In Proceedings of the Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing, Stockholm, Sweden, 11–14 September 2006. [Google Scholar]
- Vaisala CL-View Software. Available online: https://www.vaisala.com/en/products/software/cl-view100 (accessed on 21 May 2021).
- Morrille, Y.; Haeffelin, M.; Drobinski, P.; Pelon, J. STRAT: An automated algorithm to retrieve the vertical structure of the atmosphere from single-channel lidar data. J. Atmos. Ocean. Technol. 2007, 24, 761–775. [Google Scholar] [CrossRef]
- Schween, J.H.; Hirsikko, A.; Löhnert, U.; Crewell, S. Mixing-layer height retrieval with ceilometer and Doppler lidar: From case studies to long-term assessment. Atmos. Meas. Tech. 2014, 7, 3685–3704. [Google Scholar] [CrossRef]
- Kotthaus, S.; Grimmond, C.S.B. Atmospheric boundary-layer characteristics from ceilometer measurements. Part 1: A new method to track mixed layer height and classify clouds. Q. J. R. Meteorol. Soc. 2018, 144, 1525–1538. [Google Scholar] [CrossRef]
- De Arruda Moreira, G.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Foyo-Moreno, I.; Cazorla, A.; Alados, I.; Lyamani, H.; Landulfo, E.; Alados-Arboledas, L. Study of the planetary boundary layer height in an urban environment using a combination of microwave radiometer and ceilometer. Atmos. Res. 2020, 240, 104932. [Google Scholar] [CrossRef]
- Vaisala BL-View Software Package. Available online: https://www.vaisala.com/en/products/software/bl-view (accessed on 21 May 2021).
- COST Action 710. Harmonisation of the Pre-Processing of the Meteorological Data for Atmospheric Dispersion Models. Available online: http://www.dmu.dk/atmosphericenvironment/cost_710.htm (accessed on 21 May 2021).
- Fisher, B.E.A.; Erbrink, J.J.; Finardi, S.; Jeanet, P.; Joffre, S.; Morselli, M.G.; Pechinger, U.; Siebert, P.; Thomson, D.J. Harmonisation of the Pre-Processing of Meteorological Data for Atmospheric Dispersion Models; Final Report, COST Action 710; European Communities: Brussels, Belgium, 1998. [Google Scholar]
- Coen, M.C.; Praz, C.; Haefele, A.; Ruffieux, D.; Kaufmann, P.; Calpini, B. Determination and climatology of the planetary boundary layer height above the Swiss plateau by in-situ and remote sensing measurements as well as the COSMO-2 model. Atmos. Chem. Phys. 2014, 14, 13205–13221. [Google Scholar] [CrossRef]
- Holzworth, G.C. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Richardson, L.F. Some measurements of atmospheric turbulence. Philos. Trans. R. Soc. Ser. A 1921, 221, 1–28. [Google Scholar]
- Kiefer, M.T.; Heilman, W.E.; Zhong, S.; Charney, J.J.; Bian, X. Mean and turbulent flow downstream of a low-density fire: Influence of canopy and background atmospheric conditions. J. Appl. Meteorol. 2015, 54, 42–57. [Google Scholar] [CrossRef]
- Seigneur, C. Air Pollution: Concepts, Theory, and Applications; Cambridge University Press: Cambridge, UK, 2019; pp. 95–124. [Google Scholar]
- Tang, G.; Zhang, J.; Zhu, X.; Song, T.; Munkel, C.; Hu, B.; Schafer, K.; Liu, Z.; Zhang, J.; Wang, L.; et al. Mixing layer height and its implications for air pollution over Beijing, China. Atmos. Chem. Phys. 2016, 16, 12459–12475. [Google Scholar] [CrossRef]
- Eremsaa, N.; Härkönen, J.; Joffre, S.M.; Schultz, D.M.; Karppinen, A.; Kukkonen, J. A three-step method for estimating the mixing height using ceilometer data from the Helsinki testbed. J. Appl. Meteorol. Climatol. 2012, 51, 2172–2187. [Google Scholar] [CrossRef]
- Markowicz, K.M.; Flatau, P.J.; Kardas, A.E.; Remiszewska, J.; Stelmaszczyk, K.; Woeste, L. Ceilometer retrieval of the boundary layer vertical aerosol extinction structure. J. Atmos. Ocean. Technol. 2008, 25, 928–944. [Google Scholar] [CrossRef]
- Herrera-Mejía, L.; Hoyos, C.D. Characterization of the atmospheric boundary layer in a narrow tropical valley using remote-sensing and radiosonde observations and the WRF model: The Aburrá Valley case-study. Q. J. R. Meteorol. Soc. 2019, 145, 2641–2665. [Google Scholar] [CrossRef]
- Hayden, K.L.; Anlauf, K.G.; Hoff, R.M.; Strapp, J.W.; Bottenheim, J.W.; Wiebe, H.A.; Froude, F.A.; Martin, J.B.; Steyn, D.G.; McKendry, I.G. The vertical chemical and meteorological structure of the boundary layer in the Lower Fraser Valley during Pacific ’93. Atmos. Environ. 1997, 31, 2089–2105. [Google Scholar] [CrossRef]
- Flamant, C.; Pelon, J.; Flamant, P.H.; Durand, P. Lidar determination of the entrainment zone thickness at the top of the unstable marine atmospheric boundary layer. Bound. Layer Meteorol. 1997, 83, 247–284. [Google Scholar] [CrossRef]
- Menut, L.; Flamant, C.; Pelon, J.; Flamant, P.H. Urban Boundary-Layer Height determination from Lidar measurements over the Paris area. Appl. Opt. 1999, 38, 945–954. [Google Scholar] [CrossRef] [PubMed]
- Senff, C.; Bösenberg, J.; Peters, G.; Schaberl, T. Remote sensing of turbulent ozone fluxes and the ozone budget in the convective Boundary Layer with DIAL and Raman-RASS: A case study. Contr. Atmos. Phys. 1996, 69, 161–176. [Google Scholar]
- Sicard, M.; Pérez, C.; Rocadenbosch, F.; Baldasano, J.M.; García-Vizcaino, D. Mixed-layer depth determination in the Barcelona coastal area from regular Lidar measurements: Methods, results and limitations. Bound. Layer Meteorol. 2006, 119, 135–157. [Google Scholar] [CrossRef]
- University of Wyoming, Department of Atmospheric Science, USA. Available online: http://weather.uwyo.edu/upperair/sounding.html (accessed on 21 May 2021).
- Zeng, X.; Brunke, M.A.; Zhou, M.; Fairall, C.; Bond, N.A.; Lenschow, D.H. Marine atmospheric boundary layer height over the eastern Pacific: Data analysis and model evaluation. J. Climatol. 2004, 17, 4159–4170. [Google Scholar] [CrossRef]
- Yamada, T.; Mellor, G.L. A simulation of the Wangara atmospheric boundary layer data. J. Atmos. Sci. 1975, 32, 2309–2329. [Google Scholar] [CrossRef]
- Muňoz, R.C.; Undurraga, A.A. Daytime mixed layer over the Santiago basin: Description of two years of observations with a lidar ceilometer. J. Appl. Meteorol. Climatol. 2010, 49, 1728–1741. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Muneer, T.; Tzortzis, M.; Arvanitaki, S. Global and diffuse horizontal illuminance: Month-hour distribution for Athens, Greece in 1992. Lighting Res. Technol. 1998, 30, 69–74. [Google Scholar] [CrossRef]
- Kambezidis, H.D. The solar radiation climate of Athens: Variations and tendencies in the period 1992–2017, the brightening era. Sol. Energy 2018, 173, 328–347. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Oikonomou, T.I.; Zevgolis, D. Daylight climatology in the Athens urban environment: Guidance for building designers. Lighting Res. Technol. 2002, 34, 297–312. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Psiloglou, B.E. Climatology of the Linke and Unsworth-Monteith turbidity parameters for Greece: Introduction to the notion of a Typical Atmospheric Turbidity Year. Appl. Sci. 2020, 10, 4043. [Google Scholar] [CrossRef]
- Hsu, S.A. Mesoscale nocturnal jet-like winds within the Planetary Boundary Layer over a flat, open coast. Bound. Layer Meteorol. 1979, 17, 485–494. [Google Scholar] [CrossRef]
- Moreno-Garcia, M.C. Intensity and form of the urban heat island in Barcelona. Int. J. Climatol. 1993, 14, 705–710. [Google Scholar] [CrossRef]
- Kassomenos, P.A.; Koletsis, I.G. Seasonal variation of the temperature inversions over Athens, Greece. Int. J. Climatol. 2005, 25, 1651–1663. [Google Scholar] [CrossRef]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kambezidis, H.D.; Psiloglou, B.E.; Gavriil, A.; Petrinoli, K. Detection of Upper and Lower Planetary-Boundary Layer Curves and Estimation of Their Heights from Ceilometer Observations under All-Weather Conditions: Case of Athens, Greece. Remote Sens. 2021, 13, 2175. https://doi.org/10.3390/rs13112175
Kambezidis HD, Psiloglou BE, Gavriil A, Petrinoli K. Detection of Upper and Lower Planetary-Boundary Layer Curves and Estimation of Their Heights from Ceilometer Observations under All-Weather Conditions: Case of Athens, Greece. Remote Sensing. 2021; 13(11):2175. https://doi.org/10.3390/rs13112175
Chicago/Turabian StyleKambezidis, Harry D., Basil E. Psiloglou, Ariadne Gavriil, and Kalliopi Petrinoli. 2021. "Detection of Upper and Lower Planetary-Boundary Layer Curves and Estimation of Their Heights from Ceilometer Observations under All-Weather Conditions: Case of Athens, Greece" Remote Sensing 13, no. 11: 2175. https://doi.org/10.3390/rs13112175
APA StyleKambezidis, H. D., Psiloglou, B. E., Gavriil, A., & Petrinoli, K. (2021). Detection of Upper and Lower Planetary-Boundary Layer Curves and Estimation of Their Heights from Ceilometer Observations under All-Weather Conditions: Case of Athens, Greece. Remote Sensing, 13(11), 2175. https://doi.org/10.3390/rs13112175







