A New Approach to the Quality Control of Slope and Aspect Classes Derived from Digital Elevation Models

Abstract

The usefulness of the parameters (e.g., slope, aspect) derived from a Digital Elevation Model (DEM) is limited by its accuracy. In this paper, a thematic-like quality control (class-based) of aspect and slope classes is proposed. A product can be compared against a reference dataset, which provides the quality requirements to be achieved, by comparing the product proportions of each class with those of the reference set. If a distance between the product proportions and the reference proportions is smaller than a small enough positive tolerance, which is fixed by the user, it will be considered that the degree of similarity between the product and the reference set is acceptable, and hence that its quality meets the requirements. A formal statistical procedure, based on a hypothesis test, is developed and its performance is analyzed using simulated data. It uses the Hellinger distance between the proportions. The application to the slope and aspect is illustrated using data derived from a $2\times 2$ m DEM (reference) and $5\times 5$ m DEM in Allo (province of Navarra, Spain).

1. Introduction

A Digital Elevation Model (DEM) is a generic term for digital topographic and/or bathymetric data [1] and normally implies elevations of the terrain (bare earth) void of vegetation and man-made features. DEMs describe the morphological characteristics of the landforms of a terrain (topography) such as hills, ridges, cliffs, valleys, rivers, etc., and a large number of parameters can be derived (e.g., slope, aspect, curvature, etc.) [2]. DEM data can be generated through many diverse technologies (classical surveying and photogrammetry, Lidar and InSAR systems), and topographic surface modeling can be achieved using very different options such as contour lines, triangular irregular networks, gridded surfaces, parametric surfaces, etc. [3].

We are going to deal with the gridded-model case as it is currently the most widely used for DEM treatment [4]. Grid models are in conformity as a regular-rectangular array of cells, each of which stores an attribute value, so the area of each cell adopts the same elevation value, producing a sudden change in the limits of each cell (a raster model) [5]. The elevation is represented by patches, which are the cells of the grid. Thus, the size of the cell, or resolution, is a key parameter. This parameter is related to the traditional concept of scale and detail of cartographic products. Small cell sizes, giving high-spatial-resolution, are linked to large scales and great spatial detail. Large cell sizes, giving small resolution, are linked to small scales and less spatial detail.

DEMs are geospatial data products that are mostly produced by national mapping agencies (e.g., the Instituto Geográfico Nacional (IGN) in Spain, the Ordnance Survey in the U.K., etc.) and in most developed countries, the territory is covered with high-spatial-resolution DEMs. DEMs are data products at the service of entrepreneurship, public administrations, the private sector, researchers, universities, etc, to generate added value [6].

DEMs are data products with applications in an extensive set of disciplines such as civil engineering [7], hydrology [8], geomorphology [9], agriculture [10], forestry [11], etc. Some of their applications include modelling for the prevention of natural disaster (floods, fires, etc.), soil erosion studies, weather forecasting, climate change, etc. DEMs have been included as a data theme for Europe (Inspire) and as a global fundamental geospatial data theme by the United Nations Committee of Experts on Global Geospatial Information Management. Therefore, one of the fundamental premises is the need for DEMs to have sufficient quality to meet the requirements of those applications.

Two major uses of DEMs are the calculation of the slope and aspect [3,5,12]. Using relatively simple algorithms, slope and orientation models are derived from the DEMs. The calculation of these parameters is based on a local analysis of the elevation derivative. So, neither of them is directly measurable on a single point on the ground (a neighborhood is required). However, while it is not very usual, their direct measurement in the field is also possible [13,14]. Another peculiarity of the calculation of slope and orientation is that small variations in the elevations can generate notable variations in the final values of slope and orientation. The slope is relevant for engineering works and natural hazards (e.g., landslides) [15]. Orientation is related to insolation and therefore has great relevance for plants and the use of solar energy [16].

Given two digital slope or orientation models, two scenarios can be considered. In the first one, the two models to be compared have the same consideration and the interest is focused on the similarity analysis between them, while in contrast, the second scenario is related to the quality control process when one model is considered as a reference and the other must achieve the quality requirements that arise from the reference. In either of the two contexts, to overcome the possible drawbacks derived from the method used to calculate slope and orientation from elevations, it is more robust to work with a categorization of slope or orientation than with the original magnitudes which are continuous and circular (slope and orientation, respectively).

The present work is centred in the second scenario, and we propose to perform a thematic-like quality control (class based) of slope and aspect classes through a user-defined categorization process of these initial magnitudes. A statistical hypothesis test is proposed for controlling the thematic-like accuracy. For this task, it is necessary to assume that there is available a reference DEM (e.g., a sample of greater accuracy). This assumption is not as restrictive as it may seem at first sight because it does not imply a complete knowledge of the reference dataset, it is sufficient to know or to have an estimation of the proportions associated with the categorization used. Because we work with a class-based control, proportions and a multinomial statistical law are considered. In this way, the similarity between the reference and the product can be measured by comparing proportions. The novelty of our approach is that agreement will be understood as both proportions are equal except for irrelevant deviations, which means it is allowed a small enough discrepancy between the observed data and the reference ones. This is the underlying idea of an equivalence test that will be proposed in Section 2.

The rest of the paper is organized as follows. Section 2 introduces how a thematic-accuracy quality control of slope and aspect classes can be performed. To do this, an equivalence test for multinomial data based on the square Hellinger distance is developed. Because the critical region is built by using asymptotic results, that is, it is valid for infinite sample sizes, several simulation experiments are carried out to study the behaviour of the proposal for finite sample sizes. The result of this simulation analysis will help the practical use of the proposed method. As a practical example, Section 3 includes the application of the proposed statistical test to accept/reject the similarity between the observed classifications for two slope and aspect models for the area of Allo (province of Navarra, Spain). Section 4 discusses the main characteristics of the proposal, and finally, Section 5 concludes the paper.

2. Methods and Materials

2.1. Method

Let Y be a continuous random variable, as slope or orientation, and let $Y_1,Y_2,\dots ,Y_{k-1}$ be a set of thresholds defining a partition of the random variable into k disjoint intervals. So, k categories can be defined in the following way: $C_1$ for those values of Y less than or equal to $Y_1$, the categories $C_i,i=2,\dots ,k-1$ are defined by the interval $(Y_{i-1},Y_i]$ and the category $C_k$ for the rest of values of Y (greater than $Y_k$). In accordance with this categorization, given a random sample of size n from Y, the random vector whose components count the number of events falling into each category, say $X={(X_1,\dots ,X_k)}^{\top }$, follows a multinomial distribution with parameters n and $P={(p_1,\dots ,p_k)}^{\top }\in {\mathsf{\Delta }}_k=\{{(p_1,\dots ,p_k)}^{\top }:p_i>0,1\le i\le k,{\sum }_{i=1}^k{p}_i=1\}$, where $p_i$ stands for the true occurrence probability of the ith category. In short, $X\sim {\mathcal{M}}_k(n;P)$.

Let $P_0={(p_{01},\dots ,p_{0k})}^{\top }$ be a fixed point of ${\mathsf{\Delta }}_k$ which represents the classification adopted on the reference dataset. The hypothetical probabilities $p_{0i},i=1,\dots ,k$ represent the quality requirements to be achieved by the product, that is, the ideal proportions. Deciding whether or not the quality requirements are fulfilled by a product is tantamount to testing the hypotheses

$$\begin{array}{cc}{H}_{0c}:\hfill & P=P_0,\hfill \\ H_{1c}:\hfill & P\ne P_0.\hfill \end{array}$$

(1)

Recall that the critical region of a test is built so that the probability of rejecting the null hypothesis when it is true is bounded by a quantity, usually denoted by $\alpha$, called the significance level. In other words, when the null hypothesis is rejected either we are making the correct decision or we are wrong, and the probability of the latter is less than $\alpha$, that is, the probability of a false rejection is controlled. By contrast, when the null hypothesis is accepted, either we are making the correct decision or we are wrong and, in most cases, the probability of being wrong is unknown, that is, the probability of a false acceptance is unknown. Many tests are available for the testing problem (1) (see, e.g., references [17,18]). Because of the above explanation, those tests are applied when $H_{0c}$ is expected to be rejected, since when $H_{0c}$ is not rejected it cannot be concluded that $P=P_0$ because the probability of making an incorrect decision is unknown and could be arbitrarily high.

When the interest is centred in proving that $P=P_0$, the hypotheses in (1) must be adequately switched, and an equivalence test should be applied, see [19]. With this aim, the user must fix a distance or dissimilarity measure on ${\mathsf{\Delta }}_k$, say H, and a positive quantity, say $\epsilon >0$, and now the hypotheses to be tested become

$$\begin{array}{cc}{H}_{0e}:\hfill & H(P,P_0)\ge \epsilon ,\hfill \\ H_{1e}:\hfill & H(P,P_0)<\epsilon .\hfill \end{array}$$

(2)

Notice that with this approach, the equality of probability vectors has been replaced by a larger subset of ${\mathsf{\Delta }}_k$. Specifically, the subset $\{P=P_0\}$ has been enlarged through adding an indifference zone or a neighborhood around $P_0$ in the parametric space ${\mathsf{\Delta }}_k$, $H(P,P_0)<\epsilon$. In this setting, if $H_{0e}$ is rejected then it is concluded that P and $P_0$ are equal except for practically irrelevant deviations whenever $\epsilon >0$ is small enough.

Therefore, when one is interested in proving that a product meets the quality requirements stated by $P_0$, a test of (2) must be applied. In [19] a test of (2) is proposed for H the Euclidean distance. Nevertheless, other choices for H are possible. Previous research related to tests for the similarity between spatial point patterns and tests for the thematic-accuracy quality control suggested that the Hellinger distance may be an appealing choice for this goal [20,21,22]. For two multinomial probability distributions, their Hellinger distance is equal to the Euclidean norm of the difference of the square root vectors. To avoid dealing with square roots, from now on we will work with the square of the Hellinger distance, defined as follows:

$$H(P,P_0)=\sum _{i=1}^k{(\sqrt{p_i}-\sqrt{p_{0i}})}^2.$$

(3)

Notice that $0\le H(P,Q)\le 2$ and that $H(P,P_0)=0$ if and only if $P=P_0$. So, for fixed small $\epsilon >0$, P and $P_0$ will be considered equivalent according to (3) if $H(P,P_0)<\epsilon$, implying that both distributions are equal except for insignificant deviations.

To derive a critical region for (2), with H as in (3), we proceed as follows. Let $\widehat{P}={({\widehat{p}}_1,{\widehat{p}}_2,\dots ,{\widehat{p}}_k)}^{\top }$ be the vector of relative frequencies,

$${\widehat{p}}_i=\frac{X_i}{n},1\le i\le k.$$

From Corollary 3.1 in [23], for each $P\in H_{0e}$ ($P\ne P_0$), one gets

$$\sqrt{n}\left(H(\widehat{P},P_0)-H(P,P_0)\right)\stackrel{\mathcal{L}}{⟶}N(0,{\sigma }^2\left(P\right)),$$

as $n\to \infty$, where

$${\sigma }^2\left(P\right)=1-{\left(\sum _{i=1}^k\sqrt{p_i{p}_{0i}}\right)}^2,$$

and $\stackrel{\mathcal{L}}{\to }$ denotes convergence in distribution. For ${\widehat{\sigma }}^2={\sigma }^2\left(\widehat{P}\right)$, it follows that

$$\sqrt{n}\frac{H(\widehat{P},P_0)-H(P,P_0)}{\widehat{\sigma }}\stackrel{\mathcal{L}}{⟶}N(0,1),$$

as $n\to \infty$, for each $P\in H_{0e}$. So, for $\alpha \in (0,1)$, the decision rule is:

$$reject{H}_{0e}if{T}_n=\sqrt{n}\frac{(H(\widehat{P},P_0)-\epsilon )}{\widehat{\sigma }}\le Z_{\alpha },$$

(4)

where $Z_{\alpha }$ stands for the $\alpha$-percentile of the standard normal distribution. The critical point $Z_{\alpha }$ in (4) has been taken from the asymptotic distribution of $T_n$, that is, the level of the test is (exactly) equal to $\alpha$ for infinite sample sizes. To study the behaviour of test (4) for finite sample sizes, we carried out a simulation study, which is described in the next section.

Note that the equivalence test proposed is developed in the context of the multinomial law underlying a categorization scheme. So, it can be also applied not only for classifications of slopes and orientations, but also for other geospatial thematic products (e.g., land covers maps, land uses, maps, etc.).

Simulation Results

For feasibility reasons (e.g., economic, temporal, etc.), quality controls are usually carried out based on sampling. When interest is centred on proving that a product meets the quality requirements stated by $P_0$, test (4) can be applied. As observed before, that test is based on asymptotic results. To study numerically its behavior for small and moderate sample sizes, we carried out some simulation experiments.

In these experiments, we considered the testing problem $H_{0e}$ vs. $H_{1e}$ with $P_0=(1/k,\dots ,1/k)$ for $k=3,5,7$. This particular choice of $P_0$ is not casual. It has been considered in previous simulation studies involving inference research over the multinomial distribution (see [24,25,26], among others). The values of k were chosen because they conform to the most usual number of categories in the slope classifications from the literature revised [27,28,29,30,31,32]. Finally, several values for $\epsilon$ were taken, in particular, $\epsilon =0.1,0.15,0.2$ covering reasonable thresholds of closeness between P and $P_0$.

The first part of the simulation is devoted to studying the actual level of the equivalence test (4). For this task, as usual, we have to simulate data under the null hypothesis $H_{0e}$, that is, for configurations of P such that $H(P,P_0)\ge \epsilon$. Here, we considered a set of configurations of P verifying that $H(P,P_0)=\epsilon$ for $\epsilon$ as before.

Table 1. Probability distributions included in the simulation study for $k=3$.

Selected Cases	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$
Case 1: $\epsilon$ = 0.10	0.1758	0.1758	0.6483
Case 2: $\epsilon$ = 0.15	0.1433	0.1433	0.7133
Case 3: $\epsilon$ = 0.20	0.1167	0.1167	0.7667

,

Table 2. Probability distributions included in the simulation study for $k=5$.

Selected Cases	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$
Case 1: $\epsilon$ = 0.10	0.1350	0.1350	0.1350	0.1350	0.4600
Case 2: $\epsilon$ = 0.15	0.1400	0.1500	0.1400	0.1500	0.4200
Case 3: $\epsilon$ = 0.20	0.1535	0.1535	0.1535	0.1535	0.3860

and

Table 3. Probability distributions included in the simulation study for $k=7$.

Selected Cases	${\mathit{p}}_1$	${\mathit{p}}_2$	${\mathit{p}}_3$	${\mathit{p}}_4$	${\mathit{p}}_5$	${\mathit{p}}_6$	${\mathit{p}}_7$
Case 1: $\epsilon$ = 0.10	0.1300	0.1300	0.1300	0.1300	0.1300	0.1300	0.2200
Case 2: $\epsilon$ = 0.15	0.1229	0.1229	0.1229	0.1229	0.1229	0.1229	0.2629
Case 3: $\epsilon$ = 0.20	0.1155	0.1155	0.1155	0.1155	0.1155	0.1155	0.3071

display the considered configurations. For each scenario, a random sample of size $n=50$ was generated and the decision rule (4) was applied for the nominal level $\alpha =0.05$. After 100,000 repetitions, the rejection percentage was collected. The whole experiment was repeated for $n=100,200,500$ for $k=3,5$ and $n=1000,2000$ for $k=7$, respectively.

Table 4. Rejection probabilities at the nominal level $\alpha =0.05$ under the configurations in Table 1 and Table 2.

	$\mathit{k}=3$			$\mathit{k}=5$
n	Case 1	Case 2	Case 3	Case 1	Case 2	Case 3
$\mathbf{\epsilon }$	0.10	0.15	0.20	0.10	0.15	0.20
50	0.057	0.047	0.052	0.035	0.037	0.038
100	0.056	0.056	0.049	0.040	0.040	0.040
200	0.057	0.053	0.049	0.044	0.044	0.042
500	0.054	0.052	0.050	0.046	0.046	0.047

and

Table 5. Rejection probabilities at the nominal level $\alpha =0.05$ under the configurations in Table 3.

n	Case 1	Case 2	Case 3
$\mathbf{\epsilon }$	0.10	0.15	0.20
50	0.019	0.022	0.023
100	0.027	0.028	0.030
200	0.033	0.034	0.033
500	0.039	0.040	0.039
1000	0.043	0.042	0.043
2000	0.046	0.044	0.044

show the rejection percentages obtained which estimate the actual level of the test for the nominal value $\alpha =0.05$.

Looking at Table 4 and Table 5, we observe that for $k=3$ small sample sizes are needed for the actual level to match the nominal level for all considered values of $\epsilon$. However, when the number of categories increases, larger sample sizes are required for the simulation results to reach the nominal level ($n>200$ for $k=5$ and $n>2000$ for $k=7$).

To study the power of the proposal, that is, the probability of rejecting the null hypothesis when it is false, we generated a random sample of size $n=50$ from a $M(n,P_0)$ for $k=3$ and we applied the decision rule in (4) for $\alpha =0.05$ and $\epsilon =0.1$. After 100,000 repetitions, we collected the proportion of rejections which are now the estimated power associated with the nominal level $\alpha$. The experiment was repeated for $\epsilon =0.15,0.2$, $n=100,200$ and $k=5,7$.

Table 6. Estimated power.

	$\mathit{k}=3$			$\mathit{k}=5$			$\mathit{k}=7$
$\mathbf{n}\backslash \mathbf{\epsilon }$	0.1	0.15	0.2	0.1	0.15	0.2	0.1	0.15	0.2
50	0.990	0.999	0.997	0.942	0.995	0.999	0.833	0.977	0.995
100	0.998	0.999	1	0.998	0.999	1	0.899	0.997	0.999
200	1	1	1	1	1	1	0.999	1	1

shows the estimated power. As can be seen, in all the tried cases, the power is very high, that is, the procedure makes the correct decision with a probability close to 1. According to these findings, the usefulness of test (4) as a tool for quality control is evidenced.

2.2. Materials

To show an example of an application on real data, a study area around Allo (Navarra, Spain) was considered using the following digital models:

• SLM02 & ASM02. Both slope (SLM02) and aspect (ASM02) models were derived by GIS operations from a DEM (the DEM02). The DEM02 is a DEM grid with $2\times 2$ m resolution, generated in the year 2017 and its primary data source is a Lidar survey (second coverage of the PNOA-LiDAR project https://pnoa.ign.es/estado-del-proyecto-lidar/segunda-cobertura, accessed on 21 May 2021). Both datasets are considered as references in this example.
• SLM05 & ASM05. Both slope (SLM05) and aspect (ASM05) models were derived by GIS operations from a DEM (the DEM05). The DEM05 is a DEM grid with a resolution of $5\times 5$ m, generated in the year 2012 and its primary data source is a Lidar survey (first coverage of the PNOA-LiDAR project https://pnoa.ign.es/estado-del-proyecto-lidar/primera-cobertura, accessed on 21 May 2021).

Both DEM datasets come from the IGN (Spain) and are freely available. In both cases, GIS operations (slope and aspect) are those implemented by ArcGIS (TM) in its Spatial Analyst toolbox.

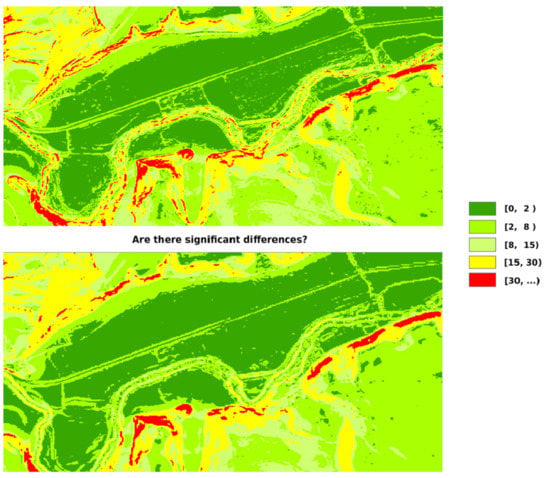
Concerning the study area, Figure 1 shows its corresponding DEM, and Figure 2 a zoom to a smaller area to have a detailed view to appreciate differences. The area is 504 km${}^2$, and it has a varied relief, but not abrupt, with valleys of different widths, and areas with different degrees of undulation. The elevation is in the interval 316–1046 m, mean value is 468 m and the standard deviation 92.8 m.

Figure 3 and Figure 4 show the observed values of slopes and aspects, respectively. In general, there are small differences between the curves corresponding to SLM02 vs. SLM05 and ASM02 vs. ASM05, respectively. The differences are minor because they are high-quality products, relatively close in time and for a territory in which there have not been major changes. The curves of the slopes (SLM02 in blue and SLM05 in red) show considerable similarity between the two datasets. Clearly, areas are observed where one curve occurs over the other, and these areas have a certain amplitude. The curves of the orientation (ASM02 in blue and ASM05 in red) show more tremor than the slope curves; this is logical since the orientation is more sensitive than the slope to small changes in elevation. On the other hand, it is observed that the curve corresponding to case ASM02 has more variability than that of case ASM05, which is also logical because it comes from a more detailed model. Furthermore, it is observed that the two curves intersect, although these crosses occur with a relatively wide length between them, which implies a certain bias. It should be remembered that the proposed analysis method is not based on the use of these frequency distributions, which have helped us to better understand the data, but on the comparison of the proportions between categories defined on them and that the differences that are worked with will be those that exist between the proportions corresponding to those classes. In this case, given the statistical control to be applied, the most important thing is to analyze whether, given a categorization of the two variables of interest (slope and orientation) applied under the two models, the hypothetical probability vector for the reference DEM02 ($2\times 2$ m) is close enough the true one of DEM05 ($5\times 5$ m). If this fact is confirmed via an equivalence test, it will mean that the quality conditions of the reference DEM02 are achieved by the product DEM05 to be controlled, except for irrelevant deviations.

3. Results

Given that in the proposed method the number k of categories to be considered is relevant to the sample size, examples with a different number of classes are presented. Thus, for the slope, two analyses with different numbers of categories (k = 3 and k = 5) will be considered, while for the orientation k = 8. In this way, with k = 3,5 and 8, the applicability of the method for the usual numbers of categories is better evidenced. In most practical situations, the probability vector $P_0$ is obtained from a previous sampling procedure or it can even be proposed by an expert.

3.1. Slope

Over this area, we considered two classification schemes for the slope in the reference data (SLM02). From the reference DEM, such classifications give the percentages of each categories as are summarized in

Table 7. Classification of slopes: Case #1.

Degrees	Classification	${\mathit{P}}_0$
0–1	Flat	0.07
1–7.5	Moderate	0.56
>7.5	Steeper	0.37

and

Table 8. Classification of slopes: Case #2.

Degrees	Classification	${\mathit{P}}_0$
0–2	Flat	0.17
2–8	Undulaing	0.48
8–15	Rolling	0.19
15–30	Moderately steep	0.13
>30	Steep	0.03

. Figure 5 and Figure 6 show the application of the classification in Table 7 and Table 8 over SLM02. These values (percentages) are considered the “pattern” ($P_0$) that the product to be controlled (SLM05) must follow.

Notice that the value of $\epsilon$ is fixed by the user. Here, applying the equivalence test for $\epsilon =0.1$,

$$\begin{array}{cc}{H}_{0e}:\hfill & H(P,P_0)\ge 0.1,\hfill \\ H_{1e}:\hfill & H(P,P_0)<0.1,\hfill \end{array}$$

which led to quality control terms raised as follows:

Null hypothesis. The distance between the distribution of proportions between the classes in the product (SLM05) and the reference (SLM02) exceeds the threshold considered; that is, the product does not achieve the quality requirements stated by the reference data.

Alternative hypothesis. The distance between the distribution of proportions between the classes in the product (SLM05) and the reference (SLM02) does not exceed the threshold considered. In other words, the quality requirements stated by the reference agree with those observed in the product (except for irrelevant deviations).

The equivalence test is applied for random samples of size 100, 200 and 500 drawn from SLM05.

Table 9. Application of the equivalence test to classification of slopes: Case #1.

Sample Size	$\widehat{\mathit{P}}$ (Observed Proportions)	${\mathit{T}}_{\mathit{n}}$	Decision
100	$(0.050,0.560,0.390)$	−27.89	Reject $H_{0e}$
200	$(0.085,0.600,0.315)$	−20.83	Reject $H_{0e}$
500	$(0.076,0.554,0.370)$	−10.26	Reject $H_{0e}$

and

Table 10. Application of the equivalence test to classification of slopes: Case #2.

Sample Size	$\widehat{\mathit{P}}$ (Observed Proportions)	${\mathit{T}}_{\mathit{n}}$	Decision
100	$(0.140,0.500,0.200,0.150,0.010)$	−10.51	Reject $H_0$
200	$(0.220,0.485,0.180,0.085,0.030)$	−14.21	Reject $H_0$
500	$(0.150,0.500,0.200,0.128,0.022)$	−72.18	Reject $H_0$

show the values of the test statistic $T_n$ and the result of the decision rules for $\alpha =0.05$ for both classifications.

As can be seen in Table 9 and Table 10, in all cases the null hypothesis is rejected at the significance level $\alpha =0.05$, which in this case means that the square Hellinger distance between both sets of DEM data is less than 0.1, so that the observed classifications on the product SLM05 agree with those indicated by the reference SLM02, except for irrelevant deviations.

3.2. Aspect

In this analysis, we considered only one classification scheme for the aspect in the reference data (ASM02). We adopted a classical eight orientation classification based on octants. From the reference model, such classification gives the percentages of each category as are summarized in

Table 11. Classification of aspect.

Aspect	Degrees	${\mathit{P}}_0$
North	337–360, 0–22.5	0.11
Northeast	22.5–67.5	0.14
East	67.5–112.5	0.13
Southeast	112.5–157.5	0.13
South	157.5–202.5	0.15
Southwest	202.5–247.5	0.15
West	247.5–292.5	0.10
Northest	292.5–337.5	0.09

(the category “Flat” does not appear in Table 11 because it is practically null). These values (percentages) are considered the “pattern” of the distribution of class proportions ($P_0$) that the product to be controlled (ASM05) must follow. Figure 7 shows the categorization in Table 11 over SLM02.

Again, the hypotheses to be tested are

$$\begin{array}{cc}{H}_{0e}:\hfill & H(P,P_0)\ge 0.1,\hfill \\ H_{1e}:\hfill & H(P,P_0)<0.1,\hfill \end{array}$$

which led to quality control terms raised as follows:

Null hypothesis. The distance between the distribution of proportions between the classes in the product (ASM05) and the reference (ASM02) exceeds the threshold considered.

Alternative hypothesis. The distance between the distribution of proportions between the classes in the product (ASM05) and the reference (ASM02) does not exceed the threshold considered. To assure the correct application of the equivalence test in this case, we got a random sample of size $n=500$ and we obtained the observed proportions given by $\widehat{P}=(0.070,0.152,0.124,0.134,0.148,0.134,0.098,0.088,0.052)$. Considering again $\epsilon =0.1$, it is obtained that $T_n=-58.30$, which implies the decision to reject the corresponding $H_{0e}$. In other words, the observed classification of orientation in the DEM05 agrees with the percentages of the classification in the reference data DEM02, so that the quality requirements are fulfilled for the orientation classification.

4. Discussion

The discussion will take place along three lines, the first on the method itself, the second on relevant aspects of the proposal as the number of categories and the relationship between the distance and the tolerance $\epsilon$, and the third on the application to the thematic-type control of slope and aspect classes.

On the first hand, recall the final objective is to decide whether a set of quality requirements stated by the reference dataset is achieved by a product or not. To reach this goal by using a hypothesis test, two points of views can be considered, say, if our interest is centred in proving that the quality requirements are not fulfilled ($P\ne P_0$) or, on the contrary, if our focus is centred in confirming that the quality requirements are achieved (in the sense of P and $P_0$ are close enough through the distance H which is bounded by $\epsilon$). Since in any hypothesis test the critical region is built so that the probability of rejecting the null hypothesis when it is true is bounded by the significance level ($\alpha$), only the probability of a false rejection is controlled. As a consequence, for the first approach, one must test $H_{0c}$ versus $H_{1c}$, whereas for the second one, the hypotheses to be tested must be $H_{0e}$ versus $H_{1e}$.

Nevertheless, the difference in the formulation (and hence in the meaning) of the null and alternative hypotheses does not imply any type of change concerning the interpretation of the level of significance and power associated with any hypothesis test.

Secondly, we highlight that the number of categories, the square Hellinger distance and the threshold $\epsilon$ are interrelated in the method and they affect the actual level of the test (2), as is shown in the simulation results. So, in the practical applications, users have to take into account that a larger number of categories requires larger sample sizes and it is suggested to take the smallest number of categories possible. In any case, we consider that the values of k used in the applications cover the most common values of the category numbers.

Finally, the hypothesis test is not carried out on a natural measure to the problem (e.g., degrees, radians, meters, etc.). The square Hellinger distance can be unknown for some users and, although its mathematical basis is understood, it is needed to manage and understand the role of $\epsilon$. That is, is $\epsilon =0.1$ a lot or a little? The answer to this question combines two things: First, the definition of $H(P,P_0)$ itself, which is related in some way to the Euclidean distance on the square roots of the observed frequencies and pattern, and second, the interest that the user puts in what should be the “indifference zone” to decide when both multinomial distributions are close enough to be considered as equal except for “irrelevant” deviations.

In any case, the use of a particular distance measure depending on the type of statistical tools is very common in their applications to geospatial data (e.g., cluster analysis, etc.), where several distances appear (Minkowski, Chebyshev, Manhattan, Mahalanobis, etc.), which are also not “natural” distances to the problem either. This entails the need to achieve sufficient sensitivity in the management of the distance that is applied. In Section 2.1 the study of the level and the power developed can guide the cases that have been considered, but it can also serve as a tool for those interested in the method who want to make their adjustments between the number of categories and $\epsilon$. Finally, about the execution of these samplings in the field, it should not be forgotten that the measurement of the slope and orientation in the field is usually carried out simultaneously or conditioned by other types of work (e.g., edaphological surveys), so their availability will be at most times conditioned by these types of actions.

5. Conclusions

A statistical procedure was proposed for the quality control of a DEM dataset to meet a reference DEM. The method is based on a categorization scheme over a continuous magnitude and on the application of an equivalence test for multinomial distributions. So, to proceed it is enough to know the values of the proportions for the reference dataset. Since there is a tradeoff between the number of classes to be considered and the size of the sample, a simulation study was carried out which allows guidance concerning the sample sizes. Those interested in applying this method could carry out their simulations to adjust the most suitable size to their case.

On the other hand, the practical example presented illustrates that the application process is quite simple. In addition, and given that statistical tests are used, one could think of carrying out a joint analysis on the slope and the orientation, for this it is enough to apply simple rules such as Holm–Bonferroni correction. The framework of the application of this method is the comparison between the proportions that correspond to the categories of a given classification system of a product and those known from a reference dataset. In this sense, the method was applied to classifications of slopes and orientations but could be applied to compare proportions of any geospatial thematic product (e.g., land covers maps, land uses maps, etc.).

Finally, it is very relevant to indicate that the formulation of the hypothesis test carried out is adequate when interest is centred on proving that a product matches the required quality requirements. The parameter $\epsilon$ that is used must be chosen by users, allowing it to be applied to multiple situations in which greater or lower flexibility is required.