Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing
Abstract
1. Introduction
2. Methodology
2.1. Basic Idea of the SBAS-InSAR Method
2.2. Derivation of Phase Time Series from Multi-Prime Interferograms
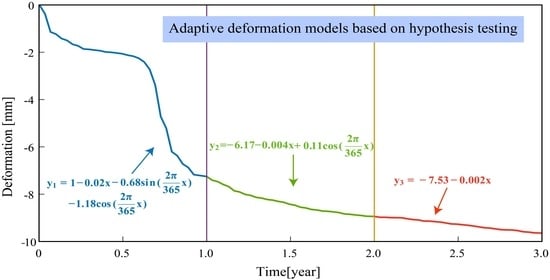
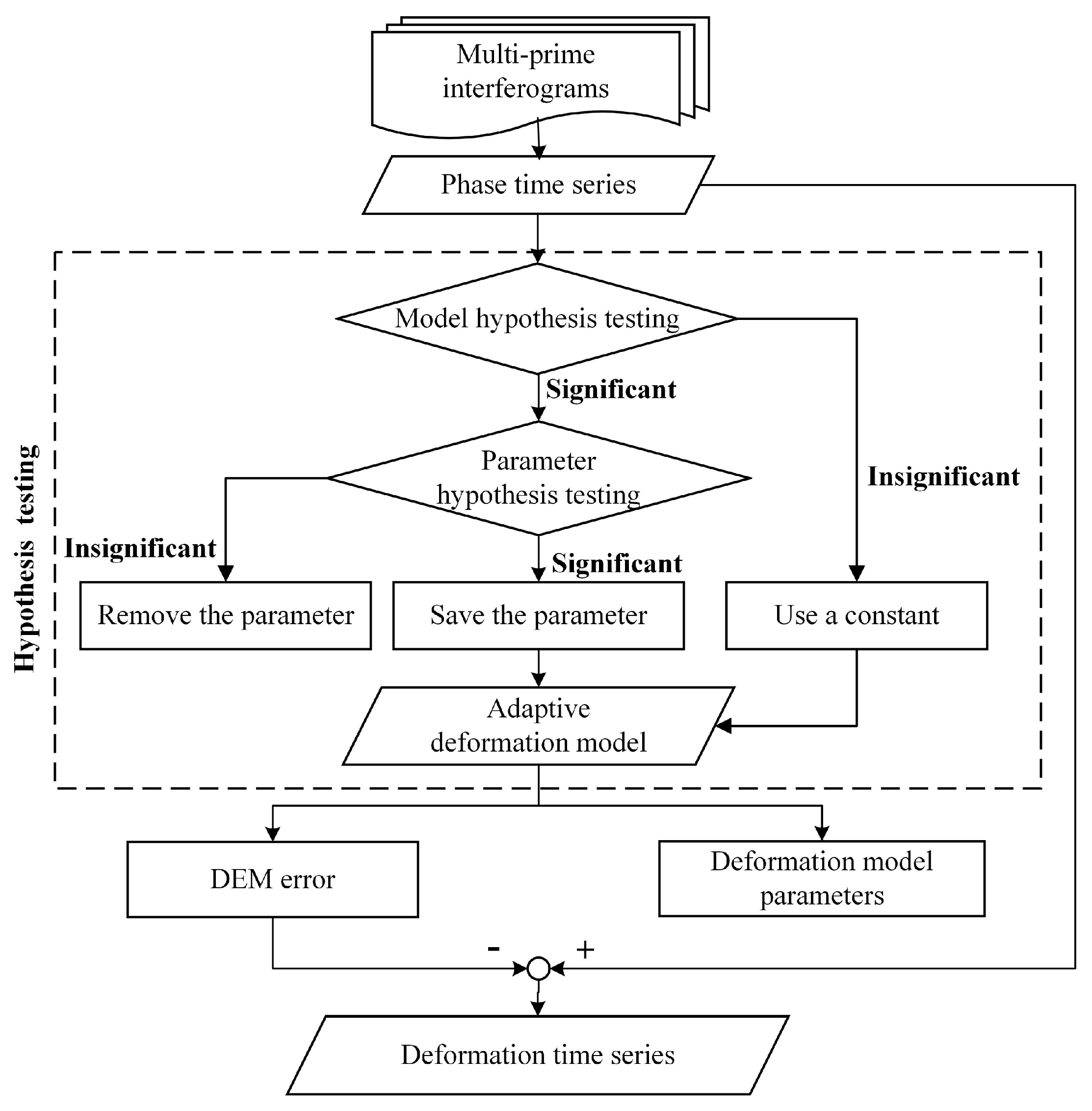
2.3. Construction of the Adaptive Deformation Model Based on Hypothesis Testing
2.4. Estimation of the Deformation Model Parameters and DEM Error
3. Results
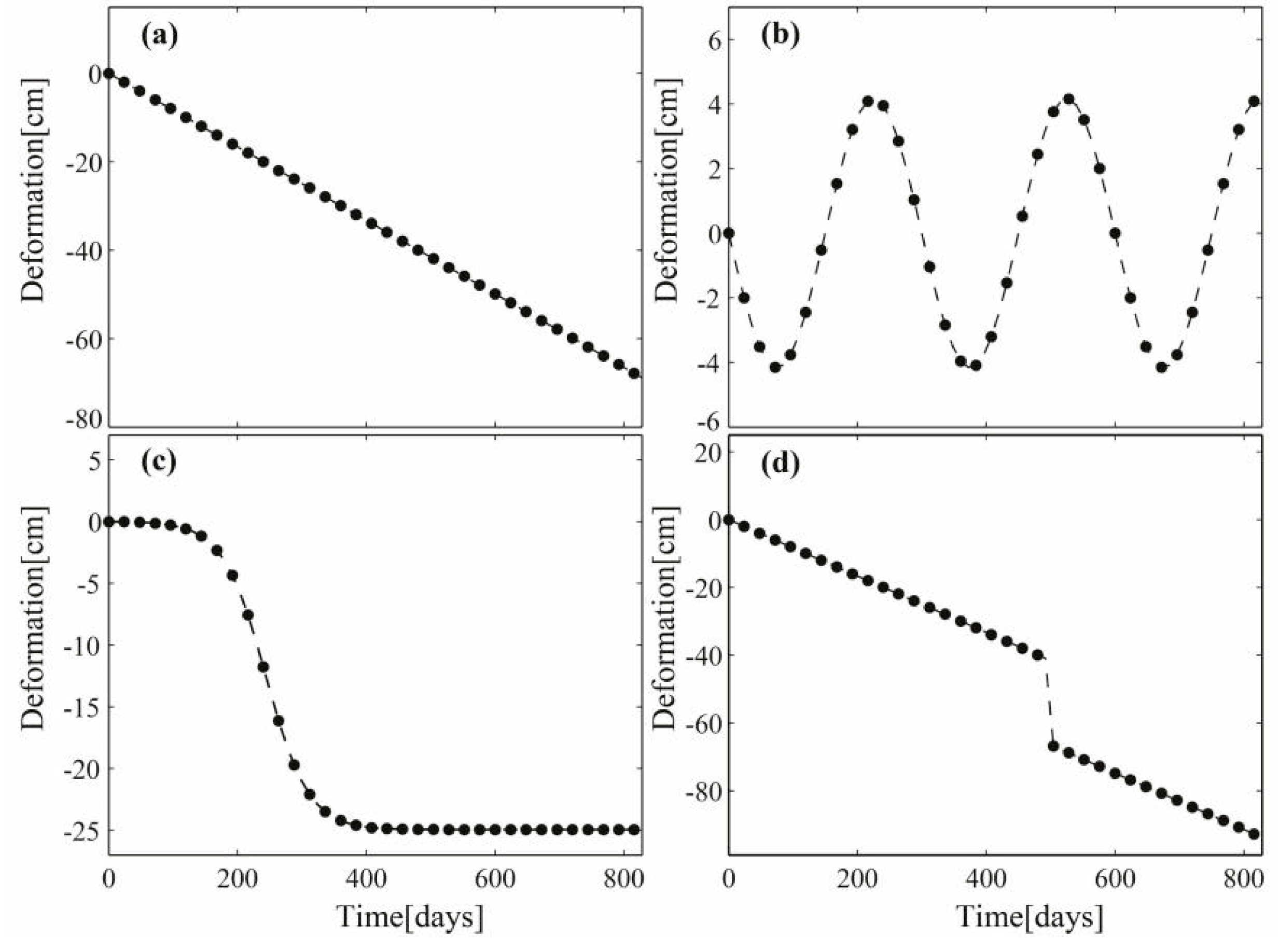
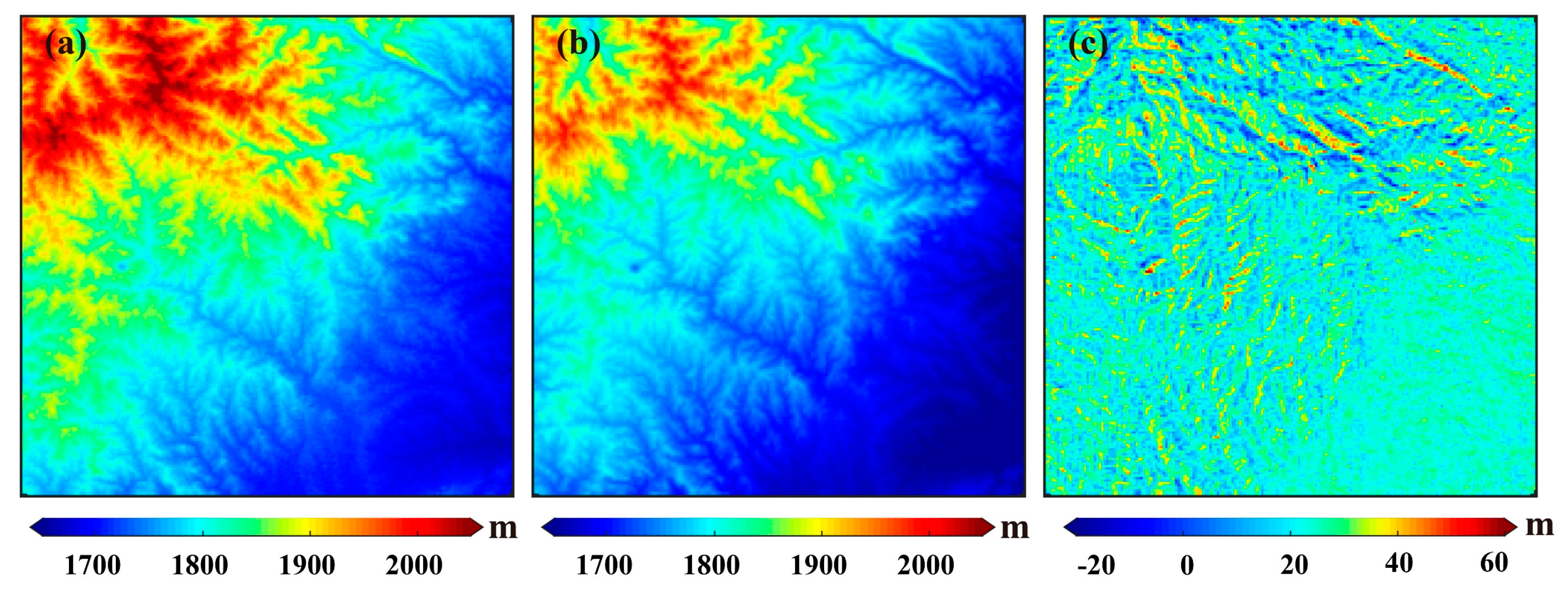
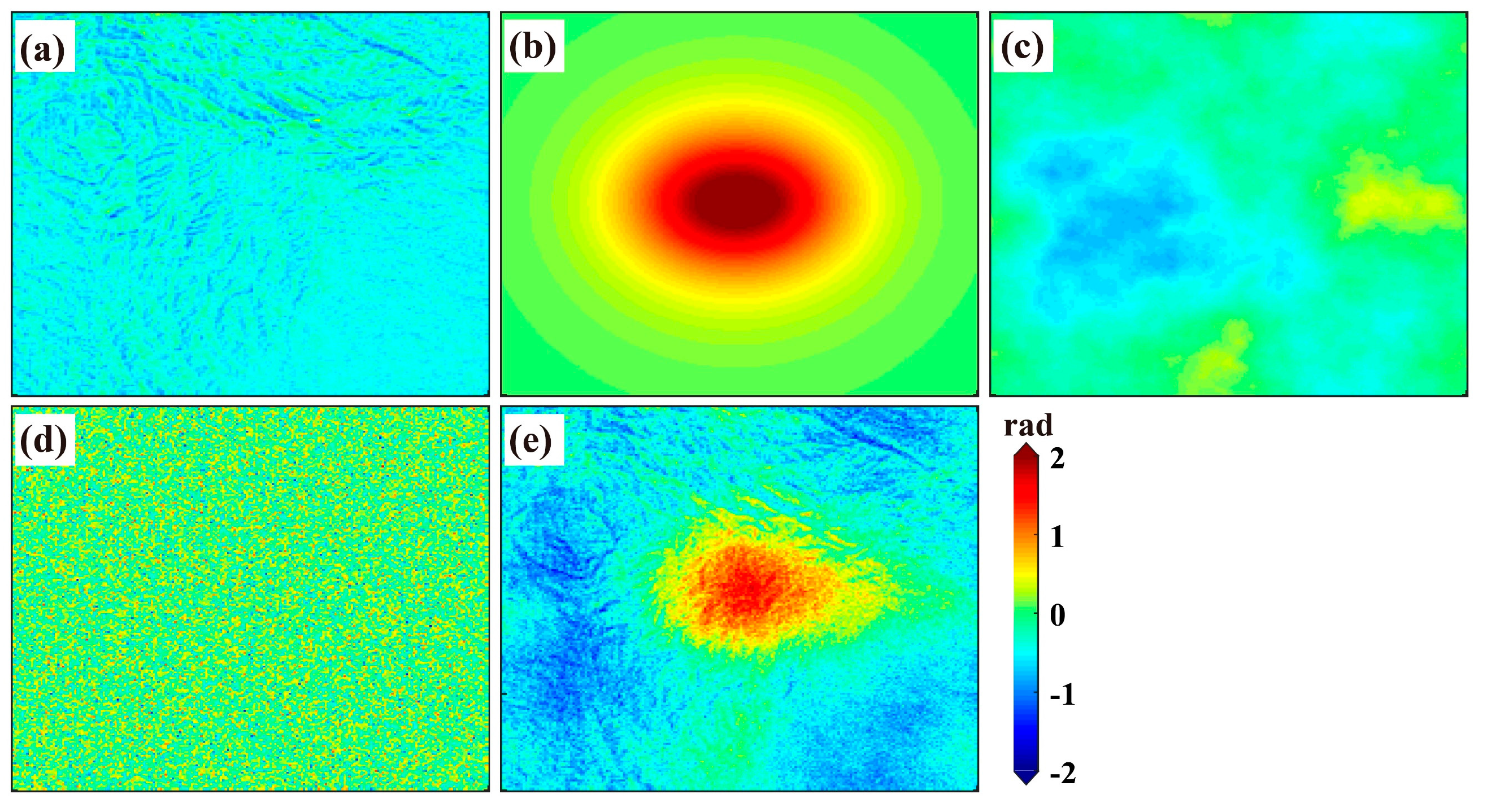
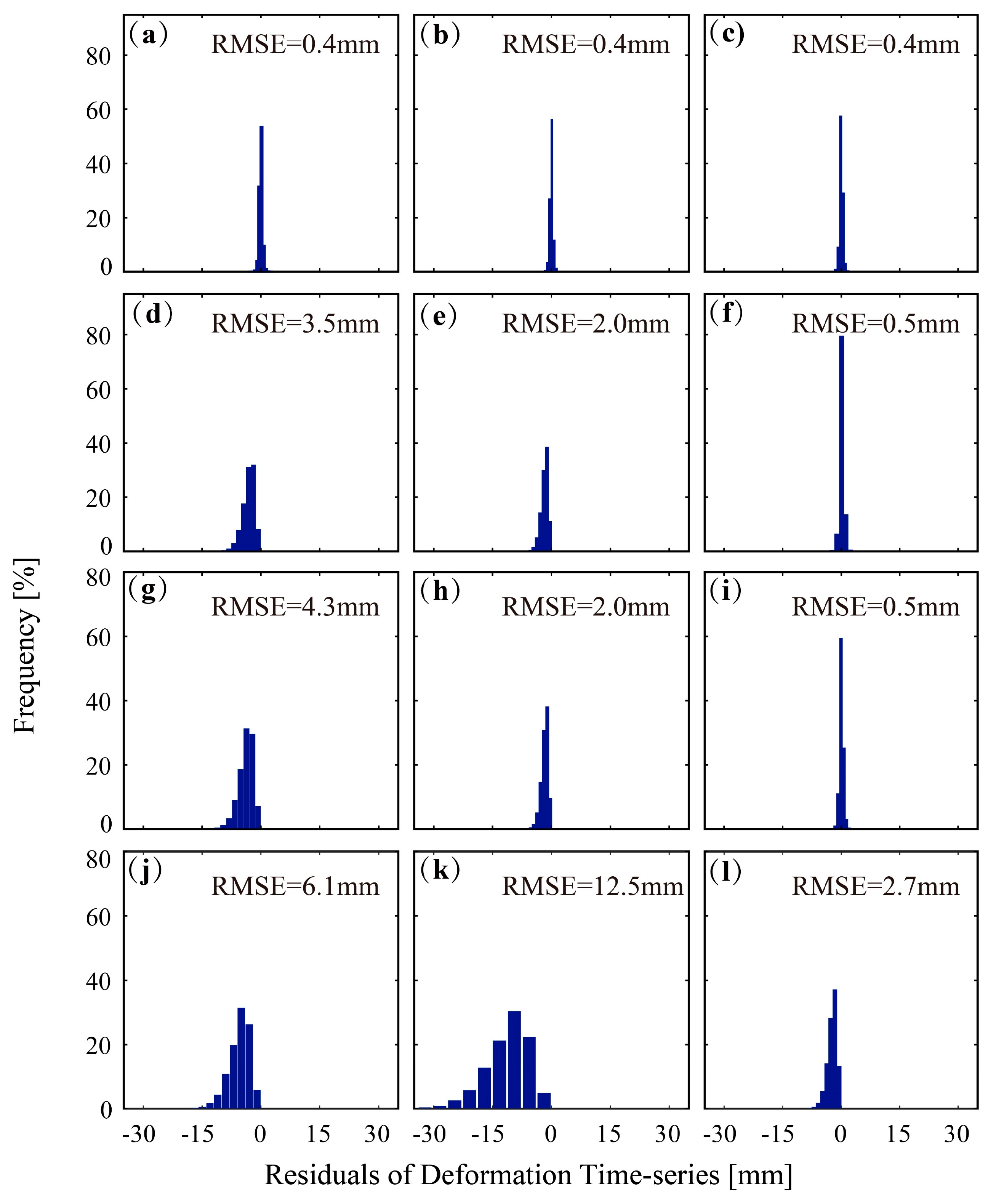
3.1. Simulated Experiments
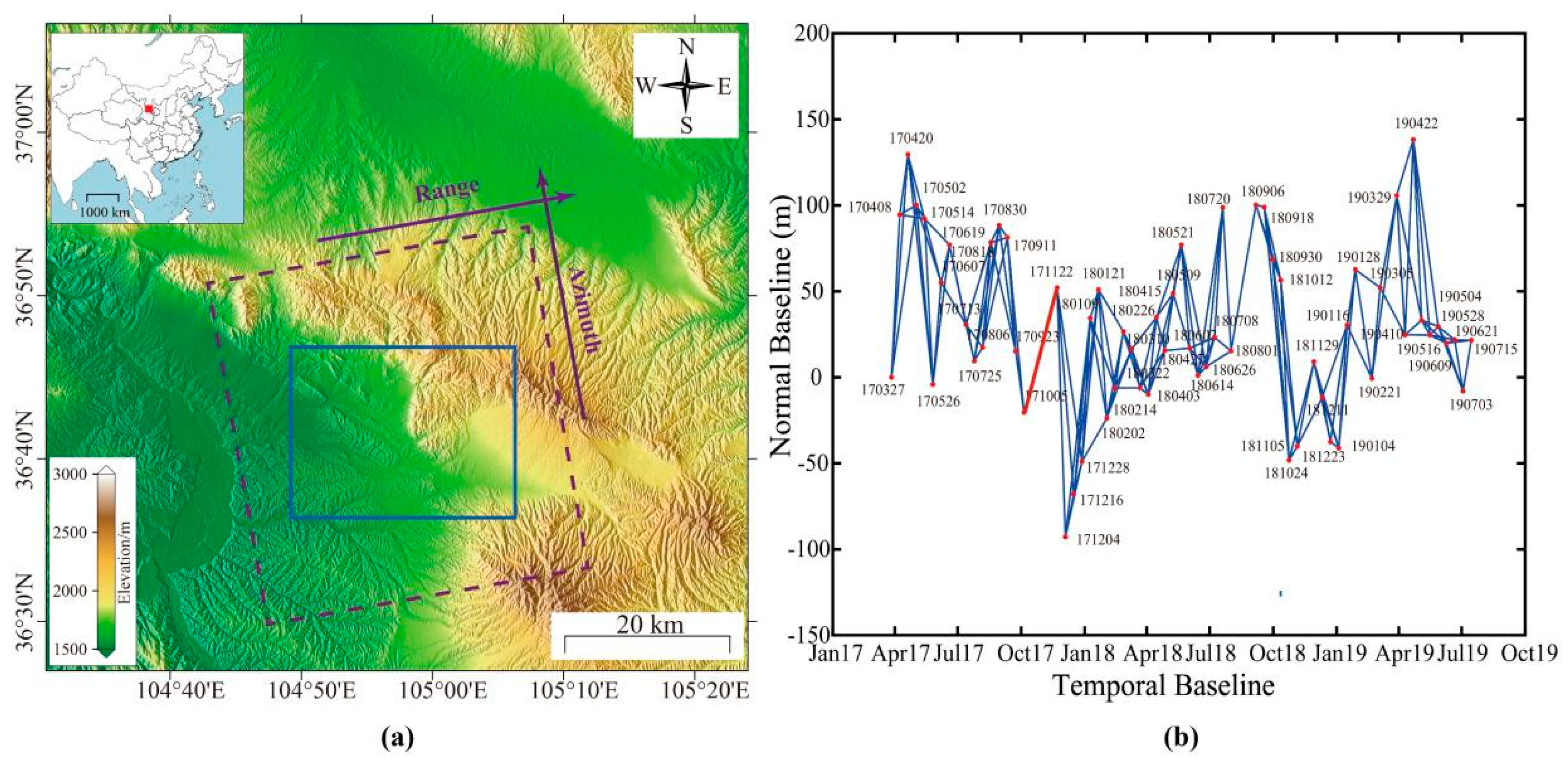
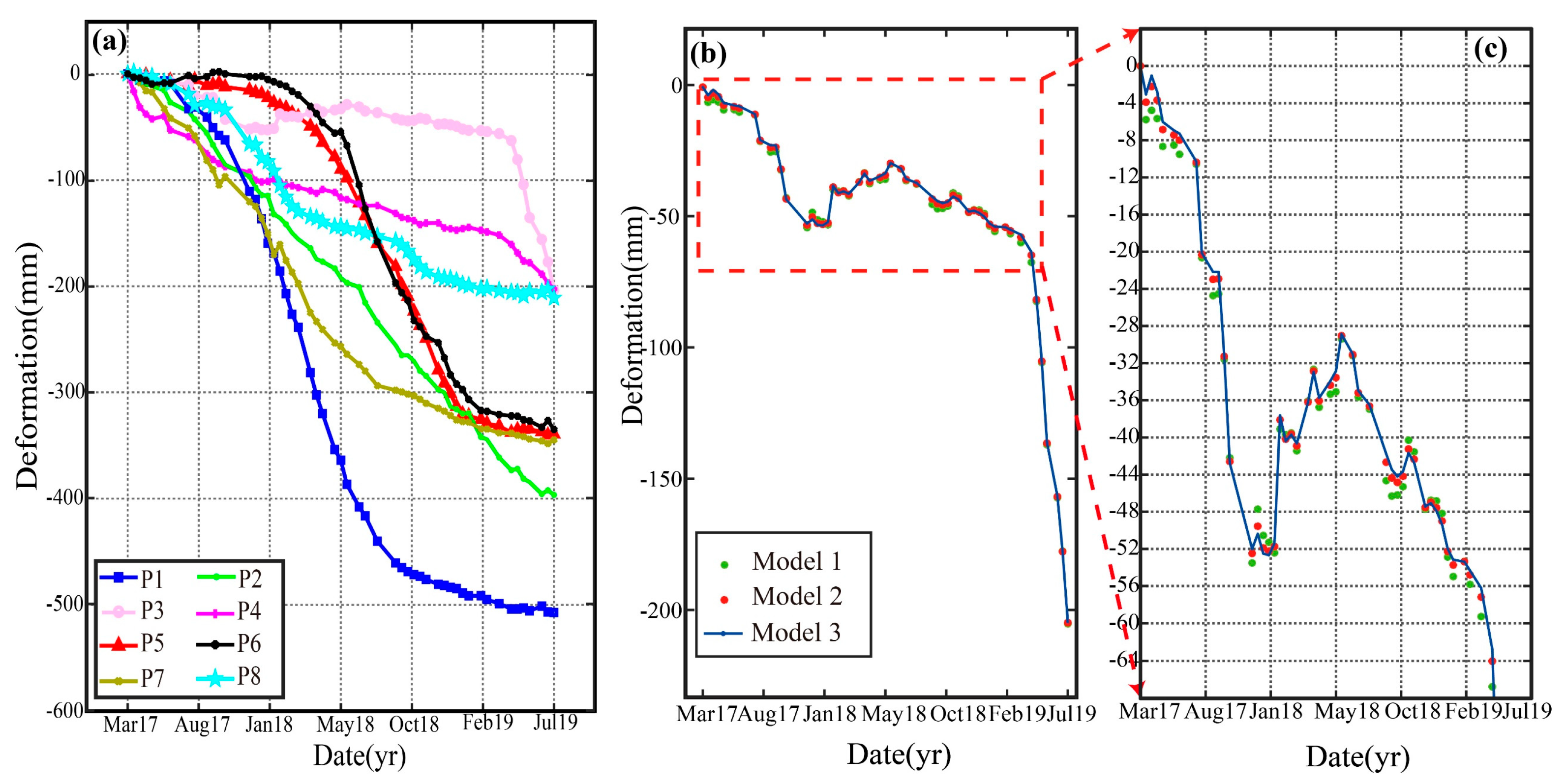
3.2. Real Data Experiments in the Pingchuan Mining Area
4. Discussion
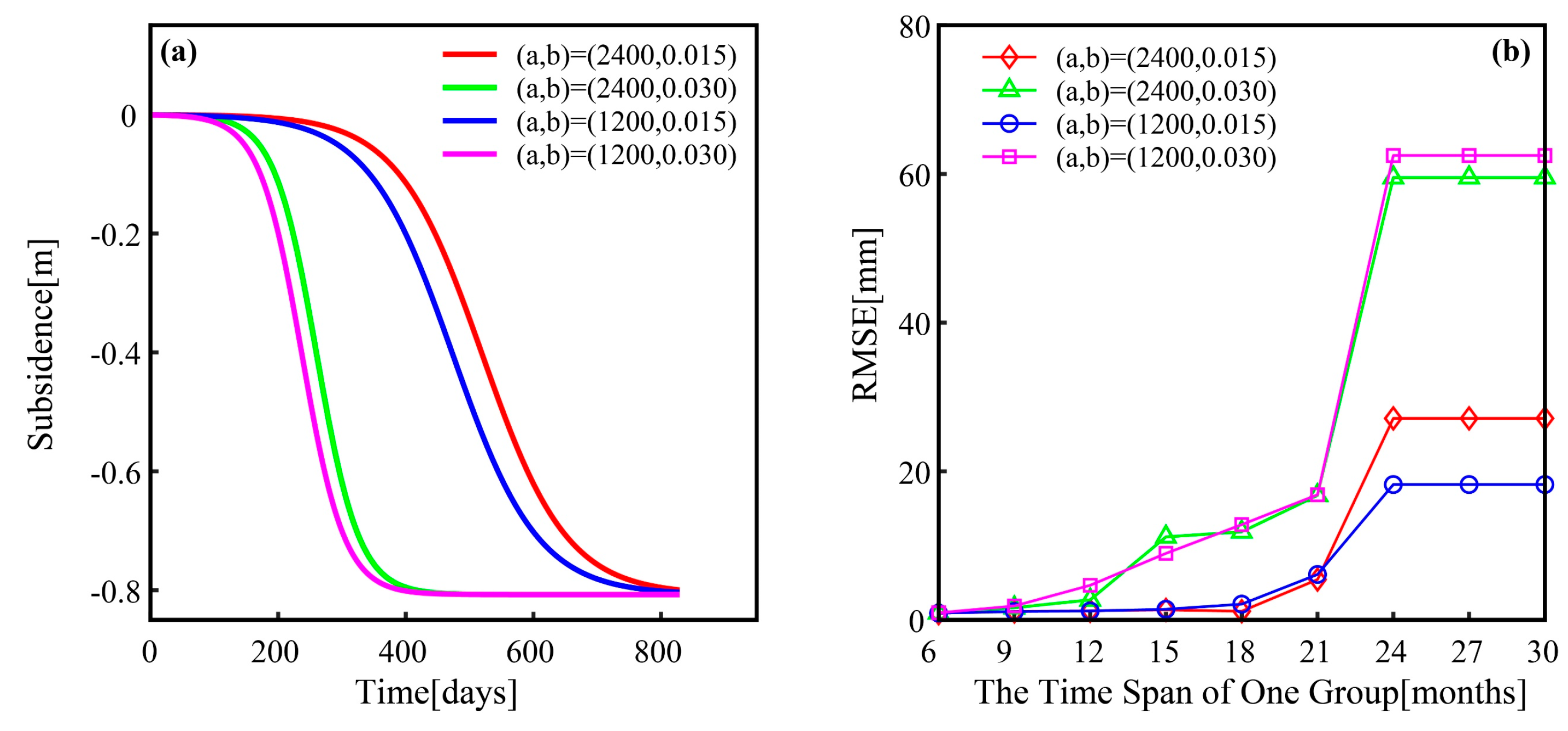
4.1. Determining the Time Span of Each Group in the Grouping Process
4.2. Decreasing Correlation between the Deformation Rate and the DEM Error Estimation Based on the Proposed Method
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ng, A.H.-M.; Ge, L.L.; Zhang, K.; Chang, H.C.; Li, X.J.; Chris, R.; Omura, M. Deformation mapping in three dimensions for underground mining using InSAR–Southern highland coalfield in New South Wales, Australia. Int. J. Remote Sens. 2011, 32, 7227–7256. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Wang, Y.D.; Wu, L.X. Use of SAR/InSAR in Mining Deformation Monitoring, Parameter Inversion, and Forward Predictions: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 71–90. [Google Scholar] [CrossRef]
- Ng, A.H.-M.; Ge, L.L.; Du, Z.Y.; Wang, S.R.; Ma, C. Satellite radar interferometry for monitoring subsidence induced by longwall mining activity using Radarsat-2, Sentinel-1 and ALOS-2 data. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 92–103. [Google Scholar] [CrossRef]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.P. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, L.; Ding, X.L.; Hu, J.; Li, Z.W.; Zhu, J.J. Slope deformation prior to Zhouqu, China landslide from InSAR time series analysis. Remote Sens. Environ. 2015, 156, 45–57. [Google Scholar] [CrossRef]
- Cigna, F.; Tapete, D. Sentinel-1 BigData Processing with P-SBAS InSAR in the Geohazards Exploitation Platform: An Experiment on Coastal Land Subsidence and Landslides in Italy. Remote Sens. 2021, 13, 885. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Sun, Q. Derivation of 3-D coseismic surface displacement fields for the 2011 Mw 9.0 Tohoku-Oki earthquake from InSAR and GPS measurements. Geophys. J. Int. 2012, 192, 573–585. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Xu, W.B.; Li, Z.W.; Zhu, J.J.; Ding, X.L.; Zhang, L. Complete Three-Dimensional Coseismic Deformation Field of the 2016 Central Tottori Earthquake by Integrating Left- and Right- Looking InSAR Observations With the Improved SM-VCE Method. J. Geophys. Res. Solid Earth 2019, 124, 12099–12115. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Q.J.; Li, Z.W.; Xie, R.A.; Zhang, X.Q.; Sun, Q. Retrieving three-dimensional coseismic displacements of the 2008 Gaize, Tibet earthquake from multi-path interferometric phase analysis. Nat. Hazards 2014, 73, 1311–1322. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Gan, J. A Method for Measuring 3-D Surface Deformations With InSAR Based on Strain Model and Variance Component Estimation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 239–250. [Google Scholar] [CrossRef]
- Solaro, G.; Acocella, V.; Pepe, S.; Ruch, J.; Neri, M.; Sansosti, E. Anatomy of an unstable volcano from InSAR: Multiple processes affecting flank instability at Mt. Etna, 1994–2008. J. Geophys. Res. Solid Earth 2010. [Google Scholar] [CrossRef]
- Richter, N.; Froger, J.L. The role of Interferometric Synthetic Aperture Radar in Detecting, Mapping, Monitoring, and Modelling the Volcanic Activity of Piton de la Fournaise, La Réunion: A Review. Remote Sens. 2020, 12, 1019. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Xue, F.Y.; Lv, X.L.; Dou, F.J.; Ye, Y. A Review of Time-Series Interferometric SAR Techniques: A Tutorial for Surface Deformation Analysis. IEEE Geosci. Remote Sens. Mag. 2020, 8, 22–42. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Li, Z.W.; Xu, W.B.; Feng, G.C.; Hu, J.; Wang, C.C.; Ding, X.L.; Zhu, J.J. Correcting atmospheric effects on InSAR with MERIS water vapour data and elevation-dependent interpolation model. Geophys. J. Int. 2012, 189, 898–910. [Google Scholar] [CrossRef]
- Mateus, P.; Nico, G.; Catalao, J. Uncertainty Assessment of the Estimated Atmospheric Delay Obtained by a Numerical Weather Model (NMW). IEEE Trans. Geosci. Remote Sens. 2015, 53, 6710–6717. [Google Scholar] [CrossRef]
- Li, Z.H.; Fielding, E.J.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.W.; Wang, Q.J.; Jiang, M. A Refined Strategy for Removing Composite Errors of SAR Interferogram. IEEE Geosci. Remote Sens. Lett. 2013, 11, 143–147. [Google Scholar] [CrossRef]
- Hu, J.; Liu, J.H.; Li, Z.W.; Zhu, J.J.; Wu, L.X.; Sun, Q.; Wu, W.Q. Estimating three-dimensional coseismic deformations with the SM-VCE method based on heterogeneous SAR observations: Selection of homogeneous points and analysis of observation combinations. Remote Sens. Environ. 2021, 255. [Google Scholar] [CrossRef]
- Du, Y.N.; Zhang, L.; Feng, G.C.; Lu, Z.; Sun, Q. On the Accuracy of Topographic Residuals Retrieved by MTInSAR. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1053–1065. [Google Scholar] [CrossRef]
- Zheng, W.J.; Hu, J.; Liu, J.H.; Sun, Q.; Li, Z.W.; Zhu, J.J.; Wu, L.X. Mapping Complete Three-Dimensional Ice Velocities by Integrating Multi-Baseline and Multi-Aperture InSAR Measurements: A Case Study of the Grove Mountains Area, East Antarctic. Remote Sens. 2021, 13, 643. [Google Scholar] [CrossRef]
- Agram, P.S.; Simons, M. A noise model for InSAR time series. J. Geophys. Res. Solid Earth 2015. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, L.; Hu, J.; Ding, X.L.; Li, Z.W.; Zhu, J.J. Characterizing sudden geo-hazards in mountainous areas by D-InSAR with an enhancement of topographic error correction. Nat. Hazards 2014, 75, 2343–2356. [Google Scholar] [CrossRef]
- Samsonov, S. Topographic Correction for ALOS PALSAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3020–3027. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. DEM Error Correction in InSAR Time Series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4249–4259. [Google Scholar] [CrossRef]
- Shanker, P.; Zebker, H. Persistent scatterer selection using maximum likelihood estimation. Geophys. Res. Lett. 2007, 34, 315–324. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, Z.; Ding, X.L.; Jung, H.S.; Feng, G.C.; Lee, C.W. Mapping ground surface deformation using temporarily coherent point SAR interferometry: Application to Los Angeles Basin. Remote Sens. Environ. 2012, 117, 429–439. [Google Scholar] [CrossRef]
- Li, S.S.; Li, Z.W.; Hu, J.; Sun, Q.; Yu, X.Y. Investigation of the seasonal oscillation of the permafrost over Qinghai-Tibet Plateau with SBAS-InSAR algorithm. Chin. J. Geophys. 2013, 56, 1476–1486. [Google Scholar] [CrossRef]
- Hetland, E.A.; Musé, P.; Simons, M.; Lin, Y.N.; Agram, P.S.; Dicaprio, C.J. Multiscale InSAR Time Series (MInTS) analysis of surface deformation. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Liang, H.Y.; Zhang, L.; Lu, Z.; Li, X. Nonparametric Estimation of DEM Error in Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10004–10014. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent Component Analysis: Algorithms and Applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Wang, J.L.; Deng, Y.K.; Wang, R.; Ma, P.F.; Lin, H. A Small-Baseline InSAR Inversion Algorithm Combining a Smoothing Constraint and L1-Norm Minimization. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Tao, B.Z. Non-linear Adjustment of Deformation Inversion Model. Geomat. Inf. Sci. Wuhan Univ. 2001, 26, 504–508. [Google Scholar] [CrossRef]
- Olive, D.J. Multiple Linear Regression. In Linear Regression; Springer International Publishing: Cham, Switzerland, 2017; pp. 17–83. [Google Scholar]
- Van Leijen, F.J.; Hanssen, R.F. Persistent scatterer density improvement using adaptive deformation models. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 2102–2105. [Google Scholar]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquí, J.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Hu, J.; Ding, X.L.; Zhang, L.; Sun, Q.; Li, Z.W.; Zhu, J.J.; Lu, Z. Estimation of 3-D Surface Displacement Based on InSAR and Deformation Modeling. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2007–2016. [Google Scholar] [CrossRef]
- Kampes, B. Radar Interferometry: Persistent Scatterer Technique; Springer Netherlands: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Li, J.H.; Tan, Z.W.; Guan, B.G. A Study on Coal Hosting Features and Prospecting Orientation in Peripheral Baojishan and Honghui Mine Areas, Jingyuan Coalfield. Coal Geol. China 2012, 24, 7–10. [Google Scholar] [CrossRef]
- Werner, M. Shuttle Radar Topography Mission (SRTM) Mission Overview. Frequenz 2001, 55, 75–79. [Google Scholar] [CrossRef]
- Yang, Z.F.; Yi, H.W.; Zhu, J.J.; Li, Z.W.; Liu, Q. Spatio-temporal evolution law analysis of whole mining subsidence basin based on InSAR-derived time-series deformation. Chin. J. Nonferrous Met. 2016, 26, 1515–1522. [Google Scholar]
- Dalaison, M.; Jolivet, R. A Kalman Filter Time Series Analysis method for InSAR. J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
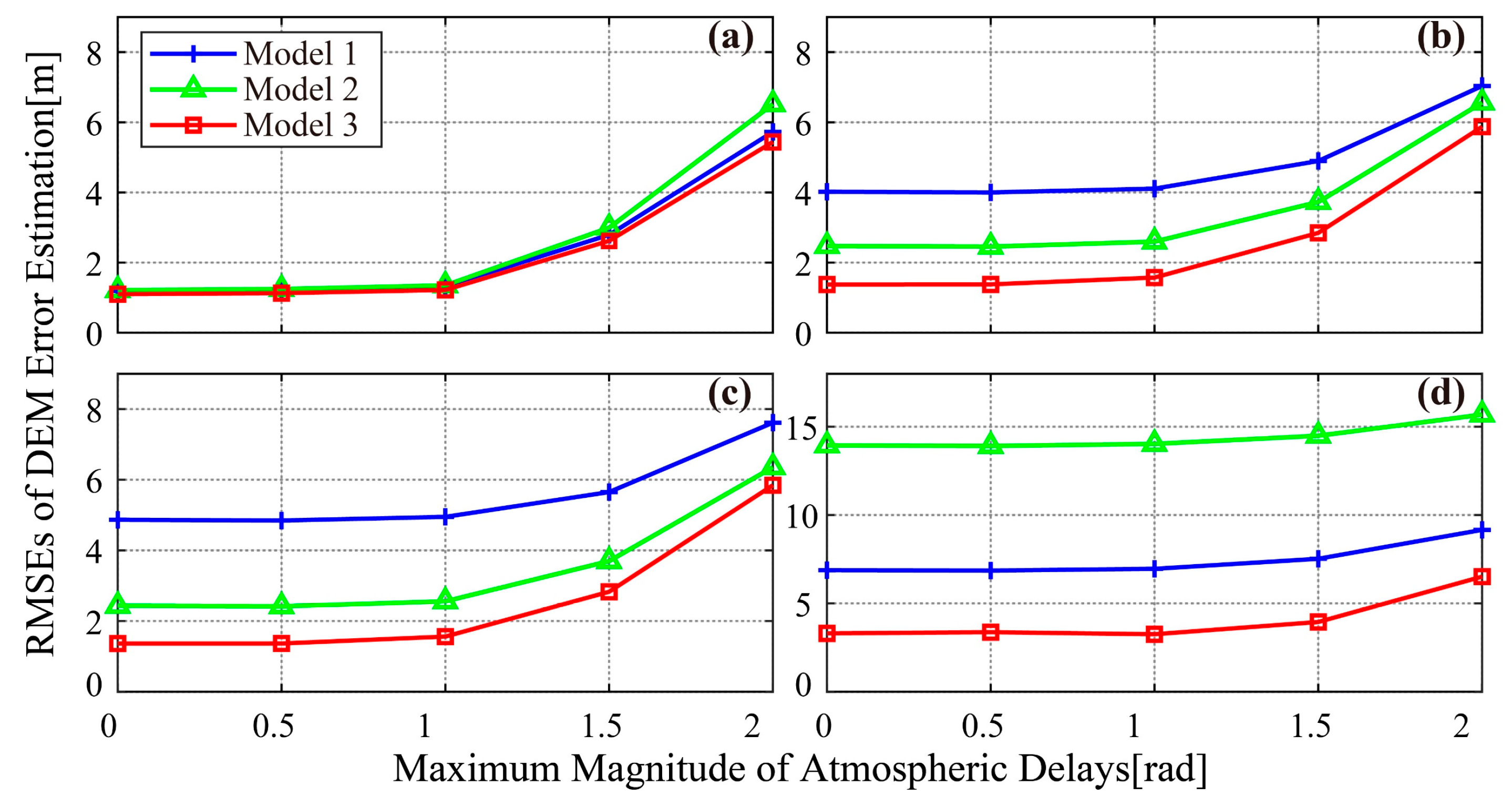

| Points | Model 1 | Model 2 | Model 3 |
|---|---|---|---|
| P1 | 0.66 | 0.62 | 0.13 |
| P2 | 0.15 | 0.14 | 0.14 |
| P3 | 0.73 | 0.60 | 0.24 |
| P4 | −0.01 | −0.02 | −0.01 |
| P5 | 0.69 | 0.65 | 0.23 |
| P6 | 0.54 | 0.35 | 0.14 |
| P7 | −0.51 | 0.39 | 0.18 |
| P8 | 0.15 | 0.15 | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Ge, Q.; Liu, J.; Yang, W.; Du, Z.; He, L. Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing. Remote Sens. 2021, 13, 2006. https://doi.org/10.3390/rs13102006
Hu J, Ge Q, Liu J, Yang W, Du Z, He L. Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing. Remote Sensing. 2021; 13(10):2006. https://doi.org/10.3390/rs13102006
Chicago/Turabian StyleHu, Jun, Qiaoqiao Ge, Jihong Liu, Wenyan Yang, Zhigui Du, and Lehe He. 2021. "Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing" Remote Sensing 13, no. 10: 2006. https://doi.org/10.3390/rs13102006
APA StyleHu, J., Ge, Q., Liu, J., Yang, W., Du, Z., & He, L. (2021). Constructing Adaptive Deformation Models for Estimating DEM Error in SBAS-InSAR Based on Hypothesis Testing. Remote Sensing, 13(10), 2006. https://doi.org/10.3390/rs13102006