DTM-Based Morphometric Analysis of Scoria Cones of the Chaîne des Puys (France)—The Classic and a New Approach
Abstract
:1. Introduction
Scoria Cone Morphometry
2. Materials and Methods
2.1. Data Used
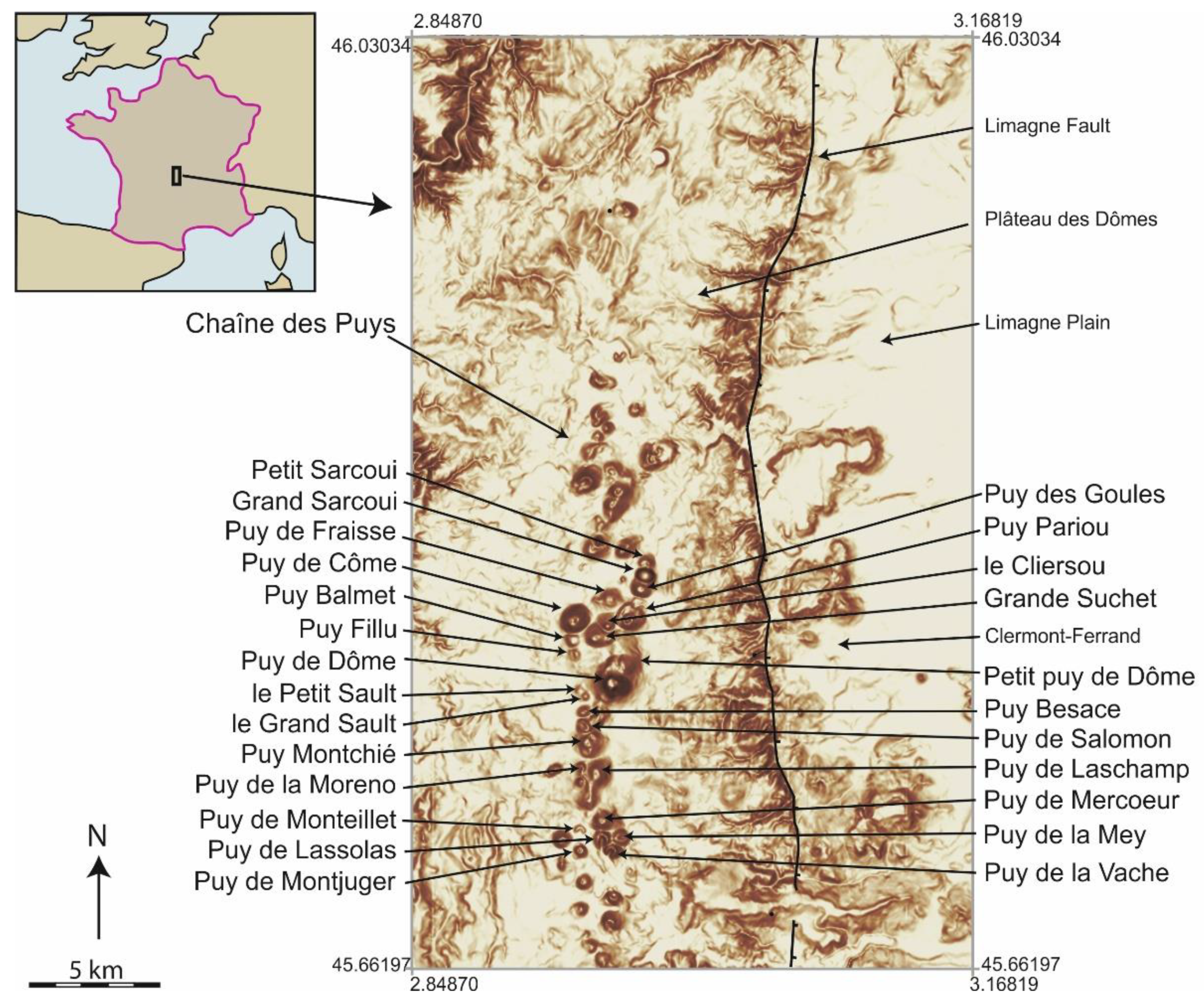
2.1.1. Chaîne des Puys Setting
2.1.2. LiDAR DTM
2.2. Methods
2.2.1. Classic Morphometry
2.2.2. Sectorization
- 1.
- determine the center of the scoria cone,
- 2.
- determine the outline of the scoria cone,
- 3.
- create the initial (basal) sectors,
- 4.
- shift/rotate the starting sectors,
- 5.
- determine the crater rim,
- 6.
- create the final sectors.
3. Results
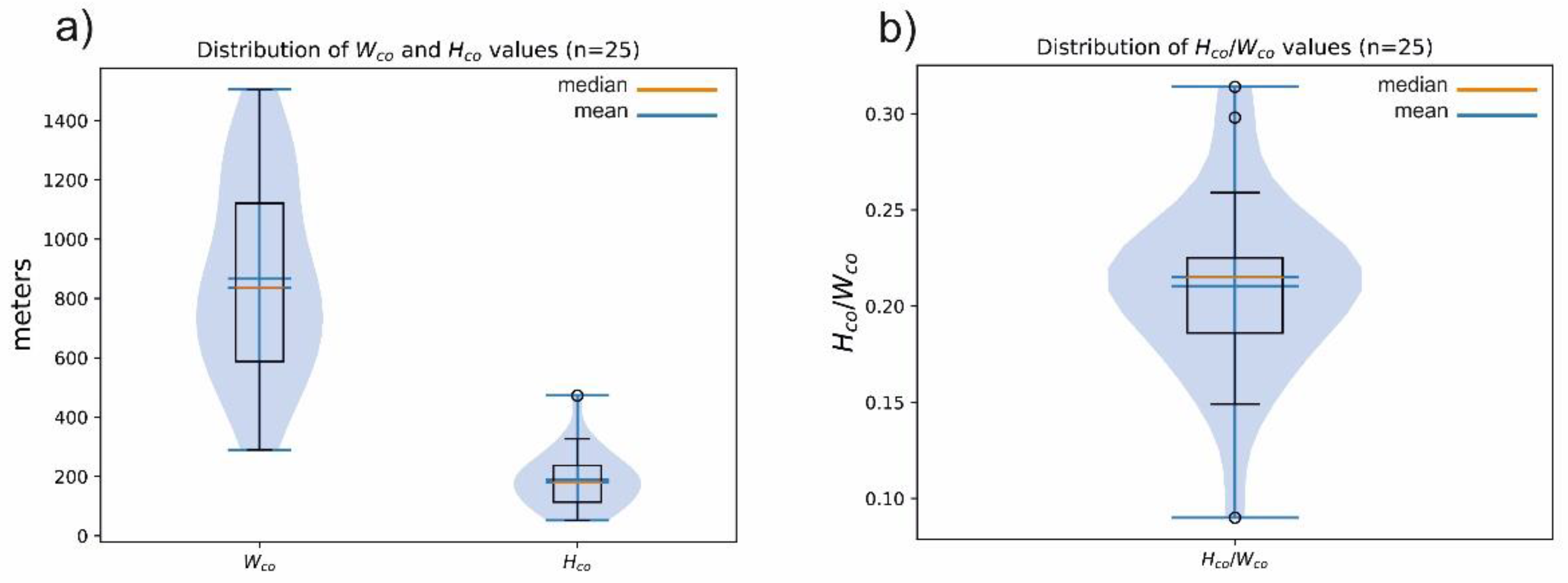
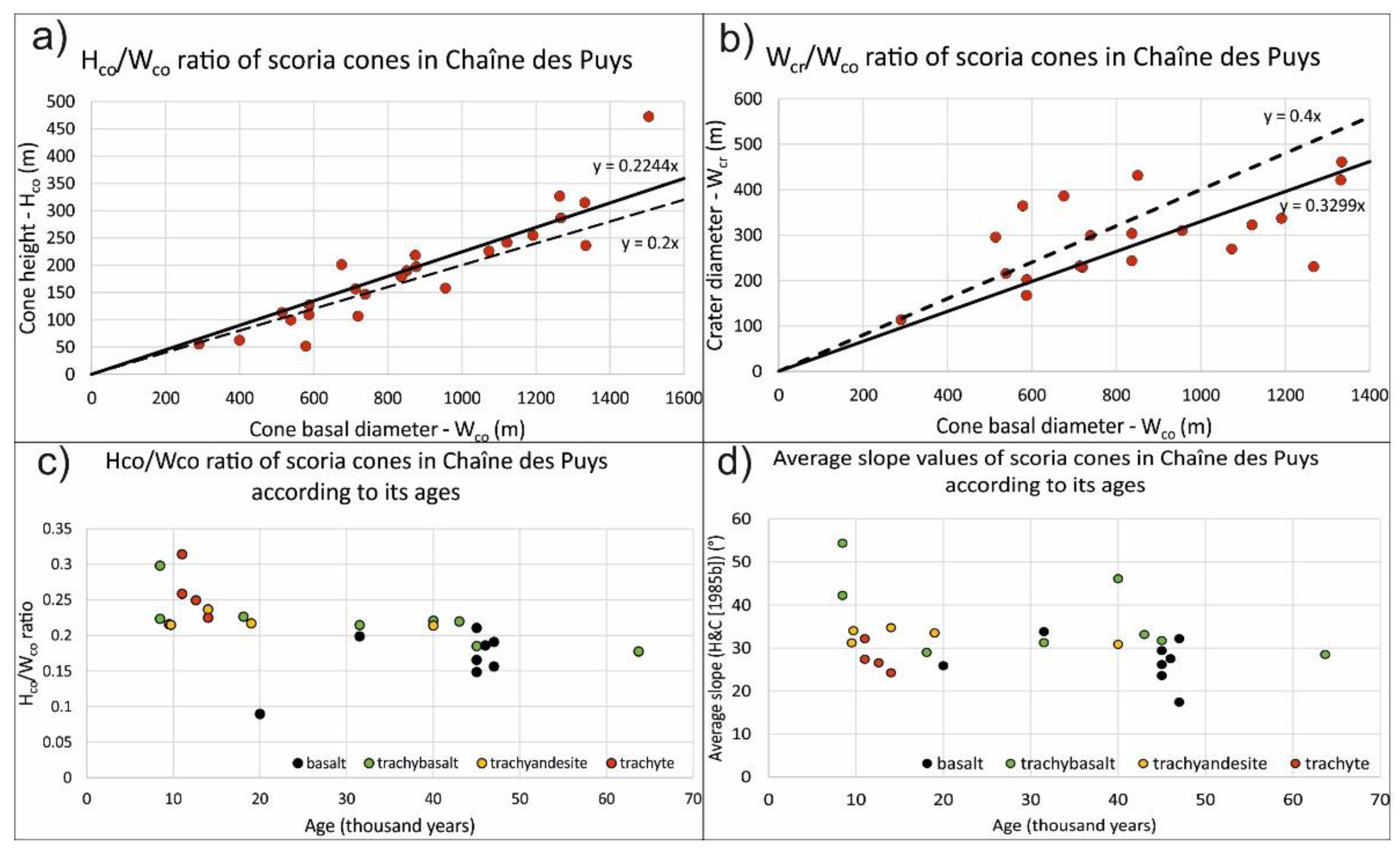
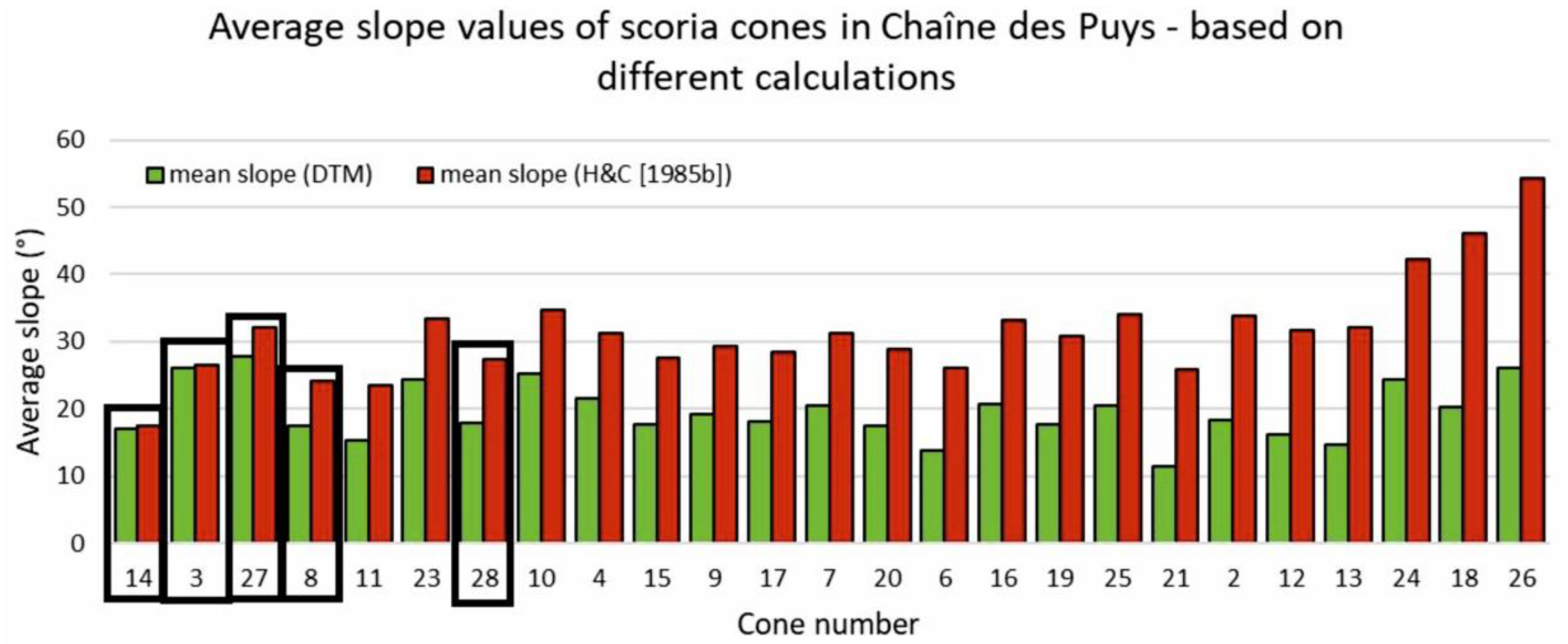
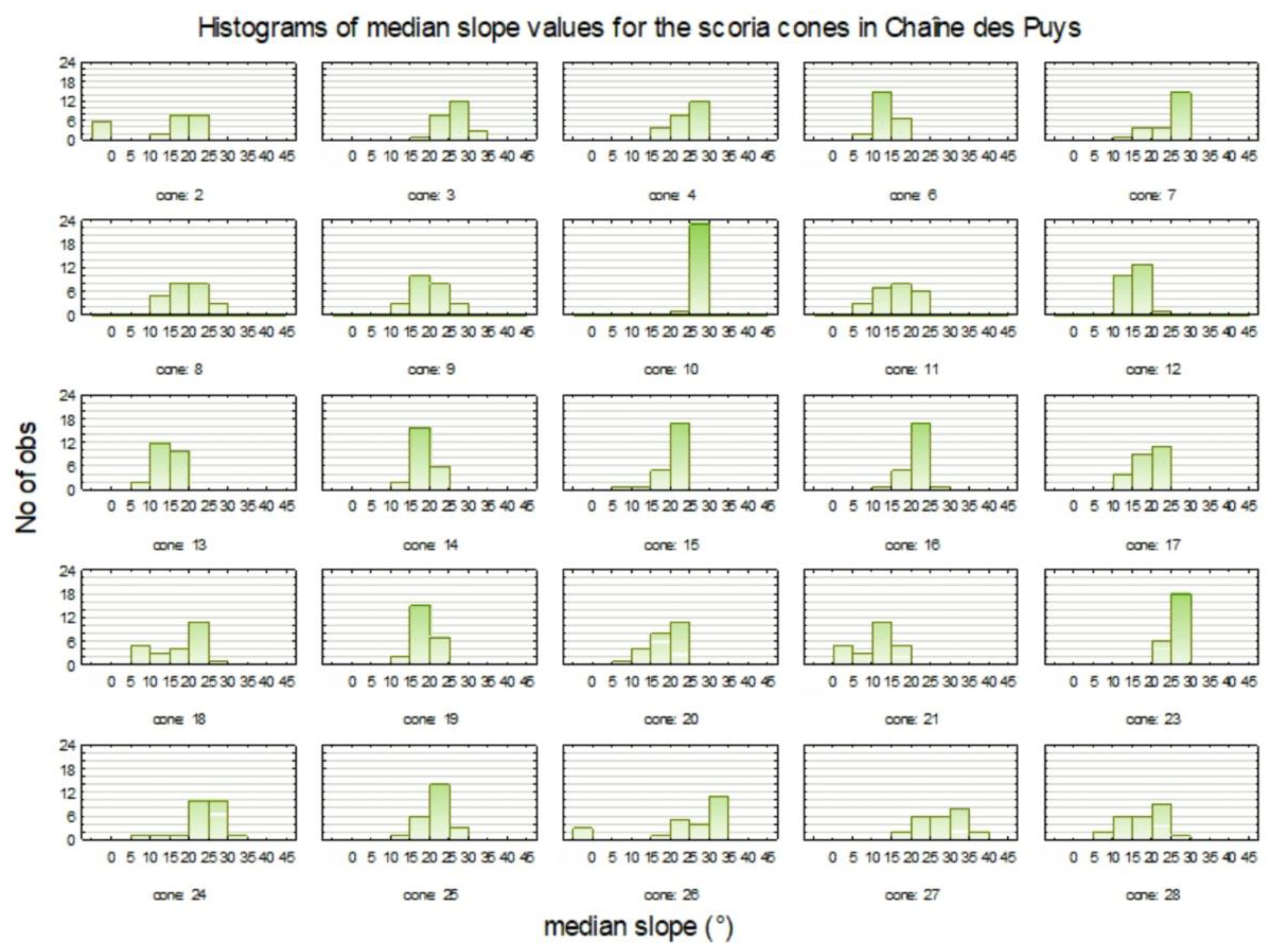
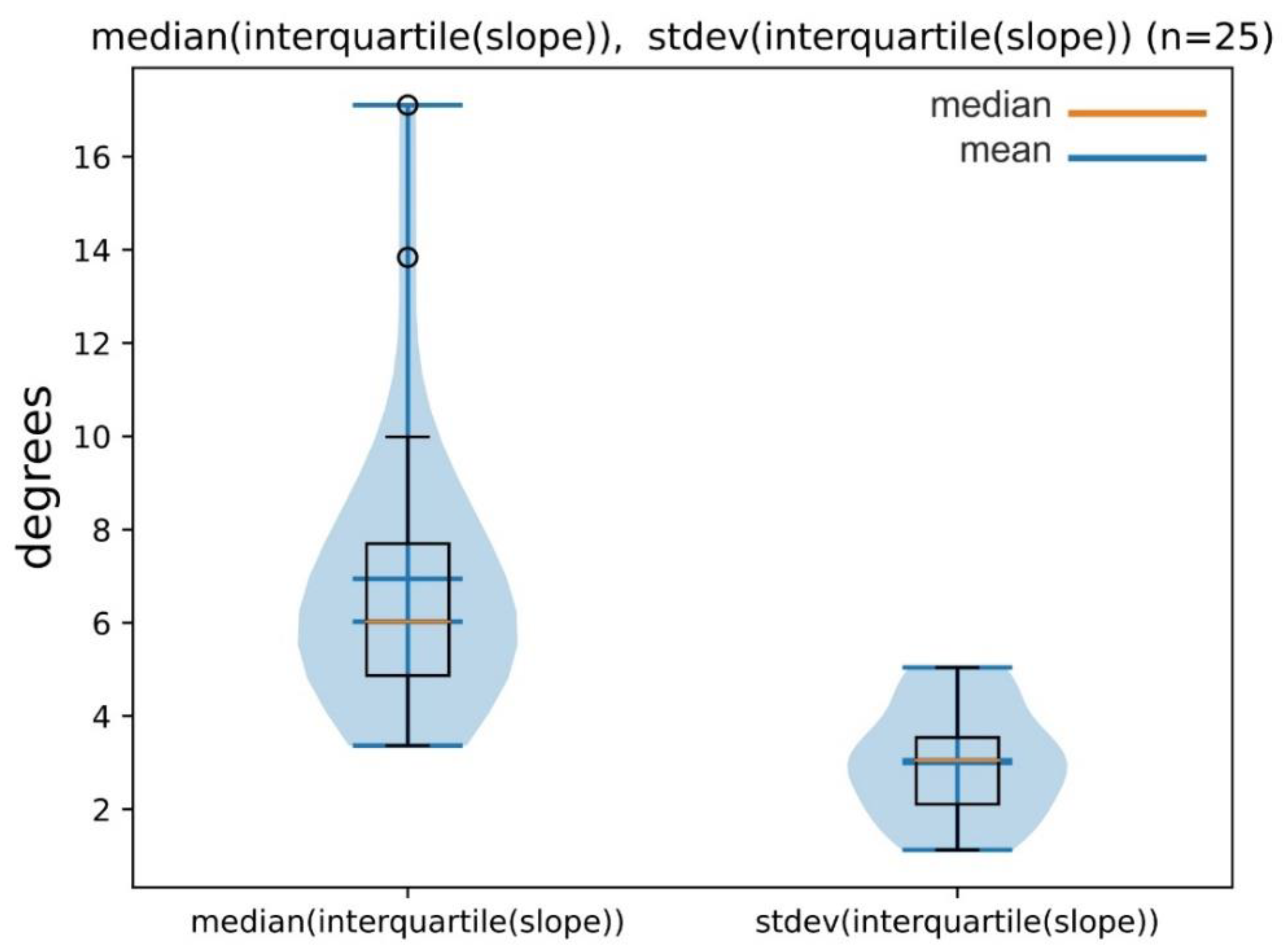
3.1. Results of the Classic Morphometry Parameters
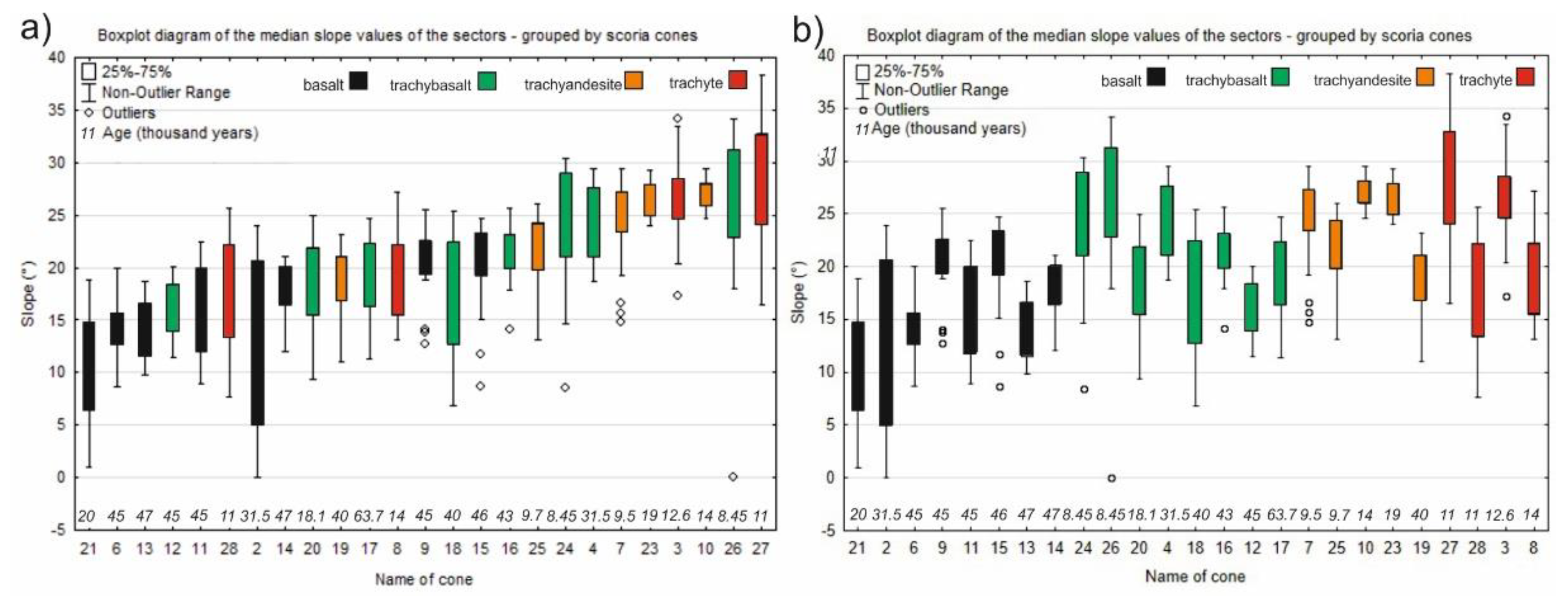
3.2. Results of Sectorization Calculations
4. Discussion
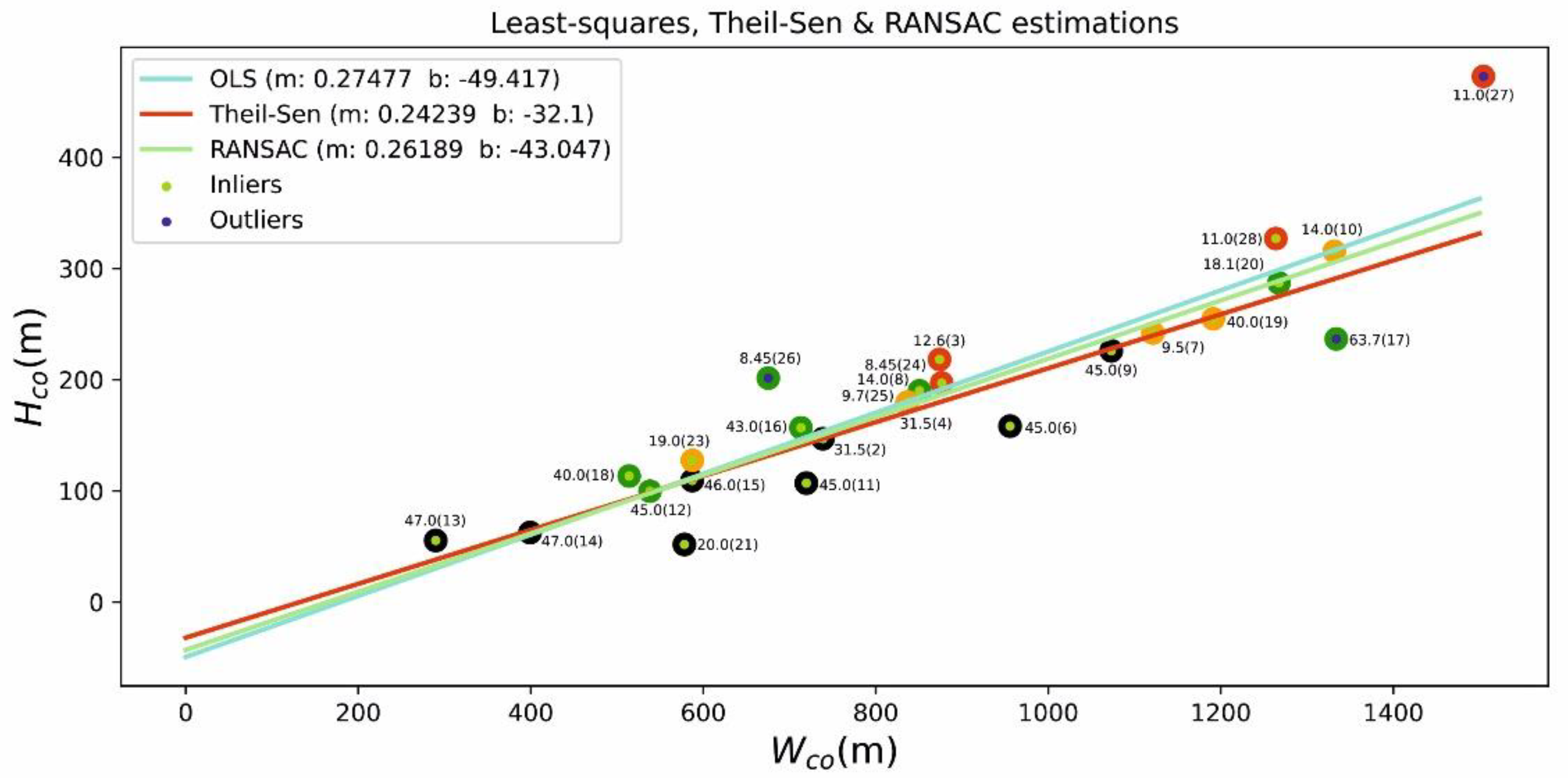
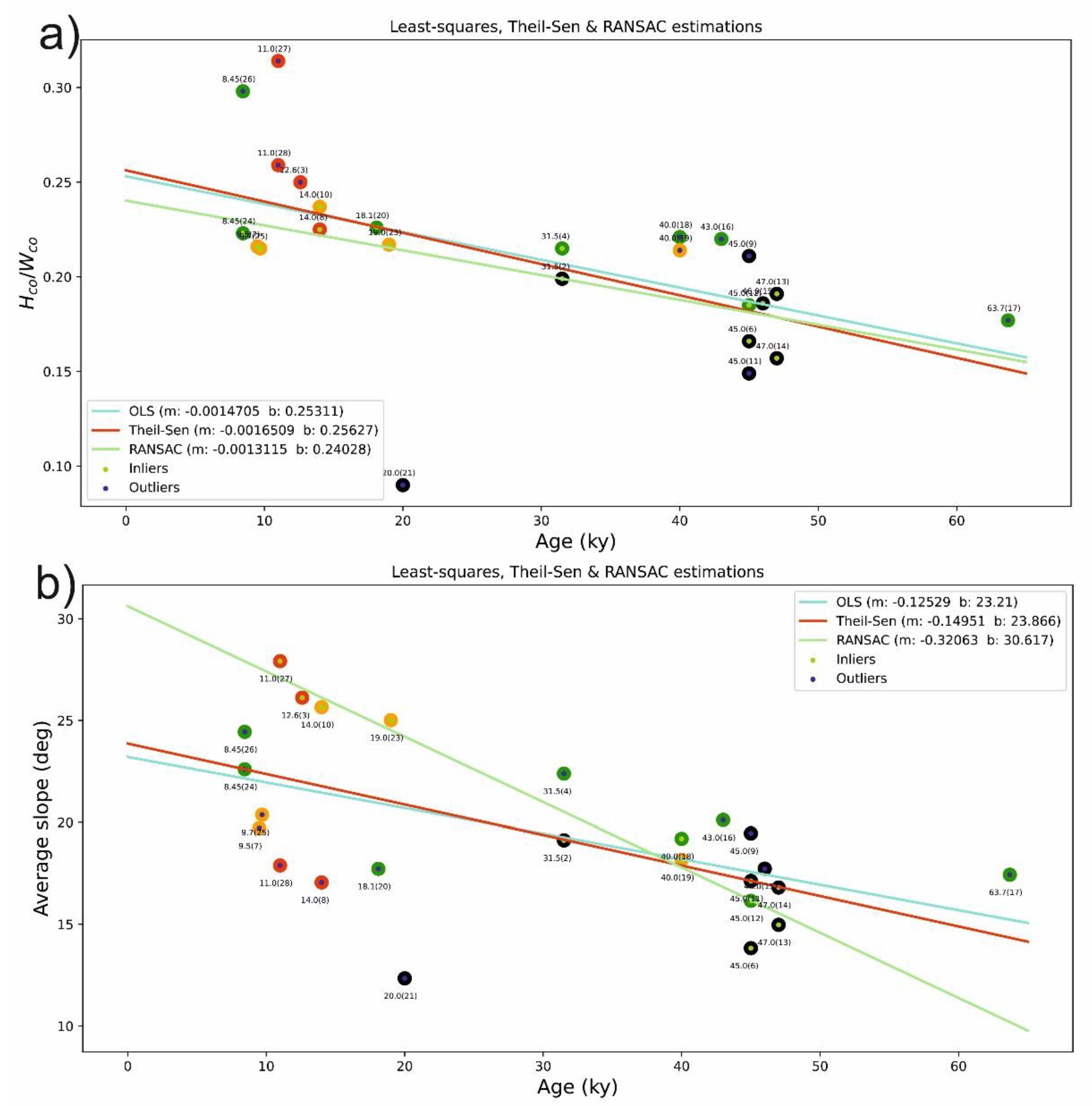
- In this case, the least squares and the Theil–Sen regression give similar results, whereas the RANSAC solution enhances the special behavior of some points too.
- The trachytic domes are well off any regression line; consequently, RANSAC identifies them as outliers in this relationship as well.
- The inliers of the RANSAC solution encompass six basaltic cones, a few trachybasaltic, and two trachyandesitic cones.
- Even if some of them are found to be outliers by RANSAC, trachybasaltic cones are mostly aligned with the trend. However, trachyandesitic cones form rather a compact group if they are considered separately.
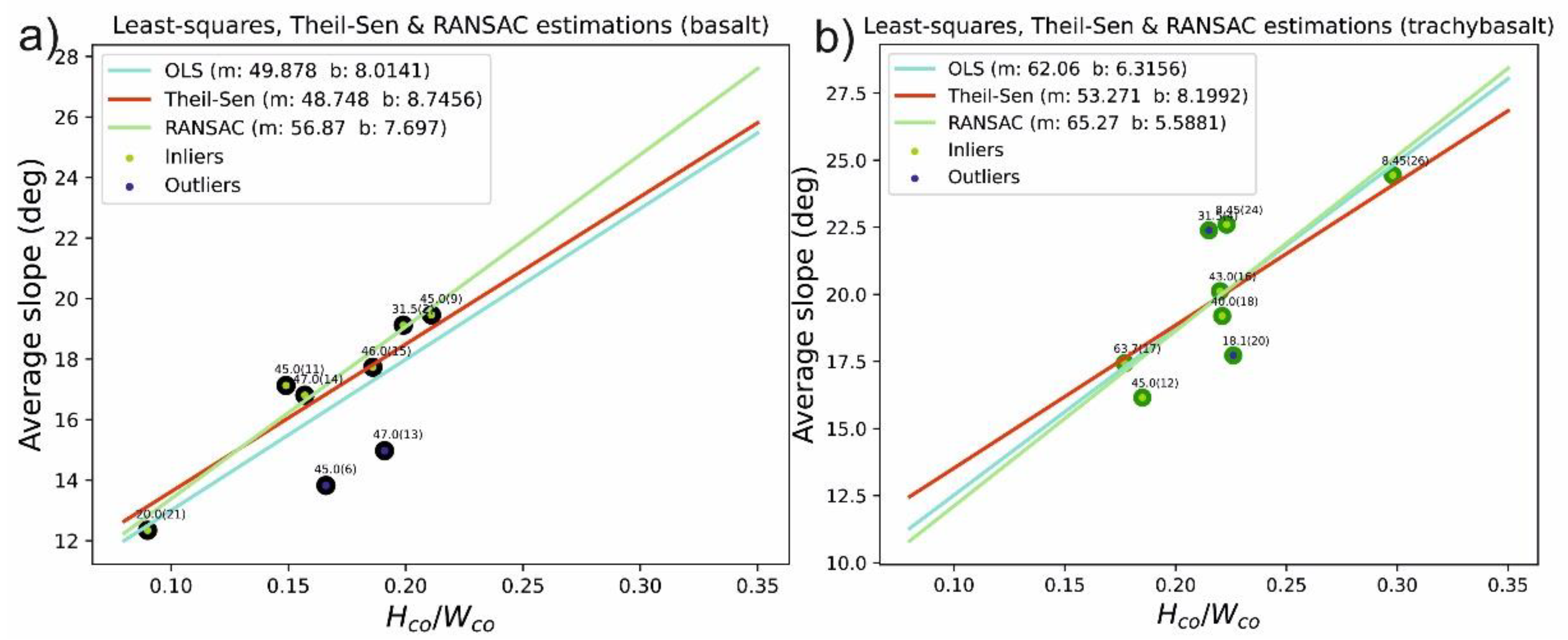
- It is interesting to note that six basaltic cones (out of 8) are strongly aligned, indicating a stronger relationship.
- The behavior of the basaltic cones motivated us to analyze them separately as well, in particular since this is the largest lithological group of eight cones. The result is presented in Figure 13a.
5. Conclusions
- The general assumption for scoria cones that the basal width (Wco) correlates with the height of the cone (Hco) could be verified. However, Hasenaka & Carmichael’s [35] calculation of average slopes overestimates the real slope values, sometimes to a great extent. We suggest that this method should be replaced by DTM-derived slope values, in agreement with a number of subsequent studies (e.g., [14]).
- In addition, a more detailed morphometric assessment that tackles the circular symmetry of the cones reveals that specific groups behave differently, and, in some cases, they define a separate trend or no trend can be detected. The slope distributions extracted from LiDAR digital terrain models indicate greater variability with lithology/composition than with age, at least over the age range of the volcanoes here.
- Nevertheless, within the same lithological group, subtle but possibly systematic trends can be detected for decreasing morphometric values (e.g., slope) with the age. Cones of different lithology/composition can have different relationships, and thus different composition cones produce slightly different shapes.
- Despite the attempt to characterize them separately, we can conclude that the time span of the trachytic cones/domes of Chaîne des Puys is too short for significant differences or correlations with the age to be detected with confidence.
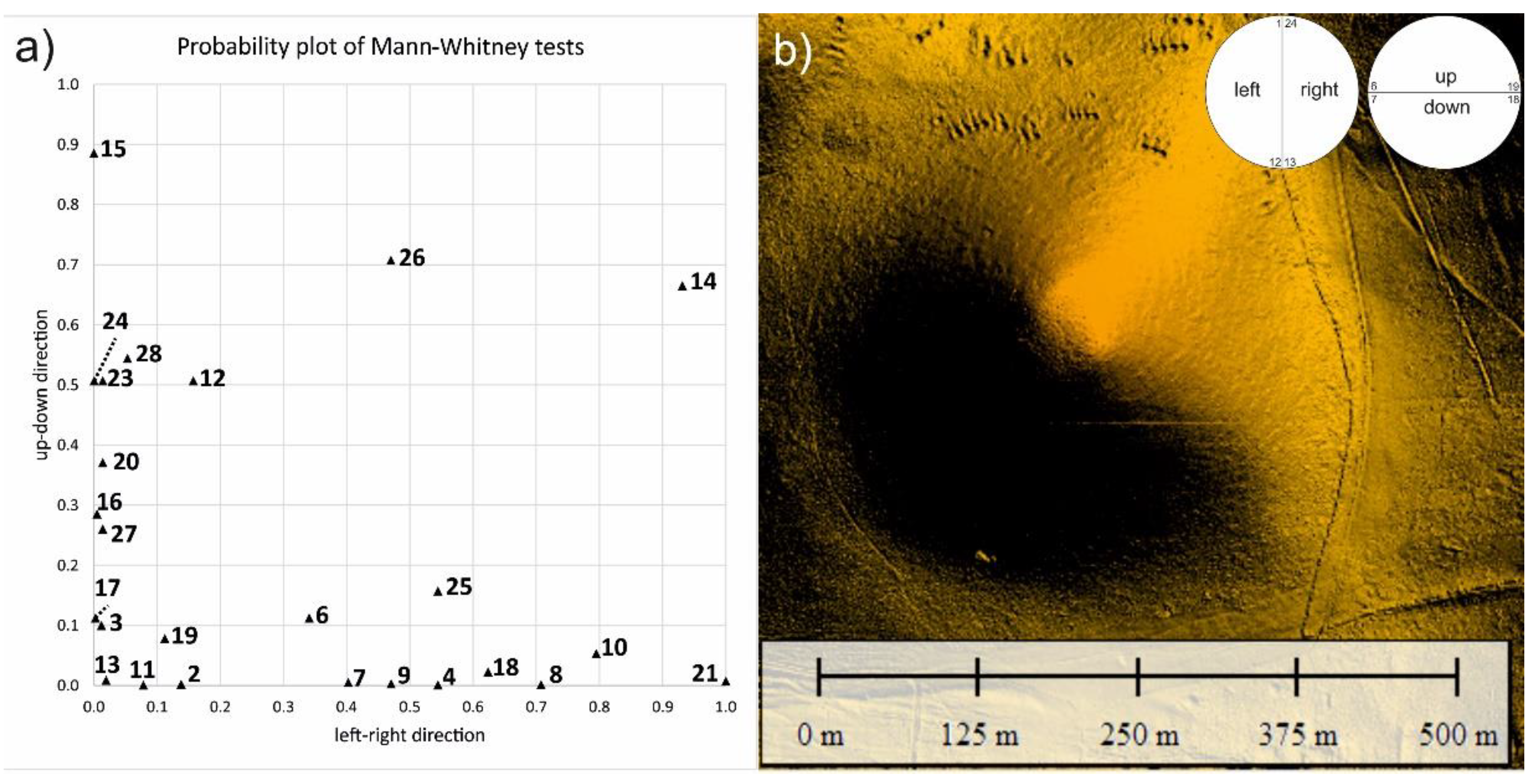
- Morphometric sectorization resulted in separation into various types of symmetries. Some cones are close to a regular shape, but the majority of the cones are not circularly symmetric. These cones, however, often show other types of symmetry. The radar diagrams of specifically processed slope distributions show similarities and dissimilarities. These observations are encouraging to perform further statistical analysis of sectorial data that might reveal further relationships with tectonics, slope or wind directions.
- The initial aim to explore relationships of age and lithology with and morphometric parameters showed that lithology is a strong control, but only a faint age effect was detectable over the timespan of just under 100,000 years. The variability of original cone morphometry led to large errors in estimated rates. More detailed geomorphological approaches integrating lithological factors would be a next step, and applying the methods to a longer time span.
- The variability depicted in the morphometry is connected largely to the lithology and thus eruptive processes, and/or potentially with the angle of repose of various types of scoria. The methods here have the potential to explore such processes over a volcanic field. Further work is needed to understand all the diverse parameters, especially how different compositions produce different shapes, and how symmetry is connected to different factors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karatson, D.; Yepes, J.; Favalli, M.; Rodríguez-Peces, M.J.; Fornaciai, A. Reconstructing eroded paleovolcanoes on Gran Canaria, Canary Islands, using advanced geomorphometry. Geomorphology 2016, 253, 123–134. [Google Scholar] [CrossRef]
- Porter, S.C. Distribution, Morphology, and Size Frequency of Cinder Cones on Mauna Kea Volcano, Hawaii. Geol. Soc. Am. Bull. 1972, 83. [Google Scholar] [CrossRef]
- Wood, C.A. Morphometric analysis of cinder cone degradation. J. Volcanol. Geotherm. Res. 1980, 8, 137–160. [Google Scholar] [CrossRef]
- Wood, C.A. Morphometric evolution of cinder cones. J. Volcanol. Geotherm. Res. 1980, 7, 387–413. [Google Scholar] [CrossRef]
- Walker, G.P.L. Basaltic volcanoes and volcanic systems. In Encyclopedia of Volcanoes; Sigurdsson, H., Ed.; Academic Press: Cambridge, UK, 2000; pp. 283–289. [Google Scholar]
- Fornaciai, A.; Favalli, M.; Karátson, D.; Tarquini, S.; Boschi, E. Morphometry of scoria cones, and their relation to geodynamic setting: A DEM-based analysis. J. Volcanol. Geotherm. Res. 2012, 217-218, 56–72. [Google Scholar] [CrossRef]
- Riedel, C.; Ernst, G.; Riley, M. Controls on the growth and geometry of pyroclastic constructs. J. Volcanol. Geotherm. Res. 2003, 127, 121–152. [Google Scholar] [CrossRef]
- de Silva, S.; Lindsay, J.M. Primary Volcanic Landforms. In The Encyclopedia of Volcanoes, 2nd ed.; Academic Press: Cambridge, UK, 2015; pp. 273–297. ISBN 9780123859389. [Google Scholar]
- Houghton, B.F.; Schmincke, H.-U. Rothenberg scoria cone, East Eifel: A complex Strombolian and phreatomagmatic volcano. Bull. Volcanol. 1989, 52, 28–48. [Google Scholar] [CrossRef]
- Calvari, S.; Pinkerton, H. Birth, growth and morphologic evolution of the ‘Laghetto’ cinder cone during the 2001 Etna eruption. J. Volcanol. Geotherm. Res. 2004, 132, 225–239. [Google Scholar] [CrossRef]
- Pioli, L.; Erlund, E.; Johnson, E.; Cashman, K.; Wallace, P.; Rosi, M.; Granados, H.D. Explosive dynamics of violent Strombolian eruptions: The eruption of Parícutin Volcano 1943–1952 (Mexico). Earth Planet. Sci. Lett. 2008, 271, 359–368. [Google Scholar] [CrossRef]
- Nemeth, K.; Kereszturi, G. Monogenetic volcanism: Personal views and discussion. Int. J. Earth Sci. 2015, 104, 2131–2146. [Google Scholar] [CrossRef]
- Németh, K. Monogenetic volcanic fields: Origin, sedimentary record, and relationship with polygenetic volcanism. In What Is A Volcano? Canon-Tapia, E., Szakacs, A., Eds.; Geological Society of America: Boulder, CO, USA, 2010; Volume 470, pp. 43–66. [Google Scholar]
- Kereszturi, G.; Németh, K. Monogenetic Basaltic Volcanoes: Genetic Classification, Growth, Geomorphology and Degradation. In Updates in Volcanology-New Advances in Understanding Volcanic Systems; Németh, K., Ed.; Intech Open: London, UK, 2012; Volume 1, pp. 3–88. [Google Scholar]
- Smith, I.E.M.; Németh, K. Source to surface model of monogenetic volcanism: A critical review. Geol. Soc. London. Spec. Publ. 2017, 446, 1–28. [Google Scholar] [CrossRef]
- Corazzato, C.; Tibaldi, A. Fracture control on type, morphology and distribution of parasitic volcanic cones: An example from Mt. Etna, Italy. J. Volcanol. Geotherm. Res. 2006, 158, 177–194. [Google Scholar] [CrossRef]
- Colton, S.H. The basaltic cinder cones and lava flows of the San Francisco Mountain volcanic field. Mus. North. Ariz. Bull. 1937, 10, 1–49. [Google Scholar]
- Scott, D.; Trask, N. Geology of the Lunar Crater volcanic field, Nye County, Nevada. Prof. Pap. 1971, 599, 22. [Google Scholar] [CrossRef]
- Settle, M. The structure and emplacement of cinder cone fields. Am. J. Sci. 1979, 279, 1089–1107. [Google Scholar] [CrossRef]
- Moore, R.B.; Wolfe, E. Geologic map of the east part of the San Francisco Volcanic Field, north-central Arizona, scale 1:50 000. USGS Misc. Investig. Ser. Map 1987. [Google Scholar] [CrossRef]
- Hooper, D.M.; Sheridan, M.F. Computer-simulation models of scoria cone degradation. J. Volcanol. Geotherm. Res. 1998, 83, 241–267. [Google Scholar] [CrossRef]
- Favalli, M.; Karátson, D.; Mazzarini, F.; Pareschi, M.T.; Boschi, E. Morphometry of scoria cones located on a volcano flank: A case study from Mt. Etna (Italy), based on high-resolution LiDAR data. J. Volcanol. Geotherm. Res. 2009, 186, 320–330. [Google Scholar] [CrossRef]
- van Wyk de Vries, B. Volcanoes of France. In Volcanoes of Europe; Jerram, D., Scarth, A., Tanguy, J.-C., Eds.; Dunedin Academic Press, Ltd.: Edinburgh, UK, 2017; p. 256. ISBN 13: 978-1780460420. [Google Scholar]
- Boivin, P.; Besson, J.C.; Briot, D.; Camus, G.; De Goër de Hervé, A.; Gourgaud, A.; Labazuy, P.; Langlois, E.; de Larouzière, F.D.; Livet, M.; et al. Volcanologie de la Chaîne des Puys, scale 1:25 000. 1 sheet. In Editions Du Parc Naturel Régional Des Volcans d’Auvergne, 5th ed.; IGN: San Francisco, CA, USA, 2017. [Google Scholar]
- Scrope, G.P. Considerations on Volcanos, the Probable Causes of Their Phenomena, the Laws Which Determine Their March, the Disposition of Their Products, and Their Connexion with the Present State and Past History of the Globe; Phillips, W., Ed.; Cambridge University Press: London, UK, 1825. [Google Scholar]
- Haut Lieu Tectonique Chaîne Des Puys-Faille De Limagne-UNESCO World Heritage Centre. Available online: http://whc.unesco.org/fr/list/1434 (accessed on 27 April 2021).
- Shields, J. The Morphometry of the Chaine des Puys; Université Blaise Pascal: Aubière, France, 2010. [Google Scholar]
- Camus, G.; Goer de Herve, A.; Kieffer, G.; Mergoil, J.; Vincent, P.M. Volcanologie de la Chaîne des Puys 1:25 000. Parc. Nat. Régional des Volcans D Auvergne Clermont Ferrand 1975. [Google Scholar]
- Delcamp, A.; Vries, B.V.W.D.; Stéphane, P.; Kervyn, M. Endogenous and exogenous growth of the monogenetic Lemptégy volcano, Chaîne des Puys, France. Geosphere 2014, 10, 998–1019. [Google Scholar] [CrossRef] [Green Version]
- Petronis, M.S.; Vries, B.V.W.D.; Garza, D. The Leaning Puy de Dôme (Auvergne, France) tilted by shallow intrusions. Volcanica 2019, 2, 161–186. [Google Scholar] [CrossRef]
- Vries, B.V.W.D.; Marquez, A.; Herrera, R.; Bruña, J.L.G.; Llanes, P.; Delcamp, A. Craters of elevation revisited: Forced-folds, bulging and uplift of volcanoes. Bull. Volcanol. 2014, 76, 875. [Google Scholar] [CrossRef]
- Vörös, F.; van Wyk de Vries, B.; Székely, B. Geomorphometric Descriptive Parameters of Scoria Cones from Different Dtms: A Resolution Invariance Study. In Proceedings of the 7th International Conference on Cartography and GIS, Sozopol, Bulgaria, 18–23 June 2018; pp. 603–612. [Google Scholar]
- Accueil|Craig. Available online: https://www.craig.fr/ (accessed on 29 April 2021).
- 2011_Site_Puy_De_Dome_Lidarverne-Fichiers-Drive Opendata Du Craig. Available online: https://drive.opendata.craig.fr/s/opendata?path=%2Flidar%2Fautres_zones%2F2011_site_puy_de_dome_lidarverne (accessed on 27 April 2021).
- Hasenaka, T.; Carmichael, I.S. The cinder cones of Michoacán—Guanajuato, central Mexico: Their age, volume and distribution, and magma discharge rate. J. Volcanol. Geotherm. Res. 1985, 25, 105–124. [Google Scholar] [CrossRef]
- Hasenaka, T.; Carmichael, I.S.E. A compilation of location, size, and geomorphological parameters of volcanoes of the Michoacan-Guanajuato Volcanic Field, Central Mexico. Geof. Int. 1985, 24, 577–607. [Google Scholar]
- Ray, R.G. Aerial photographs in geologic interpretation and mapping. Prof. Pap. 1960, 373. [Google Scholar] [CrossRef] [Green Version]
- Vörös, F.; Pál, M.; Vries, B.V.W.D.; Székely, B. Development of a New Type of Geodiversity System for the Scoria Cones of the Chaîne des Puys Based on Geomorphometric Studies. Geosciences 2021, 11, 58. [Google Scholar] [CrossRef]
- Bloomfield, K. A late-Quaternary monogenetic volcano field in central Mexico. Acta Diabetol. 1975, 64, 476–497. [Google Scholar] [CrossRef]
- Dohrenwend, J.C.; Wells, S.G.; Turrin, B.D. Degradation of Quaternary cinder cones in the Cima volcanic field, Mojave Desert, California. GSA Bull. 1986, 97, 421–427. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 1992; Volume 53, pp. 345–381. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Paradigm for Model Consensus: Applications to Image Fitting with Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
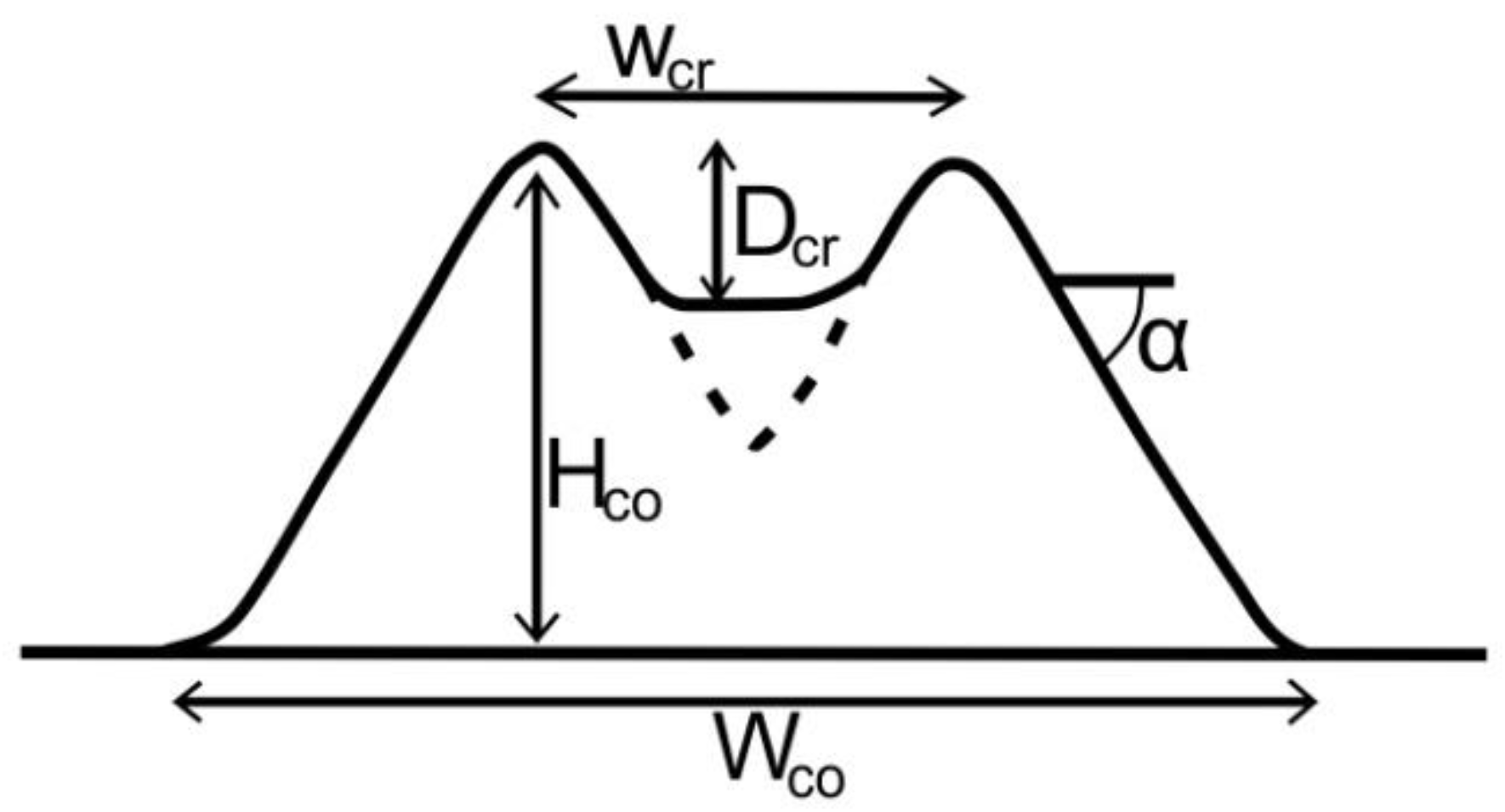




| Cone ID | Name of Cone | Age of Cone (ka) [24] | Lithology [24] | Hco/Wco | Wcr (m) | Dcr (m) | Average Slope (°) According to [35] |
|---|---|---|---|---|---|---|---|
| 2 | Petit Sarcoui | 31.5 | basalt | 0.199 | 299.49 | 54.38 | 33.8 |
| 3 | Grand Sarcoui | 12.6 | trachyte | 0.250 | No CR | No CR | 26.5 |
| 4 | Puy des Goules | 31.5 | trachybasalt | 0.215 | 243.73 | 33.42 | 31.2 |
| 6 | Puy de Fraisse | 45 | basalt | 0.166 | 310.30 | 35.13 | 26.1 |
| 7 | Puy Pariou | 9.5 | trachyandesite | 0.216 | 322.42 | 89.82 | 31.2 |
| 8 | le Cliersou | 14 | basalt | 0.225 | No CR | No CR | 24.2 |
| 9 | Grande Suchet | 45 | basalt | 0.211 | 269.58 | 40.73 | 29.4 |
| 10 | Puy de Come | 14 | trachyandesite | 0.237 | 421.42 | 75.83 | 34.7 |
| 11 | Puy Balmet | 45 | basalt | 0.149 | 229.16 | 17.06 | 23.6 |
| 12 | Puy Fillu | 45 | trachybasalt | 0.185 | 215.58 | 47.52 | 31.7 |
| 13 | le Petit Sault | 47 | basalt | 0.191 | 113.72 | 19.58 | 32.2 |
| 14 | le Grand Sault | 47 | basalt | 0.157 | No CR | No CR | 17.4 |
| 15 | Puy Besace | 46 | basalt | 0.186 | 167.60 | 32.11 | 27.5 |
| 16 | Puy de Salomon | 43 | trachybasalt | 0.220 | 232.45 | 64.14 | 33.1 |
| 17 | Puy Montchié | 63.7 | trachybasalt | 0.177 | 461.36 | 51.21 | 28.5 |
| 18 | Puy de la Moreno | 40 | trachybasalt | 0.221 | 295.71 | 103.89 | 46.1 |
| 19 | Puy Laschamp | 40 | trachyandesite | 0.214 | 337.03 | 39.56 | 30.8 |
| 20 | Puy de Mercoeur | 18.1 | trachybasalt | 0.226 | 230.84 | 38.91 | 29.0 |
| 21 | Puy de Monteillet | 20 | basalt | 0.090 | 364.45 | 40.78 | 25.9 |
| 23 | Puy de Montjuger | 19 | trachyandesite | 0.217 | 202.01 | 48.16 | 33.5 |
| 24 | Puy de Lassolas | 8.45 | trachybasalt | 0.223 | 431.69 | 152.00 | 42.2 |
| 25 | Puy de la Mey | 9.7 | trachyandesite | 0.215 | 303.37 | 111.56 | 34.0 |
| 26 | Puy de la Vache | 8.45 | trachybasalt | 0.298 | 386.05 | 152.39 | 54.3 |
| 27 | Puy de Dôme | 11 | trachyte | 0.314 | No CR | No CR | 32.1 |
| 28 | Petit puy de Dôme | 11 | trachyte | 0.259 | No CR | No CR | 27.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vörös, F.; van Wyk de Vries, B.; Karátson, D.; Székely, B. DTM-Based Morphometric Analysis of Scoria Cones of the Chaîne des Puys (France)—The Classic and a New Approach. Remote Sens. 2021, 13, 1983. https://doi.org/10.3390/rs13101983
Vörös F, van Wyk de Vries B, Karátson D, Székely B. DTM-Based Morphometric Analysis of Scoria Cones of the Chaîne des Puys (France)—The Classic and a New Approach. Remote Sensing. 2021; 13(10):1983. https://doi.org/10.3390/rs13101983
Chicago/Turabian StyleVörös, Fanni, Benjamin van Wyk de Vries, Dávid Karátson, and Balázs Székely. 2021. "DTM-Based Morphometric Analysis of Scoria Cones of the Chaîne des Puys (France)—The Classic and a New Approach" Remote Sensing 13, no. 10: 1983. https://doi.org/10.3390/rs13101983
APA StyleVörös, F., van Wyk de Vries, B., Karátson, D., & Székely, B. (2021). DTM-Based Morphometric Analysis of Scoria Cones of the Chaîne des Puys (France)—The Classic and a New Approach. Remote Sensing, 13(10), 1983. https://doi.org/10.3390/rs13101983








