Abstract
Terrestrial laser scanning (TLS) is an important part of urban reconstruction and terrain surveying. In TLS applications, 4-point congruent set (4PCS) technology is widely used for the global registration of point clouds. However, TLS point clouds usually enjoy enormous data and uneven density. Obtaining the congruent set of tuples in a large point cloud scene can be challenging. To address this concern, we propose a registration method based on the voxel grid of the point cloud in this paper. First, we establish a voxel grid structure and index structure for the point cloud and eliminate uneven point cloud density. Then, based on the point cloud distribution in the voxel grid, keypoints are calculated to represent the entire point cloud. Fast query of voxel grids is used to restrict the selection of calculation points and filter out 4-point tuples on the same surface to reduce ambiguity in building registration. Finally, the voxel grid is used in our proposed approach to perform random queries of the array. Using different indoor and outdoor data to compare our proposed approach with other 4-point congruent set methods, according to the experimental results, in terms of registration efficiency, the proposed method is more than 50% higher than K4PCS and 78% higher than Super4PCS.
1. Introduction
1.1. Background
With the ever-increasing computing power of computers in recent years, the price of TLS instruments has significantly declined. TLS point cloud data are widely used in robot navigation, three-dimensional reconstruction, terrain surveying, and other directions [1,2]. Fast and efficient TLS point cloud registration is not only a key technology but also a major research hotspot. TLS point cloud registration is the process of fusing point cloud data with different coordinate systems into a single coordinate system [3]. Since point cloud data are usually not collected all at a single time, it is often mandatory to perform a rigid transformation of three-dimensional space rotation and translation on the data from different poses.
The most commonly used algorithm in registration is Iterative Closest Point (ICP) [4]. The ICP algorithm is used to find the nearest point in the target point cloud for each data point in the origin point cloud. The rigid body transformation is estimated using the closest point pairs and is applied to the source point cloud. The closest point pair and the rigid body transformation can be determined through iterations, and the convergence can then be calculated. The ICP algorithm requires a good initial pose; otherwise, it would easily fall into the local optimum. In the past two decades, many studies have improved the convergence range and convergence speed of ICP. Popular ICP variants [5,6,7], such as Go-ICP [6] and Symmetric Objective ICP [7], both have good performance. Since the input point cloud has uneven density and incomplete overlap, there is no complete point-to-point relationship. Some scholars have carried out relevant studies on the corresponding relation for selection [8]. To solve the corresponding point problem, two types of registration methods have emerged: using feature points and without feature points.
The first type designs a robust feature descriptor by detecting keypoints of the original point cloud to obtain feature points. The corresponding point pair in the feature point cloud is determined to calculate the transformation matrix to complete the registration. However, when the original point cloud density is uneven and the overlap rate is not high, the quality and the speed of feature extraction using such methods will be limited. The second type of registration method identifies common subsets through sampling and establishes the correspondence between two subsets. One such example is the widely used 4-point congruent set algorithm. However, due to noise and outliers, this method has difficulty finding a high-quality sample subset, which will greatly affect the registration results. In recent years, some studies have proposed adopting the advantages of these two methods and combining them into a single comprehensive approach, creating a new research direction of TLS point cloud registration with a low overlap rate while a large data volume.
Based on the point cloud data of the voxel grid, a three-dimensional point cloud registration method combining local feature points and a 4-point congruent set is proposed in this paper. First, a voxel grid about the original point cloud and a linear index relationship should be established. Some outlier points are eliminated through the distribution of points in the voxel grid. Based on the point’s distance from the grid center, a density value is assigned to each grid through the Gaussian function. Using the density value of the point cloud data in the voxel grid, the density conversion rate is calculated for the different directions, and the feature points are filtered out. The way to search feature points is inspired by the Harris corner detection [9], which has been widely used for images. Compared with the keypoints detection based on the normal, the feature point based on the density conversion rate is more stable. Moreover, the use of the query advantage of the voxel grid index to filter the 4-tuple base can effectively reduce the probability of misregistration. The query advantage of the voxel grid index is used to improve the speed of verifying the congruent candidate set, the process of finding the largest common point-set (LCP) [10]. This registration method has high efficiency and accuracy for TLS point cloud data with low overlap density and uneven distribution.
The succeeding sections of this paper are arranged as follows. In chapter 1, we discuss relevant studies on point cloud registration. Section 2 presents the proposed registration method in detail, including the voxel grid establishment, keypoints extraction, base filter, and rapid search and verification method. Section 3 discusses the experiments evaluating the efficiency and accuracy of our proposed method. Finally, the discussion and conclusions of the study are presented in Section 4 and Section 5.
1.2. Reviews
Two types of registration methods have emerged: using feature points and without feature points. In this section, we review the description of features and the 4-point congruent set.
1.2.1. Keypoints and Feature Points
With smaller amounts of data, keypoints can better represent the whole information about an object. Keypoints have been widely applied in point cloud registration. The keypoints detection must be robust to rotation and noise, with unchanged resolution. Numerous keypoints extraction methods for point cloud data draw on two-dimensional image keypoints, such as the sift algorithm proposed by David Lowe [11,12]. This method uses a local feature description algorithm based on scale space and remains strong robustness. Lindeberg [13] extends a similar method in calculating the sift3D keypoints and provides the three-dimensional application of the sift operator. However, the viewpoint transformation angle of the point cloud data can change easily, and the density is uneven, resulting in unstable sift3D features.
Sipiran [14] draws on the Harris algorithm [9], Harris3D algorithm is proposed. In the point cloud data, the covariance matrix composed of the normal vector of the point cloud is used to replace the gradient change covariance matrix of the two-dimensional image. Intrinsic Shape Signature (ISS) [15] is a method that uses neighborhood information to find normal vectors to establish a local coordinate system and uses the relationship between eigenvalues to characterize the degree of point features. It satisfies the rotation invariance well and thus is used by many scholars. Similarly, Zai et al. [16] proposed adaptive covariance (ACOV) descriptor using principal component analysis, which has good robustness to noise. The normal aligned radial feature (NARF) [17] method uses the scanning attributes of the instrument to perform planar or spherical projections on the point cloud data to obtain image depths. The edges of the object area are determined by the scene edge (a sudden change in depth value). The object edge is then used as a reference to find the stable keypoints through the fractional transformation of the surface along the main direction.
Numerous studies have analyzed feature point descriptions and directly used feature descriptors to encode points of interest to match point clouds. Rusu proposed the persistent feature histograms (PFH) method in 2008 [18], which analyzes the difference in normal vectors near a point to capture the surrounding geometric information. The Fast point feature histograms (FPFH) [19] adjusted the PFH and improved the calculation efficiency. The Radius-Based Surface Descriptor (RSD) [20] fits the sphere using the normal vector of the surrounding keypoints to encode the descriptor, which also is effective. All the approaches mentioned use the normal vector, given that it can provide information around it. However, the normal vector can be computationally intensive and unstable at the corners. Dong Z et al. [21] proposed a binary shape context descriptor that can quickly and stably calculate three-dimensional feature points. In recent years, the feature point search method based on neural networks has also become popular [22,23,24]. For instance, PointNet [24] is a new deep learning model for processing point cloud data that has been used for a variety of cognitive tasks for point cloud data, such as classification semantic segmentation and target recognition. One drawback of PointNet is the inability to obtain local features, which makes it difficult to analyze complex scenarios. In PointNet++ [23], two main methods have been previously employed to improve the network and better extract local features. These methods work well, but the premise requires sufficient training data. The weakly supervised feature point detection method [25] and the unsupervised key point detection method [26] proposed by Lee et al. do not require manual labeling and ground-truth, and outstanding in terms of repeatability, distinctiveness, and computational efficiency.
Here we propose a fast keypoints detection method based on a voxel grid. The original data are unevenly distributed and have noise, and the data needs to be preprocessed. Our strategy to handle it is to grid the point cloud voxels. We assign a density value to each voxel grid according to the distribution of the number of points in the grid to normalize (unitize) the data and reduce the influence of noise and outliers. Then directly establish the Hessian matrix according to the gradient of the voxel grid density value transformation and quickly calculate the key points through the Hessian matrix, which avoids the time-consuming operation of calculating the normal vector.
1.2.2. Four-Point Congruent Sets and Related Methods
In recent years, the registration method without feature points, which uses mathematical rules to identify corresponding pairs from different clouds, has become a research hotspot. Point cloud registration requires only three sets of corresponding point pairs to calculate the transformation matrix and complete the registration. Mach proposed the Random sample consensus (RANSAC) method [27] to find three corresponding points in two point clouds and then calculate the transformation matrix based on three corresponding points. However, finding the three-point correspondence set can be difficult due to the presence of noise, and the method requires large amounts of calculations.
The 4-point congruent set (4PCS) [28] method modified the RANSAC and increased the correspondence set requirement to four points, resulting in increased robustness and less computational complexity of the cube, namely the square level. Mellado [29] proposed an intelligent search method based on this (i.e., Super4PCS method), optimizing the time complexity from square to linear. Both the 4PCS and Super4PCS use four points on the plane, which can result in wrong alignments for buildings with repeated structures and unsatisfactory registration effect. Similar findings were reported, and potential solutions were provided in [30,31,32]. For instance, two generalized 4PCS algorithms, i.e., G-4PCS and G-Super4PCS, were introduced in [30,31], where the authors exploited the richer geometry of 3-D data and generalized the four-point base by removing the planarity constraint. Zhang et al. [33] extended the G-Super4PCS method to the registration of photogrammetric and TLS point clouds in geology applications, where the scale difference between the two sources of point clouds was considered. Theiler [34,35,36] found that 4PCS is not well suited to TLS point clouds with large data volume and proposed the Keypoints-4PCS(K4PCS) that uses fewer keypoints to represent objects. Other 4-point congruent set methods have also been developed based on semantic keypoints [37]. In the past two years, numerous approaches have been developed, combining feature points with 4-point consistent set methods, such as the MSSF-4PCS [38] and A4PCS [39] methods. In addition, some scholars have used RANSAC to change the registration elements. For example, B Yang et al. [40] constructed a triangle using the intersection point of line features and carried out registration using the triangle concordant relation. Yusheng Xu et al. [41] used planar uniform sets for registration.
The above-mentioned methods have good performance in some respects. These methods are based on the mathematical ideas of RANSAC. The above methods have done a lot of research on speeding up the base query and reducing the number of candidate sets, but the experiment shows that the most time-consuming is the verification phase. In the 4PCS and Super4PCS source code, this step takes up 80–90% of the overall time. At this stage, it is necessary to find the largest common point-set (LCP) to judge whether the transformation matrix is optimal. Finding the largest common point-set is a research problem itself. We made improvements in three aspects, respectively: extracting key points, filtering out excellent bases, and improving the query method of finding the largest common point-set to effectively improve the registration efficiency.
1.3. Our Works
Although the existing methods have shortened running time and improved registration accuracy, the registration results are not satisfactory in particular cases. When the overlap rate of scanned data from two stations is not high, or the outliers are relatively large, finding the corresponding common subset can be difficult. Thus, the computational complexity becomes relatively high. In the 4-point congruent set framework, verification is mostly time-consuming. This means that reducing the times of verifications as well as time consumed by a single verification is very important. When Super4PCS is used for scenes with repeated structures or symmetrical structures such as buildings, it is easy to encounter registration misalignment, leading to low registration success rates. In response to these problems, we propose a method based on a point cloud voxel grid.
The main contributions of this paper are as follows:
1. Establish a grid for the data, and assign density values to the grid by Gaussian weighting according to the distribution of points in the grid to eliminate the adverse effects of uneven data density and noise on the registration. The keypoints are quickly calculated through the transformation gradient of the grid density value, which reduces the amount of calculation and improves the registration efficiency.
2. When the quaternion base is on the same surface, more candidate sets are generated, and thus it is easier to mismatch synthetic scenes such as buildings. To solve this problem, the four-tuple bases are selected, and the four-tuple bases on the surface of the same object are filtered out to improve the robustness of the algorithm.
3. In evaluating the candidate congruent set, we improved the determination of LCP and optimized the point search using the voxel grid random query instead of the KD-Tree search. The overall time efficiency increased by 70% compared to the original Super4PCS.
2. Materials and Methods
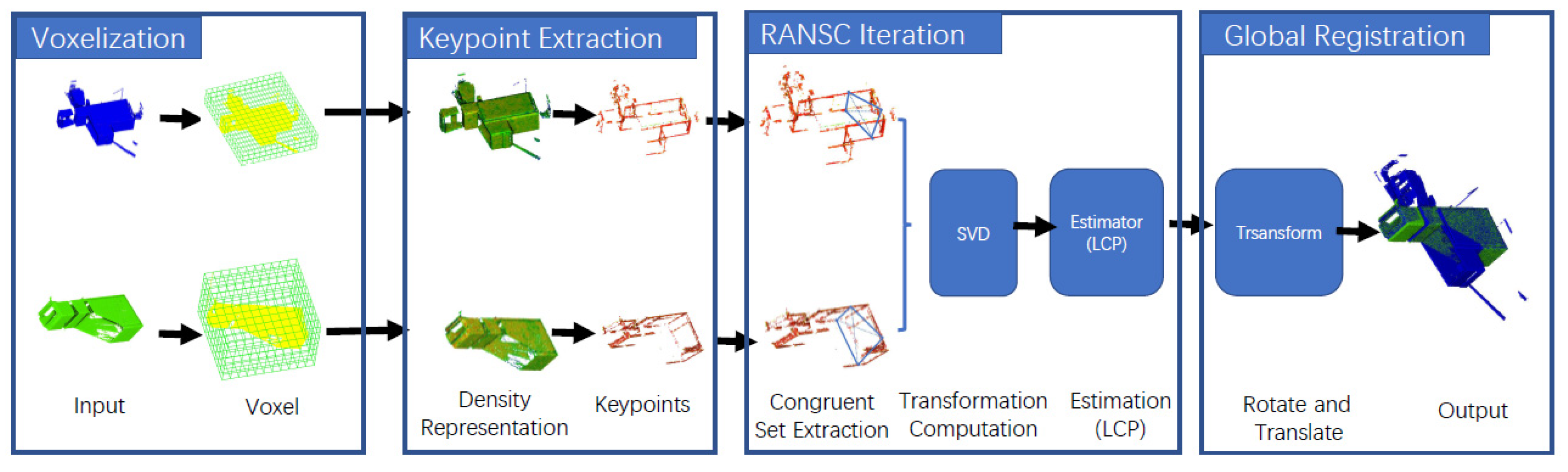
Our method follows the same framework as the 4PCS. It includes four core steps: point cloud voxelization, feature point generation, base extraction, and candidate congruent set extraction verification. First, the point cloud is voxelized into a three-dimensional grid structure, and the voxel grid is indexed. A density value is given to each voxel grid using the Gaussian function based on the density distribution of surrounding points. By calculating the second-order partial derivative of the voxel grid, the Hessian matrix of the density transformation gradient can then be obtained. Inspired by the Harris keypoints detection method [9], the keypoints are calculated and optimized using the Hessian matrix eigenvalues. The RANSAC-based strategy is adopted to find the quadruple base in the target point cloud according to the overlap rate and the size of the point cloud range. The point cloud is used to quickly query and filter out the quadruple bases on the surface of the same object (such as walls). Finally, the corresponding quaternion candidate set is determined by matching the affine transformation ratio, and the candidate transformation matrix is calculated by Singular Value Decomposition (SVD) decomposition for each candidate quaternion. We use our own voxel grid index structure to find the LCP method, evaluate the correctness of the corresponding candidate transformation matrix, and obtain the optimal transformation from the candidate transformation matrix. The parameter is employed to register the point clouds using two steps of rotation and translation. Figure 1 illustrates the process and summarizes the core steps and results involved.
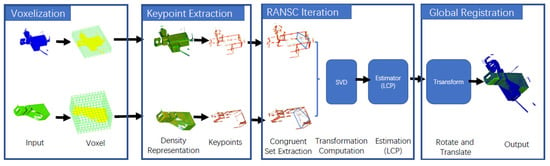
Figure 1.
Workflow of the proposed registration method.
2.1. Voxelization and Indexing Structure Generation
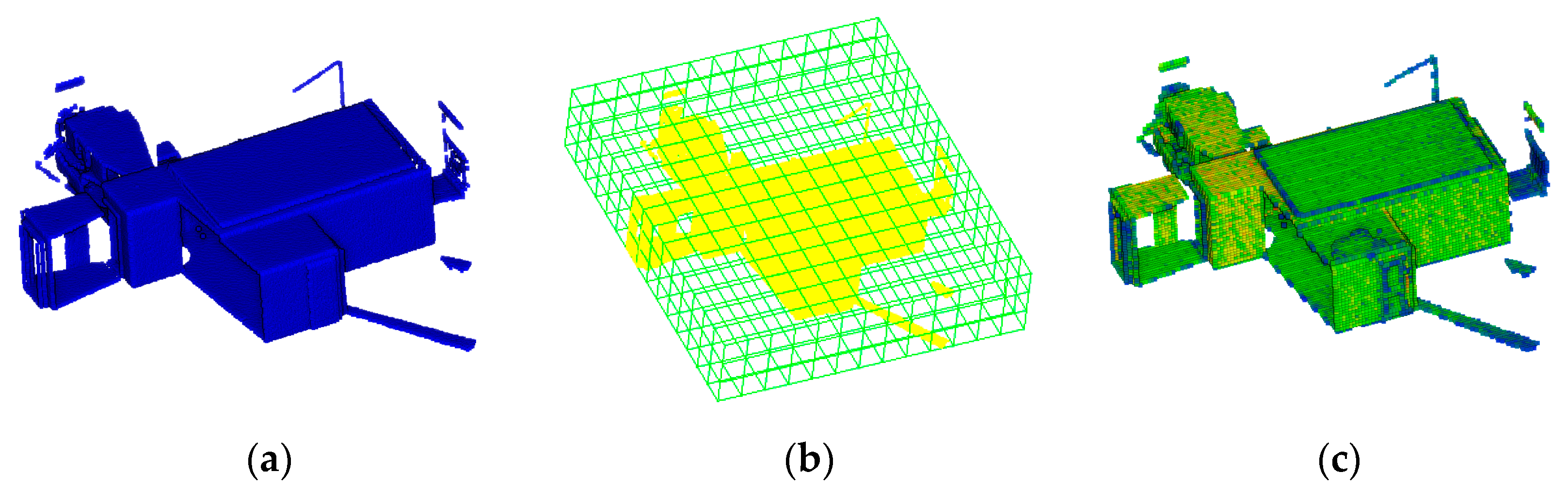
Since the TLS data have uneven density distribution and large data volume, its direct usage has very low registration efficiency, and the registration success rate is low. Generally, data preprocessing is performed before registration. The first step for these raw data is the establishment of a voxel grid. The point cloud is traversed to find the minimum (minX, MinY, minZ) and maximum (maxX, maxY, maxZ) point values in the X, Y, and Z directions. Given the voxel grid size (VoxelSize), the voxel grid can then be generated. As shown in Figure 2b, a voxel grid of is obtained, where is the rounding operation. The point cloud is traversed again to calculate the voxel grid coordinates for each point, which can be obtained using the following equation:
where is the i-th point in the point cloud. All indexes belonging to the voxel grid are saved so that the voxel grid can quickly find the points it contains. Since the voxel grid is a three-dimensional array, we can quickly determine whether the voxel grid contains points, and the time complexity is . Due to the uneven data distribution, we use the voxel grid to perform a normalization process on the data, and each voxel grid takes one point as the calculation point.
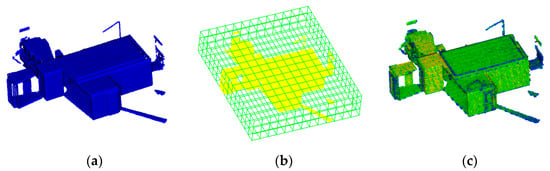
Figure 2.
Point cloud voxelization and voxel grid assignment. (a) Original point cloud; (b) Voxelization of point cloud; (c) Voxel grid with density values.
2.2. Keypoint Extraction
Keypoint detection combines the high accuracy of the registration method with feature elements and the fast registration time from the registration technique without feature elements. On the one hand, the extracted feature points retain the regular characteristics of the point cloud distribution and have good feature representation. On the other hand, it significantly reduces the number of point clouds and minimizes redundancy in the 4-point congruent set. It also limits time consumption of the 4PCS algorithm and improves feature representation of the 4-point congruent set, therefore improving registration accuracy.
2.2.1. Assign Voxel Grid Density Value by Point Distribution
Many point cloud keypoints feature point detection methods have been developed in the past two decades, and most use normal vector calculations. Normals contain local point cloud information, and their usage has multiple advantages. However, normals of areas with sudden change rates (such as wall corners and edges) and point cloud edges (occlusion edges) can be very unstable. In addition, normal calculations can be extremely time-consuming.
In the proposed framework, a density value is assigned using the number of points in each voxel grid to correspond to the gray value of the image. If the number of points in a single voxel grid is changed into a density value, the voxel grid formed by these small cubes is shown to be non-rotation-invariant, and a sawtooth effect is produced. To overcome this phenomenon, a Gaussian blur operation is performed to eliminate aliasing and smoothen the data. The following equations are used to calculate the density value of Gaussian filtering:
where i, j, and k are the neighborhood range of the current grid (the value range is i,j,k {−3, −2, −1, 0, 1, 2, 3}); n is the number of original points contained in the current grid; is the density-weighted value based on the positional relationship between the original point and the grid center; is the three-dimensional coordinate information of the current calculation point in the original point cloud; and is the current grid center. These equations can be used to calculate the 343 (7*7*7) field grid of the current grid.
If the number of original points in the grid is used in computing the density, many original point position information may be lost. To avoid the loss of the original characteristics, the weighting method can be used. Points far from the grid center contribute less to the density value, while closer points contribute more. The use of weights effectively solves the problem of grid aliasing, as shown in Figure 2b.
2.2.2. Keypoints Detection by Density Gradient
Based on the traditional Harris feature point extraction algorithm, the sudden change in density value is used as reference for the corner point measurement. Using the weighted density voxel grid, the Hessian matrix of the voxel grid point density value is expressed as:
In the formula, are the partial derivatives of the grid point density values in the x, y, and z directions, The resulting graph of the first derivative is shown in Figure 3b, respectively, and are the second-order partial derivatives. Since the density grid is continuous when constructed, the forward difference quotient (Equations (5) and (6)) can be obtained in the form of the definition formula of the derivative when calculating the partial derivative:
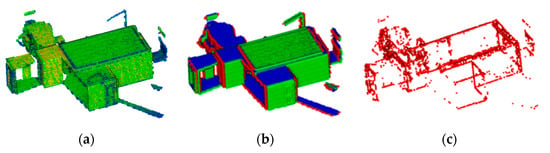
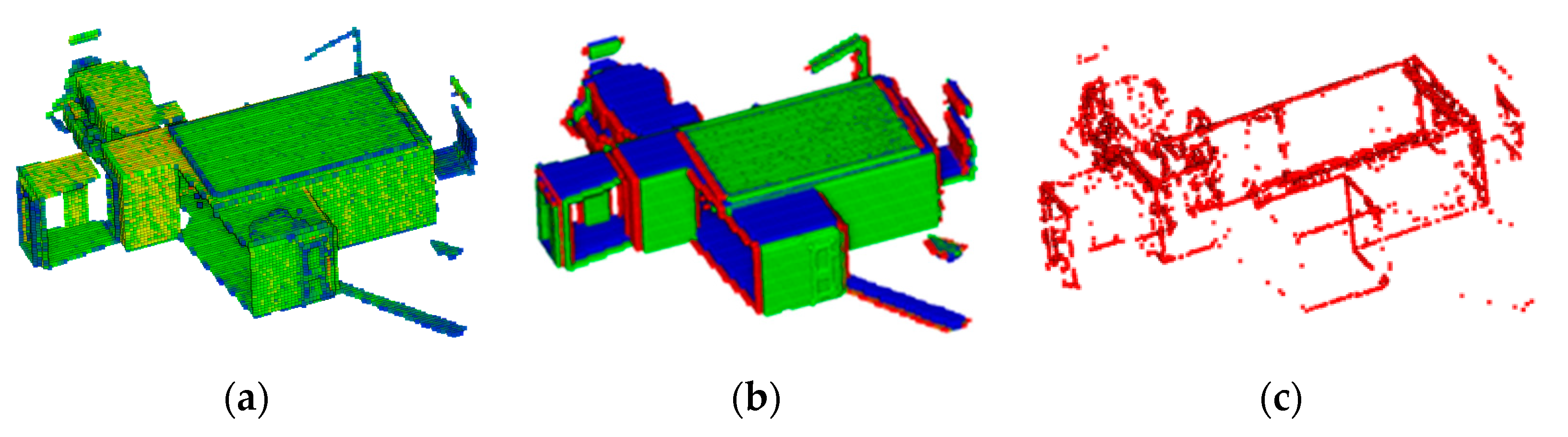
Figure 3.
Keypoints detection. (a) Voxel grid with density values; (b) First derivative of density value; (c) is the Keypoints.
To avoid large errors from the selection of on the overall result, the weighted five-point difference quotient is used to replace the two-point method forward difference quotient method in Equations (7) and (8). The weighted difference values of adjacent points are used in the following equations to generate a more accurate approximation:
If the value of each element in is obtained, the density covariance matrix M of each grid point can be calculated. The corner point value of each grid point can then be calculated using the formula:
where is the determinant of the matrix ; is the direct trace of the matrix ; α is an empirical constant with a value range of 0.04~0.06. Based on the input thresholds, when > threshold, the current point can be judged as a feature point.
2.2.3. Keypoints Location Optimization
For discretely distributed data points, the maximum value detected may not be the true maximum value for the discrete data point fitting equation. The selection of the Harris feature points is determined based on the calculated (in Equation (9)) and the threshold value of the corner point. The larger the value , the better the characteristic representativeness of the point. Specific points are more suited to represent the local characteristics, depending on whether the corner point can approach the actual maximum value in the functional relationship of the local fitting. Here, we adopt the two-step method, and the Taylor expansion formula of point in the neighborhood of () is expressed as:
where is the angle value at the grid point . The first-order derivative vector and the second-order partial derivative matrix of the density grid have been obtained in the previous stage and can be used directly in this process. If is an extreme point, has the maximum value. The derivative of Equation (10) can be obtained again. When the derivative is exactly 0, can be obtained as:
such that is the new coordinate point. Bringing Formula (9) back to Formula (7), the new value of the Harris corner at this updated coordinate point can then be obtained. In the entire iterative process, after each calculation of , should be calculated. When the value of any element of is greater than 0.5 grid units, it means that the maximum value point is closer to the neighboring grid. Position optimization is performed on the neighbor grid. is replaced with to continue the iteration process until the difference of obtained at the interval of two times is less than the given threshold, or the number of iterations reaches the upper limit (usually set to 5 times). When the value of becomes less than the corner point threshold, the iteration stops, and the nearest result is returned.
2.3. Voxel-Based 4-Point Congruent Sets
2.3.1. Base for Voxel Grid Filter
In the building’s TLS point cloud data, when looking for the base in P, the point cloud will be misregistered if the four coplanar points are set on the surface of an object. The voxel grid can be used to filter and find the coplanar 4-point-set base (a, b, c, d). First, calculate the triangle formed by points a, b, and c. For segments ab, bc, and bc, the decimal points in the line segments are taken. Query the voxel grid for each equally divided point to determine whether there is a point cloud around the point. A value of 1 means there is a point cloud and 0 for no point cloud. This means that there is a 10-dimensional code for the line segments between the points. The following is an example for the line segment ab:
where A is the three-dimensional coordinates of point a, B is the three-dimensional coordinates of point b, and is the three-dimensional coordinates of the i-th bisecting point. The bisecting points can then be calculated:
The code is obtained for line segment ab. If , , in base (a, b, c, d) are greater than 8, the base can be considered to lie on a plane. This procedure can effectively filter out the coplanar 4-point-set of non-identical object planes, therefore improving efficiency and reducing the number of calculations.
2.3.2. Voxel Grid Improved LCP Search
After more than ten years of development, significant improvements and modifications have been proposed on the 4PCS framework, such as the K4PCS and Super4PCS. Most of the improvements have focused on reducing the number of calculations by improving the search speed of candidate point pairs, increasing constraints, and reducing the number of candidate sets. In our experiments, we found that the most time-consuming procedure in the entire framework is finding the LCP, which accounts for 80% to 90% of the overall time.
In the previous method, the KD-Tree or OctoTree index relationship is established for the point cloud P. Using the correspondence between the candidate set and the base, the rotation matrix T is calculated, and the rotation is applied to the point cloud Q. For each point in the rotated point cloud Q, determine whether point cloud P exists in the range δ near the query point. If there is a midpoint P within the range δ near the query point, consider the point as a “goodPoint”. Using the ratio of goodPoint in Q, find the highest score (the one with the most goodPoint) in the candidate sets. The complexity of finding the largest common subset of a candidate set is calculated using where N is the number of points in the Q point cloud, M is the number of points in the point cloud P, and log(M) is the query time. Here, part of the computational memory space is sacrificed, and the query raster index can complete the query at complexity. The LCP can then be calculated using the formula:
where Nq is the number of points in the target point cloud, and is a single-point query (as defined in Equation (13)).
3. Results
3.1. Experimental Data Sets
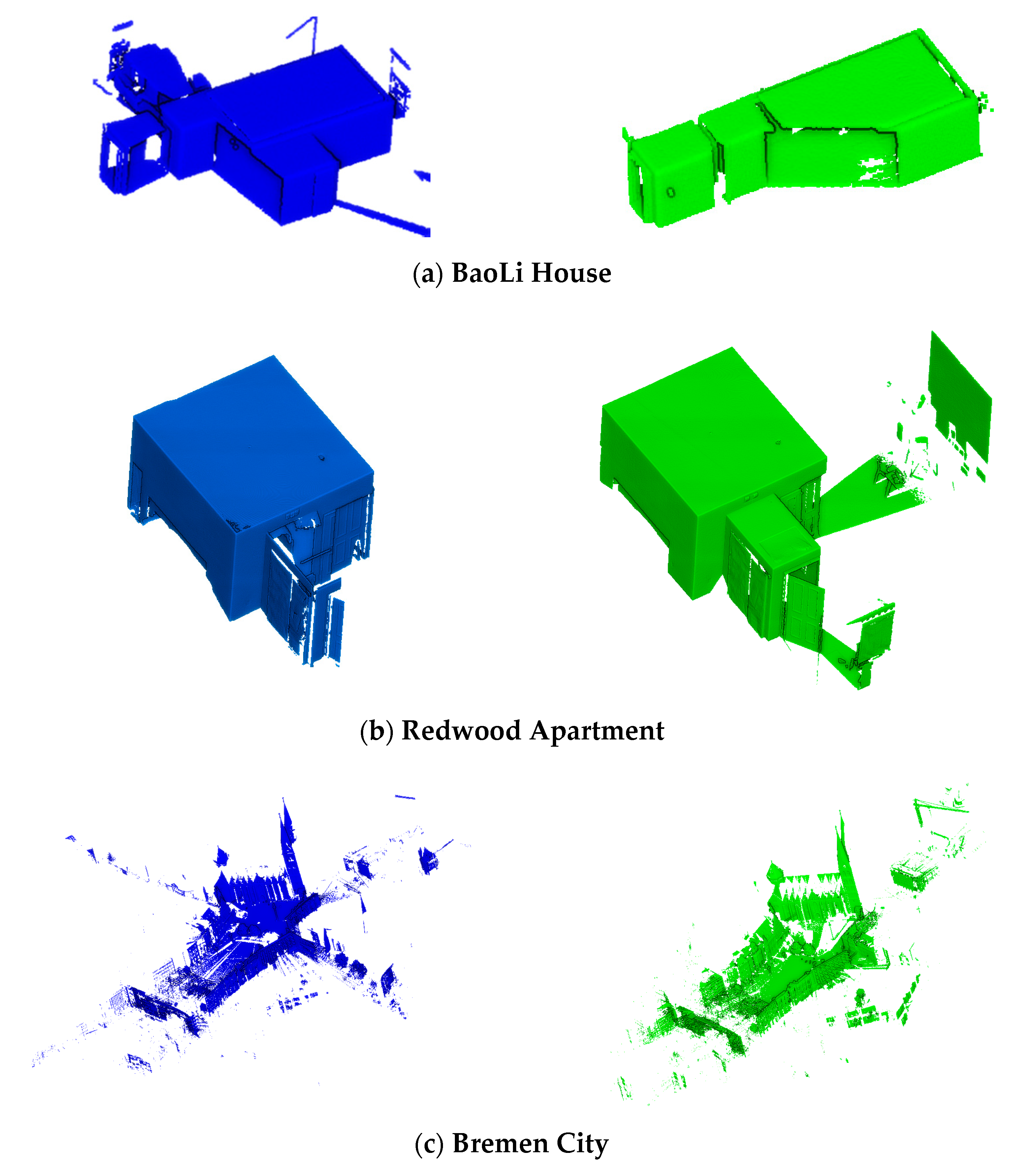
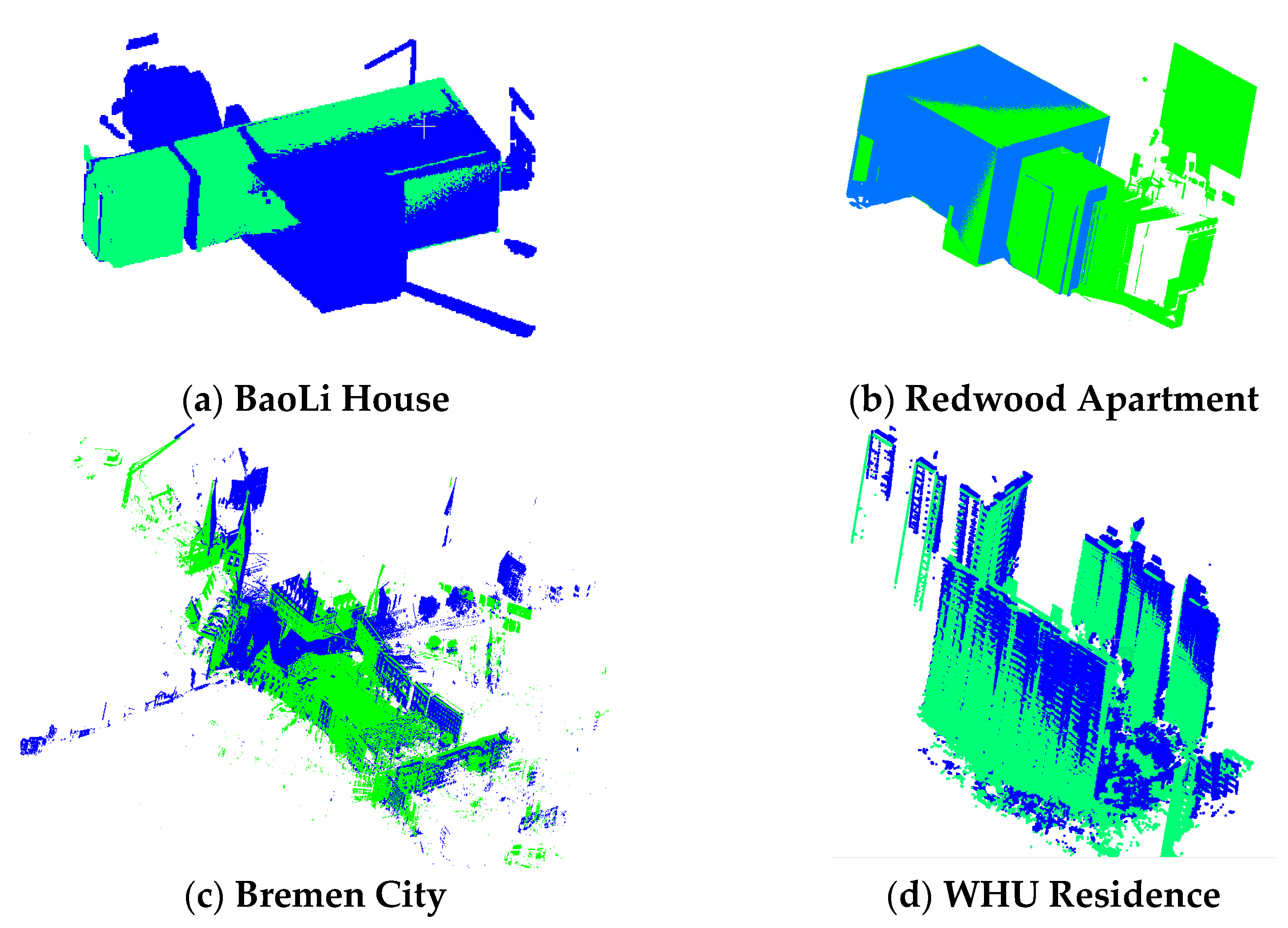
The proposed method was evaluated using different scanning instruments and TLS point clouds in different scenarios. Four data sets were analyzed, comprised of two indoor and two outdoor data. The first data are the indoor point cloud of BaoLi Commercial Housing collected by Faro Foucus3D X130. The second data were obtained from the Redwood open data set [42], which was collected using the Faro Focus 3D X330 HDR Scanner. The third data set is from Jacob University [43]. This data set was recorded using a Riegl VZ400 Scanner in the City Center of Bremen. The last data set was from the open data set of Wuhan University [44], which was collected with Leica P40 Scanner (Hereinafter referred to as WHU Residence). For two indoor data, the subsampling operation with the minimum point spacing of 0.005 was carried out; for two outdoor data, the subsampling operation with the minimum point spacing of 0.04 was adopted. We then generated the root mean square error (RMSE), as defined in Equation (17). Table 1 lists the details of the data set scenarios used in the experiments. Figure 4 is the visualization of the data.

Table 1.
Information of experimental data set (the RMSE computed on 50,000 points).
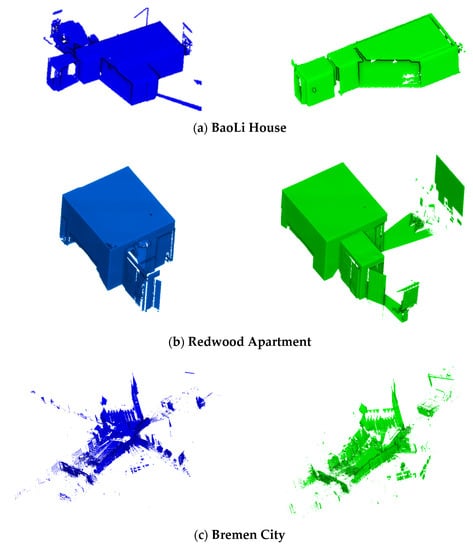

Figure 4.
Experimental data. (a,b) are indoor point cloud data; (c,d) are outdoor data. The blue is the source data, and the green is the target data.
3.2. Evaluation Metric
We mainly evaluate the keypoints extraction and registration results. All experiments were performed on a 64-bit Windows 10 mobile workstation, 8 GB RAM, and Intel (R) Core (TM) i7-9750H @2.6 GHz CPU.
3.2.1. Evaluation Metric of Keypoints Extraction
Our evaluation criteria for keypoint extraction comprise two aspects: repeatability and efficiency. Repeatability refers to the ability of a detector to detect keypoints in the same locations. This is the most important metric for a critical point detector [26].
- (1)
- Repeatability:Given point clouds of the same scene with a different viewpoint, there is a known transformation matrix between the data of the two point clouds. A keypoint detector detects a set of keypoints and from , respectively. A keypoint is repeatable if the distance between and its nearest neighbor is less than the threshold . For the value of in the experiment, we use 0.1 m for indoor data (BaoLi House and Redwood Apartment) and 0.2 m for outdoor data (Bremen City and WHU Residence). The formula for repeatable judgment of keypoint is:The formula for calculating the Repeatability is:where is the number of keypoints in point cloud .
- (2)
- Efficiency:After defining some parameters, we averaged 50 experimental running times of keypoints detection.
3.2.2. Evaluation Metric of Registration
The registration effect is evaluated using the reference registration results. The reference registration is achieved through manual calibration and then refined using standard ICP. Our evaluation criteria for registration performance comprise three aspects: time, registration accuracy rate, and success rate. These features have been adopted in similar studies (Theiler et al., 2014, [35]; Dong et al., 2018, [21]). Time performance is related to efficiency, including the time cost of the entire workflow. For the experiments, the execution times using the Super4PCS method and our method were recorded for each scan.
- (1)
- Registration Accuracy:The root mean square error (RMSE) between the reference registration results of the converted input set was used in evaluating the registration accuracy:where n is the number of points in the point cloud; the i-th point coordinate in the source point cloud S after transformation; and is the i-th point coordinate in the reference registration point cloud.
- (2)
- Success rate:Based on the root mean error, the registration success rate (RS) can be directly calculated using the formula:The RMSE threshold can be set according to the application requirements. The formula for calculating the successful registration rate (SRR) is:where is the number of successful registrations, and N is the number of experiments. Since our method involves the RANSAC process, SRR is evaluated in a series of 50 trials.
- (3)
- Computational Efficiency:The calculation efficiency is evaluated using the average total running time Tt of the entire process. Take the average of 500 experimental data for the overall coarse registration.
3.3. Keypoints Extraction
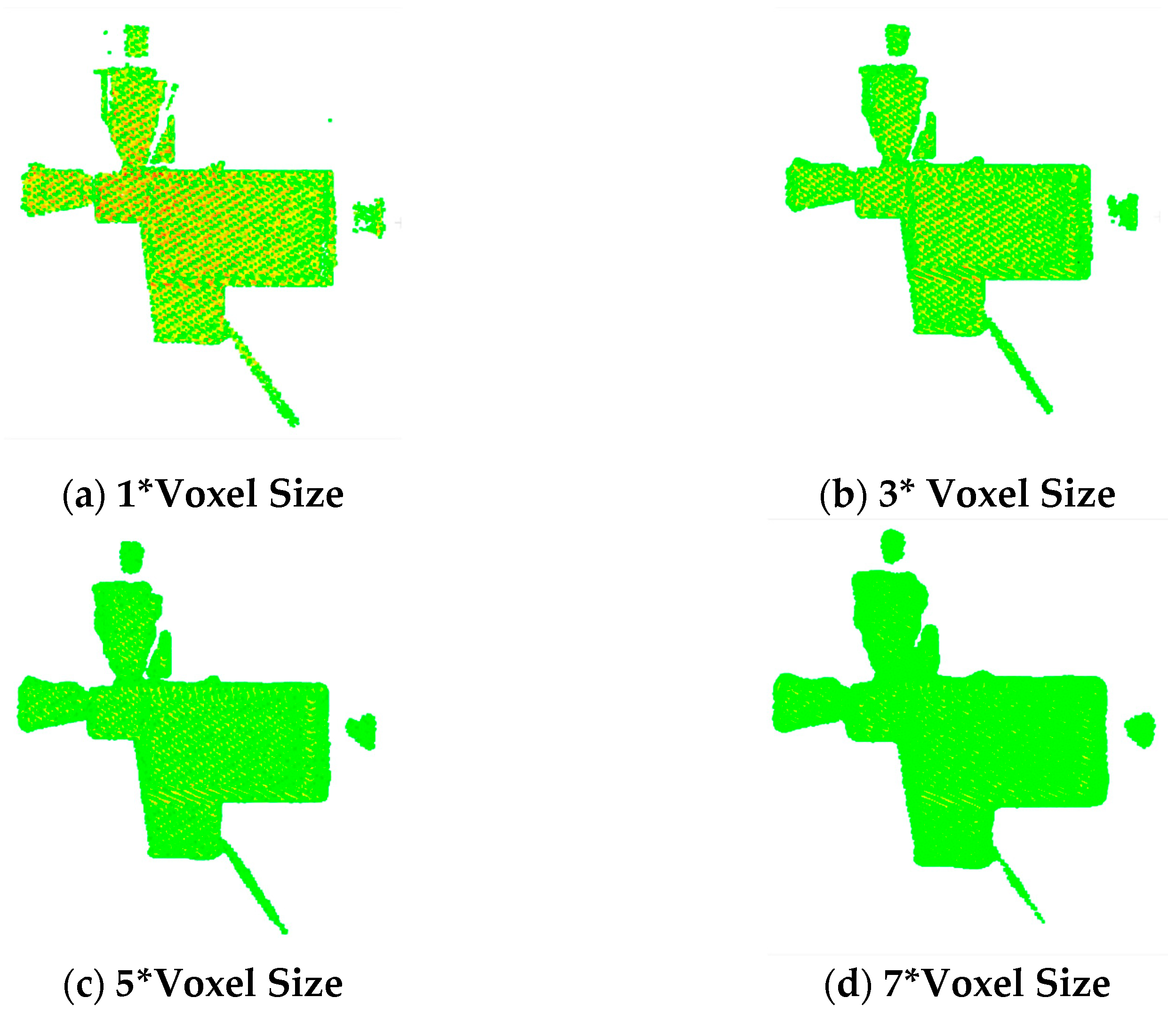
Fifty experiments were performed on each data set, and the final results were averaged as presented in Table 2. For the one object data, the larger the voxel, the smaller the voxel grid generated by the data, resulting in fewer keypoints in the final extraction. The increase of the voxel grid will lead to a decrease in repeatability because larger voxel grids increase the difficulty of location optimization, and a small number of point optimization locations also deviate. At the same time, the larger the voxel grid, the greater the time requirement since the Gaussian operation involves more points when density values are assigned to the grid.

Table 2.
Keypoint extraction under different voxel grids (repeatability defined in Section 3.2.1).
As shown in Figure 5, when the density value is assigned to the voxel grid, an excessively small radius is selected to calculate the density value of the voxel grid, which will lead to a sawtooth effect on the voxel mesh density values, resulting in a decrease in the quality of key points, therefore reducing the success rate of registration. However, too large a calculation radius will lead to an increase in time consumption, making the detection efficiency of key points low. Finally, after comprehensive consideration, the calculation radius of the field is set as three times the size of the voxel, which effectively solves the sawtooth effect caused by the voxel mesh and has high computational efficiency.
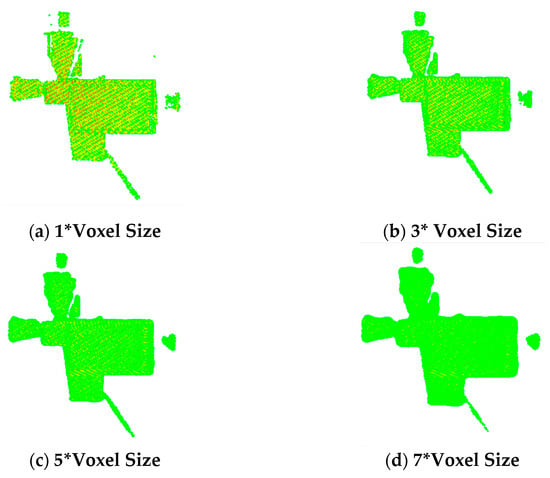
Figure 5.
Density values at different radius are calculated. The sawtooth effect occurs when the radius is small. Time consumption increases when the radius is too large. (The example is BaoLi House).
3.4. Keypoints Comparison
The keypoints extraction method in this paper is compared with other traditional keypoints extraction methods (such as SIFT3D, HARRIS3D, ISS). We debugged different parameters of the mainstream keypoints extraction methods, resulting in having acceptable experimental parameters in terms of time and keypoints quality. In consideration of calculation time and repeatability, different voxel grid sizes were used for indoor and outdoor data to participate in subsequent calculation and analysis. The results of the voxel grid size of 0.2 m were adopted for indoor data and 0.5 m for outdoor data. This is because the outdoor data scene is large, with a high number of points and plenty of noise.
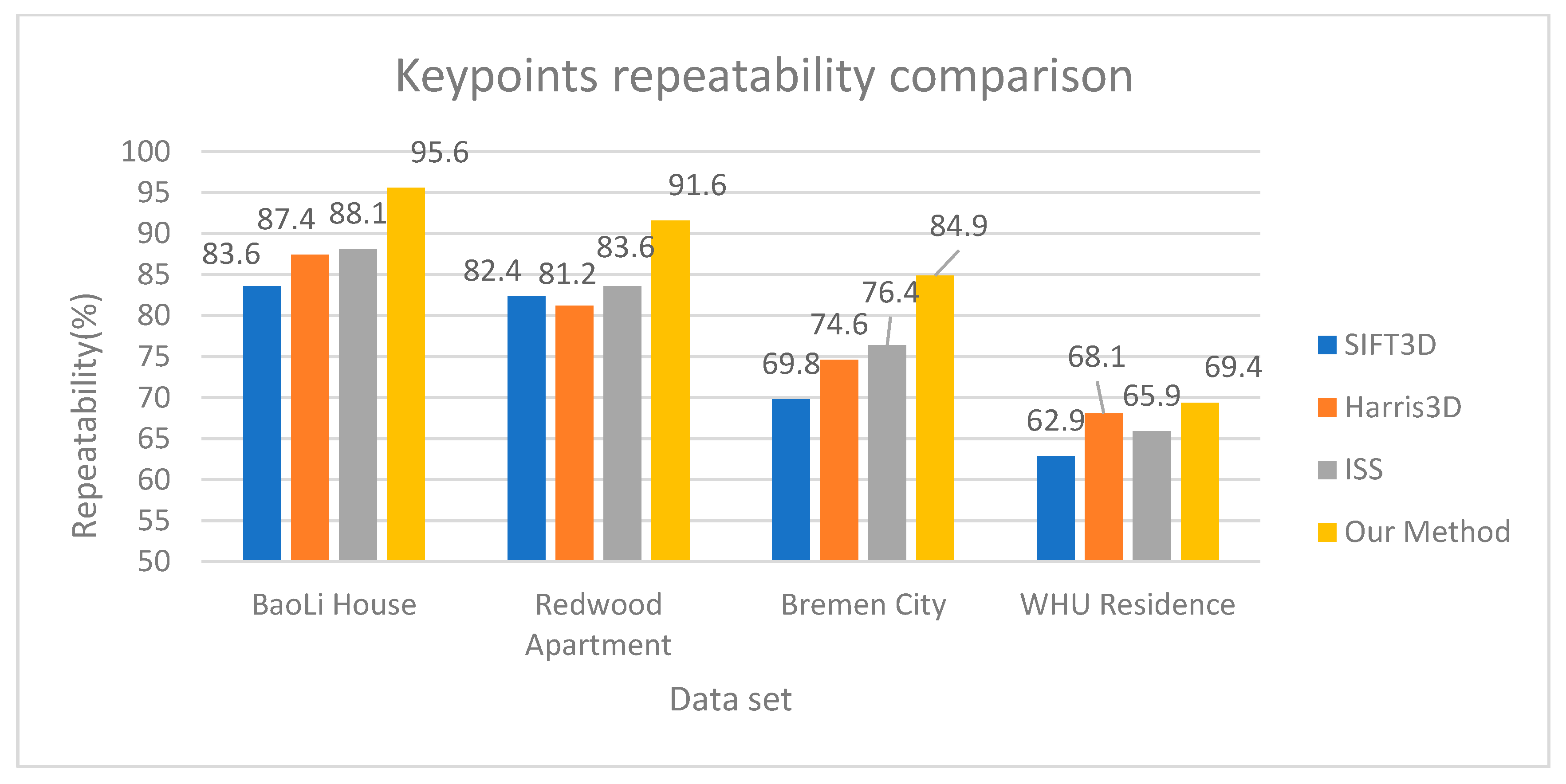
Figure 6 shows the results of the keypoints repeatability comparison. On the whole, the repeatability of indoor point cloud data is higher than that of outdoor data because there is more noise in outdoor data. For indoor data, because the building has sharp edges and corners, there is a huge change in density, so our method can stably detect the corners. Since the density value is generated by Gaussian weighting according to the distribution of points, the influence of noise can be effectively reduced. Therefore, the repeatability of the method in this paper is also better than that of the contrast method in outdoor data.
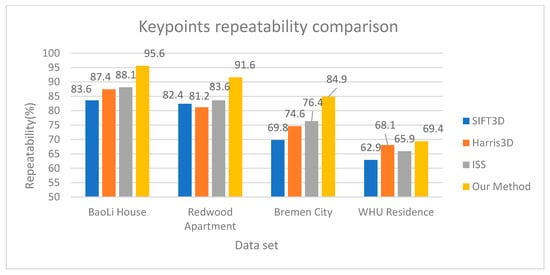
Figure 6.
Keypoints repeatability comparison. For the parameters of our method, the voxel grid size of indoor data (BaoLi House and Redwood Apartment) is 0.2 m, and that of outdoor data (Bremen City and WHU Residence) is 0.5 m.
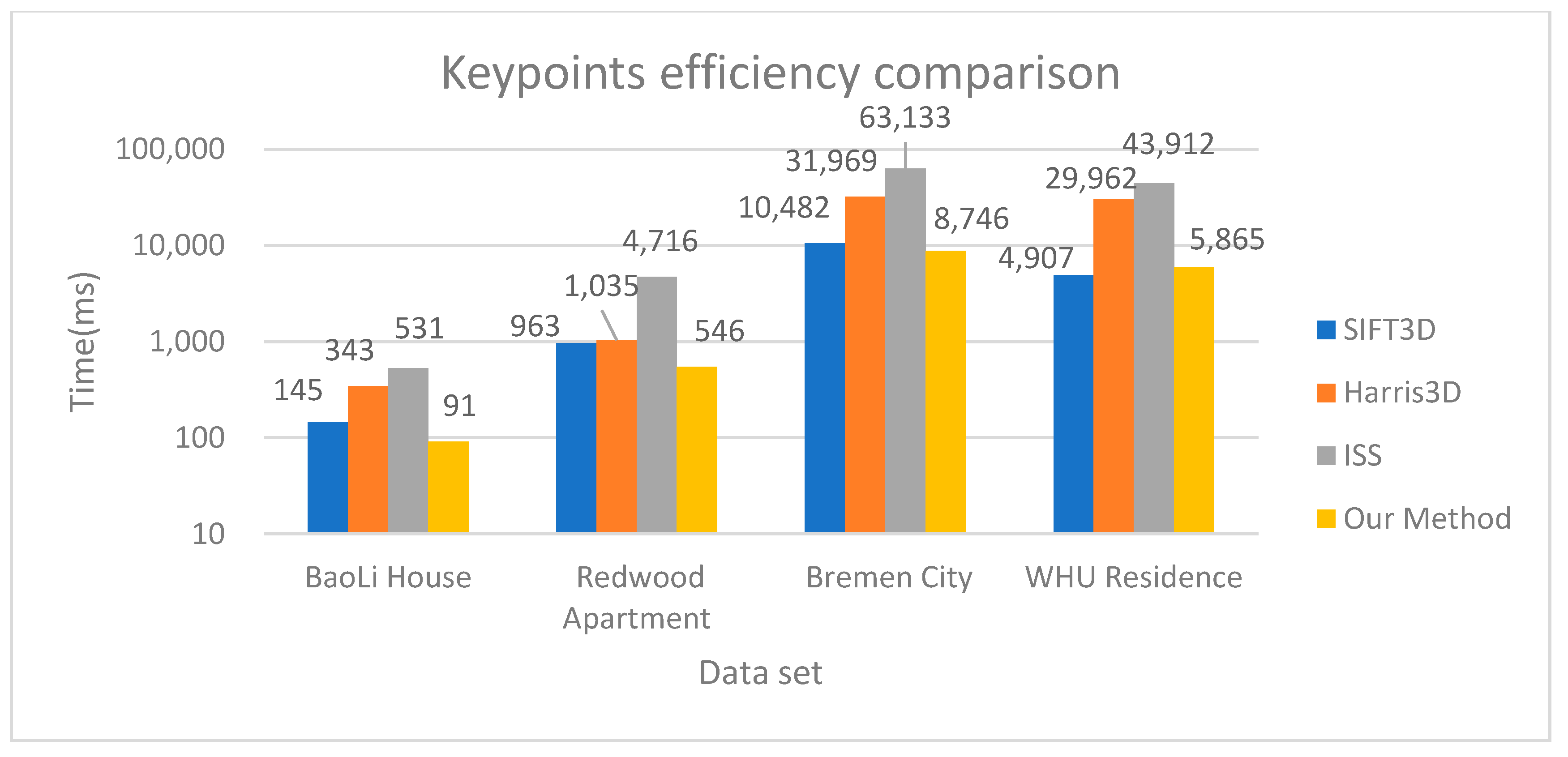
Figure 7 shows the results of the comparison of detection efficiency of keypoints. The method presented in this paper and the SIFT3D method have good efficiency. Harris3D needs to calculate the normal vector and construct the covariance matrix, while ISS needs to carry out the principal component analysis. All these steps have a significant time overhead. In WHU Residence indoor data, the efficiency of the proposed method is lower than that of the SIFT3D method, but the efficiency of the proposed method is the highest among the other three data. The results show that our method yielded good performance in keypoints quality and time efficiency.
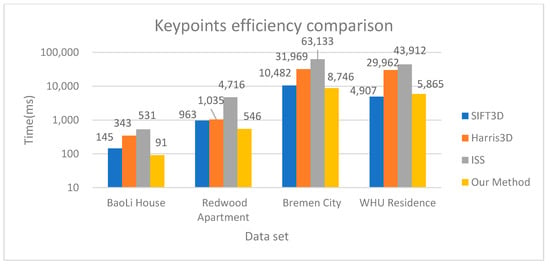
Figure 7.
Keypoints efficiency comparison. For the parameters of our method, the voxel grid size of indoor data (BaoLi House and Redwood Apartment) is 0.2 m, and that of outdoor data (Bremen City and WHU Residence) is 0.5 m. Notice that the y-coordinate is on a logarithmic scale.
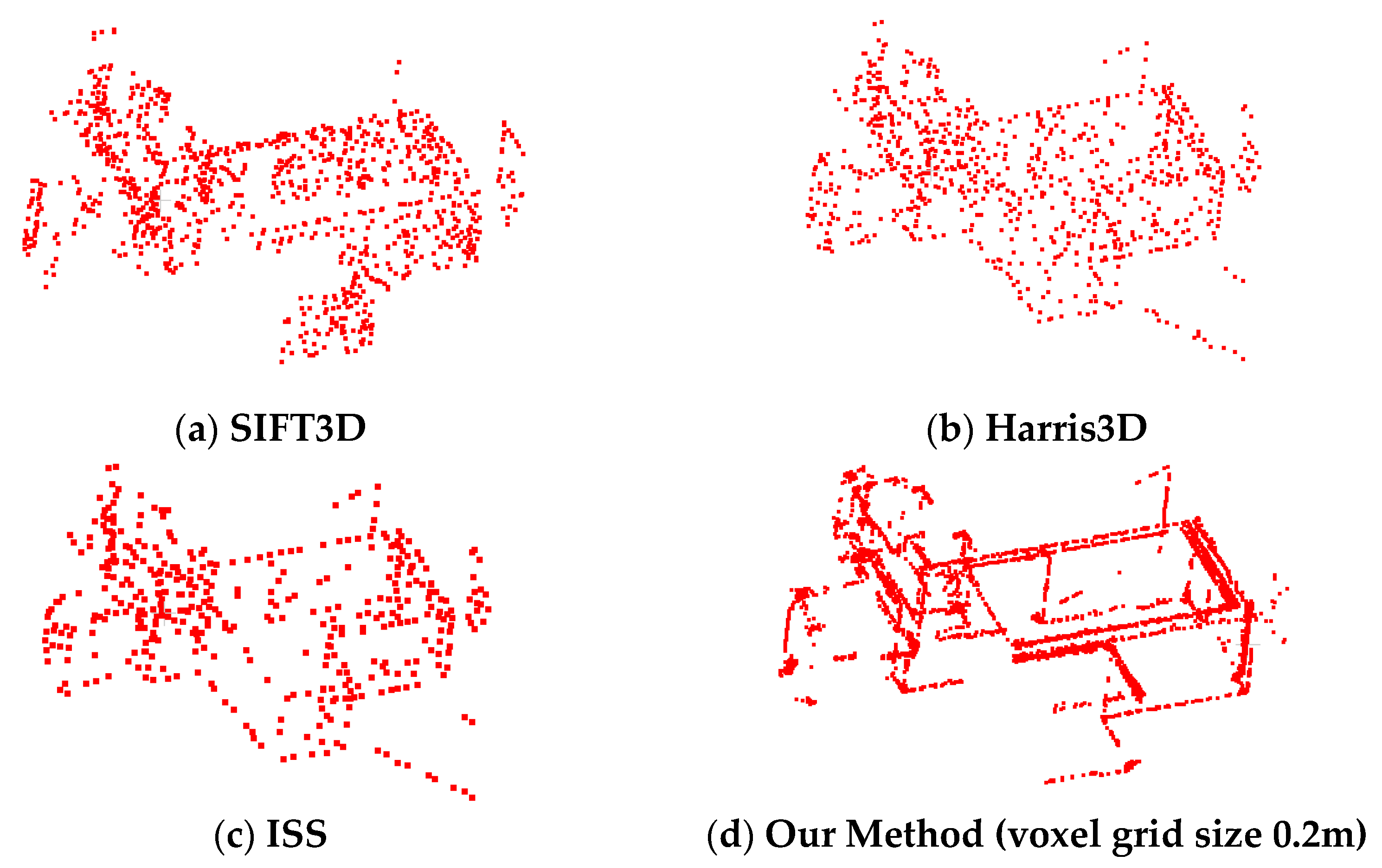
Figure 8 shows the keypoints visualization results. The example is BaoLi House source data. As mentioned above, we also adopted a voxel grid size of 0.2 m. As shown in Figure 5a, the keypoints generated by the SIFT3D method are messy, evenly distributed over the entire data, and have many redundancy problems. In Figure 5b, the traditional Harris3D method yielded missing edge features and lacked representativeness. In Figure 5c, the ISS keypoints extraction had good results but used large amounts of calculations such that its time requirement far exceeded that of our proposed approach. Figure 5d shows the results of our proposed keypoints detection. Our proposed approach yielded high-quality keypoints at the corner edges, and the feature point distribution is highly representative.
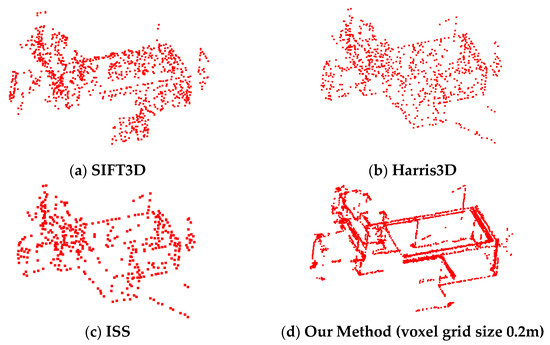
Figure 8.
Keypoints. (a) SIFT3D method; (b) Harris3D method; (c) ISS method; (d) Our method (voxel grid size 0.2 m).
3.5. Registraion Time Performance
To test the overall efficiency, we evaluated the time performance of registration for different scan data. Table 3 provides the summary of the registration time for different voxel sizes and data set. For indoor data, the speed of keypoints detection is fast. The main determinant of time consumption is the candidate set verification process. For scenes with larger voxel grids, the number of keypoints generated is comparatively less, which means fewer candidate sets used in the calculations and less time required. For outdoor data, when the voxel grid is small, the extraction time of keypoints is relatively small, but a large number of keypoints are generated, leading to heavy workload and high time consumption in post-sequence registration calculation. As stated in Section 3.1, when the voxel grid is large, the calculation time of key points increases, and the overall time consumption is high.

Table 3.
Time performance under different voxel grids.
3.6. Registration Accuracy
As shown in Figure 9, the registration results of the proposed approach on the four data set were able to achieve satisfactory results. Table 4 summarizes the quantitative evaluation results for the different voxel sizes. The RMSE threshold was given five times the value of the reference RMSE. The general results suggest, when the voxel size is small, the number of keypoints generated is large, and the registration success rate is high. For larger voxel grids, the number of keypoints generated is smaller, the required optimization cost is higher, and the quality of the keypoints obtained is comparatively lower, resulting in significantly reduced registration rates. For the same object point cloud, there is no obvious rule of RMSE with the change of different voxel mesh size.
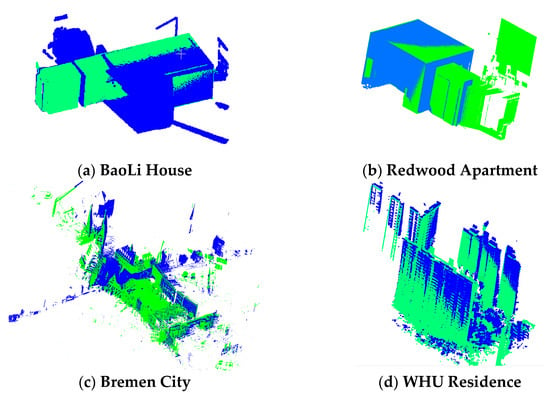
Figure 9.
Coarse registration results. For indoor data (BaoLi House and Redwood Apartment), the voxel grid size is 0.2 m, while for outdoor data (Bremen City and WHU Residence), the voxel grid size is 0.5 m.

Table 4.
Quantitative evaluation of the registration accuracy.
For each data pair, 500 experiments were performed. The BaoLi indoor data had minimal noise points. The registration effect was relatively good, with the highest registration rate at 95.0%. For the Redwood Apartment indoor data, the data overlap rate is high, but there are repeated folding structures of curtains in the data, as well as shielding of some objects, so the registration success rate is lower than that of BaoLi data, with the highest registration rate at 89.2%. For the Bremen City data, the scene is complex with high amounts of noise in the data, and its highest registration rate was 86.7%. For the WHU Residence data, trees significantly affected the registration rate, given that a third of the keypoints were distributed among the trees. The highest registration rate was 85.5%.
3.7. Registration Comparison and Analysis
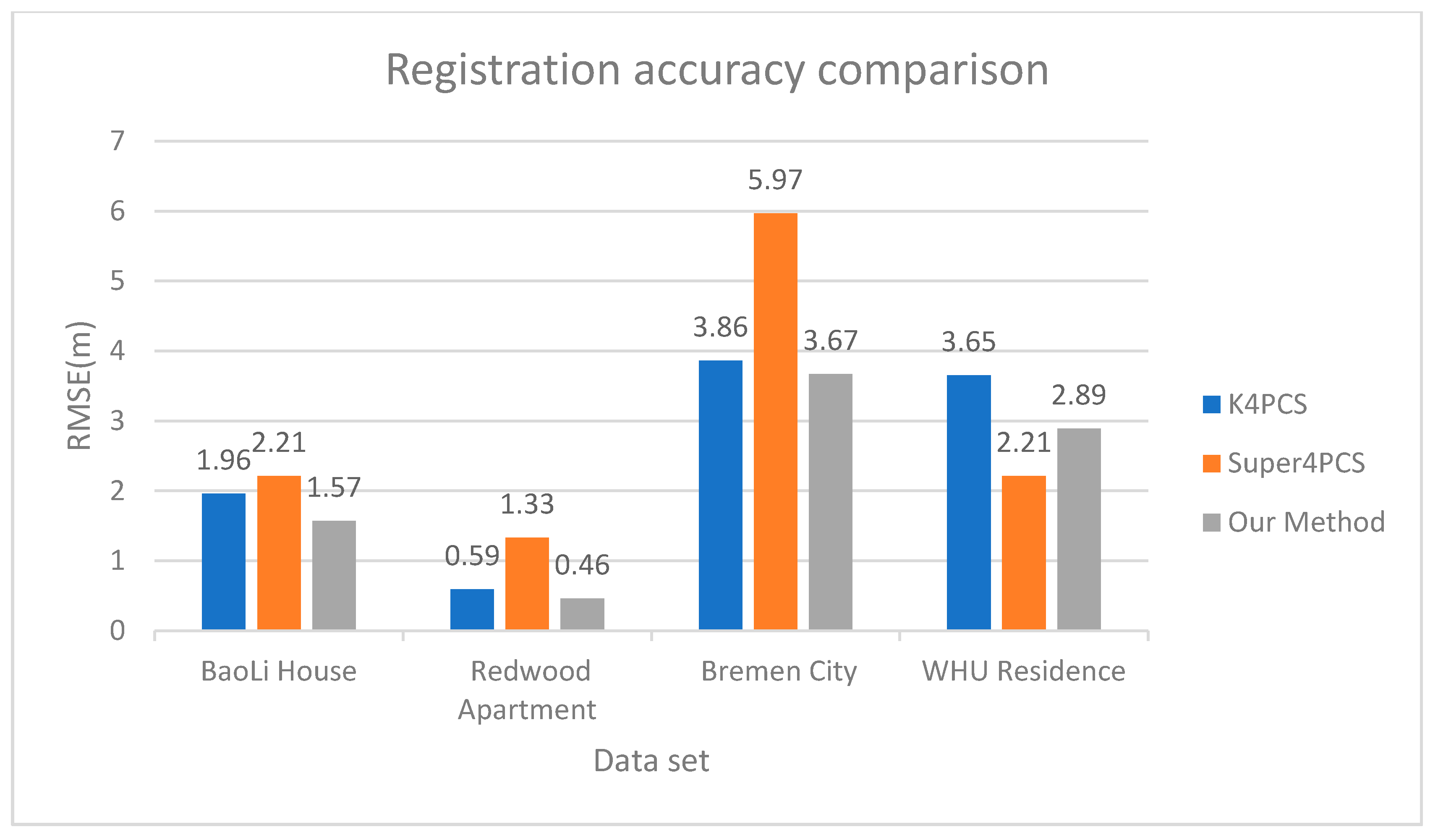
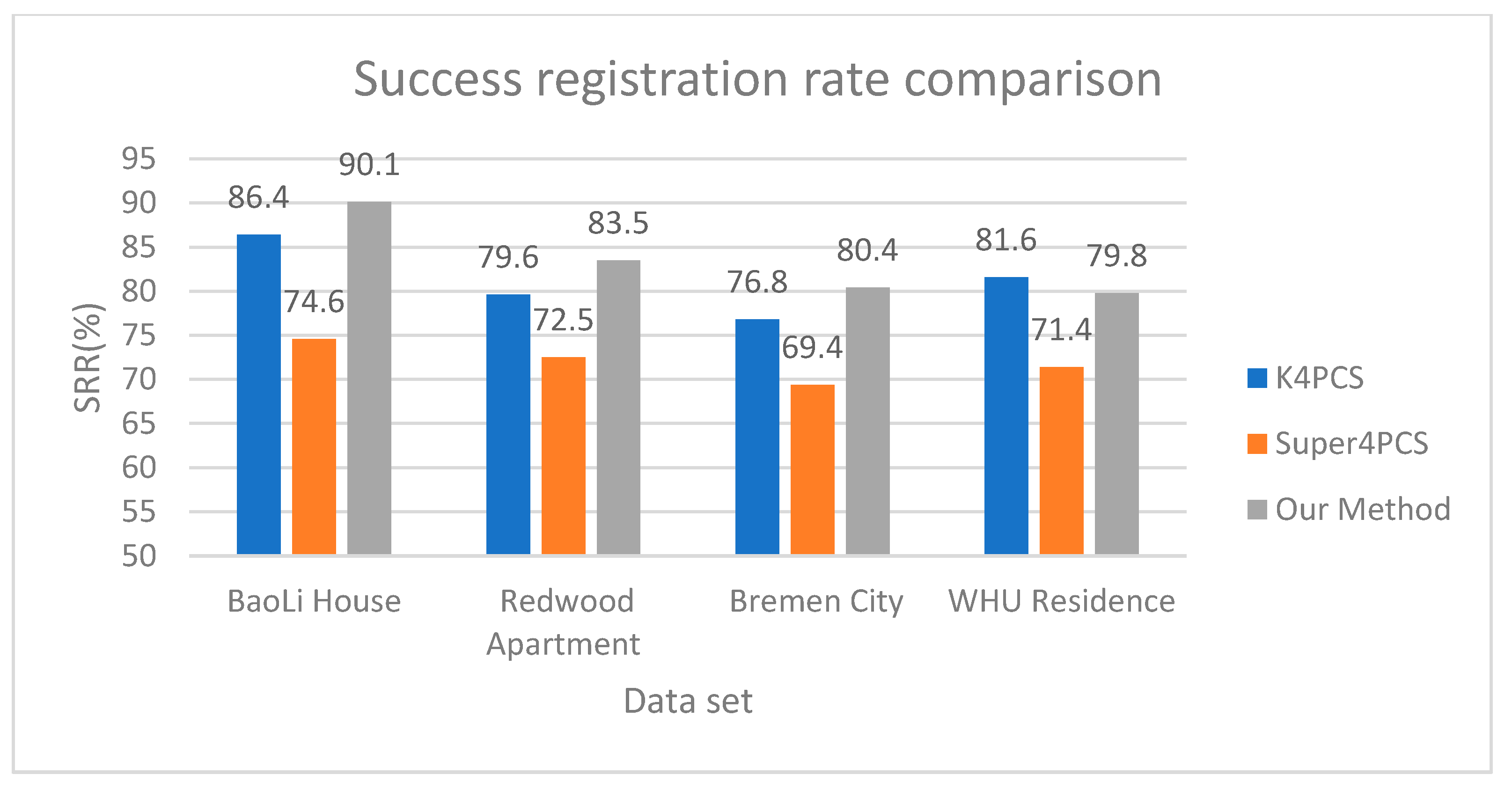
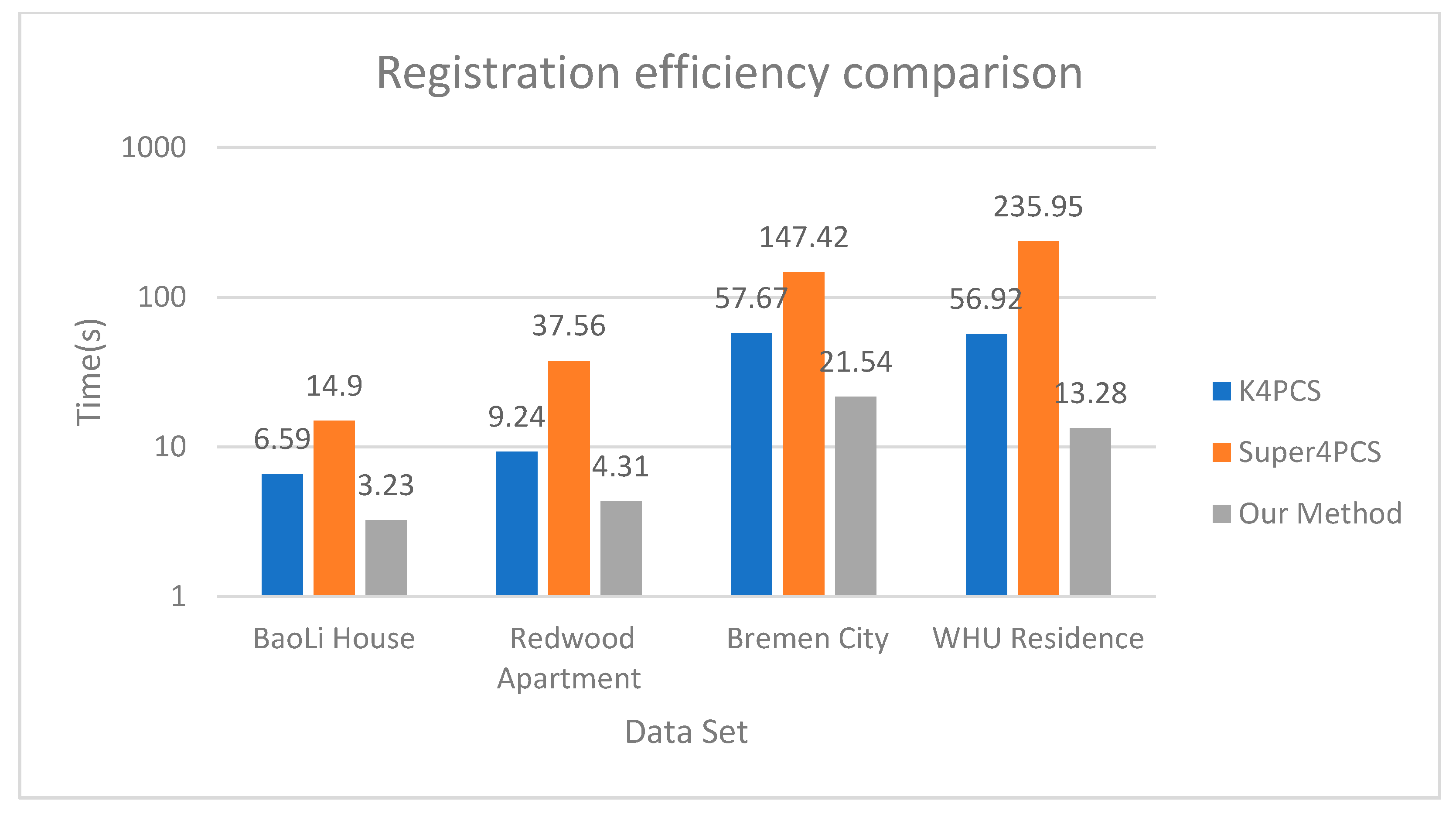
For comparison, we used the Super4PCS method. In terms of parameter settings, the estimated radius of the normal vector in K4PCS was set to five times the value of the point spacing. In the downsampling process for the Super4PCS and K4PCS, the spatial size of the voxel grid filter was set to 0.01 m. For indoor data (BaoLi House and Redwood Apartment), the voxel grid size is 0.2 m, while for outdoor data (Bremen City and WHU Residence), the voxel grid size is 0.5 m. Our analysis is based on the original coarse registration results, and there are no subsequent ICP fine registration steps. The detailed experimental results are shown in Table 5. The comparative analysis of registration accuracy, success rate, and efficiency is shown in Figure 10, Figure 11 and Figure 12.

Table 5.
Performance comparison.
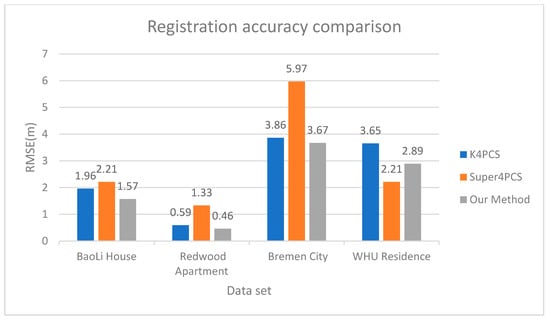
Figure 10.
Coarse registration accuracy comparison.
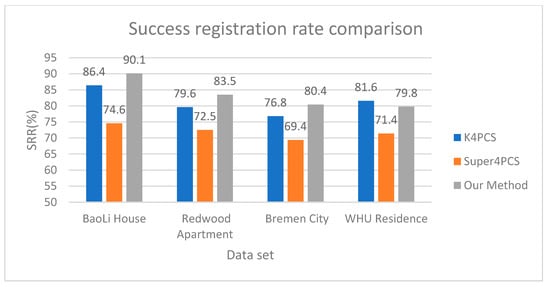
Figure 11.
Success registration rate comparison.
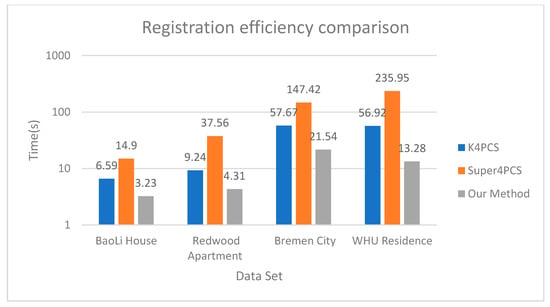
Figure 12.
Coarse Registration efficiency comparison. Notice that the y-coordinate is on a logarithmic scale.
For the comparison of the registration accuracy, different data have different performances. For WHU Residence data, the registration accuracy of Super4PCS is the highest, and the RMSE is the lowest. This is because many key points in the data appear on the tree, leading to a large RMSE of the proposed method and the K4PCS method. For the other three data, the RMSE of the Super4PCS method is the largest, and the RSME of the method in this paper is the largest.
As for the comparison of registration success rate, our method is obviously better than the Super4pcs method. In WHU data, many key points extracted by our method are in the tree, which affects the quality of the key points, and thus the registration success rate is slightly lower than that of K4PCS. For the other three data, the registration success rate of the method proposed in this paper is higher than that of the K4PCS.
As for the analysis of registration efficiency, the experimental results show that our proposed method and the K4PCS performed well with the TLS point cloud data. Since the TLS point cloud data are large, Super4PCS required many calculations and performed poorly in terms of time and accuracy. There were more noise points generated outdoors. The K4PCS calculates the keypoints. Fewer keypoints can better represent the whole point cloud. When calculating keypoints, fewer candidates were generated in the RANSAC process, which meant that in terms of time, K4PCS performed better than the Super4PCS. Compared with the K4PCS, our method was faster in calculating keypoints. Our approach was able to improve base choices, which effectively reduced the number of candidate sets. Moreover, we were able to improve the candidate set verification process using the LCP to quickly find the voxel grid. The experiments found that the set verification process was effectively improved by 35%. As shown in Table 5, it can be seen that the registration efficiency is improved by more than 50% compared with the K4PCS method and by more than 78% compared with the Super4PCS method. Overall, the experiments show that our proposed method can complete the registration quickly and reliably.
4. Discussion
Since the traditional Harris3D algorithm requires normal vector calculation, the normal contains the information of the local point cloud, which is indeed advantageous. However, experiments show that the normal vector of the sudden change rate and the edge area of the point cloud is unstable, which affects the quality of keypoint extraction. At the same time, calculating the normal vector increases the time complexity of the algorithm. This paper uses the voxel grid density value to construct the Hessian matrix, and the method of detecting key points has a good improvement in time efficiency. Theiler [34,35,36] found that 4PCS is not well applied to the ground laser point cloud data point cloud with large data volume. This paper replaces the original point cloud computing with keypoints, which can effectively improve the registration time of the TLS point cloud.
The point cloud data acquired by terrestrial laser scanning has the characteristics of large data volume and uneven distribution, and the point cloud data are disordered. In some operations, such as filtering the point cloud, calculating the normal vector and curvature, it is necessary to find the points. This requires a connection between the points and can find the points and the nearest neighbors in the domain to realize the point cloud search operation. Generally, a spatial index is established for point cloud data. The commonly used spatial index structures are the octree and KD-Tree, which are implemented in the point cloud database. Dr Hunter first proposed the octree model in 1978, which is a tree-like data structure used to describe three-dimensional space. The KD-Tree is essentially a binary search tree with constraints. In the case of uneven point cloud distribution, the performance of the KD-Tree is better than the octree, and it is more popular in practical applications. In this article, the query application is different from the nearest neighbor query and radius query of the KD-Tree in the past. We only need to judge whether there is a point within a certain range. The query time complexity of the KD-Tree of this operation is , and the voxel grid is a three-dimensional array. One of the major features of the array is that it supports random queries. The time complexity of querying whether the voxel grid contains points is . We compare and analyze the query time multiple times in the point cloud data. As shown in Table 6, it can be seen that the query time consumption of the voxel grid is 50~70% of the KD-Tree. Using a voxel grid query to improve LCP search can effectively improve the efficiency of the Super4PCS algorithm.

Table 6.
Query whether there are points in a certain range for comparative analysis.
5. Conclusions
We developed a fast point cloud registration method based on voxel grid, modifying the 4-point congruent set framework and significantly improving running time. Compared to traditional point cloud registration, the experiments show that the proposed approach could obtain faster and more accurate results than Super4PCS, particularly for TLS point cloud data with a high number of points. Our method uses a feature point detection method based on grid density gradient transformation to efficiently find keypoints of buildings. From the experimental results, our method was able to perform effective keypoints detection on point cloud data. Using our proposed approach, large-scale point cloud data can be quickly registered without preprocessing, and satisfactory performance can be obtained. One of the limitations of our method is that the entire point cloud is rasterized. One of the limitations of our method is that when the entire point cloud is rasterized, an excessively large raster size will result in very few keypoints, which cannot represent the original data well, and the registration effect is not stable enough. A grid size that is too small will result in too many grids, and there will be many empty grids, which consumes memory to a certain extent. Therefore, the next step should be to optimize the memory, eliminate empty grids during the voxel grid, and optimize the memory to reduce hardware consumption during registration.
Author Contributions
Conceptualization, B.X.; Software, W.J.; Validation, D.L.; Writing—review & editing, M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 61901311).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://redwood-data.org/; http://kos.informatik.uni-osnabrueck.de/3Dscans/; http://3s.whu.edu.cn/ybs/en/benchmark.htm accessed on 11 March 2021.
Acknowledgments
The WHU-TLS Residence set was provided by the State Key Laboratory of Information Engineering in Surveying, Mapping, and Remote Sensing, Wuhan University, Wuhan, China: http://3s.whu.edu.cn/ybs/en/index.htm accessed on 11 March 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dos Santos, D.R.; Basso, M.A.; Khoshelham, K.; de Oliveira, E.; Pavan, N.L.; Vosselman, G. Mapping indoor spaces by adaptive coarse-to-fine registration of RGB-D data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 262–266. [Google Scholar] [CrossRef]
- Ma, W.; Wu, Y.; Zheng, Y.; Wen, Z.; Liu, L. Remote sensing image registration based on multifeature and region division. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1680–1684. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, J.; Liu, L.; Wang, Y. Efficient rock mass point cloud registration based on local invariants. Remote Sens. 2021, 13, 1540. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Gelfand, N.; Ikemoto, L.; Rusinkiewicz, S.; Levoy, M. Geometrically stable sampling for the ICP algorithm. In Proceedings of the 4th International Conference on 3-D Digital Imaging and Modeling, Banff, AB, Canada, 6–10 October 2003; pp. 260–267. [Google Scholar]
- Yang, J.; Li, H.; Jia, Y. Go-icp: Solving 3d registration efficiently and globally optimally. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1457–1464. [Google Scholar]
- Rusinkiewicz, S. A symmetric objective function for ICP. ACM Trans. Graph. 2019, 38, 1–7. [Google Scholar] [CrossRef]
- Cai, Z.; Chin, T.J.; Bustos, A.P.; Schindler, K. Practical optimal registration of terrestrial LiDAR scan pairs. ISPRS J. Photogramm. Remote Sens. 2019, 147, 118–131. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detection. In Proceedings of the 4th Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–151. [Google Scholar]
- Ambühl, C.; Chakraborty, S.; Gärtner, B. Computing largest common point sets under approximate congruence. In Proceedings of the 8th Annual European Symposium, Saarbrücken, Germany, 5–8 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 52–64. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale Invariant Feature Transform. 2012. Available online: http://www.scholarpedia.org/article/Scale_Invariant_Feature_Transform (accessed on 11 May 2021).
- Sipiran, I.; Bustos, B. Harris 3D: A robust extension of the Harris operator for interest point detection on 3D meshes. Vis. Comput. 2011, 27, 963–976. [Google Scholar] [CrossRef]
- Zhong, Y. Intrinsic shape signatures: A shape descriptor for 3d object recognition. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, Kyoto, Japan, 26 September–4 October 2009; pp. 689–696. [Google Scholar]
- Zai, D.; Li, J.; Guo, Y.; Cheng, M.; Huang, P.; Cao, X.; Wang, C. Pairwise registration of TLS point clouds using covariance descriptors and a non-cooperative game. ISPRS J. Photogramm. Remote Sens. 2017, 134, 15–29. [Google Scholar] [CrossRef]
- Handte, M.; Iqbal, U.; Apolinarski, W.; Wagner, S.; Marrón, P.J. The narf architecture for generic personal context recognition. In Proceedings of the 2010 IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Newport Beach, CA, USA, 7–9 June 2010; pp. 123–130. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 224–237. [Google Scholar]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. Remote Sens. 2018, 144, 61–79. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++ deep hierarchical feature learning on point sets in a metric space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5105–5114. [Google Scholar]
- Wu, W.; Zhang, Y.; Wang, D.; Lei, Y. SK-Net: Deep learning on point cloud via end-to-end discovery of spatial keypoints. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 6422–6429. [Google Scholar]
- Yew, Z.J.; Lee, G.H. 3dfeat-net: Weakly supervised local 3d features for point cloud registration. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 607–623. [Google Scholar]
- Li, J.; Lee, G.H. Usip: Unsupervised stable interest point detection from 3d point clouds. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 361–370. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 726–740. [Google Scholar]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. ACM Trans. Graph. 2008, 1–10. [Google Scholar] [CrossRef]
- Mellado, N.; Aiger, D.; Mitra, N.J. Super 4pcs fast global pointcloud registration via smart indexing. Comput. Graph. Forum 2014, 205–215. [Google Scholar] [CrossRef]
- Mohamad, M.; Rappaport, D.; Greenspan, M. Generalized 4-points congruent sets for 3d registration. In Proceedings of the 2014 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; pp. 83–90. [Google Scholar]
- Mohamad, M.; Ahmed, M.T.; Rappaport, D.; Greenspan, M. Super generalized 4pcs for 3d registration. In Proceedings of the 2015 International Conference on 3D Vision, Lyon, France, 19–22 October 2015; pp. 598–606. [Google Scholar]
- Huang, J.; Kwok, T.-H.; Zhou, C. V4PCS: Volumetric 4PCS algorithm for global registration. J. Mech. Des. 2017, 139, 111403. [Google Scholar] [CrossRef]
- Zhang, R.; Li, H.; Liu, L.; Wu, M. A G-super4PCS registration method for photogrammetric and TLS data in geology. ISPRS Int. J. GeoInf. 2017, 6, 129. [Google Scholar] [CrossRef]
- Theiler, P.W.; Wegner, J.D.; Schindler, K.; Sciences, S.I. Markerless point cloud registration with keypoint-based 4-points congruent sets. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, 283–288. [Google Scholar] [CrossRef]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Keypoint-based 4-points congruent sets–automated marker-less registration of laser scans. ISPRS J. Photogramm. Remote Sens. 2014, 96, 149–163. [Google Scholar] [CrossRef]
- Theiler, P.W.; Wegner, J.D.; Schindler, K. Fast registration of laser scans with 4-points congruent sets-what works and what doesn’t. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 149–156. [Google Scholar] [CrossRef]
- Ge, X.; Sensing, R. Automatic markerless registration of point clouds with semantic-keypoint-based 4-points congruent sets. ISPRS J. Photogramm. Remote Sens. 2017, 130, 344–357. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, E.; Zhang, Z.; Wu, L. Multiscale sparse features embedded 4-points congruent sets for global registration of TLS point clouds. IEEE Geosci. Remote Sens. Lett. 2018, 16, 286–290. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, R.; Du, S.; Zhang, L.; Liu, Y. Global adaptive 4-points congruent sets registration for 3D indoor scenes with robust estimation. IEEE Access 2020, 8, 7539–7548. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Liang, F.; Liu, Y. Automatic registration of large-scale urban scene point clouds based on semantic feature points. ISPRS J. Photogramm. Remote Sens. 2016, 113, 43–58. [Google Scholar] [CrossRef]
- Xu, Y.; Boerner, R.; Yao, W.; Hoegner, L.; Stilla, U. Pairwise coarse registration of point clouds in urban scenes using voxel-based 4-planes congruent sets. ISPRS J. Photogramm. Remote Sens. 2019, 151, 106–123. [Google Scholar] [CrossRef]
- Park, J.; Zhou, Q.Y.; Koltun, V. Colored point cloud registration revisited. In Proceedings of the International Conference on Computer Vision, Venice, Italy, 23–29 October 2017. [Google Scholar]
- Borrmann, D.; Elseberg, J.; Lingemann, K.; Nüchter, A.; Hertzberg, J.J.R. Globally consistent 3D mapping with scan matching. Robot. Auton. Syst. 2008, 56, 130–142. [Google Scholar] [CrossRef]
- Dong, Z.; Liang, F.; Yang, B.; Xu, Y.; Zang, Y.; Li, J.; Wang, Y.; Dai, W.; Fan, H.; Hyyppä, J.; et al. Registration of large-scale terrestrial laser scanner point clouds: A review and benchmark. ISPRS J. Photogramm. Remote Sens. 2020, 163, 327–342. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).