Abstract
Canopy height serves as a good indicator of forest carbon content. Remote sensing-based direct estimations of canopy height are usually based on Light Detection and Ranging (LiDAR) or Synthetic Aperture Radar (SAR) interferometric data. LiDAR data is scarcely available for the Indian tropics, while Interferometric SAR data from commercial satellites are costly. High temporal decorrelation makes freely available Sentinel-1 interferometric data mostly unsuitable for tropical forests. Alternatively, other remote sensing and biophysical parameters have shown good correlation with forest canopy height. The study objective was to establish and validate a methodology by which forest canopy height can be estimated from SAR and optical remote sensing data using machine learning models i.e., Random Forest (RF) and Symbolic Regression (SR). Here, we analysed the potential of Sentinel-1 interferometric coherence and Sentinel-2 biophysical parameters to propose a new method for estimating canopy height in the study site of the Bhitarkanika wildlife sanctuary, which has mangrove forests. The results showed that interferometric coherence, and biophysical variables (Leaf Area Index (LAI) and Fraction of Vegetation Cover (FVC)) have reasonable correlation with canopy height. The RF model showed a Root Mean Squared Error (RMSE) of 1.57 m and R2 value of 0.60 between observed and predicted canopy heights; whereas, the SR model through genetic programming demonstrated better RMSE and R2 values of 1.48 and 0.62 m, respectively. The SR also established an interpretable model, which is not possible via any other machine learning algorithms. The FVC was found to be an essential variable for predicting forest canopy height. The canopy height maps correlated with ICESat-2 estimated canopy height, albeit modestly. The study demonstrated the effectiveness of Sentinel series data and the machine learning models in predicting canopy height. Therefore, in the absence of commercial and rare data sources, the methodology demonstrated here offers a plausible alternative for forest canopy height estimation.
1. Introduction
Understanding the role of forest carbon emissions and sequestration is needed to build a robust framework for international agreements to limit the concentration of greenhouse gases in the atmosphere [1]. The function of tropical forests is critical in the global carbon cycle because they are carbon-dense and highly productive [2]. Above-Ground Biomass (AGB) is the best indicator of the carbon content of tropical forests [3]. AGB estimation models for tropical forests generally ignore canopy height as a factor [4]. However, studies have shown that the inclusion of canopy height in the allometric models tends to improve the estimation accuracy of AGB in tropical forests [4,5,6]. Therefore, the tree canopy height of tropical forests is an essential factor in estimating its biomass, and an inaccurate estimate of canopy height can result in over- or underestimation of AGB [7].
The ground-based canopy height measurement instruments exploit the planimetric distance and the angle between the device to the base and the top of the tree, to estimate canopy height using a trigonometric relationship [8]. The laser rangefinder is quite a standard instrument that uses this method in field-based canopy height measurements [9,10]. Apart from that, instruments like altimeter and clinometer are used in some studies [11,12,13]. However, in dense tropical forests, it is often difficult to identify the top and base of the tree due to lack of direct line of sight to the canopy top, limited accessibility in rough terrains, blockage of the crown top by adjacent trees, and presence of understorey vegetation [8,14]. Therefore, the field estimated height and actual tree height often show a wide variation in the tropics [15].
The digital photogrammetry method has been used to measure canopy height in earlier remote sensing-based studies. The data used in those studies varied from aerial photogrammetry in historical cases to multispectral satellite data [16,17,18]. The advancement of LiDAR technologies was found to be more useful in measuring the tree height [19,20]. However, most of the studies were based on airborne LiDAR data, which has limited area coverage and which is costly to acquire in tropical regions [21,22]. Till now, only NASA’s Ice, Cloud, and land Elevation Satellite (ICESat-1) mission has provided world-wide spaceborne LiDAR data, obtained through Geoscience Laser Altimeter System (GLAS), which has been extensively used for vegetation mapping [23]. Many studies found that the GLAS data can be used efficiently for vegetation height monitoring of different types of forests [24,25,26,27,28]. Therefore, GLAS data alongside other remote sensing and ancillary data has been used broadly in AGB estimation [29,30,31,32]. In 2018, the Ice, Cloud, and land Elevation Satellite-2 (ICESat-2) became operational [33]. Data obtained through its Advanced Topographic Laser Altimeter System (ATLAS) sensor was made available recently. Preliminary studies with simulated ICESat-2 data have shown its effectiveness in canopy height estimation [34]. Despite having many advantages, LiDAR data, mainly spaceborne data, usually has limited spatial and temporal coverage [35]. LiDAR data is also not suitable for the wall to wall mapping as this data is usually acquired for specific footprints [36].
One of the ways by which spatially continuous height mapping can be done is by using the Synthetic Aperture Radar (SAR) interferometry (InSAR) method [37,38]. InSAR measures the surface topography and height of the surface features by using the phase information of the radar signal [39]. Coherence is measured as the magnitude of the complex cross-correlation between the constituent images of an interferometric pair [40]. Decorrelation or reduction in coherence values occurs with changes in the ground condition between the two acquisitions of the interferometric pair; thereby, reducing its ability to measure height correctly using interferrometric information. Shorter wavelength SARs have a greater tendency for greater temporal decorrelation, even for a time gap as short as one day [39]. The interferometric data with global spatial coverage became freely available with the launch of the European Space Agency’s Sentinel-1 mission. However, the Sentinel-1 mission has a maximum temporal resolution of six days [41]. There can be significant decorrelation between images while mapping dense tropical forests using Sentinel-1 repeat-pass interferometry, which may result in loss of coherence, thereby severely affecting the interferometric height measurement results.
In recent years researchers have found newer ways to estimate mean canopy height (Table 1). It was suggested that rather than using phase information of SAR images, interferometric coherence can be used to model tree height [42]. Tree height inversion from coherence data also showed improvement in biomass estimation accuracy [43]. Apart from coherence values, field-measured tree height can be correlated with SAR backscatter of different polarization to establish a canopy height model [44]. In addition to SAR, multispectral band values were also used in establishing relationship with tree canopy height. Multispectral bands of Landsat-7 and 8 showed good promise while measuring tree heights in the range of 5–20 m [45].

Table 1.
Compilation of canopy height estimation studies using different instruments and sensors.
Fraction of Vegetation Cover (FVC) has been used for vegetation height estimation. FVC is defined as the percentage of a given area that is covered by vegetation canopy [46]. MODIS derived tree cover showed a good correlation with tree height derived from GLAS data [47]. Recently, Sentinel-1 based FVC demonstrated its effectiveness in canopy height estimation [35]. LAI is measured as the total one-sided leaf area per unit ground surface area, demonstrating good correlation with tree height [48,49]. LiDAR based studies found that canopy height has a good correlation with LAI [50,51] and one could serve as proxy to other [52]. Canopy height estimation with/without a Digital Elevation Model (DEM) has been benefitted from the Shuttle Radar Topography Mission (SRTM) [53,54].
Modeling the relationship of forest parameters such as canopy height from field measured values, and remote sensing derived variables can be done in several ways. The most common are parametric regression methods [55,56,57] or machine learning models like Random Forest (RF) [58,59]. Due to their simplicity, parametric regression-based methods are widely used for modeling biophysical parameters and remote sensing variables. One major problem in parametric regression is that it assumes a standard relationship before the analysis, which may not be true, in reality. RF is a decision tree-based machine learning model used for estimation of biophysical parameters [60]. The RF model can capture the actual non-linear relationship between the predictor and predicted variables. However, the interpretation of an RF model is complicated as it consists of many trees and numerous sets of rules.
Symbolic Regression (SR) using genetic programming is a relatively modern technique that estimates a straightforward best-fit model for a given dataset by minimizing error rates while searching through all possible regression models [61,62]. Conventional machine learning algorithms work as black-boxes; implying that the internal mechanisms of these algorithms are hard to comprehend and difficult to reproduce desired results. The SR model works with the principle to determine the input-output relationship and selection of variables, which are most effective in predicting outputs [63]. The SR model’s inclination towards finding correct solutions makes it distinct from other types of regressions. SR is capable of constructing a robust and interpretable formula, which is not possible by other linear and nonlinear regressions or machine learning models.
The main objective of this study was to establish a methodology by which forest canopy height can be estimated using SAR and optical remote sensing data using machine learning models. The mangrove forest in the Bhitarkanika Wildlife Sanctuary (BWS), Odisha, India, was chosen as the study area. First, we attempted to establish canopy height models using SR and RF, and Sentinel-1 and Sentinel-2 derived parameters. Further, the canopy heights estimated using the two models were compared and validated with field measured and ICESat-2 derived data.
2. Materials and Methods
2.1. Study Area and Filed Measurement of Canopy Heights
The Bhitarkanika Wildlife Sanctuary (BWS), with 58 species, is considered as one of the vital mangrove ecosystems in the world due to its genetic diversity [64]. Dense and moderately dense mangroves cover an area of 165 km2 [65] of BWS. Some of the dominant species of BWS are Heritiera sp., Excoecaria sp., Avicennia sp., and Sonneratia sp. [66]. This area receives a high average annual rainfall of about 1642 mm, and most of it is received during June to October. BWS experiences a typical warm and humid tropical climate with temperature maxima in May and minima in January [67]. Multiple field surveys were conducted during November–December 2018 for canopy height measurement. Height measurement of all the trees in an inventory plot is time consuming, and redundant, especially if it has to be correlated with satellite derived canopy height pixels. Sullivan et al. [68] have mentioned that although an increase in the number of sampled trees results in better accuracy, the inclusion of the ten largest trees is most important. Thus, we observed the sampling frequency of the 10 largest trees per plot and measured tree height using a laser range finder instrument. The center locations were obtained using a handheld GPS for all 185 plots (Figure 1).
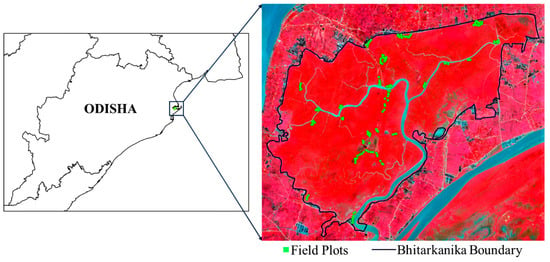
Figure 1.
Location of the Bhitarkanika Wildlife Sanctuary (Odisha state) on the eastern coast of India. The false color composite image of BWS is shown with the boundary demarcated over which the canopy height measured plot positions are overlaid with green markers.
2.2. Satellite Data and Processing
Sentinel-1 and Sentinel-2 data were downloaded from the European Space Agency’s (ESA) Copernicus Hub. The Sentinel-1 mission consists of two satellites, Sentinel-1A and Sentinel-1B, which image the earth in C-Band SAR with a six day revisit period between them. A total of six images, three each for Sentinel-1A and Sentinel-1B, were in the Single Look Complex (SLC) format. They were acquired in the interferometric wide-swath mode (IW), which contains both amplitude and phase information of the backscattered SAR signal (Table 2 and Table 3). Sentinel-1 uses the advanced Terrain Observation by Progressive Scans (TOPS) SAR mode to capture images in three sub-swaths in a total swath width of 250 km [69]. The study area falls in the second sub-swath of all the SLC images. So, each image was split to subset only the second sub-swath. Each six day pair of Sentinel-1 SLC images was co-registered in the ESA’s Sentinel Application Platform (SNAP) using orbital information and SRTM 1-sec DEM. Only the VV polarisation band of the Sentinel-1 data were selected for the study as the VH polarisation tends to lower the coherence value by introducing decorrelation due to cross-polarization noise [70]. The Sentinel-2 mission also consists of two satellites, Sentinel-2A and Sentinel-2B, with a five day revisit period in combination. Seven cloud free Sentinel-2 data were acquired in the L1C processing level, with the top of the atmosphere reflectance values. Sentinel-2 data were atmospherically corrected to the L2A processing level using the SEN2COR processor [71]. It adjusted the image to yield the bottom of the atmosphere-surface reflectance. The pre-processed Sentinel-1 and Sentinel-2 data were further used for specific parameter extraction and canopy height modeling (Figure 2).

Table 2.
The acquisition details of the Sentinel dataset used in this study.

Table 3.
Perpendicular baselines of all interferometric pairs used in the study.
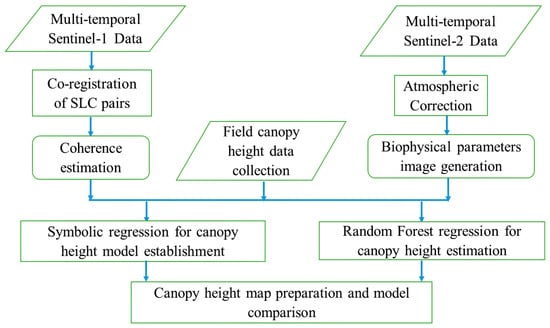
Figure 2.
Methodology flow diagram depicting the steps adopted for generating canopy height maps and comparison of model outputs.
Launched in September 2018, ICESat-2 can measure the earth surface with a 17 m diameter footprint and with 91 days temporal resolution. ICESat-2 has three pairs of beams. Each pair of beams footprint is separated by about 3 km of cross-track with a pair spacing of 90 m [72]. The ICESat-2 data were downloaded in hdf5 format from the National Snow and Ice Data Centre (NSIDC) [73]. The data product selected was ALT08, which includes the height of the surface, including the canopy. An R package was used to extract the canopy height information from the ALT08 data.
2.3. Interferometric Coherence and Biophysical Parameters Extraction
Coherence for all co-registered SLC pairs was estimated using the SNAP tool. The coherence of an image pair depends on the baseline length. A massive baseline results in low coherence and vice versa. The longest baseline for which coherence becomes zero is known as the critical baseline [39]. It can be expressed as a function of band chirp width, orbital height, and sensor operating frequency [74], as shown in Equation (1).
where, = critical baseline; = chirp width; = operating frequency; = incidence angle.
Sentinel-1 sensor characteristics vary according to observation mode [75]. The critical baseline, obtained using optimal values of parameters stands at 3.65 Km. As all the pairs have a baseline length significantly lower than the critical baseline, the coherence values fall within the acceptable range (Table 3). Backscatter images were also generated from the SLC images by converting them from the SLC image to Ground Range Detected (GRD) image.
Sentinel-2 L2A images were used to calculate LAI and FVC using the SNAP toolbox biophysical variable processor. All Sentinel-2 images were resampled to 20 m pixel size. The biophysical processor algorithm was implemented to generate biophysical products from a range of sensors [76]. An extensive database was prepared to include the top of canopy reflectance and associated vegetation characteristics in the biophysical processor algorithm. This database was used to train neural networks to estimate the canopy characteristics from the top of canopy reflectance along with the observational configuration. In SNAP, the prediction of the new variable was made based on the set of coefficients computed during the training phase.
2.4. Canopy Height Modeling
After generating the necessary variables, the next step was to establish the relationship between the variables and canopy height through regression. The values of coherence and other biophysical parameters were extracted at field plot locations to build the dataset for regression. Non-linear regression was implemented via two machine learning models, first, using the RF and then using SR. Primarily, the whole canopy height dataset was divided randomly into two parts using data partition function of CARET package. Seventy percent of it was used for model building, and the other 30 percent was used in model validation. The model building data was further divided into the model training and testing datasets in accordance with the model characteristics. Therefore, for both the models, we had separate model building, i.e., training and testing, and validation data.
2.4.1. Random Forest
The RF model was implemented via the CARET package in R [77]. In an RF model, hundreds of trees are built based on a bootstrap sample of the original data [78]. Variables were chosen randomly at each node for the split, and the final value was predicted by averaging the prediction of all the trees. The importance of the variables in the RF model was measured to find the most influential variables. As the first step of the importance measurement, the Mean Squared Error (MSE) was measured for each tree using an Out Of the Bag (OOB) sample. Thereafter a new error rate was calculated using the same procedure after permuting a variable. The difference between the two accuracies were averaged for all trees, and normalized by the standard error. This value was termed as the importance of the permuted variable to the model. The exclusion of a variable with positive importance increases the error rate of the model, while it is opposite for the variables with negative importance. After the initial run of the model, variables with negative importance were removed from the predictor list. The final model was built only on the variables with positive importance. Here one more fold cross-validation was done to reduce the chance of over-fitting. Initially, the field-measured canopy heights were correlated with the remote sensing derived variables, followed by model prediction of canopy heights.
2.4.2. Symbolic Regression
The use of SR, in retrieval of biophysical parameters has not been explored earlier. The success of machine learning algorithms in the biophysical parameters’ retrieval problem showed the existence of the non-linear relationship between remotely sensed variables and biophysical parameters. However, the establishment of an interpretable model describing the relationship was not possible with machine learning regression. The working principle of SR makes it a viable option for the establishment of such a model.
SR was implemented through genetic programming, and it consisted of several steps. First was the selection of the terminals, i.e., independent variables. Coherence, SRTM DEM, FVC, and LAI were selected as terminals for prediction of canopy height. The second step was to identify a set of functions that would be used to build the models. In this study, constant, addition, multiplication, subtraction, division, exponents and natural logarithms were selected as the primitive functions. Each of these functions has an associated complexity. The first four have a complexity of 1, division has a complexity of 2, and exponents and natural logarithm have a complexity of 4 each. The total complexity of the solution is the sum of the complexity of the functions used in the solution [79]. Each symbolic expression proposed by the genetic programming was evaluated based on its fitness, which in this case, was measured by the mean squared error between observed and predicted values. Probability values were assigned to the initial models based on their fitness. After that, a new generation of models were created by reproduction, i.e., copying an existing model to the new population and genetic recombination, i.e., building a new model by recombining parts from existing models [61]. The trial version of Eureqa pro software was used for the SR model [80]. In the absence of specific termination criteria in the software, the final model was chosen when the 50th generation was reached. After getting the final canopy height model, the efficiency of the model was checked using the test dataset. Further, canopy heights were predicted using the model for the study area.
One of the goals of the SR model was to identify the variables that provided the most significant explanatory power for the dataset. Sensitivity analysis was used to identify the variables which have the greatest contribution to the regression equation [81]. The partial derivative of the dependent variable with respect to an independent variable was taken as the first step of sensitivity analysis. The final sensitivity was obtained by multiplying the partial derivative with the ratio of the standard deviation of the independent variable and the dependent variable [79]. The sensitivity of variable x for the function y = f(x) is estimated as follows:
where = partial derivative of y with respect to x; = standard deviation of the independent variable x, and = standard deviation of the dependent variable y.
The sensitivity indicates the direction, either positive or negative, and the magnitude of the correlation between input and output variables. A positive sensitivity suggests that an increase in the input variable will increase the value of the output variable and vice versa. The magnitude of the sensitivity determines the amount of increment or reduction of the output variable due to a unit increase in the input variable. A higher magnitude of positive sensitivity denotes a high amount of increase in the output variable value and vice versa for negative sensitivity.
3. Results
3.1. Field Measured Canopy Height
The distribution of the field-measured canopy height showed that the height range of 8 to 10 m has the largest number of plots (Figure 3). The tallest canopy heights observed during the field measurement were in the range of 14–16 m and occurred in three plots, whereas the lowest measured from 2 plots were in the range of 2–3 m.
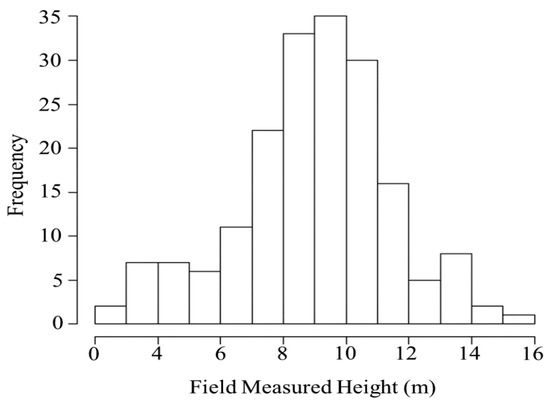
Figure 3.
Distribution of field-measured canopy heights displayed against their frequency of occurrence.
3.2. Isnterferometric Coherence and Biophysical Psarameters
The average values of SAR coherence and biophysical variable images were used as inputs to reduce the effect of temporal variation. The spatial distribution of pixel values of all the variables showed different patterns (Figure 4). The coherence values found higher and close to ‘1’ over fully correlated areas, and near ‘0’, where there is no statistical relationship between the images [40]. As vegetation loss is a significant reason explaining loss of coherence, the coherence values remained low in dense mangrove areas. The FVC and LAI images provided idea about presence and absence of vegetation. Lower values of FVC and LAI indicated sparse or no vegetation. A comparison of the coherence images with LAI and FVC images showed that areas (within yellow ellipse in Figure 4), with lower FVC and LAI values, showed a relatively higher coherence corresponding to lower DEM values. However, for some areas (under the red ellipse), FVC, and LAI showed higher values, but the coherence of the region remained high, and DEM values remained on the lower range.

Figure 4.
(a) Coherence, (b) Fraction of Vegetation Cover (FVC), (c) Leaf Area Index (LAI) images and (d) Digital Elevation Model (DEM), with a vegetated and non-vegetated patch shown under red and yellow ellipses respectively.
The frequency of pixel values in the coherence image almost shaped like a gaussian distribution (Figure 5). Most of the pixel values fall between 0.3 and 0.5. The rest of the values were distributed quite evenly on each side. Distribution of both LAI and FVC values followed a similar pattern. Due to the dense nature of mangroves, FVC also showed higher values for most of the pixels, with a much smaller number of pixels with values <0.4 and >0.6. However, LAI values remained low, between 1.5 and 2. The DEM image demonstrated flat topography with maxima of 16 m.
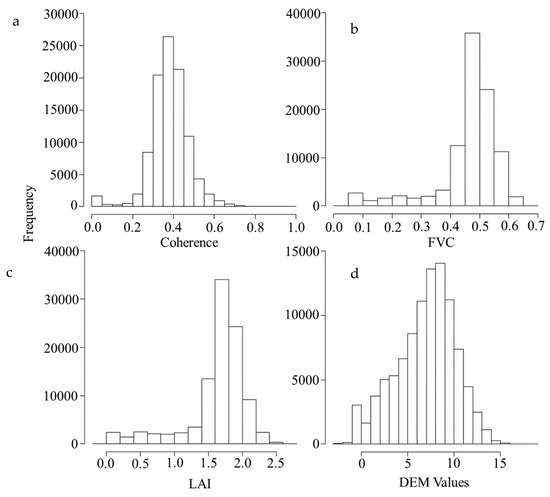
Figure 5.
Frequency distribution of the input images for the canopy height model: (a) coherence; (b) FVC; (c) LAI; (d) DEM.
3.3. Canopy Height Model Establishment Using SR
The progression of the SR showed how the mean squared error decreased by selecting different relationships between the variables (Figure 6). The final regression model (Equation (3)) is a genetic combination of seven primary relationships formed with the input data. The final model by the SR used multiplication, addition, subtraction and division to build the relationships between the dependent and independent variables.
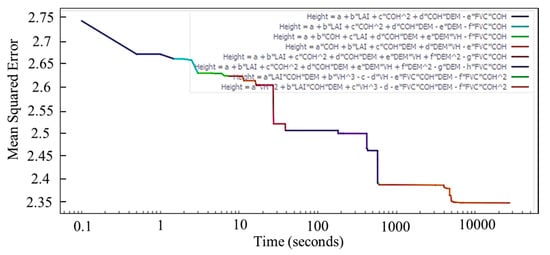
Figure 6.
Progress of Symbolic Regression (SR) over time, for canopy height model establishment, including the relationship assumed for the regression.
Considering the operators and constants used in the model, the total complexity of the model was 32. Equation (3) was used to predict canopy height for the test dataset.
The ‘variable sensitivity’ analysis gave an idea about the critical variables and their impacts on the regression model (Table 4). FVC had the highest sensitivity that means among all the variables, a unit increase in FVC caused the most significant change in estimated height. Additionally, the direction of FVC sensitivity was negative for 100% of cases, which suggested negative correlation with canopy height. A unit increase in FVC value caused a decrease of 1.122 m in estimated canopy height. LAI was also highly sensitive, but it was positively correlated to the estimated canopy height for all the cases. Thus, a unit increase in LAI increased the estimated canopy height by an amount of 1.108 m. Coherence and DEM had relatively lower sensitivity. Coherence was negatively correlated with height with a sensitivity of 0.57056. For DEM, the correlation was positive, with a sensitivity of 0.34082. VH backscatter had very low sensitivity with the estimated canopy height.

Table 4.
Variable sensitivity of the SR model that explained the relative impact a variable has on the target variable within the model.
The observed and predicted values of canopy height closely followed the identity line (Figure 7). The R2 value between observed and predicted canopy height was 0.62, and RMSE value was 1.48 m. A trend of overestimation for lower height and underestimation for higher height can be observed in the correlation plot. However, the magnitude of deviation from the identity line was pretty low, and the number of overestimated and underestimated points was almost evenly distributed. The normalized RMSE was 13.7% concerning the range of field measured canopy heights.
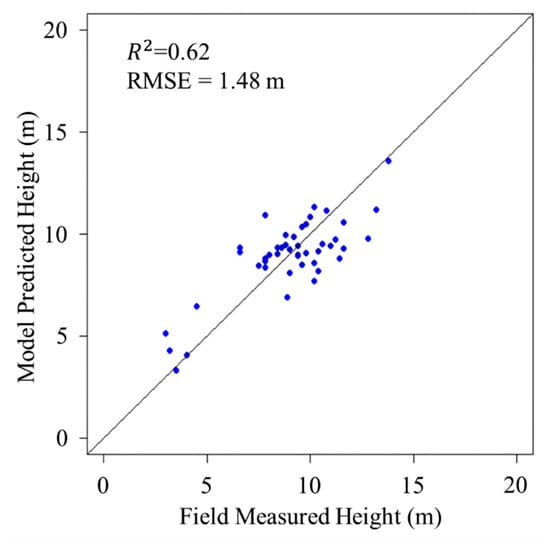
Figure 7.
Correlation plot of canopy heights between field measurements and SR model based predictions.
3.4. Canopy Height Model Establishment Using RF
RF regression was run for canopy height model establishment. The same set of training and the test dataset were used. Coherence was the most critical variable in the RF model, followed by LAI and FVC. DEM and VH backscatter acted as the variables with the lowest importance (Figure 8a). The importance of VH backscatter found much less than other variables, similar to SR model (Table 4). The correlation plot between field-measured canopy heights and model predicted canopy heights, showed that the magnitude of over- and underestimation of canopy height was more or less similar, like the SR model (Figure 8b). However, the result showed a lower of 0.6, between field measured and model predicted canopy height values, while the RMSE value of RF model was higher (1.57 m) and the normalized RMSE was 14.54%.
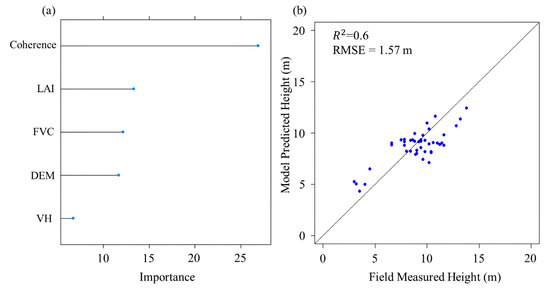
Figure 8.
(a) Variable importance of the RF model for canopy height estimation; (b) correlation plot of canopy height between field measured and RF-based model prediction.
3.5. Comparison of Canopy Height Maps Derived Using SR and RF Models
The predicted canopy height map using SR and RF models demonstrated a range between 0 to 18 m and 3 to 15 m respectively (Figure 9a,c). Areas showing the upper canopy height range distribution was less in the RF model based predicted map, while for SR prediction, a larger area was found with upper canopy height ranges. Overall, both the maps showed similar trends with the medium range of canopy height values being the same for both. The difference in the canopy height as per the two models were found largely in lower range values (Figure 9e,f).
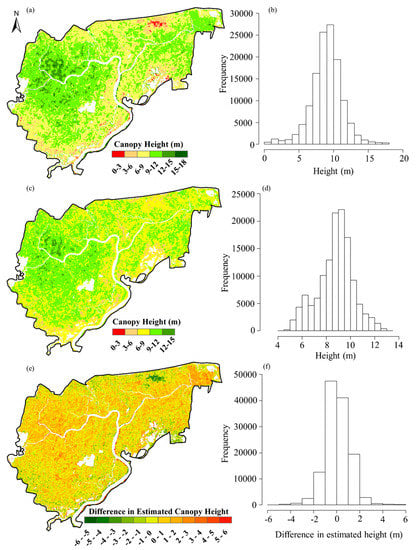
Figure 9.
(a,b) Canopy height map using the SR model and its histogram distribution; (c,d) canopy height map using RF model and its histogram distribution; (e,f) canopy height difference map derived using estimations from two models (SR–RF) and its histogram distribution.
3.6. Comparison of Canopy Heights Derived from Model Predictions with ICESat-2 Estimates
The distribution of canopy heights from ICESat-2 showed a similar pattern with SR model predictions (Figure 10a,b). However, canopy heights from ICESat-2, data demonstrated a peak at 10–12 m, whereas it was at 9–10 m for both model predictions. It can be observed that the ICESat-2 footprints lie mostly in the areas with higher canopy heights. Further, the canopy height distribution was more similar to the SR-based predictions than RF.
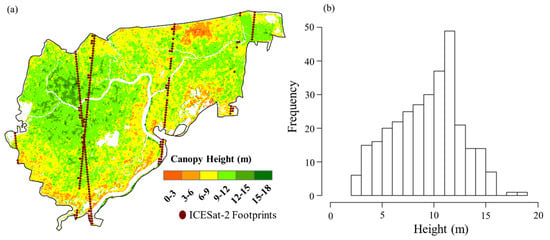
Figure 10.
(a) ICESat-2 footprints shown over the BWS on the canopy height map using SR prediction, and (b) Frequency distribution of canopy height pixels from ICESat-2 data.
The canopy height values from SR prediction showed a better correlation with ICESat-2 estimated canopy heights with an R2 value of 0.45 and RMSE of 2.24 m. The relationship with ICESat-2 based canopy height was much weaker for the RF model predicted canopy height values, where the R2 value between observed and predicted height was 0.34 with an RMSE of 2.69 m (Figure 11). There were quite a high number of footprints with extreme values, for which over- and under-estimation can be observed.
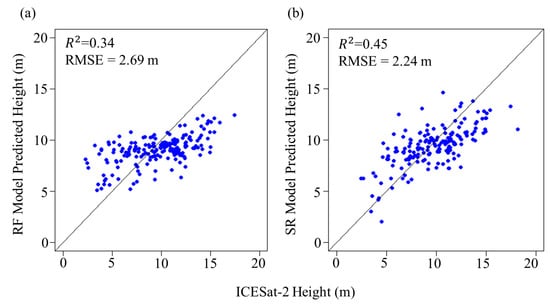
Figure 11.
Correlation plots of canopy height values between ICESat-2 footprints and (a) RF model, and (b) SR model predictions.
4. Discussion
4.1. Comparison of SR and RF Model Based Canopy Height Estimates
Although, both SR and RF can be termed as a machine learning models, the fundamental working principle is entirely different from one another. The variable importance of RF and variable sensitivity of SR varied significantly for the canopy height models, as both methods had a different perception regarding the importance of variables. The RF model determines variable importance by the change in the regression error through variable permutation [82], i.e., the change in prediction accuracy due to the presence and absence of a variable was used as a measure of importance [83]. The size of the increase or decrease in regression error due to the absence of a predictor variable measured the magnitude of importance in the RF model. A more significant increase means that the variable was more important compared to other variables. There was no separate variable importance measurement procedure in the SR model. In SR, the model undergoes through a continuous evolutionary process. Models incorporating unimportant variables will perform worse than individuals using only relevant variables. Those unimportant variables will in turn, have a lower chance of being chosen to produce highly accurate symbolic expressions [84]. Therefore, the presence of irrelevant variables was discouraged throughout the process. Hence, the presence of a variable in a sufficiently evolved population will indicate the necessity of that variable in the model.
Stijven et al. [84] had argued that the variable selection method of SR is more reliable than in RF regression. With the detailed analysis of four different datasets, they have listed several reasons for which variable selection by RF may not always be reliable. As the first reason, they concluded that when multiple variables had almost equal importance, the RF model struggles to differentiate between them and assigns random variable importance. RF can also assign considerably less significance to a variable than expected due to its correlation with other irrelevant variables present in the model. Data distribution often can influence the variable importance. SR was found to be free from all these obstacles, which were held back in the RF model. Thus, in the SR model, there was a lower chance of omitting the vital variables. Chen et al. [85] also confirmed that SR was more efficient in variable selection than RF.
4.2. Importance of Variables in the Canopy Height Models
While building the canopy height model using SR, it was found that FVC, LAI, and coherence worked as the most sensitive variable for canopy height estimation. Although, FVC was an indicator of the tree crown property, it had shown a good correlation with canopy height in some earlier studies. Simrad et al. [86] concluded that while canopy cover shows a correlation with tree height, it might not hold for tall mature tropical forests due to the saturation of canopy cover with tree height. Wang et al. [47] also produced a global canopy height map using GLAS data and RF regression. In their study, they confirmed that tree cover was closely related to canopy height. Liu et al. [35] also showed the relationship between tree height and its predictors would be a non-linear one. Korhonen et al. [87] in their study, found that on reaching a certain height, canopy height has a strong non-linear relationship with canopy cover. One more reason for this kind of result can be the species distribution in the study area. It was also observed from the results that FVC had a negative sensitivity with canopy height, which means an increase in FVC will result in a decrease of canopy height. In BWS, it was observed that trees with relatively lower height such as Excoecaria agallocha were densely packed than other taller trees, like Avicennia officinalis, and Heritiera fomes. Thus, densely packed patches could have lower canopy heights, leading to negative sensitivity of FVC to canopy height.
Several studies found that coherence showed reasonable correlation with canopy height. Olesk et al. [42] used four different models to illustrate the relationship between coherence and canopy height and found that all the models performed well in describing the relationships. In general, the coherence of an interferometric pair decreases due to the volumetric effect, among other reasons [74]. As tree height is a significant indicator of aboveground volume in forested areas, and the canopy height is highly correlated with aboveground volume, coherence must have a correlation with canopy height. Therefore, coherence can be used to estimate canopy height. Schlund et al. [88] found that volume decorrelation can be traced back to the canopy height. As a result, we found it as an essential variable in both models. In the SR model, it is negatively correlated with the canopy height. It happened so because, with the increase in height, the volume decorrelation increases leading to decrease in coherence. Therefore, decrease in coherence could indicate increase in canopy height and vice versa.
The estimation of canopy height with the help of LAI was not largely explored. Some studies have shown a possible relationship between them [52,89]. Pope and Treitz [50] showed that LiDAR predicted height could be used for LAI estimation to an acceptable extent for boreal forests. Qu et al. [51] found that even for a tropical forest site, height metrics derived from LiDAR data can estimate LAI quite efficiently. They also showed that it even performs better than MODIS LAI. Thus, these studies showed that there is a relationship that exists between canopy height and LAI. However, remote sensing based studies have not tried to use the relationship to estimate canopy height from LAI. Here, LAI was found as the second most important variable for both models, which showed good correlation of LAI with canopy height.
4.3. Canopy Height Models and Maps
Both SR and RF models demonstrated capability in predicting canopy heights with the former having better efficiency. The SR model established here is complicated with more functions and higher complexity. A complex model is more likely to map the inherent non-linearity among the predictors, while a simpler model is preferred for its easy interpretability. The relationship observed between remotely sensed parameters, and biophysical variables were generally non-linear and complex [90]. Although different machine learning algorithms, including RF, can estimate biophysical parameters efficiently, the lack of interpretability restricts the replication of their results; which can be overcome with the use of SR based models.
Though the canopy height maps differ in values, they showed similar trends for most of the areas, i.e., higher values in one map correspond to higher values in other maps, and vice versa. The difference in canopy height map showed that the values were generally higher for SR model prediction than the RF model prediction values. However, there could be exceptions (marked by a red ellipse in Figure 3), due to mainly two reasons. First, the different variable importance in different models as the RF and SR models used different set of essential variables leading to slightly different results. Second, some differences occurred due to the extrapolation problem of the RF model [91]. RF regressions cannot predict values outside the range of the training data as it is based on averaging the values of multiple outputs. In RF regression, final predictions were derived by averaging the results of many tree canopies. Additionally, each canopy output was derived as the mean values in each terminal node of a tree. The average for a set of values must be well within the value range. Therefore, the highest canopy height value remained below 14 m in the RF model predicted map (Figure 9c), whereas field-measured data reported canopy height values beyond 14 m. The RF model training sample tend to underestimate the higher canopy height values and overestimate the lower range values. The SR model can extrapolate values beyond the range of training data, therefore, a large area observed with a canopy height between 14 and 18 m for the SR model prediction (Figure 9a). Therefore, for the upper and lower canopy height values that lie beyond the training data range, the SR model prediction could be erroneous. Castillo et al. [92] also reported discouraging extrapolation with SR model.
The canopy height maps showed limited correlation with the ICESat-2 estimated canopy height. The first release of the ALT08 data product has some known issues which may affect the estimated canopy height [93]. ICESat-2 data is also found to have a vertical RMSE of 3.2 m for canopy height retrieval [94]. So, these reasons may affect the correlation between model estimated canopy height and ICESat-2 estimated height. In future, with the availability of an increased amount of more accurate footprints, an improved relationship between the two can be expected. Additionally, the canopy height models were built on field measured inputs with a laser rangefinder, which may have some instrumental error [8].
5. Conclusions
The mangroves are one of the critical storages of aboveground carbon, and they are experiencing considerable alternations due to climate change. Accurate information about the carbon storage proxies, such as canopy height, will help estimate AGB and carbon sequestration. Forest canopy height models, especially for the mangroves, were generally prepared by using airborne LiDAR, high spatial resolution stereo imagery, or SAR interferometry [20,56,95]. Nonetheless, most of these methods were not always applicable to all the areas due to a lack of proper data availability. The current study proposed a method that can be applied to anywhere else in the world as it is based on Sentinel series data having global coverage.
In this study, we have analysed the potential of Sentinel-1 interferometric coherence, Sentinel-2 biophysical parameters in predicting the canopy height for mangroves. The interferometric coherence and biophysical parameters act as good predictors due to their relationship with the canopy height. Machine learning models were found to be an excellent method for canopy height modeling. Although the RF model demonstrated its efficiency in canopy height estimation, the SR model through genetic programming was found to be the most effective. The SR also established an interpretable model, which is not possible via any other machine learning algorithms. The SR-based model outperforms commonly used machine learning models like the RF. The fraction of vegetation cover (FVC) was found to be an essential variable for predicting canopy height. It was also found that the canopy height map correlates with ICESat-2 estimated canopy height, albeit modest. Overall, this study demonstrated the effectiveness of Sentinel series data and the SR in predicting canopy height.
Author Contributions
Conceptualization, S.M.G.; and M.D.B.; methodology, S.M.G.; and S.P.; formal analysis, S.M.G.; writing—original draft preparation, S.M.G.; writing—review and editing, M.D.B.; visualization, S.P.; supervision, M.D.B. All authors have read and agreed to the published version of the manuscript.
Funding
S.M.G. and S.P. thanks Ministry of Human resources Development (MHRD), India for Fellowships for PhD research. Canopy height measurements were taken during execution of a research project funded by Space Applications Centre (ISRO), India.
Acknowledgments
We acknowledge the support received from IIT Kharagpur authorities and State Forest and Wildlife Department of Odisha, India for the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Lewis, S.L. Tropical forests and the changing earth system. Philos. Trans. R. Soc. B Biol. Sci. 2006, 361, 195–210. [Google Scholar] [CrossRef] [PubMed]
- Behera, S.K.; Sahu, N.; Mishra, A.K.; Bargali, S.S.; Behera, M.D.; Tuli, R. Aboveground biomass and carbon stock assessment in Indian tropical deciduous forest and relationship with stand structural attributes. Ecol. Eng. 2017, 99, 513–524. [Google Scholar] [CrossRef]
- Feldpausch, T.R.; Lloyd, J.; Lewis, S.L.; Brienen, R.J.W.; Gloor, M.; Monteagudo Mendoza, A.; Lopez-Gonzalez, G.; Banin, L.; Abu Salim, K.; Affum-Baffoe, K.; et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 2012, 9, 3381–3403. [Google Scholar] [CrossRef]
- Valbuena, R.; Heiskanen, J.; Aynekulu, E.; Pitkänen, S.; Packalen, P. Sensitivity of Above-Ground Biomass Estimates to Height-Diameter Modelling in Mixed-Species West African Woodlands. PLoS ONE 2016, 11, e0158198. [Google Scholar] [CrossRef] [PubMed]
- Mutwiri, F.K.; Odera, P.A.; Kinyanjui, M.J. Estimation of Tree Height and Forest Biomass Using Airborne LiDAR Data: A Case Study of Londiani Forest Block in the Mau Complex, Kenya. Open J. For. 2017, 7, 255–269. [Google Scholar] [CrossRef]
- Kearsley, E.; De Haulleville, T.; Hufkens, K.; Kidimbu, A.; Toirambe, B.; Baert, G.; Huygens, D.; Kebede, Y.; Defourny, P.; Bogaert, J.; et al. Conventional tree height-diameter relationships significantly overestimate aboveground carbon stocks in the Central Congo Basin. Nat. Commun. 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed – A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar] [CrossRef]
- Lee, W.-J.; Lee, C.-W. Forest Canopy Height Estimation Using Multiplatform Remote Sensing Dataset. J. Sens. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. Comparison of canopy volume measurements of scattered eucalypt farm trees derived from high spatial resolution imagery and LiDAR. Remote Sens. 2016, 8, 388. [Google Scholar] [CrossRef]
- St-Onge, B.A.; Achaichia, N. Measuring Forest Canopy Height Using a Combination. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2001, XXXIV, 131–137. [Google Scholar]
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of southeastern North America. For. Ecol. Manag. 2009, 257, 1136–1147. [Google Scholar] [CrossRef]
- Luoma, V.; Saarinen, N.; Wulder, M.A.; White, J.C.; Vastaranta, M.; Holopainen, M.; Hyyppä, J. Assessing precision in conventional field measurements of individual tree attributes. Forests 2017, 8, 38. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-Landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Hunter, M.O.; Keller, M.; Victoria, D.; Morton, D.C. Tree height and tropical forest biomass estimation. Biogeosciences 2013, 10, 8385–8399. [Google Scholar] [CrossRef]
- Véga, C.; St-Onge, B. Height growth reconstruction of a boreal forest canopy over a period of 58 years using a combination of photogrammetric and lidar models. Remote Sens. Environ. 2008, 112, 1784–1794. [Google Scholar] [CrossRef]
- Jensen, J.R.; Lin, H.; Yang, X.; Iii, E.R.; Davis, B.A.; Ramsey, E. The measurement of mangrove characteristics in southwest Florida using spot multispectral data The Measurement of Mangrove Characteristics in Southwest Florida Using SPOT Multispectral Data. Geocart. Int. 1991, 2, 13–21. [Google Scholar] [CrossRef]
- Miller, D.R.; Quine, C.P.; Hadley, W. An investigation of the potential of digital photogrammetry to provide measurements of forest characteristics and abiotic damage. For. Ecol. Manag. 2000, 135, 279–288. [Google Scholar] [CrossRef]
- Lee, S.; Ni-meister, W.; Yang, W.; Chen, Q. Remote Sensing of Environment Physically based vertical vegetation structure retrieval from ICESat data: Validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ. 2011, 115, 2776–2785. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.K.; Feliciano, E.; Trettin, C.; Simard, M. A comparison of mangrove Canopy height using multiple independent measurements from land, air, and space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef]
- Ballhorn, U.; Jubanski, J.; Kronseder, K.; Siegert, F. Airborne LiDAR measurements to estimate tropical peat swamp forest above Ground Biomass. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, German, 22–27 July 2012. [Google Scholar]
- Csillik, O.; Kumar, P.; Mascaro, J.; O’Shea, T.; Asner, G.P. Monitoring tropical forest carbon stocks and emissions using Planet satellite data. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Neuenschwander, A.L.; Urban, T.J.; Gutierrez, R.; Schutz, B.E. Characterization of ICESat/GLAS waveforms over terrestial ecosystems: Implications for vegetation mapping. J. Geophys. Res. Biogeosci. 2008, 113, 1–18. [Google Scholar] [CrossRef]
- Xing, Y.; de Gier, A.; Zhang, J.; Wang, L. An improved method for estimating forest canopy height using ICESat-GLAS full waveform data over sloping terrain: A case study in changbai mountains, China. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 385–392. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Forest canopy height estimation using satellite laser altimetry: A case study in the Western Ghats, India. Appl. Geomatics 2017, 9, 159–166. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar]
- Tripathi, P.; Behera, M.D. Plant height profiling in western India using LiDAR data. Curr. Sci. 2013, 7, 970–977. [Google Scholar]
- Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern china using GLAS and MODIS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 140–152. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Nelson, R.; Ranson, K.J.; Sun, G.; Kimes, D.S.; Kharuk, V.; Montesano, P. Estimating Siberian timber volume using MODIS and ICESat/GLAS. Remote Sens. Environ. 2009, 113, 691–701. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; White, L.J.T.; Abernethy, K.A.; Jeffery, K.J.; Lewis, S.L.; Collins, M.; Lefsky, M.A.; Leal, M.E.; Woodhouse, I.H.; et al. Mapping tropical forest biomass with radar and spaceborne LiDAR in Lopé National Park, Gabon: Overcoming problems of high biomass and persistent cloud. Biogeosciences 2012, 9, 179–191. [Google Scholar] [CrossRef]
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 laser altimetry mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Neuenschwander, A.; Zhou, T.; Srinivasan, S.; Harbeck, K. Estimating aboveground biomass and forest canopy cover with simulated ICESat-2 data. Remote Sens. Environ. 2019, 224, 1–11. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Xue, B.; Hu, T.; Alvarez, O.; Tao, S.; Fang, J. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Treuhaft, R.; Lei, Y.; Gonçalves, F.; Keller, M.; dos Santos, J.R.; Neumann, M.; Almeida, A. Tropical-forest structure and biomass dynamics from TanDEM-X radar interferometry. Forests 2017, 8, 277. [Google Scholar] [CrossRef]
- Solberg, S.; Hansen, E.H.; Gobakken, T.; Næssset, E.; Zahabu, E. Biomass and InSAR height relationship in a dense tropical forest. Remote Sens. Environ. 2017, 192, 166–175. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 1999, 14, R1–R54. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing with Imaging Radar; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Olesk, A.; Praks, J.; Antropov, O.; Zalite, K.; Arumäe, T.; Voormansik, K. Interferometric SAR coherence models for Characterization of hemiboreal forests using TanDEM-X dssata. Remote Sens. 2016, 8, 700. [Google Scholar] [CrossRef]
- Torano Caicoya, A.; Kugler, F.; Hajnsek, I.; Papathanassiou, K. Boreal forest biomass classification with TanDEM-X. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, German, 22–27 July 2012. [Google Scholar]
- Cougo, M.; Souza-Filho, P.; Silva, A.; Fernandes, M.; Santos, J.; Abreu, M.; Nascimento, W.; Simard, M. Radarsat-2 Backscattering for the Modeling of Biophysical Parameters of Regenerating Mangrove Forests. Remote Sens. 2015, 7, 17097–17112. [Google Scholar] [CrossRef]
- Hansen, M.C.; Potapov, P.V.; Goetz, S.J.; Turubanova, S.; Tyukavina, A.; Krylov, A.; Kommareddy, A.; Egorov, A. Mapping tree height distributions in Sub-Saharan Africa using Landsat 7 and 8 data. Remote Sens. Environ. 2016, 185, 221–232. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Fu, Y.; Niu, H.; Yang, Y.; Zhang, B. Fractional vegetation cover estimation of different vegetation types in the Qaidam Basin. Sustainability 2019, 11, 864. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A combined GLAS and MODIS estimation of the global distribution of mean forest canopy height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Welles, J.M.; Norman, J.M. Instrument for Indirect Measurement of Canopy Architecture. Agron. J. 1991, 83, 818. [Google Scholar] [CrossRef]
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Pope, G.; Treitz, P. Leaf Area Index (LAI) estimation in boreal mixedwood forest of Ontario, Canada using Light detection and ranging (LiDAR) and worldview-2 imagery. Remote Sens. 2013, 5, 5040–5063. [Google Scholar] [CrossRef]
- Qu, Y.; Shaker, A.; Silva, C.A.; Klauberg, C.; Pinagé, E.R. Remote sensing of leaf area index from LiDAR height percentile metrics and comparison with MODIS product in a selectively logged tropical forest area in Eastern Amazonia. Remote Sens. 2018, 10, 970. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, X.; Yin, F.; Zhan, J. Examination of the Quantitative Relationship between Vegetation Canopy Height and LAI. Adv. Meteorol. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Kenyi, L.W.; Dubayah, R.; Hofton, M.; Schardt, M. Comparative analysis of SRTM-NED vegetation canopy height to LIDAR-derived vegetation canopy metrics. Int. J. Remote Sens. 2009, 30, 2797–2811. [Google Scholar] [CrossRef]
- Sadeghi, Y.; St-Onge, B.; Leblon, B.; Prieur, J.F.; Simard, M. Mapping boreal forest biomass from a SRTM and TanDEM-X based on canopy height model and Landsat spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 202–213. [Google Scholar] [CrossRef]
- Wicaksono, P.; Danoedoro, P.; Hartono; Nehren, U. Mangrove biomass carbon stock mapping of the Karimunjawa Islands using multispectral remote sensing. Int. J. Remote Sens. 2016, 37, 26–52. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D.; Lee, S.K.; Fatoyinbo, T.E. Estimating mangrove canopy height and above-ground biomass in the Everglades National Park with airborne LiDAR and TanDEM-X data. Remote Sens. 2017, 9, 702. [Google Scholar] [CrossRef]
- Berninger, A.; Lohberger, S.; Stängel, M.; Siegert, F. SAR-based estimation of above-ground biomass and its changes in tropical forests of Kalimantan using L- and C-band. Remote Sens. 2018, 10, 831. [Google Scholar] [CrossRef]
- Pham, L.T.H.; Brabyn, L. Monitoring mangrove biomass change in Vietnam using SPOT images and an object-based approach combined with machine learning algorithms. ISPRS J. Photogramm. Remote Sens. 2017, 128, 86–97. [Google Scholar] [CrossRef]
- Ghosh, S.M.; Behera, M.D. Aboveground biomass estimation using multi-sensor data synergy and machine learning algorithms in a dense tropical forest. Appl. Geogr. 2018, 96, 29–40. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Iba, H.; Feng, J.; Izadi Rad, H. GP-RVM: Genetic Programing-Based Symbolic Regression Using Relevance Vector Machine. arXiv 2018, arXiv:1806.02502. [Google Scholar]
- Stijven, S.; Vladislavleva, E.; Kordon, A.; Willem, L.; Kotanchek, M.E. Prime-Time: Symbolic Regression Takes Its Place in the Real World. In Genetic Programming Theory and Practice XIII; Springer: Berlin/Heidelberg, Germany, 2016; pp. 241–260. [Google Scholar]
- Reddy, C.S.; Pattanaik, C.; Dhal, N.K.; Biswal, A.K. Vegetation and Floristic Diversity of Bhitarkanika National Park, Orissa, India. Indian For. 2006, 132, 664–680. [Google Scholar]
- Forest Survey of India (FSI). State of Forest Report; Forest Survey of India (FSI): Dehradun, India, 2017. [Google Scholar]
- Reddy, C.S. Field Identification Guide for Indian Mangroves; Bishen Singh Mahendra Pal Singh: Dehradun, India, 2008; Volume 001. [Google Scholar]
- Pattanaik, C.; Reddy, C.S.; Dhal, N.K.; Das, R. Utilisation of mangrove forests in Bhitarkanika wildlife sanctuary, Orissa. Indian J. Tradit. Knowl. 2008, 7, 598–603. [Google Scholar]
- Sullivan, M.J.P.; Lewis, S.L.; Hubau, W.; Qie, L.; Baker, T.R.; Banin, L.F.; Chave, J.; Cuni-Sanchez, A.; Feldpausch, T.R.; Lopez-Gonzalez, G.; et al. Field methods for sampling tree height for tropical forest biomass estimation. Methods Ecol. Evol. 2018, 9, 1179–1189. [Google Scholar] [CrossRef] [PubMed]
- Yague-Martinez, N.; Prats-Iraola, P.; Gonzalez, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric Processing of Sentinel-1 TOPS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef]
- Bickel, D.L. SAR Image Effects on Coherence and Coherence Estimation; Sandia National Laboratories: Albuquerque, NM, USA, 2014. [Google Scholar]
- Louis, J.; Debaecker, V.; Pflug, B.; Main-Knorn, M.; Bieniarz, J.; Mueller-Wilm, U.; Cadau, E.; Gascon, F. Sentinel-2 SEN2COR: L2A processor for users. In Proceedings of the Living Planet Symposium 2016, Prague, Czech Republic, 13 May 2016; Volume ESA SP-740. [Google Scholar]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Popescu, S.C.; Nelson, R.F.; Harding, D.; Pitts, K.L.; Robbins, J. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 1. Available online: https://doi.org/10.5067/ATLAS/ATL08.001 (accessed on 10 August 2019).
- Ferretti, A.; Monti-guarnieri, A.; Prati, C.; Rocca, F. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation, Part C. InSAR Processing: A Mathematical Approach; ESA Publications: Auckland, New Zealand, 2007. [Google Scholar]
- Geudtner, D.; Torres, R.; Snoeij, P.; Ostergaard, A.; Navas-Traver, I.; Rommen, B.; Brown, M. Sentinel-1 system overview and performance. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 13 September 2013; pp. 1719–1721. [Google Scholar]
- Weiss, M.; Baret, F. S2ToolBox Level 2 Products: LAI, FAPAR, FCOVER; Institut National de la Recherche Agronomique (INRA): Avignon, France, 2016. [Google Scholar]
- Max, K.; Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Aryadoust, V. Application of Evolutionary Algorithm-Based Symbolic Regression to Language Assessment: Toward Nonlinear Modeling. Psychol. Test Assess. Model. 2015, 57, 301. [Google Scholar]
- Schmidt, M.; Lipson, H. Distilling Free-Form Natural Laws from Experimental Data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Dyk, M. Van Identifying Patterns in Course-Leaving That Predict Student Leaving—A Comparison of Different Predictive Algorithms. Master’s Thesis, University of Oklahoma, Norman, OK, USA, 2018. [Google Scholar]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinf. 2008, 9, 307. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-inter species biomass prediction in a plantation forest: Testing the utility of high spatial resolution spaceborne multispectral RapidEye sensor and advanced machine learning algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef]
- Stijven, S.; Minnebo, W.; Vladislavleva, K. Separating the Wheat from the Chaff: On Feature Selection and Feature Importance in Regression Random Forests and Symbolic Regression. In Proceedings of the 13th annual conference companion on genetic and evolutionary computation, Dublin, Ireland, 12 July 2011; pp. 623–630. [Google Scholar]
- Chen, Q.; Zhang, M.; Xue, B. Feature selection to improve generalization of genetic programming for high-dimensional symbolic regression. IEEE Trans. Evol. Comput. 2017, 21, 792–806. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Korhonen, L.; Korhonen, K.T.; Stenberg, P.; Maltamo, M.; Rautiainen, M. Local models for forest canopy cover with beta regression. Silva Fenn. 2007, 41, 671–685. [Google Scholar] [CrossRef]
- Schlund, M.; von Poncet, F.; Hoekman, D.H.; Kuntz, S.; Schmullius, C. Importance of bistatic SAR features from TanDEM-X for forest mapping and monitoring. Remote Sens. Environ. 2014, 151, 16–26. [Google Scholar] [CrossRef]
- Jaimez, R.E.; Araque, O.; Guzman, D.; Mora, A.; Espinoza, W.; Tezara, W. Agroforestry systems of timber species and cacao: Survival and growth during the early stages. J. Agric. Rural Dev. Trop. Subtrop. 2013, 114, 1–11. [Google Scholar]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 2018, e5518. [Google Scholar] [CrossRef]
- Castillo, F.; Marshall, K.; Green, J.; Kordon, A. A methodology for combining symbolic regression and design of experiments to improve empirical model building. Lect. Notes Comput. Sci. 2003, 2724, 1975–1985. [Google Scholar]
- Neuenschwander, A.; Klotz, B.; Jelley, B. ATL08 Known Issues—Release 001. 2019. Available online: https://nsidc.org/sites/nsidc.org/files/technical-references/ATL08_Release001_Known%20Issues.2.pdf (accessed on 26 February 2020).
- Neuenschwander, A.L.; Magruder, L.A. Canopy and Terrain Height Retrievals with ICESat-2: A First Look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Wannasiri, W.; Nagai, M.; Honda, K.; Santitamnont, P.; Miphokasap, P. Extraction of Mangrove Biophysical Parameters Using Airborne LiDAR. Remote Sens. 2013, 5, 1787–1808. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).