The Impact of SMOS Soil Moisture Data Assimilation within the Operational Global Flood Awareness System (GloFAS)
Abstract
1. Introduction
2. Materials and Methods
2.1. SMOS Soil Moisture Data
2.2. GloFAS Streamflow Predictions
2.2.1. H-TESSEL Surface and Subsurface Runoff Forecasts
2.2.2. LISFLOOD Channel Routing
2.3. Streamflow Observations
2.4. GloFAS Experiment Design
2.5. Streamflow Evaluation
2.5.1. Verification against In-Situ Observations
2.5.2. Global Impact upon GloFAS
3. Results
3.1. Verification against Observed Streamflow
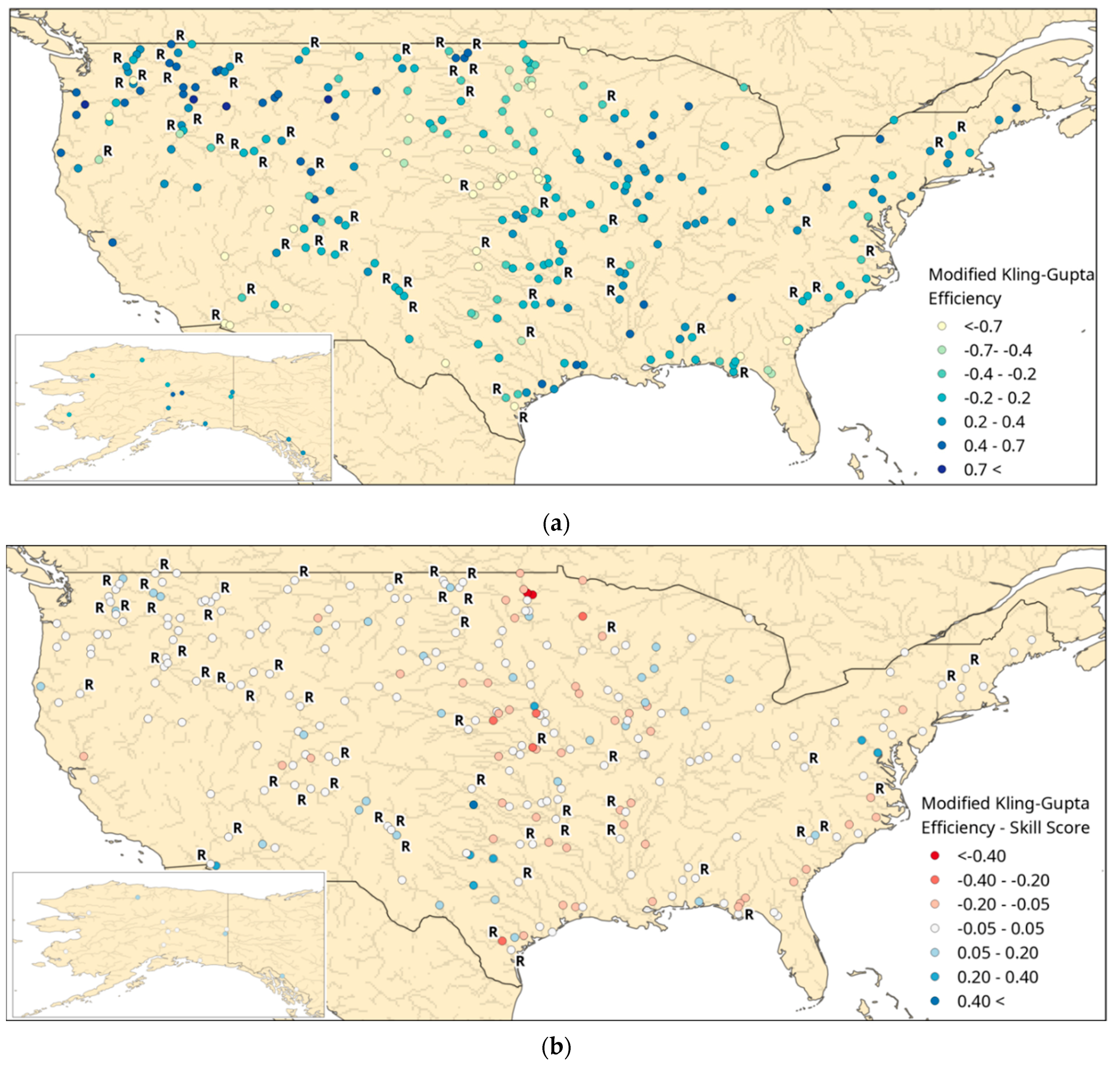
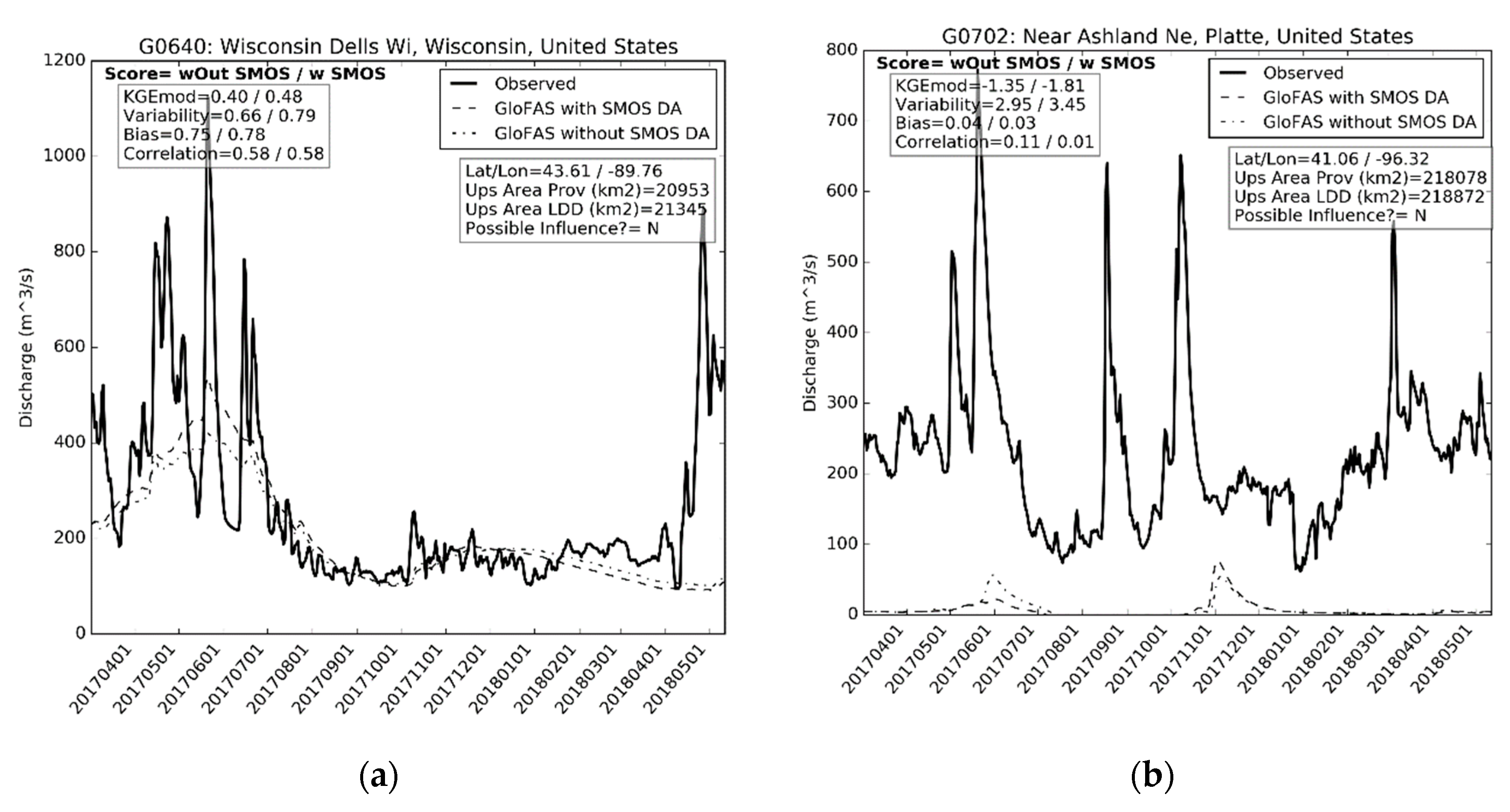
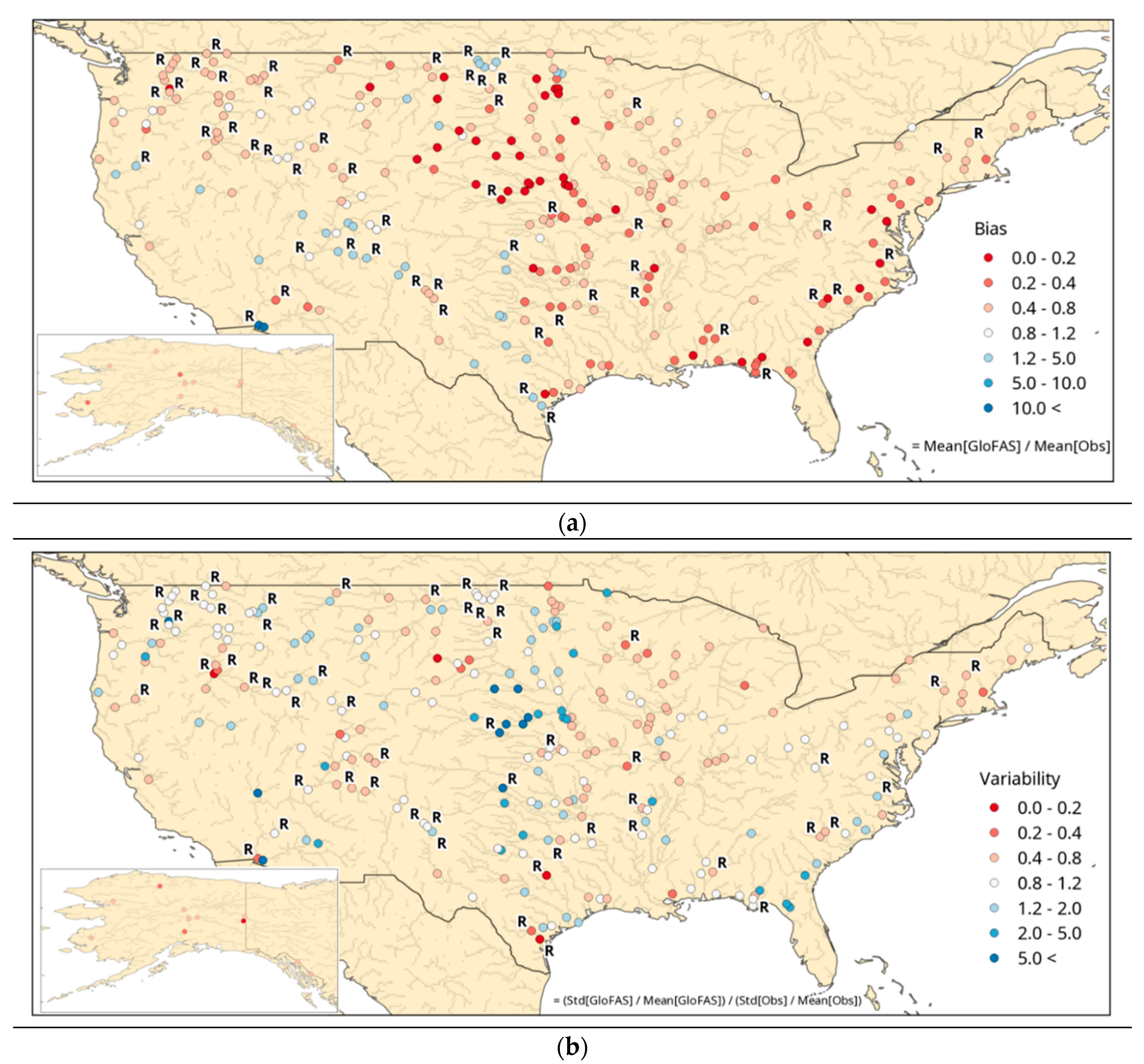
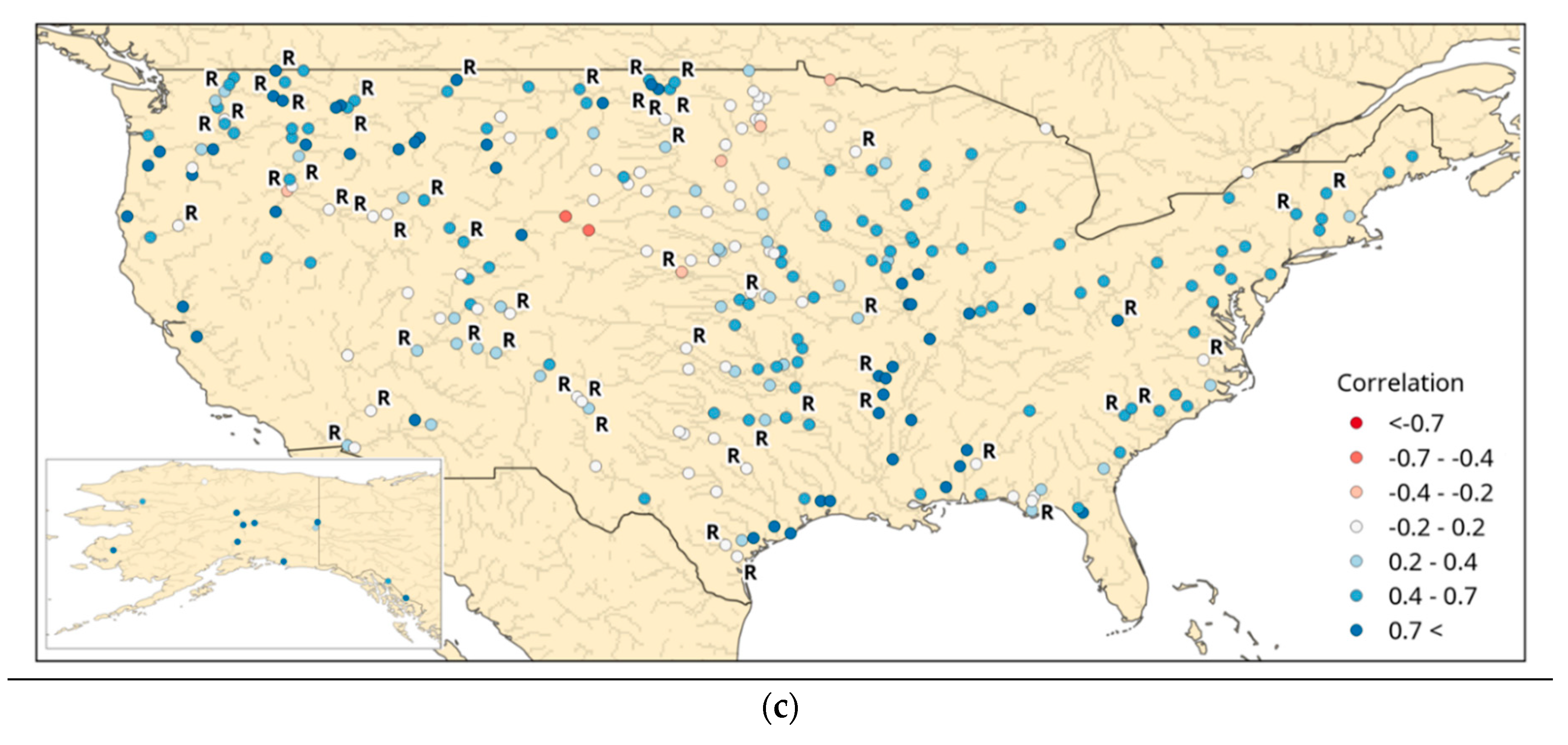
3.1.1. United States
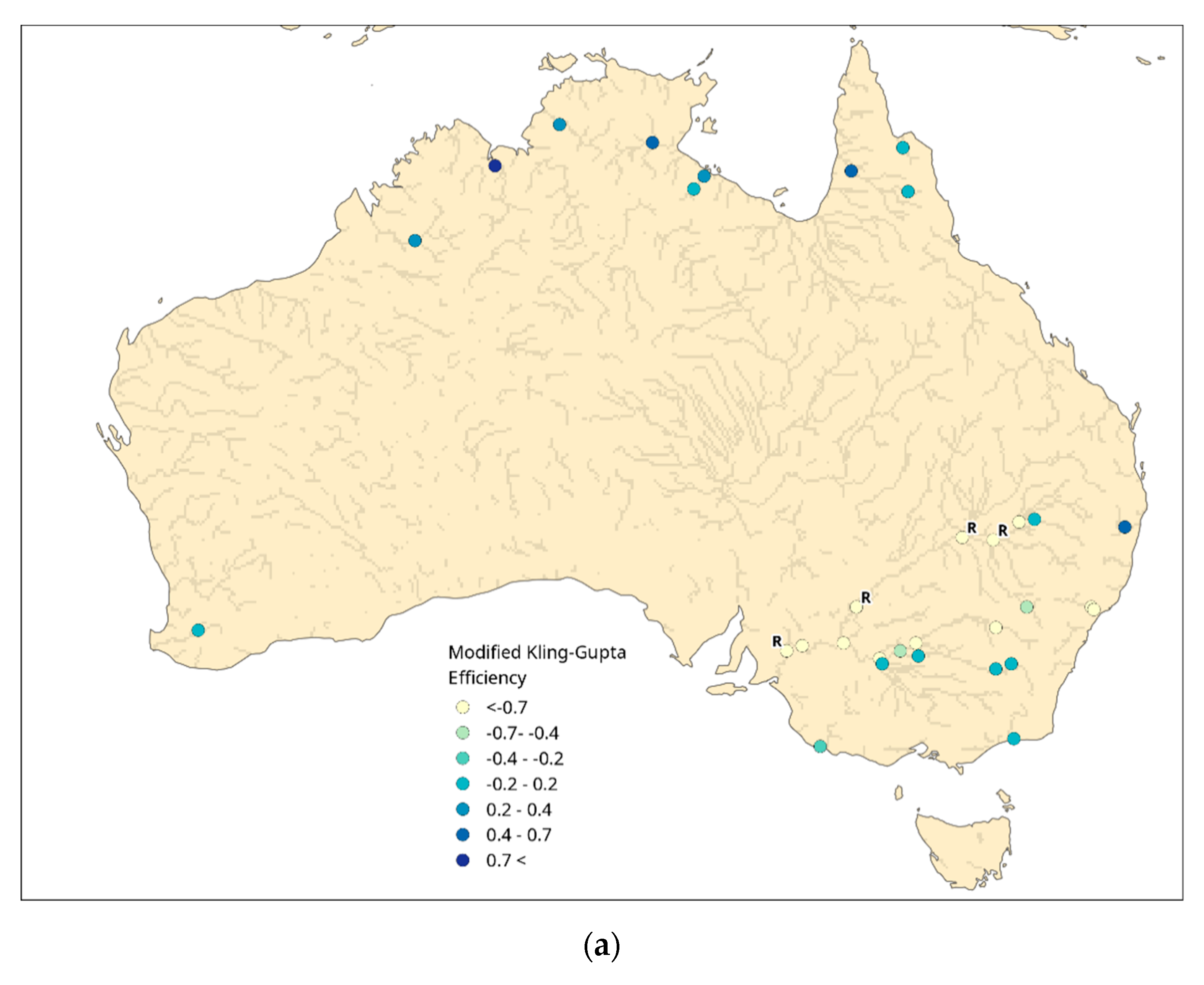
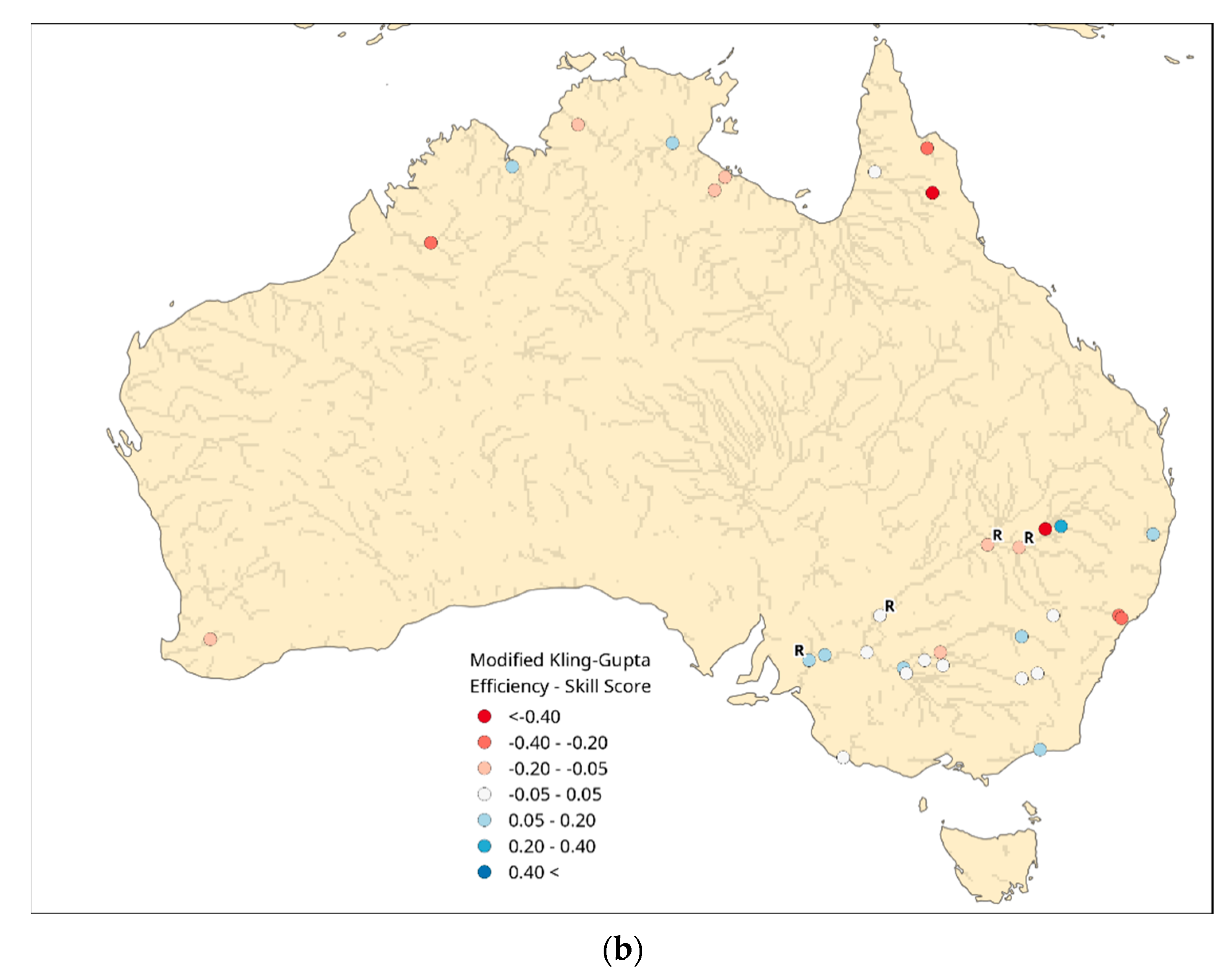
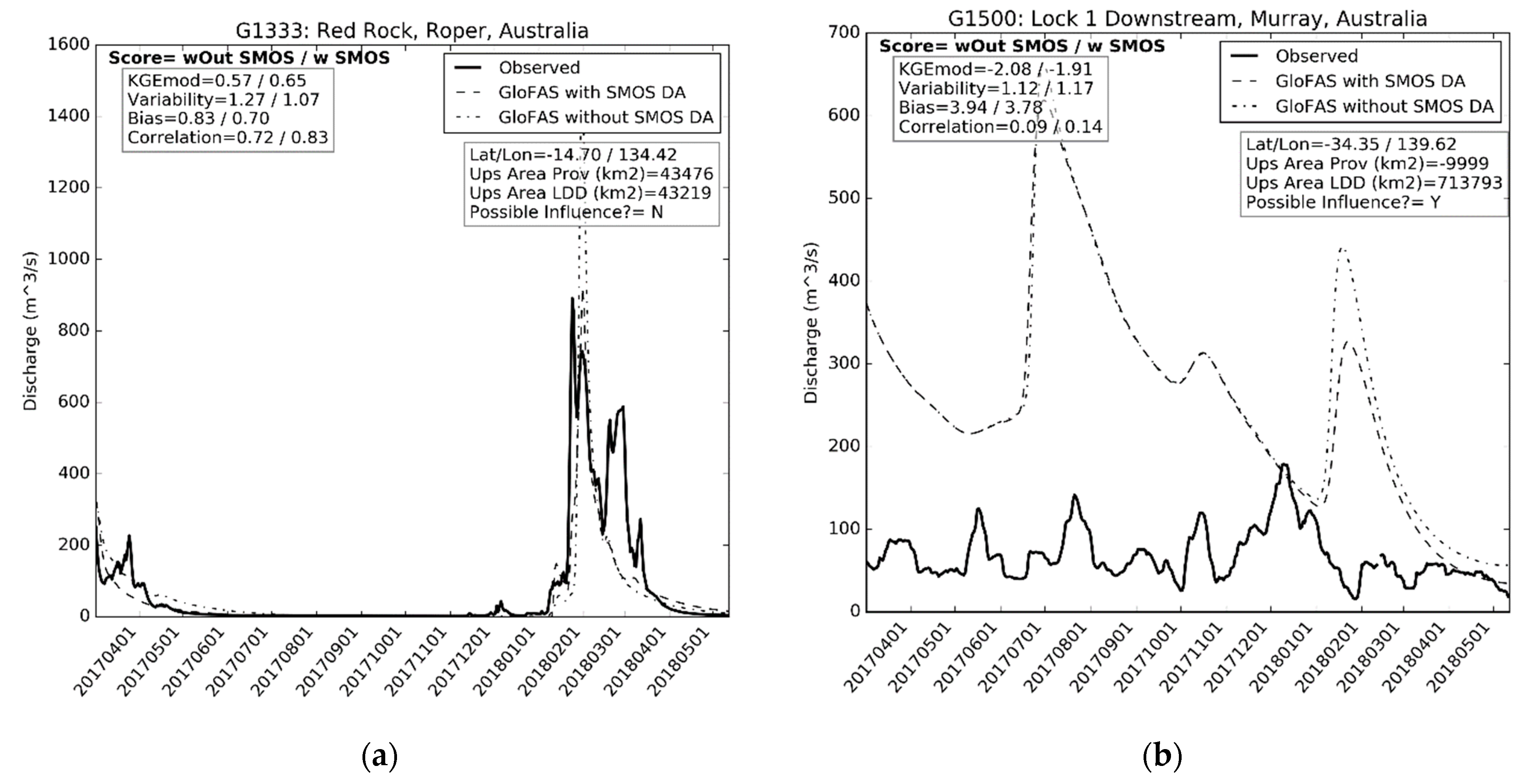
3.1.2. Australia
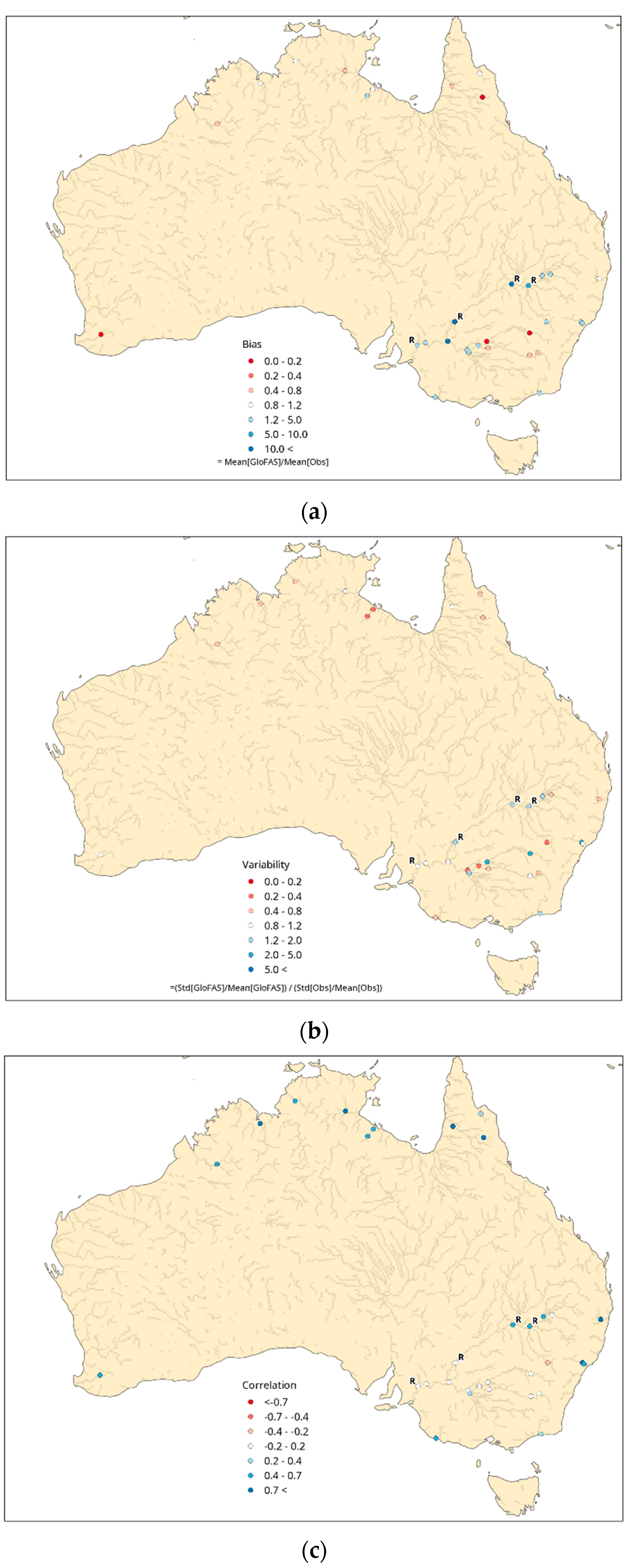
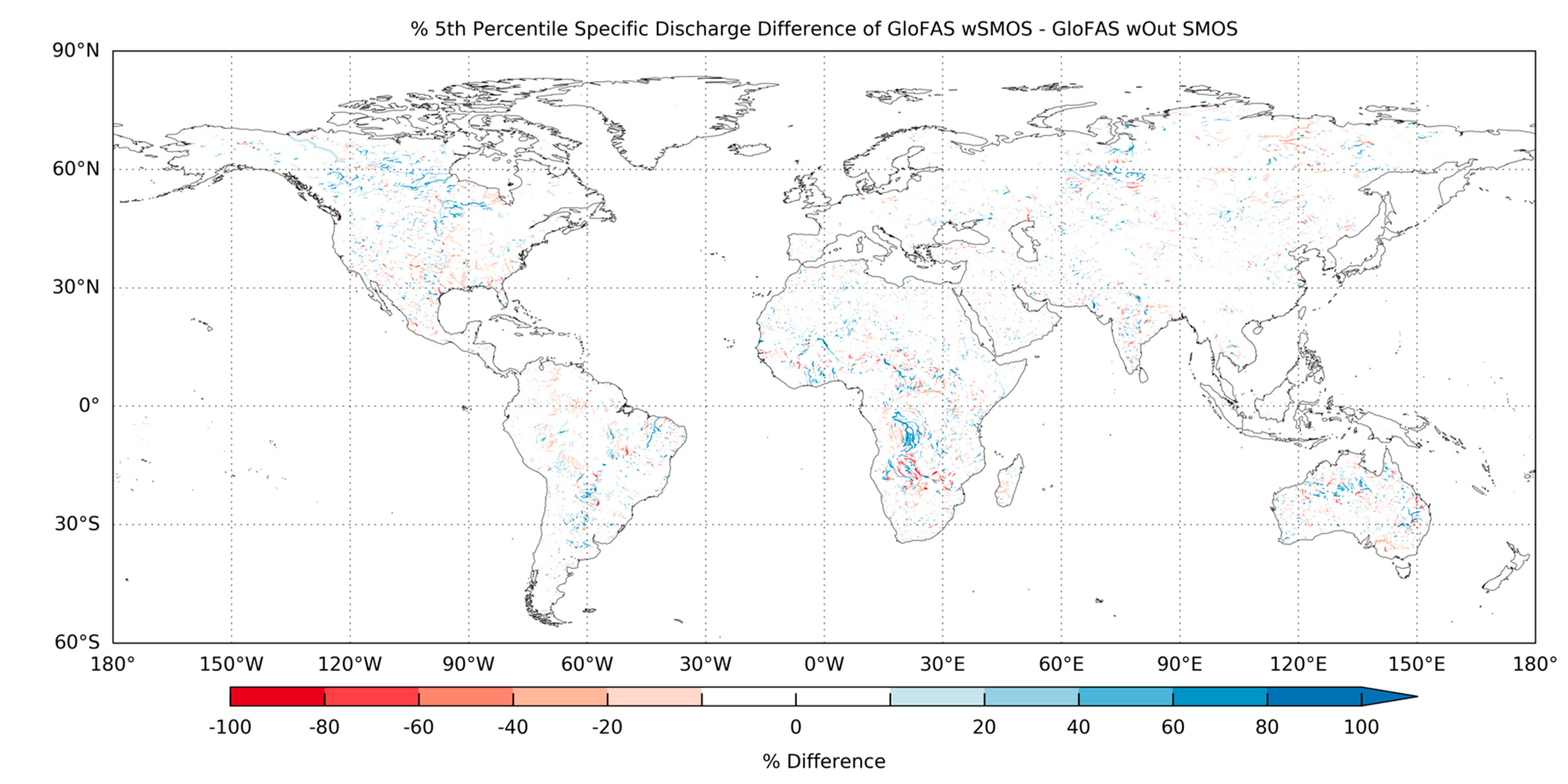
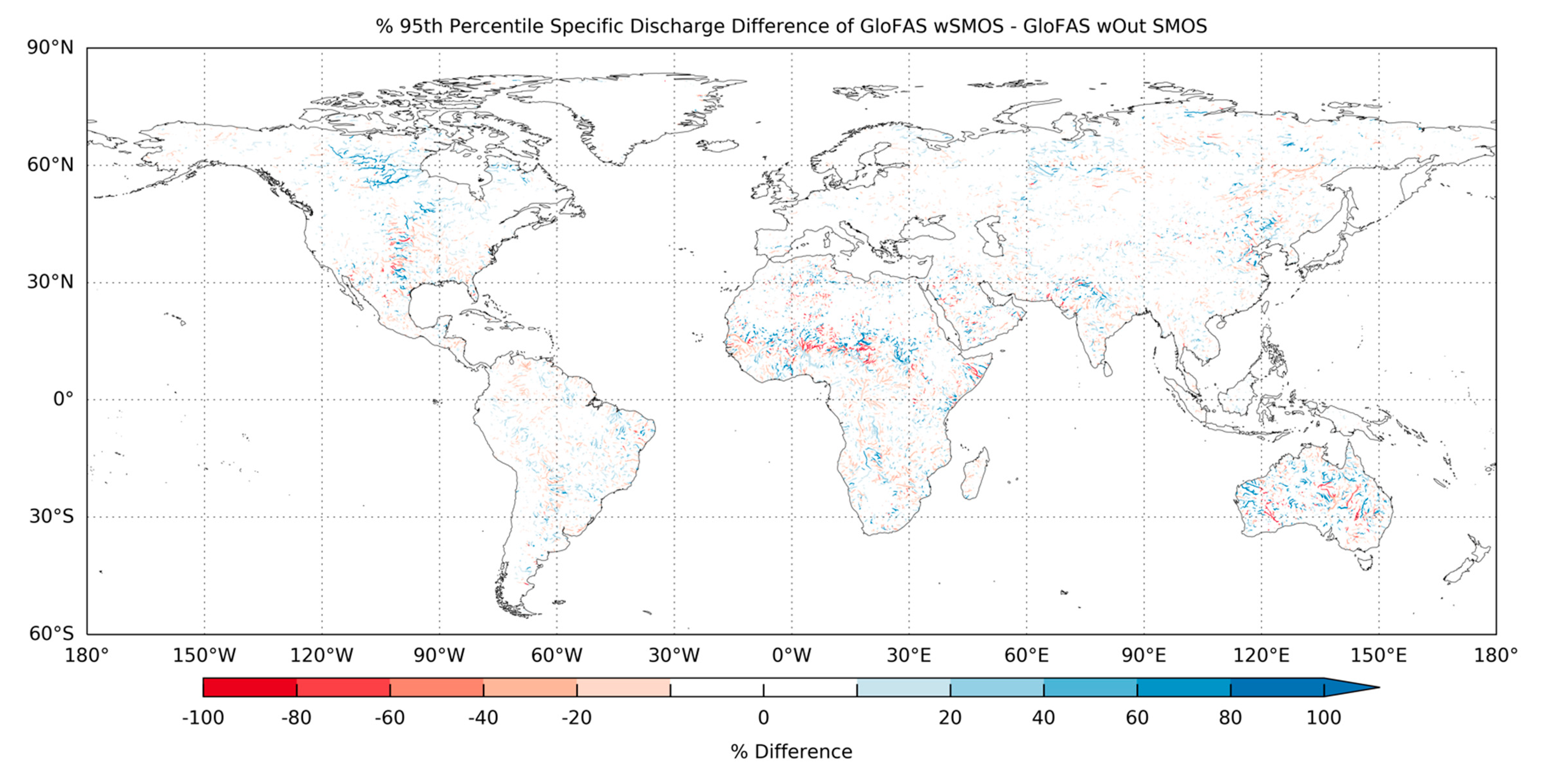
3.2. Global Impact upon GloFAS
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wood, A.W.; Lettenmeier, D.P. An ensemble approach for attribution of hydrologic prediction uncertainty. Geophys. Res. Lett. 2008, 34, 14401. [Google Scholar] [CrossRef]
- Arnal, L.; Cloke, H.L.; Stephens, E.; Wetterhall, F.; Prudhomme, C.; Neumann, J.; Krzeminski, B.; Pappenberger, F. Skillful seasonal forecasts of streamflow over Europe? Hydrol. Earth Syst. Sci. 2018, 22, 2057–2072. [Google Scholar] [CrossRef]
- Seo, D.; Lakhankar, T.; Cosgrove, B.; Khanbilvardi, R.; Zhan, X. Applying SMOS soil moisture data into the National Weather Service (NWS)’s Research Distributed Hydrologic Model (HL-RDHM) for flash flood guidance application. Remote Sens. Appl. Soc. Environ. 2017, 8, 182–192. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P.; Livneh, B.; Lettenmeier, D.P.; Reichle, R.H. Skill in streamflow forecasts derived from large-scale estimates of soil moisture and snow. Nat. Geosci. 2010, 3, 613–616. [Google Scholar] [CrossRef]
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and global scale flood forecasting systems. WIREs Water 2016, 3, 391–418. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observations: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Zreda, M.; Shuttleworth, W.J.; Zeng, X.; Zweck, C.; Desilets, D.; Franz, T.; Rosolem, R. COSMOS: The COSmic-ray Soil Moisture Observing System. Hydrol. Earth Syst. Sci. 2012, 16, 4079–4099. [Google Scholar] [CrossRef]
- Evans, J.G.; Ward, H.C.; Blake, J.R.; Hewitt, E.J.; Morrison, R.; Fry, M.; Ball, L.A.; Doughty, L.C.; Libre, J.W.; Hitt, O.E.; et al. Soil water content in southern England derived from a cosmic-ray soil moisture observing system COSMOS-UK. Hydrol. Process. 2016, 30, 4987–4999. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Barre, H.J.M.P.; Duesmann, B.; Kerr, Y.H. SMOS: The mission and system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- Kim, S.; Liu, Y.Y.; Johnson, F.M.; Parinussa, R.M.; Sharma, A. A global comparison of alternate AMSR2 soil moisture products: Why do they differ? Remote Sens. Environ. 2015, 161, 43–62. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Chen, N.; Zhang, X.; Cosh, M.H.; Wang, W. Satellite surface soil moisture from SMAP, SMOS, AMSR2 and ESA CCI: A comprehensive assessment using global ground based observations. Remote Sens. Environ. 2019, 231, 111215. [Google Scholar] [CrossRef]
- Wigneron, J.-P.; Kerr, Y.; Waldteufel, P.; Saleh, K.; Escorihuela, M.-J.; Richaume, P.; Ferrazzoli, P.; de Rosnay, P.; Gurney, R.; Calvet, J.-C.; et al. L-band microwave emission of the biosphere (L-MEB) model: Description and calibration against experimental data sets over crop fields. Remote Sens. Environ. 2007, 107, 639–655. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jiménez, C.; Mahmoodi, A.; Drusch, M. Soil moisture retrieval using neural networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.J.; Muñoz Sabater, J.; Richaume, P.; de Rosnay, P.; Kerr, Y.H.; Albergel, C.; Drusch, M.; Mecklenburg, S. SMOS near-real-time soil moisture product: Processor overview and first validation results. Hydrol. Earth Syst. Sci. 2017, 21, 5201–5216. [Google Scholar] [CrossRef]
- de Rosnay, P.; Drusch, M.; Vasiljevic, M.; Balsamo, G.; Albergel, C.; Isaksen, L. A simplified Extended Kalman Filter for the global operational soil moisture analysis at ECMWF. Q. J. R. Meteorol. Soc. 2013, 139, 1199–1213. [Google Scholar] [CrossRef]
- López López, P.; Wanders, N.; Schellekens, J.; Renzullo, L.J.; Sutanudjaja, E.H.; Bierkens, M.F.P. Improved large-scale hydrological modelling through the assimilation of streamflow and downscaled satellite soil moisture observations. Hydrol. Earth Syst. Sci. 2016, 20, 3059–3076. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting satellite-based soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W.; Hasenauer, S.; Hahn, S. Assimilation of surface- and root-zone ASCAT soil moisture products into rainfall-runoff modelling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.-H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Walker, J.P.; Pauwels, V.R.N. Application of remote sensing data to constrain operational rainfall-driven flood forecasting: A review. Remote Sens. 2016, 8, 456. [Google Scholar] [CrossRef]
- ECMWF. ECMWF. ECMWF Part II: Data Assimilation. In IFS Documentation CY46R1 Operational Implementation 6 June 2019; ECMWF, Ed.; ECMWF: Reading, UK, 2019; p. 103. Available online: https://www.ecmwf.int/en/elibrary/19306-part-ii-data-assimilation (accessed on 30 March 2020).
- de Rosnay, P.; Muñoz Sabater, J.; Albergel, C.; Isaksen, L.; English, S.; Drusch, M.; Wigneron, J.-P. SMOS brightness temperature forward modelling and long term monitoring at ECMWF. Remote Sens. Environ. 2020, 237, 111424. [Google Scholar] [CrossRef]
- Fairbairn, D.; de Rosnay, P.; Browne, P. The new stand-alone surface analysis at ECMWF: Implications for land-atmosphere DA coupling. J. Hydrometeorol. 2019, 20, 2023–2042. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.; de Rosnay, P.; Albergel, C.; Richaume, P.; Aires, F.; Prigent, C.; Kerr, Y. SMOS Neural Network Soil Moisture Data Assimilation in a Land Surface Model and Atmospheric Impact. Remote Sens. 2019, 11, 1334. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Dutra, E.; Krzeminski, B.; Muraro, D.; Thielen, J.; Pappenberger, F. GloFAS—Global ensemble streamflow forecasting and flood early warning. Hydrol. Earth Syst. Sci. 2013, 17, 1161–1175. [Google Scholar] [CrossRef]
- Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Salamon, P.; Wetterhall, F.; Barnard, C.; Cloke, H.; Pappenberger, F. GloFAS-ERA5 operational global river discharge reanalysis 1979-present. Earth Syst. Sci. Data Discuss. 2020. [Google Scholar] [CrossRef]
- Balsamo, G.; Viterbo, P.; Beljaars, A.; van den Hurk, B.; Hirschi, M.; Betts, A.K.; Scipal, K. A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the Integrated Forecast System. J. Hydrometeorol. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- van der Knijff, J.M.; Younis, J.; de Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Zsoter, E.; Cloke, H.; Stephens, E.; de Rosnay, P.; Muñoz Sabater, J.; Prudhomme, C.; Pappenberger, F. How well do operational numerical weather prediction configurations represent hydrology? J. Hydrometeorol. 2019, 20, 1533–1552. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Mecklenburg, S.; Drusch, M.; Kerr, Y.H.; Font, J.; Martín-Nuera, M.; Delwart, S.; Buenadicha, G.; Reul, N.; Daganzo-Eusebio, E.; Oliva, R.; et al. ESA’s soil moisture and ocean salinity mission: Mission performance and operations. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1354–1366. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.-P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Enache Juglea, S.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Muñoz Sabater, J.; Lawrence, H.; Albergel, C.; de Rosnay, P.; Isaksen, L.; Mecklenburg, S.; Drusch, M. Assimilation of SMOS brightness temperatures in the ECMWF integrated forecast system. Q. J. R. Meteorol. Soc. 2019, 145, 2524–2548. [Google Scholar] [CrossRef]
- ECMWF. IV: Physical Processes. In IFS Documentation CY46R1 Operational Implementation 6 June 2019; ECMWF, Ed.; ECMWF: Reading, UK, 2019; p. 223. Available online: https://www.ecmwf.int/en/elibrary/19308-part-iv-physical-processes (accessed on 30 March 2020).
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- FAO. Digital soil map of the world (DSMW). In Technical Report, Food and Agriculture Organization of the United Nations, re-issued version; FAO: Rome, Italy, 2003. [Google Scholar]
- Wu, H.; Kimball, J.S.; Li, H.; Huang, M.; Leung, L.R.; Adler, R.F. A new global river network database for macroscale hydrologic modelling. Water Resour. Res. 2012, 48, 09701. [Google Scholar] [CrossRef]
- Lehner, B.; Verdin, K.; Jarvis, A. New global hydrography derived from spaceborne elevation data. Eos Trans. 2008, 89, 93–94. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, 2004. [Google Scholar] [CrossRef]
- Yamazaki, D.; O’Loughlin, F.; Trigg, M.A.; Miller, Z.F.; Pavelsky, T.M.; Bates, P.D. Development of the Global Width Database for Large Rivers. Water Resour. Res. 2014, 50, 3467–3480. [Google Scholar] [CrossRef]
- Zajac, Z.; Revilla-Romero, B.; Salamon, P.; Burek, P.; Hirpa, F.; Beck, H. The impact of lake and reservoir parameterisation on global streamflow simulation. J. Hydrol. 2017, 548, 552–568. [Google Scholar] [CrossRef] [PubMed]
- Bollrich, G. Technische Hydromechanik: Grundlagen; Verlag Bauwesen: Wissen, Germany, 1992. [Google Scholar]
- Hirpa, F.A.; Salamon, P.; Beck, H.E.; Lorini, V.; Alfieri, L.; Zsoter, E.; Dadson, S.J. Calibration of the Global Flood Awareness System (GloFAS) using daily streamflow data. J. Hydrol. 2018, 566, 595–606. [Google Scholar] [CrossRef] [PubMed]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- WMO. The Global Water Runoff Data Project. Workshop on the Global Runoff Data Set and Grid Estimation; World Climate Programme Research: Koblenz, Germany, 1989; Volume 302, p. 96. Available online: https://www.bafg.de/GRDC/EN/01_GRDC/11_rtnle/WCRP22_WMO_TD302.pdf?__blob=publicationFile (accessed on 30 March 2020).
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical Note: Inherent benchmark or not? Comparing Nash-Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Oxford, UK, 2011. [Google Scholar]
- Verhoest, N.E.C.; van den Berg, M.J.; Martens, B.; Lievens, H.; Wood, E.F.; Pan, M.; Kerr, Y.H.; Al Bitar, A.; Tomer, S.K.; Drusch, M.; et al. Copula-based downscaling of coarse-scale soil moisture observations with implicit bias correction. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3507–3521. [Google Scholar] [CrossRef]
- Murray–Darling Basin Authority. Basin Plan Annual Report 2017–2018; Murray-Darling Basin Authority: Canberra, Australia, 2019; p. 32. Available online: https://www.mdba.gov.au/sites/default/files/pubs/basin-plan-annual-report-2017-18.pdf (accessed on 30 March 2020).
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; de Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray–Darling Basin, Australia. Remote Sens. Environ. 2015, 16, 146–162. [Google Scholar] [CrossRef]
- Lievens, H.; de Lannoy, G.J.M.; Al Bitar, A.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Tomer, S.K.; Martens, B.; Merlin, O.; et al. Assimilation of SMOS soil moisture and brightness temperature products into a land surface model. Remote Sens. Environ. 2016, 180, 292–304. [Google Scholar] [CrossRef]
- ESA. Land Cover CCI Product User Guide Version 2 Technical Report; UCL Geomatics: Louvain, Belgium, 2017; p. 105. Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 23 April 2020).
- Han, E.; Merwade, V.; Heathman, G.C. Implementation of surface soil moisture data assimilation with watershed scale distributed hydrological model. J. Hydrol. 2012, 416–417, 98–117. [Google Scholar] [CrossRef]
- Matgen, P.; Fenicia, F.; Heitz, S.; Plaza, D.; de Keyser, R.; Pauwels, V.R.N.; Wagner, W.; Savenije, H. Can ASCAT-derived soil wetness indices reduce predictive uncertainty in well-gauged areas? A comparison with in-situ observed soil moisture in an assimilation application. Adv. Water Res. 2012, 44, 49–65. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, N.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Ryu, D. Dual forcing and state correction via soil moisture assimilation for improved rainfall-runoff modelling. J. Hydrometeorol. 2014, 15, 1832–1848. [Google Scholar] [CrossRef]
| Forecast Time | Lead Time (hours) |
|---|---|
| d−1 at 18 UTC | 6–12 |
| d0 at 06 UTC | 0–12 |
| d0 at 18 UTC | 0–6 |
| Dataset | Spatial Resolution (Degrees) | Temporal Resolution (Hours) |
|---|---|---|
| SMOS level 2 Soil Moisture (trained on ECMWF neural network) | 0.50° | Instantaneous |
| H-TESSEL surface and subsurface runoff | 0.25° | 6 |
| GloFAS Streamflow | 0.10° | 24 |
| USGS streamflow observations | NA (point observations) | 24 |
| BoM streamflow observations | NA (point observations) | 24 |
| Simulation | R | Bias | KGEmod |
|---|---|---|---|
| Without SMOS DA | 0.428 | 0.840 | −0.504 |
| With SMOS DA | 0.420 | 0.812 | −0.472 |
| Simulation | R | Bias | KGEmod |
|---|---|---|---|
| Without SMOS DA | 0.410 | 2.466 | −1.248 |
| With SMOS DA | 0.356 | 2.558 | −1.340 |
| ESA CCI Land Cover Type | Number of Stations where KGEmodSS ≤ −0.05 (%) | Number of Stations where KGEmodSS ≥ 0.05 (%) |
|---|---|---|
| Grass | 16 (24%) | 28 (21%) |
| Tree | 13 (20%) | 19 (14%) |
| Urban | 7 (11%) | 12 (9%) |
| Crop | 4 (6%) | 3 (2%) |
| Vegetation | 0 (0%) | 8 (6%) |
| Herbaceous | 2 (3%) | 11 (8%) |
| Water | 11 (17%) | 24 (18%) |
| Shrub | 13 (20%) | 29 (22%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baugh, C.; de Rosnay, P.; Lawrence, H.; Jurlina, T.; Drusch, M.; Zsoter, E.; Prudhomme, C. The Impact of SMOS Soil Moisture Data Assimilation within the Operational Global Flood Awareness System (GloFAS). Remote Sens. 2020, 12, 1490. https://doi.org/10.3390/rs12091490
Baugh C, de Rosnay P, Lawrence H, Jurlina T, Drusch M, Zsoter E, Prudhomme C. The Impact of SMOS Soil Moisture Data Assimilation within the Operational Global Flood Awareness System (GloFAS). Remote Sensing. 2020; 12(9):1490. https://doi.org/10.3390/rs12091490
Chicago/Turabian StyleBaugh, Calum, Patricia de Rosnay, Heather Lawrence, Toni Jurlina, Matthias Drusch, Ervin Zsoter, and Christel Prudhomme. 2020. "The Impact of SMOS Soil Moisture Data Assimilation within the Operational Global Flood Awareness System (GloFAS)" Remote Sensing 12, no. 9: 1490. https://doi.org/10.3390/rs12091490
APA StyleBaugh, C., de Rosnay, P., Lawrence, H., Jurlina, T., Drusch, M., Zsoter, E., & Prudhomme, C. (2020). The Impact of SMOS Soil Moisture Data Assimilation within the Operational Global Flood Awareness System (GloFAS). Remote Sensing, 12(9), 1490. https://doi.org/10.3390/rs12091490






