A Pathway to the Automated Global Assessment of Water Level in Reservoirs with Synthetic Aperture Radar (SAR)
Abstract
1. Introduction
2. Data and Methods
2.1. Sentinel–1 Data Acquisition and Preprocessing
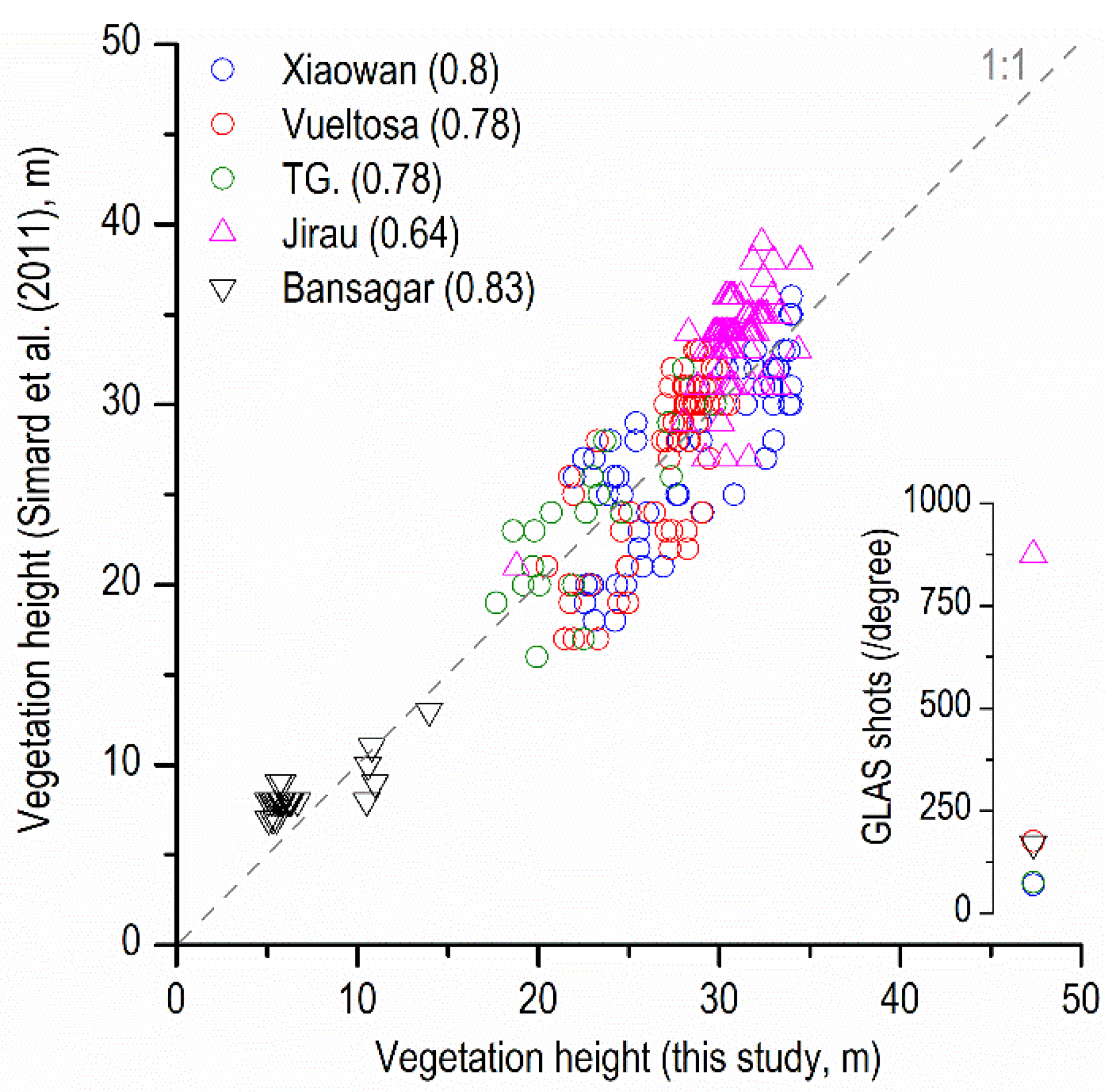
2.2. Digital Elevation Model (DEM) Processing and Validation
2.3. Water Mask Extraction and Water Level (WL) Retrieval
2.4. Validation Using Altimetry Data
3. Results
3.1. General Performance of the Proposed Approach
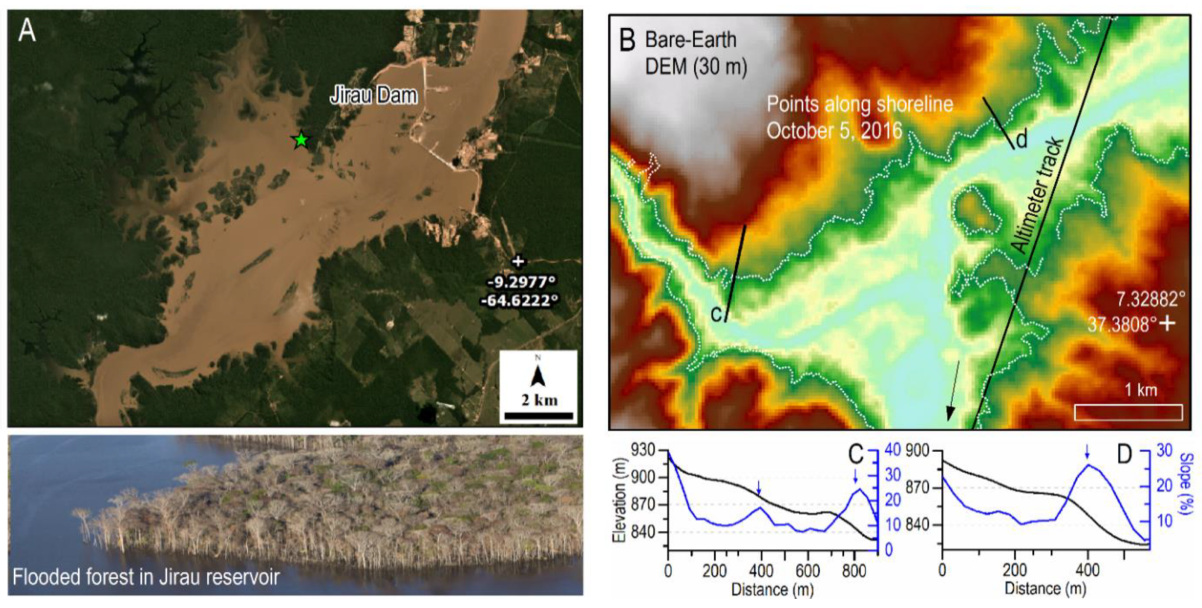
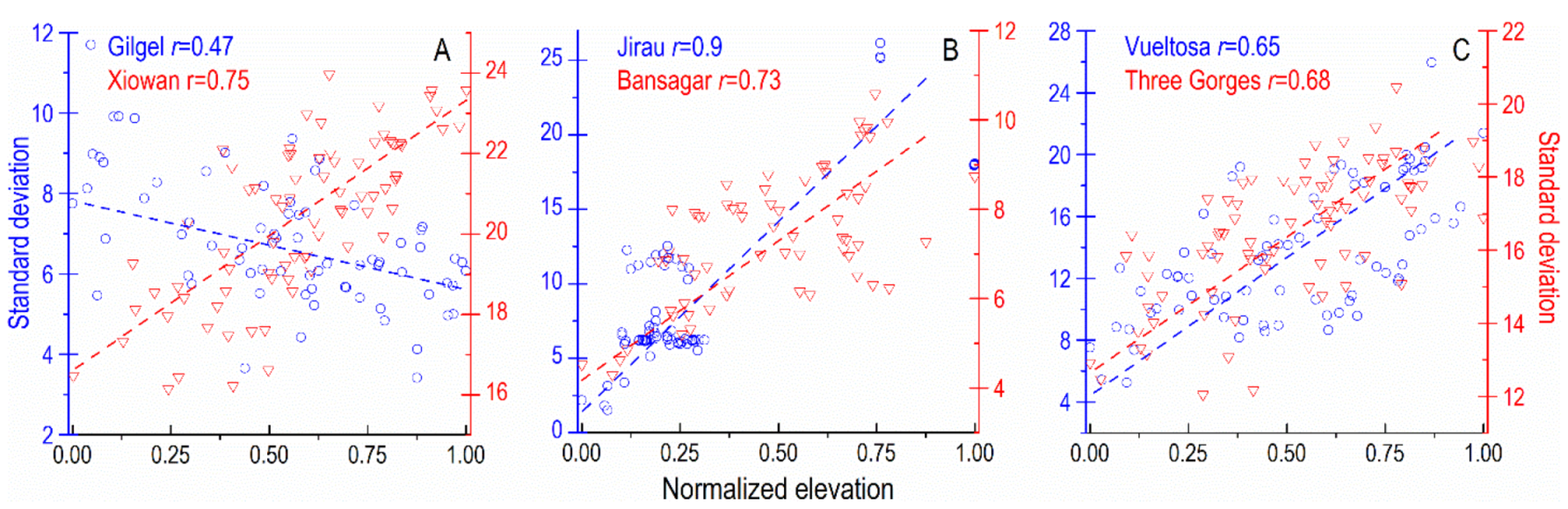
3.2. Effect of Local Slope over Different Elevation Ranges
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vörösmarty, C.I.; Meybeck, M.-H.; Fekete, B.M.; Sharma, K.; Green, P.; Syvitski, J. Anthropogenic sediment retention: Major global impact from registered river impoundments. Glob. Planet. Chang. 2003, 39, 169–190. [Google Scholar] [CrossRef]
- Zarfl, C.; Lumsdon, A.E.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- Winemiller, K.O.; Mcintyre, P.B.; Castello, L.; Fluet-Chouinard, E.; Giarrizzo, T.; Nam, S.; Baird, I.G.; Darwall, W.; Lujan, N.K.; Harrison, I.; et al. Balancing hydropower and biodiversity in the Amazon, Congo, and Mekong. Science 2016, 351, 128–129. [Google Scholar] [CrossRef] [PubMed]
- Latrubesse, E.M.; Arima, E.Y.; Dunne, T.; Park, E.; Baker, V.R.; d’Horta, F.M.; Wight, C.; Wittmann, F.; Zuanon, J.; Baker, P.A.; et al. Damming the rivers of the Amazon Basin. Nature 2017, 546, 363–369. [Google Scholar] [CrossRef]
- Fearnside, P.M. Tropical dams: To build or not to build? Science 2016, 351, 456–457. [Google Scholar] [CrossRef]
- Biemans, H.; Haddeland, I.; Kabat, P.; Ludwig, F.; Hutjes, R.; Heinke, J.; Von Bloh, W.; Gerten, D. Impact of reservoirs on river discharge and irrigation water supply during the 20th century. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Rothausen, S.G.; Conway, D. Greenhouse–gas emissions from energy use in the water sector. Nat. Clim. Chang. 2011, 1, 210–219. [Google Scholar] [CrossRef]
- Grill, G.; Lehner, B.; Thieme, M.; Geenen, B.; Tickner, D.; Antonelli, F.; Babu, S.; Borrelli, P.; Cheng, L.; Crochetiere, H.; et al. Mapping the world’s free–flowing rivers. Nature 2019, 569, 215. [Google Scholar] [CrossRef]
- Bernardo, N.; do Carmo, A.; Park, E.; Alcântara, E. Retrieval of Suspended Particulate Matter in Inland Waters with Widely Differing Optical Properties Using a Semi–Analytical Scheme. Remote Sens. 2019, 11, 2283. [Google Scholar] [CrossRef]
- Syvitski, J.P.; Vörösmarty, C.J.; Kettner, A.J.; Green, P. Impact of humans on the flux of terrestrial sediment to the global coastal ocean. Science 2005, 308, 376–380. [Google Scholar] [CrossRef]
- Park, E.; Latrubesse, E.M. A geomorphological assessment of wash–load sediment fluxes and floodplain sediment sinks along the lower Amazon River. Geology 2019, 47, 403–406. [Google Scholar] [CrossRef]
- Yang, Z.S.; Wang, H.J.; Saito, Y.; Milliman, J.D.; Xu, K.; Qiao, S.; Shi, G. Dam impacts on the Changjiang (Yangtze) River sediment discharge to the sea: The past 55 years and after the Three Gorges Dam. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Kummu, M.; Lu, X.; Wang, J.J.; Varis, O. Basin–wide sediment trapping efficiency of emerging reservoirs along the Mekong. Geomorphology 2010, 119, 181–197. [Google Scholar] [CrossRef]
- Mekonnen, M.M.; Hoekstra, A.Y. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed]
- Veldkamp, T.I.; Wada, Y.; Aerts, J.; Döll, P.; Gosling, S.N.; Liu, J.; Masaki, Y.; Oki, T.; Ostberg, S.; Pokhrel, Y.; et al. Water scarcity hotspots travel downstream due to human interventions in the 20th and 21st century. Nat. Commun. 2017, 8, 15697. [Google Scholar] [CrossRef] [PubMed]
- Khadem, M.; Rougé, C.; Harou, J.; Hansen, K.M.; Medellin-Azuara, J.; Lund, J. Estimating the economic value of inter-annual reservoir storage in water resource systems. Water Resour. Res. 2018, 54, 8890–8908. [Google Scholar] [CrossRef]
- FAO; WWC. Towards a Water and Food Secure Future, in Critical Perspective for Policy–Makers; W.W. COUNCIL: Marseille, France, 2015. [Google Scholar]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High–resolution mapping of global surface water and its long–term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Abarca-del-Río, R.; Berge-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake volume monitoring from space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef]
- Balsamo, G.; Salgado, R.; Dutra, E.; Boussetta, S.; Stockdale, T.; Potes, M. On the contribution of lakes in predicting near–surface temperature in a global weather forecasting model. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 15829. [Google Scholar] [CrossRef]
- Yang, X.; Lu, X.; Park, E.; Tarolli, P. Impacts of Climate Change on Lake Fluctuations in the Hindu Kush–Himalaya–Tibetan Plateau. Remote Sens. 2019, 11, 1082. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, S.; Durand, M.; Lee, H. Satellite Remote Sensing of Lakes and Wetlands. Hydrologic Remote Sensing; CRC Press: Boca Raton, FL, USA, 2016; pp. 57–72. [Google Scholar]
- Alsdorf, D.E.; Rodriguez, E.; Lettenmaier, D.P. Measuring surface water from space. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; May, J.; Dartevelle, S.; Birkett, C.; Lucero, E.; Russo, T.; Griffin, S.; Miller, J.; Tetrault, R.; Zentner, M. Inferring elevation variation of lakes and reservoirs from areal extents: Calibrating with altimeter and in situ data. Remote Sens. Appl. Soc. Environ. 2018, 9, 116–125. [Google Scholar] [CrossRef]
- Raclot, D. Remote sensing of water levels on floodplains: A spatial approach guided by hydraulic functioning. Int. J. Remote Sens. 2006, 27, 2553–2574. [Google Scholar] [CrossRef]
- Hostache, R.; Lai, X.; Monnier, J.; Puech, C. Assimilation of spatially distributed water levels into a shallow–water flood model. Part II: Use of a remote sensing image of Mosel River. J. Hydrol. 2010, 390, 257–268. [Google Scholar] [CrossRef]
- Westerhoff, R.S.; Kleuskens, M.P.H.; Winsemius, H.C.; Huizinga, H.J.; Brakenridge, G.R.; Bishop, C. Automated global water mapping based on wide–swath orbital synthetic–aperture radar. Hydrol. Earth Syst. Sci. 2013, 17, 651–663. [Google Scholar] [CrossRef]
- Huang, W.; DeVries, B.; Huang, C.; Lang, M.W.; Jones, J.W.; Creed, I.F.; Carroll, M.L. Automated extraction of surface water extent from Sentinel–1 data. Remote Sens. 2018, 10, 797. [Google Scholar] [CrossRef]
- Martinis, S.; Kersten, J.; Twele, A. A fully automated TerraSAR–X based flood service. ISPRS J. Photogramm. Remote Sens. 2015, 104, 203–212. [Google Scholar] [CrossRef]
- Van Bemmelen, C.W.T.; Mann, M.; De Ridder, M.; Rutten, M.; Van De Giesen, N. Determining water reservoir characteristics with global elevation data. Geophys. Res. Lett. 2016, 43, 11–278. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, H. A novel algorithm for monitoring reservoirs under all-weather conditions at a high temporal resolution through passive microwave remote sensing. Geophys. Res. Lett. 2016, 43, 8052–8059. [Google Scholar] [CrossRef]
- Sheffield, J.; Ferguson, C.R.; Troy, T.J.; Wood, E.F.; McCabe, M.F. Closing the terrestrial water budget from satellite remote sensing. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Park, E.; Lewis, Q.W.; Sanwlani, N. Large lake gauging using fractional imagery. J. Environ. Manag. 2019, 231, 687–693. [Google Scholar] [CrossRef] [PubMed]
- Amitrano, D.; Martino, G.D.; Iodice, A.; Mitidieri, F.; Papa, M.N.; Riccio, D.; Ruello, G. Sentinel–1 for monitoring reservoirs: A performance analysis. Remote Sens. 2014, 6, 10676–10693. [Google Scholar] [CrossRef]
- Chipman, J.W. A Multisensor Approach to Satellite Monitoring of Trends in Lake Area, Water Level, and Volume. Remote Sens. 2019, 11, 158. [Google Scholar] [CrossRef]
- Giustarini, L.; Matgen, P.; Hostache, R.; Montanari, M.; Plaza Guingla, D.A.; Pauwels, V.; De Lannoy, G.; De Keyser, R.; Pfister, L.; Hoffmann, L.; et al. Assimilating SAR–derived water level data into a hydraulic model: A case study. Hydrol. Earth Syst. Sci. 2011, 15, 2349–2365. [Google Scholar] [CrossRef]
- Mason, D.; Schumann, G.; Neal, J.; García-Pintado, J.; Bates, P.D. Automatic near real–time selection of flood water levels from high resolution Synthetic Aperture Radar images for assimilation into hydraulic models: A case study. Remote Sens. Environ. 2012, 124, 705–716. [Google Scholar] [CrossRef]
- Schumann, G.; Hostache, R.; Puech, C.; Hoffmann, L.; Matgen, P.; Pappenberger, F.; Pfister, L. High–resolution 3–D flood information from radar imagery for flood hazard management. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1715–1725. [Google Scholar] [CrossRef]
- Birkett, C.M.; Beckley, B. Investigating the performance of the Jason–2/OSTM radar altimeter over lakes and reservoirs. Mar. Geod. 2010, 33, 204–238. [Google Scholar] [CrossRef]
- Amazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole–Filled SRTM for the Globe Version 4. 2008. Available online: http://srtm.csi.cgiar.org/ (accessed on 20 August 2019).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.S.; Belz, J.E. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Birkett, C.; Reynolds, C.; Beckley, B.; Doorn, B. From research to operations: The USDA global reservoir and lake monitor. In Coastal Altimetry; Springer: Berlin, Heidelberg, 2011; pp. 19–50. [Google Scholar]
- Hess, L.L.; Melack, J.M.; Novo, E.M.; Barbosa, C.C.; Gastil, M. Dual–season mapping of wetland inundation and vegetation for the central Amazon basin. Remote Sens. Environ. 2003, 87, 404–428. [Google Scholar] [CrossRef]
- Birkett, C. The contribution of TOPEX/POSEIDON to the global monitoring of climatically sensitive lakes. J. Geophys. Res. Oceans 1995, 100, 25179–25204. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Ricko, M.; Carton, J.A.; Birkett, C.M.; Crétaux, J.F. Intercomparison and validation of continental water level products derived from satellite radar altimetry. J. Appl. Remote Sens. 2012, 6, 061710. [Google Scholar] [CrossRef]
- Berry, P.A.M.; Garlick, J.D.; Mathers, E.L.; Freeman, J.A. Global inland water monitoring from multi-mission altimetry. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L. Modeling and analysis of lake water storage changes on the Tibetan Plateau using multi–mission satellite data. Remote Sens. Environ. 2013, 135, 25–35. [Google Scholar] [CrossRef]
- Tong, X.; Pan, H.; Xie, H.; Xu, X.; Li, F.; Chen, L.; Luo, X.; Liu, S.; Chen, P.; Jin, Y. Estimating water volume variations in Lake Victoria over the past 22 years using multi–mission altimetry and remotely sensed images. Remote Sens. Environ. 2016, 187, 400–413. [Google Scholar] [CrossRef]
- Pham, H.T.; Marshall, L.; Johnson, F.; Sharma, A. Deriving daily water levels from satellite altimetry and land surface temperature for sparsely gauged catchments: A case study for the Mekong River. Remote Sens. Environ. 2018, 212, 31–46. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Couto, T.B.; Olden, J.D. Global proliferation of small hydropower plants–science and policy. Front. Ecol. Environ. 2018, 16, 91–100. [Google Scholar] [CrossRef]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth Parts A/B/C 2006, 31, 935–943. [Google Scholar] [CrossRef]
- Rodrigues, L.; Liebe, J. Small reservoirs depth–area–volume relationships in Savannah Regions of Brazil and Ghana. Water Resour. Irrig. Manag. 2013, 1, 1–10. [Google Scholar]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Discharge estimation and forecasting by MODIS and altimetry data in Niger–Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Park, E. Volunteered Geographic Videos in Physical Geography: Data Mining from YouTube. Ann. Am. Assoc. Geogr. 2018, 108, 52–70. [Google Scholar] [CrossRef]
- Bandini, F.; Jakobsen, J.; Olesen, D.; Reyna-Gutierrez, J.A.; Bauer-Gottwein, P. Measuring water level in rivers and lakes from lightweight Unmanned Aerial Vehicles. J. Hydrol. 2017, 548, 237–250. [Google Scholar] [CrossRef]
- Bandini, F.; Sunding, T.P.; Linde, J.; Smith, O.; Jensen, I.K.; Köppl, C.J.; Butts, M.; Bauer-Gottwein, P. Unmanned Aerial System (UAS) observations of water surface elevation in a small stream: Comparison of radar altimetry, LIDAR and photogrammetry techniques. Remote Sens. Environ. 2020, 237, 111487. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and its capabilities for land hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Wanders, N.; AghaKouchak, A.; Kuil, L.; Rangecroft, S.; Veldkamp, T.I.; Garcia, M.; van Oel, P.R.; Breinl, K.; Van Loon, A.F. Water shortages worsened by reservoir effects. Nat. Sustain. 2018, 1, 617–622. [Google Scholar] [CrossRef]


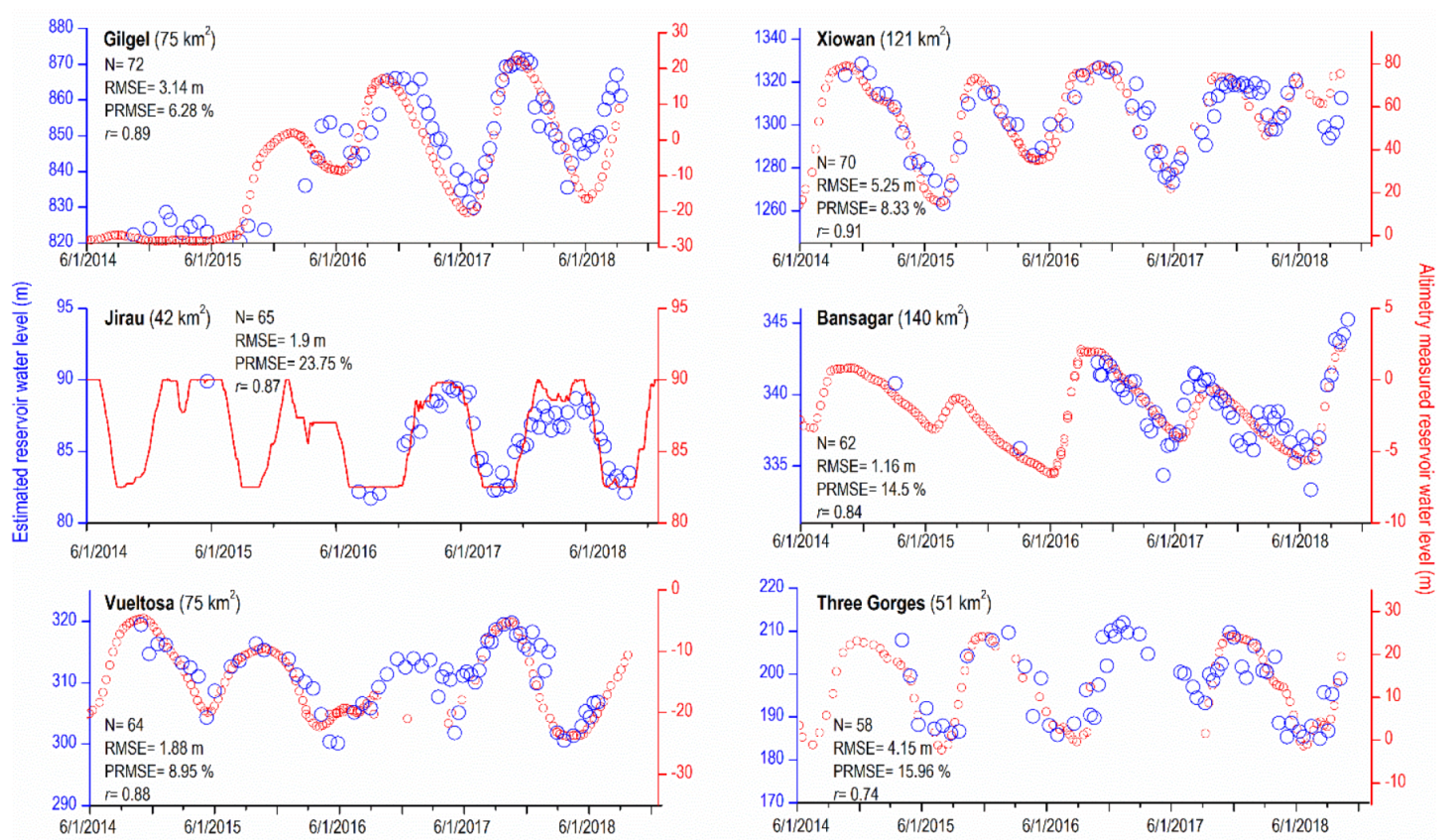

| Reservoirs | Location (Altimetry Intersection) | Country | Sentinel–1 Path | Year Started to Fill | Surface Slope (m/km) a | Water Level Variation (m) b | RMSE (m) c | pRMSE (%) d |
|---|---|---|---|---|---|---|---|---|
| Gilgel Gibe | 7°20′25”N, 37°20′77”E | Ethiopia | 152 | 2015 | 1.09 | 40 | 3.14 | 6.28 |
| Xiowan | 24°50′17”N, 100°9′49”E | China | 99 | 2009 | 1.76 | 63 | 5.25 | 8.33 |
| Jirau | 9°17′25”S, 64°41′15”W | Brazil | 156 | 2008 e | 0.46 | 8 | 1.9 | 23.75 |
| Bansagar | 24°4′27”N, 80°59′41”E. | India | 56, 92, 165 | 2011 | 0.09 | 8 | 1.16 | 14.5 |
| Vueltosa | 7°44′34”N, 71°30′58”W | Venezuela | 4, 171 | 2009 | 0.18 | 21 | 1.88 | 8.95 |
| Three Gorges | 30°49′31”N, 111°0′14”E | China | 11 | 1994 e | 0.96 | 26 | 4.15 | 15.96 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, E.; Merino, E.; W. Lewis, Q.; O. Lindsey, E.; Yang, X. A Pathway to the Automated Global Assessment of Water Level in Reservoirs with Synthetic Aperture Radar (SAR). Remote Sens. 2020, 12, 1353. https://doi.org/10.3390/rs12081353
Park E, Merino E, W. Lewis Q, O. Lindsey E, Yang X. A Pathway to the Automated Global Assessment of Water Level in Reservoirs with Synthetic Aperture Radar (SAR). Remote Sensing. 2020; 12(8):1353. https://doi.org/10.3390/rs12081353
Chicago/Turabian StylePark, Edward, Eder Merino, Quinn W. Lewis, Eric O. Lindsey, and Xiankun Yang. 2020. "A Pathway to the Automated Global Assessment of Water Level in Reservoirs with Synthetic Aperture Radar (SAR)" Remote Sensing 12, no. 8: 1353. https://doi.org/10.3390/rs12081353
APA StylePark, E., Merino, E., W. Lewis, Q., O. Lindsey, E., & Yang, X. (2020). A Pathway to the Automated Global Assessment of Water Level in Reservoirs with Synthetic Aperture Radar (SAR). Remote Sensing, 12(8), 1353. https://doi.org/10.3390/rs12081353







