Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages
Abstract
1. Introduction
2. Materials and Methods
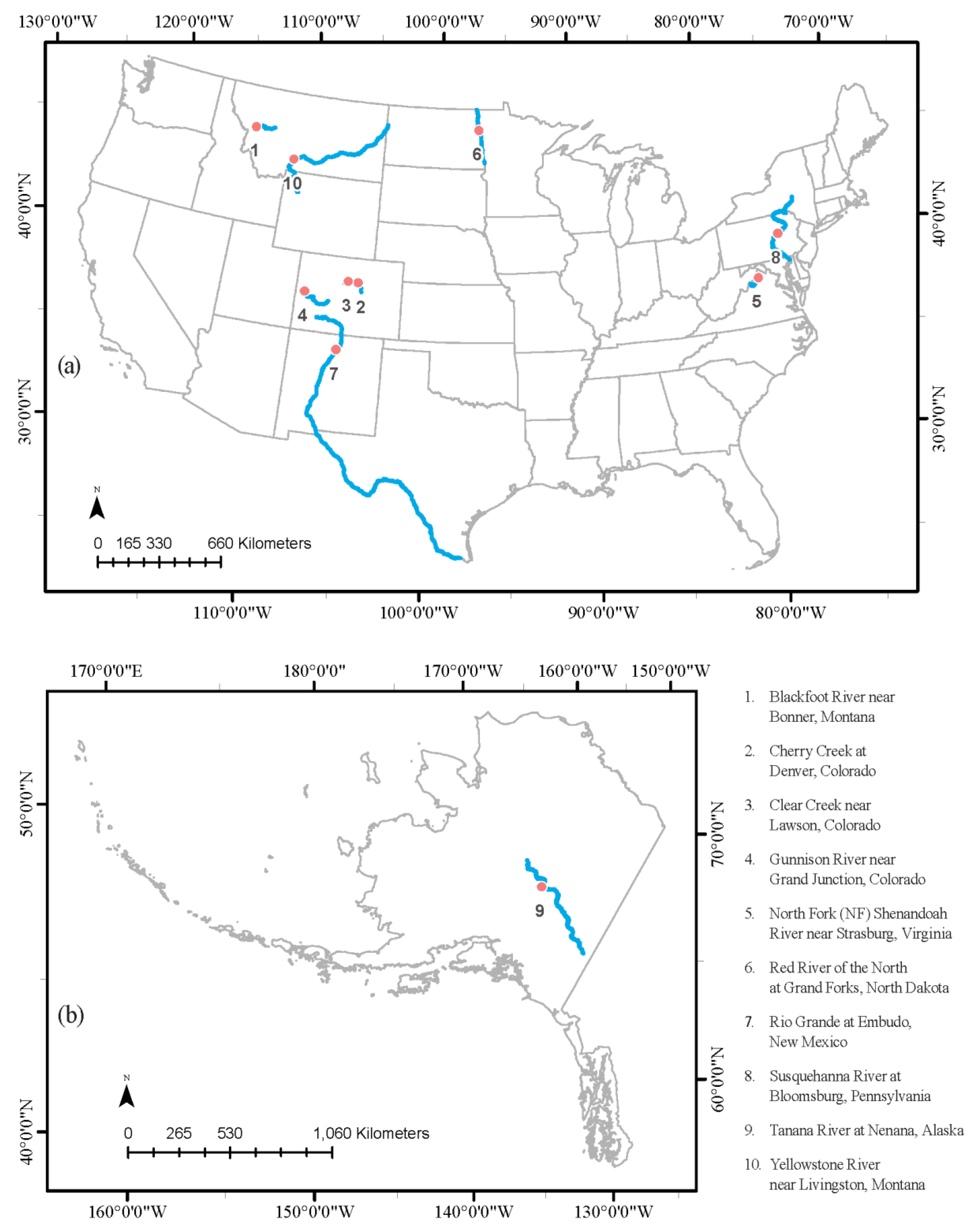
2.1. Site Selection
2.2. Doppler Radar Technology
2.3. Validation Measurements
2.4. Radar Siting
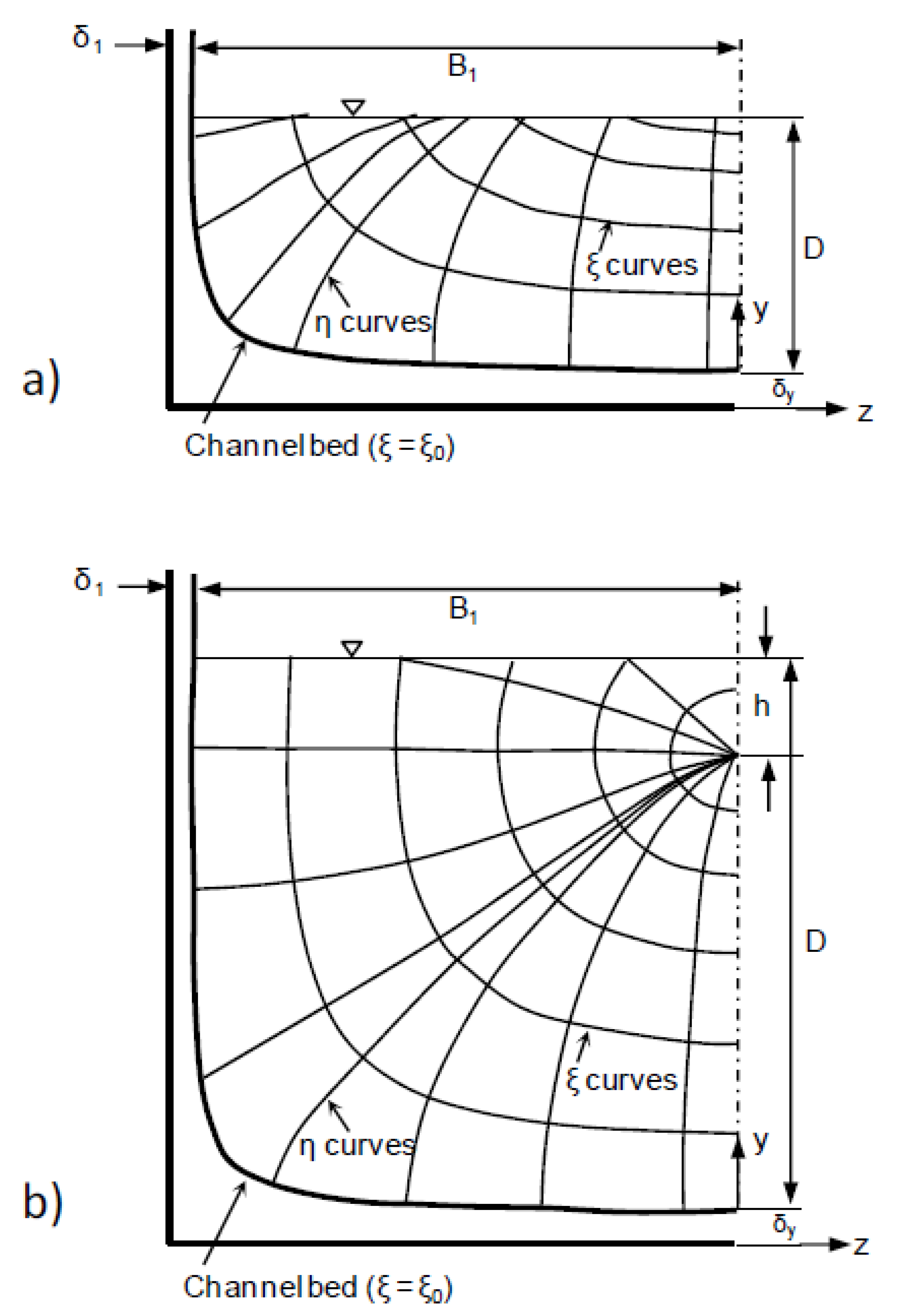
2.4.1. Velocity
2.4.2. y-axis
2.4.3. Cross-sectional Area
2.4.4. Wind Drift
2.5. Radar Deployments
2.6. Discharge Algorithms
2.6.1. Conventional Methods
2.6.2. Probability Concept
3. Results
3.1. Siting and Validation Phase
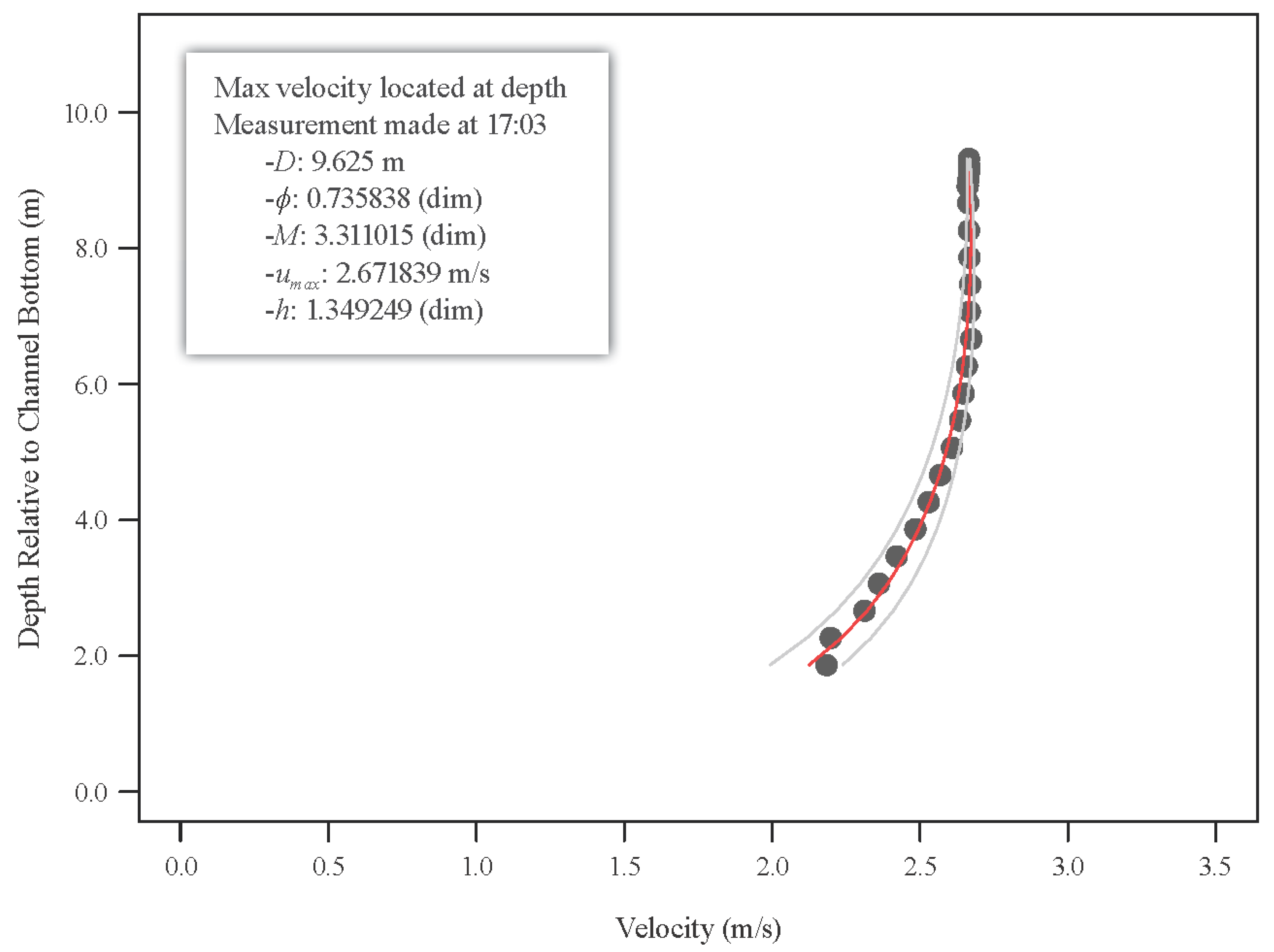
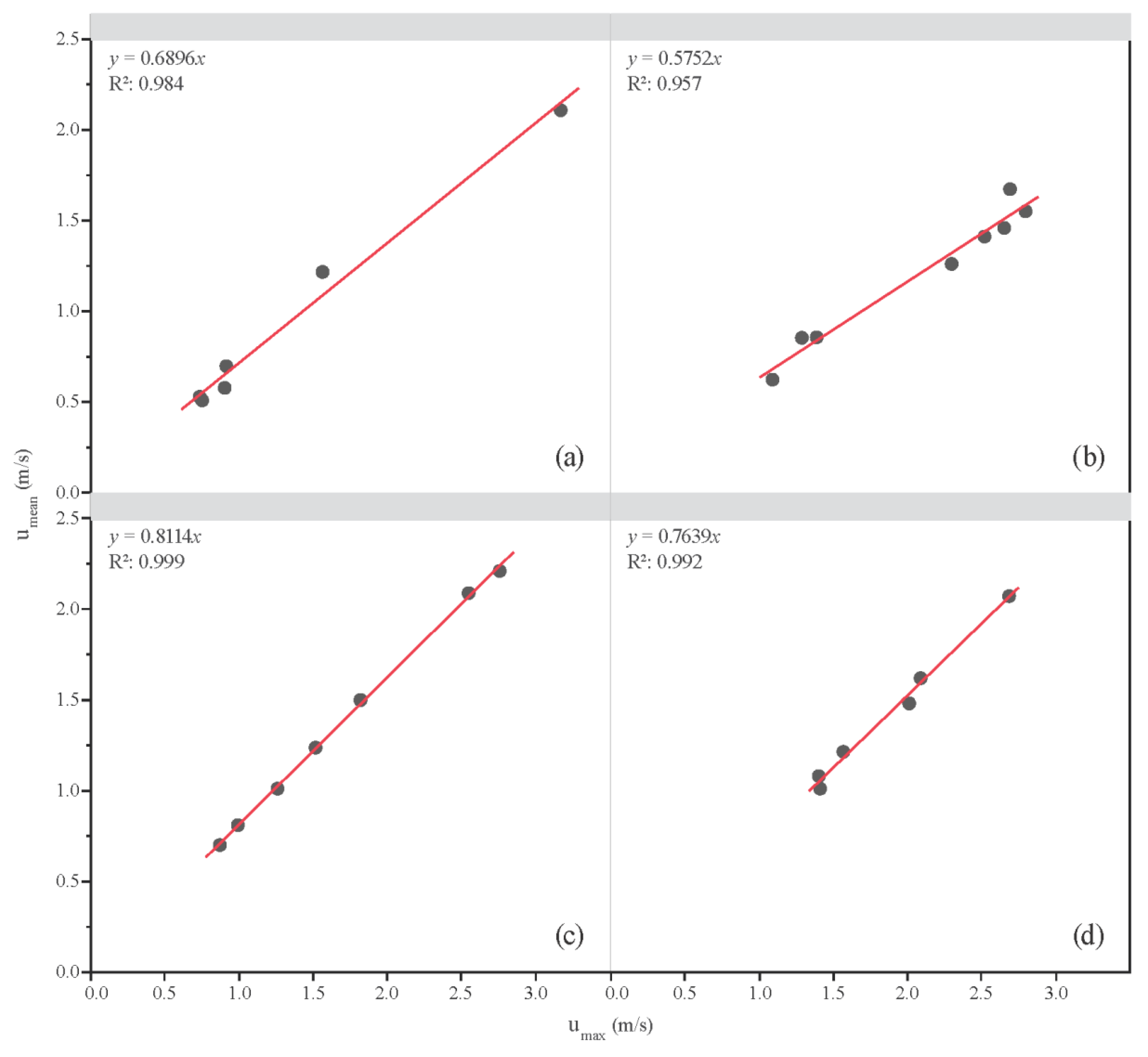
3.1.1. Velocity
3.1.2. Values of ϕ and Location of the y-axis
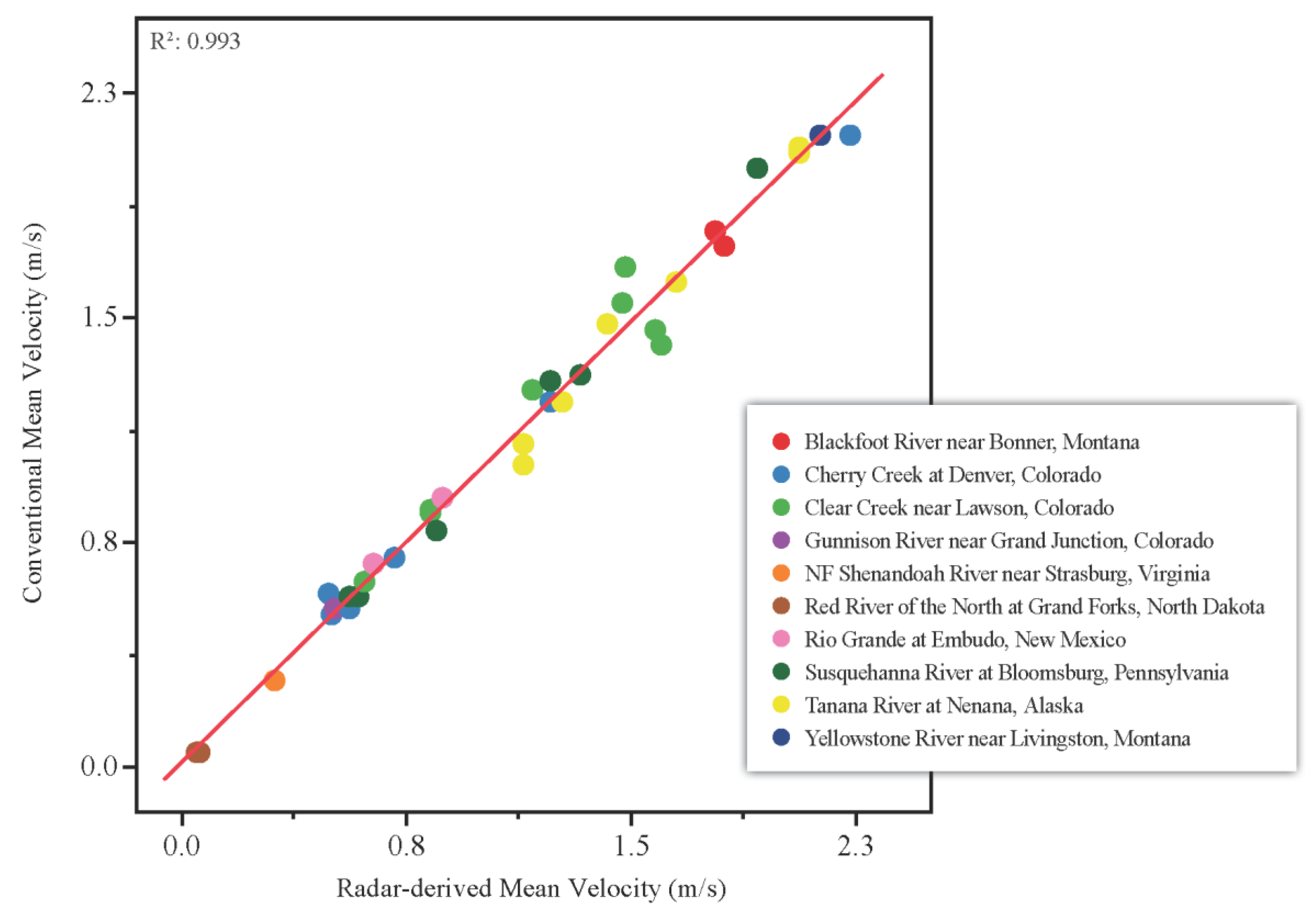
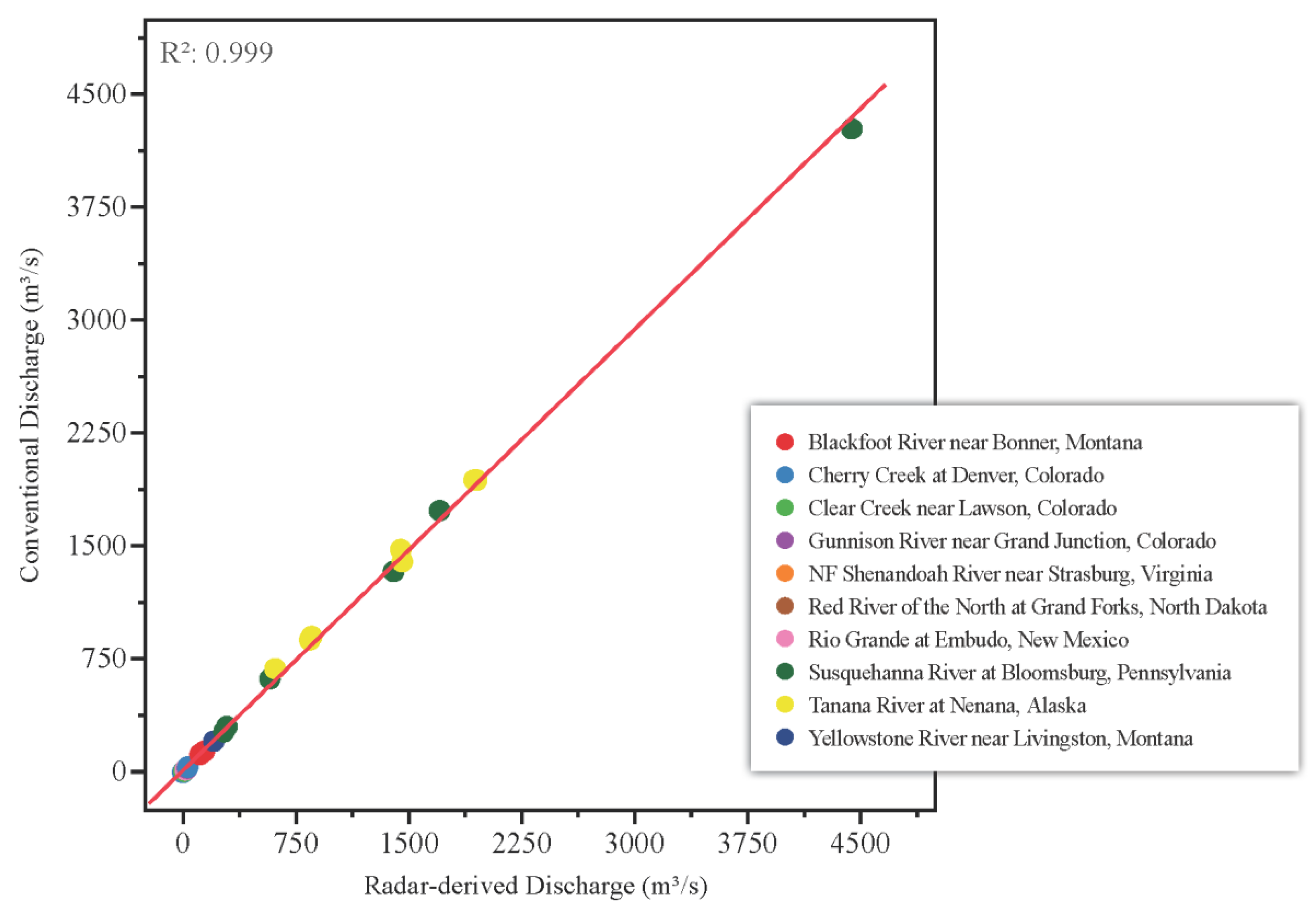
3.1.3. Discharge
3.2. Operational Phase
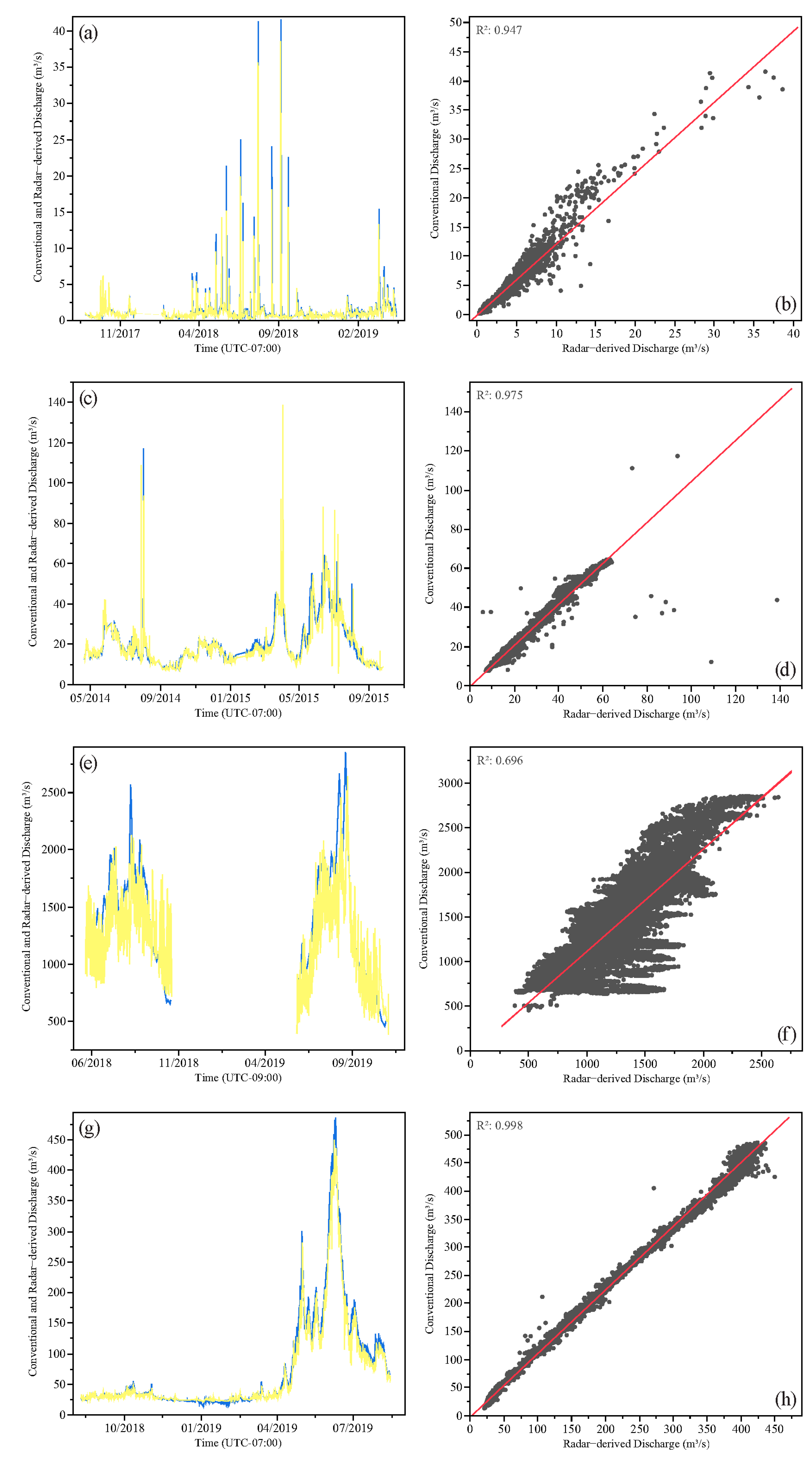
3.2.1. Velocity and Discharge
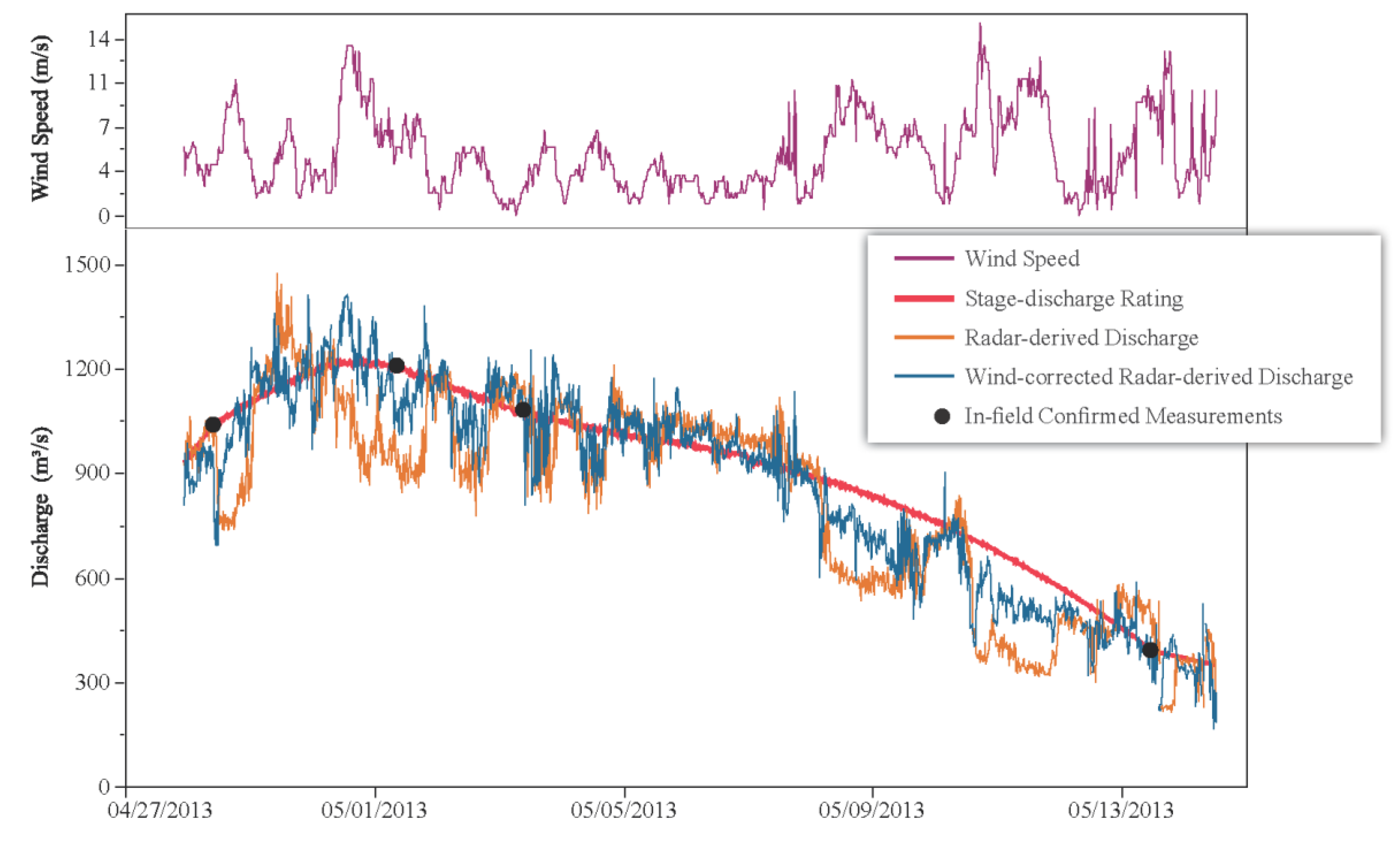
3.2.2. Wind Drift
4. Discussion
4.1. Velocity and Discharge Computations
4.2. Uncertainty
4.2.1. Variability in ϕ
4.2.2. Variability in y-axis
4.2.3. Wind drift, Sample Duration and Frequency, and Minimum-Surface Velocities
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eberts, S.; Woodside, M.; Landers, M.; Wagner, C. Monitoring the Pulse of our Nation’s Rivers and Streams—The U.S. Geological Survey Streamgaging Network; U.S. Geological Survey Fact Sheet 2018–3081; 2018. Available online: https://pubs.er.usgs.gov/publication/fs20183081 (accessed on 19 April 2020).
- Buchanan, T.J.; Somers, W.P. Discharge Measurements at Gaging Stations; U.S. Geological Survey Techniques of Water-Resources Investigations, Book 3, Chap A8; 1969; p. 65. Available online: http://pubs.usgs.gov/twri/twri3a8/ (accessed on 30 December 2019).
- Rantz, S. Measurement and Computation of Streamflow: Volume 1. Measurement of Stage and Discharge; U.S. Geological Survey Water Supply Paper 2175; United States Government Printing Office: Washington, DC, USA, 1982; p. 284.
- Turnipseed, D.P.; Sauer, V.B. Discharge Measurements at Gaging Stations; U.S. Geological Survey Techniques and Methods Book 3, Chap. A8; 2010; p. 87. Available online: http://pubs.usgs.gov/tm/tm3-a8/ (accessed on 30 December 2019).
- Christensen, J.L.; Herrick, L.E. Mississippi River Test: Volume 1. Final Rep.; DCP4400/300; the U.S. Geological Survey, AMETEK/Straza Division: El Cajon, CA, USA, 1982.
- Simpson, M.R. Evaluation of a vessel-mounted acoustic Doppler current profiler for use in rivers and estuaries. In Proceedings of the 3rd Working Conference on Current Measurement, IEEE, Washington, DC, USA, 22–24 January 1986; pp. 106–121. [Google Scholar]
- Gordon, R.L. Acoustic measurement of river discharge. J. Hydraul. Eng. 1989, 115, 925–936. [Google Scholar] [CrossRef]
- Simpson, M.R.; Oltmann, R.N. Discharge-Measurement System Using an Acoustic Doppler Current Profiler with Applications to Large Rivers and Estuaries; U.S. Geological Survey Water Supply Paper 2395; U.S. Geological Survey: Reston, VA, USA, 1993; p. 32.
- Oberg, K.A.; Morlock, S.E.; Caldwell, W.S. Quality Assurance Plan for Discharge Measurements Using Acoustic Doppler Current Profilers; U.S. Geological Survey Scientific Investigations Report 2005–5135; U.S. Geological Survey: Reston, VA, USA, 2005; p. 35.
- Mueller, D.S. QRev—Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements—User’s Manual for Version 2.8; U.S. Geological Survey Open-File Report 2016–1052; USGS: Reston, VA, USA, 2016; p. 50. Available online: https://pubs.er.usgs.gov/publication/ofr20161052 (accessed on 30 December 2019).
- Mueller, D.S. Extrap: Software to assist the selection of extrapolation methods for moving-boat ADCP streamflow measurements. Comput. Geosci. 2013, 54, 211–218. [Google Scholar] [CrossRef]
- Lin, D.; Grundmann, J.; Eltner, A. Evaluating Image Tracking Approaches for Surface Velocimetry With Thermal Tracers. Water Resour. Res. 2019, 55, 3122–3136. [Google Scholar] [CrossRef]
- Hauet, A.; Morlot, T.; Daubagnan, L. Velocity Profile and Depth-Averaged to Surface Velocity in Natural Streams: A Review over a Large Sample of Rivers. E3S Web of Conferences 40 06015 River Flow, EDP Sciences, France. 2018. Available online: https://www.e3s-conferences.org/articles/e3sconf/abs/2018/15/e3sconf_riverflow2018_06015/e3sconf_riverflow2018_06015.html (accessed on 20 January 2020).
- Fujita, I.; Komura, S. Application of video image analysis for measurements of river-surface flows. Proc. Hydraul. Eng. JSCE 1994, 38, 733–738. [Google Scholar] [CrossRef]
- Tauro, F.; Pagano, C.; Phamduy, P.; Grimaldi, S.; Porfiri, M. Large-scale particle image velocimetry from an unmanned aerial vehicle. IEEE/ASME Trans. Mechatron. 2015, 20, 3269–3275. [Google Scholar] [CrossRef]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Surface flow measurements from drones. J. Hydrol. 2016, 540, 240–245. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Legleiter, C.J. sUAS-based remote sensing of river discharge using thermal particle image velocimetry and bathymetric lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef]
- Dugan, J.P.; Anderson, S.P.; Piotrowski, C.C.; Zuckerman, S.B. Airborne infrared remote sensing of riverine currents. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3895–3907. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Estimation of discharge from three braided rivers using synthetic aperture radar satellite imagery. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
- Leon, J.G.; Calmant, S.; Seyler, F.; Bonnet, M.P.; Cauhope, M.; Frappart, F. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. J. Hydrol. 2006, 328, 481–496. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Bonnet, M.P.; Calmant, S.; Roux, H.; Filho, O.C.R.; Mansur, W.J. Hydrological monitoring of poorly gauged basins based on rainfall–runoff modeling and spatial altimetry. J. Hydrol. 2009, 379, 205–219. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Peters-Lidard, C. Estimating water discharge from large radar altimetry datasets. Hydrol. Earth Syst. Sci. 2013, 17, 923–933. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Buarque, D.C.; Colischonn, W.; Bonnet, M.-P.; Frappart, F.; Calmant, S.; Mendes, C.A.B. Large-scale hydrological and hydrodynamics modelling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River discharge estimation by using altimetry data and simplified flood routing modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Pavelsky, T.M. Using width-based rating curves from spatially discontinuous satellite imagery to monitor river discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Paris, A.; Dias de Paiva, R.; Santos da Silva, J.; Medeiros Moreira, D.; Calmant, S.; Garambois, P.-A.; Collischonn, W.; Bonnet, M.-P.; Seyler, F. Stage-discharge rating curves based on satellite altimetry and modeled discharge in the Amazon basin. Water Resour. Res. 2016, 52, 3787–3814. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.-A. Satellite remote sensing estimation of river discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.-P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.-C.; et al. Monitoring water levels and discharges using radar altimetry in an ungauged river basin: The case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Bjerklie, D.M.; Fulton, J.W.; Tarpanelli, A. River bathymetry estimate and discharge assessment from remote sensing. Water Resour. Res. 2019, 55, 6692–6711. [Google Scholar] [CrossRef]
- Birkett, C.M. Contribution of the TOPEX NASA radar altimeter to the global monitoring of large rivers and wetlands. Water Resour. Res. 1998, 34, 1223–1239. [Google Scholar] [CrossRef]
- Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. 2002, 107, 8059. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef]
- Papa, F.; Bala, S.K.; Kumar Pandey, R.; Durand, F.; Rahman, A.; Rossow, W.B. Ganga-Brahmaputra River discharge. Geophys. Res. 2012, 117, C11021. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M. Spatiotemporal dynamic of surface water bodies using Landsat time-series data from 1999 to 2011. ISPRS J. Photogramm. Remote Sens. 2013, 79, 44–52. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef]
- Kim, J.-W.; Lu, Z.; Jones, J.W.; Shum, C.K.; Lee, H.; Jia, Y. Monitoring Everglades freshwater marsh water level using L-band synthetic aperture radar backscatter. Remote Sens. Environ. 2014, 150, 66–81. [Google Scholar] [CrossRef]
- Jones, J.W. Efficient wetland surface water detection and monitoring via Landsat: Comparison with in situ data from the Everglades Depth Estimation Network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
- Carroll, M.; Wooten, M.; DiMiceli, C.; Sohlberg, R.; Kelly, M. Quantifying surface water dynamics at 30 meter spatial resolution in the North American high northern latitudes 1991–2011. Remote Sens. 2016, 8, 622. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Mic, R. Orbital microwave measurement of river discharge and ice status. Water Resour. Res. 2007, 43, W04405. [Google Scholar] [CrossRef]
- Durand, M.; Neal, J.; Rodríguez, E.; Andreadis, K.M.; Smith, L.C.; Yoon, Y. Estimating reach-averaged discharge for the River Severn from measurements of river water surface elevation and slope. J. Hydrol. 2014, 511, 92–104. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T. The SWOT Mission and its capabilities for land hydrology. Surv. Geophys. 2015, 37, 307–337. [Google Scholar] [CrossRef]
- Garambois, P.-A.; Monnier, J. Inference of effective river properties from remotely sensed observations of water surface. Adv. Water Resour. 2015, 79, 103–120. [Google Scholar] [CrossRef]
- Bonnema, M.G.; Sikder, S.; Hossain, F.; Durand, M.; Gleason, C.J.; Bjerklie, D.M. Benchmarking wide swath altimetry-based river discharge estimation algorithms for the Ganges river system. Water Resour. Res. 2016, 52, 2439–2461. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.M.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). SWOT Surface Water and Ocean Topography. Available online: https://swot.jpl.nasa.gov/home.htm (accessed on 17 July 2018).
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. Measuring stream discharge by non-contact methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Melcher, N.B.; Costa, J.E.; Haeni, F.P.; Cheng, R.T.; Thurman, E.M.; Buursink, M.; Spicer, K.R.; Hayes, E.; Plant, W.J.; Keller, W.C. River discharge measurements by using helicopter-mounted radar. Geophys. Res. Lett. 2002, 29, 41–44. [Google Scholar] [CrossRef]
- Fulton, J.W.; Anderson, I.E.; Chiu, C.-L.; Sommer, W.; Adams, J.D.; Moramarco, T.; Bjerklie, D.M.; Fulford, J.M.; Sloan, J.L. sUAS-based remote sensing of velocity and discharge using Doppler radar. (manuscript in preparation).
- Plant, W.J.; Keller, W.C.; Hayes, K. Measurement of river surface currents with coherent microwave systems. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1242–1257. [Google Scholar] [CrossRef]
- Costa, J.E.; Cheng, R.T.; Haeni, F.P.; Melcher, N.; Spicer, K.R.; Hayes, E.; Plant, W.; Hayes, K.; Teague, C.; Barrick, D. Use of radars to monitor stream discharge by noncontact methods. Water Resour. Res. 2006, 42, 14. [Google Scholar] [CrossRef]
- Fulton, J.W.; Ostrowski, J. Measuring real-time streamflow using emerging technologies: Radar, hydroacoustics, and the probability concept. J. Hydrol. 2008, 357, 1–10. [Google Scholar] [CrossRef]
- Boning, C.W. Policy Statement on Stage Accuracy; U.S. Geological Survey, Office of Surface Water Technical Memorandum 93.07; 1992. Available online: https://water.usgs.gov/admin/memo/SW/sw93.07.html (accessed on 14 February 2020).
- Sauer, V.B.; Meyer, R.W. Determination of Error in Individual Discharge Measurements; U.S. Geological Survey Open-File Report 92–144; U.S. Geological Survey: Reston, VA, USA, 1992; p. 21. [CrossRef]
- Kiang, J.E.; Gazoorian, C.; McMillan, H.; Coxon, G.; Le Coz, J.; Westerberg, I.K.; Belleville, A.; Sevrez, D.; Sikorska, A.E.; Petersen-Øverleir, A.; et al. A Comparison of Methods for Streamflow Uncertainty Estimation. Water Resour. Res. 2018, 54, 7149–7176. [Google Scholar] [CrossRef]
- Cohn, T.A.; Kiang, J.E.; Mason, R.R. Estimating Discharge Measurement Uncertainty Using the Interpolated Variance Estimator. J. Hydraul. Eng. 2013, 139, 502–510. [Google Scholar] [CrossRef]
- McMillan, H.; Krueger, T.; Freer, J. Benchmarking observational uncertainties for hydrology: Rainfall, river discharge and water quality. Hydrol. Process. 2012, 26, 4078–4111. [Google Scholar] [CrossRef]
- Welber, M.; Le Coz, J.; Laronne, J.B.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 2, 1108–1126. [Google Scholar] [CrossRef]
- Sauer, V.B. Standards for the Analysis and Processing of Surface-Water Data and Information Using Electronic Methods; U.S. Geological Survey Water-Resources Investigations Report 01–4044; U.S. Geological Survey: Reston, VA, USA, 2002; p. 91.
- Levesque, V.A.; Oberg, K.A. Computing Discharge Using the Index Velocity Method; U.S. Geological Survey Techniques and Methods 3–A23; 2012; p. 148. Available online: https://pubs.usgs.gov/tm/3a23/ (accessed on 20 January 2019).
- Fulton, J.W. Guidelines for Siting and Operating Surface-Water Velocity Radars. Available online: https://my.usgs.gov/confluence/display/SurfBoard/Guidelines+for+Siting+and+Operating+Surface-water+Velocity+Radars (accessed on 25 June 2018).
- Moramarco, T.; Barbetta, S.; Tarpanelli, A. From surface flow velocity measurements to discharge assessment by the entropy theory. Water. 2017, 9, 120. [Google Scholar] [CrossRef]
- Parsons, D.R.; Jackson, P.R.; Czuba, J.A.; Engel, F.L.; Rhoads, B.L.; Oberg, K.A.; Best, J.L.; Mueller, D.S.; Johnson, K.K.; Riley, J.D. Velocity Mapping Toolbox (VMT): A processing and visualization suite for moving-vessel ADCP measurements. Earth Surf. Process. Landf. 2013, 38, 1244–1260. [Google Scholar] [CrossRef]
- U.S. Geological Survey (USGS), Office of Surface Water Hydroacoustics Page. Available online: https://hydroacoustics.usgs.gov/movingboat/WinRiverII.shtml (accessed on 30 January 2020).
- Chiu, C.-L.; Chiou, J.-D. Structure of 3-D Flow in rectangular open channels. J. Hydraul. Eng. 1986, 112, 1050–1068. [Google Scholar] [CrossRef]
- Chiu, C.-L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Chiu, C.-L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Chiu, C.-L. Probability and Entropy Concepts in Fluid Flow Modeling and Measurement; National Taiwan University: Taipei, Taiwan, 15 March 1995. [Google Scholar]
- Chiu, C.-L.; Tung, N.C.; Hsu, S.M.; Fulton, J.W. Comparison and Assessment of Methods of Measuring Discharge in Rivers and Streams; Research Report No. CEEWR-4; Dept. of Civil & Environmental Engineering, University of Pittsburgh: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Chiu, C.-L.; Tung, N.C. Velocity and regularities in open-channel flow. J. Hydraul. Eng. 2002, 128, 390–398. [Google Scholar] [CrossRef]
- Chiu, C.-L.; Hsu, S.M.; Tung, N.C. Efficient methods of discharge measurements in rivers and streams based on the probability concept. Hydrol. Process. Wiley Intersci. 2005, 19, 3935–3946. [Google Scholar] [CrossRef]
- Chiu, C.-L.; Hsu, S.-M. Probabilistic approach to modeling of velocity distributions in fluid flows. J. Hydrol. 2006, 316, 28–42. [Google Scholar] [CrossRef]
- Moramarco, T.; Dingman, S.L. On the theoretical velocity distribution and flow resistance in natural channels. J. Hydrol. 2017, 555, 777–785. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channel based on Chiu’s velocity distribution equation. J. Hydrol. Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Fulton, J.W. Comparison of Conventional and Probability-Based Modeling of Open-Channel Flow in The Allegheny River, Pennsylvania, USA. Unpublished Thesis, Department of Civil and Environmental Engineering, University of Pittsburgh, Pittsburgh, PA, USA, April 1999. [Google Scholar]
- Lant, J.; Mueller, D.S. Stage Area Rating Application – AreaComp2, USGS. Office of Surface Water. 2012. Available online: http://hydroacoustics.usgs.gov/software/AreaComp2_Users_Guide.pdf (accessed on 21 January 2020).
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology, International Edition 1988; McGraw-Hill Inc.: Singapore, 1988; pp. 42–47. [Google Scholar]
- González, J.A.; Melching, C.S.; Oberg, K.A. Analysis of open-channel velocity measurements collected with an acoustic Doppler current profiler. Reprint from RIVERTECH 96. In Proceedings of the 1st International Conference On New/Emerging Concepts for Rivers Organized by the International Water Resources Association, Chicago, IL, USA, 22–26 September 1996. [Google Scholar]
- Murphy, E.C. Accuracy of Stream Measurements; Water-Supply and Irrigation Paper No. 95, Series M, General Hydrographic Investigations 10; United States Government Printing Office: Washington, DC, USA, 1904; pp. 58–163.
- Guo, J.; Julien, P.Y. Application of the modified log-wake law in open-Channels. J. Appl. Fluid Mech. 2008, 1, 17–23. [Google Scholar]
- Jarrett, R.D. Wading measurements of vertical velocity profiles. Geomorphology 1991, 4, 243–247. [Google Scholar] [CrossRef]
- Kundu, S.; Ghoshal, K. Velocity Distribution in Open Channels: Combination of Log-law and Parabolic-law. World Acad. Sci. Eng. Technol. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2012, 6, 1234–1241. [Google Scholar]
- Wiberg, P.L.; Smith, J.D. Velocity distribution and bed roughness in high-gradient streams. Water Resour. Res. 1991, 27, 825–838. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Xu, W.-L.; Yu, G.-L. Velocity distribution in gradually accelerating free surface flow. Adv. Water Resour. 2006, 29, 1969–1980. [Google Scholar] [CrossRef]
- Blodgett, J.C. Rock Riprap Design for Protection of Stream Channels Near Highway Structures, Volume 1: Hydraulic Characteristics of Open Channels; U.S. Geological Survey Water-Resources Investigations Report 86–4127; U.S. Geological Survey: Reston, VA, USA, 1986; p. 60. [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 9 February 2020).
- Zambrano-Bigiarini, M. HydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series. R Package Version 0.3–10. 2017. Available online: http://hzambran.github.io/hydroGOF/ (accessed on 9 February 2020).
- Fulton, J.W.; Mcdermott, W.R.; Mason, C.A. Radar-based field measurements of surface velocity and discharge from 10 USGS streamgages for various locations in the United States, 2002–2019. U.S. Geological Survey data release, (manuscript in review).
- U.S. Geological Survey. USGS Water Data for the Nation; U.S. Geological Survey National Water Information System Database; 2016. Available online: https://waterdata.usgs.gov/nwis (accessed on 15 November 2016).
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.532.2506&rep=rep1&type=pdf (accessed on 14 February 2020).
- Muleta, M.K. Model performance sensitivity to objective function during automated Calibrations. J. Hydrol. Eng. 2012, 17, 756–767. [Google Scholar] [CrossRef]
- Bechle, A.J.; Wu, C.H. An entropy-based surface velocity method for estuarine discharge measurement. Water Resour. Res. 2014, 50, 6106–6128. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C. Evidence of Bragg scattering in microwave Doppler spectra of sea return. J. Geophys. Res. 1990, 95, 16299–16310. [Google Scholar] [CrossRef]
- Plant, W.J. Bragg Scattering of Electromagnetic Waves from The air/sea Interface, in Surface Waves and Fluxes: Current Theory and Remote Sensing; Geernaert, G.L., Plant, W.J., Eds.; Kluwer: Dordrecht, The Netherlands, 1990; Volume 2, p. 336. [Google Scholar]
- Wright, J.W. A new model for sea clutter. IEEE Trans. Antennas Propag. 1968, AP-16, 217–223. [Google Scholar] [CrossRef]
- Plant, W.J.; Wright, J.W. Phase speeds of upwind and downwind traveling short gravity waves. J. Geophys. Res. 1980, 85, 3304–3310. [Google Scholar] [CrossRef]

| USGS Streamgage | USGS Streamgage Identification Number | Setting | DA (km2) | Radar Deployment Period | ||
|---|---|---|---|---|---|---|
| Start | End | Duration (Months) | ||||
| Blackfoot River near Bonner, Montana | 12340000 | High-gradient mtn stream | 5930 | May 2013 | Aug 2013 | 4 |
| Cherry Creek at Denver, Colorado | 06713500 | Urban | 1060 | Aug 2017 | Apr 2019 | 19 |
| Clear Creek near Lawson, Colorado | 06716500 | High-gradient mtn stream | 381 | Apr 2019 | Sep 2019 | 6 |
| Gunnison River near Grand Junction, Colorado | 09152500 | Mixed | 20,500 | Aug 2018 | Aug 2019 | 12 |
| NF Shenandoah River near Strasburg, Virginia | 01634000 | Mixed | 1990 | Feb 2015 | Jan 2016 | 11 |
| Red River of the North at Grand Forks, North Dakota | 05082500 | Agricultural | 66,100 | Apr 2013 | May 2013 | < 1 |
| Rio Grande at Embed, New Mexico | 08279500 | Desert | 19,300 | Apr 2014 | Sep 2015 | 17 |
| Susquehanna River at Bloomsburg, Pennsylvania | 01538700 | Mixed | 27,400 | Apr 2011 | May 2011 | < 1 |
| Tanana River at Nenana, Alaska | 15515500 | Forest | 66,200 | May 2018 | Oct 2019 | 18 |
| Yellowstone River near Livingston, Montanan | 06192500 | High-gradient mtn stream | 9200 | May 2013 | Aug 2013 | 4 |
| USGS Streamgage | Number of Visits | Top Width (m) | Hydraulic Depth (m) | ||
|---|---|---|---|---|---|
| min | max | min | max | ||
| Blackfoot River near Bonner, Montana | 2 | 44 | 58 | 0.52 | 2.1 |
| Cherry Creek at Denver, Colorado | 6 | 7.3 | 13 | 0.19 | 0.82 |
| Clear Creek near Lawson, Colorado | 8 | 7.0 | 19 | 0.34 | 0.88 |
| Gunnison River near Grand Junction, Colorado | 1 | 49 | 85 | 0.09 | 2.9 |
| NF Shenandoah River near Strasburg, Virginia | 1 | 56 | 67 | 0.40 | 1.9 |
| Red River of the North at Grand Forks, North Dakota | 2 | 87 | 160 | 5.5 | 7.0 |
| Rio Grande at Embed, New Mexico | 2 | 20 | 37 | 0.61 | 0.85 |
| Susquehanna River at Bloomsburg, Pennsylvania | 6 | 320 | 340 | 2.7 | 5.2 |
| Tanana River at Nenana, Alaska | 7 | 38 | 380 | 1.3 | 3.7 |
| Yellowstone River near Livingston, Montana | 1 | 40 | 104 | 0.98 | 1.9 |
| USGS Streamgage | Stage-Discharge (m3/s) | Streamflow Exceedance | ||
|---|---|---|---|---|
| min | med | max | % exceeded | |
| Blackfoot River near Bonner, Montana | 17.8 | 52.6 | 168 | 5.10 |
| Cherry Creek at Denver, Colorado | 0.12 | 0.79 | 41.6 | 0.00 |
| Clear Creek near Lawson, Colorado | 1.19 | 6.41 | 32.1 | 0.48 |
| Gunnison River near Grand Junction, Colorado | 13.2 | 32.4 | 486 | 0.67 |
| NF Shenandoah River near Strasburg, Virginia | 2.10 | 11.2 | 190 | 0.46 |
| Red River of the North at Grand Forks, North Dakota | 308 | 875 | 1,240 | 0.40 |
| Rio Grande at Embudo, New Mexico | 7.65 | 17.1 | 117 | 3.00 |
| Susquehanna River at Bloomsburg, Pennsylvania | 1,250 | 1,970 | 4,950 | 0.00 |
| Tanana River at Nenana, Alaska | 452 | 1,410 | 2,850 | 0.48 |
| Yellowstone River near Livingston, Montana | 57.1 | 78.1 | 113 | 5.40 |
| USGS Streamgage | Date Collected | PC Metrics | PC | Conv | % error in umean | ||||
|---|---|---|---|---|---|---|---|---|---|
| M (dim) | ϕ (dim) | uD (m/s) | umax (m/s) | Water Depth at y-axis (m) | umean (m/s) | umean (m/s) | |||
| Blackfoot River near Bonner, Montana | 05-20-2013 | 2.10 | 0.664 | 2.70 | 2.70 | 2.57 | 1.79 | 1.78 | 1.1 |
| Cherry Creek at Denver, Colorado | 08-25-2017 | 2.32 | 0.678 | 0.75 | 0.75 | 0.26 | 0.51 | 0.50 | 1.2 |
| Clear Creek near Lawson, Colorado | 04-19-2019 | 0.883 | 0.573 | na | 1.09 | 0.43 | 0.62 | 0.61 | 2.3 |
| Gunnison River near Grand Junction, Colorado | 03-27-2019 | 0.266 | 0.522 | 1.12 | 1.02 | 1.55 | 0.53 | 0.51 | 4.9 |
| NF Shenandoah River near Strasburg, Virginia | 12-04-2014 | 1.03 | 0.584 | 0.45 | 0.49 | 0.77 | 0.29 | 0.31 | −8.0 |
| Red River of the North at Grand Forks, North Dakota | 02-05-2004 | 0.60 | 0.550 | na | 0.09 | 6.34 | 0.05 | 0.05 | −0.1 |
| Rio Grande at Embudo, New Mexico | 03-21-2014 | 1.49 | 0.620 | 1.45 | 1.45 | 0.70 | 0.90 | 0.87 | 3.2 |
| Susquehanna River at Bloomsburg, Pennsylvania | 06-27-2002 | 4.35 | 0.783 | 0.73 | 0.73 | 1.83 | 0.57 | 0.59 | −4.0 |
| Tanana River at Nenana, Alaska | 05-07-2015 | 2.98 | 0.718 | 1.41 | 1.41 | 2.84 | 1.01 | 1.14 | −11 |
| Yellowstone River near Livingston, Montana | 05-22-2013 | 2.92 | 0.715 | 2.96 | 2.96 | 2.86 | 2.11 | 2.13 | −0.7 |
| Average percent error | −1.1 | ||||||||
| Absolute average percent error | 3.6 | ||||||||
| USGS Streamgage | Date Collected | Method | Discharge (m3/s) | % Error in Discharge | |
|---|---|---|---|---|---|
| PC | Conventional | ||||
| Blackfoot River near Bonner, Montana | 05-20-2013 | ADCP | 144 | 142 | 1.1 |
| Cherry Creek at Denver, Colorado | 08-25-2017 | FT | 0.85 | 0.84 | 1.2 |
| Clear Creek near Lawson, Colorado | 04-19-2019 | FT | 1.43 | 1.39 | 2.3 |
| Gunnison River near Grand Junction, Colorado | 03-27-2019 | ADCP | 30.5 | 29.1 | 4.9 |
| NF Shenandoah River near Strasburg, Virginia | 12-04-2014 | ADCP | 11.7 | 12.7 | −8.0 |
| Red River of the North at Grand Forks, North Dakota | 02-05-2004 | ADCP | 12.6 | 12.6 | −0.1 |
| Rio Grande at Embudo, New Mexico | 03-21-2014 | ADCP | 19.3 | 18.7 | 3.2 |
| Susquehanna River at Bloomsburg, Pennsylvania | 06-27-2002 | AA | 292 | 306 | −4.0 |
| Tanana River at Nenana, Alaska | 05-07-2015 | ADCP | 615 | 690 | −11 |
| Yellowstone River near Livingston, Montana | 05-22-2013 | ADCP | 208 | 209 | −0.7 |
| Average percent error | −1.1 | ||||
| Absolute average percent error | 3.6 | ||||
| USGS Streamgage | Radar-Derived Surface Velocity (m/s) | ||
|---|---|---|---|
| min | med | Max | |
| Blackfoot River near Bonner, Montana | 0.66 | 2.03 | 3.01 |
| Cherry Creek at Denver, Colorado | 0.30 | 0.62 | 3.33 |
| Clear Creek near Lawson, Colorado | 0.84 | 1.85 | 3.78 |
| Gunnison River near Grand Junction, Colorado | 0.99 | 1.16 | 3.37 |
| NF Shenandoah River near Strasburg, Virginia | 0.41 | 0.66 | 1.76 |
| Red River of the North at Grand Forks, North Dakota | 0.55 | 1.19 | 1.78 |
| Rio Grande at Embudo, New Mexico | 0.51 | 0.92 | 2.88 |
| Susquehanna River at Bloomsburg, Pennsylvania | 0.64 | 1.62 | 2.53 |
| Tanana River at Nenana, Alaska | 0.70 | 1.81 | 3.02 |
| Yellowstone River near Livingston, Montana | 1.39 | 2.49 | 3.84 |
| USGS Streamgage | Radar-Derived Discharge (m3/s) | Stage-Discharge (m3/s) | ||||
|---|---|---|---|---|---|---|
| min | med | max | min | med | max | |
| Blackfoot River near Bonner, Montana | 14.3 | 63.5 | 177 | 17.8 | 52.6 | 168 |
| Cherry Creek at Denver, Colorado | 0.17 | 0.73 | 38.6 | 0.12 | 0.79 | 41.6 |
| Clear Creek near Lawson, Colorado | 1.40 | 6.98 | 38.2 | 1.19 | 6.41 | 32.1 |
| Gunnison River near Grand Junction, Colorado | 21.0 | 31.1 | 450 | 13.2 | 32.4 | 486 |
| NF Shenandoah River near Strasburg, Virginia | 2.87 | 9.69 | 167 | 2.10 | 11.2 | 190 |
| Red River of the North at Grand Forks, North Dakota | 213 | 916 | 1470 | 308 | 875 | 1250 |
| Rio Grande at Embudo, New Mexico | 5.77 | 16.8 | 138 | 7.65 | 17.1 | 117 |
| Susquehanna River at Bloomsburg, Pennsylvania | 603 | 1780 | 4890 | 1250 | 1970 | 4950 |
| Tanana River at Nenana, Alaska | 381 | 1280 | 2640 | 452 | 1410 | 2850 |
| Yellowstone River near Livingston, Montana | 53.3 | 71.9 | 102 | 57.1 | 78.1 | 113 |
| USGS streamgage | n | MAE (m3/s) | PBIAS | NSE | (log) NSE | VE |
|---|---|---|---|---|---|---|
| Blackfoot River near Bonner, Montana | 7499 | 9.12 | 13.5 | 0.95 | 0.88 | 0.86 |
| Cherry Creek at Denver, Colorado | 151,161 | 0.13 | −9.2 | 0.91 | 0.90 | 0.86 |
| Clear Creek near Lawson, Colorado | 13,222 | 1.91 | 12 | 0.85 | 0.96 | 0.81 |
| Gunnison River near Grand Junction, Colorado | 34,628 | 7.85 | −8.6 | 0.98 | 0.99 | 0.90 |
| NF Shenandoah River near Strasburg, Virginia | 29,563 | 2.53 | −13.9 | 0.95 | 0.97 | 0.85 |
| Red River of the North at Grand Forks, North Dakota | 1558 | 122 | −3.0 | 0.71 | 0.70 | 0.86 |
| Rio Grande at Embudo, New Mexico | 41,219 | 1.13 | −2.9 | 0.97 | 0.97 | 0.94 |
| Susquehanna River at Bloomsburg, Pennsylvania | 448 | 286 | −10.6 | 0.79 | 0.61 | 0.87 |
| Tanana River at Nenana, Alaska | 28,047 | 247 | −10.6 | 0.59 | 0.60 | 0.82 |
| Yellowstone River near Livingston, Montana | 3099 1 | 6.17 | −7.8 | 0.79 | 0.81 | 0.92 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fulton, J.W.; Mason, C.A.; Eggleston, J.R.; Nicotra, M.J.; Chiu, C.-L.; Henneberg, M.F.; Best, H.R.; Cederberg, J.R.; Holnbeck, S.R.; Lotspeich, R.R.; et al. Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sens. 2020, 12, 1296. https://doi.org/10.3390/rs12081296
Fulton JW, Mason CA, Eggleston JR, Nicotra MJ, Chiu C-L, Henneberg MF, Best HR, Cederberg JR, Holnbeck SR, Lotspeich RR, et al. Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sensing. 2020; 12(8):1296. https://doi.org/10.3390/rs12081296
Chicago/Turabian StyleFulton, John W., Christopher A. Mason, John R. Eggleston, Matthew J. Nicotra, Chao-Lin Chiu, Mark F. Henneberg, Heather R. Best, Jay R. Cederberg, Stephen R. Holnbeck, R. Russell Lotspeich, and et al. 2020. "Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages" Remote Sensing 12, no. 8: 1296. https://doi.org/10.3390/rs12081296
APA StyleFulton, J. W., Mason, C. A., Eggleston, J. R., Nicotra, M. J., Chiu, C.-L., Henneberg, M. F., Best, H. R., Cederberg, J. R., Holnbeck, S. R., Lotspeich, R. R., Laveau, C. D., Moramarco, T., Jones, M. E., Gourley, J. J., & Wasielewski, D. (2020). Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sensing, 12(8), 1296. https://doi.org/10.3390/rs12081296






