A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops
Abstract
1. Introduction
2. Methodology
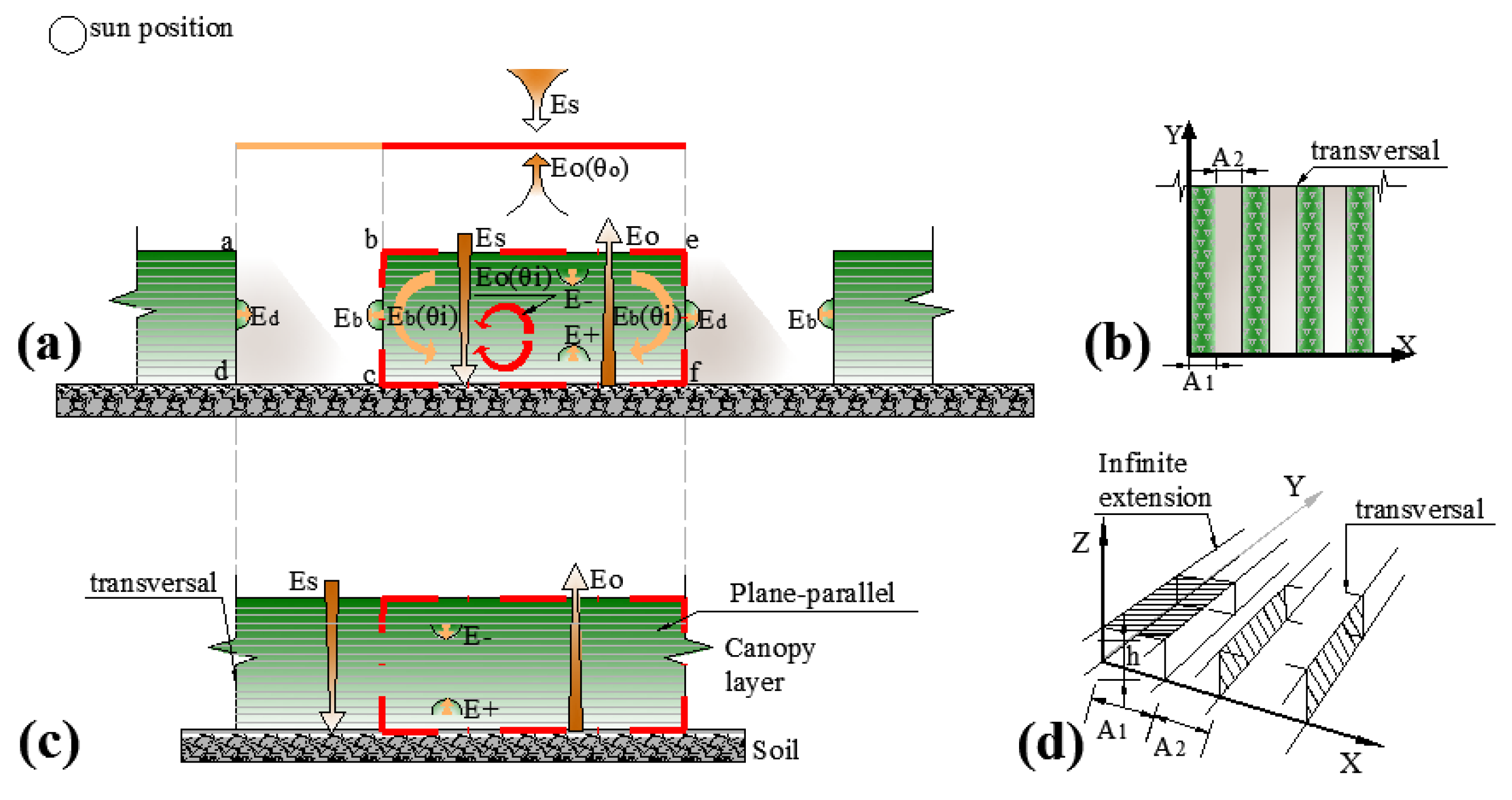
2.1. Four-Stream Radiative Transfer Equations for Continuous Crops
2.2. Refined Four-Stream Radiative Transfer Equations for Row-Planted Crops Considering Horizontal Radiative Transfer Equations
2.3. Sum of the Directional Reflectance Factor of Row-Planted Crops
2.3.1. Directional Reflectance Factor of the Canopy Closure
Single Scattering of the Canopy Closure
Multiple Scattering of the Canopy Closure
2.3.2. Directional Reflectance Factor of the Between Row Area
Single Scattering of the Between Row Area
Multiple Scattering of the Between Row Area
2.4. Input Parameters of the MFS Model
- (1)
- Geometrical parameters: solar zenith angle (), solar azimuth angle (), viewing zenith angle (), viewing azimuth angle (), and row azimuth angle ();
- (2)
- Canopy parameters: height of the canopy (), row width (), distance between rows (), leaf area index () and effective leaf area index (), average leaf inclined angle (), and canopy dimension parameter ();
- (3)
- Biochemical leaf parameters: chlorophyll content (), carotenoid content (), brown pigment content (), equivalent water thickness (), leaf mass per unit leaf area (), and structure coefficient ();
- (4)
- Canopy radiative parameters: the fraction of incoming diffuse radiation ().
3. Data
3.1. Computer-Simulated Data
3.1.1. Generation of Computer Abstract Scenes
3.1.2. Input and Output Settings for Computer-Simulated Validation
Input Setting
Output Setting
3.2. In Situ Data
3.2.1. Measurement Experiment
Directional Reflectance Factor (DRF)
Canopy Structural and Leaf Biochemical Parameters
3.2.2. Input and Output Settings for In Situ Validation
Input Setting
Output Setting
4. Results
4.1. Validation of MFS Model Using Computer-Simulated Data
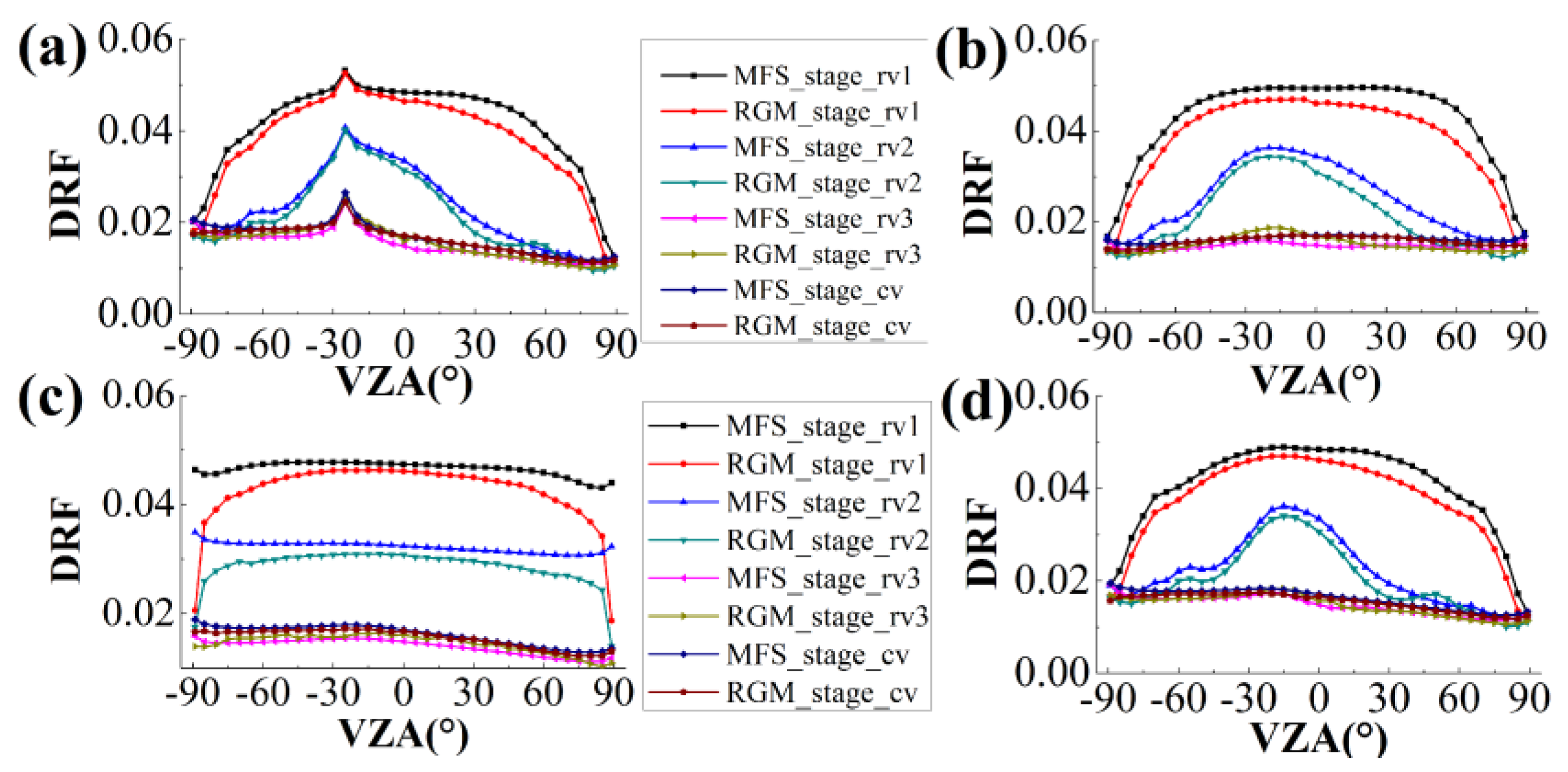
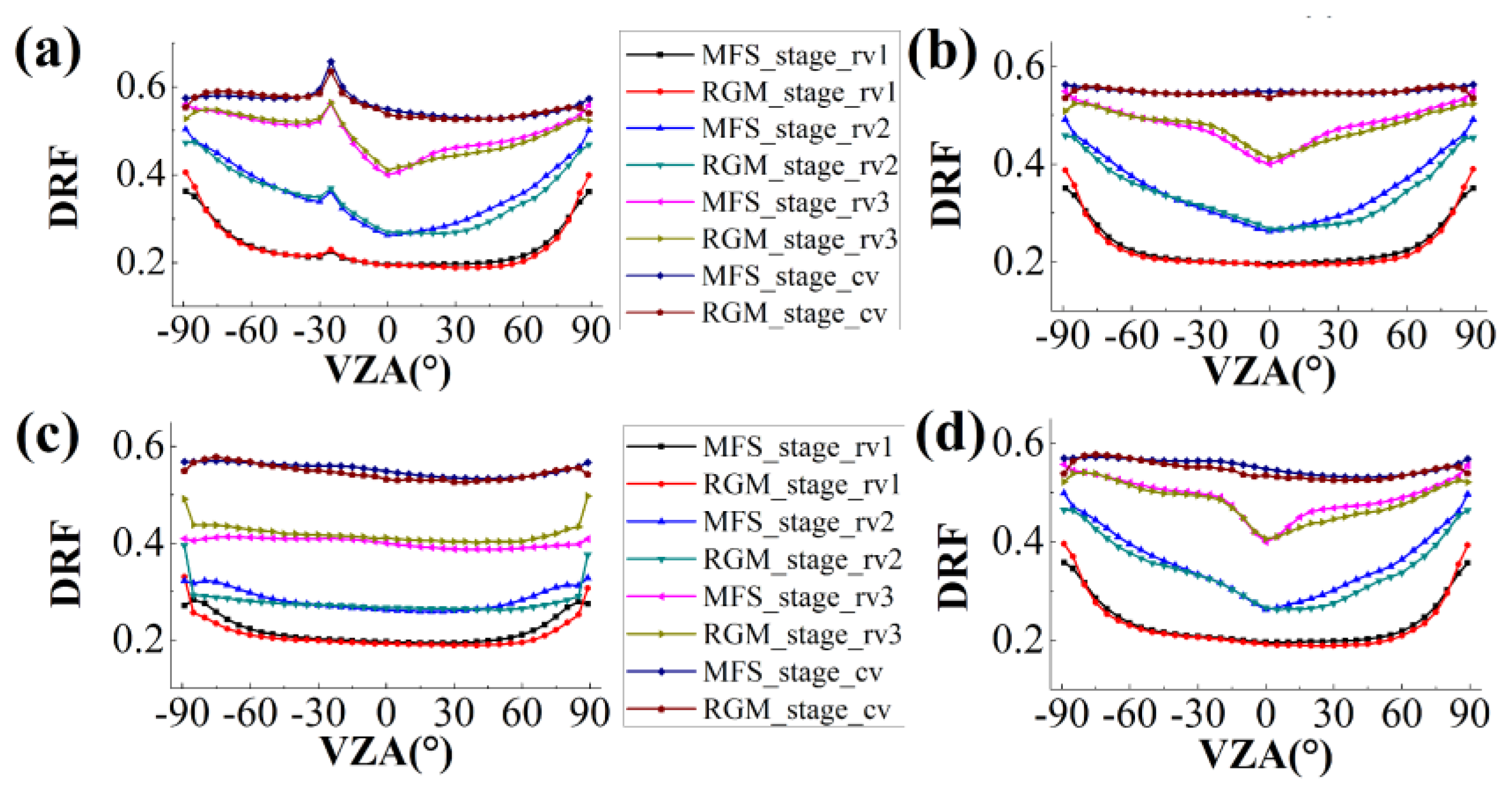
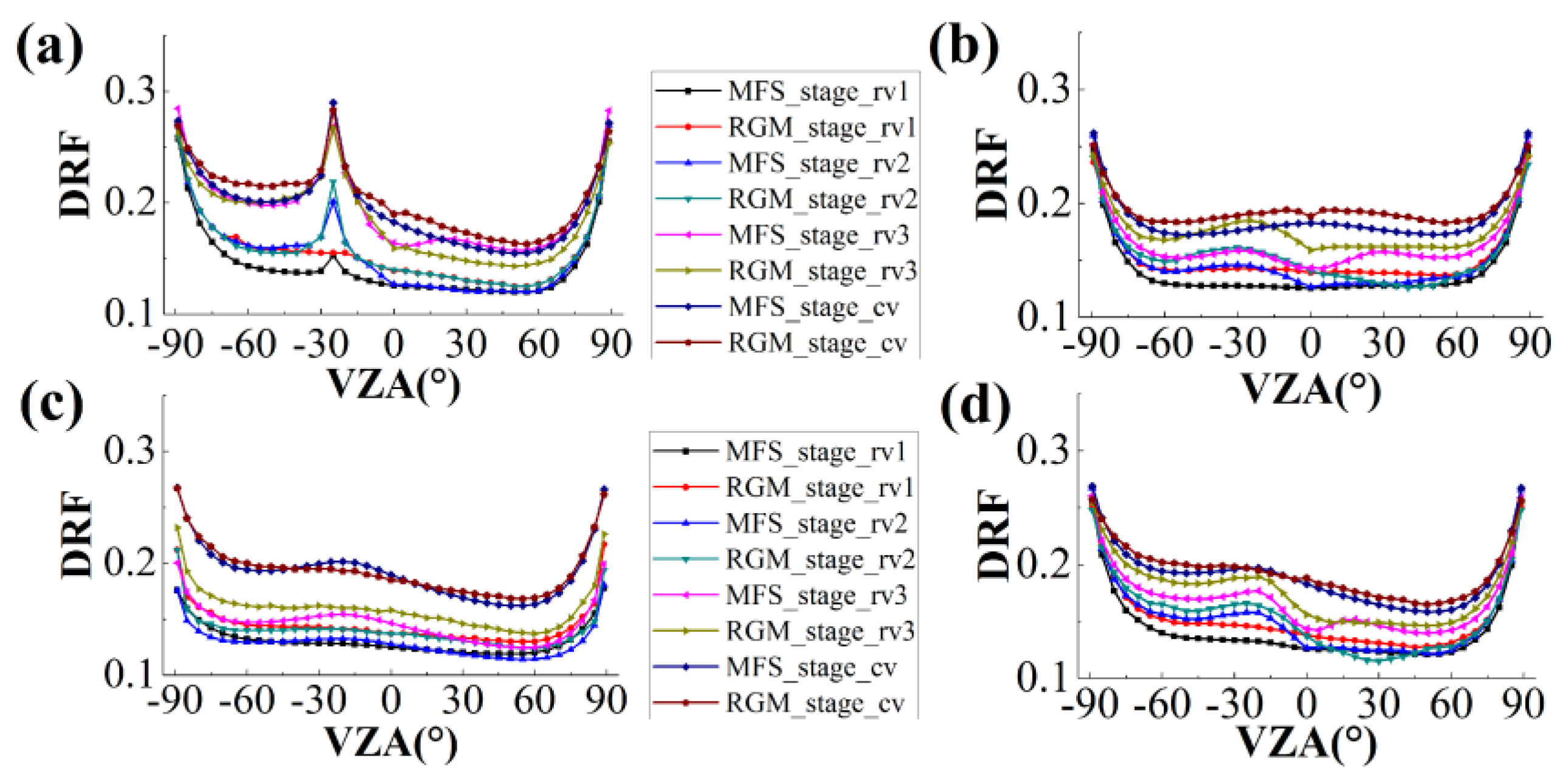
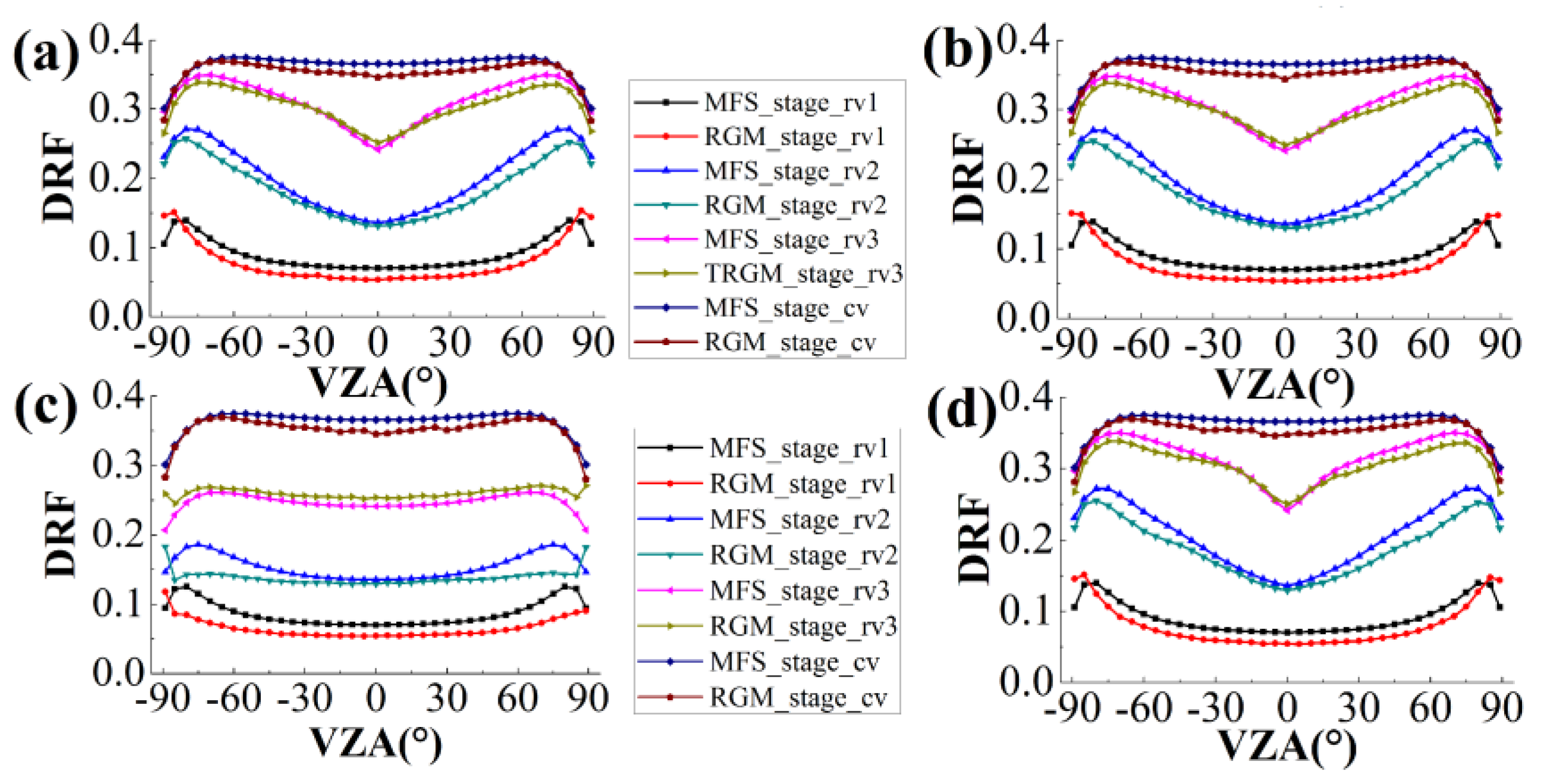
4.1.1. Results of the Qualitative Analysis of DRFs in the Red Band
4.1.2. Results of the Qualitative Analysis of DRFs in the NIR Band
4.1.3. Quantitative Analysis Results
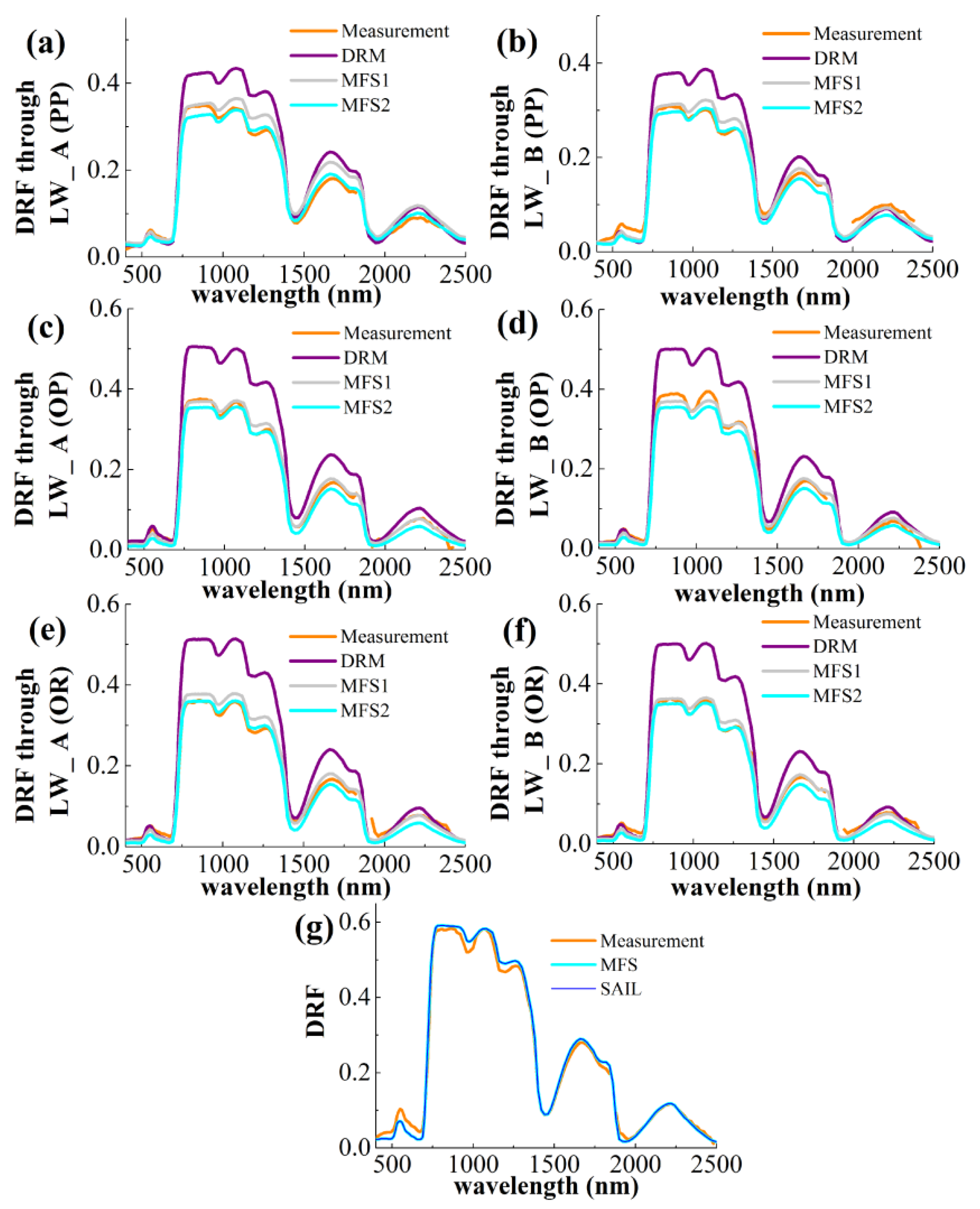
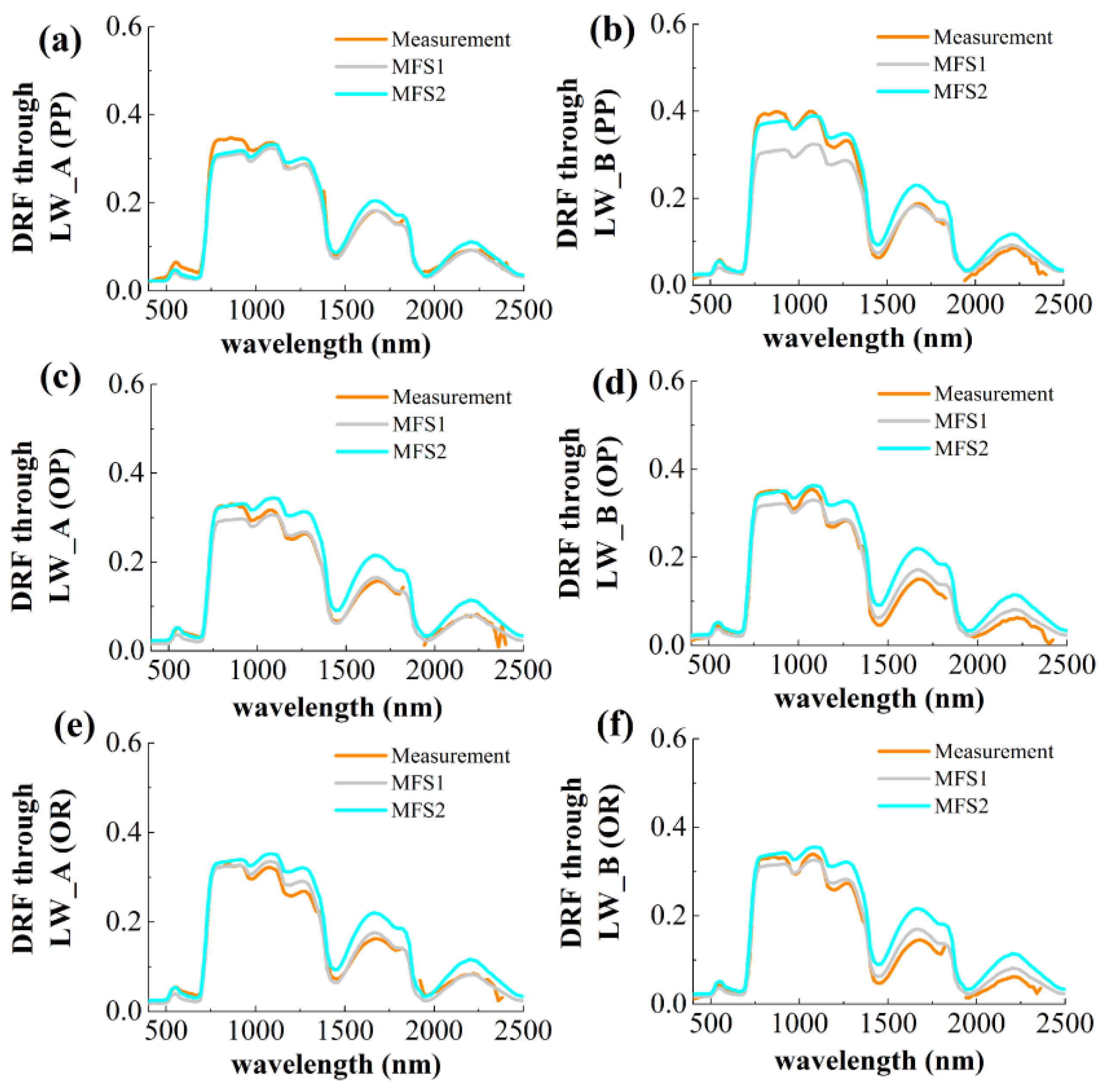
4.2. Validation of the MFS Model Using In Situ Data
5. Discussion
5.1. Systematic Deviation of the DRFs in the NIR Band at Zenith Angles Larger than 40°
5.2. Differences between MFS Model and Computer Simulation
5.3. The Relationship between the MFS Model and SAIL Model
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jackson, J.E.; Palmer, J.W. Interception of Light by Model Hedgerow Orchards in Relation to Latitude, Time of Year and Hedgerow Configuration and Orientation. J. Appl. Ecol. 1972, 9, 341. [Google Scholar] [CrossRef]
- Jackson, R.D.; Reginato, R.J.; Pinter, P.J.; Idso, S.B. Plant canopy information extraction from composite scene reflectance of row crops. Appl. Opt. 1979, 18, 3775–3782. [Google Scholar] [CrossRef] [PubMed]
- Suits, G.H. Extension of a uniform canopy reflectance model to include row effects. Remote Sens. Environ. 1981, 13, 113–129. [Google Scholar] [CrossRef]
- Annandale, J.G.; Jovanovic, N.Z.; Campbell, G.S.; Du, S.N.; Lobit, P. Two-dimensional solar radiation interception model for hedgerow fruit trees. Agric. For. Meteorol. 2004, 121, 207–225. [Google Scholar] [CrossRef]
- Liang, S.L. Quantitative Remote Sensing of Land Surfaces; John Wiley-Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Chen, J.M.; Li, X.; Nilson, T.; Strahler, A. Recent advances in geometrical optical modelling and its applications. Urban Stud. 2013, 50, 1403–1422. [Google Scholar] [CrossRef]
- Zhou, K.; Guo, Y.; Geng, Y.; Zhu, Y.; Cao, W.; Tian, Y. Development of a Novel Bidirectional Canopy Reflectance Model for Row-Planted Rice and Wheat. Remote Sens. 2014, 6, 7632–7659. [Google Scholar] [CrossRef]
- Wang, W.M.; Li, Z.L.; Su, H.B. Comparison of leaf angle distribution functions: Effects on extinction coefficient and fraction of sunlit foliage. Agric. For. Meteorol. 2007, 143, 106–122. [Google Scholar] [CrossRef]
- Wit, D.C.T. Photosynthesis of leaf canopies. J. Agric. Sci. 1965, 13, 57–59. [Google Scholar]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Goel, N.S.; Rozehnal, I.; Thompson, R.L. A computer graphics based model for scattering from objects of arbitrary shapes in the optical region. Remote Sens. Environ. 1991, 36, 73–104. [Google Scholar] [CrossRef]
- Lewis, P. Three-dimensional plant modelling for remote sensing simulation studies using the Botanical Plant Modelling System. Agronomie 1999, 19, 185–210. [Google Scholar] [CrossRef]
- Verhoef, W. Earth observation modeling based on layer scattering matrices. Remote Sens. Environ. 1985, 17, 165–178. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ross, J.; Asrar, G. A review on the theory of photon transport in leaf canopies. Agric. For. Meteorol. 1989, 45, 1–153. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ross, J. Photon-Vegetation Interactions; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Kubelka, P.; Munk, F. Ein beitrag zur optik der farbanstriche. Z. Fur Tech. Phys. 1931, 12, 593–601. [Google Scholar]
- Allen, W.A.; Gayle, T.V.; Richardson, A.J. Plant-canopy irradiance specified by the Duntley equations. J. Optic. Soc. Am. 1970, 60, 372–376. [Google Scholar] [CrossRef]
- Suits, G.H. The calculation of the directional reflectance of a vegetative canopy. Remote Sens. Environ. 1971, 2, 117–125. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Pieri, P. Modelling radiative balance in a row-crop canopy: Cross-row distribution of net radiation at the soil surface and energy available to clusters in a vineyard. Ecol. Model. 2010, 221, 802–811. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Agam, N.; Schwartz, R.C.; Kustas, W.P. Soil heat flux calculation for sunlit and shaded surfaces under row crops: 1. Model development and sensitivity analysis. Agric. For. Meteorol. 2016, 216, 115–128. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Agam, N.; Schwartz, R.C.; Kustas, W.P.; Cosh, M.H.; McKee, L. Soil heat flux calculation for sunlit and shaded surfaces under row crops: 2. Model test. Agric. For. Meteorol. 2016, 216, 129–140. [Google Scholar] [CrossRef]
- Verbrugghe, M.; Cierniewski, J. Effects of Sun and view geometries on cotton bidirectional reflectance. Test of a geometrical model. Remote Sens. Environ. 1995, 54, 189–197. [Google Scholar] [CrossRef]
- Kimes, D.S. Remote sensing of row crop structure and component temperatures using directional radiometric temperatures and inversion techniques. Remote Sens. Environ. 1983, 13, 33–55. [Google Scholar] [CrossRef]
- Kuusk, A. The hot-spot effect of a uniform vegetative cover. Sov. J. Remote Sens. 1985, 3, 645–658. [Google Scholar]
- Yan, B.Y.; Xu, X.R.; Fan, W.J. A unified canopy bidirectional reflectance (BRDF) model for row crops. Sci. China Earth Sci. 2012, 55, 824–836. [Google Scholar] [CrossRef]
- Yang, X.; Short, T.H.; Fox, R.D.; Bauerle, W.L. Plant architectural parameters of a greenhouse cucumber row crop. Agric. For. Meteorol. 1990, 51, 93–105. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Q.; Fan, W.; Li, X.; Xiao, Q.; Yan, G.; Tian, G. A bi-directional gap model for simulating the directional thermal radiance of row crops. China Sci. Earth Sci. 2002, 45, 1087–1098. [Google Scholar] [CrossRef]
- Yan, G.J.; Jiang, L.M.; Wang, J.D.; Chen, L.F.; Li, X.W. Thermal bidirectional gap probability model for row crop canopies and validation. Sci. China Earth Sci. 2003, 46, 1241–1249. [Google Scholar] [CrossRef]
- Gijzen, H.; Goudriaan, J. A flexible and explanatory model of light distribution and photosynthesis in row crops. Agric. For. Meteorol. 1989, 48, 1–20. [Google Scholar] [CrossRef]
- Goel, N.S.; Grier, T. Estimation of canopy parameters for inhomogeneous vegetation canopies from reflectance data. III. TRIM: A model for radiative transfer in heterogeneous three-dimensional canopies. Int. J. Remote Sens. 1986, 25, 255–293. [Google Scholar] [CrossRef]
- Goel, N.S.; Grier, T. Estimation of canopy parameters of row planted vegetation canopies using reflectance data for only four view directions. Remote Sens. Environ. 1987, 21, 37–51. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Modeling the gap probability of a discontinuous vegetation canopy. IEEE Trans. Geosci. Remote Sens. 1988, 26, 161–170. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H.; Woodcock, C.E. A hybrid geometric optical-radiative transfer approach for modeling albedo and directional reflectance of discontinuous canopies. IEEE Trans. Geosci. Remote Sens. 1995, 33, 466–480. [Google Scholar] [CrossRef]
- Zhao, F.; Gu, X.; Verhoef, W.; Wang, Q.; Yu, T.; Liu, Q.; Huang, H.; Qin, W.; Chen, L.; Zhao, H. A spectral directional reflectance model of row crops. Remote Sens. Environ. 2010, 114, 265–285. [Google Scholar] [CrossRef]
- Dorigo, W.A. Improving the Robustness of Cotton Status Characterisation by Radiative Transfer Model Inversion of Multi-Angular CHRIS/PROBA Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 18–29. [Google Scholar] [CrossRef]
- Andrade, J.F.; Edreira, J.I.; Mourtzinis, S.; Conley, S.P.; Ciampitti, I.A.; Dunphy, J.E.; Gaska, J.M.; Glewen, K.; Holshouser, D.L.; Kandel, H.J.; et al. Assessing the influence of row spacing on soybean yield using experimental and producer survey data. Field Crop. Res. 2019, 230, 98–106. [Google Scholar] [CrossRef]
- Cahalan, R.F.; Ridgway, W.; Wiscombe, W.J.; Bell, T.L.; Snider, J.B. The Albedo of Fractal Stratocumulus Clouds. J. Atmos. Sci. 1994, 51, 2434–2460. [Google Scholar] [CrossRef]
- Titov, G.A. Radiative Horizontal Transport and Absorption in Stratocumulus Clouds. J. Atmos. Sci. 1998, 55, 2549–2560. [Google Scholar] [CrossRef]
- Szczap, F.; Isaka, H.; Saute, M.; Guillemet, B.; Ioltukhovski, A. Effective radiative properties of bounded cascade absorbing clouds: Definition of an effective single-scattering albedo. J. Geophys. Res. Atmos. 2000, 105, 20635–20648. [Google Scholar] [CrossRef]
- Marshak, A.; Davis, A.B. Horizontal Fluxes and Radiative Smoothing; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Titov, G.A. Statistical Description of Radiation Transfer in Clouds. J. Atmos. Sci. 2010, 47, 24–38. [Google Scholar]
- Widlowski, J.L.; Pinty, B.; Lavergne, T.; Verstraete, M.M.; Gobron, N. Horizontal radiation transport in 3–D forest canopies at multiple spatial resolutions: Simulated impact on canopy absorption. Remote Sens. Environ. 2006, 103, 379–397. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Marshak, A.; Myneni, R.B. Three-dimensional radiative transfer in vegetation canopies. In 3D Radiative Transfer in Cloudy Atmospheres; Marshak, A., Davis, A., Eds.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bunnik, N.J.J. The multispectral reflectance of shortwave radiation by agricultural crops in relation with their morphological and optical properties. Ph.D. Thesis, Technische Hogeschool te Twente, Wageningen, The Netherlands, 1978. [Google Scholar]
- Campbell, G.S. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar] [CrossRef]
- Verhoef, W. Theory of Radiative Transfer Models Applied in Optical Remote Sensing of Vegetation Canopies. Ph.D. Thesis, Landbouw Universiteit Wageningen, Wageningen, The Netherlands, 1998. [Google Scholar]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; Le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Pinty, B.; Lopatka, M.; Atzberger, C.; Buzica, D.; Chelle, M.; Disney, M.; Gastellu-Etchegorry, J.P.; Gerboles, M.; Gobron, N.; et al. The fourth radiation transfer model intercomparison (RAMI-IV): Proficiency testing of canopy reflectance models with ISO-13528. J. Geophys. Res. Atmos. 2013, 118, 6869–6890. [Google Scholar] [CrossRef]
- Pinty, B.; Gobron, N.; Widlowski, J.L.; Gerstl, S.A.; Verstraete, M.M.; Antunes, M.; Bacour, C.; Gascon, F.; Gastellu, J.P.; Goel, N.; et al. Radiation transfer model intercomparison (RAMI) exercise. J. Geophys. Res. Atmos. 2001, 106, 523–538. [Google Scholar] [CrossRef]
- Pinty, B.; Widlowski, J.L.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Disney, M.; Gascon, F.; Gastellu, J.-P.; Jiang, L.; Kuusk, A.; et al. Radiation Transfer Model Intercomparison (RAMI) exercise: Results from the second phase. J. Geophys. Res. Atmos. 2004, 109, 523–538. [Google Scholar] [CrossRef]
- Pinty, B.; Widlowski, J.L.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Disney, M.; Gascon, F.; Gastellu, J.P.; Jiang, L.; Kuusk, A.; et al. The third RAdiation transfer Model Intercomparison (RAMI) exercise: Documenting progress in canopy reflectance modelling. J. Geophys. Res. Atmos. 2007, 112, 139–155. [Google Scholar]
- Liu, Q.; Huang, H.; Qin, W.; Fu, K.; Li, X. An Extended 3–D Radiosity–Graphics Combined Model for Studying Thermal-Emission Directionality of Crop Canopy. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2900–2918. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Fan, W.; Xin, X.; Yan, G.; Wang, J.; Tao, X.; Yao, Y.; Yan, B.; Shen, X.; Zhou, C.; Li, L.; et al. WATER: Dataset of LAI Measurements in the Yingke Oasis and Huazhaizi Desert Steppe Foci Experimental Areas; Heihe Plan Science Data Center: Lanzhou, China, 2010. [Google Scholar] [CrossRef]
- Li, X.; Ma, M.G.; Wang, J.; Liu, Q.; Che, T.; Hu, Z.Y.; Xiao, Q.; Liu, Q.H.; Su, P.X.; Chu, R.Z. Simultaneous remote sensing and ground-based experiment in the Heihe River Basin: Scientific objectives and experiment design. Adv. Earth Sci. 2008, 23, 897–914. [Google Scholar]
- Sandoval, C.; Kim, A.D. Extending generalized Kubelka-Munk to three-dimensional radiative transfer. Appl. Opt. 2015, 54, 7045. [Google Scholar] [CrossRef]
- Yan, G.; Ren, H.; Xin, X.; Liu, Q.; Wang, J. WATER: Dataset of Setting of the Sampling Plots and Stripes in the Yingke Oasis and Huazhaizi Desert Steppe Foci Experimental Areas; Heihe Plan Science Data Center: Lanzhou, China, 2013. [Google Scholar] [CrossRef]
- Yao, Y.; Fan, W.; Liu, Q.; Li, L.; Tao, X.; Xin, X.; Liu, Q. Improved harvesting method for corn LAI measurement in corn whole growth stages. Trans. Csae 2010, 26, 189–194. [Google Scholar]
- Li, L.; Xin, X.; Zhang, Y.; Zhou, M. WATER: Dataset of Chlorophyll Content Observations in the Yingke Oasis and Linze Grassland Foci Experimental Areas; Heihe Plan Science Data Center: Lanzhou, China, 2010. [Google Scholar] [CrossRef]
- Wu, C.; Gao, S.; Dong, J.; Wu, M. WATER: Dataset of Crop Biochemical Parameter Measurements in the Yingke Oasis Foci Experimental Area; Heihe Plan Science Data Center: Lanzhou, China, 2010. [Google Scholar] [CrossRef]
- Han, X. Quantitative Remote Sensing of Vegetation Water Based on MODIS and Spectra of Vegetation. Master’s Thesis, Chang’an University, Xi’an, China, 2009. [Google Scholar]
- Yan, G.; Zhang, W.; Wang, H.; Ren, H.; Chen, L.; Qian, Y.; Wang, J.; Wang, T. Dataset of Vegetation Cover Fraction Observations in the Yingke Oasis, Huazhaizi Desert Steppe and Biandukou Foci Experimental Areas; Heihe Plan Science Data Center: Lanzhou, China, 2010. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties EXperiment 93 (LOPEX93); Institue for Remote Sensing Applications, European Commission: Luxemberg, 1994. [Google Scholar]
- Verhoef, W. Improved modelling of multiple scattering in leaf canopies: The model SAIL++. In Proceedings of the First RAQRS Symposium, Torrent, Spain, 16–20 September 2002. [Google Scholar]

| Scene1 | Figure 2 | A1 (m) | A2 (m) | h (m) | L (m•m−1) | n△ (-) | w*△ (m) | l*△ (m) | θl (°) | φr (°) |
|---|---|---|---|---|---|---|---|---|---|---|
| Stage_rv1 | (a) | 0.4 | 0.6 | 0.48 | 0.58 | 10,419 | 0.02 | 0.02 | 44 | 0 |
| Stage_rv2 | (b) | 0.5 | 0.5 | 0.88 | 1.75 | 25,840 | 0.02 | 0.02 | 44 | 0 |
| Stage_rv3 | (c) | 0.75 | 0.25 | 1.28 | 3.51 | 48,325 | 0.02 | 0.02 | 44 | 0 |
| Stage_cv | (d) | 1 | 0 | 1.58 | 5.11 | 40,262 | 0.02 | 0.02 | 44 | 0 |
| Vegetation Type | Model | L (m•m−1) | LE (m•m−1) | LIDFa | LIDFb | A1 (m) | A2 (m) | h (m) | skyl (-) | θo (°) |
|---|---|---|---|---|---|---|---|---|---|---|
| RC | MFS1 | 2.51 | 2.51 | 0.38 | −0.02 | 0.46 | 0.46 | 0.98 | 0.1 | 60 |
| MFS2 | 2.51 | 1.73 | 0.38 | −0.02 | 0.46 | 0.46 | 0.98 | 0.1 | 60 | |
| DRM | 2.51 | - | 0.38 | −0.02 | 0.46 | 0.46 | 0.98 | 0.1 | 60 | |
| CC | MFS | 3.99 | 3.99 | 0.38 | −0.02 | 1 | 0 | 1.54 | 0.1 | 0 |
| SAIL | 3.99 | - | 0.38 | −0.02 | - | - | - | 0.1 | 0 |
| Scenes. | Statistics | DRF_red | DRF_NIR | DRF_NIR_1 | DRF_NIR_m |
|---|---|---|---|---|---|
| Stage_rv1 | R | 0.9842 | 0.9900 | 0.9881 | 0.9846 |
| RMSE | 0.0018 | 0.0082 | 0.0038 | 0.0063 | |
| Average difference | −16.69% | −7.49% | 9.41% | −22.64% | |
| Stage_rv2 | R | 0.9788 | 0.9807 | 0.9667 | 0.9864 |
| RMSE | 0.0017 | 0.0141 | 0.0087 | 0.0079 | |
| Average difference | −13.76% | −11.69% | −9.99% | 3.35% | |
| Stage_rv3 | R | 0.9341 | 0.9352 | 0.9714 | 0.9610 |
| RMSE | 0.0008 | 0.0186 | 0.0065 | 0.0112 | |
| Average difference | 4.80% | −0.48% | −1.02% | −0.10% | |
| Stage_cv | R | 0.9662 | 0.8207 | 0.9895 | 0.9084 |
| RMSE | 0.0005 | 0.0083 | 0.0035 | 0.008 | |
| Average difference | −5.25% | 1.53% | 1.16% | −3.02% |
| RC(PP) | RC(OP) | RC(OR) | CV | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lateral wall A | lateral wall B | lateral wall A | lateral wall B | lateral wall A | lateral wall B | ||||||||||
| R | RMSE | R | RMSE | R | RMSE | R | RMSE | R | RMSE | R | RMSE | R | RMSE | ||
| DRM | 0.997 | 0.012 | 0.997 | 0.011 | 0.990 | 0.026 | 0.998 | 0.010 | 0.996 | 0.017 | 0.999 | 0.008 | SAIL | 0.998 | 0.012 |
| MFS1 (60) | 0.994 | 0.013 | 0.997 | 0.008 | 0.989 | 0.020 | 0.998 | 0.009 | 0.996 | 0.017 | 0.998 | 0.006 | MFS | 0.998 | 0.012 |
| MFS2 (60) | 0.996 | 0.010 | 0.998 | 0.007 | 0.990 | 0.018 | 0.999 | 0.006 | 0.996 | 0.011 | 0.998 | 0.006 | |||
| MFS1 (50) | 0.991 | 0.016 | 0.994 | 0.012 | 0.996 | 0.012 | 0.995 | 0.013 | 0.996 | 0.011 | 0.996 | 0.011 | |||
| MFS2 (50) | 0.991 | 0.018 | 0.990 | 0.016 | 0.990 | 0.019 | 0.986 | 0.022 | 0.991 | 0.018 | 0.987 | 0.021 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Wang, T.; Lu, L. A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops. Remote Sens. 2020, 12, 1290. https://doi.org/10.3390/rs12081290
Ma X, Wang T, Lu L. A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops. Remote Sensing. 2020; 12(8):1290. https://doi.org/10.3390/rs12081290
Chicago/Turabian StyleMa, Xu, Tiejun Wang, and Lei Lu. 2020. "A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops" Remote Sensing 12, no. 8: 1290. https://doi.org/10.3390/rs12081290
APA StyleMa, X., Wang, T., & Lu, L. (2020). A Refined Four-Stream Radiative Transfer Model for Row-Planted Crops. Remote Sensing, 12(8), 1290. https://doi.org/10.3390/rs12081290






