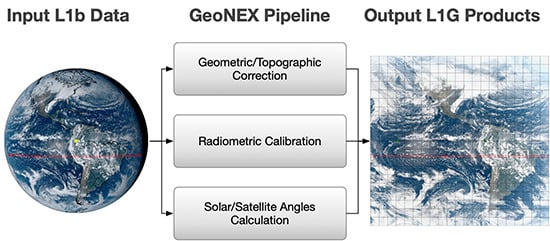
An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature
Abstract
1. Introduction
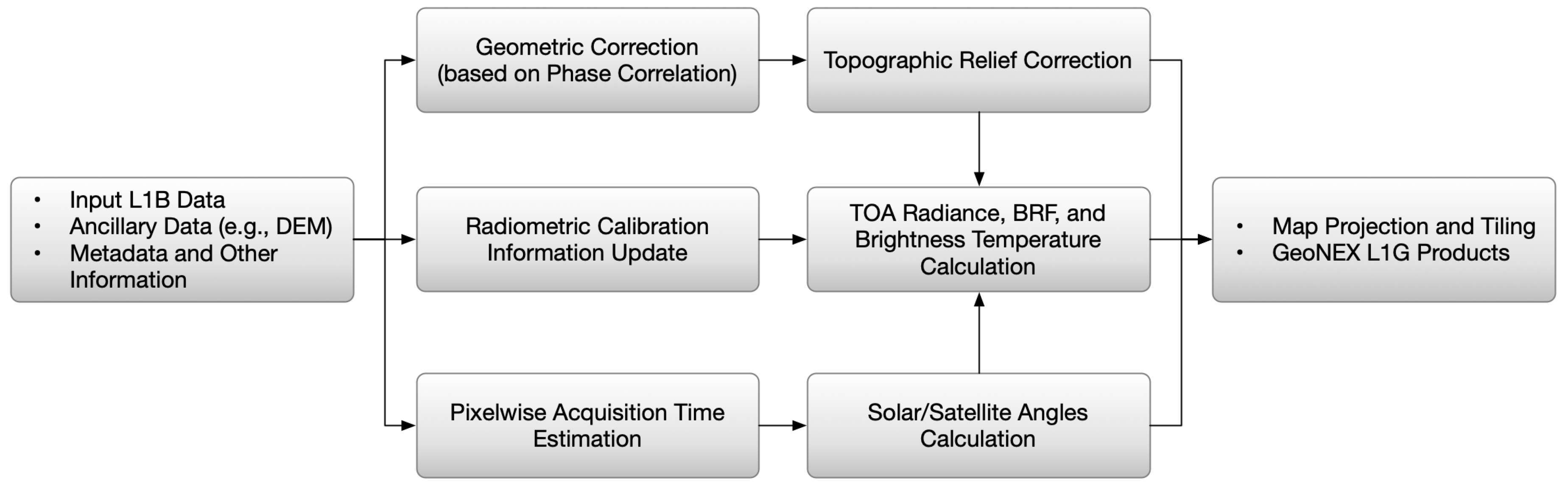
2. Materials and Methods
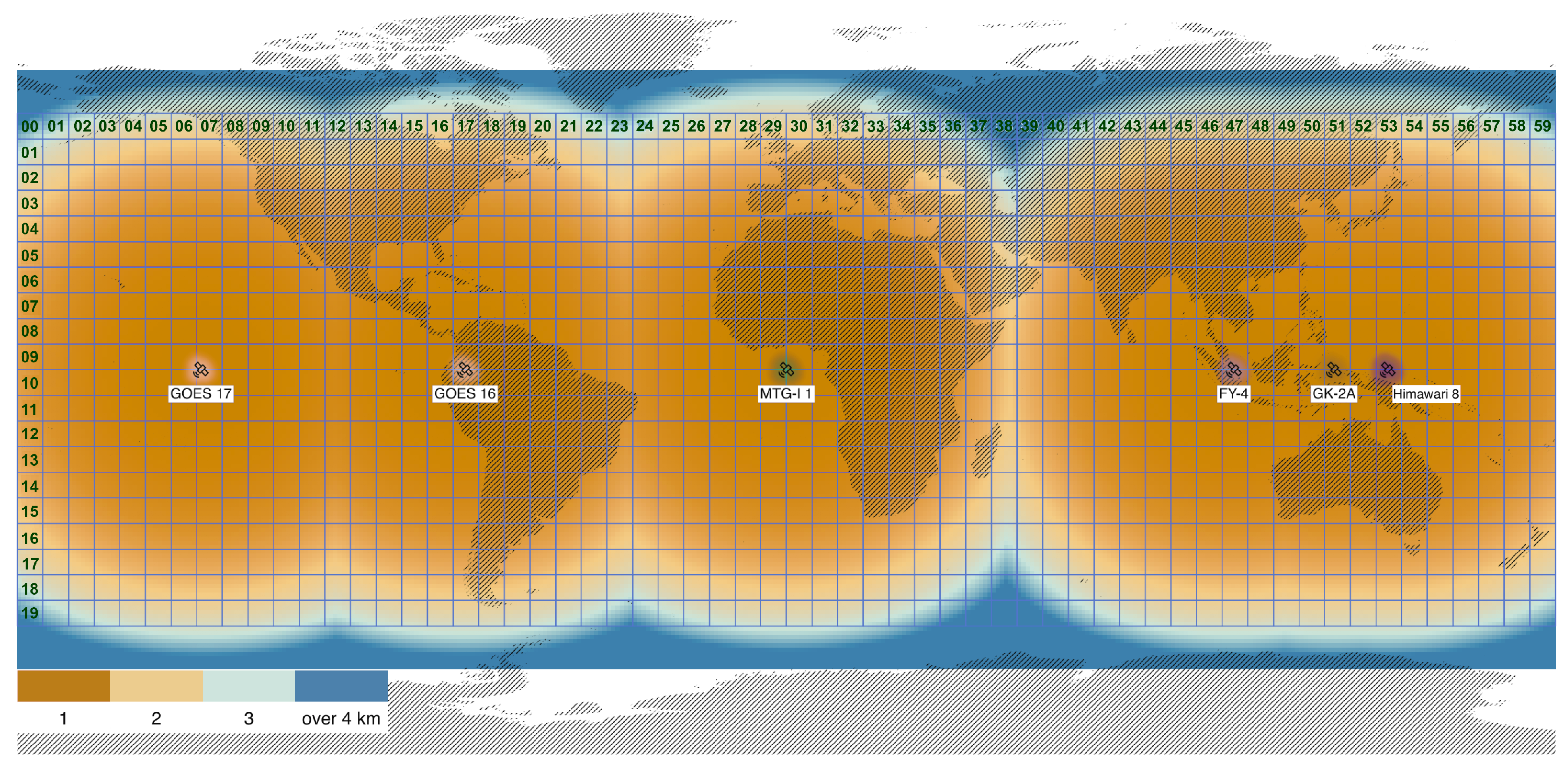
2.1. Global Geographic Tile Grid
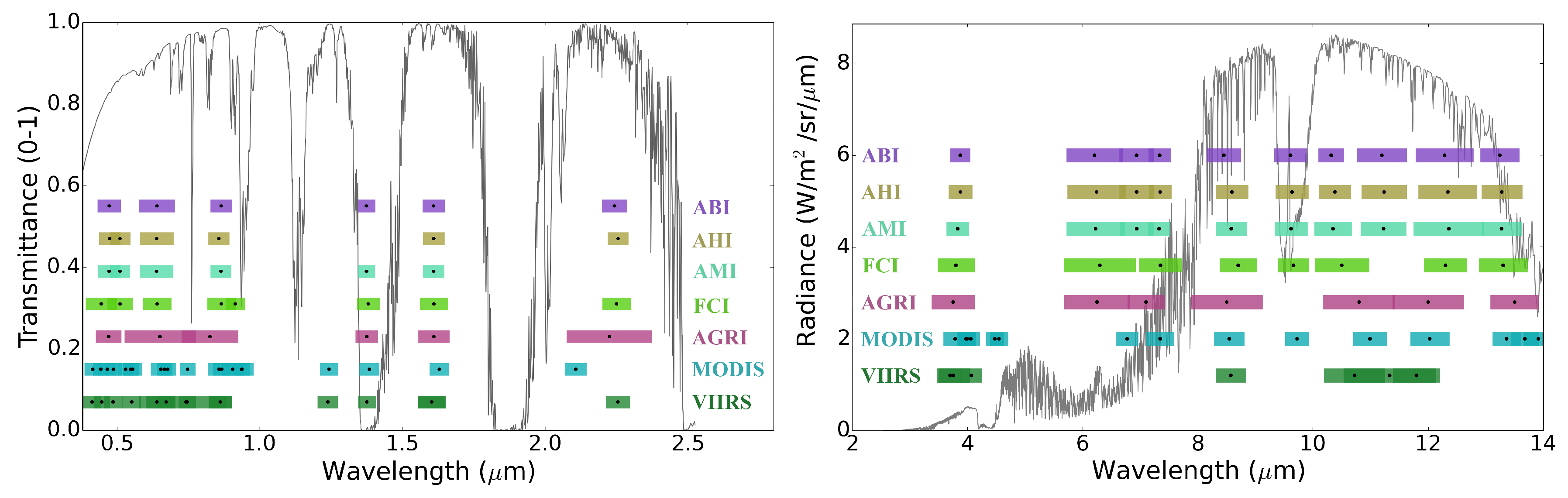
2.2. TOA Radiance
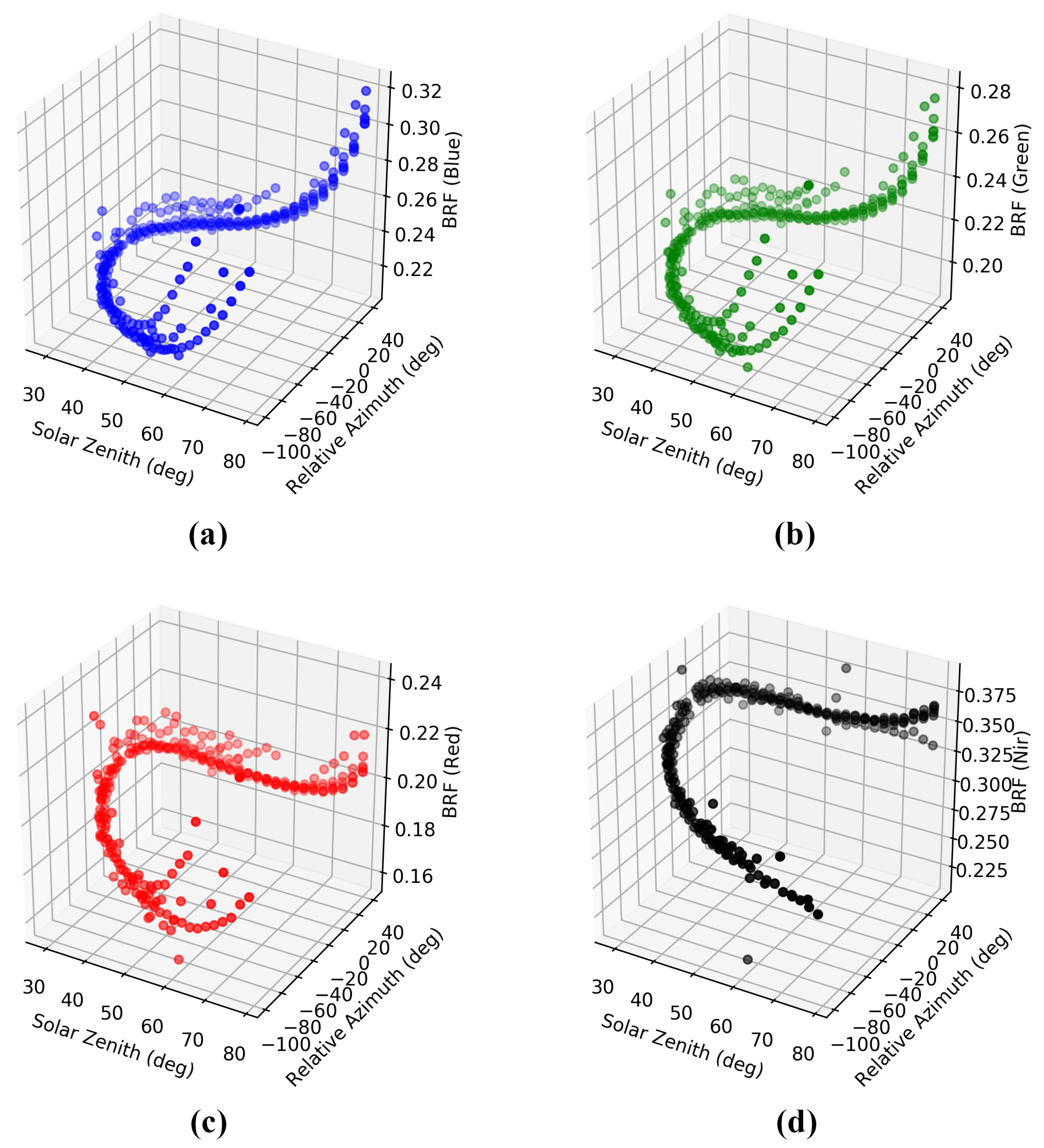
2.3. Bidirectional Reflectance Factor and Brightness Temperature
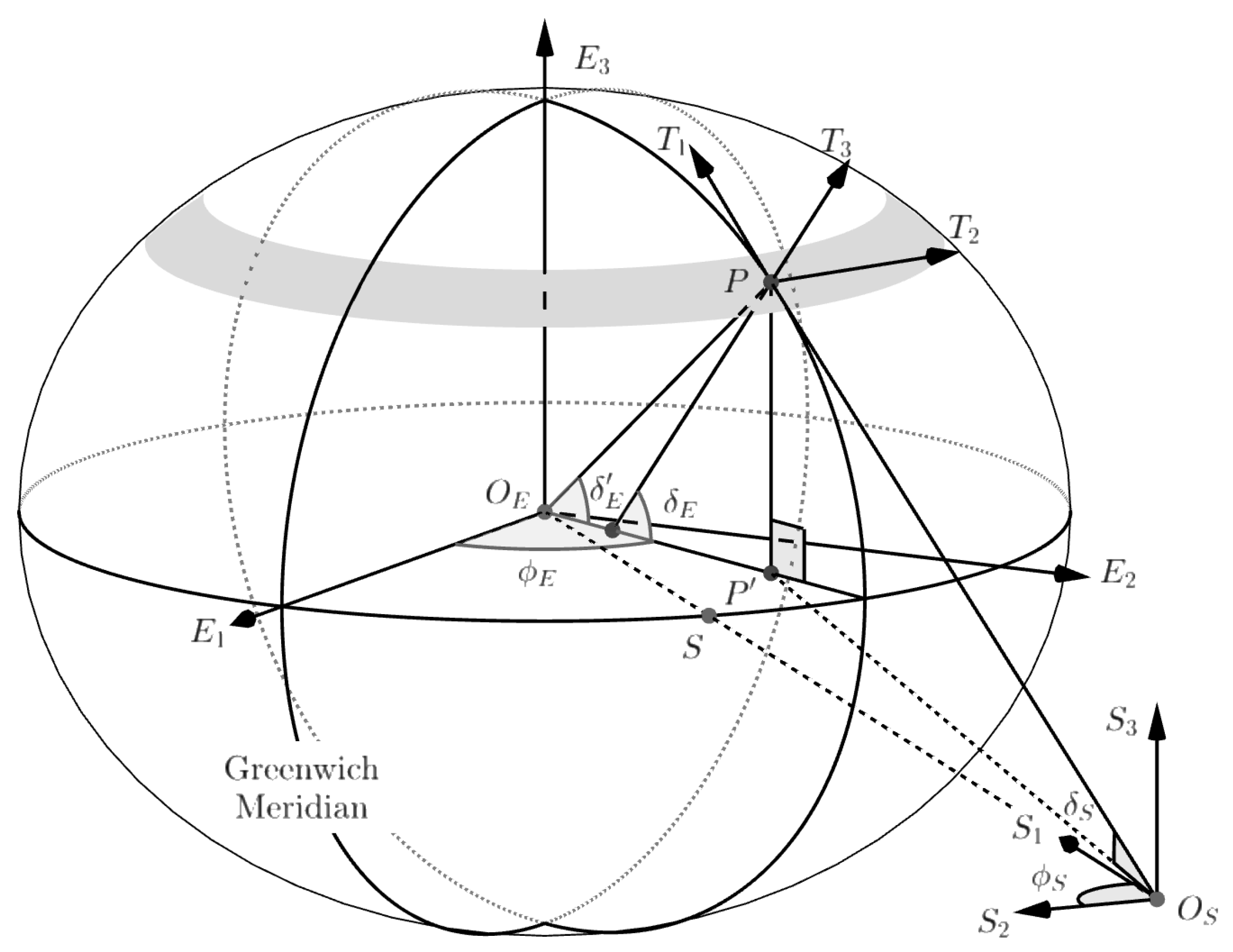
2.4. Map Projection and Coordinate Transformations
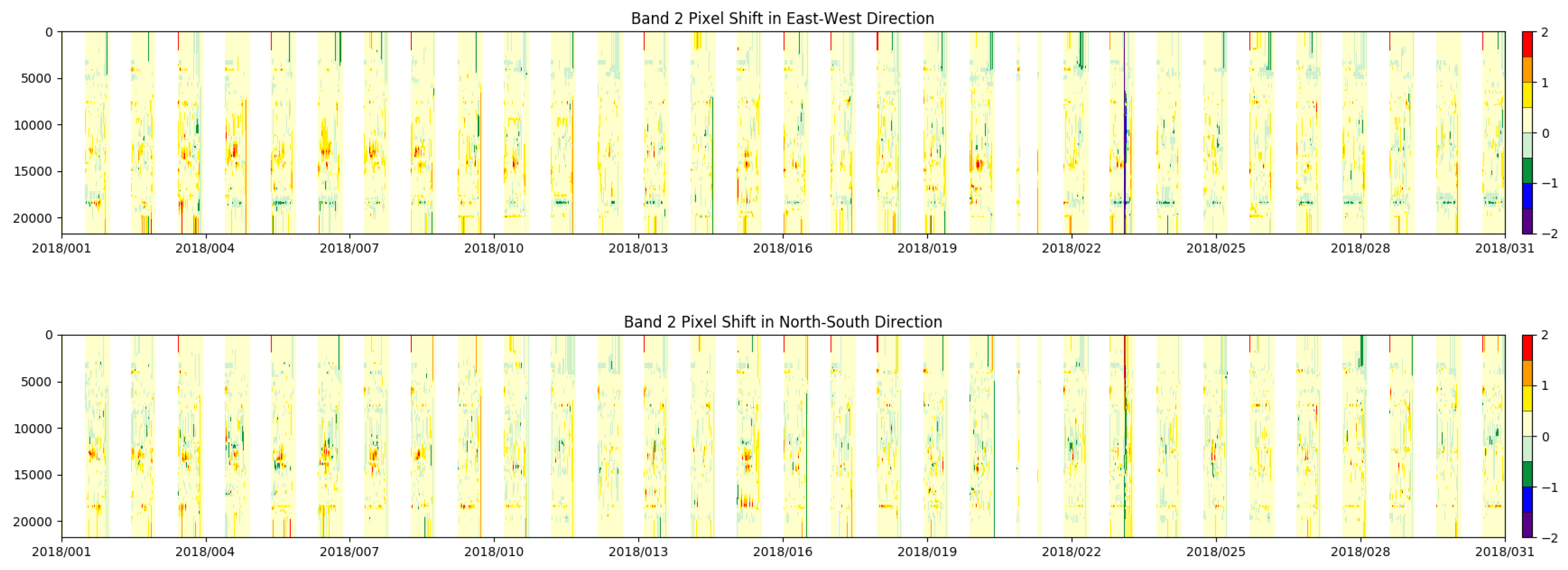
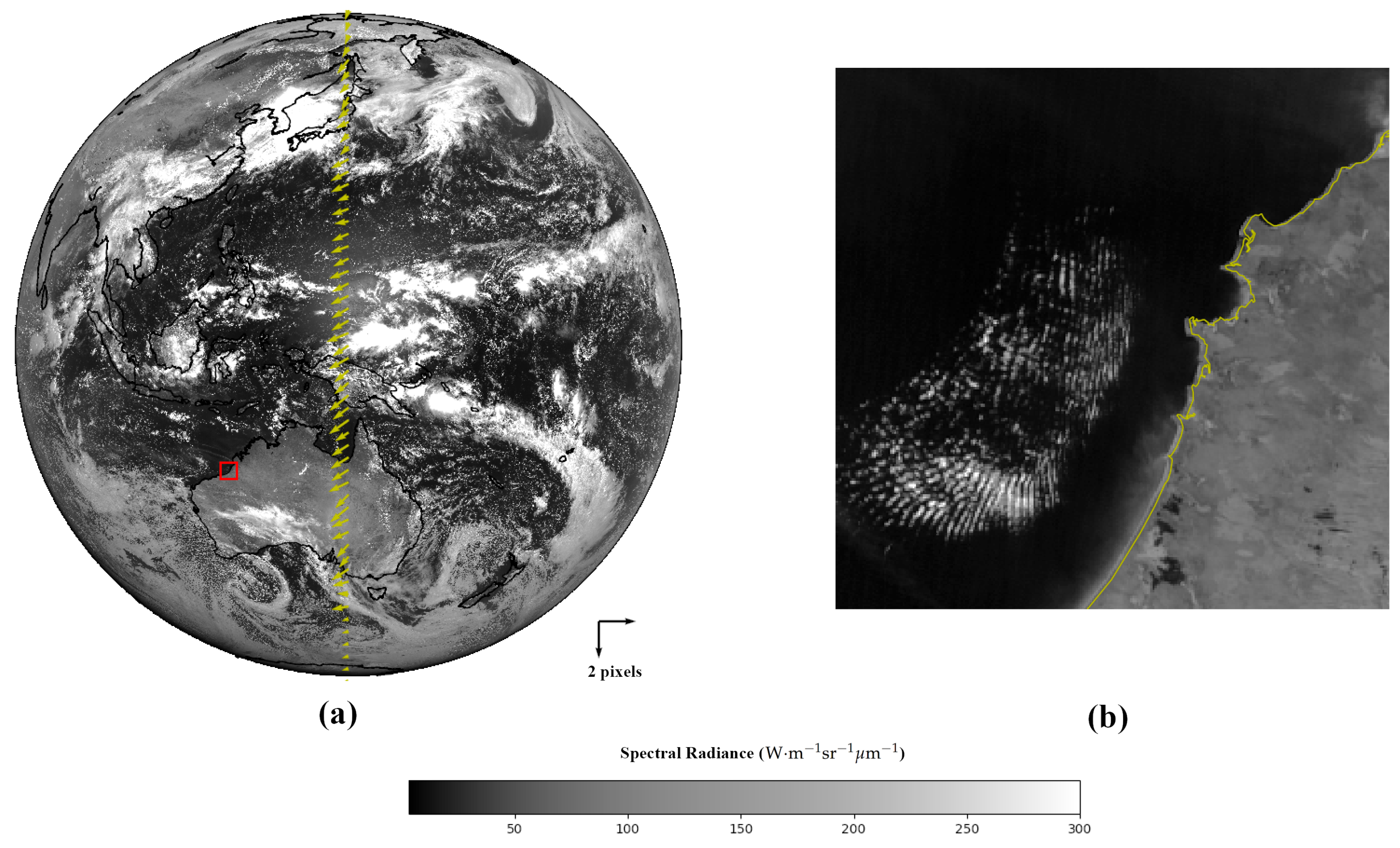
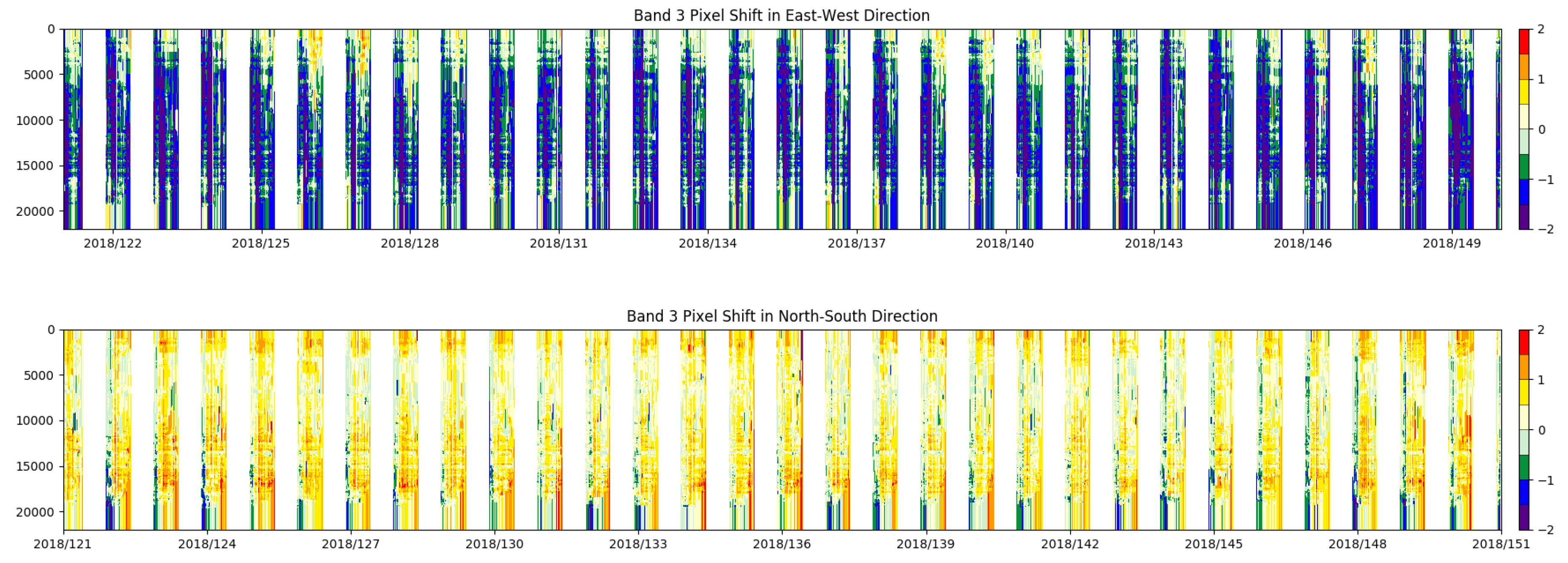
2.5. Phase Correlation Correction of Geolocations
2.6. Orthorectification for Topographic Relief
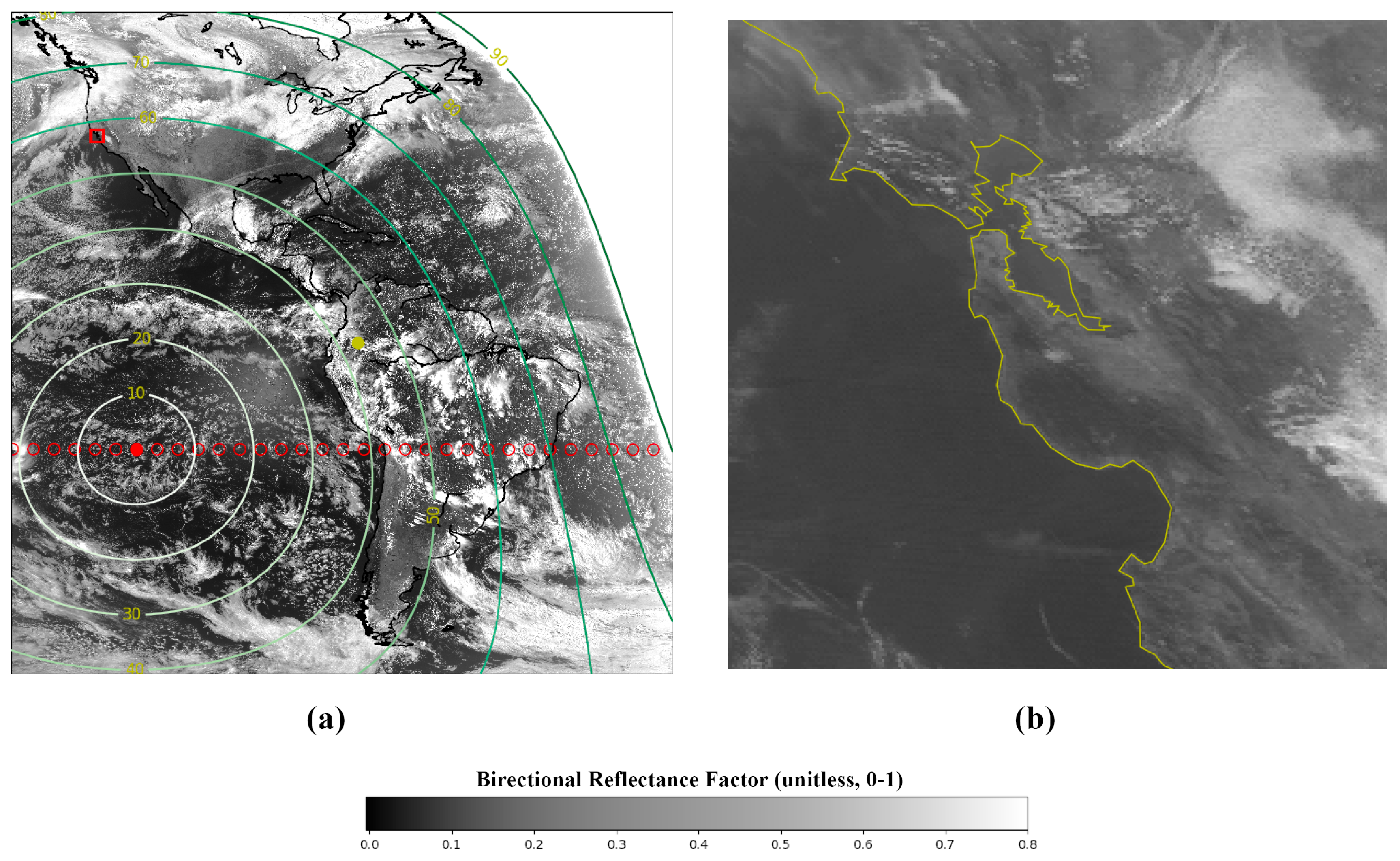
2.7. Satellite and Sun Angles
2.8. Pixelwise Data Acquisition Time
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- National Research Council (NRC). Earth Observations from Space: The First 50 Years of Scientific Achievements; The National Academies Press: Washington, DC, USA, 2008; p. 142. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine. Thriving on Our Changing Planet: A Decadal Strategy for Earth Observation from Space; National Academies Press: Washington, DC, USA, 2018. [Google Scholar]
- Fensholt, R.S.I.; Stisen, S.; Tucker, C. Analysing NDVI for the African continent using the geostationary meteosat second generation SEVIRI sensor. Remote Sens. Environ. 2006, 101, 212–229. [Google Scholar] [CrossRef]
- Fensholt, R.; Anyamba, A.; Huber, S.; Proud, S.; Tucker, C.; Small, J.; Pak, E.; Rasmussen, M.S.I.; Shisanya, C. Analysing the advantages of high temporal resolution geostationary MSG SEVIRI data compared to Polar Operational Environmental Satellite data for land surface monitoring in Africa. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 721–729. [Google Scholar] [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An Introduction to Himawari-8/9—Japan’s New-Generation Geostationary Meteorological Satellites. J. Meteorol. Soc. Jpn. Ser. 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Schmit, T.; Griffith, P.; Gunshor, M.; Daniels, J.; Goodman, S.; Lebair, W. A Closer Look at the ABI on the GOES-R Series. Bull. Am. Meteorol. Soc. 2017, 98, 681–698. [Google Scholar] [CrossRef]
- Kalluri, S.; Alcala, C.; Carr, J.; Griffith, P.; Lebair, W.; Lindsey, D.; Race, R.; Wu, X.; Zierk, S. From Photons to Pixels: Processing Data from the Advanced Baseline Imager. Remote Sens. 2018, 10, 177. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Lee, S.; Ahn, M.; Chung, S. Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager. Remote Sens. 2017, 9, 1294. [Google Scholar] [CrossRef]
- Durand, Y.; Hallibert, P.; Wilson, M.; Lekouara, M.; Grabarnik, S.; Aminou, D.; Blythe, P.; Napierala, B.; Canaud, J.; Pigouche, O.; et al. The flexible combined imager onboard MTG: From design to calibration. In Proceedings of the SPIE 9639, Sensors, Systems, and Next-Generation Satellites XIX, Toulouse, France, 21–24 September 2015; p. 963903. [Google Scholar]
- Myneni, R.; Yang, W.; Nemani, R.; Huete, A.; Dickinson, R.; Knyazikhin, Y.; Didan, K.; Fu, R.; Juárez, R.I.N.; Saatchi, S.S.; et al. Large seasonal swings in leaf area of Amazon rainforests. Proc. Natl. Acad. Sci. USA 2007, 104, 4820–4823. [Google Scholar] [CrossRef]
- Saleska, S.; Didan, K.; Huete, A.; Darocha, H. Amazon Forests Green-Up During 2005 Drought. Science 2007, 318, 612. [Google Scholar] [CrossRef]
- Samanta, A.; Ganguly, S.; Hashimoto, H.; Devadiga, S.; Vermote, E.; Knyazikhin, Y.; Nemani, R.; Myneni, R. Amazon forests did not green-up during the 2005 drought. Geophys. Res. Lett. 2010, 37, 5. [Google Scholar] [CrossRef]
- Morton, D.; Nagol, J.; Carabajal, C.; Rosette, J.; Palace, M.; Cook, B.; Vermote, E.; Harding, D.; North, P. Amazon forests maintain consistent canopy structure and greenness during the dry season. Nature 2014, 506, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Bi, J.; Knyazikhin, Y.; Choi, S.; Park, T.; Barichivich, J.; Ciais, P.; Fu, R.; Ganguly, S.; Hall, F.; Hilker, T.; et al. Sunlight mediated seasonality in canopy structure and photosynthetic activity of Amazonian rainforests. Environ. Res. Lett. 2015, 10, 064014. [Google Scholar] [CrossRef]
- Doughty, R.; Köhler, P.; Frankenberg, C.; Magney, T.; Xiao, X.; Qin, Y.; Wu, X.; Moore, B. TROPOMI reveals dry-season increase of solar-induced chlorophyll fluorescence in the Amazon forest. Proc. Natl. Acad. Sci. USA 2019, 116, 22393–22398. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, H.; Wang, W.; Dungan, J.L.; Li, S.; Takenaka, H.; Higuchi, A.; Myneni, R.B.; Nemani, R.R. GOES ABI high-frequent observation proved the basin-wide existence of the seasonality in greeness of the Amazon evergreen forest. Nat. Commun. 2020. in review. [Google Scholar]
- Martonchik, J.; Bruegge, C.; Strahler, A. A review of reflectance nomenclature used in remote sensing. Remote Sens. Rev. 2000, 19, 9–20. [Google Scholar] [CrossRef]
- Nemani, R.; Votava, P.; Michaelis, A.; Melton, F.; Milesi, C. Collaborative Supercomputing for Global Change Science. Eos, Trans. Am. Geophys. Union 2011, 92, 109–110. [Google Scholar] [CrossRef]
- Li, S.; Wang, W.; Hashimoto, H.; Xiong, J.V.; Val, T.; Yao, J.; Qian, L.; Ichii, K.; Wang, Y.; Lyapustin, A.; et al. First provisional land surface reflectance product from geostationary satellite Himawari-8 AHI. Remote Sens. 2019, 11, 2990. [Google Scholar] [CrossRef]
- Okuyama, A.; Takahashi, M.; Date, K.; Hosaka, K.; Murata, H.; Tabata, T.; Yoshino, R. Validation of Himawari-8/AHI Radiometric Calibration Based on Two Years of In-Orbit Data. J. Meteorol. Soc. Jpn. Ser. II 2018, 96B, 91–109. [Google Scholar] [CrossRef]
- Datla, R.; Shao, X.; Cao, C.; Wu, X. Comparison of the Calibration Algorithms and SI Traceability of MODIS, VIIRS, GOES, and GOES-R ABI Sensors. Remote Sens. 2016, 8, 126. [Google Scholar] [CrossRef]
- Yu, F.; Wu, X. Radiometric Inter-Calibration between Himawari-8 AHI and S-NPP VIIRS for the Solar Reflective Bands. Remote Sens. 2016, 8, 165. [Google Scholar] [CrossRef]
- Chang, T.; Xiong, X.; Keller, G.; Wu, X. GEO-LEO reflective band intercomparison with bidiretional reflectance distribution function and atmospheric scattering corrections. J. Appl. Remote Sens. 2018, 12, 014002. [Google Scholar] [CrossRef]
- Qin, Y.; Mcvicar, T. Spectral band unification and inter-calibration of Himawari AHI with MODIS and VIIRS: Constructing virtual dual-view remote sensors from geostationary and low-Earth-orbiting sensors. Remote Sens. Environ. 2018, 209, 540–550. [Google Scholar] [CrossRef]
- Coordination Group for Meteorological Satellites (CGMS). Coordination Group for Meteorological Satellites: LRIT/HRIT Global Specification; CGMS: Darmstadt, Germany, 2013; p. 54. [Google Scholar]
- Harris Corporation Space and Intelligence Systems. Product Definition and Users’ Guide (PUG), Volume 3: Level1B Products for GOES-R Series Core Ground Segment (Revision-E); Harris Corporation: Melbourne, FL, USA, 2017. [Google Scholar]
- Okuyama, A.; Andou, A.; Date, K.; Hoasaka, K.; Mori, N.; Murata, H.; Tabata, T.; Takahashi, M.; Yoshino, R.; Bessho, K. Preliminary Validation of Himawari-8/AHI Navigation and Calibration; SPIE: Bellingham, WA, USA, 2015. [Google Scholar]
- Tan, B.; Dellomo, J.; Wolfe, R.; Reth, A. GOES-16 ABI Navigation Assessment; SPIE: Bellingham, WA, USA, 2018. [Google Scholar]
- Foroosh, H.; Zerubia, J.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Skakun, S.; Roger, J.; Vermote, E.; Masek, J.; Justice, C. Automatic sub-pixel co-registration of Landsat-8 Operational Land Imager and Sentinel-2A Multi-Spectral Instrument images using phase correlation and machine learning based mapping. Int. J. Digit. Earth 2017, 10, 1253–1269. [Google Scholar] [CrossRef]
- Guizar-sicairos, M.; Thurman, S.; Fienup, J. Efficient subpixel image registration algorithms. Opt. Lett. 2008, 33, 156–158. [Google Scholar] [CrossRef]
- Rodríguez, E.; Morris, C.; Belz, J. A Global Assessment of the SRTM Performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Farr, T.; Rosen, P.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, 2. [Google Scholar] [CrossRef]
- Satge, F.; Denezine, M.; Pillco, R.; Timouk, F.; Pinel, S.; Molina, J.; Garnier, J.; Seyler, F.; Bonnet, M. Absolute and relative height-pixel accuracy of SRTM-GL1 over the South American Andean Plateau. ISPRS J. Photogramm. Remote Sens. 2016, 121, 157–166. [Google Scholar] [CrossRef]
- Toutin, T. Review article: Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2004, 25, 1893–1924. [Google Scholar] [CrossRef]
- Tucker, C.J.; Grant, D.M.; Dykstra, J.D. NASA’s Global Orthorectified Landsat Data Set. Photogramm. Eng. Remote Sens. 2004, 70, 313–322. [Google Scholar] [CrossRef]
- Soler, T.; Eisemann, D. Determination of Look Angles to Geostationary Communication Satellites. J. Surv. Eng. 1994, 120, 115–127. [Google Scholar] [CrossRef]
- Bretagnon, P.; Francou, G. Planetary Theories in rectangular and spherical variables: VSOP87 solution. Astron. Astrophys. 1988, 202, 309. [Google Scholar]
- Reda, I.; Andreas, A. Solar Position Algorithm for Solar Radiation Applications (Revised); U.S. Department of Energy: Washington, DC, USA, 2008.
- Blanc, P.; Wald, L. The SG2 algorithm for a fast and accurate computation of the position of the Sun for multi-decadal time period. Sol. Energy 2012, 86, 3072–3083. [Google Scholar] [CrossRef]
- Igly, D.A.; Virgilio, V.N.; Gounder, K. Image Navigation and Registration For GOES-R Advanced Baseline Imager. In Proceedings of the 32nd AAS Guidance and Control Conference, Breckenridge, CO, USA, 30 January–4 February 2009. [Google Scholar]
- Winkler, S.; Ramsey, G.; Frey, C.; Chapel, J.; Chu, D.; Freesl, D.; Krimchansky, A.; Concha, M. GPS Receiver On-Orbit Performance for the GOES-R Spacecraft. In Proceedings of the 10th International ESA Conference on Guidance, Navigation & Control Systems, Salzburg, Austria, 29 May–2 June 2017. [Google Scholar]
- Hasler, A. Stereographic Observations from Geosynchronous Satellites: An Important New Tool for the Atmospheric Sciences. Bull. Am. Meteorol. Soc. 1981, 62, 194–212. [Google Scholar] [CrossRef]
- Adachi, Y.; Kikuchi, R.; Obata, K.; Yoshioka, H. Relative Azimuthal-Angle Matching (RAM): A Screening Method for GEO-LEO Reflectance Comparison in Middle Latitude Forests. Remote Sens. 2019, 11, 1095. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Li, S.; Hashimoto, H.; Takenaka, H.; Higuchi, A.; Kalluri, S.; Nemani, R. An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature. Remote Sens. 2020, 12, 1267. https://doi.org/10.3390/rs12081267
Wang W, Li S, Hashimoto H, Takenaka H, Higuchi A, Kalluri S, Nemani R. An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature. Remote Sensing. 2020; 12(8):1267. https://doi.org/10.3390/rs12081267
Chicago/Turabian StyleWang, Weile, Shuang Li, Hirofumi Hashimoto, Hideaki Takenaka, Atsushi Higuchi, Satya Kalluri, and Ramakrishna Nemani. 2020. "An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature" Remote Sensing 12, no. 8: 1267. https://doi.org/10.3390/rs12081267
APA StyleWang, W., Li, S., Hashimoto, H., Takenaka, H., Higuchi, A., Kalluri, S., & Nemani, R. (2020). An Introduction to the Geostationary-NASA Earth Exchange (GeoNEX) Products: 1. Top-of-Atmosphere Reflectance and Brightness Temperature. Remote Sensing, 12(8), 1267. https://doi.org/10.3390/rs12081267