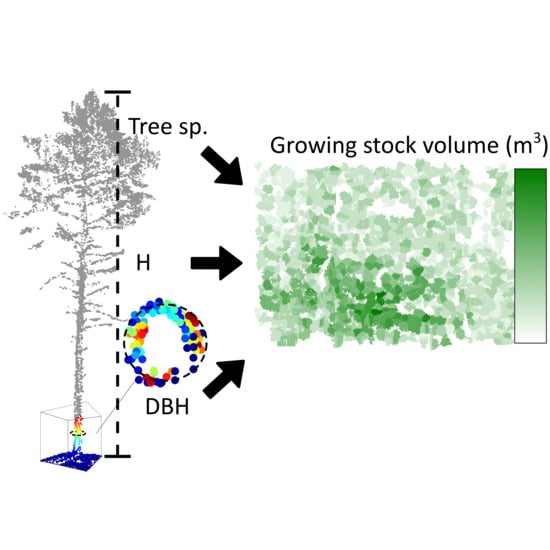
Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data?
Abstract
1. Introduction
2. Materials
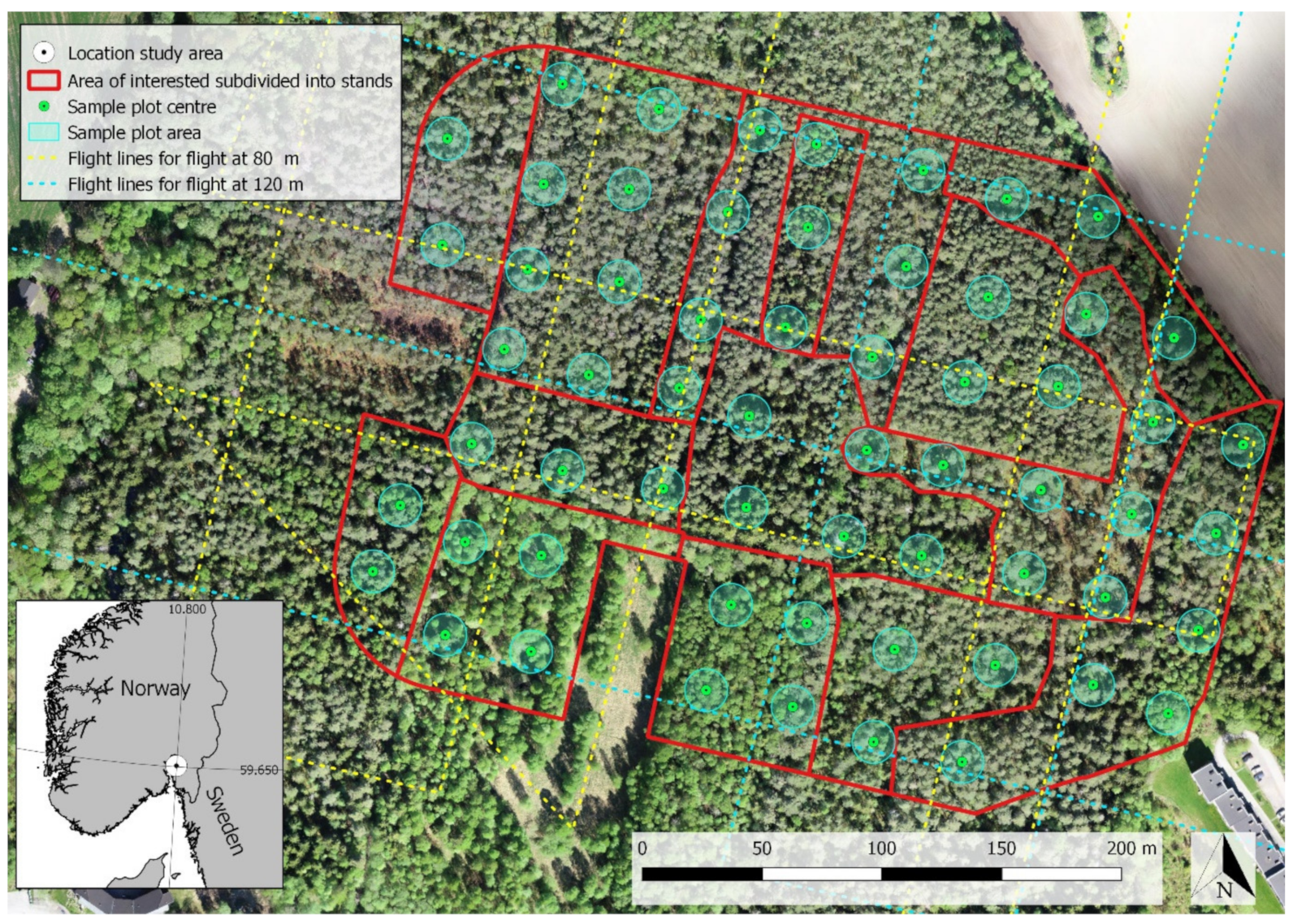
2.1. Study Area
2.2. Field Data
2.3. Remotely Sensed Data
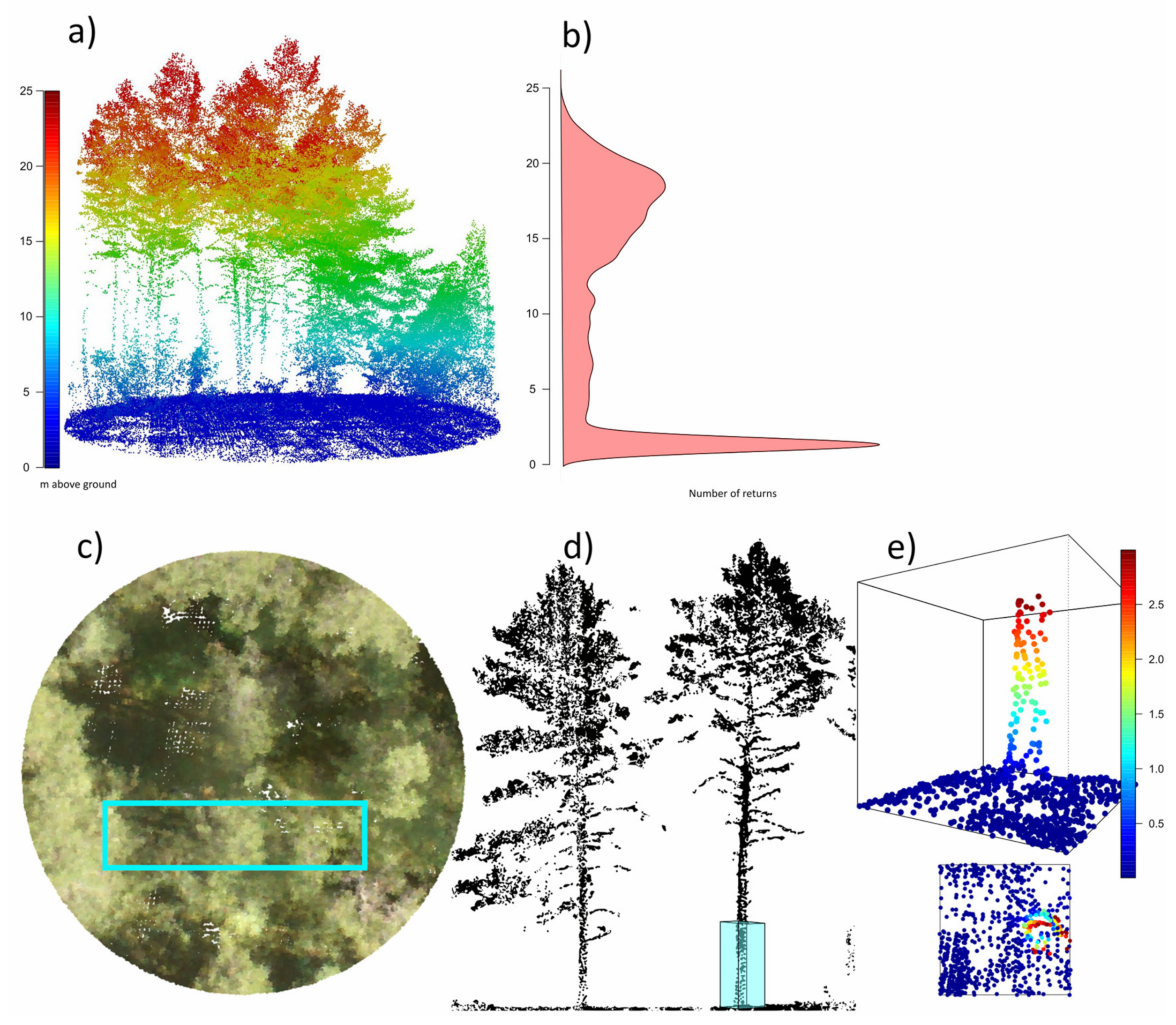
UAV-LS Data
3. Methods
3.1. Step 1: Tree Detection and Segmentation
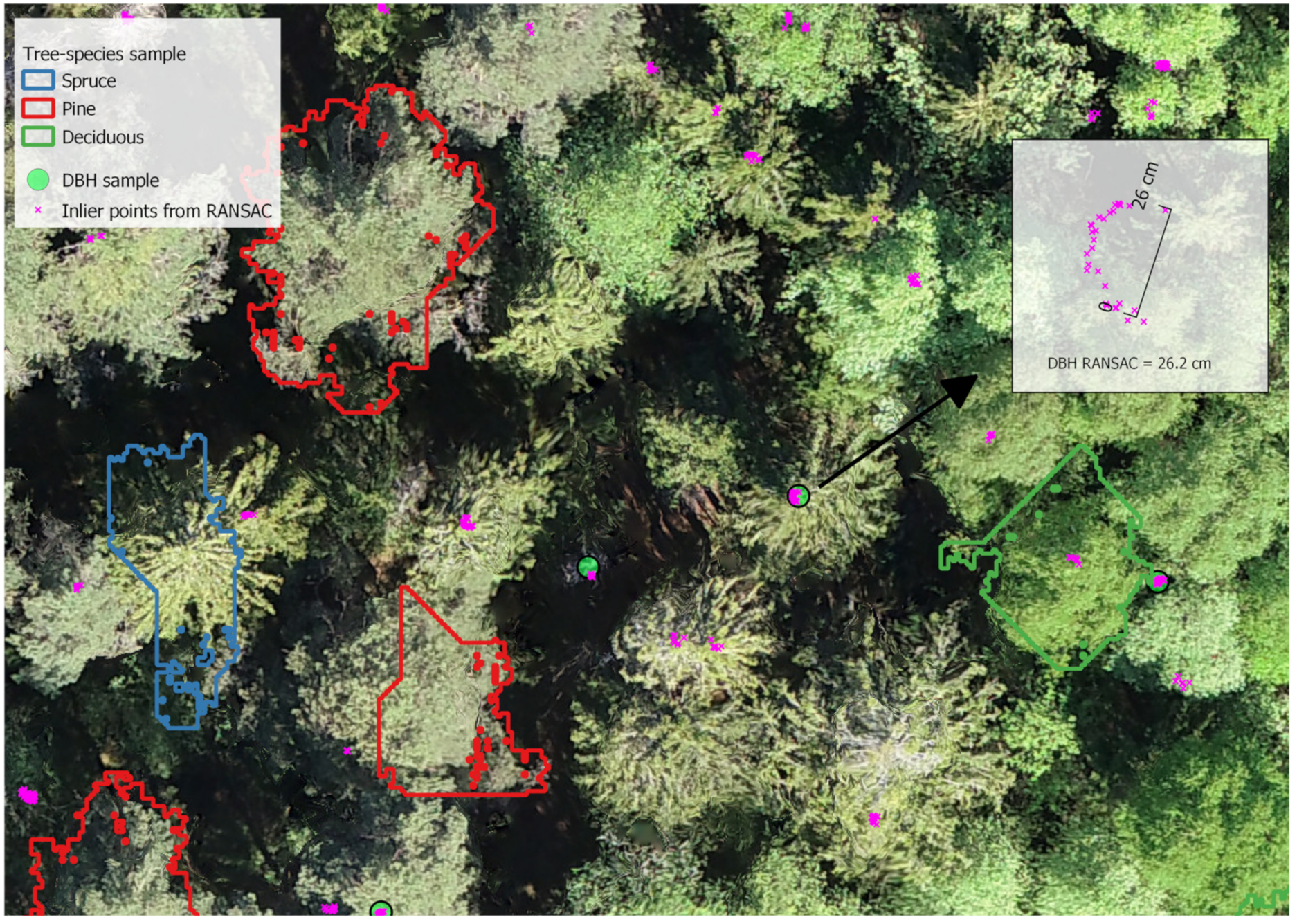
3.2. Step 2: Diameter Measurements
3.2.1. Point Cloud Clustering
3.2.2. Circumference Fitting
3.3. Step 3: DBH and Tree Species Sample Selection
- -
- Reduce the DBH measurement error, i.e., trees with little UAV-LS data occlusion and absence of branches at breast height (±1 m), with returns distributed in cylindrical shapes;
- -
- Include much of the variability in the study area, i.e., trees distributed across a wide range of DBH (5–50 cm), tree species, and geographically distributed throughout the area.
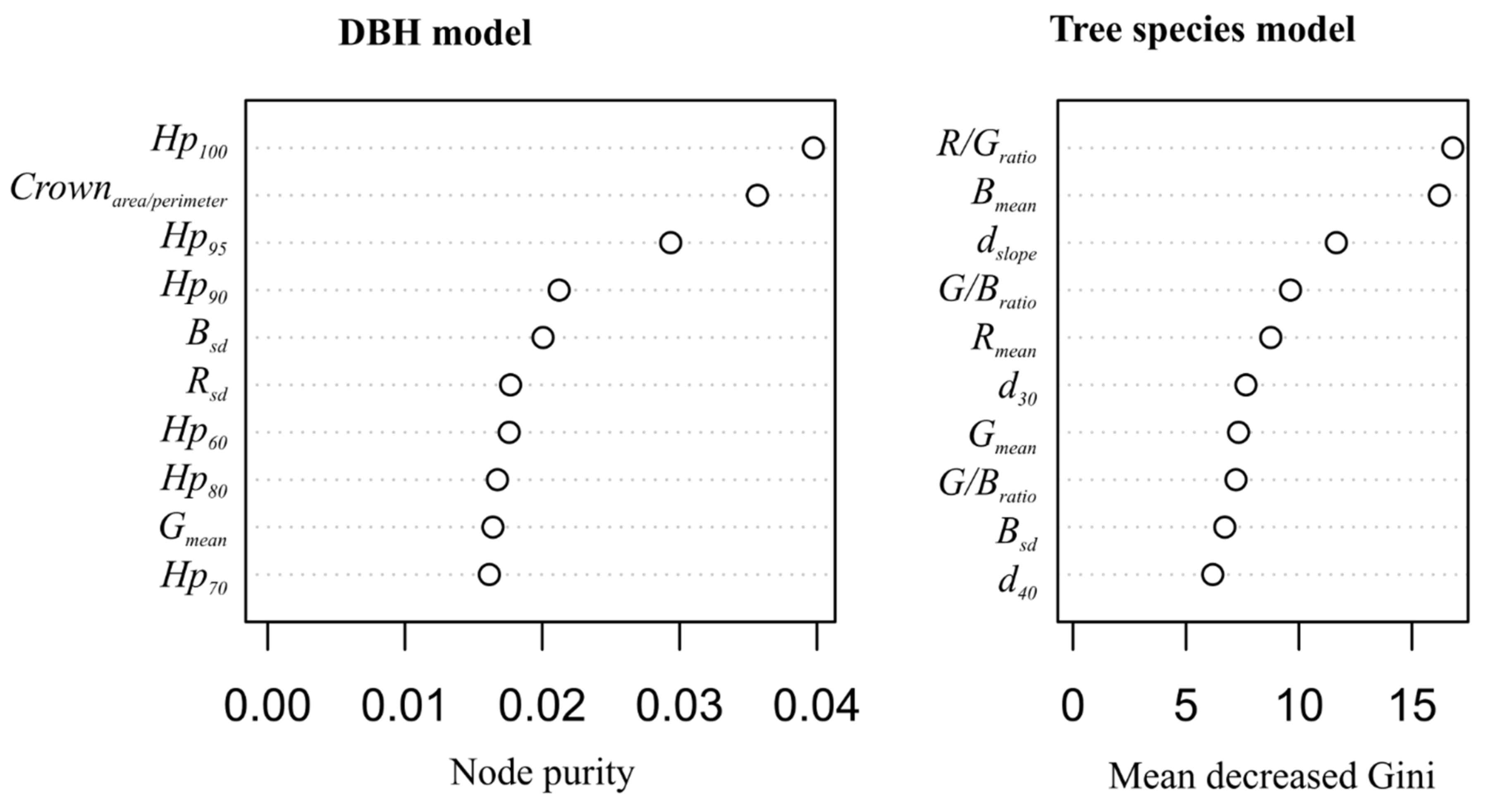
3.4. Step 4: Modelling and Predicting Tree DBH and Species
3.5. Step 5: Predicting Volume for All Detected Trees
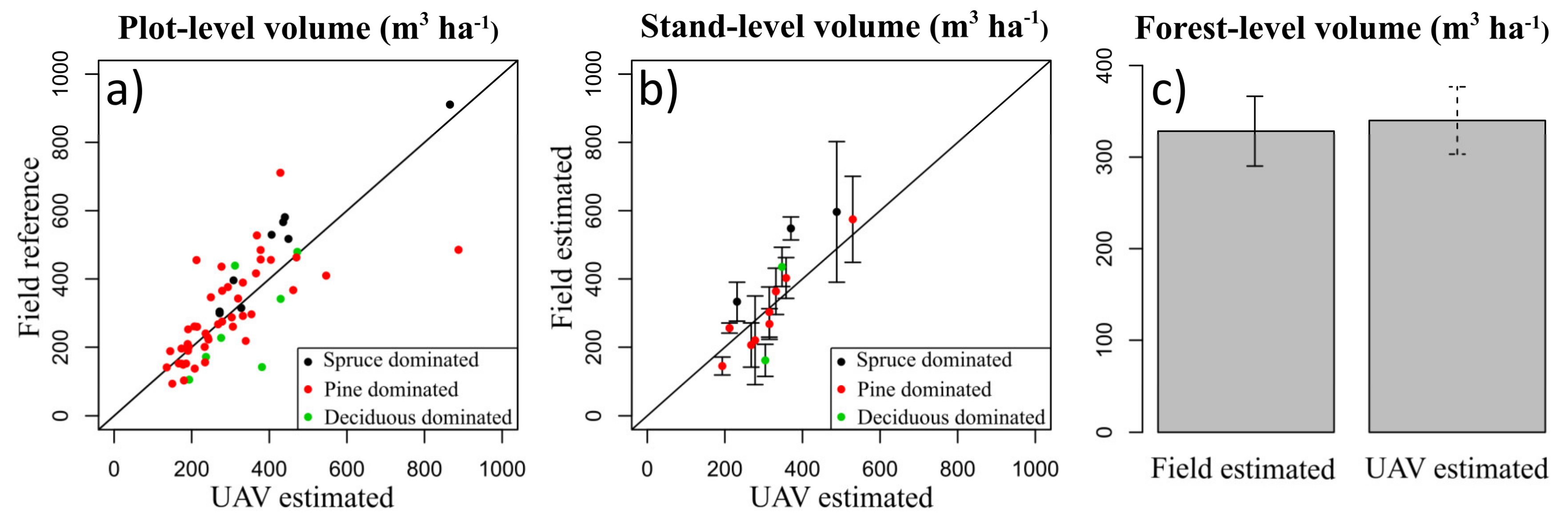
3.6. Validation
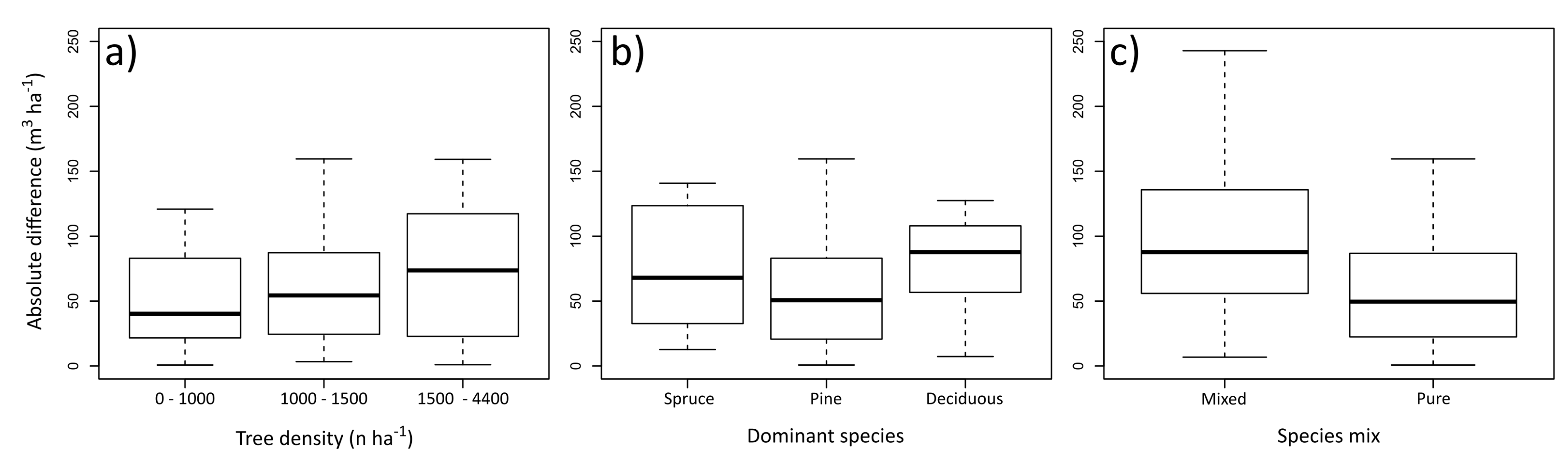
4. Results
5. Discussion
6. Conclusions
- -
- Forest growing stock volume can be estimated using UAV-LS and image data without the use of field data for calibration.
- -
- The accuracy of the UAV-LS estimates increased with the spatial scale. At the forest-scale, the UAV-LS estimates were well within the 95% confidence intervals of the estimates of an intense field survey and both estimates had similar precision.
- -
- The accuracy of the UAV-LS estimates varied given forest structure and was largest in open pine stands and smallest in dense birch or spruce stands.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Reichstein, M.; Carvalhais, N. Aspects of forest biomass in the earth system: Its role and major unknowns. Surv. Geophys. 2019, 40, 693–707. [Google Scholar] [CrossRef]
- Duncanson, L.; Armston, J.; Disney, M.; Avitabile, V.; Barbier, N.; Calders, K.; Carter, S.; Chave, J.; Herold, M.; Crowther, T.W.; et al. The importance of consistent global forest aboveground biomass product validation. Surv. Geophys. 2019, 40, 979–999. [Google Scholar] [CrossRef] [PubMed]
- Herold, M.; Carter, S.; Avitabile, V.; Espejo, A.B.; Jonckheere, I.; Lucas, R.; McRoberts, R.E.; Næsset, E.; Nightingale, J.; Petersen, R.; et al. The role and need for space-based forest biomass-related measurements in environmental management and policy. Surv. Geophys. 2019, 40, 757–778. [Google Scholar] [CrossRef]
- Chave, J.; Davies, S.J.; Phillips, O.L.; Lewis, S.L.; Sist, P.; Schepaschenko, D.; Armston, J.; Baker, T.R.; Coomes, D.; Disney, M.; et al. Ground data are essential for biomass remote sensing missions. Surv. Geophys. 2019, 40, 863–880. [Google Scholar] [CrossRef]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Jacquemoud, S.; Gonçalves, G.; Silva, C.A.; Soares, P.; Tomé, M.; Pereira, L. Airborne lidar estimation of aboveground forest biomass in the absence of field inventory. Remote Sens. 2016, 8, 653. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Wallace, L.; Hillman, S.; Reinke, K.; Hally, B. Non-destructive estimation of above-ground surface and near-surface biomass using 3d terrestrial remote sensing techniques. Methods Ecol. Evol. 2017, 8, 1607–1616. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar] [CrossRef]
- Morsdorf, F.; Kükenbrink, D.; Schneider, F.D.; Abegg, M.; Schaepman, M.E. Close-range laser scanning in forests: Towards physically based semantics across scales. Interface Focus 2018, 8, 20170046. [Google Scholar] [CrossRef]
- Kellner, J.R.; Armston, J.; Birrer, M.; Cushman, K.C.; Duncanson, L.; Eck, C.; Falleger, C.; Imbach, B.; Král, K.; Krůček, M.; et al. New opportunities for forest remote sensing through ultra-high-density drone lidar. Surv. Geophys. 2019, 40, 959–977. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Kukko, A.; Yu, X.; Kaartinen, H.; Lehtomäki, M.; Lin, Y. A low-cost multi-sensoral mobile mapping system and its feasibility for tree measurements. ISPRS J. Photogramm. Remote Sens. 2010, 65, 514–522. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a uav-lidar system with application to forest inventory. Remote Sens. 2012, 4, 1519. [Google Scholar] [CrossRef]
- Wallace, L.; Musk, R.; Lucieer, A. An assessment of the repeatability of automatic forest inventory metrics derived from uav-borne laser scanning data. IEEE Transact. Geosci. Remote Sens. 2014, 52, 7160–7169. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.; Kooistra, L. Comparing riegl ricopter uav lidar derived canopy height and dbh with terrestrial lidar. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef] [PubMed]
- Sankey, T.; Donager, J.; McVay, J.; Sankey, J.B. Uav lidar and hyperspectral fusion for forest monitoring in the southwestern USA. Remote Sens. Environ. 2017, 195, 30–43. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Watson, C. Evaluating tree detection and segmentation routines on very high resolution uav lidar data. IEEE Transact. Geosci. Remote Sens. 2014, 52, 7619–7628. [Google Scholar] [CrossRef]
- Wallace, L.; Watson, C.; Lucieer, A. Detecting pruning of individual stems using airborne laser scanning data captured from an unmanned aerial vehicle. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 76–85. [Google Scholar] [CrossRef]
- Jaakkola, A.; Hyyppä, J.; Yu, X.; Kukko, A.; Kaartinen, H.; Liang, X.; Hyyppä, H.; Wang, Y. Autonomous collection of forest field reference—the outlook and a first step with uav laser scanning. Remote Sens. 2017, 9, 785. [Google Scholar] [CrossRef]
- Wieser, M.; Mandlburger, G.; Hollaus, M.; Otepka, J.; Glira, P.; Pfeifer, N. A case study of uas borne laser scanning for measurement of tree stem diameter. Remote Sens. 2017, 9, 1154. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Pyörälä, J.; Lehtomäki, M.; Yu, X.; Kaartinen, H.; Kukko, A.; Honkavaara, E.; Issaoui, A.E.I.; Nevalainen, O.; et al. Forest in situ observations using unmanned aerial vehicle as an alternative of terrestrial measurements. For. Ecosyst. 2019, 6, 20. [Google Scholar] [CrossRef]
- Wang, Y.; Pyörälä, J.; Liang, X.; Lehtomäki, M.; Kukko, A.; Yu, X.; Kaartinen, H.; Hyyppä, J. In situ biomass estimation at tree and plot levels: What did data record and what did algorithms derive from terrestrial and aerial point clouds in boreal forest. Remote Sens. Environ. 2019, 232, 111309. [Google Scholar] [CrossRef]
- Dalponte, M.; Coomes, D.A. Tree-centric mapping of forest carbon density from airborne laser scanning and hyperspectral data. Methods Ecol. Evol. 2016, 7, 1236–1245. [Google Scholar] [CrossRef] [PubMed]
- Ferraz, A.; Saatchi, S.; Mallet, C.; Meyer, V. Lidar detection of individual tree size in tropical forests. Remote Sens. Environ. 2016, 183, 318–333. [Google Scholar] [CrossRef]
- Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M.; et al. Allometric equations for integrating remote sensing imagery into forest monitoring programmes. Global Change Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Haglöf. The dp ii computer caliper, Långsele, Sweden. 2017. Available online: http://www.haglofcg.com/index.php/en/files/leaflets/29-dp-ii-product-sheet (accessed on 14 April 2020).
- Haglöf. The vl5 vertex laser, Långsele, Sweden. 2017. Available online: http://www.haglofcg.com/index.php/en/files/leaflets/46-vl5-product-sheet (accessed on 14 April 2020).
- Topcon. Topcon gr-3. Tokio, Japan. Available online: http://www.topconcare.com/en/hardware/gnss-receivers/gr_3/specifications/ (accessed on 14 April 2020).
- Braastad, H. Volume tables for birch. Meddr norske SkogforsVes 1966, 21, 23–78. [Google Scholar]
- Brantseg, A. Volume functions and tables for scots pine. Meddr norske SkogforsVes 1967, 22, 689–739. [Google Scholar]
- Vestjordet, E. Functions and tables for volume of standing trees. Norway spruce Meddr norske SkogforsVes 1967, 22, 539–574. [Google Scholar]
- Vestjordet, E. Merchantable volume of norway spruce and scots pine based on relative height and diameter at breast height or 2.5 m above stump level. Meddr norske SkogforsVes 1968, 25, 411–459. [Google Scholar]
- Fitje, A.; Vestjordet, E. Stand height curves and new tariff tables for norway spruce. MEDDELELSER FRA NORSK INSTITUTT FOR SKOGFORSKNING 1977, 34, 27–68. [Google Scholar]
- Nordic Unmanned. Camflight Sandnes, Norway. Available online: https://nordicunmanned.com/ (accessed on 5 March 2019).
- RIEGL. Riegl-vux-1uav data sheet, Horn, Austria. 2, 2017. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/RIEGL_VUX-1UAV_Datasheet_2017-09-01_01.pdf (accessed on 23 November 2017).
- Trimble. Trimble ap20. Sunnyvale, CA, USA. Available online: https://www.applanix.com/downloads/products/specs/AP20_DS_NEW_0408_YW.pdf (accessed on 14 April 2020).
- RIEGL. Riprocess data processing software for riegl scan data, 2016, Horn, Austria. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/11_Datasheet_RiProcess_2016-09-16.pdf (accessed on 19 January 2018).
- Terrasolid. Terrascan user guide, Helsinki, Finland. 2016. Available online: https://www.terrasolid.com/download/tscan.pdf (accessed on 19 January 2018).
- Gorte, B.; Pfeifer, N. Structuring laser-scanned trees using 3d mathematical morphology. Int. Arch. Photogramm. Remote Sens. 2004, 35, 929–933. [Google Scholar]
- Gorte, B.; Winterhalder, D. Reconstruction of laser-scanned trees using filter operations in the 3d raster domain. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree stem and height measurements using terrestrial laser scanning and the ransac algorithm. Remote Sens. 2014, 6, 4323. [Google Scholar] [CrossRef]
- Roussel, J.-R.; Auty, D.; De Boissieu, F.; Meador, A.S. Lidr: Airborne lidar data manipulation and visualization for forestry applications, 1.3.1. CRAN: 2017. Available online: https://CRAN.R-project.org/package=lidR (accessed on 14 April 2020).
- de Conto, T. Treels: Tree terrestrial laser scanning processing, 1.0. CRAN: 2017. 2017. Available online: https://github.com/tiagodc/TreeLS/ (accessed on 14 April 2020).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R news 2002, 2, 18–22. [Google Scholar]
- Breidenbach, J.; Magnussen, S.; Rahlf, J.; Astrup, R. Unit-level and area-level small area estimation under heteroscedasticity using digital aerial photogrammetry data. Remote Sens. Environ. 2018, 212, 199–211. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An introduction to the bootstrap. Hall/CRC: Boca Raton, FL, USA, 1994. [Google Scholar]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Ferraz, A.; Bretar, F.; Jacquemoud, S.; Gonçalves, G.; Pereira, L.; Tomé, M.; Soares, P. 3-d mapping of a multi-layered mediterranean forest using als data. Remote Sens. Environ. 2012, 121, 210–223. [Google Scholar] [CrossRef]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, Å.; Söderman, U. Laser scanning of forest resources: The nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Disney, M.; Burt, A.; Calders, K.; Schaaf, C.; Stovall, A. Innovations in ground and airborne technologies as reference and for training and validation: Terrestrial laser scanning (tls). Surv. Geophys. 2019, 40, 937–958. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3d structure and occlusion in dense tropical and temperate forests using close-range lidar. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast automatic precision tree models from terrestrial laser scanner data. Remote Sens. 2013, 5, 491. [Google Scholar] [CrossRef]


| Number | Mean (m3 ha−1) | Minimum (m3 ha−1) | Maximum (m3 ha−1) | |
|---|---|---|---|---|
| Plot | 58 | 321.22 | 93.15 | 910.71 |
| Stand | 14 | 321.22 | 144.83 | 596.27 |
| Forest | 1 | 321.22 | 321.22 | 321.22 |
| Reference | |||||
|---|---|---|---|---|---|
| Spruce | Pine | Deciduous | User’s accuracy | ||
| Predicted | Spruce | 70 | 10 | 7 | 80.4% |
| Pine | 13 | 170 | 39 | 76.6% | |
| Deciduous | 5 | 16 | 63 | 75% | |
| Producer’s accuracy | 79.5% | 86.7% | 57.8% | Overall accuracy 77.1% | |
| Field Data | |||||||
|---|---|---|---|---|---|---|---|
| Spatial Scale | Mean | / a | a | a | a | ||
| Plot | 321.2 | 160.1 | 103.4 | 32.2 | 10.2 | 3.2 | 31.6 |
| Stand | 321.2 | 150.1 | 93.1 | 28.9 | 15.9 | 4.9 | 26.0 |
| Forest | 321.2 | 18.6 | 11.4 | 3.5 | −11.4 | −3.5 | 18.0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puliti, S.; Breidenbach, J.; Astrup, R. Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sens. 2020, 12, 1245. https://doi.org/10.3390/rs12081245
Puliti S, Breidenbach J, Astrup R. Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sensing. 2020; 12(8):1245. https://doi.org/10.3390/rs12081245
Chicago/Turabian StylePuliti, Stefano, Johannes Breidenbach, and Rasmus Astrup. 2020. "Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data?" Remote Sensing 12, no. 8: 1245. https://doi.org/10.3390/rs12081245
APA StylePuliti, S., Breidenbach, J., & Astrup, R. (2020). Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sensing, 12(8), 1245. https://doi.org/10.3390/rs12081245