Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Experiments
2.1.1. Wells Experiment
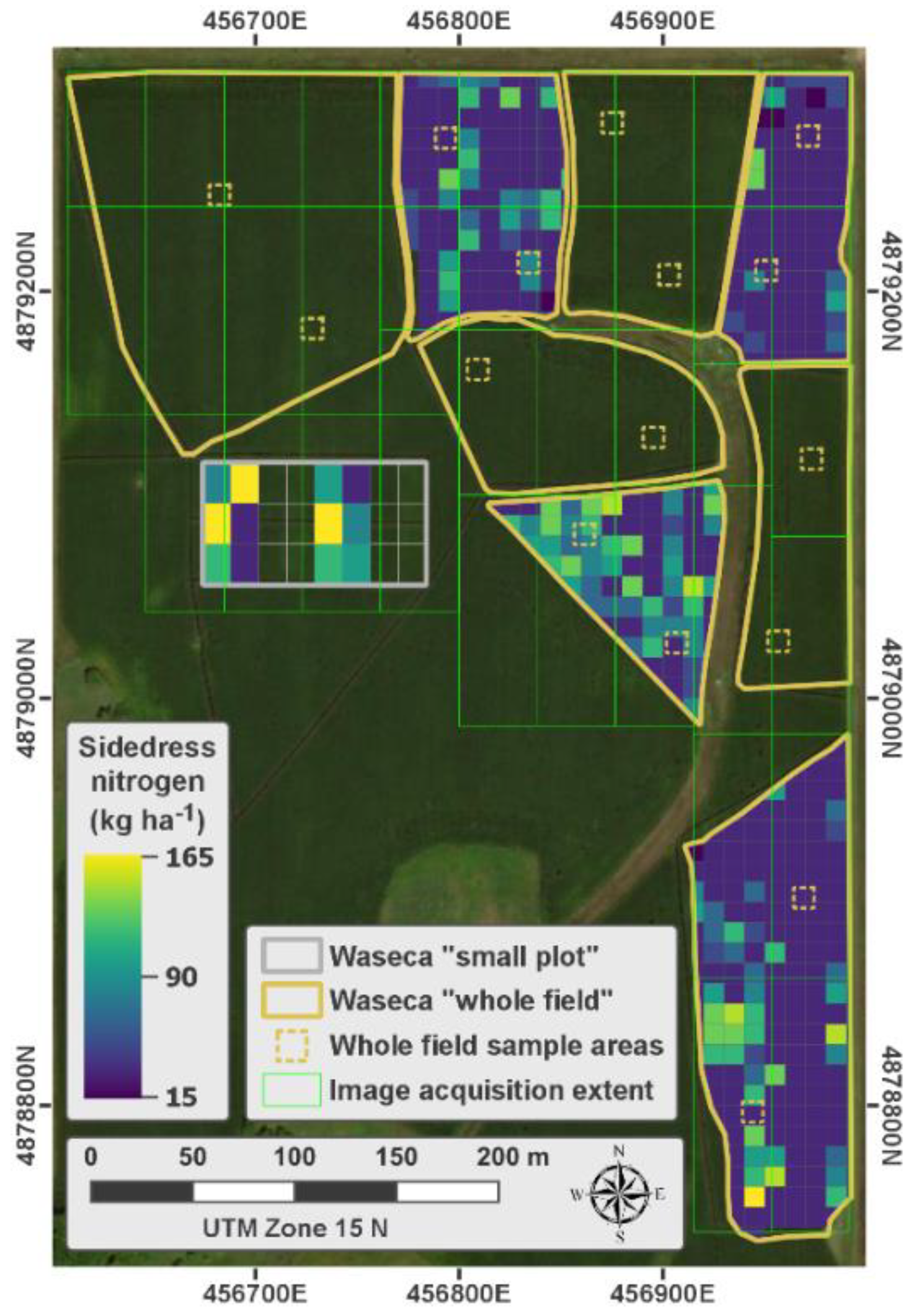
2.1.2. Waseca Experiments
2.2. Crop Nitrogen Uptake
2.3. Airborne Spectral Imaging System
2.4. Airborne Image Capture
2.5. Reference Panels
2.6. Image Pre-Processing
2.7. Image Post-Processing
2.7.1. Cropping
2.7.2. Spectral Clipping and Smoothing
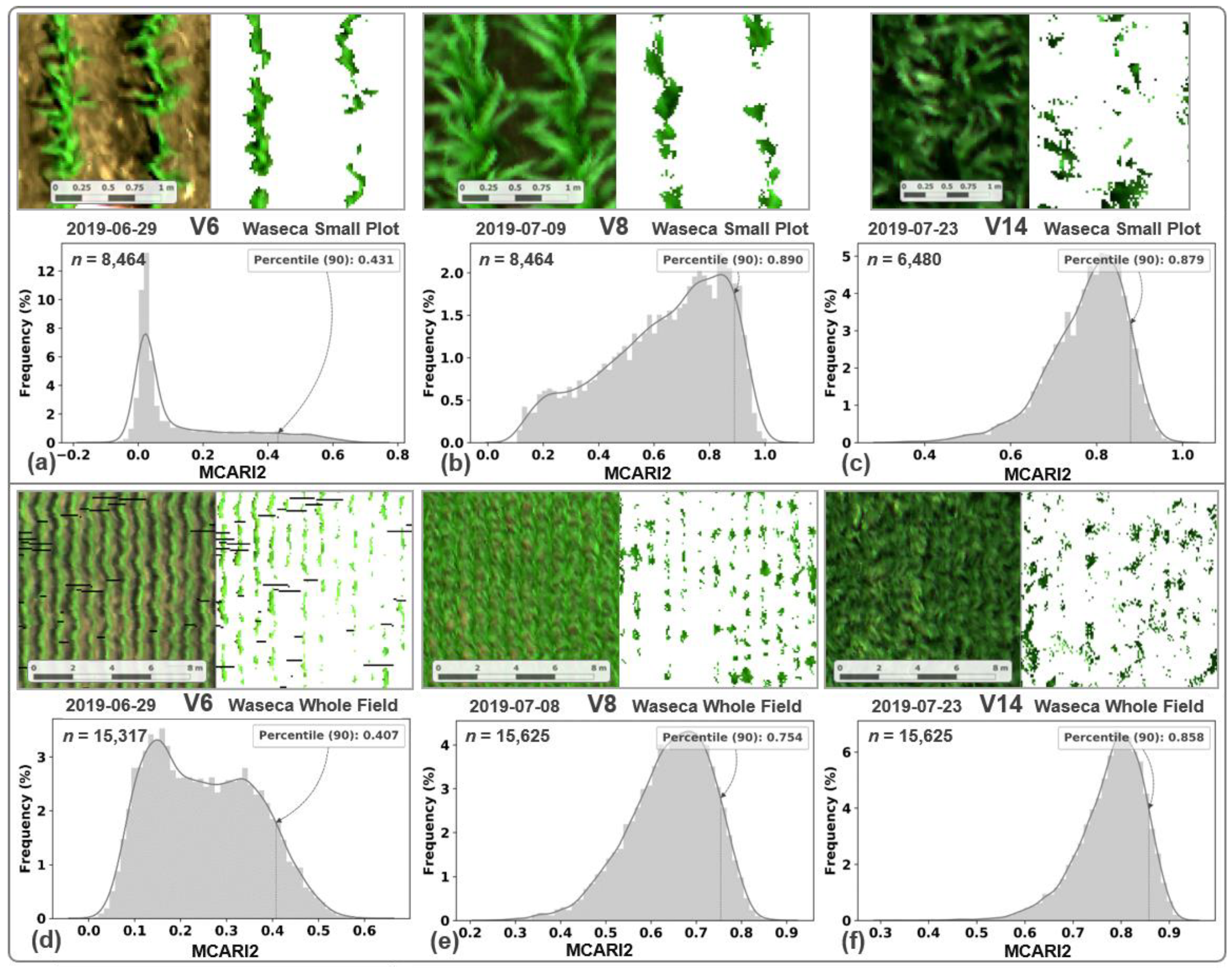
2.7.3. Choice of the Auxiliary Feature and Image Segmentation
2.8. Cross-Validation
2.9. Feature Selection
2.10. Model Tuning and Prediction
3. Results
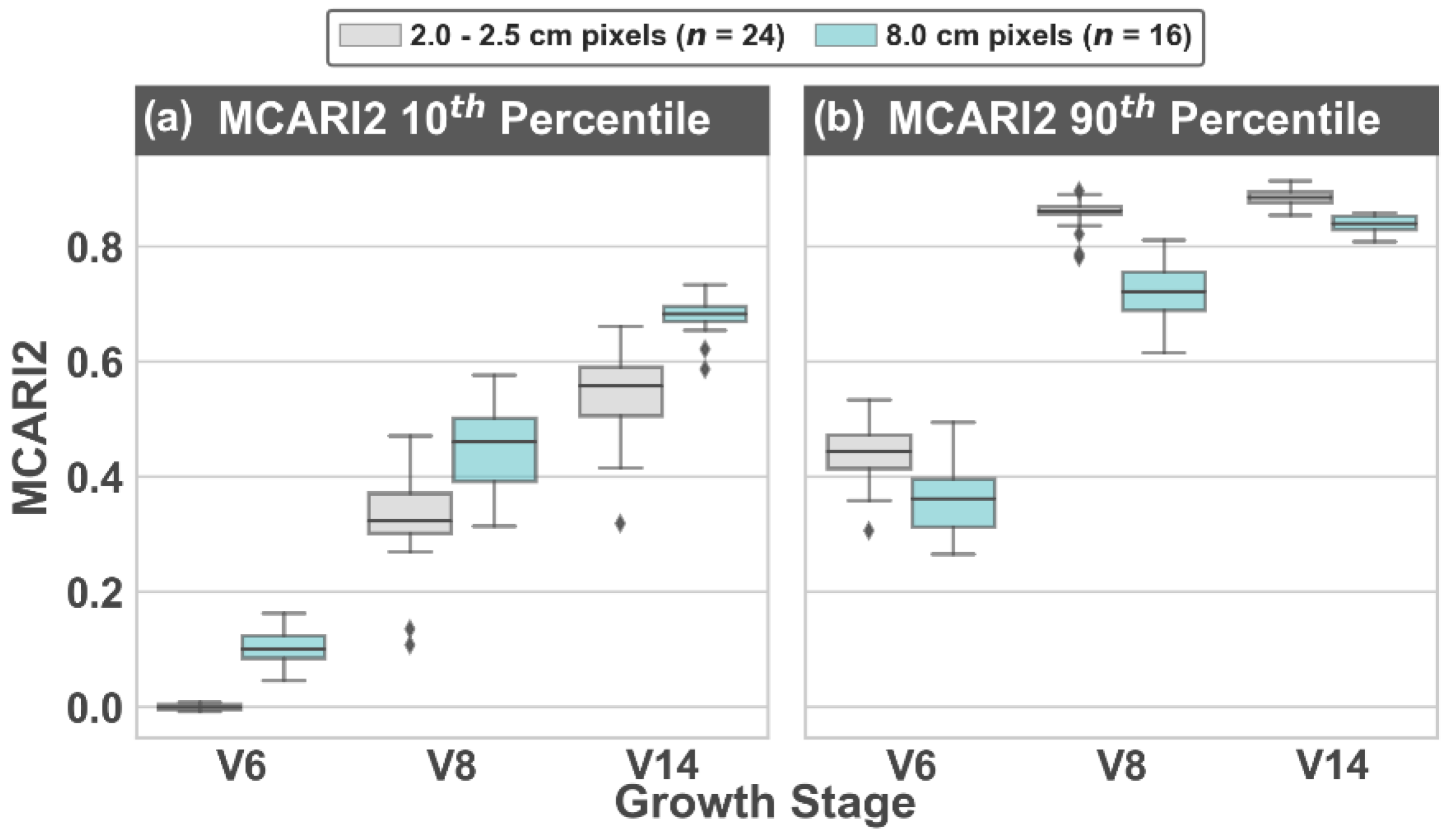
3.1. Image Segmentation and MCARI2 Analysis
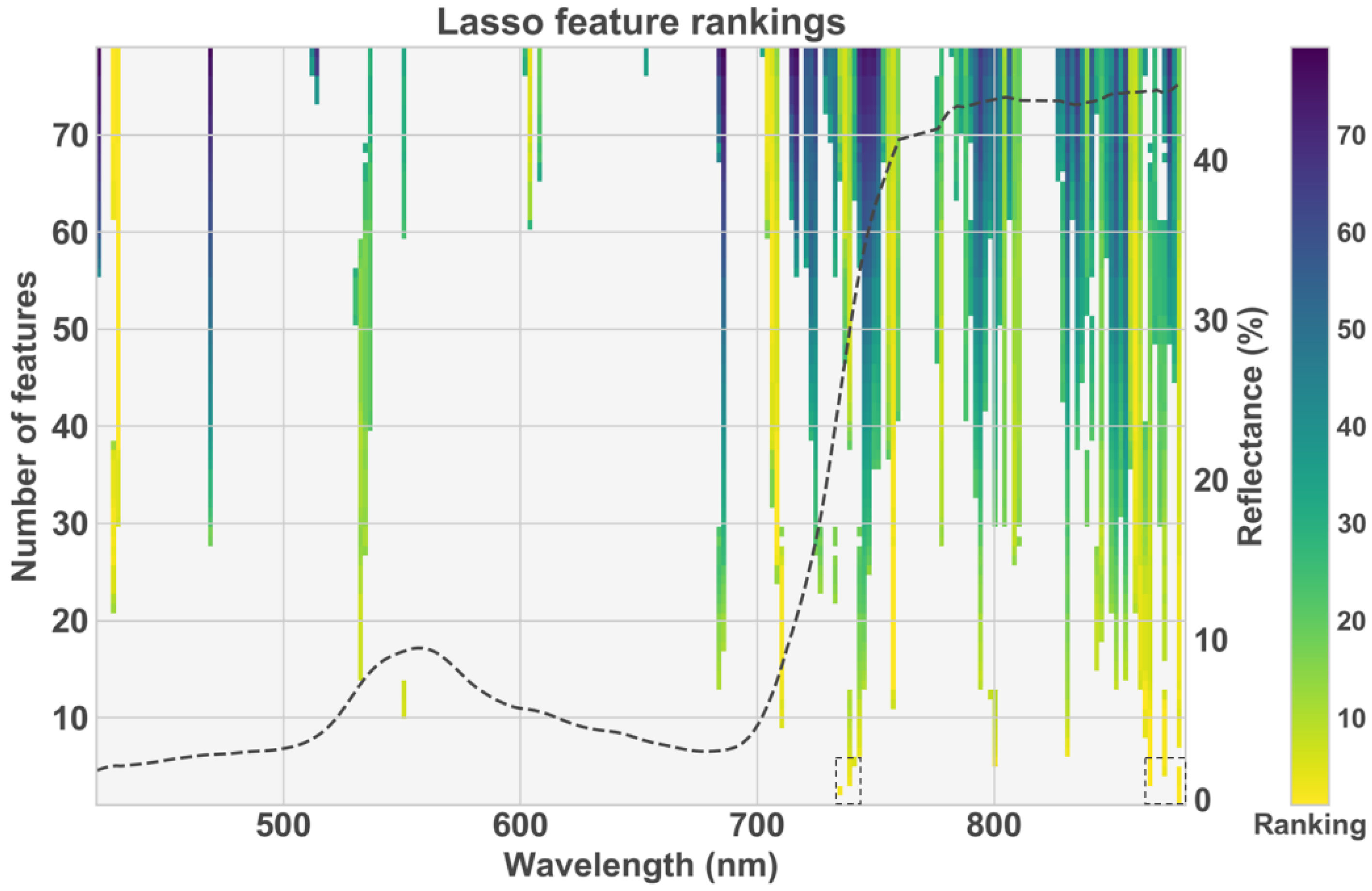
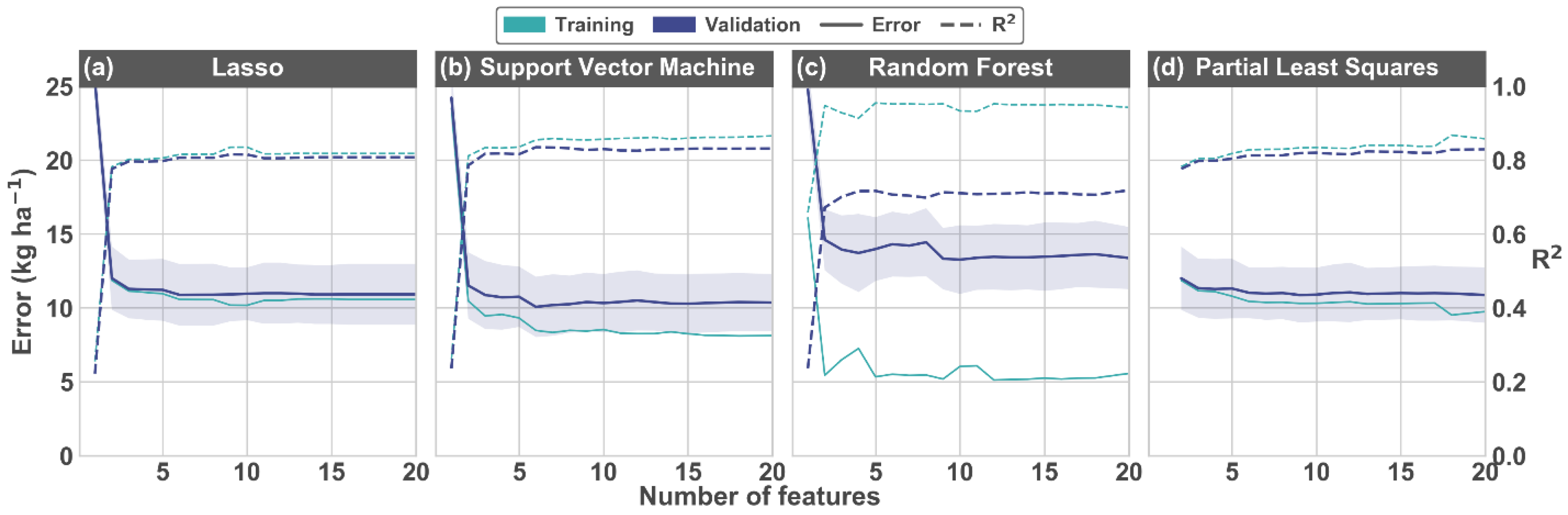
3.2. Feature Selection
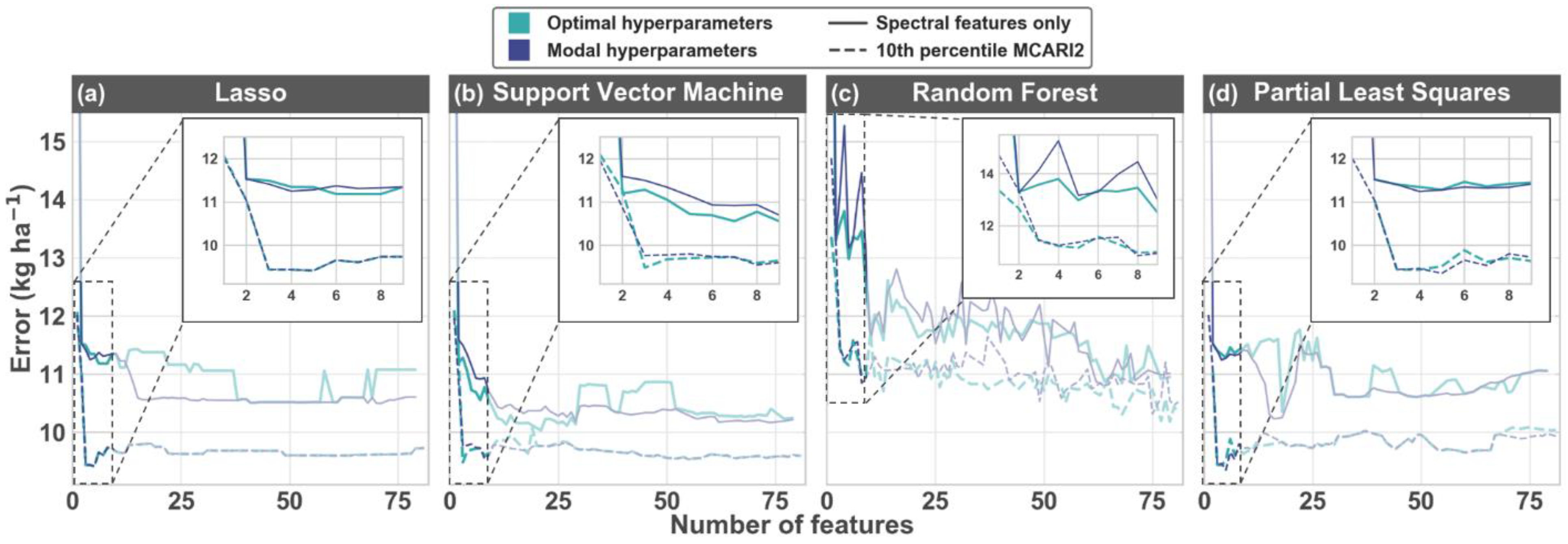
3.3. Hyperparameter Tuning
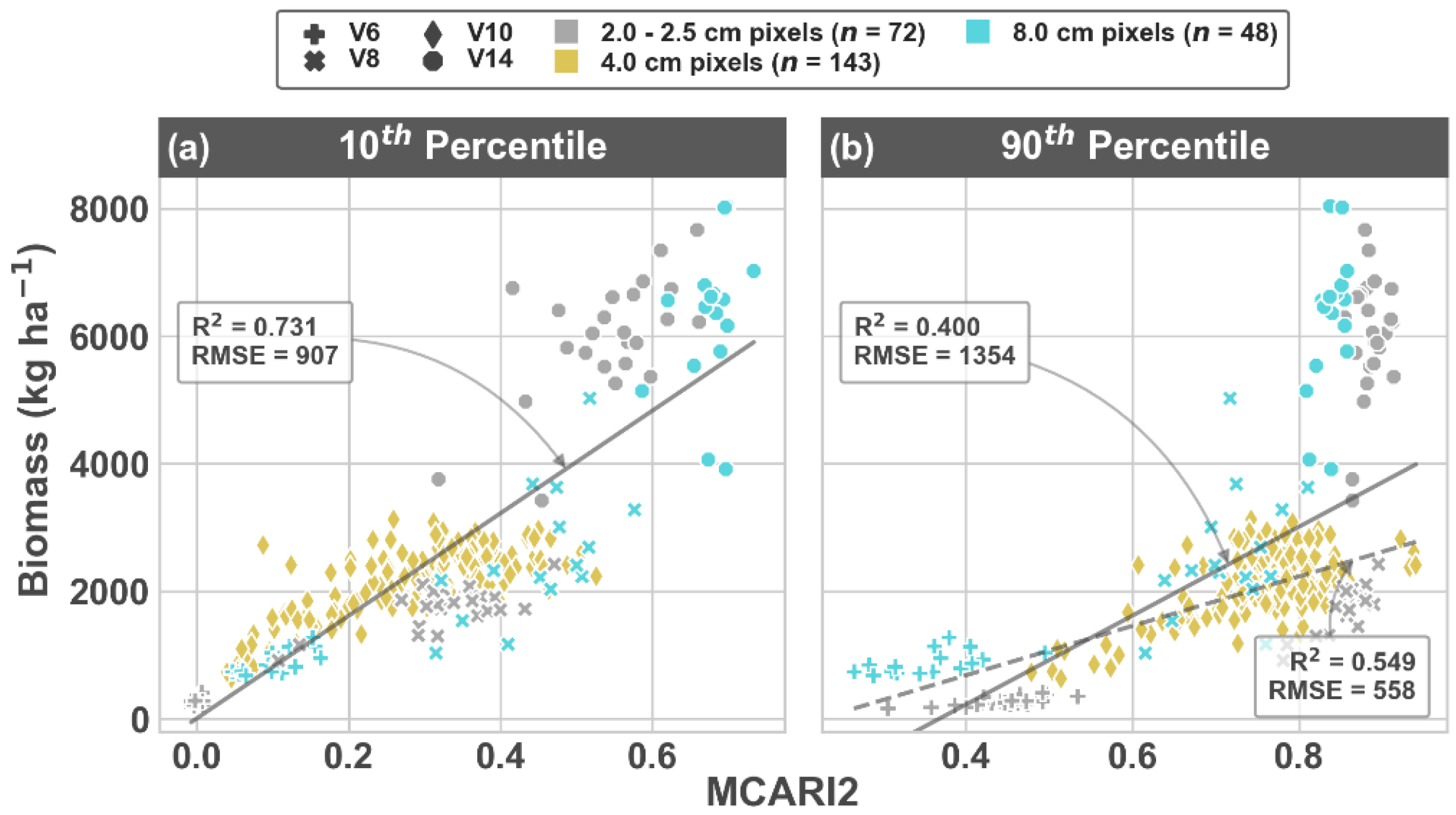
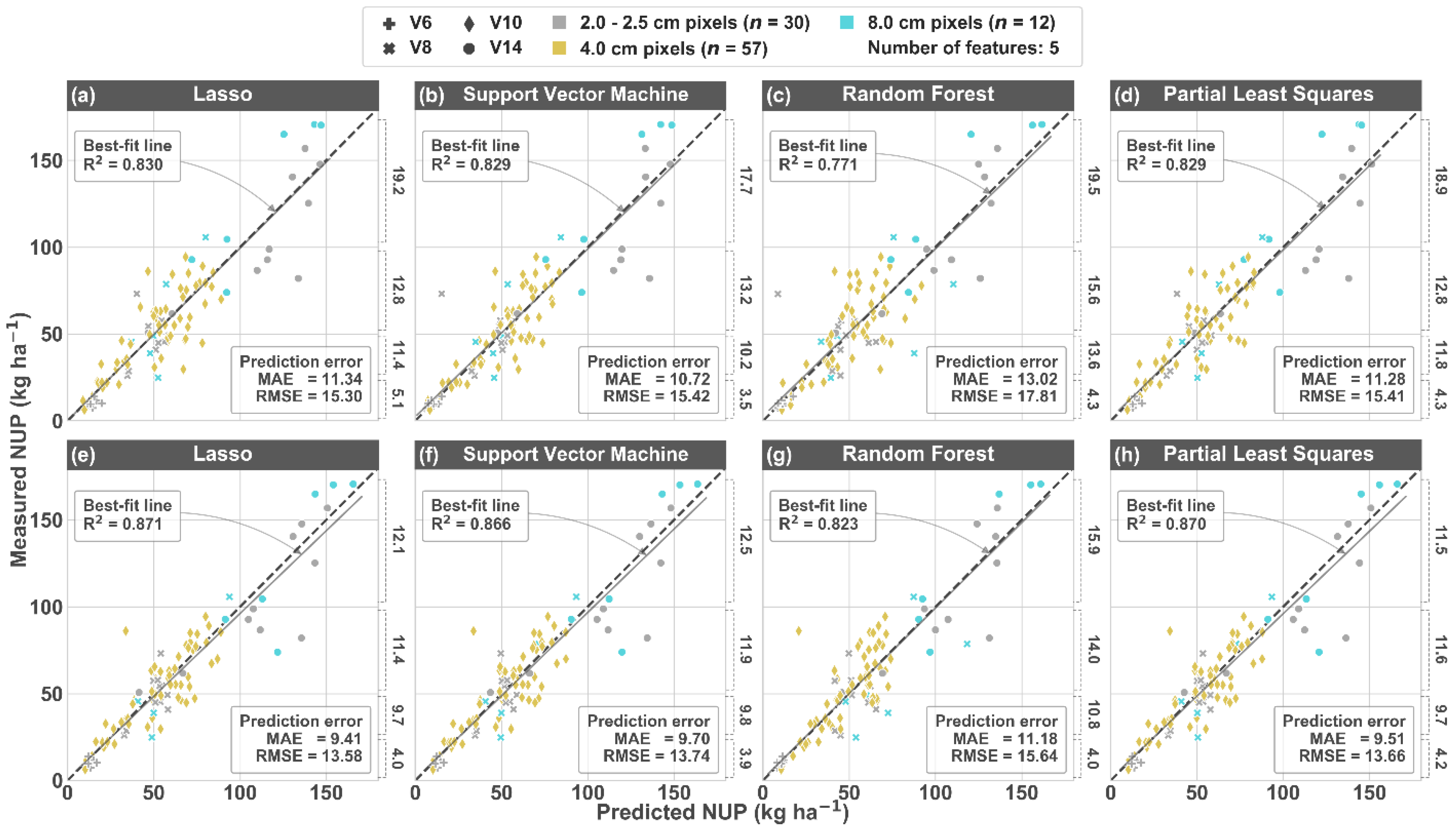
3.4. Nitrogen Uptake Predictions
4. Discussion
4.1. Model Comparison
4.2. Segmentation
4.3. Inclusion of an Auxiliary Feature
4.4. Spectral Feature Selection
4.5. Ongoing Challenges
4.5.1. Cost of Specialty Sensors
4.5.2. Timeliness
4.5.3. Making a Fertilizer Recommendation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Experiment | ID | Observation n | Stage | Sampling Date | Image Date | Image Time | Sample Area | Subsample n | Nitrogen Extraction |
|---|---|---|---|---|---|---|---|---|---|---|
| 2018 | Wells | 1 | 142 | V10 | 29 June 2018 | 28 June 2018 | 11:49–12:00 | 1.5 m × 5 m (2 rows) | 6 | Kjeldahl |
| 2019 | Waseca small-plot | 2 | 24 | V6 | 29 June 2019 | 29 June 2019 | 12:21–12:28 | 1.5 m × 2 m (2 rows) | 10 | Dry combustion |
| 2019 | 3 | 24 | V8 | 9/10 July 2019 1 | 09 July 2019 | 11:40–11:46 | 1.5 m × 2 m (2 rows) | 10 | Dry combustion | |
| 2019 | 4 | 24 | V14 | 23 July 2019 | 23 July 2019 | 12:03–12:09 | 1.5 m × 2 m (2 rows) | 6 | Dry combustion | |
| 2019 | Waseca whole-field | 5 | 16 | V8 | 10 July 2019 | 08 July 2019 | 13:06–13:17 | 5 m × 10 m (6 rows) | 6 | Dry combustion |
| 2019 | 6 | 16 | V14 | 23 July 2019 | 23 July 2019 | 12:32–12:42 | 5 m × 10 m (6 rows) | 6 | Dry combustion |
| Objective Function/Model | Spectral Features Only | With Auxiliary Feature |
|---|---|---|
| Relative 1 MAE | ||
| Lasso | 19.9% | 16.5% |
| Support vector | 18.8% | 17.0% |
| Random forest | 22.8% | 19.6% |
| Partial least squares | 19.8% | 16.7% |
| Relative 1 RMSE | ||
| Lasso | 26.8% | 23.8% |
| Support vector | 27.0% | 24.1% |
| Random forest | 31.2% | 27.4% |
| Partial least squares | 27.0% | 23.9% |
References
- Keeler, B.L.; Polasky, S. Land-use change and costs to rural households: A case study in groundwater nitrate contamination. Environ. Res. Lett. 2014, 9, 074002. [Google Scholar] [CrossRef]
- Shcherbak, I.; Millar, N.; Robertson, G.P. Global metaanalysis of the nonlinear response of soil nitrous oxide (N2O) emissions to fertilizer nitrogen. Proc. Natl. Acad. Sci. USA 2014, 111, 9199–9204. [Google Scholar] [CrossRef] [PubMed]
- Van Metre, P.C.; Frey, J.W.; Musgrove, M.; Nakagaki, N.; Qi, S.; Mahler, B.J.; Wieczorek, M.E.; Button, D.T. High Nitrate Concentrations in Some Midwest United States Streams in 2013 after the 2012 Drought. J. Environ. Qual. 2016, 45, 1696. [Google Scholar] [CrossRef]
- Keeler, B.L.; Gourevitch, J.D.; Polasky, S.; Isbell, F.; Tessum, C.W.; Hill, J.D.; Marshall, J.D. The social costs of nitrogen. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [PubMed]
- Erisman, J.W.; Galloway, J.N.; Seitzinger, S.; Bleeker, A.; Dise, N.B.; Petrescu, A.M.R.; Leach, A.M.; de Vries, W. Consequences of human modification of the global nitrogen cycle. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130116. [Google Scholar] [CrossRef] [PubMed]
- Conant, R.T.; Berdanier, A.B.; Grace, P.R. Patterns and trends in nitrogen use and nitrogen recovery efficiency in world agriculture. Global Biogeochem. Cycles 2013, 27, 558–566. [Google Scholar] [CrossRef]
- Pannell, D.J. Economic perspectives on nitrogen in farming systems: Managing trade-offs between production, risk and the environment. Soil Res. 2017, 55, 473. [Google Scholar] [CrossRef]
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef]
- Dhital, S.; Raun, W.R. Variability in optimum nitrogen rates for maize. Agron. J. 2016, 108, 2165–2173. [Google Scholar] [CrossRef]
- Mamo, M.; Malzer, G.L.; Mulla, D.J.; Huggins, D.R.; Strock, J. Spatial and temporal variation in economically optimum nitrogen rate for corn. Agron. J. 2003, 95, 958–964. [Google Scholar] [CrossRef]
- Basso, B.; Dumont, B.; Cammarano, D.; Pezzuolo, A.; Marinello, F.; Sartori, L. Environmental and economic benefits of variable rate nitrogen fertilization in a nitrate vulnerable zone. Sci. Total Environ. 2016, 545–546, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Robertson, G.P.; Vitousek, P.M. Nitrogen in Agriculture: Balancing the Cost of an Essential Resource. Annu. Rev. Environ. Resour. 2009, 34, 97–125. [Google Scholar] [CrossRef]
- Cassman, K.G.; Dobermann, A.; Walters, D.T. Agroecosystems, Nitrogen-use Efficiency, and Nitrogen Management. AMBIO A J. Hum. Environ. 2002, 31, 132–140. [Google Scholar] [CrossRef]
- Corti, M.; Cavalli, D.; Cabassi, G.; Marino Gallina, P.; Bechini, L. Does remote and proximal optical sensing successfully estimate maize variables? A review. Eur. J. Agron. 2018, 99, 37–50. [Google Scholar] [CrossRef]
- Li, F.; Wang, L.; Liu, J.; Wang, Y.; Chang, Q. Evaluation of leaf N concentration in winter wheat based on discrete wavelet transform analysis. Remote Sens. 2019, 11, 1331. [Google Scholar] [CrossRef]
- Kaiser, D.E.; Lamb, J.A.; Eliason, R. Fertilizer Guidelines for Agronomic Crops in Minnesota. Retrieved from the University of Minnesota Digital Conservancy. 2011. Available online: http://hdl.handle.net/11299/198924 (accessed on 10 April 2020).
- Wilson, G.L.; Mulla, D.J.; Galzki, J.; Laacouri, A.; Vetsch, J.; Sands, G. Effects of fertilizer timing and variable rate N on nitrate–N losses from a tile drained corn-soybean rotation simulated using DRAINMOD-NII. Precis. Agric. 2020, 21, 311–323. [Google Scholar] [CrossRef]
- Bradstreet, R.B. Kjeldahl Method for Organic Nitrogen. Anal. Chem. 1954, 26, 185–187. [Google Scholar] [CrossRef]
- Matejovic, I. Total nitrogen in plant material determinated by means of dry combustion: A possible alternative to determination by kjeldahl digestion. Commun. Soil Sci. Plant. Anal. 1995, 26, 2217–2229. [Google Scholar] [CrossRef]
- Robinson, B.F.; Biehl, L.L. Calibration procedures for measurement of reflectance factor in remote sensing field research. In Proceedings of the SPIE 0196, Measurements of Optical Radiations, San Diego, CA, USA, 27–30 August 1979; pp. 15–26. [Google Scholar]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Nigon, T.J. HS-Process. Anaconda Cloud 2020. Available online: https://hs-process.readthedocs.io/ (accessed on 10 April 2020).
- Boggs, T. Spectral Python. Anaconda Cloud 2020. Available online: http://www.spectralpython.net/ (accessed on 10 April 2020).
- GDAL/OGR contributors. GDAL/OGR Geospatial Data Abstraction Library. Open Source Geospatial Foundation 2020. Available online: https://gdal.org (accessed on 10 April 2020).
- Greenblatt, G.D.; Orlando, J.J.; Burkholder, J.B.; Ravishankara, A.R. Absorption measurements of oxygen between 330 and 1140 nm. J. Geophys. Res. 1990, 95, 18577. [Google Scholar] [CrossRef]
- Hill, C.; Jones, R.L. Absorption of solar radiation by water vapor in clear and cloudy skies: Implications for anomalous absorption. J. Geophys. Res. Atmos. 2000, 105, 9421–9428. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; ZarcoTejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Yeo, I.-K.; Johnson, R.A. A new family of power transformations to improve normality or symmetry. Biometrika 2000, 87, 954–959. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; ISBN 978-1-4757-2440-0. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; ISBN 0387848576. [Google Scholar]
- Breiman, L. Random forests. Random For. 2001, 45, 5–32. [Google Scholar]
- Helland, I.S. On the structure of partial least squares regression. Commun. Stat. Simul. Comput. 1988, 17, 581–607. [Google Scholar] [CrossRef]
- Xia, T.; Miao, Y.; Wu, D.; Shao, H.; Khosla, R.; Mi, G. Active optical sensing of spring maize for in-season diagnosis of nitrogen status based on nitrogen nutrition index. Remote Sens. 2016, 8, 605. [Google Scholar] [CrossRef]
- Morris, T.F.; Murrell, T.S.; Beegle, D.B.; Camberato, J.J.; Ferguson, R.B.; Grove, J.; Ketterings, Q.; Kyveryga, P.M.; Laboski, C.A.M.; Mcgrath, J.M.; et al. Strengths and limitations of nitrogen rate recommendations for corn and opportunities for improvement. Publ. Agron. J. 2018, 110, 1–37. [Google Scholar] [CrossRef]
- Polinova, M.; Jarmer, T.; Brook, A. Spectral data source effect on crop state estimation by vegetation indices. Environ. Earth Sci. 2018, 77, 1–12. [Google Scholar] [CrossRef]
- Scotford, I.M.; Miller, P.C.H. Applications of spectral reflectance techniques in Northern European cereal production: A review. Biosyst. Eng. 2005, 90, 235–250. [Google Scholar] [CrossRef]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Kitchen, N.R.; Sudduth, K.A.; Drummond, S.T.; Scharf, P.C.; Palm, H.L.; Roberts, D.F.; Vories, E.D. Ground-based canopy reflectance sensing for variable-rate nitrogen corn fertilization. Agron. J. 2010, 102, 71–84. [Google Scholar] [CrossRef]
- Ma, B.L.; Subedi, K.D.; Costa, C. Comparison of crop-based indicators with soil nitrate test for corn nitrogen requirement. Agron. J. 2005, 97, 462–471. [Google Scholar] [CrossRef]
- Scharf, P.C. Soil and plant tests to predict optimum nitrogen rates for corn. J. Plant. Nutr. 2001, 24, 805–826. [Google Scholar] [CrossRef]
- Scharf, P.C.; Brouder, S.M.; Hoeft, R.G. Chlorophyll meter readings can predict nitrogen need and yield response of corn in the north-central USA. Agron. J. 2006, 98, 655–665. [Google Scholar] [CrossRef]
- Schmidt, J.; Beegle, D.; Zhu, Q.; Sripada, R. Improving in-season nitrogen recommendations for maize using an active sensor. Field Crop. Res. 2011, 120, 94–101. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Dellinger, A.E.; Beegle, D.B. Nitrogen recommendations for corn: An on-the-go sensor compared with current recommendation methods. Agron. J. 2009, 101, 916–924. [Google Scholar] [CrossRef]
- Spackman, J.A.; Fernandez, F.G.; Coulter, J.A.; Kaiser, D.E.; Paiao, G. Soil texture and precipitation influence optimal time of nitrogen fertilization for corn. Agron. J. 2019, 111, 2018–2030. [Google Scholar] [CrossRef]
- Clark, J.D.; Veum, K.S.; Fernández, F.G.; Kitchen, N.R.; Camberato, J.J.; Carter, P.R.; Ferguson, R.B.; Franzen, D.W.; Kaiser, D.E.; Laboski, C.A.M.; et al. Soil sample timing, nitrogen fertilization, and incubation length influence anaerobic potentially mineralizable nitrogen. Soil Sci. Soc. Am. J. 2020. [Google Scholar] [CrossRef]
- Leirós, M.C.; Trasar-Cepeda, C.; Seoane, S.; Gil-Sotres, F. Dependence of mineralization of soil organic matter on temperature and moisture. Soil Biol. Biochem. 1999, 31, 327–335. [Google Scholar] [CrossRef]
- Puntel, L.A.; Pagani, A.; Archontoulis, S.V. Development of a nitrogen recommendation tool for corn considering static and dynamic variables. Eur. J. Agron. 2019, 105, 189–199. [Google Scholar] [CrossRef]
| Spectral Range (nm) | Spectral Resolution (nm) | Spectral Channels | Spatial Channels | Bit Depth | Field of View (Degrees) |
|---|---|---|---|---|---|
| 400–900 | 2.1 | 240 1 | 640 | 12 | 33.0 |
| Site | Altitude | Ground Speed | Ground Swath | Pixel Size | Area Captured | Cropped Plot Size |
|---|---|---|---|---|---|---|
| m | m s−1 | m | cm | ha | m | |
| Wells | 40 | 4.0 | 23.7 | 4.0 | 4.5 | 6.2 × 1.8 |
| Waseca small-plot 1 | 20–25 | 2.0–2.5 | 11.8–14.8 | 2.0–2.5 | 0.7 | 1.8 × 1.8 |
| Waseca whole-field | 80 | 8.0 | 47.4 | 8.0 | 11.2 | 10 × 10 |
| Spectral Features Only | With Auxiliary Feature | |||
|---|---|---|---|---|
| Model Parameters | Modal Value | Frequency | Modal Value | Frequency |
| Lasso | ||||
| alpha | 0.001 | 61% | 0.0001 | 100% |
| Support vector regression | ||||
| kernel | “rbf” | 82% | “linear” | 92% |
| Gamma 1 | 5 | 40% | - | - |
| C 1 | 30 | 38% | 200 | 84% |
| epsilon 1 | 0.01 | 48% | 0.01 | 86% |
| Random forest | ||||
| min_samples_split | 2 | 82% | 2 | 46% |
| max_features | 0.3 | 70% | 0.9 | 61% |
| Partial least squares | ||||
| n_components | 7 | 39% | 7 | 61% |
| scale | 1 | 77% | 1 | 79% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nigon, T.J.; Yang, C.; Dias Paiao, G.; Mulla, D.J.; Knight, J.F.; Fernández, F.G. Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery. Remote Sens. 2020, 12, 1234. https://doi.org/10.3390/rs12081234
Nigon TJ, Yang C, Dias Paiao G, Mulla DJ, Knight JF, Fernández FG. Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery. Remote Sensing. 2020; 12(8):1234. https://doi.org/10.3390/rs12081234
Chicago/Turabian StyleNigon, Tyler J., Ce Yang, Gabriel Dias Paiao, David J. Mulla, Joseph F. Knight, and Fabián G. Fernández. 2020. "Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery" Remote Sensing 12, no. 8: 1234. https://doi.org/10.3390/rs12081234
APA StyleNigon, T. J., Yang, C., Dias Paiao, G., Mulla, D. J., Knight, J. F., & Fernández, F. G. (2020). Prediction of Early Season Nitrogen Uptake in Maize Using High-Resolution Aerial Hyperspectral Imagery. Remote Sensing, 12(8), 1234. https://doi.org/10.3390/rs12081234








