Abstract
An accurate assessment of evapotranspiration (ET) is crucially needed at the basin scale for studying the hydrological processes and water balance especially from upstream to downstream. In the mountains, this term is poorly understood because of various challenges, including the vegetation complexity, plant diversity, lack of available data and because the in situ direct measurement of ET is difficult in complex terrain. The main objective of this work was to investigate the potential of a Two-Source-Energy-Balance model (TSEB) driven by the Landsat and MODIS data for estimating ET over a complex mountain region. The complexity is associated with the type of the vegetation canopy as well as the changes in topography. For validating purposes, a large-aperture scintillometer (LAS) was set up over a heterogeneous transect of about 1.4 km to measure sensible (H) and latent heat (LE) fluxes. Additionally, two towers of eddy covariance (EC) systems were installed along the LAS transect. First, the model was tested at the local scale against the EC measurements using multi-scale remote sensing (MODIS and Landsat) inputs at the satellite overpasses. The obtained averaged values of the root mean square error (RMSE) and correlation coefficient (R) were about 72.4 Wm−2 and 0.79 and 82.0 Wm−2 and 0.52 for Landsat and MODIS data, respectively. Secondly, the potential of the TSEB model for evaluating the latent heat fluxes at large scale was investigated by aggregating the derived parameters from both satellites based on the LAS footprint. As for the local scale, the comparison of the latent heat fluxes simulated by TSEB driven by Landsat data performed well against those measured by the LAS (R = 0.69, RMSE = 68.0 Wm−2), while slightly more scattering was observed when MODIS products were used (R = 0.38, RMSE = 99.8 Wm−2). Based on the obtained results, it can be concluded that (1) the TSEB model can be fairly used to estimate the evapotranspiration over the mountain regions; and (2) medium- to high-resolution inputs are a better option than coarse-resolution products for describing this kind of complex terrain.
1. Introduction
The Mediterranean region is one of the most vulnerable areas to climate variability and change [1], which seriously influences the water resources. In Morocco, additional factors such as population growth, urban expansion, tourism development, and more importantly the intensification of agriculture are likely to increase the frequency of water shortages in this region. In several Mediterranean basins, water originates from the mountains and is diverted to irrigated crop areas from upstream to downstream through networks of traditional canals or collected within dams for later use. One of the most important components of water balance in such area is the evapotranspiration (ET). Refs. [2] and [3] have stated that ET is the second largest term in the terrestrial water budget after precipitation, and that it is expected to increase with global warming. Recently, a great deal of research has been done on either measurements or estimates of ET over irrigated crops located downstream, as evidenced by the numerous studies carried out on irrigated crops of the Haouz plain in the Tensift catchment near Marrakech [4,5,6,7,8,9,10,11]. Unfortunately, over mountain regions, this term is still poorly investigated. The reasons are numerous: agriculture in mountainous areas is very heterogeneous (small fields, a large variety of crops including mixed crops) and data are lacking in these poorly gauged areas. Additionally, topography leads to complex heat and mass transfers with the importance of advection processes compared to homogeneous and flat terrain. There is thus an urgent need to develop new methodologies for monitoring the evapotranspiration over agricultural mountainous areas.
Over homogeneous areas, direct measurements of turbulent fluxes can be obtained by the eddy covariance (EC) method or other local point measurement techniques such as lysimeter or Bowen ratio [12,13,14]. Due to its robustness, EC is considered to be a reference technique for measuring sensible (H) and latent (LE) heat fluxes with high temporal resolution. It has been tested for various land surface conditions [15]. However, such a system is very costly and demanding with respect to manpower, requiring a competent staff for data processing and maintenance, as well as an important power supply. When the area is heterogeneous, such as an agricultural landscape, large-scale measurement of ET requires the installation of a system on each field which is often unaffordable. By contrast, large or extra-large scintillometers (LAS or XLAS) provide spatially averaged turbulent fluxes along transects that can reach 10 km [16,17,18,19]. Success in validating remote sensing-based ET against LAS measurements has already been demonstrated in some other areas of the world [20,21,22,23,24,25].
When direct measurements of evapotranspiration are lacking, energy balance models forced by remotely sensed Land Surface Temperature (LST) have long since been shown to be valuable tools for estimating ET at larger scales [26,27,28] without needing any information about rainfall or soil hydraulic properties. In irrigated areas, another significant asset is that ET can be retrieved without any information on irrigation inputs that are likely to be unknown at the field scale over large areas. Consequently, energy balance approaches present a huge benefit in mountainous areas characterized by data scarcity and by a strong heterogeneity. Generally speaking, these models can be classified into two groups: (1) single-source energy balance models which consider the land surface as a single big leaf, with no distinction between vegetation and soil sources (SEBS [29], METRIC [30], SEBAL [31]); and (2) two-source energy balance models that distinguish, at minimum, between soil and vegetation sources and relate their contributions to the composite radiometric surface temperature and surface energy fluxes (TSEB [32], and SPARSE [33]). For sparse vegetation and complex canopies, two-source modeling schemes provide a more realistic representation of the turbulent and radiation exchanges with the lower atmosphere [9,32,34,35,36,37,38,39]. These models also avoid empirical corrections for the excess resistance used in the single-source models and can further incorporate the effects of view geometry [40]. Moreover, two-source model groups generally do not require any additional information beyond that required for single-source models and can use a single measurement of LST. Consequently, these models and their subsequent refinements [10,25,41,42] have been found to be practical for estimating surface energy fluxes for a wide variety of vegetation cover, climates, and spatial scales in which LST was obtained from ground-based, airborne, and satellite instruments. Among the existing two-source models (SPARSE [33], ESVEP [41], ALEXI [43], TSEB [32]), the thermal-based two-source energy balance (TSEB) [32] was chosen for its simplicity and because it has been shown to accurately predict LE in different contexts, including sparse canopy in semi-arid areas [9,21,25,34,38]. Until the launch of a future high-resolution and high-repetitiveness mission in the thermal infrared domain [44], the possibilities in terms of LST products are limited to the Moderate Sensors Resolution Imaging Spectroradiometer (MODIS) (1 km and a daily revisit time) and Landsat (60 to 100 m resolution, 16 days). The question arises as to what is the required level of heterogeneity representation in terms of input surface variables to get accurate predictions of convective fluxes (H and LE) with the TSEB model based on the available remote sensing products?
In this context, this paper evaluated for the first time the performance of TSEB for predicting ET in mountainous agricultural areas using MODIS and Landsat input data. Water management institutions are often interested in ET estimates aggregated over several fields (an irrigated perimeter, such as a farm or a district). The scale of our study is thus twofold: field and multi-field. For the multi-scale evaluation of TSEB, a LAS and two eddy covariance systems were installed during two growing seasons in the foothills of the Atlas mountains near Marrakech. This paper is organized as follows: firstly, a brief physical background of the key formulations used by the scintillation method is presented. Then, the TSEB algorithm model and the data used are presented in the second section. The results are discussed and commented on in Section 3. Finally, the conclusion and perspectives are drawn.
2. Materials and Methods
2.1. Site and Experimental Data
The study area is located in the foothills of the High Atlas mountain range close to the village of Tahanaout, about 35 km south of Marrakech, Morocco (Figure 1a). It is characterized by a semi-arid climate with a low annual rainfall amount of around 230 mm/year. Figure 1 also shows the land use mapping of the study area carried out in February 2018. The surface is heterogeneous and composed of small fields planted with olive trees with heights ranging from 3 to 12 m, which were measured in every field using the 45° Triangle Method. The map of tree height is displayed in Figure 1b. Below the trees, some farmers cultivate wheat, alfalfa and corn. Other crops include apricot trees, plum trees, orange trees and peach trees are cultivated. The bare soil is mainly present on the sides of the river of Rherhaya and on the North-West part of the area. Plots are irrigated using the flooding technique.
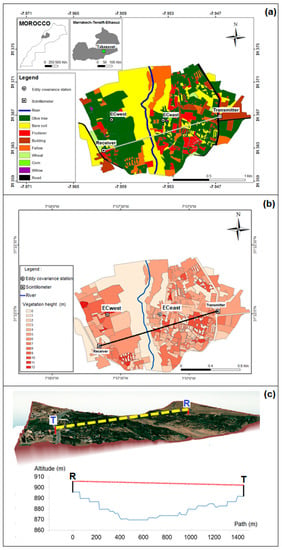
Figure 1.
(a) Location of the eddy covariance stations and of the scintillometer transmitter (T) and receiver (R) superimposed on the land use map of the study site. (b) Vegetation height map of the study site. (c) Google Earth image draped on the DEM of the area (8-m DEM derived from PLEIADE data), scintillometer path and elevation along the scintillometer path.
The experiment started in October 2016. Firstly, a large-aperture scintillometer was installed over a transect of 1464 m. For the stability of the LAS signal, the transmitter and receiver were put on two buildings at heights of 10.5 and 10 m, respectively. The frequency of the measurements was 1 Hz, from which half-hourly fluxes were computed. Generally speaking, the heterogeneity in topography causes a variation in the LAS beam height along its path ranging between 10 and 50 m above the ground. This means that the LAS measurements represent not only a horizontal, but also a vertical average of the structure parameter of temperature (). Therefore, the use of the averaged height of transmitter and receiver of the LAS can affect the application of Monin-Obukhov similarity theory (MOST), and thus the sensible heat flux (). Indeed, this height does not represent the vertically averaged due to its non-linearity with height, and the LAS signal is weighted towards the middle of the path. To overcome this problem, it is necessary to introduce in the H calculation an effective height [45], taking into account the variation of the LAS beam along its path (see Section 2.2).
The site was also equipped with two eddy covariance (EC) systems installed on two olive fields on towers with heights of about 17.5 m (hereafter referred to as ECwest and ECeast; Figure 1a) in October 2016 and April 2017, respectively. The two plots were covered by different land uses, where ECwest contained a row of olive trees and wheat. By contrast, ECeast was more heterogeneous and was characterized by a mix of various tree crops and wheat. The EC systems were composed of a three-dimensional sonic anemometer (CSAT3, Campbell Scientific Ltd.) and a Krypton hygrometer (KH20, Campbell Scientific Ltd.). Raw data were sampled at a rate of 20 Hz and processed using the ECpack software to compute turbulent fluxes. Air temperature and humidity were measured by an HMP155 manufactured by Vaisala and the four components of the net radiation were measured by a CNR4 sensor manufactured by Campbell Scientific. The in situ LST was derived from the emitted long wavelength component measured by the CNR4 instrument at the time of the satellites overpass. The in situ daily albedo was computed as the ratio between incoming and outgoing short-wave components averaged between 11:00 a.m. and 3:00 p.m. In addition, each station was equipped with Time Domain Reflectometry (TDR) and heat flux plate (HPF01) sensors to measure the soil water content at different depths and heat conduction fluxes G, respectively. Note that ECwest was outside the LAS footprint but is representative of olive orchards with wheat cropped inter-row, which is the predominant land use within the footprint.
The wind speed and direction were measured at 10 m next to the LAS receiver. The prevailing winds come from the North, with a speed ranging mostly from 0 to 4 m/s (not shown). Figure 2 reports the daily pattern of the meteorological data including solar radiation, rainfall, humidity and temperature of the air during the study period. The atmosphere is very dry, with an average humidity of 30% and an average air temperature of 35 °C during spring, summer and early autumn. By contrast, the rest of the year is milder and wet with an average humidity of 60% and an average air temperature of 15 °C. Precipitation fell mainly during winter and spring, from the beginning of November until the middle of May, with a total amount of about 218 mm for 2017 and 325 mm for 2018.
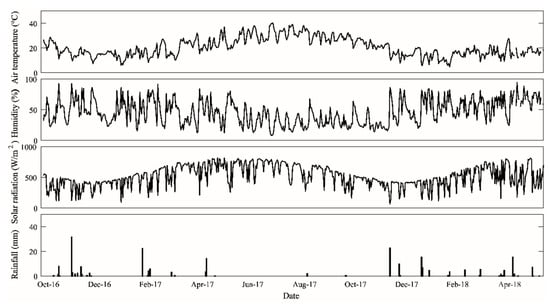
Figure 2.
Time series of the main meteorological variables measured at the study site, Morocco.
2.2. Scintillometry Theoretical Background
2.2.1. Determining the Sensible and Latent Heat Flux from LAS
The turbulence in the boundary layer of the atmosphere causes a variation in the refractive index of the air. This variation produces fluctuations in the intensity of the electromagnetic wave emitted by the transmitter. The wave attenuations allow the calculation of the variation of the structure parameter of the refractive index along the path and analyzed at the receiver. For the scintillometers operating at the visible or near-infrared wavelengths, the structure parameter of the temperature can be related to as follows [46]:
where is the refractive index coefficient for air (7.8*10−7 K·Pa−1), and is the Bowen ratio computed in this study by the iterative procedure of the Bowen closure method (BCM) [47]. is the air temperature (K), and P is the atmospheric pressure (Pa). The final bracketed term is a correction factor considering the effects of humidity. and are given in m−2/3 and K2m−2/3, respectively.
In unstable conditions, very likely during the day, the Monin-Obikhov similarity theory can be used to link the temperature structure parameter to the temperature scale as follows [16,48]:
is the Obukhov length, defined as:
where = 0.41 is the Von Karman constant, = 9.81 m·s−2 is the gravitational acceleration and is the friction velocity, given by:
where is the integrated stability function [49], is the displacement height and is the roughness length, the latter two being calculated as a fraction of the vegetation height (hveg). The displacement height and roughness length were then computed from the vegetation height with the rule of thumb and [50]. The range of wind direction (WD) was split into 18 twenty-degree intervals. For each interval, the LAS footprint is computed considering the average value of the friction velocity (0.3 m/s). Finally, the average vegetation height over the LAS footprint was computed using the vegetation height map at the field scale and the LAS footprint. U is the wind speed, is the measurement height corrected by adopting the formulae developed by [45] in order to take into account the variation of the path height between the transmitter and the receiver.
where is the normalized path at each point, Z(u) is the scintillometer beam height along the path, and is the weighting function.
The sensible heat flux (W·m−2) is then calculated iteratively using Equations (1) to (4) and the following relationship:
where (kg·m−3) and (J·kg−1K−1) are the air density and heat capacity, respectively. The latent heat flux from the LAS is obtained as the residual term of the energy balance equation:
where (W·m−2) and (W·m−2) are the net radiation and soil heat flux, respectively.
The available energy () used in the Equation (7) can be a measurement value which represents a local scale, or estimated according to satellite data. In this latter case, the spatial scale of available energy can represent the source area of the LAS footprint. The net radiation is estimated as follows:
where is the albedo, is the surface emissivity, is the solar radiation, is the atmospheric radiation (W·m−2) and is the Stefan-Boltzmann constant. Finally, the soil conduction flux is estimated as a constant fraction of following [32]:
2.2.2. Scintillometer Footprint
The LAS measurement is the average of an entire area, with each part of it contributing a percentage depending on its position, weight and wind speed. To obtain this contribution, several analytical and Lagrangian models of footprint have been developed [51,52,53,54]. In this work, we used the model of [52], which relates the flux measured at to the surface distribution of the flux:
where f is the footprint function relates the flux measured at , to the spatial distribution of surface fluxes, . and are the downwind and crosswind distances (m) from the point where the measurements are taken, respectively. As already mentioned, each point is weighted according to the spatial weighting function of the LAS [55]:
where is the LAS footprint, and is the flux footprint for a point located at distance from the transmitter. is the scintillometer path-weighting function for the position located at distance.
2.3. The Two-Source Energy Balance Model
The two-source energy balance (TSEB) model estimates sensible and latent heat fluxes, for soil and canopy, distinctly. This model has been described in [32] and [42]. It combines the biophysical characteristics of vegetation with the energy balance of the canopy and soil. As with most soil–plant–atmosphere energy balance algorithms, TSEB considers the available energy () to be equal to the sum of the turbulent fluxes () for both components and assumes other energy components to be negligible, such as canopy heat storage and photosynthesis. Two input variables derived from remote sensing instruments are key to the TSEB model. The first is the surface temperature, which is used in the estimation of sensible heat flux. The second is the vegetated cover fractional, which controls the partitioning of energy between surface vegetation and the underlying soil. In the TSEB model, , , and are further partitioned to their canopy and soil components as follows:
where the flux components are distinguished by the following subscripts: the canopy c, and the soil s. The canopy is assumed to transpire at his potential rate (Equation (14)) using the equation in [56]:
where is the Priestley-Taylor coefficient, is the fraction of green vegetation, is the thermodynamic psychrometric constant (≈ 67 Pa·K−1), and Δ is the slope of the temperature saturation vapor pressure curve. Canopy sensible heat flux, , is determined as the residual term of Equation (13), and canopy temperature (Equation (15)) is computed from :
Soil temperature, Ts (Equation (16)) is then derived from the surface temperature allowing for the computation of the soil sensible heat (Equation (17)) as follows:
The resistances to surface energy fluxes are strongly affected by atmospheric stability. Resistance is adjusted based upon Obukhov stability length, L, but this length is in turn dependent upon surface fluxes. By iteration, L and the aerodynamic resistance () and the resistance to heat flux above the soil surface () are determined. If is negative, meaning condensation on the soil, which is very unlikely during the day, its value is set to zero, and a new value of is calculated as a residual term of the vegetation energy balance. Likewise, when negative values for are found, the normal evaluation procedure is overridden by setting and to 0 and the remaining flux components are balanced.
2.4. Satellite Products and Data
2.4.1. MODIS Products
Moderate Resolution Imaging Spectroradiometer (MODIS) is a key instrument aboard the Terra and Aqua satellites. It views the entire surface of the earth every one to two days and it acquires data at three spatial resolutions—250 m, 500 m and 1000 m—between 0.405 and 14.385 µm. The collection version 6 of the products was used in the present study. The MOD11A1 product, which corresponds to the daily level 3 LST and emissivity at 1 km spatial resolution, is derived from the MODIS sensor on board Terra. It is constructed with the daily LST pixel values in each granule retrieved by the generalized split-window algorithm under clear-sky conditions defined in MOD35. The MCD43A3 product, which jointly uses MODIS sensor data on board the Terra and Aqua satellites, is the daily albedo Model product at 500 m resolution. It provides both directional hemispherical reflectance (black sky albedo) and bihemispherical reflectance (white sky albedo) for each of the MODIS surface reflectance bands [57,58]. Each daily image is generated using 16 days of data, centered on the given day. In our case, we considered 85% direct light and 15% diffuse to compute a blue-sky albedo following [21]:
The MYD13Q1 product provides Vegetation Index (NDVI, EVI) values at 250 m resolution every 16 days. The Normalized Difference Vegetation Index (NDVI) was chosen for this study. This index is computed from atmospherically corrected bidirectional surface reflectances that have been masked for water, clouds, heavy aerosols, and cloud shadows.
2.4.2. Landsat Products
In this study, data from Landsat 7 and 8 were collected. The repeated cycle for these two satellites is 16 days. However, eight-day repeatability can be achieved by combining images from both satellites. The Enhanced Thematic Mapper Plus (ETM+) is installed on board Landsat 7. It acquires images in the nadir direction in the VNIR, the short-wave infrared (SWIR) at a resolution of 30 m and the thermal infrared (TIR) ranges at a resolution of 60 m. The Landsat 8 satellite is equipped with multispectral sensors including: (i) Operational Land Imager (OLI), which acquires imagery in nine spectral bands ranging from visible to medium infrared at a resolution of 30 m; and (ii) Thermal Infrared Sensor (TIRS), which provides TIR bands at a 100 m spatial resolution. In what follows, NDVI and Land Surface Temperature are derived from the ETM+ sensor data on board Landsat 7, while for Landsat 8, NDVI and LST are derived from the OLI and the TIRS, respectively.
Image data for this study were downloaded from the USGS website (http://earthexlorar.com/). Please note that all Landsat thermal data provided by the USGS were projected using the Universal Transverse Mercator (UTM), Zone 29N, World Geodetic System (WGS) 84 coordinate system. Actual LST were derived from Landsat thermal radiance using the processing chain developed at CESBIO following the correction steps described in [59]. The corrections associated with the radiation emitted by the atmosphere and to the atmospheric attenuation are based on the vertical atmospheric conditions (temperature, pressure, water vapor and ozone) of the ERA-Interim dataset. The atmospheric correction parameters were finally computed using the commercial RTM software MODTRAN. The surface emissivity was determined according to [59]. This formula is based on the vegetation index, as follows:
and are the vegetation and the soil emissivity, which are 0.99 and 0.96, respectively, in our study. and , which represent the maximum and the minimum values of , are equal to 0.99 and 0.17, following [59]. The parameter was fixed arbitrarily to 2 in accordance with [60]. To derive the albedo from Landsat data, all combinations of bands acquired in the visible and the near-infrared domains were tested through a multi-linear regression based on the in situ albedo computed from the shortwave components of the CNR4 instrument. The best combination (Table 1) was obtained from the Red (R) and the InfraRed (IR) bands, which is in agreement with similar studies carried out for other sensors like FORMOSAT [61] and SPOT4 [9].

Table 1.
Best reflectance combinations to retrieve albedo from Landsat data. R is for red and IR is for infrared.
3. Results and Discussion
3.1. Experimental Data Analysis
3.1.1. Energy Balance Closure
Before evaluating the TSEB model on the LAS transect, a validation at local scale was carried out with the eddy covariance (EC) measurements. For that reason, verification of the closure of the energy balance was a prerequisite to assessing the quality of the EC fluxes. Generally speaking, it is usually checked that the sum of these fluxes is close to the available energy () by assuming that the energy stored in the canopy is negligible. Figure 3 presents the scatter plot of () as a function of the sum of the sensible () and latent () heat fluxes for the two stations at a daily timestep. The comparison shows that the available energy overestimates the turbulent fluxes by approximately the same statistical metrics for both sites. However, the sum of the turbulent fluxes only reaches 60% of the available energy, and this non-closure is similar to what has been observed in previous studies over crops [62,63,64,65]. However, the obtained correlation is still acceptable due to the complexity of the study sites. Indeed, the non-accounting of the stored energy within the canopy can have a significant impact on the imbalance due to the existence of mixed vegetation (trees and seasonal vegetation). Likewise, a large part of this overestimation could be related to the underestimation of the EC measurements [4,6,66,67,68,69] which resulted from an angle-of-attack dependent calibration error in the sonic anemometer and from the use of coordinate rotation, which can act as a high-pass filter when applied to short measurement periods [70]. To correct the non-closure, particularly for the use of these turbulent fluxes to evaluate energy balance models, several studies have adopted the assumption suggested by [62], which stated that despite the underestimation of and by the EC system, their ratio (Bowen ratio) is correctly measured [11,21,23,68,70]. Herein, this approach was used to recompute and by forcing the energy balance closure with the measured values of Bowen ratio and AE ().
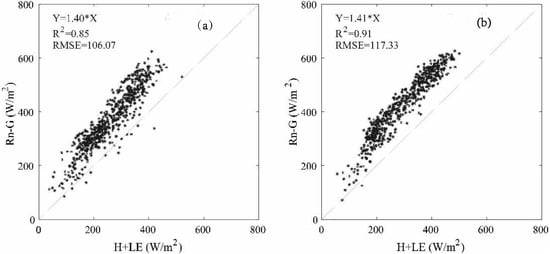
Figure 3.
Assessment of energy balance closure. Daily average fluxes of (Rn-G) are plotted against the sum of sensible (H) and latent heat (LE) measured under unstable conditions by the western EC system (a) and the eastern EC system (b).
3.1.2. Seasonal Course of Convective Fluxes
Figure 4 displays the time series of daily convective fluxes and derived from LAS and EC systems, available energy (), soil moisture, and rainfall, collected from November 2016 to April 2018 over both sites. Figure 5 provides the differences between EC stations and LAS for and in ten days steps for easy comparison. First, the shape of the available energy, which is controlled by solar radiation, is characteristic of semi-arid continental climates with high values in summer (maximum about 623 Wm−2) and low values in winter (85 Wm−2). Additionally, the Eastern site shows slightly higher values of the , particularly in summer and during early autumn, which can be justified by the lower albedo values measured over this station. Indeed, during this period, the albedo measured over the Western site was higher by 0.01 compared to that of the Eastern site (not shown). This is due to the increase in clear bare soil surface and to the decrease in vegetation cover fraction resulting from the wheat harvest that occurred in June at the Western site. Results reported in other experimental studies have shown that measurement of net radiation above a complex ecosystem is not representative because the vegetation structure around the measurement location can be highly variable. Depending on the location, various fractions of the upwelling radiation from the soil are intercepted by vegetation and do not reach the measurement device [71].
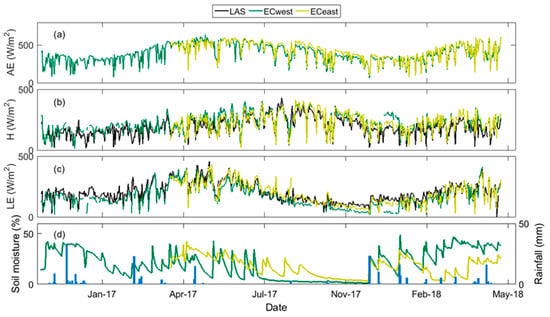
Figure 4.
Daily variation of (a) Available energy (AE); (b) Sensible heat (H); (c) Latent heat (LE) and (d) Soil moisture from October 2016 to May 2018. ECwest, ECeast and LAS measurements were superimposed for comparison purposes.
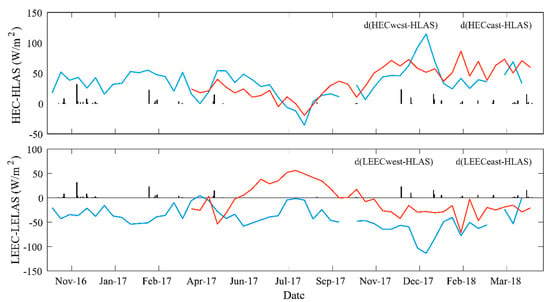
Figure 5.
10-day differences between scintillometer and eddy covariance measurements.
For the sensible heat fluxes, as expected, their curves followed approximately that of the available energy: high values were recorded during summer, with a peak of 421 Wm−2 (LAS measurement), due to the increase in bare soil surface associated with the senescence and the harvest of annual crops; while low values were measured during the winter season or after irrigation/rainfall events. Likewise, the latent heat flux decreased significantly during dry periods and increased immediately after rainfall or irrigation events. It peaked at the end of April, with a maximum value of about 403 Wm−2 (LAS measurement), which corresponds to very humid conditions, and high available energy and vegetation cover fraction (i.e., development peak of annual crops). Afterwards, the curves of decreased continuously until their minimum values during early autumn, when the soil moisture was low and when there was no water anymore in the river to irrigate the crops, resulting in a higher fraction of bare soils. In addition, there was no annual vegetation (wheat, corn) or irrigation of olive trees, and the fruit trees dropped their leaves in this period.
At the seasonal scale (Figure 4 and Figure 5), we note an acceptable agreement between LAS and eddy covariance daily turbulent fluxes ( and ) for ECwest, with differences of less than 50 Wm−2 from December 2017. The shift observed on the ECwest measurements of and could highlight an instrument acquisition problem (Figure 4) in this period of the year. By contrast, differences between ECeast and LAS exhibited a seasonal signal with higher deviation during the summer months. Indeed, during this period of the year, the dominant signal acquired by the LAS came from olive orchards that were no longer irrigated, while the wheat underneath had already been harvested. Th ECeast footprint was dominated by fruit trees with fully developed leaves that transpire at high rates. The higher soil moisture and watering events that can be observed in Figure 4 support this assumption. Stated differently, the values of the LAS were higher than those of the western station and lower than those measured at the eastern station. Indeed, the West station contained olive trees cropped in rows and separated by bare soil. By contrast, the East station contained fruit trees in the maturation stage in addition to the olive trees. Consequently, the LAS measurement values lay in between the values for the two stations, since the LAS footprint covered a mix of land use. Interestingly enough, some differences between the LAS and eddy covariance values could be observed for specific periods: precipitation and irrigation events introduced a difference in the surface conditions of the source area between LAS and EC. For irrigation, this was because none of the plots were irrigated at the same time, while for precipitation this was due to the source surface of the LAS, which contained more bare soil than the EC stations. In this case, the amount of precipitation easily evaporates from over the bare soil, because there is no vegetation to stock it or prevent the solar radiation from reaching the soil, which is in contrast to the vegetation-covered area of the EC stations’ footprints. Additionally, whatever the wind direction, the source area of the LAS contains the river (marked as blue color in Figure 1a), which may strongly affect the LAS signal, resulting in the lower values of sensible heat fluxes measured by LAS compared to the EC systems. Unfortunately, the quantity of evaporation from the river was not quantified, due to the difficulty in installing an EC system. Indeed, particularly after a huge rainfall in the mountain, the river can flood, thus damaging the instruments. A variety of studies [14,20,72,73,74,75,76] have reported the disagreement between EC and LAS for H measurements. The reasons for such differences have been attributed to a variety of explanations, including the difference in the size and the heterogeneity of the EC and LAS source areas [5,63,77,78], the stability of the surface layer conditions [14,63], the sensitivity of the LAS to the aerodynamic roughness length [79], and the energy balance closure issues [5,63]. The sensible heat flux was measured directly with LAS, whereas the latent heat flux was estimated from the energy balance equation. Consequently, the accuracy of LE measured by LAS is ultimately limited by good quality Rn and G measurements, which are representative of the LAS footprint. In fact, the measurements of G are difficult and have relatively large errors because they depend on different factors, such as soil moisture, soil thermal properties, and vegetation canopy, which may have large spatial variability. Furthermore, Evans et al. [80] reported that the LE derived from LAS can be improved with the inclusion of the energy storage terms in the energy balance equation, but other driving parameters would be required that were not available at our study site.
3.2. Evaluation of Satellites Products
A comparison of the land surface temperature and albedo (α) derived from the remote sensing data and in situ measurements was carried out at the station scale. Figure 6a,b display the scatter plot of the in situ LST against those derived from Landsat 7/8 and MODIS satellites over both sites, respectively. The obtained statistical metrics clearly show that the LST derived from Landsat 7/8 are in good agreement with in situ measurements for both sites, despite a slight overestimation that is prominent at high values of LST (bias = 1.7 K for ECwest, bias = 2.8 K for ECeast). The RMSE and R² values were approximately the same for both sites and were about 4.5 K (4.4 K) and 0.93 (0.84) for ECwest (ECeast), respectively. These results are in accordance with those reported in the literature [9,10,81]. The overestimation of LST from Landsat can be explained by the mismatch between the Landsat resolution and the footprint of CNR4. The CNR4 radiometer has a much smaller footprint and was installed to get representative measurements of the canopy, while the 100 m pixel may “see” a larger part of bare soil surface exhibiting higher temperature. The observed overestimation occurring particularly during the senescence or after the harvest of seasonal corps like wheat supports this assumption. Likewise, LST from MODIS also shows a strong overestimation (bias = 6.6 K for ECwest, bias = 10.8 K for ECeast) with significant discrepancies compared to LST of Landsat for both sites. The RMSE and R² values are lower than for Landsat, but still acceptable, with about 8.2 K (9.1 K) and 0.77 (0.66) for ECwest (ECeast). In fact, these statistical metrics were expected, due to the large pixel size of MODIS (1 km) compared to the footprint of CNR4. The high values of MODIS LST can be explained by the large percentage of the bare soil in the observed pixel. However, the slightly better statistics obtained at ECwest in comparison to ECeast suggests a higher degree of homogeneity within the ECwest footprint. Figure 1 shows that the ECwest station is surrounded only by olive trees and wheat crops, while the surface around the ECeast station is a mix of several types of vegetation (apricot trees, plum trees, peach trees, alfalfa and wheat).
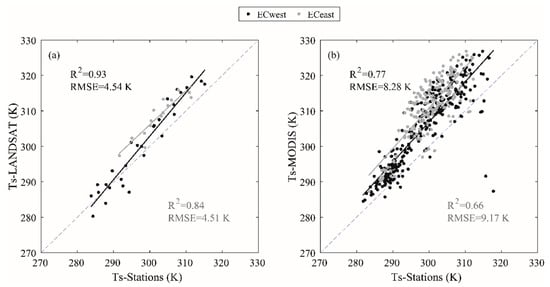
Figure 6.
Scatterplot of Landsat LST (a) and MODIS LST (b) versus in situ data.
Figure 7a,b show the comparison between the measured albedo and that derived from Landsat and MODIS. The statistical metrics show that the agreement between MODIS albedos and in situ measurements is relatively poor compared to the Landsat products, with a significant overestimation for both sites (RMSE = 0.04, R2 = 0.54 for ECwest and RMSE = 0.04, R2 = 0.03 for ECeast). As already underscored, this may be attributed to the lack of representativity of the in situ measurements, which covered relatively dense vegetation, unlike the pixel MODIS, which was mainly composed of bare soil. However, the high spatial resolution of Landsat values provides significantly better agreement with in situ measurements (RMSE=0.01, R2 = 0.51 for ECwest and RMSE = 0.003, R2 = 0.32 for ECeast). Another major issue that could explain the differences between Landsat and MODIS albedo is the fact that Landsat albedo is computed based on regression equations using field measurements, contrarily to MODIS. In addition, the assumption of the constant partition between direct and diffuse incoming radiation (85/15 in this study) may also alter the quality of the MODIS products. Interestingly enough, the range of values is more limited for ECeast than for ECwest. This may be attributed to a higher dynamic of land use on ECwest with large fraction of bare soil after wheat harvest that exhibit a higher range of albedo values in response to rainfall and vegetation completely covering the soil during the winter core.
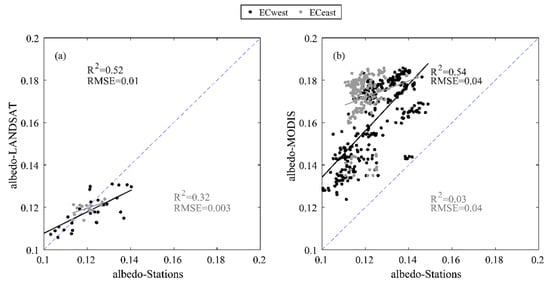
Figure 7.
Scatterplot of Landsat albedo (a) and MODIS albedo (b) versus in situ data.
3.3. TSEB Results
As a preliminary step, the TSEB predictions were evaluated at the EC scale. Focus was then placed on the evaluation of TSEB at the LAS scale using both Landsat- and MODIS-derived products. To this end, satellite images were used in combination with the analytical footprint models of LAS and EC systems to compute LST, albedo and emissivity inputs for TSEB using different options, namely high resolution (Landsat) and moderate resolution (MODIS).
3.3.1. Field Scale
The scatterplots between the predicted and the EC-measured components of the energy balance at the time of the satellite overpass are displayed in Figure 8, with inputs derived from Landsat data. Figure 9 is the same as Figure 8, but using MODIS products. Figure 10 displays the typical footprint of the LAS and of the EC station for prominent wind directions, superimposed on Landsat (Figure 10a) and MODIS (Figure 10b) images. Please note that in order to compare TSEB estimates with EC measurements, the model was run, on one hand, using Landsat data weighted using the EC footprint and, on the other hand, using MODIS data using the pixel value with the closest coordinates. The EC footprint was not used on MODIS data, since the spatial resolution is very high, and the value of each pixel is an average of 1 km, which could overestimate or underestimate the value of the model inputs on the surface covered by the footprint. The TSEB model correctly estimates the net radiation, especially when it is derived using Landsat data (Figure 8a) with RMSE of about 40.6 and 58.1 Wm−2 for ECwest and ECeast, respectively. By contrast, the estimation of net radiation is less reliable when it is computed with MODIS data (Figure 9a) as RMSE increased to about 78.1 and 90.8 Wm−2 for ECwest and ECeast, respectively. This result was expected, as the low spatial resolution of MODIS is unable to represent a local measurement, especially over heterogeneous surfaces (Figure 10). Additionally, the underestimation of at the eastern station is attributed to the observed overestimation of LST and albedo (Figure 6 and Figure 7). The performance of the TSEB model for predicting the soil heat flux was lower (Figure 8b and Figure 9b). Indeed, the soil heat flux was linearly related to the soil net radiation in the TSEB model, meaning that any difference between simulated and measured can be translated into a comparison of . Moreover, the soil heat flux is the most difficult variable of the energy budget to estimate. Several studies have pointed out the difficulty of comparing predicted to point-scale measurements, especially on sparse vegetation [21,23], because of surface heterogeneity and changing incoming radiation in relation to vegetation screening. In addition, measurements at 5 cm are difficult, because the plates must be totally covered to ensure that it is not directly exposed to the sunlight.
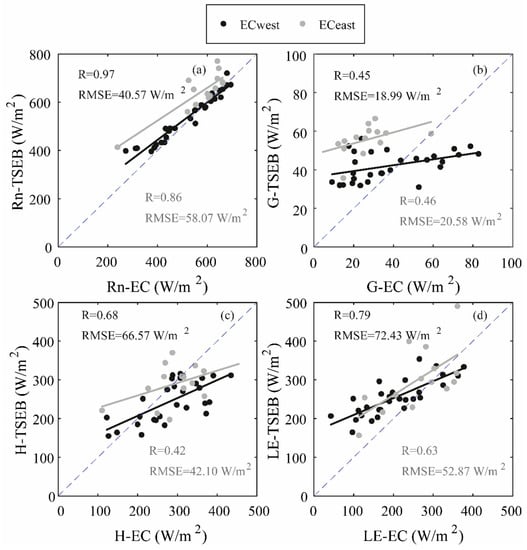
Figure 8.
Net radiation (a), soil heat flux (b), sensible heat flux (c) and latent heat flux (d), scatterplots of the comparison between the Eddy covariance measurements and TSEB predictions based on Landsat products at satellite overpass time.
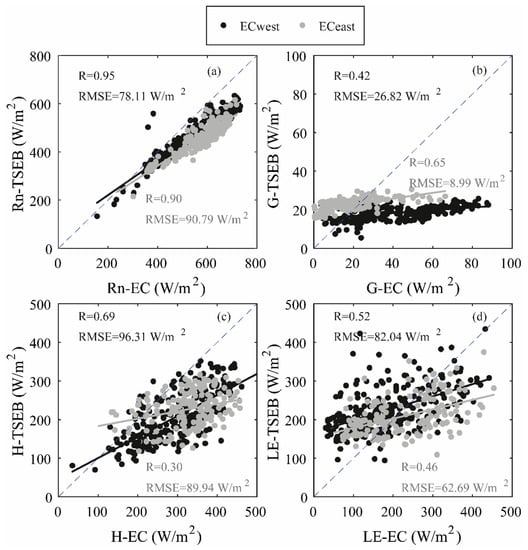
Figure 9.
Same as Figure 8 but for MODIS products.
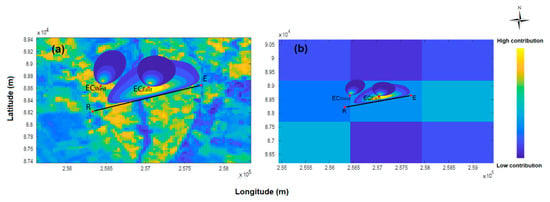
Figure 10.
Footprint of the LAS computed using the footprint model of Horst and Weil superimposed on a surface temperature images derived from Landsat (a) and MODIS (b).
Despite the significant dispersion, the correlation coefficients and RMSEs are encouraging for sensible flux (Figure 8c and Figure 9c). Even if RMSE are always lower for ECeast (66.6 Wm−2 versus 42.1 Wm−2 for ECwest and ECeast, respectively, for Landsat and 96.36 Wm−2 versus 89.96 Wm−2 for ECwest and ECeast, respectively, for MODIS), the temporal dynamic is much better for ECwest, as illustrated by the significant differences in terms of correlation coefficient (R = 0.68 versus R = 0.42 for ECwest and ECeast, respectively, for Landsat and R = 0.69 versus R = 0.30 for ECwest and ECeast, respectively, for MODIS). This is probably related to the heterogeneity level, as the ECeast is more heterogeneous than ECwest. In addition, other parameters, such as roughness length () and displacement height (d), which are used in the calculation of , are estimated as a fraction of the vegetation height ( = 0.14*hveg and d = 0.66*hveg following [22,82]). These equations have been established for homogeneous and dense covers while the study site is heterogeneous and sparse. Therefore, the use of these formulas may lead to an extra discrepancy between simulated and observed values. The latent heat flux values illustrated in Figure 8d and Figure 9d show a significant scatter, especially when TSEB is derived by MODIS data, which can be explained by the fact that is a residual term affected by errors in estimated , and . Furthermore, several model parameters have been used in the TSEB model, which require calibration according to the specific conditions of the study area; in particular, the Priestley-Taylor parameter, which relates the transpiration to the vegetation net radiation (Equation (14)). In this work, the Priestley-Taylor parameter is set to be constant throughout the study period because of the difficulty in calibrating it under such conditions. Generally speaking, previous studies have pointed out that it varies over time depending on surface and atmospheric conditions related, for instance, to water deficit, vegetation fraction, and advective conditions [10,21,81,82]. In contrast, TSEB driven by Landsat shows acceptable results on compared to the EC measurements (RMSE = 72.4 Wm−2 and R = 0.79 for ECwest and RMSE = 52.8 Wm−2 and R = 0.63 for ECeast). Agam et al. [83] found high errors in LE estimates using TSEB under low to moderate vapor water pressure deficit conditions (0 < VPD < 4), and they suggested that the reduction of the value of to a value under that taken usually (1.3) could be considered as a possible solution in order to reduce these errors. Colaizzi et al. [84] proposed a revised version of TSEB, replacing the Priestley-Taylor formulation with the Penman-Monteith equation in order to better account for large variations of vapor water pressure deficits and advection. Boulet et al. [33] thus built the SPARSE model based on Penman-Monteith, obtaining satisfying performances on several wheat sites in Morocco and Tunisia. Morillas et al. [85] reported that other factors different from those related to the Priestley-Taylor assumption could be causing the TSEB-derived LE errors. One of these factors is the fact that the TSEB estimates LE as a residual of the energy balance equation, biases from H, Rn, and G might accumulate in the LE estimates, and higher non-systematic errors could be expected [86], in addition to the errors in input values.
As a conclusion, while some dispersion is observed, TSEB is able to predict sensible and latent heat flux with reasonable accuracy at the station scale when it is forced by high-resolution inputs derived from Landsat. The best performance is obtained when the site is homogeneous. The question arises now as to how the model behaves with a heterogeneous landscape. To this end, several options for deriving TSEB inputs from Landsat and MODIS are evaluated in the next section.
3.3.2. Multi-Field Scale
To estimate convective fluxes at the landscape scale, two options for the key inputs variables of TSEB are compared: the simple approach consisting of using coarse-resolution MODIS products directly; and high-resolution Landsat variables weighted on the LAS footprint (Figure 10). Figure 11 shows the time series of the convective fluxes simulated by TSEB based on Landsat and on MODIS inputs superimposed with the LAS measurements at the time of the satellite’s overpasses (11:00 a.m.). TSEB predicted the seasonal course of sensible and latent heat fluxes correctly for both Landsat and MODIS options, but with a much smoother dynamic with MODIS, while with Landsat inputs, the predictions followed the day-to-day variability more closely. TSEB estimated the sensible and latent heat fluxes appropriately during the period from November 2016 to July 2017, especially when the model inputs were driven by Landsat with RMSE = 60.7 Wm−2 and R = 0.58 for sensible heat flux and RMSE = 68.0 Wm−2 and R = 0.69 for latent heat flux. By contrast, TSEB driven by MODIS generated obviously less reliable values for the same days of Landsat overpass with RMSE = 101.5 Wm−2 and R = 0.38 for sensible heat flux and RMSE = 99.8 Wm−2 and R = 0.38 for latent heat flux. This was expected, as Landsat products can take into consideration the contribution of each type of land use. TSEB became less consistent in the period from August 2017 to November 2017, which may be justified by the fact that Priestley-Taylor parameter is set to a constant value during the study period despite the variation in the green vegetation cover. Indeed, during this period, the fruit trees lose their leaves and wheat is harvested, while Priestley-Taylor used within TSEB assumes that plants transpire at their potential rate. Several studies have highlighted the trend of TSEB to overestimate [83,87], as observed after July 2017. During this period, change in the radiative properties (albedo) of the plants associated with senescence may also impact net radiation and, ultimately, evapotranspiration. Even if the number of available Landsat images after July 2017 is low, it seems that better predictions are obtained again when using Landsat than with MODIS.
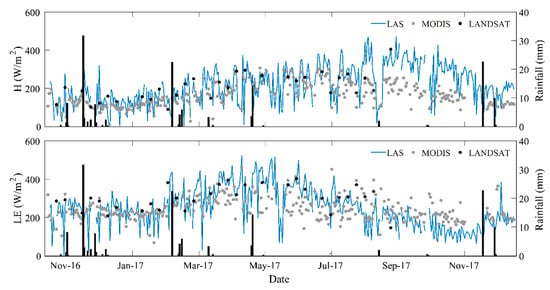
Figure 11.
Time series of the LAS convective flux measurements (H and LE) at 11:00 a.m. and TSEB predictions based on MODIS and Landsat products.
The reliability and the representativeness of the available energy values are very important in the evapotranspiration calculation with the LAS since is a residual term gathering errors linked to the other component measurements. Figure 12 displays the scatter plots between sensible heat flux and latent heat flux predicted by TSEB (driven by Landsat) and the LAS measurements as Figure 11, but using obtained from Landsat instead of the EC station. The comparison between TSEB based on Landsat inputs and LAS evapotranspiration using Landsat available energy led to a drastic drop in terms of RMSE (104.7 versus 68 Wm−2). The accuracy of the available energy was affected by errors with respect to surface temperature and albedo products. Figure 6a shows that Landsat overestimated the surface temperature, which led to an underestimation of the net radiation. Consequently, low net radiation values generate low values of evapotranspiration and higher RMSE. Additionally, the may be strongly affected by the error in , which is estimated here as 15% of the net radiation. Other methods have been tested for estimating such as [88,89,90], but they were less reliable (not shown). By contrast, the correlation coefficient R on is improved (0.75 versus 0.69). The results of the comparison for sensible heat was also slightly better with Landsat (RMSE of 58 Wm−2 versus 60.7 Wm−2 and R of 0.71 versus 0.58). We are aware that this is an indirect evaluation of choosing between station and Landsat , but the systematic improvement of correlation coefficients is an argument in favor of the choice of available energy computed with high-resolution remote sensing products such as Landsat. Stated differently, although the use of station inputs for AE may reduce bias, the better spatial representativeness of high-resolution products such as those derived from Landsat may improve the measured evapotranspiration dynamic. Finally, installing instruments such as CNR4, or NR01 from Campbell to measure net radiation and flux plates along the LAS path with an effective sampling strategy is complex and costly, while the use of high-resolution Landsat products may be a valuable option.
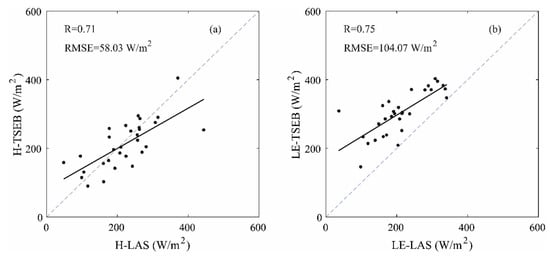
Figure 12.
Scatterplots between TSEB predictions H (a) and LE (b) based on Landsat and LAS measurements using available energy driven by Landsat.
4. Conclusions
In this investigation, the aim was to quantify the evapotranspiration of the agricultural landscape in mountainous areas. In this context, the energy balance TSEB model was evaluated for the first time in such terrain at a field and multi-field scale. For the multi-scale evaluation, a large-aperture scintillometer (LAS) was installed over a transect of about 1.4 km to measure the convective fluxes. Two eddy covariance systems were deployed over different sites along the LAS path. Firstly, a seasonal analysis and a comparison between convective fluxes measurements using LAS and EC were performed. The results show the accuracy of the LAS measurements in the mountain foothill region, where the calculation of the effective height of the path is extremely important. Then, the LAS and EC measurements were used to evaluate the performance of the thermal-based TSEB forced by Landsat and MODIS remote sensing products over semi-arid region. The remotely sensed inputs, including surface temperature, albedo and surface emissivity, were weighted using the LAS and EC footprint. The proposed approach can be considered acceptable for the estimation of the turbulent fluxes at large scale over heterogeneous landscape especially, with inputs derived at high spatial resolution from Landsat. By contrast, the agreement decreases when using MODIS inputs, which have a low-resolution incompatible with heterogeneous areas. In fact, the heterogeneous character of the study site and the uncertainties of the similarity stability functions over mountain regions strongly impact the estimation of turbulent fluxes. This study also gives some insight into experimental design for LAS measurements. Indeed, sampling net radiation and soil heat flux for available energy estimates along the LAS path is often complex and costly. It is shown in this study that available energy derived from Landsat provided a valuable option. Finally, TSEB model parameters rely on the strong assumption of plants transpiring at their potential rate through the Priestley Taylor parameterization. It is shown that under specific climate conditions such as highly changing land use, and are poorly reproduced. Ongoing work aims to evaluate the added value of the Penman-Monteith approach in place of the PT approximation as proposed by [84] in order to improve predictions under these specific conditions thanks to the use of the SPARSE model [33]. This study opens up new perspectives on the monitoring of convective fluxes over heterogeneous landscapes based on high-resolution satellite products, as well as monitoring irrigation and the groundwater level through simple water balance approach constrained by evapotranspiration estimates.
Author Contributions
Conceptualization, J.E.; Formal analysis, J.E.; Investigation, J.E.; Resources, S.R., A.B. and R.V.; Software, J.E. and B.A.H.; Supervision, J.E., S.E.-R. and L.J.; Validation, J.E., S.E.-R., B.A.H. and L.J.; Visualization, J.E.; Writing—original draft, J.E.; Writing—review & editing, J.E., S.E.-R., V.S., A.B., S.K., A.C. and L.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was carried out within the frame of the Joint International Laboratory TREMA (www.lmi-trema.ma). Setup was funded by CNRST SAGESSE project and German Cooperation Giz within the frame of the Hydraulic Basin Agency of the Tensift (ABHT). Additional funding was provided by the European Commission Horizon 2020 Programme for Research and Innovation (H2020) in the context of the Marie Sklodowska-Curie Research and Innovation Staff Exchange (RISE) action (REC project, grant agreement no: 645642). followed by ACCWA project, grant agreement no. 823965). PHC TBK/18/61 project is acknowledged for providing Jamal Elfarkh a travel grant. The authors wish to thank also the ERANETMED03-62 CHAAMS for partly funding the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. CRC Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.B.; Er-Raki, S.; Chehbouni, A.; Boulet, G.; Bonnefond, J.M.; De Bruin, H.A.R. The use of the scintillation technique for monitoring seasonal water consumption of olive orchards in a semi-arid region. Agric. Water Manag. 2007, 89, 173–184. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.C.B.; Chehbouni, A. On the application of scintillometry over heterogeneous grids. J. Hydrol. 2007, 334, 493–501. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Er-Raki, S.; Hanich, L. Combining a large aperture scintillometer and estimates of available energy to derive evapotranspiration over several agricultural fields in a semi-arid region. Plant Biosyst. 2009, 143, 209–221. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A.; Hoedjes, J.; Ramier, D.; Boulain, N.; Boubkraoui, S.; Cappelaere, B.; Descroix, L.; Mougenot, B.; Timouk, F. Combining scintillometer measurements and an aggregation scheme to estimate area-averaged latent heat flux during the AMMA experiment. J. Hydrol. 2009, 375, 217–226. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining satellite remote sensing data with the FAO-56 dual approach for water use mapping in irrigated wheat fields of a semi-arid region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef]
- Diarra, A.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Aouade, G.; Tavernier, A.; Boulet, G.; Ezzahar, J.; Merlin, O.; Khabba, S. Performance of the two-source energy budget (TSEB) model for the monitoring of evapotranspiration over irrigated annual crops in North Africa. Agric. Water Manag. 2017, 193, 71–88. [Google Scholar] [CrossRef]
- Hssaine, B.A.; Merlin, O.; Rafi, Z.; Ezzahar, J.; Jarlan, L.; Khabba, S.; Er-Raki, S. Calibrating an evapotranspiration model using radiometric surface temperature, vegetation cover fraction and near-surface soil moisture data. Agric. For. Meteorol. 2018, 256–257, 104–115. [Google Scholar] [CrossRef]
- Rafi, Z.; Merlin, O.; Le Dantec, V.; Khabba, S.; Mordelet, P.; Er-Raki, S.; Amazirh, A.; Olivera-Guerra, L.; Ait Hssaine, B.; Simonneaux, V.; et al. Partitioning evapotranspiration of a drip-irrigated wheat crop: Inter-comparing eddy covariance-, sap flow-, lysimeter- and FAO-based methods. Agric. For. Meteorol. 2019, 265, 310–326. [Google Scholar] [CrossRef]
- Lee, X.; Finnigan, J.; Paw U, K.T. Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Springer: Berlin, Germany, 2005; Volume 29, pp. 33–66. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Zeweldi, D.A.; Gebremichael, M.; Wang, J.; Sammis, T.; Kleissl, J.; Miller, D. Intercomparison of sensible heat flux from large aperture scintillometer and eddy covariance methods: Field experiment over a homogeneous semi-arid region. Bound.-Layer Meteorol. 2010, 135, 151–159. [Google Scholar] [CrossRef]
- Vesala, T.; Eugster, W.; Ojala, A. Eddy Covariance Measurements over Lakes. In Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer: Berlin, Germany, 2012; pp. 365–376. [Google Scholar] [CrossRef]
- Odhiambo, G.O.; Savage, M.J. Sensible heat flux by surface layer scintillometry and eddy covariance over a mixed grassland community as affected by Bowen ratio and MOST formulations for unstable conditions. J. Hydrometeorol. 2009, 10, 479–492. [Google Scholar] [CrossRef]
- Jacobs, C.; Elbers, J.; Brolsma, R.; Hartogensis, O.; Moors, E.; Rodríguez-Carretero Márquez, M.T.; van Hove, B. Assessment of evaporative water loss from Dutch cities. Build. Environ. 2015, 83, 27–38. [Google Scholar] [CrossRef]
- Crawford, B.; Grimmond, C.S.B.; Ward, H.C.; Morrison, W.; Kotthaus, S. Spatial and temporal patterns of surface–atmosphere energy exchange in a dense urban environment using scintillometry. Q. J. R. Meteorol. Soc. 2017, 143, 817–833. [Google Scholar] [CrossRef]
- Rotach, M.W.; Stiperski, I.; Fuhrer, O.; Goger, B.; Gohm, A.; Obleitner, F.; Rau, G.; Sfyri, E.; Vergrgeiner, J. Investigating exchange processes over complex topography: The Innsbruck box (i-Box). Bull. Am. Meteorol. Soc. 2017, 98, 787–805. [Google Scholar] [CrossRef]
- Duchemin, B.; Hagolle, O.; Mougenot, B.; Benhadj, I.; Hadria, R.; Simonneaux, V.; Ezzahar, J.; Hoedjes, J.; Khabba, S.; Kharrou, M.H.; et al. Agrometerological study of semi-ard areas: An experiment for analysing the potential of time series of FORMOSAT-2 images (Tensift-Marrakech plain). Int. J. Remote Sens. 2008, 29, 5291–5300. [Google Scholar] [CrossRef]
- Hssaine, B.A.; Ezzahar, J.; Jarlan, L.; Merlin, O.; Khabba, S.; Brut, A.; Er-Raki, S.; Elfarkh, J.; Cappelaere, B.; Chehbouni, G. Combining a two source energy balance model driven by MODIS and MSG-SEVIRI products with an aggregation approach to estimate turbulent fluxes over sparse and heterogeneous vegetation in Sahel region (Niger). Remote Sens. 2018, 10, 974. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Chehbouni, A.; Ezzahar, J.; Escadafal, R.; De Bruin, H.A.R. Comparison of Large Aperture Scintillometer and Eddy Covariance Measurements: Can Thermal Infrared Data Be Used to Capture Footprint-Induced Differences? J. Hydrometeorol. 2007, 8, 144–159. [Google Scholar] [CrossRef]
- Ezzahar, J.; Chehbouni, A. The use of scintillometry for validating aggregation schemes over heterogeneous grids. Agric. For. Meteorol. 2009, 149, 2098–2109. [Google Scholar] [CrossRef]
- Saadi, S.; Boulet, G.; Bahir, M.; Brut, A.; Delogu, É.; Fanise, P.; Mougenot, B.; Simonneaux, V.; Chabaane, Z.L. Assessment of actual evapotranspiration over a semiarid heterogeneous land surface by means of coupled low-resolution remote sensing data with an energy balance model: Comparison to extra-large aperture scintillometer measurements. Hydrol. Earth Syst. Sci. 2018, 22, 2187–2209. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, Z.; Zhong, L.; Wang, B.; Han, C.; Wang, Z.; Wang, Y.; Lu, L.; Amatya, P.M.; Ma, W.; et al. Combining MODIS, AVHRR and in situ data for evapotranspiration estimation over heterogeneous landscape of the Tibetan Plateau. Atmos. Chem. Phys. 2014, 14, 1507–1515. [Google Scholar] [CrossRef]
- Song, L.; Liu, S.; Zhang, X.; Zhou, J.; Li, M. Estimating and validating soil evaporation and crop transpiration during the HiWATER-MUSOEXE. IEEE Geosci. Remote Sens. Lett. 2015, 12, 334–338. [Google Scholar] [CrossRef]
- Castelli, M.; Anderson, M.C.; Yang, Y.; Wohlfahrt, G.; Bertoldi, G.; Niedrist, G.; Hammerle, A.; Zhao, P.; Zebisch, M.; Notarnicola, C. Two-source energy balance modeling of evapotranspiration in Alpine grasslands. Remote Sens. Environ. 2018, 209, 327–342. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.J.; Robison, C.W. Journal of Irrigation and Drainage Engineering Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)— Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van Der Wal, T. A remote sensing surface energy balance algorithm for land (SEBAL): 2. Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef]
- Anderson, M.; Kustas, W. Thermal Remote Sensing of Drought and Evapotranspiration.pdf. Eos Trans. Am. Geophys. Union 2008, 89, 233–240. [Google Scholar] [CrossRef]
- Choi, M.; Kustas, W.P.; Anderson, M.C.; Allen, R.G.; Li, F.; Kjaersgaard, J.H. An intercomparison of three remote sensing-based surface energy balance algorithms over a corn and soybean production region (Iowa, U.S.) during SMACEX. Agric. For. Meteorol. 2009, 149, 2082–2097. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; McCabe, M.F.; Li, F.; et al. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) at the Iowa 2002 SMACEX site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Jia, Y.; Li, C.; Sun, X.; Kustas, W.P.; Anderson, M.C. An intercomparison of three remote sensing-based energy balance models using Large Aperture Scintillometer measurements over a wheat-corn production region. Remote Sens. Environ. 2011, 115, 3187–3202. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L. An End-Member-Based Two-Source Approach for Estimating Land Surface Evapotranspiration from Remote Sensing Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5818–5832. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ. 1997, 60, 195–216. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Bhattacharya, B.K.; Crébassol, P.; Gamet, P.; Babu, S.S.; Boulet, G.; Briottet, X.; Buddhiraju, K.M.; Cherchali, S.; Dadou, I.; et al. The Indian-French Trishna mission: Earth observation in the thermal infrared with high spatio-temporal resolution. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 4078–4081. [Google Scholar]
- Hartogensis, O.K.; Watts, C.J.; Rodriguez, J.-C.; De Bruin, H.A.R. Derivation of an Effective Height for Scintillometers: La Poza Experiment in Northwest Mexico. J. Hydrometeorol. 2003, 4, 915–928. [Google Scholar] [CrossRef]
- Wesely, M.L. Combined effect of temperature and humidity fluctuations on refractive index. J. Appl. Meteorol. 1976, 15, 43–49. [Google Scholar] [CrossRef]
- Solignac, P.A.; Brut, A.; Selves, J.-L.; Béteille, J.-P.; Gastellu-Etchegorry, J.-P.; Keravec, P.; Béziat, P.; Ceschia, E. Uncertainty analysis of computational methods for deriving sensible heat flux values from scintillometer measurements. Atmos. Meas. Tech. 2009, 2, 741–753. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Kohsiek, W.; Van Den Hurk, B.J.J.M. A verification of some methods to determine the fluxes of momentum, sensible heat, and water vapour using standard deviation and structure parameter of scalar meteorological quantities. Bound.-Layer Meteorol. 1993, 53, 231–257. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Jensen, N.O.; Jackson, P.S. Introduction to wind characteristics: Flow over hills and ridges. In Wind Engineering 1983; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the atmosphere. Theory, history, and applications; Springer: Dordrecht, The Netherlands, 1982; pp. 1223–1224. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J.C. Footprint estimation for scalar flux measurements in the atmospheric surface layer. Bound.-Layer Meteorol. 1992, 59, 279–296. [Google Scholar] [CrossRef]
- Horst, T.W.; Weil, J.C. How far is far enough? The fetch requirements for micrometeorological measurement of surface fluxes. J. Atmos. Ocean. Technol. 1994, 11, 1018–1025. [Google Scholar] [CrossRef]
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Bound.-Layer Meteorol. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Rannik, U.; Aubinet, M.; Kurbanmuradov, O.; Sabelfeld, K.K.; Markkanen, T.; Vesala, T. Footprint analysis for measurements over a heterogeneous forest. Bound.-Layer Meteorol. 2000, 97, 137–166. [Google Scholar] [CrossRef]
- Meijninger, W.M.L. Surface Fluxes over Natural Landscapes Using Scintillometry; Wageningen UR Publication: Wageningen, The Netherlands, 2003; pp. 1–176. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Román, M.O.; Schaaf, C.B.; Lewis, P.; Gao, F.; Anderson, G.P.; Privette, J.L.; Strahler, A.H.; Woodcock, C.E.; Barnsley, M. Assessing the coupling between surface albedo derived from MODIS and the fraction of diffuse skylight over spatially-characterized landscapes. Remote Sens. Environ. 2010, 114, 738–760. [Google Scholar] [CrossRef]
- Wittich, K.P. Some simple relationships between land-surface emissivity, greenness and the plant cover fraction for use in satellite remote sensing. Int. J. Biometeorol. 1997, 41, 58–64. [Google Scholar] [CrossRef]
- Tardy, B.; Rivalland, V.; Huc, M.; Hagolle, O.; Marcq, S.; Boulet, G. A software tool for atmospheric correction and surface temperature estimation of Landsat infrared thermal data. Remote Sens. 2016, 8, 696. [Google Scholar] [CrossRef]
- Courault, D.; Bsaibes, A.; Kpemlie, E.; Hadria, R.; Hagolle, O.; Marloie, O.; Hanocq, J.F.; Olioso, A.; Bertrand, N.; Desfonds, V. Assessing the potentialities of FORMOSAT-2 data for water and crop monitoring at small regional scale in South-Eastern France. Sensors 2008, 8, 3460–3481. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Mauder, M.; Liebethal, C.; Göckede, M.; Leps, J.P.; Beyrich, F.; Foken, T. Processing and quality control of flux data during LITFASS-2003. Bound.-Layer Meteorol. 2006, 121, 67–88. [Google Scholar] [CrossRef]
- Finnigan, J.J.; Clement, R.; Malhi, Y.; Leuning, R.; Cleugh, H.A. Re-evaluation of long-term flux measurement techniques. Part I: Averaging and coordinate rotation. Bound.-Layer Meteorol. 2003, 107, 1–48. [Google Scholar] [CrossRef]
- Gash, J.H.C.; Dolman, A.J. Sonic anemometer (co)sine response and flux measurement. Agric. For. Meteorol. 2003, 119, 195–207. [Google Scholar] [CrossRef]
- Nakai, T.; Van Der Molen, M.K.; Gash, J.H.C.; Kodama, Y. Correction of sonic anemometer angle of attack errors. Agric. For. Meteorol. 2006, 136, 19–30. [Google Scholar] [CrossRef]
- Van Der Molen, M.K.; Gash, J.H.C.; Elbers, J.A. Sonic anemometer (co)sine response and flux measurement: II. The effect of introducing an angle of attack dependent calibration. Agric. For. Meteorol. 2004, 122, 95–109. [Google Scholar] [CrossRef]
- Chehbouni, A.; Ezzahar, J.; Watts, C.J.; Garatuza-Payan, J. Estimating area-averaged surface fluxes over contrasted agricultural patchwork in a semi-arid region. In Recent Advances in Remote Sensing and Geoinformation Processing for Land Degradation Assessment; CRC Press: Boca Raton, FL, USA, 2009; pp. 73–86. [Google Scholar] [CrossRef]
- Anthoni, P.M.; Lae, B.E.; Unsworth, M.H.; Vong, R.J. Variation of net radiation over heterogeneous surfaces: Measurements and simulation in a juniper-sagebrush ecosystem. Agric. For. Meteorol. 2000, 102, 275–289. [Google Scholar] [CrossRef]
- Kleissl, J.; Gomez, J.; Hong, S.H.; Hendrickx, J.M.H.; Rahn, T.; Defoor, W.L. Large aperture scintillometer intercomparison study. Bound.-Layer Meteorol. 2008, 128, 133–150. [Google Scholar] [CrossRef]
- Chehbouni, A.; Kerr, Y.H.; Dedieu, G.; Cayrol, P.; Boulet, G.; Lagouarde, J.P.; Goodrich, D.; Moran, S.M.; Nouvellon, Y.; Watts, C.; et al. Synthèse des découvertes et des principaux résultats scientifiques obtenus pendant le programme SALSA. AMA 1999, 19, 285–288. [Google Scholar]
- Liu, S.M.; Xu, Z.W.; Zhu, Z.L.; Jia, Z.Z.; Zhu, M.J. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Samain, B.; Ferket, B.V.A.; Defloor, W.; Pauwels, V.R.N. Estimation of catchment averaged sensible heat fluxes using a large aperture scintillometer. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H. Comparison of Turbulent Sensible Heat Flux Determined by Large-Aperture Scintillometer and Eddy Covariance over Urban and Suburban Areas. Bound.-Layer Meteorol. 2015, 154, 119–136. [Google Scholar] [CrossRef]
- Schüttemeyer, D.; Moene, A.F.; Holtslag, A.A.M.; de Bruin, H.A.R.; van de Giesen, N. Surface fluxes and characteristics of drying semi-arid terrain in West Africa. Bound.-Layer Meteorol. 2006, 118, 583–612. [Google Scholar]
- Griebel, A.; Bennett, L.T.; Metzen, D.; Cleverly, J.; Burba, G.; Arndt, S.K. Effects of inhomogeneities within the flux footprint on the interpretation of seasonal, annual, and interannual ecosystem carbon exchange. Agric. For. Meteorol. 2016, 221, 50–60. [Google Scholar] [CrossRef]
- Su, Z.; Timmermans, W.J.; Van Der Tol, C.; Dost, R.; Bianchi, R.; Gómez, J.A.; House, A.; Hajnsek, I.; Menenti, M.; Magliulo, V.; et al. EAGLE 2006 - Multi-purpose, multi-angle and multi-sensor in-situ and airborne campaigns over grassland and forest. Hydrol. Earth Syst. Sci. 2009, 13, 833–845. [Google Scholar] [CrossRef]
- Evans, J.G.; McNeil, D.D.; Finch, J.W.; Murray, T.; Harding, R.J.; Ward, H.C.; Verhoef, A. Determination of turbulent heat fluxes using a large aperture scintillometer over undulating mixed agricultural terrain. Agric. For. Meteorol. 2012, 166–167, 221–233. [Google Scholar] [CrossRef]
- Blyth, E.; Gash, J.; Lloyd, A.; Pryor, M.; Weedon, G.P.; Shuttleworth, J. Evaluating the JULES land surface model energy fluxes using FLUXNET data. J. Hydrometeorol. 2010, 11, 509–519. [Google Scholar] [CrossRef]
- Napoly, A.; Boone, A.; Samuelsson, P.; Gollvik, S.; Martin, E.; Seferian, R.; Carrer, D.; Decharme, B.; Jarlan, L. The interactions between soil-biosphere-atmosphere (ISBA) land surface model multi-energy balance (MEB) option in SURFEXv8 - Part 2: Introduction of a litter formulation and model evaluation for local-scale forest sites. Geosci. Model Dev. 2017, 10, 1621–1644. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Colaizzi, P.D.; Howell, T.A.; Prueger, J.H.; Meyers, T.P.; Wilson, T.B. Application of the priestley-taylor approach in a two-source surface energy balance model. J. Hydrometeorol. 2010, 11, 185–198. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A.; Kustas, W.P.; Anderson, M.C. Two-source energy balance model to calculate E, T, and ET: Comparison of priestley-taylor and penman-monteith formulations and two time scaling methods. Trans. ASABE 2014, 57, 479–498. [Google Scholar]
- Morillas, L.; Leuning, R.; Villagarcía, L.; García, M.; Serrano-Ortiz, P.; Domingo, F. Improving evapotranspiration estimates in Mediterranean drylands: The role of soil evaporation. Water Resour. Res. 2013, 49, 6572–6586. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. Regionalization of Surface Flux Densities and Moisture Indicators in Composite Terrain: A Remote Sensing Approach under Clear Skies in Mediterranean Climates. Ph.D. Thesis, Wageningen Agricultural University, Wageningen, The Netherlands, 1995; p. 273. [Google Scholar]
- Choudhury, B.J. Relationships between vegetation indices, radiation absorption, and net photosynthesis evaluated by a sensitivity analysis. Remote Sens. Environ. 1987, 22, 209–233. [Google Scholar] [CrossRef]
- Jackson, R.D.; Moran, M.S.; Gay, L.W.; Raymond, L.H. Evaluating evaporation from field crops using airborne radiometry and ground-based meteorological data. Irrig. Sci. 1987, 8, 81–90. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).