Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification
Abstract
1. Introduction
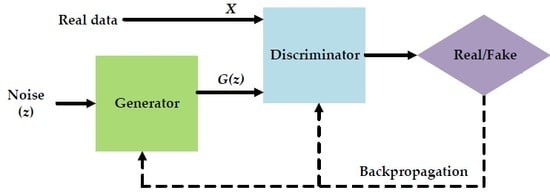
2. Generative Adversarial Networks
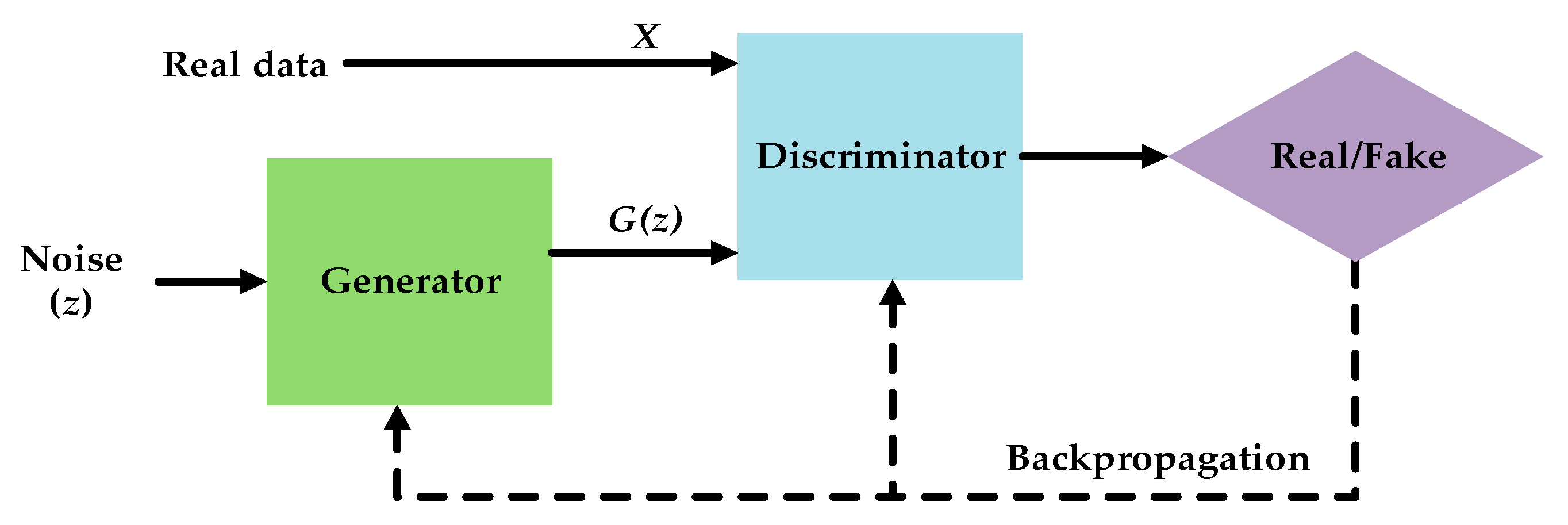
3. The Proposed CA-GAN Method
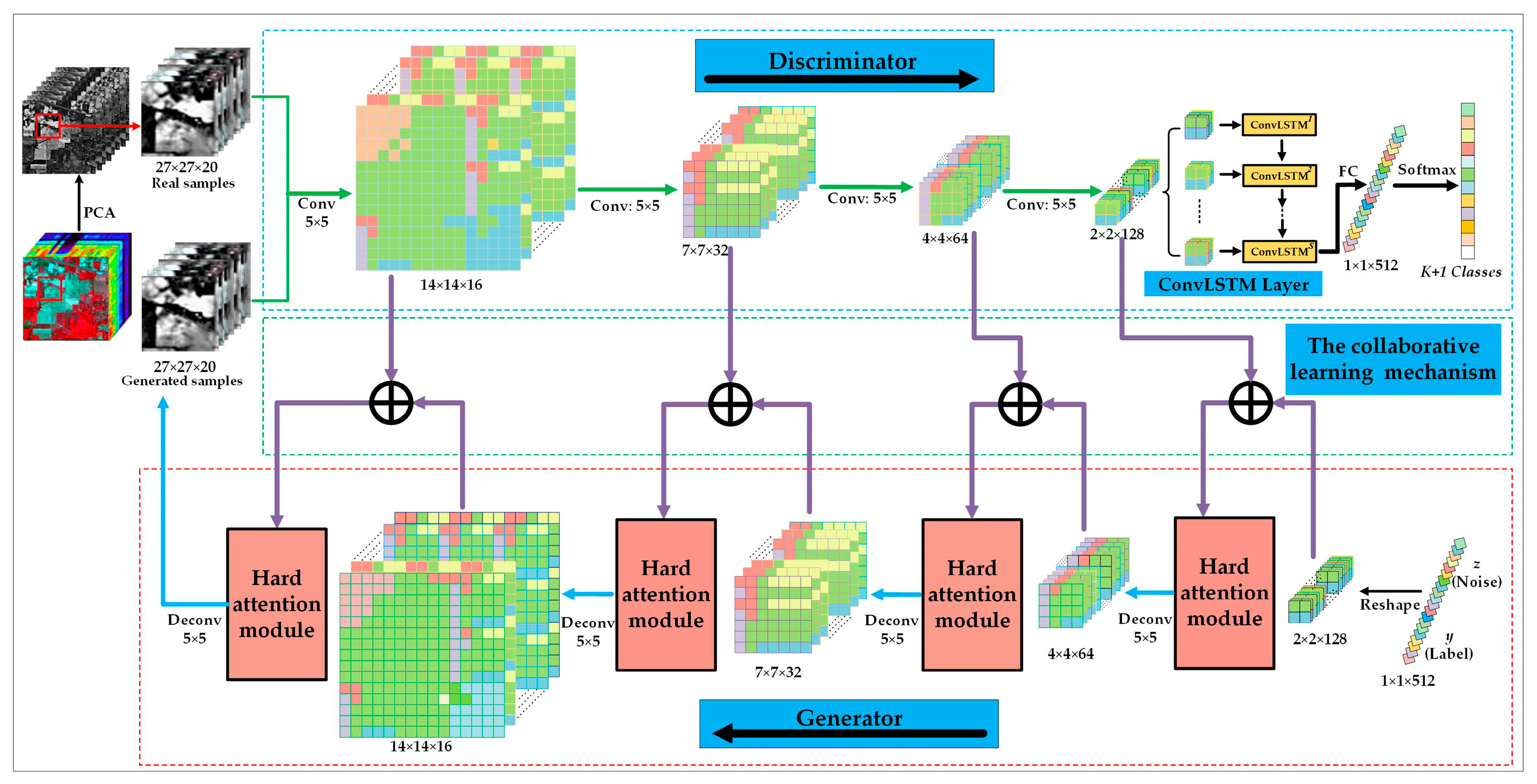
3.1. The Generator in CA-GAN Based on Joint Spatial–Spectral Hard Attention Module
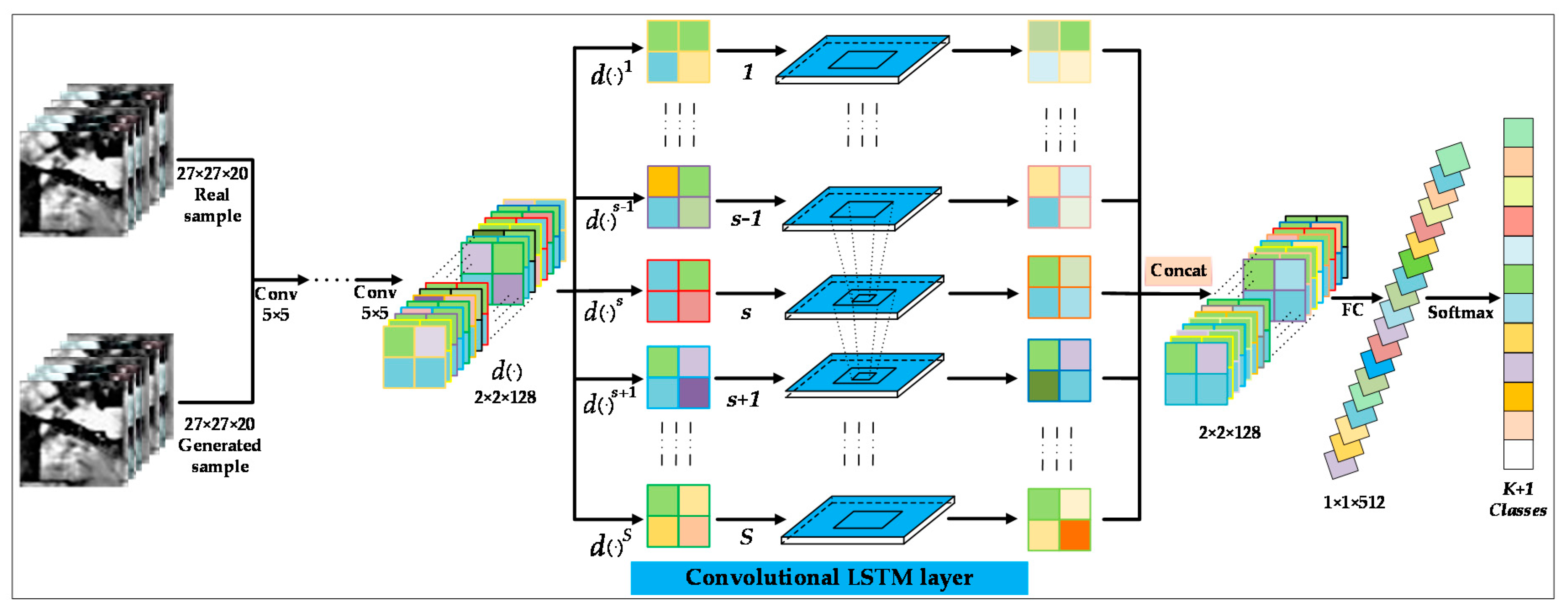
3.2. The Discriminator in CA-GAN Based on Convolutional LSTM for Joint Spatial–Spectral Feature Extraction
3.3. Classification of CA-GAN Based on Collaborative and Competitive Learning
3.4. The Procedure of CA-GAN
4. Experimental Results
4.1. Data Description
4.2. Experimental Setting
4.3. Experimental Results
4.4. Analysis on Running Time
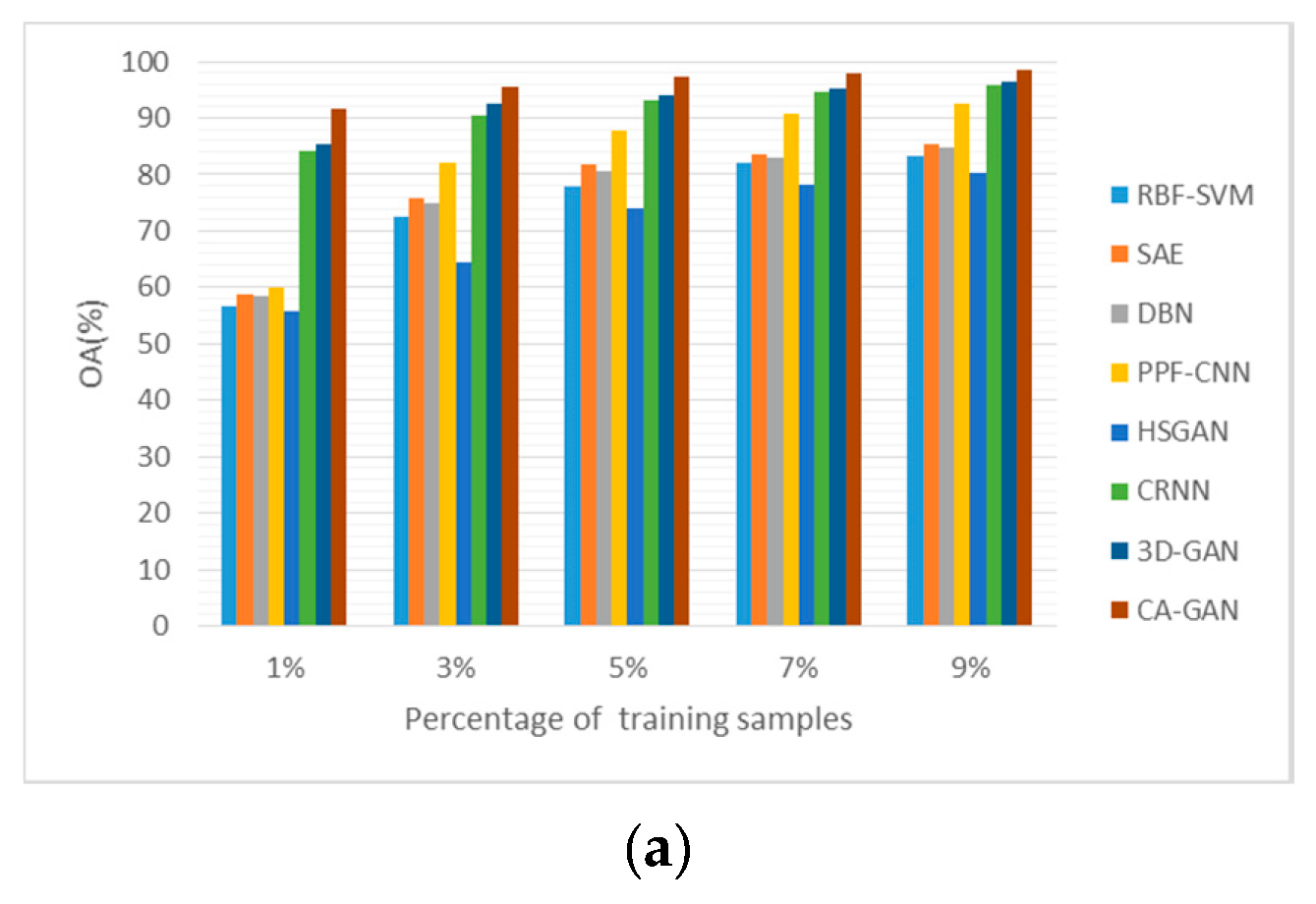
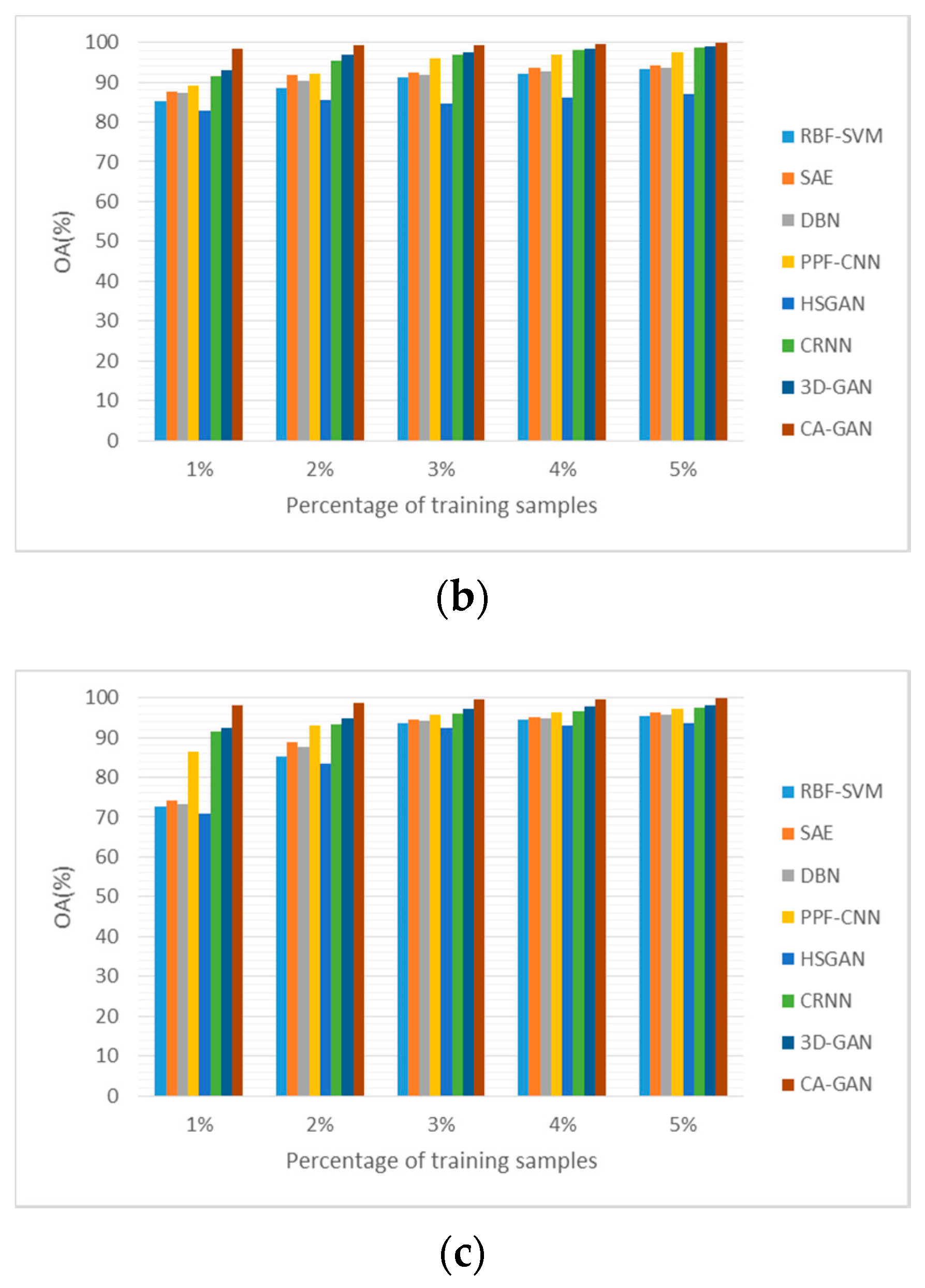
4.5. Sensitivity to the Proportion of Training Samples
4.6. Influence of Different Number of Principle Components in CA-GAN
4.7. Effectiveness of Each Step in CA-GAN
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, C.I. Hyperspectral Data Exploitation: Theory and Applications; Wiley: Hoboken, NJ, USA, 2007; pp. 441–442. [Google Scholar]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A survey of landmine detection using hyperspectral imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of spectral-temporal response surfaces by combining multispectral satellite and hyperspectral UAV imagery for precision agriculture applications. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Brown, A.J.; Walter, M.R.; Cudahy, T.J. Hyperspectral imaging spectroscopy of a Mars analogue environment at the North Pole Dome, Pilbara Craton, Western Australia. Austral. J. Earth Sci. 2005, 52, 353–364. [Google Scholar] [CrossRef]
- Kang, X.D.; Xiang, X.L.; Li, S.T.; Benediktsson, J.A. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L.; Zhang, L. Dimensionality reduction and classification of hyperspectral images using ensemble discriminative local metric learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2509–2524. [Google Scholar] [CrossRef]
- Chen, P.; Jiao, L.; Liu, F.; Gou, S.; Zhao, J.; Zhao, Z. Dimensionality reduction of hyperspectral imagery using sparse graph learning. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2017, 10, 1165–1181. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, T.; Jia, X.; Benediktsson, J.A.; Chanussot, J. Nonlinear multiple kernel learning with multiple-structure-element extended morphological profiles for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3235–3247. [Google Scholar] [CrossRef]
- Xue, Z.; Li, J.; Cheng, L.; Du, P. Spectral-spatial classification of hyperspectral data via morphological component analysis-based image separation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 70–84. [Google Scholar]
- Jia, S.; Zhang, X.; Li, Q. Spectral-Spatial Hyperspectral Image Classification Using Regularized Low-Rank Representation and Sparse Representation-Based Graph Cuts. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 2473–2484. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral-spatial information of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral-spatial classification of hyperspectral images with a superpixel-based discriminative sparse model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Wei, Z.; Xiao, L.; Sun, L. Spatial-spectral kernel sparse representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2462–2471. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Haest, B.; Spanhove, T.; Borre, J.V.; Mücher, C.A. Heathland conservation status mapping through integration of hyperspectral mixture analysis and decision tree classifiers. Remote Sens. 2012, 126, 222–231. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Gualtieriand, J.A.; Chettri, S. Support vector machines for classification of hyperspectral data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; pp. 813–815. [Google Scholar]
- Zhong, S.; Chang, C.I.; Zhang, Y. Iterative Support Vector Machine for Hyperspectral Image Classification. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 3309–3312. [Google Scholar]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Jia, K.; Sun, L.; Gao, S.; Song, Z.; Shi, B.E. Laplacian auto-encoders: An explicit learning of nonlinear data manifold. Neurocomputing 2015, 160, 250–260. [Google Scholar] [CrossRef]
- Zabalza, J.; Ren, J.; Zheng, J.; Zhao, H.; Qing, C.; Yang, Z.; Marshall, S. Novel segmented stacked autoencoder for effective dimensionality reduction and feature extraction in hyperspectral imaging. Neurocomputer 2016, 185, 1–10. [Google Scholar] [CrossRef]
- Zhou, P.; Han, J.; Cheng, G.; Zhang, B. Learning compact and discriminative stacked autoencoder for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4823–4833. [Google Scholar] [CrossRef]
- Chen, Y.S.; Zhao, X.; Jia, X. Spectral-spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.B. Learning to diversify deep belief networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Ghassemi, M.; Ghassemian, H.; Imani, M. Deep Belief Networks for Feature Fusion in Hyperspectral Image Classification. In Proceedings of the IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 20–21 September 2018; pp. 1–6. [Google Scholar]
- Mughees, A.; Tao, L. Multiple deep-belief-network-based spectral-spatial classification of hyperspectral images. Tsinghua Sci. Technol. 2018, 24, 183–194. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef]
- Chen, Y.S.; Jiang, H.L.; Li, C.Y. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral image classification with deep feature fusion network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Reed, S.; Akata, Z.; Yan, X.; Logeswaran, L.; Schiele, B.; Lee, H. Generative adversarial text-to-image synthesis. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Mathieu, M.; Couprie, C.; LeCun, Y. Deep multi-scale video prediction beyond mean square error. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Che, T.; Li, Y.; Zhang, R.; Hjelm, R.D.; Li, W.; Song, Y.; Bengio, Y. Maximum-likelihood augmented discrete generative adversarial networks. arXiv 2017, arXiv:1702.07983. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34 th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of Wasserstein GANs. In Proceedings of the Advances in Neural Information Processing Systems. (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5769–5779. [Google Scholar]
- Zhao, J.; Mathieu, M.; LeCun, Y. Energy-based generative adversarial network. In Proceedings of the International Conference on Learning Representations. (ICLR), Toulon, France, 24–26 April 2017; pp. 1–17. [Google Scholar]
- Wang, D.; Vinson, R.; Holmes, M.; Seibel, G.; Bechar, A.; Nof, S.; Tao, Y. Early Tomato Spotted Wilt Virus Detection using Hyperspectral Imaging Technique and Outlier Removal Auxiliary Classifier Generative Adversarial Nets (OR-AC-GAN). In 2018 ASABE Annual International Meeting; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2018; p. 1. [Google Scholar]
- Ma, D.; Tang, P.; Zhao, L. SiftingGAN: Generating and sifting labeled samples to improve the remote sensing image scene classification baseline in vitro. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1046–1050. [Google Scholar] [CrossRef]
- Denton, E.; Chintala, S.; Szlam, A.; Fergus, R. Deep generative image models using a laplacian pyramid of adversarial networks. arXiv 2015, arXiv:1506.05751. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. In Proceedings of the International Conference on Learning Representations ICLR, Toulon, France, 20 January 2016; pp. 1–16. [Google Scholar]
- Durugkar, I.; Gemp, I.; Mahadevan, S. Generative multi-adversarial networks. In Proceedings of the International Conference on Learning Representations. (ICLR), Toulon, France, 24–26 April 2017; pp. 1–14. [Google Scholar]
- Neyshabur, B.; Bhojanapalli, S.; Chakrabarti, A. Stabilizing GAN Training With Multiple Random Projections. arXiv 2017, arXiv:1705.07831. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training GANs. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2234–2242. [Google Scholar]
- Zhong, Z.; Li, J.; Clausi, D.A.; Wong, A. Generative adversarial networks and conditional random fields for hyperspectral image classification. IEEE Trans. Cybernetics 2019, 1–12. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative adversarial networks-based semi-supervised learning for hyperspectral image classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef]
- Zhan, Y.; Hu, D.; Wang, Y.; Yu, X. Semisupervised hyperspectral image classification based on generative adversarial networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 212–216. [Google Scholar] [CrossRef]
- Zhan, Y.; Wu, K.; Liu, W.; Qin, J.; Yang, Z.; Medjadba, Y.; Yu, X. Semi-supervised classification of hyperspectral data based on generative adversarial networks and neighborhood majority voting. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5756–5759. [Google Scholar]
- Zhan, Y.; Qin, J.; Huang, T.; Wu, K.; Hu, D.; Zhao, Z.; Wang, G. Hyperspectral Image Classification Based on Generative Adversarial Networks with Feature Fusing and Dynamic Neighborhood Voting Mechanism. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 811–814. [Google Scholar]
- Gao, H.; Yao, D.; Wang, M.; Li, C.; Liu, H.; Hua, Z.; Wang, J. A Hyperspectral Image Classification Method Based on Multi-Discriminator Generative Adversarial Networks. Sensors 2019, 19, 3269. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative adversarial networks for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Feng, J.; Yu, H.; Wang, L.; Cao, X.; Zhang, X.; Jiao, L. Classification of Hyperspectral Images Based on Multiclass Spatial-Spectral Generative Adversarial Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5329–5343. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems: Annual Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]


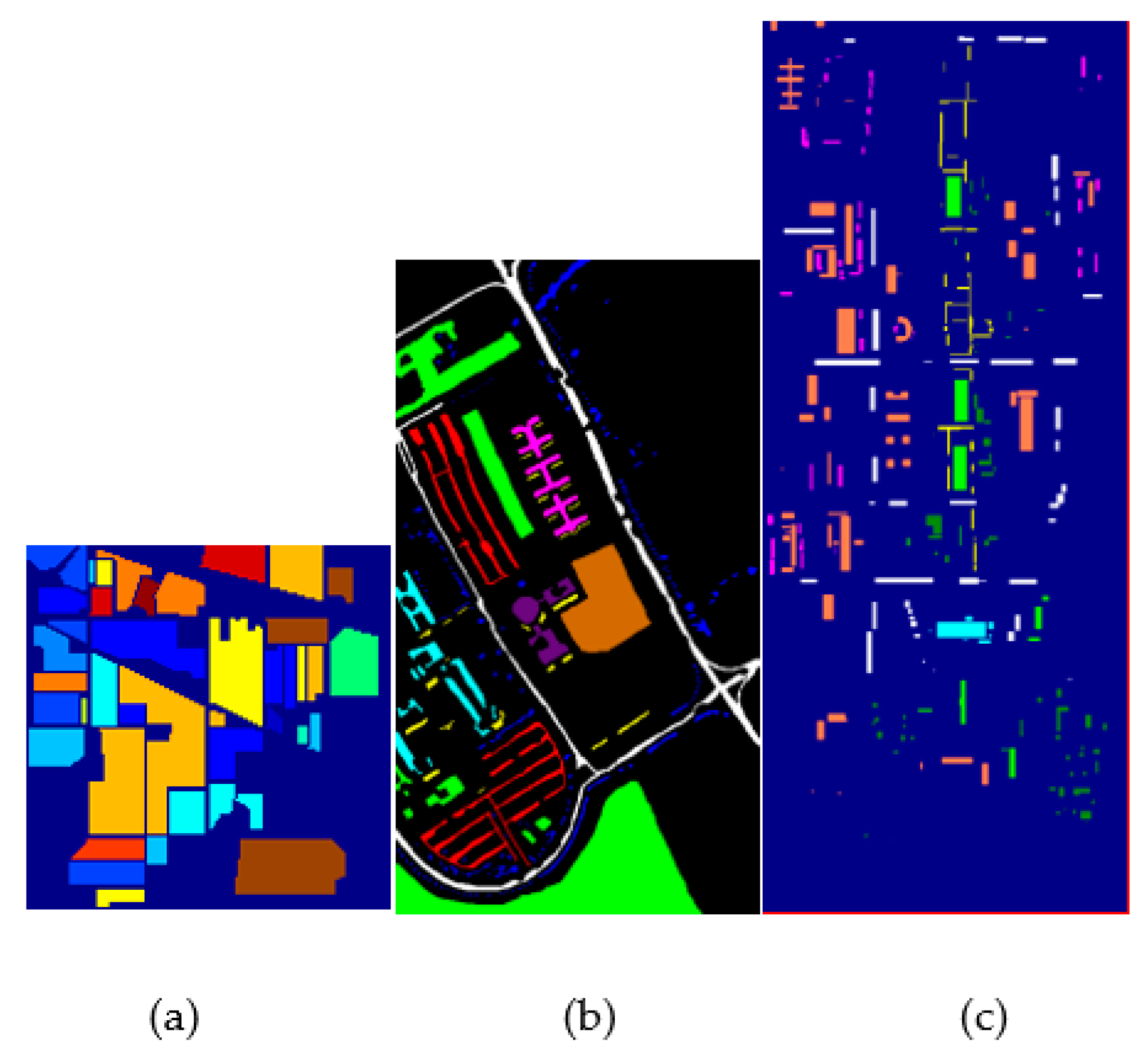
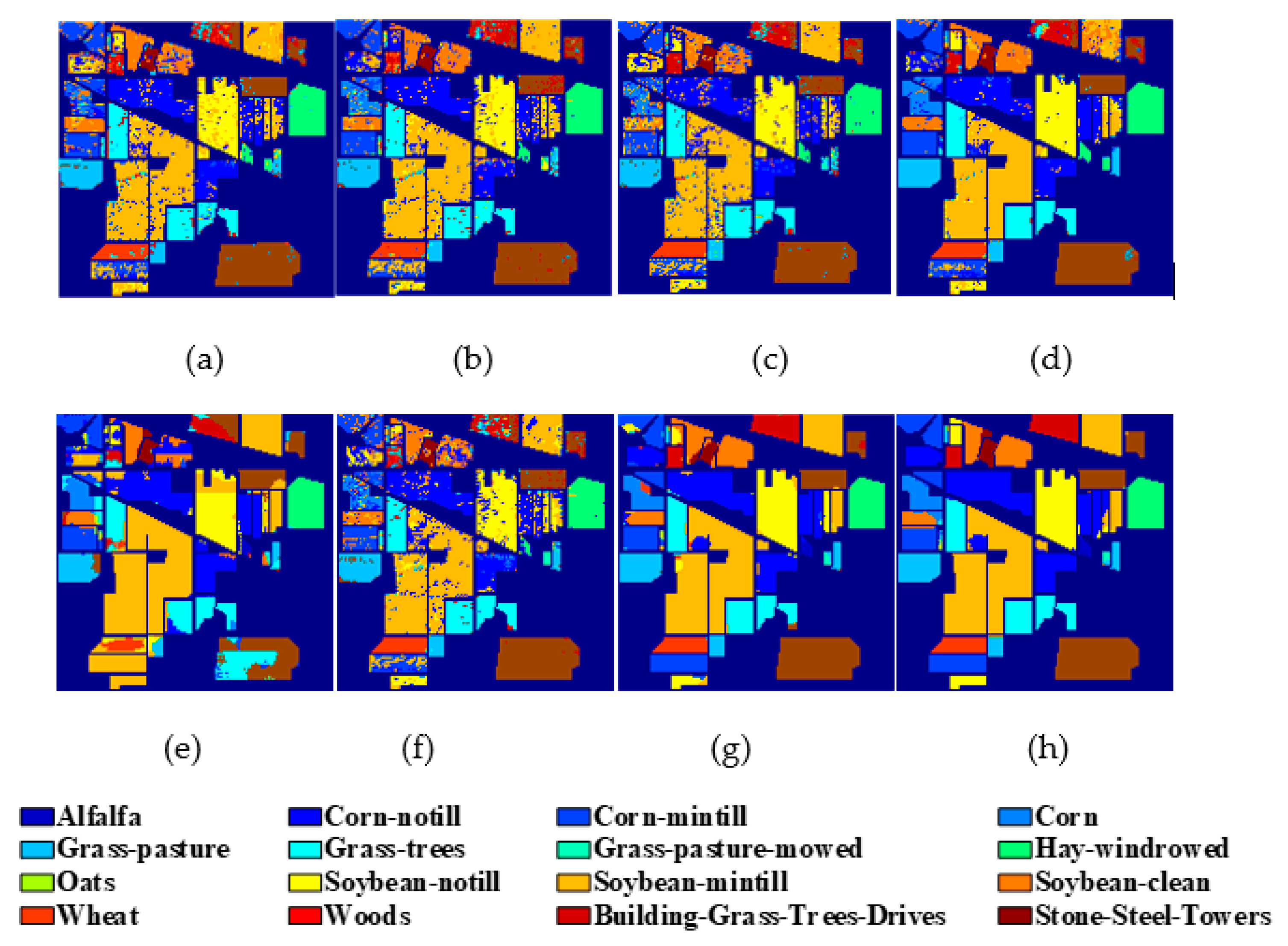

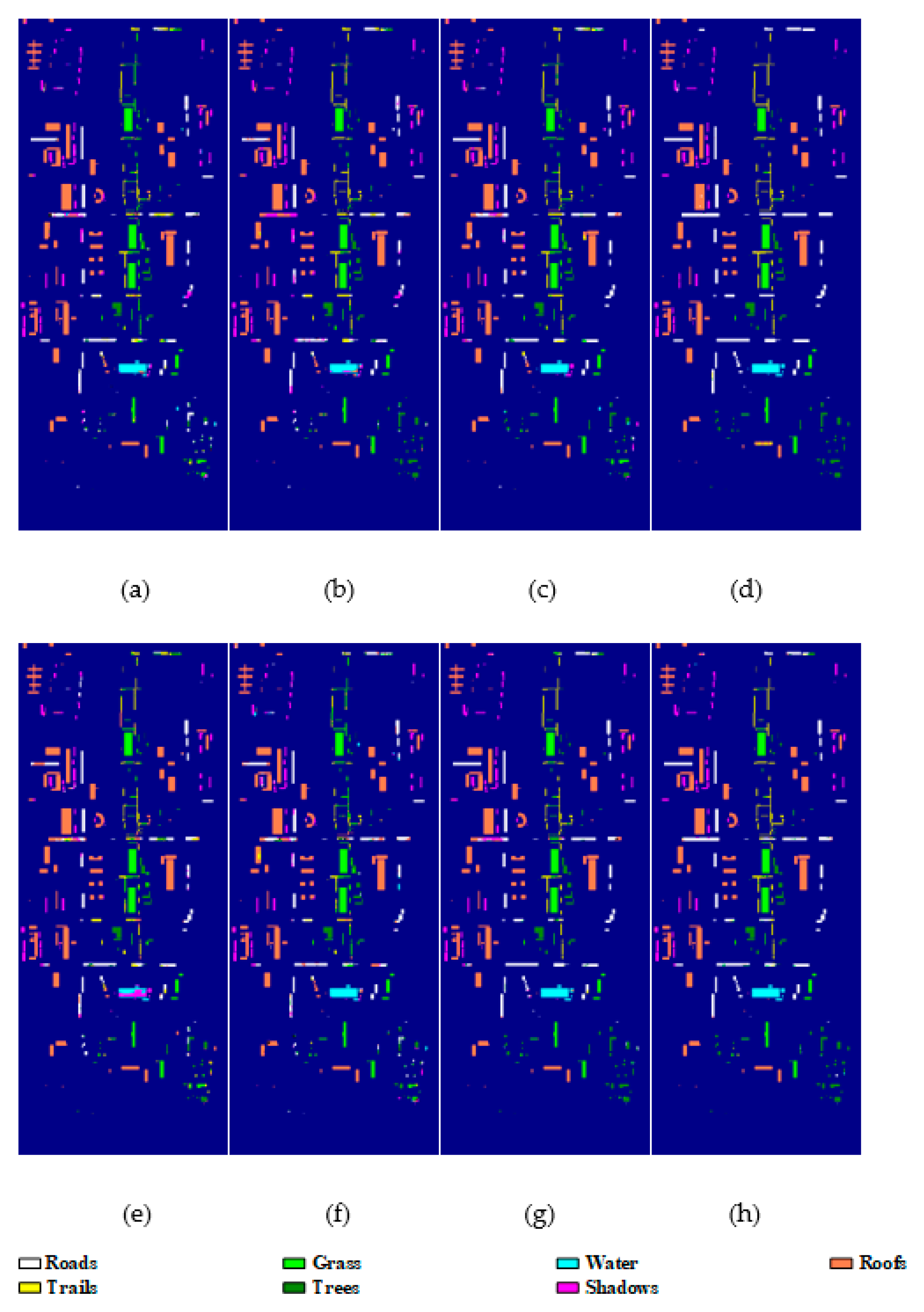
|
| Network | No | Layer | Operation | Activation | Output Size |
|---|---|---|---|---|---|
| G | 1 | Hard Attention | |||
| 2 | Deconvolution | ReLU | |||
| 3 | Hard Attention | ||||
| 4 | Deconvolution | ReLU | |||
| 5 | Hard Attention | ||||
| 6 | Deconvolution | ReLU | |||
| 7 | Hard Attention | ||||
| 8 | Deconvolution | Tanh | |||
| D | 1 | Convolution | ReLU | ||
| 2 | Convolution | ReLU | |||
| 3 | Convolution | ReLU | |||
| 4 | Convolution | Tanh | |||
| 5 | ConvLSTM | Tanh/Sigmoid | |||
| 6 | FC | - | - | ||
| 7 | - | - | Softmax | classes |
| Class | Number of Samples | |||
|---|---|---|---|---|
| No | Name | Training | Test | Total |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | Alfalfa Corn-notill Corn-mintill Corn Grass-pasture Grass-trees Grass-pasture-mowed Hay-windrowed Oats Soybean-notill Soybean-mintill Soybean-clean Wheat Woods Buildings-Grass-Trees-Drives Stone-Steel-Towers | 2 71 42 12 24 36 1 24 1 49 123 30 10 63 19 5 | 42 1357 788 225 459 694 27 454 19 923 2332 563 195 1202 367 88 | 46 1428 830 237 483 730 28 478 20 972 2455 593 205 1265 386 93 |
| Total | 512 | 9737 | 10,249 | |
| Class | RBF-SVM | SAE | DBN | PPF-CNN | CRNN | HSGAN | 3D-GAN | CA-GAN |
|---|---|---|---|---|---|---|---|---|
| 1 | 6.1 ± 11.2 | 10.0 ± 6.4 | 13.6 ± 5.6 | 30.4 ± 8.4 | 81.8 ± 6.7 | 17.7 ± 5.2 | 90.9 ± 5.2 | 95.5 ± 4.5 |
| 2 | 72.9 ± 3.6 | 79.7 ± 2.3 | 79.8 ± 2.9 | 89.2 ± 2.1 | 91.5 ± 1.4 | 66.3 ± 1.1 | 91.0 ± 1.7 | 96.4 ± 2.1 |
| 3 | 68.0 ± 3.6 | 74.9 ± 4.8 | 70.5 ± 2.2 | 77.1 ± 2.7 | 91.8 ± 2.1 | 60.2 ± 2.9 | 90.4 ± 2.1 | 96.5 ± 2.3 |
| 4 | 59.0 ± 15.0 | 62.8 ± 8.3 | 71.3 ± 6.6 | 87.7 ± 3.7 | 86.3 ± 0.4 | 57.8 ± 4.7 | 93.7 ± 4.3 | 95.0 ± 4.7 |
| 5 | 87.0 ± 4.5 | 84.2 ± 3.3 | 80.1 ± 4.1 | 94.7 ± 1.0 | 94.1 ± 0.7 | 82.0 ± 6.1 | 93.2 ± 4.5 | 96.1 ± 4.0 |
| 6 | 92.4 ± 2.0 | 94.3 ± 1.7 | 94.2 ± 2.4 | 93.1 ± 1.9 | 95.2 ± 1.0 | 94.3 ± 2.2 | 95.4 ± 0.7 | 99.6 ± 0.4 |
| 7 | 0.0 ± 0.0 | 24.4 ± 18.8 | 28.1 ± 22.6 | 0.0 ± 0.0 | 64.1 ± 12.4 | 23.8 ± 12.2 | 94.9 ± 0.1 | 94.9 ± 0.1 |
| 8 | 98.1 ± 1.4 | 98.8 ± 0.4 | 98.5 ± 1.5 | 99.6 ± 0.3 | 100 ± 0.0 | 98.8 ± 0.3 | 99.9 ± 0.1 | 100 ± 0.0 |
| 9 | 0.0 ± 0.0 | 11.1 ± 10.1 | 9.5 ± 2.4 | 0.0 ± 0.0 | 33.1 ± 9.3 | 13.7 ± 12.1 | 53.5 ± 1.4 | 55.7 ± 9.8 |
| 10 | 65.8 ± 3.7 | 73.6 ± 3.8 | 73.2 ± 4.7 | 85.6 ± 2.8 | 87.6 ± 12.1 | 68.5 ± 3.6 | 94.2 ± 0.3 | 98.6 ± 0.3 |
| 11 | 85.3 ± 2.9 | 83.4 ± 2.0 | 82.7 ± 2.2 | 83.8 ± 1.6 | 98.4 ± 0.2 | 79.7 ± 0.5 | 94.7 ± 1.5 | 99.7 ± 0.2 |
| 12 | 69.6 ± 6.5 | 70.4 ± 8.0 | 62.0 ± 5.8 | 91.4 ± 3.1 | 84.7 ± 2.7 | 48.8 ± 4.5 | 92.1 ± 2.3 | 92.3 ± 3.4 |
| 13 | 92.3 ± 4.1 | 94.2 ± 4.3 | 95.7 ± 10.6 | 97.8 ± 0.9 | 78.7 ± 3.4 | 89.2 ± 2.7 | 95.5 ± 0.2 | 97.9 ± 1.6 |
| 14 | 96.6 ± 1.0 | 94.2 ± 1.5 | 94.4 ± 1.6 | 95.5 ± 1.1 | 92.5 ± 0.1 | 96.0 ± 1.1 | 95.6 ± 0.3 | 98.7 ± 0.4 |
| 15 | 41.7 ± 7.0 | 66.1 ± 5.6 | 64.2 ± 6.5 | 78.0 ± 2.4 | 83.1 ± 3.7 | 37.9 ± 11.4 | 87.7 ± 2.1 | 92.3 ± 1.0 |
| 16 | 75.2 ± 9.0 | 87.6 ± 8.1 | 80.5 ± 13.2 | 97.3 ± 1.3 | 94.3 ± 0.5 | 73.0 ± 5.3 | 92.6 ± 2.3 | 98.9 ± 1.1 |
| OA (%) | 77.8 ± 0.8 | 81.9 ± 0.1 | 80.6 ± 0.1 | 87.9 ± 0.8 | 93.0 ± 0.5 | 74.0 ± 0.9 | 93.5 ± 0.3 | 97.4 ± 0.5 |
| AA (%) | 61.3 ± 1.4 | 69.4 ± 1.9 | 68.3 ± 1.7 | 76.5 ± 0.6 | 92.1 ± 2.1 | 60.2 ± 2.6 | 84.8 ± 2.7 | 95.2 ± 2.2 |
| Kappa (%) | 74.5 ± 1.0 | 79.3 ± 1.1 | 77.8 ± 1.3 | 86.3 ± 0.9 | 92.9 ± 0.8 | 70.0 ± 1.0 | 93.1 ± 1.2 | 97.0 ± 0.6 |
| Class | Number of Samples | |||
|---|---|---|---|---|
| No | Name | Training | Test | Total |
| 1 2 3 4 5 6 7 8 9 | Asphalt Meadows Gravel Trees Painted metal sheets Bare Soil Bitumen Self-Blocking Bricks Shadows | 199 559 63 92 40 151 40 110 28 | 6233 17,531 1973 2880 1265 4727 1250 3462 891 | 6631 18,649 2099 3064 1345 5029 1330 3682 947 |
| Total | 1282 | 40,212 | 42,776 | |
| Class | RBF-SVM | SAE | DBN | PPF-CNN | CRNN | HSGAN | 3D-GAN | CA-GAN |
|---|---|---|---|---|---|---|---|---|
| 1 | 89.1 ± 1.0 | 91.7 ± 0.3 | 90.6 ± 0.7 | 97.1 ± 0.8 | 90.2 ± 0.1 | 80.7 ± 38.3 | 88.9 ± 0.1 | 99.1 ± 0.2 |
| 2 | 95.3 ± 0.3 | 96.1 ± 0.7 | 96.9 ± 0.1 | 95.2 ± 0.7 | 99.0 ± 0.4 | 94.4 ± 1.5 | 99.8 ± 0.1 | 99.9 ± 0.1 |
| 3 | 61.6 ± 4.8 | 70.2 ± 1.5 | 68.4 ± 2.7 | 67.4 ± 6.8 | 87.4 ± 0.7 | 83.4 ± 4.6 | 89.6 ± 0.4 | 99.2 ± 0.2 |
| 4 | 89.1 ± 1.1 | 89.4 ± 1.4 | 89.7 ± 1.4 | 90.7 ± 6.8 | 88.7 ± 1.3 | 90.9 ± 1.9 | 94.8 ± 0.2 | 97.0 ± 2.3 |
| 5 | 96.2 ± 0.7 | 96.1 ± 0.7 | 96.0 ± 0.9 | 100.0 ± 0.0 | 90.7 ± 0.7 | 80.2 ± 10.1 | 99.8 ± 0.1 | 100 ± 0.0 |
| 6 | 77.0 ± 2.3 | 85.1 ± 0.9 | 84.0 ± 1.4 | 79.4 ± 2.8 | 96.5 ± 1.1 | 76.2 ± 3.3 | 99.8 ± 0.1 | 99.6 ± 0.3 |
| 7 | 73.9 ± 3.1 | 76.9 ± 2.3 | 74.1 ± 3.8 | 76.0 ± 7.2 | 83.1 ± 0.9 | 83.0 ± 2.0 | 96.1 ± 0.1 | 99.8 ± 0.2 |
| 8 | 84.5 ± 1.2 | 83.8 ± 0.9 | 84.0 ± 0.7 | 86.4 ± 3.9 | 84.2 ± 10.3 | 83.1 ± 3.9 | 88.4 ± 0.2 | 97.5 ± 0.3 |
| 9 | 98.5 ± 0.1 | 97.4 ± 0.7 | 98.0 ± 0.2 | 94.4 ± 1.7 | 67.8 ± 1.5 | 92.7 ± 2.4 | 90.8 ± 5.3 | 96.5 ± 1.7 |
| OA (%) | 88.5 ± 0.8 | 91.8 ± 0.1 | 90.2 ± 0.1 | 92.2 ± 0.7 | 95.4 ± 0.4 | 85.4 ± 2.4 | 97.0 ± 0.1 | 99.2 ± 0.6 |
| AA (%) | 85.6 ± 0.3 | 88.4 ± 0.6 | 89.1 ± 0.2 | 87.8 ± 0.9 | 83 ± 4.5 | 81.0 ± 1.0 | 92.1 ± 0.4 | 98.6 ± 1.2 |
| Kappa (%) | 86.1 ± 0.6 | 88.7 ± 0.3 | 88.9 ± 0.3 | 89.5 ± 0.9 | 92.5 ± 0.4 | 80.9 ± 3.2 | 96.0 ± 0.3 | 99.2 ± 0.7 |
| Class | Number of Samples | |||
|---|---|---|---|---|
| No | Name | Training | Test | Total |
| 1 2 3 4 5 6 7 | Roads Grass Water Roofs Trails Trees Shadows | 86 51 19 31 38 35 168 | 2787 1663 611 1005 1240 1118 5443 | 2873 1714 630 1036 1278 1153 5611 |
| Total | 428 | 13,867 | 14,295 | |
| Class | RBF-SVM | SAE | DBN | PPF-CNN | CRNN | HSGAN | 3D-GAN | CA-GAN |
|---|---|---|---|---|---|---|---|---|
| 1 | 94.1 ± 3.1 | 92.7 ± 1.8 | 94.2 ± 2.7 | 97.9 ± 0.6 | 92.2 ± 0.1 | 92.8 ± 3.1 | 96.1 ± 0.1 | 99.9 ± 0.1 |
| 2 | 93.4 ± 0.6 | 93.5 ± 0.1 | 92.6 ± 0.5 | 97.6 ± 0.1 | 93.5 ± 4.5 | 94.9 ± 0.1 | 95.4 ± 3.8 | 99.5 ± 0.3 |
| 3 | 98.3 ± 0.1 | 92.7 ± 0.5 | 91.5 ± 0.8 | 100.0 ± 0.0 | 86.6 ± 0.1 | 95.8 ± 0.3 | 99.6 ± 0.0 | 100 ± 0.0 |
| 4 | 88.2 ± 3.9 | 90.1 ± 2.4 | 92.9 ± 3.4 | 95.6 ± 3.1 | 93.8 ± 2.4 | 90.8 ± 3.5 | 99.0 ± 1.1 | 98.8 ± 2.1 |
| 5 | 95.6 ± 0.4 | 99.0 ± 0.6 | 98.9 ± 1.1 | 99.9 ± 0.1 | 96.9 ± 0.3 | 90.0 ± 0.0 | 99.5 ± 0.3 | 99.9 ± 0.1 |
| 6 | 91.6 ± 3.5 | 92.8 ± 1.6 | 91.1 ± 1.8 | 97.5 ± 1.2 | 91.5 ± 4.7 | 91.6 ± 1.1 | 97.0 ± 1.0 | 99.2 ± 0.5 |
| 7 | 98.2 ± 1.5 | 93.2 ± 0.5 | 93.5 ± 0.3 | 94.9 ± 0.1 | 99.3 ± 0.3 | 94.7 ± 1.3 | 98.2 ± 0.7 | 99.6 ± 0.1 |
| OA (%) | 93.7 ± 0.4 | 94.6 ± 0.4 | 94.1 ± 0.9 | 95.7 ± 0.3 | 95.9 ± 0.4 | 92.5 ± 1.6 | 97.2 ± 0.3 | 99.5 ± 0.5 |
| AA (%) | 92.3 ± 0.8 | 94.2 ± 0.6 | 94.6 ± 1.0 | 95.9 ± 0.5 | 94.7 ± 0.1 | 90.8 ± 1.8 | 97.0 ± 0.5 | 98.9 ± 0.7 |
| Kappa (%) | 93.7 ± 0.6 | 94.2 ± 0.5 | 93.9 ± 1.1 | 95.5 ± 0.3 | 94.7 ± 0.3 | 90.3 ± 1.6 | 96.7 ± 0.4 | 99.2 ± 0.4 |
| Dataset | Method | Training Time (s) | Test Time (s) |
|---|---|---|---|
| Indian Pines | RBF-SVM | 0.4 ± 0.1 | 1.2 ± 0.1 |
| SAE | 76.3 ± 8.4 | 0.2 ± 0.1 | |
| DBN | 114.3 ± 20.1 | 0.2 ± 0.1 | |
| PPF-CNN | 2056.0 ± 36.7 | 5.3 ± 0.3 | |
| CRNN | 2184.5 ± 75.7 | 49.9 ± 12.3 | |
| HSGAN | 444.7 ± 73.1 | 0.3 ± 0.0 | |
| 3D-GAN | 597.67 ± 60.8 | 0.3 ± 0.0 | |
| CA-GAN | 712.9 ± 3.1 | 0.3 ± 0.1 |
| Dataset | Method | Training Time (s) | Test Time (s) |
|---|---|---|---|
| Pavia University | RBF-SVM | 0.5 ± 0.1 | 1.4 ± 0.2 |
| SAE | 12.9 ± 0.9 | 0.5 ± 0.0 | |
| DBN | 27.4 ± 0.9 | 0.5 ± 0.0 | |
| PPF-CNN | 2414.0 ± 374.0 | 19.8 ± 6.2 | |
| CRNN | 2717.6 ± 54.6 | 127.2 ± 4.3 | |
| HSGAN | 580.2 ± 20.5 | 0.5 ± 0.1 | |
| 3D-GAN | 724.4 ± 50.7 | 0.6 ± 0.1 | |
| CA-GAN | 949.9 ± 80.2 | 0.6 ± 0.1 |
| Dataset | Method | Training Time (s) | Test Time (s) |
|---|---|---|---|
| Washington | RBF-SVM | 0.3 ± 0.0 | 0.2 ± 0.0 |
| SAE | 28.9 ± 0.4 | 0.2 ± 0.0 | |
| DBN | 29.2 ± 0.1 | 0.2 ± 0.0 | |
| PPF-CNN | 926.8 ± 29.5 | 5.2 ± 0.5 | |
| CRNN | 1328.1 ± 56.9 | 64.8 ± 12.3 | |
| HSGAN | 493.4 ± 73.8 | 0.2 ± 0.1 | |
| 3D-GAN | 673.3 ± 23.7 | 0.3 ± 0.1 | |
| CA-GAN | 814.2 ± 7.2 | 0.3 ± 0.1 |
| Dataset | CA-GAN Method | OA (%) | Training Time (s) |
|---|---|---|---|
| Indian Pines | PCA-20 | 97.4 ± 0.5 | 712.9 ± 3.1 |
| PCA-50 | 97.6 ± 0.3 | 1296.8 ± 59.8 | |
| PCA-100 | 97.4 ± 0.3 | 2183.2 ± 101.7 | |
| PCA-150 | 97.3 ± 0.2 | 3924.7 ± 241.5 | |
| without PCA | 97.1 ± 0.5 | 6396.8 ± 148.3 |
| Dataset | CA-GAN Method | OA (%) | Training Time (s) |
|---|---|---|---|
| Pavia University | PCA-20 | 99.2 ± 0.6 | 949.9 ± 80.2 |
| PCA-40 | 99.4 ± 0.4 | 1457.1 ± 83.4 | |
| PCA-60 | 99.3 ± 0.4 | 2676.8 ± 129.8 | |
| PCA-80 | 99.1 ± 0.3 | 4713.4 ± 185.3 | |
| without PCA | 99.0 ± 0.5 | 8034.8 ± 192.1 |
| Dataset | CA-GAN Method | OA (%) | Training Time (s) |
|---|---|---|---|
| Washington | PCA-20 | 99.5 ± 0.5 | 814.2 ± 7.2 |
| PCA-50 | 99.8 ± 0.2 | 1389.4 ± 36.8 | |
| PCA-100 | 99.5 ± 0.3 | 2435.4 ± 74.1 | |
| PCA-150 | 99.4 ± 0.2 | 4382.1 ± 183.5 | |
| without PCA | 99.2 ± 0.4 | 7274.1 ± 278.4 |
| Dataset | Method | CA-GAN-WCAC | CA-GAN-WCA | CA-GAN-WC | CA-GAN |
|---|---|---|---|---|---|
| Indian Pines | OA (%) | 94.0 ± 0.1 | 96.0 ± 0.3 | 97.0 ± 0.1 | 97.4 ± 0.5 |
| AA (%) | 89.9 ± 1.6 | 94.2 ± 0.5 | 94.7 ± 0.8 | 95.2 ± 2.2 | |
| Kappa (%) | 92.3 ± 2.0 | 96.0 ± 0.1 | 96.6 ± 0.2 | 97.0 ± 0.6 | |
| Pavia University | OA (%) | 96.0 ± 0.1 | 97.4 ± 0.5 | 98.7 ± 0.4 | 99.2 ± 0.6 |
| AA (%) | 95.9 ± 0.2 | 97.1 ± 0.1 | 98.0 ± 0.3 | 98.6 ± 1.2 | |
| Kappa (%) | 96.0 ± 0.4 | 97.3 ± 1.0 | 98.5 ± 0.2 | 99.2 ± 0.7 | |
| Washington | OA (%) | 96.3 ± 0.1 | 97.8 ± 0.3 | 99.1 ± 0.4 | 99.5 ± 0.5 |
| AA (%) | 96.1 ± 0.2 | 97.5 ± 0.6 | 98.3 ± 0.1 | 98.9 ± 0.7 | |
| Kappa (%) | 96.3 ± 0.1 | 97.6 ± 0.1 | 98.8 ± 0.4 | 99.2 ± 0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Feng, X.; Chen, J.; Cao, X.; Zhang, X.; Jiao, L.; Yu, T. Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1149. https://doi.org/10.3390/rs12071149
Feng J, Feng X, Chen J, Cao X, Zhang X, Jiao L, Yu T. Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification. Remote Sensing. 2020; 12(7):1149. https://doi.org/10.3390/rs12071149
Chicago/Turabian StyleFeng, Jie, Xueliang Feng, Jiantong Chen, Xianghai Cao, Xiangrong Zhang, Licheng Jiao, and Tao Yu. 2020. "Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification" Remote Sensing 12, no. 7: 1149. https://doi.org/10.3390/rs12071149
APA StyleFeng, J., Feng, X., Chen, J., Cao, X., Zhang, X., Jiao, L., & Yu, T. (2020). Generative Adversarial Networks Based on Collaborative Learning and Attention Mechanism for Hyperspectral Image Classification. Remote Sensing, 12(7), 1149. https://doi.org/10.3390/rs12071149