The Ability of Sun-Induced Chlorophyll Fluorescence From OCO-2 and MODIS-EVI to Monitor Spatial Variations of Soybean and Maize Yields in the Midwestern USA
Abstract
1. Introduction
2. Materials and Methods
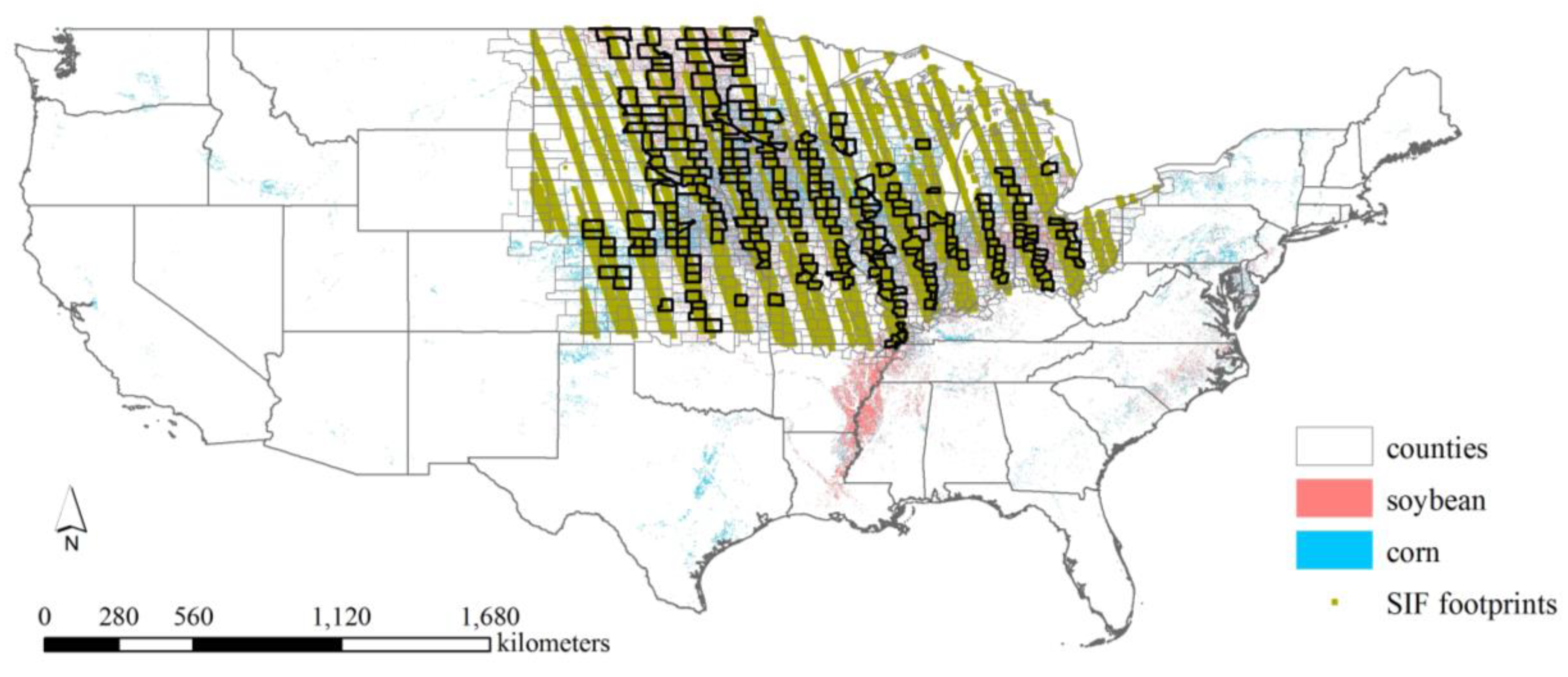
2.1. Study Area
2.2. Data
2.2.1. Satellite Data
2.2.2. Climate Data
2.2.3. Crop Classification and Yield Data
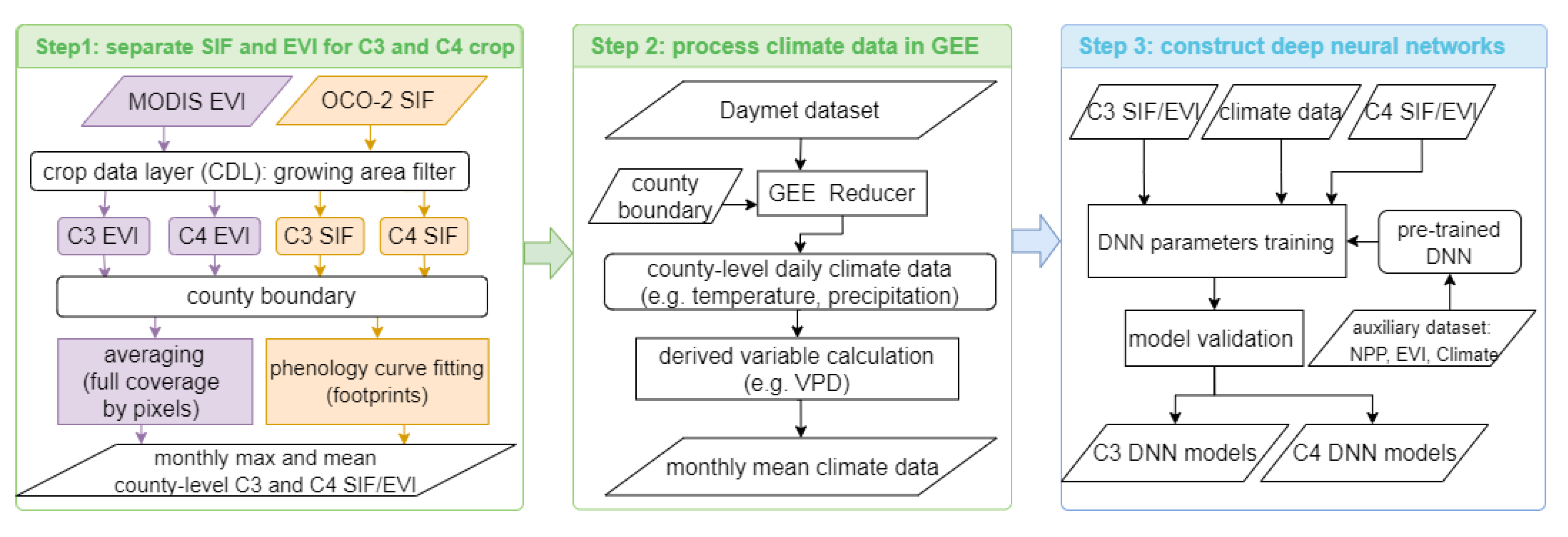
2.3. Method
2.3.1. SIF Phenology Fitting
2.3.2. Model Construction and Validation
2.3.3. Importance Determination of Different Variables
3. Results
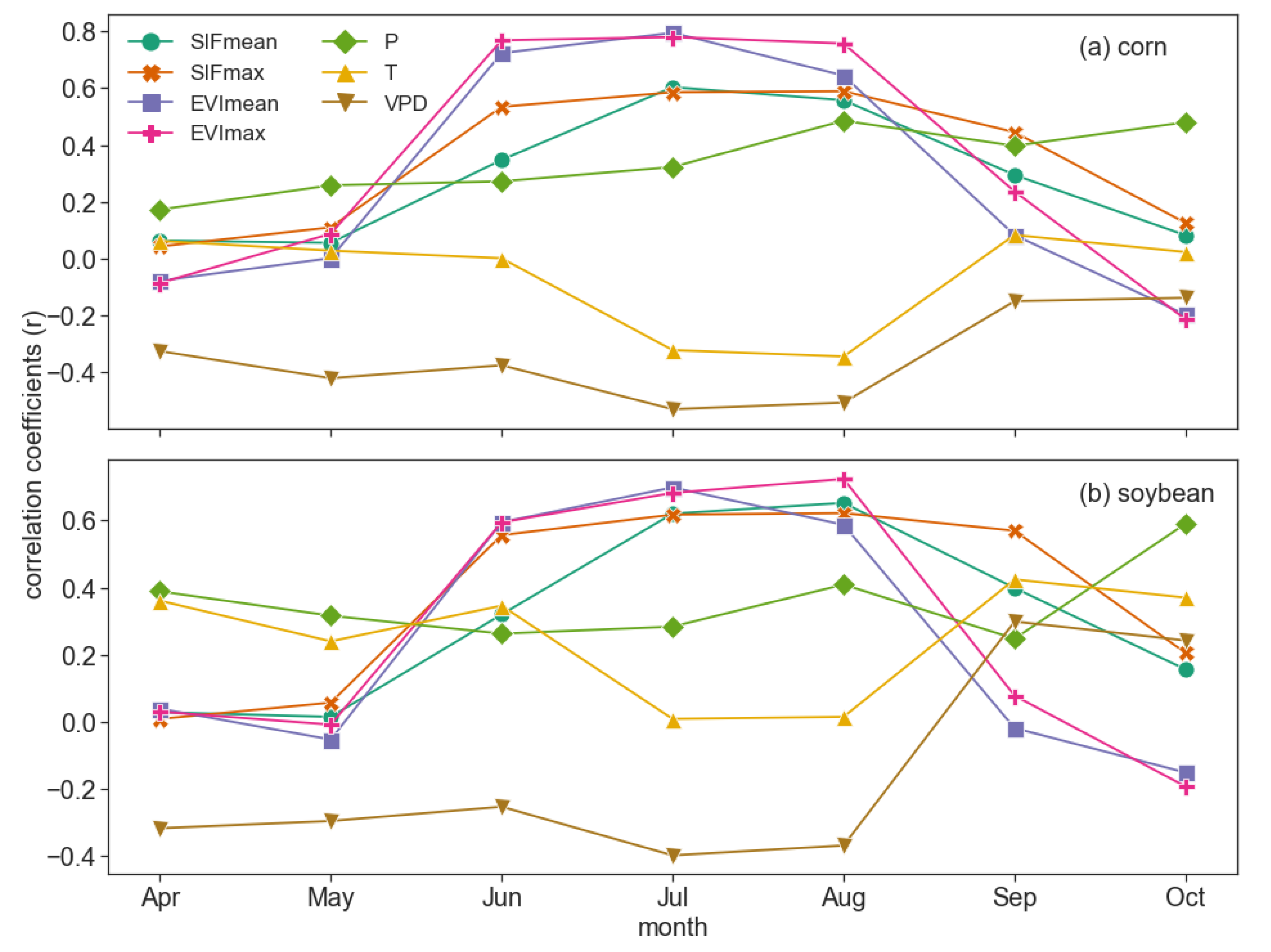
3.1. Relationships Between Crop Yields and Different Variables
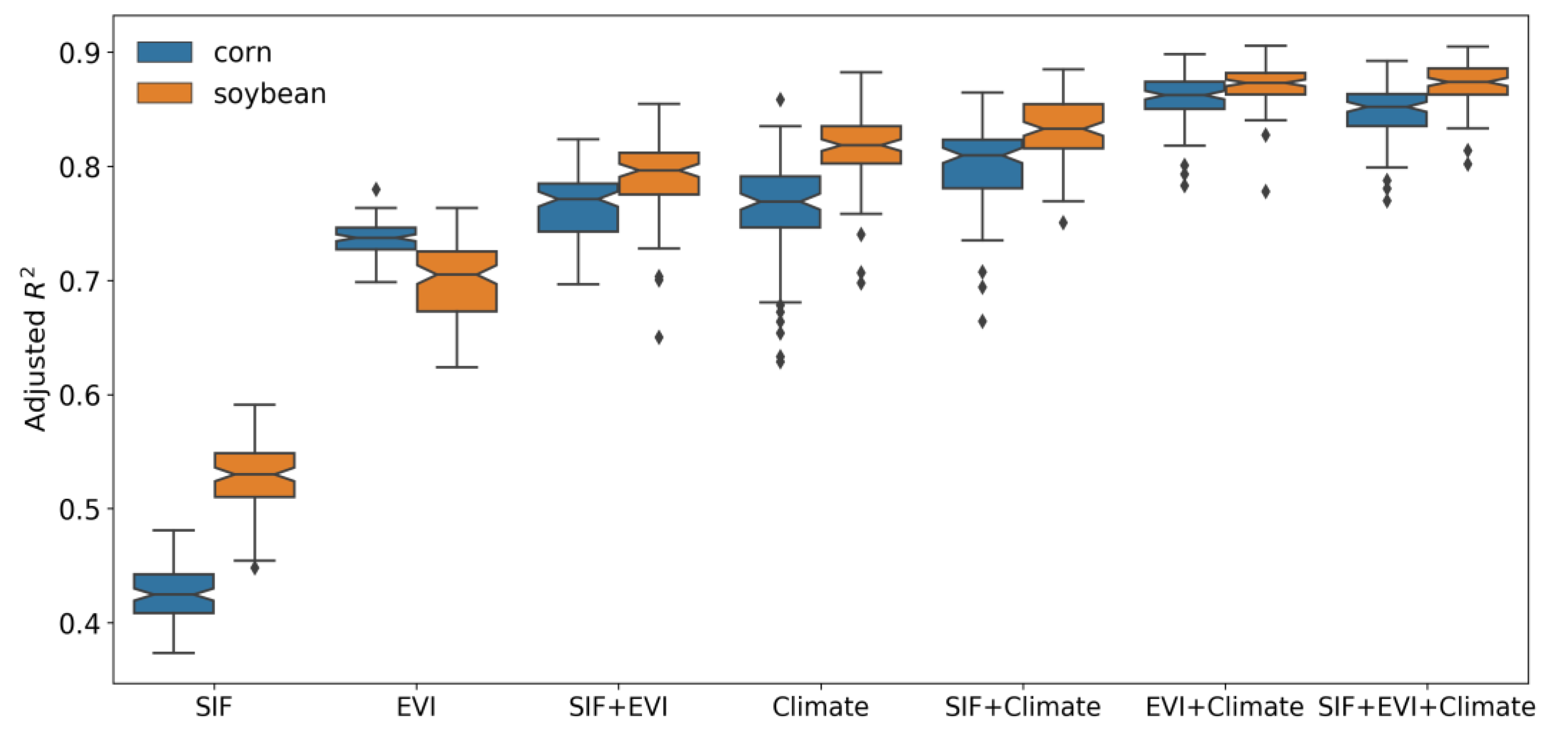
3.2. Performances of DNNs for Corn and Soybean Yield Prediction
3.3. Spatial Differences in Performances of the DNN Models
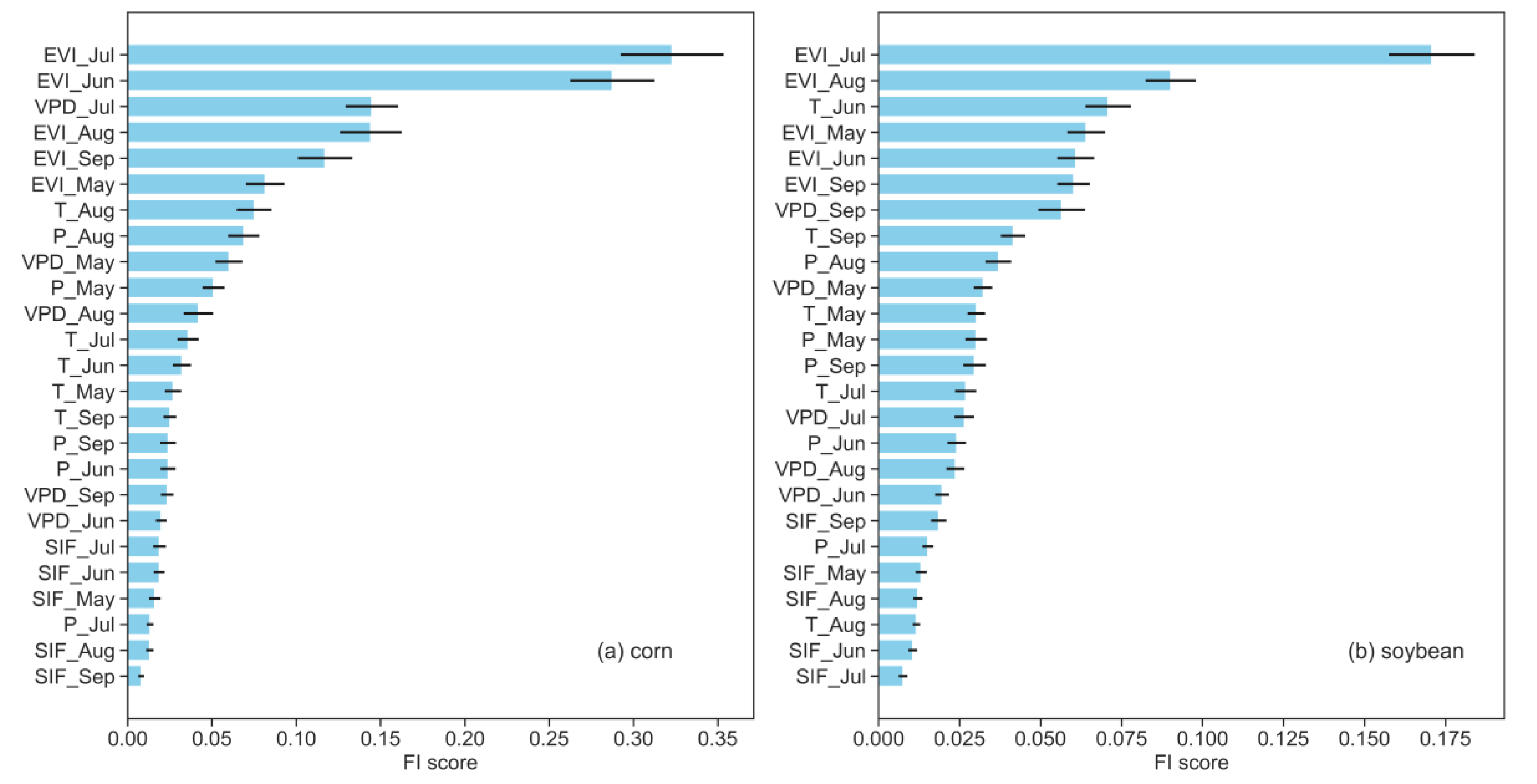
3.4. Importance of Different Variables
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A: Pre-train DNN and the Auxiliary Dataset
References
- Horie, T.; Yajima, M.; Nakagawa, H. Yield Forecasting. Agric. Syst. 1992, 40, 211–236. [Google Scholar] [CrossRef]
- Basso, B.; Cammarano, D.; Carfagna, E. Review of crop yield forecasting methods and early warning systems. In Proceedings of the First Meeting of the Scientific Advisory Committee of the Global Strategy to Improve Agricultural and Rural Statistics, FAO Headquarters, Rome, Italy, 18–19 July 2013; pp. 18–19. [Google Scholar]
- Adjemian, M.K.; Smith, A. Using USDA Forecasts to Estimate the Price Flexibility of Demand for Agricultural Commodities. Am. J. Agric. Econ. 2012, 94, 978–995. [Google Scholar] [CrossRef]
- Hoffman, L.A.; Etienne, X.L.; Irwin, S.H.; Colino, E.V.; Toasa, J.I. Forecast performance of WASDE price projections for US corn. Agric. Econ. 2015, 46, 157–171. [Google Scholar] [CrossRef]
- Mkhabela, M.S.; Mkhabela, M.S.; Mashinini, N.N. Early maize yield forecasting in the four agro-ecological regions of Swaziland using NDVI data derived from NOAA’s-AVHRR. Agric. For. Meteorol. 2005, 129, 1–9. [Google Scholar] [CrossRef]
- Challinor, A. AGRICULTURE Forecasting food. Nat. Clim. Chang. 2011, 1, 103–104. [Google Scholar] [CrossRef]
- Lobell, D.B.; Hammer, G.L.; McLean, G.; Messina, C.; Roberts, M.J.; Schlenker, W. The critical role of extreme heat for maize production in the United States. Nat. Clim. Chang. 2013, 3, 497–501. [Google Scholar] [CrossRef]
- Iizumi, T.; Luo, J.J.; Challinor, A.J.; Sakurai, G.; Yokozawa, M.; Sakuma, H.; Brown, M.E.; Yamagata, T. Impacts of El Nino Southern Oscillation on the global yields of major crops. Nat. Commun. 2014, 5, 3712. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef]
- Muller, C.; Elliott, J.; Chryssanthacopoulos, J.; Arneth, A.; Balkovic, J.; Ciais, P.; Deryng, D.; Folberth, C.; Glotter, M.; Hoek, S.; et al. Global gridded crop model evaluation: Benchmarking, skills, deficiencies and implications. Geosci. Model Dev. 2017, 10, 1403–1422. [Google Scholar] [CrossRef]
- Peng, B.; Guan, K.Y.; Chen, M.; Lawrence, D.M.; Pokhrel, Y.; Suyker, A.; Arkebauer, T.; Lu, Y.Q. Improving maize growth processes in the community land model: Implementation and evaluation. Agric. For. Meteorol. 2018, 250, 64–89. [Google Scholar] [CrossRef]
- Bassu, S.; Brisson, N.; Durand, J.L.; Boote, K.; Lizaso, J.; Jones, J.W.; Rosenzweig, C.; Ruane, A.C.; Adam, M.; Baron, C. How do various maize crop models vary in their responses to climate change factors? Glob. Chang. Boil. 2014, 20, 2301–2320. [Google Scholar] [CrossRef] [PubMed]
- Van der Werf, W.; Keesman, K.; Burgess, P.; Graves, A.; Pilbeam, D.; Incoll, L.; Metselaar, K.; Mayus, M.; Stappers, R.; van Keulen, H. Yield-SAFE: A parameter-sparse, process-based dynamic model for predicting resource capture, growth, and production in agroforestry systems. Ecol. Eng. 2007, 29, 419–433. [Google Scholar] [CrossRef]
- Iizumi, T.; Yokozawa, M.; Nishimori, M. Parameter estimation and uncertainty analysis of a large-scale crop model for paddy rice: Application of a Bayesian approach. Agric. For. Meteorol. 2009, 149, 333–348. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Shi, W.J.; Tao, F.L.; Zhang, Z. A review on statistical models for identifying climate contributions to crop yields. J. Geogr. Sci. 2013, 23, 567–576. [Google Scholar] [CrossRef]
- Li, Y.; Guan, K.Y.; Yu, A.; Peng, B.; Zhao, L.; Li, B.; Peng, J. Toward building a transparent statistical model for improving crop yield prediction: Modeling rainfed corn in the U.S. Field Crop. Res. 2019, 234, 55–65. [Google Scholar] [CrossRef]
- Mirschel, W.; Wieland, R.; Wenkel, K.-O.; Nendel, C.; Guddat, C. YIELDSTAT–a spatial yield model for agricultural crops. Eur. J. Agron. 2014, 52, 33–46. [Google Scholar] [CrossRef]
- Kern, A.; Barcza, Z.; Marjanovic, H.; Arendas, T.; Fodor, N.; Bonis, P.; Bognar, P.; Lichtenberger, J. Statistical modelling of crop yield in Central Europe using climate data and remote sensing vegetation indices. Agric. For. Meteorol. 2018, 260, 300–320. [Google Scholar] [CrossRef]
- Gornott, C.; Wechsung, F. Statistical regression models for assessing climate impacts on crop yields: A validation study for winter wheat and silage maize in Germany. Agric. For. Meteorol. 2016, 217, 89–100. [Google Scholar] [CrossRef]
- Lobell, D.B. Changes in diurnal temperature range and national cereal yields. Agric. For. Meteorol. 2007, 145, 229–238. [Google Scholar] [CrossRef]
- Johnson, M.D.; Hsieh, W.W.; Cannon, A.J.; Davidson, A.; Bedard, F. Crop yield forecasting on the Canadian Prairies by remotely sensed vegetation indices and machine learning methods. Agric. For. Meteorol. 2016, 218, 74–84. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.L.; Mouazen, A.M. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Cai, Y.P.; Guan, K.Y.; Lobell, D.; Potgieter, A.B.; Wang, S.W.; Peng, J.; Xu, T.F.; Asseng, S.; Zhang, Y.G.; You, L.Z.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- You, J.; Li, X.; Low, M.; Lobell, D.; Ermon, S. Deep gaussian process for crop yield prediction based on remote sensing data. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Bose, P.; Kasabov, N.K.; Bruzzone, L.; Hartono, R.N. Spiking Neural Networks for Crop Yield Estimation Based on Spatiotemporal Analysis of Image Time Series. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 6563–6573. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Mikolov, T.; Deoras, A.; Povey, D.; Burget, L.; Černocký, J. Strategies for training large scale neural network language models. In Proceedings of the 2011 IEEE Workshop on Automatic Speech Recognition & Understanding, Waikoloa, HA, USA, 11–15 December 2011; pp. 196–201. [Google Scholar]
- Farabet, C.; Couprie, C.; Najman, L.; Lecun, Y. Learning hierarchical features for scene labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef]
- Tompson, J.J.; Jain, A.; LeCun, Y.; Bregler, C. Joint training of a convolutional network and a graphical model for human pose estimation. In Proceedings of the Advances in neural information processing systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1799–1807. [Google Scholar]
- Ma, J.; Sheridan, R.P.; Liaw, A.; Dahl, G.E.; Svetnik, V. Deep neural nets as a method for quantitative structure–activity relationships. J. Chem. Inf. Model. 2015, 55, 263–274. [Google Scholar] [CrossRef]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 13–18 July 2015; pp. 858–861. [Google Scholar]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep Transfer Learning for Crop Yield Prediction with Remote Sensing Data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies (COMPASS)—COMPASS ’18, Association for Computing Machinery (ACM), California, CA, USA, 20–22 June 2018. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Guan, K.Y.; Wu, J.; Kimball, J.S.; Anderson, M.C.; Frolking, S.; Li, B.; Hain, C.R.; Lobe, D.B. The shared and unique values of optical, fluorescence, thermal and microwave satellite data for estimating large-scale crop yields. Remote. Sens. Environ. 2017, 199, 333–349. [Google Scholar] [CrossRef]
- Newlands, N.K.; Zamar, D.S.; Kouadio, L.A.; Zhang, Y.; Chipanshi, A.; Potgieter, A.; Toure, S.; Hill, H.S. An integrated, probabilistic model for improved seasonal forecasting of agricultural crop yield under environmental uncertainty. Front. Environ. Sci. 2014, 2, 17. [Google Scholar] [CrossRef]
- Cane, M.A.; Eshel, G.; Buckland, R.W. Forecasting Zimbabwean Maize Yield Using Eastern Equatorial Pacific Sea-Surface Temperature. Nature 1994, 370, 204–205. [Google Scholar] [CrossRef]
- Soler, C.M.T.; Sentelhas, P.U.; Hoogenboom, G. Application of the CSM-CERES-maize model for planting date evaluation and yield forecasting for maize grown off-season in a subtropical environment. European Eur. J. Agron. 2007, 27, 165–177. [Google Scholar] [CrossRef]
- Urban, D.W.; Roberts, M.J.; Schlenker, W.; Lobell, D.B. The effects of extremely wet planting conditions on maize and soybean yields. Clim. Chang. 2015, 130, 247–260. [Google Scholar] [CrossRef]
- Tack, J.; Barkley, A.; Nalley, L.L. Effect of warming temperatures on US wheat yields. Proc. Natl. Acad. Sci. USA 2015, 112, 6931–6936. [Google Scholar] [CrossRef] [PubMed]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef]
- Pena-Gallardo, M.; Vicente-Serrano, S.M.; Quiring, S.; Svoboda, M.; Hannaford, J.; Tomas-Burguera, M.; Martin-Hernandez, N.; Dominguez-Castro, F.; El Kenawy, A. Response of crop yield to different time-scales of drought in the United States: Spatio-temporal patterns and climatic and environmental drivers. Agric. For. Meteorol. 2019, 264, 40–55. [Google Scholar] [CrossRef]
- Gond, V.; Fayolle, A.; Pennec, A.; Cornu, G.; Mayaux, P.; Camberlin, P.; Doumenge, C.; Fauvet, N.; Gourlet-Fleury, S. Vegetation structure and greenness in Central Africa from Modis multi-temporal data. Philos. Trans. R. Soc. B Boil. Sci. 2013, 368, 20120309. [Google Scholar] [CrossRef]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. Near real-time prediction of US corn yields based on time-series MODIS data. Remote. Sens. Environ. 2014, 147, 219–231. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Peng, B.; Guan, K.Y.; Pan, M.; Li, Y. Benefits of Seasonal Climate Prediction and Satellite Data for Forecasting US Maize Yield. Geophys. Res. Lett. 2018, 45, 9662–9671. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Minh, V.Q.; Trung, N.H. A comparative analysis of multitemporal MODIS EVI and NDVI data for large-scale rice yield estimation. Agric. For. Meteorol. 2014, 197, 52–64. [Google Scholar] [CrossRef]
- Guan, K.; Berry, J.A.; Zhang, Y.; Joiner, J.; Guanter, L.; Badgley, G.; Lobell, D.B. Improving the monitoring of crop productivity using spaceborne solar-induced fluorescence. Glob. Chang. Boil. 2016, 22, 716–726. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.E.; et al. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef] [PubMed]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; Van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.R. Chlorophyll fluorescence: A probe of photosynthesis in vivo. Annu. Rev. Plant Boil. 2008, 59, 89–113. [Google Scholar] [CrossRef] [PubMed]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote. Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gomez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote. Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Jung, M.; Joiner, J.; Guanter, L.; Kohler, P.; Magney, T. Overview of Solar-Induced chlorophyll Fluorescence (SIF) from the Orbiting Carbon Observatory-2: Retrieval, cross-mission comparison, and global monitoring for GPP. Remote. Sens. Environ. 2018, 209, 808–823. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: Methodology, simulations, and application to GOME-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Yoshida, Y.; Corp, L.A.; Middleton, E.M. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef]
- Kohler, P.; Guanter, L.; Joiner, J. A linear method for the retrieval of sun-induced chlorophyll fluorescence from GOME-2 and SCIAMACHY data. Atmos. Meas. Tech. 2015, 8, 2589–2608. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Walther, S.; Voigt, M.; Thum, T.; Gonsamo, A.; Zhang, Y.; Köhler, P.; Jung, M.; Varlagin, A.; Guanter, L. Satellite chlorophyll fluorescence measurements reveal large-scale decoupling of photosynthesis and greenness dynamics in boreal evergreen forests. Glob. Chang. Boil. 2016, 22, 2979–2996. [Google Scholar] [CrossRef]
- Verma, M.; Schimel, D.; Evans, B.; Frankenberg, C.; Beringer, J.; Drewry, D.T.; Magney, T.; Marang, I.; Hutley, L.; Moore, C. Effect of environmental conditions on the relationship between solar-induced fluorescence and gross primary productivity at an OzFlux grassland site. J. Geophys. Res. Biogeosciences 2017, 122, 716–733. [Google Scholar] [CrossRef]
- Wood, J.D.; Griffis, T.J.; Baker, J.M.; Frankenberg, C.; Verma, M.; Yuen, K. Multiscale analyses of solar-induced florescence and gross primary production. Geophys. Res. Lett. 2017, 44, 533–541. [Google Scholar] [CrossRef]
- Guan, K.; Pan, M.; Li, H.; Wolf, A.; Wu, J.; Medvigy, D.; Caylor, K.K.; Sheffield, J.; Wood, E.F.; Malhi, Y. Photosynthetic seasonality of global tropical forests constrained by hydroclimate. Nat. Geosci. 2015, 8, 284. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kohler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Boil. 2014, 20, 3727–3742. [Google Scholar] [CrossRef]
- Gu, L.; Han, J.; Wood, J.D.; Chang, C.Y.Y.; Sun, Y. Sun-induced Chl fluorescence and its importance for biophysical modeling of photosynthesis based on light reactions. New Phytol. 2019. [Google Scholar] [CrossRef]
- Liu, L.Y.; Guan, L.L.; Liu, X.J. Directly estimating diurnal changes in GPP for C3 and C4 crops using far-red sun-induced chlorophyll fluorescence. Agric. For. Meteorol. 2017, 232, 1–9. [Google Scholar] [CrossRef]
- Köhler, P.; Frankenberg, C.; Magney, T.S.; Guanter, L.; Joiner, J.; Landgraf, J. Global retrievals of solar-induced chlorophyll fluorescence with TROPOMI: First results and intersensor comparison to OCO-2. Geophys. Res. Lett. 2018, 45, 410,456–410,463. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R. Daymet: Daily surface weather on a 1 km grid for North America, 1980–2008, Oak Ridge National Laboratory (ORNL) Distributed Active Archive Center for Biogeochemical Dynamics (DAAC) 2012. Available online: https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1328 (accessed on 9 December 2019).
- Grassini, P.; Specht, J.E.; Tollenaar, M.; Ciampitti, I.; Cassman, K.G. High-yield maize–soybean cropping systems in the US Corn Belt. In Crop Physiology, 2nd ed.; Calderini, V.S.D., Ed.; Academic Press: Massachusetts, MA, USA, 2014. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Joiner, J.; Migliavacca, M. Angle matters: Bidirectional effects impact the slope of relationship between gross primary productivity and sun-induced chlorophyll fluorescence from Orbiting Carbon Observatory-2 across biomes. Glob. Chang. Boil. 2018. [Google Scholar] [CrossRef] [PubMed]
- Robinson, N.P.; Allred, B.W.; Smith, W.K.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Running, S.W. Terrestrial primary production for the conterminous United States derived from Landsat 30 m and MODIS 250 m. Remote. Sens. Ecol. Conserv. 2018, 4, 264–280. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 56, p. e156. [Google Scholar]
- Wang, S.; Ju, W.; Peñuelas, J.; Cescatti, A.; Zhou, Y.; Fu, Y.; Huete, A.; Liu, M.; Zhang, Y. Urban− rural gradients reveal joint control of elevated CO2 and temperature on extended photosynthetic seasons. Nat. Ecol. Evol. 2019, 1. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; D’Odorico, P. Deriving land surface phenology indicators from CO2 eddy covariance measurements. Ecol. Indic. 2013, 29, 203–207. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M.; Ooi, Y.W. Peak season plant activity shift towards spring is reflected by increasing carbon uptake by extratropical ecosystems. Glob. Chang. Boil. 2018, 24, 2117–2128. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Mhaskar, H.; Liao, Q.; Poggio, T.A. When and why are deep networks better than shallow ones; AAAI: California, CA, USA,, 2017; pp. 2343–2349. [Google Scholar]
- Lu, J.; Behbood, V.; Hao, P.; Zuo, H.; Xue, S.; Zhang, G.Q. Transfer learning using computational intelligence: A survey. Knowledge-Based Syst. 2015, 80, 14–23. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Aghighi, H.; Azadbakht, M.; Ashourloo, D.; Shahrabi, H.S.; Radiom, S. Machine Learning Regression Techniques for the Silage Maize Yield Prediction Using Time-Series Images of Landsat 8 OLI. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 4563–4577. [Google Scholar] [CrossRef]
- Putin, E.; Mamoshina, P.; Aliper, A.; Korzinkin, M.; Moskalev, A.; Kolosov, A.; Ostrovskiy, A.; Cantor, C.; Vijg, J.; Zhavoronkov, A. Deep biomarkers of human aging: Application of deep neural networks to biomarker development. Aging (Albany NY) 2016, 8, 1021–1033. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
- Giam, X.; Olden, J.D. A new R2-based metric to shed greater insight on variable importance in artificial neural networks. Ecol. Model. 2015, 313, 307–313. [Google Scholar] [CrossRef]
- Tukey, J.W. Comparing individual means in the analysis of variance. Biom. 1949, 5, 99–114. [Google Scholar] [CrossRef]
- Mishra, V.; Cherkauer, K.A. Retrospective droughts in the crop growing season: Implications to corn and soybean yield in the Midwestern United States. Agric. For. Meteorol. 2010, 150, 1030–1045. [Google Scholar] [CrossRef]
- Sacks, W.J.; Kucharik, C.J. Crop management and phenology trends in the US Corn Belt: Impacts on yields, evapotranspiration and energy balance. Agric. For. Meteorol. 2011, 151, 882–894. [Google Scholar] [CrossRef]
- Pettigrew, W.; Hesketh, J.; Peters, D.; Woolley, J. A vapor pressure deficit effect on crop canopy photosynthesis. Photosynth. Res. 1990, 24, 27–34. [Google Scholar] [CrossRef]
- Lobell, D.B.; Roberts, M.J.; Schlenker, W.; Braun, N.; Little, B.B.; Rejesus, R.M.; Hammer, G.L. Greater sensitivity to drought accompanies maize yield increase in the US Midwest. Sci. 2014, 344, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Board, J.E.; Kahlon, C.S. Soybean yield formation: What controls it and how it can be improved. Soybean Physiol. Biochem. 2011, 1–36. [Google Scholar]
- Southworth, J.; Randolph, J.; Habeck, M.; Doering, O.; Pfeifer, R.; Rao, D.G.; Johnston, J. Consequences of future climate change and changing climate variability on maize yields in the midwestern United States. Agric. Ecosyst. Environ. 2000, 82, 139–158. [Google Scholar] [CrossRef]
- Schauberger, B.; Archontoulis, S.; Arneth, A.; Balkovic, J.; Ciais, P.; Deryng, D.; Elliott, J.; Folberth, C.; Khabarov, N.; Muller, C.; et al. Consistent negative response of US crops to high temperatures in observations and crop models. Nat .Commun. 2017, 8, 13931. [Google Scholar] [CrossRef] [PubMed]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Kohler, P.; Pollock, R.; Taylor, T.E. Prospects for chlorophyll fluorescence remote sensing from the Orbiting Carbon Observatory-2. Remote. Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef]
- Drusch, M.; Moreno, J.; Del Bello, U.; Franco, R.; Goulas, Y.; Huth, A.; Kraft, S.; Middleton, E.M.; Miglietta, F.; Mohammed, G. The fluorescence explorer mission concept—ESA’s Earth explorer 8. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1273–1284. [Google Scholar] [CrossRef]
- Buis, A. GeoCarb: A New View of Carbon Over the Americas. Available online: https://www.nasa.gov/feature/jpl/geocarb-a-new-view-of-carbon-over-the-americas (accessed on 18 April 2019).
- Zhang, Y.; Joiner, J.; Alemohammad, S.H.; Zhou, S.; Gentine, P. A global spatially contiguous solar-induced fluorescence (CSIF) dataset using neural networks. Biogeosciences 2018, 15, 5779–5800. [Google Scholar] [CrossRef]
- Yu, L.; Wen, J.; Chang, C.; Frankenberg, C.; Sun, Y. High-Resolution Global Contiguous SIF of OCO-2. Geophys. Res. Lett. 2019, 46, 1449–1458. [Google Scholar] [CrossRef]
- Gentine, P.; Alemohammad, S. Reconstructed solar-induced fluorescence: A machine learning vegetation product based on MODIS surface reflectance to reproduce GOME-2 solar-induced fluorescence. Geophys. Res. Lett. 2018, 45, 3136–3146. [Google Scholar] [CrossRef]
- Guan, K.Y.; Wood, E.F.; Medvigy, D.; Kimball, J.; Pan, M.; Caylor, K.K.; Sheffield, J.; Xu, X.T.; Jones, M.O. Terrestrial hydrological controls on land surface phenology of African savannas and woodlands. J. Geophys. Res. Biogeosciences 2014, 119, 1652–1669. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Jones, L.A. Passive microwave remote sensing of soil moisture based on dynamic vegetation scattering properties for AMSR-E. IEEE Trans. Geosci. Remote Sens. 2015, 54, 597–608. [Google Scholar] [CrossRef]
- Anderson, M.C.; Hain, C.; Otkin, J.; Zhan, X.W.; Mo, K.; Svoboda, M.; Wardlow, B.; Pimstein, A. An Intercomparison of Drought Indicators Based on Thermal Remote Sensing and NLDAS-2 Simulations with US Drought Monitor Classifications. J. Hydrometeorol. 2013, 14, 1035–1056. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Gao, F.; Otkin, J.A.; Tetrault, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote. Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
| Models | N | Corn | Soybean | ||||
|---|---|---|---|---|---|---|---|
| R2 | MAE | MAPE (%) | R2 | MAE | MAPE (%) | ||
| SIF | 5 | 0.43 | 16.50 | 8.99 | 0.53 | 4.73 | 8.90 |
| EVI | 5 | 0.74 | 10.26 | 5.59 | 0.70 | 3.51 | 6.79 |
| SIF + EVI | 10 | 0.76 | 9.62 | 5.24 | 0.79 | 3.05 | 5.89 |
| Climate | 15 | 0.76 | 9.76 | 5.34 | 0.82 | 2.87 | 5.55 |
| SIF + Climate | 20 | 0.80 | 8.98 | 4.90 | 0.83 | 2.68 | 5.18 |
| EVI + Climate | 20 | 0.86 | 7.27 | 3.97 | 0.87 | 2.36 | 4.56 |
| SIF + EVI + Climate | 25 | 0.85 | 7.49 | 4.08 | 0.87 | 2.30 | 4.45 |
| Corn | Min | 15% | 50% | 85% | Max | Mean | Std a |
|---|---|---|---|---|---|---|---|
| SIF | −20.25 | −10.03 | −1.87 | 13.91 | 47.03 | 0.83 | 11.97 |
| EVI | −26.11 | −6.39 | −0.64 | 6.32 | 46.09 | 0.05 | 7.84 |
| SIF + EVI | −20.20 | −5.69 | −0.50 | 5.70 | 47.83 | 0.13 | 6.89 |
| Climate | −15.68 | −4.52 | −0.11 | 4.24 | 30.85 | 0.09 | 5.78 |
| SIF + Climate | −12.46 | −4.72 | −0.65 | 3.78 | 21.90 | −0.07 | 5.12 |
| EVI + Climate | −12.28 | −3.48 | −0.17 | 3.75 | 15.93 | 0.15 | 3.97 |
| SIF + EVI + Climate | −11.44 | −3.55 | −0.08 | 3.39 | 17.83 | 0.02 | 4.23 |
| Soybean | Min | 15% | 50% | 85% | Max | Mean | Std a |
| SIF | −36.86 | −9.42 | 0.03 | 12.67 | 40.62 | 1.73 | 12.37 |
| EVI | −28.96 | −6.18 | 0.07 | 7.14 | 29.35 | 0.67 | 8.43 |
| SIF + EVI | −17.06 | −5.23 | 0.27 | 6.29 | 25.18 | 0.79 | 6.49 |
| Climate | −13.80 | −5.35 | −0.15 | 5.54 | 23.48 | 0.44 | 5.94 |
| SIF + Climate | −14.53 | −4.80 | 0.12 | 5.11 | 21.94 | 0.27 | 5.44 |
| EVI + Climate | −15.64 | −4.37 | −0.16 | 4.65 | 18.68 | 0.39 | 4.89 |
| SIF + EVI + Climate | −11.30 | −3.63 | −0.25 | 4.27 | 16.74 | 0.41 | 4.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Wang, S.; Guan, K.; Wolanin, A.; You, L.; Ju, W.; Zhang, Y. The Ability of Sun-Induced Chlorophyll Fluorescence From OCO-2 and MODIS-EVI to Monitor Spatial Variations of Soybean and Maize Yields in the Midwestern USA. Remote Sens. 2020, 12, 1111. https://doi.org/10.3390/rs12071111
Gao Y, Wang S, Guan K, Wolanin A, You L, Ju W, Zhang Y. The Ability of Sun-Induced Chlorophyll Fluorescence From OCO-2 and MODIS-EVI to Monitor Spatial Variations of Soybean and Maize Yields in the Midwestern USA. Remote Sensing. 2020; 12(7):1111. https://doi.org/10.3390/rs12071111
Chicago/Turabian StyleGao, Yun, Songhan Wang, Kaiyu Guan, Aleksandra Wolanin, Liangzhi You, Weimin Ju, and Yongguang Zhang. 2020. "The Ability of Sun-Induced Chlorophyll Fluorescence From OCO-2 and MODIS-EVI to Monitor Spatial Variations of Soybean and Maize Yields in the Midwestern USA" Remote Sensing 12, no. 7: 1111. https://doi.org/10.3390/rs12071111
APA StyleGao, Y., Wang, S., Guan, K., Wolanin, A., You, L., Ju, W., & Zhang, Y. (2020). The Ability of Sun-Induced Chlorophyll Fluorescence From OCO-2 and MODIS-EVI to Monitor Spatial Variations of Soybean and Maize Yields in the Midwestern USA. Remote Sensing, 12(7), 1111. https://doi.org/10.3390/rs12071111






