The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty
Abstract
1. Introduction
2. Experimental Site and Data
2.1. Significance of Weather Radar Surveillance in Central Missouri
2.2. System and Dataset Description
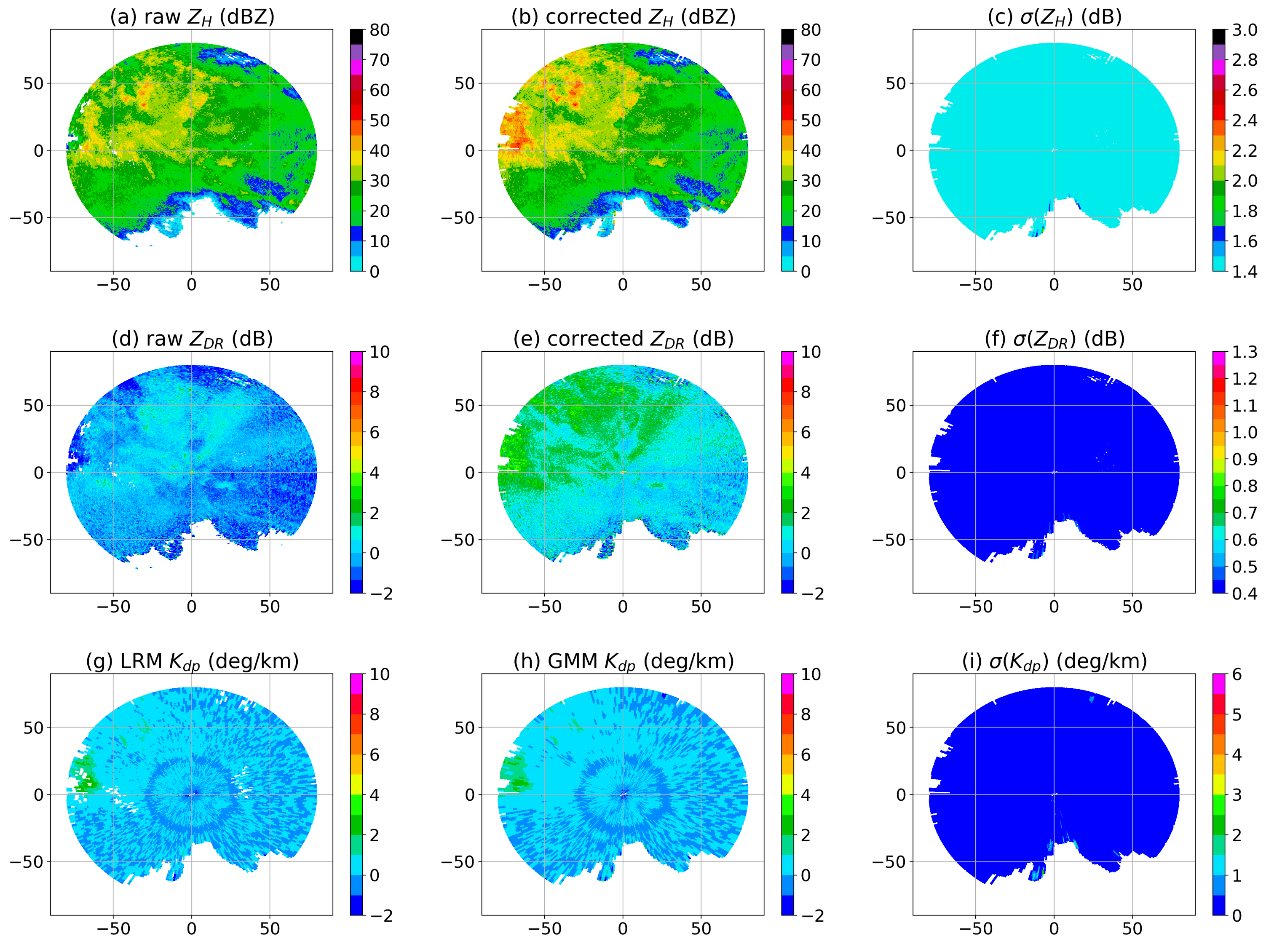
3. Quality Control
3.1. Clutter Removal
3.2. Estimation
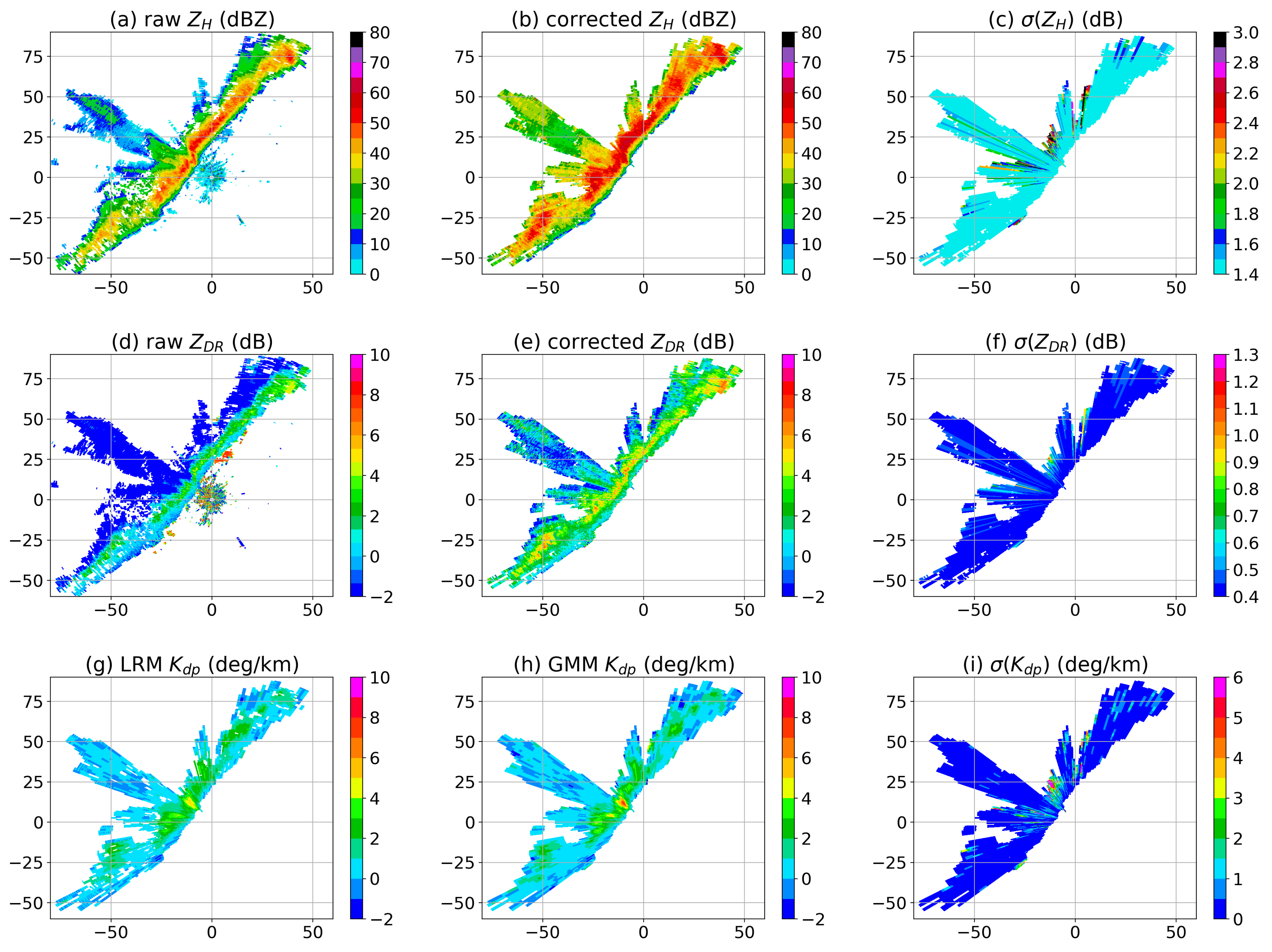
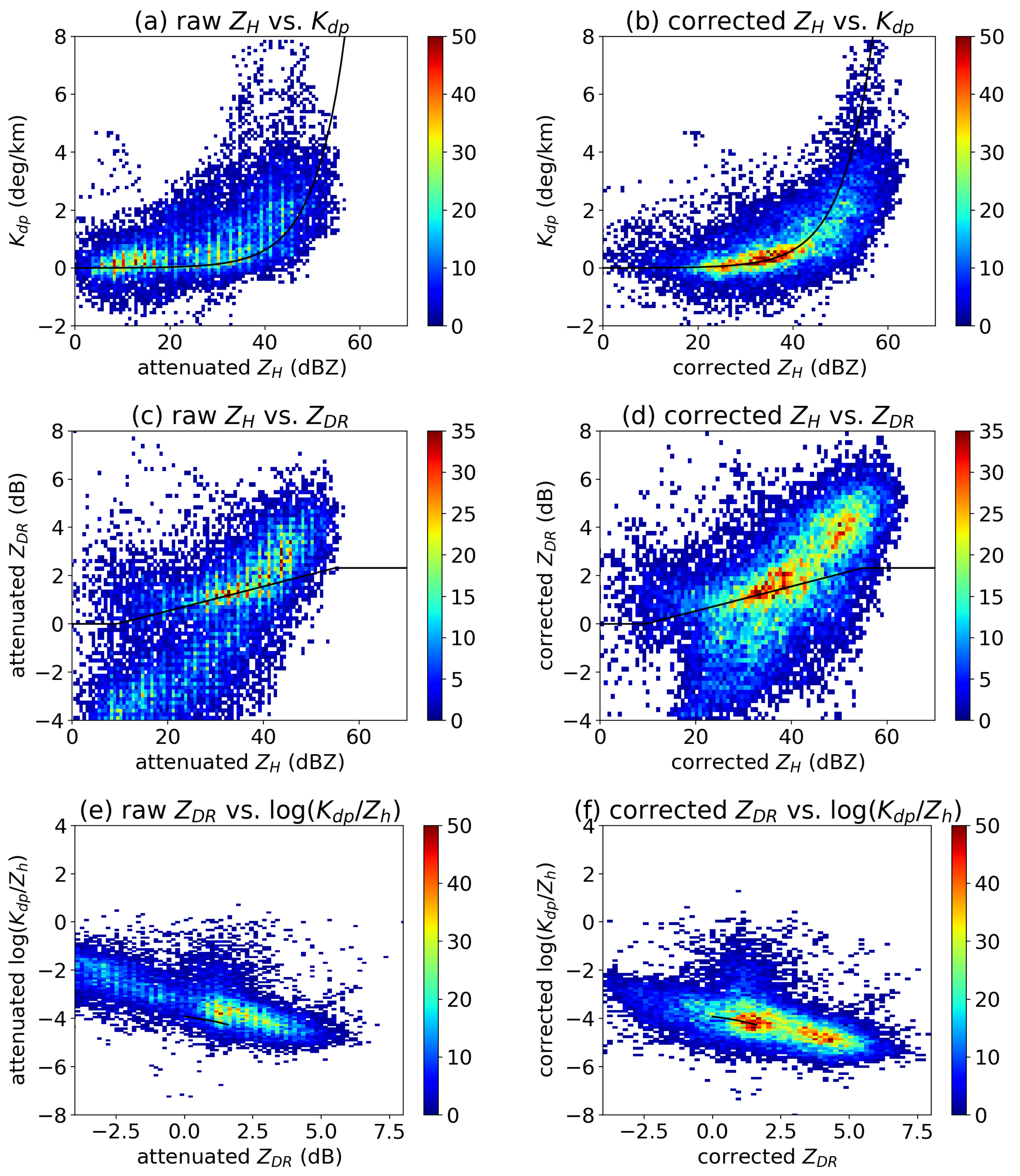
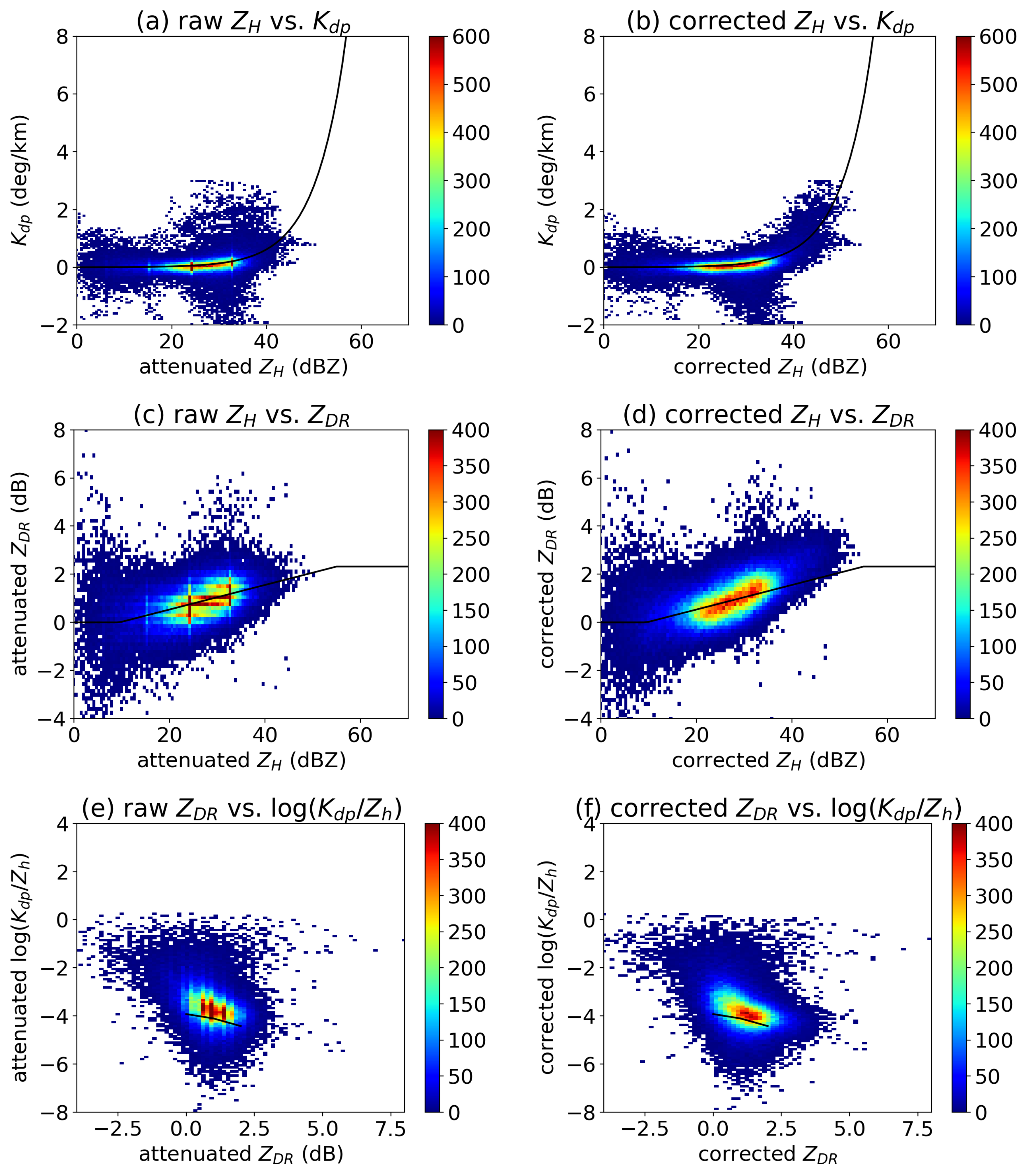
3.3. Attenuation Correction
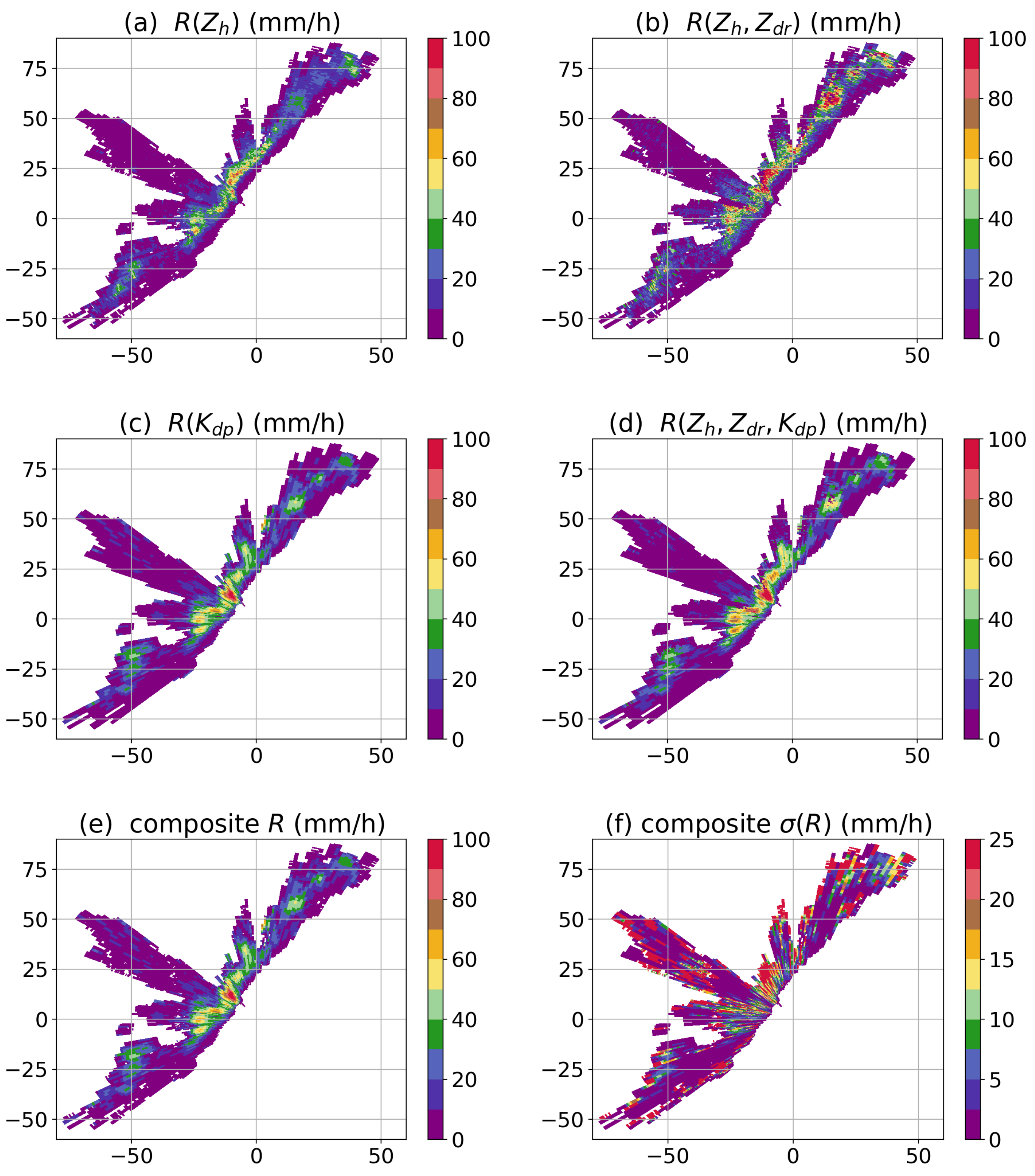
4. Rain Rate Estimation
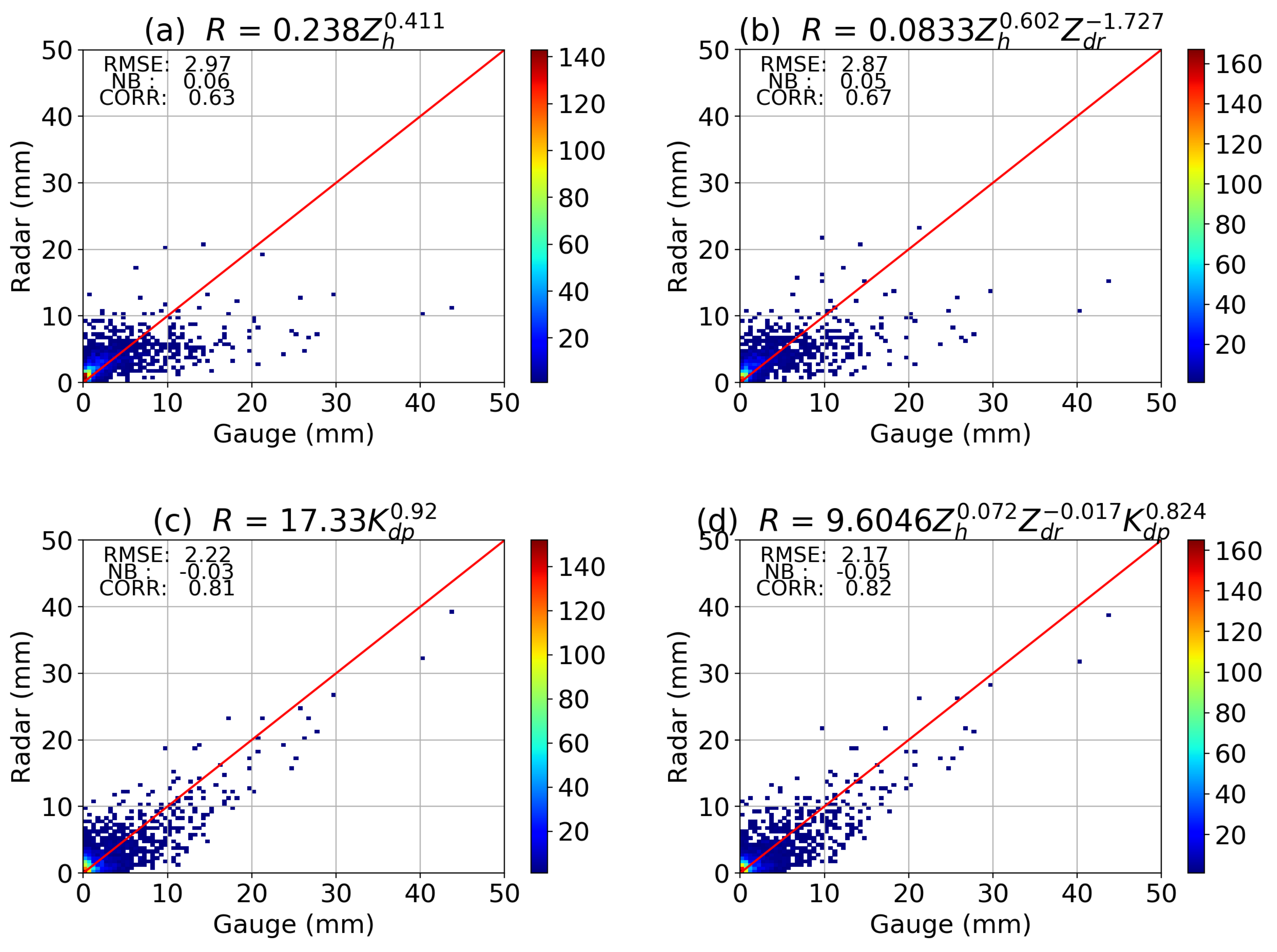
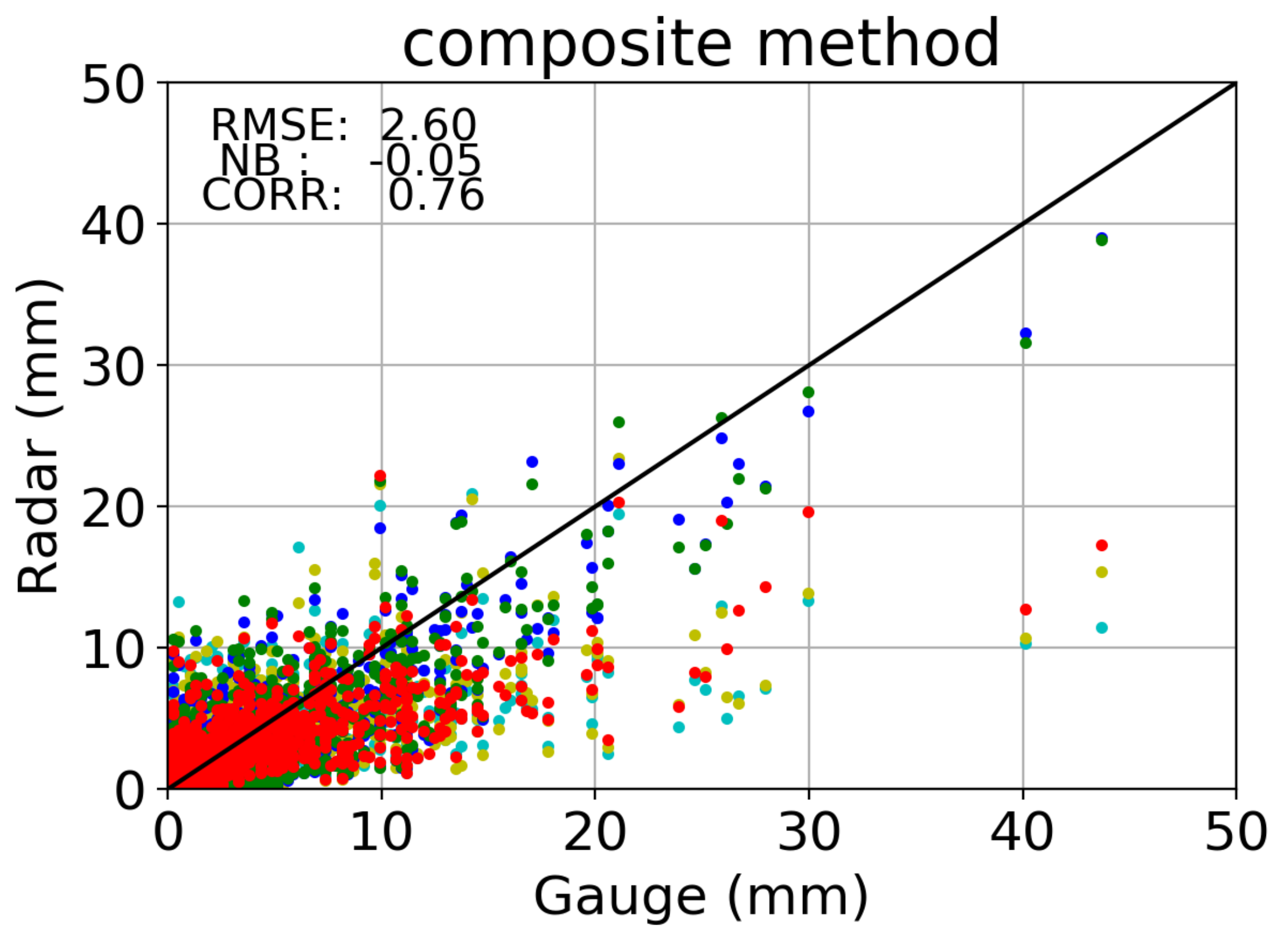
4.1. Retrieval of R
4.2. Retrieval of
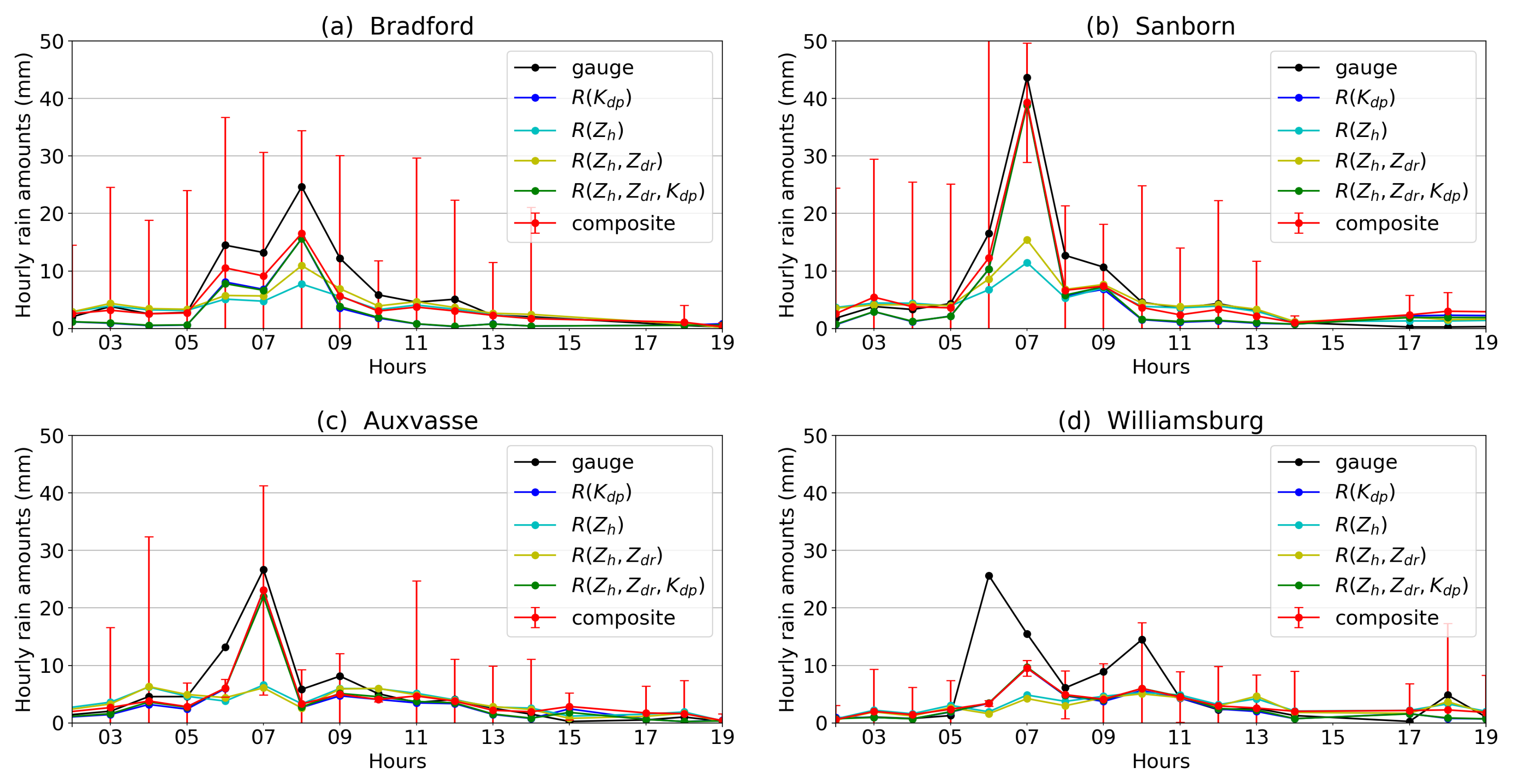
5. Case Studies
5.1. Squall Line Event: 7 March 2017
5.2. Prolonged Rain Event: 2–4 July 2016
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Attenuation-Based Rain Rate Estimation
References
- Anagnostou, E.N.; Anagnostou, M.N.; Krajewski, W.F.; Kruger, A.; Miriovsky, B.J. High-resolution rainfall estimation from X-band polarimetric radar measurements. J. Hydrometeorol. 2004, 5, 110–128. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Wang, Y.; Chen, H. The CASA quantitative precipitation estimation system: A five year validation study. Nat. Hazards Earth Syst. Sci. 2012, 12, 2811–2820. [Google Scholar] [CrossRef]
- Dolan, B.; Rutledge, S.A. A theory-based hydrometeor identification algorithm for X-Band polarimetric radars. J. Atmos. Ocean. Technol. 2009, 26, 2071–2088. [Google Scholar] [CrossRef]
- Lim, S.; Cifelli, R.; Chandrasekar, V.; Matrosov, S.Y. Precipitation Classification and Quantification Using X-Band Dual-Polarization Weather Radar: Application in the Hydrometeorology Testbed. J. Atmos. Ocean. Technol. 2013, 30, 2108–2120. [Google Scholar] [CrossRef]
- Raupach, T.H.; Berne, A. Retrieval of the raindrop size distribution from polarimetric radar data using double-moment normalisation. Atmos. Meas. Tech. 2017, 10, 2573–2594. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Application of the Generalized Gamma Model to Represent the Full Rain Drop Size Distribution Spectra. J. Appl. Meteorol. Climatol. 2018, 57, 1197–1210. [Google Scholar] [CrossRef]
- Hall, M.P.M.; Cherry, S.M.; Goddard, J.W.F.; Kennedy, G.R. Rain drop sizes and rainfall rate measured by dual-polarization radar. Nature 1980, 285, 195. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation. J. Appl. Meteorol. 1976, 15, 69–76. [Google Scholar] [CrossRef]
- Seliga, T.A.; Bringi, V.N. Differential reflectivity and differential phase shift: Applications in radar meteorology. Radio Sci. 1978, 13, 271–275. [Google Scholar] [CrossRef]
- Zrnić, D.S. Estimation of Spectral Moments for Weather Echoes. IEEE Trans. Geosci. Electron. 1979, 17, 113–128. [Google Scholar] [CrossRef]
- Bringi, V.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001; p. 636. [Google Scholar]
- Bringi, V.N.; Chandrasekar, V.; Balakrishnan, N.; Zrnić, D.S. An Examination of Propagation Effects in Rainfall on Radar Measurements at Microwave Frequencies. J. Atmos. Ocean. Technol. 1990, 7, 829–840. [Google Scholar] [CrossRef]
- Koffi, A.; Gosset, M.; Zahiri, E.P.; Ochou, A.; Kacou, M.; Cazenave, F.; Assamoi, P. Evaluation of X-band polarimetric radar estimation of rainfall and rain drop size distribution parameters in West Africa. Atmos. Res. 2014, 143, 438–461. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Kennedy, P.C.; Cifelli, R. Experimentally based estimates of relations between X-band radar signal attenuation characteristics and differential phase in rain. J. Atmos. Ocean. Technol. 2014, 31, 2442–2450. [Google Scholar] [CrossRef][Green Version]
- Matrosov, S.Y.; Kingsmill, D.E.; Martner, B.E.; Ralph, F.M. The utility of X-band polarimetric radar for quantitative estimates of rainfall parameters. J. Hydrometeorol. 2005, 6, 248–262. [Google Scholar] [CrossRef]
- Carey, L.D.; Rutledge, S.A.; Ahijevych, D.A.; Keenan, T.D. Correcting Propagation Effects in C-Band Polarimetric Radar Observations of Tropical Convection Using Differential Propagation Phase. J. Appl. Meteorol. 2000, 39, 1405–1433. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnić, D.S. Precipitation and Attenuation Measurements at a 10-cm Wavelength. J. Appl. Meteorol. 1995, 34, 2121–2134. [Google Scholar] [CrossRef]
- Testud, J.; Bouar, E.L.; Obligis, E.; Ali-Mehenni, M. The Rain Profiling Algorithm Applied to Polarimetric Weather Radar. J. Atmos. Ocean. Technol. 2000, 17, 332–356. [Google Scholar] [CrossRef]
- Smyth, T.J.; Illingworth, A.J. Correction for attenuation of radar reflectivity using polarization data. Q. J. R. Meteorol. Soc. 1998, 124, 2393–2415. [Google Scholar] [CrossRef]
- Bringi, V.N.; Keenan, T.; Chandrasekar, V. Correcting C-band radar reflectivity and differential reflectivity data for rain attenuation: A self-consistent method with constraints. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1906–1915. [Google Scholar] [CrossRef]
- Park, S.; Bringi, V.; Chandrasekar, V.; Maki, M.; Iwanami, K. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part I: Theoretical and empirical basis. J. Atmos. Ocean. Technol. 2005, 22, 1621–1632. [Google Scholar] [CrossRef]
- Park, S.; Maki, M.; Iwanami, K.; Bringi, V.; Chandrasekar, V. Correction of radar reflectivity and differential reflectivity for rain attenuation at X band. Part II: Evaluation and application. J. Atmos. Ocean. Technol. 2005, 22, 1633–1655. [Google Scholar] [CrossRef]
- Gorgucci, E.; Chandrasekar, V. Evaluation of attenuation correction methodology for dual-polarization radars: Application to X-band systems. J. Atmos. Ocean. Technol. 2005, 22, 1195–1206. [Google Scholar] [CrossRef]
- Anagnostou, M.N.; Kalogiros, J.; Anagnostou, E.N.; Tarolli, M.; Papadopoulos, A.; Borga, M. Performance evaluation of high-resolution rainfall estimation by X-band dual-polarization radar for flash flood applications in mountainous basins. J. Hydrol. 2010, 394, 4–16. [Google Scholar] [CrossRef]
- Cifelli, R.; Chandrasekar, V.; Lim, S.; Kennedy, P.C.; Wang, Y.; Rutledge, S.A. A new dual-polarization radar rainfall algorithm: Application in Colorado precipitation events. J. Atmos. Ocean. Technol. 2011, 28, 352–364. [Google Scholar] [CrossRef]
- Giangrande, S.E.; Ryzhkov, A.V. Estimation of rainfall based on the results of polarimetric echo classification. J. Appl. Meteorol. Climatol. 2008, 47, 2445–2462. [Google Scholar] [CrossRef]
- Gorgucci, E.; Baldini, L. Influence of Beam Broadening on the Accuracy of Radar Polarimetric Rainfall Estimation. J. Hydrometeorol. 2015, 16, 1356–1371. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Clark, K.A.; Martner, B.E.; Tokay, A. X-band polarimetric radar measurements of rainfall. J. Appl. Meteorol. 2002, 41, 941–952. [Google Scholar] [CrossRef]
- Mishra, K.V.; Krajewski, W.F.; Goska, R.; Ceynar, D.; Seo, B.C.; Kruger, A.; Niemeier, J.J.; Galvez, M.B.; Thurai, M.; Bringi, V.N.; et al. Deployment and Performance Analyses of High-Resolution Iowa XPOL Radar System during the NASA IFloodS Campaign. J. Hydrometeorol. 2016, 17, 455–479. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Giangrande, S.E.; Schuur, T.J. Rainfall Estimation with a Polarimetric Prototype of WSR-88D. J. Appl. Meteorol. 2005, 44, 502–515. [Google Scholar] [CrossRef]
- McLaughlin, D.; Pepyne, D.; Chandrasekar, V.; Philips, B.; Kurose, J.; Zink, M.; Droegemeier, K.; Cruz-Pol, S.; Junyent, F.; Brotzge, J.; et al. Short-Wavelength Technology and the Potential For Distributed Networks of Small Radar Systems. Bull. Am. Meteorol. Soc. 2009, 90, 1797–1818. [Google Scholar] [CrossRef]
- Sachidananda, M.; Zrnić, D.S. Differential propagation phase shift and rainfall rate estimation. Radio Sci. 1986, 21, 235–247. [Google Scholar] [CrossRef]
- Wang, Y.; Chandrasekar, V. Algorithm for estimation of the specific differential phase. J. Atmos. Ocean. Technol. 2009, 26, 2565–2578. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Zrnić, D.S. Comparison of Dual-Polarization Radar Estimators of Rain. J. Atmos. Ocean. Technol. 1995, 12, 249–256. [Google Scholar] [CrossRef]
- Zrnić, D.S.; Ryzhkov, A. Advantages of Rain Measurements Using Specific Differential Phase. J. Atmos. Ocean. Technol. 1996, 13, 454–464. [Google Scholar] [CrossRef]
- Wen, G.; Fox, N.I.; Market, P.S. A Gaussian mixture method for specific differential phase retrieval at X-band frequency. Atmos. Meas. Tech. 2019, 12, 5613–5637. [Google Scholar] [CrossRef]
- Decker, W.L. Climate of Missouri 2019, Missouri Climate Center Home Page. Available online: http://climate.missouri.edu/climate.php (accessed on 26 March 2020).
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Ellerbæk Nielsen, J.; ten Veldhuis, M.C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F. Radar-rain gauge comparisons under observational uncertainties. J. Appl. Meteorol. 1999, 38, 1519–1525. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.F.; Kruger, A. Sampling errors of tipping-bucket rain gauge measurements. J. Hydrol. Eng. 2001, 6, 159–166. [Google Scholar] [CrossRef]
- May, P.T.; Keenan, T.D.; Zrnić, D.S.; Carey, L.D.; Rutledge, S.A. Polarimetric Radar Measurements of Tropical Rain at a 5-cm Wavelength. J. Appl. Meteorol. 1999, 38, 750–765. [Google Scholar] [CrossRef]
- May, P.T.; Strauch, R.G. Reducing the Effect of Ground Clutter on Wind Profiler Velocity Measurements. J. Atmos. Ocean. Technol. 1998, 15, 579–586. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Karstens, C.; Krause, J.; Tang, L. Quality Control of Weather Radar Data Using Polarimetric Variables. J. Atmos. Ocean. Technol. 2014, 31, 1234–1249. [Google Scholar] [CrossRef]
- Rennie, S.J.; Curtis, M.; Peter, J.; Seed, A.W.; Steinle, P.J.; Wen, G. Bayesian Echo Classification for Australian Single-Polarization Weather Radar with Application to Assimilation of Radial Velocity Observations. J. Atmos. Ocean. Technol. 2015, 32, 1341–1355. [Google Scholar] [CrossRef]
- Williams, C.R.; May, P.T. Uncertainties in Profiler and Polarimetric DSD Estimates and Their Relation to Rainfall Uncertainties. J. Atmos. Ocean. Technol. 2008, 25, 1881–1887. [Google Scholar] [CrossRef]
- Hubbert, J.; Bringi, V.N. An Iterative Filtering Technique for the Analysis of Copolar Differential Phase and Dual-Frequency Radar Measurements. J. Atmos. Ocean. Technol. 1995, 12, 643–648. [Google Scholar] [CrossRef]
- Van de Beek, C.; Leijnse, H.; Stricker, J.; Uijlenhoet, R.; Russchenberg, H. Performance of high-resolution X-band radar for rainfall measurement in The Netherlands. Hydrol. Earth Syst. Sci. 2010, 14, 205–221. [Google Scholar] [CrossRef]
- Wen, G.; Xiao, H.; Yang, H.; Bi, Y.; Xu, W. Characteristics of summer and winter precipitation over northern China. Atmos. Res. 2017, 197, 390–406. [Google Scholar] [CrossRef]
- Gorgucci, E.; Chandrasekar, V.; Baldini, L. Correction of X-band radar observation for propagation effects based on the self-consistency principle. J. Atmos. Ocean. Technol. 2006, 23, 1668–1681. [Google Scholar] [CrossRef]
- Green, A.W. An Approximation for the Shapes of Large Raindrops. J. Appl. Meteorol. 1975, 14, 1578–1583. [Google Scholar] [CrossRef]
- Matrosov, S.Y. Evaluating Polarimetric X-Band Radar Rainfall Estimators during HMT. J. Atmos. Ocean. Technol. 2010, 27, 122–134. [Google Scholar] [CrossRef]
- Wen, G.; Chen, H.; Zhang, G.; Sun, J. An Inverse Model for Raindrop Size Distribution Retrieval with Polarimetric Variables. Remote Sens. 2018, 10, 1179. [Google Scholar] [CrossRef]
- Sachidananda, M.; Zrnić, D.S. Rain Rate Estimates from Differential Polarization Measurements. J. Atmos. Ocean. Technol. 1987, 4, 588–598. [Google Scholar] [CrossRef]
- Matrosov, S.Y.; Cifelli, R.; Kennedy, P.C.; Nesbitt, S.W.; Rutledge, S.A.; Bringi, V.N.; Martner, B.E. A Comparative Study of Rainfall Retrievals Based on Specific Differential Phase Shifts at X- and S-Band Radar Frequencies. J. Atmos. Ocean. Technol. 2006, 23, 952–963. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef]
- Pepler, A.S.; May, P.T.; Thurai, M. A Robust Error-Based Rain Estimation Method for Polarimetric Radar. Part I: Development of a Method. J. Appl. Meteorol. Climatol. 2011, 50, 2092–2103. [Google Scholar] [CrossRef]
- Pepler, A.S.; May, P.T. A robust error-based rain estimation method for polarimetric radar. Part II: Case study. J. Appl. Meteorol. Climatol. 2012, 51. [Google Scholar] [CrossRef]
- Bringi, V.N.; Williams, C.R.; Thurai, M.; May, P.T. Using dual-polarized radar and dual-frequency profiler for DSD characterization: A case study from Darwin, Australia. J. Atmos. Ocean. Technol. 2009, 26, 2107–2122. [Google Scholar] [CrossRef]
- Otto, T.; Russchenberg, H.W. Estimation of specific differential phase and differential backscatter phase from polarimetric weather radar measurements of rain. IEEE Geosci. Remote Sens. Lett. 2011, 8, 988–992. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; May, P.T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia. J. Atmos. Ocean. Technol. 2010, 27, 932–942. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Beard, K.V. A wind tunnel investigation of the internal circulation and shape of water drops falling at terminal velocity in air. Q. J. R. Meteorol. Soc. 1970, 96, 247–256. [Google Scholar] [CrossRef]
- Pallardy, Q.; Fox, N.I. Accounting for rainfall evaporation using dual-polarization radar and mesoscale model data. J. Hydrol. 2018, 557, 573–588. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Zrnić, D. Assessment of Rainfall Measurement That Uses Specific Differential Phase. J. Appl. Meteorol. 1996, 35, 2080–2090. [Google Scholar] [CrossRef]
- Chen, H.; Cifelli, R.; White, A. Improving operational radar rainfall estimates using profiler observations over complex terrain in Northern California. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1821–1832. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F.; Smith, J. Uncertainty Quantification of Mean-Areal Radar-Rainfall Estimates. J. Atmos. Ocean. Technol. 1999, 16, 206–215. [Google Scholar] [CrossRef]
- Diederich, M.; Ryzhkov, A.; Simmer, C.; Zhang, P.; Trömel, S. Use of Specific Attenuation for Rainfall Measurement at X-Band Radar Wavelengths. Part II: Rainfall Estimates and Comparison with Rain Gauges. J. Hydrometeorol. 2015, 16, 503–516. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N.; Manić, A.B.; Šekeljić, N.J.; Notaroš, B.M. Investigating raindrop shapes, oscillation modes, and implications for radio wave propagation. Radio Sci. 2014, 49, 921–932. [Google Scholar] [CrossRef]
- Jameson, A. The effect of temperature on attenuation-correction schemes in rain using polarization propagation differential phase shift. J. Appl. Meteorol. 1992, 31, 1106–1118. [Google Scholar] [CrossRef]
- Ryzhkov, A.; Diederich, M.; Zhang, P.; Simmer, C. Potential utilization of specific attenuation for rainfall estimation, mitigation of partial beam blockage, and radar networking. J. Atmos. Ocean. Technol. 2014, 31, 599–619. [Google Scholar] [CrossRef]

| Date | Type | Phenomena | Movement | Shape and Size | Duration |
|---|---|---|---|---|---|
| 7 March 2017 | Convection | Rain, hail, and tornado | Southeast | Squall line, small scale | 5 h |
| 2–4 July 2016 | Stratiform | Rain | Northeast | Mesoscale | 27 h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, G.; Fox, N.I.; Market, P.S. The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty. Remote Sens. 2020, 12, 1072. https://doi.org/10.3390/rs12071072
Wen G, Fox NI, Market PS. The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty. Remote Sensing. 2020; 12(7):1072. https://doi.org/10.3390/rs12071072
Chicago/Turabian StyleWen, Guang, Neil I. Fox, and Patrick S. Market. 2020. "The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty" Remote Sensing 12, no. 7: 1072. https://doi.org/10.3390/rs12071072
APA StyleWen, G., Fox, N. I., & Market, P. S. (2020). The Quality Control and Rain Rate Estimation for the X-Band Dual-Polarization Radar: A Study of Propagation of Uncertainty. Remote Sensing, 12(7), 1072. https://doi.org/10.3390/rs12071072






