Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem
Abstract
1. Introduction
2. Materials and Methods
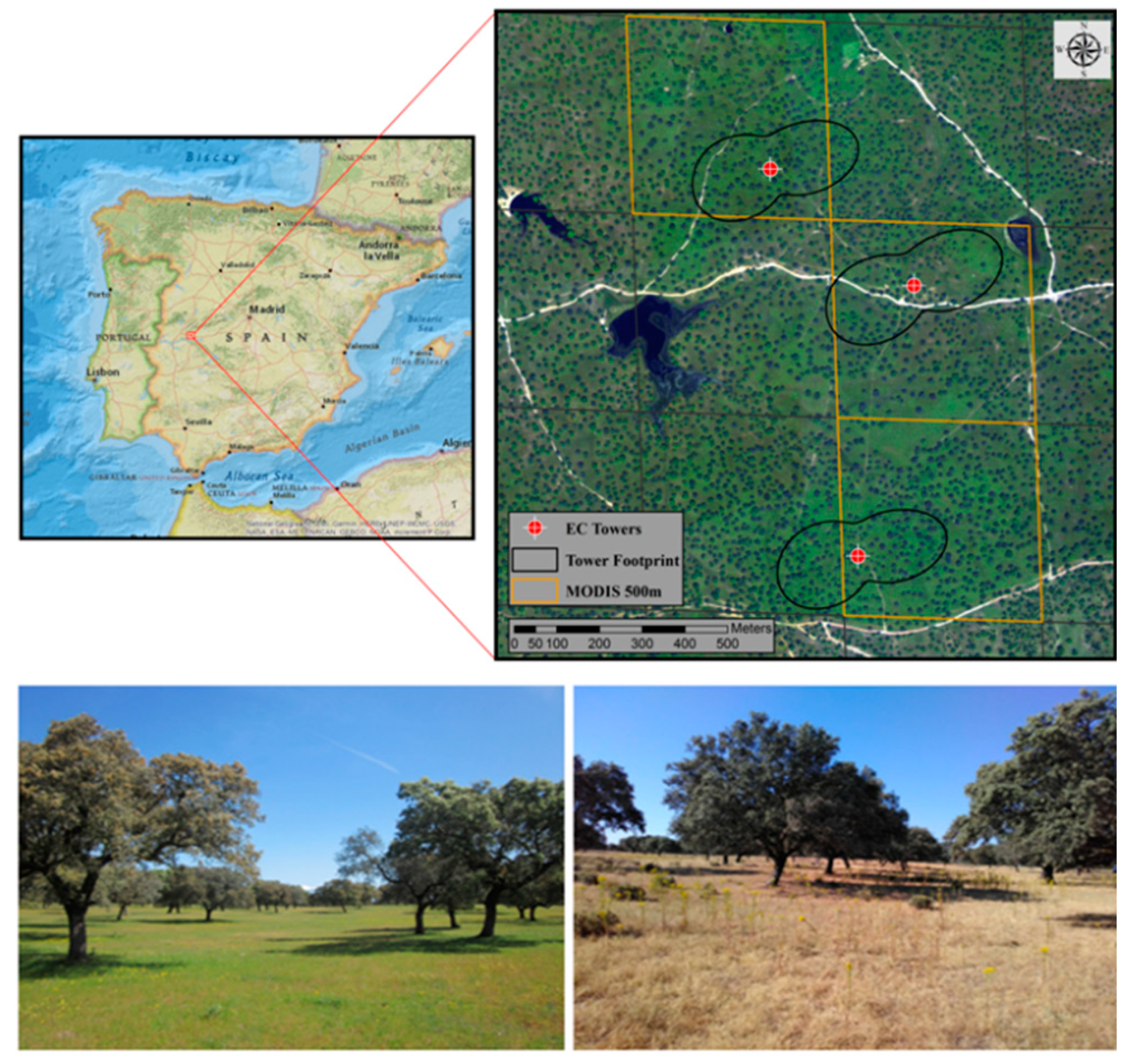
2.1. Study Site
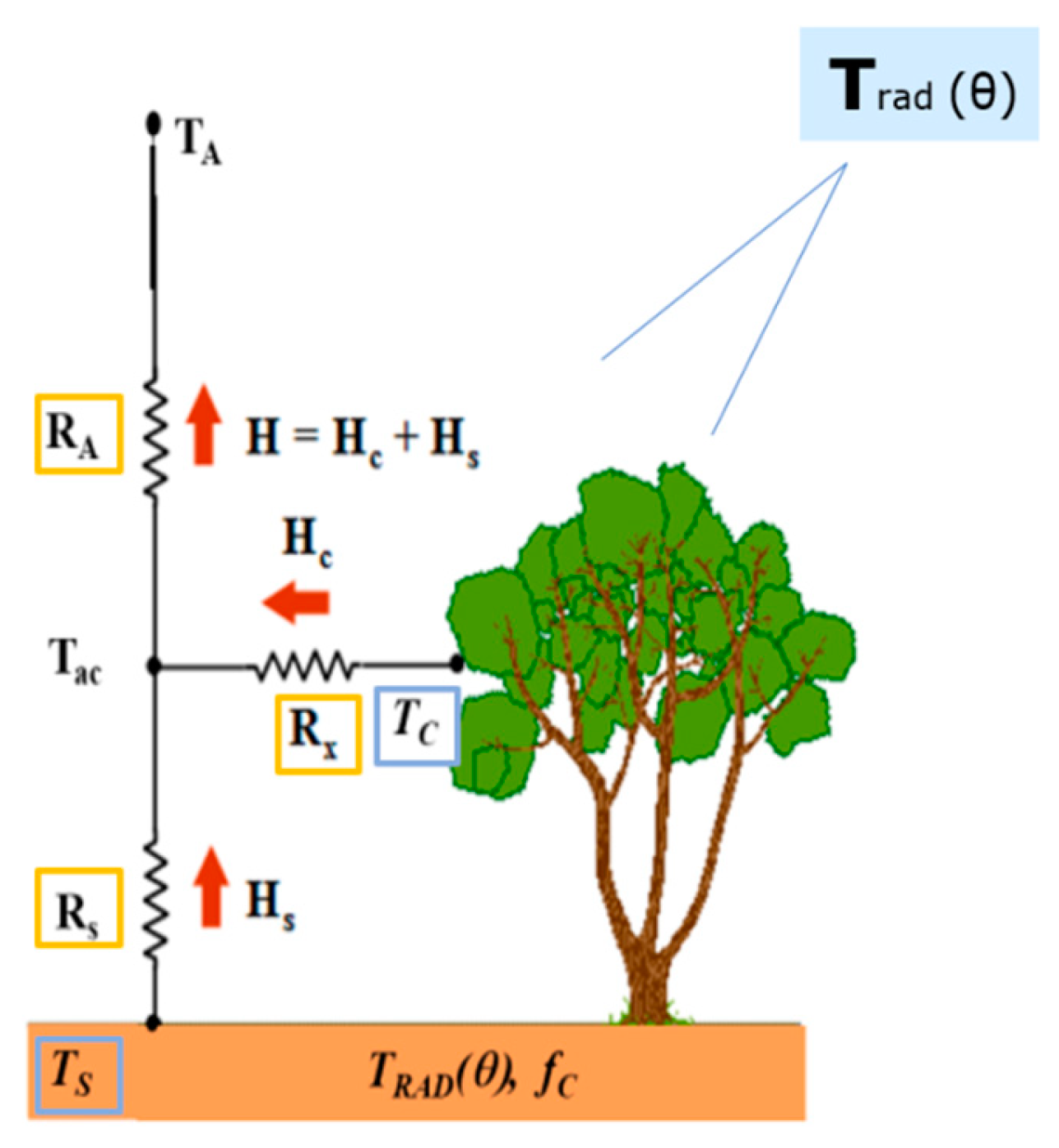
2.2. TSEB Model Overview
2.2.1. Radiation Transmission in Sparse Vegetation
2.2.2. Resistances within and below Canopy
2.3. Data
2.3.1. Eddy Covariance and Bio-Meteorological Measurements
2.3.2. Vegetation Biophysical Measurements
2.4. Model Simulations and Evaluation
2.4.1. Default TSEB Model Configuration
2.4.2. Sensitivity Analysis
Sobol´ Global Parameter Sensitivity Analysis
Input Local Sensitivity Analysis
2.4.3. End Member Simulations
2.4.4. Two-Season Modeling Approach
2.4.5. Model Evaluation
3. Results
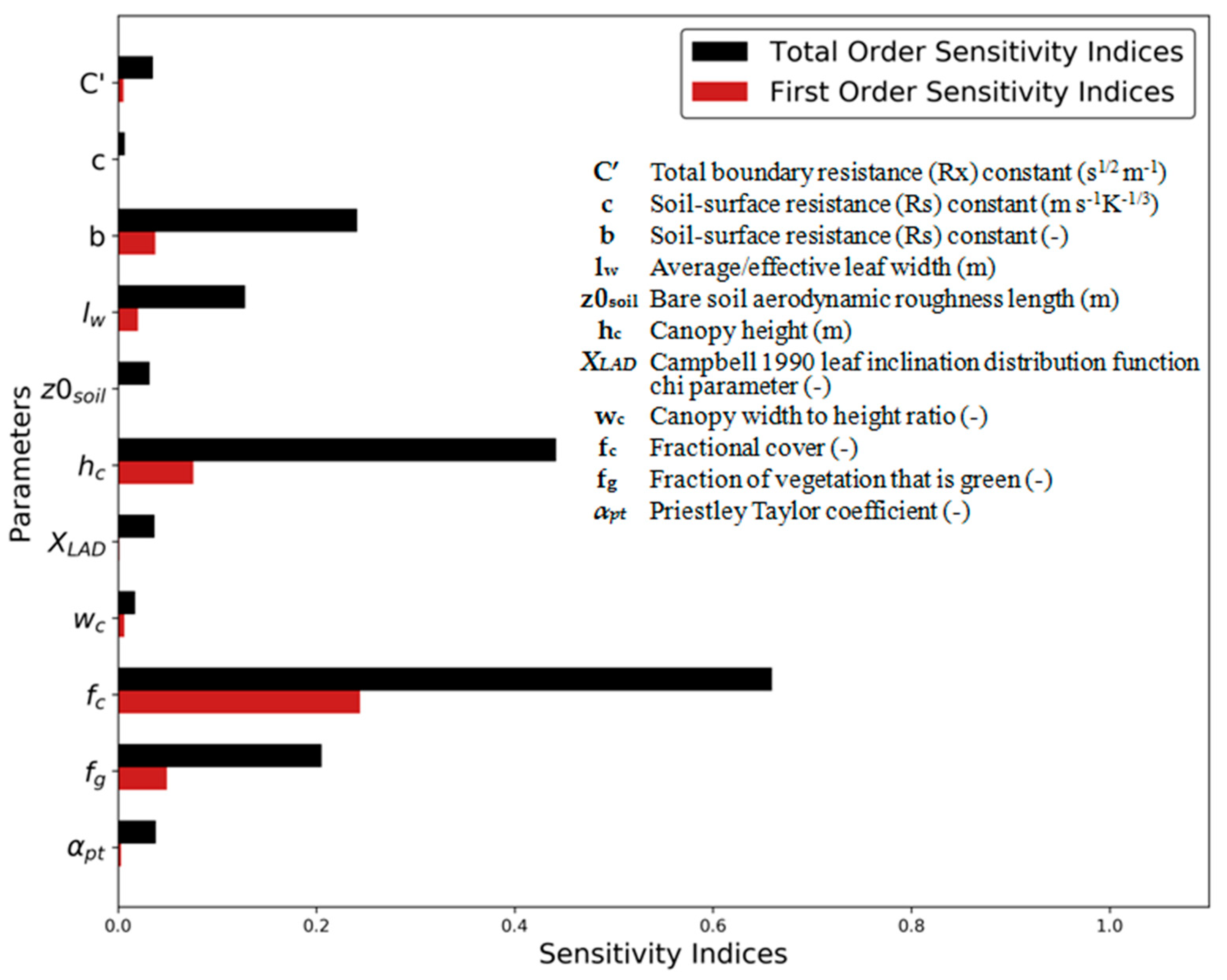
3.1. Sensitivity Analysis
3.1.1. Global Sobol´ Parameter SA
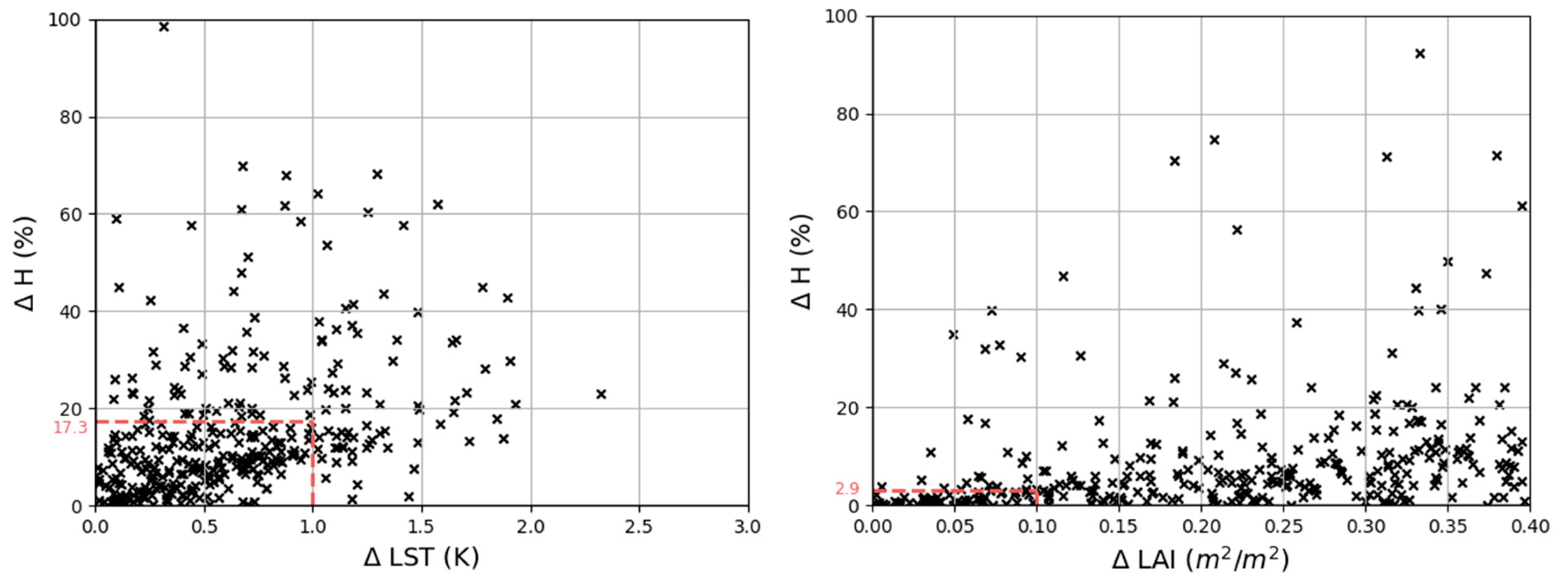
3.1.2. Local Input SA
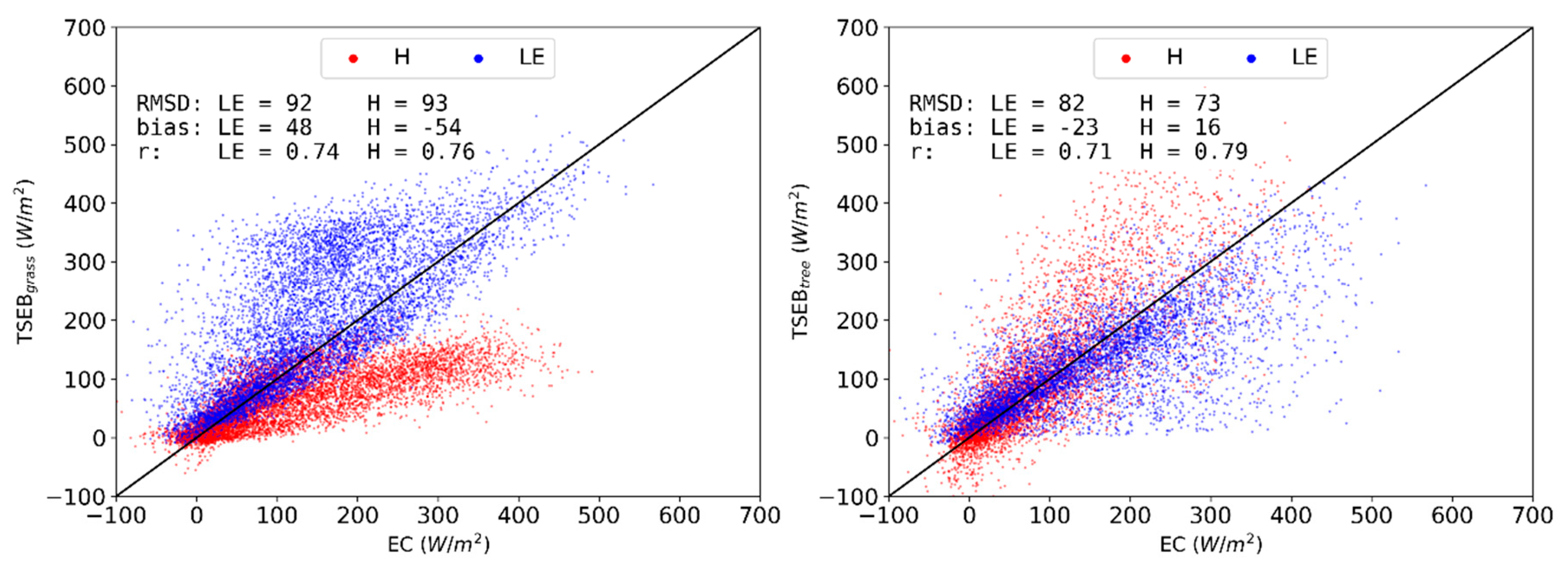
3.1.3. TSEBgrass, TSEBtree and TSEB-2S Model Configuration
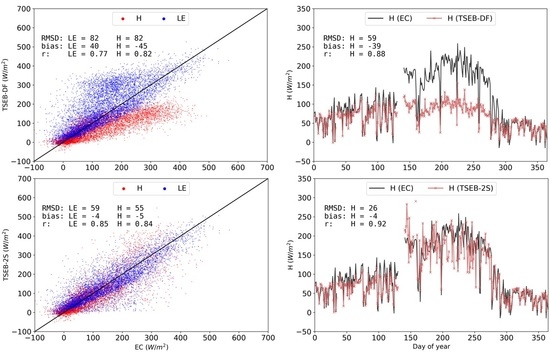
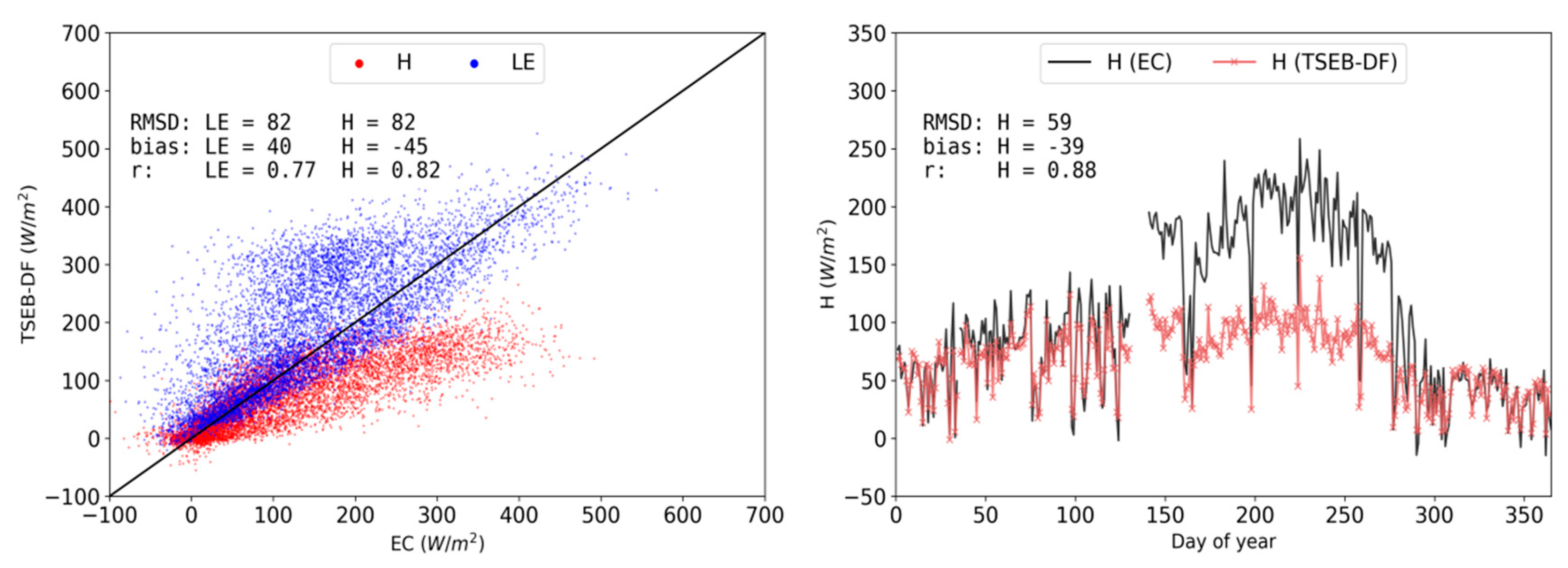
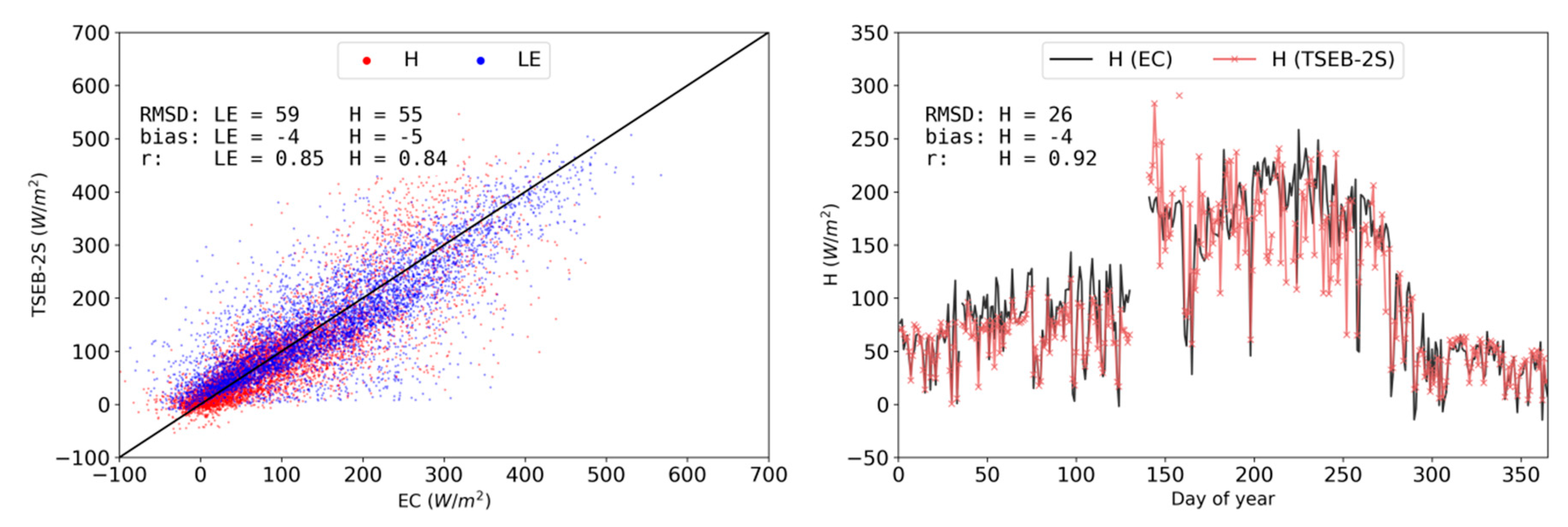
3.2. Model Evaluations for Main Simulation Period (2015 CT)
3.3. TSEB-2S Validation
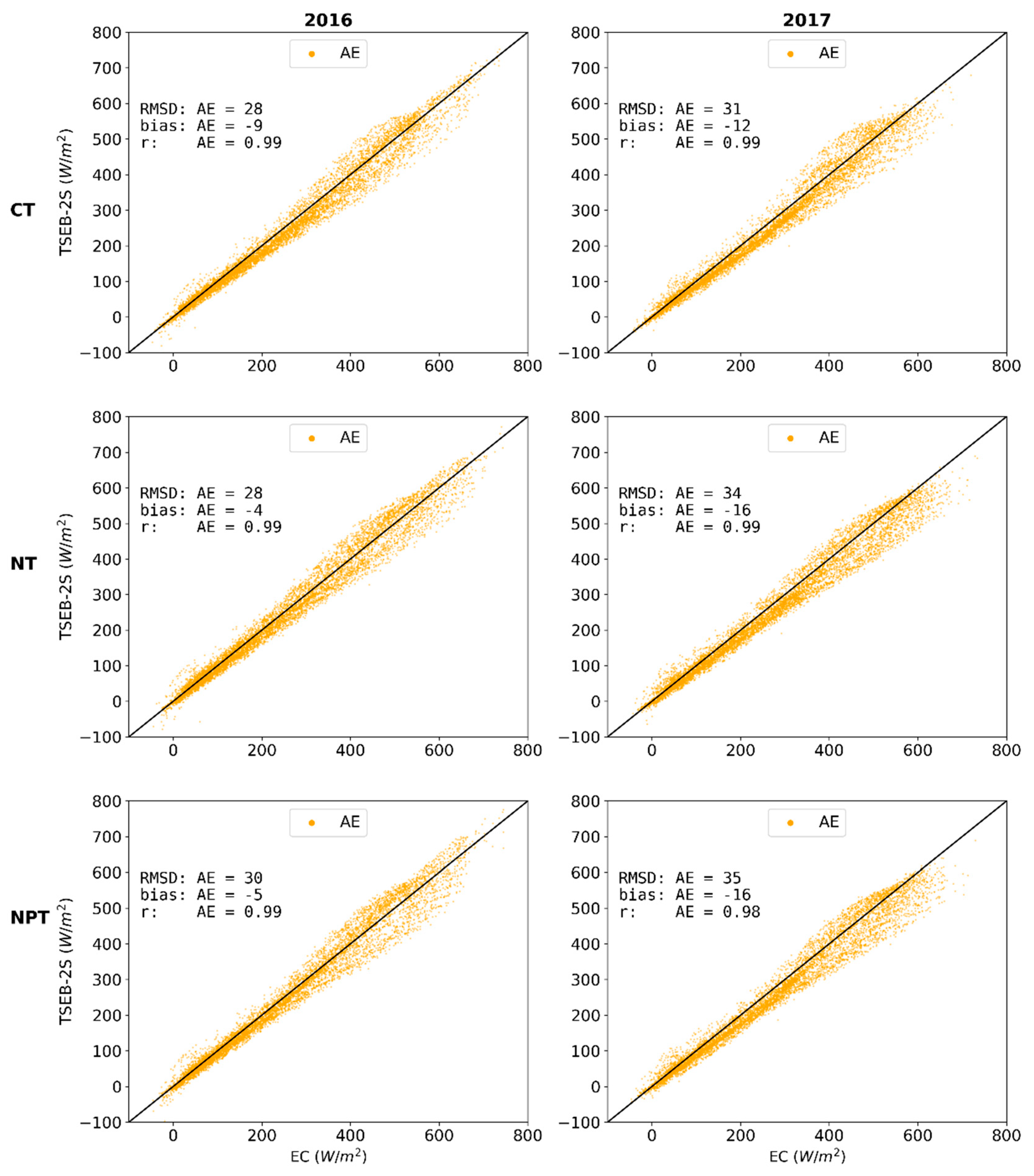
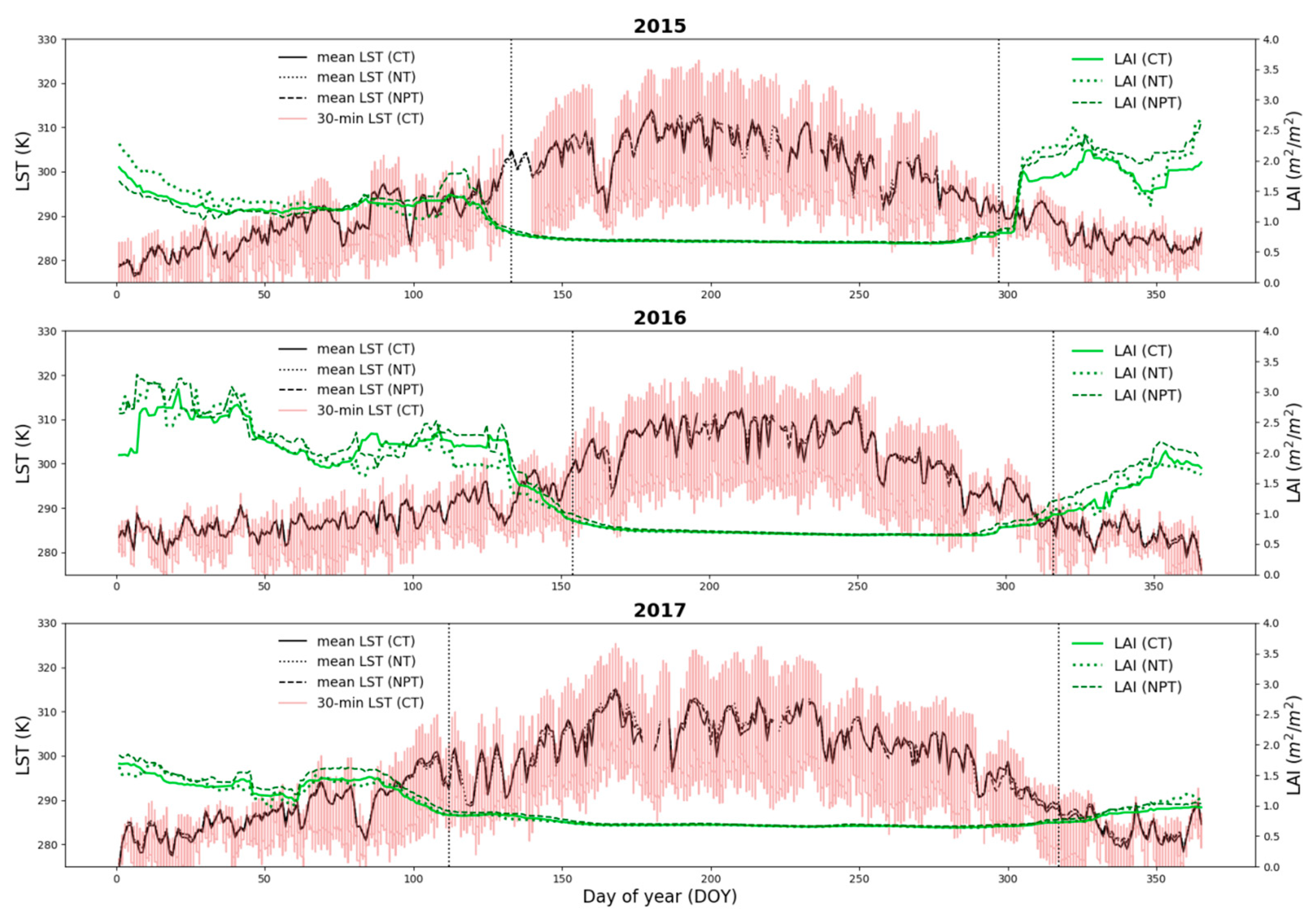
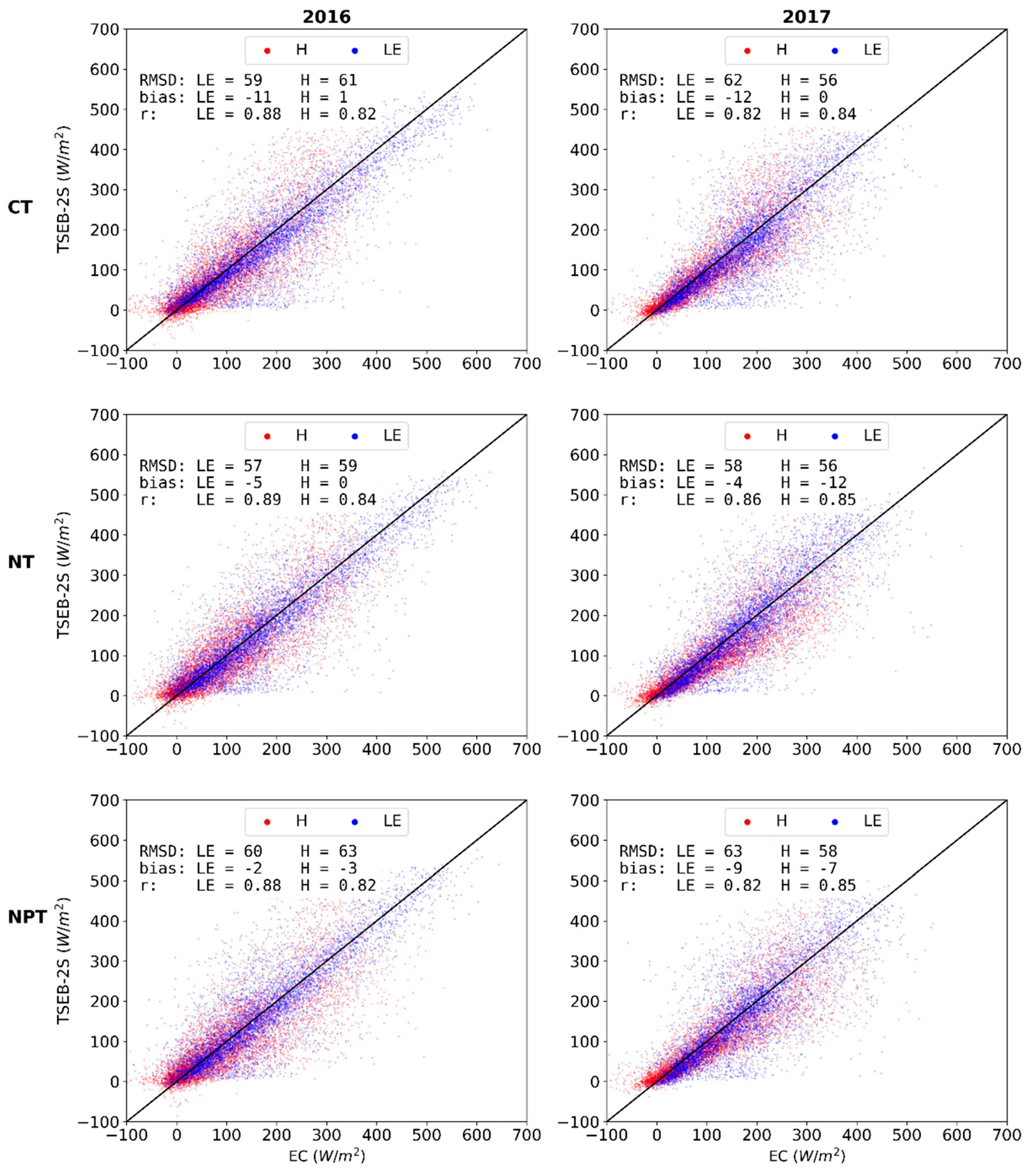
3.3.1. Independent Evaluations for 2016 and 2017 over CT, NT and NPT Towers
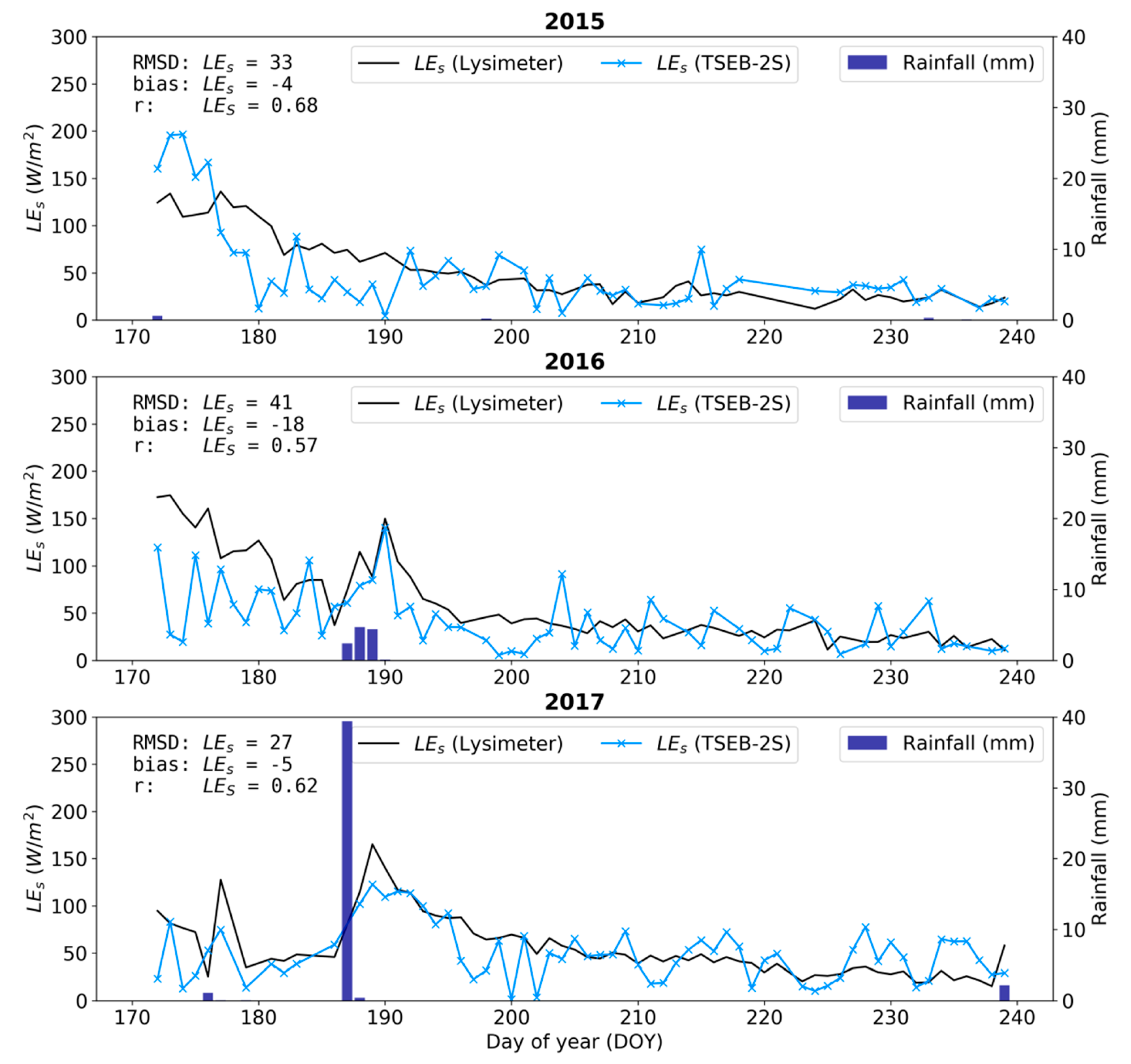
3.3.2. LE Partitioning
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
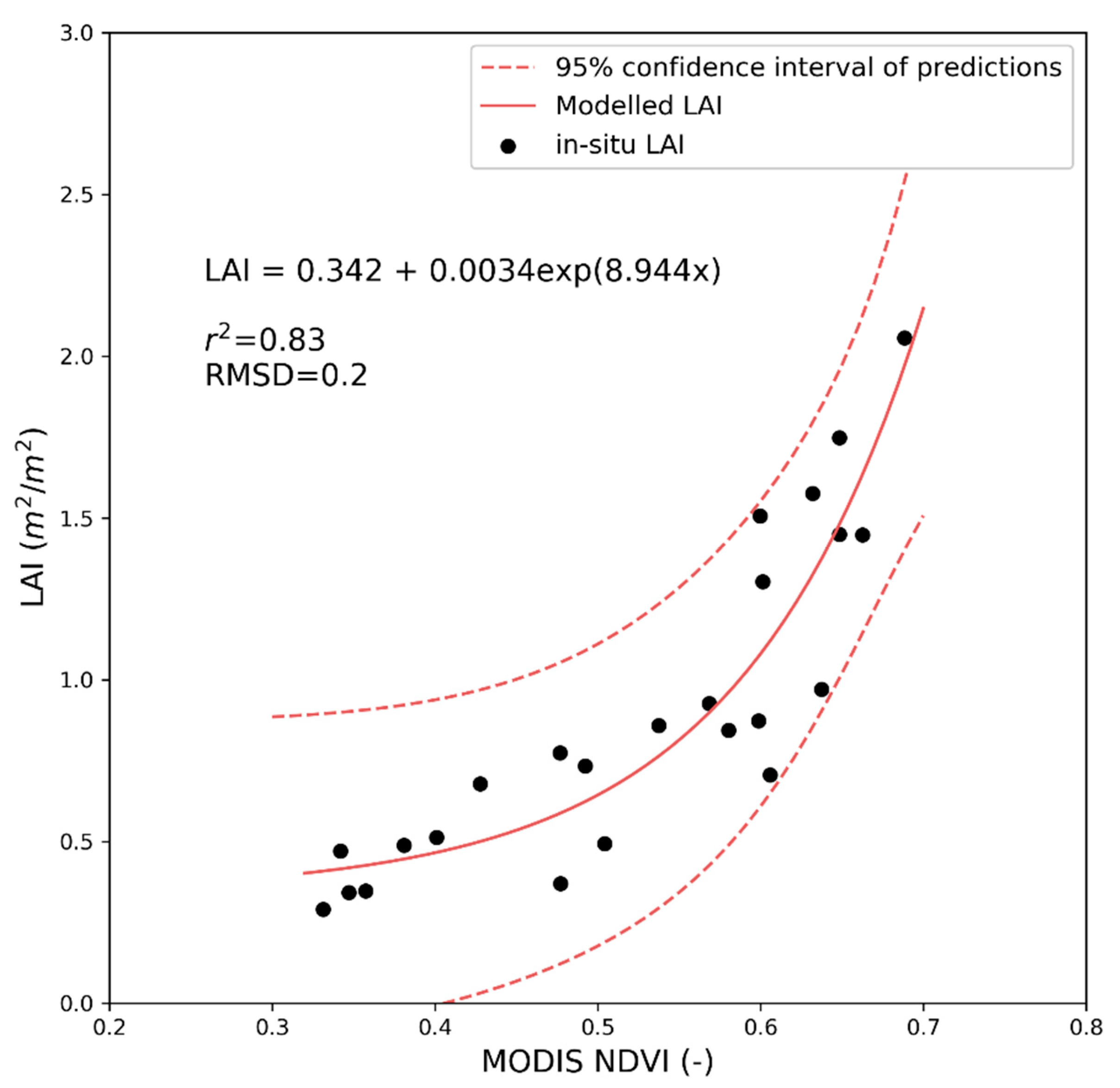
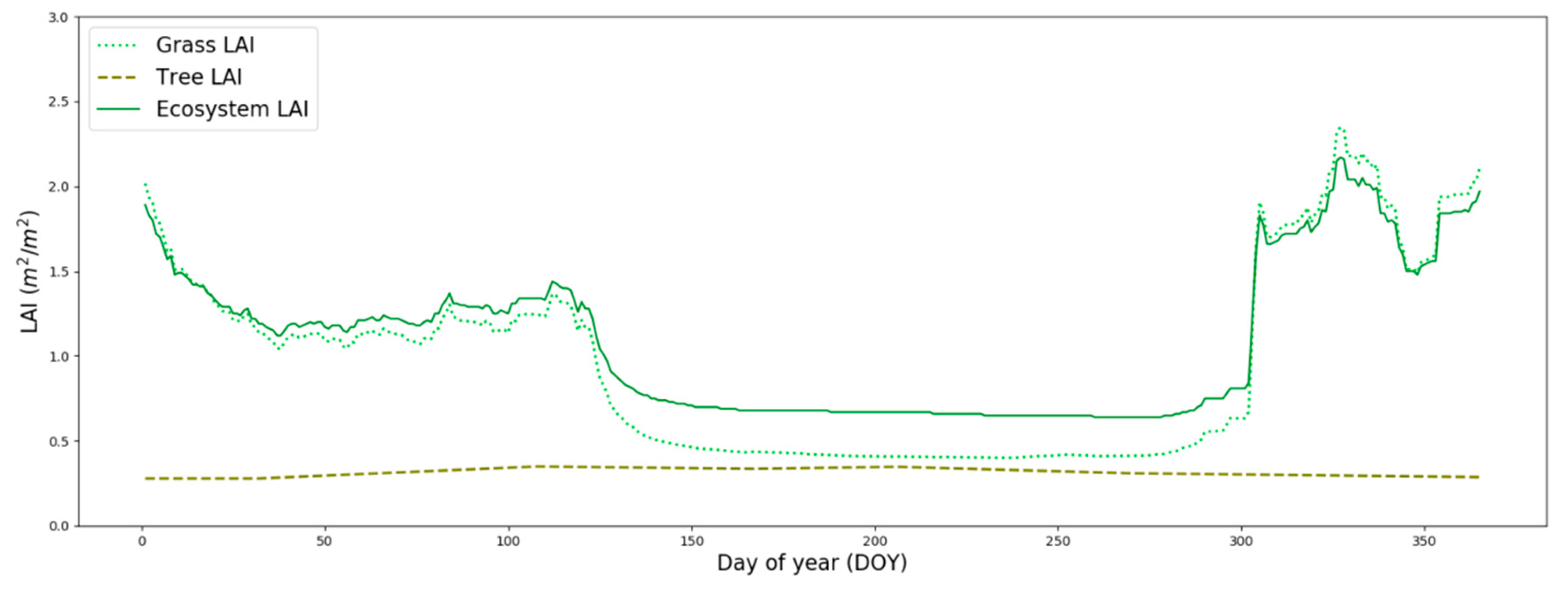
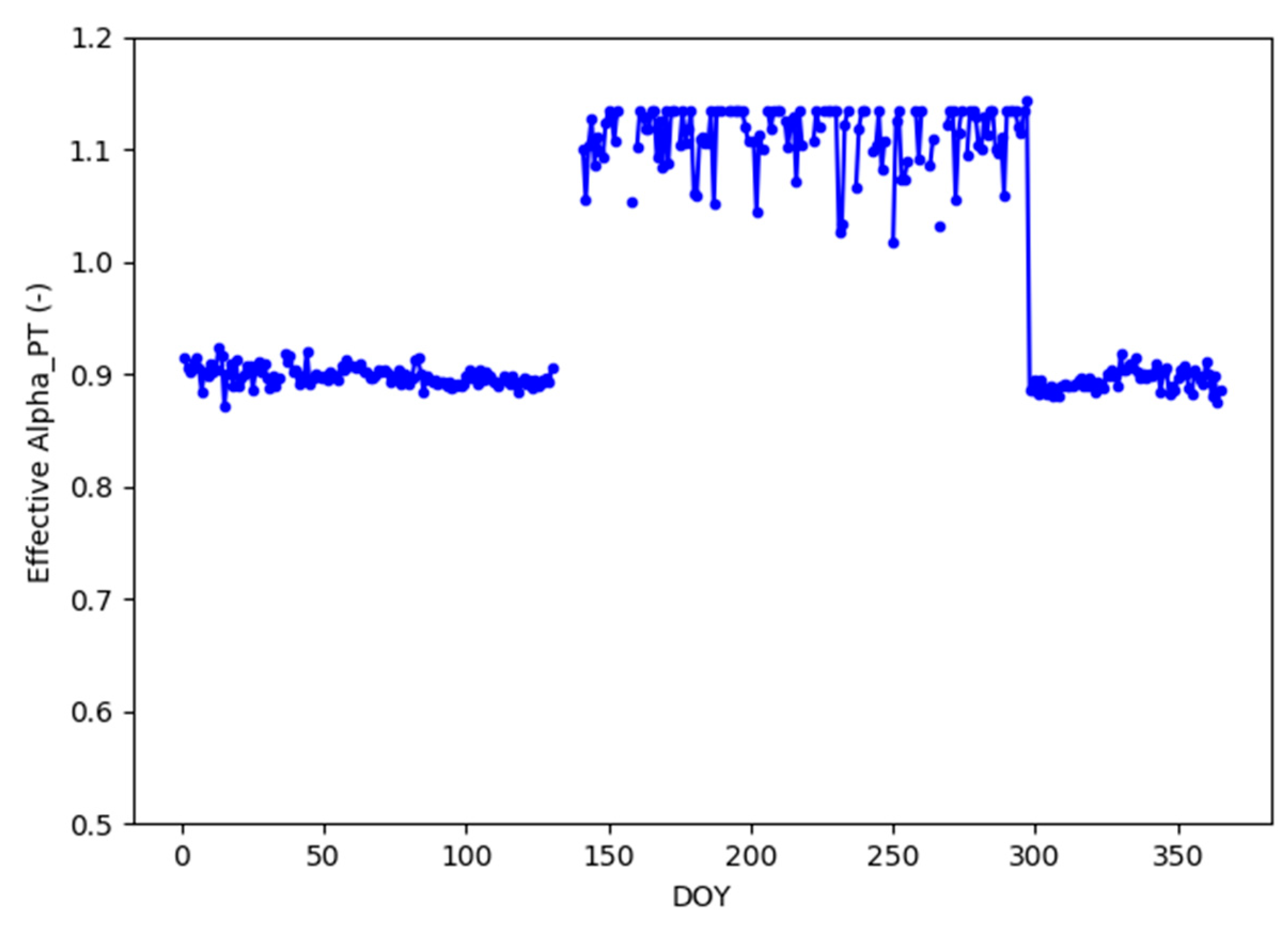
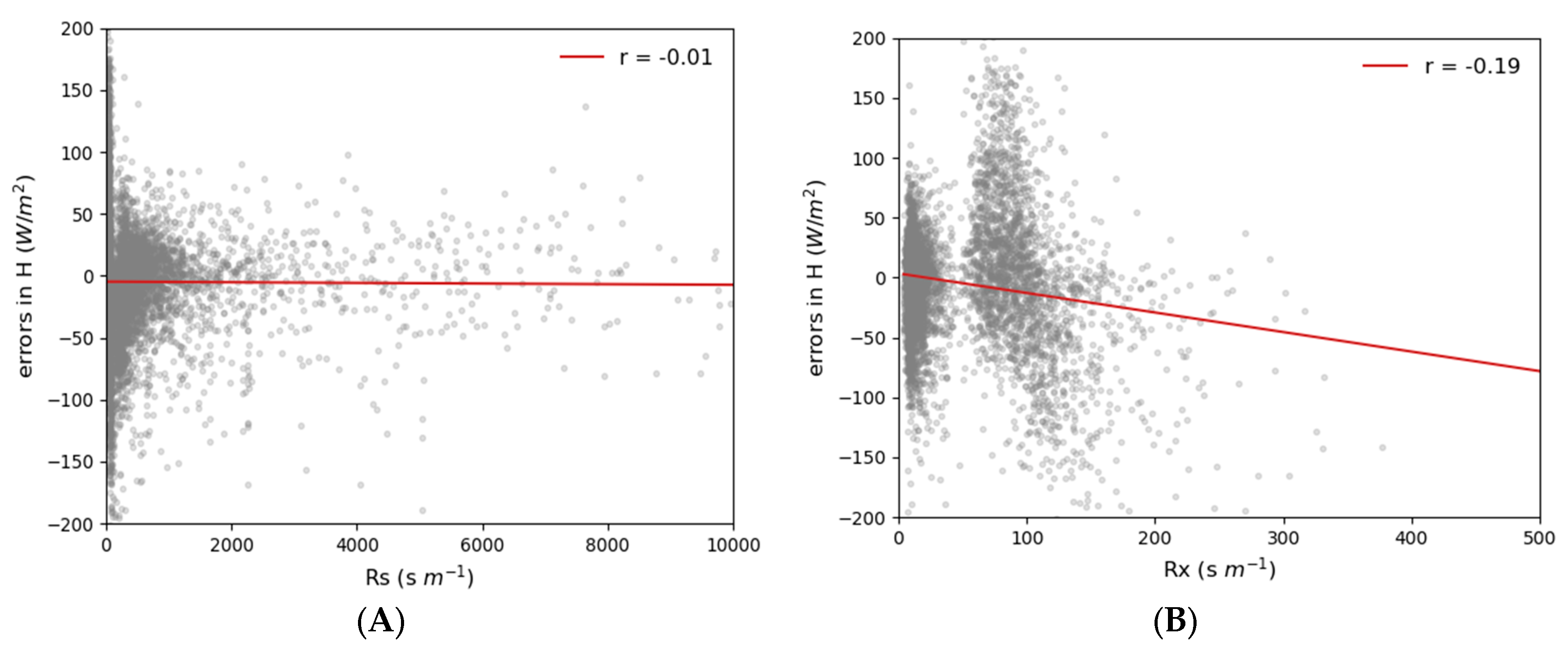
Appendix B
References
- Bonan, G.B.; Doney, S.C. Climate, ecosystems, and planetary futures: The challenge to predict life in Earth system models. Science 2018, 359, eaam8328. [Google Scholar] [CrossRef] [PubMed]
- Krinner, G.; Viovy, N.; de Noblet-Ducoudré, N.; Ogée, J.; Polcher, J.; Friedlingstein, P.; Ciais, P.; Sitch, S.; Prentice, I.C. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles 2005, 19. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Stoy, P.C.; El-Madany, T.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Liu, S.; Miralles, D.G.; Perez-Priego, O.; Skaggs, T.H. Reviews and syntheses: Turning the challenges of partitioning ecosystem evaporation and transpiration into opportunities. Biogeosci. Discuss. 2019, 10, 3747–3775. [Google Scholar] [CrossRef]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial water fluxes dominated by transpiration. Nature 2013, 496, 347. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Walker, J.P. Effects of spatial aggregation on the multi-scale estimation of evapotranspiration. Remote Sens. Environ. 2013, 131, 51–62. [Google Scholar] [CrossRef]
- Li, Y.; Huang, C.; Hou, J.; Gu, J.; Zhu, G.; Li, X. Mapping daily evapotranspiration based on spatiotemporal fusion of ASTER and MODIS images over irrigated agricultural areas in the Heihe River Basin, Northwest China. Agric. For. Meteorol. 2017, 244–245, 82–97. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C. Advances in thermal infrared remote sensing for land surface modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Su, Z. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. Discuss. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Trezza, R. Satellite-Based energy balance for mapping evapotranspiration with internalized calibration (METRIC)\97Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Guzinski, R.; Anderson, M.C.; Kustas, W.P.; Nieto, H.; Sandholt, I. Using a thermal-based two source energy balance model with time-differencing to estimate surface energy fluxes with day-night MODIS observations. Hydrol. Earth Syst. Sci. 2013, 17, 2809–2825. [Google Scholar] [CrossRef]
- Kustas, W.P.; Alfieri, J.G.; Nieto, H.; Wilson, T.G.; Gao, F.; Anderson, M.C. Utility of the two-source energy balance (TSEB) model in vine and interrow flux partitioning over the growing season. Irrig. Sci. 2019, 37, 375–388. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Alsina, M.M.; Prueger, J.H.; et al. Evaluation of TSEB turbulent fluxes using different methods for the retrieval of soil and canopy component temperatures from UAV thermal and multispectral imagery. Irrig Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef]
- Diarra, A.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Aouade, G.; Tavernier, A.; Boulet, G.; Ezzahar, J.; Merlin, O.; Khabba, S. Performance of the two-source energy budget (TSEB) model for the monitoring of evapotranspiration over irrigated annual crops in North Africa. Agric. Water Manag. 2017, 193, 71–88. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Norman, J.M.; Colaizzi, P.D.; Howell, T.A.; Prueger, J.H.; Meyers, T.P.; Wilson, T.B. Application of the Priestley-Taylor approach in a two-source surface energy balance model. J. Hydrometeor. 2010, 11, 185–198. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; García, M. Revisiting the paper “Using radiometric surface temperature for surface energy flux estimation in Mediterranean drylands from a two-source perspective”. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef]
- Li, Y.; Kustas, W.P.; Huang, C.; Nieto, H.; Haghighi, E.; Anderson, M.C.; Domingo, F.; Garcia, M.; Scott, R.L. Evaluating soil resistance formulations in thermal-based two-source energy balance (TSEB) model: Implications for heterogeneous semiarid and arid regions. Water Resour. Res. 2019, 55, 1059–1078. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the surface energy balance algorithm for land (SEBAL) and the two-source energy balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Jung, M.; Henkel, K.; Herold, M.; Churkina, G. Exploiting synergies of global land cover products for carbon cycle modeling. Remote Sens. Environ. 2006, 101, 534–553. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Schnabel, S.; Dahlgren, R.A.; Moreno-Marcos, G. Soil and water dynamics. In Mediterranean Oak Woodland Working Landscapes: Dehesas of Spain and Ranchlands of California; Campos, P., Huntsinger, L., Oviedo Pro, J.L., Starrs, P.F., Diaz, M., Standiford, R.B., Montero, G., Eds.; Landscape Series; Springer: Dordrecht, The Netherlands, 2013; pp. 91–121. ISBN 978-94-007-6707-2. [Google Scholar]
- Luo, Y.; El-Madany, T.; Filippa, G.; Ma, X.; Ahrens, B.; Carrara, A.; Gonzalez-Cascon, R.; Cremonese, E.; Galvagno, M.; Hammer, T. Using near-infrared-enabled digital repeat photography to track structural and physiological phenology in Mediterranean tree-grass ecosystems. Remote Sens. 2018, 10, 1293. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Xu, L.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak-grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Perez-Priego, O.; Katul, G.; Reichstein, M.; El-Madany, T.S.; Ahrens, B.; Carrara, A.; Scanlon, T.M.; Migliavacca, M. Partitioning eddy covariance water flux components using physiological and micrometeorological approaches. J. Geophys. Res. Biogeosci. 2018, 123. [Google Scholar] [CrossRef]
- Andreu, A.; Kustas, W.; Polo, M.; Carrara, A.; González-Dugo, M. Modeling surface energy fluxes over a dehesa (Oak Savanna) ecosystem using a thermal based two-source energy balance model (TSEB) I. Remote Sens. 2018, 10, 567. [Google Scholar] [CrossRef]
- Jin, X.; Xu, C.-Y.; Zhang, Q.; Singh, V.P. Parameter and modeling uncertainty simulated by GLUE and a formal Bayesian method for a conceptual hydrological model. J. Hydrol. 2010, 383, 147–155. [Google Scholar] [CrossRef]
- Migliavacca, M.; Sonnentag, O.; Keenan, T.F.; Cescatti, A.; O’Keefe, J.; Richardson, A.D. On the uncertainty of phenological responses to climate change, and implications for a terrestrial biosphere model. Biogeosciences 2012, 9, 2063–2083. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Pianosi, F.; Iwema, J.; Rosolem, R.; Wagener, T. A multimethod global sensitivity analysis approach to support the calibration and evaluation of land surface models. In Sensitivity Analysis in Earth Observation Modelling; Elsevier: Amsterdam, The Netherlands, 2017; pp. 125–144. [Google Scholar]
- Rosolem, R.; Hoshin, G.; Shuttleworth, J.W.; Xubin, Z.; Gonçalves, L.G. A fully multiple-criteria implementation of the Sobol’ method for parameter sensitivity analysis. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Kustas, W.P.; Nieto, H.; Prueger, J.H.; Hipps, L.E.; McKee, L.G.; Gao, F.; Los, S. Influence of wind direction on the surface roughness of vineyards. Irrig. Sci. 2019, 37, 359–373. [Google Scholar] [CrossRef]
- Gan, G.; Gao, Y. Estimating time series of land surface energy fluxes using optimized two source energy balance schemes: Model formulation, calibration, and validation. Agric. For. Meteorol. 2015, 208, 62–75. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.; Jackson, T.J. Utility of remote sensing-based two-source energy balance model under low-and high-vegetation cover conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Sobol’, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Perez-Priego, O.; El-Madany, T.S.; Migliavacca, M.; Kowalski, A.S.; Jung, M.; Carrara, A.; Kolle, O.; Martín, M.P.; Pacheco-Labrador, J.; Moreno, G.; et al. Evaluation of eddy covariance latent heat fluxes with independent lysimeter and sapflow estimates in a Mediterranean savannah ecosystem. Agric. For. Meteorol. 2017, 236, 87–99. [Google Scholar] [CrossRef]
- El-Madany, T.S.; Reichstein, M.; Perez-Priego, O.; Carrara, A.; Moreno, G.; Pilar Martín, M.; Pacheco-Labrador, J.; Wohlfahrt, G.; Nieto, H.; Weber, U.; et al. Drivers of spatio-temporal variability of carbon dioxide and energy fluxes in a Mediterranean savanna ecosystem. Agric. For. Meteorol. 2018, 262, 258–278. [Google Scholar] [CrossRef]
- Casals, P.; Gimeno, C.; Carrara, A.; Lopez-Sangil, L.; Sanz, M. Soil CO2 efflux and extractable organic carbon fractions under simulated precipitation events in a Mediterranean Dehesa. Soil Biol. Biochem. 2009, 41, 1915–1922. [Google Scholar] [CrossRef]
- Migliavacca, M.; Perez-Priego, O.; Rossini, M.; El-Madany, T.S.; Moreno, G.; van der Tol, C.; Rascher, U.; Berninger, A.; Bessenbacher, V.; Burkart, A. Plant functional traits and canopy structure control the relationship between photosynthetic CO2 uptake and far-red sun-induced fluorescence in a Mediterranean grassland under different nutrient availability. New Phytol. 2017, 214, 1078–1091. [Google Scholar] [CrossRef] [PubMed]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of aerodynamic and radiometric surface temperature using precision weighing lysimeters. In Proceedings of the Remote Sensing and Modeling of Ecosystems for Sustainability; International Society for Optics and Photonics: Washington, DC, USA, 2004; Volume 5544, pp. 215–230. [Google Scholar]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Li, F.; Prueger, J.H.; Mecikalski, J.R. Effects of vegetation clumping on two-source model estimates of surface energy fluxes from an agricultural landscape during SMACEX. J. Hydrometeorol. 2005, 6, 892–909. [Google Scholar] [CrossRef]
- García, M.; Gajardo, J.; Riaño, D.; Zhao, K.; Martín, P.; Ustin, S. Canopy clumping appraisal using terrestrial and airborne laser scanning. Remote Sens. Environ. 2015, 161, 78–88. [Google Scholar] [CrossRef]
- Sauer, T.J.; Norman, J.M. Simulated canopy microclimate using estimated below-canopy soil surface transfer coefficients. Agric. For. Meteorol. 1995, 75, 135–160. [Google Scholar] [CrossRef]
- Kondo, J.; Ishida, S. Sensible heat flux from the Earth’s surface under natural convective conditions. J. Atmos. Sci. 1997, 54, 498–509. [Google Scholar] [CrossRef]
- McNaughton, K.G.; Van Den Hurk, B.J.J.M. A ‘Lagrangian’ revision of the resistors in the two-layer model for calculating the energy budget of a plant canopy. Bound. Layer Meteorol. 1995, 74, 261–288. [Google Scholar] [CrossRef]
- Goudriaan, J. Crop Micrometeorology: A Simulation Study; Center for Agricultural Publications and Documentation: Wageningen, The Netherlands, 1977. [Google Scholar]
- Schaudt, K.J.; Dickinson, R.E. An approach to deriving roughness length and zero-plane displacement height from satellite data, prototyped with BOREAS data. Agric. For. Meteorol. 2000, 104, 143–155. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound. Layer Meteorol. 1994, 71, 211–216. [Google Scholar] [CrossRef]
- Lindroth, A. Aerodynamic and canopy resistance of short-rotation forest in relation to leaf area index and climate. Bound. Layer Meteorol. 1993, 66, 265–279. [Google Scholar] [CrossRef]
- Weligepolage, K.; Gieske, A.S.M.; van der Tol, C.; Timmermans, J.; Su, Z. Effect of sub-layer corrections on the roughness parameterization of a Douglas fir forest. Agric. For. Meteorol. 2012, 162, 115–126. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Orgaz, F.; Testi, L.; Fereres, E. Measurement and modeling of evapotranspiration of olive (Olea europaea L.) orchards. Eur. J. Agron. 2000, 13, 155–163. [Google Scholar] [CrossRef]
- Foken, T.; Göockede, M.; Mauder, M.; Mahrt, L.; Amiro, B.; Munger, W. Post-Field data quality control. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 181–208. [Google Scholar]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T. Towards a standardized processing of net ecosystem exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Foken, T.; Aubinet, M.; Finnigan, J.J.; Leclerc, M.Y.; Mauder, M.; Paw, U.K.T. Results of a panel discussion about the energy balance closure correction for trace gases. Bull. Am. Meteorol. Soc. 2011, 92, ES13–ES18. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Jensen, R.; Mendiguren, G. Remotely sensed land-surface energy fluxes at sub-field scale in heterogeneous agricultural landscape and coniferous plantation. Biogeosciences 2014, 11, 5021–5046. [Google Scholar] [CrossRef]
- Kustas, W.P.; Alfieri, J.G.; Anderson, M.C.; Colaizzi, P.D.; Prueger, J.H.; Evett, S.R.; Neale, C.M.; French, A.N.; Hipps, L.E.; Chávez, J.L. Evaluating the two-source energy balance model using local thermal and surface flux observations in a strongly advective irrigated agricultural area. Adv. Water Resour. 2012, 50, 120–133. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Rashid Niaghi, A.; Jia, X.; Steele, D.D.; Scherer, T.F. Drainage water management effects on energy flux partitioning, evapotranspiration, and crop coefficients of corn. Agric. Water Manag. 2019, 225, 105760. [Google Scholar] [CrossRef]
- Santanello, J.A.; Friedl, M.A. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteorol. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; Hipps, L.E.; Los, S.; Prueger, J.H.; McKee, L.G.; Anderson, M.C. Impact of different within-canopy wind attenuation formulations on modelling sensible heat flux using TSEB. Irrig. Sci. 2019, 37, 315–331. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Verhoef, W. Canopy directional emissivity: Comparison between models. Remote Sens. Environ. 2005, 99, 304–314. [Google Scholar] [CrossRef]
- Sauer, T.J.; Norman, J.M.; Tanner, C.B.; Wilson, T.B. Measurement of heat and vapor transfer coefficients at the soil surface beneath a maize canopy using source plates. Agric. For. Meteorol. 1995, 75, 161–189. [Google Scholar] [CrossRef]
- Mendiguren, G.; Pilar Martín, M.; Nieto, H.; Pacheco-Labrador, J.; Jurdao, S. Seasonal variation in grass water content estimated from proximal sensing and MODIS time series in a Mediterranean Fluxnet site. Biogeosciences 2015, 12, 5523–5535. [Google Scholar] [CrossRef]
- Pacheco-Labrador, J.; El-Madany, T.S.; Martín, M.P.; Migliavacca, M.; Rossini, M.; Carrara, A.; Zarco-Tejada, P.J. Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem. Remote Sens 2017, 9, 608. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; de Miguel, E. Land surface temperature derived from airborne hyperspectral scanner thermal infrared data. Remote Sens. Environ. 2006, 102, 99–115. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H. Evaluating the feasibility of using Sentinel-2 and Sentinel-3 satellites for high-resolution evapotranspiration estimations. Remote Sens. Environ. 2019, 221, 157–172. [Google Scholar] [CrossRef]
- Defourny, P.; Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C.; Schlerf, M.; Santoro, M. Land Cover CCI: Product User Guide Version 2. Available online: https://www.esa-landcover-cci.org/?q=webfm_send/84 (accessed on 10 March 2020).
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; van Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; van Gorsel, E.; Knohl, A.; Law, B.E.; et al. Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
- Boulet, G.; Mougenot, B.; Lhomme, J.-P.; Fanise, P.; Lili-Chabaane, Z.; Olioso, A.; Bahir, M.; Rivalland, V.; Jarlan, L.; Merlin, O.; et al. The SPARSE model for the prediction of water stress and evapotranspiration components from thermal infra-red data and its evaluation over irrigated and rainfed wheat. Hydrol. Earth Syst. Sci. 2015, 19, 4653–4672. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. A two-source energy balance approach using directional radiometric temperature observations for sparse canopy covered surfaces. Agron. J. 2000, 92, 847–854. [Google Scholar] [CrossRef]
| Parameter/Variable | Description | Source | Purpose |
|---|---|---|---|
| LST | Land surface temperature (K) estimated from longwave radiation using Equation (13) | 4-component radiometer (CNR4, Kipp & Zonen, Delft, Netherlands) | Remote sensing input |
| LAI | Leaf area index (m2/m2) based on NDVI (Appendix A) | MODIS/Terra and Aqua Nadir BRDF-adjusted Reflectance Daily L3 500m v006 (MCD43A4) product | Remote sensing input |
| Ta | Air temperature (K) measured at 15m | Hygro.Thermo transmitter | Input forcing |
| RH | Relative humidity (%) measured at 15m | Hygro.Thermo transmitter | Input forcing |
| u | Wind speed (m/s) measured at 15m | Sonic anemometer (Gill R3-50, Lymington UK) | Input forcing |
| P | Atmospheric pressure (mb) | Barometric pressure sensor | Input forcing |
| Sdn | Incoming shortwave irradiance (W m−2) | 4-component radiometer (CNR4, Kipp & Zonen, Delft, Netherlands) | Input forcing |
| G | Soil heat flux (W m−2) | Soil heat flux plates | Input forcing |
| Lin | Incoming longwave irradiance (W m−2) | 4-component radiometer (CNR4, Kipp & Zonen, Delft, Netherlands) | Input forcing |
| Lout | Outgoing longwave irradiance (W m−2) | 4-component radiometer (CNR4, Kipp & Zonen, Delft, Netherlands) | Estimate LST |
| Priestley Taylor coefficient (-) | 1.26 (Default value from [10,14]) | Model parameter | |
| Fraction of vegetation that is green (-) | Study site information [43] | Model parameter | |
| Fractional cover (-) | Study site information [43] | Model parameter | |
| Canopy width to height ratio (-) | 1 (Default value from [48]) | Model parameter | |
| Campbell 1990 leaf inclination distribution function chi parameter (-) | 1 (Default value from [48]) | Model parameter | |
| Canopy height (m) | Study site information [43] | Model parameter | |
| Bare soil aerodynamic roughness length (m) | 0.01 (Default value from [10]) | Model parameter | |
| Average/effective leaf width (m) | 0.01 (Default value from [10]) | Model parameter | |
| b | Soil-surface resistance (Rs) constant (-) | 0.012 (Default value from [14,70]) | Model parameter |
| Soil-surface resistance (Rs) constant (m s−1K−1/3) | 0.0025 (Default value from [14,52]) | Model parameter | |
| C’ | Total boundary resistance (Rx) constant (s1/2 m−1) | 90 (Default value from [14,53]) | Model parameter |
| H | Sensible heat flux (W m−2) | 3D sonic anemometer (Gill R3-50, Lymington UK) | Model evaluation |
| LE | Latent heat flux (W m−2) | IRGA (Li-7200, Licor, Lincoln Nebraska, USA) and 3D sonic anemometer (Gill R3-50, Lymington UK) | Model evaluation |
| LElys | Latent heat flux from the understory measured by lysimeters (W m−2) | Weighing-lysimeters [42] | Model evaluation |
| Parameters | TSEB-DF | Source |
|---|---|---|
| (-) | 1.26 | [10,14] |
| (-) | 0.7 | [43] |
| (-) | 1 | [43] |
| (-) | 1 | [48] |
| (-) | 1 | [48] |
| (m) | 2 | [43] |
| (m) | 0.01 | [10] |
| (m) | 0.01 | [10] |
| b (-) | 0.012 | [14,51] |
| (m s−1 K−1/3) | 0.0025 | [14,52] |
| C’ (s1/2 m−1) | 90 | [14,53] |
| Parameter | Lower Bound | Upper Bound | Sub-module within TSEB | Reference |
|---|---|---|---|---|
| 1.26 | 2 | Initial canopy transpiration estimate | [14] | |
| 0.01 | 1 | Initial canopy transpiration estimate | ||
| 0.1 | 1 | Radiation transfer through canopy | ||
| 0.5 | 3 | Radiation transfer through canopy | ||
| 0.5 | 3 | Radiation transfer through canopy | [48] | |
| 0.1 | 20 | Aerodynamic resistances (Ra, Rs, Rx) | ||
| 0.005 | 0.2 | Aerodynamic resistances (Rs) | [10] | |
| 0.005 | 0.1 | Aerodynamic resistances (Rs, Rx) | ||
| 0.012 | 0.087 | Aerodynamic resistances (Rs) | [51] | |
| 0.0011 | 0.0038 | Aerodynamic resistances (Rs) | [52] | |
| C‘ | 50 | 150 | Aerodynamic resistances (Rx) | [53] |
| Parameters | End-Member | |
|---|---|---|
| TSEBgrass | TSEBtree | |
| (-) | 1.26 | 1.26 |
| (-) | 0.7 | 0.9 |
| (-) | 1 | 0.2 |
| (-) | 1 | 1 |
| (-) | 1 | 1 |
| (m) | 0.5 | 8 |
| (m) | 0.01 | 0.01 |
| (m) | 0.01 | 0.05 |
| b (-) | 0.012 | 0.034 |
| (m s−1 K−1/3) | 0.0025 | 0.0025 |
| C’ (s1/2 m−1) | 90 | 90 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burchard-Levine, V.; Nieto, H.; Riaño, D.; Migliavacca, M.; El-Madany, T.S.; Perez-Priego, O.; Carrara, A.; Martín, M.P. Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem. Remote Sens. 2020, 12, 904. https://doi.org/10.3390/rs12060904
Burchard-Levine V, Nieto H, Riaño D, Migliavacca M, El-Madany TS, Perez-Priego O, Carrara A, Martín MP. Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem. Remote Sensing. 2020; 12(6):904. https://doi.org/10.3390/rs12060904
Chicago/Turabian StyleBurchard-Levine, Vicente, Héctor Nieto, David Riaño, Mirco Migliavacca, Tarek S. El-Madany, Oscar Perez-Priego, Arnaud Carrara, and M. Pilar Martín. 2020. "Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem" Remote Sensing 12, no. 6: 904. https://doi.org/10.3390/rs12060904
APA StyleBurchard-Levine, V., Nieto, H., Riaño, D., Migliavacca, M., El-Madany, T. S., Perez-Priego, O., Carrara, A., & Martín, M. P. (2020). Seasonal Adaptation of the Thermal-Based Two-Source Energy Balance Model for Estimating Evapotranspiration in a Semiarid Tree-Grass Ecosystem. Remote Sensing, 12(6), 904. https://doi.org/10.3390/rs12060904