Raman Spectroscopy from Laboratory and Proximal to Remote Sensing: A Tool for the Volcanological Sciences
Abstract
1. Introduction
2. Raman Basics
3. Raman Spectral Analysis of Natural Glasses
4. Volcanological Applications
4.1. Estimating Composition and Redox State of Silicate Glasses and Melts
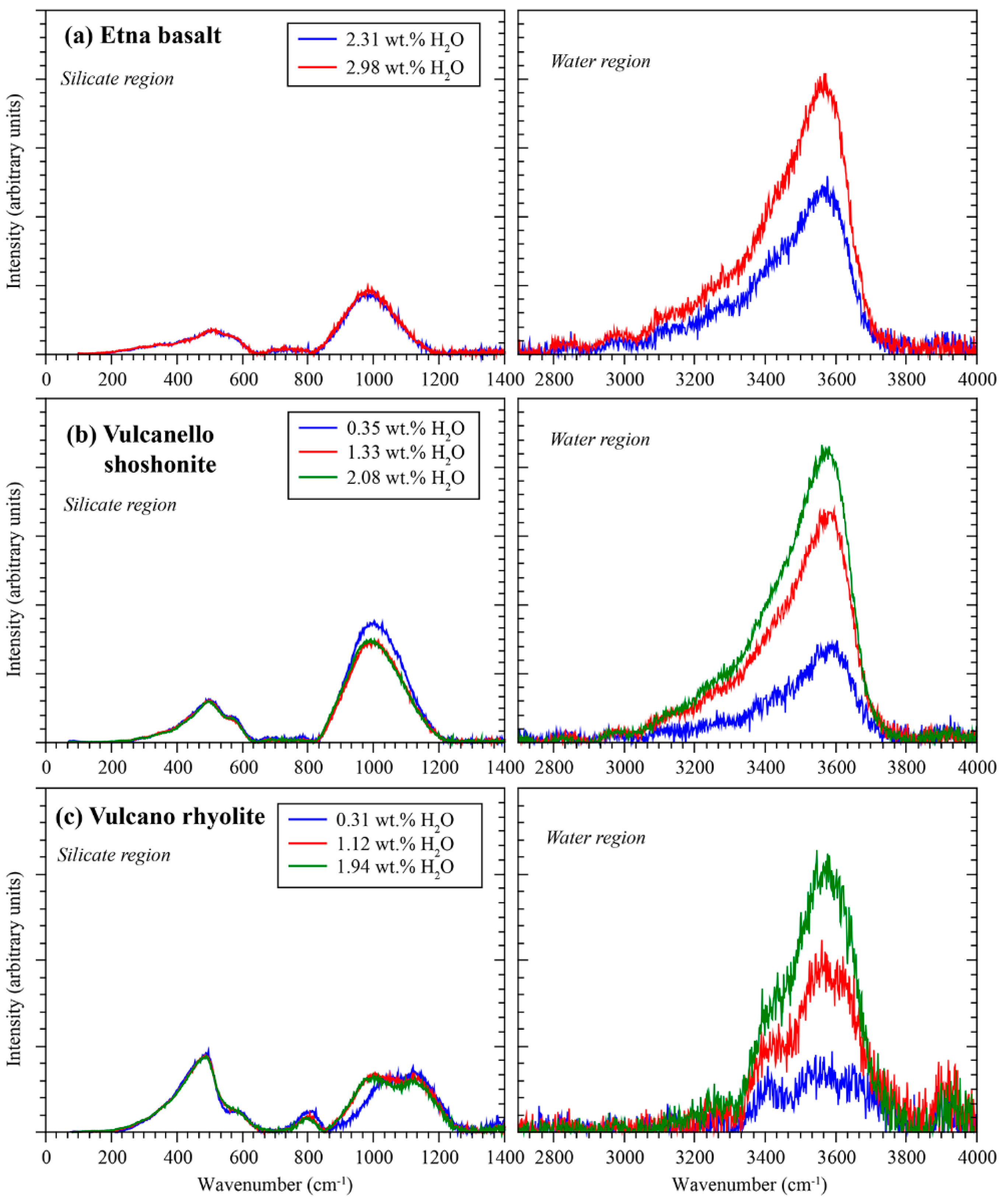
4.2. Predicting Dissolved Volatile Contents in Silicate Glasses and Melts
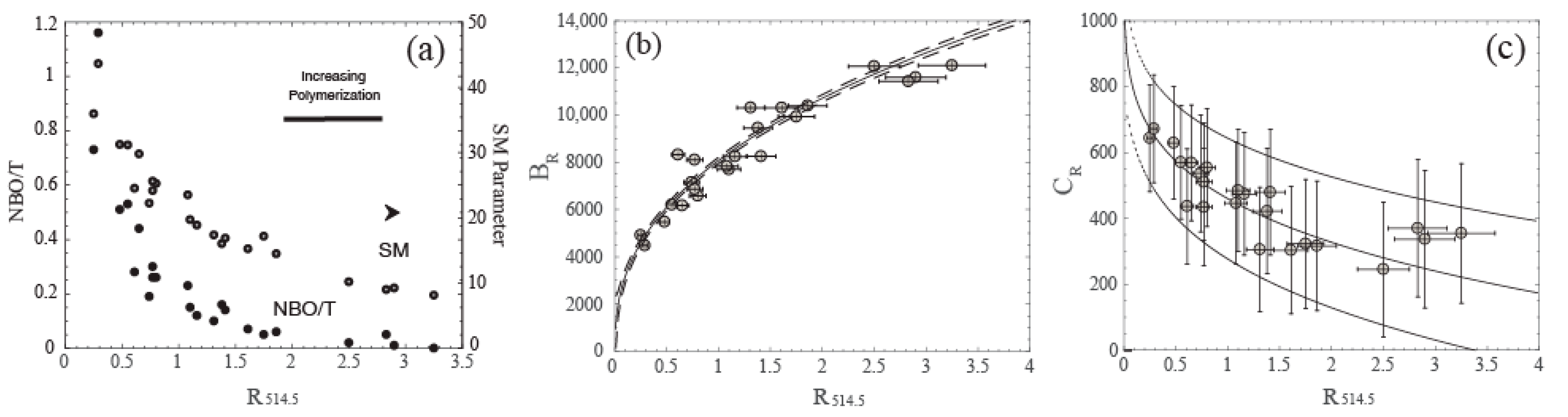
4.3. Toward a Structural Viscosity Model for Silicate Melts
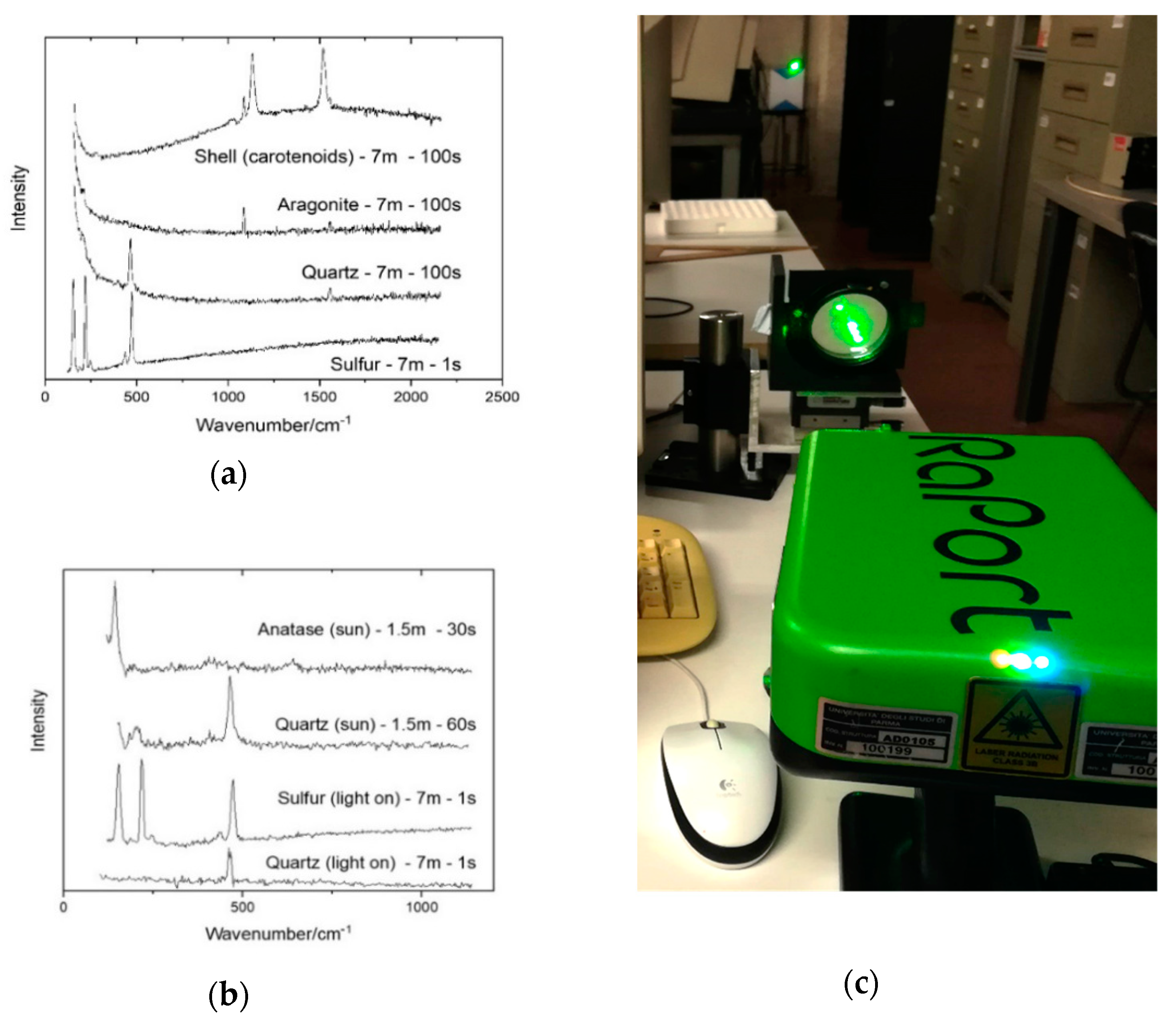
4.4. Raman in the Field: Proximal and Remote Sensing Campaigns
5. The Future for Field-Based Raman Spectroscopy in Volcanological Science
- The RRUFF Project website (http://rruff.info/about/about_general.php).
- The Handbook of Raman Spectra for geology (http://www.geologie-lyon.fr/Raman/index.php).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Main Vibrational Modes
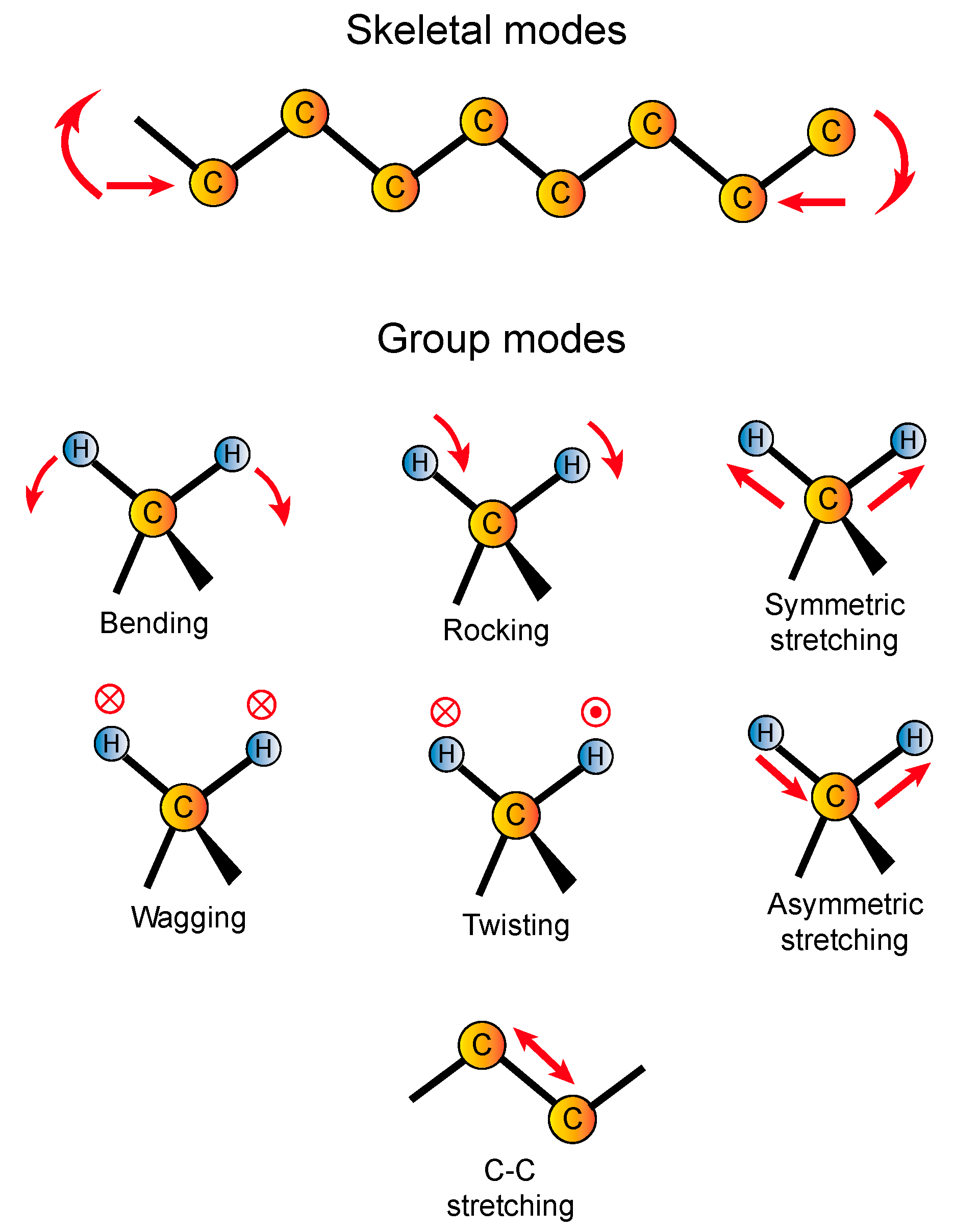
Appendix A.2. LW, MW and HW Bands in Silicate Melts and Glasses
| Wavenumber (cm−1) | Features | References |
|---|---|---|
| LW Region (200–700 cm−1) | ||
| 400–650 | Bending vibration of BO bonds of SiO2 | [9] |
| 440–495 | Oxygen breathing in SiO4 units in Q4 | [9] |
| 550–590 | Si-O-Si bending in Q3 | [14] |
| 565–595 | Si-O-Si bending in Q2 | [9] |
| 605 | Oxygen breathing in SiO4 in Q4 | [9] |
| 450, 500, 600 | Motions of BO in T-O-T linkages | |
| 580 | Si-O0 rocking motions in fully polymerized SiO2 (Q4) units | |
| 600 | Si-O-Si bending vibration in depolymerized structural units | |
| HW region (650–850 cm−1) | ||
| 700 | Si-O-Si bending in Q0/Q1 | [9] |
| 779 | Si-O-Si network, AlO4 units with three BOs and 1 NBO | |
| 790 | Si-O-Si symmetric stretching | |
| 807 | Si-O-Si bending | |
| 810–820 | Si-O stretching involving oxygen motions in Si-O-Si plane or the motion of of the Si | |
| 850 | Antisymmetric stretch Si-O- (NBO) in Q0/Q1 | [9] |
| HW region 850–1300 cm−1 | ||
| 890 | ||
| 900 | Antisymmetric Si-O- stretch (NBO) in Q1 | [9] |
| 935 | ||
| 950–960 | Antisymmetric stretching vibration of Si-O tetrahedral with two corners shared with aluminium-oxygen or calcium-oxygen polyhedra (Q2 units) | |
| 965–980 | Fe3+ band related to the Fe3+ abundance likely related to the stretching of F3+ possibly in four-fold coordination | [36,37] |
| 980 | ||
| 1035 | ||
| 1050 | Antisymmetric Si-O- stretch (NBO) in Q2 | |
| 1060−1200 (1060, 1120, 1150, 1170, 1190−1200) | Antisymmetric Si-O stretching vibrations of SiO4 tetrahedra (Q4 units) | [9] |
| 1070 | C-O symmetric stretch in CO3 groups | [9] |
| 1083 | SiO4 asymmetric stretching vibration | [9] |
| 1100 | Antisymmetric Si-O- (NBO) in Q3 | [9] |
| Volatile bearing compositions | ||
| 900−970 | Si-OH stretching mode | [7,9] |
| 1280 | Molecular CO2 | [9] |
| 1600−1650 | H-O-H bending of molecular H2O | [9] |
| 2350 | Si-OH groups involved in intratetrahedral hydrogen bonding across an edge of the SiO4 tetrahedron | |
| 2800−4000 | O-H+H2O stretch (wide band) | [9] |
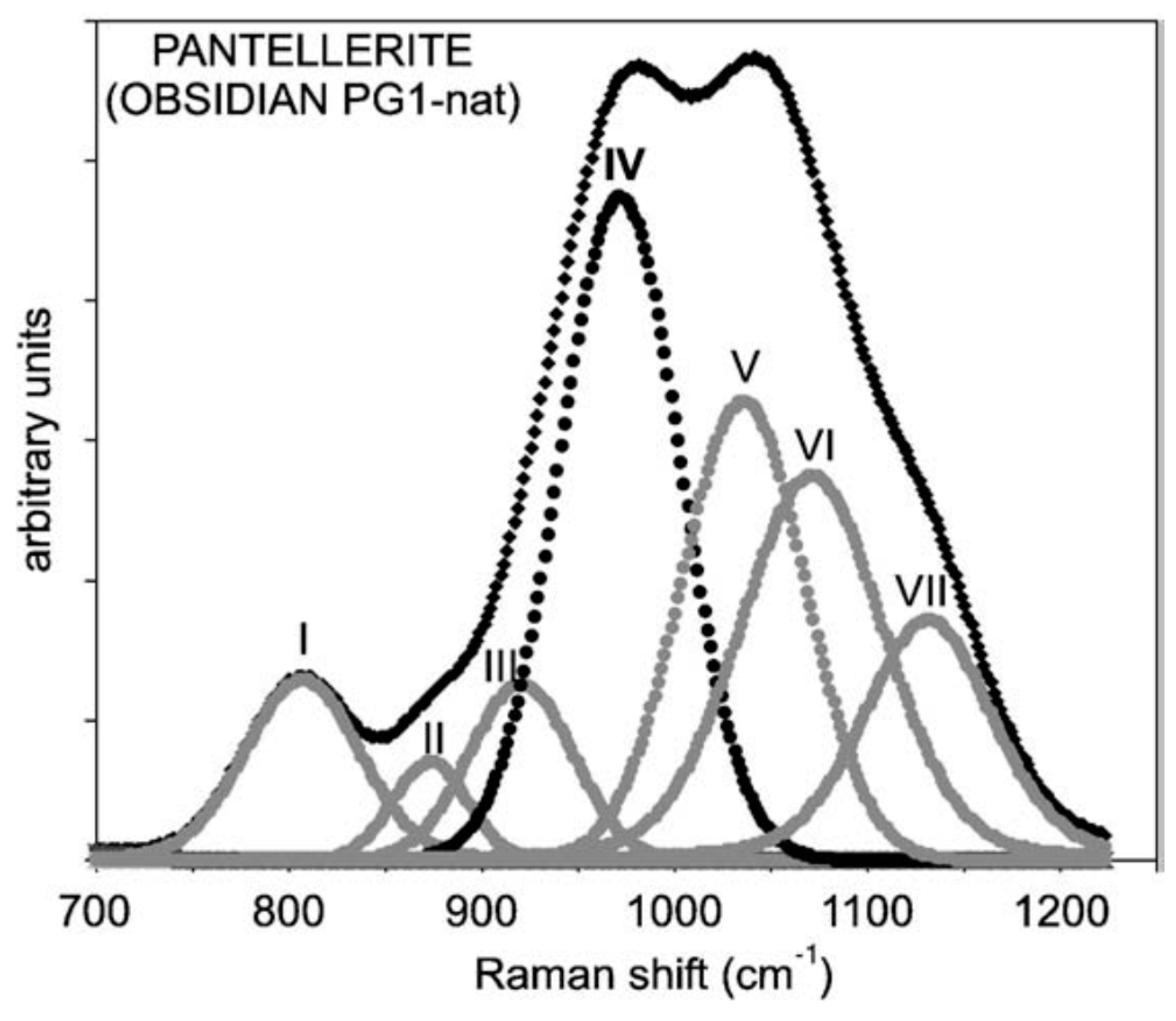
References
- Giordano, D.; Polacci, M.; Longo, A.; Papale, P.; Digwell, D.B.; Boschi, E.; Kasereka, M. Thermo-rheological magma control on the impact of highly fluid lava flows at Mt. Nyiragongo. Geophys. Res. Lett. 2007, 34, L06301. [Google Scholar] [CrossRef]
- Giordano, D.; González-García, D.; Russell, J.K.; Raneri, S.; Bersani, D.; Fornasini, L.; Di Genova, D.; Ferrando, S.; Kaliwoda, M.; Lottici, P.P.; et al. A calibrated database of Raman spectra for natural silicate glasses: Implications for modelling melt physical properties. J. Raman Spectrosc. 2019, 1–17. [Google Scholar] [CrossRef]
- Kolzenburg, S.; Giordano, D.; Hess, K.U.; Dingwell, D.B. Shear Rate−Dependent Disequilibrium Rheology and Dynamics of Basalt Solidification. Geophys. Res. Lett. 2018, 45, 6466–6475. [Google Scholar] [CrossRef]
- Kolzenburg, S.; Giordano, D.; Di Muro, A.; Dingwell, D.B. Equilibrium viscosity and disequilibrium rheology of a high magnesium basalt from Piton de la Fournaise volcano, La Reunion, Indian Ocean, France. Ann. Gephys. 2019, 62, VO218. [Google Scholar] [CrossRef]
- Sharma, S.K.; Misra, A.K.; Clegg, S.M.; Barefield, J.E.; Wiens, R.C.; Acosta, T.E.; Bates, D.E. Remote-Raman spectroscopic study of minerals under supercritical CO2 relevant to Venus exploration. Spectr. Acta Part A 2011, 80, 75–81. [Google Scholar] [CrossRef]
- Sharma, S.K.; Porter, J.N.; Misra, A.K.; Helsley, C.E.; Bates, D.E. Scanning time-resolved standoff Raman instrument for large-area mineral detection on planetary surfaces. Eur. J. Mineral. 2013, 25, 715–720. [Google Scholar] [CrossRef]
- McMillan, P.F.; Poe, B.T.; Stanton, T.R.; Remmele, R.L. A Raman spectroscopic study of H/D isotopically substituted hydrous aluminosilicate glasses. Phys. Chem. Miner. 1993, 19, 454–459. [Google Scholar] [CrossRef]
- Angel, S.M.; Gomer, N.R.; Sharma, S.K.; McKay, C. Remote Raman Spectroscopy for Planetary Exploration: A Review. Appl. Spectrosc. 2012, 66, 137–150. [Google Scholar] [CrossRef]
- Rossano, S.; Mysen, B. Raman spectroscopy of silicate glasses and melts in geological systems. EMU Notes Mineral. 2012, 12, 319–364. [Google Scholar] [CrossRef]
- Malfait, W. Vibrational Properties of Glasses and Melts. In Magmas Under Pressure. Advances in High-Pressure Experiments on Structure and Properties of Melts; Kono, Y., Sanloup, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 211–236. [Google Scholar]
- Hurai, V.; Huraiová, M.; Slobodnik, M.; Thomas, R. Raman and Infrared Spectroscopic Analysis. In Geofluids. Developments in Microthermometry, Spectroscopy, Thermodynamics, and Stable Isotopes; Elsevier: Amsterdam, The Netherlands, 2015; pp. 231–280. [Google Scholar] [CrossRef]
- Neuville, D.R.; de Ligny, D.; Henderson, G.S. Advances in Raman Spectrosscopy Applied to Earth and Material Sciences. Rev. Mineral. Geochem. 2014, 78, 509–541. [Google Scholar] [CrossRef]
- Thomas, R. Determination of water contents of granite melt inclusions by confocal laser Raman microprobe spectroscopy. Am. Mineral. 2000, 85, 868–872. [Google Scholar] [CrossRef]
- Mercier, M.; Di Muro, A.; Giordano, D.; Métrich, N.; Lesne, P.; Pichavant, M.; Scaillet, B.; Clocchiatti, R.; Montagnac, G. Influence of glass po¬lymerisation and oxidation on micro-Raman water analysis in alumino-silicate glasses. Geochim. Cosmochim. Acta 2009, 73, 197–217. [Google Scholar] [CrossRef]
- Mercier, M.; Muro, A.D.; Métrich, N.; Giordano, D.; Belhadj, O.; Mandeville, C.W. Spectroscopic analysis (FTIR, Raman) of water in mafic and intermediate glasses and glass inclusions. Geochim. Cosmochim. Acta 2010, 74, 5641–5656. [Google Scholar] [CrossRef]
- Di Genova, D.; Sicola, S.; Romano, C.; Vona, A.; Fanara, S.; Spina, L. Effect of iron and nanolites on Raman spectra of volcanic glasses: A reassessment of existing strategies to estimate the water content. Chem. Geol. 2017, 475, 76–86. [Google Scholar] [CrossRef]
- Bernard, S.; Beyssac, O.; Benzerara, K. Raman Mapping Using Advanced Line-Scanning Systems: Geological Applications. Appl. Spectrosc. 2008, 62, 1180–1188. [Google Scholar] [CrossRef]
- Yesiltas, M.; Jaret, S.; Young, J.; Wright, S.P.; Glotch, T.D. Three dimensional Raman tomographic microspectroscopy: A novel imaging technique. Earth Space Sci. 2018, 5, 380–392. [Google Scholar] [CrossRef]
- Roskosz, M.; Toplis, M.J.; Neuville, D.R.; Mysen, B.O. Quantification of the kinetics of iron oxidation in silicate melts using Raman spectroscopy and assessment of the role of oxygen diffusion. Am. Mineral. 2008, 93, 1749–1759. [Google Scholar] [CrossRef]
- Luth, R.W.; Mysen, B.O.; Virgo, D. Raman spectroscopic study of the solubility behavior of H2 in the system Na2O-Al2O3-SiO2-H2. Am. Mineral. 1987, 72, 481–486. [Google Scholar]
- Manara, D.; Gradjean, A.; Pinet, O.; Dussossoy, J.L.; Neuville, D.R. Sulfur behavior in silicate glasses and melts: Implications for sulfate incorporation in nuclear waste glasses as a function of alkali cation and V2O5 content. J. Non-Cryst. Solids 2007, 353, 12–23. [Google Scholar] [CrossRef]
- Klimm, K.; Botcharnikov, R.E. The determination of sulfate and sulfide species in hydrous silicate glasses using Raman spectroscopy. Am. Mineral. 2010, 95, 1574–1579. [Google Scholar] [CrossRef]
- Amalberti, J.; Neuville, D.R.; Sarda, P.; Sator, N.; Guillot, B. Quantification of CO2 dissolved in silicate glasses and melts using Raman spectroscopy: Implications for geodynamics. Mineral. Mag. 2012, 76, 430. [Google Scholar]
- Morizet, Y.; Brooker, R.A.; Iacono-Marziano, G.; Kjarsgaard, B.A. Quantification of dissolved CO2 in silicate glasses using micro-Raman spectroscopy. Am. Mineral. 2013, 98, 1788–1802. [Google Scholar] [CrossRef]
- Chabiron, A.; Pironon, J.; Massare, D. Characterization of water in synthetic rhyolitic glasses and natural melt inclusions by Raman spectroscopy. Contrib. Mineral. Petr. 2004, 146, 485–492. [Google Scholar] [CrossRef]
- Zajacz, Z.; Halter, W.; Malfait, W.J.; Bachmann, O.; Bodnar, R.J.; Hirschmann, M.M.; Mandeville, C.W.; Morizet, Y.; Müntener, O.; Ulmer, P.; et al. A composition-independent quantitative determination of the water content in silicate glasses and silicate melt inclusions by confocal Raman spectroscopy. Contrib. Mineral. Petr. 2005, 150, 631–642. [Google Scholar] [CrossRef]
- Behrens, H.; Roux, J.; Neuville, D.; Siemann, M. Quantification of dissolved H2O in silicate glasses using confocal microRaman spectroscopy. Chem. Geol. 2006, 229, 96–112. [Google Scholar] [CrossRef]
- Thomas, R.; Metrich, N.; Scaillet, B.; Kamenetsky, V.S.; Davidson, P. Determination of water in Fe-rich basalt glasses with confocal micro-Raman spectroscopy. Z. Geol. Wissenschaft. 2008, 36, 31–37. [Google Scholar]
- Schiavi, F.; Bolfan-Casanova, N.; Withers, A.C.; Médard, E.; Laumonier, M.; Laporte, D.; Flaherty, T.; Gómez-Ulla, A. Water quantification in silicate glasses by Raman spectroscopy: Correcting for the effects of confocality, density and ferric iron. Chem. Geol. 2018, 483, 312–331. [Google Scholar] [CrossRef]
- Dubessy, J.; Caumon, M.-C.; Rull, F. Raman Spectroscopy Applied to Earth Sciences and Cultural Heritage; EMU Notes Mineralogy: London, UK, 2012. [Google Scholar]
- Chou, I.-M.; Wang, A. Application of laser Raman micro-analyses to Earth and planetary materials. J. Asian Earth Sci. 2017, 145, 309–333. [Google Scholar] [CrossRef]
- Mysen, B.O.; Richet, P. Silicate Glasses and Melts—Properties and Structure; Elsevier: Amsterdam, The Netherlands, 2005; Volume 10. [Google Scholar]
- Di Muro, A.; Métrich, N.; Mercier, M.; Giordano, D.; Massare, D.; Montagnac, G. Micro-Raman determination of iron redox state in dry natural glasses: Application to peralkaline rhyolites and basalts. Chem. Geol. 2009, 259, 78–88. [Google Scholar] [CrossRef]
- Giordano, D.; Russell, J.K. Toward a Structural Model for the Viscosity of Geological Melts. Earth Planet. Sci. Lett. 2018, 501, 202–212. [Google Scholar] [CrossRef]
- Long, D.A. Raman Spectroscopy; McGraw-Hill: New York, NY, USA, 1977; p. 275. [Google Scholar]
- Magnien, V.; Neuville, D.R.; Cormier, I.; Roux, J.; Pinet, O.; Richet, P. Kinetics of iron redox reactions: A high temperature XANES and Raman spectroscopy study. J. Nucl. Mater. 2006, 352, 190–195. [Google Scholar] [CrossRef]
- Cochain, B.; Neuville, D.R.; Henderson, G.S.; McCammon, C.; Pinet, O.; Richet, P. Iron content, redox state and structure of sodium borosilicate glasses: A Raman, Mössbauer and boron K-edge XANES spectroscopy study. J. Am. Soc. 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Di Genova, D.; Kolzenburg, S.; Vona, A.; Chevrel, M.O.; Hess, K.-U.; Neuville, D.R.; Ertel-Ingrisch, W.; Romano, C.; Dingwell, D.B. Raman spectra of Martian glass analogues: A tool to approximate their chemical composition. J. Geophys. Res. Planets 2016, 121, 740–752. [Google Scholar] [CrossRef] [PubMed]
- Di Genova, D.; Hess, K.-U.; Chevrel, M.O.; Dingwell, D.B. Models for the estimation of Fe3+/Fetot ratio in terrestrial and extraterrestrial alkali- and iron-rich silicate glasses using Raman spectroscopy. Am. Mineral. 2016, 101, 943–952. [Google Scholar] [CrossRef]
- Di Genova, D.; Morgavi, D.; Hess, K.-U.; Neuville, D.R.; Borovkov, N.; Perugini, D.; Dingwell, D.B. Approximate chemical analysis of volcanic glasses using Raman spectroscopy. J. Raman Spectrosc. 2015, 46, 1235–1244. [Google Scholar] [CrossRef]
- González-García, D.; Giordano, D.; Russell, J.K.; Dingwell, D.B. A Raman spectroscopic tool to estimate chemical composition of natural volcanic glasses. 2020; Submitted. [Google Scholar]
- Mysen, B.O.; Virgo, D. Structure and properties of fluorine-bearing aluminosilicate melts: The system Na2O-Al2O3-SiO2-F at 1 atm. Contrib. Mineral. Petrol. 1985, 91, 205–220. [Google Scholar] [CrossRef]
- Di Muro, A.; Villemant, B.; Montagnac, G.; Scaillet, B.; Reynard, B. Quantification of water content and speciation in natural silicic glasses (phonolite, dacite, rhyolite) by confocal microRaman spectrometry. Geochim Cosmochim. Acta 2006, 70, 2868–2884. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R.; Moretti, R.; Roux, J. Determination of water content in silicate glasses using Raman spectrometry: Implications for the study of explosive volcanism. Am. Mineral. 2012, 97, 779–790. [Google Scholar] [CrossRef]
- Severs, M.J.; Azbej, T.; Thomas, J.B.; Mandeville, C.W.; Bodnar, R.J. Experimental determination of H2O loss from melt inclusions during laboratory heating: Evidence from Raman spectroscopy. Chem. Geol. 2007, 237, 358–371. [Google Scholar] [CrossRef]
- Morizet, Y.; Paris, M.; Gaillard, F.; Scaillet, B. Raman quantification factor calibration for CO–CO2 gas mixture in synthetic fluid inclusions: Application to oxygen fugacity calculation in magmatic systems. Chem. Geol. 2009, 264, 58–70. [Google Scholar] [CrossRef]
- Morizet, Y.; Paris, M.; Sifre, D.; Di Carlo, I.; Ory, S.; Gaillard, F. Towards the reconciliation of viscosity change and CO2-induced polymerization in silicate melts. Chem. Geol. 2017, 458, 38–47. [Google Scholar] [CrossRef]
- Le Losq, C.; Neuville, D.R. Molecular structure, configurational entropy and viscosity of silicate melts: Link through the Adam and Gibbs theory of viscous flow. J. Non-Cryst. Solids 2017, 463, 175–188. [Google Scholar] [CrossRef]
- Sharma, S.K.; Lucey, P.G.; Gosh, M.; Hubble, H.W.; Horton, K.A. Stand-off Raman spectroscopic detection of minerals on planetary surfaces. Spectrochim. Acta A 2003, 59, 2391–2407. [Google Scholar] [CrossRef]
- Clegg, S.M.; Wiens, R.; Misra, A.K.; Sharma, S.K.; Lambert, J.; Bender, S.; Newell, R.; Nowak-Lovato, K.; Smrekar, S.; Dyar, M.D.; et al. Planetary geochemical investigations using Raman and laser-induced breakdown spectroscopy. Appl. Spectrosc. 2014, 68, 925–936. [Google Scholar] [CrossRef] [PubMed]
- Wiens, R.C.; Sharma, S.K.; Thompson, J.; Misra, A.; Lucey, P.G. Joint analyses by laser-induced breakdown spectroscopy (LIBS) and Raman spectroscopy at stand-off distances. Spectrochim. Acta A 2005, 61, 2324–2334. [Google Scholar] [CrossRef]
- Sharma, S.K.; Misra, A.K.; Lucey, P.G.; Wiens, R.G.; Clegg, S.M. Combined remote LIBS and Raman spectroscopy at 8.6 m of sulfur-containing minerals, and minerals coated with hematite or covered with basaltic dust. Spectrochim. Acta A 2007, 68, 1036–1045. [Google Scholar] [CrossRef]
- Guimbretière, G.; Canizarès, A.; Finzola, A.; Delcher, E.; Raimboux, N.; Di Muro, A.; Simon, P.; Devouard, B.; Bertil, A. Raman spectroscopy as suitable tool for the field study of recent volcanic environments. J. Raman Spectrosc. 2016, 47, 740–742. [Google Scholar] [CrossRef]
- Hutchinson, I.; McHugh, M.; Lerman, H.; Ingley, R.; Edwards, H.; Moral, A.; Ramos, G.; Perez, C.; Malherbe, C.; Wang, A. Spectrometer Development for Planetary and Terrestrial Exploration. In Proceedings of the XIII International Conference GeoRaman, Catania, Italy, 10–14 June 2018. [Google Scholar]
- Rees, J.M.; Bonafous, M.; Lapauw, L.; Humeau, O.; Fouchet, T.; Bernardi, P.; Cais, P.; Deleuze, M.; Forni, O.; Maurice, S.; et al. The SuperCam infrared instrument on the NASA MARS2020 mission: Performance and qualification results. Int. Conf. Space Opt. 2018, 11180. [Google Scholar] [CrossRef]
- Acosta-Maeda, T.E.; Misra, A.K.; Muzangwa, L.G.; Berlanga, G.; Muchow, D.; Poerter, J.; Sharma, S.K. Remote Raman measurements of minerals, organics, and inorganics at 430 m range. Appl. Opt. 2016, 55, 10283–10289. [Google Scholar] [CrossRef]
- Berlanga, G.; Acosta-Maeda, T.E.; Sharma, S.K.; Porter, J.N.; Dera, P.; Shelton, H.; Taylor, G.J.; Misra, A. Remote Raman spectroscopy of natural rocks. Appl. Opt. 2019, 58, 8971–8980. [Google Scholar] [CrossRef]
- Porter, J.N.; Helsley, C.E.; Sharma, S.K.; Misra, A.K.; Bates, D.E.; Lienart, B.R. Two-dimensional standoff Raman measurements of distant samples. J. Raman Spectrosc. 2012, 43, 165–167. [Google Scholar] [CrossRef]
- Wu, M.; Ray, M.K.; Fung, H.; Ruckman, M.W.; Harder, D.; Sedllacek, A.J. Stand-off Detection of Chemicals by UV Raman Spectroscopy. Appl. Spectrsosc. 2000, 54, 800–806. [Google Scholar] [CrossRef]
- Pettersson, A.; Johansson, I.; Wallin, S.; Nordberg, M.; Ostmark, H. Near Real-Time Standoff Detection of Explosives in a Realistic Outdoor Environment at 55 m Distance. Propellants Explos. Protech. 2009, 34, 297. [Google Scholar] [CrossRef]
- Giordano, D. Advances in the rheology of natural multiphase silicate melts and implications for magma transport and lava flow emplacement. Ann. Geophys. 2019. [Google Scholar] [CrossRef]
- Simon, P.; Moulin, B.; Buixaderas, E.; Raimboux, N.; Herault, E.; Chazallon, B.; Cattey, H.; Magneron, N.; Oswalt, J.; Hocrelle, D. High temperatures and Raman scattering through pulsed spectroscopy and CCD detection. J. Raman Spectrosc. 2003, 34, 497–504. [Google Scholar] [CrossRef]
- Wunderlich, B. The ATHAS database on heat capacities of polymers. Pure Appl. Chem. 1995, 87, 1019–1026. [Google Scholar] [CrossRef]
- McMillan, P. Structural studies of silicate glasses and melts-applications and limitations of Raman spectroscopy. Am. Mineral. 1984, 69, 622–644. [Google Scholar]
- Colomban, P. Polymerization degree and Raman identification of ancient glasses used for jewelrym, ceramic enamels and mosaics. J. Non-Cryst. Solids 2003, 323, 180–187. [Google Scholar] [CrossRef]
- Colomban, P. On-site Raman identification and dating of ancient glasses: A review of procedures and tools. J. Cult. Herit. 2008, 9, e55–e60. [Google Scholar] [CrossRef]
- Bykov, V.N.; Koroleva, O.N.; Osipov, A.A. Structure of silicate melts: Raman spectroscopic data and thermodynamic simulation results. Geochem. Inter. 2009, 47, 1067. [Google Scholar] [CrossRef]
- Galeneer, F.L. Planar rings in glasses. Solid State Commun. 1982, 44, 1037–1040. [Google Scholar] [CrossRef]
- Neuville, D.; Mysen, B. Role of aluminium in the silicate network: In situ, high-temperature study of glasses and melts on the join SiO2-NaAlO2 Geochim. Cosmochim. Acta 1996, 60, 1727–1737. [Google Scholar] [CrossRef]
- Sharma, S.K.; Mammone, J.F.; Nicol, M.F. Raman investigation of ring configurations in vitreous silica. Nature 1981, 292, 140–141. [Google Scholar] [CrossRef]
- Matson, D.W.; Sharma, S.K.; Philpotts, J.A. The structure of high-silica alkali-silicate glasses. A Raman spectroscopic investigation. J. Non Cryst. Solids 1983, 56, 323–352. [Google Scholar] [CrossRef]
- Kalampounias, A.G.; Yannopoulos, S.N.; Papatheodorou, G.N. A high-temperature Raman spectroscopic investigation of the potassium tetrasilicate in glassy, supercooled, and liquid states. J. Chem. Phys. 2006, 125, 164502. [Google Scholar] [CrossRef] [PubMed]
- Seifert, F.; Mysen, B.O.; Virgo, D. Three-dimensional network structure of quenched melts (glass) in the systems SiO2–NaAlO2, SiO2–CaAl2O4 and SiO2–MgAl2O4. Am. Mineral. 1982, 67, 696–717. [Google Scholar]
- Mysen, B.O.; Finger, L.W.; Virgo, D.; Seifert, F.A. Curve-fitting of Raman spectra of silicate glasses. Am. Mineral. 1982, 67, 686–695. [Google Scholar]
- Ardia, P.; Di Muro, A.; Giordano, D.; Massare, D.; Sanchez-Valle, C.; Schmidt, M.W. Densification mechanisms of haplogranite glasses as a function of water content and pressure based on density and Raman data. Geochim. Cosmochim. Acta 2014, 138, 158–180. [Google Scholar] [CrossRef][Green Version]
- Le Losq, C.; Berry, A.J.; Kendrick, M.A.; Neuville, F.R.; O’Neill, H.C. Determination of the oxidation state of iron in Mid-Ocean Ridge basalt glasses by Raman spectroscopy. Am. Mineral. 2019, 104, 1032–1042. [Google Scholar] [CrossRef]
- Di Genova, D.; Caracciolo, A.; Kolzenburg, S. Measuring the degree of “nanotilization” of volcanic glasses: Understanding syn-eruptive processes recorded in melt inclusions. Lithos 2018, 318–319, 209–218. [Google Scholar] [CrossRef]
- Furukawa, T.; Fox, K.E.; White, W.B. Raman spectroscopic investigation of the structure of silicate glasses. III. Raman intensities and structural units in sodium silicate glasses. J. Chem. Phys. 1981, 75, 3226–3237. [Google Scholar] [CrossRef]
- Giordano, D.; Dingwell, D.B. Viscosity of hydrous Etna basalt: Implications for Plinian-style basaltic eruptions. Bull. Volcanol. 2003, 65, 8–14. [Google Scholar] [CrossRef]
- González-García, D.; Behrens, H.; Petrelli, M.; Vetere, F.; Morgavi, D.; Zhang, C.; Perugini, D. Water-enhacned interdiffusion of major elements between natural shoshonite and high-K rhyolite melts. Chem. Geol. 2017, 466, 86–101. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giordano, D.; Russell, J.K.; González-García, D.; Bersani, D.; Dingwell, D.B.; Del Negro, C. Raman Spectroscopy from Laboratory and Proximal to Remote Sensing: A Tool for the Volcanological Sciences. Remote Sens. 2020, 12, 805. https://doi.org/10.3390/rs12050805
Giordano D, Russell JK, González-García D, Bersani D, Dingwell DB, Del Negro C. Raman Spectroscopy from Laboratory and Proximal to Remote Sensing: A Tool for the Volcanological Sciences. Remote Sensing. 2020; 12(5):805. https://doi.org/10.3390/rs12050805
Chicago/Turabian StyleGiordano, Daniele, James K. Russell, Diego González-García, Danilo Bersani, Donald B. Dingwell, and Ciro Del Negro. 2020. "Raman Spectroscopy from Laboratory and Proximal to Remote Sensing: A Tool for the Volcanological Sciences" Remote Sensing 12, no. 5: 805. https://doi.org/10.3390/rs12050805
APA StyleGiordano, D., Russell, J. K., González-García, D., Bersani, D., Dingwell, D. B., & Del Negro, C. (2020). Raman Spectroscopy from Laboratory and Proximal to Remote Sensing: A Tool for the Volcanological Sciences. Remote Sensing, 12(5), 805. https://doi.org/10.3390/rs12050805







