1. Introduction
Mangrove forests are among the most important components of natural ecosystems. They perform a wide range of crucial functions, such as mitigating the effects of tropical typhoons and tsunami, reducing coastal erosion, and storing huge amounts of blue carbon [
1,
2]. Despite their functions and benefits, mangrove forests have been reduced and degraded worldwide, more seriously in South East Asia, where the decimation rate reached its highest level in the last 50 years [
3,
4]. The driving factors of mangrove deforestation and degradation are conversion to shrimp aquaculture, agriculture (particularly rice and oil palm in West Africa and Southeast Asia), urban development, poor governance, and overexploitation [
3,
5]. Unfortunately, the loss of mangrove carbon on large spatial scales is little understood. Without this knowledge, we cannot mitigate the global loss of mangrove habitats [
6].
Land-cover change is thought to alter the above-ground biomass (AGB) in the tropical areas [
7,
8,
9]. By mapping the spatial distribution of mangrove AGB and the carbon stocks associated with external factors, we could detect the changes in mangrove ecosystems, better understand the drivers of these changes, and reduce the uncertainty in estimating the loss of mangrove ecosystem services. A precise estimation of mangrove AGB is required for sustainably preserving and protecting mangrove ecosystems from loss and degradation under climate change and accelerated global warming. However, the complex structure of mangrove ecosystems hindered quantitative estimates of mangrove AGB. Especially, the biosphere reserves of mangroves are characterized by multiple species, very high diversity, and large spatial distributions. During the last 30 years, AGB retrieval of mangroves has been investigated worldwide [
10,
11,
12,
13,
14]. Mangrove AGB can be accurately estimated from field-based measurements or forest inventory data. However, these approaches are disadvantaged by high cost and site-selection biases [
15]. Cost-effective and accurate retrieval techniques for mangrove AGB in tropical and semi-tropical areas would provide baseline data for the monitoring, reporting, and verification schemes adopted in climate-change mitigation strategies, such as Blue Carbon projects and the United Nations’ Reducing Emissions from Deforestation and Forest Degradation (REDD+) program in the tropics [
16].
In recent years, mangrove AGBs have been increasingly mapped using earth observation (EO) data collected by optical sensors [
17,
18,
19], synthetic aperture radar (SAR) data [
13,
20,
21], airborne LiDAR [
22,
23], and LiDAR data acquired form unmanned aerial vehicles (UAV) [
24,
25]. A few attempts combined the data of multispectral and SAR sensors for mangrove AGB retrieval in tropical regions. Fused data are particularly useful in biosphere reserves comprising multiple mangrove species and rich biodiversity. In such systems, the spatial distribution of the mangrove AGB is difficult to estimate with sufficient accuracy. By accurately estimating the mangrove AGB in biosphere reserves, we could effectively monitor their mangrove ecosystems and implement sustainable mangrove conservation and management.
Models for estimating AGB range from simple to multi-linear regression approaches [
13,
21,
24] to sophisticated machine learning (ML) methods [
17,
18,
26]. For mapping and estimating forest AGBs, non-parametric approaches using various ML algorithms have proven more effective than parametric methods using linear models. Meanwhile, numerous EO datasets have been compiled from optical, SAR, and LiDAR data. These data are commonly retrieved from non-parametric regression techniques such as the random forest regression (RFR) algorithm [
17,
25,
27], artificial neuron networks (ANN) [
26], and support vector regression (SVR) [
28,
29]. Recently, gradient boosting decision trees (GBDT) effectively solved regression problems such as evaporation prediction [
30] and oil price estimation [
31]. The extreme gradient boosting regression (XGBR) algorithm is a particularly potent tool in environmental problems in environmental problems such as urban heat islands [
32], algal blooming [
33], and energy-supply security issues [
34]. However, to our knowledge, the usefulness of the XGBR algorithm in forest AGB estimation, particularly in tropical mangrove habitats, has not been quantified. Especially, the current literature seems to lack a quantitative comparison of state-of-the-art ML techniques for estimating AGBs in different forest ecosystems.
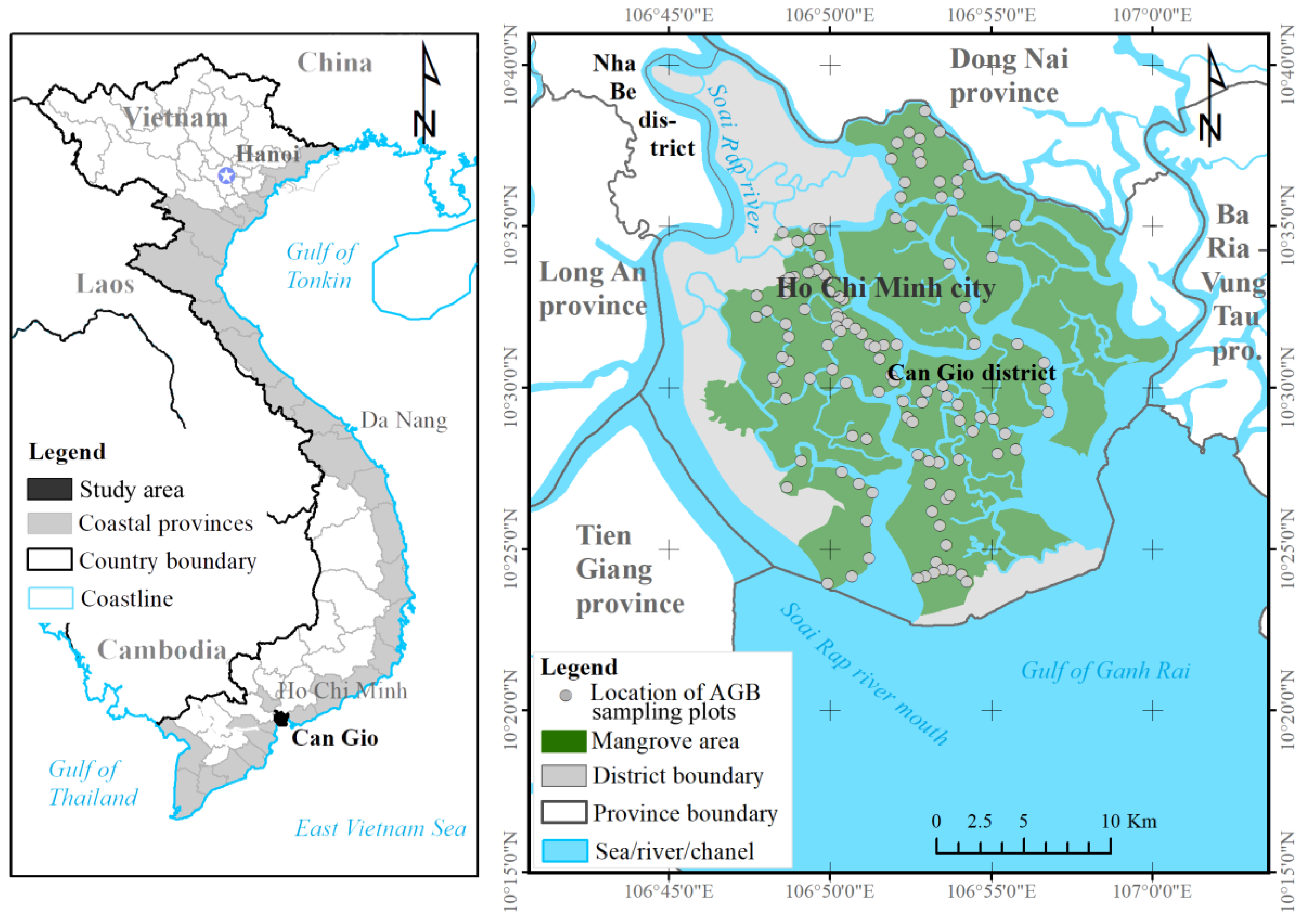
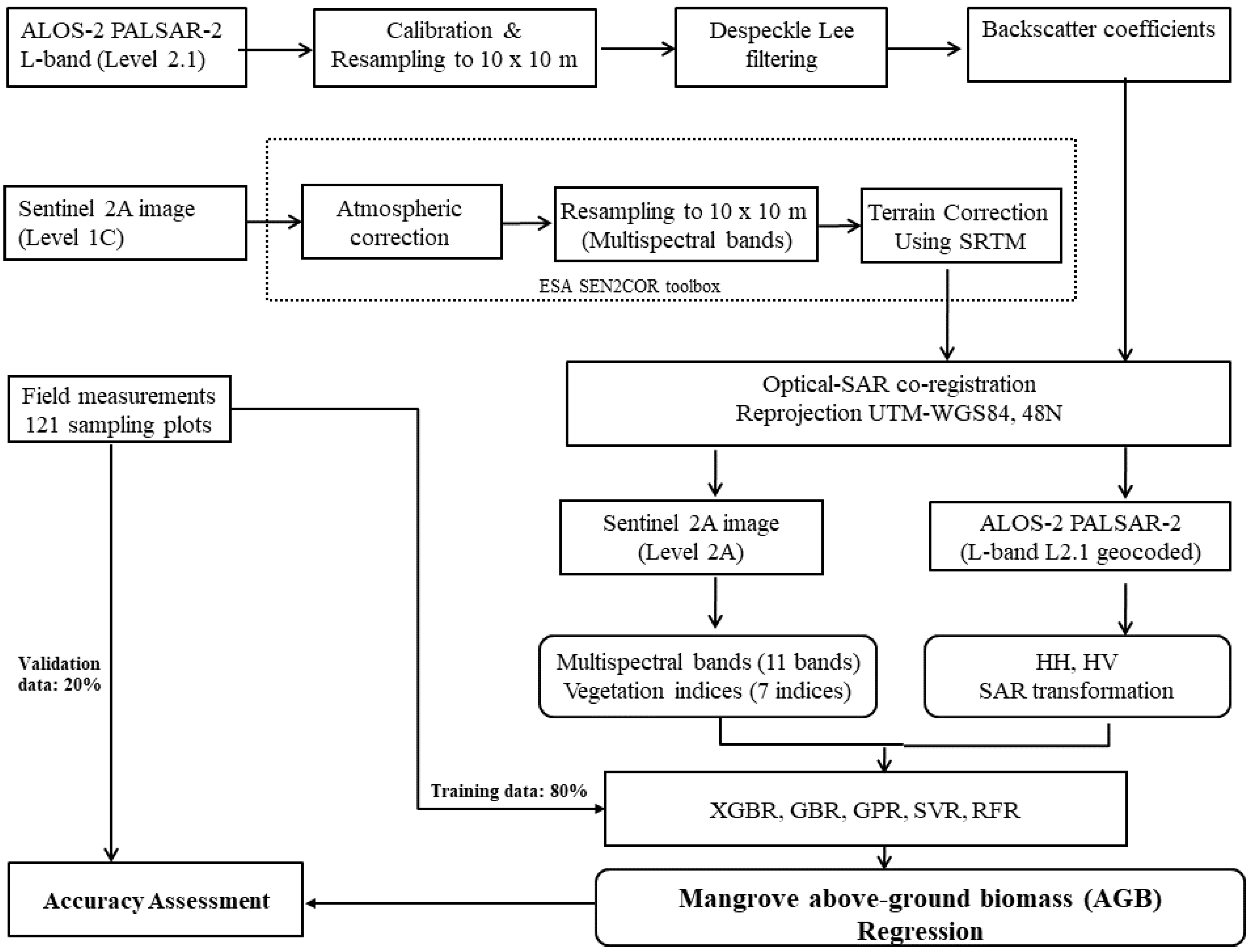
To overcome these challenges, we estimated the mangrove AGB in the Can Gio biosphere reserve (South Vietnam) using an ML model and the fused data of the Sentinel-2 (S2) MSI and ALOS-2 PALSAR-2 sensors. We selected Sentinel-2 MSI because the multispectral bands of S-2 reflect the forest stand structures such as stem volume, whereas the longer wavelengths of the dual polarimetric (HH, HV) mode of the ALOS-2 PALSAR-2 sensor can penetrate mangrove forest canopies. The fused S2 MSI and ALOS-2 PALSAR-2 data were processed by a nonlinear regression model in the XGBR algorithm, providing the first estimation of mangrove AGB in the Can Gio biosphere reserve (CGBRS). Additionally, the performance of the XGBR model was compared with those of other GBDT techniques and several well-known ML algorithms (SVR, GPR, and RFR) on mangrove AGB estimation in the same study area. Incorporating the S-2 MSI and ALOS-2 PALSAR-2 data into the proposed model was found to improve the mangrove AGB estimation in a Vietnamese biosphere reserve and is potentially applicable to mangrove conservation in other biosphere reserves.
4. Discussion
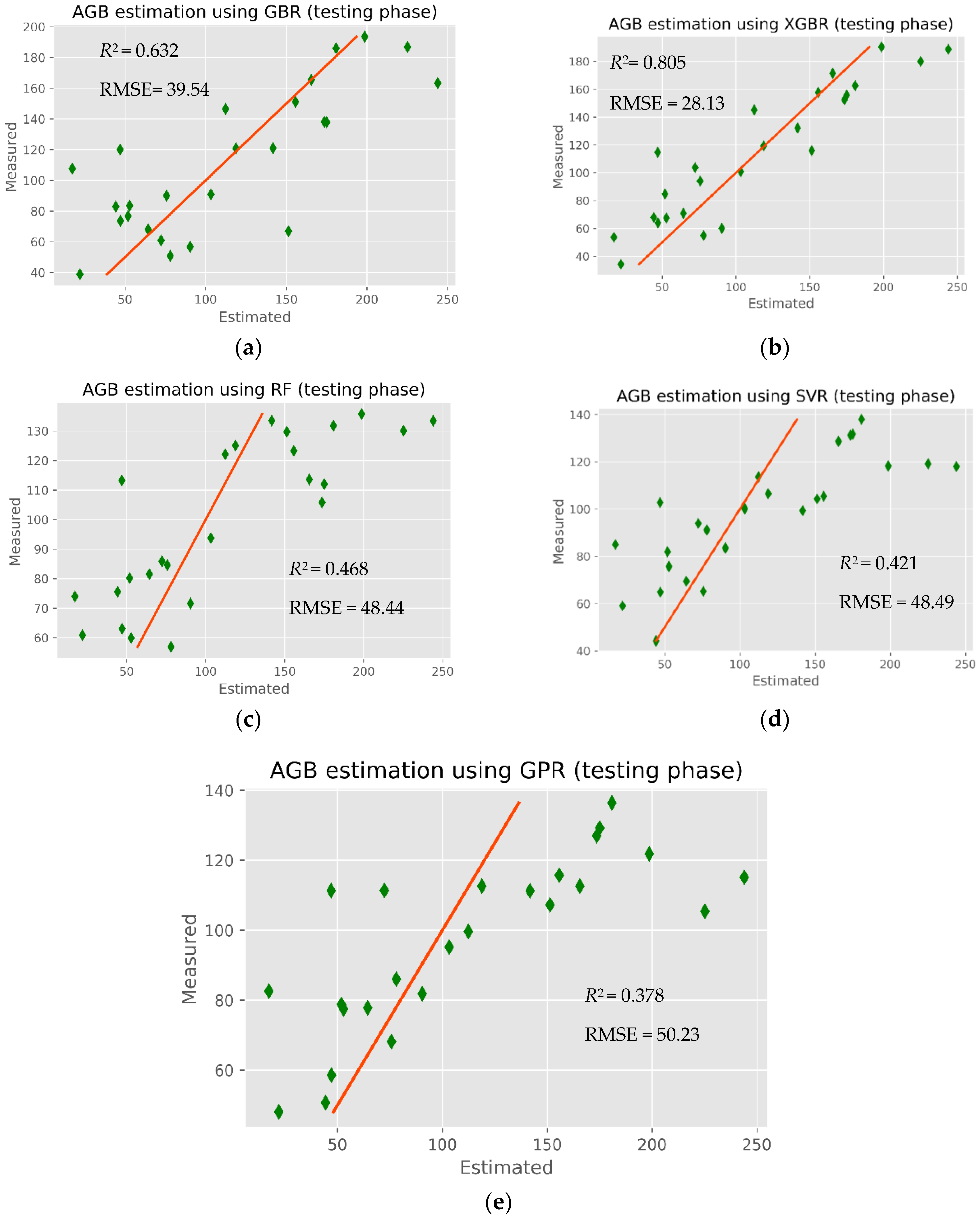
The modeling results of mangrove AGB retrieval in the CGBSR obtained by the five ML models (XGBR, GBR, GPR, SVR, and RFR) are given in
Table 6. Clearly, the XGBR model yielded the highest performance, with an
R2 and RMSE of 0.805 and 28.13 Mg ha
−1, respectively. The worst performing model was GPR, with an
R2 and RMSE of 0.378 and 50.23 Mg ha
−1, respectively. Both the XGBR model (
R2 = 0.805) and GBR model (
R2 = 0.632) were good predictors of mangrove AGB, indicating that the GBDT regression models were applicable to the study area, where the mangrove biomass is higher than in other mangrove regions of Vietnam. As shown in
Table 7, the combined S-2 and ALOS-2 PALSAR data significantly improved the performance of estimating the mangrove AGB in the study area. These results are consistent with a recent previous study [
50]. Overall, the XGBR model outperformed the existing algorithms in retrieving the mangrove AGB in a Vietnamese biosphere reserve.
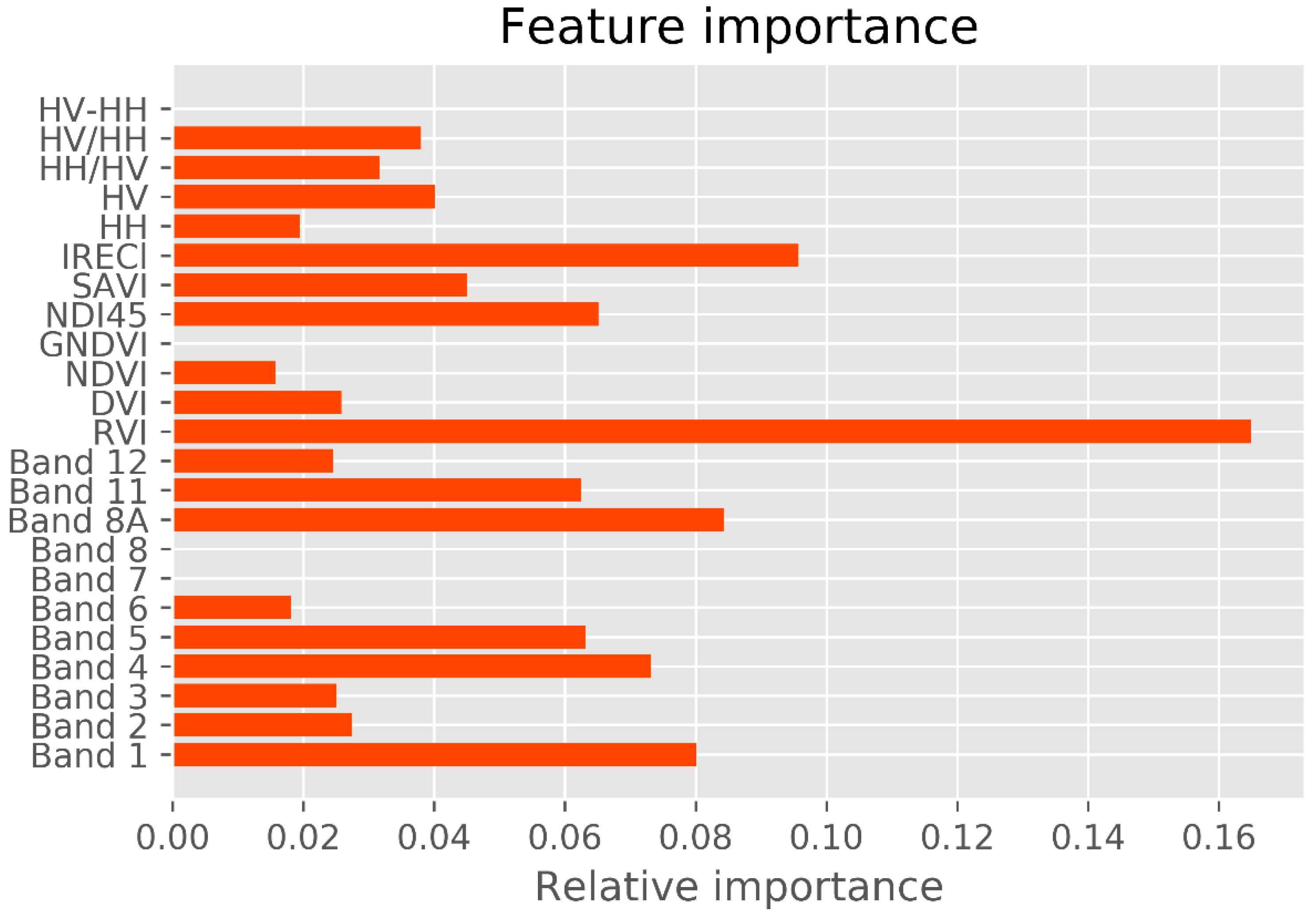
Previous studies reported that long-wavelength PolSAR data, such as the L and the P bands, are well correlated with mangrove forest structures. Among these data, crossed-polarized HV appears to be most correlated with biophysical attributes [
13,
66,
67]. The variable-importance analysis revealed that crossed-polarization HV is more sensitive to mangrove AGB in the study area than HH polarization (
Figure 6), consistent with previous results [
26,
29]. However, mangrove forests in a biosphere reserve exhibit unique stand structures and species compositions that may saturate multispectral and SAR sensors. Data saturation of multispectral sensors such as Landsat TM, ETM+ or OLI, and the S-2 sensor degrades the prediction accuracy of mangrove AGBs in dense forest canopies. The saturation range of multispectral data reaches 100–150 Mg ha
−1 in complex tropical forests, much higher than in mixed and pine forest ecosystems (with a saturation range of >150 to <160 Mg ha
−1) [
68,
69]. In several recent investigations, the saturation levels of the mangrove AGBs retrieved from SAR data ranged from above 100 Mg ha
−1 [
20] to below 150 Mg ha
−1 [
21,
26]. This large range probably manifests from the root systems of different mangrove species in intertidal tropical and sub-tropical regions [
13]. The sigma backscatter coefficients of the dual polarimetric data of ALOS-2 PALSAR-2 increased when the mangrove AGB fell below 100 Mg ha
−1 and then saturated at a higher AGB because the high mangrove cover density extinguished the radar signals [
70,
71].
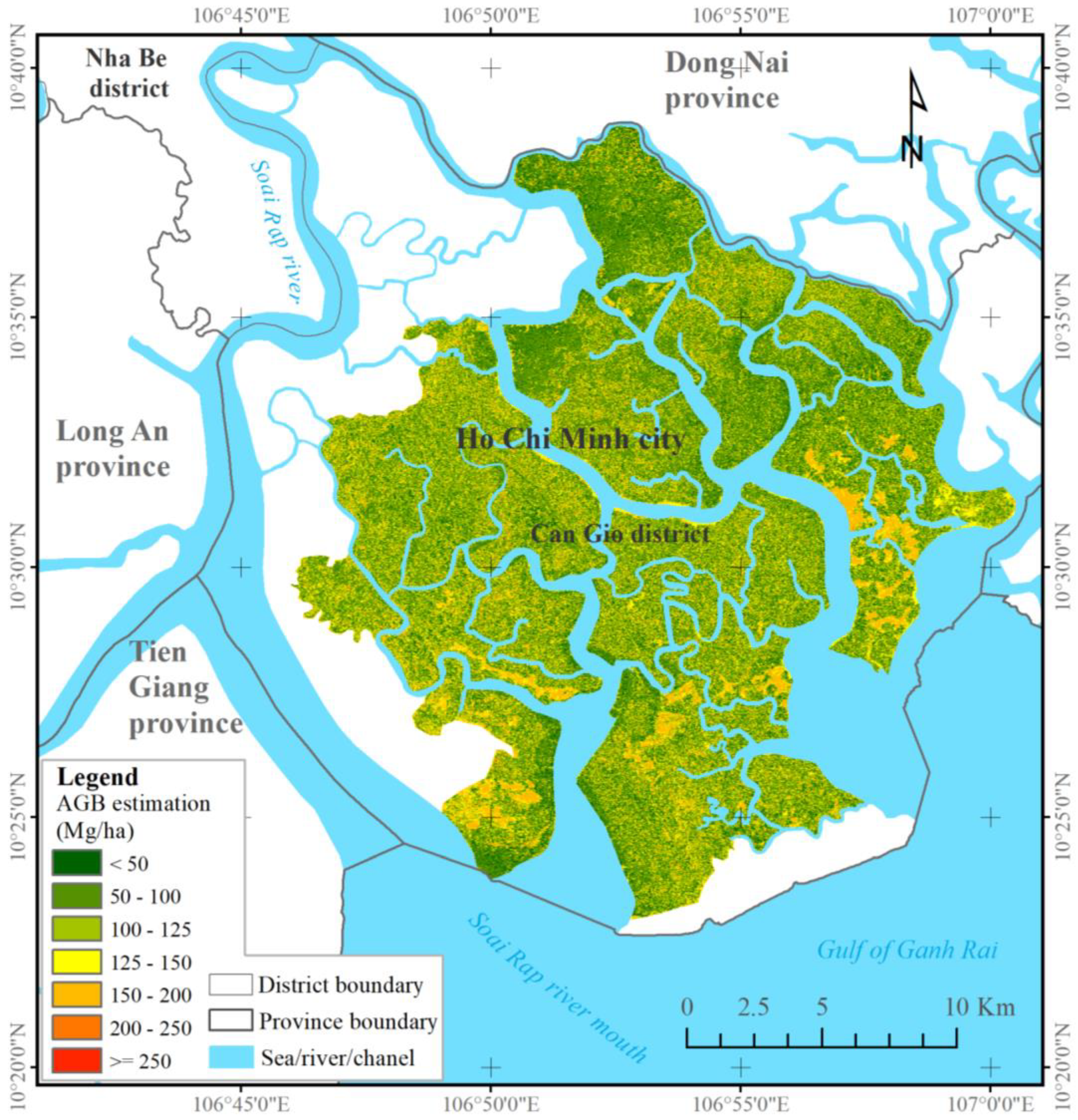
Biosphere reserves often consist of various mangrove species. The species types (i.e.,
R. appiculata,
B. gymnorrhiza, and
S. caseolaris) are densely grown and characterized by high DBH and tall height. Some species, such as
A. germinans and
C. decandra, form small but high-density mangrove patches in which high and low biomasses are easily underestimated and overestimated, respectively, by machine learning algorithms. In the current study, the XGBR model possibly over-estimated the low mangrove AGBs (below 50 Mg ha
−1) and under-estimated the high values (over 250 Mg ha
−1). Despite these limitations, the combined ALOS-2 PALSAR-2 and S-2 data sensitively detected mangrove AGBs exceeding 200 Mg ha
−1 in the CGBRS (See
Figure 5). Our findings agree with the conclusions of prior research on biosphere reserves [
17,
65]. Given the species complexity in mangrove biosphere reserves, we recommend the inclusion of species classification or richness indices for improved mangrove AGB estimation in future work [
19,
21].
In the variable-importance results, the mangrove AGB in the study area was largely retrieved from the Red band and the Vegetation Red Edge band. A similar result was reported elsewhere [
18,
72]. The vegetation red edge, narrow NIR, and SWIR reflectance are likely to be more strongly correlated with forest biomass and carbon stock volume than visible reflectance [
17]. Accordingly, the new vegetation index ND145, which is computed from the Sentinel-2 data bands, is a probable sensitive indicator of mangrove AGB. Band 8A in the narrow NIR and band 11 in the SWIR (1613 nm) also played a crucial role in the AGB retrieval. Interestingly, the IRECl derived from S-2 was strongly correlated with mangrove AGB in the biosphere reserve. More in-depth studies would elucidate the effectiveness of image transformations involving new vegetation indices derived from the Narrow NIR bands, SWIR of S-2 data, and other image transformations computed from the fully polarized data (HH, HV, VH, and VV) of the Gaofeng-3 and the ALOS-2 PALSAR-2 sensors in biosphere reserves.
To accurately estimate mangrove AGBs, researchers attempted multi-linear regression, which performed poorly with
R2 ranging from 0.43–0.65 [
13,
21,
73], and various ML algorithms such as GPR, MLPNN, SVR, and RFR [
17,
18,
29]. ML approaches have proven more successful in mangrove AGB than multi-linear regression and other parametric methods [
18,
47], but the
R2 has rarely exceeded 0.70. Therefore, novel approaches for mangrove AGB estimation are urgently needed. In this research, the performance of the XGBR model was boosted by incorporating data from the ALOS-2 PALSAR-2, S-2 sensors. The result (
R2 = 0.805 for the AGB of a mangrove biosphere reserve in the tropics) demonstrates the promise of this approach. Despite the good fit between the XGBR-predicted and measured-mean mangrove AGBs, the range of the predicted mangrove AGBs did not reach the extrema of the actual distribution range, which was maximized at 305.41 Mg ha
−1 and minimized at 26 Mg ha
−1 (
Table 5). The predicted results may have been degraded by the saturation levels of the S2 MSI sensor and the dual polarimetric L-band ALOS-2 PALSAR-2 when retrieving mangrove AGB in intertidal areas. Although the AGB was well predicted by the XGBR model, the
R2 values in the training and testing phases were significantly different (
Table 6). This difference is likely attributable to the mixed mangrove species planted in the CGBRS and the number of plots. To archive a more accurate forest AGB map, we should exploit the advantages of various novel GBDT algorithms with multi-sensor data integration [
74]. In more intensive works, novel boosting decision tree techniques should exploit the full capability of multi-source EO data in different mangrove communities occupying tropical intertidal areas at different geographical locations, particularly those of biosphere reserves. Such developments are needed for rapid mangrove AGB monitoring in the future.