Lunar Regolith Temperature Variation in the Rümker Region Based on the Real-Time Illumination
Abstract
1. Introduction
2. Methods
2.1. Heat Conduction Equation
2.2. Boundary Conditions
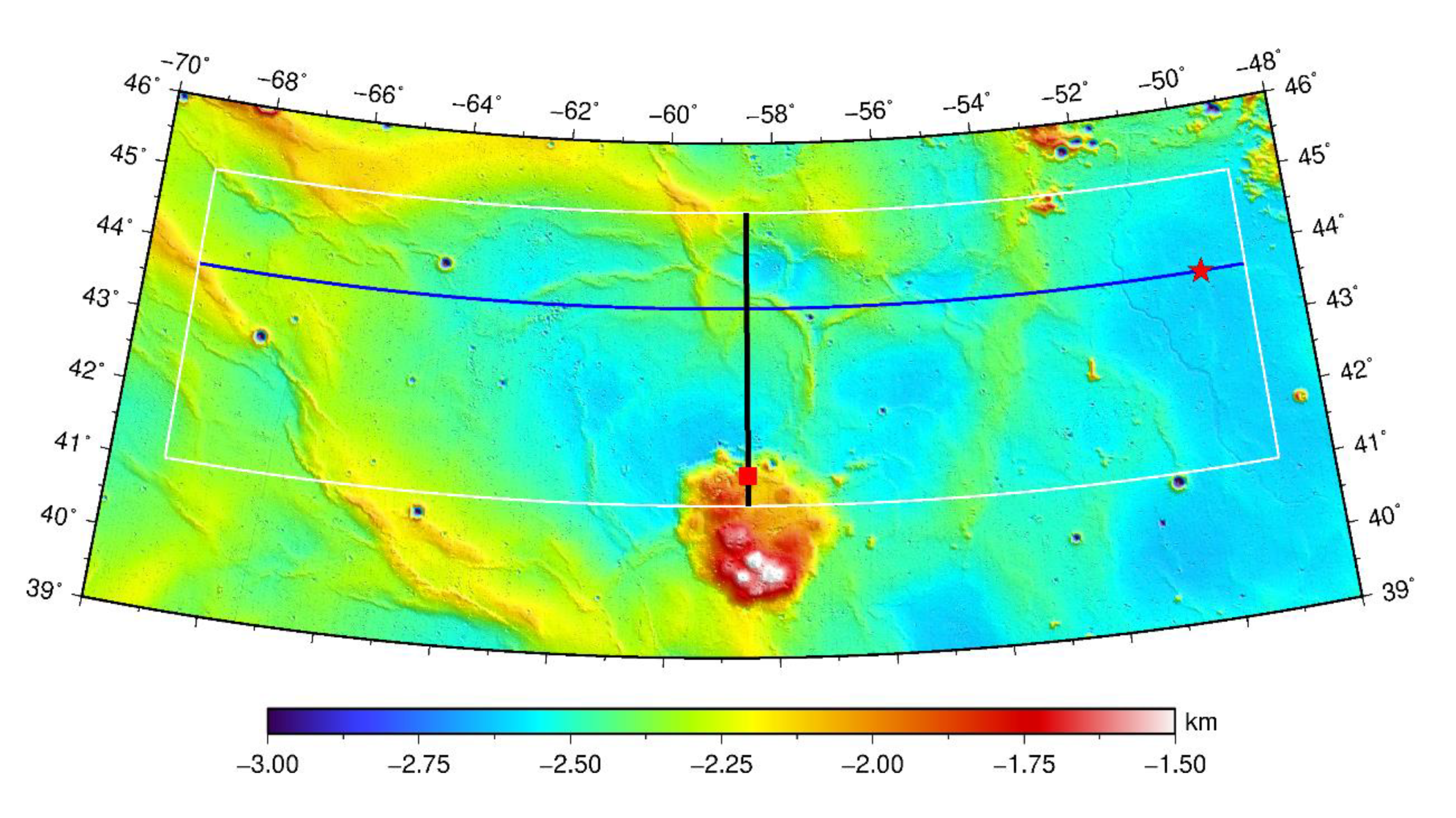
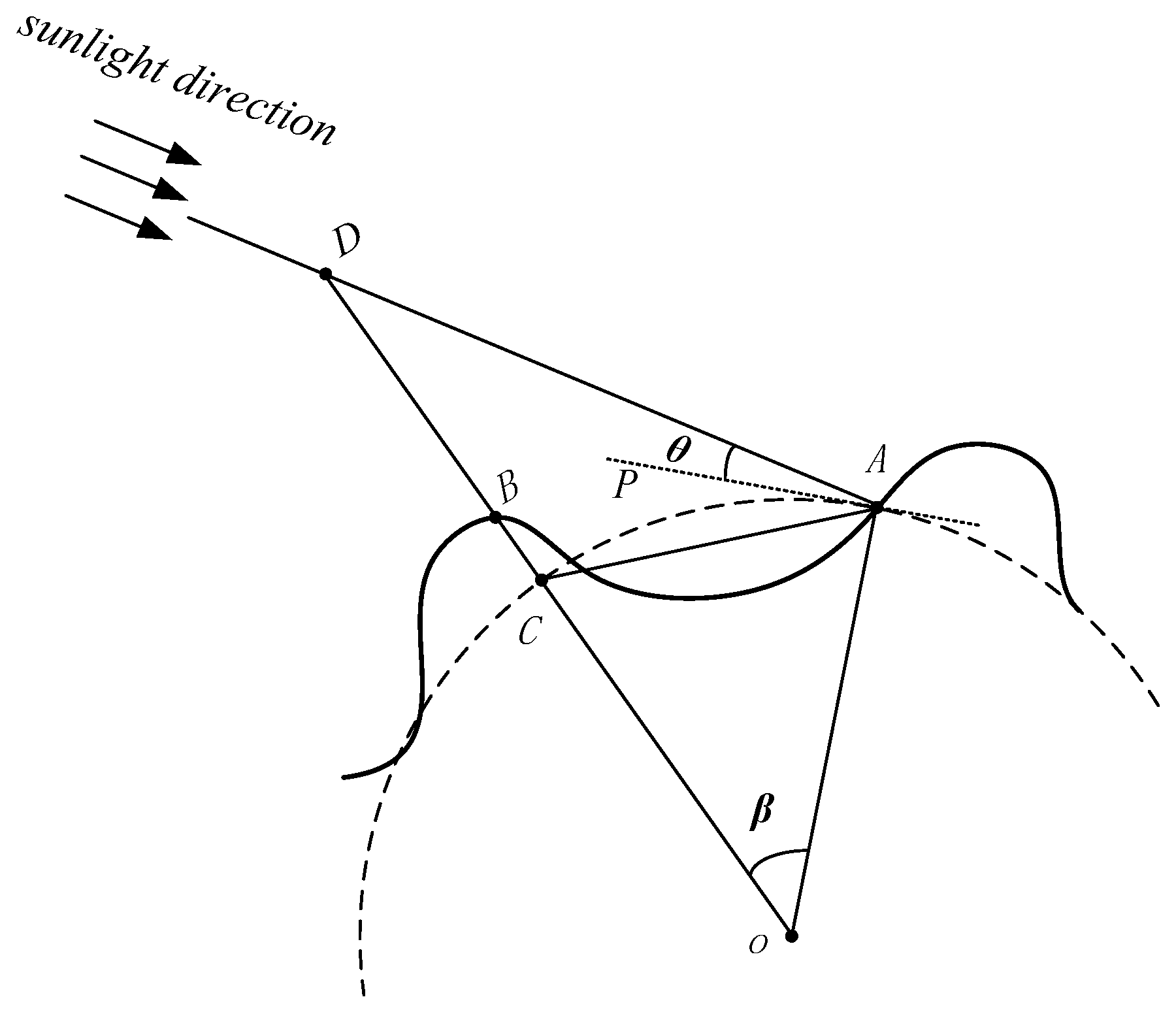
2.3. Illumination
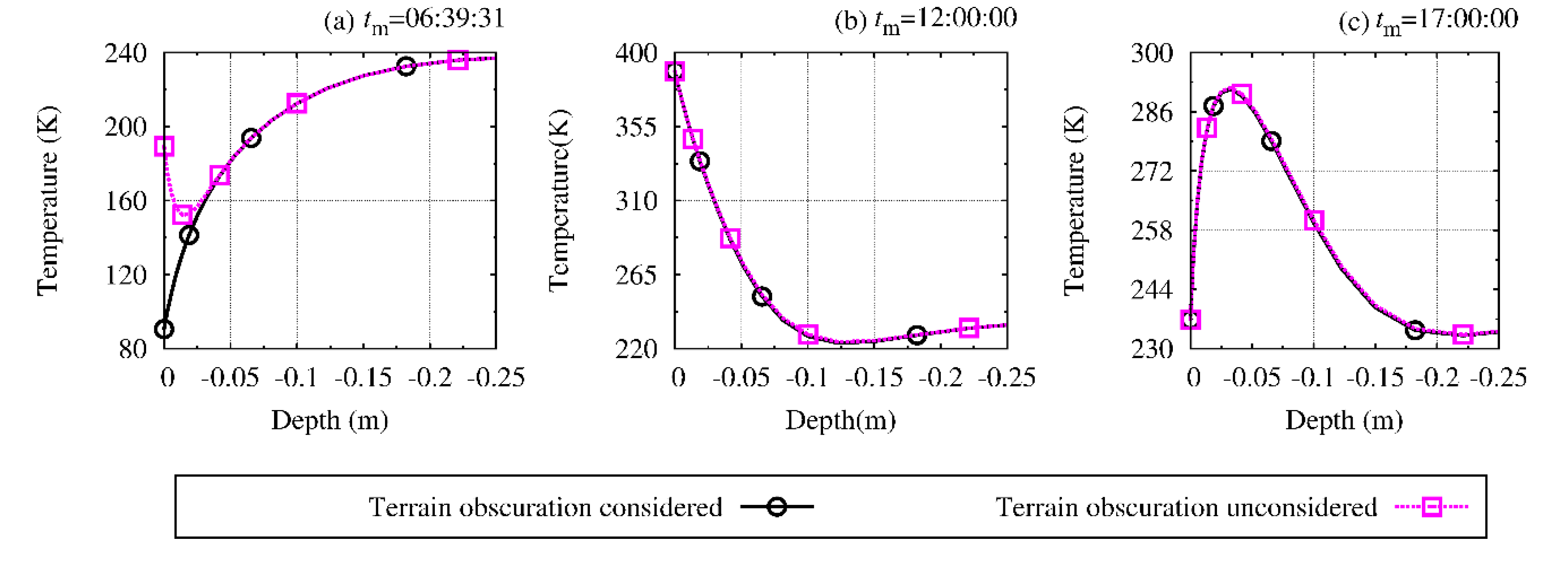
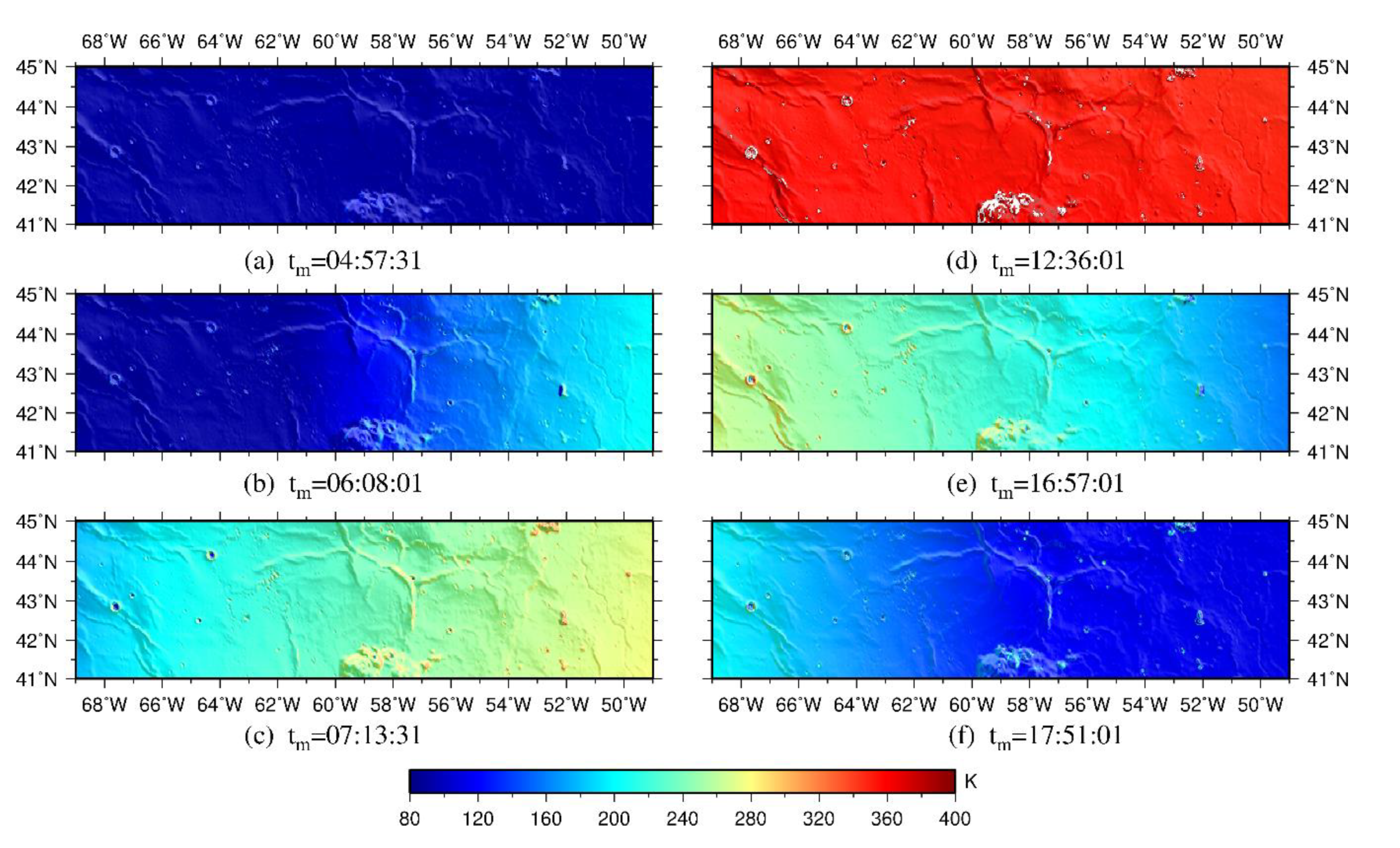
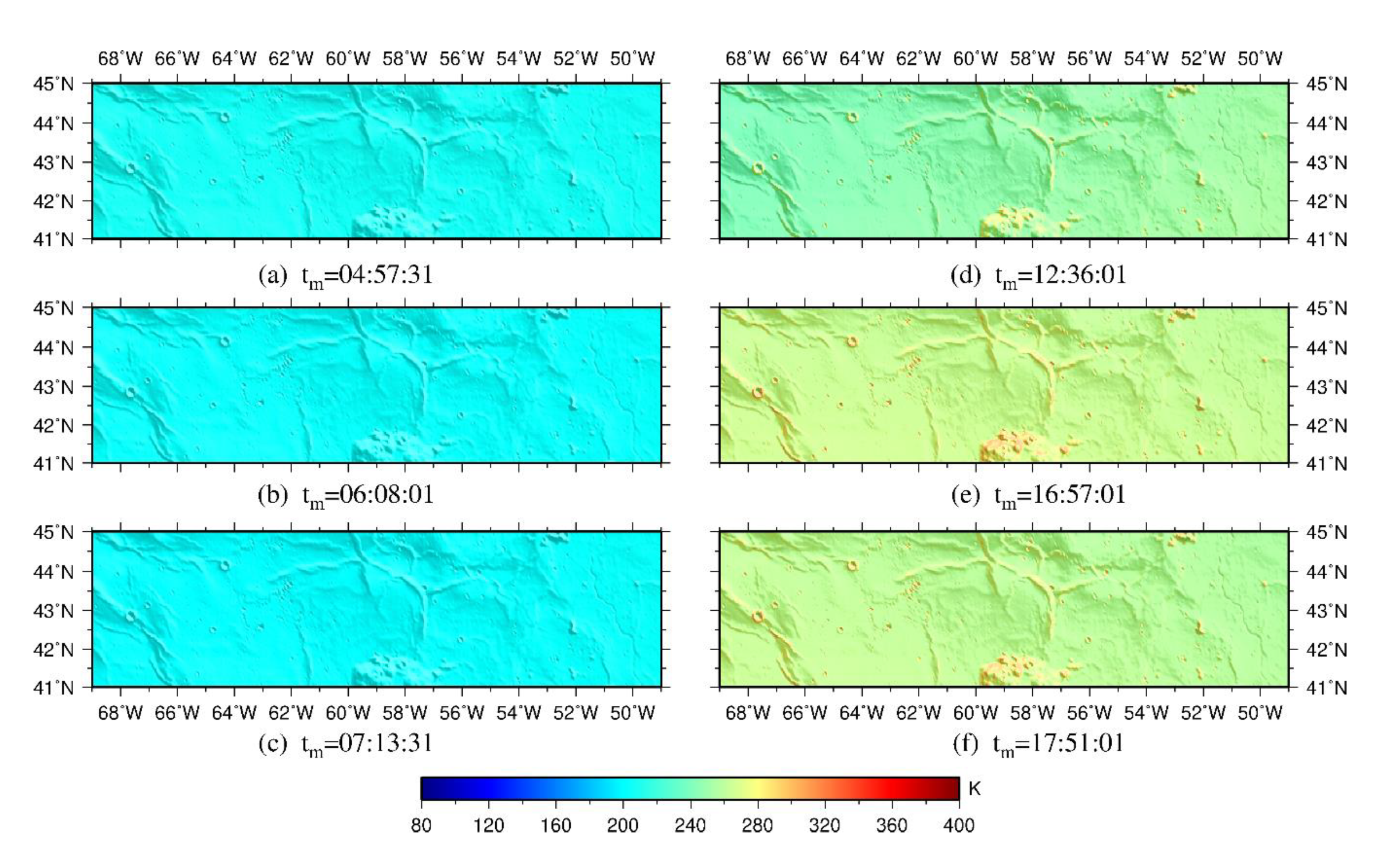
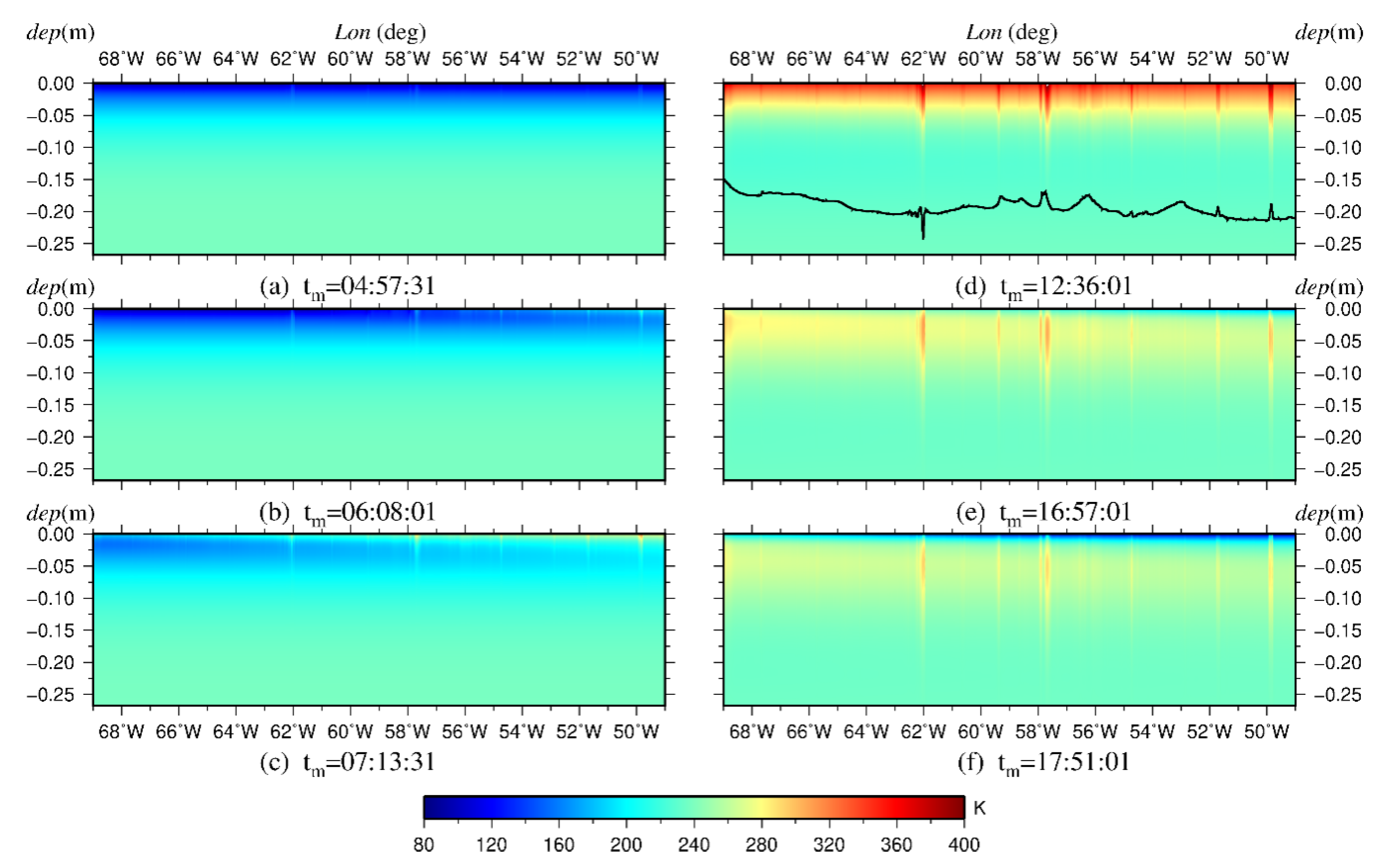
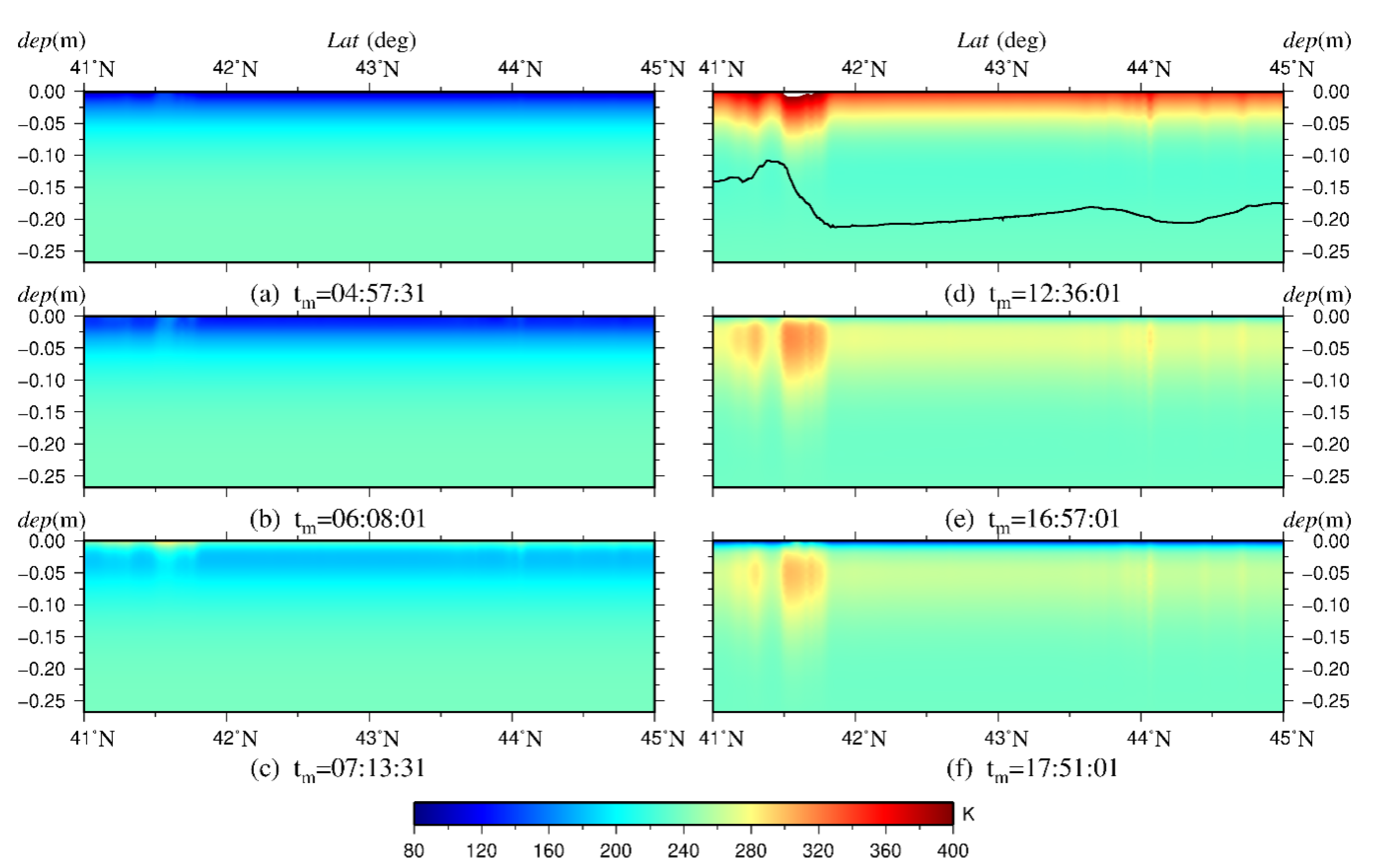
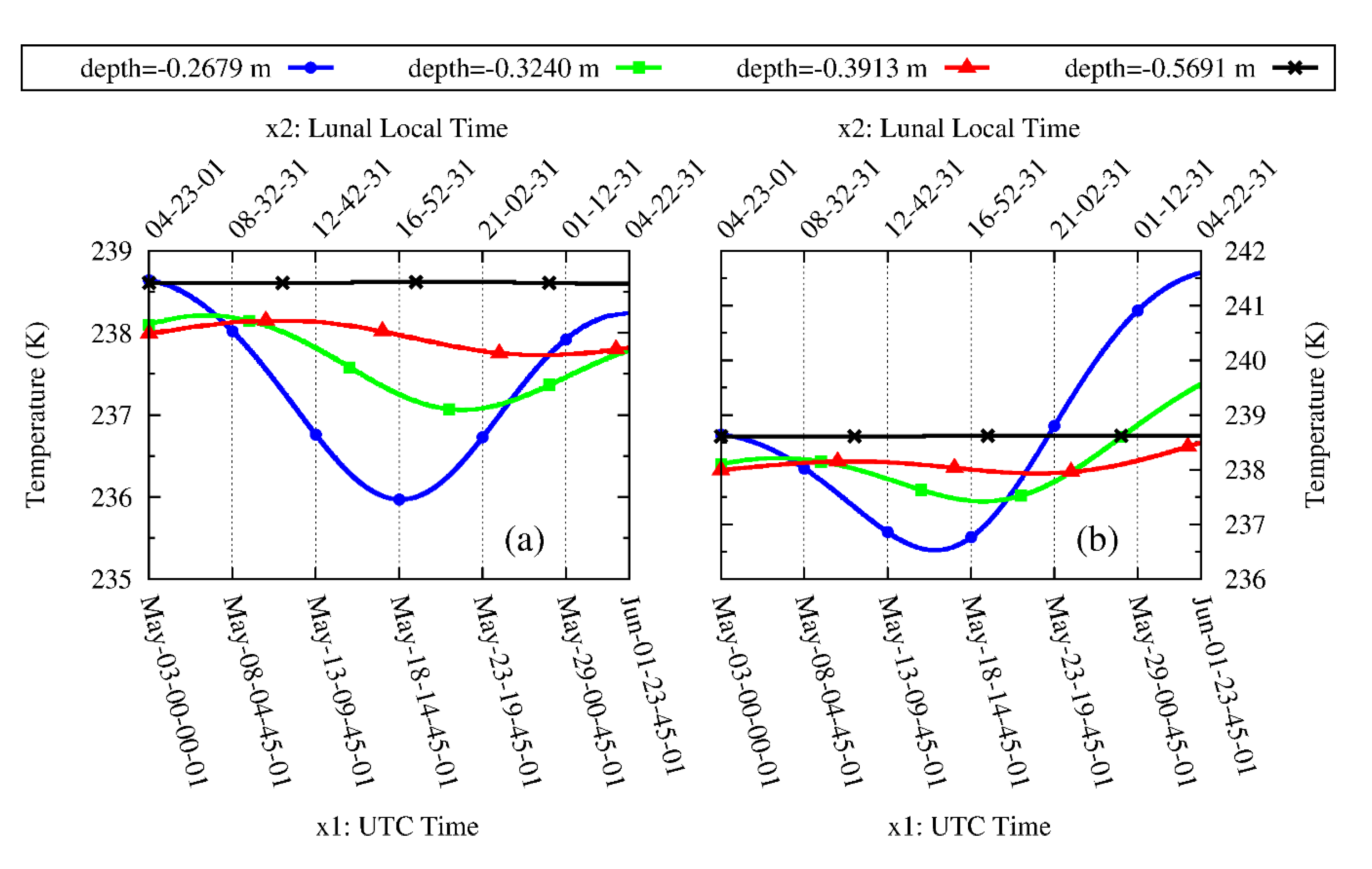
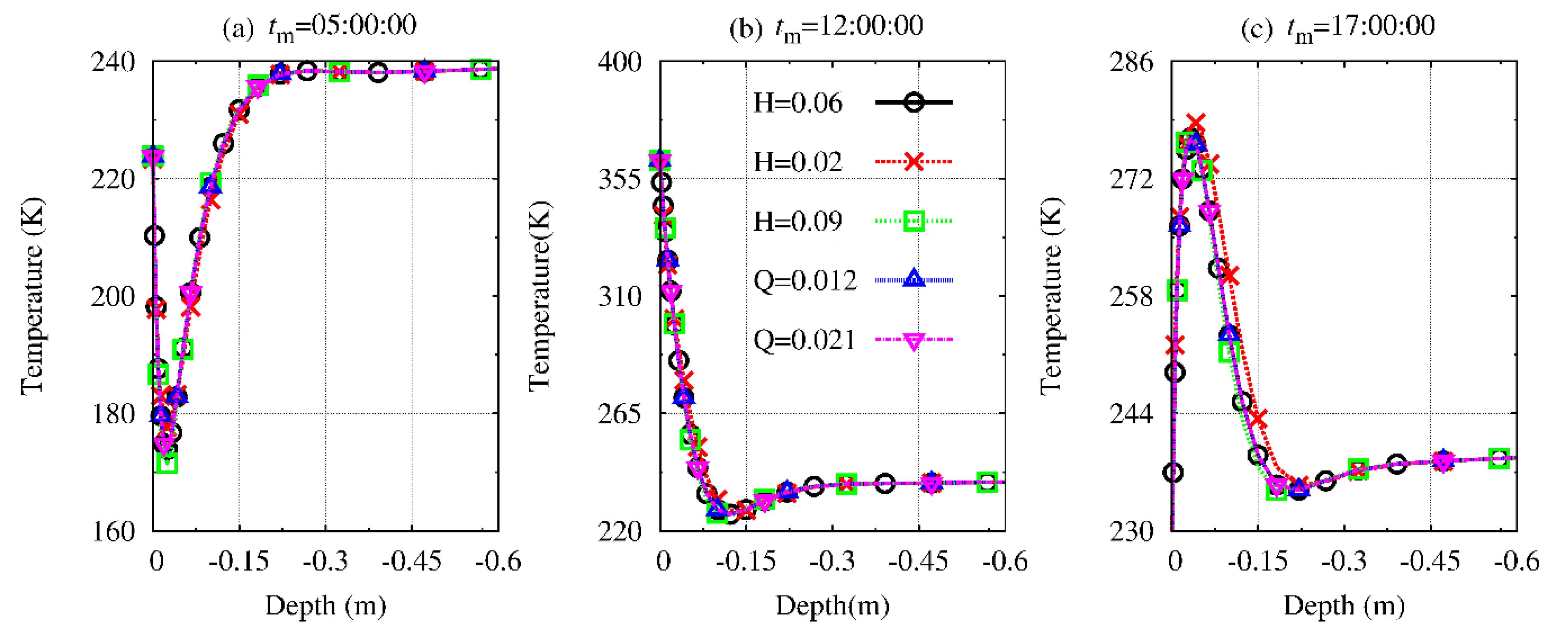
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, J.; Xiao, L.; Qiao, L.; Glotch, T.D.; Huang, Q. The Mons Rümker volcanic complex of the Moon: A candidate landing site for the Chang’E-5 mission. J. Geophys. Res. Planets 2017, 122, 1419–1442. [Google Scholar] [CrossRef]
- Qian, Y.; Xiao, L.; Zhao, S.Y.; Zhao, J.; Huang, J.; Flahaut, J.; Martinot, M.; Head, J.; Hiesinger, H.; Wang, G.X. Geology and Scientific Significance of the Rümker Region in Northern Oceanus Procellarum: China’s Chang’E-5 Landing Region. J. Geophys. Res. Planets 2018, 123, 1407–1430. [Google Scholar] [CrossRef]
- Chisenga, C.; Yan, J.; Zhao, J.; Atekwana, E.A.; Steffen, R. Density Structure of the Rümker Region in the Northern Oceanus Procellarum: Implications for Lunar Volcanism and Landing Site Selection for the Chang’E-5 Mission. J. Geophys. Res. Planets 2020, 125. [Google Scholar] [CrossRef]
- Yue, Z.; Di, K.; Liu, Z.; Michael, G.; Jia, M.; Xin, X.; Liu, B.; Peng, M.; Liu, J. Lunar regolith thickness deduced from concentric craters in the CE-5 landing area. Icarus 2019, 329, 46–54. [Google Scholar] [CrossRef]
- Zhang, T.; Ding, X. Drilling forces model for lunar regolith exploration and experimental validation. Acta Astronaut. 2017, 131, 190–203. [Google Scholar] [CrossRef]
- Tang, J.; Quan, Q.; Jiang, S.; Liang, J.; Lu, X.; Yuan, F. Investigating the soil removal characteristics of flexible tube coring method for lunar exploration. Adv. Space Res. 2018, 61, 799–810. [Google Scholar] [CrossRef]
- Langseth, M.G.; Keihm, S.J.; Peters, K. Revised lunar heat flow values. In Proceedings of the International Conference on Lunar and Planetary Science, Pergamon, Houston, TX, USA, 15−19 March 1976; pp. 3143–3171. [Google Scholar]
- Mitchell, J.K.; Carrier, W.D., III; Costes, N.C.; Houston, W.N.; Scott, R.F. Surface soil variability and stratigraphy at the Apollo 16 site. In Proceedings of the International Conference on Lunar and Planetary Science, Pergamon, Houston, TX, USA, 5−8 March 1973; pp. 2437–2445. [Google Scholar]
- Paige, D.A.; Siegler, M.A.; Zhang, J.A.; Hayne, P.O.; Foote, E.; Bennett, K.A.; Vasavada, A.R.; Greenhagen, B.T.; Schofield, J.T.; McCleese, D.J.; et al. Diviner lunar radiometer observations of cold traps in the Moon’s south polar region. Science 2010, 330, 479–482. [Google Scholar] [CrossRef]
- Yu, S.; Fa, W. Thermal conductivity of surficial lunar regolith estimated from Lunar Reconnaissance Orbiter Diviner Radiometer data. Planet. Space Sci. 2016, 124, 48–61. [Google Scholar] [CrossRef]
- Williams, J.; Paige, D.; Greenhagen, B.T.; Sefton-Nash, E. The global surface temperatures of the Moon as measured by the Diviner Lunar Radiometer Experiment. Icarus 2017, 283, 300–325. [Google Scholar] [CrossRef]
- Vasavada, A.; Bandfield, J.L.; Greenhagen, B.; Hayne, P.O.; Siegler, M.; Williams, J.; Paige, D.A. Lunar equatorial surface temperatures and regolith properties from the Diviner Lunar Radiometer Experiment. J. Geophys. Res. Space Phys. 2012, 117, 1–12. [Google Scholar] [CrossRef]
- Hayne, P.; Bandfield, J.L.; Siegler, M.A.; Vasavada, A.R.; Ghent, R.R.; Williams, J.; Greenhagen, B.T.; Aharonson, O.; Elder, C.; Lucey, P.G.; et al. Global Regolith Thermophysical Properties of the Moon From the Diviner Lunar Radiometer Experiment. J. Geophys. Res. Planets 2017, 122, 2371–2400. [Google Scholar] [CrossRef]
- Paige, D.A. The thermal stability of near-surface ground ice on Mars. Nature 1992, 356, 43–45. [Google Scholar] [CrossRef]
- Mitchell, D.L.; De Pater, I. Microwave imaging of Mercury’s thermal emission at wavelengths from 0 3 to 20.5 cm. Icarus 1994, 110, 2–32. [Google Scholar]
- Vasavada, A. Near-Surface Temperatures on Mercury and the Moon and the Stability of Polar Ice Deposits. Icarus 1999, 141, 179–193. [Google Scholar] [CrossRef]
- Hayne, P.O.; Greenhagen, B.; Foote, M.C.; Siegler, M.; Vasavada, A.R.; Paige, D.A. Diviner Lunar Radiometer Observations of the LCROSS Impact. Science 2010, 330, 477–479. [Google Scholar] [CrossRef] [PubMed]
- Kieffer, H.H. Thermal model for analysis of Mars infrared mapping. J. Geophys. Res. Planets 2013, 118, 451–470. [Google Scholar] [CrossRef]
- Bussey, B.; Spudis, P.D.; Robinson, M.S. Illumination conditions at the lunar South Pole. Geophys. Res. Lett. 1999, 26, 1187–1190. [Google Scholar] [CrossRef]
- Noda, H.; Araki, H.; Goossens, S.; Ishihara, Y.; Matsumoto, K.; Tazawa, S.; Kawano, N.; Sasaki, S. Illumination conditions at the lunar polar regions by KAGUYA(SELENE) laser altimeter. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Mazarico, E.; Neumann, G.A.; Smith, D.; Zuber, M.T.; Torrence, M. Illumination conditions of the lunar polar regions using LOLA topography. Icarus 2011, 211, 1066–1081. [Google Scholar] [CrossRef]
- Gläser, P.; Scholten, F.; De Rosa, D.; Figuera, R.M.; Oberst, J.; Mazarico, E.; Neumann, G.A.; Robinson, M. Illumination conditions at the lunar south pole using high resolution Digital Terrain Models from LOLA. Icarus 2014, 243, 78–90. [Google Scholar] [CrossRef]
- Woods-Robinson, R.; Siegler, M.; Paige, D.A. A Model for the Thermophysical Properties of Lunar Regolith at Low Temperatures. J. Geophys. Res. Planets 2019, 124, 1989–2011. [Google Scholar] [CrossRef]
- Acton, C.H., Jr. Ancillary data services of NASA’s Navigation and Ancillary Information Facility, Planet. Space Sci. 1996, 44, 65–70. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.; Duxbury, T.H.; et al. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA). Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Mazarico, E.; Lemoine, F.G.; Iii, J.W.H.; Lucey, P.G.; Aharonson, O.; Robinson, M.S.; Sun, X.; et al. Summary of the results from the lunar orbiter laser altimeter after seven years in lunar orbit. Icarus 2017, 283, 70–91. [Google Scholar] [CrossRef]
- Carrier, W.D.; Olhoeft, G.R.; Mendell, W. Physical properties of the lunar surface. In Lunar Sourcebook; Cambridge University Publishers: Cambridge, UK, 1991; pp. 475–594. ISBN 0-521-33444-6. [Google Scholar]
- Whipple, F.L. A comet model. I. The acceleration of Comet Encke. Astrophys. J. 1950, 111, 375–394. [Google Scholar] [CrossRef]
- Fountain, J.A.; West, E.A. Thermal conductivity of particulate basalt as a function of density in simulated lunar and Martian environments. J. Geophys. Res. Space Phys. 1970, 75, 4063–4069. [Google Scholar] [CrossRef]
- Ledlow, M.J.; Zeilik, M.; Burns, J.O.; Gisler, G.R.; Zhao, J.H.; Baker, D.N. Subsurface emissions from Mercury-VLA radio observations at 2 and 6 centimeters. Astrophys. J. 1992, 384, 640–655. [Google Scholar] [CrossRef]
- Hemingway, B.S.; Krupka, K.M.; Robie, R.A. Heat capacities of the alkali feldspars between 350 and 1000 K from differential scanning calorimetry, the thermodynamic functions of the alkali feldspars from 298.15 to 1400 K, and the reaction quartz + jadeite = analbite. Am. Mineral. 1981, 66, 1202–1215. [Google Scholar]
- Keihm, S.J. Interpretation of the lunar microwave brightness temperature spectrum: Feasibility of orbital heat flow mapping. Icarus 1984, 60, 568–589. [Google Scholar] [CrossRef]
- Kopp, G.; Lean, J.L. A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 2011, 38, 541–551. [Google Scholar] [CrossRef]
- Braun, J.; Mitchell, J. Solar geometry for fixed and tracking surfaces. Sol. Energy 1983, 31, 439–444. [Google Scholar] [CrossRef]
- Hao, W.; Zhu, C.; Li, F.; Yan, J.; Ye, M.; Barriot, J.P. Illumination and communication conditions at the Mons Rümker region based on the improved Lunar Orbiter Laser Altimeter data. Planet. Space Sci. 2019, 168, 73–82. [Google Scholar] [CrossRef]
- Siegler, M.A.; Smrekar, S.E. Lunar heat flow: Regional prospective of the Apollo landing sites. J. Geophys. Res. Planets 2014, 119, 47–63. [Google Scholar] [CrossRef]
- Rasmussen, K.L.; Warren, P.H. Megaregolith thickness, heat flow, and the bulk composition of the Moon. Nature 1985, 313, 121–124. [Google Scholar] [CrossRef]
- Warren, P.H.; Rasmussen, K.L. Megaregolith insulation, internal temperatures, and bulk uranium content of the moon. J. Geophys. Res. Space Phys. 1987, 92, 3453–3465. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Yan, J.; Xiao, Z. Lunar Regolith Temperature Variation in the Rümker Region Based on the Real-Time Illumination. Remote Sens. 2020, 12, 731. https://doi.org/10.3390/rs12040731
Zhong Z, Yan J, Xiao Z. Lunar Regolith Temperature Variation in the Rümker Region Based on the Real-Time Illumination. Remote Sensing. 2020; 12(4):731. https://doi.org/10.3390/rs12040731
Chicago/Turabian StyleZhong, Zhen, Jianguo Yan, and Zhiyong Xiao. 2020. "Lunar Regolith Temperature Variation in the Rümker Region Based on the Real-Time Illumination" Remote Sensing 12, no. 4: 731. https://doi.org/10.3390/rs12040731
APA StyleZhong, Z., Yan, J., & Xiao, Z. (2020). Lunar Regolith Temperature Variation in the Rümker Region Based on the Real-Time Illumination. Remote Sensing, 12(4), 731. https://doi.org/10.3390/rs12040731






